Open Access Article
Open Access ArticleMachine learning assisted construction of a shallow depth dynamic ansatz for noisy quantum hardware†
Sonaldeep
Halder
a,
Anish
Dey
b,
Chinmay
Shrikhande
a and
Rahul
Maitra‡
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India. E-mail: rmaitra@chem.iitb.ac.in
bDepartment of Chemical Sciences, Indian Institute of Science Education and Research Kolkata, West Bengal 741246, India
First published on 17th January 2024
Abstract
The development of various dynamic ansatz-constructing techniques has ushered in a new era, making the practical exploitation of Noisy Intermediate-Scale Quantum (NISQ) hardware for molecular simulations increasingly viable. However, such ansatz construction protocols incur substantial measurement costs during their execution. This work involves the development of a novel protocol that capitalizes on regenerative machine learning methodologies and many-body perturbation theoretical measures to construct a highly expressive and shallow ansatz within the variational quantum eigensolver (VQE) framework with limited measurement costs. The regenerative machine learning model used in our work is trained with the basis vectors of a low-rank expansion of the N-electron Hilbert space to identify the dominant high-rank excited determinants without requiring a large number of quantum measurements. These selected excited determinants are iteratively incorporated within the ansatz through their low-rank decomposition. The reduction in the number of quantum measurements and ansatz depth manifests in the robustness of our method towards hardware noise, as demonstrated through numerical applications. Furthermore, the proposed method is highly compatible with state-of-the-art neural error mitigation techniques. This resource-efficient approach is quintessential for determining spectroscopic and other molecular properties, thereby facilitating the study of emerging chemical phenomena in the near-term quantum computing framework.
1 Introduction
Quantum computing platforms provide an elegant solution to the formidable task posed by the exponential growth of the Hilbert space encountered in the realms of many-body physics and chemistry.1–3 In recent years, a plethora of state-of-the-art methods have been developed that aim to produce accurate energies and wavefunctions for molecular systems utilizing quantum hardware. Leading the pack are the variational algorithms,4–17 which rely on the dynamic construction and deployment of shallow depth parameterized ansatzes to generate the molecular wavefunctions. They are highly suitable for Noisy Intermediate-Scale Quantum (NISQ)18 devices that suffer from limited coherence time, state preparation and measurement (SPAM) errors, and poor gate fidelity. However, most of these methods typically demand extensive pre-circuit measurements, significantly contributing to the computational overhead. Additionally, noise from NISQ architecture can fundamentally alter the design of dynamic circuits. The selection of operators from the pool and the resulting unitary operation may deviate significantly from the optimal outcome as its construction is highly dependent on measurements (which have errors when utilizing NISQ hardware). Therefore, it is crucial to reduce the utilization of quantum resources when constructing dynamic ansatzes. In this regard, we should prioritize using approaches grounded in first principles or aided by machine learning. These methods have the potential to navigate around any challenges posed by the NISQ architecture, avoiding potential pitfalls. In this work, we have introduced a novel approach that combines unsupervised machine learning (ML) techniques with a first-principles-based strategy rooted in many-body perturbation theory. The outcome is a dynamically constructed ansatz that strikes an exceptional balance between compactness and expressiveness, all achieved without the burden of extensive pre-circuit measurements. This compact ansatz provides us with access to molecular energies and wavefunctions, which are fundamental for accurately assessing various molecular properties. It enables the exploration of new chemical compounds and phenomena that are currently beyond the reach of classical computers.The use of neural network-based ML models to represent quantum states has been widespread in the realm of classical many-body theories and error mitigation protocols.19–33 The ability of these models to proactively learn the intricate interrelation between different basis functions that span the N-electron Hilbert space corresponding to a quantum state can be leveraged to generate its low complexity representation in quantum computers. The learned state, often called the neural quantum state (NQS), forms the backbone of neural quantum state tomography (NQST)34 and neural error mitigation35 (NEM). This manuscript entails the utilization of a Restricted Boltzmann Machine (RBM),36–38 a powerful regenerative ML model, to construct an expanded wavefunction in terms of the dominant many-body basis after learning the correlation from what may be ascribed as the “primary excitation subspace”. Simple many-body perturbative measures intimately guide this process. The generated ansatz corresponding to this expanded wavefunction further involves the inclusion of a suite of two-body operators with an effective one hole–one particle excitation – the so-called scatterers – resulting in an extremely low-depth yet highly expressive ansatz. Additionally, our method can be efficiently integrated with NEM, enhancing its efficacy for NISQ implementation.
In section 2.1, we briefly introduce the RBM's functioning and the generative process deployed to produce the dominant contributors (many-body basis) for the wavefunction expansion. In section 2.2, we set the background for the disentangled Unitary Coupled Cluster (dUCC) ansatz39 and Variational Quantum Eigensolver (VQE),4 which will be used to generate and optimize the wavefunction. In section 2.3, we introduce an innovative protocol that combines RBM and second-order Möller–Plesset perturbation theory (MP2) to craft a compact ansatz, leveraging the use of scatterer operators.
2 Theory
2.1 Restricted Boltzmann machine (RBM): a brief overview
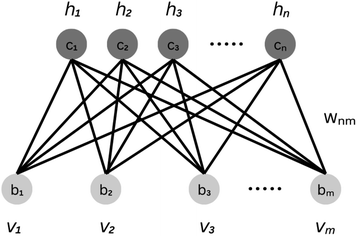
Characterizing a correlated wavefunction as a neural network model has been widely embraced as an effective strategy to mitigate its inherent complexity. Within this framework, the neural network's weights and biases, distributed across distinct layers, effectively encode the diverse contributions of various bases to the given wavefunction. In light of this, a regenerative neural network can effectively generate the dominant contributors to a wavefunction by training on an initial approximate state of the given system. To implement this approach, we utilize the Restricted Boltzmann Machines (RBMs). They are probabilistic graphical models that can be interpreted as stochastic neural networks. RBM comprises two layers, a visible and a hidden layer. This topology is depicted in Fig. 1. The visible layer (vi ∈ {0, 1}) corresponds to observations from the training data, which comprises the binary vector representation of the basis expansion of an initial approximate wavefunction. A more detailed description of the form and source of the training dataset can be found in sections 2.2 and 2.3. The hidden layer (hi ∈ {0, 1}) captures the hidden patterns underlying in-between the components of the visible layer.To model a probability distribution of m-dimensional training data in the form of computational basis measurements, an n-dimensional hidden representation of the state is constructed. A bias is assigned to each visible and hidden unit. A weight matrix is set to establish a connection between the visible and the hidden layers, which are of dimensions n × m. Connections only exist between the visible and hidden units, not between the units of the same layer. This restriction in the network topology makes RBMs different from conventional Boltzmann machines. RBM aims to find the optimal values of the biases and the weight matrix so that the probability distribution modeled explains the observed data well. RBM constructs a joint probability distribution for the configuration {v, h}
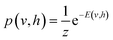 | (1) |
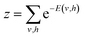 | (2) |
E(v, h) is parameterized by the biases and weights. The parameterized form of E(v, h) is written as
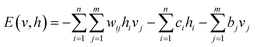 | (3) |
The model is trained to minimize E(v, h). To do that, the log of likelihood function 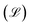 is constructed
is constructed
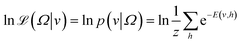 | (4) |
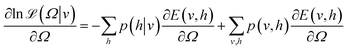 | (5) |
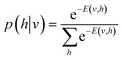 | (6) |
It must be noted that obtaining the derivative of a log-likelihood function can become intractable. Contrastive Divergence (CD), Persistent Contrastive Divergence (PCD) and Parallel Tempering (PT) are some of the approximations that are commonly employed to overcome this.
The model is trained on a collection of binary vectors (representing a many-body basis), with their probability distribution ascertained by measuring an initially prepared approximate wavefunction. The hidden layers of the model decipher the correlation existing within this wavefunction. Once the training is complete, the model generates new binary vectors, preserving the correlation it learned before. The generation is accomplished through Gibbs sampling. Starting from a given binary input vector (v0), a hidden layer representation (h0) is calculated based on p(h|v0). This, in turn, generates a new representation of the visible layer based on p(v|h0). This recursive process generates new binary vectors v′. They correspond to the most dominant contributors to the wavefunction of a given many-fermion system. The exact parametric representation of this state is built up using the dUCC ansatz, which is further variationally optimized. This leads to section 2.2, where we briefly discuss the composition of the dUCC ansatz and the variational principle employed to optimize the ansatz parameters.
2.2 Disentangled unitary coupled cluster ansatz (dUCC) and variational quantum eigensolver
A trial wavefunction can be generated in a quantum computer by the action of a parameterized unitary on a reference state (|Φo〉)| |ψ(θ)〉 = Û(θ)|Φo〉. | (7) |
For the dUCC ansatz, this unitary is characterized by a pool of ordered, non-commuting, anti-hermitian particle–hole operators ({![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) }) with the reference state taken to be the single Hartree–Fock (HF) determinant |Φo〉 = |χiχj…〉, with χs being the spin-orbitals. The ansatz can be written as
}) with the reference state taken to be the single Hartree–Fock (HF) determinant |Φo〉 = |χiχj…〉, with χs being the spin-orbitals. The ansatz can be written as
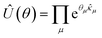 | (8) |
![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) μ = μ = ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) μ − μ − ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) †μ †μ | (9) |
![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) μ = μ = ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) †a †a![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) †b… †b…![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) j j![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) i i | (10) |
In the above equations, μ represents a multi-index particle–hole excitation structure as defined by the string of creation (![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) †) and annihilation (
†) and annihilation (![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) ) operators with the indices {i, j, …} denoting the occupied spin-orbitals in the Hartree–Fock state and {a, b, …} denoting the unoccupied spin-orbitals.
) operators with the indices {i, j, …} denoting the occupied spin-orbitals in the Hartree–Fock state and {a, b, …} denoting the unoccupied spin-orbitals. ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) μ acts on the reference state to generate a many-body basis,
μ acts on the reference state to generate a many-body basis,
![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) μ|Φo〉 = |Φμ〉 μ|Φo〉 = |Φμ〉 | (11) |
In a quantum computing framework, the operators described in eqn (7)–(11) are realized in terms of quantum gates and computational basis. Required transformations are carried out using standard mapping techniques. As such, these many-body bases ({|Φμ〉}) can also be represented as binary vectors (or bit strings). In this work, these vectors are often referred to as configurations.
For all practical applications, the dUCC ansatz is constructed using only a subset of the total possible excitation operators (![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) μ). The corresponding parameters are optimized by invoking variational minimization of the electronic energy.
μ). The corresponding parameters are optimized by invoking variational minimization of the electronic energy.
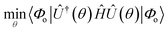 | (12) |
In adherence to the Rayleigh–Ritz principle, the variationally obtained minimum energy gives the upper bound to the exact ground state energy (Eo) for the given molecular Hamiltonian.
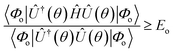 | (13) |
The inherent expressibility40 of the chosen ansatz assumes a pivotal role in generating a trial state that recovers a substantial amount of correlation energy. It can be achieved through the incorporation of higher-order excitations (![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) μ) in the ansatz. However, implementing such an ansatz on quantum hardware requires very deep quantum circuits. In light of the limitations posed by current quantum devices, the execution of such circuits becomes unfeasible. Developing novel techniques to generate a compact and expressive ansatz becomes essential for practically utilizing quantum computing platforms for accurate molecular energy calculations.
μ) in the ansatz. However, implementing such an ansatz on quantum hardware requires very deep quantum circuits. In light of the limitations posed by current quantum devices, the execution of such circuits becomes unfeasible. Developing novel techniques to generate a compact and expressive ansatz becomes essential for practically utilizing quantum computing platforms for accurate molecular energy calculations.
2.3 Utilization of RBM and many-body perturbation theory towards the construction of RBM-dUCC
The construction of the dUCC ansatz, utilizing either true hole–particle or general excitations, gives rise to quantum circuits with substantial depth. Several sophisticated methodologies have been developed to incorporate dominant operators exclusively, effectively capturing a significant portion of the many-fermion correlation effects within a given molecular system. These protocols rely on quantum measurements at each stage to dynamically interlace the ansatz. This leads to a considerable measurement overhead that significantly prolongs the overall runtime of the procedure on quantum hardware. In this section, we present a comprehensive method involving judicious utilization of RBM guided by MP2 measures to achieve a compact and highly expressive ansatz. It encompasses the following steps:| |ΨSD〉 = ÛSD(θopt)|Φo〉 | (14) |
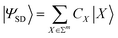 | (15) |
Here, Σm denotes the set of bit strings of length m. Eqn (15) denotes the expansion of |ΨSD〉 in the computational basis ({|X〉}). During the variational optimization of parameters associated with ÛSD(θ), one may choose to do a partial optimization. As will be evident in the subsequent steps, it is the relative |CX|2 (eqn (21)) that are important and not their exact values.
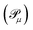 , sorted in descending order. Operators with corresponding probabilities below a selected threshold of 10−5 are excluded from the ansatz. The arrangement of excitation operators follows the order of rank two excitations (denoted by superscript D) first, followed by rank one (superscript S).
, sorted in descending order. Operators with corresponding probabilities below a selected threshold of 10−5 are excluded from the ansatz. The arrangement of excitation operators follows the order of rank two excitations (denoted by superscript D) first, followed by rank one (superscript S).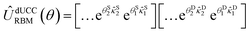 | (16) |
{![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) S} → single excitations S} → single excitations | (17) |
{![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) D} → double excitations D} → double excitations | (18) |
The probability order for the singles and doubles operator blocks independently follows
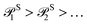 | (19) |
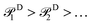 | (20) |
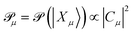 | (21) |
The ground and various excited determinants are mapped from the many-body basis to the computational basis:
 | (22) |
|Φμ〉 = ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) μ|Φo〉 ∀ μ|Φo〉 ∀![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) μ ∈ ÛSD μ ∈ ÛSD | (23) |
The wavefunction generated using ÛdUCCRBM(θ) at this stage spans what can be called as the primary excitation subspace. An approximate wavefunction, which only occupies the primary excitation subspace, captures limited correlation.
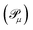 incorporated in |ΨSD〉. The HF state is never taken during training since it has a high associated probability and may result in improper training.33 Since we are taking only a subset of the computational basis, these probabilities are further normalized. This constitutes the training phase where the ML model deciphers the correlation folded within the wavefunction. At this point, one may use powerful NEM techniques to learn a better representation of |ΨSD〉 if it has errors folded within it.
incorporated in |ΨSD〉. The HF state is never taken during training since it has a high associated probability and may result in improper training.33 Since we are taking only a subset of the computational basis, these probabilities are further normalized. This constitutes the training phase where the ML model deciphers the correlation folded within the wavefunction. At this point, one may use powerful NEM techniques to learn a better representation of |ΨSD〉 if it has errors folded within it.
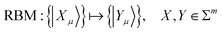 | (24) |
{|Yμ}〉 represents the dominant contributors to the secondary excitation space.
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ) on the primary excitation subspace functions generated previously. This implies that a given high-rank excitation is factorized into two low-rank operators. The scatterer here needs some more clarification: the inherent structural characteristics of the scatterer enable it to act upon a set of low-rank excited determinants and generate an excitation manifold of one rank higher. Thus, the scatterers may be perceived as two-body operators with an effective hole–particle excitation rank of one. Mathematically, these operators can be represented as:
) on the primary excitation subspace functions generated previously. This implies that a given high-rank excitation is factorized into two low-rank operators. The scatterer here needs some more clarification: the inherent structural characteristics of the scatterer enable it to act upon a set of low-rank excited determinants and generate an excitation manifold of one rank higher. Thus, the scatterers may be perceived as two-body operators with an effective hole–particle excitation rank of one. Mathematically, these operators can be represented as: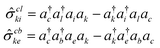 | (25) |
![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) D represents a rank two excitation operator, its commutator with a suitable scatterer results in the generation of a rank three excitation operator (
D represents a rank two excitation operator, its commutator with a suitable scatterer results in the generation of a rank three excitation operator (![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) T):
T):[![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) , , ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) D] → D] → ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) T T | (26) |
The scatterers can be configured in a nested commutator form to generate even higher-order excitations such as quadruples.
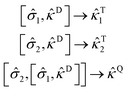 | (27) |
![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) D,
D, ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) T, and
T, and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) Q represent connected double, triple, and quadruple excitations, respectively.
Q represent connected double, triple, and quadruple excitations, respectively.
Such implicit generation of the high-rank excitations is only possible when the scatterers possess specific destruction orbital labels that are common to one of the indices of the cluster operators such that they satisfy non-commutativity. Let us say we only account for dominant triples generated by RBM. In that case, we take suitable non-commuting scatterers that combine with rank two excitation operators already present in ÛdUCCRBM leading to the desired triples. The appearance of the high-rank excitations through the nested commutators is a direct consequence of the disentangled structure of the unitary (see S2 in the ESI†). Thus, the chosen scatterer and the excitation operator (with which the scatterer is non-commutative) are paired up in a factorized manner. After such incorporation, ÛdUCCRBM can be written as:
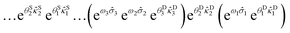 | (28) |
The overall depth of ÛdUCCRBM is greatly reduced due to the introduction of scatterers and will be evident in the Results and discussion section.
The interwoven structure of the ansatz that includes high rank correlation through its decomposition into lower rank operators is reminiscent of a double exponential (factorized) coupled cluster ansatz41 and its unitarized variant.7 Such double exponential structure of the waveoperator in terms of two-body operators is crucial for the exactness of the wavefunction for which the variational minimum analytically satisfies the contracted Schrödinger equation (CSE)42 – a necessary and sufficient condition for the wavefunction to satisfy the Schrödinger equation. Contrarily, the wavefunctions generated from a single exponential with generalized two-body operators43,44 do not satisfy the CSE.42 The CSE and its anti-hermitian variant (ACSE) leads to the direct determination of energy and two-electron reduced density matrices of many-electron molecules45,46 and is shown to be more expressive and efficient than the UCC ansatz. The ACSE has been implemented for quantum simulations, both on simulators and devices47–51 at the cost of shallow quantum circuits.
![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) Di and
Di and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) Dj may combine with
Dj may combine with ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) i and
i and ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) j to generate the same triple excitation operator
j to generate the same triple excitation operator ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) T
T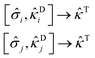 | (29) |
The most dominant combination is ascertained by the largest value of the product of the MP2 measures of the associated scatterers, given it exceeds a predefined threshold (set to 10−6 here). The higher-order excitation (![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) T in eqn (29)) is excluded from the ansatz when no combination meets this criterion. This approach is based on the rationale that a more substantial MP2 value of the scatterer enhances its ability to facilitate connections between the low-rank and high-rank excitations, which should be from a many-body perturbation theory viewpoint. Subsequently, the included high-rank excitations are reintroduced to the model (in the form of binary vectors) for further training. The probabilities for these high-rank excitations are determined by the product of two factors: the probability of the double excitation from |ΨSD〉 and the squared modulus of the MP2 values of the scatterers involved in creating the desired high-rank excitation. Steps 4 to 6 are iterated with the improved training set until the RBM ceases to generate new high-rank configurations. This marks the termination of our protocol. The resultant ansatz (ÛdUCCRBM), which we will call the RBM-dUCC ansatz, represents the final output of this protocol.
T in eqn (29)) is excluded from the ansatz when no combination meets this criterion. This approach is based on the rationale that a more substantial MP2 value of the scatterer enhances its ability to facilitate connections between the low-rank and high-rank excitations, which should be from a many-body perturbation theory viewpoint. Subsequently, the included high-rank excitations are reintroduced to the model (in the form of binary vectors) for further training. The probabilities for these high-rank excitations are determined by the product of two factors: the probability of the double excitation from |ΨSD〉 and the squared modulus of the MP2 values of the scatterers involved in creating the desired high-rank excitation. Steps 4 to 6 are iterated with the improved training set until the RBM ceases to generate new high-rank configurations. This marks the termination of our protocol. The resultant ansatz (ÛdUCCRBM), which we will call the RBM-dUCC ansatz, represents the final output of this protocol.
The expansion of the initial wavefunction to incorporate the contribution from high-order excitations occurs in steps. First, we run the sequence of the abovementioned steps, starting from |ΨSD〉 to target all dominant triply excited configurations. When RBM does not produce any new such configurations, we stop the generation procedure. The ansatz, (ÛdUCCRBM), at this stage, can be denoted as RBM-dUCCSDTS, where the subscript S on T signifies that this ansatz generates triply excited configurations through the utilization of scatterers. It may be noted that while we focus on generating the secondary subspace through triply excited configurations at the leading order, a scatterer that is present later in ÛdUCCRBM may combine with it to form a quadruply excited configuration. Although we call our ansatz RBM-dUCCSDTS, it may still implicitly produce some higher excited configurations, such as quadruples. This event is fortuitous and results in higher-than-desired expressibility.
The optimization of the RBM-dUCCSDTS parameters is performed in the VQE framework. The resultant state, which now expands the secondary subspace, contains dominant triply excited configurations and may contain higher order excitations due to fortuitous combinations. This state can be fed to the protocol described in steps 2 to 6 to further produce explicit quadruples by constructing RBM-dUCCSDTSQS. This would require explicit cascades of scatterers as described in eqn (27). Such a procedure can be continued to make the ansatz even more expressive. It is to be noted that as the single excitation operators appear at the end, no scatterer can act on them to produce redundant configurations. A real quantum device has inherent noise, potentially introducing errors in obtaining |ΨSD〉. However, once a regenerative ML model (such as RBM) learns the probability distribution, it can mitigate the errors by employing powerful NEM. As the remaining steps do not involve any quantum measurement, no additional error accumulates. The ease of integrating NEM into our method adds to its elegance.
Before proceeding further, it is important to discuss the feasibility and costs associated with learning a quantum state using a neural network, specifically in the context of Step-3 in our protocol. This process draws parallels with Neural Quantum State Tomography (NQST),34 an efficient machine learning-based Quantum State Tomography (QST) technique that sidesteps the substantial computational costs of traditional brute-force QST methods. In their work, Torlai et al.34 showcased the effectiveness of optimal Restricted Boltzmann Machine (RBM) models in efficiently performing QST for highly entangled states described by over a hundred qubits. Consequently, our approach, similarly employing RBM to learn the initial quantum state, holds promise for application in large-scale systems. Once the machine learning (ML) model is trained, it deciphers correlations within the learned state and symbolically generates dominant excited determinants. This generative process utilizes Gibbs sampling37 to directly generate dominant determinants based on the weights and biases of visible and hidden nodes set during training. Importantly, we avoid exhaustive searches through the entire space of possible determinants to identify dominance. The symbolic knowledge of dominant determinants is then used to construct an appropriate shallow depth ansatz. Hence, using an optimal RBM structure in terms of the number of hidden nodes, learning rate, etc.,52 one can efficiently learn an approximate state and accurately generate dominant determinants. Enhancing the efficiency of the generation process involves configuring the model or its components to preserve the spatial and spin symmetry of the generated determinants. In our study, as detailed in the Results and discussion section, we implement tower sampling to retain spin symmetry. Generating dominant determinants using RBM is conceptually a variant of selected configuration interaction. As elucidated by Herzog et al.,33 the main challenge in this RBM-based approach arises from verifying whether the RBM-generated excited determinants are already incorporated within the ansatz at a given step. For every proposed determinant, this scales as O(Ndet2),33 with Ndet being the number of determinants already incorporated “within” the ansatz. With the increase in system size, this does not requisitely approach the complexity of Full Configuration Interaction (FCI) as Ndet represents the set of dominant configurations, which practically increases sub-exponentially with the system size, even for highly correlated systems.
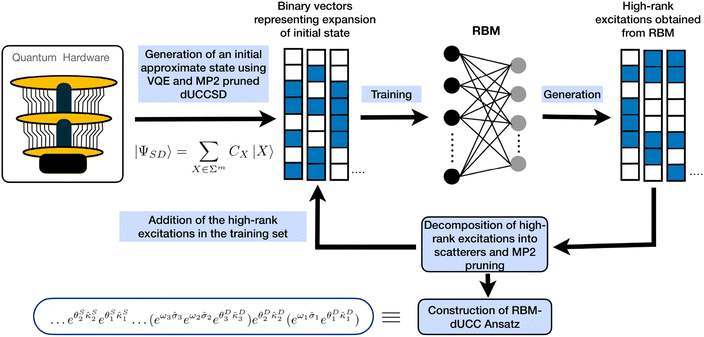
To summarize our procedure, we first obtain a low-level approximation to the wavefunction (using a low-rank ansatz such as dUCCSD) from a quantum device and learn the probability distribution using RBM. The learned wavefunction is now expanded iteratively with the help of many body perturbative measures. We end up with a highly compact ansatz capable of inducing high-order configurations required to describe the correlation effects properly. The overview of our procedure is depicted in Fig. 2. In section 3, we showcase the efficacy of this method by generating dominant triply excited configurations starting from a dUCCSD ansatz. Moreover, we describe the significantly low gate depth of the constructed ansatz. We consider a variety of molecules at various geometries to carry out this study, highlighting our method's general applicability.
3 Results and discussion
3.1 Accuracy and cost efficiency of RBM-dUCC
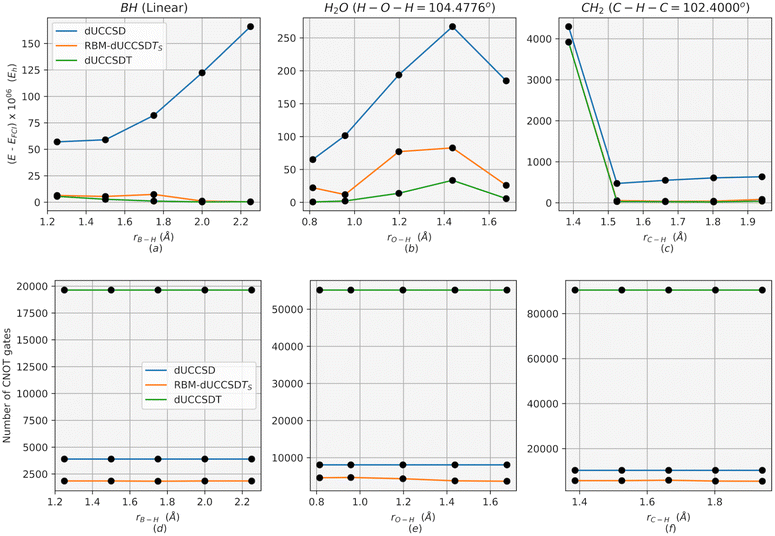
As a demonstration of the remarkable capabilities of Restricted Boltzmann Machines (RBM) in acquiring the knowledge of a wavefunction and generating dominant configurations, we compare the energy accuracy obtained using RBM-dUCCSDTS with that of conventional dUCCSDT in Fig. 3. The latter consists of all triples excitations (which is of the order of no3nv3, where no represents the number of occupied orbitals and nv the number of unoccupied orbitals). We also plot the converged energies using the conventional dUCCSD ansatz for reference. The comparison is depicted in Fig. 3 for three molecules viz. H2O, BH and CH2 with their core orbitals frozen. For all calculations, we have used the orbitals obtained from the restricted Hartree–Fock method provided by PySCF53 using the STO-3G basis set. The required Jordan–Wigner transformation for the hamiltonian and the ansatz is obtained from the qiskit-nature54 modules. All simulations have been performed on the statevector simulator (which mimics a noiseless quantum device) provided by qiskit. The conventional dUCCSD and dUCCSDT ansatzes and required MP2 values of the scatterers are also obtained from qiskit modules. All variational optimizations have been done using a conjugate gradient (CG) optimizer with an initial point set to zero for all parameters. Of course, one may choose an initial point of zero only for the parameters associated with scatterers and set the values of singles and doubles from the ÛSD(θopt) (eqn (14)). The construction of the RBM has been carried out using the sklearn modules.55 A detailed description of this construction, along with its various hyper-parameters, has been included in the ESI (point S1†).Apart from the energy accuracy, we also provide the circuit depth for conventional dUCCSD, dUCCSDT, and RBM-dUCCSDTS. As can be discerned from Fig. 3, the energy obtained after variationally optimizing RBM-dUCCSDTS is very close to that obtained using conventional dUCCSDT with a difference of 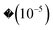 Hartree, all while using far fewer CNOT gates (a measure of circuit depth). The former even has fewer CNOT gates than conventional dUCCSD. This tremendous reduction in the number of CNOT gates reflects the high suitability of the RBM-generated ansatz for the NISQ hardware. As the energy for RBM-dUCCSDTS is not below the conventional dUCCSDT for any of the tested systems, the fortuitous generation of higher-than-desired configurations (that is, beyond triples) has not occurred here. As we explicitly target triply excited configurations, another important assessment would be to check the overlap between the optimized wavefunctions generated using conventional dUCCSDT and RBM-dUCCSDTS ansatzes. Thus, we provide the overlap between these two wavefunctions in Fig. 4. It can be discerned from this plot that the overlap difference from unity is
Hartree, all while using far fewer CNOT gates (a measure of circuit depth). The former even has fewer CNOT gates than conventional dUCCSD. This tremendous reduction in the number of CNOT gates reflects the high suitability of the RBM-generated ansatz for the NISQ hardware. As the energy for RBM-dUCCSDTS is not below the conventional dUCCSDT for any of the tested systems, the fortuitous generation of higher-than-desired configurations (that is, beyond triples) has not occurred here. As we explicitly target triply excited configurations, another important assessment would be to check the overlap between the optimized wavefunctions generated using conventional dUCCSDT and RBM-dUCCSDTS ansatzes. Thus, we provide the overlap between these two wavefunctions in Fig. 4. It can be discerned from this plot that the overlap difference from unity is 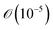 or less. This indicates the ability of RBM to recognize the dominant triply excited configurations properly. Additionally, it highlights the efficacy of MP2 theory in guiding ML predictions.
or less. This indicates the ability of RBM to recognize the dominant triply excited configurations properly. Additionally, it highlights the efficacy of MP2 theory in guiding ML predictions.
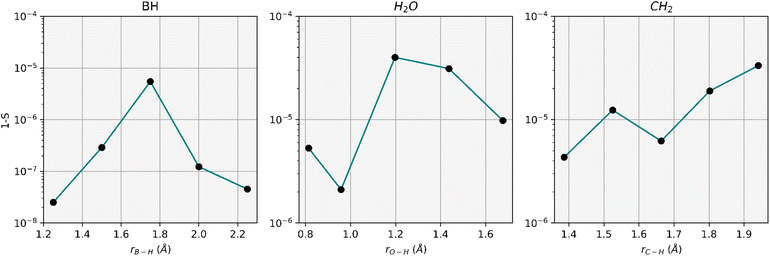 | ||
| Fig. 4 Difference of the overlap (S) of optimized wavefunctions generated by the RBM-dUCCSDTS ansatz (ΨdUCCSDTRBMS) and that by conventional dUCCSDT (ΨdUCCSDTConv) from unity. Here, S = 〈ΨdUCCSDTRBMS|ΨdUCCSDTConv〉 and the molecular systems taken are identical to that used during the study depicted in Fig. 3. | ||
A comparison of our protocol with the popular ADAPT-VQE6 is presented in Fig. S1 of the ESI.† Under the noiseless case, the ADAPT protocol does produce an exceptionally compact ansatz capable of capturing large correlation energy (with minutely less accuracy than RBM-dUCCSDTS). However, the noise present in NISQ hardware can impair ADAPT's ability to generate an optimum ansatz with sufficient expressibility.40 This point is further elaborated in section 3.2. RBM-dUCC construction only requires measurements during the initial state preparation and, thereby, is substantially resilient to noise (corroborated by Fig. 5 and Table S1 of the ESI†).
Another challenge that requires scrutiny is the capacity of our devised method to effectively handle systems characterized by pronounced multireference traits in their ground states against other known to be parameter-efficient methods. For this purpose, we test our protocol on a linear chain H6 (STO-3G) with the nearest neighbor bond distance set to 2 Å. We compare our results with the k-uCJ ansatz,56 which is known for exceptional performance within multireference systems. As can be discerned from Table 1, the results produced by RBM-dUCCSDTS are comparable in terms of variational parameters (an indirect indication of circuit depth) and accuracy. However, our dynamic methodology possesses the advantage of tailoring the ansatz based on the specific correlations inherent in a molecular system. This flexibility is in contrast to fixed-size ansatzes like k-uCJ, which only consider the molecular size while building the ansatz. This adaptive nature is crucial for constructing a shallow depth ansatz while dealing with low to moderately correlated systems.
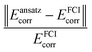 , where Ecorr represents the correlation energy obtained using the ansatz or method described in the superscript
, where Ecorr represents the correlation energy obtained using the ansatz or method described in the superscript
| Ansatz used for ground state energy evaluation | Number of variational parameters | Error in correlation energy (in percentage) |
|---|---|---|
| 1-uCJ | 77 | 1.40 |
| 2-uCJ | 154 | 0.05 |
| RBM-dUCCSDTS | 127 | 0.48 |
3.2 Implementation of RBM-dUCC under noise
The remarkable efficiency of the RBM-dUCC ansatz to produce highly correlated wavefunctions while employing only a fraction of CNOT gates has been demonstrated in section 3.1. In this section, we implement RBM-dUCCSDTS to calculate the ground state energy using VQE in a noisy backend. To construct this backend, we incorporate the shot-based estimator54 with noise model imported from IBM's FakeMelbourne. This includes:1. Single qubit gate errors composed of a depolarizing error channel followed by the thermal relaxation error channel on the respective qubit.
2. Two qubit gate errors composed of a two-qubit depolarizing error channel followed by single qubit thermal relaxation error on the involved qubits.
3. Single qubit readout-errors on measurement.
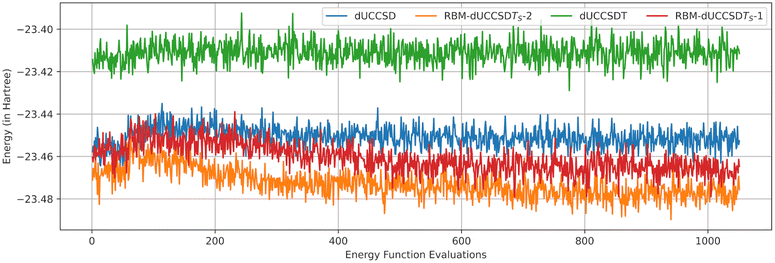
Under the same noisy backend, we also provide a comparative performance of conventional dUCCSD and dUCCSDT ansatzes. For variational optimization of the ansatz parameters, we use the Simultaneous Perturbation Stochastic Approximation (SPSA)57 with the maximum iteration set to 500 and the initial point taken to be zero for all parameters. In general, SPSA is considered to be a good optimizer under noise as it requires fewer measurements during the optimization as compared to CG. The number of shots used to obtain the requisite expectation values was set to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. To reduce the time of measurement simulations, we levied the normal distribution approximation on the expectation values.54 The resultant outcomes are portrayed through the graphical representation in Fig. 5. For this study, we used linear BH (rB–H = 2.25 Å). The large number of CNOT gates in the dUCCSDT ansatz (≈19
000. To reduce the time of measurement simulations, we levied the normal distribution approximation on the expectation values.54 The resultant outcomes are portrayed through the graphical representation in Fig. 5. For this study, we used linear BH (rB–H = 2.25 Å). The large number of CNOT gates in the dUCCSDT ansatz (≈19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) results in a substantial accumulation of error. This renders the VQE optimization scheme completely useless. Even in the case of conventional dUCCSD, the trajectory is not well-behaved and leads to higher energy. RBM-dUCCSDTS provides the best results in terms of accuracy and stability. This is a direct effect of exceptionally few gates in this ansatz. We performed analysis on two variations of RBM-dUCCSDTS.
000) results in a substantial accumulation of error. This renders the VQE optimization scheme completely useless. Even in the case of conventional dUCCSD, the trajectory is not well-behaved and leads to higher energy. RBM-dUCCSDTS provides the best results in terms of accuracy and stability. This is a direct effect of exceptionally few gates in this ansatz. We performed analysis on two variations of RBM-dUCCSDTS.
1. RBM-dUCCSDTS – 1: the initial state (|ΨSD〉) was prepared under the noise and was used to train RBM. The final ansatz obtained after the sequence of steps outlined in section 2.3 was also variationally optimized under the same noise.
2. RBM-dUCCSDTS – 2: the initial state (|ΨSD〉) was prepared with noiseless simulation. However, the final ansatz generated through RBM was optimized under noise.
For both variations, the accuracy is superior to conventional dUCCSD. Although we cannot produce a noiseless initial state in real quantum hardware, our study aims to show the deteriorating effect of using a noisy initial wavefunction during the generation of the RBM-dUCC ansatz. However, in this case, one can seamlessly use NEM to mitigate the errors and obtain a well-trained RBM. This would make the red curve (Fig. 5) move down towards the orange one. One can easily extend NEM to the final generated ansatz, too. This would further enhance the accuracy. It must be noted that in the study depicted in Fig. 5, we are not focussing on the absolute accuracy of the various ansatzes but their relative behavior on average. One must apply layers of error mitigation protocols (including NEM) to bring the results within the chemical accuracies. As the depth of the RBM-dUCC ansatz is substantially low, the cost overhead when applying such error-mitigating protocols would, in general, also decrease.
A standout feature of our methodology lies in its ability to operate without expectation-value evaluations once an approximate initial state is established. This provides two significant advantages: it reduces the measurement overhead and becomes particularly beneficial when considering the inherent errors associated with measurements on NISQ hardware. Any ansatz constructing methodology that heavily relies on such expectation terms to tailor the ansatz would inevitably grapple with these errors, resulting in a final ansatz that significantly deviates from the ideal one. Hence, an optimal protocol must generate an ansatz well-suited to the coherence time of NISQ hardware and achieve this in a manner that minimizes susceptibility to noise. The protocol expounded in this article adeptly incorporates both of these essential features as exemplified in Fig. 3 and 5. Methods such as ADAPT-VQE,6 which depend on expectation value measurements during ansatz construction, are highly likely to show some complications under hardware noise. In the ESI,† we present a comparison of the performance between the ADAPT ansatz and RBM-dUCCSDTS. It is noted that the ADAPT ansatz exhibits some sensitivity to noise despite generating an impressively shallow depth ansatz in noiseless simulations. In contrast, RBM-dUCCSDTS performs consistently well both with and without noise. For this comparison, we do not use additional error mitigation techniques.35,58–63
4 Conclusions and future outlook
In this study, we have demonstrated the application of Restricted Boltzmann Machines (RBMs) to acquire a concise and expressive ansatz specifically tailored to individual molecules at their various nuclear–nuclear separations. Our approach involves generating dominant configurations starting from an initial wavefunction derived from a lower-level approximation. To refine the output obtained from the RBM, we have employed MP2 measures as filtering criteria. The resultant configurations are fed back into the RBM, enabling iterative learning and facilitating the generation of an increasingly accurate expansion of the wavefunction. Furthermore, we have leveraged the utilization of scatterer operators to incorporate high-rank excitations, resulting in an ansatz with exceedingly shallow depth. Notably, our methodology circumvents the necessity for quantum measurements in all steps beyond the initial wavefunction approximation. These characteristics contribute to the exceptional potency of our approach for implementation within the realm of NISQ devices. A comparison of our method with the well-known ADAPT-VQE and k-uCJ presented in this work corroborates these advantages. Additionally, the RBM can be combined with NEM techniques to effectively mitigate the detrimental impacts of noise inherent in present-day quantum hardware. Thus, utilizing our protocol, one can determine accurate molecular wavefunctions and energies using noisy quantum hardware, which is essential for understanding the behavior of molecules and materials. A meticulous examination of the various hyperparameters associated with the RBM and their influence on the final ansatz represents a promising avenue for future investigation. Furthermore, exploring alternative regenerative models beyond RBMs holds significant potential in advancing this field of study.Data availability
The data supporting this study's findings are available from the corresponding author upon reasonable request.Author contributions
Sonaldeep Halder: conceptualization, formal analysis, investigation, methodology, software, writing – original draft. Anish Dey: data curation, formal analysis, investigation, methodology, software. Chinmay Shrikhande: data curation, methodology, software. Rahul Maitra: conceptualization, funding acquisition, project administration, resources, supervision, validation, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dipanjali Halder (Indian Institute of Technology Bombay) for all the stimulating discussions regarding the use of scatterers in the dUCC framework. SH acknowledges the Council of Scientific & Industrial Research (CSIR) for their fellowship. RM acknowledges the financial support from the Industrial Research and Consultancy Centre, IIT Bombay and Science and Engineering Research Board, Government of India.Notes and references
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed
.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre and N. P. Sawaya,
et al.
, Chem. Rev., 2019, 119, 10856–10915 CrossRef CAS PubMed
.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Rev. Mod. Phys., 2020, 92, 015003 CrossRef CAS
.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O'brien, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed
.
- A. Delgado, J. M. Arrazola, S. Jahangiri, Z. Niu, J. Izaac, C. Roberts and N. Killoran, Phys. Rev. A, 2021, 104, 052402 CrossRef CAS
.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, Nat. Commun., 2019, 10, 3007 CrossRef PubMed
.
- D. Halder, V. S. Prasannaa and R. Maitra, J. Chem. Phys., 2022, 157, 174117 CrossRef CAS PubMed
.
- D. Halder, S. Halder, D. Mondal, C. Patra, A. Chakraborty and R. Maitra, J. Chem. Sci., 2023, 135, 41 CrossRef CAS
.
- D. Mondal, D. Halder, S. Halder and R. Maitra, J. Chem. Phys., 2023, 159, 014105 CrossRef CAS PubMed
.
- C. Feniou, M. Hassan, D. Traoré, E. Giner, Y. Maday and J.-P. Piquemal, Commun. Phys., 2023, 6, 192 CrossRef CAS
.
- L. Zhao, J. Goings, K. Shin, W. Kyoung, J. I. Fuks, J.-K. Kevin Rhee, Y. M. Rhee, K. Wright, J. Nguyen and J. Kim,
et al.
, npj Quantum Inf., 2023, 9, 60 CrossRef
.
- H. L. Tang, V. Shkolnikov, G. S. Barron, H. R. Grimsley, N. J. Mayhall, E. Barnes and S. E. Economou, PRX Quantum, 2021, 2, 020310 CrossRef
.
- Y. S. Yordanov, V. Armaos, C. H. Barnes and D. R. Arvidsson-Shukur, Commun. Phys., 2021, 4, 228 CrossRef
.
- M. Ostaszewski, E. Grant and M. Benedetti, Quantum, 2021, 5, 391 CrossRef
.
- N. V. Tkachenko, J. Sud, Y. Zhang, S. Tretiak, P. M. Anisimov, A. T. Arrasmith, P. J. Coles, L. Cincio and P. A. Dub, PRX Quantum, 2021, 2, 020337 CrossRef
.
- F. Zhang, N. Gomes, Y. Yao, P. P. Orth and T. Iadecola, Phys. Rev. B, 2021, 104, 075159 CrossRef CAS
.
- S. Sim, J. Romero, J. F. Gonthier and A. A. Kunitsa, Quantum Sci. Technol., 2021, 6, 025019 CrossRef
.
- J. Preskill, Quantum, 2018, 2, 79 CrossRef
.
- M. Schuld, I. Sinayskiy and F. Petruccione, Quantum Inf. Process., 2014, 13, 2567–2586 CrossRef
.
- G. Carleo and M. Troyer, Science, 2017, 355, 602–606 CrossRef CAS PubMed
.
- K. Hornik, Neural Netw., 1991, 4, 251–257 CrossRef
.
- N. Le Roux and Y. Bengio, Neural Comput., 2008, 20, 1631–1649 CrossRef PubMed
.
- K. Choo, A. Mezzacapo and G. Carleo, Nat. Commun., 2020, 11, 2368 CrossRef CAS PubMed
.
-
A. Szabo and N. S. Ostlund, Modern quantum chemistry: introduction to advanced electronic structure theory, Courier Corporation, 2012 Search PubMed
.
- T. D. Barrett, A. Malyshev and A. Lvovsky, Nat. Mach. Intell., 2022, 4, 351–358 CrossRef
.
- J. Han, L. Zhang and E. Weinan, J. Comput. Phys., 2019, 399, 108929 CrossRef CAS
.
- J. Hermann, Z. Schätzle and F. Noé, Nat. Chem., 2020, 12, 891–897 CrossRef CAS PubMed
.
- D. Pfau, J. S. Spencer, A. G. Matthews and W. M. C. Foulkes, Phys. Rev. Res., 2020, 2, 033429 CrossRef CAS
.
- J. Kessler, F. Calcavecchia and T. D. Kühne, Adv. Theory Simul., 2021, 4, 2000269 CrossRef CAS
.
- J. P. Coe, J. Chem. Theory Comput., 2018, 14, 5739–5749 CrossRef CAS PubMed
.
- G. E. Hinton and R. R. Salakhutdinov, Science, 2006, 313, 504–507 CrossRef CAS PubMed
.
- R. G. Melko, G. Carleo, J. Carrasquilla and J. I. Cirac, Nat. Phys., 2019, 15, 887–892 Search PubMed
.
- B. Herzog, B. Casier, S. Lebègue and D. Rocca, J. Chem. Theory Comput., 2023, 19, 2484–2490 CrossRef CAS PubMed
.
- G. Torlai, G. Mazzola, J. Carrasquilla, M. Troyer, R. Melko and G. Carleo, Nat. Phys., 2018, 14, 447–450 Search PubMed
.
- E. R. Bennewitz, F. Hopfmueller, B. Kulchytskyy, J. Carrasquilla and P. Ronagh, Nat. Mach. Intell., 2022, 4, 618–624 Search PubMed
.
-
G. Montúfar, Information Geometry and Its Applications, Cham, 2018, pp. 75–115 Search PubMed
.
-
A. Fischer and C. Igel, Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications, Berlin, Heidelberg, 2012, pp. 14–36 Search PubMed
.
-
Y. Freund and D. Haussler, Advances in Neural Information Processing Systems, 1991 Search PubMed
.
- F. A. Evangelista, G. K.-L. Chan and G. E. Scuseria, J. Chem. Phys., 2019, 151, 244112 CrossRef PubMed
.
- S. Sim, P. D. Johnson and A. Aspuru-Guzik, Adv. Quantum Technol., 2019, 2, 1900070 CrossRef
.
- R. Maitra, Y. Akinaga and T. Nakajima, J. Chem. Phys., 2017, 147, 074103 CrossRef PubMed
.
- D. A. Mazziotti, Phys. Rev. A, 2004, 69, 012507 CrossRef
.
- M. Nooijen, Phys. Rev. Lett., 2000, 84, 2108 CrossRef CAS PubMed
.
- H. Nakatsuji, Phys. Rev. A, 1976, 14, 41 CrossRef CAS
.
- D. A. Mazziotti, Phys. Rev. Lett., 2006, 97, 143002 CrossRef PubMed
.
- D. A. Mazziotti, Phys. Rev. A, 2007, 75, 022505 CrossRef
.
- S. E. Smart and D. A. Mazziotti, Phys. Rev. Lett., 2021, 126, 070504 CrossRef CAS PubMed
.
- S. E. Smart and D. A. Mazziotti, Phys. Rev. A, 2022, 105, 062424 CrossRef CAS
.
- S. E. Smart, J.-N. Boyn and D. A. Mazziotti, Phys. Rev. A, 2022, 105, 022405 CrossRef CAS
.
- Y. Wang, L. M. Sager-Smith and D. A. Mazziotti, New J. Phys., 2023, 25, 103005 CrossRef
.
- C. L. Benavides-Riveros, Y. Wang, S. Warren and D. A. Mazziotti, arXiv, 2023, preprint, arXiv:2311.05058, DOI:10.48550/arXiv.2311.05058.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed
.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova and S. Sharma,
et al.
, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed
.
-
H. Abraham
et al.
, Qiskit: An Open-source Framework for Quantum Computing, 2021 Search PubMed
.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg,
et al.
, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed
.
- Y. Matsuzawa and Y. Kurashige, J. Chem. Theory Comput., 2020, 16, 944–952 CrossRef CAS PubMed
.
- J. C. Spall, Johns Hopkins APL Tech. Dig., 1998, 19, 482–492 Search PubMed
.
- K. Temme, S. Bravyi and J. M. Gambetta, Phys. Rev. Lett., 2017, 119, 180509 CrossRef PubMed
.
- S. Endo, S. C. Benjamin and Y. Li, Phys. Rev. X, 2018, 8, 031027 CAS
.
- S. Halder, C. Shrikhande and R. Maitra, J. Chem. Phys., 2023, 159, 114115 CrossRef CAS PubMed
.
- A. Kandala, K. Temme, A. D. Córcoles, A. Mezzacapo, J. M. Chow and J. M. Gambetta, Nature, 2019, 567, 491–495 CrossRef CAS PubMed
.
- H. Liao, D. S. Wang, I. Sitdikov, C. Salcedo, A. Seif and Z. K. Minev, arXiv, 2023, preprint, arXiv:2309.17368, DOI:10.48550/arXiv.2309.17368.
- Z. Cai, R. Babbush, S. C. Benjamin, S. Endo, W. J. Huggins, Y. Li, J. R. McClean and T. E. O'Brien, arXiv, 2022, preprint, arXiv:2210.00921, DOI:10.48550/arXiv.2210.00921.
Footnotes |
| † Electronic supplementary information (ESI) available: A detailed description of the construction of the Restricted Boltzmann Machine (RBM), a brief discussion on scatterer operators and a comparison between RBM-dUCC and ADAPT ansatzes. See DOI: https://doi.org/10.1039/d3sc05807g |
| ‡ Centre of Excellence in Quantum Information, Computing, Science & Technology, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India (Email: E-mail: rmaitra@chem.iitb.ac.in). |
| This journal is © The Royal Society of Chemistry 2024 |