 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accessing the electronic structure of liquid crystalline semiconductors with bottom-up electronic coarse-graining†
Chun-I
Wang
 ,
J. Charlie
Maier
and
Nicholas E.
Jackson
,
J. Charlie
Maier
and
Nicholas E.
Jackson
 *
*
Department of Chemistry, University of Illinois at Urbana-Champaign, 505 S Mathews Avenue, Urbana, Illinois 61801, USA. E-mail: jacksonn@illinois.edu
First published on 2nd May 2024
Abstract
Understanding the relationship between multiscale morphology and electronic structure is a grand challenge for semiconducting soft materials. Computational studies aimed at characterizing these relationships require the complex integration of quantum-chemical (QC) calculations, all-atom and coarse-grained (CG) molecular dynamics simulations, and back-mapping approaches. However, these methods pose substantial computational challenges that limit their application to the requisite length scales of soft material morphologies. Here, we demonstrate the bottom-up electronic coarse-graining (ECG) of morphology-dependent electronic structure in the liquid-crystal-forming semiconductor, 2-(4-methoxyphenyl)-7-octyl-benzothienobenzothiophene (BTBT). ECG is applied to construct density functional theory (DFT)-accurate valence band Hamiltonians of the isotropic and smectic liquid crystal (LC) phases using only the CG representation of BTBT. By bypassing the atomistic resolution and its prohibitive computational costs, ECG enables the first calculations of the morphology dependence of the electronic structure of charge carriers across LC phases at the ∼20 nm length scale, with robust statistical sampling. Kinetic Monte Carlo (kMC) simulations reveal a strong morphology dependence on zero-field charge mobility among different LC phases as well as the presence of two-molecule charge carriers that act as traps and hinder charge transport. We leverage these results to further evaluate the feasibility of developing mesoscopic, field-based ECG models in future works. The fully CG approach to electronic property predictions in LC semiconductors opens a new computational direction for designing electronic processes in soft materials at their characteristic length scales.
1 Introduction
Significant strides have been made in the design of organic semiconductors (OSCs), with diverse applications such as organic light-emitting diodes (OLEDs),1,2 organic photovoltaics (OPVs),3,4 organic field-effect transistors (OFETs),5–7 and biomedical devices.8–10 The success of OSCs hinges upon gaining insights into the interplay between optoelectronic properties and multiscale structural attributes, spanning molecular conformations (1–10 Å), primary structural features (1–10 nm), mesoscale morphology (10 nm–10 μm), and thin-film morphology (>10 μm).11–21 Multiscale simulations have emerged as an essential tool, shedding light on complex structure–function relationships in OSCs.22–25 Traditional multiscale simulations often employ a bottom-up coarse-grained (CG) procedure to model the bulk morphology of OSCs, followed by a series of back-mapping procedures aimed at converting CG coordinates to atomistic resolution.26–34 The atomistic coordinates retrieved from the CG resolution facilitate subsequent quantum chemistry (QC) calculations to characterize electronic structure. However, the widespread utilization of multiscale simulations for OSC design has been hampered by the complex workflow, challenges associated with the one-to-many nature of backmapping, and the prohibitive computational cost of QC calculations. While recent efforts have utilized machine learning (ML) approaches to streamline back-mapping,35–37 the computation of morphology-dependent electronic properties remains intractable due to the demanding nature of quantum chemistry calculations.The recent emergence of interest in liquid-crystal-forming semiconductors highlights the computational challenges intrinsic to OSCs. Simply put, the computational challenge of modeling OSCs can be stated as the need to assess quantum-mechanically-derived electronic properties at multiple thermodynamic state points for large (∼10–100 nm), often glassy morphologies with robust statistical sampling.38–43 While the manipulation of liquid crystal (LC) phases in OSCs for enhanced device performance is a common theme throughout the community,44–46 recent work has explored morphology-dependent conductivity in asymmetric benzothienobenzothiophene-based compounds, a promising type of LC-forming OSCs used in field-effect transistors.47–66 These compounds exhibit a remarkable combination of attributes, including high charge mobility, superior solubility and processability, robust thermal durability, and the capability to regulate molecular orientation. While layered smectic phases with head-to-head bilayer (lipid-like) structures have been reported in the asymmetric benzothienobenzothiophene family, recent work by Han et al. introduced a derivative, 2-(4-methoxyphenyl)-7-octyl-benzothienobenzothiophene (BTBT),56,57 that exhibited a rare nematic phase (long-range order without layered structure) when inserted into rubbed planar anchoring sandwich cells. However, the mechanisms underlying phase transitions between crystals and different smectic phases or the formation of the nematic phase remain unclear.59–66 Importantly, large changes in the electronic conductivities were observed in transitioning benzothienobenzothiophene-based molecules through different LC phases. For traditional multiscale computational methods, the analysis of such conductivity trends would represent an effort warranting state-of-the-art computing resources; slow relaxation times would necessitate CG modeling, which would need to be connected with all-atom (AA) backmapping and molecular dynamics, followed by ad nauseam QC characterization at the ∼10–100 nm scale to compute morphology dependent electronic properties.
To circumvent the convoluted back-mapping processes and resource-intensive QC calculations, recent efforts have explored the evaluation of quantum mechanical (QM) properties at CG resolutions using a “top-down” approach.67–71 This approach leverages anisotropic CG simulations to capture π–π stacking interactions between aromatic moieties and the torsional conformational changes within conjugated backbones. These CG collective variables serve as the basis for estimating structure-dependent electronic properties like electronic coupling using physically-motivated approximations. While these top-down CG approaches have been effective at accessing electronic properties such as charge mobility and molecular orbital delocalization at mesoscopic simulation length scales, they are restricted to simple analytical forms that do not capture the complexity of real chemistries. Additionally, research has highlighted that the collective structural variables based on π–π stacking and backbone torsion alone may not suffice to model structure-dependent electronic properties at the CG level.72–75
Recently, data-driven approaches have emerged for the “bottom-up” prediction of electronic properties of soft materials at the CG resolution.76–84 These electronic CG (ECG) models leverage ML to establish a mapping from AA electronic structure to CG representation, eliminating the complexities and computational costs associated with back-mapping processes and ad nauseam QC. A fundamental insight driving the development of ECG models is the recognition that a single CG configuration encompasses a range of AA configurations, resulting in a “one-to-many” mapping (Fig. S1†). This mapping implies that any property derived from the AA model inherently becomes a probabilistic distribution at the CG resolution. The noise on this distribution can be related to (i) the degeneracy of the CG mapping operator (dictating how atoms are grouped into CG beads) and (ii) the thermodynamic state of the system (reflecting the extent of thermal fluctuations within the AA model). Recently, our group has extended the ECG framework through the incorporation of deep kernel learning (DKL) with approximate Gaussian processes81,82 to predict noisy, heteroscedastic distributions as a function of CG representation, facilitating the rigorous bottom-up connection of ECG predictions with an underlying, QC-accurate AA model.
In this work, we demonstrate the first bottom-up CG study of the bulk electronic structure of the molecular semiconductor BTBT,55–58 as a function of the LC morphology using ECG methods. Our comprehensive structural characterization of the simulations reveal the presence of smectic A and smectic E phases, instead of the experimentally observed nematic phase under planar anchoring conditions, which suggests a general preference for the benzothienobenzothiophene family to exhibit smectic characteristics. We further explore the dependence of charge delocalization on LC morphology by explicitly constructing density functional theory (DFT)-quality electronic Hamiltonians using only the CG model resolution, from which electronic structure at the ∼20 nm length scale is derived with statistical robustness. Analyses of these Hamiltonians reveal the presence of three distinct types of charge carriers, the distributions of which vary between LC phases. We trace the origin of these charge carriers to multi-molecule descriptors of local electronic and structural environments. The zero-field charge mobility across LC phases, as determined by kinetic Monte Carlo (kMC) simulations, not only underscores a pronounced dependence on morphology but also indicates that two-molecule charge carriers serve as traps, impeding effective charge transport pathways. As ECG methods exhibit approximately 105 reduced cost relative to existing multiscale computational paradigms, a statistically robust characterization of the electronic structure of LC phases at large-length scales is achieved without invoking vast computational resources. Lastly, we examine the potential for connecting bottom-up CG predictions of electronic structure with field-based order parameters that serve as the workhorses of the soft materials theory community. Altogether, this fully “bottom-up” approach to morphology and electronic structure calculations facilitates the systematic design of OSCs across diverse morphologies at mesoscopic length scales with statistical robustness and low computational cost.
2 Methods
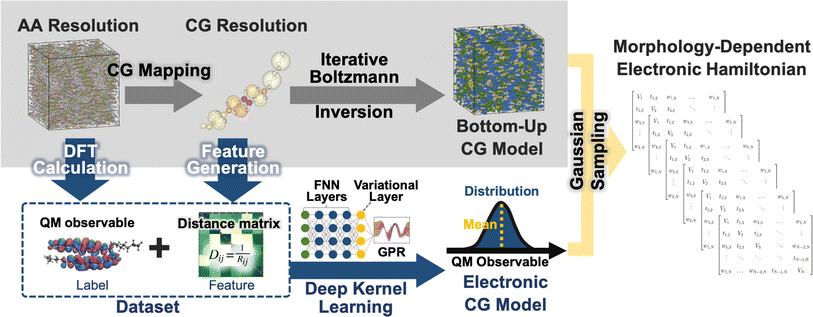
The workflow for the fully bottom-up CG method for the LC phases of BTBT is illustrated in Fig. 1. AA molecular dynamics (MD) simulations are performed in the isotropic (700 K and 1 bar), smectic A (555 K and 1 bar),‡ and smectic E (515 K and 1 bar)‡ phases to parameterize CG models using iterative Boltzmann inversion (IBI)85,86 and an electronic structure-optimized CG mapping.87 CG structural prediction models are coupled with bottom-up ECG models derived from AA MD trajectories and ωB97XD/cc-pVDZ DFT calculations. CG representations were converted to CG distance matrices, providing translational and rotational invariance, that served as input features for the DKL method underlying ECG. ECG models were trained to reproduce (i) conformation-dependent, single-molecule highest occupied molecular orbital (HOMO) energies of BTBT as well as (ii) HOMO–HOMO electronic couplings between BTBT dimers. Comprehensive details regarding the parameterization and validation of the AA force field and the creation of BTBT training data sets can be found in previous work.872.1 Bottom-up CG models for morphology prediction
Iterative Boltzmann Inversion (IBI)85,86 with pressure correction88 is used to construct CG intermolecular potentials for BTBT in the isotropic and smectic phases. IBI was selected due to the importance of structural prediction accuracy in ECG that was recently reported,80 though in principle more rigorous bottom-up CG methods can be utilized as long as structural distribution functions are accurately reproduced.As CG non-bonded potentials are expected to exhibit limited thermodynamic transferability between isotropic and smectic phases, two CG non-bonded potentials were developed for the isotropic (700 K and 1 bar) and smectic A phases (at 555 K and 1 bar), respectively. Achieving transferability in bottom-up CG necessitates a similarity in the effective interaction domain, such as isotropic to isotropic or anisotropic to anisotropic, rather than transitioning from isotropic to anisotropic phases. This requirement arises from the collective interaction of mapped atoms, encapsulated by an effective CG potential of mean force, which in turn represents the corresponding free energy attributes.89–92 Therefore, for the smectic E phase (at 515 K and 1 bar), the CG non-bonded potentials were adopted from those designed for the smectic A phase, which demonstrated excellent transferability in reproducing both short-range and long-range structural properties, as discussed in the ESI.† A single set of CG bonded potentials of BTBT, encompassing CG bond, CG angle, and CG dihedral interactions, were determined through direct Boltzmann inversion using the reference AA isotropic morphology; previous works have demonstrated the low sensitivity of CG bonded parameters to thermodynamic state changes.86,93,94 All AA and CG MD simulations were conducted using LAMMPS,95 with a custom IBI implementation adhering to established procedures.96–98 Additional details regarding the construction of CG structural prediction models and a comprehensive evaluation including the radial distribution function (RDFs) of the center of mass, nematic order parameters, structure factor analyses, and RDFs of the 120 distinctive CG pairs are available in the ESI.†
While the IBI methodology and its derivatives have been extensively utilized in the development of bottom-up CG models for liquid-crystal-forming materials,99–111 we observed significant limitations in its application to the complex intermolecular interactions of BTBT. Specifically, the extensive fused ring motifs of BTBT, coupled with the flexible alkyl side chain, induce strongly anisotropic intermolecular interactions. This asymmetric molecular architecture poses challenges for the convergence of the IBI procedure, particularly in high-order LC phases. The presence of a rigid fused ring, a floppy alkyl side chain, along with the highly asymmetric structure necessitates the treatment of all 15 CG particles as distinct types. This results in the requirement for 120 CG non-bonded potentials, further complicating the challenge of the IBI parameterization. We observed that IBI convergence for BTBT in the smectic A phase was slow and extremely sensitive to initializations and damping factors compared to the isotropic phase. Although the CG non-bonded potentials derived for the smectic A phase exhibit excellent transferability to the smectic E phase, we attempted to further refine the smectic E CG non-bonded potentials. Unfortunately, the convergence of the IBI approach proved intractable in this more anisotropic system. We note that the development of CG potentials for BTBT or similar fused-ring materials112,113 in condensed phases is uncommon in the literature to-date. Recent research on anisotropic CG models114–122 or ML-derived CG potentials123,124 has explored their potential to accommodate the strong anisotropy of the polycyclic aromatic hydrocarbon systems, but this topic falls beyond the scope of the present work.
2.2 Development of electronic (ECG) models
We employ the DKL version of ECG81 to create CG electronic predictions models that capture configurational variations of BTBT's HOMO energy as well as the HOMO–HOMO electronic coupling between BTBT dimers, eliminating the need for backmapping or ad nauseam QC. The DKL-ECG model consists of a feed-forward neural network (FNN), a variational layer, and Gaussian process regression (GPR), as illustrated in the inset of Fig. 1. The FNN transforms CG conformations (distance matrices) followed by a variational layer that maps the FNN results to a latent space. From this latent space, approximate GPR is used to map to the electronic prediction task. Critically, DKL-ECG allows the noisy observables at the CG resolution to be treated as heteroscedastic Gaussian distributions, with predicted means and widths varying as functions of positions in CG configuration space. Accurately representing these CG probability distributions of electronic properties is essential to achieving an accurate “bottom-up” reproduction of the electronic structure of the system. Stochastic sampling of these Gaussian distributions as a function of CG configuration allows the reproduction of the correction AA ensemble of DFT-quality electronic structure without the need for backmapping or ad nauseam QC, providing the critical computational cost advantage without loss of accuracy. For in-depth methodological details of DKL-ECG, the reader is referred to ref. 81.Training sets for DKL-ECG models are obtained from previous AA simulations of BTBT.87 These trajectories encompass isotropic and smectic morphologies, followed by electronic structure calculations of single molecule and dimer pairs at the ωB97XD/cc-pVDZ level of theory. In subsequent discussions, we refer to the data set extracted from the isotropic morphology as training-isotropic/testing-isotropic, and the data set originating from the smectic A morphology as training-smectic A/testing-smectic A. Comprehensive details regarding the training procedure of the DKL-ECG models for HOMO energy prediction can be found in the ESI.† Training ML models for predicting electronic coupling has consistently posed a formidable challenge, even when including full AA featurization.125–128 This challenge stems from the electronic coupling's intricate dependence on both the separation distance and mutual orientation between molecular pairs.11,129 To address this challenge, we explored many approaches (see ESI†) and settled on learning the logarithm of the absolute value of the electronic coupling combined with a phase classifier that predicts the sign of the HOMO–HOMO electronic coupling for a given CG molecular pair conformation using a FNN. Detailed information on the model parameters and the training procedures for the DKL-ECG models and the FNN classifier can be found in the ESI.†
2.3 Valence Hamiltonian construction at the CG resolution
We integrate CG structural prediction models and ECG models to construct tight-binding Hamiltonians for the isotropic and smectic phases in a basis of HOMO orbitals using only the CG representation of BTBT. 9000 BTBT molecules are simulated at the CG resolution in the isotropic and smectic LC phases within cubic boxes measuring 199 Å, 190 Å, and 188 Å, respectively. Ten replicas of each CG simulation (40 ns) were performed for each phase. 120 snapshots of the CG configuration of the system were collected from each simulation. These snapshots served to define the morphology-dependent electronic Hamiltonian at the CG level.130–132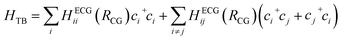 | (1) |
A tight-binding Hamiltonian in the basis of BTBT's HOMO orbitals was employed to model the valence band electronic structure relevant to hole transport in BTBT morphologies (eqn (1)), where HECGii(RCG) and HECGij(RCG) represent the on-site ECG-derived HOMO energy prediction and dimer HOMO–HOMO electronic coupling predictions, respectively. Provided the single-molecule and dimer configurations extracted from the CG simulations, ECG models predict the Gaussian means and variances of the HOMO energy and HOMO–HOMO electronic coupling as illustrated in Fig. 1 resulting in population of all matrix elements of the Hamiltonian. For each single-molecule CG configuration, we performed Gaussian sampling using the predicted mean and variance, generating 20 distinct samples of the HOMO energies that served as the individual diagonal elements of 20 unique Hamiltonians. The off-diagonal elements of these Hamiltonians underwent the same Gaussian sampling process, with the coupling value set to zero when the distance between the center of mass (COM) of the pair molecules exceeded 7 Å. This sampling process explicitly addresses the one-to-many mapping influenced by thermodynamic fluctuations and mapping degeneracy, reproducing the correct AA-ensemble of thermodynamically averaged electronic predictions without backmapping. Subsequently, these ECG-determined Hamiltonians were diagonalized to compute the delocalized electronic states in the isotropic and smectic LC phases, from which subsequent analysis occurred.
The ECG approach to construct electronic tight-binding Hamiltonians at the CG resolution exhibits dramatic computational cost benefits relative to traditional multiscale modeling paradigms. Establishing an individual Hamiltonian using this method is conservatively estimated to be at least 105 times faster than equivalent DFT calculations, and this estimation does not account for the computational cost of backmapping procedures or additional sampling with AA MD. In this study, the task of creating a single Hamiltonian involved handling 9000 single-molecule configurations and roughly 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecular pairs (within a COM distance of 7 Å) for the evaluation of HOMO energy and electronic coupling, respectively. To characterize the electronic structure of 7200 Hamiltonians with ad nauseam DFT calculations at the ωB97XD/cc-pVDZ level, executed on a single CPU core, would require approximately 83
000 molecular pairs (within a COM distance of 7 Å) for the evaluation of HOMO energy and electronic coupling, respectively. To characterize the electronic structure of 7200 Hamiltonians with ad nauseam DFT calculations at the ωB97XD/cc-pVDZ level, executed on a single CPU core, would require approximately 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520
520![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CPU hours (∼7.2 × 107 individual calculations). In contrast, the DKL-ECG method accomplishes this computation in just 107 CPU hours. Relative to the computational cost of training set generation for all ECG models used in this work (cumulatively ∼7.5 × 105 DFT calculations), this amounts to a two order of magnitude advantage that only improves with additional statistical sampling and application of the trained ECG models. This outstanding computational efficiency empowers us to generate 2400 Hamiltonians (comprising 120 CG snapshots multiplied by 20 rounds of Gaussian sampling) for each LC system. This extensive characterization provides a comprehensive and statistically significant understanding of electronic structure in the LC phases, a level of detail that was previously beyond the reach of traditional multiscale simulation methods due to intractable computational costs.
000 CPU hours (∼7.2 × 107 individual calculations). In contrast, the DKL-ECG method accomplishes this computation in just 107 CPU hours. Relative to the computational cost of training set generation for all ECG models used in this work (cumulatively ∼7.5 × 105 DFT calculations), this amounts to a two order of magnitude advantage that only improves with additional statistical sampling and application of the trained ECG models. This outstanding computational efficiency empowers us to generate 2400 Hamiltonians (comprising 120 CG snapshots multiplied by 20 rounds of Gaussian sampling) for each LC system. This extensive characterization provides a comprehensive and statistically significant understanding of electronic structure in the LC phases, a level of detail that was previously beyond the reach of traditional multiscale simulation methods due to intractable computational costs.
3 Results and discussion
In this work, we employ bottom-up CG models to study the morphology of a system of 9000 BTBT molecules at temperatures of 700 K, 555 K, and 515 K, followed by the assessment of ECG models for predicting HOMO energy and HOMO–HOMO electronic coupling. Subsequently, we systematically explore the relationship between different LC structures and their charge transport properties by integrating the bottom-up CG approach and ECG models.3.1 Morphology characterization
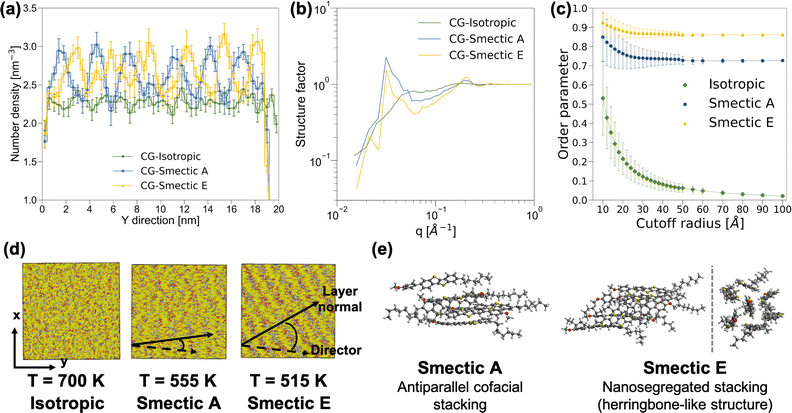
Based on the observation of differential scanning calorimetry with the insertion of BTBT into rubbed planar anchoring sandwich cells,56,57 our simulation should yield distinct phases at temperatures of 700 K, 555 K, and 515 K, corresponding to isotropic, nematic, and smectic A phases, respectively. The structural characterization of the morphology at 700 K, as depicted in Fig. 2, confirms the anticipated isotropic features. However, an unexpected discovery emerged when clear layered structures were observed in both AA and CG simulations at 555 K and 515 K, meeting the key criteria for distinguishing smectic phases from the nematic phase. Fig. 2a and b reveal oscillating patterns in number density along the y-axis direction and a distinct peak at q = 0.03 Å−1 in the structure factor analyses,§ indicating smectic phases at 555 K and 515 K. An additional AA MD simulation was performed with the system temperature linearly decreasing at a rate of 3.5 K ns−1 from 700 K to 350 K. As illustrated in Fig. S8,† we observed changes in the slope of the nematic order parameters for both the molecular long-axis and short-axis around 640 K, and another change in the slope of the order parameter of the molecular short-axis around 520 K. Fig. S8† also shows a clear change in the structure factor peak at q = 0.03 Å−1, corresponding a layered structure of period 33 Å, at both phase transition temperatures. The persistent presence of layered-structure below 640 K in the structure factor analysis suggests the absence of the nematic phase in our simulations. Given that the major difference between BTBT and the well-studied benzothienobenzothiophene family is the methoxy group at the tail of the phenyl ring, we suspect that the nematic phase can only be achieved under specific boundary conditions, such as those provided by the rubbed planar anchoring sandwich cells.56,57Further analyses were conducted to differentiate between the two smectic phases at 555 K and 515 K. The nematic order parameter analysis revealed that the CG morphology at 555 K exhibited an order parameter of 0.733 ± 0.008 along with a principal director vector (−0.093 ± 0.009, 0.994 ± 0.001, −0.048 ± 0.012), and a tilt angle between the principal director vector and layer normal of 17.1 ± 16.0°. The similar mean value and standard deviation of the tilt angle imply parallel alignment and suggest a smectic A phase. Conversely, for the 515 K CG morphology, a larger order parameter of 0.867 ± 0.004 was observed along with a principal director vector (−0.114 ± 0.003, 0.986 ± 0.002, −0.123 ± 0.010), and a clear deviation between the principal director vector and layer normal with the tilt angle of 34.1 ± 12.2°, as shown in Fig. 2d, indicates a smectic E phase. In addition, snapshots extracted from AA MD simulations at 555 K and 515 K illustrate the differences between smectic A and smectic E phases. While BTBT molecules form antiparallel cofacial π–π stacking in the smectic A phase, a herringbone-like structure with offset π–π stacking is observed in the smectic E phase, reminiscent of the crystal structure observed in the benzothienobenzothiophene family.47–55,59–66 These features are consistent with CG structure factor analyses and the characterization of the nematic order parameter as a function of cutoff radius, as depicted in Fig. 2b and c. Specifically, the smectic E phase exhibits a stronger peak at q = 0.21 Å−1 and a larger order parameter with smaller standard deviation, reflecting more ordered π–π stacking in the herringbone-like structure. The decreasing peak intensity at q around 0.03 Å−1 and its shift to the low q regime indicates offset π–π stacking monolayer structure.
The observation of monolayers with a length scale around 33 Å, featuring antiparallel π–π stacking within these layered structures, provides insights into the phase transition mechanisms between smectic and crystal phases. Since the initial use of asymmetric benzothienobenzothiophene in field-effect transistors, a head-to-head bilayer (lipid-like) unit structure in the crystal phase has consistently been reported. It was conventionally believed that the head-to-head bilayer should be a common feature in smectic phases as well.47–55 However, recent studies have presented more evidence of monolayer structures along with antiparallel π–π stacking in smectic phases. Our simulation results align with these recent findings.59–66 Specifically, the transition from antiparallel cofacial π–π stacking133 to offset π–π stacking (also known as nanosegregated stacking)134,135 within the monolayers from smectic A to smectic E, accompanied by a considerable increase in the tilt angle between the principal director and the layer normal, may serve as a precursor to the formation of the lipid-like bilayer structure observed in the crystal phase.65,66
3.2 Evaluation of ECG models
We first scrutinize the performance of the DKL-ECG model in predicting the HOMO energy and HOMO–HOMO electronic coupling as inputs for constructing the tight-binding Hamiltonian (eqn (1)).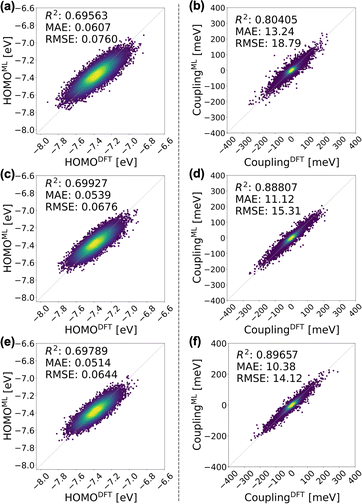 | ||
| Fig. 3 Evaluation of the DKL-ECG models for predicting HOMO energy (left panels) and HOMO–HOMO electronic coupling (right panels). The mean values of HOMO energy predicted by the DKL-ECG models are compared with values obtained through DFT calculations across the (a) testing-isotropic, (c) testing-smectic A, and (e) testing-smectic E data sets. The right panels assess HOMO–HOMO electronic coupling predictions, utilizing DFT calculations as benchmarks, and contrasting values derived from the DKL-predicted mean and a FNN sign classifier, for the (b) testing-isotropic (d) testing-smectic A, and (f) testing-smectic E data sets. The heatmap visually represents the density of data points. The DKL-ECG model for HOMO energy prediction was trained on the training-isotropic data set. ECG for electronic coupling predictions are derived from the DKL regression model trained on the training-smectic A data set and the FNN classification model trained on the training-isotropic data set. Detailed evaluations of these ECG models are discussed in the ESI.† | ||
It is crucial to underscore the significantly reduced computational cost offered by the DKL-ECG approach. The DKL-ECG predicts the HOMO–HOMO coupling of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecular pairs in 80 CPU seconds at single-time execution, while DFT calculations demand 4200 CPU seconds for a single pair, equating to 11
000 molecular pairs in 80 CPU seconds at single-time execution, while DFT calculations demand 4200 CPU seconds for a single pair, equating to 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 CPU hours for 10
600 CPU hours for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecular pairs with repeating executions. The computational efficiency of ECG models empowers the establishment of over 4000 morphology-dependent electronic Hamiltonians in this work, facilitating an in-depth exploration of bulk electronic structure with robust statistical sampling.
000 molecular pairs with repeating executions. The computational efficiency of ECG models empowers the establishment of over 4000 morphology-dependent electronic Hamiltonians in this work, facilitating an in-depth exploration of bulk electronic structure with robust statistical sampling.
3.3 Characterization of electronic structure in the isotropic and smectic phases
The combination of bottom-up CG structural prediction models with ECG models enables the generation of electronic Hamiltonians at the scale of ∼20 nm that can be used to explore the interplay between morphology and electronic structure in the LC phases of BTBT. We first employed bottom-up CG models to simulate 9000 BTBT molecules in the isotropic and smectic phases. The resulting ensemble-averaged nematic order parameters are 0.018 ± 0.005, 0.733 ± 0.008, and 0.867 ± 0.004 for the isotropic, smectic A, and smectic E phases, respectively. Subsequently, we sampled 2400 electronic Hamiltonians for each LC phase based on ECG predictions derived from the collected snapshots of CG configurations. The diagonalization of these Hamiltonians provided eigenstates (Ej) and eigenvectors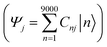 , where Ej represents the energy of the jth eigenstate, and Cnj is the wave function coefficient of the nth BTBT molecule for the jth eigenstate. Subsequently, we computed the inverse participation ratio (IPR) defined as
, where Ej represents the energy of the jth eigenstate, and Cnj is the wave function coefficient of the nth BTBT molecule for the jth eigenstate. Subsequently, we computed the inverse participation ratio (IPR) defined as 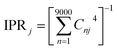 , to quantify the delocalization of the wavefunction throughout the LC phases.
, to quantify the delocalization of the wavefunction throughout the LC phases.
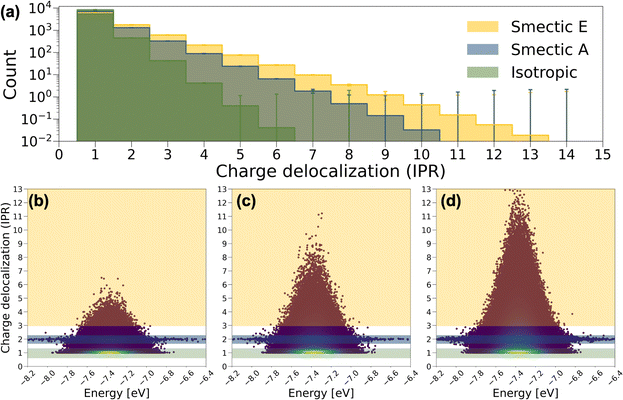
In Fig. 4a, the averaged histogram of the number of charge-delocalized molecules (IPR) over the 9000 eigenstates reveals that charge carriers are predominantly localized on one or two molecules in all LC phases. However, in smectic morphologies, there is a notable increase in the presence of delocalized states, allowing charge carriers to extend across 6 to 10 BTBT molecules for smectic A and 6 to 13 BTBT molecules for smectic E. This observation aligns with experimental findings indicating enhanced mobility with increased ordering of the LC phases in BTBT.56–58 It is noteworthy that among the IPR analyses derived from the 2400 Hamiltonians for smectic morphologies, a small number of Hamiltonians do not exhibit the 6 to 13-molecule charge delocalization observed in the majority of cases. Such statistical fluctuations can be critical in soft materials theory, and our effort provides the first robust analysis of the ensemble averaged electronic properties of soft materials, ensuring reliable insights.
To further understand the electronic structure of BTBT in each LC phase, the IPR values for the 9000 charge transport (CT) states derived from each Hamiltonian are depicted as a function of their energies in Fig. 4b–d. Notably, a pronounced concentration of CT states is observed in the IPR ∼ 1 region, particularly prominent in the isotropic and smectic phases. Furthermore, a consistent pattern in the IPR ∼ 2 region is identified across each LC phase, where CT energies span a broad range from −8.2 to −6.4 eV. These distinctive patterns serve as the basis for categorizing CT states into “one-molecule charge carriers” and “two-molecule charge carriers,” while CT states that delocalize over more than three molecules are labeled as “delocalized charge carriers.” To further dissect structural and electronic contributions to the appearance of these charge carrier motifs, we recalculated and diagonalized the Hamiltonians for all systems by setting all diagonal elements to the mean value of HOMO energy across all molecules in the training set (site-energy disorder equal to zero). As shown in Fig. S17,† elimination of site energy disorder (implying identical conformations for all BTBT molecules) facilitates dramatically increased delocalization across 10 to 3000 molecules in 9% of CT states for both isotropic and smectic A phases, and 4.3% for the smectic phase. This result is important for the field of LC material modeling as nearly all simulation approaches employ anisotropic ellipsoids or field-based descriptors, for which such molecule-specific energetic disorder is absent. Moreover, HOMO energy disorder is observed to be smaller in the smectic E phase followed by the smectic A and the isotropic phase, which likely drives the increased charge delocalization. Interestingly, the pattern of two-molecule charge carriers remains unchanged by the manipulation of on-site energy disorder, implying a more detailed interplay of structural and electronic properties in charge delocalization.
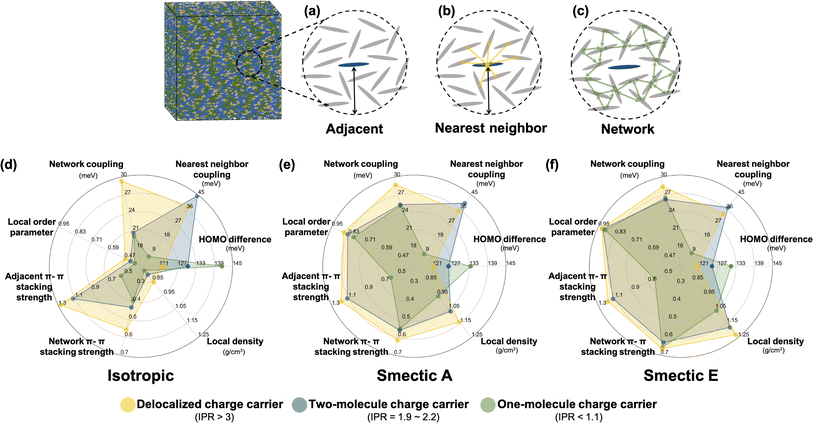
To further investigate the formation of the three primary charge carrier types, we conducted a comprehensive structural characterization based on the local molecular environment of the charge carrier. In the subsequent analyses, to minimize uncertainties arising from CG representation or thermal fluctuations, charge carriers were categorized based on their IPR values: one-molecule charge carriers with IPR values below 1.1, two-molecule charge carriers with IPR values ranging from 1.9 to 2.2, and delocalized charge carriers with IPR values larger than 3. For each charge carrier type, the charge center of the jth electronic state was determined by the center of mass of the molecule possessing the largest Cnj coefficient. We included Nadj adjacent molecules within a 13 Å radius, corresponding to the second molecular shell determined by the RDFs shown in Fig. S2b,† to estimate adjacent structural and electronic characteristics, as illustrated in Fig. 5a–c. These properties included the averaged absolute value of HOMO energy differences between the charge center and all adjacent molecules, local order parameters derived from the nematic order tensor,38 the local density, the averaged absolute value of the electronic coupling between the charge center molecule and its nearest neighbor (NN) molecules, the network coupling, representing the averaged absolute value of the electronic coupling between molecules within the cutoff radius (13 Å), and the averaged adjacent π–π stacking strength68 between the charge center molecules and adjacent molecules defined by eqn (2):
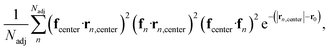 | (2) |
In Fig. 5d–f, the radar plots depict the mean values of all computed electronic descriptors for the three types of charge carriers. These mean values are averaged over the results obtained from 2400 Hamiltonians for the isotropic and smectic phases, respectively. One-molecule charge carriers exhibit the largest HOMO energy difference (141 meV isotropic, 133 meV smectic A, 131 meV smectic E) but the lowest nearest neighbor coupling (6 meV isotropic, 8 meV both smectic phases), as well as the smallest network coupling (20 meV isotropic, 25 meV smectic A). In contrast, delocalized charge carriers exhibit the smallest HOMO energy difference (121 meV isotropic, 121 meV smectic A, 120 meV smectic E) but the largest network coupling (29 meV isotropic, 29 meV smectic A, 28.5 meV smectic E). These findings imply that an effective charge transport network, characterized by strong network coupling, moderate nearest neighbor coupling, and low onsite energy disorder, facilitates charge delocalization. Two-molecule charge carriers demonstrate the strongest nearest neighbor coupling (44 meV isotropic, 39 meV smectic A, 37 meV smectic E) among the three classes, surpassing even their network coupling (21 meV isotropic, 25 meV smectic A, 26 meV smectic E). This result suggests that a stronger nearest neighbor coupling compared to network coupling can result in the localization of charge carriers onto two molecules, which may act as a trap during charge transport. Notably, the prevalence of two-molecule charge carriers aligns with the results of quantum dynamics simulations crystalline organic semiconductors136–138 and the model framework of transient localization theory.139–143 As LCs are intermediate between isotropic and crystalline systems, the presence of such electronic states is of crucial importance for understanding charge carrier transport in LC materials.
The three types of charge carriers directly reflect their local structural environments. As depicted in Fig. 5d–f, delocalized charge carriers in the isotropic and smectic phases exhibit large values of the local nematic order parameter, local density, and adjacent and network π–π stacking strengths. In contrast, one-molecule charge carriers display the lowest values for all structural features, particularly in terms of adjacent π–π stacking strength. In both smectic phase, even though one-molecule charge carriers demonstrate a similar level of network π–π stacking strength, their small adjacent π–π stacking strength indicates a poor connection between nearest neighbors that substantially impedes charge delocalization. Notably, the large nearest neighbor coupling observed in two-molecule charge carriers does not necessarily correlate with adjacent π–π stacking strength, as only a single molecular pair has a large π–π stacking strength. This result suggests that averaged structural characterizations can wash out the contribution of critical local molecular aggregates even at the 1–10 nm length scale.
3.4 Correlation between morphology and charge mobility
To explore the variation in charge mobility across different LC morphologies and understand the impact of the three identified charge carriers on the charge transport mechanism, we conducted rejection-free kMC simulations to estimate the zero-field charge mobility following the methodology outlined in ref. 144–146 (details provided in the ESI†). For each LC phase, kMC charge hopping trajectories were run for 105 steps based on 100 CG configurations/Hamiltonians, utilizing 9000 molecules as different initial hopping sites, resulting in 900![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kMC trajectories per LC phase. Analysis of the kMC trajectories with different initial hopping sites revealed that in the isotropic phase, 65.0 ± 1.0% of the initial sites exhibited zero mobility, indicating that the charge carriers were trapped near these initial sites within 105 steps, attributed to either one-molecule or two-molecule charge localized carrier states. Furthermore, the partition of zero mobility due to the localized initial charge carriers in the smectic A and smectic E phases was 35.4 ± 1.2% and 17.9 ± 1.2%, respectively, indicating the inability of these carriers to establish effective charge transport pathways in all phases, but with a portion that decreased as a function of increase LC ordering.
000 kMC trajectories per LC phase. Analysis of the kMC trajectories with different initial hopping sites revealed that in the isotropic phase, 65.0 ± 1.0% of the initial sites exhibited zero mobility, indicating that the charge carriers were trapped near these initial sites within 105 steps, attributed to either one-molecule or two-molecule charge localized carrier states. Furthermore, the partition of zero mobility due to the localized initial charge carriers in the smectic A and smectic E phases was 35.4 ± 1.2% and 17.9 ± 1.2%, respectively, indicating the inability of these carriers to establish effective charge transport pathways in all phases, but with a portion that decreased as a function of increase LC ordering.
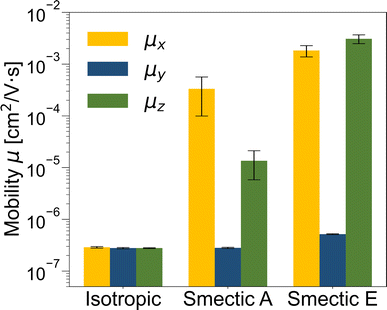
The zero-field charge mobilities along the three Cartesian coordinates (μx, μy, and μz) for each LC phase are illustrated in Fig. 6. In the isotropic phase, the mobilities along the three coordinates exhibit similar values (<10−6 cm2 V−1 s−1) that are systematically smaller than both smectic phases due to strong disorder. Notably, the mobilities in the both smectic phases display anisotropic characteristics, with the lowest mobility observed along the y-direction (μy < 10−6 cm2 V−1 s−1) due to disruptions in the effective charge transport path caused by the lamellar spacing. Conversely, the μx value, approximately 10−3 cm2 V−1 s−1, can be attributed to the alignment of π–π stacking perpendicular to the LC director, as depicted in Fig. 2d. Importantly, only in the smectic E phase does μz surpass 10−3 cm2 V−1 s−1 due to the presence of a herringbone-like structure.
The isotropic mobilities (averaged over μx, μy, and μz) for the isotropic, smectic A, and smectic E phases are ∼10−7, ∼10−4, and ∼10−3 cm2 V−1 s−1, respectively. Given that zero-field charge mobility is generally 103 to 104 times smaller than the field-effect mobility,147–149 the isotropic mobility obtained from our kMC simulation aligns well with the mobility trend and order of magnitudes observed for the benzothienobenzothiophene family in distinct LC phases through experimental measurements.45,56 These results underscore the robustness of our ECG approach in elucidating the relationship between morphology and electronic properties at CG resolution in a more efficient manner compared to typical multiscale approaches.
3.5 Examining the potential for bottom-up electronic coarse-graining over fields
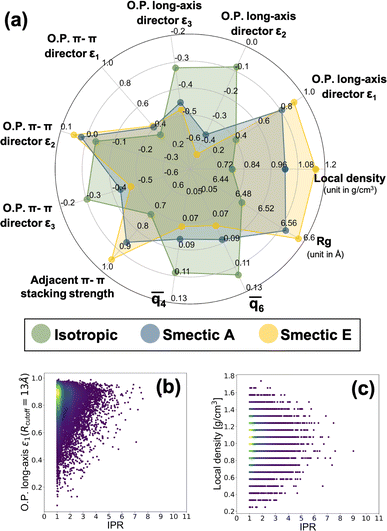
Provided the scalable electronic structure predictions enabled by use of a particle-based CG model for the LC material BTBT, we assess the potential for moving into field-based CG models of electronic structure parameterized from the “bottom-up” to further extend accessible spatiotemporal simulation scales. Such field-based models are the workhorses of the Chemical Engineering and Materials Science communities, with recent work being performed to introduce systematic “bottom-up” CG approaches for structural and thermodynamic predictions.34 Notably, simulations of LC materials have historically been the domain of such field-based descriptions,150,151 motivating the assessment of the question within the specific context of LC materials.To explore this, we computed a broad array of local order parameters within a characteristic radius of 13 Å, including nematic tensor order parameters of BTBT's long and π-system axes, multiple Steinhardt order parameters,152–154 the local density, and the local π–π-stacking strength. Fig. 7 a shows the average values of all computed field-based local order parameters for the isotropic and smectic phases, respectively, and the distributions of all field-based parameters as a function of IPR value are demonstrated in Fig. S19–S21.† Clearly, each phase can be distinguished by multiple different types of order parameters when coarse-grained from the “bottom-up.” To probe the feasibility of field-based CG descriptions of electronic structure, we assembled a data set of IPR calculated from the extracted local environments within the CG simulations of Fig. 7. As the local density and nematic order parameter are two common field-based descriptors used in soft materials theory, we analyzed whether these descriptors possessed any correlation with the resulting local electronic structure of BTBT in either LC phase. A weak visual correlation between the nematic order parameter of the long axis and the IPR was observed (Fig. 7b) but quantitative regression analysis using LASSO regression for feature selection elicited no meaningful predictive relationships. No visual correlation was observed between the local density and the ECG-computed IPR (Fig. 7c). LASSO regression and visual examination of all computed structural metrics further showed little correlation with the resulting IPR (see Fig. S19–S21 in the ESI†). This result suggests that while particle-based CG representations can be productive in scaling up electronic predictions to the mesoscale for disordered materials, field-based descriptors for the electronic structure of molecular LC are untenable at present.
Such a negative result should not be taken as evidence of a complete lack of potential for such models, but is sensible provided the standard densities and weak intermolecular couplings between LC molecules in this study. In more strongly coupled systems (higher densities, polymer chains) field-based descriptors of local electronic structure may be more predictive. Notably, in the context of semi-crystalline systems including grain boundaries and crystallites, a field-based descriptor would likely be a fruitful characterization of the local electronic structure.
4 Conclusions
In this work, we have integrated bottom-up CG and ECG techniques to provide the first quantitative characterization of the morphology-dependence of electronic structure in a LC semiconductor at the ∼20 nm length scale. Importantly, this framework provided such characterization with minimal computational resources and without the need for ad nauseam QC or complicated backmapping protocols, which enabled robust statistical analysis averaging over the full thermodynamic ensemble. This investigation revealed increased wavefunction delocalization in both smectic phases relative to the isotropic phase, as well as a recurrent two-site charge carrier motif common to the LC semiconductor BTBT. Using the CG electronic Hamiltonian, the zero-field mobility obtained via kMC simulations agrees semi-quantitatively with experimental mobility trends, validating the mesoscale electronic structure predictions from ECG. Importantly, we analyzed the potential for field-based ECG methods moving forward and concluded that significant work remains to be done to connect bottom-up electronic structure predictions with the mesoscopic scales that dictate soft materials function. This work marks a significant advancement in the ability to quantitatively model the relationships between multiscale morphology and electronic structure in organic semiconductors.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
C. I. Wang: methodology, software, validation, formal analysis, investigation, writing – original draft, visualization, J. C. Maier: writing – methodology, review and editing, N. E. Jackson: conceptualization, writing – review and editing, resources, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The development of the coarse-grained electronic models described in this article was supported by the National Science Foundation Chemical Theory, Models, and Computation division under award CHE-2154916. The authors acknowledge support from the Dreyfus Program for Machine Learning in the Chemical Sciences and Engineering during this project. The establishment of the ML data set was done using services provided by the OSG Consortium,155–157 which is supported by the National Science Foundation awards #2030508 and #1836650. We also appreciate the support from David Friday for the structure factor analysis.References
- G. Hong, X. Gan, C. Leonhardt, Z. Zhang, J. Seibert, J. M. Busch and S. Bräse, Adv. Mater., 2021, 33, 2005630 CrossRef CAS PubMed.
- Y.-Z. Shi, H. Wu, K. Wang, J. Yu, X.-M. Ou and X.-H. Zhang, Chem. Sci., 2022, 13, 3625–3651 RSC.
- D. Luo, W. Jang, D. D. Babu, M. S. Kim, D. H. Wang and A. K. K. Kyaw, J. Mater. Chem. A, 2022, 10, 3255–3295 RSC.
- G. Bernardo, T. Lopes, D. G. Lidzey and A. Mendes, Adv. Energy Mater., 2021, 11, 2100342 CrossRef CAS.
- K. Liu, B. Ouyang, X. Guo, Y. Guo and Y. Liu, npj Flexible Electron., 2022, 6, 1–19 CrossRef CAS.
- W. Tang, Y. Huang, L. Han, R. Liu, Y. Su, X. Guo and F. Yan, J. Mater. Chem. C, 2019, 7, 790–808 RSC.
- H. Li and J.-L. Brédas, Natl. Sci. Rev., 2021, 8, nwaa167 CrossRef CAS PubMed.
- T. Yokota, K. Fukuda and T. Someya, Adv. Mater., 2021, 33, 2004416 CrossRef CAS PubMed.
- J. Rivnay, R. M. Owens and G. G. Malliaras, Chem. Mater., 2014, 26, 679–685 CrossRef CAS.
- W.-K. Tsai, C.-I. Wang, C.-H. Liao, C.-N. Yao, T.-J. Kuo, M.-H. Liu, C.-P. Hsu, S.-Y. Lin, C.-Y. Wu, J. R. Pyle, J. Chen and Y.-H. Chan, Chem. Sci., 2019, 10, 198–207 RSC.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef PubMed.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- Y. Olivier, D. Niedzialek, V. Lemaur, W. Pisula, K. Müllen, U. Koldemir, J. R. Reynolds, R. Lazzaroni, J. Cornil and D. Beljonne, Adv. Mater., 2014, 26, 2119–2136 CrossRef CAS PubMed.
- F. Laquai, D. Andrienko, R. Mauer and P. W. M. Blom, Macromol. Rapid Commun., 2015, 36, 1001–1025 CrossRef CAS PubMed.
- D. Andrienko, in Multiscale Concepts in Simulations of Organic Semiconductors, ed. W. Andreoni and S. Yip, Springer International Publishing, Cham, 2020, pp. 1431–1442 Search PubMed.
- Y. Kim, S. Cook, S. M. Tuladhar, S. A. Choulis, J. Nelson, J. R. Durrant, D. D. C. Bradley, M. Giles, I. McCulloch, C.-S. Ha and M. Ree, Nat. Mater., 2006, 5, 197–203 CrossRef CAS.
- L. Zhu, M. Zhang, J. Xu, C. Li, J. Yan, G. Zhou, W. Zhong, T. Hao, J. Song, X. Xue, Z. Zhou, R. Zeng, H. Zhu, C.-C. Chen, R. C. I. MacKenzie, Y. Zou, J. Nelson, Y. Zhang, Y. Sun and F. Liu, Nat. Mater., 2022, 21, 656–663 CrossRef CAS PubMed.
- Z. Hu, R. T. Haws, Z. Fei, P. Boufflet, M. Heeney, P. J. Rossky and D. A. Vanden Bout, Proc. Natl. Acad. Sci. U.S.A., 2017, 114, 5113–5118 CrossRef CAS PubMed.
- J. K. Sowa, T. C. Allen and P. J. Rossky, Phys. Chem. Chem. Phys., 2023, 25, 20808–20816 RSC.
- A. Landi, M. Reisjalali, J. D. Elliott, M. Matta, P. Carbone and A. Troisi, J. Mater. Chem. C, 2023, 11, 8062–8073 RSC.
- C. K. Lee, L. Shi and A. P. Willard, J. Phys. Chem. C, 2019, 123, 306–314 CrossRef CAS.
- P. Gemünden, C. Poelking, K. Kremer, K. Daoulas and D. Andrienko, Macromol. Rapid Commun., 2015, 36, 1047–1053 CrossRef PubMed.
- B. J. Boehm, H. T. L. Nguyen and D. M. Huang, J. Phys.: Condens. Matter, 2019, 31, 423001 CrossRef CAS PubMed.
- P. Friederich, A. Fediai, S. Kaiser, M. Konrad, N. Jung and W. Wenzel, Adv. Mater., 2019, 31, 1808256 CrossRef PubMed.
- V. Bhat, C. P. Callaway and C. Risko, Chem. Rev., 2023, 123, 7498–7547 CrossRef CAS PubMed.
- N. E. Jackson, J. Phys. Chem. B, 2021, 125, 485–496 CrossRef CAS PubMed.
- S. Dhamankar and M. A. Webb, J. Polym. Sci., 2021, 59, 2613–2643 CrossRef CAS.
- J. Jin, A. J. Pak, A. E. P. Durumeric, T. D. Loose and G. A. Voth, J. Chem. Theory Comput., 2022, 18, 5759–5791 CrossRef CAS PubMed.
- W. G. Noid, J. Phys. Chem. B, 2023, 127, 4174–4207 CrossRef CAS PubMed.
- M. Reisjalali, R. Manurung, P. Carbone and A. Troisi, Mol. Syst. Des. Eng., 2022, 7, 294–305 RSC.
- R. Alessandri, S. Sami, J. Barnoud, A. H. de Vries, S. J. Marrink and R. W. A. Havenith, Adv. Funct. Mater., 2020, 30, 2004799 CrossRef CAS.
- P. Liu and G. A. Voth, J. Chem. Phys., 2007, 126, 045106 CrossRef PubMed.
- P. Liu, Q. Shi, E. Lyman and G. A. Voth, J. Chem. Phys., 2008, 129, 114103 CrossRef PubMed.
- N. Sherck, K. Shen, M. Nguyen, B. Yoo, S. Köhler, J. C. Speros, K. T. Delaney, M. S. Shell and G. H. Fredrickson, ACS Macro Lett., 2021, 10, 576–583 CrossRef CAS PubMed.
- M. Stieffenhofer, M. Wand and T. Bereau, Mach. Learn.: Sci. Technol., 2020, 1, 045014 Search PubMed.
- M. Stieffenhofer, T. Bereau and M. Wand, APL Mater., 2021, 9, 031107 CrossRef CAS.
- M. Stieffenhofer, C. Scherer, F. May, T. Bereau and D. Andrienko, Front. Chem., 2022, 10, 982757 CrossRef CAS PubMed.
- D. Andrienko, J. Mol. Liq., 2018, 267, 520–541 CrossRef CAS.
- S. Inoue, H. Minemawari, J. Tsutsumi, M. Chikamatsu, T. Yamada, S. Horiuchi, M. Tanaka, R. Kumai, M. Yoneya and T. Hasegawa, Chem. Mater., 2015, 27, 3809–3812 CrossRef CAS.
- M. Yoneya, H. Minemawari, T. Yamada and T. Hasegawa, J. Phys. Chem. C, 2017, 121, 8796–8803 CrossRef CAS.
- T. Okamoto, C. P. Yu, C. Mitsui, M. Yamagishi, H. Ishii and J. Takeya, J. Am. Chem. Soc., 2020, 142, 9083–9096 CrossRef CAS PubMed.
- P. A. Banks, A. M. Dyer, A. C. Whalley and M. T. Ruggiero, Chem. Commun., 2022, 58, 12803–12806 RSC.
- M. P. Allen, Mol. Phys., 2019, 117, 2391–2417 CrossRef CAS.
- P. Xie, T. Liu, J. Sun and J. Yang, Adv. Funct. Mater., 2022, 32, 2200843 CrossRef CAS.
- M. J. Han, D.-W. Lee, E. K. Lee, J.-Y. Kim, J. Y. Jung, H. Kang, H. Ahn, T. J. Shin, D. K. Yoon and J.-I. Park, ACS Appl. Mater. Interfaces, 2021, 13, 11125–11133 CrossRef CAS PubMed.
- K. S. Park, X. Luo, J. J. Kwok, A. Khasbaatar, J. Mei and Y. Diao, ACS Cent. Sci., 2023, 9, 2096–2107 CrossRef CAS PubMed.
- H. Minemawari, J. Tsutsumi, S. Inoue, T. Yamada, R. Kumai and T. Hasegawa, Appl. Phys. Express, 2014, 7, 091601 CrossRef CAS.
- S. Inoue, H. Minemawari, J. Tsutsumi, M. Chikamatsu, T. Yamada, S. Horiuchi, M. Tanaka, R. Kumai, M. Yoneya and T. Hasegawa, Chem. Mater., 2015, 27, 3809–3812 CrossRef CAS.
- H. Iino, T. Usui and J.-I. Hanna, Nat. Commun., 2015, 6, 6828 CrossRef CAS PubMed.
- M. Yoneya, H. Minemawari, T. Yamada and T. Hasegawa, J. Phys. Chem. C, 2017, 121, 8796–8803 CrossRef CAS.
- S. Inoue, S. Shinamura, Y. Sadamitsu, S. Arai, S. Horiuchi, M. Yoneya, K. Takimiya and T. Hasegawa, Chem. Mater., 2018, 30, 5050–5060 CrossRef CAS.
- T. Okamoto, C. P. Yu, C. Mitsui, M. Yamagishi, H. Ishii and J. Takeya, J. Am. Chem. Soc., 2020, 142, 9083–9096 CrossRef CAS PubMed.
- M. N. Gueye, A. Vercouter, R. Jouclas, D. Guérin, V. Lemaur, G. Schweicher, S. Lenfant, A. Antidormi, Y. Geerts, C. Melis, J. Cornil and D. Vuillaume, Nanoscale, 2021, 13, 3800–3807 RSC.
- P. Pandey, L. Fijahi, N. McIntosh, N. Turetta, M. Bardini, S. Giannini, C. Ruzié, G. Schweicher, D. Beljonne, J. Cornil, P. Samorì, M. Mas-Torrent, Y. H. Geerts, E. Modena and L. Maini, J. Mater. Chem. C, 2023, 11, 7345–7355 RSC.
- P. Pandey, L. Fijahi, N. McIntosh, N. Turetta, M. Bardini, S. Giannini, C. Ruzié, G. Schweicher, D. Beljonne, J. Cornil, P. Samorì, M. Mas-Torrent, Y. H. Geerts, E. Modena and L. Maini, J. Mater. Chem. C, 2023, 11, 7345–7355 RSC.
- M. J. Han, D. Wei, Y. H. Kim, H. Ahn, T. J. Shin, N. A. Clark, D. M. Walba and D. K. Yoon, ACS Cent. Sci., 2018, 4, 1495–1502 CrossRef CAS PubMed.
- M. J. Han, D. Wei, H. S. Yun, S.-H. Lee, H. Ahn, D. M. Walba, T. J. Shin and D. K. Yoon, NPG Asia Mater., 2022, 14, 1–12 CrossRef.
- P. Xie, T. Liu, J. Sun and J. Yang, Adv. Funct. Mater., 2022, 32, 2200843 CrossRef CAS.
- M. Yoneya, J. Phys. Chem. C, 2018, 122, 22225–22231 CrossRef CAS.
- A. Baggioli, M. Casalegno, G. Raos, L. Muccioli, S. Orlandi and C. Zannoni, Chem. Mater., 2019, 31, 7092–7103 CrossRef CAS.
- S. Hofer, W. Bodlos, J. Novák, A. Sanzone, L. Beverina and R. Resel, Liq. Cryst., 2021, 1888–1896 CrossRef CAS.
- S. Hofer, A. Hofer, J. Simbrunner, M. Ramsey, M. Sterrer, A. Sanzone, L. Beverina, Y. Geerts and R. Resel, J. Phys. Chem. C, 2021, 125, 28039–28047 CrossRef CAS PubMed.
- N. Shioya, M. Yoshida, M. Fujii, T. Shimoaka, R. Miura, S. Maruyama and T. Hasegawa, J. Phys. Chem. Lett., 2022, 13, 11918–11924 CrossRef CAS PubMed.
- K. Nikaido, S. Inoue, R. Kumai, T. Higashino, S. Matsuoka, S. Arai and T. Hasegawa, Adv. Mater. Interfaces, 2022, 9, 2201789 CrossRef CAS.
- T. Oka, N. Shioya, T. Shimoaka and T. Hasegawa, J. Phys. Chem. C, 2023, 127, 7560–7564 CrossRef CAS.
- T. Suzuki, A. De Nicola, S. Inoue, T. Okada, T. Hasegawa, G. Milano and H. Matsui, Chem. Commun., 2024, 60, 2192–2195 RSC.
- P. Gemünden, C. Poelking, K. Kremer, D. Andrienko and K. Ch. Daoulas, Macromolecules, 2013, 46, 5762–5774 CrossRef.
- D. M. Friday and N. E. Jackson, Macromolecules, 2022, 55, 1866–1877 CrossRef CAS.
- D. M. Friday and N. E. Jackson, Mol. Syst. Des. Eng., 2023, 8, 743–755 RSC.
- A. Khot and B. M. Savoie, Macromolecules, 2021, 54, 4889–4901 CrossRef CAS.
- A. Khot and B. M. Savoie, J. Polym. Sci., 2022, 60, 610–620 CrossRef CAS.
- K. F. Wong, M. S. Skaf, C.-Y. Yang, P. J. Rossky, B. Bagchi, D. Hu, J. Yu and P. F. Barbara, J. Phys. Chem. B, 2001, 105, 6103–6107 CrossRef CAS.
- E. Hennebicq, C. Deleener, J.-L. Brédas, G. D. Scholes and D. Beljonne, J. Chem. Phys., 2006, 125, 054901 CrossRef PubMed.
- H. Ma, T. Qin and A. Troisi, J. Chem. Theory Comput., 2014, 10, 1272–1282 CrossRef CAS PubMed.
- C. I. Wang, C. H. Hsu and C. C. Hua, Phys. Chem. Chem. Phys., 2017, 19, 20818–20828 RSC.
- C.-I. Wang and N. E. Jackson, Chem. Mater., 2023, 35, 1470–1486 CrossRef CAS.
- N. E. Jackson, A. S. Bowen, L. W. Antony, M. A. Webb, V. Vishwanath and J. J. de Pablo, Sci. Adv., 2019, 5, eaav1190 CrossRef CAS PubMed.
- N. E. Jackson, A. S. Bowen and J. J. de Pablo, Macromolecules, 2020, 53, 482–490 CrossRef CAS.
- L. Simine, T. C. Allen and P. J. Rossky, Proc. Natl. Acad. Sci. U.S.A., 2020, 117, 13945–13948 CrossRef CAS PubMed.
- R. Alessandri and J. J. de Pablo, Macromolecules, 2023, 56, 3574–3584 CrossRef CAS.
- J. C. Maier and N. E. Jackson, J. Chem. Phys., 2022, 157, 174102 CrossRef CAS PubMed.
- G. Sivaraman and N. E. Jackson, J. Chem. Theory Comput., 2022, 18, 1129–1141 CrossRef CAS PubMed.
- Z. Yu and N. E. Jackson, Machine learning quantum-chemical bond scission in thermosets under extreme deformation, Appl. Phys. Lett., 2023, 122, 211906 CrossRef CAS.
- Z. Yu and N. E. Jackson, Exploring thermoset fracture with a quantum chemically accurate model of bond scission, Macromolecules, 2024, 57, 1414–1425 CrossRef CAS.
- A. K. Soper, Chem. Phys., 1996, 202, 295–306 CrossRef CAS.
- D. Reith, M. Pütz and F. Müller-Plathe, J. Comput. Chem., 2003, 24, 1624–1636 CrossRef CAS PubMed.
- C.-I. Wang, J. C. Maier and N. E. Jackson, J. Chem. Theory Comput., 2023, 19, 4982–4990 CrossRef CAS PubMed.
- H. Wang, C. Junghans and K. Kremer, Eur. Phys. J. E, 2009, 28, 221–229 CrossRef PubMed.
- N. J. H. Dunn, T. T. Foley and W. G. Noid, Acc. Chem. Res., 2016, 49, 2832–2840 CrossRef CAS PubMed.
- N. J. H. Dunn and W. G. Noid, J. Chem. Phys., 2016, 144, 204124 CrossRef PubMed.
- D. Rosenberger and N. F. A. van der Vegt, Phys. Chem. Chem. Phys., 2018, 20, 6617–6628 RSC.
- J. Jin, A. Yu and G. A. Voth, J. Chem. Theory Comput., 2020, 16, 6823–6842 CrossRef CAS PubMed.
- T. C. Moore, C. R. Iacovella and C. McCabe, J. Chem. Phys., 2014, 140, 224104 CrossRef PubMed.
- V. Agrawal, P. Peralta, Y. Li and J. Oswald, J. Chem. Phys., 2016, 145, 104903 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- V. Rühle, C. Junghans, A. Lukyanov, K. Kremer and D. Andrienko, J. Chem. Theory Comput., 2009, 5, 3211–3223 CrossRef PubMed.
- S. Bevc, C. Junghans and M. Praprotnik, J. Comput. Chem., 2015, 36, 467–477 CrossRef CAS PubMed.
- N. Dunn, K. M. Lebold, M. R. DeLyser, J. F. Rudzinski and W. G. Noid, J. Phys. Chem. B, 2018, 122, 3363–3377 CrossRef CAS PubMed.
- C. Peter, L. Delle Site and K. Kremer, Soft Matter, 2008, 4, 859–869 RSC.
- K. R. Hadley and C. McCabe, J. Chem. Phys., 2010, 132, 134505 CrossRef CAS PubMed.
- A. Brasiello, S. Crescitelli and G. Milano, Phys. Chem. Chem. Phys., 2011, 13, 16618–16628 RSC.
- G. Megariotis, A. Vyrkou, A. Leygue and D. N. Theodorou, Ind. Eng. Chem. Res., 2011, 50, 546–556 CrossRef CAS.
- B. Mukherjee, L. Delle Site, K. Kremer and C. Peter, J. Phys. Chem. B, 2012, 116, 8474–8484 CrossRef CAS PubMed.
- G. Saielli, G. A. Voth and Y. Wang, Soft Matter, 2013, 9, 5716–5725 RSC.
- J. Zhang and H. Guo, J. Phys. Chem. B, 2014, 118, 4647–4660 CrossRef CAS PubMed.
- G. Saielli, A. Bagno and Y. Wang, J. Phys. Chem. B, 2015, 119, 3829–3836 CrossRef CAS PubMed.
- S.-P. Ju, S.-C. Huang, K.-H. Lin, H.-Y. Chen and T.-K. Shen, J. Phys. Chem. C, 2016, 120, 14277–14288 CrossRef CAS.
- J. Moon, B. Kim, J. Choi and M. Cho, Macromolecules, 2019, 52, 2033–2049 CrossRef CAS.
- T. D. Potter, M. Walker and M. R. Wilson, Soft Matter, 2020, 16, 9488–9498 RSC.
- M. Sakamoto and I. Hanasaki, Phys. Rev. E, 2021, 104, 024704 CrossRef CAS PubMed.
- M. R. Wilson and G. Yu, Crystals, 2023, 13, 502 CrossRef CAS.
- C. Yan, S. Barlow, Z. Wang, H. Yan, A. K.-Y. Jen, S. R. Marder and X. Zhan, Nat. Rev. Mater., 2018, 3, 18003 CrossRef CAS.
- H. Wang, J. Cao, J. Yu, Z. Zhang, R. Geng, L. Yang and W. Tang, J. Mater. Chem. A, 2019, 7, 4313–4333 RSC.
- R. Berardi, S. Orlandi and C. Zannoni, Chem. Phys. Lett., 1996, 261, 357–362 CrossRef CAS.
- K. C. Chan, Z. Li and W. Wenzel, J. Chem. Theory Comput., 2023, 19, 910–923 CrossRef CAS PubMed.
- M. Ricci, O. M. Roscioni, L. Querciagrossa and C. Zannoni, Phys. Chem. Chem. Phys., 2019, 21, 26195–26211 RSC.
- H. T. L. Nguyen and D. M. Huang, J. Chem. Phys., 2022, 156, 184118 CrossRef CAS PubMed.
- B. J. Boehm and D. M. Huang, Soft Matter, 2022, 18, 1843–1857 RSC.
- M. O. Wilson and D. M. Huang, J. Chem. Phys., 2023, 159, 024110 CrossRef CAS PubMed.
- W. Chen, Y. Zhu, F. Cui, L. Liu, Z. Sun, J. Chen and Y. Li, PLoS One, 2016, 11, e0151704 CrossRef PubMed.
- J. Jin, Y. Han and G. A. Voth, J. Chem. Phys., 2019, 150, 154103 CrossRef PubMed.
- O. M. Roscioni, M. Ricci, C. Zannoni and G. D'Avino, J. Phys. Chem. C, 2023, 127, 9225–9235 CrossRef CAS.
- S. T. John and G. Csányi, J. Phys. Chem. B, 2017, 121, 10934–10949 CrossRef CAS PubMed.
- J. Wang, N. Charron, B. Husic, S. Olsson, F. Noé and C. Clementi, J. Chem. Phys., 2021, 154, 164113 CrossRef CAS PubMed.
- L. E. Ratcliff, L. Grisanti, L. Genovese, T. Deutsch, T. Neumann, D. Danilov, W. Wenzel, D. Beljonne and J. Cornil, J. Chem. Theory Comput., 2015, 11, 2077–2086 CrossRef CAS PubMed.
- C.-I. Wang, M. K. E. Braza, G. C. Claudio, R. B. Nellas and C.-P. Hsu, J. Phys. Chem. A, 2019, 123, 7792–7802 CrossRef CAS PubMed.
- C.-I. Wang, I. Joanito, C.-F. Lan and C.-P. Hsu, J. Chem. Phys., 2020, 153, 214113 CrossRef CAS PubMed.
- M. Rinderle, W. Kaiser, A. Mattoni and A. Gagliardi, J. Phys. Chem. C, 2020, 124, 17733–17743 CrossRef CAS.
- T. Vehoff, B. Baumeier, A. Troisi and D. Andrienko, J. Am. Chem. Soc., 2010, 132, 11702–11708 CrossRef CAS PubMed.
- D. L. Cheung and A. Troisi, Phys. Chem. Chem. Phys., 2008, 10, 5941–5952 RSC.
- A. Troisi, D. L. Cheung and D. Andrienko, Phys. Rev. Lett., 2009, 102, 116602 CrossRef PubMed.
- E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman and J.-L. Brédas, J. Am. Chem. Soc., 2006, 128, 9882–9886 CrossRef CAS PubMed.
- S. Diele, S. Tosch, S. Mahnke and D. Demus, Cryst. Res. Technol., 1991, 26, 809–817 CrossRef CAS.
- T. Miyazawa, Y. Yamamura, M. Hishida, S. Nagatomo, M. Massalska-Arodź and K. Saito, J. Phys. Chem. B, 2013, 117, 8293–8299 CrossRef CAS PubMed.
- K. Saito, T. Miyazawa, A. Fujiwara, M. Hishida, H. Saitoh, M. Massalska-Arodź and Y. Yamamura, J. Chem. Phys., 2013, 139, 114902 CrossRef PubMed.
- S. Giannini, A. Carof, M. Ellis, H. Yang, O. G. Ziogos, S. Ghosh and J. Blumberger, Nat. Commun., 2019, 10, 1–12 CrossRef CAS PubMed.
- S. Giannini, O. G. Ziogos, A. Carof, M. Ellis and J. Blumberger, Adv. Theory Simul., 2020, 3, 2000093 CrossRef CAS.
- M. Ellis, H. Yang, S. Giannini, O. G. Ziogos and J. Blumberger, Adv. Mater., 2021, 33, 2104852 CrossRef CAS PubMed.
- S. Ciuchi, S. Fratini and D. Mayou, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 081202 CrossRef.
- S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2016, 26, 2292–2315 CrossRef CAS.
- S. Fratini, S. Ciuchi, D. Mayou, G. T. de Laissardière and A. Troisi, Nat. Mater., 2017, 16, 998–1002 CrossRef CAS PubMed.
- T. Nematiaram, S. Ciuchi, X. Xie, S. Fratini and A. Troisi, J. Phys. Chem. C, 2019, 123, 6989–6997 CrossRef CAS.
- A. J. Sneyd, D. Beljonne and A. Rao, J. Phys. Chem. Lett., 2022, 13, 6820–6830 CrossRef CAS PubMed.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef PubMed.
- V. Rühle, A. Lukyanov, F. May, M. Schrader, T. Vehoff, J. Kirkpatrick, B. Baumeier and D. Andrienko, J. Chem. Theory Comput., 2011, 7, 3335–3345 CrossRef PubMed.
- H. Oberhofer, K. Reuter and J. Blumberger, Chem. Rev., 2017, 117, 10319–10357 CrossRef CAS PubMed.
- H. Bässler, Phys. Status Solidi B, 1993, 175, 15–56 CrossRef.
- S. D. Baranovskii, Phys. Status Solidi B, 2014, 251, 487–525 CrossRef CAS.
- X. Chen, J. Guo, L. Peng, Q. Wang, S. Jiang and Y. Li, Mater. Today Electron., 2023, 6, 100077 CrossRef.
- M. Ravnik and S. Žumer, Liq. Cryst., 2009, 36, 1201–1214 CrossRef CAS.
- D. M. Sussman and D. A. Beller, Front. Phys., 2019, 7, 485161 Search PubMed.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 784–805 CrossRef CAS.
- W. Lechner and C. Dellago, J. Chem. Phys., 2008, 129, 114707 CrossRef PubMed.
- V. Ramasubramani, B. D. Dice, E. S. Harper, M. P. Spellings, J. A. Anderson and S. C. Glotzer, Comput. Phys. Commun., 2020, 254, 107275 CrossRef CAS.
- R. Pordes, D. Petravick, B. Kramer, D. Olson, M. Livny, A. Roy, P. Avery, K. Blackburn, T. Wenaus, F. Würthwein, I. Foster, R. Gardner, M. Wilde, A. Blatecky, J. McGee and R. Quick, J. Phys.: Conf. Ser., 2007, 012057 CrossRef.
- I. Sfiligoi, D. C. Bradley, B. Holzman, P. Mhashilkar, S. Padhi and F. Wurthwein, 2009 WRI World Congress on Computer Science and Information Engineering, 2009, pp. 428–432 Search PubMed.
- OSG, OSPool, 2006, https://osg-htc.org/services/open_science_pool.html Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc06749a |
| ‡ Both smectic phases exhibit a layered structure, but in the smectic A phase, the primary director and layer normal are parallel, whereas in the smectic E phase, there is a tilt angle between them, along with a unit pattern among the layer structure. A detailed structural characterization of various LC phases is provided in the subsequent section. |
| § The structure factor analysis in this study is based on the Fourier transform of particle density averaged across the three Cartesian coordinates. Due to the inherent anisotropic nature of both smectic phases, we evaluated the structure factor separately along each Cartesian axis and then normalized the results across all three axes. |
| This journal is © The Royal Society of Chemistry 2024 |

![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif)