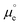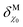Open Access Article
Open Access ArticleUnderstanding electrochemical interfaces through comparing experimental and computational charge density–potential curves
Nandita
Mohandas†
ab,
Sumit
Bawari†
a,
Jani J. T.
Shibuya
b,
Soumya
Ghosh
a,
Jagannath
Mondal
 a,
Tharangattu N.
Narayanan
a,
Tharangattu N.
Narayanan
 a and
Angel
Cuesta
a and
Angel
Cuesta
 *bc
*bc
aTata Institute of Fundamental Research-Hyderabad, Hyderabad 500046, India
bAdvanced Centre for Energy and Sustainability (ACES), School of Natural and Computing Sciences, University of Aberdeen, AB24 3UE Aberdeen, Scotland, UK. E-mail: angel.cuestaciscar@abdn.ac.uk
cCentre for Energy Transition, University of Aberdeen, AB24 3FX, Aberdeen, Scotland, UK
First published on 23rd April 2024
Abstract
Electrode–electrolyte interfaces play a decisive role in electrochemical charge accumulation and transfer processes. Theoretical modelling of these interfaces is critical to decipher the microscopic details of such phenomena. Different force field-based molecular dynamics protocols are compared here in a view to connect calculated and experimental charge density–potential relationships. Platinum–aqueous electrolyte interfaces are taken as a model. The potential of using experimental charge density–potential curves to transform cell voltage into electrode potential in force-field molecular dynamics simulations, and the need for that purpose of developing simulation protocols that can accurately calculate the double-layer capacitance, are discussed.
1. Introduction
In electrochemistry, interfacial potential differences drive chemical reactions involving the transfer of charge. These interfacial charge transfer processes are reasonably well understood at a qualitative level and often require an electrocatalyst, i.e., a material which, in addition to acting as a source or drain of electrons, can also act as a catalyst that lowers the apparent activation energy of the process by providing easy paths to the rupture and formation of bonds. Platinum group metals (PGM) are probably the most common components of such electrocatalysts, particularly regarding reactions relevant for energy conversion and storage.1In recent years, experimental techniques have been able to probe much deeper into these processes at smaller spatial resolution and timescales. In parallel, computational approaches have also been optimised with new methods that can simulate larger system sizes and longer timescales. For electrocatalysts, the intrinsic activity is defined by the positioning of d-orbitals, bonding efficacy, or specific binding sites. However, to understand an overall electrochemical reaction, all aspects of it, including charging, chemical interactions, and solvent dynamics need to be considered. Classical and ab initio molecular dynamics (MD) have the potential to simulate an entire reaction, and in this perspective, we aim to discuss the applicability of electrochemical force-field based MD approaches from an experimentalist's point of view.
In the absence of specific adsorption and at the Potential of Zero Free Charge (pzfc), the potential at the outer Helmholtz plane (OHP) is the same as in the bulk of the electrolyte, ϕOHP = ϕS, and there is no charge accumulation at the electrode–electrolyte interface.2 The potential of zero charge (pzc) is a fundamental property of the electrode–electrolyte interface, whose knowledge is a key requirement for a detailed understanding of double layer phenomena and related properties. Accumulation of charge at the interface is the expected outcome if the electrode potential differs from the pzc. To rationally model electrochemical systems we need a fair experimental estimation of the pzc and of the capacitance that controls the magnitude of charge accumulation at the electrodes at any given potential away from it.
Although methods to describe ions and solvent in classical MD are well developed, modelling of the electrode is still quite challenging. The interfacial potential difference, ΔϕMS, can be controlled by the externally applied potential on the electrode. Depending on the sign and amount of this difference, mere charge accumulation, specific adsorption, or charge transfer reactions can take place at the interface, but such phenomena cannot be accurately described with a single set of force field parameters in force field-based MD simulations. In this perspective, we aim to understand electrode potentials (Section 2), how charge is induced on an electrode (Section 3) and how potentials and the charging process can be modelled using classical MD (Section 4). In force field-based MD simulations, certain methods exist to induce an electrochemical potential on the electrode.3 In the simplest approximation, the Fixed Charge Method (FCM),4–8 a partial charge can be added to the surface atoms of the electrode. In Section 4, we discuss and compare this method and two other approximations, namely, the Constant Potential Method (CPM)9 and the Electro Chemical Dynamics with Implicit Degrees of freedom (EchemDID).10 In Section 5, we assess the agreement of these methods with experimental results and emphasise the relevance of using experimental values of pzc in combination with accurately computed capacitances for a correct translation of simulated applied voltage biases into simulated applied potentials.
2. Measuring potentials, the Galvani, Volta and surface potentials, work function, the potential of zero charge and absolute potentials
We cannot measure absolute potentials; we always measure potential differences between two electrodes. When one of the electrodes has a well-defined (though unknown and unknowable) potential that can be used as the zero in a potential scale (i.e., when it can work as a reference electrode), we usually ignore this fact, although we need to specify the reference potential scale used. Otherwise, we identify the potential difference as a voltage. In any case, measured potential differences (whether potentials in a scale or voltages) are nothing but the difference, in eV per electron, between the Fermi levels (EF's) of the measuring device's terminals. Taking the energy of an electron in vacuum at infinity as reference, −EF corresponds to the minimum energy needed to extract an electron from the corresponding material into the vacuum. It can be decomposed into a chemical contribution,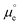 , corresponding to the standard chemical potential of electrons in that material, and an electrostatic contribution given by the material's inner or Galvani potential, −eϕ (where e is the elementary charge). In other words, the electrochemical potential of the electrons in a given material, defined as
, corresponding to the standard chemical potential of electrons in that material, and an electrostatic contribution given by the material's inner or Galvani potential, −eϕ (where e is the elementary charge). In other words, the electrochemical potential of the electrons in a given material, defined as 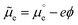 , and that material's EF are one and the same thing.11
, and that material's EF are one and the same thing.11
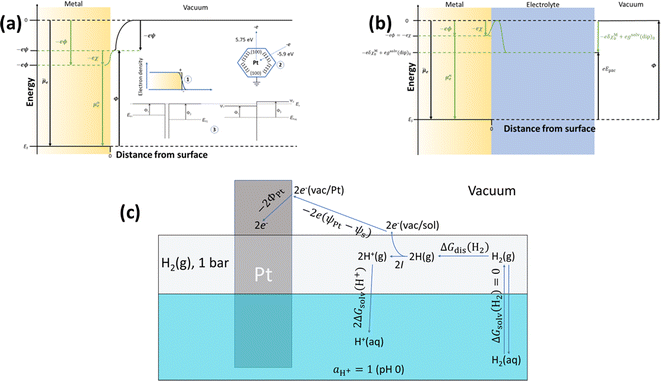
Although ϕ cannot be measured experimentally, it is worth decomposing it into different contributions by analysing the energies involved in transferring an electron from infinity in vacuum to the bulk of the material at the metal-ultra-high vacuum (UHV) interface (Fig. 1a) and comparing with the case of the metal–electrolyte interface (Fig. 1b). Because, in general, the metal surface in UHV may be charged (positively in the case of Fig. 1a), as the electron approaches the surface it will feel the potential created by the surface charge density. This is the Volta potential (ψ) and can be measured. The electronic density does not drop to zero at the metal UHV interface. Instead, electrons spill over the interface (inset 1 of Fig. 1a) resulting in a surface dipole and a surface potential, χ, which cannot be measured. Therefore, the electrostatic contribution to the energy of the electron in the metal, taking the energy of the electron at infinity in the vacuum as reference, is eϕ = eψ + eχ. Like χ, we insist that ϕ cannot be measured.
The energy needed to extract an electron from the bulk of the metal to a point in vacuum just outside the metal surface is the work function, Φ, which can be measured and differs from EF by eψ. This apparently trivial difference is very relevant, because it renders Φ a magnitude sensitive to the atomic structure of the metal surface.12 For example, the work function of Pt(111) is 5.9 eV, whereas that of Pt(100) is 5.75 eV. The absurdity of defining Φ as the energy needed to extract an electron from the bulk of the metal to a point at infinity in vacuum (i.e., of identifying Φ with EF), as sometimes found even in textbooks, is easily shown by a simple gedankenexperiment (inset 2 of Fig. 1a): extracting an electron from the bulk of, say, platinum, through a (100) facet and then letting that electron fall to the Fermi level through a (111) facet would result in the net release of 0.15 eV, which violates the First Law of thermodynamics. Defining Φ as the energy needed to extract an electron from the bulk of the metal to a point in vacuum just outside the metal surface also makes this magnitude insensitive to the state of charge of the metal surface, which is obviously not true for EF. This can be shown with another simple gedankenexperiment (inset 3 in Fig. 1a): two metal pieces exposing to the vacuum initially uncharged surfaces are put in contact, forcing electrons to flow from the higher to the lower EF, until both Fermi levels are aligned, and resulting in a net positive charge on the surface of the metal with the initially higher EF and a net negative charge on the surface of the metal with the initially lower EF. Φ1 and Φ2, however, remain unaltered, and the difference between them can be measured by simply measuring the difference between the Volta potentials of the two surfaces when in contact:
| Φ1 − Φ2 = e(ψ2 − ψ1) | (1) |
Differences or changes in Φ can therefore be measured very accurately, while absolute measurements of Φ typically carry a large error due to the loose definition of the reference energy. In Fig. 1b, a metal surface is in direct contact with an electrolyte layer which is in contact with a UHV at the pzc (please note that because at the pzc the charge density on the electrode surface is zero, ψ = 0). The energy necessary to extract an electron from the bulk of the metal to a point in vacuum just outside the surface of the electrolyte at the pzc is eEpzc, and differs from Φ by −δχM0 + gsolv(dip)0, i.e.,13–15
| eEpzc = Φ − δχM0 + gsolv(dip)0 | (2) |
The energy of an electron just outside the surface of the electrolyte provides a reference level for the definition of an absolute potential, for which a new gedankenexperiment, illustrated in Fig. 1c for the case of the standard hydrogen electrode (SHE), is needed. Thermodynamic cycles like that illustrated in Fig. 1c have recently been used in the development of several computational reference electrodes as well as the calculation of pzc's.18–22
Take a piece of Pt immersed in and in equilibrium with an aqueous solution of pH 0 in equilibrium with 1 bar H2. Because the system is in equilibrium, ΔG for
| 2H+(aq) + 2e−(Pt) ⇌ H2(g) | (3) |
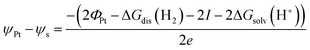 | (4) |
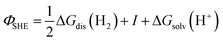 | (5) |
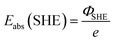 . Please note that, as demonstrated by Hansen and Kolb,17 the energy required to extract an electron from the Fermi level of Pt (or any other metal) to a point in vacuum just outside the surface of the electrolyte scales linearly with the applied potential.24 Only when reaction (3) is in equilibrium will this energy coincide with ΦSHE (for example, at the pzc, it will correspond to eEpzc, as shown above, with Epzc the potential of zero charge in the absolute scale).
. Please note that, as demonstrated by Hansen and Kolb,17 the energy required to extract an electron from the Fermi level of Pt (or any other metal) to a point in vacuum just outside the surface of the electrolyte scales linearly with the applied potential.24 Only when reaction (3) is in equilibrium will this energy coincide with ΦSHE (for example, at the pzc, it will correspond to eEpzc, as shown above, with Epzc the potential of zero charge in the absolute scale).
The accepted value of Eabs(SHE) is 4.5 ± 0.2 V. The large uncertainty is due to the error associated with the experimental determination of work functions and/or the computational calculation of the thermodynamic magnitudes included in the definition (see eqn (4) and (5)). It is also the reason why we keep using arbitrary reference potential scales like the SHE instead of the absolute potential scale. However, this definition of the absolute potential is crucial for the development of computational reference electrodes.
3. Experimental determination of the pzc and of the potential–charge relationship
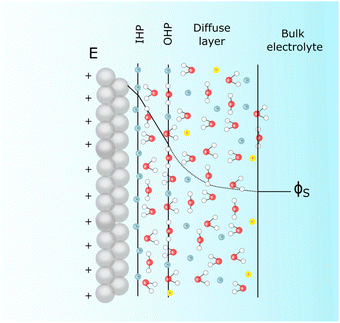
The effect of the electrostatic potential difference between the electrode surface and the bulk of the electrolyte on the solvent and ions constituting that electrolyte has been studied by Gouy,23 Chapman,24 Stern,25 and Grahame,26 resulting in increasingly complex models describing charge separation and distribution at the electrochemical interface. The difference (ΔϕMS) between the Galvani or inner potential of the electrode (ϕM), and the Galvani or inner potential of the electrolyte (ϕS), accounts for the electrostatic contribution to the Gibbs free energy of any interfacial charge transfer reaction. This potential difference (ΔϕMS = ϕM − ϕS) can be precisely changed by any desired amount and in either direction by externally controlling the difference between the electrochemical potential of electrons in our electrode (which is usually denoted as the working electrode, WE),![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) WEe, and the electrochemical potential of electrons in a reference electrode (RE),
WEe, and the electrochemical potential of electrons in a reference electrode (RE), ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) REe. The latter is pinned by an electrochemical equilibrium as determined by Nernst equation (e.g., in the SHE it is pinned by the H+/H2 equilibrium when pH is 0 and PH2 = 1 bar). Because this potential difference, ΔϕMS, happens across a very short distance, it generates a huge electric field that can, for example, polarise any chemical species present in this spatial region, including interfacial water molecules. Please note that
REe. The latter is pinned by an electrochemical equilibrium as determined by Nernst equation (e.g., in the SHE it is pinned by the H+/H2 equilibrium when pH is 0 and PH2 = 1 bar). Because this potential difference, ΔϕMS, happens across a very short distance, it generates a huge electric field that can, for example, polarise any chemical species present in this spatial region, including interfacial water molecules. Please note that 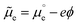 (where
(where 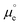 is the standard chemical potential of electrons in the material, e is the elementary charge and ϕ is the Galvani potential of the material) has both chemical
is the standard chemical potential of electrons in the material, e is the elementary charge and ϕ is the Galvani potential of the material) has both chemical 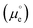 and electrostatic (ϕ) contributions and, therefore, the measured or applied potential difference between WE and RE does not in general correspond to the difference in electrostatic Galvani potentials between them, unless both electrodes are made of the same material, in which case
and electrostatic (ϕ) contributions and, therefore, the measured or applied potential difference between WE and RE does not in general correspond to the difference in electrostatic Galvani potentials between them, unless both electrodes are made of the same material, in which case 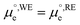 .
.
The interfacial capacitance (C), defined as the slope of a plot of the charge density on the electrode (σM) vs. the applied potential (ΔϕMS),
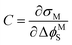 | (6) |
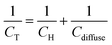 | (7) |
 | ||
| Fig. 2 Scheme depicting Stern's description of the electrochemical interface in the presence of specifically adsorbing anions for the particular case of a positively charged surface. | ||
If there is specific adsorption, accumulation of charge in the adsorption bond behaves as a third capacitor (Cad) in parallel to CH and Cdiffuse, and the CT is given by:
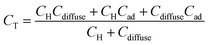 | (8) |
Even though various general phenomena are successfully described by these theories, the quantitative study of the effect of ion concentration and type requires the explicit atomistic description of the electrolyte.
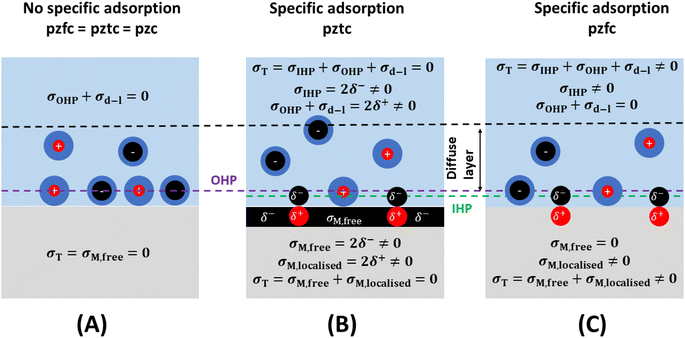
From the preceding paragraphs, it is evident that a good experimental estimation of the pzc and the interfacial capacitance is required, as they control the magnitude of charge accumulation at the interface, a clear understanding of which is essential for modelling electrochemical systems. At this point, the definition of two types of pzc results convenient (see Fig. 3):27,28
(1) The potential of zero free charge (pzfc), at which the free electronic excess charge density on the metal surface is zero.
(2) The potential of zero total charge (pztc), at which the sum of the free electronic charge density plus the charge density localised in polar adsorption bonds is zero. The pztc can also be defined as the potential at which no charge will flow in or out of the interface (i.e., no current would be measured) upon changing its area.28 In the absence of specific adsorption, pztc = pzfc.
It must be noted that, because the presence of an adlayer on the electrode surface will modify its surface potential, and therefore also its work function (see preceding section) the pzfc of an electrode surface in the absence of specific adsorption (Fig. 3A) will be different to the pzfc of the very same surface covered by specifically adsorbed species (even if those are neutral, e.g., the pzfc of Pt(111) is 0.26 ± 0.03 V vs. SHE, while the pzfc of CO-covered Pt(111) is 1.10 ± 0.04 V (ref. 29)). Specific adsorption can also lead to an electrode surface having two pzfc's. For example, Pt(111) has a pzfc around 0.26 V vs. SHE corresponding to the adsorbate-free metal surface,29 and a second pzfc around 0.84 V vs. RHE corresponding to the OH-covered Pt(111) surface.30 Obviously, as the charge density on Pt(111) must become increasingly positive when crossing over 0.26 V in the positive direction but then must return to zero at 0.84 V, at some point between these two potentials the positive free charge density on the surface of this electrode will reach a maximum after which it will start decreasing to then become zero at E = 0.84 V (in other words, there will be a negative capacitance contribution to the total interfacial capacitance of Pt(111) in this potential region30).
Possibly the most classical method of determining the pzfc of an electrode–electrolyte interface is that based on the determination of the Gouy–Chapman capacitance minimum. As the name of the method implies, the method is based on Gouy–Chapman's theory of double-layer structure and, consequently, can only be applied under conditions in which Gouy–Chapman's model applies, i.e., sufficiently low electrolyte concentration and absence of specific adsorption, under which the distinction between pzfc and pztc is unnecessary. Using this method, significant differences between the experimentally measured capacitance and that calculated using Gouy–Chapman's theory were revealed in the 1980's for metals other than Hg, specifically, for Ag(111).31–33 Similar differences have been found recently for Pt(111) and have reignited the interest in the topic.34–36
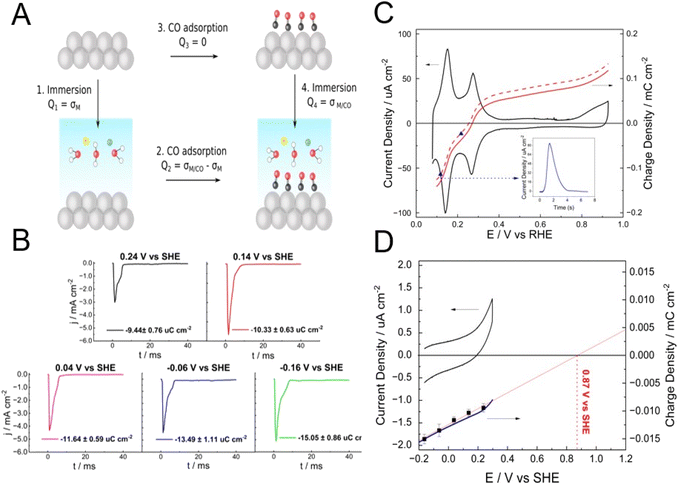
It is worth briefly discussing here two methods of determining the pztc, namely, the CO-charge displacement and the immersion methods, as both rely on the thermodynamic definition of the pztc as the potential at which no charge will flow in or out of the interface upon changing its area and can be considered as the two sides of the same coin (Fig. 4). The CO-charge displacement method, developed by the Alicante group,37,38 can be considered as the reverse of the immersion method, as it attempts to measure the charge flowing across the interface when the double layer is quenched (Arrow 2 in Fig. 4a), rather than when its formed (Arrow 1 in Fig. 4a). It does so by measuring the current transient resulting from the adsorption of CO on a metal electrode and works well with metals on which CO adsorbs strongly and forms a dense adlayer that completely separates the metal substrate from the electrolyte, like Pt37–40 and the Pt-group metals.41
If the charge density on the CO-covered metal surface is much smaller than that present on the CO-free surface, the former can be neglected (i.e., Q2 = σM/CO − σM ≈ −σM, see Fig. 4) and the charge obtained by integrating the current transient measured during the adsorption process corresponds to the total charge density on the metal surface at the potential at which the experiment is performed. The precision of the method can be improved by determining the charge density on the CO-covered metal (i.e., Q4 = σM/CO, Arrow 4 in Fig. 4a) and subsequently correcting Q2.29,42 Performing experiments at different potentials and/or integrating a current–potential curve using Q2 (if necessary, corrected by Q4) at a given potential as the integrating constant, allows to obtain a charge–potential curve, from which the pztc can be determined as the point at which the curve crosses through zero.
The immersion method involves measuring the current transient when immersing the electrode surface in the electrolyte at a constant applied potential (Arrows 1 and 4 in Fig. 4a). When immersing a pristine, clean metal surface, the potential at which integration of the immersion current transient returns zero charge density corresponds to the pztc of that metal surface, because upon immersion species that can adsorb specifically will do so until the equilibrium coverage corresponding to the applied potential is reached, and the charge corresponding to the adsorption up to that coverage will be included in the transient (as discussed above, in the absence of specific adsorption, that pztc will also be the pzfc).
As all metals but gold are too reactive to remain free of any adsorbate when exposed to an atmosphere containing oxygen and/or water vapour, Au is the only metal for which its pzfc can be detected by this method. For example, no charge density flows when immersing a UHV-prepared clean and well-ordered reconstructed Au(111) surface in 0.1 M HClO4 at 0.53 ± 0.04 V vs. SHE,43 which is therefore the pzfc (ClO4− does not adsorb specifically on Au, or does so very weakly) of reconstructed Au(111), in good agreement with values obtained from the Gouy–Chapman capacity minimum. However, when the same group tried to determine the pzfc of Pt(111) in the same solution by the same method, they did not obtain the correct value of 0.26 V vs. SHE.29 Instead, a zero charge transient was obtained at 0.78 V vs. SHE,43 corresponding to the pzfc of Pt(111) covered by a complete OH adlayer, which must have formed when the Pt(111) electrode was extracted from the UHV chamber and put in contact with the atmosphere in the electrochemical cell.30 The immersion method can be used to determine the charge density present at a specific potential (Q4 = σM/CO, in Fig. 4a) on a CO-covered Pt electrode. Using this strategy, one of us29 was able to determine that the charge density on a CO-covered Pt(111) electrode at 0.04 V vs. SHE is −16.6 μC cm−2 ± 0.9, which results in an error of 0.05 V in the determination of the pztc of Pt(111) in 0.1 HClO4 by the CO-charge displacement method if this charge density is not taken into account. Fig. 4b shows transients measured upon immersion of a CO-overed polycrystalline Pt electrode (Pt(poly)) in 0.1 M acetate buffer (pH 4.76). The charge density obtained by integrating any of these transients can be used to correct the charge density–potential curve of Pt(poly) in the same solution obtained using the CO-charge displacement method. Fig. 4c shows the characteristic CV of Pt(poly) in 0.1 M acetate buffer together with the corrected (red solid line) and uncorrected (dashed solid lines) charge density vs. potential curves, which result, respectively in corrected and uncorrected pztc's of 0.270 and 0.254 V vs. RHE.
Because any localised charge density associated to the formation of the CO adlayer is already present on the electrode surface before immersion, the charge that flows in the immersion transients necessarily has to be free charge. Therefore, extrapolation to zero charge density delivers the pzfc of the CO-covered electrode. Fig. 4d shows the CV (black line) of CO-covered Pt(poly) between −0.16 V and the onset of the oxidation of the CO adlayer. The black squares correspond to the charge density on the CO-covered electrode at −0.16, −0.06, 0.04, 0.14 and 0.24 V vs. SHE as obtained from the transients shown in Fig. 4b. The blue line is the charge-density vs. potential curve of CO-covered Pt(poly) obtained by integrating the CV using the charge from the immersion transient at −0.16 V as the integration constant. The excellent agreement between the interfacial capacitance obtained from a linear fit to the charge density as determined from the potentiostatic immersion transients with that obtained from integrating the CV is evidence of the internal consistency of our data. Extrapolation of the charge-density vs. potential curve to charge density zero delivers the pzfc of CO-covered Pt(poly), which is 0.87 V vs. SHE. This is, as expected, more negative than the pzfc of CO-covered Pt(111) (1.10 V vs. SHE29), because the polycrystalline surface will contain a multiplicity of sites with different local atomic structures, all of which will have a work function smaller (and therefore, a more negative pzfc) than CO-covered Pt(111). Although, at the pzfc, the charge summed over the whole surface will add up to zero, locally the surface will have negatively and positively charged sites. Even if there were a considerable fraction of (111) terraces on the Pt(poly) surface, the presence of sites with a different local atomic structure, including a variety of steps, kinks and border grains, must necessarily shift the overall pzfc negatively. The immersion method has also been used to determine the pzfc's of Au(111) electrodes modified by alkanethiol44 and mercaptoalkanoic acid SAMs.45 As demonstrated by all this work, preparation in UHV is thankfully not always a prerequisite for the immersion method.
Some electrochemical reactions have proven to also be good pztc probes. For example, the reduction of peroxodisulphate is strongly inhibited on Pt(111), Pt(100) and Pt(110) single-crystal electrodes except at potentials around the corresponding pztc.46 Much more interesting is the case of the reduction of N2O, which has been shown to be an excellent probe of the local pztc.47 N2O reduction has been used in combination with CO-charge displacement experiments to identify the pztc of step and terrace sites of stepped Pt single-crystal electrodes and improve our understanding of the effect of introducing steps on the global pztc.48,49
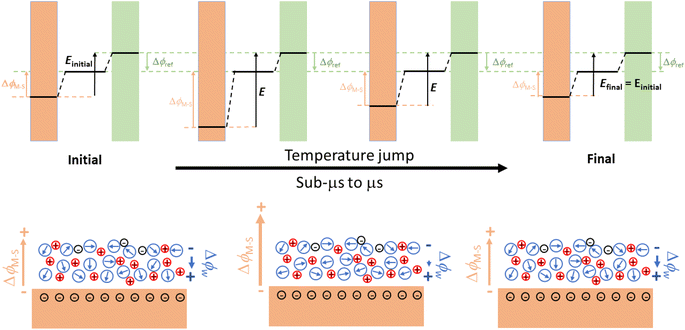
The determination of the pzfc by classical electrochemical methods is impossible when it falls within a potential region in which specific adsorption occurs and requires coupling with non-electrochemical methods. Probably the most successful of these is the measurement of coulostatic potential transients after a laser-induced temperature jump (T-jump) at the electrode electrolyte interface.50–53 The cartoon in Fig. 5 illustrates the interfacial processes generating the coulostatic potential transient measured upon inducing an interfacial T-jump with a short laser pulse in an aqueous electrolyte. At any applied potential, interfacial water dipoles will orient to shield the charge density accumulated at the electrode surface, resulting in a potential drop across the electrode–electrolyte interface smaller than what would exist for the same charge density in the absence of interfacial dipoles. The T-jump resulting from a short laser pulse inciding on the electrode surface randomises the orientation of the interfacial water dipoles, thereby decreasing the degree to which the charge density on the electrode surface can be screened by them. Because under coulostatic conditions charge cannot flow to keep the potential drop across the interface constant during the experiment (this is what would happen if the experiment were done potentiostatically instead, and would result in a current transient), the interfacial drop will change during the T-jump and will return to the initial value when the interface cools down back to the initial temperature. Because the potential drop across the reference electrode–electrolyte interface remains constant, this results in a potential transient. If the electrode surface is negatively charged, as in the example in Fig. 5, a negative potential transient will occur, while a positive potential transient will be measured for a positively charged electrode surface. There will however be a potential at which the orientation of the interfacial water dipoles is as random as can be, and at which therefore the T-jump will not result in a coulostatic potential transient. This will be the Potential of Maximum Entropy (pme). Because the orientation of the interfacial water dipoles must be determined by the free charge density on the electrode surface, the pme must be closely related to the pzfc. Actually, because in most metals interfacial water has a negative contribution to the interfacial potential drop at the pzfc,19 the pme is slightly negative of the pzfc.52
Very recently, Xu et al.54 have reported an optical method for the determination of the pzfc of metal electrodes based on measuring the phase shift of the electrode's second harmonic generation (SHG) signal, which must scale with the interfacial electric field. Therefore, by comparing the potential dependence of the phase of an electrode's SHG, ϕ1, with the phase of the SHG generated by the same, uncharged, surface (e.g., the SHG of same surface either in vacuum or exposed to an inert atmosphere, instead of immersed in an electrolyte), ϕ0, the pzfc can be identified as the potential at which ϕ1−ϕ0 = 0. Xu et al.54 tested their method with a polycrystalline Pt electrode and, although they find the expected independence of the pzfc on pH and a −0.36 V shift of the pzfc when Ni is deposited on Pt, the absolute value obtained for the pzfc of Pt(poly), 0.231 V vs. SHE ± 0.076 is essentially identical to that of Pt(111). As discussed above, due to the presence on the surface of Pt(poly) of sites with a local work function necessarily smaller than that of Pt(111), the pzfc of Pt(poly) should be expected to be lower than that of Pt(111) (see, e.g., the 0.23 V difference noted above between the pzfc of CO-covered Pt(poly), 0.87 V vs. SHE, and that of CO-covered Pt(111), 1.10 V vs. SHE). It must be noted, though, that even in perchloric acid solutions, only (111) terraces will be free of adsorbates in the so-called double-layer region of Pt(poly). For any other site with a different local atomic structure, hydrogen desorption is concomitant to OH adsorption.55 Because the presence of adsorbed OH will lead to a different, probably more positive, pzfc (see discussion above noting that the pzfc of OH-covered Pt(111) is 0.84 V vs. RHE in 0.1 M HClO4), an overall pzfc of Pt(poly) very similar to that of Pt(111) is still possible. In any case, the validity of Xu et al.'s54 method for the determination of the pzfc needs to be tested with model surfaces like Pt(111) and Au single-crystal electrodes, for which the pzfc's are well known and free of ambiguities.
4. Computational electrochemistry: modelling the electrode–electrolyte interface with classical force fields-based molecular dynamics
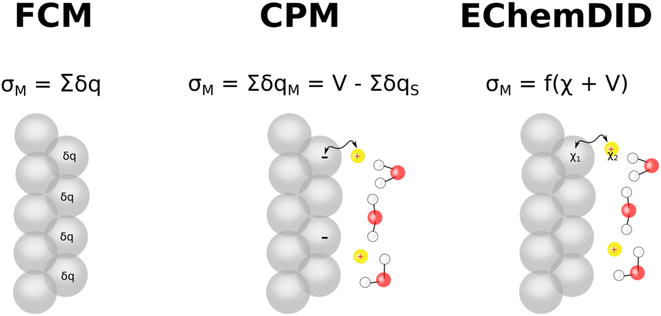
Force field-based Molecular Dynamics (MD) are versatile and powerful computational methods. Although the quantum mechanical ab initio alternative can provide a more detailed description of the electrode at the atomic level, we need to resort to force field-based MD simulations to study significantly larger spatial and temporal scales, at which the computational cost of ab initio MD becomes prohibitive.In force field-based MD simulations of electrochemical systems, modelling the electrode, including an appropriate way of describing the electrode's charge density and potential, is a particular challenge of critical importance.3 Here, we discuss three ways of including the voltage between the two electrodes enclosing the simulation cell in classical MD: (i) ElectroChemical Dynamics with Implicit Degrees of freedom (EchemDID), (ii) the fixed charge method (FCM), and (iii) the constant potential method (CPM) (Fig. 6). Even though other methods have been reported,56 we feel that these three are particularly important and more widely used among computational electrochemists. We then discuss the challenge of translating the cell voltage into individual electrode potentials and how comparison with experimental results like those discussed in the preceding sections can help in this task.
4.1 EChemDID
This method is applied particularly within the framework of reactive force-field (ReaxFF) type potentials, which are empirical.10,57–59 In ReaxFF, bond breaking/formation and partial charges (q) are described through the bond order, bonding and charge interactions.10 Two atom-dependent electronic parameters are then introduced, electronegativity (χ0) and hardness (H), to describe the electronic energy of the system, which is then combined with the coulombic interactions to yield the total energy of the system,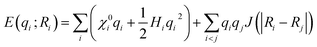 | (9) |
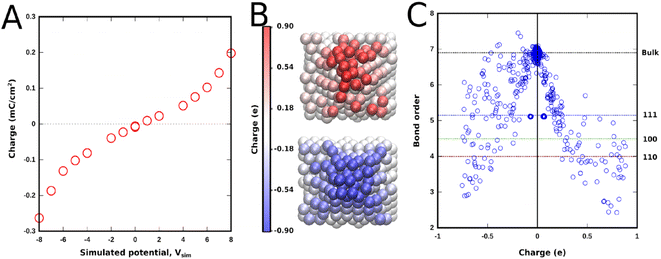
The method relies on the electronegativity parameter, χ, to induce an external voltage. Onofrio et al.60 introduced externally applied voltages using χ +1/2 V and χ −1/2 V for each one of the opposing slabs describing the two electrodes enclosing the simulation cell. This change in the electronegativity of the atoms in the slab changes the Fermi level of the metal electrode. This method was initially developed to elucidate the mechanism of potential-dependent contact formation/breaking in solid state electro-metallisation cells.61 Surface chemical interactions can be studied in this framework because ReaxFF also describes bonding interactions. This method can, in principle, capture both the capacitive and faradaic responses corresponding to the various surface reactions that can take place in an aqueous electrolytic solution. As an example, a system consisting of two polycrystalline platinum electrodes (modelled as protruding conical electrodes) in a weakly acidic pH (carbonic acid) in the electrochemical window between hydrogen and oxygen evolution is studied here. Using ReaxFF parameters for Pt/C/H/O, the EchemDID module is used to simulate an externally applied voltage Vsim between two platinum electrodes (Fig. 7),10 which results in charge accumulation on the surfaces of the electrodes.
A maximum simulated bias of 16 Vsim (between −8 and +8 V) is applied between the two electrodes, above which the interactions seen in simulations are deemed unrealistic. The charge accumulation across the surface of either one of the electrodes at positive and negative voltages is reported in Fig. 7a. An almost linear dependence of charge density on Vsim, that becomes exponential at high simulated voltage due to the contribution from surface reactions, is obtained. It is important to note that faradaic reactions, e.g., hydrogen- and oxygen evolution reactions, cannot be simulated in force-field based MD. Nevertheless, it is interesting to note that the trend of the charge density–voltage relationship in Fig. 7a is consistent with the charge density–potential curve in Fig. 4c, even though the voltage range in the simulations is highly unrealistic.62,63
Another aspect that can be studied in simulations is the plane dependent behaviour of different interactions. Protruding conical electrodes are used to simulate a rugged surface which is closer to a real polycrystalline platinum surface, where the effect of edges and different planes can be studied. These polycrystalline surfaces contain local regions which can be ascribed to different Pt crystallographic orientations.63Fig. 7c shows a clear dependence of accumulated charges on the bond order of the platinum atom in question. Atoms buried inside the electrode, which form the bulk phase, have no charge on them, showing that, as expected for a metal, only the surface gets charged. Polarised charge is bond-order dependent and increases with decreasing bond order. Thus based on the bond order of surface atoms of different planes the following trend for charge accumulation can be inferred: Pt(110) > Pt(100) > Pt(111). This behaviour is entirely dependent on the bond order and surface chemical interactions, and any correlation with the pzc of these surfaces cannot be inferred from these results. The edges that form between these phases accumulate even more charge, as they have lower coordination. A notable difference in the spread of charge is also seen between the positive (anode) and negative (cathode) electrodes, where negative charge is more delocalised than positive charge.
4.2 FCM
This is the most straight-forward way to incorporate charges computationally on the electrode surface. The method applies a partial charge to the surface atoms of an electrode and neglects charge fluctuations on the electrode induced by local density fluctuations in the electrolyte solution. From the electrostatics point of view, two oppositely charged electrodes induce an electric field between them, and hence FCM, in principle, may be considered as an equivalent to directly applying an electric field to the electrochemical system. Even though FCM is fairly uncomplicated and relies on a crude approximation, the method has been successfully adapted to various systems,4–8,64–69 where it is reported to give promising results in most of the cases.4.3 CPM
CPM was developed initially by Reed et al.70 to explicitly consider local charge fluctuations while maintaining the potential constant over the electrode surface.68 The method is based on earlier work by Siepmann and Sprik,71 in which the constraint of constant electrode potential was enforced on average using an extended Hamiltonian approach. This is similar to the Nosé method72 for constant temperature, with the main difference that in CPM the constraint is applied instantaneously at every step. The electric potential Ψl on each electrode atom is constrained at each simulation step to be equal to the applied bias, which is constant for a given electrode. This constraint leads to the following equation: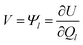 | (10) |
The interaction potential of an electrode/electrolyte system is given by:
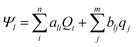 | (11) |
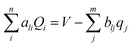 | (12) |
For each electrode atom a similar linear equation can be obtained, and solving these well-determined linear equation systems, the explicit charge for all the electrode atoms can be determined. In CPM simulations, equal and opposite potentials were assigned on the positive and negative electrodes, so that ΔΨ = Ψ+ − Ψ− = 2Ψ+ = 2Ψ−.
In the simulations discussed here, two water models with nonpolarizable (SPC/E73) and polarisable (SWM4-NDP74) force fields are considered. While the SPC/E model contains constant charges on atomic positions, the SWM4-NDP water model is represented as a rigid object imposing the experimental gas phase molecular geometry, with four interaction sites: the oxygen, carrying the molecular polarizability but no net charge, the two hydrogens, and an additional site located along the HOH bisector. An isotropic polarizability is introduced by adding an auxiliary mobile charged particle attached to the oxygen atom by a harmonic spring, generally referred to as a classical ‘Drude’ oscillator. Comparison between a polarizable and a non-polarizable water models is essential because the electronic polarization of water is highly sensitive to its environment and polarizability has shown essential to accommodate the local disruption of the hydrogen bond network created by anions or to reproduce the polarization effects of small multivalent cations on the first hydration shell.75–80 Studies have shown that polarization of water may play a crucial role for the specific water–water interactions near small nonpolar moieties.81–84
Charge vs. voltage curves can be obtained by simulating two Pt(111) surfaces with the CPM model, which is compared in Fig. 8 with results for the same system using EChemDID. In the CPM simulations the charge follows a linear response up to bias voltages of around 5 V, after which the charge appears to saturate. The maximum surface charge is found to be slightly higher for the polarisable SWM4-NDP water model. Nevertheless, the polarizability of the water model does not seem to have a huge impact on the charging of the electrode. The order of magnitude of charge density that we have calculated by employing the CPM, 10 μC cm−2, is comparable to the charge density that had been reported in previous studies employing the same method.85,86 Even though the SWM4-NDP water model, partially accounts for the polarizability of water and better estimates the viscosity (η) and hydration free energy (ΔG) within the range of experimental estimates, it is still unable to induce charging of the electrode any better than the non-polarizable SPC/E model. We find that the blj and qj terms in eqn (12), which describe the position and charge of species, respectively, in the electrolyte in the CPM, were not altered as expected due to the polarization of water. We speculate that the origin of this result lies in the rigid setup of SWM4-NDP water model as well as in the rigid setup of the electrode. For this reason, the polarizability of water does not have a significant impact on the charge induced on the electrode, i.e., on the Qi term in eqn (12).
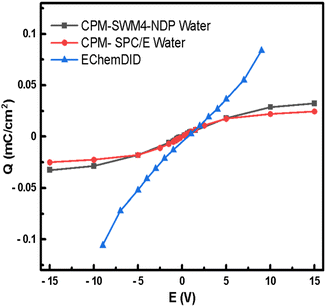 | ||
| Fig. 8 Charge–potential relationship curves using classical MD simulations on Pt(111) surface, with the CPM using SWM4-NDP water model and SPC/E water models; and EChemDID method with reactive water. | ||
In the case of EChemDID, the accumulated charge on the electrode also increases linearly with the applied bias but with an larger slope (i.e., a larger capacitance) which is likely due to the added contributions of surface reactions and water alignment in the vicinity of the electrode. This behaviour is similar to the experimental result, which contains capacitive and pseudo-capacitive contributions in and at both sides, respectively, of the double-layer region. In contrast to the CPM method, different charges were induced at positive and negative bias in EchemDID, because this model takes into account the intrinsic electronegativity difference of Pt–O and Pt–H interactions. In the FCM (fixed charge method) and CPM (constant potential method), the surface charge density increases with voltage through accumulation of non-specifically adsorbing ions in the double layer, which eventually reaches dielectric saturation as no other processes can be described. On the contrary, bond breaking is allowed in the EChemDID method, and surface bonds like Pt–O at the anode and Pt–H at the cathode allow for a further increase in charge density at higher cell voltages. This effect mirrors experimental charge increment due to surface reactions, which is why the charge density–potential profile is consistent with experiments, even though the underlying computational voltages are unrealistic.
FCM and CPM have been previously compared for modelling electric double layer capacitors (EDLC). Laird and co-workers9 reported that for an ionic liquid electrolyte system at a graphite electrode, at low voltage (≤2 V), the two methods yield essentially identical results, but at higher voltages (>4 V) significant differences appear. Another work by Merlet et al.87 examined the differences between the two methods by examining the relaxation kinetics and the electrolyte structure at the interface in EDLC with nanoporous carbide-derived carbon electrodes and planar graphite electrodes. They showed that CPM predicted more reasonable relaxation time than FCM, while the qualitative features in the electrolyte structure remained unchanged in both cases. Yet another work on the same line by Yang et al.,88 on a very similar system, also reported that both methods yielded essentially similar results for electric double layer (EDL) structures in the charged nanometre and sub-nanometre spaces, consistent with previous observations in bulk electrolytes. Their results also suggest that the dynamics of the formation of EDL, i.e., the evolution of ion concentration with time during the charging process, is more reliable in CPM. In a recent work by Tee and Searles,89 the theoretical framework of CPM-MD was extended to the case in which the total charge of each electrode is controlled, instead of their potential difference, with a typical ionic liquid–graphene supercapacitor. They too observed statistically identical plots of charge against bias voltage in both cases.
A recent review by Zeng et al.56 discussed various scenarios where different classical MD approaches are applicable in modelling electrochemical systems. They review applications of MD to supercapacitors, capacitive deionization, batteries, and electrical double layer transistors. We refer the reader interested in the rationality and possible applicability of the three different ways of including the voltage in classical MD to this review. Surface reactions are routinely studied with EChemDID method, and voltage provides another descriptor for simulating surface chemistry. Some of us62,63 have recently demonstrated, for the first time to the best of our knowledge, the possibility of modelling electrochemical interfaces using reactive force field-based EChemDID MD simulations.
5. Comparison of charge density–voltage curves computed using classical force fields-based MD with experiments
As mentioned in Section 4, all the force field-based MD methods discussed above allow inclusion of the electrode charge density in the simulation, but none of them allows to translate this into an electrode potential. The ability of experimental methods, as shown in Section 3, to determine very precise and accurate charge density vs. potential curves, however, offers the possibility to estimate the potential in force field-based MD, or at least to test the agreement of simulated interfacial capacitances with experimental values.Double layer capacitances obtained computationally and experimentally in this work and a few others from the literature are summarised in Table 1. The computed interfacial capacitances were calculated in all the cases as the slope of the charge density vs. voltage plot in the region where the dependence is linear, taking into account that the cell voltage is composed of two potentials identical in magnitude but opposed in sign at each of the electrodes (i.e., a cell voltage of 4 V corresponds to polarising the negative electrode −2 V below and the positive electrode +2 V above, the pzc). This is simply the capacitance as defined in eqn (6). We can clearly see that computational methods considerably underestimate the double layer capacitance. For example, the experimental double layer capacitance of Pt(111) in 0.1 M HClO4 is ∼65 μF cm−2 in the double layer region.90 In contrast, our simulations with Pt(111) and pure water delivered 4–5 μF cm−2 with CPM MD and ∼8 μF cm−2 when reactive force fields were used. Similarly, if we compare the experimental double-layer capacitance of polycrystalline Pt in acetate buffer (see Fig. 4c and corresponding discussion) with the computational result (see Fig. 7a), the latter is more than four times smaller than the former.
| Method | Electrode | Electrolyte | Capacitance/μF cm−2 | Reference |
|---|---|---|---|---|
| Computation-CPM | Pt(111) | SPC/E water | 4.705 | This work |
| Computation-CPM | Pt(111) | SWM4-NDP water | 4.475 | This work |
| Computation-EChemDID | Pt(111) | Reactive water | 8.584 | This work |
| Computation-EChemDID | Pt(poly) | Reactive water & acetic acid | 18.07 | This work |
| Experiment-CO charge displacement | Pt(poly) | 0.1 M acetic acid | 82.11 | This work |
| Experiment-CO charge displacement | Pt(111) | 0.1 M HClO4 | ∼65 | Ref. 90 |
Such a discrepancy between the experimental and computational double layer capacitance is majorly overlooked in most of the cases. In most of the simulation studies we can find unrealistically high potentials being used which do not make sense from the experimental point of view, without any clear justification or charge induced being discussed. Both computational and experimental electrochemists should have a clear understanding of this discrepancy and be very careful when using either computational results to explain experiments or experimental results to support computations. Rather than simply reporting applied voltages in the simulation results, the charge densities induced by those voltages also need to be discussed and compared with the experiments. This is extremely important because potentials in force field-based simulations are not referred to any reference electrode scale, but to the pzc of the electrode in question. In experimental conditions, the charge density on the electrode surface is zero only at the potential of zero charge (pzc), which is characteristic of each electrode and electrolyte combination. In both classical CPM and EChemDID simulations, the charge induced on the electrode is zero at a cell voltage of 0 V, a situation which has no equivalent in experiment. Furthermore, along with non-specific ion adsorption, interfacial charge-transfer processes associated to bond breaking and formation (i.e., specific adsorption) and reorientation of interfacial water are concomitant to charging the electrode surface. In CPM, none of the processes involved in specific adsorption are taken into consideration, thereby yielding the smallest double layer capacitance. In EChemDID method, bond breaking and formation is modelled, which leads to a better estimation of the double layer capacitance than CPM. However, charge transfer processes cannot be modelled, which leads to an underestimation of adsorption capacitance. This shows the limitations of the existing classical MD methods.
The problem of how to refer the computed electrode potentials to a reference electrode in MD simulations of electrode–electrolyte interfaces is non-trivial. There are several ways to solve this issue in the case of ab initio MD. The oldest of these methods implies, for aqueous electrolytes, explicitly modelling the water–vapour interface and the use of the vacuum potential as reference.91–94 The work function (i.e., the energy required to extract an electron from the metal to the water–vacuum interface, see Fig. 2b and the corresponding discussion), which corresponds to the electrode potential in the absolute scale, is converted to the SHE scale by subtracting the experimental value of the absolute SHE potential (see Fig. 2c and the corresponding discussion). A related approach, using surface dipole correction, has been employed to study systems under constant charge95 or constant potential conditions.96 An alternative is the computational reference electrode method developed by Cheng and Sprik for the SHE.20,21 This method avoids the explicit modelling of the water–vapour interface and does not require any experimental input. It uses the free energy of solvation of aqueous H+, calculated using thermodynamic integration over a set of ensembles sampled by DFT-MD,97,98 as reference. The method has been used to compute the pzfc's of metal electrodes and can be used for reference electrodes other than the SHE18 as well as for non-aqueous media.22 The simulated electrode surface can be charged by adding explicit ions in the electrolyte to the simulation cell,99 and has been successfully employed to study the double layer properties of metal–electrolyte interfaces.100–102 A similar internal reference has been employed in simulations with implicit solvent environment.103
Similar methods are unfortunately not available for including a computational reference electrode in classical force field-based MD. However, because at zero simulated applied voltage the charge density on both electrodes in the simulation cell is zero, the potential of both electrodes can be identified with the experimental pzc. The electrode potential corresponding to any other simulated applied bias can be identified then by comparing the simulated and experimental charge-density vs. potential curves, hence the critical relevance of accurately describing the capacitance of the electrode–electrolyte interface discussed above. This is needed because, while AIMD methods are now able to reliably simulate electrochemical surfaces, the allowed timescales and system sizes are still limited by the computational power required. Simulating double-layer dynamics in relevant time scales or non-planar geometries is only possible in classical force field-based MD.
6. Conclusions, outlook and perspective
Using the Pt-aqueous electrolyte system as a prototype, we compare in this perspective the charge density–potential relationships from three classical MD methods to experimental data. We stress the importance of understanding the charge–potential relationship obtained from simulations as well as experiments to get a better understanding of the proxy variable for potential used in the simulations. While each of the three classical MD methods analysed has its own merit, their limitations are equally important and should not be overlooked.FCM is the simplest and fastest method to induce an electrochemical potential on the electrode, with little difference in terms of static properties when compared to CPM. FCM also allows for direct comparison with experimental charge values, while polarisation effects like charge inhomogeneity at the electrode surface and dynamic properties are better modelled with CPM. EChemDID allows to incorporate surface reactions and can be useful to model charged states of polarisable ions and reaction processes.
We found a consistent mismatch between the computed and experimental capacitance with all the simulation methods analysed. This is a serious problem, as this is a proxy variable commonly used to define potentials in classical force field-based MD. The situation in which the simulated applied voltage and charge density are zero can still be identified with the experimental pzc. However, determination of the potential of both the positive and negative electrodes at non-zero simulated applied voltages and charge densities requires as accurate a simulation of the interfacial capacitance as possible. Although it is promising that the computational methods reproduce the almost constant experimental capacitance in the double-layer potential window, their performance still requires further improvement if they are to provide sensible insights into the structure and dynamics of real electrode–electrolyte interfaces.
MD simulations are a robust method for exploring EDLs at solid–liquid interfaces, even though accurately simulating electrode polarization is a notable hurdle. Looking ahead, though the CPM is a promising strategy for capturing EDL behaviours precisely, further improvement is essential to provide valuable insights for optimizing electrochemical devices. Another critical aspect is integrating chemical reactions into MD simulations, by employing reactive force fields (ReaxFF) within CPM-MD framework. With the greater timescales and system complexities available to classical MD, the effects of electrolytes, electrode geometry, etc. can be studied and these mechanistic insights can complement experiments. Despite significant advancements, it is important to be cautious to prevent erroneous results, by giving meticulous attention to system design, method selection, parameter accuracy, and data collection. Through these measures, even within its limitations, classical MD simulations can still offer valuable insights about EDL and electrochemical processes.
7. Methods
7.1 Experiments
The immersion and CO charge-displacement experiments were conducted using a polycrystalline Pt bead which was cut and polished with alumina paste of 1.0, 0.3, and 0.05 μm particle size in succession. Contact with the electrolyte was made through a hanging meniscus so that only the polished flat surface of known area is covered by the solution.For the CO charge-displacement experiments, the crystal was first annealed in an open propane flame then quickly placed in a clean flask containing CO-saturated ultra-pure water. The crystal was allowed to cool down for at least 10 seconds in the closed atmosphere of the flask, lowered into the water, then raised to form a drop on the surface to protect it during transfer to the electrochemical cell, which contained 0.1 M acetate buffer (0.1 M CH3COOH + 0.1 M Na(CH3COO)) deaerated with Ar (N5.0, supplied by BOC). Once transferred to the electrochemical cell, the CO-covered surface was immersed in the electrolyte at 0.1 V vs. RHE and Ar was bubbled for some minutes to remove excess CO present in the protecting drop before starting a cyclic voltammogram. Then, a CO-stripping voltammogram was done to oxidise the CO-adlayer and expose a clean polycrystalline Pt surface. The CO charge-displacement experiment was then performed by applying the desired potential and blowing CO through a Pasteur pipette into the meniscus, thus allowing rapid transport of CO to the electrode–electrolyte interface. The resulting current transient was recorded and the experiment was repeated at least four times per set potential. The data used, including those presented in Fig. 4c, are the average of these four measurements.
In the immersion experiments, after annealing the polycrystalline Pt bead was introduced directly in the electrochemical cell containing a CO atmosphere and a CO-saturated electrolyte solution. The electrode surface was then positioned directly over the tip of the Luggin capillary, which points upwards, and the desired potential was applied. A KCl-saturated Ag/AgCl reference electrode with a glass joint fitting created an overpressure in the Luggin capillary when inserted into the air-tight joint that closes the compartment where the reference electrode is hosted. By slowly opening the Teflon or glass key separating that compartment form the capillary tip, a jet of solution was shot up directly to the crystal surface, allowing to form a hanging meniscus and to wet the electrode surface without wetting the walls of the bead. The current transient resulting from forming the electrode–electrolyte interface was recorded and integrated to obtain the charge density on the CO-covered polycrystalline Pt electrode at that potential. As with the CO charge-displacement experiments, each transient was repeated at least four times per set potential. The charge densities presented in Fig. 4b and used in Fig. 4d, are the average of these four measurements. The experimental errors and error bars, respectively, presented in those figures, are the corresponding standard deviations.
Solutions were prepared using ultra-pure water (18.2 MΩ cm, 1–3 ppb TOC, from an ELGA-VEOLIA PURELAB Chorus 1 Life Science water purification system), Acetic acid (glacial) 100% Suprapur (Merck) and Sodium acetate (anhydrous 99.99%) Suprapur (Merck).
7.2 MD simulation
All the MD simulations employing FCM and CPM were performed using the LAMMPS104 2020 code. For EChemDID simulations LAMMPS105 2015 code was used. The MD system consists of water enclosed between two oppositely charged Pt electrodes. Each electrode is modelled as three layers of Pt (111) sheets with an area of 9.8582 nm2, with the distance between the innermost layers of the two electrodes 75.4 Å. Simulations were performed in the NVT ensemble with the electrolyte temperature maintained at 300 K using the Nose–Hoover106 thermostat. A cut-off length of 1.2 nm was used in the calculation of electrostatic interactions in the real space. The electrostatic potential is treated using the particle–particle particle-mesh approach. The Pt sheets were treated with fix command, so as to make them immobile. To reach equilibrium, the NVT simulation was first run for 200 ps and then a 20 ns production run was performed. For modelling water SPC/E73 parameters were used in the non-polarizable case. The polarizable SWM4-NDP74 model was constructed as an explicit 4-point model, with the Drude oscillator added by the Python tool polarizer.py.104 A rectangular simulation box of dimension 34 × 30 × 80 Å3 used in all the simulations, was periodically replicated in the x and y-directions while a fixed boundary condition was employed for the z-direction containing the platinum electrodes. The constant potential method implemented in the LAMMPS code by Wang et al.9 was used. For the EChemDID simulations, LAMMPS 2015 code was used as it is compatible with the USER-EChemDID package.60,61 A similar system as described above (Pt(111) with water) and a system consisting of two conical electrodes with 3–4 passive Pt layers were simulated with a solvent containing water and carbonic acid (as HCO3− and H3O+) to simulate a pH ∼5. Up to 320 ps were run at a particular applied potential, in an NVT ensemble where a temperature of 300 K is maintained using the Berendsen107 thermostat.Data availability
The experimental and computational datasets generated for this article are available from the authors on reasonable request.Author contributions
NM: conceptualization, investigation, methodology, MD simulations, writing – original draft. SB: conceptualization, investigation, methodology, MD simulations, writing – original draft. JJTS: electrochemical experiments and corresponding analysis – CO-charge displacement and immersion transients. SG: supervision, writing – editing. JM: conceived the idea, conceptualization, resources, supervision. TNN: conceived the idea, conceptualization, funding acquisition, resources, supervision, writing – original draft. AC: conceptualization methodology, resources, supervision, writing – review and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
N. M., S. B., S. G., J. M. and T. N. N. acknowledge the support of the Department of Atomic Energy, Government of India, under Project Identification No. RTI 4007. J. J. T. S. and A. C. thank the University of Aberdeen for continued support.References
- A. Raveendran, M. Chandran and R. Dhanusuraman, A comprehensive review on the electrochemical parameters and recent material development of electrochemical water splitting electrocatalysts, RSC Adv., 2023, 13, 3843–3876 RSC.
- S. Trasatti and E. Lust, in Modern Aspects of Electrochemistry, ed. R. E. White, J. O. Bockris and B. E. Conway, Springer US, Boston, MA, 1999, pp. 1–215 Search PubMed.
- L. Scalfi, M. Salanne and B. Rotenberg, Molecular Simulation of Electrode-Solution Interfaces, Annu. Rev. Phys. Chem., 2021, 72, 189–212 CrossRef CAS PubMed.
- L. Yang, B. H. Fishbine, A. Migliori and L. R. Pratt, Molecular simulation of electric double-layer capacitors based on carbon nanotube forests, J. Am. Chem. Soc., 2009, 131, 12373–12376 CrossRef CAS PubMed.
- G. Feng and P. T. Cummings, Supercapacitor capacitance exhibits oscillatory behavior as a function of nanopore size, J. Phys. Chem. Lett., 2011, 2, 2859–2864 CrossRef CAS.
- G. Feng, S. Li, J. S. Atchison, V. Presser and P. T. Cummings, Molecular insights into carbon nanotube supercapacitors: capacitance independent of voltage and temperature, J. Phys. Chem. C, 2013, 117, 9178–9186 CrossRef CAS.
- L. Yang, B. H. Fishbine, A. Migliori and L. R. Pratt, Dielectric saturation of liquid propylene carbonate in electrical energy storage applications, J. Chem. Phys., 2010, 132, 044701 CrossRef PubMed.
- Y. Shim, H. J. Kim and Y. Jung, Graphene-based supercapacitors in the parallel-plate electrode configuration: Ionic liquids versus organic electrolytes, Faraday Discuss., 2012, 154, 249–263 RSC.
- Z. Wang, Y. Yang, D. L. Olmsted, M. Asta and B. B. Laird, Evaluation of the constant potential method in simulating electric double-layer capacitors, J. Chem. Phys., 2014, 141, 184102 CrossRef PubMed.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, ReaxFF: A Reactive Force Field for Hydrocarbons, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- S. W. Boettcher, S. Z. Oener, M. C. Lonergan, Y. Surendranath, S. Ardo, C. Brozek and P. A. Kempler, Potentially Confusing: Potentials in Electrochemistry, ACS Energy Lett., 2021, 6, 261–266 CrossRef CAS.
- A. Kahn, Fermi level, work function and vacuum level, Mater. Horiz., 2016, 3, 7–10 RSC.
- S. Trasatti, Work function, electronegativity, and electrochemical behaviour of metals, J. Electroanal. Chem., 1971, 33, 351–378 CrossRef CAS.
- S. Trasatti, in Advances in Electrochemistry and Electrochemical Engineering, ed. H. Gerischer and C. W. Tobias, Wiley, New York, 1977, vol. 10, p. 213 Search PubMed.
- S. Trasatti, in Comprehensive Treatise of Electrochemistry, ed. J. O. Bockris, B. E. Conway and E. Yeager, Springer, Boston, 1980, pp. 45–81 Search PubMed.
- A. N. Frumkin, Sven. Kem. Tidskr., 1965, 77, 300 CAS.
- W. N. Hansen and D. M. Kolb, The work function of emersed electrodes, J. Electroanal. Chem., 1979, 100, 493–500 CrossRef CAS.
- X.-H. Yang, A. Cuesta and J. Cheng, Computational Ag/AgCl Reference Electrode from Density Functional Theory-Based Molecular Dynamics, J. Phys. Chem. B, 2019, 123, 10224–10232 CrossRef CAS PubMed.
- J. Le, M. Iannuzzi, A. Cuesta and J. Cheng, Determining Potentials of Zero Charge of Metal Electrodes versus the Standard Hydrogen Electrode from Density-Functional-Theory-Based Molecular Dynamics, Phys. Rev. Lett., 2017, 119, 016801 CrossRef PubMed.
- J. Cheng and M. Sprik, Aligning electronic energy levels at the TiO2/H2O interface, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081406 CrossRef.
- J. Cheng and M. Sprik, Alignment of electronic energy levels at electrochemical interfaces, Phys. Chem. Chem. Phys., 2012, 14, 11245–11267 RSC.
- X.-H. Yang, M. Papasizza, A. Cuesta and J. Cheng, Water-In-Salt Environment Reduces the Overpotential for Reduction of CO2 to CO2– in Ionic Liquid/Water Mixtures, ACS Catal., 2022, 12, 6770–6780 CrossRef CAS.
- M. Gouy, Sur la constitution de la charge électrique à la surface d’un électrolyte, J. Phys. Theor. Appl., 1910, 9, 457–468 CrossRef.
- D. L. Chapman, LI. A contribution to the theory of electrocapillarity, London, Edinburgh Dublin Philos. Mag. J. Sci., 1913, 25, 475–481 CrossRef.
- O. Stern, Zur Theorie Der Elektrolytischen Doppelschicht, Z. Elektrochem. Angew. Phys. Chem., 1924, 30, 508–516 CrossRef CAS.
- D. C. Grahame, The Electrical Double Layer and the Theory of Electrocapillarity, Chem. Rev., 1947, 41, 441–501 CrossRef CAS PubMed.
- A. N. Frumkin and O. A. Petrii, Potentials of zero total and zero free charge of platinum group metals, Electrochim. Acta, 1975, 20, 347–359 CrossRef CAS.
- A. N. Frumkin, O. A. Petrii and B. B. Damaskin, in Comprehensive Treatise of Electrochemistry, ed. J. O'M. Bockris, B. E. Conway, and E. Yeager, Plenum Press, New York, 1980, vol. 1, p. 221 Search PubMed.
- A. Cuesta, Measurement of the surface charge density of CO-saturated Pt(111) electrodes as a function of potential: The potential of zero charge of Pt(111), Surf. Sci., 2004, 572, 11–22 CrossRef CAS.
- J. Huang, A. Malek, J. Zhang and M. H. Eikerling, Non-monotonic Surface Charging Behavior of Platinum: A Paradigm Change, J. Phys. Chem. C, 2016, 120, 13587–13595 CrossRef CAS.
- W. Schmickler, The Effect of Weak Adsorption on the Double Layer Capacitance, ChemElectroChem, 2021, 8, 4218–4222 CrossRef CAS.
- G. Valette, Double layer on silver single crystal electrodes in contact with electrolytes having anions which are slightly specifically adsorbed, J. Electroanal. Chem., 1989, 269, 191–203 CrossRef CAS.
- W. Schmickler, D. Henderson and H. D. Hurwitz, Ionic Adsorption at Low Concentrations, Z. Phys. Chem., 1988, 160, 191–198 CrossRef CAS PubMed.
- K. Ojha, K. Doblhoff-Dier and M. T. M. Koper, Double-layer structure of the Pt(111)–aqueous electrolyte interface, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(3), e2116016119 CrossRef CAS PubMed.
- K. Ojha, N. Arulmozhi, D. Aranzales and M. T. M. Koper, Double Layer at the Pt(111)–Aqueous Electrolyte Interface: Potential of Zero Charge and Anomalous Gouy–Chapman Screening, Angew. Chem., Int. Ed., 2020, 132, 721–725 CrossRef.
- V. Briega-Martos, F. J. Sarabia, V. Climent, E. Herrero and J. M. Feliu, Cation Effects on Interfacial Water Structure and Hydrogen Peroxide Reduction on Pt(111), ACS Meas. Sci. Au, 2021, 1, 48–55 CrossRef CAS PubMed.
- J. Clavilier, R. Albalat, R. Gómez, J. M. Orts and J. M. Feliu, Displacement of adsorbed iodine on platinum single-crystal electrodes by irreversible adsorption of CO at controlled potential, J. Electroanal. Chem., 1993, 360, 325–335 CrossRef CAS.
- J. M. Orts, R. Gómez, J. M. Feliu, A. Aldaz and J. Clavilier, Potentiostatic charge displacement by exchanging adsorbed species on Pt(111) electrodes—acidic electrolytes with specific anion adsorption, Electrochim. Acta, 1994, 39, 1519–1524 CrossRef CAS.
- J. M. Feliu, J. M. Orts, R. Gómez, A. Aldaz and J. Clavilier, New information on the unusual adsorption states of Pt(111) in sulphuric acid solutions from potentiostatic adsorbate replacement by CO, J. Electroanal. Chem., 1994, 372, 265–268 CrossRef CAS.
- V. Climent, R. Gómez, J. M. Orts, A. Rodes, A. Aldaz and J. M. Feliu, in Interfacial Electrochemistry, ed. A. Wieckowski, Marcel Dekker, New York, 1999, p. 463 Search PubMed.
- R. Gómez, J. M. Feliu, A. Aldaz and M. J. Weaver, Validity of double-layer charge-corrected voltammetry for assaying carbon monoxide coverages on ordered transition metals: comparisons with adlayer structures in electrochemical and ultrahigh vacuum environments, Surf. Sci., 1998, 410, 48–61 CrossRef.
- M. J. Weaver, Potentials of zero charge for platinum (111)−aqueous interfaces: a combined assessment from in-situ and ultrahigh-vacuum measurements, Langmuir, 1998, 14, 3932–3936 CrossRef CAS.
- U. W. Hamm, D. Kramer, R. S. Zhai and D. M. Kolb, The pzc of Au(111) and Pt(111) in a perchloric acid solution: an ex situ approach to the immersion technique, J. Electroanal. Chem., 1996, 414, 85–89 CrossRef.
- P. Ramírez, R. Andreu, Á. Cuesta, C. J. Calzado and J. J. Calvente, Determination of the Potential of Zero Charge of Au(111) Modified with Thiol Monolayers, Anal. Chem., 2007, 79, 6473–6479 CrossRef PubMed.
- P. Ramírez, A. Granero, R. Andreu, A. Cuesta, W. H. Mulder and J. J. Calvente, Potential of zero charge as a sensitive probe for the titration of ionizable self-assembled monolayers, Electrochem. Commun., 2008, 10, 1548–1550 CrossRef.
- V. Climent, M. D. Maciá, E. Herrero, J. M. Feliu and O. A. Petrii, Peroxodisulphate reduction as a novel probe for the study of platinum single crystal/solution interphases, J. Electroanal. Chem., 2008, 612, 269–276 CrossRef CAS.
- G. A. Attard and A. Ahmadi, Anion—surface interactions Part 3. N2O reduction as a chemical probe of the local potential of zero total charge, J. Electroanal. Chem., 1995, 389, 175–190 CrossRef.
- G. A. Attard, O. Hazzazi, P. B. Wells, V. Climent, E. Herrero and J. M. Feliu, On the global and local values of the potential of zero total charge at well-defined platinum surfaces: stepped and adatom modified surfaces, J. Electroanal. Chem., 2004, 568, 329–342 CrossRef CAS.
- V. Climent, G. A. Attard and J. M. Feliu, Potential of zero charge of platinum stepped surfaces: a combined approach of CO charge displacement and N2O reduction, J. Electroanal. Chem., 2002, 532, 67–74 CrossRef CAS.
- V. Climent, B. A. Coles, R. G. Compton and J. M. Feliu, Coulostatic potential transients induced by laser heating of platinum stepped electrodes: influence of steps on the entropy of double layer formation, J. Electroanal. Chem., 2004, 561, 157–165 CrossRef CAS.
- V. Climent, B. A. Coles and R. G. Compton, Coulostatic Potential Transients Induced by Laser Heating of a Pt(111) Single-Crystal Electrode in Aqueous Acid Solutions. Rate of Hydrogen Adsorption and Potential of Maximum Entropy, J. Phys. Chem. B, 2002, 106, 5988–5996 CrossRef CAS.
- V. Climent, B. A. Coles and R. G. Compton, Laser-Induced Potential Transients on a Au(111) Single-Crystal Electrode. Determination of the Potential of Maximum Entropy of Double-Layer Formation, J. Phys. Chem. B, 2002, 106, 5258–5265 CrossRef CAS.
- V. Climent, B. A. Coles and R. G. Compton, Laser Induced Current Transients Applied to a Au(111) Single Crystal Electrode. A General Method for the Measurement of Potentials of Zero Charge of Solid Electrodes, J. Phys. Chem. B, 2001, 105, 10669–10673 CrossRef CAS.
- P. Xu, A. D. von Rueden, R. Schimmenti, M. Mavrikakis and J. Suntivich, Optical method for quantifying the potential of zero charge at the platinum–water electrochemical interface, Nat. Mater., 2023, 22, 503–510 CrossRef CAS PubMed.
- M. J. T. C. van der Niet, N. Garcia-Araez, J. Hernández, J. M. Feliu and M. T. M. Koper, Water dissociation on well-defined platinum surfaces: The electrochemical perspective, Catal. Today, 2013, 202, 105–113 CrossRef CAS.
- L. Zeng, J. Peng, J. Zhang, X. Tan, X. Ji, S. Li and G. Feng, Molecular dynamics simulations of electrochemical interfaces, J. Chem. Phys., 2023, 159, 9 Search PubMed.
- Y. K. Shin, L. Gai, S. Raman and A. C. T. van Duin, Development of a ReaxFF Reactive Force Field for the Pt–Ni Alloy Catalyst, J. Phys. Chem. A, 2016, 120, 8044–8055 CrossRef CAS PubMed.
- M. L. Urquiza, M. M. Islam, A. C. T. van Duin, X. Cartoixà and A. Strachan, Atomistic Insights on the Full Operation Cycle of a HfO2-Based Resistive Random Access Memory Cell from Molecular Dynamics, ACS Nano, 2021, 15, 12945–12954 CrossRef CAS PubMed.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, The ReaxFF reactive force-field: development, applications and future directions, npj Comput. Mater., 2016, 2, 15011 CrossRef CAS.
- N. Onofrio and A. Strachan, Voltage equilibration for reactive atomistic simulations of electrochemical processes, J. Chem. Phys., 2015, 143, 054109 CrossRef PubMed.
- N. Onofrio, D. Guzman and A. Strachan, Atomic origin of ultrafast resistance switching in nanoscale electrometallization cells, Nat. Mater., 2015, 14, 440–446 CrossRef CAS PubMed.
- S. Bawari, A. Guha, T. N. Narayanan and J. Mondal, Understanding water structure and hydrogen association on platinum–electrolyte interface, Oxford Open Mater. Sci., 2022, 2(1), itac014 CrossRef.
- S. Bawari, T. N. Narayanan and J. Mondal, Insights into the reaction pathways of platinum dissolution and oxidation during electrochemical processes, Electrochem. Commun., 2023, 147, 107440 CrossRef CAS.
- K. Xu, X. Ji, B. Zhang, C. Chen, Y. Ruan, L. Miao and J. Jiang, Charging/Discharging Dynamics in Two-Dimensional Titanium Carbide (MXene) Slit Nanopore: Insights from molecular dynamic study, Electrochim. Acta, 2016, 196, 75–83 CrossRef CAS.
- K. Xu, Z. Lin, C. Merlet, P. Taberna, L. Miao, J. Jiang and P. Simon, Tracking Ionic Rearrangements and Interpreting Dynamic Volumetric Changes in Two-Dimensional Metal Carbide Supercapacitors: A Molecular Dynamics Simulation Study, ChemSusChem, 2018, 11, 1892–1899 CrossRef CAS PubMed.
- K. Xu, C. Merlet, Z. Lin, H. Shao, P.-L. Taberna, L. Miao, J. Jiang, J. Zhu and P. Simon, Effects of functional groups and anion size on the charging mechanisms in layered electrode materials, Energy Storage Mater., 2020, 33, 460–469 CrossRef.
- X. Jiang, J. Huang, H. Zhao, B. G. Sumpter and R. Qiao, Dynamics of electrical double layer formation in room-temperature ionic liquids under constant-current charging conditions, J. Phys.: Condens. Matter, 2014, 26, 284109 CrossRef PubMed.
- L. Zeng, T. Wu, T. Ye, T. Mo, R. Qiao and G. Feng, Modeling galvanostatic charge–discharge of nanoporous supercapacitors, Nat. Comput. Sci., 2021, 1, 725–731 CrossRef PubMed.
- G. Feng, D. Jiang and P. T. Cummings, Curvature Effect on the Capacitance of Electric Double Layers at Ionic Liquid/Onion-Like Carbon Interfaces, J. Chem. Theory Comput., 2012, 8, 1058–1063 CrossRef CAS PubMed.
- S. K. Reed, O. J. Lanning and P. A. Madden, Electrochemical interface between an ionic liquid and a model metallic electrode, J. Chem. Phys., 2007, 8, 126 Search PubMed.
- J. I. Siepmann and M. Sprik, Influence of surface topology and electrostatic potential on water/electrode systems, J. Chem. Phys., 1995, 102, 511–524 CrossRef CAS.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- G. Lamoureux, E. Harder, I. V. Vorobyov, B. Roux and A. D. MacKerell, A polarizable model of water for molecular dynamics simulations of biomolecules, Chem. Phys. Lett., 2006, 418, 245–249 CrossRef CAS.
- I. Bako, J. Hutter and G. Palinkas, Car–Parrinello molecular dynamics simulation of the hydrated calcium ion, J. Chem. Phys., 2002, 117, 9838–9843 CrossRef CAS.
- M. Sprik, M. L. Klein and K. Watanabe, Solvent polarization and hydration of the chlorine anion, J. Phys. Chem., 1990, 94, 6483–6488 CrossRef CAS.
- R. A. Bryce, M. A. Vincent, N. O. J. Malcolm, I. H. Hillier and N. A. Burton, Cooperative effects in the structuring of fluoride water clusters: Ab initio hybrid quantum mechanical/molecular mechanical model incorporating polarizable fluctuating charge solvent, J. Chem. Phys., 1998, 109, 3077–3085 CrossRef CAS.
- T. P. Lybrand and P. A. Kollman, Water–water and water–ion potential functions including terms for many body effects, J. Chem. Phys., 1985, 83, 2923–2933 CrossRef CAS.
- T. Ikeda, Infrared absorption and Raman scattering spectra of water under pressure via first principles molecular dynamics, J. Chem. Phys., 2014, 141, 044501 CrossRef PubMed.
- W. H. Robertson, E. G. Diken, E. A. Price, J. W. Shin and M. A. Johnson, Spectroscopic Determination of the OH− Solvation Shell in the OH−·(H2O)n Clusters, Science, 2003, 299, 1367–1372 CrossRef CAS PubMed.
- S. W. Rick and B. J. Berne, Free energy of the hydrophobic interaction from molecular dynamics simulations: the effects of solute and solvent polarizability, J. Phys. Chem. B, 1997, 101, 10488–10493 CrossRef CAS.
- M. H. New and B. J. Berne, Molecular dynamics calculation of the effect of solvent polarizability on the hydrophobic interaction, J. Am. Chem. Soc., 1995, 117, 7172–7179 CrossRef CAS.
- I.-C. Yeh and M. L. Berkowitz, Effects of the polarizability and water density constraint on the structure of water near charged surfaces: Molecular dynamics simulations, J. Chem. Phys., 2000, 112, 10491–10495 CrossRef CAS.
- A. Kohlmeyer, W. Witschel and E. Spohr, Molecular dynamics simulations of water/metal and water/vacuum interfaces with a polarizable water model, Chem. Phys., 1996, 213, 211–216 CrossRef CAS.
- Z. Li, G. Jeanmairet, T. Méndez-Morales, B. Rotenberg and M. Salanne, Capacitive Performance of Water-in-Salt Electrolytes in Supercapacitors: A Simulation Study, J. Phys. Chem. C, 2018, 122, 23917–23924 CrossRef CAS.
- G. F. L. Pereira, R. G. Pereira, M. Salanne and L. J. A. Siqueira, Molecular Dynamics Simulations of Ether-Modified Phosphonium Ionic Liquid Confined in between Planar and Porous Graphene Electrode Models, J. Phys. Chem. C, 2019, 123, 10816–10825 CrossRef CAS.
- C. Merlet, C. Péan, B. Rotenberg, P. A. Madden, P. Simon and M. Salanne, Simulating Supercapacitors: Can We Model Electrodes As Constant Charge Surfaces?, J. Phys. Chem. Lett., 2013, 4, 264–268 CrossRef CAS PubMed.
- J. Yang, Z. Bo, H. Yang, H. Qi, J. Kong, J. Yan and K. Cen, Reliability of Constant Charge Method for Molecular Dynamics Simulations on EDLCs in Nanometer and Sub-Nanometer Spaces, ChemElectroChem, 2017, 4, 2486–2493 CrossRef CAS.
- S. R. Tee and D. J. Searles, Constant Potential and Constrained Charge Ensembles for Simulations of Conductive Electrodes, J. Chem. Theory Comput., 2023, 19, 2758–2768 CrossRef CAS PubMed.
- R. Rizo, E. Sitta, E. Herrero, V. Climent and J. M. Feliu, Towards the understanding of the interfacial pH scale at Pt(111) electrodes, Electrochim. Acta, 2015, 162, 138–145 CrossRef CAS.
- S. Sakong and A. Groß, The electric double layer at metal-water interfaces revisited based on a charge polarization scheme, J. Chem. Phys., 2018, 149, 8 CrossRef PubMed.
- S. Sakong, K. Forster-Tonigold and A. Groß, The structure of water at a Pt(111) electrode and the potential of zero charge studied from first principles, J. Chem. Phys., 2016, 144, 19 CrossRef PubMed.
- O. M. Magnussen and A. Groß, Toward an Atomic-Scale Understanding of Electrochemical Interface Structure and Dynamics, J. Am. Chem. Soc., 2019, 141, 4777–4790 CrossRef CAS PubMed.
- C. G. Van de Walle and R. M. Martin, Theoretical study of band offsets at semiconductor interfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 8154–8165 CrossRef CAS PubMed.
- S. Surendralal, M. Todorova, M. W. Finnis and J. Neugebauer, First-principles approach to model electrochemical reactions: understanding the fundamental mechanisms behind Mg corrosion, Phys. Rev. Lett., 2018, 120, 246801 CrossRef CAS PubMed.
- F. Deißenbeck, C. Freysoldt, M. Todorova, J. Neugebauer and S. Wippermann, Dielectric properties of nanoconfined water: A canonical thermopotentiostat approach, Phys. Rev. Lett., 2021, 126, 136803 CrossRef PubMed.
- J. Cheng, X. Liu, J. VandeVondele, M. Sulpizi and M. Sprik, Redox Potentials and Acidity Constants from Density Functional Theory Based Molecular Dynamics, Acc. Chem. Res., 2014, 47, 3522–3529 CrossRef CAS PubMed.
- J. Cheng, M. Sulpizi and M. Sprik, Redox potentials and pKa for benzoquinone from density functional theory based molecular dynamics, J. Chem. Phys., 2009, 15, 131 Search PubMed.
- C. Y. Li, J. B. Le, Y. H. Wang, S. Chen, Z. L. Yang, J. F. Li, J. Cheng and Z. Q. Tian, In situ probing electrified interfacial water structures at atomically flat surfaces, Nat. Mater., 2019, 18, 697–701 CrossRef CAS PubMed.
- J. B. Le, Q. Y. Fan, J. Q. Li and J. Cheng, Molecular origin of negative component of Helmholtz capacitance at electrified Pt(111)/water interface, Sci. Adv., 2020, 6, eabb1219 CrossRef CAS PubMed.
- J. B. Le, A. Chen, L. Li, J. F. Xiong, J. Lan, Y. P. Liu, M. Iannuzzi and J. Cheng, Modeling electrified Pt(111)-Had/water interfaces from ab initio molecular dynamics, JACS Au, 2021, 1, 569–577 CrossRef CAS PubMed.
- P. Li, Y. Liu and S. Chen, Microscopic EDL structures and charge–potential relation on stepped platinum surface: Insights from the ab initio molecular dynamics simulations, J. Chem. Phys., 2022, 156, 104701 CrossRef CAS PubMed.
- J. Haruyama, T. Ikeshoji and M. Otani, Electrode potential from density functional theory calculations combined with implicit solvation theory, Phys. Rev. Mater., 2018, 2, 095801 CrossRef.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A, 1985, 31, 1695–1697S CrossRef PubMed.
- A. Dequidt, J. Devémy and A. A. H. Pádua, Thermalized Drude Oscillators with the LAMMPS Molecular Dynamics Simulator, J. Chem. Inf. Model., 2016, 56, 260–268 CrossRef CAS PubMed.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
Footnote |
| † Equal contributing authors. |
| This journal is © The Royal Society of Chemistry 2024 |