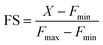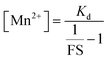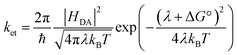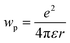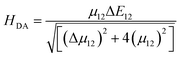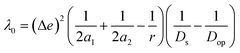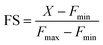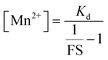A water-soluble, cell-permeable Mn(II) sensor enables visualization of manganese dynamics in live mammalian cells

Abstract

Central roles of Mn²⁺ ions in immunity, brain function, and photosynthesis necessitate probes for tracking this essential metal ion in living systems. However, developing a cell-permeable, fluorescent sensor for selective imaging of Mn²⁺ ions in the aqueous cellular milieu has remained a challenge. This is because Mn²⁺ is a weak binder to ligand-scaffolds and Mn²⁺ ions quench fluorescent dyes leading to turn-off sensors that are not applicable for in vivo imaging. Sensors with a unique combination of Mn²⁺ selectivity, μM sensitivity, and response in aqueous media are necessary for not only visualizing labile cellular Mn²⁺ ions live, but also for measuring Mn²⁺ concentrations in living cells. No sensor has achieved this combination thus far. Here we report a novel, completely water-soluble, reversible, fluorescent turn-on, Mn²⁺ selective sensor, M4, with a K_d of 1.4 μM for Mn²⁺ ions. M4 entered cells within 15 min of direct incubation and was applied to image Mn²⁺ ions in living mammalian cells in both confocal fluorescence intensity and lifetime-based set-ups. The probe was able to visualize Mn²⁺ dynamics in live cells revealing differential Mn²⁺ localization and uptake dynamics under pathophysiological versus physiological conditions. In a key experiment, we generated an in-cell Mn²⁺ response curve for the sensor which allowed the measurement of the endogenous labile Mn²⁺ concentration in HeLa cells as 1.14 ± 0.15 μM. Thus, our computationally designed, selective, sensitive, and cell-permeable sensor with a 620 nM limit of detection for Mn²⁺ in water provides the first estimate of endogenous labile Mn²⁺ levels in mammalian cells.

---

Introduction

The biological importance of manganese (Mn) is undisputed, evident from its distinct roles in brain function, immunity against pathogens, all the way to one of the most crucial processes on the planet, photosynthesis.^1–5 Since Mn is an essential nutrient, the uptake, distribution, and removal of Mn ions are tightly regulated in all forms of life, ranging from bacteria to animals and plants.⁵ The playground of Mn cell biology encompasses the Mn ion labile pool, Mn dependent proteins and enzymes, and Mn transporters.^1,2,4–13 The concerted interplay of these players maintains the total mammalian cellular levels of Mn ions between low μM to sub mM levels.^5,14 Due to the reducing cellular environment, the major oxidation state of the labile Mn ion pool is +2.¹⁵ The labile Mn²⁺ pool can act as an antioxidant as per in vitro studies.^2,15 Recent reports have shown that the antioxidant properties of the labile pool are linked to the mobilization of Mn²⁺ ions during cancer and the early stages of microbial infection.^3,4,16–18 Further, mutations in Mn²⁺ transporters can lead to early-onset Parkinsonism, due to accumulation of Mn ions in the blood, brain, and liver.^19–23 Mn-induced Parkinsonism is also observed in miners and welders who are occupationally exposed to Mn.^5,24–26 In this intricate backdrop of Mn essentiality and pathophysiology, Mn²⁺ sensitive fluorescent sensors are key chemical tools that can help chalk out Mn regulatory pathways in both physiological and disease contexts. Importantly, in theory fluorescent Mn²⁺ sensors should be able to afford estimates of labile Mn²⁺ ions in living mammalian cells; however, no sensor has achieved this goal to date.

The requirements for an ideal Mn²⁺ sensor for tracking, imaging, and estimating endogenous Mn²⁺ ions in living systems are: (1) selectivity over other biologically essential metal ions especially Ca²⁺ and Mg²⁺ ions which have very similar coordination properties to Mn²⁺ ions but are present in overlapping to higher concentration ranges in living systems;²⁷ (2) sensitivity to detect μM levels of the labile Mn²⁺ ion pool; (3) cell permeability; and finally (4) water-solubility to generate in vitro/in-cell fluorescence calibration curves and obtain dissociation constants for the sensor in aqueous buffer replicating the aqueous cellular milieu. The last feature would allow the key estimation of labile Mn²⁺ levels in living cells. To date no Mn²⁺ sensor has shown the combination of all of the aforementioned properties (Fig. 1). The very few small molecule-based Mn²⁺ sensors either suffer from selectivity issues or have low water-solubility.^28–31 The only two macromolecular sensors, one protein-based and another DNA-based, either rely on transfection for cell incorporation or are cell impermeable.^32,33 In addition, the protein-based sensor did not have the desired selectivity toward Mn²⁺ over Ca²⁺ and Mg²⁺ and especially given that the intra-cellular concentration of Mg²⁺ ions is in the mM range, competition would be expected. Thus far the protein-based sensor has only been applied to detect Mn²⁺ in bacterial cells (Fig. 1a).³³ The DNA-based cell-impermeable sensor is selective toward Mn²⁺ but has low sensitivity allowing imaging of only high, mM levels of Mn²⁺ ions (Fig. 1a).³² A reason for the lack of fluorescent sensors for detecting Mn²⁺ ions is the fact that Mn²⁺ ions lie at the bottom of the Irving–Williams series which ranks the stability of metal complexes of divalent transition metal ions in ascending order from Mn²⁺ to Cu²⁺ in water.³⁴ Apart from the Irving–Williams series, a more significant challenge is to design selective binders for Mn²⁺ over Ca²⁺ and Mg²⁺ ions which are present in sub μM (Ca²⁺) to mM (Mg²⁺) concentrations in cells within mammalian systems. Finally, Mn²⁺ ions can quench the fluorescence of fluorophores leading to turn-off sensors which are not suitable for tracking metals in living systems.³⁵

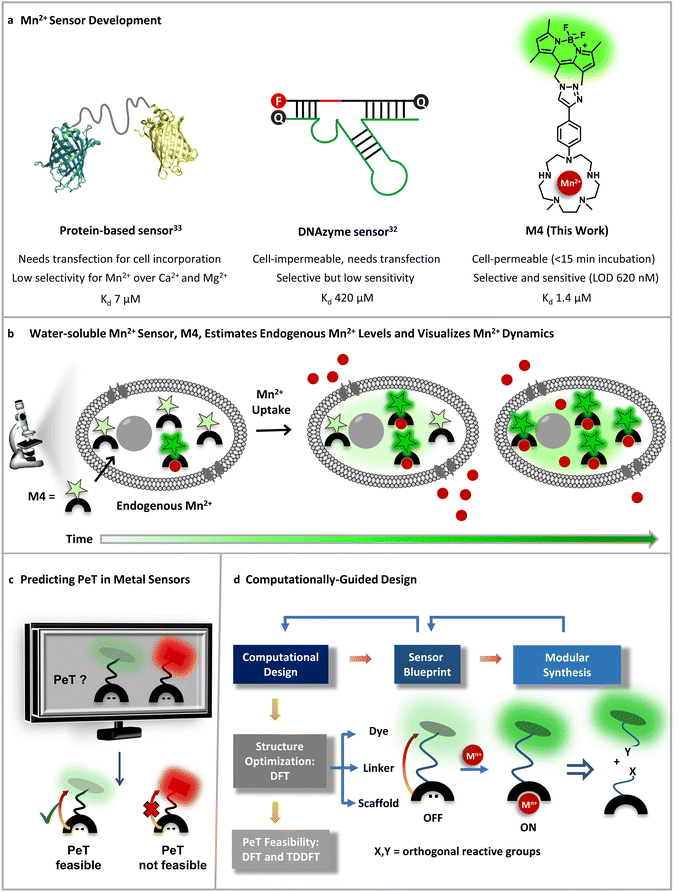Fig. 1 Designing an Mn²⁺ sensor. (a) Comparison of previous Mn²⁺ probes with this work. A fluorescent protein-based sensor requires transfection and has limited selectivity for Mn²⁺ over Ca²⁺ making it only applicable to Mn²⁺ detection in bacterial cells thus far.³³ A DNAzyme sensor exhibits Mn²⁺ selectivity, but is cell-impermeable and has low sensitivity only allowing imaging of high, mM levels of Mn²⁺ ions.³² A novel small-molecule based turn-on fluorescent water-soluble sensor, in this work, directly permeates cell-membranes and exhibits Mn²⁺ selectivity and sensitivity to enable imaging of Mn²⁺ dynamics in living mammalian cells. (b) Schematic depicting the cell-permeable small-molecule based sensor described in (a), which is sensitive to and can estimate physiological levels of Mn²⁺ and can also visualize Mn²⁺ uptake dynamics in live cells. (c) A computational workflow devised to predict PeT, central to the design of turn-on fluorescent metal ion sensors. (d) Schematic representing the utilization of the computational workflow to predict PeT in any metal ion sensor blueprint, highlighting the feedback between design guided by chemical intuition, synthetic feasibility, and computations. The general workflow was leveraged to develop a water-soluble, cell-permeable Mn²⁺ sensor.

To address all of the aforementioned challenges and develop a cell-permeable, water-soluble, fluorescent sensor for Mn²⁺ ions we devised a general computational workflow to design a turn-on fluorescent sensor for any metal ion. Specifically, we noted that none of the previously reported sensors had a combination of water-solubility, selectivity, and sensitivity toward μM levels of Mn²⁺ ions. In order to visualize endogenous levels of Mn²⁺ ions in living cells and estimate the levels of labile Mn²⁺ ions in mammalian cells we needed a ‘turn-on’ fluorescent sensor that would respond to μM levels of Mn²⁺ ions in aqueous buffer with high selectivity. We thus went to the drawing board and designed putative water-soluble Mn²⁺ sensors that could be synthesized via modular synthetic strategies amenable to easy modifications. The computational workflow was applied to these sensor blueprints (Fig. 1c and d). In this proof-of-concept study, we successfully combined our predictive computational workflow in conjunction with a modular synthetic approach, to obtain a novel, selective, sensitive, completely water-soluble, and cell-permeable turn-on fluorescent sensor for Mn²⁺ ions (Fig. 1a and b). The sensor had a dissociation constant of 1.4 ± 0.2 μM toward Mn²⁺ ions in aqueous buffer and a limit of detection (LOD) of 620 ± 70 nM for Mn²⁺ ions. The sensor, henceforth referred to as M4, entered mammalian cells within 15 min of direct incubation in aqueous media. M4 showed a distinct selective increase in fluorescence intensity (Fig. 1b) and fluorescence lifetime in the presence of Mn²⁺ ions. The cell-permeable sensor was applied to image Mn²⁺ ions in confocal fluorescence microscopy setups in both fluorescence intensity and lifetime modes, a first for Mn²⁺ imaging. Importantly, we were able to apply the sensor to not only visualize endogenous Mn²⁺ ions but also performed an in-cell calibration of the fluorescence response of the sensor. By utilizing the information on the dissociation constant of the sensor in aqueous buffer and performing a key live cell Mn²⁺ uptake imaging experiment we provide the first estimate of labile Mn²⁺ ions in mammalian cells as 1.14 ± 0.15 μM.

Finally, the probe was used to visualize live Mn²⁺ uptake dynamics in mammalian cells lacking a critical Mn²⁺ ion transporter implicated in early onset Parkinsonism via excess Mn accumulation. Comparison of cells with and without the transporter revealed significant differences in Mn²⁺ uptake rates and visual differences in localization in physiological versus pathophysiological contexts. The study indicates that the sensor would be clearly applicable to the elucidation of Mn²⁺ regulation not only under physiological conditions but also in the context of neurodegeneration, immunity, and cancers in the future.

Results and discussion

A computational workflow for designing metal ion sensors

Small-molecule based cell-permeable metal ion sensors are attractive chemical tools for deciphering the cell-biology of metal ions. However, the lack of predictability in design principles leads to emphasis on intuitive design which might often lead to unpredictable outcomes. A popular approach to develop turn-on fluorescent metal ion sensors relies upon photo-induced electron transfer (PeT).^35,36 The basic blueprint of any PeT based metal ion sensor is a metal-binding ligand conjugated to a fluorescent dye via a linker (Fig. 1c). The sensor should remain in the quenched or off state in the absence of metal ions due to PeT from the metal binding ligand to the dye (Fig. 1c). Upon metal binding, PeT should be abolished leading to an increase in emission. Key to the design of PeT based sensors is the initial off state of the probe. Any random dye–scaffold combination would not lead to a fluorescence quenched apo probe which is a necessary condition for turn-on fluorescence sensors. Realizing that a major challenge in the field of metal ion probe design, including Mn²⁺ ion sensor design, is predictability in the sensing strategy, we devised a computational workflow to predict PeT in the metal unbound state of a sensor (Fig. 1c, d and 2).

Fig. 2 Computational insights guide Mn²⁺ sensor design. (a) Blueprints of water-soluble ‘turn-on’ fluorescent Mn²⁺ ion sensors. (b) Optimized geometry of M4 in water (DFT B3LYP with a 6-311++G** basis set). The three parts of the molecule (the dye, the linker, and the scaffold) are at different planes marked in green, yellow and orange respectively. (c) Plot depicting the energy levels of optimized ground state geometry, most probable transitions, and possible PeT donor levels in the molecules shown in (a) [TP – Transition Probability]. Due to extensive delocalization of MOs across the M3 molecule, the donor and acceptor states localized on the dye and scaffold are not available for M3. (d) MOs of M4 which are localized on either the dye or the scaffold part of the molecule and can participate as PeT donor/acceptor states.

The requirements for PeT to occur in a metal unbound initial state or apo sensor are: (1) no electron delocalization between the metal-binding ligand and the dye, as PeT is a through-space electron transfer process;³⁷ (2) favorable driving force between PeT donor and acceptor states that have electron densities localized on the metal-binding scaffold and dye, respectively. To predict if PeT would be feasible in a candidate metal ion sensor, we employed density functional theory (DFT) to optimize the proposed sensor geometries in appropriate solvents and obtain electronic energies and wavefunctions (Fig. 1d). Following DFT calculations, time-dependent DFT (TD-DFT) calculations were performed to identify the most probable electronic transitions within the sensor. The workflow that we devised to determine the feasibility of PeT in any designed metal ion sensor (Fig. 1c and d) therefore included: (1) identifying dye-centered orbitals within the sensor conducive to photo-absorption which can act as PeT acceptors; (2) identifying ligand-centered orbitals with favorable driving forces to act as PeT donors. To test the efficacy of the computational workflow, we decided to apply it toward solving a long-standing challenge in metal ion imaging: the development of a water-soluble, cell-permeable Mn²⁺ ion probe.

Design of a water-soluble, turn-on fluorescent Mn²⁺ selective probe

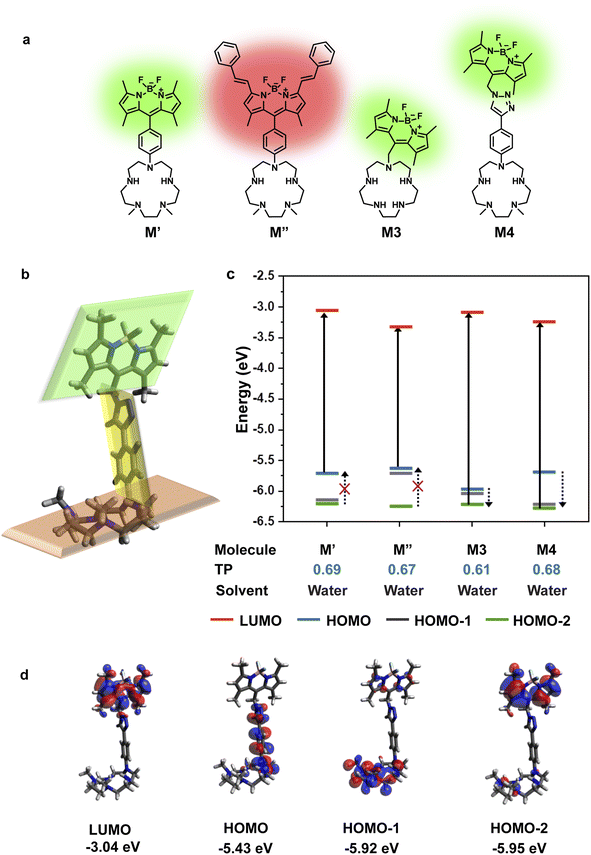
To design a water-soluble, cell-permeable, turn-on fluorescent Mn²⁺ ion sensor, we applied the computational workflow to blueprints of potential Mn²⁺ ion sensors (Fig. 2). Blueprints of Mn²⁺ selective, water-soluble fluorescent sensors were chalked out based on the following considerations: (1) an appropriate Mn²⁺ binding scaffold with high aqueous solubility; (2) a visible emitting fluorescent dye; (3) feasibility of PeT in the final sensor design as predicted by our computational workflow. For the Mn²⁺ binding scaffold design, we selected a penta-aza macrocyclic ligand (Fig. 2a). The design was based on the possibility of attaining a hepta-coordinate Mn²⁺ binding geometry via equatorial N-atom coordination and axial coordination to O-atom donor containing molecules like water or anions like phosphate or citrate^2,13,15 that would be present in the cellular milieu. An aza-macrocycle with amine moieties would have inherently high water-solubility. The preference of Mn²⁺ ions toward a hepta-coordinate geometry has been observed in Mn²⁺ binding proteins and small-molecule based complexes.^38,39 Further, Mn²⁺ is a borderline ion, that is, it is neither as hard as Ca²⁺ ions nor as soft as Zn²⁺ ions.⁵ Hence, we reckoned that a planar pentagonal N-atom coordination sphere providing a suitable metal-binding core size to fit Mn²⁺ ions along with axial O-donor coordination would provide the appropriate N,O donor mix for selective Mn²⁺ ion coordination. We designed four potential water-soluble Mn²⁺ sensors, M′, M′′, M3, and M4 (Fig. 2a), by combining synthetically feasible pentaaza macrocycles with BODIPY based visible emitting dyes via either aliphatic or aromatic linkers. Amongst these designs, M3 would be attainable via a modular S_N2 based scheme to join the metal-binding scaffold to the dye. M4 would be accessible via a “click” reaction based modular synthetic strategy involving conjugation of an alkyne-tagged metal binding scaffold to an azide-tagged dye. Modular synthetic schemes (Fig. 1d) were more preferable since modifications in either the dye or scaffold would be easily accessible in the future.

Before employing the computational workflow on the newly designed water-soluble sensor blueprints, the workflow was validated on a previously reported PeT-based Mn²⁺ ion sensor, M1, that had afforded a selective turn-on response toward Mn²⁺ ions in acetonitrile (Fig. S1 and Table S1†).³⁰ We employed Gaussian D.01 for all electronic structure calculations, Gaussview 6.0.16 for initial modelling, Avogadro 1.1.1 for visualization, and Gaussview and Avogadro for analysis, for all computations described henceforth. The results from the DFT calculations of M1 in acetonitrile indicated that HOMO−2 and LUMO had electron densities centered on the dye (Fig. S1†). The DFT optimized structure of M1 showed that the dye and the ligand were not in the same plane, thereby indicating a possibility of through-space PeT from the ligand to the dye (Fig. S1†). The most probable transition was from HOMO−2 to LUMO (Table S1†), resulting in two energetically favorable donor orbitals, HOMO and HOMO−1 which were dimethylaniline (DMA) and macrocycle-centered respectively, to fill the hole in HOMO−2 (Fig. S1†). We note here that the DMA amine is a part of the metal binding scaffold. Hence, the computations indicated that PeT would occur in apo M1. Indeed, PeT had been found to be operational in M1, based on the low quantum yield, 0.0038, of the apo sensor in acetonitrile.³⁰ Having validated our workflow, we carried out calculations for all the designed water-soluble Mn²⁺ sensor molecules with water as solvent (Fig. 2c and S2–S4, and Table S1†). For M′ and M′′ the most probable transitions were from the HOMO to LUMO (Fig. 2c, S2, and S3, and Table S1†). Hence, no favorable PeT donor levels were available. For M3, the most probable transition was from HOMO−2 to LUMO, allowing HOMO and HOMO−1 to act as potential PeT donor levels (Fig. 2c and S4, and Table S1†). However, MOs were delocalized over the dye and the scaffold, making PeT less likely in this molecule.

Finally, for M4, we observed that the dye and the ligand were distinctly out-of-plane with respect to each other which was a favorable configuration for PeT (Fig. 2b). The most probable transition was from dye-centered HOMO−2 to LUMO (Fig. 2c and d, and Table S1†). Hence, the DMA-centered HOMO or macrocycle-centered HOMO−1 would act as PeT donor orbitals (Fig. 2c and d). Therefore, based on computations, M4 should exhibit PeT based quenching of the BODIPY unit in its metal unbound state, fulfilling the necessary initial criterion for turn-on sensing. The thermodynamic driving force associated with PeT (ΔG°) and electron transfer rates (k_et) were calculated using the Rehm–Weller equation⁴⁰ and Marcus theory,⁴¹ respectively (details in Computational methods, Fig. S5 and Tables S2–S4†). For M4, during excitation, the most probable transition took place from the dye-centered HOMO−2 to LUMO with a hole created on the former, enabling it to act as an electron acceptor state. The potential donor states for PeT were the scaffold centered HOMO and HOMO−1. ΔG° for electron transfer from HOMO to HOMO−2 was calculated to be −2.27 eV and k_et was 4.09 × 10¹² s⁻¹. ΔG° for electron transfer from HOMO−1 to HOMO−2 was −2.77 eV and k_et was 9.13 × 10⁹ s⁻¹. The negative ΔG° values indicated that PeT would be functional in apo M4. The electron transfer rates calculated for M4 were also similar to experimental values obtained for a previously reported BODIPY based Ca²⁺ ion sensor that functioned via PeT in water.⁴² Since the computations convincingly predicted that PeT would be feasible in apo M4, we decided to proceed with the evaluation of M4 as a potential water-soluble Mn²⁺ sensor.

M4 is a water-soluble, Mn²⁺ ion selective and sensitive turn-on fluorescent sensor

The probe M4, shortlisted from the computational predictions, was next synthesized (Fig. S6†). The synthesis involved a Cu ion assisted “click” reaction to conjugate the BODIPY azide 10 to the Boc-protected alkyne-tagged penta-aza macrocycle 7 (Fig. S7†) to afford the Boc-protected sensor 11 (Fig. S8†) which was then deprotected to afford M4 (Fig. S9†). M4 was characterized by LC-ESI-MS for purity (Fig. S9†), followed by HR-ESI-MS, ¹H-NMR, and ¹³C NMR (Fig. S32–S41†). The molecule was completely water-soluble as designed, with an experimentally determined log P value of −0.2 (Fig. S10†). Hence, all further experiments were performed in aqueous buffer without the addition of any organic solvent.

The presence of the secondary amines in the macrocycle along with the triazole moiety in the linker in M4 (Fig. 2a), we believe, are responsible for the high water-solubility of the molecule. We observed that an aqueous solution of the M4 sensor showed very low fluorescence intensity indicating that PeT was occurring in the apo sensor (Fig. 3a). Importantly, the quantum yield of the apo sensor was 0.027 ± 0.005 (Fig. S11†). Hence, our experimental observations were in line with the computational predictions for M4 indicating that the workflow (Fig. 1d) could be employed successfully to predict PeT in metal ion sensors.

Fig. 3 Visualizing and quantifying endogenous labile Mn²⁺ in mammalian cells. (a) Fluorescence response of M4 (2 μM) to Mn²⁺ (0 μM to 28 μM) in HEPES (20 mM) and KNO₃ (100 mM) buffer (pH 7.1), λ_ex 480 nm. Inset: Observed fluorescence intensity (F) over initial fluorescence intensity in the absence of Mn²⁺ (F₀) at 514 nm over an Mn²⁺ ion concentration range of 0–28 μM (black circles; the red line is the fitted curve). (b) Observed fluorescence intensity (F), in the presence of different biologically relevant metal ions, including Mn²⁺ ([Mⁿ⁺] = 15 μM), over initial fluorescence intensity in the absence of any metal ion (F₀) at 514 nm. Data are presented as SEM where n = 3 in each set. (c) Representative confocal single z plane images of HEK293T cells. Cells were incubated with: M4 (5 μM) in aqueous buffer (pH 7.4) for 15 min (upper panel); with 25 μM Mn²⁺ in aqueous buffer (pH 7.4) for 1 h, washed and then incubated with M4 in aqueous buffer (pH 7.4) for 15 min (lower panel). Both the sets were washed with aqueous buffer (pH 7.4) and imaged; differential interference contrast (DIC) images are in the right columns for the respective confocal images. Scale bar = 20 μm. (d) Representative confocal single z plane images of HeLa cells. Cells were incubated with: M4 (5 μM) in aqueous buffer (pH 7.4) for 15 min (upper panel); with 25 μM Mn²⁺ in aqueous buffer (pH 7.4) for 1 h, washed and then incubated with M4 in aqueous buffer (pH 7.4) for 15 min (lower panel). Both the sets were washed with aqueous buffer (pH 7.4) and imaged; DIC images are in the right columns for the respective confocal images. Scale bar = 20 μm. (e) Confocal fluorescence and DIC overlay images and bar plots representing the mean intensities obtained from intensity analysis of confocal images of five sets of HeLa cells. The first set of HeLa cells were incubated with M4 (5 μM) in aqueous buffer (pH 7.4) for 15 min, washed and then TPEN (50 μM) was added and the cells were imaged after 40 min. The second set of cells were incubated with M4 (5 μM) in aqueous buffer (pH 7.4) for 15 min, washed and then imaged. The third, fourth, and fifth set of cells were first incubated with Mn²⁺ (5 μM (third), 10 μM (fourth) and 25 μM (fifth), respectively) for 1 h, washed and then incubated with M4 (5 μM) in aqueous buffer (pH 7.4) for 15 min, washed and imaged. Fluorescence intensity analyses of confocal images were carried out by using ImageJ software. Data are presented as SEM where n = 5 in each set. (f) Average titration curve for intracellular Mn²⁺ responses with M4. Cells were incubated with M4 (5 μM) in aqueous buffer (pH 7.4) for 15 min, washed and imaged for 5 min to get the resting state. Next the cells were treated with TPEN (50 μM) and subsequent time-dependent images were taken. After 30 min, cells were washed with aqueous buffer and Mn²⁺ (25 μM) was added and subsequent time-dependent images were taken till saturation was achieved. n = 4 cells (for each independent experiment, N = 3).

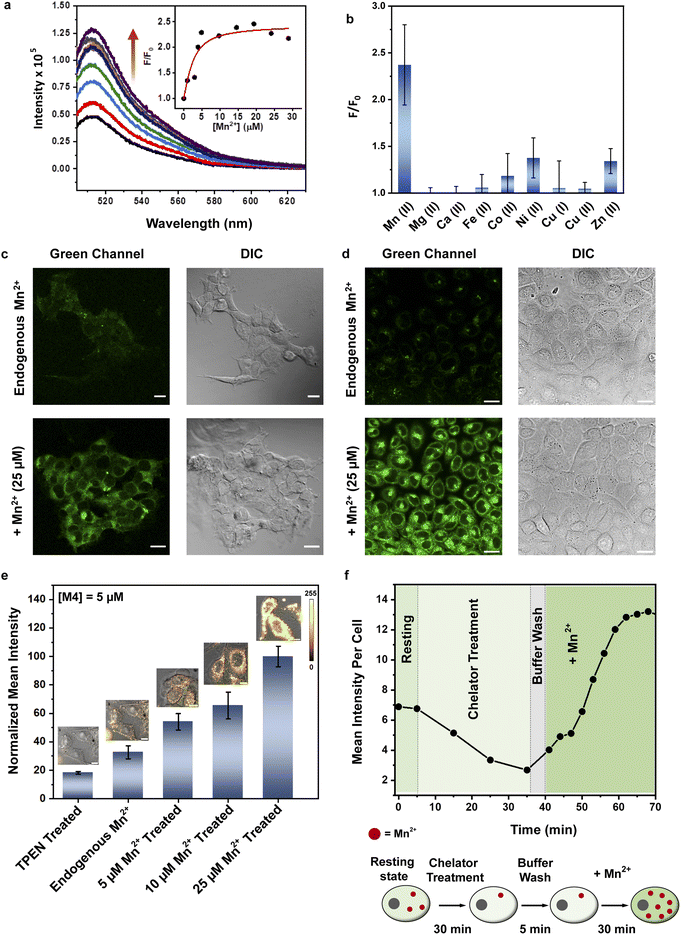
The absorption spectrum of M4 showed a maxima at 508 nm in HEPES buffer (Fig. S9b†) with an extinction coefficient of 2673 ± 127 M⁻¹ cm⁻¹ (Fig. S12†). When excited at 480 nm, the sensor afforded an emission spectrum with a maxima at 514 nm (Fig. 3a). Upon addition of Mn²⁺ ions in the form of MnCl₂, we observed a 2.4-fold increase in emission intensity of M4 at pH 7.1, in aqueous buffer (Fig. 3a and b). The quantum yield of the sensor in the presence of Mn²⁺ was 0.055 ± 0.005 (Fig. S11†) which was also twice that of the apo sensor matching with the observed fluorescence enhancement in the presence of Mn²⁺ ions. The extent of enhancement remained unaltered even when other Mn²⁺ salts, perchlorate and acetate, were used as Mn²⁺ ion sources, indicating that the response of M4 was not altered when the counterion was changed (Fig. S13†). Further, the response of the sensor toward Mn²⁺ ions remained unchanged in acetonitrile (Fig. S14†) indicating that the response would not be affected by the polarity of the medium. Studies in other organic solvents could not be performed since the sensor was highly water-soluble and could not be dissolved in other organic solvents. The pH response of M4 was a critical parameter that would govern its applicability in physiological contexts. pH dependent studies of M4 indicated that the emission of the apo sensor remained constant within the physiological pH range of 5–8 (Fig. S15†).

We next tested the response of M4 in the presence of other biologically essential metal ions (Fig. 3b and S16†). The sensor did not respond at all to Mg²⁺ (up to a tested concentration of 1 mM, Fig. S16a†) and Ca²⁺ ions (up to a tested concentration of 15 μM) (Fig. 3b) which was a necessary criterion for any designed probe to be applied for imaging Mn²⁺ ions in living cells especially mammalian cells. M4 also barely responded to all other tested metal ions (Fig. 3b). The only other metal ions that showed minimal response were Ni²⁺ (maximum 1.4-times at saturation concentrations) and Zn²⁺ (maximum 1.3-times at saturation concentrations) ions. Notably, for both these ions the emission increase was significantly lower compared to that afforded by Mn²⁺ ions (Fig. 3b). The dissociation constant of M4 toward Mn²⁺ ions was obtained as 1.4 ± 0.2 μM (Fig. 3a, inset, and Table S5†). Ni²⁺ ions afforded a 2-times higher K_d value while Zn²⁺ ions showed a 6-times higher K_d value when compared to the dissociation constant of M4 toward Mn²⁺ ions (Table S5 and Fig. S17†). The dissociation constant values for Ni²⁺ and Zn²⁺ were further validated by performing fluorescence competition titrations with the Mn²⁺ complex of M4 (Fig. S18†). The putative levels of labile Zn²⁺ ions within cellular systems are pM and intracellular labile Ni²⁺ levels are in the sub nM range.^35,43–45 Hence, we expect no interference from these ions when imaging Mn²⁺ ions which are present in μM levels in cellular systems. Na⁺ and K⁺ ions were already present in high mM amounts in the buffer. No change in the fluorescence response of M4 was observed after addition of excess buffer to an aqueous solution of M4 (Fig. S16b†). Any possibility of interference from Na⁺ and K⁺ ions was thus eliminated. Finally, the response of M4 toward Mn²⁺ ions remained unaffected in the presence of a representative protein, bovine serum albumin (Fig. S19†). Therefore, no interference from the proteins in the biological context is expected. Hence, M4 was an Mn²⁺ selective sensor that afforded a distinct turn-on response in the presence of Mn²⁺ ions in water. Importantly, based on the binding affinity (0.7 × 10⁶ M⁻¹) of M4 toward Mn²⁺ ions and a LOD for Mn²⁺ ions of 620 ± 70 nM in water (Fig. S20†), M4 had the apt sensitivity required to detect Mn²⁺ ions in biological systems.

The cell-permeable, Mn²⁺ ion selective probe images physiologically relevant levels of Mn²⁺ ions in living cells

We next tested whether M4 could be applied to image Mn²⁺ ions in living mammalian cells (Fig. 3c–f). An MTT assay for cellular toxicity in HEK293T cells indicated that the sensor was not toxic up to a tested concentration of 15 μM, till the maximum tested incubation time of 1 h (Fig. S21†). Hence, concentrations lower than 15 μM and incubation times less than 1 h were used for all cell studies. When living HEK293T and HeLa cells were treated with aqueous solutions of M4 (5 μM), we observed that the sensor efficiently entered cells within 15 min of direct incubation (Fig. 3c and d, S22, and S23†). Fluorescence emission from cells that were not exogenously treated with Mn²⁺ indicated that M4 could be used to detect Mn²⁺ ions inherently present in living cells (Fig. 3c and d, top panels, and Fig. 3e). A distinct increase in fluorescence emission was observed in both HEK293T and HeLa cells exogenously treated with low μM (25 μM) levels of Mn²⁺ ions (Fig. 3c and d, bottom panels). Intensity analysis of cell images indicated significant 2.2-fold overall emission enhancement in Mn-treated HEK293T cells and 2.7-fold emission enhancement in Mn-treated HeLa cells versus untreated cells. Furthermore, when N,N,N′,N′-tetrakis(2-pyridylmethyl)ethylenediamine (TPEN), a cell-permeable, divalent metal ion chelator that can bind to Mn²⁺, was added to cells that were not exogenously treated with Mn²⁺, a clear decrease in fluorescence intensity was observed (Fig. 3e and f, and S24†). A similar decrease in fluorescence intensity was also observed when TPEN was added to cells that were exogenously treated with Mn²⁺ (Fig. S25†), thus establishing M4 as a reversible sensor for detecting Mn²⁺ ions within living cells. Hence, M4 was a water-soluble, reversible, cell-permeable sensor that could clearly image μM, physiologically relevant levels of Mn²⁺ ions in living mammalian cells.

In both cell types, increased emission was observed in the cytoplasm and in the perinuclear regions, in Mn-treated cells. The presence of Mn in these regions of Mn-treated mammalian cells has been reported previously via Mn elemental maps generated using nano-synchrotron X-ray fluorescence imaging.^23,46,47 This fact further validated the ability of M4 toward Mn²⁺ ion imaging in living cells.

Although the labile Zn²⁺ levels in mammalian cells are in pM,^35,43,45 to further confirm that there was no interference from Zn²⁺ ions in the in-cell response of M4, a control experiment was performed on Zn²⁺ treated cells. No increase in fluorescence intensity was observed in cells exogenously treated with Zn²⁺ (Fig. S26†), again confirming the in-cell Mn²⁺ specificity of M4. Finally, we wanted to confirm that M4 was not localized in lysosomes as an acidic environment might lead to fluorescence enhancement in PeT based sensors. No colocalization was observed between M4 and LysoTracker Red (Fig. S27†). These experiments distinctly confirmed the in-cell Mn²⁺ specificity of M4.

In order to test whether M4 could detect changes in Mn²⁺ concentration inside living mammalian cells in the physiologically relevant Mn²⁺ concentration range and if the sensor could afford an Mn²⁺ concentration dependent response in living mammalian cells, different sets of HeLa cells were incubated with varying concentrations of Mn²⁺ ions. The lowest intensity was observed when cells were treated with the chelator TPEN (Fig. 3e). A step-wise increase in cellular Mn²⁺ levels from untreated cells containing endogenous Mn²⁺ to cells treated with up to 25 μM Mn²⁺ could be distinctly observed via a concomitant increase in the fluorescence intensity of the sensor. Therefore, M4 could report on endogenous levels of Mn²⁺ and importantly track changes in Mn²⁺ ion concentrations inside living cells (Fig. 3e).

Encouraged by this result we next set forth to apply the water-soluble, cell-permeable sensor, M4, to estimate labile Mn²⁺ levels by a method first introduced by Tsien et al.⁴⁸ and applied by Palmer et al.⁴⁹ to metal-based sensors to determine the levels of intracellular Zn²⁺ ions. The method involved determining the fractional saturation of the sensor in resting cells that had not been externally treated with any Mn²⁺ ions. The fractional saturation could then be plugged in to an equation relating the dissociation constant of the sensor and fractional saturation to the concentration of the labile metal ion. In brief, the experiment involved temporal imaging of fluorescence intensity within living mammalian cells starting from the resting state, chelator treatment, and wash, followed by Mn²⁺ addition (Fig. 3f). The experiment was repeated and analyzed for multiple individual cells to afford the average minimum fluorescence intensity (F_min), fluorescence intensity in resting cells (X), and maximum fluorescence intensity (F_max) in living cells. To obtain the minimum in-cell fluorescence intensity of apo-M4, cells were treated with TPEN, a chelator that can bind to Mn²⁺ ions. Subsequently, the maximum fluorescence intensity corresponding to the bound form of M4 inside the cells was obtained by adding Mn²⁺ ions to the same set of cells. The titration curves (Fig. 3f and S28†) indicate that M4 responds to both the decrease in Mn²⁺ levels upon chelator treatment and increase in Mn²⁺ levels due to exogenously added Mn²⁺. Fractional saturation FS was calculated from:

Since we could measure the dissociation constant of the sensor for Mn²⁺ ions in aqueous media owing to the water-solubility of the sensor, the concentration of labile Mn²⁺ ions in resting cells could be estimated from the equation

Thus, by generating in-cell Mn²⁺ responses we obtained the average labile Mn²⁺ concentration in living mammalian HeLa cells as 1.14 ± 0.15 μM which to the best of our knowledge is the first estimate of labile Mn²⁺ ion concentration in a living mammalian cell.

Fluorescence lifetime imaging of Mn²⁺ ions in living cells

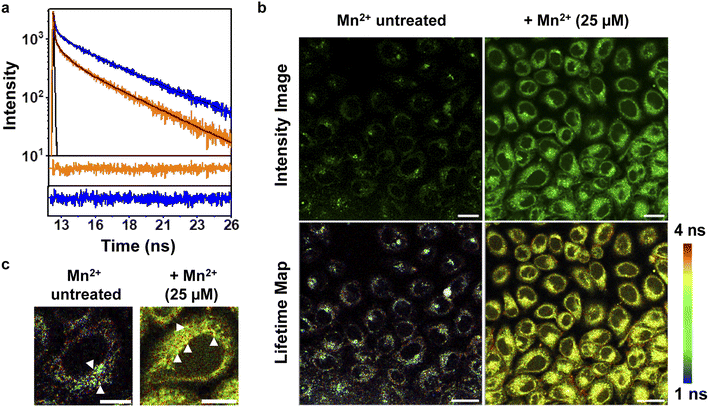
To further increase the repertoire of applications of M4 toward imaging biological Mn²⁺ in living cells, we next explored fluorescence lifetime imaging microscopy (FLIM) (Fig. 4). Intensity based fluorescence imaging with a turn-on fluorescence sensor cannot distinguish between intracellular regions of high sensor accumulation versus regions with high analyte concentration. Since FLIM is inherently concentration and intensity independent, this technique in conjunction with intensity images can provide distinct information on intracellular analyte-localization.^50,51 Hence, we imaged Mn²⁺ untreated and exogenously Mn²⁺ treated mammalian cells on a FLIM setup in the presence of M4 (Fig. 4b, and S29†). We first performed in vitro lifetime measurements of M4 in the absence and presence of Mn²⁺ ions and observed a 2.3-fold increase in the lifetime value of the sensor in the presence of Mn²⁺ ions (Fig. 4a, and Table S6†). This result was clearly in line with the in vitro fluorescence titration results in Fig. 3a. In live cell FLIM experiments, we observed significantly lower lifetime values in certain regions in Mn²⁺ untreated cells (Fig. 4b, bottom left panel, Fig. 4c, left panel) compared to Mn²⁺ treated cells (Fig. 4b, bottom right panel, Fig. 4c, right panel) indicating the presence of the apo sensor in cells that were not exogenously treated with Mn²⁺. We note that the IRFs of the TCSPC measurement setup and FLIM setup were different, with the FLIM IRF (224 ps) being significantly longer than the TCSPC IRF (68 ps). Hence, we have not compared the absolute average lifetime values between in vitro TCSPC and FLIM and reported the relative increase in average lifetime values of the probe in the absence and presence of Mn²⁺ ions. The lifetime values were uniformly higher throughout the cytoplasm and peri-nuclear regions in the Mn²⁺ treated cells showing the localization of Mn²⁺ ions in these regions (Fig. 4c, white arrows, right panel). In contrast, in Mn²⁺ untreated cells, few punctate regions showed high lifetime values attributable to the bound sensor, hinting toward perhaps a more compartmentalized Mn²⁺ ion localization (Fig. 4c, white arrows, left panel). Hence, M4 provides an unprecedented handle into imaging Mn²⁺ localization in living cells via both intensity and lifetime image maps (Fig. 4b).

Fig. 4 FLIM with M4 in living mammalian cells affords lifetime maps revealing Mn²⁺ distribution. (a) Experimental (orange) and fitted (black) fluorescence intensity decay curves of M4 (2 μM) in the absence of Mn²⁺; experimental (blue) and fitted (black) fluorescence intensity of M4 (2 μM) in the presence of Mn²⁺ (20 μM). The black curve represents the instrument response function. Residuals from the fitted fluorescence intensity decay of M4 in the presence of Mn²⁺ (blue) and residuals from the fitted fluorescence intensity decay of M4 in the absence of Mn²⁺ (orange) are presented below the decay curves. (b) Representative confocal single z plane intensity images (upper panel) and lifetime maps (lower panel) of HeLa cells. Cells were incubated: with M4 (5 μM) in aqueous buffer (pH 7.4) for 15 min (left panel); with 25 μM Mn²⁺ in aqueous buffer (pH 7.4) for 1 h, washed and then incubated with M4 in aqueous buffer (pH 7.4) for 15 min (right panel). Both the sets were washed with aqueous buffer (pH 7.4) and imaged. Scale bar = 20 μm. (c) Zoomed-in representative confocal single z plane lifetime maps of single cells, incubated with only M4 (left image) and with Mn²⁺ and M4 (right image), respectively.

Visualization of Mn²⁺ uptake dynamics in live mammalian cells reveals pathophysiologically relevant differences

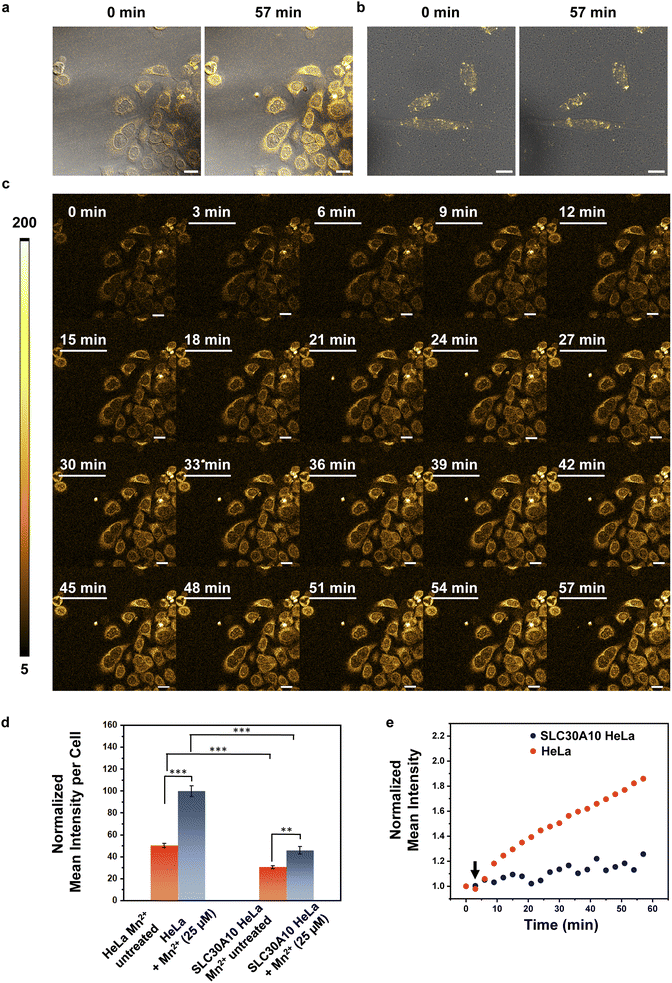
Finally, since M4 is a turn-on, cell-permeable, fluorescent sensor for Mn²⁺ ions that can detect Mn²⁺ ions in aqueous media, we wanted to challenge the sensor by testing if the probe could be used to image Mn²⁺ dynamics in living mammalian cells (Fig. 5, ESI Videos S1 and S2†). Mutations in the cell-surface localized Mn²⁺ ion efflux transporter SLC30A10 causes hypermanganesemia, leading to liver damage and Parkinson's like dystonia.^19–21,23 We reasoned that tracking differences in Mn²⁺ ion uptake rates in cells with low levels of SLC30A10 mRNA versus cells overexpressing SLC30A10 would afford information on the spatio-temporal dynamics of Mn²⁺ ions and its link to Mn-transport disorders reported in children and adults. HeLa cells have inherently very low levels of SLC30A10 and can be used to study disorders caused by deactivating mutations in the Mn²⁺ efflux transporter SLC30A10.²⁰ For comparison, SLC30A10 wild-type (WT) was expressed in HeLa cells, based on a previously reported procedure.²⁰ To apply M4 for spatiotemporal imaging of Mn²⁺ uptake, we first tested the photostability of the sensor under a fluorescence confocal microscope and we found that the probe was photostable up to the tested time of 1 h (Fig. S30†). For imaging Mn²⁺ uptake dynamics, cells were first treated with M4 for 15 min in aqueous media. Excess M4 was carefully washed out. The M4 treated cells were placed under a confocal microscope and imaged. Following the acquisition of the first image, Mn²⁺ ions were added to the media and images were recorded every 3 min for 1 h (Fig. 5c). We could distinctly image the live uptake dynamics of Mn²⁺ ions in living HeLa cells which mimic pathophysiological conditions in which the SLC30A10 efflux transporter does not function (Fig. 5a and c, and ESI Video S1†). A sequential increase in the fluorescence intensity was observed within these cells along with a significant 1.9-fold increase in emission intensity over 1 h (Fig. 5a and c–e, and ESI Video S1†). Importantly, the basal fluorescence intensity in HeLa cells (Fig. 5a and d) was 1.6 times higher than that of HeLa cells expressing SLC30A10-WT (Fig. 5b and d) indicating that the presence of the transporter was necessary to regulate endogenous Mn²⁺ ion levels. When the identical Mn²⁺ uptake experiment was performed on HeLa cells expressing SLC30A10-WT, we observed fluctuating fluorescence intensities, with a significantly slower, gradual increase in emission intensity (Fig. 5b and e, and ESI Video S2†). The final intensity in SLC30A10-WT expressing HeLa cells was significantly lower (2.2 times) than control HeLa cells (Fig. 5d and e). These results proved that M4 could be applied to visualize Mn²⁺ dynamics in living mammalian cells. Further, since SLC30A10 is a proven Mn²⁺ efflux transporter, this study validated the exquisite in-cell selectivity of the M4 probe toward sensing, tracking, and imaging Mn²⁺ ions.

Fig. 5 Visualizing Mn²⁺ dynamics in living cells. (a) Representative DIC and fluorescence overlay single z plane images of HeLa cells, incubated with M4 (5 μM), before and 57 min after addition of Mn²⁺ (25 μM), respectively. (b) Representative overlay single z plane images of HeLa cells expressing SLC30A10-WT, incubated with M4 (5 μM), before and 57 min after addition of Mn²⁺ (25 μM) respectively. (c) Cells were incubated with M4 (5 μM) in aqueous buffer (pH 7.4) for 15 min, washed with aqueous buffer and imaged (0 min). Following that, 25 μM Mn²⁺ in aqueous buffer (pH 7.4) was added and time-dependent images were taken at intervals of 3 min. The frames after addition of Mn²⁺ are underlined. Scale bar 20 μm. (d) Bar plots representing the mean intensities obtained from intensity analysis of confocal images of HeLa cells and HeLa cells expressing SLC30A10-WT. Intensity data were normalized to the intensity of Mn²⁺ treated HeLa cells. Data are presented as SEM, where n = 5 for each set. *p < 0.05, **p < 0.01 and ***p < 0.001. Fluorescence intensity analyses of confocal images were carried out by using ImageJ software. (e) Variation of mean intensity with time (HeLa cells: orange circles; SLC30A10 HeLa cells: blue circles). Addition of Mn²⁺ is marked by the black arrow. Intensity data were normalized to the intensity of the first frame (0 min) of the two cell lines. Fluorescence intensity analyses of confocal images were carried out by using ImageJ software.

We also observed visual differences in the fluorescence intensity distribution under pathophysiologically relevant conditions with low expression of an Mn²⁺ efflux transporter versus cells expressing the transporter (Fig. S31†). In the case of HeLa cells, the emission intensity of M4 increased in the cytoplasm, peri-nuclear, and nuclear regions revealing regions of Mn²⁺ ion accumulation (Fig. S31a†). In HeLa cells expressing SLC30A10-WT, a more punctate intensity distribution was observed, with a significantly lower increase in overall emission intensity and barely any Mn²⁺ ion accumulation in the regions where Mn²⁺ ions had accumulated in the HeLa cells (Fig. S31b†). These results indicated that M4 was applicable for spatiotemporal imaging of Mn²⁺ ions in living mammalian cells, in both physiological and pathophysiological contexts. This study places M4 in a unique vantage position as a chemical tool for deciphering Mn²⁺ ion regulation in living systems, finally filling a critical gap by affording a water-soluble, cell-permeable Mn²⁺ ion selective probe.

Conclusions

In conclusion, we have successfully devised and employed a general computational workflow to design a novel, highly water-soluble, selective, and sensitive, turn-on fluorescent sensor, M4, for detecting Mn²⁺ ions in aqueous media. The sensor entered living mammalian cells within 15 min of direct incubation, hence was distinctly cell-permeable, and could image Mn²⁺ ion localization in living cells. M4 was used to image Mn²⁺ ions in both intensity and significantly in lifetime fluorescence imaging setups, making it a valuable chemical tool for probing Mn²⁺ ion regulation in both turn-on intensity-based and ratiometric lifetime-based approaches. Importantly, M4 could not only be applied to image Mn²⁺ ion localization but also afforded live spatiotemporal visualization of Mn²⁺ ion uptake dynamics in mammalian cells. The experiments revealed visual differences in Mn²⁺ ion localization and significant differences in uptake rates in cells with differential expression levels of an Mn²⁺ transporter implicated in Mn²⁺-induced early-onset Parkinsonism. Hence, these results open the gateway to tracking and imaging Mn²⁺ ion dynamics in living systems with our easy to apply, cell-permeable probe. In a key experiment, we generated an in-cell Mn²⁺ fluorescence response curve for the M4 sensor which afforded imaging of endogenous Mn²⁺ ions within living mammalian cells thus providing the first estimate of labile Mn²⁺ ions to be 1.14 ± 0.15 μM in a mammalian cell.

Looking into the future, the probe design principle is modular and provides a route for easy modifications to incorporate features of sub-cellular targetability and further tuning of probe sensitivity, based on the biological setting. Any design modification can be wetted through our predictive computational workflow. Therefore, our study starting from the computational design of a sensor, to synthesis, all the way to biological applicability in visualizing live intracellular dynamics forms a general rational sensor design workflow and provides a feedback loop between computational design and experiments. We believe that this workflow can guide the design and development of fluorescent sensors for any metal ion and can be further developed to specifically aid fine-tuning of sensors based on biological contexts and compartments which is the next challenge in deciphering metallobiology.

Experimental section

Computational workflow

The following workflow (Fig. 1d), based on DFT and TD-DFT calculations, for predicting PeT in the designed water-soluble Mn²⁺ sensors in the metal unbound or apo state, was drafted: (1) the ground state geometries of the molecules were optimized using DFT calculations in a suitable solvent model (acetonitrile or water depending on the predicted solubility of the candidate sensor molecule); (2) the ground state energy levels and orbital maps of the molecules were obtained from DFT calculations using a suitable solvent model; (3) the localization of molecular orbitals in the ground state sensor geometry, on the dye or on the scaffold unit of the molecule, was investigated. Delocalization of orbitals over the dye and scaffold may lead to a decreased possibility of PeT since PeT is a through-space process; (4) the most probable transitions during excitation of the molecule were identified using TD-DFT calculations (transitions corresponding to wavelengths close to the reported absorption of dye were chosen; 400–550 nm for M1, M′, M3 and M4 and 500–650 nm for M′′). Transitions with the maximum oscillator strength were considered as the most probable transition in each case; (5) the orbitals (localized on the dye) involved in the most probable transition were identified, thereby also locating the orbital vacated during excitation, i.e., PeT acceptor orbital; (6) potential PeT donor orbitals, i.e., orbitals localized on either the linker or the scaffold with favorable energies from where electron transfer to the dye-centered orbital vacated during excitation was possible, were identified; (7) ΔG° and k_et for the molecules in which potential PeT donor orbitals were available were calculated using the Rehm–Weller equation⁴⁰ and Marcus theory,⁴¹ respectively (see details below).

Geometry optimizations and electronic structure calculations

The starting point of the geometry optimizations was a planar geometry of the sensor generated by GaussView 6.0.16 software. DFT optimized ground state geometries and electronic structure of the molecules were generated in a vacuum and other suitable dielectric media modelled via the polarizable continuum model (PCM) using the B3LYP exchange–correlation functional and the 6-311++G** basis set in Gaussian D.01 software. Solvents, water and acetonitrile, were modelled using PCM. Frontier molecular orbitals (MOs) of the molecules were visualized in Avogadro 1.1.1. software for the optimized ground state geometries. TD-DFT calculations were performed on each DFT optimized sensor geometry to extract the most probable (highest oscillator strength) transition and its MO compositions showing the initial and final electronic states following photoexcitation. A total of 150 singlet transitions were considered for each sensor.

PeT rate calculations

The electron transfer rates were estimated using the semiclassical Marcus theory in the nonadiabatic limit as⁴¹:
which depends on the thermodynamic driving force ΔG° of the reaction, the electronic coupling H_DA between donor and acceptor states, and the reorganization energy λ. In the above equation, k_B, T, and ℏ are Boltzmann's constant, temperature (298 K), and the reduced Planck's constant respectively.

The free energy changes (driving force) associated with PeT were calculated according to the Rehm–Weller equation:⁴⁰

ΔG° = E_D − E_A − ΔE_0,0 − w_p

where E_D and E_A are the ground state redox potentials of the donor and the acceptor states, respectively. Here, we have approximated E_D and E_A by the ground state energies of the potential donor and acceptor molecular orbitals, respectively, which holds in the weak coupling limit. ΔE_0,0 is the electronic excitation energy between vibrationally relaxed ground and excited states and is estimated from the absorption maxima predicted by TD-DFT calculations for each molecule. The work term, w_p, corresponds to the electrostatic stabilization energy for the radical ion pair formed as a result of PeT, such that
where e is the electronic charge, r is the distance between the centroids of the donor and acceptor orbitals and ε is the permittivity of the suitable solvent (ACN for M1 and water for M4). The value of r was calculated using Multiwfn 3.8.⁵²

H _DA is the electronic coupling matrix element between the donor and the acceptor states that can be expressed as:

in the generalized Mulliken Hush scheme within a two-state approximation.⁵³μ₁₂ is the transition dipole moment between the two donor and acceptor orbitals and Δμ₁₂ is the difference between the permanent dipole moment of the two orbitals. Both μ₁₂ and Δμ₁₂ have been obtained from Multiwfn 3.8.⁵² ΔE₁₂ has been considered to be the difference in energy of the two orbitals. The coupling H_DA then represents the coupling between diabatic states (D/A) localized on the scaffold and the dye respectively. λ is the reorganization energy,

λ = λ_i + λ₀

where λ_i is the inner sphere contribution arising from the relaxation of molecular degrees of freedom and λ₀ is outer sphere contribution from solvent reorganization.⁴¹ Typically, the inner sphere reorganization energy contributions are much smaller than those of the outer sphere. Therefore, we assumed λ ≈ λ₀, which is calculated (using the simplified spherical cavity model given by Marcus) as⁴¹:
where Δe is the charge of one electron. Here, we have assumed the potential donor and acceptor orbitals as spherical moieties described by radii a₁ and a₂ respectively. To calculate a₁ and a₂, we determined the spatial distribution of electron density of each orbital and manually calculated the distance between the atoms at the extremes of this spatial distribution in both horizontal and vertical directions. We then took an average of the horizontal and vertical values to get 2a₁ and 2a₂, respectively for each orbital (Fig. S5†). r is the distance between the centroids of the donor and acceptor orbitals. r has been obtained from Multiwfn 3.8.⁵²D_s and D_op are the static and optical dielectric constants of the suitable solvent (ACN for M1 and water for M4).

Synthesis and characterization of molecules

Details of synthetic procedures are available in the ESI.† Novel molecules were characterized via liquid chromatography (LC), low resolution mass spectrometry (LRMS), high resolution mass spectrometry (HRMS), ¹H NMR and ¹³C NMR. Data are provided in the ESI.†

In vitro fluorescence measurements

All spectroscopic measurements were performed at room temperature. Since M4 was completely water-soluble, all stock solutions were prepared in aqueous media. A solution of 2 μM M4 was prepared from a primary stock (3 mM) in water, by further dissolving in aqueous buffer consisting of HEPES (20 mM) and KNO₃ (100 mM); pH was adjusted to 7.1. Fluorescence spectra were recorded on a FluoroLog®-3 (Horiba Jobin Yvon Inc.) spectrofluorometer using quartz cuvettes with 10 mm × 2 mm inner dimensions (Hellma® Analytics). Fluorescence spectra were obtained by excitation at 480 nm with a slit width of 5 nm for both excitation and emission, for M4. Mn²⁺ was used in the form of MnCl₂·4H₂O from a stock solution of 1 mM MnCl₂·4H₂O in water. Other biologically relevant metal ions were used to test the selectivity of M4 towards Mn²⁺ ions. Mg²⁺, Ca²⁺, Fe²⁺, Co²⁺, Ni²⁺, and Cu²⁺ ions were used in the form of their chlorides as MgCl₂·6H₂O, CaCl₂·2H₂O, FeCl₂·4H₂O, CoCl₂, NiCl₂, and CuCl₂ from 1 mM stock solutions prepared in water. Zn²⁺ ions were used in the form of nitrate as Zn(NO₃)₂·6H₂O from 1 mM stock solution prepared in water. Cu⁺ ions were used in the form of tetrakis(acetonitrile)copper(I) hexafluorophosphate from 1 mM stock in degassed acetonitrile. In order to check the effect of anions on the fluorescence response of M4 toward Mn²⁺ ions, Mn²⁺ was also used in the form of Mn(ClO₄)₂·H₂O and Mn(OAc)₂. All stock solutions were diluted in aqueous buffer consisting of HEPES (20 mM) and KNO₃ (100 mM) (pH was adjusted to 7.1) when required, to prepare 0.2 mM secondary stocks. The stock solution of Cu⁺ was diluted in degassed buffer. The apparent dissociation constants (K_d) corresponding to each metal ion were determined from a plot of observed fluorescence intensity (F) over fluorescence intensity of the sensor in the absence of any metal ion (F₀) at 514 nm versus [M²⁺]. The data were fitted to eqn (1) (ESI†). For fluorescence studies of the probe with varying pH, experiments were carried out with probe M4 (2 μM) prepared from the primary stock (3 mM) in water, further dissolved in aqueous buffer consisting of HEPES (20 mM) and KNO₃ (100 mM) (pH 4, 4.5, 5, 6, 7, 8). Buffers of different pH were made by adding concentrated HCl or NaOH solutions.

Cell viability experiments

For testing whether M4 affected the viability of cells, HEK293T cells were seeded and grown for 36 h in 96 well plates (cell density 10 000 cells per well) in Dulbecco's Modified Eagle's Medium (DMEM, Sigma-Aldrich®) with phenol red supplemented with fetal bovine serum (10%, Gibco®), and antibiotic (100×, 10 mL L⁻¹) at 37 °C under humidified air containing 5% CO₂. Solutions of different concentrations (2.5 μM, 5 μM, 10 μM, 15 μM) of the sensor were prepared from a stock in water. Cells were incubated with the abovementioned concentrations of M4 in aqueous buffer (pH 7.4) (200 μL per well). The incubation with the sensor was continued for 15 min, 30 min and 1 h at 37 °C in an incubator. As control, cells were incubated with media containing no sensor. After incubation, the medium containing the sensor was removed and the wells were filled with 3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide (MTT) solution (0.5 mg mL⁻¹, 180 μL per well) in DMEM, pH 7.4. MTT treated cells were kept at 37 °C in an incubator for 3–4 h for the formation of formazan crystals. Then the medium from each well was removed and the wells were filled with DMSO (200 μL per well) and the plates were shaken for 5 min to dissolve the crystal. Absorption values at 570 nm of the resultant purple solutions were recorded for each well using Cytation 5 Cell Imaging Multimode Reader (Biotek, Agilent). As background control, absorbance of only DMSO was also recorded.

Cell viability was calculated as follows:

% cell viability = [(experimental value − background control)/(control − background control)] × 100

Confocal fluorescence imaging

HEK293T and HeLa cells were cultured in DMEM (Sigma-Aldrich®), supplemented with fetal bovine serum (10%, Gibco®), and antibiotic (100×, 10 mL L⁻¹) in T25 culture plates at 37 °C under humidified air containing 5% CO₂. For HeLa cells, additional glucose (3.5 mg L⁻¹) was added to the medium. A day before the imaging, the cells were plated on home-made glass coverslip bottomed Petri plates (35 mm diameter, Tarsons) coated with polylysine (200 μg mL⁻¹). Fluorescence images of the cells were recorded on either a confocal microscope (LSM 510, Carl Zeiss, Germany) using 40× oil immersion objectives and a 488 nm laser (argon source) as the excitation source for M4 and emission was collected from 500 to 600 nm or confocal microscope (LEICA TCS SP8 X) using 60× oil immersion objectives and a white light laser set at 514 nm as the excitation source for M4 and emission was collected from 540 to 650 nm. Modified Thomson's buffer (TB) consisting of sodium HEPES (20 mM), NaCl (146 mM), KCl (5.4 mM), MgSO₄ (0.8 mM), KH₂PO₄ (0.4 mM), Na₂HPO₄ (0.3 mM) and glucose (5.5 mM) (pH adjusted to 7.4) was used during the confocal studies. A stock solution of M4 (5 mM) was prepared in water. The cells were washed with TB and incubated with M4 (5 μM in TB) for 15 min at 37 °C under humidified air containing 5% CO₂. After staining, the cells were washed with TB and imaged. For Mn treatment, cells were incubated with MnCl₂ (25 μM in TB) for 1 h at 37 °C under humidified air containing 5% CO₂. Then the cells were washed with TB to remove excess MnCl₂, incubated with M4 as mentioned above and imaged. For concentration dependent experiments, five sets of cells were used. The first set of cells were incubated with M4 (5 μM) in TB for 15 min and washed, and TPEN (50 μM) was added and the cells were imaged 40 min after addition of TPEN. The second set of cells were incubated with M4 (5 μM) in TB for 15 min, washed with TB and imaged. The third, fourth and fifth sets were incubated with Mn²⁺ (5 μM (third), 10 μM (fourth) and 25 μM (fifth) respectively) for 1 h, washed and then incubated with M4 (5 μM) in TB for 15 min, washed with TB and imaged.

Estimation of intracellular labile Mn²⁺ concentration

For estimation of intracellular labile Mn²⁺ concentration, analysis was done using ImageJ software. Background-subtracted mean fluorescence intensity was calculated taking individual cells as regions of interest (ROIs) during the resting state, 30 min after TPEN addition, and at the saturation level after Mn²⁺ addition respectively.

Fractional saturation (FS) was calculated according to the following equation:⁴⁹

where X is the mean fluorescence intensity at the resting state, F_min is the mean fluorescence intensity 30 min after addition of TPEN and F_max is the mean fluorescence intensity at the saturation level after Mn²⁺ addition.

From the FS, intracellular labile Mn²⁺ concentration was estimated according to the following equation:⁴⁹

where K_d is the dissociation constant of M4 in aqueous buffer with Mn²⁺.

FS and [Mn²⁺] for 12 individual unique cells from three different independent experiments (4 from each experiment) were calculated and the average value has been reported as an estimate of the intracellular labile Mn²⁺ concentration.

Time resolved fluorescence measurements

For fluorescence lifetime measurements, the probe solution was excited at 480 nm by using a DeltaFlex Time Correlated Single Photon Counting (TCSPC) spectrometer. The vertically polarized second harmonic of the output of a Mai-Tai laser, with a repetition rate of 10 MHz, was used to excite the samples. Emission was collected (at 90° to the excitation beam) at 514 nm using a 32 nm slit width. No filter was used. The instrument response function (IRF) was taken at 480 nm and was calculated to be 68 ps (FWHM). For all the fluorescence lifetime measurements, peak counts of 3000 were collected with the emission polarizer oriented at the magic angle (54.7°) with respect to the excitation polarizer. Fluorescence lifetimes of samples containing only M4 (2 μM) and samples containing both M4 (2 μM) and Mn²⁺ (20 μM) were recorded. The decay was de-convoluted with respect to the IRF and fitted using a three-exponential model.

I(t) = Σα_i exp(−t/τ_i)

where I(t) is the fluorescence intensity at time t and α_i is the amplitude of the i^th lifetime τ_i such that Σα_i = 1. The goodness of fit was determined by monitoring the χ² values and residuals.

Average lifetime (τ_m) values were calculated from the equation:

τ_m = Σα_iτ_i

All lifetime data for M4 and M4 with Mn²⁺ were recorded in triplicate. Error bars represent standard deviations.

Fluorescence lifetime imaging microscopy

Fluorescence lifetime images were recorded in a Leica TCS SP8 X equipped with a FLIM module. Live cells were excited using a white light laser set at 514 nm. The confocal image was captured with a 60× oil objective and then the FLIM images were recorded by switching the excitation laser to a pulsed laser. For FLIM imaging, a 514 nm picosecond pulse laser at 80 MHz pulse frequency was used for excitation. Emission was collected from 540 to 650 nm until the photon count reached 500 per pixel. The instrument response function (IRF) was taken at 514 nm and was calculated to be 224 ps (FWHM). The cells were washed with TB and incubated with M4 (5 μM in TB) for 15 min at 37 °C. After incubation, the cells were washed with TB and imaged. For Mn treatment, cells were incubated with MnCl₂ (25 μM in TB) for 1 h at 37 °C. Then the cells were washed with TB to remove excess MnCl₂, stained with M4 as mentioned above and imaged. Fluorescence lifetime distributions in cells were analyzed on Leica Lax X software. Data from each image pixel was fitted to a three-component exponential decay function to extract the average fluorescence lifetime at each pixel. Color-coded representation of the average lifetime distribution within living cells under both Mn²⁺ untreated and exogenously treated conditions is presented in Fig. 4b.

Imaging Mn²⁺ dynamics in living cells

HeLa cells were used in a pathophysiological context mimicking conditions of hypermanganesemia and Mn induced Parkinsonism caused by deactivating mutations in SLC30A10. To generate cells expressing the transporter, SLC30A10 plasmid with an ampicillin resistant insert was amplified in DH5α cells in agar medium containing ampicillin. The extracted, amplified SLC30A10 plasmid was then transiently transfected into a suspension of HeLa cells, using Lipofectamine 3000 in OptiMEM. The suspension was then plated on home-made glass coverslip bottomed Petri plates (35 mm diameter, Tarsons) coated with polylysine (200 μg mL⁻¹). To check whether M4 had the requisite photo-stability for prolonged time-dependent dynamic uptake studies, cells were incubated with M4 (5 μM in TB) for 15 min. After 15 min, cells were washed with TB and imaged for 1 h at intervals of 3 min. For time-dependent Mn²⁺ uptake imaging studies, cells were incubated with M4 (5 μM in TB) for 15 min. After 15 min, cells were washed with TB three times and imaged. MnCl₂ (25 μM in TB) was then added and time-dependent imaging was started immediately after addition. Images were recorded at an interval of 3 min for 1 h. The image recorded before addition of MnCl₂ was taken as the image at 0 min.

Data availability

All datasets supporting this article have either been uploaded as part of the ESI† or are available upon request to the corresponding author.

Author contributions

A. D., S.·K., and S. K. D. designed and conceptualized the project, performed the experiments, analyzed the data, and wrote the paper. K. G. participated in optimizations of control experiments. Raj. K. participated in cell experiments. R. V., S. K., S. K. D., Rav. K., and K. G. participated in computational studies. A. N. and B.·B. participated in FLIM experiments. All authors checked the results and the manuscript and approved the final version of the manuscript.

Conflicts of interest

The authors declare no competing interest.

Acknowledgements

A. D. acknowledges the support of the Department of Atomic Energy, Government of India, under Project Identification No. RTI4003 and Indo-French Centre for the Promotion of Advanced Research – CEFIPRA under Project No. 6505-1. The authors acknowledge Prof. Anindya Datta, Arkaprava Chowdhury and the TCSPC facility, S.A.I.F, I.I.T. Bombay for help with TCSPC experiments; Prof. Deepak Saini, Suchetha K. S. and the Bio-Imaging facility, Department of Biological Sciences, IISc, Bangalore for help with FLIM experiments; Prof. Somshuvra Mukhopadhyay for sharing SLC30A10 WT plasmids and Ms Deepika Furtado for help with plasmid amplification and isolation; Ms Mamata Joshi and Mr Devidas Jadhav, National NMR facility, TIFR, and NMR facility, I.I.T. Bombay; DCS Cell Culture facility; and Mass Laboratory, Chemistry Dept., I.I.T. Bombay and I.I.S.E.R., Pune.

References

1. Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Crystal structure of oxygen-evolving photosystem II at a resolution of 1.9 Å, Nature, 2011, 473(7345), 55–60,  DOI:10.1038/nature09913.
2. K. Barnese, E. B. Gralla, J. S. Valentine and D. E. Cabelli, Biologically relevant mechanism for catalytic superoxide removal by simple manganese compounds, Proc. Natl. Acad. Sci. U.S.A., 2012, 109(18), 6892–6897,  DOI:10.1073/pnas.1203051109.
3. S. M. Damo, T. E. Kehl-Fie, N. Sugitani, M. E. Holt, S. Rathi, W. J. Murphy, Y. Zhang, C. Betz, L. Hench and G. Fritz, et al., Molecular basis for manganese sequestration by calprotectin and roles in the innate immune response to invading bacterial pathogens, Proc. Natl. Acad. Sci. U.S.A., 2013, 110(10), 3841–3846,  DOI:10.1073/pnas.1220341110.
4. M. B. Brophy and E. M. Nolan, Manganese and Microbial Pathogenesis: Sequestration by the Mammalian Immune System and Utilization by Microorganisms, ACS Chem. Biol., 2015, 10(3), 641–651,  DOI:10.1021/cb500792b.
5. S. Das, K. Khatua, A. Rakshit, A. Carmona, A. Sarkar, S. Bakthavatsalam, R. Ortega and A. Datta, Emerging chemical tools and techniques for tracking biological manganese, Dalton Trans., 2019, 48(21), 7047–7061,  10.1039/C9DT00508K.
6. Y. Chiba, T. Miyakawa, Y. Shimane, K. Takai, M. Tanokura and T. Nozaki, Structural comparisons of phosphoenolpyruvate carboxykinases reveal the evolutionary trajectories of these phosphodiester energy conversion enzymes, J. Biol. Chem., 2019, 294(50), 19269–19278,  DOI:10.1074/jbc.RA119.010920.
7. V. C. Culotta, M. Yang and T. V. O'Halloran, Activation of superoxide dismutases: putting the metal to the pedal, Biochim. Biophys. Acta Mol. Cell Res., 2006, 1763(7), 747–758,  DOI:10.1016/j.bbamcr.2006.05.003.
8. M. J. Daly, E. K. Gaidamakova, V. Y. Matrosova, A. Vasilenko, M. Zhai, A. Venkateswaran, M. Hess, M. V. Omelchenko, H. M. Kostandarithes and K. S. Makarova, et al., Accumulation of Mn(II) in Deinococcus radiodurans Facilitates Gamma-Radiation Resistance, Science, 2004, 306(5698), 1025–1028,  DOI:10.1126/science.1103185.
9. L. Di Costanzo, M. E. Pique and D. W. Christianson, Crystal Structure of Human Arginase I Complexed with Thiosemicarbazide Reveals an Unusual Thiocarbonyl μ-Sulfide Ligand in the Binuclear Manganese Cluster, J. Am. Chem. Soc., 2007, 129(20), 6388–6389,  DOI:10.1021/ja071567j.
10. A. R. Reddi, L. T. Jensen and V. C. Culotta, Manganese Homeostasis in Saccharomyces cerevisiae, Chem. Rev., 2009, 109(10), 4722–4732,  DOI:10.1021/cr900031u.
11. A. Sharma, E. K. Gaidamakova, V. Y. Matrosova, B. Bennett, M. J. Daly and B. M. Hoffman, Responses of Mn²⁺ speciation in Deinococcus radiodurans and Escherichia coli to γ-radiation by advanced paramagnetic resonance methods, Proc. Natl. Acad. Sci. U.S.A., 2013, 110(15), 5945–5950,  DOI:10.1073/pnas.1303376110.
12. Y. Sheng, I. A. Abreu, D. E. Cabelli, M. J. Maroney, A.-F. Miller, M. Teixeira and J. S. Valentine, Superoxide Dismutases and Superoxide Reductases, Chem. Rev., 2014, 114(7), 3854–3918,  DOI:10.1021/cr4005296.
13. L. C. Tabares and S. Un, In situ Determination of Manganese(II) Speciation in Deinococcus radiodurans by High Magnetic Field EPR: Detection of High Levels of Mn(II) Bound to Proteins, J. Biol. Chem., 2013, 288(7), 5050–5055,  DOI:10.1074/jbc.C112.444992.
14. A. B. Bowman and M. Aschner, Considerations on manganese (Mn) treatments for in vitro studies, Neurotoxicology, 2014, 41, 141–142,  DOI:10.1016/j.neuro.2014.01.010.
15. R. L. McNaughton, A. R. Reddi, M. H. S. Clement, A. Sharma, K. Barnese, L. Rosenfeld, E. B. Gralla, J. S. Valentine, V. C. Culotta and B. M. Hoffman, Probing in vivo Mn²⁺ speciation and oxidative stress resistance in yeast cells with electron-nuclear double resonance spectroscopy, Proc. Natl. Acad. Sci. U.S.A., 2010, 107(35), 15335–15339,  DOI:10.1073/pnas.1009648107.
16. P. A. Doble and G. L. G. Miklos, Distributions of manganese in diverse human cancers provide insights into tumour radioresistance, Metallomics, 2018, 10(9), 1191–1210,  10.1039/c8mt00110c.
17. M. Lv, M. Chen, R. Zhang, W. Zhang, C. Wang, Y. Zhang, X. Wei, Y. Guan, J. Liu and K. Feng, et al., Manganese is critical for antitumor immune responses via cGAS-STING and improves the efficacy of clinical immunotherapy, Cell Res., 2020, 30(11), 966–979,  DOI:10.1038/s41422-020-00395-4.
18. J. M. Rozenberg, M. Kamynina, M. Sorokin, M. Zolotovskaia, E. Koroleva, K. Kremenchutckaya, A. Gudkov, A. Buzdin and N. Borisov, The Role of the Metabolism of Zinc and Manganese Ions in Human Cancerogenesis, Biomedicines, 2022, 10(5), 1072,  DOI:10.3390/biomedicines10051072.
19. K. Tuschl, P. T. Clayton, S. M. Gospe, S. Gulab, S. Ibrahim, P. Singhi, R. Aulakh, R. T. Ribeiro, O. G. Barsottini and M. S. Zaki, et al., Syndrome of Hepatic Cirrhosis, Dystonia, Polycythemia, and Hypermanganesemia Caused by Mutations in SLC30A10, a Manganese Transporter in Man, Am. J. Hum. Genet., 2012, 90(3), 457–466,  DOI:10.1016/j.ajhg.2012.01.018.
20. L.-I. Dinorah, C. Pan, E. Z. Charles, H. Steven, M. M. Jonathan, D. S. Caleb, A. M. Richard, B. B. Aaron, A. Michael and M. Somshuvra, SLC30A10 Is a Cell Surface-Localized Manganese Efflux Transporter, and Parkinsonism-Causing Mutations Block Its Intracellular Trafficking and Efflux Activity, J. Neurosci., 2014, 34(42), 14079,  DOI:10.1523/JNEUROSCI.2329-14.2014.
21. K. Tuschl, E. Meyer, L. E. Valdivia, N. Zhao, C. Dadswell, A. Abdul-Sada, C. Y. Hung, M. A. Simpson, W. K. Chong and T. S. Jacques, et al., Mutations in SLC39A14 disrupt manganese homeostasis and cause childhood-onset parkinsonism–dystonia, Nat. Commun., 2016, 7(1), 11601,  DOI:10.1038/ncomms11601.
22. C. E. Zogzas, M. Aschner and S. Mukhopadhyay, Structural Elements in the Transmembrane and Cytoplasmic Domains of the Metal Transporter SLC30A10 Are Required for Its Manganese Efflux Activity, J. Biol. Chem., 2016, 291(31), 15940–15957,  DOI:10.1074/jbc.M116.726935.
23. A. Carmona, C. E. Zogzas, S. Roudeau, F. Porcaro, J. Garrevoet, K. M. Spiers, M. Salomé, P. Cloetens, S. Mukhopadhyay and R. Ortega, SLC30A10 Mutation Involved in Parkinsonism Results in Manganese Accumulation within Nanovesicles of the Golgi Apparatus, ACS Chem. Neurosci., 2019, 10(1), 599–609,  DOI:10.1021/acschemneuro.8b00451.
24. C. J. da Silva, A. José da Rocha, M. F. Mendes, A. P. S. d. M. Braga and S. Jeronymo, Brain Manganese Deposition Depicted by Magnetic Resonance Imaging in a Welder, Arch. Neurol., 2008, 65(7), 983,  DOI:10.1001/archneur.65.7.983.
25. S. Bakthavatsalam, S. Das Sharma, M. Sonawane, V. Thirumalai and A. Datta, A zebrafish model of manganism reveals reversible and treatable symptoms that are independent of neurotoxicity, Dis. Models Mech., 2014, 7(11), 1239–1251,  DOI:10.1242/dmm.016683.
26. S. L. O'Neal and W. Zheng, Manganese Toxicity Upon Overexposure: a Decade in Review, Curr. Environ. Health Rep., 2015, 2(3), 315–328,  DOI:10.1007/s40572-015-0056-x.
27. R. Bagur and G. Hajnóczky, Intracellular Ca²⁺ Sensing: Its Role in Calcium Homeostasis and Signaling, Mol. Cell, 2017, 66(6), 780–788,  DOI:10.1016/j.molcel.2017.05.028.
28. J. Liang and J. W. Canary, Discrimination between Hard Metals with Soft Ligand Donor Atoms: An On-Fluorescence Probe for Manganese(II), Angew. Chem., Int. Ed., 2010, 49(42), 7710–7713,  DOI:10.1002/anie.201002853.
29. F. Gruppi, J. Liang, B. B. Bartelle, M. Royzen, D. H. Turnbull and J. W. Canary, Supramolecular metal displacement allows on-fluorescence analysis of manganese(II) in living cells, Chem. Commun., 2012, 48(87), 10778–10780,  10.1039/C2CC34742C.
30. S. Bakthavatsalam, A. Sarkar, A. Rakshit, S. Jain, A. Kumar and A. Datta, Tuning macrocycles to design ‘turn-on’ fluorescence probes for manganese(II) sensing in live cells, Chem. Commun., 2015, 51(13), 2605–2608,  10.1039/C4CC09542A.
31. S. Adhikari, A. Ghosh, A. Sahana, S. Guria and D. Das, Tailoring Ligand Environment toward Development of Colorimetric and Fluorescence Indicator for Biological Mn(II) Imaging, Anal. Chem., 2016, 88(2), 1106–1110,  DOI:10.1021/acs.analchem.5b03551.
32. H. Fan, C. E. McGhee, R. J. Lake, Z. Yang, Z. Guo, X.-B. Zhang and Y. Lu, A Highly Selective Mn(II)-Specific DNAzyme and Its Application in Intracellular Sensing, JACS Au, 2023, 3(6), 1615–1622,  DOI:10.1021/jacsau.3c00062.
33. J. Park, M. B. Cleary, D. Li, J. A. Mattocks, J. Xu, H. Wang, S. Mukhopadhyay, E. M. Gale and J. A. Cotruvo, A genetically encoded fluorescent sensor for manganese(II), engineered from lanmodulin, Proc. Natl. Acad. Sci. U.S.A., 2022, 119(51), e2212723119,  DOI:10.1073/pnas.2212723119.
34. H. Irving and R. J. P. Williams, 637. The stability of transition-metal complexes, J. Chem. Soc., 1953, 3192–3210,  10.1039/JR9530003192.
35. K. P. Carter, A. M. Young and A. E. Palmer, Fluorescent sensors for measuring metal ions in living systems, Chem. Rev., 2014, 114(8), 4564–4601,  DOI:10.1021/cr400546e.
36. J. Cody, S. Mandal, L. Yang and C. J. Fahrni, Differential Tuning of the Electron Transfer Parameters in 1,3,5-Triarylpyrazolines: A Rational Design Approach for Optimizing the Contrast Ratio of Fluorescent Probes, J. Am. Chem. Soc., 2008, 130(39), 13023–13032,  DOI:10.1021/ja803074y.
37. S. Das, A. Sarkar, A. Rakshit and A. Datta, A Sensitive Water-Soluble Reversible Optical Probe for Hg²⁺ Detection, Inorg. Chem., 2018, 57(9), 5273–5281,  DOI:10.1021/acs.inorgchem.8b00310.
38. A. M. McGuire, B. J. Cuthbert, Z. Ma, K. D. Grauer-Gray, M. Brunjes Brophy, K. A. Spear, S. Soonsanga, J. I. Kliegman, S. L. Griner and J. D. Helmann, et al., Roles of the A and C Sites in the Manganese-Specific Activation of MntR, Biochemistry, 2013, 52(4), 701–713,  DOI:10.1021/bi301550t.
39. D. Salvemini, D. P. Riley and S. Cuzzocrea, Sod mimetics are coming of age, Nat. Rev. Drug Discovery, 2002, 1(5), 367–374,  DOI:10.1038/nrd796.
40. D. Rehm and A. Weller, Kinetics of Fluorescence Quenching by Electron and H-Atom Transfer, Isr. J. Chem., 1970, 8, 259–271,  DOI:10.1002/ijch.197000029.
41. R. A. Marcus and N. Sutin, Electron transfers in chemistry and biology, Biochim. Biophys. Acta Bioenerg., 1985, 811(3), 265–322,  DOI:10.1016/0304-4173(85)90014-X.
42. P. Batat, G. Vives, R. Bofinger, R.-W. Chang, B. Kauffmann, R. Oda, G. Jonusauskas and N. D. McClenaghan, Dynamics of ion-regulated photoinduced electron transfer in BODIPY-BAPTA conjugates, Photochem. Photobiol. Sci., 2012, 11(11), 1666–1674,  10.1039/c2pp25130b.
43. C. E. Outten and T. V. O’Halloran, Femtomolar Sensitivity of Metalloregulatory Proteins Controlling Zinc Homeostasis, Science, 2001, 292(5526), 2488–2492,  DOI:10.1126/science.1060331.
44. A. W. Foster, R. Pernil, C. J. Patterson, A. J. P. Scott, L.-O. Pålsson, R. Pal, I. Cummins, P. T. Chivers, E. Pohl and N. J. Robinson, A tight tunable range for Ni(II) sensing and buffering in cells, Nat. Chem. Biol., 2017, 13(4), 409–414,  DOI:10.1038/nchembio.2310.
45. E. L. Que, D. W. Domaille and C. J. Chang, Metals in Neurobiology: Probing Their Chemistry and Biology with Molecular Imaging, Chem. Rev., 2008, 108(5), 1517–1549,  DOI:10.1021/cr078203u.
46. A. Carmona, S. Roudeau, L. Perrin, G. Veronesi and R. Ortega, Environmental manganese compounds accumulate as Mn(II) within the Golgi apparatus of dopamine cells: relationship between speciation, subcellular distribution, and cytotoxicity, Metallomics, 2014, 6(4), 822–832,  10.1039/c4mt00012a.
47. S. Das, A. Carmona, K. Khatua, F. Porcaro, A. Somogyi, R. Ortega and A. Datta, Manganese Mapping Using a Fluorescent Mn²⁺ Sensor and Nanosynchrotron X-ray Fluorescence Reveals the Role of the Golgi Apparatus as a Manganese Storage Site, Inorg. Chem., 2019, 58(20), 13724–13732,  DOI:10.1021/acs.inorgchem.9b01389.
48. R. Tsien and T. Pozzan, Measurement of cytosolic free Ca2+ with quin2, Methods Enzymol., 1989, 172, 230–262,  DOI:10.1016/s0076-6879(89)72017-6.
49. L. Sanford and A. E. Palmer, Dissociated Hippocampal Neurons Exhibit Distinct Zn²⁺ Dynamics in a Stimulation-Method-Dependent Manner, ACS Chem. Neurosci., 2020, 11(4), 508–514,  DOI:10.1021/acschemneuro.0c00006.
50. A. Kaur, M. A. Haghighatbin, C. F. Hogan and E. J. New, A FRET-based ratiometric redox probe for detecting oxidative stress by confocal microscopy, FLIM and flow cytometry, Chem. Commun., 2015, 51(52), 10510–10513,  10.1039/C5CC03394B.
51. D. Rupsa, G. Amani, S. Matthew and C. S. Melissa, Recent innovations in fluorescence lifetime imaging microscopy for biology and medicine, J. Biomed. Opt., 2021, 26(7), 070603,  DOI:10.1117/1.JBO.26.7.070603.
52. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592,  DOI:10.1002/jcc.22885.
53. R. J. Cave and M. D. Newton, Generalization of the Mulliken-Hush treatment for the calculation of electron transfer matrix elements, Chem. Phys. Lett., 1996, 249(1), 15–19,  DOI:10.1016/0009-2614(95)01310-5.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of DFT and TDDFT calculations, synthesis, and characterization of novel molecules via LC-ESI-MS, ¹H-NMR and ¹³C-NMR, fluorescence experiments, cytotoxicity assay, cell studies, photostability assay, Mn²⁺ uptake studies, TCSPC and FLIM experiments (PDF). Supporting videos of live imaging of Mn²⁺ dynamics: Videos S1 and S2 (MP4). See DOI: https://doi.org/10.1039/d4sc00907j

‡ Equal contribution.

---