Open Access Article
Open Access ArticleCluster analysis as a tool for quantifying structure–transport properties in simulations of superconcentrated electrolyte†
Sheng
Bi
 ab and
Mathieu
Salanne
ab and
Mathieu
Salanne
 *abc
*abc
aSorbonne Université, CNRS, Physicochimie des Électrolytes et Nanosystèmes Interfaciaux, F-75005 Paris, France. E-mail: mathieu.salanne@sorbonne-universite.fr
bRéseau sur le Stockage Electrochimique de l'Energie (RS2E), FR CNRS 3459, 80039 Amiens Cedex, France
cInstitut Universitaire de France (IUF), 75231 Paris, France
First published on 10th June 2024
Abstract
Using molecular dynamics simulations and graph-theory-based cluster analysis, we investigate the structure–transport properties of typical water-in-salt electrolytes. We demonstrate that ions exhibit distinct dynamics across different ionic clusters—namely, solvent-separated ion pairs (SSIPs), contact ion pairs (CIPs), and aggregates (AGGs). We assess the average proportions of various ionic species and their lifetimes. Our method reveals a dynamic decoupling of ion kinetics, with each species independently contributing to the overall molecular motion. This is evidenced by the fact that the total velocity autocorrelation function (VACF) and power spectrum can be expressed as a weighted sum of independent functions for each species. The experimental data on the ionic conductivity of the studied LiTFSI electrolytes align well with our theoretical predictions at various concentrations, based on the proportions and diffusion coefficients of free ions derived from our analysis. The insights gained into the solvation structures and dynamics of different ionic species enable us to elucidate the physical mechanisms driving ion transport in such superconcentrated electrolytes, providing a comprehensive framework for the future design and optimization of electrolytes.
1 Introduction
Water-in-salt electrolytes (WiSEs) represent a significant advancement in electrochemical energy storage, emerging as a promising alternative to traditional organic electrolytes in applications such as lithium metal batteries (LMBs).1–9 These electrolytes typically contain small alkali cations, such as lithium ions (Li+), and often incorporate large fluorinated anions like bis(trifluoromethane)sulfonimide (TFSI−). However, there exist ones that feature halogen-free anions.10 WiSEs are characterized by their very high salt concentration, where the salt content exceeds that of the solvent in both mass and volume. This unique property affects the reactivity of water11 and allow for the formation of a SEI, which leads to enhanced electrochemical stability windows (ESW) compared to diluted aqueous electrolytes.12,13 Moreover, WiSEs offer advantages in terms of safety, cost-effectiveness, and environmental sustainability, along with superior transport properties compared to most traditional organic electrolytes.14Many experimental and computational studies have depicted the unconventional ion solvation structures in WiSEs as distinct from those in dilute aqueous solutions.2,15–18 For instance, in a 21 m LiTFSI WiSE, water molecules primarily bind in Li+ solvation shells, which inhibits the undesired reactions involving free water.2,19 Furthermore, contrary to dilute solutions where ions typically exist as solvent-separated ion pairs (SSIPs), the water content in the 21 m LiTFSI WiSE is insufficient to fully solvate all Li+ ions.2,15 This results in direct contact between Li+ and TFSI− ions, leading to forming contact ion pairs (CIPs) and ionic aggregates (AGGs).
As reported, ion species wherein TFSI− coordinate with multiple Li+ ions positively contribute to the formation of a robust and conductive solid electrolyte interphase (SEI).20 Consequently, recent explorations in electrolyte design are focusing on manipulating solvation structures.21–23 For example, recent studies on the binary ionic liquid/Li salt electrolytes demonstrated that the Li+ transport mechanism can be tailored through the coordination of Li ions to the ionic liquid ions.24,25 Other approaches have also been explored, including mixing different salts26–28 and incorporating diluent into WiSEs to produce localized high-concentration electrolytes (LHCEs).29–31 The idea is to tailor chemical species around the ions' primary solvation shell, which facilitates controlled SEI formation and enhancing LMB performance.
The proportion of ionic species in form of SSIP, CIP, and AGG can be evaluated through both experimental and computational methods, including high-resolution spectral deconvolution16,32 and cluster analysis in molecular simulations.15,33–36 In particular, several simulation/theoretical studies have attempted to capture ionic associations in ionic liquids and salt-in-ionic liquid electrolytes.37–41 For instance, Feng et al. revealed that ions in ionic liquids may reside in the free and bound states, and the ionic conductivity can be well-predicted by their modified Nernst–Einstein equation, neglecting correlations and only accounting for free ions.37 Molinari et al. investigated the spatial ionic coordination in the salt-in-ionic liquid electrolytes, and developed a single-linkage cluster analysis method to compute the effective lithium charge.38 They further developed the spectral denoising method for the short-time ionic displacement covariance to identify diffusing clusters.39 These approaches appear applicable for computing the transport properties of WiSEs; however, questions such as the dynamics of ions in various ionic species and their role in transport remain largely unclear.
To address this, we conducted molecular dynamics (MD) simulations on aqueous lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) electrolyte at various concentrations. We explored the distinctive dynamics of SSIPs, CIPs, and AGGs (identified using a graph theory-based method) in both highly concentrated and diluted conditions. We found that the kinetics of ions in the studied systems are dynamically decoupled, with each species contributing independently to the overall molecular motion. Additionally, our findings suggest that the mechanism of ionic conductivity in the LiTFSI electrolytes, regardless of salt concentrations, is primarily driven by the vehicular movement of SSIPs.
2 Results
2.1 Ion clustering in the water-in-salt case
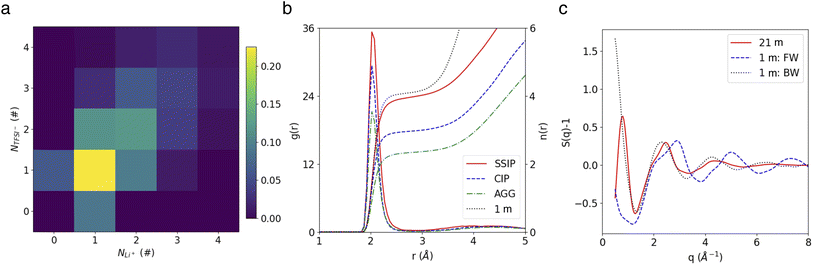
Our MD trajectories were analyzed using a graph theory-based method, in order to extract all the relevant species. In the highly concentrated 21 m LiTFSI electrolyte, in which the dissolved salts significantly outnumber water molecules, ion paring and clustering are intricate. As depicted in Fig. 1a, the studied WiSE hosts a variety of clusters, ranging from free Li+ and TFSI− ions to ion pairs and larger clusters like Li3(TFSI)4−. Analysis of cluster populations reveals that ion pairs (LiTFSI) make up 22.5% of the total, followed by neutral ion tetramers (Li2(TFSI)2) at 12.1%. Ion triplets, specifically Li(TFSI)2− and Li2TFSI+, account for 11.6% and 9.6%, respectively. Notably, free Li+ and TFSI− ions constitue only marginal fractions of 9.0% and 6.2%, respectively. The aggregate Li2(TFSI)3− forms 6.2% of total, exceeding the free TFSI−, while other higher-order aggregates are less common, each representing less than 5% of total.Fig. 1b shows the radial distribution functions (RDFs) of O atom in water molecule regarding Li+ in different species. Note that here and after, the group AGGs include all aggregates involving three or more ions. It shows that the lone Li+ ions identified by our cluster analysis method (see Methods) are fully solvated, as indicated by the number of water molecules in their primary solvation shell, which matches the value observed in the diluted (1 m) electrolyte case (both have 4H2O). In contrast, the water coordination numbers for Li+ ions in ion pairs and aggregates are reduced to 3 and 2, respectively. Representative snapshots highlighting different solvation structures are shown in Fig. S4.†
The water network structure in the 21 m WiSE was also analyzed in terms of partial water O–O structure factors (SOO(Q)), comparing it to the dilute 1 m electrolyte (Fig. 1c). First, a virtual diffraction experiment was conducted for the 1 m case to measure the SOO(Q) of water in the Li+ first solvation shells (bound water) and beyond (free water), c.f., blue dashed line and black dotted line in Fig. 1c. It reveals distinct peaks for free and bound water in their SOO(Q) (∼2.4 Å−1 and 2.9 Å−1, respectively), which can be attributed to changes in water topology (Fig. S5b†), as previously explained in a recent study.42
In the 21 m WiSE, peaks similar to the ones observed for bound water in the 1 M electrolyte are present in its SOO(Q), reflecting the fact that there is very few free water in such a concentrated condition. Additionally, a small low-Q peak (∼0.8 Å−1) is observed in the 21 m electrolyte but absent in the 1 m case, that indicates the presence of a nanostructure on the scale of ∼8 Å. The SOO(Q) of water bound to different ionic species reveal that this peak arises from water bound to AGGs (Fig. S5c†). Moreover, a third coordination shell located at ∼8 Å is observed in the RDF of AGG-bound water (Fig. S5d†), suggesting the formation of hydrogen-bond chains with a third water molecule. The existence of such nano-heterogeneity has also been highlighted in the work of Borodin et al.15
The velocity autocorrelation function (VACF), denoted as 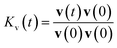 , has been computed for Li+ and TFSI− in various ionic species to further characterize their dynamics. As illustrated in Fig. 2a, the Kv(t) of Li+ ions displays a pattern of damped oscillations, alternating between positive and negative correlations over time. This could be attributed to backscattering caused by Li+ oscillations within a cage (see Fig. S4†) formed by the surrounding solvation molecules. This oscillatory behavior is more noticeable for free Li+ ions compared to those CIPs and AGGs. Regarding Li+ in ionic clusters, as the number of TFSI− in the solvation shell increases, cation's backscattering effect weakens, suggesting an easier escape of Li+ from the cage. In contrast, the Kv(t) of TFSI− does not show such alternating oscillations in any species. They transition from 1 to a negative value and then asymptotically approach zero. This pattern results from their weaker interaction with water compared to Li+ ions, leading to less pronounced ion rattling. Nevertheless, deviations can still be observed in the Kv(t) curves for anions in different species, indicating diverse dynamical behaviors among the distinct ionic species.
, has been computed for Li+ and TFSI− in various ionic species to further characterize their dynamics. As illustrated in Fig. 2a, the Kv(t) of Li+ ions displays a pattern of damped oscillations, alternating between positive and negative correlations over time. This could be attributed to backscattering caused by Li+ oscillations within a cage (see Fig. S4†) formed by the surrounding solvation molecules. This oscillatory behavior is more noticeable for free Li+ ions compared to those CIPs and AGGs. Regarding Li+ in ionic clusters, as the number of TFSI− in the solvation shell increases, cation's backscattering effect weakens, suggesting an easier escape of Li+ from the cage. In contrast, the Kv(t) of TFSI− does not show such alternating oscillations in any species. They transition from 1 to a negative value and then asymptotically approach zero. This pattern results from their weaker interaction with water compared to Li+ ions, leading to less pronounced ion rattling. Nevertheless, deviations can still be observed in the Kv(t) curves for anions in different species, indicating diverse dynamical behaviors among the distinct ionic species.
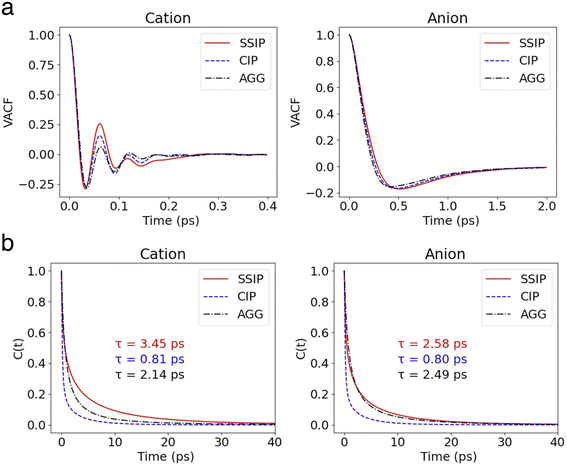 | ||
| Fig. 2 (a) VACFs of cations and anions in different states. (b) The survival probability functions of cations and anions in different states. Their corresponding lifetime are labeled in the figure. | ||
We further delved into the interstate exchange processes among the ionic species. These processes could be quantified by the survival probability function c(t),37 defined as 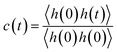 , where h(t) is a population variable set to one if an ion continuously remains in the same species for a time duration t, and zero otherwise. The mean residence time τ is then computed as
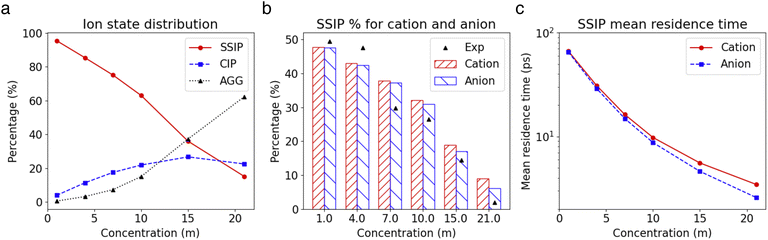
, where h(t) is a population variable set to one if an ion continuously remains in the same species for a time duration t, and zero otherwise. The mean residence time τ is then computed as 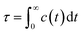 for each ionic species. The c(t) as well as τ for Li+ and TFSI− in the forms of SSIPs, CIPs and AGGs are depicted in Fig. 2b. Notably, the computed residence time is on the order of 1 ps, which is significant in the sense that by the time τ elapses, the corresponding Kv(t) of each type of species has already damped to near zeros (Fig. 2a). In other words, the VACFs die out faster than the transitions between ionic species occur. Moreover, the residence time of ions in AGGs is similar to that of SSIPs (e.g., 2.49 ps vs. 2.28 ps for the AGG and SSIP anions). However, a more detailed breakdown of AGGs into specific ionic clusters reveals that the residence time decreases exponentially with increasing cluster size (as shown in Fig. S6†), suggesting that processes like the merging of smaller clusters into larger ones and the reverse are prevalent in AGGs.
for each ionic species. The c(t) as well as τ for Li+ and TFSI− in the forms of SSIPs, CIPs and AGGs are depicted in Fig. 2b. Notably, the computed residence time is on the order of 1 ps, which is significant in the sense that by the time τ elapses, the corresponding Kv(t) of each type of species has already damped to near zeros (Fig. 2a). In other words, the VACFs die out faster than the transitions between ionic species occur. Moreover, the residence time of ions in AGGs is similar to that of SSIPs (e.g., 2.49 ps vs. 2.28 ps for the AGG and SSIP anions). However, a more detailed breakdown of AGGs into specific ionic clusters reveals that the residence time decreases exponentially with increasing cluster size (as shown in Fig. S6†), suggesting that processes like the merging of smaller clusters into larger ones and the reverse are prevalent in AGGs.
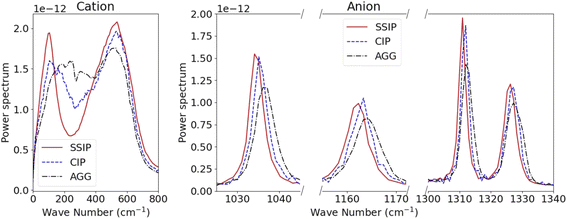
The power spectrum S(w) of Li+ and TFSI− in SSIPs, CIPs and AGGs are compared to understand the impact of solvation structures on the ions' vibrational modes. In the case of Li+ ions, a bi-modal spectral distribution is observed for SSIP Li+ – the lower frequency mode, observed near 100 cm−1, corresponds to the ‘rattling mode’ of a Li+ confined within the surrounding water cage; the higher frequency mode, occurring near 600 cm−1, is likely associated with the Li+ ion engaging in the scissoring motion of an adjacent oxygen atom in a water molecule (Fig. 3). For Li+ in CIPs and AGGs, this bi-modal vibration pattern becomes less pronounced.
For TFSI− ions, the influence of ion clustering on their intramolecular vibrations is evident in three distinct frequency modes, as shown in Fig. 3b. The mode at approximately 1035 cm−1 is linked to asymmetric S–N–S stretching; the modes at ∼1165 cm−1 and the bi-modal mode at ∼1310 cm−1 and 1325 cm−1 are associated with S–O(SO2) stretching.15,43 A notable observation is the shift of these vibrational peaks to higher frequencies for TFSI− in CIPs compared to SSIP ones, with an even more pronounced shift for those in AGGs. Such blue-shifts can be attributed to the intensified cation–TFSI− interaction, which makes some of the bonds in TFSI− stiffer.
Given that the SSIPs, CIPs, and AGGs exhibit unique dynamics and their reasonably long mean residence time, the overall kinetics of such systems could potentially be modelled by integrating the kinetics of individual species with inter-species exchanges.37 For instance, the overall Kv(t) for Li+ or TFSI− ions might be expressed as a combination of the partial VACFs for each type of ionic species and their respective survival probability c(t), provided the dynamics within each species are independent. However, formulating such an expression can be complex, even when considering only two states.37 Fortunately, an approximation can be made as we observed that the kinetics of ionic species decay more rapidly than the transitions between different species (c.f., Fig. 2), denoted as Kv(t) = ∑psKvs(t), where s denotes the ionic species and ps represents its proportion. Leveraging the linearity of the Laplace transform, the overall power spectrum S(w) can be expressed as S(w) = ∑psSs(w). This approximation is verified in Fig. 4 for both cations and anions, as the MD-derived overall S(w) closely align with the sum of three distinct Ss(w) weighted by their proportions. Such strong agreement supports the notion of “dynamic decoupling” in molecular motion in the studied WiSE, as the time correlation functions for different ionic species are statistically independent.
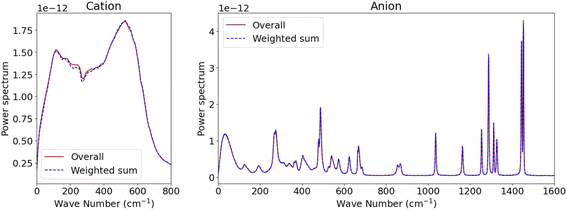 | ||
| Fig. 4 Comparison between the overall power spectrum derived from all ions and the weighted sum of partial power spectra for distinct ion species. | ||
2.2 A broader view on clustering
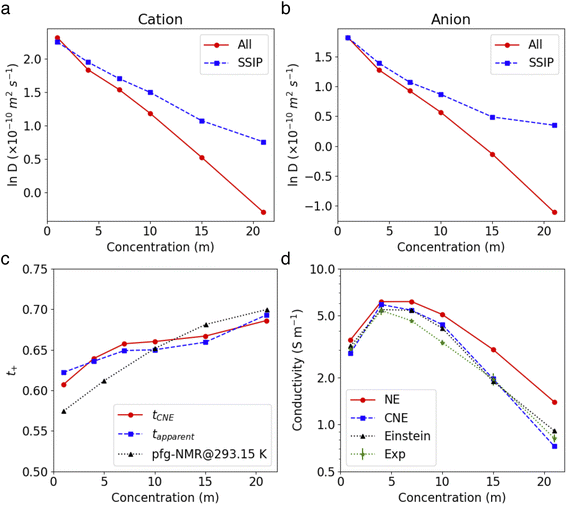
The insights gained from the analysis of the highly concentrated 21 m electrolyte underscore the accurate cluster differentiation and distinctive dynamics of ions in diverse clusters. This naturally raises subsequent questions regarding how clustering evolves across a broader range of concentrations. Fig. 5a shows the proportion of the SSIPs, CIPs, and AGGs as a function of LiTFSI concentration. As expected, in dilute solutions (i.e., cases below 10 m), ions predominantly exist as SSIPs. Conversely, in highly concentrated solutions (i.e., the 15 m and 21 m cases), there is a remarkable increase in the presence of CIPs and AGGs. Interestingly, the fractions of Li+ and TFSI− in SSIPs are nearly identical at lower salt concentrations, however, the disparity between them becomes more evident at higher concentrations, with SSIP TFSI− become consistently less prevalent than SSIP Li+ (Fig. 5b). This aligns with the finding that the mean residence time t for SSIP anions is consistently shorter than that for SSIP cations across all concentrations, and the difference grows with increasing concentration, as illustrated in Fig. 5c. Moreover, our MD predictions are also consistent with the fractions of SSIP TFSI− obtained in experiments (c.f., Fig. 5b),15 evidencing the accuracy of the obtained structure and of the cluster analysis method.The diffusion coefficients for both overall ions and SSIPs-only were computed using Green–Kubo relation, 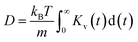 , utilizing the previously obtained overall and partial VACFs. The reason that diffusion coefficients were not obtained for CIPs and AGGs is insufficient samplings for those species in diluted cases, attributed to their scarcity. For the 1 m case, the discrepancy between the overall and SSIP-only diffusion coefficients is minimal, which can be attributed to the dominance of SSIPs in such a diluted condition. However, as the salt concentration increases, a remarkable acceleration in the diffusion of SSIPs compared to the overall average is observed. This deviation becomes increasingly pronounced with higher concentrations. This is probably due to the larger size (Fig. S7a†) and reduced mobility of AGGs in more condensed solutions, which collectively lower the overall value.
, utilizing the previously obtained overall and partial VACFs. The reason that diffusion coefficients were not obtained for CIPs and AGGs is insufficient samplings for those species in diluted cases, attributed to their scarcity. For the 1 m case, the discrepancy between the overall and SSIP-only diffusion coefficients is minimal, which can be attributed to the dominance of SSIPs in such a diluted condition. However, as the salt concentration increases, a remarkable acceleration in the diffusion of SSIPs compared to the overall average is observed. This deviation becomes increasingly pronounced with higher concentrations. This is probably due to the larger size (Fig. S7a†) and reduced mobility of AGGs in more condensed solutions, which collectively lower the overall value.
Ionic conductivity is also found to be intricately influenced by ion pairing and clustering. To compute ionic conductivity based on MD-derived trajectories, one usually uses the Nernst–Einstein (NE), i.e., 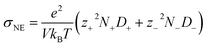 , where e is the elementary charge and kBT is Boltzmann constant, V the box volume and T the temperature. N+/N− and D+/D− are the number and self-diffusion coefficients of cations and anions, respectively. While NE equation is effective for diluted solutions, it tends to significantly overestimate the conductivity in condensed systems such as WiSEs because it does not account for ion–ion interactions.
, where e is the elementary charge and kBT is Boltzmann constant, V the box volume and T the temperature. N+/N− and D+/D− are the number and self-diffusion coefficients of cations and anions, respectively. While NE equation is effective for diluted solutions, it tends to significantly overestimate the conductivity in condensed systems such as WiSEs because it does not account for ion–ion interactions.
Nevertheless, since the overall kinetics can be approximated by summing the contributions of individual ionic species (as indicated in Fig. 4), one may modify the original NE equation to consider ionic species as independent, non-interacting species (also called cluster Nernst–Einstein (CNE) method).44 This modified equation is denoted as 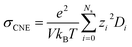 , where Ns is the total number of ionic species in the system, zi and Di are, respectively, the charge number and the diffusion coefficient of the ith ionic species. Also, note that the CIPs are neutral in charge, and for AGGs, part of them are neutral clusters, while the charged ones have small effective charge (mostly ±1, see Fig. 1 and S7b†) and diffuse much slower than the free ions (as shown in Fig. 6). Thus, the contribution from CIPs and AGGs should be marginal, and the formula can be further simplified to only account for SSIPs. In practice, we divided SSIPs into SSIP Li+ and TFSI−, as,
, where Ns is the total number of ionic species in the system, zi and Di are, respectively, the charge number and the diffusion coefficient of the ith ionic species. Also, note that the CIPs are neutral in charge, and for AGGs, part of them are neutral clusters, while the charged ones have small effective charge (mostly ±1, see Fig. 1 and S7b†) and diffuse much slower than the free ions (as shown in Fig. 6). Thus, the contribution from CIPs and AGGs should be marginal, and the formula can be further simplified to only account for SSIPs. In practice, we divided SSIPs into SSIP Li+ and TFSI−, as,
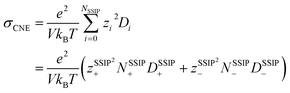 | (1) |
Fig. 6c demonstrates that the modified NE equation significantly outperforms the original NE equation in terms of precision, providing ionic conductivity values that are comparable to experimental data.15,45,46 The results obtained by Fig. 1 are also close to the values using the accurate Einstein form,45 evidencing that the dominant effect of ion–ion correlations on conductivity is the short range interactions within the clustering whereas correlations between different clusters has a minor impact. The good agreement with experimental values also justifies the effectiveness of our approach in capturing the essential dynamics of SSIPs in such electrolyte systems.
Li+ transference number was further calculated using two definitions. First, the apparent Li+ transference number is defined as 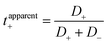 , where D+/D− are the over self-diffusion coefficients of Li+ and TFSI−, respectively. Although this definition relies on ideal solution assumptions and does not rigorously account for ion–ion and solvent–ion correlations,47 it is widely used due to the routine measurement of self-diffusion coefficients using PFG-NMR. The second definition, the Li+ transference number based on self-diffusion coefficients for each ionic species, is given as
, where D+/D− are the over self-diffusion coefficients of Li+ and TFSI−, respectively. Although this definition relies on ideal solution assumptions and does not rigorously account for ion–ion and solvent–ion correlations,47 it is widely used due to the routine measurement of self-diffusion coefficients using PFG-NMR. The second definition, the Li+ transference number based on self-diffusion coefficients for each ionic species, is given as 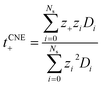 ,44,48 in which z+ is the is charge of all cations in the ith ionic species (e.g., 2 if there are 2Li+ in the cluster). One can simply the definition as
,44,48 in which z+ is the is charge of all cations in the ith ionic species (e.g., 2 if there are 2Li+ in the cluster). One can simply the definition as 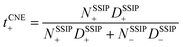 , assuming that the contribution from CIPs and AGGs is small.
, assuming that the contribution from CIPs and AGGs is small.
As demonstrated in Fig. 6d, both the theoretical and experimental apparent Li+ transference number see an increase with rising concentration. As both simulations (see Fig. 6a and b) and experiments15 show that the diffusivity of Li+ is consistently higher than that of TFSI− in these electrolytes, the tapparent+ and tPFG-NMR+ are above 0.5 across all LiTFSI concentrations. As the concentration increases, tapparent+ shows a monotonous rise, reaching about 0.69 at 21 m, which aligns excellently with experimental values (0.70). Interestingly, despite their different definitions, the computed tCNE+ is closely aligned with the tapparent+ values. Note that the tCNE+ should ideally be compared with experimental values that are based on directly measured electrophoretic mobility (e.g., through electrophoretic NMR47), but such data are yet to be reported for a direct comparison. In similar systems composed of LiTFSI–DMC, the Li+ transference number measured by eNMR did show an increase with rising salt concentration.47
The observed increase in the tCNE+ value can be attributed to two main factors: (1) a higher proportion of SSIP Li+ ions compared to SSIP TFSI− ions, and (2) the faster diffusivity of SSIP Li+ ions relative to TFSI− ions. In the cases we studied, if we were to consider only the latter aspect (the faster diffusivity of SSIP Li+), we would not observe a monotonic increase in tCNE+ as shown in Fig. S8.† This implies that the increase in tCNE+ at higher concentrations is primarily due to the rising ratio of SSIP Li+ to SSIP TFSI− ions, as indicated in Fig. 5b. This can be explained by the stronger interaction between Li+ and H2O compared to that between TFSI− and H2O. In highly concentrated systems, where the amount of water molecules is limited, this stronger interaction means that more Li+ ions are likely to be fully solvated than the TFSI− ions. Consequently, the proportion of solvated Li+ ions compared to SSIP TFSI− increases, contributing to the higher tCNE+ values observed at higher concentrations.
We further investigate the effects of salt concentration on the vibrational modes of ions. For Li+ ions, the distinct bi-modal spectral distribution becomes less pronounced as the salt concentration increases. Concurrently, TFSI− ions exhibit blue-shifts in their spectra with increasing salt concentration. These observations are consistent with our earlier findings comparing the spectra of SSIP ions and ion clusters in the 21 m electrolyte (referenced in Fig. 3). These trends can be largely attributed to the increased presence of ion pairs and clusters in more concentrated electrolytes. Interestingly, the vibrational modes of free ions in the WiSEs (i.e., 15 m and 21 m cases), for both SSIP Li+ and TFSI−, remain identical to those of the fully solvated ions in the most diluted case (as shown in Fig. 7a). This indicates that the primary motion of SSIPs is vehicular motion, which remains consistent across different salt concentration. A similar pattern is observed for AGGs; the vibrations of ions (both Li+ and TFSI−) in AGGs in the 15 m electrolyte closely resemble those in the 21 m WiSE, as depicted in Fig. 7b, suggesting the cluster size effect on ion's local bonding is minor.
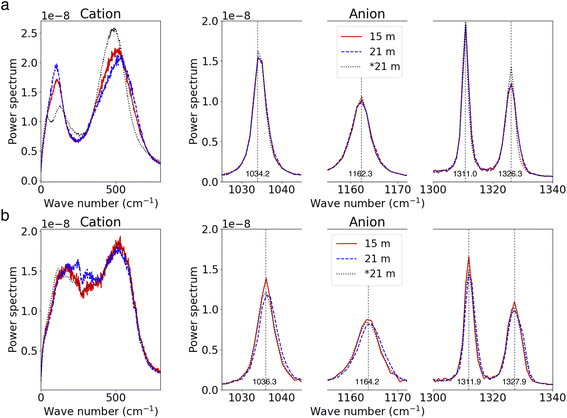 | ||
| Fig. 7 (a and b) Power spectra for SSIP ions (a) and AGG ions (b) at high and moderate salt concentrations. | ||
3 Conclusion
We have thoroughly investigated the ion solvation structures and dynamics of different ionic species in the LiTFSI–H2O system in a wide concentration range via MD simulations. For the diluted solutions, solvent-separated ion pairs are the dominant ionic species. As concentration increases, ion pairs and aggregates start to be formed and prevailing. These distinct ionic species are found to have different kinetics, in which the SSIPs diffuse faster than the CIPs and AGGs. More importantly, one could conclude that the kinetics of ions in our studied systems can be decoupled in the sense that the kinetics of each ionic species are statistically independent – the total VACF and power spectrum can be expressed as a weighted sum of independent functions of each species. Mechanism of ionic conductivity in LiTFSI–H2O systems seems mostly driven by the motion of SSIPs, as the modified NE equation accounting only SSIP ions could well reproduce conductivity computed using Einstein form (considering the cross-correlation between ions) and measured in experiments. These results not only deepen our understanding of ion transport mechanism in the condensed aqueous electrolytes but also provide a valuable framework for predicting and tailoring electrolyte properties under diverse conditions. In particular, it is worth noting that in a recent ab initio molecular dynamics study of LiTFSI at large concentration (21 m), we have observed the formation of polymer-like chains of lithium ions within the aqueous nanodomains. Although current force fields do not enable to observe their formation, the extension of our method to the analysis of the dynamics of such complex species would be straightforward.49 Other new electrolytes, that comprises even more complex species such as high entropy liquids,50 can also be studied within a similar framework, which would enable systematic comparisons of the dynamics of each species within these liquids.4 Methods
MD simulations of aqueous LiTFSI at concentrations of 1, 4, 7, 10, 15, 21 m were conducted using GROMACS MD package.51 Detailed information about the simulation cells is summarized in Table S1.† The force fields for LiTFSI were adopted from the work by Canongia Lopes et al.,52 except for the charges are uniformly scaled by a factor of 0.8 to yield accurate dynamics.45 The SPC/E model was used for water.53 The cells were cubic and set up with 3D periodic boundary conditions. The temperature was maintained at 298 K using the Nose–Hoover thermostat with a relaxation time of 0.2 ps. The Parrinello–Rahman barostat was employed to maintain a pressure of 1 bar, with a relaxation time of 2 ps, in the isothermal–isobaric (NPT) ensemble. The electrostatic interactions were computed using the particle mesh Ewald (PME) method, utilizing a fast Fourier transformation grid spacing of 0.12 nm and cubic interpolation for charge distribution in the reciprocal space. A cutoff distance of 1.2 nm was used for calculating electrostatic interactions in real space. For each concentration case, the simulation was repeated three times. Each simulation began with an initial equilibration for 10 ns in the NPT ensemble, followed by a 20 ns production run in the canonical ensemble (NVT). To compute and ensure the accuracy of the velocity autocorrelation functions and survival probability functions, each case was replicated ten times for a 100 ps production run, with atomic coordinates saved at every step and different initial configurations used for each repetition.A graph-theory-based cluster analysis method was developed and used to differentiate ionic species (see ESI†). Each ion was labeled by its belonging ionic species throughout the trajectory points. Thus, each ion trajectory contains shorter and longer fragments that can be attributed to one specific ionic species. The statistics of these states are quantified by the survival probability function (see Fig. 2b and S6†). For each ionic species, we did step-wise average across multiple corresponding trajectory fragments, ensuring that the average at each time step only includes values from fragments that have an value at that step. For example, almost all Li+ ions that are labeled as free at time t = 0 contribute to the initial part of the VACF of free Li+. At longer time, fewer such ions remain in the free state and contribute to the VACF. To obtain good statistics, an averaging of the results over many runs is a must, however, we always have enough free ions to describe the asymptotic decay of the VACF to zero because of their relatively long mean residential time (see Fig. 5c).
Data availability
The codes of the graph-theory-based cluster analysis method are made available open-source at https://github.com/Sheng-Bi/graph-theory-based-cluster-analysis.Author contributions
Conceptualization: S. B. and M. S.; investigation: S. B.; methodology: S. B.; supervision: M. S.; writing – review & editing: S. B. and M. S.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie actions Grant Agreement No. 945298 – ParisRegionFP. S. B. is a Fellow of Paris Region Fellowship Programme supported by the Paris Region.References
- Y. Yamada, K. Furukawa, K. Sodeyama, K. Kikuchi, M. Yaegashi, Y. Tateyama and A. Yamada, Unusual Stability of Acetonitrile-Based Superconcentrated Electrolytes for Fast-Charging Lithium-Ion Batteries, J. Am. Chem. Soc., 2014, 136, 5039–5046 CrossRef CAS PubMed
.
- L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, “Water-in-salt” electrolyte enables high-voltage aqueous lithium-ion chemistries, Science, 2015, 350, 938–943 CrossRef CAS PubMed
.
- L. Suo, O. Borodin, W. Sun, X. Fan, C. Yang, F. Wang, T. Gao, Z. Ma, M. Schroeder, A. von Cresce, S. M. Russell, M. Armand, A. Angell, K. Xu and C. Wang, Advanced High-Voltage Aqueous Lithium-Ion Battery Enabled by “Water-in-Bisalt” Electrolyte, Angew. Chem., Int. Ed., 2016, 55, 7136–7141 CrossRef CAS PubMed
.
- J. Wang, Y. Yamada, K. Sodeyama, C. H. Chiang, Y. Tateyama and A. Yamada, Superconcentrated electrolytes for a high-voltage lithium-ion battery, Nat. Commun., 2016, 7, 1–9 Search PubMed
.
- M. R. Lukatskaya, J. I. Feldblyum, D. G. Mackanic, F. Lissel, D. L. Michels, Y. Cui and Z. Bao, Concentrated mixed cation acetate ”water-in-salt” solutions as green and low-cost high voltage electrolytes for aqueous batteries, Energy Environ. Sci., 2018, 11, 2876–2883 RSC
.
- Y. Yamada, J. Wang, S. Ko, E. Watanabe and A. Yamada, Advances and issues in developing salt-concentrated battery electrolytes, Nat. Energy, 2019, 4, 269–280 CrossRef CAS
.
- L. Chen, J. Zhang, Q. Li, J. Vatamanu, X. Ji, T. P. Pollard, C. Cui, S. Hou, J. Chen, C. Yang, L. Ma, M. S. Ding, M. Garaga, S. Greenbaum, H. S. Lee, O. Borodin, K. Xu and C. Wang, A 63 m Superconcentrated Aqueous Electrolyte for High-Energy Li-Ion Batteries, ACS Energy Lett., 2020, 5, 968–974 CrossRef CAS
.
- M. Chen, G. Feng and R. Qiao, Water-in-salt electrolytes: An interfacial perspective, Curr. Opin. Colloid Interface Sci., 2020, 47, 99–110 CrossRef CAS
.
- T. Liang, R. Hou, Q. Dou, H. Zhang and X. Yan, The Applications of Water-in-Salt Electrolytes in Electrochemical Energy Storage Devices, Adv. Funct. Mater., 2021, 31, 1–23 Search PubMed
.
- D. Xiao, L. Zhang, Z. Li, H. Dou and X. Zhang, Design strategies and research progress for Water-in-Salt electrolytes, Energy Storage Mater., 2022, 44, 10–28 CrossRef
.
- A. Serva, N. Dubouis, A. Grimaud and M. Salanne, Confining Water in Ionic and Organic Solvents to Tune Its Adsorption and Reactivity at Electrified Interfaces, Acc. Chem. Res., 2021, 54, 1034–1042 CrossRef CAS PubMed
.
- T. Lv and L. Suo, Water-in-salt widens the electrochemical stability window: Thermodynamic and kinetic factors, Curr. Opin. Electrochem., 2021, 29, 100818 CrossRef CAS
.
- X. Fan and C. Wang, High-voltage liquid electrolytes for Li batteries: progress and perspectives, Chem. Soc. Rev., 2021, 50, 10486–10566 RSC
.
- M. Amiri and D. Bélanger, Physicochemical and Electrochemical Properties of Water-in-Salt Electrolytes, ChemSusChem, 2021, 14, 2487–2500 CrossRef CAS PubMed
.
- O. Borodin, L. Suo, M. Gobet, X. Ren, F. Wang, A. Faraone, J. Peng, M. Olguin, M. Schroeder, M. S. Ding, E. Gobrogge, A. Von Wald Cresce, S. Munoz, J. A. Dura, S. Greenbaum, C. Wang and K. Xu, Liquid Structure with Nano-Heterogeneity Promotes Cationic Transport in Concentrated Electrolytes, ACS Nano, 2017, 11, 10462–10471 CrossRef CAS PubMed
.
- J. Lim, K. Park, H. Lee, J. Kim, K. Kwak and M. Cho, Nanometric Water Channels in Water-in-Salt Lithium Ion Battery Electrolyte, J. Am. Chem. Soc., 2018, 140, 15661–15667 CrossRef CAS PubMed
.
- M. McEldrew, Z. A. H. Goodwin, S. Bi, M. Z. Bazant and A. A. Kornyshev, Theory of ion aggregation and gelation in super-concentrated electrolytes, J. Chem. Phys., 2020, 152, 234506 CrossRef CAS PubMed
.
- M. McEldrew, Z. A. H. Goodwin, S. Bi, A. A. Kornyshev and M. Z. Bazant, Ion Clusters and Networks in Water-in-Salt Electrolytes, J. Electrochem. Soc., 2021, 168, 050514 CrossRef CAS
.
- M. McEldrew, Z. A. Goodwin, A. A. Kornyshev and M. Z. Bazant, Theory of the Double Layer in Water-in-Salt Electrolytes, J. Phys. Chem. Lett., 2018, 9, 5840–5846 CrossRef CAS PubMed
.
- L. Suo, D. Oh, Y. Lin, Z. Zhuo, O. Borodin, T. Gao, F. Wang, A. Kushima, Z. Wang, H.-C. Kim, Y. Qi, W. Yang, F. Pan, J. Li, K. Xu and C. Wang, How Solid-Electrolyte Interphase Forms in Aqueous Electrolytes, J. Am. Chem. Soc., 2017, 139, 18670–18680 CrossRef CAS PubMed
.
- X.-Q. Zhang, X. Chen, L.-P. Hou, B.-Q. Li, X.-B. Cheng, J.-Q. Huang and Q. Zhang, Regulating Anions in the Solvation Sheath of Lithium Ions for Stable Lithium Metal Batteries, ACS Energy Lett., 2019, 4, 411–416 CrossRef CAS
.
- Z. Piao, R. Gao, Y. Liu, G. Zhou and H. M. Cheng, A Review on Regulating Li+ Solvation Structures in Carbonate Electrolytes for Lithium Metal Batteries, Adv. Mater., 2023, 35, 1–22 Search PubMed
.
- H. Cheng, Q. Sun, L. Li, Y. Zou, Y. Wang, T. Cai, F. Zhao, G. Liu, Z. Ma, W. Wahyudi, Q. Li and J. Ming, Emerging Era of Electrolyte Solvation Structure and Interfacial Model in Batteries, ACS Energy Lett., 2022, 7, 490–513 CrossRef CAS
.
- P. Nürnberg, J. Atik, O. Borodin, M. Winter, E. Paillard and M. Schönhoff, Superionicity in Ionic-Liquid-Based Electrolytes Induced by Positive Ion–Ion Correlations, J. Am. Chem. Soc., 2022, 144, 4657–4666 CrossRef PubMed
.
- M. Brinkkötter, A. Mariani, S. Jeong, S. Passerini and M. Schönhoff, Ionic Liquid in Li Salt Electrolyte: Modifying the Li+ Transport Mechanism by Coordination to an Asymmetric Anion, Adv. Energy Sustainability Res., 2021, 2, 2000078 CrossRef
.
- L. Suo, O. Borodin, W. Sun, X. Fan, C. Yang, F. Wang, T. Gao, Z. Ma, M. Schroeder, A. von Cresce, S. M. Russell, M. Armand, A. Angell, K. Xu and C. Wang, Advanced High-Voltage Aqueous Lithium-Ion Battery Enabled by “Water-in-Bisalt” Electrolyte, Angew. Chem., 2016, 128, 7252–7257 CrossRef
.
- H. Li, T. Kurihara, D. Yang, M. Watanabe and T. Ishihara, A novel aqueous dual-ion battery using concentrated bisalt electrolyte, Energy Storage Mater., 2021, 38, 454–461 CrossRef
.
- T. A. Nigatu, H. K. Bezabh, B. W. Taklu, B. W. Olbasa, Y. T. Weng, S. H. Wu, W. N. Su, C. C. Yang and B. J. Hwang, Synergetic effect of water-in-bisalt electrolyte and hydrogen-bond rich additive improving the performance of aqueous batteries, J. Power Sources, 2021, 511, 230413 CrossRef CAS
.
- X. Ren, S. Chen, H. Lee, D. Mei, M. H. Engelhard, S. D. Burton, W. Zhao, J. Zheng, Q. Li, M. S. Ding, M. Schroeder, J. Alvarado, K. Xu, Y. S. Meng, J. Liu, J. G. Zhang and W. Xu, Localized High-Concentration Sulfone Electrolytes for High-Efficiency Lithium-Metal Batteries, Chem, 2018, 4, 1877–1892 CAS
.
- S. Chen, J. Zheng, D. Mei, K. S. Han, M. H. Engelhard, W. Zhao, W. Xu, J. Liu and J. G. Zhang, High-Voltage Lithium-Metal Batteries Enabled by Localized High-Concentration Electrolytes, Adv. Mater., 2018, 30, 1–7 CAS
.
- C. M. Efaw, Q. Wu, N. Gao, Y. Zhang, H. Zhu, K. Gering, M. F. Hurley, H. Xiong, E. Hu, X. Cao, W. Xu, J.-G. Zhang, E. J. Dufek, J. Xiao, X.-Q. Yang, J. Liu, Y. Qi and B. Li, Localized high-concentration electrolytes get more localized through micelle-like structures, Nat. Mater., 2023, 22, 1531–1539 CrossRef CAS PubMed
.
- W. A. Henderson, D. M. Seo, S.-D. Han and O. Borodin, Electrolyte Solvation and Ionic Association. VII. Correlating Raman Spectroscopic Data with Solvate Species, J. Electrochem. Soc., 2020, 167, 110551 CrossRef CAS
.
- Y. Zhang, N. H. Lewis, J. Mars, G. Wan, N. J. Weadock, C. J. Takacs, M. R. Lukatskaya, H. G. Steinrück, M. F. Toney, A. Tokmakoff and E. J. Maginn, Water-in-Salt LiTFSI Aqueous Electrolytes. 1. Liquid Structure from Combined Molecular Dynamics Simulation and Experimental Studies, J. Phys. Chem. B, 2021, 125, 4501–4513 CrossRef CAS PubMed
.
- Z. Yu, L. A. Curtiss, R. E. Winans, Y. Zhang, T. Li and L. Cheng, Asymmetric Composition of Ionic Aggregates and the Origin of High Correlated Transference Number in Water-in-Salt Electrolytes, J. Phys. Chem. Lett., 2020, 11, 1276–1281 CrossRef CAS PubMed
.
- R. Andersson, F. Arén, A. A. Franco and P. Johansson, CHAMPION: Chalmers hierarchical atomic, molecular, polymeric and ionic analysis toolkit, J. Comput. Chem., 2021, 42, 1632–1642 CrossRef CAS PubMed
.
- M. Vatin, M. Duvail, P. Guilbaud and J.-F. Dufrêche, Thermodynamics of Malonamide Aggregation Deduced from Molecular Dynamics Simulations, J. Phys. Chem. B, 2021, 125, 3409–3418 CrossRef CAS PubMed
.
- G. Feng, M. Chen, S. Bi, Z. A. Goodwin, E. B. Postnikov, N. Brilliantov, M. Urbakh and A. A. Kornyshev, Free and Bound States of Ions in Ionic Liquids, Conductivity, and Underscreening Paradox, Phys. Rev. X, 2019, 9, 21024 CAS
.
- N. Molinari, J. P. Mailoa and B. Kozinsky, General Trend of a Negative Li Effective Charge in Ionic Liquid Electrolytes, J. Phys. Chem. Lett., 2019, 10, 2313–2319 CrossRef CAS PubMed
.
- N. Molinari, Y. Xie, I. Leifer, A. Marcolongo, M. Kornbluth and B. Kozinsky, Spectral Denoising for Accelerated Analysis of Correlated Ionic Transport, Phys. Rev. Lett., 2021, 127, 025901 CrossRef CAS PubMed
.
- N. Molinari, J. P. Mailoa, N. Craig, J. Christensen and B. Kozinsky, Transport Anomalies Emerging from Strong Correlation in Ionic Liquid Electrolytes, J. Power Sources, 2019, 428, 27–36 CrossRef CAS
.
- M. McEldrew, Z. A. H. Goodwin, N. Molinari, B. Kozinsky, A. A. Kornyshev and M. Z. Bazant, Salt-in-Ionic-Liquid Electrolytes: Ion Network Formation and Negative Effective Charges of Alkali Metal Cations, J. Phys. Chem. B, 2021, 125, 13752–13766 CrossRef CAS PubMed
.
- C. Zhang, S. Yue, A. Z. Panagiotopoulos, M. L. Klein and X. Wu, Dissolving salt is not equivalent to applying a pressure on water, Nat. Commun., 2022, 13, 8–13 CrossRef PubMed
.
- I. Rey, P. Johansson, J. Lindgren and J. C. Lasse, Spectroscopic and Theoretical Study of (CF 3 SO 2 ) 2 N - (TFSI - ) and (CF 3 SO 2 ) 2 NH (HTFSI), J. Phys. Chem. A, 1998, 102, 3249–3258 CrossRef CAS
.
- A. France-Lanord and J. C. Grossman, Correlations from Ion Pairing and the Nernst-Einstein Equation, Phys. Rev. Lett., 2019, 122, 136001 CrossRef CAS PubMed
.
- Z. Li, R. Bouchal, T. Mendez-Morales, A. L. Rollet, C. Rizzi, S. Le Vot, F. Favier, B. Rotenberg, O. Borodin, O. Fontaine and M. Salanne, Transport Properties of Li-TFSI Water-in-Salt Electrolytes, J. Phys. Chem. B, 2019, 123, 10514–10521 CrossRef CAS PubMed
.
- M. Zhang, H. Hao, D. Zhou, Y. Duan, Y. Wang and H. Bian, Understanding the Microscopic Structure of a ”water-in-Salt” Lithium Ion Battery Electrolyte Probed with Ultrafast IR Spectroscopy, J. Phys. Chem. C, 2020, 124, 8594–8604 CrossRef CAS
.
- H. K. Bergstrom and B. D. McCloskey, Ion Transport in (Localized) High Concentration Electrolytes for Li-Based Batteries, ACS Energy Lett., 2024, 373–380 CrossRef CAS PubMed
.
- C. Fang, A. Mistry, V. Srinivasan, N. P. Balsara and R. Wang, Elucidating the Molecular Origins of the Transference Number in Battery Electrolytes Using Computer Simulations, JACS Au, 2023, 3, 306–315 CrossRef CAS PubMed
.
- K. Goloviznina, A. Serva and M. Salanne, Formation of Polymer-Like Nanochains with Short Lithium-Lithium Distances in a Water-in-Salt Electrolyte, J. Am. Chem. Soc., 2024, 146, 8142–8148 CrossRef CAS PubMed
.
- W. Zhang, H. Xia, Z. Zhu, Z. Lv, S. Cao, J. Wei, Y. Luo, Y. Xiao, L. Liu and X. Chen, Decimal Solvent-Based High-Entropy Electrolyte Enabling the Extended Survival Temperature of Lithium-Ion Batteries to -130 °C, CCS Chem., 2020, 3, 1245–1255 CrossRef
.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed
.
- J. N. Canongia Lopes, J. Deschamps and A. A. Pádua, Modeling Ionic Liquids Using a Systematic All-Atom Force Field, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef
.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc01491j |
| This journal is © The Royal Society of Chemistry 2024 |