Open Access Article
Open Access ArticleRadical ligand transfer: mechanism and reactivity governed by three-component thermodynamics†
Zuzanna
Wojdyla
 and
Martin
Srnec
and
Martin
Srnec
 *
*
J. Heyrovský Institute of Physical Chemistry, The Czech Academy of Sciences, Dolejškova 3, Prague 8, 18223, Czech Republic. E-mail: martin.srnec@jh-inst.cas.cz
First published on 10th May 2024
Abstract
Here, we demonstrate that the relationship between reactivity and thermodynamics in radical ligand transfer chemistry can be understood if this chemistry is dissected as concerted ion-electron transfer (cIET). Namely, we investigate radical ligand transfer reactions from the perspective of thermodynamic contributions to the reaction barrier: the diagonal effect of the free energy of the reaction, and the off-diagonal effect resulting from asynchronicity and frustration, which we originally derived from the thermodynamic cycle for concerted proton-electron transfer (cPET). This study on the OH transfer reaction shows that the three-component thermodynamic model goes beyond cPET chemistry, successfully capturing the changes in radical ligand transfer reactivity in a series of model FeIII–OH⋯(diflouro)cyclohexadienyl systems. We also reveal the decisive role of the off-diagonal thermodynamics in determining the reaction mechanism. Two possible OH transfer mechanisms, in which electron transfer is coupled with either OH− and OH+ transfer, are associated with two competing thermodynamic cycles. Consequently, the operative mechanism is dictated by the cycle yielding a more favorable off-diagonal effect on the barrier. In line with this thermodynamic link to the mechanism, the transferred OH group in OH−/electron transfer retains its anionic character and slightly changes its volume in going from the reactant to the transition state. In contrast, OH+/electron transfer develops an electron deficiency on OH, which is evidenced by an increase in charge and a simultaneous decrease in volume. In addition, the observations in the study suggest that an OH+/electron transfer reaction can be classified as an adiabatic radical transfer, and the OH−/electron transfer reaction as a less adiabatic ion-coupled electron transfer.
Introduction
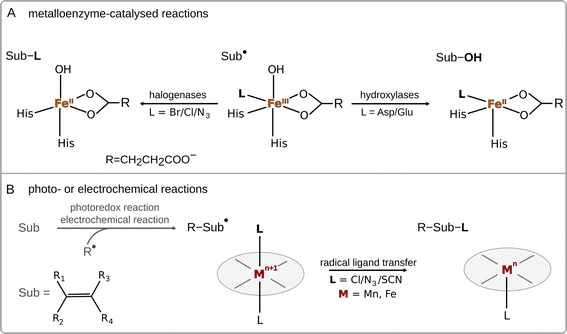
Radical ligand transfer reactions play an important role in biological processes, such as biosynthesis of natural products1–6 and collagen,7 or neutralization of toxins (see Scheme 1A).8,9 It is also an important step in organic synthesis enabling late-stage functionalization and synthesis of possible high-value products via photo- or electrochemical activation of alkenes or carboxylic acids (see Scheme 1B).10,11 This strategy opens the way for selective formation of difunctionalized products, which might later serve as intermediates in synthetic processes.10–14 To date, radical ligand transfer reactions are performed with the use of redox-active metal (manganese or iron) complexes. On the other hand, metal-independent reactions typically proceed via electron transfer, with the only – to our knowledge – exception of thyil group transfer performed by a disulfide bearing tetrafluoropyridinyl group in reaction with alkyl radicals.15A prototypical example of (biological) radical-ligand transfer is OH group transfer, better known as radical hydroxylation or the OH rebound reaction, which is a part of the catalytic cycle of many metal-containing oxygenases.16 This type of reaction was also subjected to an intensive study in enzymatic and biomimetic chemistry.17–20 Transfer of the OH group in enzymes (and their biomimetics) is preceded by hydrogen atom abstraction (HAA) from the substrate by a high-valent metal-oxo site, which produces a substrate radical intermediate and a metal–OH moiety. In the next step, the hydroxyl group is transferred onto the substrate radical, forming the hydroxylated product.21 Apart from radical hydroxylation, other examples of radical ligand transfer reactions can involve halogenation,22–25 azidation26–29 or alkoxidation.30 These reactions can be carried out using the same molecular scaffold as that for radical hydroxylation, as has been shown in the examples of enzymes that can convert their native ability for radical hydroxylation into the ability to carry out other radical ligand transfers by changing the reaction conditions or the substrate for the reaction, or through directed evolution.31–35 This indicates that transfers of different radical ligands may follow the same mechanism.
As far as the mechanism of radical ligand transfer is concerned, it was computationally investigated in the study of non-heme iron halogenase SyrB2, an enzyme capable of halogenation as well as hydroxylation of its non-native substrates. For this system it was demonstrated that the preference for halogen vs. hydroxyl radical transfer from the SyrB2 HO–FeIII–Cl active site to the substrate radical is a joint result of the energy difference between two key redox-active dπ* frontier molecular orbitals (one along the Fe–Cl bond vs. one along the Fe–OH bond) and the position of the substrate relative to the HO–Fe–Cl plane.36 Yet, in both cases, the radical transfer mechanism has been shown to involve rather non-intuitive electron transfer (ET) from the substrate to FeIII through the super-exchange mediating R− ligand, with the concomitant transfer of R− to the substrate.36 Thus, the ET was proposed to be an integral part of radical halogenation/hydroxylation. Similarly, experimental studies on a series of para-substituted radicals in reaction with heme and non-heme FeIII–OH complexes revealed a slight dependence of the rate constant on the redox potential of the radical – a lower reaction rate was observed for radicals hosting more strongly electron withdrawing substituents,18,37 which again indicates that ET is an important component of radical ligand transfer. Moreover, as shown for a biomimetic non-heme azide–FeIII–OH complex, the ET component of the radical ligand transfer may play a role in the product selectivity of the reaction.38 In this system a switch from hydroxylation towards azidation was observed upon change of the substrate to a more electron rich one (i.e. with the lowest redox potential). On a similar note, Savéant et al. found that the release of radicals from butyl and benzyl halides mechanistically involves ET coupled to bond cleavage.38,39 Based on all these studies, the radical ligand transfer reaction can thus be thought of as an electron transfer (ET) coupled to the transfer of the corresponding ion (IT) – concerted electron-ion transfer (cIET), which might be viewed as analogous to the canonical concerted proton-electron transfer (cPET).40–42
In contrast to cIET, the chemistry of cPET has been studied much more intensively and thus offers a possible starting point for the study of cIET.40–57 One of the key aspects of cPET chemistry is the variable degree of concertedness between ET and proton transfer (PT) from the fully concerted mode to an asynchronous mode in favor of ET or PT; the limiting case is then the stepwise ET/PT or PT/ET mode. This feature and its connection to reactivity was first qualitatively described via More O'Ferrall–Jencks diagrams58–60 and later was more quantitatively but empirically captured by Bernasconi's principle of non-perfect synchronization.61,62
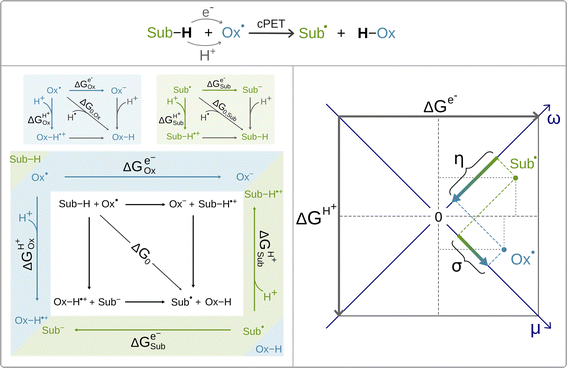
Recently, it was shown by one of us that the extent to which the cPET reaction is asynchronous in favor of ET or PT, can be quantitatively and non-empirically determined by the energetics associated with the full-reaction thermodynamic cycle depicted in black in Scheme 2 (bottom, left).63 The cycle includes three thermodynamically equivalent pathways for H-atom (H+/e−) abstraction from the substrate Sub-H to the oxidant Ox˙, two of which are the stepwise (off-diagonal) ET/PT and PT/ET pathways with the ET and PT states as intermediates along the respective reaction coordinates. Although these ET and PT states are never formed during the single-step cPET reaction, the energetics of these ET and PT states influences concertedness of ET and PT in cPET and thus shapes cPET reactivity. All this is encoded in the acid–base and redox properties of the reaction partners, which compete for the H-atom (i.e. the H+/e− pair). The competition is described by the free energies of one-electron reduction vs. protonation of the oxidant and the substrate radical (Ox˙ and Sub˙).63 These free energies are associated with the half-reaction thermodynamic cycles, one for the oxidant (blue panel in Scheme 2) and one for the substrate radical (green panel in Scheme 2). The three ‘tug-of-wars’ between Ox˙ and Sub˙ for three different particles (hydrogen atom, electron and proton) can then be evaluated simply as a subtractive combination of the half-reaction thermodynamic cycles for the oxidant and the substrate radical.64 This is indicated in Scheme 2 by combining the blue and green panels into one diagram, which also provides a link to the full reaction thermodynamic cycle. The competition between Ox˙ and Sub˙ for a hydrogen atom directly determines the free energy of the reaction, which corresponds to the total thermodynamic driving force for cPET. The two remaining tug-of-wars, one for the proton and one for the electron, together predetermine two additional reaction characteristics – frustration and asynchronicity, as indicated in the right plot in Scheme 2. Explicitly, the plot shows that free energies of one-electron reduction and protonation, ΔGe− and ΔGH+, of the two competitors X˙ (Ox˙ and Sub˙) are first combined into two composite quantities – potential duality μ and potential disparity ω. The potential duality of X˙ reflects the joint height of the reduced and protonated states above X˙ and describes the ability of X˙ to act together as the oxidant and base. The potential disparity of X˙ reflects the difference in the height of the reduced vs. protonated state above X˙ and thus captures to what extent the species X˙ is a stronger/weaker oxidant than a base.
Finally, the two off-diagonal thermodynamic reaction factors, frustration σ and asynchronicity η, are given as the respective differences between potential dualities and between potential disparities of Ox˙ and Sub˙ (Scheme 2, right). Asynchronicity captures the relative height of the ET vs. PT state in the respective stepwise (off-diagonal) ET/PT and PT/ET pathways and thus quantifies the thermodynamic preference for ET vs. PT, which controls the concertedness of ET and PT in cPET.‡ On the other hand, frustration reflects the joint thermodynamic (in)accessibility of the two off-diagonal ET and PT states in these off-diagonal pathways. The data-driven implementation of σ and η in the linearized Marcus model for the barrier revealed that the more asynchronous reaction yields higher reaction rates than the equally exergonic synchronous reaction, whereas a more frustrated reaction is less effective than an unfrustrated one.64 Both frustration σ and asynchronicity η, together with free energy of the reaction ΔG0, provide a complete three-component basis for the thermodynamic contribution to cPET reactivity.
In this work we demonstrate that the framework developed for cPET can be employed also for cIET to correctly predict its reactivity. Moreover, the framework is substantially extended for cIET by considering mechanistic scenarios that have not been previously observed in cPET chemistry. For this purpose, we utilize a series of axially substituted model (TMC)FeIII–OH complexes in reaction with cyclohexadienyl (CHD˙) and 3,3-difluorocyclohexadienyl (2F-CHD˙) radicals. On the basis of the two substrates, we investigate the link between the mechanism of the radical ligand transfer reaction and the contributions originating from the off-diagonal states, associated with ion and electron transfers (IT and ET). The major finding is that of the several distinct thermodynamic cycles that may be associated with radical ligand transfer, the one with the most energetically accessible off-diagonal states is functional and controls not only cIET reactivity but also decides on the reaction mechanism.
The structure of this paper is as follows. The first part presents the theoretical framework derived for the cIET reactions. The second section deals with the use of a thermodynamic model to predict the barriers for OH rebound reactions. The third section contains a characterization of the evolution of the electronic structure along the reaction coordinate and its relation to the thermodynamic description of the reaction. The fourth section provides insight into the reaction mechanism based on asynchronicity. The final section discusses the role of adiabatic coupling in the reactions.
Computational methods
The calculations were performed for the L axially ligated and 1,4,8,11-tetramethylcyclam supported iron(III)–OH complexes65 ((L)(TMC)FeIII–OH complexes with L listed in Fig. 1A) in reaction with cyclohexadienyl (CHD˙) and 3,3-difluorocyclohexadienyl (2F-CHD˙) radicals. TMC can adapt two conformations – ‘parallel’ and ‘crossed’, which differ by the arrangement of two opposite C–C bonds (marked in purple in ESI – Fig. S1†). The parallel conformation is presented in the main text due to lower Gibbs free energies of the parallel (L)(TMC)FeIII–OH complexes as compared to their crossed cognates (for the ‘crossed’ set see the ESI†). Note that the same observations as for the parallel set can be obtained from the crossed one. For both parallel and crossed sets, the two electronic configurations of the reactant complex (RC) were considered: (i) the high-spin (S = 5/2) (L)(TMC)FeIII–OH complex coupled antiferromagnetically with (2F-)CHD˙ (S = −1/2) and (ii) the intermediate-spin (S = 3/2) (L)(TMC)FeIII–OH complex coupled ferromagnetically with (2F-)CHD˙ (S = 1/2). Throughout both the parallel and crossed sets, the S = 5/2 (L)(TMC)FeIIIOH complexes were characterized by lower G, and thus we focus in the main text on the high-spin systems (for S = 3/2 alternatives see the ESI†). Visual inspection of frontier molecular orbitals was performed to ensure that the investigated radical ligand transfer reaction consistently follows the π-channel, that is the electron is accepted (or donated) by one of the dπ* orbitals of the FeIII–OH moiety.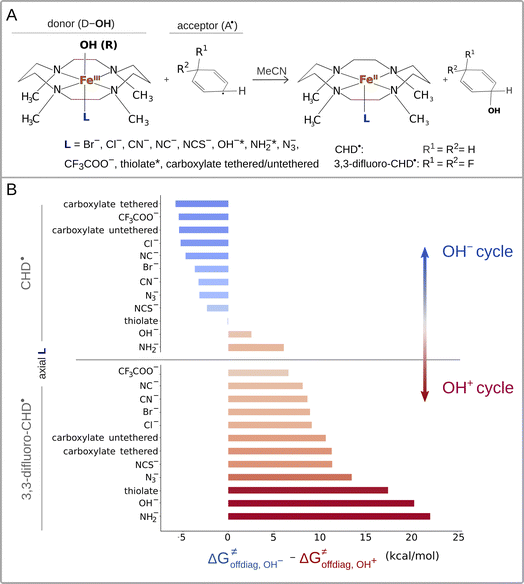 | ||
| Fig. 1 (A) Reaction between the tetramethylcyclam (TMC)-supported, axial-ligand (L)-perturbed FeIII–OH systems and the substrates CHD˙ and 3,3-diflouroCHD˙ used in the study. Note that for FeIII–OH complexes with L marked with an asterisk, we calculated the free-energy barriers ΔG≠ only for the 2F-CHD-based systems, as we were not able to optimize the respective transition states of the CHD-based systems in the appropriate spin state (i.e. S = 5/2 FeIII–OH complex coupled antiferromagnetically with the substrate radical). (B) The difference between off-diagonal energetics (ΔG≠offdiag from eq (7)): negative values indicate preference for the OH− cycle (blue), positive – for OH+ (red). | ||
The calculations were performed with Gaussian 16 revision C.01.66 The B3LYP functional67 with Grimme's D3 dispersion correction68 and the def2-SVP basis set69 was used. The solvation effects were described with the conductor-like polarizable continuum model (CPCM)70 using ε = 35.7 (acetonitrile). The Gibbs free energies for the optimized structures were calculated as the sum of potential electronic energies (Eel) calculated at the B3LYP-D3/def2-SVP level with CPCM and the thermal enthalpic and entropic contributions to the Gibbs free energy (at 298.15 K) obtained from frequency analysis performed at the same level of theory: G = Eel + [EZPE + pV + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q], where Eel and Q are the zero-point vibrational energy and the molecular partition function, respectively.
Q], where Eel and Q are the zero-point vibrational energy and the molecular partition function, respectively.
The Gibbs free energy barriers for the reactions were calculated as the difference between the Gibbs free energy of the transition state (TS) and the isolated reactants (kcal mol−1). A value of 1.9Δn kcal mol−1 has been applied to correct the computed values to the 1 mol L−1 standard state (a value of 1.9 kcal mol−1 corresponds to the conversion of a 1 bar standard state in the gas phase to 1 mol L−1 concentration in solution at 298 K; Δn is the change in the number of moles). The half-reaction thermodynamic cycles were calculated according to the same computational protocol, using the free energies of the ground spin states (structures and spin states are shown in the ESI†).
The atoms-in-molecules (AIM) approach implemented in the AIMAll program71 was employed to assess the redistribution of electron densities during the reaction in the investigated systems. The atomic charges (calculated as the difference between the atomic nuclear charge and its associated electron density) were computed based on the DFT-calculated electron densities of the optimized structures of the transition states and reactant complexes. Densities were integrated using the Proaim method with a ‘very fine’ interatomic surface mesh and a basin outer angular quadrature of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 grid points (using 15-point Gaussian quadrature GS15). The AIM properties of the atoms with a Lagrangian L(A) > 0.001 au were recalculated with the Promega algorithm. The AIM charges and volumes of the atoms were used to characterize the reaction, i.e. the amount of electron density transferred upon transition from the RC to the TS between the substrate and the (L)(TMC)FeIII–OH complex.
400 grid points (using 15-point Gaussian quadrature GS15). The AIM properties of the atoms with a Lagrangian L(A) > 0.001 au were recalculated with the Promega algorithm. The AIM charges and volumes of the atoms were used to characterize the reaction, i.e. the amount of electron density transferred upon transition from the RC to the TS between the substrate and the (L)(TMC)FeIII–OH complex.
Results and discussion
Thermodynamic cycles for concerted ion-electron transfer; determination of the valid cycle
According to the conventional view of cPET and cIET, these two reaction types differ in the charge of the ion that is transferred between the H-atom/radical donor and acceptor; in the former case it is cation (i.e. proton) transfer, whereas in the latter case it is anion transfer, as we have learned from mechanistic studies of halogen/hydroxyl radical transfer in SyrB2. This difference also determines the difference in the ET direction. For ET associated with cation transfer, the electron is transferred in the same direction as ion transfer (IT), i.e. from the radical group donor D˙ to the radical group acceptor A˙. Alternatively, if ET is coupled to anion transfer, ET proceeds in the opposite direction to IT, i.e. from A˙ to D˙. Thus, the two interconnected ET/IT transfers can proceed in either uni- or bidirectional fashion. These scenarios are illustrated for radical ligand (R˙) transfer in Scheme 3 (top). For R˙ transfer, which takes place as concerted and co-directional transfer of the cation R+ and electron, we further use the notation R+→/e−→ transfer (with ‘→’ indicating the direction of transfer from the D˙ to A˙). For R˙ transfer, which is realized as the concerted and contra-directional transfer of the anion R− and electron, we further use the notation R−→/e−← transfer (with ‘←’ indicating the direction from A˙ to D˙). In the case of R−→/e−← transfer, the species that accepts the electron is D–R, and the electron thus flows in the direction opposite to anion transfer. The R+→/e−→ transfer scenario resembles the canonical cPET described in Scheme 2, i.e. the electron flows in the direction of cation transfer and is accepted by the acceptor A˙. Importantly, two distinct concerted ion-electron transfer scenarios (R+→/e−→ and R−→/e−←) are associated with two distinct reaction thermodynamic cycles assembled from the respective half-reaction thermodynamic cycles for the acceptor and donor of the radical group R˙ shown in Scheme 3.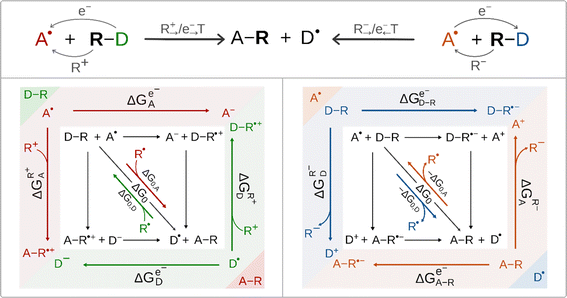 | ||
| Scheme 3 Top: two mechanistic scenarios for radical ligand transfers between the R˙ donor (D–R) and acceptor (A˙): one involving concerted and co-directional transfer of R+ and the electron denoted as R+→/e−→ transfer, and one with concerted contra-directional transfer of R− and the electron denoted as R−→/e−← (left and right, respectively). The group R˙ corresponds to OH˙ in this study. Bottom: the full-reaction thermodynamic cycles associated with the two R+→/e−→ transfer and R−→/e−← transfer mechanisms (left and right, respectively) are depicted together with their constituent blocks – half-reaction thermodynamic cycles (color coded in the figure). For each half-reaction thermodynamic cycle, three key free energy quantities are shown. Their meaning and importance are explained in the main text. Note the left scenario is fully analogous to cPET presented in Scheme 2. The half-reaction cycles are presented in Fig. S2.† | ||
Regardless of the mechanistic scenario, the diagonal path connecting the initial and the final state of a reaction corresponds to a transfer of the radical R˙ as an intact moiety. In analogy to cPET, the thermodynamic driving force for such a transfer is simply the free energy of the reaction ΔG0 = ΔG0,A − ΔG0,D (Scheme 3). Still the two scenarios are very different in terms of the off-diagonal thermodynamics in the respective half-reaction cycles. Importantly, the crux of the mechanism, as described by the half-reaction cycles, is to correctly identify the electron-accepting species, which are the initial states in these cycles. In the co-directional R+→/e−→ transfer, they are A˙ and D˙, whereas in contra-directional R−→/e−← transfer, they are D–R and A–R.
In Scheme 3, we present subtractive combinations of the half-reaction cycles to form the respective full-reaction thermodynamic cycles which reflect the competition between the electron-accepting species for the electron (in analogy to Scheme 2 for cPET). Thus, for the R+→/e−→ transfer full-reaction cycle, the half-reaction cycle of the radical ligand acceptor starts with electron-accepting A˙ in the upper left corner, while the half-reaction cycle of the radical ligand donor is oppositely oriented starting with electron-accepting D˙ in the lower right corner (Scheme 3, left). In this relative orientation of the two half-reaction cycles, the upper and lower horizontal off-diagonals, opposing each other, stand for one-electron reduction of the A˙ and D˙ (ΔGe−A˙ and ΔGe−D˙), respectively, while the left and right vertical off-diagonals, again opposing each other, account for the binding of the R+ cation to D˙ and A˙ (ΔGR+D˙ and ΔGR+A˙), respectively.
On the other hand, for the R−→/e−← transfer full-reaction cycle, the half-reaction cycle of the radical ligand donor starts with electron-accepting D–R in the upper left corner, while the half-reaction cycle of the radical ligand acceptor is reversed starting with electron-accepting A–R in the lower right corner (Scheme 3, right). In this arrangement, the mutually opposed upper and lower horizontal off-diagonals correspond to the one-electron reduction of the D–R and A–R, (ΔGe−D–R and ΔGe−A–R), respectively, while the mutually opposed vertical left and right off-diagonals account for the abstraction of the R− anion from D–R and A–R (ΔGR−D−R and ΔGR−A−R), respectively. We note in passing that the mutually opposed half-reaction off-diagonals in the case of R+→/e−→ transfer reflects the nature of the competition between A˙ vs. D˙, which corresponds to the tug-of-war for both the electron and R+ cation, as mentioned in the introduction for canonical cPET. Analogously, the mutually opposed half-reaction off-diagonals in the case of R−→/e−← reflects the tug-of-war and push-of-war nature of the competition between D–R and A–R for the electron and anion R−, respectively. In any case, the opposite orientation of the half-reaction diagonals captures the competition for the radical R˙. Specifically, for the OH transfer between the Fe-complex and organic substrate radical, the respective half-reaction thermodynamic cycles are described in Fig. S2.†
Following the concept of asynchronicity and frustration in ref. 64, which is briefly described in the introduction, half-reaction cycles are used to derive potential disparity ω and duality μ (in analogy to Scheme 2) for both unidirectional and bidirectional transfer scenarios from Scheme 3:
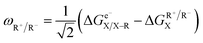 | (1) |
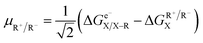 | (2) |
| ηR+ = ωA˙ − ωD˙ | (3) |
| ηR− = ωD–R − ωA–R | (4) |
The second reaction off-diagonal thermodynamic factor is frustration, σ, which is defined as:
| σR+ = μA˙ − μD˙ | (5) |
| σR− = μD–R − μA–R | (6) |
The critical point of the concept is the implementation of σ and η into the Marcus-type reactivity model as follows:
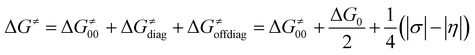 | (7) |
Eqn (7) shows that, for a homologous set of reactions (presumably featuring similar intrinsic reaction barriers), the total barrier is decisively modulated by the LFER together with the off-diagonal term ΔG≠offdiag. Because radical ligand transfer is conceived to follow one of the two distinct mechanistic scenarios from Scheme 3, we here formulate and testify a hypothesis: the operative mechanism and kinetics of a reaction is the one that features the thermodynamic cycle associated with the most favorable off-diagonal contribution to the barrier, i.e. the most favorable ΔG≠offdiag. To assess this, we consider substituted (L)(TMC)FeIII–OH complexes (with L as a variable axial ligand) in reaction with two substrates, CHD˙ and 2F-CHD˙ (Fig. 1A), as these two sets exhibit a mostly mutually opposite preference for the off-diagonal component ΔG≠offdiag (Fig. 1B). Specifically, most of the (L)(TMC)FeIII–OH/CHD˙ systems favor the bidirectional OH−→/e−← cycle (or shortly the OH− cycle), whereas the fluorinated form of CHD˙ switches the preference for unidirectional OH+→/e−→ (or shortly the OH+ cycle). The preference for the OH−vs. OH+ cycle was assessed as a difference between 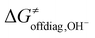 and
and 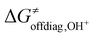 from the respective cycles (Fig. 1B).
from the respective cycles (Fig. 1B).
Application of the thermodynamic model to predict ΔG≠ of the hydroxyl transfer reactions
In the first step, we investigated the applicability of the thermodynamic (three-component) model to predict the change in ΔG≠ in two sets of reactions. The two sets are (L)(TMC)FeIII–OH series with CHD˙ denoted as the ‘OH− set’ due to the preference for the OH− cycle, and (L)(TMC)FeIII–OH series with 2F-CHD˙, which shows preference towards the OH+ cycle and is therefore called the ‘OH+ set’ (Fig. 1). For each set, we looked into the following correlations: (i) ΔG≠versus ΔG≠diag alias LFER; (ii) ΔG≠versus LFER together with the effect of asynchronicity of the reaction; and (iii) ΔG≠versus ΔG≠thermo including the LFER along with the complete off-diagonal thermodynamic term. The correlations are shown in Fig. 2. | ||
| Fig. 2 ΔG≠vs. linear free energy relationship (LFER) (left); LFER with the effect of asynchronicity (middle); LFER together with the complete off-diagonal term (right) for the OH− (top) and OH+ (bottom) sets. The quality of correlations is assessed by using the squared Pearson's coefficient (R2). For the plot with the points labeled according to the axial ligand of the (L)(TMC)FeIII–OH complex see ESI – Fig. S3,† and the detailed decomposition of the barriers into the non-thermodynamic and thermodynamic (diagonal and off-diagonal) components is shown in Fig. S4.† The barriers and thermodynamic descriptors are given in Tables S1–S3.† For the details on all systems investigated in this work see Fig. S5–S7 and Tables S4–S10.† Further details on the performance of the models are presented in Tables S11 and S12.† | ||
The results show that ΔG≠thermo allows the evolution of ΔG≠ within both of the sets (as indicated by R2 > 0.7) to be captured very well. The off-diagonal term seems indispensable for an accurate prediction of ΔG≠ as the LFER alone does not perform satisfactorily (as shown by an R2 of 0.05 and 0.28 for the OH− and OH+ set, respectively). The reason for poor performance of the LFER may be a relatively small span of the ΔG0 values (ca. 4 kcal mol−1), which does not allow the variability of ΔG≠ to be effectively grasped and suggests that the reactivity is shaped by other factors (notably, in datasets featuring a larger span of ΔG0 values, the role of LFER is more significant, see the ESI†). In both OH−→/e−← and OH+→/e−→ cases, asynchronicity is the crucial ingredient to describe the barriers (improving correlations with R2 > 0.6). However, in the OH− set, frustration further improves the prediction, as ΔG≠thermo provides a noticeably better correlation than ΔG≠diag − |η|/4 (R2 = 0.71 vs. R2 = 0.62), whereas in the OH+ set frustration acts more as a perturbation to the ΔG≠diag − |η|/4 (lowering the R2 from 0.90 to 0.76). We note that we also tested how much the correlation between ΔG≠ and ΔG≠thermo deteriorates if we apply ΔG≠thermo from the inappropriate cycle associated with the higher ΔG≠offdiag. For the OH− set, the correlation based on the ΔG≠thermo obtained from the OH+ cycle (featuring higher ΔG≠offdiag) performs noticeably worse as the R2 for ΔG≠vs. ΔG≠thermo decreases from 0.7 to 0.5 (Fig. S8 and Table S13†). For the OH+ set, once the ‘inappropriate’ OH− ΔG≠offdiag is applied, the model performs comparably well as in case of the application of the appropriate cycle. We traced the source of the seeming fitness of the ‘mismatched’ model to strong correlation between ηR− and ηR+ obtained from the two thermodynamic cycles (R2 of 0.87). This can be further narrowed down to the linear correlation of ω values for the (L)(TMC)FeIII–OH systems obtained from the OH− and OH+ half-reaction cycles (Fig. S9†).
Finally, it must be stressed that the two sets feature different slopes in the correlation with ΔG≠diag − |η|/4 and ΔG≠thermo, which indicates that the two reactions feature fundamentally different mechanisms. The OH− set is analogous to the previously studied cPET reactions, where asynchronicity is the barrier-lowering contribution, whereas the OH+ set displays a change in the sign of the correlation slope in going from the left to the right plots in Fig. 2. The change is counterintuitive as it indicates that the more asynchronous reaction as well as the reaction featuring a more favorable off-diagonal term will be associated with a higher ΔG≠. Behind this apparent contradiction, however, lies one more effect, which is discussed later in the text.
Agreement between the observed mechanism of cIET and the mechanism indicated by thermodynamic contributions
To gain insight into the mechanism of the reaction and distinguish between the OH−→/e−← and OH+→/e−→ featured radical ligand transfers, we examined the changes in electronic properties of the reacting system along the reaction coordinate, more specifically, the AIM charges and volumes of the OH group. The change in the AIM charge (Δq) and volume (ΔV) in going from the RC to the TS, is plotted in Fig. 3. The figure shows that each of the OH− and OH+ sets is associated with a well-defined range of Δq and ΔV values (also see the plots of individual descriptors Δq and ΔV versus the difference between two mechanisms in terms of their off-diagonal energetics in Fig. S11†). Namely, systems characterized by the off-diagonal energetics favoring the OH− cycle (blue points) form a cluster featuring a negligible change in the OH volume and an only slightly negative change in charge in transition from the RC to the TS (Δq ∈ [−0.04e, 0.02e] and ΔV ∈ [−3.7 a.u.3, 1.2 a.u.3]). This is in good agreement with the mechanism where the (L)(TMC)FeIII–OH moiety accepts the electron from the substrate, and thus the anionic character of the OH group remains essentially preserved. There is one outlier (azide-ligated TMC system), which features a slightly positive change in charge and negative change in volume and presumably demonstrates the limitations of the change-of-charge/volume method. Alternatively, this system exhibits the least asynchronous OH rebound in favor of substrate-to-FeIII electron transfer (the least negative η), which might explain the largest radical character of OH at the TS and hence its most pronounced change in charge and volume in going from the RC to the TS in the series of reactions.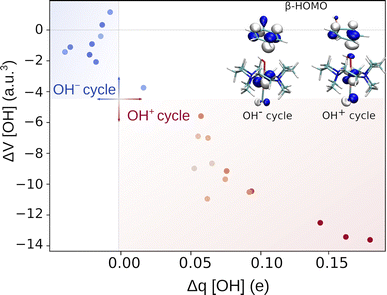 | ||
| Fig. 3 Characterization of the OH rebound reaction by change in volume and charge on the transferred OH group upon the RC → TS transition. The points are colored and shaded from dark blue (favored OH−) to dark red (favored OH+) to reflect the difference in off-diagonal thermodynamic contributions to the barrier (ΔG≠offdiag) originating from the OH− and OH+ cycles. The HOMO for the OH− and OH+ cycle driven reaction is shown in the inset. For the plot with the points labeled according to the axial ligand of the (L)(TMC)FeIII–OH complex see Fig. S10,† and the AIM charges and volumes of the studied systems are listed in Tables S16–S17.† | ||
In contrast, the systems whose off-diagonal contributions to the barrier originate from the OH+ cycle gather in the other region of the plot, displaying a considerably larger decrease in the volume of the OH moiety and positive change in charge during the RC-to-TS transition. This is in line with the expectation that in the reaction linked to the OH+ cycle, the transfer of the electron from the FeIII–OH moiety to the substrate leads to electron deficiency on the OH radical group, which is reflected by a rather significant build-up of positive charge, Δq ∈ [0.06e, 0.18e]. Moreover, the observed change in volume is consistent with the expectation that the OH group with some OH+ character is less bulky than that with the OH− character, which corresponds to a larger decrease in volume of OH in the OH+-favored reaction, ΔV ∈ [−13.6 a.u.3, −5.6 a.u.3].
Electron deficiency of the OH radical group in reactions associated with the OH+ cycle correlates with the character of the frontier molecular orbital at the TS structures. Throughout the OH+ set of reactions, the β-HOMO features a contribution from the p orbital of the oxygen of the OH group, which is not present in the OH−-favored TSs (inset of Fig. 3, for details see Tables S14 and S15†). This additional contribution indicates that the OH moiety features an electron vacancy, which enables a partial delocalization of the unpaired β electron to the OH moiety. The presence of such a vacancy may suggest that the OH has a partial OH+ character, which in turn is in line with the change in charge and volume of OH.
Detailed insight into the concertedness of cIET as given by asynchronicity
Apart from qualitative agreement between the preference for one of the cycles and the observed changes along the reaction coordinate, the three-component thermodynamic model also provides a quantitative insight into the mechanism for the reaction. It turns out that asynchronicity allows to describe the extent to which ET is more advanced in the reaction. As shown in Fig. S12,† the change in charge upon the RC-to-TS transition correlates with asynchronicity – the systems more asynchronous towards ET feature a larger change in charge of the OH moiety. The correlation is much more pronounced in the OH+→/e−→ featured reactions (R2 = 0.80), yet it is also noticeable in the OH− set (R2 = 0.56). The weaker correlation observed for the OH−→/e−← reactions can be explained by a mechanism that involves ET from the substrate to FeIII and thus less dramatic changes in the character of the OH moiety. Additionally, the OH+→/e−→ featured reactions exhibit more pronounced changes in Δq (and ΔV) than their OH−→/e−← counterparts, even though they are characterized by smaller magnitudes of asynchronicity as compared to reactions of the OH− set. This suggests (in addition to the change in the sign of the correlation slope in Fig. 2) that some other factors may be at work, such as stronger interactions between reactants that are part of the non-thermodynamic component of the barrier (see the next section).Moreover, asynchronicity allows us to distinguish between a concerted and stepwise mechanism of the OH transfer reaction. The investigated transition states correspond to a concerted process as indicated by a single imaginary frequency related to OH group motion from the donor to the acceptor and a retained radical character of the (2F-)CHD˙ fragment. For all these cases, the energies of both ET and PT states are higher than the energy of the TS (see Fig. S13†), which is clear evidence that the preferred route is concerted electron-ion transfer. As can be expected, there is a strong relationship between the energy of the ET (and IT) state and asynchronicity such that large negative values indicate a low energy of the ET state (and a high energy of the IT state; Fig. S14†). The investigation of additional TMC systems with neutral axial ligands (e.g. carbon monoxide, water, and acetonitrile) in reaction with CHD˙ showed that if the asynchronicity reaches very negative values (in this particular case less than −70 kcal mol−1), the energy of the ET state becomes lower than the energy of the (separated) reactants, meaning that the reaction is driven by spontaneous ET between the substrate and the oxidant.
Difference between two reaction sets in terms of the interplay between the thermodynamic and non-thermodynamic component of the barrier
From Fig. 2, it is apparent that two reaction sets – one associated with the OH− cycle and the other with the OH+ cycle – differ by the barrier heights. While the range for ΔG≠ in the first set is 5–9 kcal mol−1, the latter set exhibits higher barriers (in the range of 15–19 kcal mol−1 as shown in Fig. S15†). We note that such a difference in ranges comes neither from the LFER nor from the overall thermodynamic contribution to the barriers, since the range for ΔG≠diag or ΔG≠thermo in both reaction sets is essentially the same (Fig. 2). In fact, a different barrier range is mostly due to the non-thermodynamic component of the reaction barrier (that is ΔG≠00 from eq (7)), which is higher in the OH+ set of reactions than in the concurrent OH− set (Fig. 4 and Fig. S4†). Moreover, Fig. 4 reveals a striking difference between the two reaction sets in terms of the relation between ΔG≠00 and asynchronicity. Namely, ΔG≠00 correlates well with ηR+ in the OH+ space so that a larger value of |ηR+| yields a higher ΔG≠00, while ΔG≠00 within the OH− set of reactions remains approximately constant.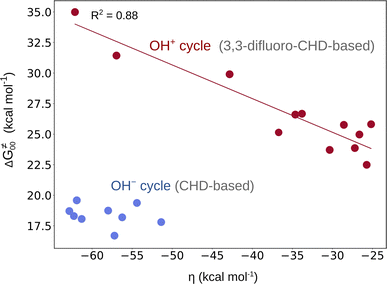 | ||
| Fig. 4 ΔG≠00vs. asynchronicity for radical ligand transfers linked to the OH− (blue) and OH+ (red) thermodynamic cycles. For the OH−/OH+ sets, the ηR− and ηR+ from eqn (3) and (4) were employed, respectively. For the plot with the points labeled according to the axial ligand of the (L)(TMC)FeIII–OH complex see Fig. S22A.† | ||
To rationalize this, we note the important features of the TS geometries: first; the angle between the FeIII–OH moiety and the radical carbon atom of the substrate for both of the OH− and OH+ sets consistently facilitates the reaction following the π-channel for the reaction, that is with the electron accepted (donated) by one of the dπ* orbitals of the FeIII–OH moiety (dπ*: dxz/yz antibonding with px/y with the z-axis along the Fe–OH bond). In the OH+ set, however, the Fe–OH–C axis is more bent (Fig. S16†), allowing a more favorable overlap of the dπ* orbital with pC, but also causing a larger steric strain between the reactants, which contributes, at least in part, to the higher values of ΔG≠00 in the OH+ set. Second, the key C–OH–Fe distances at TSs in the OH+ set are noticeably shorter than those in the OH− set (Tables S18–S21 and Fig. S16–S21†), implying that during the OH+-flavored radical transfer the OH donor and acceptor interact more strongly than in the reaction following the OH− cycle (as already indicated by the more pronounced change in charge and volume). All these observations suggest that there is a significant difference in the role of adiabatic coupling between concerted OH−→/e−← and OH+→/e−→ transfers.
To better understand this, let us recall the meaning of such a coupling well known from cPET chemistry, where ET and PT are recognized to be electronically adiabatic or non-adiabatic. The former means that the reaction takes place on a single electronic ground state surface, which results from the mixing of the two originally non-interacting (diabatic) surfaces, which retain the electronic structure of the reactant and product state along the reaction coordinate, respectively. Strong mixing leads to a strong response of electrons to a change in the position of the nuclei and therefore a strong adiabatic coupling. On the other hand, the weaker the mixing, the less adiabatic the process becomes, until it eventually reaches the limit of a non-adiabatic reaction, which involves thermally accessible excited electronic states. At this point, it is worth mentioning that, in cPET chemistry, the reaction is often electronically less adiabatic (with a smaller adiabatic coupling), when the electron travels a longer distance through a proton transfer interface.50 Conversely, a shorter distance between the reactants indicates a larger adiabatic coupling. This, based on the parallel between cPET and cIET, signals that for the tighter TSs of the OH+ reactions we can expect stronger adiabatic couplings, as compared to those associated with the OH− set. The adiabatic coupling depends on the reaction coordinate73 and thus it should be integrated in the non-thermodynamic component of the reaction barrier ΔG≠00.
According to our current understanding, thermodynamic asynchronicity affects adiabatic coupling. As we demonstrated in ref. 63, thermodynamic asynchronicity in cPET controls the redistribution of the positive vs. negative charge along the reaction coordinate going from the RC to the TS. Namely, we found that a higher asynchronicity in favor of ET leads to electron dislocation from the H-atom donor to the acceptor, which is more pronounced than the competitive build-up of a more positive charge on the transferred H group. The opposite is true for a higher asynchronicity in favor of PT. This behavior is also consistent with the position of the H-atom in between the H-atom donor and acceptor at the TS. Comparing two reactions having similar ΔG0, ET- vs. PT-driven cPET tends to exhibit a shorter donor—H vs. a shorter H—acceptor distance, respectively. All this may witness that more asynchronous reactions have a weaker responsivity of electron rearrangement to proton (nucleus) motion, and vice versa. As a consequence, a smaller adiabatic coupling expected for more asynchronous reactions should then reduce the magnitude of ΔG≠00 to a lower extent.
This is consistent with the observation for the OH+ set in Fig. 4, where ΔG≠00 increases with increasing |η|. This effect is evidently also responsible for the change in the correlation slope in the OH+ set seen in Fig. 2. On the other hand, the OH− set of reactions exhibit a more or less constant ΔG≠00 (independent of asynchronicity) due to weaker interaction between the OH˙ donor and acceptor, which is also reflected by much smaller electronic changes in the FeIII–OH moiety in going from the RC to the TS as compared to the OH+ set, which we demonstrated in the previous sections.
The ferro- vs. antiferromagnetic interaction of the OH donor and acceptor and thermodynamics
The unpaired electron of the substrate CHD˙ (or 2F-CHD˙) radical can interact antiferromagnetically with the high-spin (S = 5/2) (L)(TMC)FeIII–OH complex, or ferromagnetically with its intermediate-spin (S = 3/2) form. In the TMC-supported FeIII–OH complexes, the S = 3/2 state lies 3–10 kcal mol−1 above its S = 5/2 counterpart, which is otherwise the focus of this study. This spin state energetics translates into relative energies of the respective TSs for OH group transfer: the ferromagnetic TS is higher in energy than the corresponding antiferromagnetic TS (Fig. S10†). Nevertheless, we found that the relationship between ΔG≠ and the appropriate ΔG≠thermo obtained from the favored OH− or OH+ cycle, is well preserved throughout these ferromagnetically coupled sets (Fig. S5 and S7†). We note in passing that the observed relationship is largely given by the canonical LFER, that is the role of the off-diagonal term is slightly less important than in antiferromagnetically coupled systems (for details see Fig. S5 and S7†). This can be possibly attributed to the more negative ΔG0 of ferromagnetically coupled reactive systems. Importantly, we conclude here that the energy difference between two related ferro- and antiferromagnetic TSs appear less important compared to the difference between barriers of two related OH+ and OH− featured radical ligand transfers, which is given by the three-component thermodynamics (Fig. S10†).As for the unidirectional OH+→/e−→ transfer vs. bidirectional OH−→/e−← transfer mechanism, OH group transfer is not affected by the spin state of FeIII–OH: the ferromagnetically as well as antiferromagnetically coupled pairs of reactants feature a negative and positive change in charge on OH in going from the RC to the TS in reactions following the OH− and OH+ cycle, respectively. The change in volume of OH also follows the same pattern in the space of ferromagnetically and antiferromagnetically coupled systems, i.e. there is only a modest change in the case of reactions linked to the OH− cycle, and a noticeable decrease in volume for the OH+ counterpart. The only significant difference is that the absolute changes in the charge and the volume in the ferromagnetic space are more shifted towards positive values (see Fig. S23, S24 and Tables S22, S23† as well as the related discussion on the origin of the shift).
Conclusions
In this work we investigated the role of three thermodynamic factors contributing to the barrier of radical ligand transfer reactions using the example of OH group transfer reactions. The three-component thermodynamics and its effect on reactivity were originally investigated for concerted proton-electron transfer reactions. This includes, besides the well-known so-called diagonal effect – LFER, two other off-diagonal components – asynchronicity (η) and frustration (σ), the first of which measures the inequality in thermodynamic preference for electron vs. proton transfer, whereas the latter reflects the overall thermodynamic (in)accessibility of the two separate transfers. Here, we applied the concept to radical transfer chemistry viewing it as a concerted ion-electron transfer (cIET) and elucidated the following.First, the three-component thermodynamic framework works well for chemistry beyond the concerted proton-electron transfer and clearly shows that the barrier for the reaction is affected by the joint contribution originating from free energy of the reaction, asynchronicity and frustration (yet the exact effect of asynchronicity appears to strongly depend on the adiabatic coupling between ion and electron transfer in cIET, vide infra).
Second, it is the energetics of the off-diagonal states (ion transfer vs. electron transfer state) that determines the mechanism of the reaction. More importantly, two mechanistic scenarios can be well recognized – unidirectional cation and electron transfer from the radical donor to the radical acceptor and bidirectional anion and electron transfer, where the anion moves from the radical donor to the acceptor and the electron flows in the opposite direction. One of the two scenarios is observed in the reaction if its associated thermodynamic cycle has preferred off-diagonal thermodynamics (i.e. off-diagonal states are lower in energy in comparison to those of the competing thermodynamic cycle). This conclusion was derived from the correlation of the evolution of the charge and volume of the OH group upon the RC-to-TS transition and the preference for a given thermodynamic cycle. In the case of bidirectional anion-electron transfer, the OH group retains its anionic character and only slightly changes its volume. In contrast, in the case of unidirectional cation-electron transfer, the OH group develops an electron deficiency, which is also accompanied by a noticeable decrease in the volume of this moiety. These findings render the three-component thermodynamic model not only a tool to predict cIET reactivity, but also to gain insight into the mechanism of the reaction.
Third, we have revealed the role of the non-thermodynamic component of the barrier, which may be the dominant factor ruling the barrier difference between two reactions in the case of strongly interacting reacting moieties (manifested by more compact TS structures). This is the situation that we observed for unidirectional cation-electron transfer reactions. For them, large values of η result in a high reaction barrier, which presumably can be attributed to strong modulation of adiabatic coupling by asynchronicity. Namely, a large asynchronicity in favor of electron transfer in the unidirectional OH+/electron process results in reduced adiabatic coupling and, thus a larger non-thermodynamic component of the barrier. For a bidirectional anion-electron transfer reaction with a weaker interaction of reacting moieties, the non-thermodynamic component remains quite constant. These observations eventually suggest that a unidirectional OH+/electron transfer reaction can be classified as an adiabatic radical transfer, and the bidirectional OH−/electron transfer reaction as a less adiabatic ion-coupled electron transfer. From this perspective, we may partially perceive a parallel with the mechanistic distinction between adiabatic hydrogen atom transfer and non-adiabatic proton-coupled electron transfer.57,74,75 Finally, in light of the presented study, it seems pertinent to revisit concerted proton-electron transfer reactions and validate the possibility of the mechanism analogous to bidirectional OH−/electron transfer, that is the mechanism where electron transfer flowing from the oxidant to the X–H substrate is coupled to the hydride transfer in the opposite direction. This will be the aim of future studies.
Data availability
A data set collection of computational results (including transition state structures and reactant complexes) is available in the ioChem-BD repository76 and can be accessed viahttps://doi.org/10.19061/iochem-bd-4-73.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project was supported by the Grant Agency of the Czech Republic (Grant No. 21-10383S). MS also acknowledges the Praemium Academiae award by the Czech Academy of Sciences.Notes and references
- J. E. Baldwin, R. M. Adlington, J. B. Coates, M. J. C. Crabbe, N. P. Crouch, J. W. Keeping, G. C. Knight, C. J. Schofield, H. H. Ting, C. A. Vallejo, M. Thorniley and E. P. Abraham, Biochem. J., 1987, 245, 831–841 CrossRef CAS PubMed
.
- M. D. Lloyd, K. D. Merritt, V. Lee, T. J. Sewell, B. Wha-Son, J. E. Baldwin, C. J. Schofield, S. W. Elson, K. H. Baggaley and N. H. Nicholson, Tetrahedron, 1999, 55, 10201–10220 CrossRef CAS
.
- B. Tudzynski, M. C. Rojas, P. Gaskin and P. Hedden, J. Biol. Chem., 2002, 277, 21246–21253 CrossRef CAS PubMed
.
- R. Lukačin, F. Wellmann, L. Britsch, S. Martens and U. Matern, Phytochemistry, 2003, 62, 287–292 CrossRef PubMed
.
- M. Mizutani and D. Ohta, Annu. Rev. Plant Biol., 2010, 61, 291–315 CrossRef CAS PubMed
.
- J. Li, M. J. van Belkum and J. C. Vederas, Bioorg. Med. Chem., 2012, 20, 4356–4363 CrossRef CAS PubMed
.
-
K. I. Kivirikko and T. Pihlajaniemi, in Advances in Enzymology and Related Areas of Molecular Biology, John Wiley & Sons, Ltd, 1998, pp. 325–398 Search PubMed
.
- J. R. Chekan, C. Ongpipattanakul, T. R. Wright, B. Zhang, J. M. Bollinger, L. J. Rajakovich, C. Krebs, R. M. Cicchillo and S. K. Nair, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 13299–13304 CrossRef CAS
.
- J. Huang, D. Chen and J. Jiang, Environ. Microbiol., 2020, 22, 286–296 CrossRef CAS
.
- K.-J. Bian, D. Jr. Nemoto, S.-C. Kao, Y. He, Y. Li, X.-S. Wang and J. G. West, J. Am. Chem. Soc., 2022, 144, 11810–11821 CrossRef CAS PubMed
.
- S.-C. Kao, K.-J. Bian, X.-W. Chen, Y. Chen, A. A. Martí and J. G. West, Chem Catal., 2023, 3, 100603 CrossRef CAS PubMed
.
- K.-J. Bian, S.-C. Kao, D. Nemoto, X.-W. Chen and J. G. West, Nat. Commun., 2022, 13, 7881 CrossRef CAS PubMed
.
- N. Fu, G. S. Sauer and S. Lin, J. Am. Chem. Soc., 2017, 139, 15548–15553 CrossRef CAS PubMed
.
- N. Fu, G. S. Sauer, A. Saha, A. Loo and S. Lin, Science, 2017, 357, 575–579 CrossRef CAS PubMed
.
- L. I. Panferova, M. O. Zubkov, V. A. Kokorekin, V. V. Levin and A. D. Dilman, Angew. Chem., 2021, 133, 2885–2890 CrossRef
.
- W. Nam, Y.-M. Lee and S. Fukuzumi, Acc. Chem. Res., 2018, 51, 2014–2022 CrossRef CAS PubMed
.
- J. Pan, E. S. Wenger, M. L. Matthews, C. J. Pollock, M. Bhardwaj, A. J. Kim, B. D. Allen, R. B. Grossman, C. Krebs and J. M. Jr. Bollinger, J. Am. Chem. Soc., 2019, 141, 15153–15165 CrossRef CAS
.
- J. P. T. Zaragoza, T. H. Yosca, M. A. Siegler, P. Moënne-Loccoz, M. T. Green and D. P. Goldberg, J. Am. Chem. Soc., 2017, 139, 13640–13643 CrossRef CAS
.
- V. Yadav, J. B. Gordon, M. A. Siegler and D. P. Goldberg, J. Am. Chem. Soc., 2019, 141, 10148–10153 CrossRef CAS
.
- V. Yadav, R. J. Rodriguez, M. A. Siegler and D. P. Goldberg, J. Am. Chem. Soc., 2020, 142, 7259–7264 CrossRef CAS
.
- J. M. Bollinger Jr, J. C. Price, L. M. Hoffart, E. W. Barr and C. Krebs, Eur. J. Inorg. Chem., 2005, 2005, 4245–4254 CrossRef
.
- M. L. Hillwig and X. Liu, Nat. Chem. Biol., 2014, 10, 921–923 CrossRef CAS PubMed
.
- C. Y. Kim, A. J. Mitchell, C. M. Glinkerman, Fu-S. Li, T. Pluskal and J.-K. Weng, Nat. Commun., 2020, 11, 1867 CrossRef CAS PubMed
.
- R. K. Quinn, Z. A. Könst, S. E. Michalak, Y. Schmidt, A. R. Szklarski, A. R. Flores, S. Nam, D. A. Horne, C. D. Vanderwal and E. J. Alexanian, J. Am. Chem. Soc., 2016, 138, 696–702 CrossRef CAS PubMed
.
- J. K. Bower, A. D. Cypcar, B. Henriquez, S. C. E. Stieber and S. Zhang, J. Am. Chem. Soc., 2020, 142, 8514–8521 CrossRef CAS PubMed
.
- X. Zhang, H. Yang and P. Tang, Org. Lett., 2015, 17, 5828–5831 CrossRef CAS PubMed
.
- R. R. Karimov, A. Sharma and J. F. Hartwig, ACS Cent. Sci., 2016, 2, 715–724 CrossRef CAS PubMed
.
- K.-J. Bian, Y. Li, K.-F. Zhang, Y. He, T.-R. Wu, C.-Y. Wang and X.-S. Wang, Chem. Sci., 2020, 11, 10437–10443 RSC
.
- K. Wang, Y. Li, X. Li, D. Li and H. Bao, Org. Lett., 2021, 23, 8847–8851 CrossRef CAS PubMed
.
- T. M. Pangia, C. G. Davies, J. R. Prendergast, J. B. Gordon, M. A. Siegler, G. N. L. Jameson and D. P. Goldberg, J. Am. Chem. Soc., 2018, 140, 4191–4194 CrossRef CAS PubMed
.
- M. L. Matthews, W. Chang, A. P. Layne, L. A. Miles, C. Krebs and J. M. Bollinger, Nat. Chem. Biol., 2014, 10, 209–215 CrossRef CAS PubMed
.
- R. J. Martinie, J. Livada, W. Chang, M. T. Green, C. Krebs, J. M. Jr. Bollinger and A. Silakov, J. Am. Chem. Soc., 2015, 137, 6912–6919 CrossRef CAS PubMed
.
- A. J. Mitchell, N. P. Dunham, J. A. Bergman, B. Wang, Q. Zhu, W. Chang, X. Liu and A. K. Boal, Biochemistry, 2017, 56, 441–444 CrossRef CAS PubMed
.
- A. Papadopoulou, J. Meierhofer, F. Meyer, T. Hayashi, S. Schneider, E. Sager and R. Buller, ChemCatChem, 2021, 13, 3914–3919 CrossRef CAS
.
- M. E. Neugebauer, E. N. Kissman, J. A. Marchand, J. G. Pelton, N. A. Sambold, D. C. Millar and M. C. Y. Chang, Nat. Chem. Biol., 2022, 18, 171–179 CrossRef CAS
.
- M. Srnec and E. I. Solomon, J. Am. Chem. Soc., 2017, 139, 2396–2407 CrossRef CAS
.
- T. M. Pangia, V. Yadav, E. F. Gérard, Y.-T. Lin, S. P. de Visser, G. N. L. Jameson and D. P. Goldberg, Inorg. Chem., 2019, 58, 9557–9561 CrossRef CAS
.
- J.-M. Savéant, Acc. Chem. Res., 1993, 26, 455–461 CrossRef
.
- C. Costentin, M. Robert and J. M. Savéant, Chem. Phys., 2006, 324, 40–56 CrossRef CAS
.
- J. M. Mayer, D. A. Hrovat, J. L. Thomas and W. T. Borden, J. Am. Chem. Soc., 2002, 124, 11142–11147 CrossRef CAS
.
- J. W. Darcy, B. Koronkiewicz, G. A. Parada and J. M. Mayer, Acc. Chem. Res., 2018, 51, 2391–2399 CrossRef CAS
.
- M. Galeotti, M. Salamone and M. Bietti, Chem. Soc. Rev., 2022, 51, 2171–2223 RSC
.
- G. A. Parada, Z. K. Goldsmith, S. Kolmar, B. P. Rimgard, B. Q. Mercado, L. Hammarström, S. Hammes-Schiffer and J. M. Mayer, Science, 2019, 364, 471–475 CrossRef CAS PubMed
.
- M. Salamone, M. Galeotti, E. Romero-Montalvo, J. A. van Santen, B. D. Groff, J. M. Mayer, G. A. DiLabio and M. Bietti, J. Am. Chem. Soc., 2021, 143, 11759–11776 CrossRef CAS PubMed
.
- J. H. Skone, A. V. Soudackov and S. Hammes-Schiffer, J. Am. Chem. Soc., 2006, 128, 16655–16663 CrossRef CAS PubMed
.
- A. V. Soudackov and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2014, 5, 3274–3278 CrossRef CAS PubMed
.
- S. Hammes-Schiffer and A. A. Stuchebrukhov, Chem. Rev., 2010, 110, 6939–6960 CrossRef CAS PubMed
.
- A. Sirjoosingh and S. Hammes-Schiffer, J. Chem. Theory Comput., 2011, 7, 2831–2841 CrossRef CAS PubMed
.
- A. Sirjoosingh and S. Hammes-Schiffer, J. Phys. Chem. A, 2011, 115, 2367–2377 CrossRef CAS PubMed
.
- S. Hammes-Schiffer, ChemPhysChem, 2002, 3, 33–42 CrossRef CAS PubMed
.
- T. Liu, R. Tyburski, S. Wang, R. Fernández-Terán, S. Ott and L. Hammarström, J. Am. Chem. Soc., 2019, 141, 17245–17259 CrossRef CAS PubMed
.
- R. Tyburski, T. Liu, S. D. Glover and L. Hammarström, J. Am. Chem. Soc., 2021, 143, 560–576 CrossRef CAS PubMed
.
- N. Zhao, M. K. Goetz, J. E. Schneider and J. S. Anderson, J. Am. Chem. Soc., 2023, 145, 5664–5673 CrossRef CAS
.
- J. E. Schneider, M. K. Goetz and J. S. Anderson, Chem. Sci., 2021, 12, 4173–4183 RSC
.
- M. Salamone and M. Bietti, Acc. Chem. Res., 2015, 48, 2895–2903 CrossRef CAS PubMed
.
- M. Galeotti, M. Salamone and M. Bietti, Chem. Soc. Rev., 2022, 51, 2171–2223 RSC
.
- M. Mazzonna, M. Bietti, G. A. Dilabio, O. Lanzalunga and M. Salamone, J. Org. Chem., 2014, 79, 5209–5218 CrossRef CAS PubMed
.
- R. A. More O'Ferrall, J. Chem. Soc. B, 1970, 274–277 RSC
.
- W. P. Jencks, Chem. Rev., 1972, 72, 705–718 CrossRef CAS
.
- A. Cembran, M. R. Provorse, C. Wang, W. Wu and J. Gao, J. Chem. Theory Comput., 2012, 8, 4347–4358 CrossRef CAS PubMed
.
- C. F. Bernasconi, Acc. Chem. Res., 1992, 25, 9–16 CrossRef CAS
.
- C. F. Bernasconi, J. Phys. Org. Chem., 2004, 17, 951–956 CrossRef CAS
.
- D. Bím, M. Maldonado-Domínguez, L. Rulíšek and M. Srnec, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E10287–E10294 CrossRef PubMed
.
- M. Maldonado-Domínguez and M. Srnec, Inorg. Chem., 2022, 61, 18811–18822 CrossRef PubMed
.
- E. Kent Barefield, F. Wagner and E. K. Barefield, Inorg. Chem., 1973, 12, 723 CrossRef
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed
.
-
T. A. Keith, AIMAll (Version 19.10.12), TK Gristmill Software, Overland Park KS, USA, 2019 Search PubMed
.
- J. M. Mayer, Acc. Chem. Res., 2011, 44, 36–46 CrossRef CAS PubMed
.
- U. Raucci, M. G. Chiariello, F. Coppola, F. Perrella, M. Savarese, I. Ciofini and N. Rega, J. Comput. Chem., 2020, 41, 1835–1841 CrossRef CAS PubMed
.
- D. Usharani, D. C. Lacy, A. S. Borovik and S. Shaik, J. Am. Chem. Soc., 2013, 135, 17090–17104 CrossRef CAS PubMed
.
- O. Tishchenko, D. G. Truhlar, A. Ceulemans and M. T. Nguyen, J. Am. Chem. Soc., 2008, 130, 7000–7010 CrossRef CAS PubMed
.
- M. Álvarez-Moreno, C. de Graaf, N. Lopez, F. Maseras, J. M. Poblet and C. J. Bo, J. Chem. Inf. Model., 2015, 55, 95–103 CrossRef PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc01507j |
| ‡ Despite the thermodynamic definition of asynchronicity, it is directly related to the asynchronicity between ET and PT in time because, as we showed earlier in ref. 63, thermodynamic asynchronicity controls the redistribution of positive and negative charge in the reaction system during its transition to the transition state, and this can be considered as a stopwatch measuring the extent of ET vs. PT transfer over time required to reach the transition state. |
| This journal is © The Royal Society of Chemistry 2024 |