Non-Aufbau electronic structure in radical enzymes and control of the highly reactive intermediates

Abstract

Radicals are highly reactive, short-lived chemical species that normally react indiscriminately with biological materials, and yet, nature has evolved thousands of enzymes that employ radicals to catalyze thermodynamically challenging chemistry. How these enzymes harness highly reactive radical intermediates to steer the catalysis to the correct outcome is a topic of intense investigation. Here, the results of detailed QM/MM calculations on archetype radical B₁₂-enzymes are presented that provide new insights into how these enzymes control the reactivity of radicals within their active sites. The catalytic cycle in B₁₂-enzymes is initiated through the formation of the 5′-deoxyadenosyl (Ado˙) moiety, a primary carbon-centred radical, which must migrate up to 8 Å to reach the target substrate to engage in the next step of the catalytic process, a hydrogen atom abstraction. Our calculations reveal that Ado˙ within the protein environment exhibits an unusual non-Aufbau electronic structure in which the singly occupied molecular orbital is lower in energy than the doubly occupied orbitals, an uncommon phenomenon known as SOMO–HOMO inversion (SHI). We find that the magnitude of SHI in the initially formed Ado˙ is larger compared to when the Ado˙ is near the intended substrate, leading to the former being relatively less reactive. The modulation of the SHI originates from Coulombic interactions of a quantum nature between a negative charge on a conserved glutamate residue and the spin on the Ado˙. Our findings support a novel hypothesis that these enzymes utilize this quantum Coulombic effect as a means of maintaining exquisite control over the chemistry of highly reactive radical intermediates in enzyme active sites.

---

Introduction

Radicals are highly reactive chemical systems that have drawn sustained interest in all branches of chemistry due to their widespread applications.^1–5 The electronic structure of radicals is a key factor responsible for their distinctive characteristics.^6–8 Recently, there have been reports of persistent organic radical systems having electronic structures that apparently do not obey the Aufbau principle resembling the electronic structure found in some transition metal complexes.^9–11 Friend, Bredas, Li et al. characterized a series of donor–acceptor organic radical systems that possess a non-Aufbau electronic configuration.¹² These radicals were found to have high emission yields while also having high photostability. Coote and coworkers reported that some radical anions such as 4-carboxy-TEMPO show unprecedented stabilization which is accompanied by a non-Aufbau electronic structure.^13,14 This stabilization seems to be correlated with the enhanced acidity of some radicals observed by Walton; i.e., nearby spins stabilize the negative charge in radical anions.^15,16 Other examples include relatively persistent aza-thia[7]helicene radical species and cationic radical bicarbazoles, all of which have been verified to possess non-Aufbau configurations by experimental and theoretical methods.¹⁷ These radical systems are described by Autschbach and others as displaying electronic structures wherein their singly occupied molecular orbitals (SOMOs) are lower in energy than their highest-occupied molecular orbitals (HOMOs) exhibiting SOMO–HOMO inversion (SHI).^18,19 The studies of systems displaying SHI suggest a tantalizing connection between radical stability/persistence and non-Aufbau electronic structure.^14,18–21

The unusual stability of radicals displaying SHI led us to hypothesize that the effect could be operating in radical enzymes. There are thousands of known radical enzymes including a large family of radical SAM (rSAM) enzymes that utilize highly reactive radical species to effect thermodynamically challenging chemical transformations, such as 1,2-isomerizations.^22,23 Many of these enzymes are responsible for key biochemical transformations required to sustain life in a diversity of species.²² In general, radical enzymes must utilize a mechanism that takes advantage of the high reactivity of radicals while also controlling unwanted, damaging side reactions.²⁴ One prime example of such radicals is the fleeting primary 5′-deoxyadenosyl (Ado˙) radical, which evaded spectroscopic detection until recently.²⁵ Therefore, understanding the control mechanism can provide invaluable insights into the activity of radical enzymes and assist in the design of artificial enzymes and of novel catalysts.^26–28

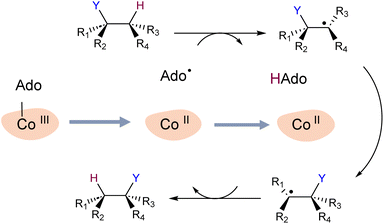
To explore our hypothesis, we undertook a simulation study of two B₁₂-dependent radical enzymes: glutamate mutase (GLM) and methylmolonyl-Co-A mutase (MCM). The catalytic cycles in both enzymes begin with the homolytic scission of the Co–C bond in the adenosylcobalamin co-enzyme,^29–32 and generation of the primary carbon-centred radical Ado˙. The highly reactive Ado˙ must then migrate to the intended substrate, a journey of up to 8 Å.³³ Ado˙ then abstracts a hydrogen atom from the substrate, allowing the latter to undergo isomerization, after which the hydrogen atom is transferred back to the rearranged substrate (Scheme 1). The mechanistic details of the catalytic cycle of these enzymes, particularly Co–C bond dissociation, have been extensively investigated experimentally and computationally.^29–37 However, the enzymatic control of highly reactive intermediates has not been elucidated in these studies.

Scheme 1 General catalytic cycle in B₁₂-dependent enzymes. Homolysis of adenosylcobalamin generates the 5′-deoxyadenosyl radical (Ado˙), which then migrates to, and abstracts a hydrogen atom from, the substrate. The substrate radical subsequently undergoes a 1,2 rearrangement. The cycle is completed when the rearranged substrate radical abstracts the hydrogen atom from 5′-deoxyadenosine to form the Ado˙, which then recombines with cob(II)alamin.

The high reactivity of Ado˙, which is central for the B₁₂-dependent and the large family of rSAM enzymes, is essential for catalysis but is also potentially detrimental to the functioning of enzymes that utilize it. Some have suggested that perfect positioning of the Ado˙ and substrate in certain radical enzymes reduces the potential for unwanted side reactions of the radical through tight van der Waals contacts.^38–41 However, the general lack of specificity associated with van der Waals interactions lend doubt to these suggestions, in particular given the large distances that the Ado˙ must migrate in some enzymes. Other radical control mechanisms proposed include Retey's negative catalysis,⁴² interactions with enzyme's active site residues to guide the radical toward the target substrate,³⁷ the effect of ion coordination on the radical stability,⁴³ and control through conformational constraints (e.g. preventing planarization of radical centres).^44,45

Here we show that the GLM and MCM enzymes generate Ado˙ species that have non-Aufbau electronic structures that are consistent with SHI, suggesting that the enzymes could make use of the effect to control the reactivity of the radical. Our simulations reveal that modulation of the SHI in Ado˙ occurs through changes in the degree of hydrogen bonding between a conserved active site glutamate residue (Glu⁻) and the ribose ring of the radical. When Ado˙ is first formed in the active site, hydrogen bonding between the radical and Glu⁻ is minimal. In this instance, the Ado˙ SOMO energy is relatively low (SHI is more significant) and consequently the reactivity of the radical is relatively low. Conversely, when Ado˙ is close to the intended substrate, there is strong hydrogen bonding between Glu⁻ and Ado˙. In this case, the Ado˙ SOMO energy is relatively high (SHI is less pronounced) and the reactivity of the radical increases by 1–3 orders of magnitude. The results align with the previous experimental and theoretical evidence, which underscores the importance of Ado˙ and Glu⁻ interactions.^30,32,37,46 Our findings suggest that viewing radical enzyme catalysis through the lens of SHI will provide novel insights into the biochemistry of a large class of poorly understood systems.

Computational details

GLM models

For simulations involving the GLM enzyme, models were obtained from the X-ray crystallographic structure (pdb id: 1I9C) in which the substrate is bound in the active site. This X-ray structure has mixed populations of two distinct conformations for the Ado˙ group (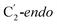 and 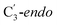orientation of the ribose ring) corresponding to two different stages of the catalytic cycle, pre-migration and post-migration of the Ado˙ (Fig. 1).^47–49 The two conformers differ from each other by the Co–C(Ado) bond distances, the geometry of the Ado˙ ribose ring, and more importantly the degree to which Ado˙ interacts with the nearby conserved glutamate residue (E330) in the active site. In the pre-migration conformation 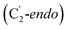the Ado˙ forms a partial hydrogen bond with E330 (Glu⁻, Fig. 1b, left). We refer to this conformation as GLM-Pre. In the post-migration conformation 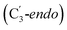, the Ado˙ group has nearly completed its migration toward the substrate by pseudorotation of the Ado˙ ribose ring and forms a stronger hydrogen bond with E330 (Glu⁻, Fig. 1b, right). This conformation is labelled GLM-Post and has the Ado˙ group within vdW distance of the substrate and so it is in position to abstract the intended hydrogen. The GLM-Pre and GLM-Post conformations provide ideal model systems for exploring our hypothesis: the GLM-Pre model represents the structure prior to migration in which the reactivity of Ado˙ should be reduced to prevent unintended reactions. On the other hand, the GLM-Post model represents the structure near the hydrogen abstraction step in which the enzyme should be able to exploit the reactivity of the Ado˙ in order to effectively engage in the hydrogen atom abstraction reaction. As both GLM-Pre and GLM-Post models are identical except only in the position of the Ado˙, and consequently the extent of its hydrogen bonding with E330, it is possible to make direct comparisons between their electronic structures and molecular orbital (MO) energies. These two models were used for our QM/MM electronic structure calculations described below.

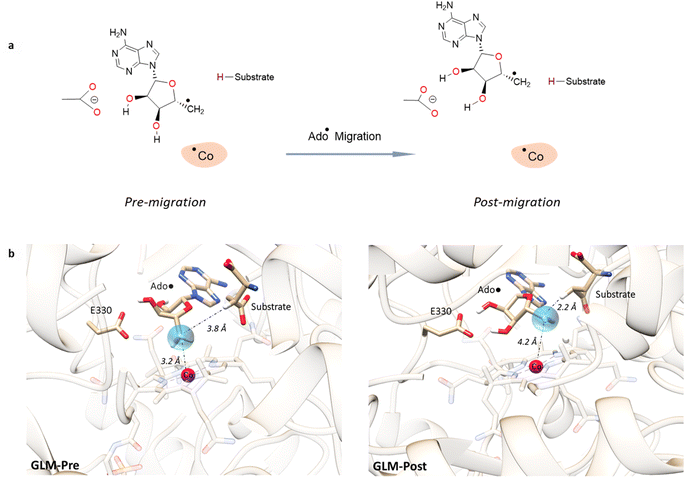Fig. 1 Models of GLM enzyme before and after migration. (a) Representations of the active site components prior to the migration of the Ado˙ (“Pre-migration”) and after the migration of the Ado˙ (“Post-migration”). (b) The GLM models (Pre and Post) obtained from the X-ray crystal structure (Protein Data Bank entry code 1I9C) that show the active site just after the Ado is formed and before the hydrogen abstraction. In (b, left, GLM-Pre) the ribose group has a 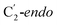sugar ring orientation, and E330:Ado˙ forms a partial hydrogen bond with a distance of 2.1 Å. In (b, right, GLM-Post) the ribose group is in the 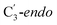puckered state, and E330:Ado˙ forms a stronger pair of hydrogen bonds with distances of 1.5 and 1.7 Å. In both cases, the carbon radical centre of Ado˙ is shown with a teal sphere.

QM/MM calculations

The GLM-Pre and GLM-Post models were modified by the following steps to acquire the initial structures for our eventual QM/MM electronic structure calculations. Starting from these crystal structures, the protonation states of the standard residues were predicted at pH 7.0 using the PROPKA 3.1 (ref. 50) and PDBPQR⁵¹ programs, and based on this prediction and visual inspection, the hydrogens were added. Hydrogen atoms on the non-standard residues (the Ado˙, the substrate and the B₁₂ cofactor) were added using the Gaussview version 6.1.1 software package.⁵² The prepared structures (GLM-Pre and GLM-Post) were then subjected to two sets of QM/MM optimization using the ChemShell⁵³ interface combining Orca 5.0 (ref. 54) for the QM region calculations and DL_POLY⁵⁵ for the MM region calculations. Hydrogen link atoms and the electronic embedding scheme were employed to treat the QM/MM boundaries and to polarize the QM region, respectively. The QM region was treated by unrestricted Kohn–Sham density functional theory⁵⁶ (UKS-DFT) with the BP86 functional, whereas for the MM region the CHARMM36 forcefield⁵⁷ was used. The choice of the BP86 functional is heavily justified in the KS-DFT framework of B₁₂ enzymes' studies.^58,59 The CHARMM parameters required for the B₁₂ cofactor and Ado˙ were obtained from Pavlova et al.⁶⁰ and the parameters for the substrate were generated by analogy to the available similar molecules. In the first set of our DFT/MM optimizations only the positions of all hydrogen atoms were optimized using BP86/def2-SVP:CHARMM. This choice was made to maintain the geometries of the pre-migration and post-migration conformers to allow for direct comparisons of their electronic structures and MO energies. However, in another set of calculations using the same methodology the heavy atoms of residues within 5 Å of the Ado radical in both of the models were also optimized: it was found that the heavy atom optimization does not have a significant influence on the conclusion drawn in this work, i.e. SHI is more significant in the Pre model than Post model (see ESI and Fig. S12).† Both of the optimizations were done using the DL-FIND⁶¹ geometry optimizer implemented in ChemShell. The QM region in both cases consisted of the truncated B₁₂ cofactor, the substrate, Ado˙ and the side chain of E330. In order to acquire the electronic structures of the models, UKS-DFT/CHARMM single point computations were carried out with BP86, M06-2X, and PBE0 functionals in conjunction with the 6-311+G(d,p) basis set. A very large QM region constructed from residues in proximity of the Ado˙ was used, resulting in a total of 480 atoms. The list of residues included in the QM region is provided in Fig. S1.† The choice of M06-2X functional in obtaining a reliable electronic structure for SHI radicals was justified in previous work that showed the M06-2X functional reproduces the electronic structure obtained by using the multi-configurational self-consistent field (MCSCF) method for SHI radicals.^13,14 Additional justification for the use of the M06-2X functional is provided by benchmarking our own systems against complete active space self-consistent field calculations (for details of CASSCF calculations see the ESI†). The hybrid PBE0 functional has also been used by Morgante and Autschbach²⁰ in previous calculations to study the SHI radicals, so the PBE0 functional was also used for comparison purposes. The MO values and the electronic structures reported here are based on M06-2X unless otherwise stated.

MCM models

The model structures were obtained from a previous QM/MM MD study in which the reaction coordinate between the carbon-centre of Ado˙ and the target hydrogen atom of the substrate had been studied.⁶² The details of these calculations are given in ref. 62. This study has shown that in the pre-migration stage no significant hydrogen bonding is present between the conserved glutamate and Ado˙, but as the Ado˙ migrates toward the substrate it forms a hydrogen bond with the glutamate side chain. From this study two structures that were associated with pre-migration and post-migration of Ado˙ were taken from the reaction coordinate and were subjected to the same UKS-DFT:MM electronic structure calculations mentioned for the GLM enzyme. To be consistent with our naming conventions we call these models MCM-Pre and MCM-Post. Fig. S7† illustrates the two MCM models with several important structural parameters. It should be noted that the calculations on these MCM models are done to separately see the generality of our conclusions. Direct comparison of the electronic structure and MO energies between GLM and MCM is not possible due to the structurally different systems, and these comparisons were not made in this work in any form. Moreover, since the MCM models are derived from long dynamic simulations resulting in numerous structural differences between MCM-Pre and MCM-Post, a cautious approach is necessary when making direct comparisons of their electronic structures.

Electronic configurations

The electronic structures and molecular orbital configurations reported in this work were obtained from UKS-DFT:MM calculations at the levels mentioned above. In UKS-DFT, α and β spin orbitals are represented by separate wave functions. Therefore, α and β orbitals calculated for a doubly occupied orbital will not necessarily have identical shapes or energies but are expected to be approximately the same. In order to determine if an MO is doubly or singly occupied, the α orbitals and β orbitals should be matched as far as it is possible in terms of energy and MO shape (by visual inspection or calculations of the overlap integral). An MO is doubly occupied if an occupied α orbital (approximately) matches an occupied β orbital. If an occupied α orbital has a β counterpart that is unoccupied (β-spin hole), the α orbital is considered to be the SOMO. To determine the SOMO that is associated with the Ado˙ in our models, we visualized the high energy MOs extracted from the UKS-DFT:MM or full UKS-DFT calculations. The MO that had the most electron density localized on the CH₂ of the Ado fragment was identified as the SOMO. The RCC value (described in the ESI†), which estimates the contribution of the atomic p-type orbital of the Ado˙ to the SOMO, was also calculated for extra verification. All the orbital configuration representations reported in this work have α and β signs on each MO representation to emphasize that they were obtained using unrestricted calculations.

QM calculations

The described models were truncated to only the Ado˙ and the glutamate side-chain (ethoxylate anion) without any modification to the positions of the atoms. The corrin ring was removed to see the influence of the E330 on just the electronic structure of the Ado˙ (the influence of the corrin ring could be seen in our large QM/MM calculations described above). These models are labelled with “s” at the end of their naming throughout this work. These models were subjected to full QM calculations including single point calculations to obtain the electronic structures, barrier height calculations with the wild-type substrate to estimate the reactivity, and density of states (DOS). The majority of these calculations were done at the UM06-2X/6-311+G(d,p) level; however, other functionals BP86 and PBE0 were also employed occasionally for comparison. The performance of the M06-2X functional has been found to be one of the most accurate benchmarked functionals for predicting hydrogen atom transfer barriers against the HTBH38 data set of Truhlar and coworkers.^63,64 The full QM calculations described here were performed using the Gaussian 16 software package.⁶⁵ Technical details for each of the mentioned calculations are provided in the ESI.†

Results and discussion

Electronic structure in the GLM enzyme

The orbital configurations predicted for the GLM-Pre and GLM-Post models from the QM/MM calculations are illustrated in Fig. 2. The calculations reveal that these structures have the unexpected non-Aufbau electronic structures. In the GLM-Pre model the SOMO associated with the Ado˙ is HOMO-19, with an absolute energy (ε) of −231 kJ mol⁻¹. The radical centre contribution (RCC, which is the contribution of the p_z atomic orbital associated with the radical center to the canonical orbital identified as the SOMO, see the ESI†) to the SOMO is ∼11%. In the GLM-Post model, the SOMO is HOMO-6, the RCC is ∼7%, and the energy associated with this MO is −145 kJ mol⁻¹. The seemingly small RCCs to these MOs are because of the inherent delocalized nature of the MOs; nevertheless, these RCCs are the largest among all of the orbitals in the GLM models, which confirms that they are associated with the Ado˙ (RCC to HOMO is 0% in both cases). The HOMOs for both of the models are provided in Fig. S2.†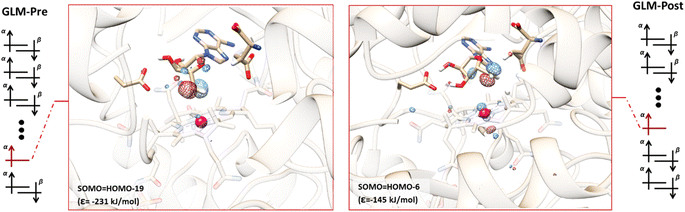

Fig. 2 Representative electronic configurations, and MO plots of the SOMO associated with Ado˙ with the absolute MO energy for GLM model systems. Left: Electronic configuration of GLM-Pre and the plot of its HOMO-19 (isovalue = 0.1). The orbital is distributed over the radical centre, indicating that this MO is the SOMO (RCC = 10%). Right: Electronic configuration of GLM-Post and the plot of its HOMO-6 (isovalue = 0.1). The orbital is distributed over the radical centre, indicating that this MO is the SOMO (RCC = 7%). The MO plots of the HOMO are illustrated in Fig. S2.† Orbital configurations are represented by separated α and β orbitals to reiterate that the configurations were obtained by unrestricted DFT calculations. The SOMO associated with Co and cobalamin is beneath the other doubly occupied MOs and is omitted for clarity.

The electronic configurations we calculated for the GLM models indicates that SHI is operating in these systems. By taking the absolute energies of SOMOs as a measure of the SHI effect, we make the following two key observations:

SHI is more significant in the GLM-Pre model than in the GLM-Post model. The absolute energy of SOMO in GLM-Pre (−231 kJ mol⁻¹) is lower compared to GLM-Post (−145 kJ mol⁻¹). While different computational methods (density-functionals) predict different absolute SOMO energies (as expected), the energy difference between the SOMOs of GLM-Pre and GLM-Post is almost independent of the functional employed (ca. 86 to 92 kJ mol⁻¹, see Table S1 in the ESI†).

Hydrogen bonding controls the degree of SHI. Recalling that one of the principal differences between these GLM-Pre and GLM-Post models is the degree of hydrogen bonding between the Ado˙ and the Glu⁻ (E330) residue, it therefore appears that the stronger hydrogen bonding in the GLM-Post model reduces the degree of SHI by delocalizing the negative charge associated with the conserved Glu⁻ residue. This was tested by rotating the Glu⁻ to alter the strength of hydrogen bonding (see the ESI and Fig. S3†). The results strongly support the notion that SHI is reduced when the negatively charged centre is engaged in hydrogen bonding with the radical. This is also consistent with reports showing that SHI associated with distonic radical anions mostly occurs in gas-phase and solid-state systems, but not in aqueous solutions,^13,66 wherein hydrogen bonding by water molecules will quench SHI. It is well known that the active sites of enzymes are shielded from the aqueous environment, which suggests that the B₁₂-enzymes are able to control the degree of SHI over the course of Ado˙ migration through hydrogen bonding between the conserved Glu⁻ residue and the Ado˙.

Previous works by Brunk et al. and Croft et al. speak to the possibility that ribose puckering conformations and structural changes may play an important role in radical control.^44,62 The GLM-Pre and GLM-Post models exhibit differences not only in the degree of hydrogen bonding with the Glu⁻ moiety (see above) but also in ribose puckering conformation. Thus, different ribose conformations may also contribute to the observed SHI differences in the models: Coote et al. showed that structural changes lead to variations in spin and charge delocalization within distonic radicals that can modulate SHI.¹³ We therefore conducted a spin-density analysis to explore the influence of ribose structure on the degree of spin delocalization. Our results for both models indicate minimal spin delocalization and negligible differences in delocalization between the two models (Fig. S11†). From these observations, and the above hydrogen bonding analysis we conclude that hydrogen bonding to Glu⁻, and the accompanying delocalization of its negative charge, is the major contributor to the observed SHI differences in the two models.

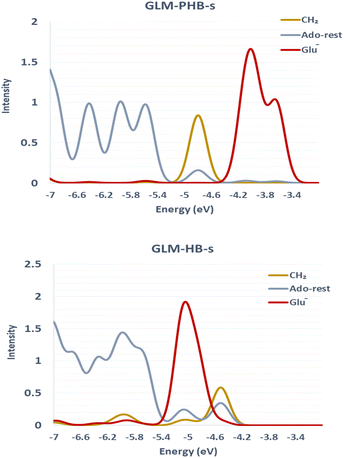
We sought to verify that the SHI we observe in the large GLM models is not an artifact due to the presence of other negatively charged groups in the model, which would contribute high-energy doubly occupied molecular orbitals to the electronic structure manifold. For this purpose, we explored the role of SHI in enzyme catalysis, using small models (labelled with “-s”) of the moieties directly involved in the hydrogen atom transfer reaction, specifically just the Ado˙ and an ethoxylate group to represent E330. The SOMO and HOMO plots with MO energies obtained from calculations on these smaller systems are reported in Fig. 3 (see also Fig. S4† for other high energy level MOs). The calculations reveal that the electronic structure of the GLM-Pre-s model exhibits SHI, in contrast to GLM-Post-s in which the SOMO is the highest energy MO. In GLM-Pre-s, the SOMO was found to be HOMO-3 (RCC = 33%) with the absolute energy of −460 kJ mol⁻¹. In contrast, for GLM-Post-s the HOMO is the SOMO (RCC = 17%) in which the MO energy is −425 kJ mol⁻¹. The persistence of SHI in the small models provides strong validation that the effect is genuine. The results also show that the difference in hydrogen bonding between the Glu⁻ and the Ado˙ results in this change in the electronic structure, as was the case for the larger enzyme models. The difference in hydrogen bonding not only results in the stabilization of the radical SOMO, but also in the destabilization of some of the doubly occupied MOs, particularly those associated with the Glu⁻ moiety. This fact was verified using density-of-states plots displayed in Fig. 4.

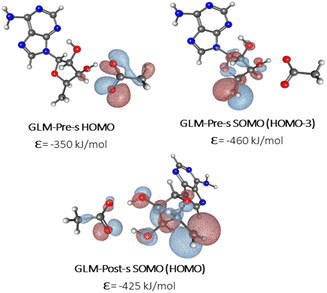Fig. 3 MO plots of α-HOMO and α-SOMO associated with Ado˙ with the absolute MO energy in kJ mol⁻¹ for -s models of GLM enzymes.

Fig. 4 The DOS plots of GLM models. Top: DOS plots of GLM-Pre-s. The MOs associated with the ˙CH₂ moiety are lower in energy than those associated with the Glu⁻ moiety. The orbitals associated with rest of the system are shown as Ado-rest. Bottom: DOS of GLM-Post-s. The MO associated with the ˙CH₂ groups are relatively higher in energy and reside above most of the MOs associated with the Glu⁻ residue. These plots indicate that SHI in GLM-Pre-s is a result of SOMO stabilization and doubly occupied orbital destabilization, particularly the negatively charged Glu⁻ side-chain MOs.

The results of the calculations on the small models follow the same trend found in the large models. That is, the degree of SHI is larger in the Pre model than in the Post model. We conclude from these simulations that these small models can be used to explore the influence of SHI on the catalysis of hydrogen atom transfer.

The impact and role of the SHI on reactivity and the enzymatic catalysis

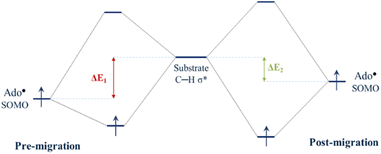
Since the degree of SHI operating in the Ado˙ influences the SOMO energy, it follows that SHI activity also impacts the reactivity of the radical. To explore this we calculated the barrier height associated with the hydrogen abstraction by Ado˙ from the native substrate of the enzyme (L-threo-3-methylaspartate). Calculations were performed to obtain the relative reactivity of GLM-Pre-s and GLM-Post-s models (the transition state structures are provided in Fig. S5†). We found that the structure in which SHI is present (i.e. GLM-Pre-s) has a hydrogen atom transfer barrier height that is 7.1 kJ mol⁻¹ higher than GLM-Post in which the SHI is smallest (31.8 vs. 24.7 kJ mol⁻¹). The barrier height difference lends support to the hypothesis that at the early stages of the catalysis when Ado˙ is first formed, the degree of SHI is relatively high and the reactivity of the radical is relatively low. This SHI-induced reactivity lowering will benefit the enzyme by reducing the likelihood of the radical engaging in aberrant side reactions. Likewise, the calculated barrier height associated with the GLM-Post model aligns with the notion that when the Ado˙ is near the substrate its reactivity must be restored in order to effectively abstract the target hydrogen atom. Therefore, it is apparent that the degree to which SHI is active is inversely related to reactivity, which suggests that GLM enzyme can employ SHI to control the reactivity of the Ado˙ radical. That is, when the magnitude of SHI is large, the SOMO has lower energy and the reactivity of Ado˙ is reduced. Conversely, when the magnitude of the SHI is lowered through increased hydrogen bonding between the Glu⁻ and the Ado˙, both the energy of the SOMO and the reactivity of the radical are increased.

Concepts in FMOT can be utilized to develop an understanding of how changes in the energy level of the SOMO can alter reactivity. Fig. 5 qualitatively illustrates how the degree of the interaction of the orbital associated with the carbon-centred radical of the Ado˙ with the C–H σ* orbital of the substrate changes with the energy level of the SOMO. The higher the energy of the SOMO associated with Ado˙, the more strongly it can interact with the substrate C–H σ* orbital and the lower the reaction barrier. The calculations show that the GLM-Pre model, which is associated with the initial formation of the Ado˙ in the enzyme, has relatively low-energy SOMOs and the structure is consequently less reactive. The GLM-Post model, in which the radical is in position to react with the substrate, has a relatively high-energy SOMO and is relatively more reactive.

Fig. 5 Simple MO energy diagram illustrating the interaction between the Ado˙ SOMO in pre-migration and post-migration models and the substrate C–H σ*. Because the energy gap (ΔE) between Ado˙ SOMO and C–H σ* is smaller in Post models compared to Pre models (ΔE₁ > ΔE₂), these two MOs can interact with each other more efficiently in Post models. The more favorable interaction in the Post model compared to Pre results in the reactivity difference observed between the two.

Although the results of published experimental studies do not provide definitive proof that the presented SHI effects are operative in the enzymes, they are certainly aligned with our findings.^46,67,68 Experimental mutation studies on GLM show definitively that replacing E330 with Asp or Gln results in decreases in tritium-abstraction rate constants between Ado˙ and the substrate, indicating that the mutants have larger hydrogen abstraction barrier heights.^68,69 Using our models we calculated the barrier heights associated with these mutants and we found a clear correspondence between our calculated relative barrier heights and experimental data (Table S2†).

Electronic structure of MCM enzyme

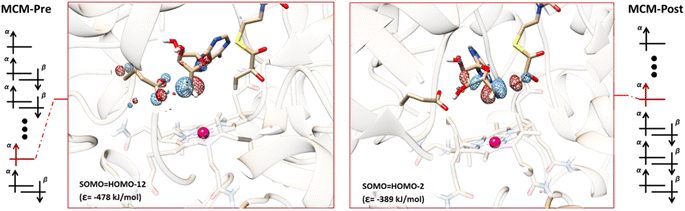
We also explored the role of SHI in the MCM enzyme, which has a similar hydrogen atom transfer reaction to that of GLM. Our calculations for the MCM enzyme are based on prior QM/MM studies that examined the reaction pathway involving the carbon center of Ado˙ and the target hydrogen atom of the substrate.⁶² Two models with a QM region containing 551 atoms (Fig. S6 and S7†) were extracted from this previous work to represent the pre-migration (MCM-Pre) and post-migration (MCM-Post) of Ado˙, and similar electronic structure calculations were performed on these two models (see the ESI†). The calculated electronic configurations for MCM-Pre and MCM-Post are illustrated in Fig. 6. In MCM-Pre the unpaired electron on the Ado˙ resides in HOMO-12 (ε = −478 kJ mol⁻¹). For the MCM-Post model, the MO associated with the unpaired electron of the Ado˙ is HOMO-2 (ε = −389 kJ mol⁻¹). As was found for GLM, the orbital energies we obtained show that the SHI is more pronounced in the MCM-Pre system when compared to the MCM-Post system. This observation can also be attributed to the interactions of Ado˙ with the nearby glutamate residue (E370 in the case of MCM), i.e. degree of Ado˙:E370 hydrogen bonding. In the MCM-Pre model no significant hydrogen bonding is present, whereas in MCM-Post the Ado˙ is hydrogen bonded to the negatively charged E370. It is important to note that we cannot rule out the potential influence of the other interactions within the active site as this hydrogen bonding is not the only difference between the MCM-Pre and MCM-Post. This is in contrast to the GLM systems in which both systems were identical with the exception of the Ado˙:Glu⁻ hydrogen bonding magnitude caused by the orientation of the Ado˙.

Fig. 6 Representative electronic configurations, and MO plots of SOMO associated with Ado˙ with the absolute MO energy for MCM model systems. Left: Electronic configuration of MCM-Pre and the plot of its HOMO-12 (isovalue = 0.1). Right: Electronic configuration of MCM-Post and the plot of its HOMO-2 (isovalue = 0.1). The HOMO was found to be associated with the cobalt centre and corrin ring.

To assess the reactivity of these systems, we performed calculations using the same methodology that was applied to the GLM models. The calculated barrier heights revealed that the reactivity for MCM-Pre-s is larger than that of MCM-Post-s in agreement with our SHI control hypothesis. The relative barrier height difference for MCM is 11.7 kJ mol⁻¹ (27.0 kJ mol⁻¹ compared to 15.3 kJ mol⁻¹), which translates to a difference in reactivity of almost three orders of magnitude. The high energy MOs and the predicted MO configurations for MCM-Pre-s and MCM-Post-s are depicted in Fig. S8.†

The origin and nature of the observed SHI

Several additional calculations were conducted on GLM to determine the underlying cause behind the shift in SOMO energies and the observed reactivity difference. Initially, we eliminated the Glu⁻ (E330 sidechain) to assess the significance of a negative charge on both the electronic structure and reactivity. Upon the removal of Glu⁻, the electronic structure no longer exhibits the SHI electronic configuration, and the hydrogen abstraction barrier heights associated with the GLM-Pre and GLM-Post models increase to 46.6 and 45.3 kJ mol⁻¹, respectively. The negligible difference in the barrier heights for the two models strongly suggests that the negative charge on the glutamate residue is central to both the SHI and the catalysis of hydrogen atom transfer. We further explored the possibility that classical electrostatic effects could be responsible for the observed changes in electronic structure and reactivity by substituting the Glu⁻ moiety with classical partial point charges (refer to ESI Fig. S9 and S10†). Once again, the resulting electronic structure adhered to the Aufbau principle and, accordingly, SHI was absent. The SOMO energies calculated for both the Pre and Post models were similar, differing by less than 10 kJ mol⁻¹. Using the partial classical point charges, we re-evaluated the barrier heights for hydrogen abstraction. The results showed that the barrier height for the Pre and Post models increased to 49.1 and 49.0 kJ mol⁻¹, respectively, representing an approximately 4 kJ mol⁻¹ elevation compared to the barrier when Glu⁻ is entirely removed. These outcomes indicate that the observed effects cannot be reproduced when: (1) the negative charge is not present, and (2) the glutamate moiety is not treated quantum-mechanically. This shows that both the negative charge (Coulomb interactions) and the quantum treatment of the Glu⁻ moiety are necessary to reproduce the effect, so this effect can be regarded as a quantum Coulombic effect. In agreement with this conclusion, we found via DFT energy decomposition analysis that over 80 percent of the total reactivity difference emerged from the exchange component of the energy. Since the exchange and correlation components of electronic energy are a direct consequence of quantum mechanics, this provides further evidence that the observed effect can be quantum-mechanical in nature.

Conclusion

Our calculated results provide support for the hypothesis that B₁₂-enzymes utilize a Coulombic effect with quantum origin to control the reactivity of radicals generated in their catalytic cycle. The effect manifests through a SOMO–HOMO inversion in the Ado˙ radical species generated in the enzyme active site and is modulated by the degree of hydrogen bonding between the Ado˙ and a conserved, nearby Glu⁻ residue. At the first stage of the catalysis, when Ado˙ is initially generated, the interaction between the radical and the Glu⁻ causes significant SHI and the energy of the orbital associated with the unpaired electron is relatively low in energy. In this state, the reactivity of the Ado˙ is relatively low and this benefits the enzyme by reducing the probability of Ado˙ engaging in deleterious side reactions. When the radical has completed its migration to the active site bound substrate, strong hydrogen bonding occurs between the nearby Glu⁻ and the Ado˙, resulting in a reduction in the degree of SHI, and a concomitant increase in the reactivity of Ado˙ toward hydrogen abstraction. We describe the observed interactions between the unpaired electron and the nearby negative charge as a quantum Coulombic effect (QCE).

The QCE, which manifests through stabilization of the SOMO relative to doubly occupied orbitals in the enzyme system, is an elegant control mechanism that appears to be exploited by B₁₂-enzymes (GLM and MCM) to control and manipulate the reactivity of Ado˙. The characteristics of this effect are such that it gives the B₁₂-enzymes the ability to control the Ado˙ reactivity simply by altering the hydrogen bonding between Ado˙ and a nearby conserved Glu⁻ residue. While previous modeling studies have elucidated the important role of classical electrostatics in enhancing enzyme catalytic activity (catalytic power),³⁰ the present work shows for the first time that quantum mechanical electrostatics are also central to controlling the reactivity/selectivity of reactions involving radical intermediates. These findings may be generalizable to other families of radical enzymes, which, in conjunction with structural/conformational factors, can address the question of how radical enzymes drive their reactions toward the correct outcome. These insights can ultimately lead to new approaches in enzyme engineering.⁷⁰ Our future work in this area will be focused on understanding the interplay between enzyme dynamics and the observed effects.

Data availability

The Cartesian coordinates associated with the calculations are provided as xyz files. Additional computational details are also provided in the ESI.†

Author contributions

MHK conducted the investigation and curated the data. GAD was responsible for conceptualization, funding acquisition, and supervision. Both authors conducted the analysis and authored the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors wish to thank the National Sciences and Engineering Research Council (NSERC) of Canada, the Canadian Foundation for Innovation, and The University of British Columbia for financial support, and Digital Research Alliance of Canada and University of British Columbia Advanced Research Computing for computational resources. We would also like to acknowledge Elizabeth Brunk for providing us with the coordinates of the MCM enzyme and Kirsten Wolthers for many insightful discussions. We are also grateful to an anonymous reviewer who provided very helpful comments.

Notes and references

1. L. A. Pham-Huy, H. He and C. Pham-Huy, Int. J. Biomed. Sci., 2008, 4, 89–96.
2. M. Smeu and G. A. DiLabio, J. Phys. Chem. C, 2010, 114, 17874–17879.
3. K. J. Romero, M. S. Galliher, D. A. Pratt and C. R. J. Stephenson, Chem. Soc. Rev., 2018, 47, 7851–7866.
4. G. Moad, E. Rizzardo and S. H. Thang, Polymer, 2008, 49, 1079–1131.
5. I. Ratera and J. Veciana, Chem. Soc. Rev., 2012, 41, 303–349.
6. I. Novak, L. J. Harrison, B. Kovač and L. M. Pratt, J. Org. Chem., 2004, 69, 7628–7634.
7. G. d. P. Gomes, Y. Loginova, S. Z. Vatsadze and I. V. Alabugin, J. Am. Chem. Soc., 2018, 140, 14272–14288.
8. J. Zhang, Y. Li, F. Zhang, C. Hu and Y. Chen, Angew. Chem., Int. Ed., 2016, 55, 1872–1875.
9. T. Kusamoto, S. Kume and H. Nishihara, J. Am. Chem. Soc., 2008, 130, 13844–13845.
10. B. L. Westcott, N. E. Gruhn, L. J. Michelsen and D. L. Lichtenberger, J. Am. Chem. Soc., 2000, 122, 8083–8084.
11. M. J. Białek and L. Latos-Grażyński, Inorg. Chem., 2016, 55, 1758–1769.
12. H. Guo, Q. Peng, X.-K. Chen, Q. Gu, S. Dong, E. W. Evans, A. J. Gillett, X. Ai, M. Zhang, D. Credgington, V. Coropceanu, R. H. Friend, J.-L. Brédas and F. Li, Nat. Mater., 2019, 18, 977–984.
13. G. Gryn’ova and M. L. Coote, J. Am. Chem. Soc., 2013, 135, 15392–15403.
14. G. Gryn’ova, D. L. Marshall, S. J. Blanksby and M. L. Coote, Nat. Chem., 2013, 5, 474–481.
15. J. C. Walton, J. Phys. Chem. A, 2017, 121, 7761–7767.
16. J. C. Walton, Chem. Soc. Rev., 2021, 50, 7496–7512.
17. Y. Wang, H. Zhang, M. Pink, A. Olankitwanit, S. Rajca and A. Rajca, J. Am. Chem. Soc., 2016, 138, 7298–7304.
18. S. Kasemthaveechok, L. Abella, J. Crassous, J. Autschbach and L. Favereau, Chem. Sci., 2022, 13, 9833–9847.
19. L. Abella, J. Crassous, L. Favereau and J. Autschbach, Chem. Mater., 2021, 33, 3678–3691.
20. P. Morgante and J. Autschbach, J. Chem. Theory Comput., 2023, 19, 3929–3942.
21. S. Kasemthaveechok, L. Abella, M. Jean, M. Cordier, T. Roisnel, N. Vanthuyne, T. Guizouarn, O. Cador, J. Autschbach, J. Crassous and L. Favereau, J. Am. Chem. Soc., 2020, 142, 20409–20418.
22. B. J. Landgraf, E. L. McCarthy and S. J. Booker, Annu. Rev. Biochem., 2016, 85, 485–514.
23. R. Banerjee, Chem. Rev., 2003, 103, 2083–2094.
24. N. Shibata and T. Toraya, J. Biochem., 2015, 158, 271–292.
25. H. Yang, E. C. McDaniel, S. Impano, A. S. Byer, R. J. Jodts, K. Yokoyama, W. E. Broderick, J. B. Broderick and B. M. Hoffman, J. Am. Chem. Soc., 2019, 141, 12139–12146.
26. V. Nanda and R. L. Koder, Nat. Chem., 2010, 2, 15–24.
27. V. V. Welborn, L. Ruiz Pestana and T. Head-Gordon, Nat. Catal., 2018, 1, 649–655.
28. K. Chen and F. H. Arnold, Nat. Catal., 2020, 3, 203–213.
29. P. Schopf, M. J. L. Mills and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4328–4333.
30. P. K. Sharma, Z. T. Chu, M. H. M. Olsson and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9661–9666.
31. W. D. Robertson, M. Wang and K. Warncke, J. Am. Chem. Soc., 2011, 133, 6968–6977.
32. K. P. Jensen and U. Ryde, J. Am. Chem. Soc., 2005, 127, 9117–9128.
33. V. Bandarian and G. H. Reed, Biochemistry, 2002, 41, 8580–8588.
34. A. P. Ghosh, M. J. Toda and P. M. Kozlowski, ACS Catal., 2021, 11, 7943–7955.
35. C. R. Wick and D. M. Smith, J. Phys. Chem. A, 2018, 122, 1747–1755.
36. B. Kovačević, D. Barić, D. Babić, L. Bilić, M. Hanževački, G. M. Sandala, L. Radom and D. M. Smith, J. Am. Chem. Soc., 2018, 140, 8487–8496.
37. D. Bucher, G. M. Sandala, B. Durbeej, L. Radom and D. M. Smith, J. Am. Chem. Soc., 2012, 134, 1591–1599.
38. N. S. Lees, D. Chen, C. J. Walsby, E. Behshad, P. A. Frey and B. M. Hoffman, J. Am. Chem. Soc., 2006, 128, 10145–10154.
39. M. Horitani, K. Shisler, W. E. Broderick, R. U. Hutcheson, K. S. Duschene, A. R. Marts, B. M. Hoffman and J. B. Broderick, Science, 2016, 352, 822–825.
40. P. Amara, J. M. Mouesca, M. Bella, L. Martin, C. Saragaglia, S. Gambarelli and Y. Nicolet, J. Am. Chem. Soc., 2018, 140, 16661–16668.
41. J. R. Chen, T. X. Ke, P. A. Frey and S. C. Ke, ACS Catal., 2021, 11, 14352–14368.
42. J. Rétey, Angew. Chem., Int. Ed. Engl., 1990, 29, 355–361.
43. C. M. Jäger and A. K. Croft, Chem.–Eur. J., 2017, 23, 953–962.
44. C. J. Suess, F. L. Martins, A. K. Croft and C. M. Jäger, J. Chem. Inf. Model., 2019, 59, 5111–5125.
45. M. Hanževački, A. K. Croft and C. M. Jäger, J. Chem. Inf. Model., 2022, 62, 3401–3414.
46. C. Makins, A. V. Pickering, C. Mariani and K. R. Wolthers, Biochemistry, 2013, 52, 878–888.
47. K. Gruber, R. Reitzer and C. Kratky, Angew. Chem., Int. Ed., 2001, 40, 3377–3380.
48. D. P. Dowling, A. K. Croft and C. L. Drennan, Annu. Rev. Biophys., 2012, 41, 403–427.
49. R. Banerjee and S. W. Ragsdale, Annu. Rev. Biochem., 2003, 72, 209–247.
50. M. H. M. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537.
51. T. J. Dolinsky, J. E. Nielsen, J. A. McCammon and N. A. Baker, Nucleic Acids Res., 2004, 32, W665–W667.
52. R. Dennington II, T. A. Keith and J. M. Millam, GaussView, Version 6.1.1, Semichem Inc., Shawnee Mission, KS, 2016.
53. Y. Lu, M. R. Farrow, P. Fayon, A. J. Logsdail, A. A. Sokol, C. R. A. Catlow, P. Sherwood and T. W. Keal, J. Chem. Theory Comput., 2019, 15, 1317–1328.
54. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
55. W. Smith, C. W. Yong and P. M. Rodger, Mol. Simul., 2002, 28, 385–471.
56. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
57. J. Huang and A. D. MacKerell, J. Comput. Chem., 2013, 34, 2135–2145.
58. K. P. Kepp, J. Phys. Chem. A, 2014, 118, 7104–7117.
59. M. J. Toda, A. P. Ghosh, S. Parmar and P. M. Kozlowski, in Methods in Enzymology, Elsevier Inc., 1st edn, 2022, vol. 669, pp. 119–150.
60. A. Pavlova, J. M. Parks and J. C. Gumbart, J. Chem. Theory Comput., 2018, 14, 784–798.
61. J. Kästner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865.
62. E. Brunk, W. F. Kellett, N. G. J. Richards and U. Rothlisberger, Biochemistry, 2014, 53, 3830–3838.
63. Y. Zhao, N. González-García and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 2012–2018.
64. N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372.
65. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
66. P. Franchi, E. Mezzina and M. Lucarini, J. Am. Chem. Soc., 2014, 136, 1250–1252.
67. Z. G. Chen, M. A. Zietek, H. J. Russell, S. Tait, S. Hay, A. R. Jones and N. S. Scrutton, ChemBioChem, 2013, 14, 1529–1533.
68. G. D. Román-Meléndez, P. Von Glehn, J. N. Harvey, A. J. Mulholland and E. N. G. Marsh, Biochemistry, 2014, 53, 169–177.
69. H. W. Chih, E. Neil and N. G. Marsh, Biochemistry, 2001, 40, 13060–13067.
70. Y. Nicolet, Nat. Catal., 2020, 3, 337–350.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc01785d

---