Internal strain-driven bond manipulation and band engineering in Bi_2−xSb_xYO₄Cl photocatalysts with triple fluorite layers

Abstract

In extended solid-state materials, the manipulation of chemical bonds through redox reactions often leads to the emergence of interesting properties, such as unconventional superconductivity, which can be achieved by adjusting the Fermi level through, e.g., intercalation and pressure. Here, we demonstrate that the internal ‘biaxial strain’ in tri-layered fluorite oxychloride photocatalysts can regulate bond formation and cleavage without redox processes. We achieve this by synthesizing the isovalent solid solution Bi_2−xSb_xYO₄Cl, which undergoes a structural phase transition from the ideal Bi₂YO₄Cl structure to the Sb₂YO₄Cl structure with (Bi,Sb)₄O₈ rings. Initially, substitution of smaller Sb induces expected lattice contraction, but further substitution beyond x > 0.6 triggers an unusual lattice expansion before the phase transition at x = 1.5. Detailed analysis reveals structural instability at high x values, characterized by Sb–O underbonding, which is attributed to tensile strain exerted from the inner Y sublayer to the outer (Bi,Sb)O sublayer within the triple fluorite block – a concept well-recognized in thin film studies. This concept also explains the formation of zigzag Bi–O chains in Bi₂MO₄Cl (M = Bi, La). The Sb substitution in Bi_2−xSb_xYO₄Cl elevates the valence band maximum, resulting in a minimized bandgap of 2.1 eV around x = 0.6, which is significantly smaller than those typically observed in oxychlorides, allowing the absorption of a wider range of light wavelengths. Given the predominance of materials with a double fluorite layer in previous studies, our findings highlight the potential of compounds endowed with triple or thicker fluorite layers as a novel platform for band engineering that utilizes biaxial strain from the inner layer(s) to finely control their electronic structures.

---

Introduction

In photocatalysis, precise control of both the valence band maximum (VBM) and the conduction band minimum (CBM) is critical. Mixed-anion compounds, such as oxynitrides, are well-suited for enabling a response to visible light.^1–4 For example, in BiOX oxyhalides (X = Cl, Br, I),¹ the halogen p orbitals reside above the O-2p orbitals, elevating the VBM in the sequence of decreasing electronegativity. Recently, structurally related Sillén and Sillén-Aurivillius layered oxyhalides with double fluorite layers, such as PbBiO₂X⁵ and Bi₄NbO₈X (X = Cl, Br), have emerged as promising photocatalysts for water splitting under visible light irradiation, due to their outstanding stability against self-oxidation by photogenerated holes.^6,7 This stability arises from the formation of VBM composed primarily of the O-2p orbitals, unlike in BiOX. The high energy levels of the O-2p orbitals stem from the lone pair interaction between the Bi-6s and O-2p orbitals,⁸ coupled with electrostatic repulsion between the fluorite layer and adjacent layers.^6,9

While tunning CBM in compounds with the double fluorite layer is not straightforward,^10,11 we recently demonstrated a drastic CBM change by replacing the M cation in Bi₂MO₄Cl (M = Y, La, Bi),¹⁰ comprising a triple fluorite Bi₂MO₄ slab. Bi₂YO₄Cl has the ideal structure (Fig. 1a), whereas Bi₂LaO₄Cl and Bi₃O₄Cl¹⁰ contain broken Bi–O bonds, resulting in double and single zigzag chains, respectively, composed of BiO₃ units (Fig. S1†). The CBM shifts higher with Y → La → Bi due to the anti-bonding interaction allowed by breaking the mirror symmetry at the Bi site. However, the fundamental queries regarding the mechanism of the Bi–O bond cleavage and its exclusive occurrence in compounds with the triple-layer fluorite block remain unresolved.

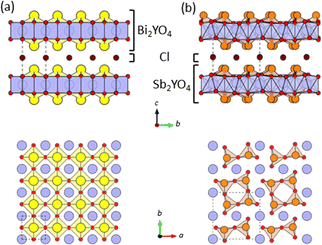Fig. 1 The crystal structures of (a) Bi₂YO₄Cl²⁸ and (b) Sb₂YO₄Cl²⁹ with triple fluorite slabs, viewed along the [100] direction (top) and the [001] direction (bottom). Yellow, orange, blue, red, and brown spheres indicate Bi, Sb, Y, O and Cl atoms, respectively. Broken lines represent the unit cell. Bi/Sb–O bonds with negligible bond valence (<0.1) are not drawn (Table S5†).

From a broader perspective, manipulating the formation and cleavage of chemical bonds is generally important in solid-state chemistry since it often induces a variety of novel properties.^12–15 For example, in SrCo₂(Ge_1−xP_x)₂,¹⁴ a ferromagnetic phase appears in the vicinity of the so-called collapse phase transition (x ≈ 0.5). In IrTe₂, the chemical substitution of Pt causes the Ir–Ir bonds of the triangular lattice to break, resulting in superconductivity.¹⁶ More recently, anion redox involving bond formation of an anion such as oxygen and sulfur has attracted much attention for the development of high-capacity battery materials.^17,18 In these examples, the underlying mechanism of the formation/breaking of chemical bonds in extended solids is attributed to the electron transfer between transition metal and the (molecular) anions, and hence they can be controlled by adjusting the relative energy of transition metal d states and anti-bonding states of molecular anions through, for example, intercalation, high pressure, and chemical substitutions.^{12,14,16–21}

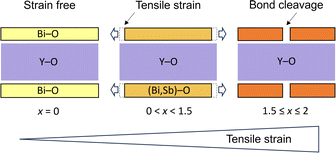
On the other hand, the mechanism and control of bond breaking in Bi₂MO₄Cl remain to be elucidated, but an interesting mechanism different from the above examples involving redox processes is expected. In this study, we newly synthesized an entire isovalent solid solution Bi_2−xSb_xYO₄Cl and investigated its phase transition behavior from the ideal Bi₂YO₄Cl structure to Sb₂YO₄Cl with isolated Sb₄O₈ rings (Fig. 1)^22,23 to elucidate the bond breaking process of the (Bi,Sb)–O square net. We found that upon substituting smaller Sb³⁺, the expected lattice contraction is observed for x < 0.6, but further substitution leads to unexpected lattice expansion, ultimately inducing a transition to the Sb₂YO₄Cl phase at x = 1.5. Similar to the well-studied oxide thin films, where biaxial strain from a substrate affects and controls properties,^24–29 the structural instability, featured by lattice expansion (0.6 < x < 1.5), can be regarded as tensile strain from the middle YO₂ sublayer to outer (Bi,Sb)O sublayers in the triple fluorite slab (Fig. 2). With this concept, the crystal structures of Bi₂LaO₄Cl and Bi₃O₄Cl with zigzag chains¹⁰ can also be reasonably explained. The variation in bandgap of Bi_2−xSb_xYO₄Cl corroborates with the lattice parameter evolution, with a minimum bandgap of 2.1 eV at around x = 0.5, suggesting the potential for enhanced catalytic activity at shorter wavelengths.

Fig. 2 Schematic illustration showing ‘tensile strain’ by Sb substitution in Bi₂YO₄Cl. With the Sb substitution of Bi, tensile strain is imposed from the inner YO₂ sublayer (blue) to the outer (Bi,Sb)O sublayer within the (Bi,Sb)₂YO₄ triple fluorite slab, eventually leading to a phase transition with bond-cleaved Sb₂YO₄Cl-type structure.

Results and discussion

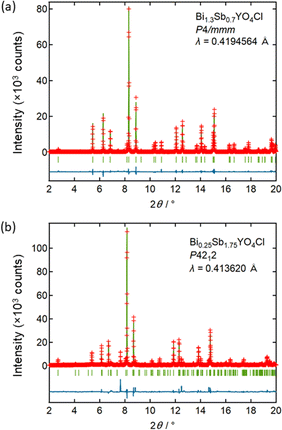
Let us start by comparing the crystal structures of Bi₂YO₄Cl²⁸ and Sb₂YO₄Cl,²⁹ as shown in Fig. 1. Bi₂YO₄Cl is of tetragonal symmetry (space group: P4/mmm), with outer sublayers composed of corner-sharing BiO₄ square pyramids connected by eight-coordinate Y ions, forming a triple fluorite slab. These slabs stack along the c axis, with a Cl layer in between. In the case of Sb₂YO₄Cl, the outer sublayers are heavily distorted, yielding SbO₃ units that assemble into Sb₄O₈ ring.²⁹ This results in a 2a × 2b × c superstructure compared to Bi₂YO₄Cl (space group: P42₁2).^28,29 Thus, Sb₂YO₄Cl manifests as a zero-dimensional (0D) system comprising isolated rings, differing from the one-dimensional (1D) zigzag chains in distorted Bi₃O₄Cl and Bi₂LaO₄Cl and the two-dimensional (2D) square net of ideal Bi₂YO₄Cl (Fig. S1†).¹⁰

Synchrotron powder X-ray diffraction (SPXRD) patterns of Bi_2−xSb_xYO₄Cl are presented in Fig. 3. For x ≤ 1.25, all peaks can be indexed based on the ideal Bi₂YO₄Cl structure without superlattice peaks, except for small unidentified impurity peaks for x = 0.2 and x ≥ 0.8. This suggests the successful formation of the solid solution with the ideal P4/mmm structure. The absence of second harmonic generation (SHG) in x = 0.7–1.25 is consistent with the centrosymmetric structure. For all compositions, peaks are sharp, indicating high crystallinity of our samples. The local structure does not show any deviation from the average structure, as shown by the analysis of pair distribution function (PDF) for 0 ≤ x ≤ 1 (Fig. S6 and Table S3†). For x ≥ 1.5, the 2a × 2b × c superlattice peaks are observed, indicating a phase transition to the P42₁2 structure (Fig. 3 and S2†). Energy dispersive X-ray (EDX) analysis showed that the Bi, Sb, and Cl ratios in all samples closely match with the stoichiometry of the target compounds (Table S1†). The selected area electron diffraction (SAED) pattern of BiSbYO₄Cl (x = 1.0) along the [001] direction shows no superlattice reflection, consistent with the P4/mmm structure (Fig. S3†).

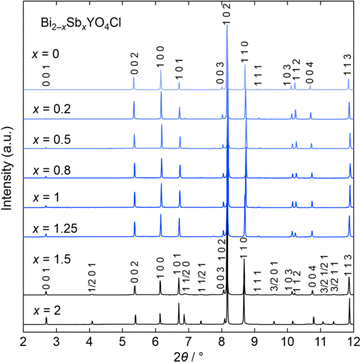Fig. 3 Room temperature SPXRD patterns of Bi_2−xSb_xYO₄Cl (0 ≤ x ≤ 2). The samples with x ≤ 1.25 are indexed with the P4/mmm space group (Bi₂YO₄Cl structure). Peaks are indexed based on the ideal tetragonal structure of Bi₂YO₄Cl. See Fig. S2† showing the absence of superlattice peaks for x ≤ 1.25. The data was collected at a wavelength of λ = 0.41946 Å (x ≤ 1) or 0.41362 Å (1 < x ≤ 2).

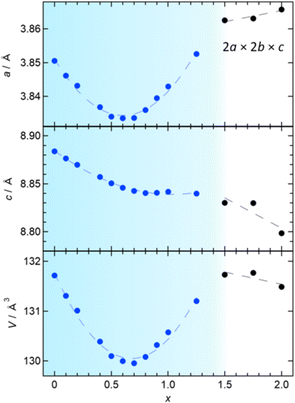
The P4/mmm phase (0 ≤ x ≤ 1.25) has an anomaly in the x dependence of lattice constants, as shown in Fig. 4. Initially, both the a and c axes display a linear decrease with increasing x (≤0.4), consistent with the variance in ionic radii between Sb³⁺ and Bi³⁺ (0.76 Å vs. 1.17 Å).³⁰ Upon further Sb-substitution, the a-axis decreases more slowly, reaching a minimum at x = 0.6 and then increases. At the same time, the c-axis departs from linear dependence and becomes nearly constant above x = 0.7. As a result, the volume change reaches a minimum around x = 0.7 and then increases up to x = 1.25. In the P42₁2 region (1.5 ≤ x ≤ 2), the c-axis and (normalized) volume decrease as anticipated from the difference in ionic radii, while the normalized a-axis increases, continuing the trend observed in the later region of the Bi₂YO₄Cl structure.

Fig. 4 The x dependence of the lattice parameters in Bi_2−xSb_xYO₄Cl (0 ≤ x ≤ 2): (top) a-axis, (middle) c-axis, and (bottom) volume. For 1.5 ≤ x ≤ 2, the a-axis and volume are normalized to the ideal P4/mmm unit cell.

To understand the unconventional evolution of lattice parameters, Rietveld refinement was conducted on SPXRD data in the range of 0 ≤ x ≤ 1.25, assuming the ideal Bi₂YO₄Cl structure (P4/mmm),^10,28 where distribution of Bi and Sb atoms was randomized and their isotropic atomic displacement parameters (U_iso) were restricted to be equal. The refinement converged smoothly, yielding reasonable reliability factors, for example, GOF = 2.87%, R_p = 8.73%, and R_wp = 11.71% for Bi_1.3Sb_0.7YO₄Cl (Fig. 5a and Table S2†). The results are summarized in Fig. S4,† with the refined parameters listed in Table S2.† No discernible deviations from the average crystal structure were identified from pair-distribution function (PDF) analysis (Fig. S6 and Table S3†) and high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) images (Fig. S3†). For 1.5 ≤ x ≤ 2, Rietveld refinement was performed, assuming the Sb₂YO₄Cl structure (P42₁2),²⁹ where similar restrictions on U_iso of randomly distributed Bi and Sb were applied. This also converged smoothly (Fig. 5b and Table S2†).

Fig. 5 The Rietveld refinement on SPXRD data of (a) Bi_1.3Sb_0.7YO₄Cl, assuming the Bi₂YO₄Cl (P4/mmm) model, and (b) Bi_0.25Sb_1.75YO₄Cl, assuming the Sb₂YO₄Cl (P42₁2) model. The red markers, the green solid line, and the blue solid line represent observed, calculated and difference intensities, respectively. The green ticks indicate the calculated Bragg reflections.

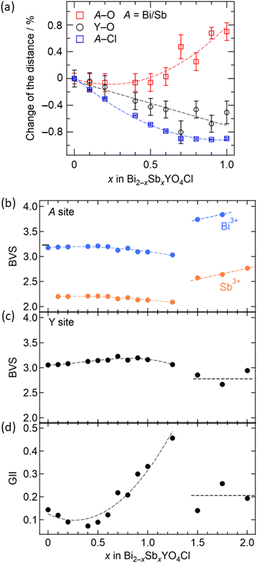
The information obtained from the structural refinement provides insight into the anomalous lattice evolution near the phase boundary and the mechanism behind the bond cleavage of the (Bi,Sb)O sublayer. A crucial observation is the gradual growth of lattice volume above x = 0.7 without a significant jump, even in close proximity to the phase boundary. This suggests an intimate relationship between lattice expansion for 0.5 < x < 1.5 and (Bi,Sb)–O bond cleavage in the Sb₂YO₄Cl-type structure. Bond valence sum (BVS) calculations (Fig. 6b and c) reveal that Y³⁺ maintains nearly ideal values in the entire solid solution, while Sb³⁺ is fairly underbonded in the tetragonal structure (x ≤ 1.25) but becomes closer to the ideal coordination in Sb₂YO₄Cl structure (1.5 ≤ x ≤ 2). This difference implies for the higher flexibility of Sb³⁺ coordination compared to Y³⁺, allowing stretching of (Bi,Sb)–O prior to the phase transition. It possibly enhances the structural instability as clearly seen in the global instability index (GII), which is the summation of the deviation of BVS from the formal charge (Fig. 6d).

Fig. 6 (a) The x dependence (0 ≤ x ≤ 1) of A–O (red), A–Cl (blue) and Y–O (black) distances obtained from the Rietveld refinement of the Bi_2−xSb_xYO₄Cl solid solution (where A = Bi, Sb). The relative change with respect to x = 0 is shown. For A–Cl, error bars are within the markers. The x dependence of (b) the BVS of the A site assuming full occupation of Bi³⁺ (blue) and Sb³⁺ (orange) cations, and (c) the Y site, and (d) the global instability index (GII) for 0 ≤ x ≤ 2. Dashed lines are guides for the eyes.

Combining these observations with the fact that Bi₂YO₄Cl is a stable structure, we propose that the substitution of smaller Sb³⁺ can lead to a mismatch between the outer (Bi,Sb)O and the inner YO₂ sublayer within the triple fluorite slab. This mismatch gives a tensile strain to the outer (Bi,Sb)O sublayer, which is exerted from the central YO₂ sublayer (Fig. 2). In the low substitution region (x < 0.5), the (Bi,Sb)O₄ pyramidal volume changes only slightly due to the increase of its height (Fig. S5†). However, as the tensile strain to the outer (Bi,Sb)O sublayer increases (x > 0.5), the (Bi,Sb)O₄ pyramid expands rapidly, enhancing the structural instability (Fig. 6d and S5†).

The manipulation of chemical bonds can lead to unique properties including unconventional superconductivity of BaNi₂(Ge_1−xP_x)₂ and BaTi₂Pn₂O (Pn = As, Sb)^13,20 in the vicinity of P–P/Pn–Pn bond breaking and in high-energy-density cathode materials (e.g., La_1.2Sr_1.8Mn₂O_7−δF₂) involving anion redox.^17,31,32 In these cases, the bond breaking involves redox of transitions metal and anions (e.g., 2Pn³⁻ ⇔ (Pn–Pn)⁴⁻ + 2e⁻) and thus the relative energy between d orbitals of transition metals and p orbitals of (molecular) anions, which is controlled, for example, by intercalation, application of pressure and chemical substitution. In contrast, in the present study, the formation/breaking of chemical bonds in the (Bi,Sb)O₂ square net occurs free of redox processes and originates from the biaxial strain exerted from the inner Y sublayer. The strain concept is ubiquitous in thin film research: physical properties can be controlled by applying compressive or tensile strain from the substrate.^24–29 Strain effects in compounds with alternating layers are commonly addressed to alter physical properties,^33,34 but the occurrence of drastic bond formation/cleavage is, to the best of our knowledge, unknown.

The strain concept introduced above provides a plausible explanation of the Bi₂MO₄Cl structures, wherein only M = La and Bi induce bond breaking, resulting in 1D zigzag chains, unlike when M = Y.¹⁰ In the case of Bi₂MO₄Cl, the M cations in the central MO₂ sublayer vary while maintaining the outer BiO sublayer.¹⁰ By substituting M from Y³⁺ (1.02 Å) to the larger La³⁺ (1.16 Å) or Bi³⁺ (1.17 Å)³⁰ (Fig. 7), the outer BiO sublayer is subject to tensile strain, which causes the Bi–O bonds to break, forming 1D single or double zigzag chains. We anticipate that this strain effect can occur in compounds with n ≥ 3 fluorite layers that are yet to be developed. Hence, this approach can be a useful strategy in the quest for novel photocatalysts and other functions. Indeed, the presence of corrugated sextuple fluorite blocks (n = 6), with partial inclusion of the rock-salt 1D block, can also be considered to appear as a consequence of strain between outer and inner layers of the hypothetical ideal n = 6 fluorite structure.³⁵

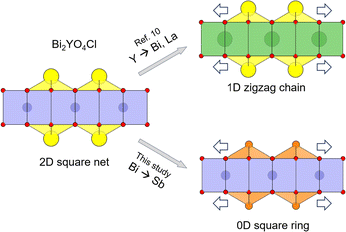Fig. 7 Scheme of manipulating Bi₂YO₄Cl structure by substitution-induced tensile strain from the inner sublayer to the outer sublayer within the Bi₂YO₄ triple-fluorite slab. (top) Y-site substitution of the inner sublayer with larger Bi or La cations (Bi₂LaO₄Cl and Bi₃O₄Cl) transforms the outer BiO sublayer (2D square net) into 1D zigzag chains.¹⁰ (bottom) In this study, Bi-site substitution of the outer sublayer to smaller Sb cation (Bi_2−xSb_xYO₄Cl) transforms the outer sublayer into 0D square rings for x ≥ 1.5. Yellow, orange, blue, green, and red spheres indicate Bi, Sb, Y, La, and O atoms, respectively.

To understand the impact of Sb substitution and strain effect on the electronic structures, we measured diffuse reflectance spectra (Fig. S7†). Tauc plots revealed that the bandgap reduces from 2.5 eV for x = 0 to 2.1 eV for x = 0.5 (Fig. 8a). With a further increase in Sb, however, the bandgap expands to 2.35 eV for x = 1, correlating with the anomalous change in lattice constants. This change is consistent with the observed coloration of the samples: yellow for x = 0 and 1, and bright orange for x = 0.5 (Fig. S8†). Fig. 8b shows the positions of the VBM and CBM, determined from absorption spectra and photoelectron yield spectroscopy (PYS) measurements (Fig. S9†). The VBM shifts upward from 2.07 V (x = 0) to 1.7 V (x = 0.5) and then downward to 1.95 V (x = 1), whereas the CBM value, obtained by subtracting the bandgap from the ionization energy, remains almost constant. Hence, the change in VBM predominantly accounts for the narrowed bandgap. It is notable that the bandgaps for 0.2 ≤ x ≤ 0.8 are among the smallest of oxychloride photocatalysts, with the exception of Bi_2.8Y_0.2O₄Cl with 2.0 eV.^36–38

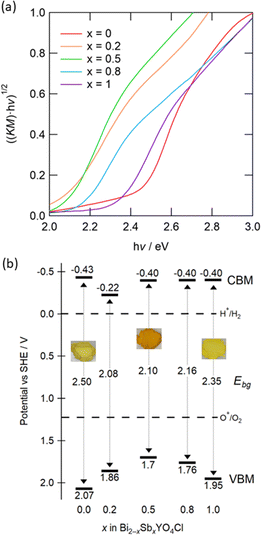Fig. 8 (a) Tauc plots of Bi_2−xSb_xYO₄Cl (0 ≤ x ≤ 1) obtained from UV-visible diffuse reflectance spectra. Corresponding reflectance spectra are shown in Fig. S7.† (b) Schematic band diagrams estimated from the bandgap and the lowest ionization energy. Values in the middle between the CBM and the VBM represent the bandgap (E_bg). The standard electrode potential is converted to −([absolute electron potential in a vacuum] + 4.44 V) (vs. SHE at the isoelectric point). Embedded photos demonstrate the colour of samples with x = 0, 0.5, 1 (see Fig. S8† for details).

In addition, we conducted DFT calculations for Bi₂YO₄Cl and Bi_1.5Sb_0.5YO₄Cl (see Fig. S10 and Table S4† for details). As shown in Fig. 9a, it is evident that the VBM of Bi₂YO₄Cl primarily comprises O-2p orbitals, with a certain contribution from Bi-6s/6p orbitals, indicating that the VBM is formed by the lone pair interaction of Bi.^8,11,39,40 In contrast, in Bi_1.5Sb_0.5YO₄Cl (Fig. 9b), the VBM contribution mainly stems from the Sb-5s/5p orbitals rather than Bi orbitals. Furthermore, the bonding orbitals between Sb-5s and O-2p (around –8 eV) are higher than those of the Bi-6s states (–9–12 eV), likely due to relativistic effects,⁴¹ leading to higher energy levels of atomic Sb-5s orbitals compared to Bi-6s orbitals.^41,42 Therefore, the energy rise of VBM upon minor Sb substitution can be attributed to the closer energy levels between Sb-5s and O-2p orbitals, enabling stronger lone pair interactions (Fig. 9a).

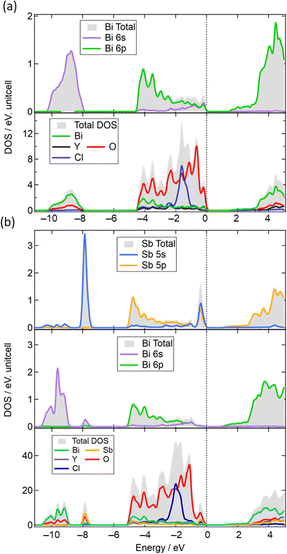Fig. 9 (a) Density of states (DOS) of Bi₂YO₄Cl and partial DOS (PDOS) for Bi 6s and Bi 6p states. (b) DOS of Bi_1.5Sb_0.5YO₄Cl and PDOS for Sb and Bi.

Interestingly, the bandgaps of Sb-substituted Bi₂YO₄Cl (x ∼0.5) are remarkably narrow, even when compared to Sb-based oxychlorides (e.g., 3.5 eV for Sb₄O₅Cl₂,⁴³ and 4.0 eV for SbOCl⁴²). In addition, the downshift of VBM occurs at x > 0.5 despite the increase in the Sb ratio (Fig. 8b), an observation that cannot be solely explained by simply considering the higher atomic levels of Sb-5s (vs. Bi-6s). In general, the stereochemical activity of LPEs can be enhanced when the lone-pair containing cations (e.g., Bi³⁺, Sb³⁺) occupy a larger space.^44–46 Given that Sb³⁺ is relatively small for the Bi³⁺ site,³⁰ the lone pair interaction of Sb in the lower x region may be enhanced. However, further substitution beyond x = 0.5 elongates the (Bi,Sb)–O bonds (Fig. 6a), weakens the Sb–O lone pair interaction and lowers the VBM level. This scenario resembles that of perovskite CsSnBr₃, where the off-centring is suppressed by competition with octahedral tilting distortions upon cooling.⁴⁶ In our case, competition with bond-breaking distortion may elongate the Sb–O distance and hence weaken the Sb–O lone pair interactions.

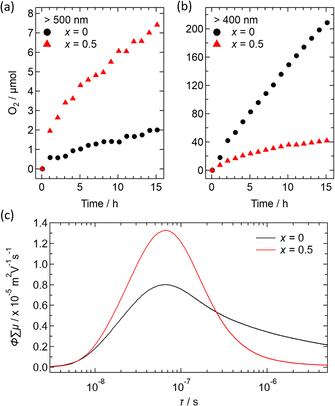
Fig. 10 illustrates preliminary photocatalytic results for O₂ evolution from water using Ir-loaded Bi_2−xSb_xYO₄Cl (x = 0 and 0.5), with AgNO₃ as a sacrificial reagent. When irradiated with light longer than 500 nm, Bi_1.5Sb_0.5YO₄Cl showed approximately 5 times higher activity than parent Bi₂YO₄Cl (Fig. 10a and b). This increase in activity indicates that the Sb-substituted sample can utilize a wider range of light wavelengths due to its narrower bandgap. However, the oxygen evolution is not very high, indicating the need for surface improvements. When exposed to the light with λ > 400 nm, the activity is enhanced but remains lower than that of pristine Bi₂YO₄Cl.

Fig. 10 Time course of O₂ production over Bi₂YO₄Cl (x = 0) and Bi_1.5Sb_0.5YO₄Cl (x = 0.5) from water, containing 4 mM of AgNO₃ as an Ag⁺ electron acceptor under the visible light irradiation with wavelengths (a) >500 nm and (b) >400 nm, produced by Xe lamp with L52 and L42 cutoff filters respectively. Photocatalysts had been initially loaded with 5 wt% of Ir as cocatalyst. (c) Transient conductivities of Bi₂YO₄Cl (x = 0) and Bi_1.5Sb_0.5YO₄Cl (x = 0.5) upon 355 nm laser excitation. The vertical axis represents the product of the quantum efficiency φ and the sum of photogenerated carrier mobilities ∑μ. The horizontal axis represents the lifetime in logarithmic scale.

The transient conductivity measurements revealed an improved mobility of photogenerated carries for x = 0.5, in comparison to x = 0 (Fig. 10c). This enhancement could be ascribed to a shorter (Bi,Sb)–O distance, leading to increased band dispersion. On the other hand, the x = 0.5 sample exhibits faster decay of the photoconductivity, suggesting that Sb-substitution increases the number of defects acting as recombination centers. Addressing this issue may involve adjusting the synthesis conditions and the choice of cocatalyst, as demonstrated in other materials,^47,48 though this is beyond the scope of our current study and remains a future challenge.

Conclusions

We have successfully synthesized the entire solid solution Bi_2−xSb_xYO₄Cl containing the triple fluorite layer, unveiling a clue of (Bi,Sb)–O bond breaking, a phenomenon that never occurs in compounds with conventional double fluorite layers. A small Sb substitution (x ≤ 0.5) induces the anticipated lattice contraction, but further substitutions lead to lattice expansion, finally causing a phase transition to the Sb₂YO₄Cl-type structure with 0D (Bi,Sb)₄O₈ rings. The structural instability observed in the high x region, characterized by Sb–O underbonding (which eventually leads to bond cleavage at x ≥ 1.5), can be rationalized as a result of biaxial tensile strain exerted from the central YO₂ sublayer to the outer (Bi,Sb)O sublayers within the triple fluorite block. This is similar to a strategy widely used in thin film studies, i.e., strain from a substrate, and can also reasonably explain the structure evolution to Bi₂MO₄Cl (M = Bi, La) with 1D zigzag chains. While the VBM remained uncontrolled in Bi₂MO₄Cl, Sb substitution in Bi_2−xSb_xYO₄Cl varies the VBM alongside a nonlinear change in lattice constants, narrowing the bandgap from 2.5 eV (x = 0) to 2.1 eV (x = 0.5). Our findings highlight the potential of fluorite structures comprising triple or more layers for bandgap engineering by introducing biaxial strain from the inner slab to the outer slab, or vice versa. This unique situation is absent in layered perovskites, which have been extensively studied as functional materials, and this study encourages the search for materials with thicker fluorite layers toward realizing new functions in a variety of fields.

Experimental

Synthesis and characterization

A series of Bi_2−xSb_xYO₄Cl solid solutions were obtained using the flux method or by solid-state reaction (SSR). For the SSR synthesis, powders of BiOCl (Wako, 95.0+%), Sb₂O₃ (Wako, 99.99%), Bi₂O₃ (Wako, 99.99%), and Y₂O₃ (Wako, 99.99%) were mixed in stoichiometric ratio, thoroughly grinded, and pelletized. Then, the pellet was loaded in an alumina tube, which was placed in a silica tube and vacuum-sealed. The pellets were heated twice to 800 °C with intermediate grinding. For flux synthesis, CsCl (Wako, 99.0%) was chosen as flux following the previous studies of oxyhalide photocatalysts.^10,29 19 times CsCl was added to the stoichiometric mixture of other starting materials. After 20 hours of reaction at 800 °C, the products were carefully washed with water and dried overnight at 100 °C followed by heating in air at 400 °C for 1 hour. SPXRD and SHG data were obtained from samples synthesized by solid state reaction, while photocatalytic measurements were performed with samples obtained by flux synthesis.

Synchrotron powder XRD (SPXRD) patterns were collected at the BL02B2 beamline in SPring-8, Japan (λ = 0.41327(1) Å) and were analysed using Jana2006.⁴⁹ High-angle annular dark-field scanning transmission electron microscopy images (HAADF-STEM) and selected area diffraction pattern (SAED) were collected using a JEM-ARM200CF, JEOL microscope operating at an accelerating voltage of 80 kV. UV-vis spectrophotometer (UV-2600, Shimadzu) was used to measure reflectance spectra, then the data were transformed to Kubelka–Munk, F(R), function.⁵⁰ The band gaps were obtained by Tauc plots, where (F(R) × hν)ⁿ is plotted against energy hν (eV) assuming n = 0.5 for a indirect bandgap transition.^51,52 The ionization energy was measured by photoelectron yield spectroscopy (PYS; BIP-KV201, Bunkoukeiki) in vacuum (<5 × 10⁻² Pa). The experimental pair distribution function (PDF), G(r), were obtained from the total scattering structure function S(Q) in variable Q ranges measured at the BL13XU beamline in SPring-8, Japan (λ = 0.334614(1) Å). Fourier transformation was carried out using the PDFgetX3 program.⁵³ Further refinement was performed using PDFfit2 software.⁵⁴

Optical second harmonic generation (SHG) measurements were performed at room temperature. As the light source, a pulsed Nd:YAG laser with a wavelength of 1064 nm was used. Pulse duration was 25 ps with repetition frequency of 10 Hz. A photomultiplier tube with a 532 nm narrow band-pass filter was used to detect the SHG light from the sample.

Time-resolved microwave conductivity (TRMC) measurements were conducted on samples synthesized via the flux method under ambient conditions using a third harmonic generator (THG; 355 nm).⁵⁵ A Nd:YAG laser (Continuum Inc., Surelite II) emitting pulses with a duration of 5–8 ns pulse duration and a frequency of 10 Hz served as the excitation source (4.6 × 10¹⁵ photons per cm² per pulse). An X-band microwave with a frequency of ∼9.1 GHz acted as the probe. The transient photoconductivity Δσ was calculated using the formula ΔP_r/A × P_r, where ΔP_r, A, and P_r represent the transient power change of the reflected microwave power, the sensitivity factor, and the reflected microwave power, respectively. The transient photoconductivity Δσ was then converted to the product of the quantum yield and the sum of charge carrier mobilities, ∑μ = μ₊ + μ₋, using the formula φ × ∑μ = Δσ × (e × I₀ × F_light)⁻¹, where e and F_light denote the unit charge of a single electron and a correction (or filling) factor, respectively.

DFT calculations

The electronic structures of Bi₂YO₄Cl and Bi_1.5Sb_0.5YO₄Cl were calculated using the VASP Package.^56,57 For Bi_1.5Sb_0.5YO₄Cl, a 2 × 2 × 1 superlattice was constructed, wherein Sb and Bi atoms were alternatively positioned in the triple fluorite layer (Fig. S10†) The exchange and correlation energies were evaluated within the generalized gradient approximation (GGA) of density functional theory (DFT), as proposed by Perdew, Burke, and Ernzerhof (PBE).^58,59 The supercell of Bi_1.5Sb_0.5O₄Cl (Fig. S10†) is generated using SHRY.⁶⁰ The electronic states were expanded by using a plane-wave basis set with a cutoff energy of 800 eV. The 12 × 12 × 6 k-points were used. Geometry optimization was performed before calculating the electronic structures using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm.^61–64 The calculated lattice parameters reasonably agree with the lattice parameters obtained from diffraction experiments (Table S4†).

Photocatalytic reaction

In prior to the photocatalytic measurements, Bi₂YO₄Cl and Bi_1.5Sb_0.5YO₄Cl powder samples were impregnated with Ir as cocatalyst. In this process, a photocatalyst was mixed with certain amount of Na₂IrCl₆·6H₂O (Strem Chemicals) water solution, corresponding to 0.5 wt% of Ir (assuming, for simplicity, a metallic state of cocatalyst). After that, the mixture was heated on a hot water bath until dry. Then, the result powder was heated under Ar flow at 450 °C for 30 min.

Photocatalytic reactions were performed in a closed gas-circulation system using a Pyrex reaction vessel, which had been degassed and purged with Ar gas before measurements. The evolved gases were analysed using online gas chromatography (GC3210, GL Sciences, Ar carrier gas). For photocatalytic O₂ evolution, the Bi_2−xSb_xYO₄Cl photocatalyst (0.1 g) preliminary loaded with Ir (0.5 wt%) as cocatalyst was suspended in a 250 ml of 4 mM aqueous solution of AgNO₃ (Wako, 99.9%). A Xe lamp (LAMP HOUSE R300-3J, Eagle engineering, 300 W) equipped with a cold mirror (CM-1, Kenko) and a cut-off filter was used as a light source. For irradiation of λ > 400 nm and λ > 500 nm light, cut-off filters L-42 and L-52 (HOYA Corporation) were used, respectively.

Data availability

ICSD 2343994–2344007 contain the supplementary crystallographic data for this paper.

Author contributions

A. G., D. K., H. K., S. K., designed the project. A. G., N. K. synthesized the samples. D. K. performed DFT calculations. A. G., H. U., D. K. collected and analysed SPXRD data and PDF data. R. A., D. K. carried out TEM measurements. K. F. carried out SHG measurement. A. G. performed the measurement of physical properties. H. S., O. T., R. A. contributed to the measurement of photocatalytic properties. A. S. and H. S. performed the TRMC measurements. A. G., D. K., H. K. wrote the manuscript, with comments from other authors.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by JST PRESTO (JPMJPR21A5), JSPS Core-to-Core Program (A) Advanced Research Networks (JPJSCCA20200004), the Grant-in-Aid for Scientific Research on Innovative Areas “Mixed Anion” project (16H06438, 16H06439), JSPS KAKENHI (JP21K20556, JP20H00398, JP22H04914, JP23H04860), and CREST (JPMJCR1421). TEM measurement was supported by “Advanced Research Infrastructure for Materials and Nanotechnology in Japan (ARIM)” of the Ministry of Education, Culture, Sports, Science and Technology (MEXT) (Proposal No. JPMXP1222KU0040 and JPMXP1223KU0023). The SPXRD experiments were performed at the BL02B2 of SPring-8 (Proposal No. 2022A1081 and 2022B1964). AG and SZK have received funding from the Project 309827 within the International Partnerships for Excellent Education, Research and Innovation Program of the Research Council of Norway. Special recommendation: COOL LONGBOAT project.

References

1. H. Kunioku, M. Higashi and R. Abe, Sci. Rep., 2016, 6, 32664.
2. T. Takata, C. Pan and K. Domen, Sci. Technol. Adv. Mater., 2015, 16, 33506.
3. K. Maeda, F. Takeiri, G. Kobayashi, S. Matsuishi, H. Ogino, S. Ida, T. Mori, Y. Uchimoto, S. Tanabe, T. Hasegawa, N. Imanaka and H. Kageyama, Bull. Chem. Soc. Jpn., 2022, 95, 26–37.
4. J. Cui, C. Li and F. Zhang, ChemSusChem, 2019, 12, 1872–1888.
5. H. Suzuki, H. Kunioku, M. Higashi, O. Tomita, D. Kato, H. Kageyama and R. Abe, Chem. Mater., 2018, 30, 5862–5869.
6. D. Kato, K. Hongo, R. Maezono, M. Higashi, H. Kunioku, M. Yabuuchi, H. Suzuki, H. Okajima, C. Zhong, K. Nakano, R. Abe and H. Kageyama, J. Am. Chem. Soc., 2017, 139, 18725–18731.
7. H. Fujito, H. Kunioku, D. Kato, H. Suzuki, M. Higashi, H. Kageyama and R. Abe, J. Am. Chem. Soc., 2016, 138, 2082–2085.
8. H. Kunioku, M. Higashi, O. Tomita, M. Yabuuchi, D. Kato, H. Fujito, H. Kageyama and R. Abe, J. Mater. Chem. A, 2018, 6, 3100–3107.
9. D. Kato, R. Abe and H. Kageyama, J. Mater. Chem. A, 2019, 7, 19846–19851.
10. A. Nakada, D. Kato, R. Nelson, H. Takahira, M. Yabuuchi, M. Higashi, H. Suzuki, M. Kirsanova, N. Kakudou, C. Tassel, T. Yamamoto, C. M. Brown, R. Dronskowski, A. Saeki, A. Abakumov, H. Kageyama and R. Abe, J. Am. Chem. Soc., 2021, 143, 2491–2499.
11. K. Ogawa, H. Suzuki, A. Walsh and R. Abe, Chem. Mater., 2023, 35, 5532–5540.
12. K. Kudo, H. Ishii, M. Takasuga, K. Iba, S. Nakano, J. Kim, A. Fujiwara and M. Nohara, J. Phys. Soc. Jpn., 2013, 82, 2–5.
13. D. Hirai, F. Von Rohr and R. J. Cava, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 100505.
14. S. Jia, P. Jiramongkolchai, M. R. Suchomel, B. H. Toby, J. G. Checkelsky, N. P. Ong and R. J. Cava, Nat. Phys., 2011, 7, 207–210.
15. H. Yamamoto, T. Ogata, Y. Sakai and M. Azuma, Inorg. Chem., 2019, 58, 2755–2760.
16. S. Pyon, K. Kudo and M. Nohara, J. Phys. Soc. Jpn., 2012, 81, 053701.
17. H. Miki, K. Yamamoto, H. Nakaki, T. Yoshinari, K. Nakanishi, S. Nakanishi, H. Iba, J. Miyawaki, Y. Harada, A. Kuwabara, Y. Wang, T. Watanabe, T. Matsunaga, K. Maeda, H. Kageyama and Y. Uchimoto, J. Am. Chem. Soc., 2024, 146, 3844–3853.
18. J. J. Zak, S. S. Kim, F. A. L. Laskowski and K. A. See, J. Am. Chem. Soc., 2022, 144, 10119–10132.
19. S. Jia, A. J. Williams, P. W. Stephens and R. J. Cava, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 165107.
20. T. Yamamoto, T. Yajima, Z. Li, T. Kawakami, K. Nakano, T. Tohyama, T. Yagi, Y. Kobayashi and H. Kageyama, Inorg. Chem., 2021, 60, 2228–2233.
21. R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1987, 26, 846–878.
22. M. Schmidt, M. Oppermann, H. Hennig, C. Henn, R. W. Gmelin, E. Soeger and N. Binnewies, Z. Anorg. Allg. Chem., 2000, 626, 125–135.
23. R. J. C. Locke, F. C. Goerigk, M. J. Schäfer, H. A. Höppe and T. Schleid, RSC Adv., 2022, 12, 640–647.
24. J. P. Locquet, J. Perret, J. Fompeyrine, E. Mächler, J. W. Seo and G. Van Tendeloo, Nature, 1998, 394, 453–456.
25. Y. Konishi, Z. Fang, M. Izumi, T. Manako, M. Kasai, H. Kuwahara, M. Kawasaki, K. Terakura and Y. Tokura, J. Phys. Soc. Jpn., 1999, 68, 3790–3793.
26. K. J. Choi, M. Biegalski, Y. L. Li, A. Sharan, J. Schubert, R. Uecker, P. Reiche, Y. B. Chen, X. Q. Pan, V. Gopalan, L. Q. Che, D. C. Schlom and C. B. Eom, Science, 2004, 306, 1005–1009.
27. J. H. Lee, L. Fang, E. Vlahos, X. Ke, Y. W. Jung, L. F. Kourkoutis, J. W. Kim, P. J. Ryan, T. Heeg, M. Roeckerath, V. Goian, M. Bernhagen, R. Uecker, P. C. Hammel, K. M. Rabe, S. Kamba, J. Schubert, J. W. Freeland, D. A. Muller, C. J. Fennie, P. Schiffer, V. Gopalan, E. Johnston-Halperin and D. G. Schlom, Nature, 2010, 466, 954–958.
28. T. Yamamoto, A. Chikamatsu, S. Kitagawa, N. Izumo, S. Yamashita, H. Takatsu, M. Ochi, T. Maruyama, M. Namba, W. Sun, T. Nakashima, F. Takeiri, K. Fujii, M. Yashima, Y. Sugisawa, M. Sano, Y. Hirose, D. Sekiba, C. M. Brown, T. Honda, K. Ikeda, T. Otomo, K. Kuroki, K. Ishida, T. Mori, K. Kimoto, T. Hasegawa and H. Kageyama, Nat. Commun., 2020, 11, 5923.
29. M. Namba, H. Takatsu, R. Mikita, Y. Sijia, K. Murayama, H. B. Li, R. Terada, C. Tassel, H. Ubukata, M. Ochi, R. Saez-Puche, E. P. Latasa, N. Ishimatsu, D. Shiga, H. Kumigashira, K. Kinjo, S. Kitagawa, K. Ishida, T. Terashima, K. Fujita, T. Mashiko, K. Yanagisawa, K. Kimoto and H. Kageyama, J. Am. Chem. Soc., 2023, 145, 21807–21816.
30. R. D. Shannon, Acta Crystallogr., 1976, 32, 751–767.
31. C. J. Hansen, J. J. Zak, A. J. Martinolich, J. S. Ko, N. H. Bashian, F. Kaboudvand, A. Van Der Ven, B. C. Melot, J. Nelson Weker and K. A. See, J. Am. Chem. Soc., 2020, 142, 6737–6749.
32. G. Assat and J. M. Tarascon, Nat. Energy, 2018, 3, 373–386.
33. I. D. Brown, Phys. C, 1990, 169, 105–106.
34. G. H. Kwei, P. C. Canfield, Z. Fisk, J. D. Thompson and R. B. Von Dreele, Phys. C, 1991, 176, 57–63.
35. D. Kato, O. Tomita, R. Nelson, M. A. Kirsanova, R. Dronskowski, H. Suzuki, C. Zhong, C. Tassel, K. Ishida, Y. Matsuzaki, C. M. Brown, K. Fujita, K. Fujii, M. Yashima, Y. Kobayashi, A. Saeki, I. Oikawa, H. Takamura, R. Abe, H. Kageyama, T. E. Gorelik and A. M. Abakumov, Adv. Funct. Mater., 2022, 32, 2204112.
36. Y. Jiang, Y. Mi, C. Li, W. Fang, X. Li, X. Zeng, Y. Liu and W. Shangguan, J. Alloys Compd., 2021, 884, 161036.
37. C. Zhao, L. Sun, Y. Xu, B. Dong, Y. Luo, J. Li, J. Chen and Z. Zhang, Chem.–Eur. J., 2022, 28, 202202004.
38. K. Ogawa, R. Abe and A. Walsh, J. Am. Chem. Soc., 2024, 146, 5806–5810.
39. C. Zhong, D. Kato, K. Ogawa, C. Tassel, F. Izumi, H. Suzuki, S. Kawaguchi, T. Saito, A. Saeki, R. Abe and H. Kageyama, Inorg. Chem., 2021, 60, 15667–15674.
40. R. Kuriki, T. Ichibha, K. Hongo, D. Lu, R. Maezono, H. Kageyama, O. Ishitani, K. Oka and K. Maeda, J. Am. Chem. Soc., 2018, 140, 6648–6655.
41. A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463.
42. Z. Ran, X. Wang, Y. Li, D. Yang, X.-G. Zhao, K. Biswas, D. J. Singh and L. Zhang, npj Comput. Mater., 2018, 4, 14.
43. L. Yang, J. Huang, L. Cao, L. Shi, Q. Yu, X. Kong and Y. Jie, Sci. Rep., 2016, 6, 27765.
44. X. Li, Y. Guan, X. Li and Y. Fu, J. Am. Chem. Soc., 2022, 144, 18030–18042.
45. U. Dang, W. Zaheer, W. Zhou, A. Kandel, M. Orr, R. W. Schwenz, G. Laurita, S. Banerjee and R. T. MacAluso, Chem. Mater., 2020, 32, 7404–7412.
46. D. H. Fabini, G. Laurita, J. S. Bechtel, C. C. Stoumpos, H. A. Evans, A. G. Kontos, Y. S. Raptis, P. Falaras, A. Van Der Ven, M. G. Kanatzidis and R. Seshadri, J. Am. Chem. Soc., 2016, 138, 11820–11832.
47. K. Ogawa, A. Nakada, H. Suzuki, O. Tomita, M. Higashi, A. Saeki, H. Kageyama and R. Abe, ACS Appl. Mater. Interfaces, 2019, 11, 5642–5650.
48. J. Yu, S. Chang, L. Shi and X. Xu, ACS Catal., 2023, 13, 3854–3863.
49. V. Petricek, L. Palatinus, J. Plasil and M. Dusek, Z. Kristallogr., 2023, 238, 271–282.
50. E. L. Simmons, Appl. Opt., 1976, 15, 951–954.
51. P. Makuła, M. Pacia and W. Macyk, J. Phys. Chem. Lett., 2018, 9, 6814–6817.
52. A. E. Morales, Rev. Mex. Fis., 2007, 53, 18–22.
53. P. Juhás, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Crystallogr., 2013, 46, 560–566.
54. C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Boin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219.
55. A. Saeki, Polym. J., 2020, 52, 1307–1321.
56. G. Kresse and J. Hafner, J. Phys.: Condens.Matter, 1994, 6, 8245–8257.
57. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1774.
58. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
59. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
60. G. I. Prayogo, A. Tirelli, K. Utimula, K. Hongo, R. Maezono and K. Nakano, J. Chem. Inf. Model., 2022, 62, 2909–2915.
61. D. Goldfarb, Math. Comput., 1970, 24, 23–26.
62. C. G. Broyden, IMA J. Appl. Math., 1970, 6, 76–90.
63. R. Fletcher, Comput. J., 1970, 13, 317–322.
64. D. F. Shanno, Math. Comput., 1970, 24, 647–656.

---

Footnote

† Electronic supplementary information (ESI) available: Reflectance spectra, refinement data. See DOI: https://doi.org/10.1039/d4sc02092h

---