Open Access Article
Open Access ArticleArtificial intelligence driven molecule adsorption prediction (AIMAP) applied to chirality recognition of amino acid adsorption on metals†
Zi-Xing
Guo
a,
Guo-Liang
Song
*a and
Zhi-Pan
Liu
 *abc
*abc
aCollaborative Innovation Center of Chemistry for Energy Material, Shanghai Key Laboratory of Molecular Catalysis and Innovative Materials, Key Laboratory of Computational Physical Science, Department of Chemistry, Fudan University, Shanghai 200433, China. E-mail: guoliangsong@fudan.edu.cn; zpliu@fudan.edu.cn
bKey Laboratory of Synthetic and Self-Assembly Chemistry for Organic Functional Molecules, Shanghai Institute of Organic Chemistry, Chinese Academy of Sciences, Shanghai 200032, China
cShanghai Qi Zhi Institution, Shanghai 200030, China
First published on 18th July 2024
Abstract
Predicting the adsorption structure of molecules has long been a challenging topic given the coupled complexity of surface binding sites and molecule flexibility. Here, we develop AIMAP, an Artificial Intelligence Driven Molecule Adsorption Prediction tool, to achieve the general-purpose end-to-end prediction of molecule adsorption structures. AIMAP features efficient exploration of the global potential energy surface of the adsorption system based on global neural network (G-NN) potential, by rapidly screening qualified adsorption patterns and fine searching using stochastic surface walking (SSW) global optimization. We demonstrate the AIMAP efficiency in constructing the Cu-HCNO6 adsorption database, encompassing 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182
182![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 351 distinct adsorption configurations of 9592 molecules on three copper surfaces. AIMAP is then utilized to identify the best adsorption structure for 18 amino acids (AAs) on achiral Cu surfaces and the chiral Cu(3,1,17)S surface. We find that AAs chemisorb on copper surfaces in their highest deprotonated state, through both the carboxylate-amino skeleton and side groups. The chiral recognition is identified for the D-preference of Asp, Glu, and Tyr, and L-preference for His. The physical origin for the enantiospecific adsorption is thus rationalized, pointing to the critical role of the competitive adsorption between functional side groups and the carboxylate-amino skeleton at surface low-coordination sites.
351 distinct adsorption configurations of 9592 molecules on three copper surfaces. AIMAP is then utilized to identify the best adsorption structure for 18 amino acids (AAs) on achiral Cu surfaces and the chiral Cu(3,1,17)S surface. We find that AAs chemisorb on copper surfaces in their highest deprotonated state, through both the carboxylate-amino skeleton and side groups. The chiral recognition is identified for the D-preference of Asp, Glu, and Tyr, and L-preference for His. The physical origin for the enantiospecific adsorption is thus rationalized, pointing to the critical role of the competitive adsorption between functional side groups and the carboxylate-amino skeleton at surface low-coordination sites.
1 Introduction
The molecule–surface interaction is at the heart of many branches of science. Molecular adsorption not only can modify the surface electronic/optical properties, but also may reshape the surface structures, and dictate the molecular reactivity.1,2 The characterization of molecular adsorption, including molecule conformation, the anchoring site, and the adsorption strength, is however very challenging in experiments due to the dynamic nature of molecules on surfaces at finite temperatures. From a theoretical point of view, the molecule–surface adsorption system can be defined as a complex thermodynamic ensemble that encompasses a vast array of energetically nearly degenerate configurations (usually within a few tenths of eV), the population of which exponentially scales with varied adsorption sites, coordination atoms, and molecule conformations. As a result, the fast prediction of the molecule–surface interaction remains not feasible to date.As a representative molecule–surface system, amino acid (AA) adsorption on metals has important applications in template synthesis,3–6 enantiospecific adsorption,7–11 and metal corrosion inhibition.12–16 To date, the investigation has been limited to relatively small-sized AAs, e.g., Gly, Ala, Ser17–22 where the “brute-intuition”23 heuristic protocol is utilized to find the adsorption configuration, i.e., the local optimization with pre-guessed geometries.19,21,24,25 Even for the simplest AA, such as Gly, there is a considerable number of likely adsorption geometries, for instance, 45 tridentate-configurations on Cu(3,1,17)S as enumerated by Rankin et al.19 For larger AAs such as Asp, and His, the structure search becomes prohibitive since multi-dentate adsorption configurations are coupled with the inherent flexible molecular geometry to generate a huge configuration space.
The rigorous way to find the adsorption structure would require quantum-mechanics-based26–28 either global optimization29,30 or long-time molecular dynamics (MD) simulations,31–35 which is often computationally too demanding even for medium-sized molecules (e.g., 10 atoms). Indeed, there are only a few reports, less than 30 systems (a molecule on a surface), in the literature.23,36 For example, Peterson searched the global minima (GM) of 17 CxHyOz molecules on the Cu(211) surface by using DFT calculations and the constrained minima hopping (CMH) global optimization algorithm.23 The recent effort is thus directed to the database construction of adsorption structures using density functional theory (DFT) calculations without seeking the most stable configuration, such as the OC20 database (Open Catalyst 2020) project that contains a total of 1.28 million DFT results of simple molecule adsorption on a wide swath of materials (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 451 materials in total, 95% are binary or ternary, with up to 55 unique elements).29 The molecule types in the OC20 dataset are limited to only 82 small-sized adsorbates, mainly C1/C2 compounds and N/O-containing intermediates, less than 7.0 × 10−5 percent of the vast molecular space recorded in PubChem (117 million unique chemical structures).37 The lack of molecule generality is understandable since the database generation is both labor and computation intensive where the precursors for each adsorbate have to be generated by enumerating many likely adsorption sites, followed by DFT-level local geometry optimization to identify favorable adsorption sites and energetics. In the OC20 generation, to reduce the computational costs, only ca. 0.07% of the possible precursors are selected randomly, each with one local minimum (LM).
451 materials in total, 95% are binary or ternary, with up to 55 unique elements).29 The molecule types in the OC20 dataset are limited to only 82 small-sized adsorbates, mainly C1/C2 compounds and N/O-containing intermediates, less than 7.0 × 10−5 percent of the vast molecular space recorded in PubChem (117 million unique chemical structures).37 The lack of molecule generality is understandable since the database generation is both labor and computation intensive where the precursors for each adsorbate have to be generated by enumerating many likely adsorption sites, followed by DFT-level local geometry optimization to identify favorable adsorption sites and energetics. In the OC20 generation, to reduce the computational costs, only ca. 0.07% of the possible precursors are selected randomly, each with one local minimum (LM).
Recent advances in machine learning (ML) based algorithms provide a new avenue for theoretical simulations to fast explore the PES of complex systems.38,39 For instance, our group showed in recent years that the stochastic surface walking (SSW) global optimization based on the global neural network (G-NN) potential (SSW-NN) can explore global PES unbiasedly via the smooth structure perturbation with an accuracy comparable to DFT calculations.40–42 The SSW-NN has been utilized to explore the molecule reaction network on metal surfaces, which yields not only the GM of molecular adsorption structures but also the reaction transition state (TS).43–48
Here we introduce AIMAP, an artificial intelligence (AI)-based end-to-end tool for predicting molecular adsorption energetics and configurations. We demonstrate the power of AIMAP by establishing the first molecule-Cu database, which encompasses 9592 distinct adsorbates of up to 6 skeleton atoms (i.e., C, N, and O) on Cu(111), Cu(100), and Cu(211) surfaces with all results released online (http://laspmol.lasphub.com/laspmol_surf.asp). With this new tool, we explore the adsorption of 18 AAs on three achiral copper surfaces and also predict the enantioselectivity of AAs on intrinsic chiral Cu(3,1,17)S. Our results pave the way for fully automated computational prediction of molecule adsorption and surface reaction energetics via AI-based methods.
2 AIMAP method and Cu-HCNO6 database
2.1 AIMAP method
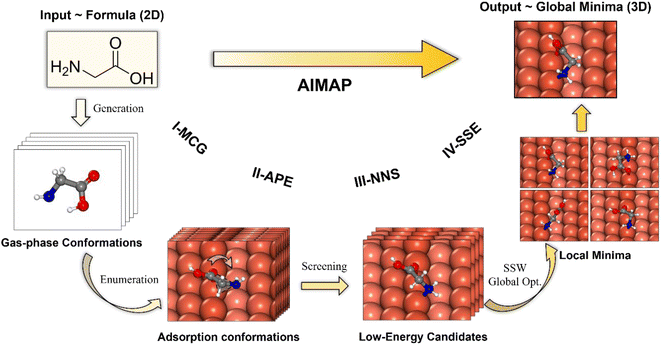
Our AIMAP method is developed to determine, in an automated way, energetically-favored molecule configurations on surfaces with simple inputs, e.g., starting from the chemical name of the adsorbate and surface Miller index. The hierarchy workflow of the method is depicted in Fig. 1, which contains four stages, namely, (i) Molecular Conformation Generation (I-MCG); (ii) Adsorption Precursor Enumeration (II-APE); (iii) Neural Network potential based precursor Screening (III-NNS); (iv) SSW-NN-based Structural Space Exploration (IV-SSE). Unlike previous methods, AIMAP considers all likely chemisorption connectivity in generating surface precursors and incorporates a neural network potential to speed up the precursor screening (at the stage III-NNS), and employs the SSW-NN method for the GM global exploration (at the stage IV-SSE). More details about the G-NN potential and SSW-NN method can be found in ESI Section 1.† The four stages are outlined in the following with the adsorption of the non-deprotonated glycine on the Cu(211) surface as the example.Fig. 1 illustrates one of the typical arrangements of glycine on the Cu(211) surface, which incorporates three atoms, i.e., carboxyl oxygen, α-hydrogen, and amino nitrogen. The adsorbate is arranged 2.0 Å above the surface, with the oxygen atom located at the top site on the step edge. Each 60° rotation through the Cu–O axis produces one brute precursor. A total number of 263 structures are enumerated with other arrangements and rotations. A 1.0 Å cutoff is set to rule out duplicate structures and finally produce 57 distinct adsorption conformations.
Fig. 1 illustrates the selected precursors for the glycine/Cu(211) system after the screening. A total number of 10 structures are identified (NIS = 10). The most favorable precursor can directly produce multi-dentation configurations with a single-step optimization.
Fig. 1 illustrates the GM and top 4 LM for the glycine/Cu(211) system, which are obtained by 5 steps of SSW global search (NSSW = 5). The GM features the μ2 configuration (μn(X): ‘n’ signifies the number of adsorbed atoms with X labeling their elements) with O and N atoms binding on the step edge.
In Table 1, we list the statistics for AIMAP in identifying the adsorption GM for methanol, non-deprotonated glycine, and mono-deprotonated asparagine (aspartate) on Cu(211) surfaces. It can be seen that with the increase of molecular complexity from methanol to aspartate, the parameters NIS (III-NNS) and NSSW (IV-SSE) need to be increased to identify the GM. The computation time in the fully automated AIMAP search also increases from 67 s to 701 s on a typical 28 CPU workstation, which is understandable as both glycine and aspartate prefer multidentate adsorption, e.g., μ2, μ5, which was typically a formidable task52 in the adsorption structure search. It should be emphasized that not only the GM is identified, but a set of LM with relatively low energy are also obtained from AIMAP, which is very useful for understanding the adsorption behavior of molecules and is exemplified in ESI Fig. S2.†. In the following sections, we set NIS (III-NNS) = NSSW (IV-SSE) = 15 for generating the Cu-HCNO6 database. For careful investigation of adsorption structures of AAs, the parameters are raised to NIS = NSSW = 30 on achiral surfaces and are further expanded on the more complex chiral Cu(3,1,17)S surface (e.g., NIS = NSSW = 45 for asparagine).
| a GM identified by AIMAP is further confirmed by long SSW global optimization (>2000 steps). b Distinguished by root mean square deviation (RMSD) of Cartesian coordinates with the periodicity and symmetry considered. c Data in parentheses is the number of LM within +0.20 eV above the GM. d Measured on a single workstation computer: Xeon E5-2695 V3, 3.3 GHz, 2 packages, 28 cores. | |||
|---|---|---|---|
| Molecule name | Methanol | Glycine | Aspartate |
| Molecule size | 2 | 5 | 9 |
| N IS | 3 | 10 | 15 |
| N SSW | 3 | 5 | 15 |
| N LM | 9 | 50 | 225 |
| N DLM | 3 (2)c | 11 (2)c | 34 (3)c |
| Conf. | μ 1(O) | μ 2(N,O) | μ 5(4O,N) |
| t /s | 67 | 274 | 701 |
2.2 Cu-HCNO6 database
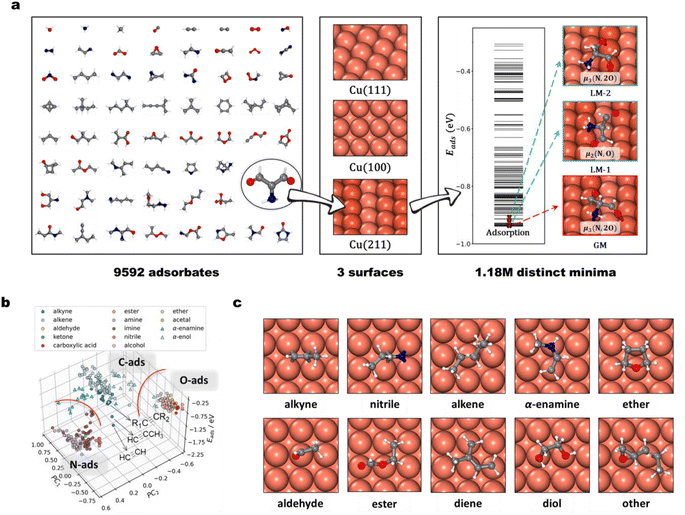
The power of the AIMAP method is then proved by constructing a large database named Cu-HCNO6, which contains 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182
182![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 351 distinct adsorption structures on copper surfaces. Fig. 2a summarizes the content and key features of the Cu-HCNO6 database: three typical Cu surfaces are considered, including planar Cu(111) and Cu(100), and stepped Cu(211); 9592 distinct adsorbates are included, encompassing nearly all neutral species composed of up to six C/N/O (non-H) heavy atoms in the PubChem database, where 76.2% of them possess one or more double or triple bonds (unsaturated C, e.g., CH2
351 distinct adsorption structures on copper surfaces. Fig. 2a summarizes the content and key features of the Cu-HCNO6 database: three typical Cu surfaces are considered, including planar Cu(111) and Cu(100), and stepped Cu(211); 9592 distinct adsorbates are included, encompassing nearly all neutral species composed of up to six C/N/O (non-H) heavy atoms in the PubChem database, where 76.2% of them possess one or more double or triple bonds (unsaturated C, e.g., CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), and 75.7% contain at least two N/O atoms. Detailed composition analysis is provided in ESI Section 4.†
CH2), and 75.7% contain at least two N/O atoms. Detailed composition analysis is provided in ESI Section 4.†
Not only the GM but also low-energy LM obtained from AIMAP are included in the Cu-HCNO6 database, which are screened out of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 301
301![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277 local relaxations in IV-SSE. Using these adsorption structures, the adsorption energy (Eads) of the molecule can thus be predicted and stored in the database. Since all the energetics in the database are based on G-NN calculations, we have benchmarked the precision of adsorption energy with DFT results. On 10
277 local relaxations in IV-SSE. Using these adsorption structures, the adsorption energy (Eads) of the molecule can thus be predicted and stored in the database. Since all the energetics in the database are based on G-NN calculations, we have benchmarked the precision of adsorption energy with DFT results. On 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 randomly selected adsorption structures, the RMSD of adsorption energy from G-NN results and DFT results is 0.19 eV per structure (see ESI Section 5†).
000 randomly selected adsorption structures, the RMSD of adsorption energy from G-NN results and DFT results is 0.19 eV per structure (see ESI Section 5†).
Because of the huge content of the Cu-HCNO6 database, in the following, we provide a database profile by focusing on selected molecules. We choose 311 different molecules, 14 types in total, from the database, distinct in the functional group feature, including alkyne, alkene, aldehyde, ketone, carboxylic acid, ester, amine, imine, nitrile, alcohol, ether, acetal, α-enamine, and α-enol. Taking these molecules on the Cu(100) surface as an example, we analyze their adsorption geometry features by using Principal Component Analysis (PCA). 450 power-type symmetry descriptors (PTSD) used in G-NN potential are utilized as the component for constructing the PCA basis, from which the top 2 highest weight components are generated (PC1, PC2) that provide the main geometric feature. Fig. 2b plots the scatter diagram between the Eads energetic and PC main geometrical features, which shows an obvious clustering of the data points in the Eads ∼ PC1 ∼ PC2 plot molecules with similar functional groups that tend to behave similarly.
Specifically, the adsorption geometry can be divided into three broad regions along the x/y-axis, featuring N, O, and unsaturated C atoms in their functional groups. For those with two more functional groups, for example, α-enamine and α-enol, they also appear as separate clusters, indicating the participation of multiple functional groups in adsorption (e.g., both unsaturated C and N/O atoms involved in bonding with the surface). Within the same type of functional group, the adsorption energy varies in a range of typically a few tenths of eV, due to the different alkyl fragments attached to the functional group (e.g., acetylene, propyne, and other alkynes, as exemplified in Fig. 2b).
We further examine carefully the adsorption structures out of the 311 molecules on the Cu(100) surface. As illustrated in Fig. 2c, we found that alkyne, alkene, nitrile, α-enamine, and α-enol adsorb strongly with their unsaturated C (N) atoms, and the molecule adopts the flat-lying geometry. On Cu(100) each triple-bonded C/N atom is located typically at one bridge site, as alkyne and in nitrile, forming a tetrahedron binding geometry (μ2, Fig. 2c alkyne, nitrile); the double-bonded C atoms can adopt the top–top site geometry (μ2, Fig. 2c alkene) or the top–bridge–top site (μ3Fig. 2c α-enamine). For N/O-containing molecules, the N/O end also prefers to bond with Cu, where the O and N atoms are typically located at the top site on Cu(100) (Fig. 2c ether, aldehyde). For molecules with multiple adsorption linker atoms (i.e., O, N and unsaturated C), they can have the multidentate adsorption geometry, where by rotating the flexible single-bond of the molecule, each linker atom could achieve monodentate adsorption. For example, both two oxygen atoms bind on the top sites in ester adsorption (Fig. 2c ester). This rule applies to multiple functional group molecules, such as glycol (Fig. 2c, diol), cis-pentadiene (Fig. 2c, diene), and 4,5-epoxy-2-pentene (Fig. 2c, other). These molecules often form ring structures with surface Cu atoms, which further stabilize the adsorption geometry (e.g., six-membered ring Cu–O–C–C–O–Cu in glycol).
It should be noted that the above analysis takes only 3.4% of adsorbates in the Cu-HCNO6 database, and on a single Cu(100) surface. For a broader range of molecule adsorption on varied surfaces, we refer to the database http://laspmol.lasphub.com/laspmol_surf.asp for any specific research.
3 Amino acid adsorption on Cu surfaces
Not limited to relatively small molecules involved in the Cu-HCNO6 database, we go further to predict the AA adsorption structure on Cu, which is of great significance in many applications.3–16 Except for cysteine and methionine with the sulfur atom (not supported by the Cu–C–H–O–N G-NN potential), adsorption of all AAs (18 molecules) on the three achiral Cu surfaces (Cu(111), Cu(100) and Cu(211)) and one chiral Cu surface (Cu(3,1,17)S), including their neutral, anionic, and di-anionic forms, in total 43 distinct adsorbates, is investigated and their adsorption free energies under ambient conditions are evaluated to compare the relative stability. DFT calculations are further utilized to fully optimize the low-energy structures obtained from AIMAP (see ESI Section 2†). All DFT data (using PBE-D3 exchange–correlation functional) can be found in ESI Sections 6 and 7.†To align to the same deprotonation level of adsorbates the adsorption free energy (Gads) is calculated using eqn (1),
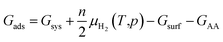 | (1) |
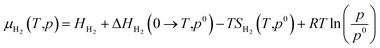 | (2) |
3.1 Adsorption on achiral surfaces
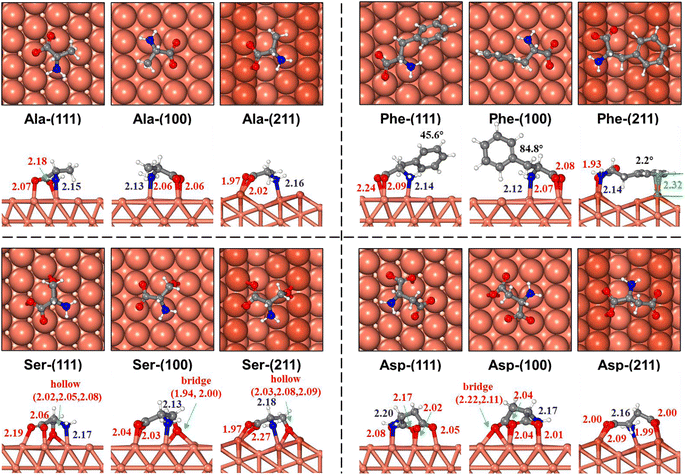
We only focus on L-AAs in this part, given that the adsorption structure of D/L-AAs is equivalent on achiral surfaces. As listed in Table 2, for the best adsorption structure and energetics in the GM, we find that all AAs undergo deprotonation upon adsorption on all three achiral surfaces (also see ESI Table S6†). They all achieve the multi-dentate adsorption geometry, at least tridentate, relating two O in the carboxylate group and N in the amino group. Among them, anion species are favored for 13 types of AAs, including Gly, Ala, Val, Leu, Ile, Pro, Phe, Trp, Gln, Asn, Lys, Arg, and His; and the di-anionic form is preferred for Ser, Thr, Tyr, Glu, and Asp where the hydroxyl or carboxyl groups in the side chains also undergo deprotonation on adsorption.| Class | Molecule name | Deprotonation number | Cu(111) | Cu(100) | Cu(211) | |||
|---|---|---|---|---|---|---|---|---|
| G ads | Conf. | G ads | Conf. | G ads | Conf. | |||
| Alkyl | Gly | 1 | −1.49 | μ 3(2O,N) | −1.88 | μ 3(2O,N) | −2.06 | μ 3(2O,N) |
| Ala | 1 | −1.62 | −2.03 | −2.20 | ||||
| Pro | 1 | −1.73 | −2.06 | −2.23 | ||||
| Val | 1 | −1.70 | −2.29 | −2.29 | ||||
| Leu | 1 | −1.83 | −2.26 | −2.35 | ||||
| Ile | 1 | −1.89 | −2.29 | −2.35 | ||||
| Aryl | Phe | 1 | −2.05 | μ 3(2O,N) | −2.45 | μ 3(2O,N) | −2.65 | μ 3(O,N,Ar) |
| Trp | 1 | −2.49 | μ 3(2O,N) | −2.72 | μ 3(2O,N) | −3.20 | μ 3(O,N,Ar) | |
| Tyr | 2 | −2.48 | μ 4(2O,N,Ar) | −3.33 | μ 3(2O,Ar) | −3.56 | μ 4(2O,N,Ar) | |
| Other N/O containing functional | Ser | 2 | −2.18 | μ 4(3O,N) | −2.54 | μ 4(3O,N) | −2.68 | μ 4(3O,N) |
| Thr | 2 | −2.32 | μ 4(3O,N) | −2.67 | μ 4(3O,N) | −2.77 | μ 4(3O,N) | |
| Gln | 1 | −2.36 | μ 3(2O,N) | −2.89 | μ 4(3O,N) | −3.08 | μ 4(3O,N) | |
| Asn | 1 | −1.85 | μ 3(2O,N) | −2.34 | μ 4(3O,N) | −2.49 | μ 4(3O,N) | |
| Glu | 2 | −2.59 | μ 5(4O,N) | −3.17 | μ 5(4O,N) | −3.65 | μ 5(4O,N) | |
| Asp | 2 | −2.30 | μ 5(4O,N) | −2.86 | μ 5(4O,N) | −3.11 | μ 5(4O,N) | |
| Lys | 1 | −2.63 | μ 4(2O,2N) | −3.39 | μ 4(2O,2N) | −3.36 | μ 4(2O,2N) | |
| Arg | 1 | −2.25 | μ 4(2O,2N) | −2.90 | μ 4(2O,2N) | −3.17 | μ 3(2O,N) | |
| His | 1 | −2.26 | μ 4(2O,2N) | −2.84 | μ 3(2O,N) | −3.20 | μ 4(2O,2N) | |
The adsorption energy is generally large, greater than 1.4 eV, where the lower coordinated surface provides higher adsorption energy in general, i.e., Gads follows Cu(111) < Cu(100) < Cu(211), with average value as −2.11 eV, −2.61 eV, and −2.80 eV, respectively. It is interesting to note that the van der Waals (vdW) contribution from D3 correction contributes 66.5% on average to Gads in Cu(111), 46.0% in Cu(100) and 44.5% in Cu(211), suggesting the significant contribution of vdW interactions for the large molecule adsorption on metals.
In the following, we elaborate on the adsorption results of 18 AAs, which can be divided broadly into three classes according to their side chains, alkyl, aryl, and N/O containing functional groups.
It is interesting to compare our theoretical results with experimental observations. First, the deprotonation state of AA adsorption has been observed in many experiments (above 300 K), including Gly/Cu(100), Gly/Cu(110), Ala/Cu(110), Ser/Cu(110), Asp/Cu(110), and Pro/Cu(111) systems.17,54–62 For example, Dutta et al. found that the α-carboxyl group undergoes deprotonation in the Pro/Cu(111) system through C 1s X-ray photoelectron spectroscopy (XPS) measurements61 and the deprotonation of side-chain groups is also observed by XPS measurements in other AAs (e.g., hydroxyl in Ser and carboxyl in Asp).60,63 This is consistent with our results that the highest deprotonation form is preferred for all AAs on copper surfaces. Second, the multi-dentate adsorption geometry of AAs has also been deduced from experiments. By using PhD and LEED, Williams et al. observed a pair of equidistance oxygen atoms and N lone-pair interaction in the low-coverage Ala/Cu(110) system,54 which suggests a μ3 configuration. Eralp et al. observed a low binding-energy shoulder (530.8 eV) of O 1s XPS in the Ser/Cu(531) system, which suggests that the adsorption involves hydroxyl oxygen and thus the μ4 configuration is proposed.21
3.2 Adsorption on the chiral surface
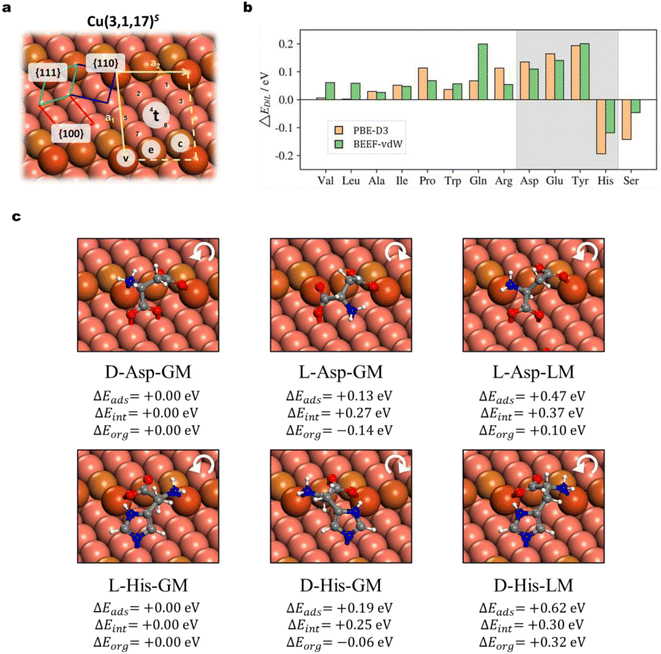
The chirality recognition via the molecule–surface interaction is an important topic in chemistry. By switching the achiral Cu surfaces to a chiral surface, Cu(3,1,17)S, as shown in Fig. 4a, we can utilize AIMAP to predict whether the chirality recognition is present for AA adsorption on the chiral Cu surface. The Cu(3,1,17)S surface features kinked steps formed by {110} and {111} microfacets, separated by {100} terraces. The kinked structure is the chiral center, which is designated R and S with clockwise and counter-clockwise rotations in the sequence of {111} → {100} → {110}. On the S surface, D-adsorbates are equivalent to L-adsorbates on the R surface (and vice versa). Without losing generality, we focus on the adsorption of D/L-AA on the Cu(3,1,17)S surface, where their highest deprotonated AA forms are taken as the adsorbates based on the knowledge gleaned from the previous section.In Fig. 4a, all distinctive sites, including the step vertex site v, step edge site e, step corner site c, and terrace sites t1–t7, are labeled. The defective atoms on the step edge (v, e, and c) are primarily considered on arranging the surface precursors, as inspired by the adsorption behavior on the defective Cu(211) surface. A total number of 6420 distinct minima are considered for all 35 types of D/L-AA species, with 346 adsorption structures selected out for further DFT investigations. The adsorption structures are modeled at low-coverage, as the (2 × 1) supercell is utilized for these with relatively small skeleton size (Ala, Val, Pro, Leu, Ile, Ser, Thr, Glu, Gln, Asp, Asn) whereas a (2 × 2) supercell is applied for the other 6 types (Phe, Trp, Tyr, His, Lys, Arg). All the adsorption structures and the adsorption energy of D and L forms are provided in ESI S7.1 and S7.2† and it is obvious that all D/L-enantiomers adopt distinct local geometry from each other. The relative stability of the most stable D/L-enantiomers is given by:
| ΔEL/D = Eads(L) − Eads(D) | (3) |
Fig. 4b shows that 11 types of AAs have a preference for the D-enantiomer, including Ala, Val, Leu, Ile, Pro, Asp, Glu, Gln, and Tyr, while 2 types of AAs show a preference for the L-enantiomer, i.e. His and Ser. Notably, four types of D/L-enantiomers, i.e., Asp, Glu, Tyr, and His, possess relatively strong ΔEads (>0.10 eV, shadowed in Fig. 4b) under both the two DFT functionals. From our results, the most chiral recognition system always involves the chemical binding on all three microfacets, {111}, {110}, and {100} (i.e., Asp, Glu, Thr, His; Fig. 4 and ESI Fig. S10, S11†), in which the side-chain must also strongly bind with copper atoms through the N/O-containing groups (i.e., carboxylate, imidazole, and phenolic hydroxide). Molecules with poor binding side chains possess relatively small ΔEL/D as they only involve chemisorption on {110} and {111} microfacets (e.g., Ala, Leu, Val, see ESI Fig. S9†).
To better understand the chiral recognition, we decompose the adsorption energy Eads into two parts, the one from the structure reorganization energy Eorg of the individual molecule and the surface in the adsorption system compared to the gas phase molecule and the clean surface, respectively; and the other Eint from the interaction of the adsorbed molecule and the surface (Eads = Eorg + Eint). By using the most stable adsorption system as the reference (e.g., D-Asp-GM for Asp, Fig. 4c), we thus can obtain the ΔEads (=ΔEorg + ΔEint) to compare the adsorption energy difference between the most stable form and the other less stable form. For illustration, Fig. 4c shows the adsorption structures of two representative chirality recognition systems, Asp and His, which prefer the D- and L-enantiomer adsorption, respectively. The most stable D- (e.g., D-Asp-GM) and L-forms (e.g., L-Asp-GM) for the two AAs are depicted in this figure, together with the less stable L-form of Asp and D-form of His (L-Asp-LM and D-His-LM), which have the closest adsorbate–surface connectivity with their most stable form (D-Asp-GM and L-His-GM, respectively). The ΔEads, ΔEorg and ΔEint are also indicated for these less stable adsorption structures.
Our results highlight four AAs (Asp, Glu, Tye, and His) with a strong tendency of chiral recognition on Cu(3,1,17)S. They share the same structural feature that the side chain containing N/O groups also binds strongly with the surface. We note that the D-preference of Asp has been revealed through the TPD experiment: on the Cu(3,1,17)S surface, Yun et al. observed a higher coverage of D-Asp against L-Asp on equilibrium adsorption and estimated a 3.2 ± 0.3 kJ mol−1 energetic discrimination through the ratio of D/L-coverage (θD/θL).65 On the other hand, experiments also indicate non-enantioselective adsorption for some AAs. For example, when the Cu(3,1,17)R&S surfaces are exposed to the Ala mixture with different D/L ratios (i.e., 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2
2, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, racemic), the ratio of D- and L-Ala on surface coverages equals the value in the gas phase (θD/θL = pD/pL).66 This also agrees with our theoretical prediction of the poor chiral recognition for Ala as reflected by the low ΔEL/D.
1, racemic), the ratio of D- and L-Ala on surface coverages equals the value in the gas phase (θD/θL = pD/pL).66 This also agrees with our theoretical prediction of the poor chiral recognition for Ala as reflected by the low ΔEL/D.
One has to keep in mind that a high PES accuracy (e.g., <0.05 eV) is generally required to predict correctly the enantioselectivity, which remains extremely challenging for electronic structure calculations. Our results show that two different DFT functionals could lead to the qualitative discrepancy in the sign of ΔEL/D in the adsorption of four types of AAs (Thr, Asn, Phe, and Lys). Among them, Phe is known to be non-enantioselective and the D-form of Lys is 2.6 ± 0.3 kJ mol−1 more favorable,10,67 a magnitude below the typically regarded chemical accuracy. Finally, we would like to point out that Ser is an interesting case, where theory predicts a 0.14 eV preference for the L-enantiomer by the PBE-D3 method (0.05 eV by BEEF-vdW), but no enantiomeric excess was observed in experiment for the saturated adsorption of Ser on Cu(3,1,17)S.67 While it may still originate from DFT error, we suspect that the chiral recognition of the aggregation forms of adsorbates17,19,21,68,69 (high coverages with lateral interactions) might be the key reason since only low coverage adsorption is considered in this work.
4 Conclusions
This work develops AIMAP, an AI-based tool, to predict molecule adsorption on surfaces, where SSW-NN global optimization as implemented in LASP software in combination with other cheminformatics tools is utilized to speed up the global potential energy scan of molecular adsorption systems. To demonstrate the efficiency of AIMAP, we create the Cu-HCNO6 adsorption database, including over one million distinct adsorption structures of 9592 adsorbates on three representative low-Miller-index Cu surfaces. This database allows us to obtain comprehensive knowledge on molecule adsorption geometry and the sites with the copper surface, The whole database is openly accessible on the LASP website http://laspmol.lasphub.com/laspmol_surf.asp. We are currently working on to expand the database with more metal/material surfaces.We apply AIMAP in a challenging problem in surface science, the adsorption and the chiral recognition of AAs on surfaces. Multidentate adsorption structures for 18 types of AAs on three achiral copper surfaces are identified, showing that the deprotonated state is generally preferred in adsorption. For AAs on the intrinsic chiral Cu(3,1,17)S surface, we predict the D-preference of Asp, Glu, and Tyr, and a L-preference of His. We show that the binding competition effect between the carboxylate-amino skeleton and the side-chain functional side groups for the kinked Cu sites is critical for achieving enantioselectivity.
Data availability
The data supporting this article have been included as part of the ESI.† The CuCHON and other adsorption databases are available from the website http://laspmol.lasphub.com/laspmol_surf.asp.Author contributions
Z.-P. L. and G.-L. S. conceived the project and contributed to the design of the calculations and analyses of the data. Z.-X. G. carried out most of the calculations and wrote the draft of the paper. All authors discussed the results and commented on the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work received financial support from the National Science Foundation of China (12188101, 22033003, 91745201, 91945301, and 223B2302), the Fundamental Research Funds for the Central Universities (20720220011), the National Key Research and Development Program of China (2018YFA0208600), and the Tencent Foundation for XPLORER PRIZE.Notes and references
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24 RSC.
- T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- P. A. Mirau, R. R. Naik and P. Gehring, J. Am. Chem. Soc., 2011, 133, 18243–18248 CrossRef CAS PubMed.
- R. Coppage, J. M. Slocik, M. Sethi, D. B. Pacardo, R. R. Naik and M. R. Knecht, Angew. Chem., Int. Ed., 2010, 22, 3767–3770 CrossRef PubMed.
- I. A. Banerjee, L. Yu and H. Matsui, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14678–14682 CrossRef CAS PubMed.
- C.-Y. Chiu, Y. Li, L. Ruan, X. Ye, C. B. Murray and Y. Huang, Nat. Chem., 2011, 3, 393–399 CrossRef CAS PubMed.
- Y. Fang, X. Liu, Z. Liu, L. Han, J. Ai, G. Zhao, O. Terasaki, C. Cui, J. Yang, C. Liu, Z. Zhou, L. Chen and S. Che, Chem, 2023, 9, 460–471 CAS.
- N. Shukla and A. J. Gellman, Nat. Mater., 2020, 19, 939–945 CrossRef CAS PubMed.
- X. Zhao, J. Am. Chem. Soc., 2000, 122, 12584–12585 CrossRef CAS.
- W. Y. Cheong and A. J. Gellman, J. Phys. Chem. C, 2011, 115, 1031–1035 CrossRef CAS.
- D. S. Sholl, A. Asthagiri and T. D. Power, J. Phys. Chem. B, 2001, 105, 4771–4782 CrossRef CAS.
- M. M. Antonijevic and M. B. Petrovic, Int. J. Electrochem. Sci., 2008, 3, 1–28 CrossRef CAS.
- D. Kumar, N. Jain, V. Jain and B. Rai, Appl. Surf. Sci., 2020, 514, 145905 CrossRef CAS.
- Z. Zhang, N. Tian, L. Zhang and L. Wu, Corros. Sci., 2015, 98, 438–449 CrossRef CAS.
- A. Kasprzhitskii, G. Lazorenko, T. Nazdracheva, A. Kukharskii, V. Yavna and A. Kochur, New J. Chem., 2021, 45, 3610–3629 RSC.
- A. Kasprzhitskii and G. Lazorenko, J. Mol. Liq., 2021, 331, 115782 CrossRef CAS.
- M. Sacchi, D. J. Wales and S. J. Jenkins, Phys. Chem. Chem. Phys., 2017, 19, 16600–16605 RSC.
- Y. Wang, S. Yang, M. Fuentes-Cabrera, S. Li and W. Liu, J. Am. Chem. Soc., 2017, 139, 8167–8173 CrossRef CAS PubMed.
- R. B. Rankin and D. S. Sholl, J. Chem. Phys., 2006, 124, 074703 CrossRef PubMed.
- H. S. Song and J. W. Han, J. Phys. Chem. C, 2015, 119, 15195–15203 CrossRef CAS.
- T. Eralp, A. Ievins, A. Shavorskiy, S. J. Jenkins and G. Held, J. Am. Chem. Soc., 2012, 134, 9615–9621 CrossRef CAS PubMed.
- J. W. Han, J. N. James and D. S. Sholl, J. Chem. Phys., 2011, 135, 034703 CrossRef PubMed.
- A. A. Peterson, Top. Catal., 2014, 57, 40–53 CrossRef CAS.
- R. B. Rankin and D. S. Sholl, J. Phys. Chem. B, 2005, 109, 16764–16773 CrossRef CAS PubMed.
- C. Chen, S. Yang, G. Su, Q. Ji, M. Fuentes-Cabrera, S. Li and W. Liu, J. Phys. Chem. C, 2020, 124, 742–748 CrossRef CAS.
- K.-S. Yun, S. J. Pai, B. C. Yeo, K.-R. Lee, S.-J. Kim and S. S. Han, J. Phys. Chem. Lett., 2017, 8, 2812–2818 CrossRef CAS PubMed.
- P. K. Biswas, N. A. Vellore, J. A. Yancey, T. G. Kucukkal, G. Collier, B. R. Brooks, S. J. Stuart and R. A. Latour, J. Comput. Chem., 2012, 33, 1458–1466 CrossRef CAS PubMed.
- H. Heinz, T.-J. Lin, R. Kishore Mishra and F. S. Emami, Langmuir, 2013, 29, 1754–1765 CrossRef CAS PubMed.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11, 6059–6072 CrossRef CAS.
- A. Kolluru, M. Shuaibi, A. Palizhati, N. Shoghi, A. Das, B. Wood, C. L. Zitnick, J. R. Kitchin and Z. W. Ulissi, ACS Catal., 2022, 12, 8572–8581 CrossRef CAS.
- M. Kleber, I. C. Bourg, E. K. Coward, C. M. Hansel, S. C. B. Myneni and N. Nunan, Nat. Rev. Earth Environ., 2021, 2, 402–421 CrossRef.
- T. Sedghamiz, M. Bahrami and M. H. Ghatee, Chem. Phys., 2017, 487, 48–58 CrossRef CAS.
- S.-H. Park and G. Sposito, Phys. Rev. Lett., 2002, 89, 085501 CrossRef PubMed.
- L. Guo, S. Kaya, I. B. Obot, X. Zheng and Y. Qiang, J. Colloid Interface Sci., 2017, 506, 478–485 CrossRef CAS PubMed.
- S. Kr. Saha, A. Dutta, P. Ghosh, D. Sukul and P. Banerjee, Phys. Chem. Chem. Phys., 2015, 17, 5679–5690 RSC.
- K. Krautgasser, C. Panosetti, D. Palagin, K. Reuter and R. J. Maurer, J. Chem. Phys., 2016, 145, 084117 CrossRef PubMed.
- S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, Nucleic Acids Res., 2023, 51, D1373–D1380 CrossRef PubMed.
- J. Lan, A. Palizhati, M. Shuaibi, B. M. Wood, B. Wander, A. Das, M. Uyttendaele, C. L. Zitnick and Z. W. Ulissi, npj Comput. Mater., 2023, 9, 172 CrossRef CAS.
- H. Jung, L. Sauerland, S. Stocker, K. Reuter and J. T. Margraf, npj Comput. Mater., 2023, 9, 144 CrossRef.
- S. Huang, C. Shang, P. Kang, X. Zhang and Z. Liu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9(6), e1415 CAS.
- C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 1838–1845 CrossRef CAS PubMed.
- P.-L. Kang, Z.-X. Yang, C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2023, 19, 7972–7981 CrossRef CAS PubMed.
- D. Chen, L. Chen, Q.-C. Zhao, Z.-X. Yang, C. Shang and Z.-P. Liu, Nat. Catal., 2024, 1–10 Search PubMed.
- J.-L. Li, Y.-F. Li and Z.-P. Liu, JACS Au, 2023, 3, 1162–1175 CrossRef CAS PubMed.
- Q.-Y. Liu, C. Shang and Z.-P. Liu, J. Am. Chem. Soc., 2021, 143, 11109–11120 CrossRef CAS PubMed.
- S. Ma, S.-D. Huang and Z.-P. Liu, Nat. Catal., 2019, 2, 671–677 CrossRef CAS.
- P.-L. Kang, C. Shang and Z.-P. Liu, J. Am. Chem. Soc., 2019, 141, 20525–20536 CrossRef CAS PubMed.
- Y.-F. Shi, P.-L. Kang, C. Shang and Z.-P. Liu, J. Am. Chem. Soc., 2022, 144, 13401–13414 CrossRef CAS PubMed.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33 Search PubMed.
- S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 15665–15673 CrossRef CAS PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11(2), e1493 CAS.
- J. R. Boes, O. Mamun, K. Winther and T. Bligaard, J. Phys. Chem. A, 2019, 123, 2281–2285 CrossRef CAS PubMed.
- W. M. Haynes, D. R. Lide and T. J. Bruno, Handbook of Chemistry and Physics, CRC Press, Boca Raton, 97th edn, 2016 Search PubMed.
- J. Williams, S. Haq and R. Raval, Surf. Sci., 1996, 368, 303–309 CrossRef CAS.
- X. Zhao, Z. Gai, R. G. Zhao, W. S. Yang and T. Sakurai, Surf. Sci., 1999, 424, L347–L351 CrossRef CAS.
- S. M. Barlow, K. J. Kitching, S. Haq and N. V. Richardson, Surf. Sci., 1998, 401, 322–335 CrossRef CAS.
- M. Nyberg, J. Hasselström, O. Karis, N. Wassdahl, M. Weinelt, A. Nilsson and L. G. M. Pettersson, J. Chem. Phys., 2000, 112, 5420–5427 CrossRef CAS.
- N. A. Booth, D. P. Woodruff, O. Schaff, T. Gießel, R. Lindsay, P. Baumgärtel and A. M. Bradshaw, Surf. Sci., 1998, 397, 258–269 CrossRef CAS.
- G. Jones, L. B. Jones, F. Thibault-Starzyk, E. A. Seddon, R. Raval, S. J. Jenkins and G. Held, Surf. Sci., 2006, 600, 1924–1935 CrossRef CAS.
- T. Eralp, A. Shavorskiy, Z. V. Zheleva, G. Held, N. Kalashnyk, Y. Ning and T. R. Linderoth, Langmuir, 2010, 26, 18841–18851 CrossRef CAS PubMed.
- S. Dutta and A. J. Gellman, Chirality, 2020, 32, 200–214 CrossRef CAS PubMed.
- J.-H. Kang, R. L. Toomes, M. Polcik, M. Kittel, J.-T. Hoeft, V. Efstathiou, D. P. Woodruff and A. M. Bradshaw, J. Chem. Phys., 2003, 118, 6059–6071 CrossRef CAS.
- B. S. Mhatre, Super-Enantiospecific Autocatalytic Decomposition of Tartaric Acid and Aspartic Acid on Cu Surfaces, PhD thesis, Carnegie Mellon University, Pittsburgh, PA, 2013.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- Y. Yun and A. J. Gellman, Angew. Chem., Int. Ed., 2013, 52, 3394–3397 CrossRef CAS PubMed.
- Y. Yun, D. Wei, D. S. Sholl and A. J. Gellman, J. Phys. Chem. C, 2014, 118, 14957–14966 CrossRef CAS.
- Y. Yun and A. J. Gellman, Langmuir, 2015, 31, 6055–6063 CrossRef CAS PubMed.
- Y. Yun and A. J. Gellman, J. Phys. Chem. C, 2016, 120, 27285–27295 CrossRef CAS.
- R. B. Rankin and D. S. Sholl, Langmuir, 2006, 22, 8096–8103 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Theoretical methods; training and benchmark for the Cu–C–H–O–N quinary G-NN potential; insight on the Cu-HCNO6 database; structural and energetic details for AA adsorption on achiral Cu(111), Cu(100), and Cu(211) surfaces, as well as the chiral Cu(3,1,17)S surface; the snapshots of the enantio-specific adsorption of Glu and Tyr on the Cu(3,1,17)S surface. See DOI: https://doi.org/10.1039/d4sc02304h |
| This journal is © The Royal Society of Chemistry 2024 |