Data-driven discovery of active phosphine ligand space for cross-coupling reactions

Abstract

The design of highly active catalysts is a main theme in organic chemistry, but it still relies heavily on expert experience. Herein, powered by machine-learning global structure exploration, we forge a Metal–Phosphine Catalyst Database (MPCD) with a meticulously designed ligand replacement energy metric, a key descriptor to describe the metal–ligand interactions. It pushes the rational design of organometallic catalysts to a quantitative era, where a ±10 kJ mol⁻¹ window of relative ligand binding strength, a so-called active ligand space (ALS), is identified for highly effective catalyst screening. We highlight the chemistry interpretability and effectiveness of ALS for various C–N, C–C and C–S cross-coupling reactions via a Sabatier-principle-based volcano plot and demonstrate its predictive power in discovering low-cost ligands in catalyzing Suzuki cross-coupling involving aryl chloride. The advent of the MPCD provides a data-driven new route for speeding up organometallic catalysis and other applications.

---

Introduction

Metal–ligand (M–L) complexes demonstrate great value in homogeneous catalysis towards a wide range of reactions, e.g. C–C/C–N cross-coupling, olefin carbonylation reactions, etc.^1–4 Finding the optimal ligand for a target reaction is, however, a fundamental challenge, which relies largely on labor-intensive trial-and-error experiments.^5–8 Naturally, it would be highly desirable to develop a rational strategy that can pre-screen all available ligands on the market (>1000) to meet the target reactivity. Catalyst design could be boosted by quantum mechanics calculations, particularly density functional theory (DFT) calculations, which can resolve the lowest energy reaction profile for a designed catalyst thus to identify the suitable ligand. The major difficulty is the low efficiency in establishing the quantitative linkage between metal–ligand catalysts for a specific reaction, not least because of the complexity of the reaction mechanism under realistic experimental conditions and the high computational cost of quantum mechanics calculations.

In the past few decades, various strategies have been developed to speed up ligand screening. For instance, Fey^9–13 and Gensch groups^14,15 have constructed ligand knowledge bases (LKB) and a kraken design platform, which parameterize ligands from both electronic and geometric perspectives. These databases contain commonly utilized geometrical features of the Tolman cone,¹⁶ buried volume (V_bur),¹⁷ and the electronic features of the energy level of the lowest/highest (un)occupied molecule orbital, natural bond orbital charge etc.¹⁸ These efforts in feature engineering facilitate the development of quantitative structure–activity relationship (QSAR) models, correlating experimental activity (selectivity) data with computable quantities.^5,19,20 Consequently, this could minimize the number of experimental trials required to identify optimal ligands. However, these features often lack a direct connection with reaction kinetics, and thus, for reactions with unknown mechanisms, it is not possible to identify the feature-activity correlation in advance.

Other strategies, such as the molecular volcano plot,^21–24 virtual ligand-assisted screening,²⁵ AARON,²⁶ CatVS²⁷etc., have made important progress to incorporate reaction mechanism information in building feature-activity correlation, which improves the accuracy in predicting a series of important organic reactions, such as cross-coupling, hydroformylation of a terminal olefin and asymmetric hydrogenation reactions.^28–33 Nevertheless, these approaches generally require the 3-dimensional conformation geometry of metal–ligand complexes and knowledge of the reaction mechanism, which are often too computationally intensive to obtain and thus their application is much limited compared to the more user-friendly QSAR models.

In recent years, our group has combined the stochastic surface walking (SSW) global optimization method^34,35 with the machine-learning global neural network potential (G-NN)^36–41 method (SSW-NN) for exploring the vast phase space of materials. Based on the method, the LASP (Large-Scale Atomic Simulation based on Neural Network Potential) software package has been developed and is now widely utilized in different research fields.⁴² The SSW-NN method features the high speed (3–4 orders of magnitude faster than DFT calculations) and the high accuracy of G-NN potential for potential energy surface (PES) computation and the high efficiency of the SSW method for structure global optimization and reaction exploration.^43–46 This provides a new opportunity for the metal–ligand catalysis design, where, by fast computing the conformation space of metal–ligand complexes, the reaction information may be obtained efficiently for quantifying ligand reaction features and thus facilitating ligand screening.

For this purpose, in this work we have developed G-NN potentials capable of describing metal–P-ligand (M–L_P) catalysts and further established the Metal Phosphine-ligand Catalyst Database (MPCD) that contains over ten thousand M–L_P interaction strength metrics (accessible through an open online platform, https://www.lasphub.com/database/#/MPCD). By using the MPCD data, we designed a general strategy, the so-called active ligand space (ALS) approach, for the quick construction of a volcano plot. We demonstrate the efficiency of the ALS approach by applying it to various cross-coupling reactions. By combining synthetic experiments, we identified a series of cost-effective P-ligands from the existing commercial P-ligand pool for C–C cross-coupling reactions, which can achieve aryl chloride activation.

Results

Sabatier principle for catalyst screening

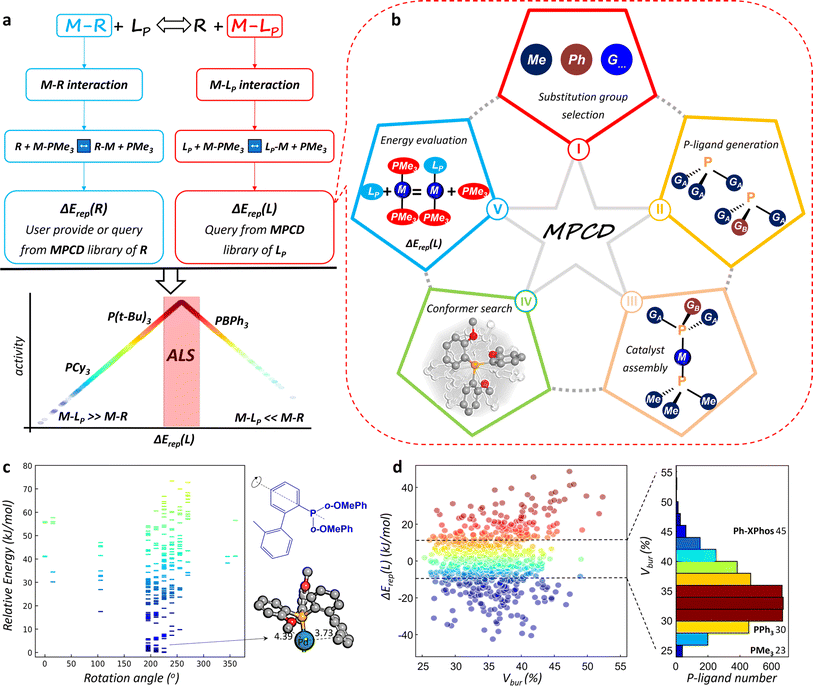
For metal-catalyzed homogeneous reactions, a catalytic cycle is commonly initiated by the formation of an active metal catalytic center surrounded by various ligands, followed by a series of redox reactions, such as oxidative addition and reductive elimination. The ligands of the central metal constitute the essential chemical environment for the reaction, which can leave and rejoin the metal center dynamically as the reaction proceeds. The dynamics behavior of the catalyst follows exactly the well-known Sabatier principle—good catalysts should have neither too-strong nor too-weak binding for metal–reaction species (M–R) and M–L.

This fundamental principle has inspired us to design a universal ligand library for describing their interactions with metal atoms. As depicted in Fig. 1a, the energetics of the binding of molecule X to the metal can be defined as the relative binding strength with respect to a reference state (S), which is connected to the replacement energy (ΔE_rep) of the reaction X + MS → MX + S. This definition indirectly compares the interactions between M–R and M–L by referencing both the reactants and ligands to the same reference state. Here, we use simplified and generic trimethyl phosphine (PMe₃) as the reference state. In this manner, we can establish two databases for measuring the binding energies of different reaction species and P-ligands with metals by calculating the ΔE_rep(R) and ΔE_rep(L), respectively, as shown in eqn (1) and (2).

L_P + M(PMe₃)₂ → L_PMPMe₃ + PMe₃, ΔE_rep(L) (1)

R + M(PMe₃)₂ → RMPMe₃ + PMe₃, ΔE_rep(R) (2)

Fig. 1 MPCD construction and analysis. (a) The methodology for defining the active ligand space (ALS) via calculating the interaction of M–L_P and M–R, respectively, and plotting the volcano plot. (b) The entire MPCD construction process: substitution group selection, P-ligand generation, catalyst assembly, conformer search, energy evaluation and online visualization. (c) Energy spectrum of L_P–M–PMe₃ conformers collected from SSW-NN global search, where L_P is composed of a 2′-methyl biphenyl (2MeBPh) group and two o-methoxy phenyl (o-OMePh) groups. These conformers are viewed from the rotation angle of the 2MeBPh substitution group along the P–C axis. (d) The variations of ΔE_rep(L) against the V_bur value for Pd–L_P catalysts, along with the statistical histograms of P-ligand numbers in the MPCD. The dark blue, pink, red, gray and white balls represent the Pd, P, O, C and H atoms, respectively.

In catalyst design for a target reaction, a Sabatier volcano map can be easily constructed. To avoid the expensive transition state search and the fabrication of a linear relationship, we define a simple −|ΔE_rep(L) − ΔE_rep(R)| descriptor as the reaction activity metric (eqn (3)) with ΔE_rep(L) as the ligand descriptor. As illustrated in Fig. 1a, the left and right sides of the volcano curve represent the poor catalyst region (i.e. M–L_P ≫ M–R or M–L_P ≪ M–R). When the interaction of M–R is greater than that of M–L_P, the reaction species tends to replace all P-ligand ligands, rendering the ligands unable to bind to the metal center and thus losing their catalytic functionalities. Conversely, when the interaction of M–R is smaller than that of M–L_P, the ligand preferentially binds to the metal center, preventing the reaction intermediate from being activated by the central metal. Only the apex of the volcano curve corresponds to an ALS, where the P-ligand is well-matched with the reaction species and has the potential to activate the reaction intermediate. We will show later using different examples that the typical ALS is rather small, typically within ±10 kJ mol⁻¹ for the |ΔE_rep(L) − ΔE_rep(R)|.

Activity ∝ −|ΔE_rep(L) − ΔE_rep(R)| (3)

Establishment of the MPCD

Using the above catalyst design strategy, we undertook a systematic five-step procedure to construct the MPCD for ΔE_rep(L), as illustrated in Fig. 1b, namely substitution group selection, P-ligand generation, catalyst assembly, best conformer search, and energy evaluation. In the following, we elaborate these steps by using the typical monodentate P-ligand with three substitution groups as an example (also see Fig. 1b texts in the star shape).

Step I. It starts from a careful selection of fundamental substitution group building blocks that are widely used on the market, including alkyl (–C_sp³R, e.g. –cyclohexyl), aryl (–C_sp²R, e.g. –benzyl), alcohols (–OR, e.g. –methoxy) and amino (–NR, e.g. pyridyl). The detailed introduction of these substitution groups is presented in Fig. S1.†

Step II. We combine distinct substitution groups to yield an array of diverse P-ligands. Each P-ligand contains at most two types of substitution groups connecting to the phosphorus atom. This considers the fact that P-ligands with three distinct substitution groups are generally much more difficult to synthesize and thus rare on the market.

Step III. The P-ligand is then assembled with the center metal and PMe₃ ligand to form an L_P–M–PMe₃ complex. The metal atom is thus coordinated with two P-ligands, a common geometry for catalyst intermediates during organic reactions.^5,19 Since the PMe₃ ligand is generally small in size, the ligand–ligand steric repulsion can be largely avoided in computing ligand binding strength.

Step IV. The global PES exploration is performed to identify the most stable conformer for each L_P–M–PMe₃ complex by using the global G-NN-based^42,44,47,48 stochastic surface walking³⁴ method (SSW-NN).

Step V. After the low energy structures are generated, the DFT calculations are performed to refine the selected most stable structures to yield the final ΔE_rep(L) values. It might be mentioned that as the LASP project⁴² aims to speed up the atomic simulation for a wide range of elements, including both materials and molecules, thus the LASP dataset is constructed using the same plane-wave DFT calculations (e.g. VASP software⁴⁹) with the same generalized gradient approximation exchange–correlation functional at the Perdew–Burke–Ernzerhof (GGA-PBE) level. In this work, as the system is metal–ligand complexes, where the atomic-orbital-based B3LYP functional (e.g. Gaussian 09 software⁵⁰) is more popular, we have carefully benchmarked the energy difference between two different setups. We found that there is only a small mean absolute error of 3.9 kJ mol⁻¹ for the ΔE_rep(L) values (more details can be found in the Methods section) and this does not affect the fast ligand screening purpose of our ALS approach.

The thus-established MPCD is openly accessible from the online platform (see Movie S1†) with a user-friendly interface for search. To date, more than >4 million conformers for around 8200 assembled P-ligands have been explored and their most stable conformers and their energetics are now included in the MPCD. The online platform provides access to ∼60 000 ΔE_rep(L) values of >8200 P-ligands with different metals (Pd, Pt, Rh etc.). The ΔE_rep(R) for a molecule, e.g. ArX, can be similarly obtained following the above procedure, and some data are stored in the MPCD of molecules (Table S1†).

In Step IV, the advent of the SSW-NN method allows efficient and automatic identification of the most stable conformers for a large number of P-ligands in L_P–M–PMe₃ complexes. Fig. 1c illustrates the energy spectrum of L_P–M–PMe₃ conformers collected from SSW-NN global search, where the P-ligand is composed of a 2′-methyl biphenyl (2MeBPh) and two o-methoxy phenyl (o-OMePh) groups. These conformers can be better viewed from the rotation angle of the 2MeBPh substitution group along the P–C axis. As shown, even a small rotation would generate an excessive number of distinct conformers with a substantial energy change (∼80 kJ mol⁻¹). The most stable conformer appears when the rotation angle approaches 225°, where the 2MeBPh group is as far away as possible from the adjacent o-OMePh substitution group (Fig. 1c). The total cost for finding the global minima of each P-ligand needs approximately 10 core-hours by using SSW-NN methods, reducing the cost by 3–4 orders of magnitude relative to the DFT calculations.

Data analysis can be quickly conducted on ΔE_rep(L) magnitude for different P-ligands to compare with other descriptors. Fig. 1d depicts the energy variations of ΔE_rep(L) for the Pd–L_P catalysts against the widely employed V_bur steric occupation descriptor.¹⁷ The V_bur quantifies the steric occupation of any given ligand structure within a radius of 3.5 Å around the central metal atom. It is obvious that a lack of correlation emerges between ΔE_rep(L) and V_bur, which can be attributed to their distinct conceptual foundations in terms of energetic and steric attributes. It is particularly noteworthy that the distribution of these P-ligands spans a significant range in both energetic and volumetric dimensions, consequently allowing the screening and design of optimum P-ligands. The statistical distribution in terms of P-ligand numbers, presented in the histogram of Fig. 1d, indicates that within a narrow ΔE_rep(L) variation region from −10 kJ mol⁻¹ to 10 kJ mol⁻¹, approximately 4500 distinct P-ligands are present that have a diverse steric occupation. There are not only approximately 700 compact P-ligands with V_bur values below 30% but also around 250 bulky P-ligands with V_bur values exceeding 42%. This implies that the ΔE_rep(L) is a very sensitive descriptor for judging the interaction strength of P-ligands with the metal and thus facilitates identifying any trivial structural variation of P-ligands.

MPCD applications

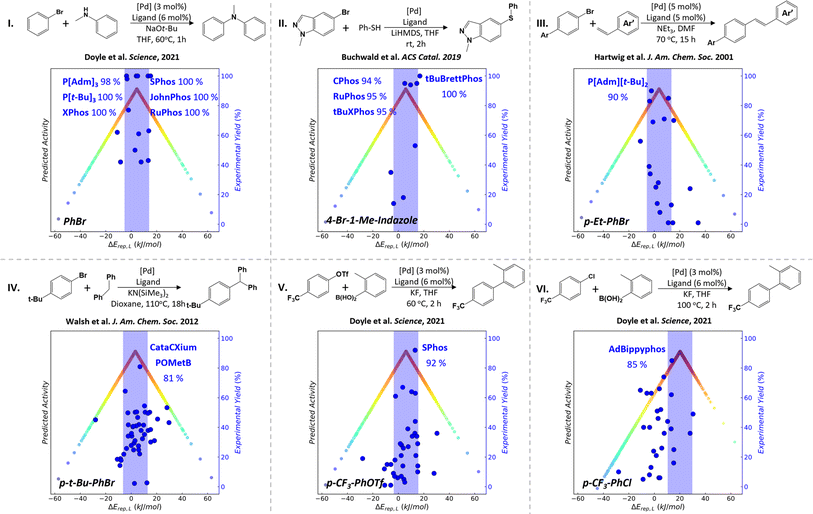
Based on the MPCD, we can now apply the ALS approach of P-ligand screening to metal–ligand catalyzed organic reactions. The palladium-catalyzed cross-coupling of aryl halides (ArX + Ar′LG → Ar–Ar′ + X + LG; X: I, Cl and Br; LG: leaving group) is selected as the target reaction, which is well-known as a powerful method to make carbon–carbon and carbon–heteroatom bonds. ΔE_rep(L) and ΔE_rep(R) (eqn (1) and (2)) quantify the relative strength of M–L_P and M–R bonds, respectively, and can be utilized to assess quantitatively the competition between reaction species and P-ligands in binding with the central metal atom. By calculating ArX reactants, the coupling partners with the leaving group and the coupling products binding with the central Pd metal atom, we found that both the coupling partners and products bond weakly with the ΔE_rep(R) being larger than +50 kJ mol⁻¹, resulting in no suitable P-ligands with ΔE_rep(L) (generally below + 40 kJ mol⁻¹) compatible with ΔE_rep(R) (Fig. S2 and S3†). We therefore utilize ArX binding with metal Pd to compute ΔE_rep(R) in this work, which is then compared with the ΔE_rep(L) in the MPCD to obtain the theoretically predicted ALSs. This is consistent with the general knowledge that ArX is the molecule to be activated by the catalyst. Six C–N, C–S or C–C cross-coupling reactions are analyzed to construct the volcano plots. The experimental activity data in the literature are collected to compare with the theoretically predicted ALS to verify the correctness of ALS.^5,51–53 The phosphine ligands that are not included in our MPCD and illustrate less prominent experimental activity in the literature are ignored (Fig. 2).

Fig. 2 The MPCD-based volcano plot analysis for Pd catalyzed cross-coupling reactions with the reactants as the key reaction species to match with P-ligands. Each colored dot represents a theoretically calculated P-ligand with redder colors closer to the peak of the volcano plot and bluer colors further away from the peak. The light blue region represents the predicted ALSs based on volcano plots. The dark blue circles are the experimental yields of different P-ligands reported in the literature. The reactions I–IV, V and VI involve the activation of ArBr, ArOTf and ArCl with the ALS ranges from −5 to 15 kJ mol⁻¹, from −4 to 16 kJ mol⁻¹ and from 11 to 21 kJ mol⁻¹, respectively.

Reaction I is the Pd-catalyzed Buchwald–Hartwig amination of bromobenzene (PhBr) as reported by Doyle and coworkers.⁵ By comparing ΔE_rep(PhBr) with ΔE_rep(L), we reveal the theoretically predicted ALS in between −5.2 and 14.8 kJ mol⁻¹ with respect to ΔE_rep(PhBr) (4.8 kJ mol⁻¹). Experimental data encompass a dataset of 26 screened P-ligands, of which six demonstrate remarkable product yield (>98%). Interestingly, our analysis reveals that five of these P-ligands—namely P[t-Bu]₃ (t-Bu: tert-butyl), P[Adm]₃ (Adm: adamantyl), XPhos, RuPhos and SPhos—fall in the ALS of PhBr, exhibiting ΔE_rep(L) values of −3.9, −2.9, 3.9, 4.2 and 13.5 kJ mol⁻¹, respectively. Even the only exception, the JohnPhos ligand, is located just at the ALS boundary with ΔE_rep(L) values of 15.4 kJ mol⁻¹.

The same agreement between theory and experiment can be extended to other reactions involving the activation of aryl bromides (ArBr), such as the Pd-catalyzed C–S cross-coupling reaction conducted by Buchwald and collaborators (reaction II),⁵¹ the Pd-catalyzed C–C Heck cross-coupling reaction conducted by Hartwig and collaborators (reaction III)⁵² and the Pd-catalyzed C_sp³–H arylation elucidated by Zhang et al. (reaction IV).⁵³ The ALS ranges of ΔE_rep(L) are from −4 to 16 kJ mol⁻¹ for reaction II, from −6 to 14 kJ mol⁻¹ for reaction III and from −7 to 13 kJ mol⁻¹ for reaction IV, suggesting that the substitution group of ArBr does not much alter ALS. Notably, the CPhos, RuPhos and tBuXPhos with product yield > 94% for reaction II fall in the ALS of 4-bromo-1-methylindazole (4-Br-3-Me-indazole). Even the exception the tBuBrettPhos ligand is located just at the ALS boundary with ΔE_rep(L) values of 17.3 kJ mol⁻¹. Moreover, P[Adm][t-Bu]₂ and the CataCXium POMetB boasting the highest product yields have ΔE_rep(L) values of −3.9 and 6.8 kJ mol⁻¹ for reactions III and IV, respectively, also well falling in the predicted ALS region.

For Suzuki–Miyaura coupling (SMC) reactions in reactions V and VI, they feature a diverse array of ArX reactants: p-trifluoromethyl benzene triflates (p-CF₃-PhOTf) and p-trifluoromethyl chlorobenzene (p-CF₃-PhCl). The theoretically predicted ALS ranges from −4 to 16 kJ mol⁻¹ and from 11 to 31 kJ mol⁻¹ for the reactions V and VI, respectively, involving the activation of the p-CF₃-PhOTf and p-CF₃-PhCl reactants. In the literature, the SPhos and AdBippyphos ligands emerge as the best P-ligands with product yields of 92% and 85% for reactions V and VI, respectively. These optimal ligands also match well with the corresponding ALSs. These good alignments of experimental ligands with theoretical ALSs provide strong evidence for the predictive power of the MPCD-based blind ligand design.

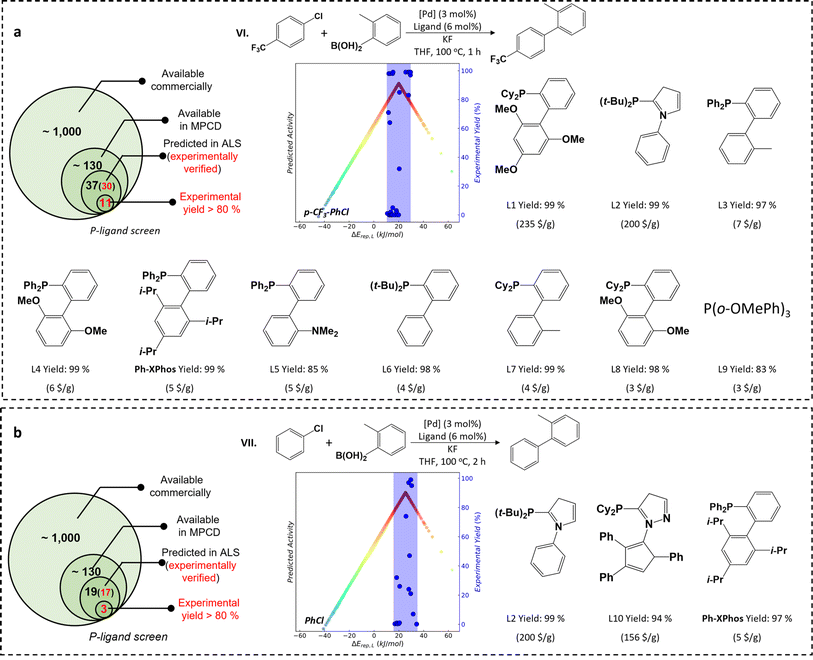
Considering the significance of aryl chloride activation in industrial applications, our next investigation focuses on the SMC reaction involving aryl chloride activation (reactions VI and VII). Although some active P-ligands have been reported in the literature for aryl chloride activation, they suffer from either low turnover frequency (TOF) of reaction activity (e.g., PCy₃)⁵⁴ or high costs (e.g. AdBippyphos with a market price of 257 $ per g).⁵ Therefore, there is a strong need for active yet cost-effective P-ligands. For the reaction VI involving the activation of p-CF₃-PhCl, by using the MPCD-based volcano plot, the theoretically predicted ALS range of the p-CF₃-PhCl spans from 11 to 21 kJ mol⁻¹. Among a pool of 130 commercially available P-ligands (Table S2†), the ALS-guided prediction indicates that 37 of them are likely to activate p-CF₃-PhCl (Fig. 3a and Table S3†). 30 of these predictions are then experimentally carried out via reaction VI, where the reaction time is shortened to 1 hour to better reflect the activity of ligands (Fig. S4†). The AdBippyphos ligand, reported as the best ligand in literature,⁵ indeed exhibits noteworthy catalytic performance with a product yield of 98% in our experiments. More interestingly, we discover ten novel P-ligands that all lead to product yields exceeding 80% (Fig. 3a). Of special interest is the Ph-XPhos ligand, showing an impressive 99% product yield and a price of only 5 $ per g. The TOF is 33 h⁻¹, which ranks top among known catalysts (Table S4†).

Fig. 3 The ALS-guided experiment P-ligand screening for SMC reactions of (a) p-CF₃PhCl (reaction VI) and (b) PhCl (reaction VII). The experimental verifications are under the guidance of ALSs of p-CF₃PhCl and PhCl. The P-ligands with a product yield higher than 80% are illustrated in the figure.

For the reaction VII involving PhCl activation, the theoretically predicted ALS range for PhCl is from 15 to 35 kJ mol⁻¹ (Fig. 3b), located in the higher ΔE_rep(L) region relative to the ALS of p-CF₃-PhCl. This suggests a weaker M–R interaction and thus a reduced pool of active P-ligands for PhCl compared to p-CF₃-PhCl. A subset of 19 commercial P-ligands fall within the ALS of PhCl (Table S5†), and 17 of them are then verified through experiments (Fig. S5†). Among them, we identify three P-ligands with high catalytic performance with product yields exceeding 94% after 2 hours of reaction time. Again, the cost-efficient Ph-XPhos ligand emerges as a frontrunner, exhibiting a TOF of approximately 16 h⁻¹, notably higher than that of known catalysts (Table S4†). We emphasize that the Ph-XPhos ligand shows consistently high yields across broad aryl chloride substrates with diverse functional groups (Fig. S6†) which ranks top among known catalysts (Table S6†).

To further understand the detailed structural evolution of metal Pd during the reaction, the ³¹P nuclear magnetic resonance (NMR) spectrum is used to characterize the electron structure variation of P-ligands. We selected the best P-ligand for reactions VI and VII, Ph-XPhos, to demonstrate the structural changes of metal Pd during the activation process of PhCl. As shown in Fig. S7,† the ³¹P NMR spectrum of Ph-XPhos shows a chemical shift at −18 ppm, indicating the initial state of the P-ligand. Upon adding metal Pd to the solution, a new peak appears at 18 ppm in the ³¹P NMR spectrum. This shift confirms the formation of the Pd–L_P complex, where Ph-XPhos bonds with the Pd atom. Introducing the PhCl reactant into the solution at room temperature does not cause any change in the ³¹P NMR spectrum, which remains at 18 ppm. This observation indicates that PhCl does not interact with the Pd atom under these conditions. When the solution with PhCl is heated to 100 °C for 1 hour, a new peak emerges at 36 ppm, and the original peak at 18 ppm disappears. This significant shift demonstrates that PhCl is activated by the Pd–L_P catalyst, resulting in the formation of the Ph–Pd–(Cl)–L_P complex. These experimental results clearly show the structural evolution of the Pd–L_P catalyst during the activation of PhCl, which is consistent with the observations on Ni-catalyzed C–C coupling and Pd-catalyzed direct arylation reactions with aryl chlorides.^55,56

We note that ligands with identical binding strengths to the metal can exhibit vastly different catalytic performance. For example, the P[Tol]₃ and L8 ligands both have a ΔE_rep(L) value of 13.5 kJ mol⁻¹ but result in vastly different product yields of 1% and 98% for reaction VI, respectively. This suggests that the complexity of catalysis activity cannot be simply described by a single ΔE_rep(L) parameter. To take into account more ligand properties, we have tentatively incorporated geometrical factors in our ligand design, such as the V_bur descriptor for the steric effect as utilized in the literature.⁵ Interestingly, by using the V_bur threshold larger than 32% as a criterion to screen for a valid catalyst, we found that the success rates can further increase to ∼60% and 25% for reactions VI and VII, respectively (Fig. S8 and Tables S3 and S4†). This indicates that the geometrical factor is indeed important for the activity of some P-ligands. However, it is important to recognize that the V_bur descriptor thresholds, e.g. 32%, are empirically derived from experimental data, which limits their predictive capability prior to experimental validation. In contrast, our ΔE_rep(L) energy descriptors do not depend on experimental data and can be utilized for pre-screening purposes before conducting actual experiments. Therefore, the other descriptors can act as key complements after the ALS-guided ligand screening. By considering both the binding strengths and steric conformations of ligands, one can gain a deeper understanding of the catalyst and make better decisions to design better ligands for catalytic applications.

Discussion

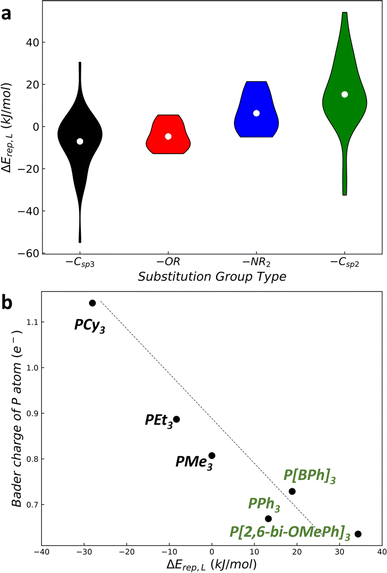
As illustrated in Fig. 4a, a violin sequence diagram illustrates the relationship between ΔE_rep(L) and different types of substitution groups. Each violin bar represents the distribution of ΔE_rep(L) values for P[G_a]₃ ligands with the same type of substitution group. Four categories of substitution groups –C_sp³R alkyl, –C_sp²R aryl, –OR alcohol, and –NR₂ amino are classified. These four categories of substitution groups exhibit distinct distributions. Alkyl groups predominate in regions of strong M–L_P interactions (ΔE_rep(L) = −40 to 15 kJ mol⁻¹), whereas aryl groups are more prevalent in areas with weaker M–L_P interactions (ΔE_rep(L) = −10 to 60 kJ mol⁻¹). Alcohol and amino groups, in contrast, occupy intermediate small regions with the ΔE_rep(L) range of approximately −13 to 10 kJ mol⁻¹ and −5 to 25 kJ mol⁻¹, respectively.

Fig. 4 The analysis of ΔE_rep(L) against different types of substitution groups. (a) The violin plot of ΔE_rep(L) against different types of substitution groups. Each violin represents the distributions of ΔE_rep(L) for the P[G_a]₃ ligands with the same type of substitution group. (b) The relationship between ΔE_rep(L) and the Bader charge on P atoms for some typical P-ligands.

By performing electronic structure analysis of P-ligands, we found that in general the more electrons on the P atom are present, the stronger the interaction between the metal and P-ligand. This can be attributed to the electron transfer from the ligand to the metal. By plotting the atomic charge (Bader charge of P) versus the ΔE_rep(L) of Pd–L_P complexes in Fig. 4b, we note that there is an inverse proportional relationship. Specifically, alkyl substituent groups such as Cy, Et, and Me (electron donors) induce a larger atomic charge on the P atom, while aryl groups such as Ph, BPh, and 2,6-bi-OMePh (electron acceptor) lead to a smaller atomic charge on the P atom. This indicates that alkyl substituent groups by donating electrons to the P atom can strengthen the metal–ligand binding. It is therefore possible to design effective ligands by utilizing their electronic structures as descriptors, as has been performed previously by other groups.¹⁰

This sequence of substitution groups can serve as a general guide for fast searching for optimal P-ligands. In reaction I–V, the active P-ligands can be broadly categorized into two groups: aryl-type P-ligands that incorporate aryl substitution groups (such as XPhos, SPhos, JohnPhos, RuPhos, CPhos, tBuXPhos, tBuBrettPhos, CataCXium POMetB, and rac-BI-DIME) and alkyl-type P-ligands composed exclusively of alkyl groups (P[Adm]₃, P[t-Bu]₃, and P[Adm][t-Bu]₂). The ΔE_rep(R) values for both aryl bromides and aryl triflates are around 5 kJ mol⁻¹, which correspond to an intermediate region in the violin sequence diagram with the presence of both aryl and alkyl groups. This explains why P-ligands of both aryl and alkyl types can exhibit exceptional catalytic performance in these reactions.

In the case of reactions VI and VII, which involve the activation of aryl chloride, the active P-ligands can be classified into four subgroups: the Buchwald-type characterized by the presence of a biphenyl group and its derivatives (L1, L3–L8, and Ph-XPhos); the CataCXium-type featuring a 1-Ph-pyrrolyl group (L2); the aryl-type with an o-OMe-Ph group (L9); and the Singer-type with a pyrazol group and its derivatives (e.g., L10 and AdBippyphos). All these P-ligands contain aryl-type substation groups to weaken the M–L interaction. This energy range aligns adeptly with the Pd-aryl chloride interaction (ΔE_rep(R) = ∼21 kJ mol⁻¹), consequently yielding a high catalytic performance in aryl chloride activation. Therefore, the distribution of ALS varies in a catalytic system depending on the specific reactants involved which should be carefully considered.

Conclusion

We have established an MPCD, featuring a meticulously designed ligand replacement energy metric that serves as a universal descriptor for characterizing metal–ligand interactions. Utilizing this energy descriptor, we have devised a strategy for predicting active P-ligands for specific target reactions, achieved through the construction of volcano plots and the delineation of ALS. It offers a quick and economical means of effectively narrowing down the P-ligand screening space, thereby enhancing catalyst design efficiency. We have effectively applied this approach to screen out a range of cost-effective P-ligands which can catalyze the SMC reaction involving aryl chloride. The MPCD will motivate synthetic chemists to perform computer-assisted interactive ligand exploration and provide new insights into relevant properties to solve a given problem.

Methods

SSW-NN simulations

Our approach for P-ligand conformer exploration is based on the recently developed SSW-NN method as implemented using the LASP code.⁴² The machine learning NN potential is generated by iterative self-learning of the plane wave density functional theory (DFT) global potential energy surface dataset generated from SSW exploration. The SSW-NN simulation can be divided into three steps: global dataset generation based on DFT calculations using selected structures from SSW simulation, NN potential fitting and SSW global optimization using NN potential. These steps are iteratively performed until the NN potential is transferable and robust enough to describe the global potential energy surface. The procedure is briefly summarized below.

At first, the global dataset is built iteratively during the self-learning of NN potential. The initial data of the global dataset comes from the DFT-based SSW simulation and all the other data are taken from NN-based SSW exploration. In order to cover all the likely compositions of M–P–C–N–O–H systems (M: Pd, Pt and Ni), SSW simulations have been carried out for different structures (including organic molecules and metal–phosphine complexes), compositions and atom numbers per unit cell. Overall, these SSW simulations generate more than 10⁷ structures on potential energy surfaces. The final global dataset that is computed from high accuracy DFT calculations contains >100 000 structures. Then, the NN potential is generated using the method introduced in our previous work.^36,57 To pursue a high accuracy for potential energy surfaces, we have adopted a large set of power-type structure descriptors, which contains 912 descriptors for every element, including 224 2-body, 508 3-body, and 180 4-body descriptors, and compatibly, the network utilized is also large involving two-hidden layers (912-50-50-1 net), equivalent to ∼290 000 network parameters in total. The min–max scaling is utilized to normalize the training data sets. Hyperbolic tangent activation functions are used for the hidden layers, while a linear transformation is applied to the output layer of all networks. The limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) method is used to minimize the loss function to match DFT energy, force and stress. The final energy and force criteria of the root mean square errors are 6.7 meVper atom and 0.19 eV Å⁻¹ respectively. Finally, SSW-NN simulations are performed on all MLPMe₃ (L: different P-ligands) structures and P-ligands to identify the most stable conformer. Thus, a large variety of structures have been obtained. All the low energy structure candidates from SSW-NN exploration are finally verified using plane wave DFT calculations and thus the energetic data reported in the work, without specifically mentioning, are from DFT.

DFT calculations

All DFT calculations are performed by using the plane wave VASP code,⁵⁸ where electron–ion interaction is represented by the projector augmented wave pseudopotential.^59,60 The exchange functional utilized is the spin-polarized GGA-PBE.⁶¹ The kinetic energy cutoff is set at 450 eV. The first Brillion zone k-point sampling utilizes the 1 × 1 × 1 gamma-centered mesh grid. The energy and force criterion for convergence of the electron density and structure optimization are set at 10⁻⁵ eV and 0.05 eV Å⁻¹, respectively.

Considering that organic calculations typically utilize programs with atomic orbitals as basis sets, we therefore choose a ∼100 M–L catalyst and compared the ΔE_rep(L) results obtained from the PBE functional with those from the B3LYP functional calculated using the Gaussian 09 package,⁵⁰ as shown in Table S7.† The geometry optimizations and single-point calculations are performed using the B3LYP functional. The SDD effective core potential method is used as the basis set for Pd, and the 6-31G(d,p) basis set is used for all other atoms (H, C, O, P and N). The mean absolute error of ΔE_rep(L) between PBE and B3LYP functionals is only 3.9 kJ mol⁻¹.

Experimental testing

All procedures were carried out under a dry and inert atmosphere using a nitrogen-filled glovebox. Aryl chloride, potassium fluoride and tetrahydrofuran (THF, SafeDry, water ≤30 ppm (by K.F.), 99.9%, stabilized with BHT, Safeseal) were purchased from Adamas. o-tolylboronic acid was purchased from Leyan. Tris-(di-benzylidene-acetone)-dipalladium(0) (Pd₂(dba)₃) was purchased from Bokachem. Unless otherwise noted, P-ligands were purchased from Bidepharm or Aladdin.

In a nitrogen-filled glovebox, p-trifluoromethylbenzyl chloride (1 mmol, 1.0 equiv) or chlorobenzene (1 mmol, 1.0 equiv), o-tolylboronic acid (2 mmol, 2.0 equiv), KF (3 mmol, 3.0 equiv), Pd₂(dba)₃ (1.5 mol%), P-ligands (6 mol%), THF 3 mL and a magnetic stir bar were added to a 10 mL Schlenk tube. The Schlenk tube was then sealed with a PTFE-lined cap, removed from the glovebox, and heated for 1 hour at 100 °C for p-trifluoromethylbenzyl chloride and for 2 hours at 100 °C for chlorobenzene. Afterwards, the reaction was stopped and diluted with ethyl acetate. The yields of biphenyls were determined by GC (Agilent 7820A with a flame ionization detector equipped with a HP-5 column) using dodecane as the calibrated internal standard. The experimental standard curves can be found in Fig. S9 and S10.†

Web application technical

The fore-end web development is based on vue.js, which is an open-source fore-end JavaScript framework with a user-friendly start and easy integration with third-party libraries. The back-end data storage is based on MySQL database software. The fore-end and back-end interface is implemented using Django, which is a free and open-source web app framework written in Python.

Data availability

All data are available within the article (and its ESI†) and from the corresponding authors upon reasonable request and can also be found at the online webpage of https://www.lasphub.com/database/#/MPCD. The software code of LASP and NN potential used within the article is available from the corresponding author upon request or on the website http://www.lasphub.com.

Author contributions

Z.-P. L. conceived the project and contributed to the design and analyses of the data. S. M. carried out most of the calculations and web app development and wrote the draft of the paper. Y. C. and L. H. performed the experimental tests. Y.-F. S. and C. S. carried out the code development. All the authors discussed the results and commented on the manuscript.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This work was supported by the National Science Foundation of China (12188101, 22203101, and 22033003), Youth Innovation Promotion Association CAS (No. 2023265) and the Science & Technology Commission of Shanghai Municipality (23ZR1476100).

References

1. T. Hayashi, Acc. Chem. Res., 2000, 33, 354–362.
2. H. Tomori, J. M. Fox and S. L. Buchwald, J. Org. Chem., 2000, 65, 5334–5341.
3. L. C. Liang, Coord. Chem. Rev., 2006, 250, 1152–1177.
4. J. Yang, J. W. Liu, H. Neumann, R. Franke, R. Jackstell and M. Beller, Science, 2019, 366, 1514–1517.
5. S. H. Newman-Stonebraker, S. R. Smith, J. E. Borowski, E. Peters, T. Gensch, H. C. Johnson, M. S. Sigman and A. G. Doyle, Science, 2021, 374, 301–308.
6. I. P. Beletskaya, F. Alonso and V. Tyurin, Coord. Chem. Rev., 2019, 385, 137–173.
7. C. A. Malapit, J. R. Bour, C. E. Brigham and M. S. Sanford, Nature, 2018, 563, 100–104.
8. N. H. Angello, V. Rathore, W. Beker, A. Wolos, E. R. Jira, R. Roszak, T. C. Wu, C. M. Schroeder, A. Aspuru-Guzik, B. A. Grzybowski and M. D. Burke, Science, 2022, 378, 399–405.
9. D. J. Durand and N. Fey, Acc. Chem. Res., 2021, 54, 837–848.
10. D. J. Durand and N. Fey, Chem. Rev., 2019, 119, 6561–6594.
11. N. Fey, A. G. Orpen and J. N. Harvey, Coord. Chem. Rev., 2009, 253, 704–722.
12. N. Fey, Dalton Trans., 2010, 39, 296–310.
13. N. Fey, M. F. Haddow, J. N. Harvey, C. L. McMullin and A. G. Orpen, Dalton Trans., 2009, 8183–8196.
14. T. Gensch, G. D. Gomes, P. Friederich, E. Peters, T. Gaudin, R. Pollice, K. Jorner, A. Nigam, M. Lindner-D'Addario, M. S. Sigman and A. Aspuru-Guzik, J. Am. Chem. Soc., 2022, 144, 1205–1217.
15. T. Gensch, S. R. Smith, T. J. Colacot, Y. N. Timsina, G. L. Xu, B. Glasspoole and M. S. Sigman, ACS Catal., 2022, 12, 7773–7780.
16. C. A. Tolman, Chem. Rev., 1977, 77, 313–348.
17. H. Clavier, A. Correa, L. Cavallo, E. C. Escudero-Adán, J. Benet-Buchholz, A. M. Z. Slawin and S. P. Noaln, Eur. J. Inorg. Chem., 2009, 1767–1773.
18. F. Weinhold, J. Comput. Chem., 2012, 33, 2363–2379.
19. Z. L. Niemeyer, A. Milo, D. P. Hickey and M. S. Sigman, Nat. Chem., 2016, 8, 611–618.
20. S. H. Newman-Stonebraker, J. Y. Wang, P. D. Jeffrey and A. G. Doyle, J. Am. Chem. Soc., 2022, 144, 1205–1217.
21. M. Busch, M. D. Wodrich and C. Corminboeuf, Chem. Sci., 2015, 6, 6754–6761.
22. M. D. Wodrich, B. Sawatlon, M. Busch and C. Corminboeuf, Acc. Chem. Res., 2021, 54, 1107–1117.
23. M. D. Wodrich, M. Busch and C. Corminboeuf, Chem. Sci., 2016, 7, 5723–5735.
24. L. C. Yang and X. Hong, Dalton Trans., 2020, 49, 3652–3657.
25. W. Matsuoka, Y. Harabuchi and S. Maeda, ACS Catal., 2022, 12, 3752–3766.
26. Y. Guan, V. M. Ingman, B. J. Rooks and S. E. Wheeler, J. Chem. Theory Comput., 2018, 14, 5249–5261.
27. A. R. Rosales, J. Wahlers, E. Limé, R. E. Meadows, K. W. Leslie, R. Savin, F. Bell, E. Hansen, P. Helquist, R. H. Munday, O. Wiest and P.-O. Norrby, Nat. Catal., 2018, 2, 41–45.
28. S. M. Maley, D. H. Kwon, N. Rollins, J. C. Stanley, O. L. Sydora, S. M. Bischof and D. H. Ess, Chem. Sci., 2020, 11, 9665–9674.
29. R. N. Straker, Q. Peng, A. Mekareeya, R. S. Paton and E. A. Anderson, Nat. Commun., 2016, 7, 10109.
30. M. C. Nielsen, K. J. Bonney and F. Schoenebeck, Angew. Chem., Int. Ed., 2014, 53, 5903–5906.
31. S. Ahn, M. Hong, M. Sundararajan, D. H. Ess and M. H. Baik, Chem. Rev., 2019, 119, 6509–6560.
32. T. Sperger, I. A. Sanhueza and F. Schoenebeck, Acc. Chem. Res., 2016, 49, 1311–1319.
33. S. E. Wheeler, Acc. Chem. Res., 2013, 46, 1029–1038.
34. C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 1838–1845.
35. C. Shang, X.-J. Zhang and Z.-P. Liu, Phys. Chem. Chem. Phys., 2014, 16, 17845–17856.
36. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
37. B. G. Sumpter and D. W. Noid, Chem. Phys. Lett., 1992, 192, 455–462.
38. T. H. Fischer, W. P. Petersen and H. P. Lüthi, J. Comput. Chem., 1995, 16, 923–936.
39. L. Raff, M. Malshe, M. Hagan, D. Doughan, M. Rockley and R. Komanduri, J. Chem. Phys., 2005, 122, 084104.
40. S. Manzhos, X. Wang, R. Dawes and T. Carrington, J. Phys. Chem. A, 2006, 110, 5295–5304.
41. K. Ohno and S. Maeda, Chem. Phys. Lett., 2004, 384, 277–282.
42. S. D. Huang, C. Shang, P. L. Kang, X. J. Zhang and Z. P. Liu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, e1415.
43. S. Ma, S.-D. Huang, Y.-H. Fang and Z.-P. Liu, ACS Catal., 2018, 8, 9711–9721.
44. S. Ma, S.-D. Huang and Z.-P. Liu, Nat. Catal., 2019, 2, 671–677.
45. S. Ma, C. Shang, C.-M. Wang and Z.-P. Liu, Chem. Sci., 2020, 11, 10113–10118.
46. P. L. Kang, C. Shang and Z. P. Liu, J. Am. Chem. Soc., 2019, 141, 20525–20536.
47. S. Ma and Z.-P. Liu, Nat. Commun., 2022, 13, 1–8.
48. S. Ma, C. Shang and Z.-P. Liu, J. Chem. Phys., 2019, 151, 050901.
49. J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078.
50. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, 9, 2009.
51. J. Xu, R. Y. Liu, C. S. Yeung and S. L. Buchwald, ACS Catal., 2019, 9, 6461–6466.
52. J. P. Stambuli, S. R. Stauffer, K. H. Shaughnessy and J. F. Hartwig, J. Am. Chem. Soc., 2001, 123, 2677–2678.
53. J. D. Zhang, A. Bellomo, A. D. Creamer, S. D. Dreher and P. J. Walsh, J. Am. Chem. Soc., 2012, 134, 13765–13772.
54. W. Shen, Tetrahedron Lett., 1997, 38, 5575–5578.
55. R. M. Oechsner, J. P. Wagner and I. Fleischer, ACS Catal., 2022, 12, 2233–2243.
56. M. Wakioka, K. Hatakeyama, S. Sakai, T. Seki, K.-i. Tada, Y. Mizuhata, T. Nakazato, S. Koguchi, Y. Shibuya, Y. Maruyama and M. Ayabe, Organometallics, 2023, 42, 3454–3465.
57. S.-D. Huang, C. Shang, X.-J. Zhang and Z.-P. Liu, Chem. Sci., 2017, 8, 6327–6337.
58. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
59. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
60. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
61. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc02327g

‡ These authors contributed equally to this work.

---