Open Access Article
Open Access ArticleConstruction of intermolecular σ-hole interactions in rare earth metallocene complexes using a 2,3,4,5-tetraiodopyrrolyl anion†
Francis
Delano
IV
 a,
Florian
Benner
a,
Florian
Benner
 a,
Seoyun
Jang
a,
Seoyun
Jang
 a,
Samuel M.
Greer
a,
Samuel M.
Greer
 b and
Selvan
Demir
b and
Selvan
Demir
 *a
*a
aDepartment of Chemistry, Michigan State University, 578 South Shaw Lane, East Lansing, Michigan 48824, USA. E-mail: sdemir@chemistry.msu.edu
bLos Alamos National Laboratory (LANL), Los Alamos, New Mexico 87545, USA
First published on 26th July 2024
Abstract
The generation of noncovalent intermolecular interactions represents a powerful method to control molecular vibrations and rotations. Combining these with the axial ligand field enforced by the metallocene ligand scaffold provides a dual-pronged approach in controlling the magnetic-relaxation pathways for dysprosium-based single-molecule magnets (SMMs). Here, we present the first implementation of 2,3,4,5-tetraiodopyrrole (TIPH) in its anionic form [TIP]− as a ligand in three isostructural rare-earth metal complexes Cp*2RE(TIP) (1-RE, RE = Y, Gd, and Dy; Cp* = pentamethylcylopentadienyl), where the TIP ligand binds through the nitrogen and one iodine atom κ2(N,I) to the metal centre. The shallow potential energy surface of the intermolecular σ-hole interaction yields distortions of the interatomic distances at elevated temperatures which were investigated by variable-temperature SCXRD. 1-RE constitute the first crystallographically characterized molecules containing TIP as a ligand for any metal ion, and 1-Dy is the first SMM that employs the TIP ligand. The structural dependence on temperature allowed the mechanism of magnetic relaxation to be explored through ab initio calculations at different temperatures. The electronic influence of the coordinated iodine substituent was probed via magnetometry and cw-EPR spectroscopy on 1-Gd. To further scrutinize the impact of the iodine substituents on the physical properties, a second set of new complexes Cp*2RE(DMP) (2-RE, RE = Y, and Dy) where DMP = 2,5-dimethylpyrrolyl were synthesized. Here, the DMP ligand binds similarly to the TIP ligand and represents an all-hydrocarbon analogue to 1-RE. 2-Dy constitutes the first SMM bearing a DMP ligand.
Introduction
Anionic heterocyclic rings represent attractive ligands for the generation of rare earth (RE) metal complexes, as they are typically isoelectronic to the ubiquitous cyclopentadienyl ligand. RE complexes bearing five-membered heterocyclic rings are rarer relative to the all-hydrocarbon analogues. The isolated examples comprise borolyl,1,2 silolyl,3 germolyl,3,4 plumbolyl,5 phospholyl,6–9 arsolyl10 and bismolyl11 anions. Thus, exploring the interactions of substituted five-membered heterocyclic ligands with the RE metals represents a fundamental frontier of research as the synthetic strategies for the generation of substituted heterocyclic rings are typically well-investigated.12–14 Recently, other pentadentate organometallic ligands such as carborane ligands have also been employed to construct dysprosium single-molecule magnets.15–17The generation of noncovalent inter- and intramolecular interactions represents a powerful tool for (supra)molecular chemistry and crystal engineering.18 Halogen bonding originates from a net attractive interaction between a charge depleted region of a halogen atom and a nucleophilic region of a molecule or molecular fragment.19 σ-holes, or areas of positive electrostatic potential along the extensions of covalently bonded halogen atoms, stem from the charge density anisotropy of the heavy halogens. Consequently, negative electrostatic potential accumulate on the equatorial regions of the atom.20 This phenomenon is typically observed for the heavy halogen atoms due to the increased polarizability ascribed to the larger ionic radii. Intermolecular interactions of this class have garnered enormous attention in supramolecular chemistry and related fields.21
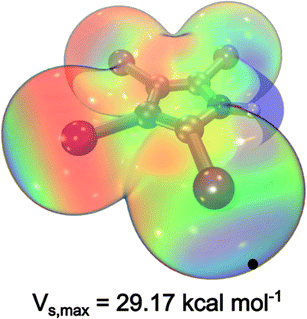
Our search for ligand scaffolds suitable for fostering halogen bonding stabilization interaction led to the attractive 2,3,4,5-tetraiodopyrrole ligand (TIPH), Fig. 1. Excitingly, its electrostatic potential map reveals a region of depleted electron density, a key observable of σ-holes.19 Generally, the positive extrema of the electrostatic potential, Vs,max, corresponds to the location of the σ-hole.20 Notably, co-crystals containing TIPH and tetraphenylphosphonium iodide, tri(n-propyl)ammonium or 1,3,5-trimethylpyridinium iodide exhibit short I⋯TIP interatomic distances,22,23 indicative of halogen bonding. Discrete installation of both halogen atoms and halogen-containing substituents has enabled a controlled design of catalysts and supramolecular structures. Remarkably, halogen bonding interactions were integral for the production of molecular motors and catalysts,24 by helping maintain a specific geometry that best favours the rotational behaviour of said molecule.
We are intrigued to implement non-covalent interactions in the realm of the rare earth (RE) metals, using TIP, which is hitherto unexplored in coordination chemistry at large. In particular, our interest is to generate new single-molecule magnets (SMMs) featuring such non-covalent interactions and study their impact on the mechanism of magnetic relaxation.
Albeit its scarce use, TIPH is an intriguing molecule that was first discovered by Ciamician and Dennstedt in 1882.25 The molecule itself is generally stable, however decomposes releasing I2 at elevated temperatures (140–150 °C). As such, TIPH represents a promising material as an agent defeat weapon,26 a molecule designed to destroy or neutralize active agents by releasing large amounts of biocides such as I2 after detonation, owing to its inherent high iodine content, and impact sensitivity.
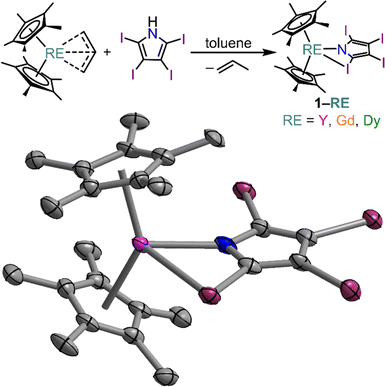
Herein, the synthesis and characterization of three unprecedented mononuclear yttrium, gadolinium, and dysprosium tetraiodopyrrole complexes Cp*2RE(TIP) (1-RE, RE = Y, Gd, and Dy; Cp* = pentamethylcyclopentadienyl, TIP = 2,3,4,5-tetraiodopyrrolyl) are presented. The three isostructural complexes represent the first crystallographically characterized compounds containing TIP as a ligand for any metal ion. Noteworthy, the TIP ligand formally binds κ2(N,I) to the metal centre involving both the nitrogen atom and the iodine atom of the 2-position of the heterocyclic ring. This binding motif was unambiguously confirmed through single-crystal X-ray diffraction (SCXRD) analysis and density functional theory calculations. As intermolecular halogen-bonding interactions may be prone to depend strongly on temperature,27,28 the structure of 1-Dy was thoroughly examined through variable temperature SCRXD. This strong intermolecular interaction manifests itself in a significant distortion to the primary crystal field of the DyIII ion, as a result of the elongation of the intermolecular I⋯I interactions over the investigated temperature range. Excitingly, The DyIII congener, 1-Dy, displays out-of-phase components of the ac magnetic susceptibility, indicative of slow magnetic relaxation. The observed structural distortions with respect to temperature affords the opportunity to investigate how small alterations to the Dy–I distance influences the mechanism of magnetic relaxation through ab initio calculations at three different temperatures. Additionally, the electronic structure of 1-Gd was probed through both magnetometry and cw-EPR spectroscopy, in order to assess the influence of the proximal iodine atom on the electronic structure of the GdIII centre. The analogous 2,5-dimethylpyrrolyl complexes Cp*2RE(DMP) (2-RE, RE = Y, Dy, DMP = 2,5-dimethylpyrrolyl) were additionally isolated. Here, the DMP ligand binds in a similar fashion to the tetraiodopyrrole ligand and represent excellent hydrocarbon analogues to the halogen substituted complexes.
Experimental methods
General information
All manipulations described below were performed under an inert N2 or Ar atmosphere with rigorous exclusion of oxygen and moisture using Schlenk and glovebox techniques, unless otherwise noted. House nitrogen was purified through a MBraun HP-500-MO-OX gas purifier prior to use. Toluene was dried by refluxing over potassium and distilled prior to use. The absence of water and oxygen was confirmed by testing with a drop of potassium benzophenone radical solution in the glovebox. Dichloromethane was dried by refluxing over calcium hydride and distilled prior to use. Potassium bis(trimethylsilylamide), K[N(SiMe3)2], was purchased from Sigma-Aldrich, dissolved in toluene at 90 °C and subsequently recrystallized at −35 °C. Pentamethylcyclopentadiene (HCp*) and H-2,5-dimethylpyrrole were purchased from Sigma-Aldrich and was dried over 4 Å sieves prior to use. Anhydrous rare earth chlorides (RECl3, RE = Y, Gd, and Dy), 28–30% NH4OH solution, and allylmagnesium chloride (2.0 M in THF) were purchased from Sigma-Aldrich and used as received. I2 was purchased from Alfa-Aesar and purified by sublimation prior to use. H-pyrrole was purchased from Alfa-Aesar and dried over 4 Å molecular sieves prior to use. KCp* and K[DMP] were synthesized by deprotonation of HCp* and DMPH with K[N(SiMe3)2], respectively.29 A similar synthetic approach has been used for the synthesis of Li[DMP].30 Cp*2RE(η3-C3H5) (RE = Y, Gd, and Dy) and Cp*2RE(BPh4) (RE = Y, and Dy) were prepared according to literature procedures.31,32 IR spectra were collected on solid crystalline samples with an Agilent Cary 630 FTIR spectrometer. UV-vis spectra were taken on an Agilent Cary 60 instrument, in 1 cm cuvette cells equipped with Schlenk adaptors. A PerkinElmer 2400 Series II CHNS/O analyser was used for CHN elemental analyses. All NMR spectra were recorded on a Bruker Avance NEO 500 MHz spectrometer in toluene-d8. NMR samples were prepared under an argon atmosphere and sealed using J-Young tubes. Chloroform-d and DMSO-d6 were purchased from Cambridge Isotope Lab. Toluene-d8 was purchased from Sigma-Aldrich and was subsequently dried over a sodium–potassium alloy and filtered prior to use. Chloroform-d was dried over 4 Å molecular sieves prior to use.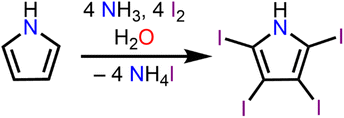 | (1) |
X-ray crystallography
Data were collected on a XtaLAB Synergy, Dualflex, HyPix diffractometer using Cu or Mo Kα radiation. Plate-shaped crystals with dimensions 0.2 × 0.14 × 0.06, 0.38 × 0.22 × 0.08, and 0.353 × 0.275 × 0.111 mm3 for 1-Y, 1-Gd, and 1-Dy and block-shaped crystals with dimensions of 0.524 × 0.329 × 0.196, and 0.283 × 0.174 × 0.138 mm3 for 2-Y and 2-Dy respectively, were suspended in n-paratone oil and mounted on a nylon loop. The temperature was controlled using an Oxford Cryosystems low-temperature device. The structural refinement parameters for 1-RE and 2-RE are provided in Tables S1–S9.†The data collection strategy, unit cell determination, and data reduction were performed by the CrysAlisPro software,33 which corrects for Lorentz-polarization. Absorption effects were accounted for through use of a numerical absorption correction based on Gaussian integration over a multifaceted crystal model using spherical harmonics implemented in the SCALE3 ABSPACK34 scaling algorithm.
The structure of 1-RE and 2-RE were solved in the space group P21/c by using dual methods with the ShelXT35 and refined by least squares using version 20189/2 of XL36 incorporated in Olex2.37 All non-hydrogen atoms were refined anisotropically. Hydrogen atom positions were calculated geometrically and refined using the riding model.
Synthesis of tetraiodopyrrole (TIPH)
The synthesis of TIPH was performed under aerobic condition (thus, without the precautions of an inert atmosphere) following a literature procedure, eqn (1).38 6.0 mL of 28–30% NH4OH was diluted with 25 mL of H2O and cooled to −78 °C in a 250 mL round bottom flask. To this, 667.0 mg (9.94 mmol) of H-pyrrole and 1.762 g (10.61 mmol) of KI was added. 10.112 g (39.83 mmol) of I2 was dissolved in 75 mL of EtOH and added dropwise to the stirring pyrrole solution at −78 °C. The reaction was allowed to proceed under darkness at −78 °C. After 1 h, the light-brown reaction mixture was warmed up to room temperature and the product was precipitated by addition of 200 mL of H2O and subsequently isolated by filtration. The crude solids were collected and dissolved in 12 mL EtOH. The ethanol solution was brought to a boil and 50 mg of activated charcoal was added. The mixture was allowed to heat for 1 h, and then filtered into a cold KI solution (0 °C, 207 mg, 1.25 mmol, 200 mL). The final product was isolated as a white solid from filtration of the KI/TIPH mixture in 30% yield (1.696 g, 2.97 mmol). Anal. calcd for C4HNI4: C 8.42, H 0.18, N 2.45. Found: C 8.71, H 0.31, N 2.46. 1H (500 MHz, ppm, DMSO-d6, 25 °C) δ 12.35 (s, 1H,![[H with combining low line]](https://www.rsc.org/images/entities/i_char_0048_0332.gif) NC4I4). 13C (126 MHz, ppm, DMSO-d6, 25 °C) δ 87.25 (N
NC4I4). 13C (126 MHz, ppm, DMSO-d6, 25 °C) δ 87.25 (N![[C with combining low line]](https://www.rsc.org/images/entities/i_char_0043_0332.gif) 4H4), 80.34 (N
4H4), 80.34 (N![[C with combining low line]](https://www.rsc.org/images/entities/i_char_0043_0332.gif) 4H4). (ATR, cm−1) 3379s, 3360m, 2846w, 1469m, 1383m, 1333w, 1282m, 1224m, 1207w, 1005m, 941s, 911w, 842w.
4H4). (ATR, cm−1) 3379s, 3360m, 2846w, 1469m, 1383m, 1333w, 1282m, 1224m, 1207w, 1005m, 941s, 911w, 842w.
Synthesis of Cp*2Y(TIP), 1-Y
405.8 mg (1.01 mmol) of Cp*2Y(C3H5) was dissolved in 3 mL of toluene in a 20 mL scintillation vial and subsequently, cooled to −78 °C. To this, 577.3 mg (1.01 mmol) of TIPH was added. The total volume of toluene was increased to 8 mL and the reaction was allowed to proceed at −78 °C, causing the initial yellow coloured mixture to turn green. After three hours, the green reaction was allowed to warm to room temperature, accompanied by the formation of a yellow-green precipitate. The toluene was removed under reduced pressure to yield a yellow-green solid. Yellow crystals of Cp*2Y(TIP), 1-Y, suitable for single-crystal X-ray diffraction analysis were obtained at −35 °C from a concentrated dichloromethane solution in 56% crystalline yield (575.4 mg, 0.57 mmol). 1-Y crystallized with one CH2Cl2 molecule in the unit cell. 1H NMR (500 MHz, ppm, chloroform-d, 25 °C) δ 2.00 (s, 30H,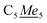 ). 13C NMR (126 MHz, ppm, chloroform-d, 25 °C) δ 121.48, (
). 13C NMR (126 MHz, ppm, chloroform-d, 25 °C) δ 121.48, (![[C with combining low line]](https://www.rsc.org/images/entities/i_char_0043_0332.gif) 5Me5), 82.55, 82.33 (TIP), 12.23
5Me5), 82.55, 82.33 (TIP), 12.23 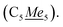 Anal. calcd for C24H30NI4Y·CH2Cl2: C 29.61, H 3.18, N 1.38. Found: C 29.61, H 3.05, N 1.37. (ATR, cm−1) 2898m, 1853m, 1429m, 1413w, 1377m, 1367w, 1356m, 1246w, 1213s, 1190s, 1163s, 1017m, 943s, 924s, 892w, 724s, 693s. Note for 1-Y: the initial precipitation of the yellow-green solid during warm-up of the reaction from −78 °C to room temperature, was additionally isolated through centrifugation in one event for further investigation. The solid amounted to approximately 76% crude yield, and both 1H NMR studies on the solid as well as single-crystals grown from this solid unambiguously have proven it to be 1-Y.
Anal. calcd for C24H30NI4Y·CH2Cl2: C 29.61, H 3.18, N 1.38. Found: C 29.61, H 3.05, N 1.37. (ATR, cm−1) 2898m, 1853m, 1429m, 1413w, 1377m, 1367w, 1356m, 1246w, 1213s, 1190s, 1163s, 1017m, 943s, 924s, 892w, 724s, 693s. Note for 1-Y: the initial precipitation of the yellow-green solid during warm-up of the reaction from −78 °C to room temperature, was additionally isolated through centrifugation in one event for further investigation. The solid amounted to approximately 76% crude yield, and both 1H NMR studies on the solid as well as single-crystals grown from this solid unambiguously have proven it to be 1-Y.
Synthesis of Cp*2Gd(TIP), 1-Gd
Following the synthetic procedure for 1-Y, 1-Gd (143.0 mg) was crystallized from dichloromethane solution at −35 °C in 43% crystalline yield (0.13 mmol). 1-Gd is isostructural to 1-Y and crystallized with one CH2Cl2 molecule in the unit cell. Used masses: Cp*2Gd(C3H5) (140.9 mg, 0.30 mmol), TIPH (173.9 mg, 0.30 mmol). Anal. Calcd for C24H30NI4Gd·CH2Cl2: C 27.74, H 2.98, N 1.29. Found: C 27.60, H 3.00, N 1.30. (ATR, cm−1) 2888m, 2851m, 1444m, 1414w, 1379m, 1366w, 1355m, 1261m, 1213s, 1180s, 1019m, 943s, 922s, 736s, 704s, 688s.Synthesis of Cp*2Dy(TIP), 1-Dy
Following the synthetic procedure for 1-Y, 1-Dy (251.0 mg) was crystallized as yellow crystals from dichloromethane solution at −35 °C in 47% crystalline yield (0.23 mmol). 1-Dy is isostructural to 1-Y and 1-Gd and crystallized with one CH2Cl2 molecule in the unit cell. Used masses: Cp*2Dy(C3H5) (231.8 mg, 0.49 mmol), TIPH (280.2 mg, 0.49 mmol). Anal. calcd for C24H30NI4Dy·CH2Cl2: C 27.61, H 2.97, N 1.29. Found: C 27.09, H 3.08, N 1.30. (ATR, cm−1) 2892m, 2851m, 1429m, 1412w, 1377m, 1366w, 1354m, 1211w, 1189s, 1179s, 1162s, 1017m, 943s, 922s, 890w, 725s, 693s.Synthesis of Cp*2Y(DMP), 2-Y
In a 20 mL scintillation vial, 22.4 mg (0.16 mmol) of K[DMP] was added to a stirring 16 mL Et2O solution containing 105.5 mg (0.16 mmol) of Cp*2Y(BPh4). After addition of K[DMP], 4 mL of Et2O was added, increasing the total volume of the reaction to 20 mL. The reaction mixture was allowed to stir at room temperature for 1 h, concurrent with the production of a white precipitate, presumably KBPh4. The cloudy reaction mixture was centrifuged, and the supernatant was filtered through a Celite plug. The toluene was removed under reduced pressure, yielding an oily solid which was redissolved in 4 mL of n-hexane. The resulting, yellow-coloured solution contained white particulates which were removed via filtration through a Kimwipe plug. All hexane was removed in vacuo give a crystalline solid. Yellow crystals of Cp*2Y(DMP), 2-Y, suitable for single-crystal X-ray diffraction analysis were grown from concentrated n-hexane solution at −35 °C in 42% crystalline yield (29.9 mg, 0.07 mmol). 1H NMR (500 MHz, ppm, toluene-d8, 25 °C) δ 1.79 (s, 30H,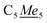 ), 2.04 (s, 6H,
), 2.04 (s, 6H, 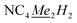 ), 6.26 (s, 2H, NC4Me2
), 6.26 (s, 2H, NC4Me2![[H with combining low line]](https://www.rsc.org/images/entities/i_char_0048_0332.gif) 2). 13C{1H} NMR (126 MHz, ppm, toluene-d8, 25 °C) δ 120.45, (
2). 13C{1H} NMR (126 MHz, ppm, toluene-d8, 25 °C) δ 120.45, (![[C with combining low line]](https://www.rsc.org/images/entities/i_char_0043_0332.gif) 5Me5), 109.33 (N
5Me5), 109.33 (N![[C with combining low line]](https://www.rsc.org/images/entities/i_char_0043_0332.gif) 4Me2H2), 108.04 (N
4Me2H2), 108.04 (N![[C with combining low line]](https://www.rsc.org/images/entities/i_char_0043_0332.gif) 4Me2H2), 9.25–12.24 (q, 1JC–H: 125.83 Hz,
4Me2H2), 9.25–12.24 (q, 1JC–H: 125.83 Hz, 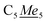 ), 15.00–17.92 (q, 1JC–H: 121.90 Hz,
), 15.00–17.92 (q, 1JC–H: 121.90 Hz,  ). Anal. calcd for C26H38NY: C 68.86, H 8.45, N 3.09. Found: C 68.48, H 8.81, N 3.05. (ATR, cm−1) 3083w, 2965w, 2902m, 2858m, 2719w, 1484w, 1433m, 1373m, 1307w, 1254m, 1051w, 1021w, 949w, 745s.
). Anal. calcd for C26H38NY: C 68.86, H 8.45, N 3.09. Found: C 68.48, H 8.81, N 3.05. (ATR, cm−1) 3083w, 2965w, 2902m, 2858m, 2719w, 1484w, 1433m, 1373m, 1307w, 1254m, 1051w, 1021w, 949w, 745s.
Synthesis of Cp*2Dy(DMP), 2-Dy
Following the synthetic procedure for 2-Y, yellow crystals of 2-Dy (23.4 mg, 0.04 mmol) were crystallized from n-hexane solution at −35 °C in 37% crystalline yield. Used masses: Cp*2Dy(BPh4) (64.0 mg, 0.09 mmol), K[DMP] (11.6 mg, 0.09 mmol). Anal. calcd for C26H38NDy: C 59.25, H 7.27, N 2.66. Found: C 58.92, H 7.66, N 2.65. (ATR, cm−1) 3081w, 2964w, 2901m, 2855m, 2718w, 1486w, 1432m, 1371m, 1305w, 1253m, 1051w, 1020w, 948w, 743s.Magnetic measurements
Magnetic data were collected on a Quantum Design MPMS3 SQUID magnetometer. Polycrystalline Cp*2Gd(TIP) (1-Gd), Cp*2Dy(TIP) (1-Dy), and Cp*2Dy(DMP) (2-Dy) were first dried under high vacuum, and then 25.3 mg (0.02 mmol), 16.8 mg (0.02 mmol) and 12.3 mg (0.02 mmol) respectively, were immobilized with molten eicosane (60 °C) prior to the experiment. After ensuring an airtight seal, the sample was transferred out of the glovebox and mounted onto the SQUID sample holder.Dc magnetic susceptibility data were collected at temperatures ranging from 2 to 300 K. Ac magnetic susceptibility data were collected under a 3 Oe oscillating magnetic field. All data were corrected for diamagnetic contributions from the eicosane and core diamagnetism estimated using Pascal's constants.39 The molar masses used to work up the raw magnetic data for all compounds are based on the molar mass determined by single-crystal X-ray diffraction study and matching elemental analysis.
Continuous wave electron paramagnetic resonance spectroscopy
Continuous-wave X-band EPR spectra were recorded at 5 K using a Bruker Elexsys E500 spectrometer. Temperature control was provided by a Lakeshore temperature controller and an ESR 900 cryostat in combination with a ColdEdge Stinger system. All simulations of EPR spectra were performed using EasySpin.40Computational methods
The pKa values of H-tetraiodopyrrole, H-pyrrole, and H-2,5-dimethylpyrrole were evaluated based on a theoretical proton transfer reaction between the protonated heterocycle and one water molecule using the computational derived thermodynamic parameters. The effectiveness of this method has previously been shown in a series of carboxylic acids.41 H-tetraiodopyrrole, H-pyrrole, H-2,5-dimethylpyrrole, H2O, and H3O+ were calculated at the def2-TZVP level,42 retrieved through Basis Set Exchange,43 employing the CAMB3LYP functional.44 A 28 electron in-core pseudo potential was used for the iodine substituents of the TIP ligand.45 To account for the effects of solvation, a CPCM (H2O) solvent model was included.46,47 Further details are provided in the ESI.†The electronic structure of 1-Y and 2-Y were studied by density functional theory (DFT) calculations through use of the Gaussian software suite.48 A suitable functional for the characterization of 1-Y and 2-Y was determined through comparison of the experimental and computed bond metrics of various functionals employing the def2-SVP basis set, Tables S26, S27 and S30, S31.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42,49 It was determined that the hybrid meta-GGA functional TPSSh, most accurately described the structure of 1-Y, and thus, a final geometry optimization was performed using the larger def2-TZVP functional on all atoms, as well as a 28 in-core electron pseudopotential (ECP28MDF45) and GD3 (ref. 50 and 51) empirical dispersion correction on both the central Y ion, as well as the ancillary iodine substituents. TDDFT calculations were conducted on the optimized structure of 1-Y for 50 excited states on the def2-TZVP/ECP28MDF(Y,I) level of theory using the TPSSh functional with GD3 dispersion correction. A CPCM implicit solvent model for dichloromethane was included.46,47 In the case of 2-Y, multiple functionals accurately predicted the experimentally determined geometry, Tables S30 and S31.† Owing to the success of the TPSSh functional in the optimization of 1-Y, the final geometry of 2-Y was also completed using this description. Final optimizations were performed employing the very-tight optimization criteria. The minimum structures were confirmed through analytical frequency calculations. One small, imaginary frequency (10i cm−1) was found for 1-Y, owing to the flat potential energy surface regarding the rotation of the [Cp*]− ligands. This phenomenon has also been observed in similar RE metal organometallic complexes, and is considered benign if the frequency in question does not concern the atoms of interest.52 The bonding situation of 1-Y and 2-Y were investigated through a natural localized molecular orbital (NLMO)53 analysis, at def2-TZVP/ECP28MDF(Y,I) level of theory using the TPSSh functional with GD3 dispersion correction. The relevant donor/acceptor NLMO interactions are provided in Tables S29 and S32,† respectively. Only strongest interactions between the pyrrolyl ligand and metal ion are depicted (>1 kcal mol−1).
42,49 It was determined that the hybrid meta-GGA functional TPSSh, most accurately described the structure of 1-Y, and thus, a final geometry optimization was performed using the larger def2-TZVP functional on all atoms, as well as a 28 in-core electron pseudopotential (ECP28MDF45) and GD3 (ref. 50 and 51) empirical dispersion correction on both the central Y ion, as well as the ancillary iodine substituents. TDDFT calculations were conducted on the optimized structure of 1-Y for 50 excited states on the def2-TZVP/ECP28MDF(Y,I) level of theory using the TPSSh functional with GD3 dispersion correction. A CPCM implicit solvent model for dichloromethane was included.46,47 In the case of 2-Y, multiple functionals accurately predicted the experimentally determined geometry, Tables S30 and S31.† Owing to the success of the TPSSh functional in the optimization of 1-Y, the final geometry of 2-Y was also completed using this description. Final optimizations were performed employing the very-tight optimization criteria. The minimum structures were confirmed through analytical frequency calculations. One small, imaginary frequency (10i cm−1) was found for 1-Y, owing to the flat potential energy surface regarding the rotation of the [Cp*]− ligands. This phenomenon has also been observed in similar RE metal organometallic complexes, and is considered benign if the frequency in question does not concern the atoms of interest.52 The bonding situation of 1-Y and 2-Y were investigated through a natural localized molecular orbital (NLMO)53 analysis, at def2-TZVP/ECP28MDF(Y,I) level of theory using the TPSSh functional with GD3 dispersion correction. The relevant donor/acceptor NLMO interactions are provided in Tables S29 and S32,† respectively. Only strongest interactions between the pyrrolyl ligand and metal ion are depicted (>1 kcal mol−1).
The magnetic properties of 1-Dy and 2-Dy were calculated via a complete active space self-consistent field (CASSCF) +N-valence perturbation theory (NEVPT2) approach implemented in the ORCA 5.0.4 package.54,55
Results and discussion
Synthesis and structural characterization
The development of materials featuring non-covalent interactions is currently of large interest given the desire to promote stability and the appearance of unique physical and chemical properties of new crystal forms. Halogen bonding, a subset of the σ-hole interactions, is particularly intriguing as many covalently bonded halogens have regions of positive electrostatic potential along the axes of the covalent bond.To implement these interactions into crystals containing bis-cyclopentadienyl scaffolds containing rare-earth centres, we turned to the halogenated heterocycle 2,3,4,5-tetraiodopyrrole. Complexes innate to tetraiodopyrrole ligands are unknown, rendering them intriguing synthetic targets for the development of new multifunctional materials. The synthesis of 2,3,4,5-tetraiodopyrrole (TIPH) was first described in 1882,25eqn (1), and has since been investigated in the development of building blocks for halogen bond-assisted supramolecular structures.23
The installation of RE metallocene units into larger molecules benefits from the isolation of materials that have prolific use in various applications such as in catalysis and magnetism.56,57 An attractive synthetic strategy utilizes allylic complexes Cp*2RE(η3-C3H5), where the allyl component can readily extrude the relatively inert propene gas by adding an acidic proton. The use of this particular driving force has been demonstrated for RE and other early transition metals giving rise to both mono- and multi-nuclear complexes including, Cp*2Y(NH2)THF, [Cp′2Zr(μ3-S)DyCp*2]2, [Cp*2Dy(μ-CNC6H4O-κC:κO)]2,58 [((η5-Cp*)2RE)2(μ-1η2-pyr-2κN)(μ-2η2-pyr-1κN)],59 and dinuclear complexes in the presence of H2.60,61
Capitalizing on this fruitful synthetic approach, the bis(pentamethylcyclopentadienyl) RE tetraiodopyrrole complexes Cp*2RE(TIP), 1-RE, (RE = Y (1-Y), Gd (1-Gd), and Dy (1-Dy)) were isolated from a protonolysis reaction of H-tetraiodopyrrole and the respective RE allyl complexes in toluene, Fig. 2. Notably, 1-RE is poorly soluble in toluene, causing it to precipitate as a yellow-green solid as the reaction progresses (where the isolated solid amounted to approximately 76% crude yield for 1-Y). Yellow crystals suitable for single-crystal X-ray diffraction analysis were grown from concentrated dichloromethane solution at −35 °C in 56, 43, and 47% crystalline yields, for 1-Y, 1-Gd, and 1-Dy, respectively. All three complexes are isostructural and crystalize in the space group P21/c with four molecules in the unit cell, Fig. S8.† In all cases the first coordination sphere of the eight-coordinate metal centre is comprised of two pentamethylcyclopentadienyl ligands, the nitrogen and one iodine atom of the TIP ligand.
In order to assess the influence of the ancillary iodine atoms we pursued the synthesis of an all-hydrocarbon alternative in the first coordination sphere. For this, we turned to 2,5-dimethylpyrrole (DMPH). Here, the differing substitution has a dramatic influence on the basicity of the N-atom of the heterocycle. In order to estimate the pKa of the TIPH, pyrrole, and DMPH ligands, we computationally determined the thermodynamic parameters for the proton transfer reaction between the heterocycle and one water molecule. This approach has been described in the estimation of pKa for several carboxylic acids.41,62 The relevant thermodynamic values are provided in Tables S24 and S25,† resulting in estimated pKa values of 6.19, 21.10, and 23.45 for TIPH, H-pyrrole, and H-2,5-dimethylpyrrole respectively. Interestingly, when DMPH is reacted directly with Cp*2RE(η3-C3H5) no reaction is observed likely because of the decreased acidity of the N-proton.
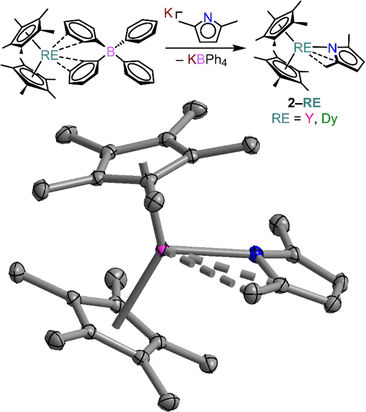
Thus, we pursued an alternative synthetic approach to isolate the unprecedented Cp*2RE(DMP) (RE = Y (2-Y) and Dy (2-Dy), DMP = 2,5-dimethylpyrrolyl), which were obtained from salt-metathesis reactions of Cp*2RE(BPh4) (RE = Y, Dy) and the potassium salt of 2,5-dimethylpyrrolyl, K[DMP], Fig. 3. Similar approaches have been employed to implement the [CpR2RE]+ cation (where R = alkyl) to obtain both mono- and multinuclear RE compounds.31,63–69 Notably, we recently extended this approach to systems bearing guanidinate anions.70,71 Recently, both guanidinate and the structurally and electronically related amidinate ions have been shown to be attractive ligands for the design of single-molecule magnets.70,72–75 Yellow single-crystals of 2-RE were grown from concentrated n-hexane solutions at −35 °C in 42 and 37% crystalline yield for 2-Y and 2-Dy, respectively. 2-RE are isostructural and crystalize in the monoclinic space group P21/c akin to 1-RE. The structure of 2-RE is topologically similar to that of 1-RE as each metal centre is seven-coordinate and ligated by two pentamethylcyclopentadienyl anions and one asymmetrically coordinated DMP substituent with one main interaction to the nitrogen atom, and two weak agostic interactions to one of the methyl groups of the pyrrole ring, and the adjacent C2 carbon of the pyrrole ring.
Excitingly, 1-RE represent the first report of tetraiodopyrrole as a ligand for any metal ion. Notably, the σ- and π-type Lewis basicity of pyrrolyl ligands allows a wide range of coordination modes from η1–η5.76 Recently, the first report of an η1:η2-bridging coordination mode of the pyrrolyl ligand was reported by some of us, resulting from a highly strained dinuclear complex.59 However, in both 1-RE and 2-RE, the N-atom of the pyrrolyl ligand forms a σ-type interaction with the metal centre, without any additional interactions arising from the π-system. Notably, the RE–N interaction in 1-RE is significantly elongated with 2.367(6), 2.410(3) and 2.376(3) Å for 1-Y, 1-Gd, and 1-Dy, respectively, compared to 2.289(1) and 2.299(2) Å for 2-Y and 2-Dy, respectively. This is attributed to the significant differences in basicity of the coordinating nitrogen atom in TIP vs. DMP. The small differences in interatomic distances across isostructural complexes are attributed to the slight variations in ionic radii for Y, Gd, and Dy (YIII = 1.019, GdIII = 1.053, and DyIII = 1.027 Å; CN = 8).77 Remarkably, neither pyrrolyl ligand coordinates symmetrically to the metal centre. In both cases, one substituent in the 2-position of the heterocyclic ring lies substantially closer to the metal than the other. The shortest interatomic RE–I distances in 1-RE (RE–I1) amount to 3.238(1) (1-Y), 3.253(1) (1-Gd), and 3.233(1) (1-Dy) Å, hinting at a significant metal iodine interaction, see Fig. S7† for relevant atom labels. These interatomic distances are significantly longer than other complexes bearing direct Dy–I bonding interactions such as (NNTBS)DyI(THF)2,78 (NNTBS = Fc(NHSitBuMe2)2; Dy–I = 3.09 Å), Cp*2DyI(THF),79 (Dy–I = 2.982 Å), and Dy(Cy3PO)3I3 (Dy–I = 3.055–3.097 Å).80 In contrast, the nearest methyl substituent of the DMP ligand in 2-RE resides significantly closer to the metal centre, with distances of 2.993(2) and 2.996(2) Å in 2-Y and 2-Dy, respectively. The Cnt–RE distances in 1-RE (where Cnt centroid of the pentamethylcyclopentadienyl ring) are 2.355 and 2.344 Å for 1-Y, 2.391 and 2.390 Å for 1-Gd, and 2.357 2.359 Å for 1-Dy. By contrast, the respective Cnt–RE distances in 2-RE are marginally shorter with 2.342 and 2.338 Å for 2-Y, and 2.347 and 2.341 Å for 2-Dy. For both set of compounds, the ∠Cnt–RE–Cnt metallocene angle is slightly larger than 131.8° found in [Cp*2Y(μ-pyr)]2 (139.4°, 139.3°, 139.9°, 139.5°, and 139.7° for 1-Y, 1-Dy, 1-Gd, 2-Y, and 2-Dy, respectively).
Intriguingly, the closest intermolecular I⋯I interaction is 3.838(1) Å, observed in 1-Y, which is approximately 0.15 Å less than the van der Waals radii for two I atoms (3.98 Å).81 In addition to the reduced I⋯I interatomic distance, another key observable of a σ-hole interaction is the interatomic distance between the C and halogen substituent.82 A σ-hole interaction typically changes the length of the C–I covalent bond that is colinear with the σ-hole interaction by ±0.03 Å or less.83–85 The C–I interatomic distances in free TIPH range from 2.060(6) to 2.054(6) Å,38 which is 0.039 Å shorter than the C–I1 distance of 2.099(8) Å observed in 1-Y. Typically, halogen⋯halogen interactions are separated into two types: type I and type II.82 There are clear chemical and geometric criteria for the designation of which classification is most appropriate for a given interaction.82 Interactions of type I are typically geometry-based and arise from close crystal packing, which are observed for all halogen atoms. By contrast, type II interactions originate from electrophile-nucleophile pairings, which is a direct consequence of the increased polarizability of the I atom. Since the region of positive electrostatic potential lies along the same axis of the covalent bond, the σ-hole interaction is normally colinear with the covalent C–I bond. For 1-Y, the ∠C–I–I angle is 166.5(2)°, where the deviation from linearity is attributed to crystal-packing affects.
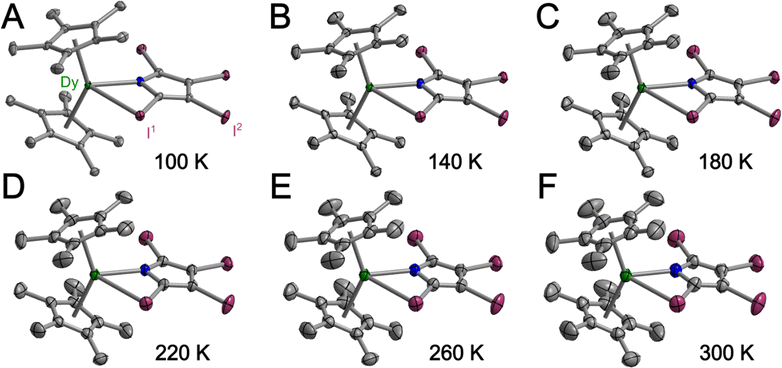
In general, weak interactions with shallow potential energy wells do not cost much energy, thus have large deformation with changing temperatures. Notably, the interatomic distances of halogen bonding interactions are extremely dependent on temperature.28 To probe the temperature dependence of the structure of the complex in the solid state, a single-crystal X-ray diffraction analysis of 1-Dy was conducted at varying temperatures from 100 to 300 K, Fig. 4, S5 and S6.† The monotonic changes in unit cell dimensions, Fig. 5, preclude any potential phase transition over the probed temperature range. Traversing the temperature from 100 to 300 K, the unit cell parameters for 1-Dy elongate (Δa = 0.1106 Å, Δb = 0.1754 Å, and Δc = 0.3346 Å) causing an expansion of 3.6% for the unit cell volume (compare V = 3058.4(1) and 3168.2(2) Å3 for 100 and 300 K, respectively). Over the entire probed temperature range, the TIP ligand maintains a κ2-coordination mode, Fig. 4. Noteworthy, the Dy–I1 interatomic distance increases substantially (ΔDy–I1 = 0.024 Å), Fig. 5B, whereas the Dy–N interatomic distance remains unchanged, as it relates to the magnitude of the standard deviation, Fig. S9.† The displacement of the coordinated iodine atom is also observed in the I1–I2 interatomic distance, Fig. 5C, which declines substantially with increasing temperature. In addition, the N–C and C–C distances around the pyrrole ring remain invariant as a function of temperature, suggesting that this phenomenon is localized to the ancillary I-substituents, Fig. S10.†
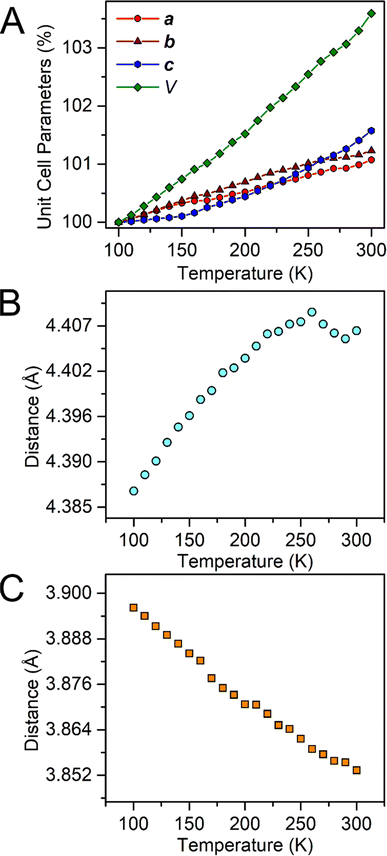 | ||
| Fig. 5 Plots of the temperature dependence of the unit cell parameters (A), and interatomic Dy–I1 (B), and I1–I2 (C) distances of Cp*2Dy(TIP)·CH2Cl2. The error bars are within the radius of the symbols. Please see Fig. S7† for relevant atom labels. Graphical representations of the intermolecular halogen⋯halogen interactions are provided in Fig. S11–S13.† | ||
Several description of halogen bonding have been developed, including those based on the natural orbitals of chemical valence (ETS-NOCV), which provides a quantitative picture of the electronic and electrostatic influences at play between donor and acceptor units.86 One description of intermolecular halogen⋯halogen bonding invokes molecular orbital theory along the X⋯X axis.21 Due to the energy lowering arising from the favourable orbital overlap between the two halogen substituents, the formation of both a formally bonding and antibonding molecular orbital is observed.87 Notably, the closest intermolecular I⋯I interaction (I1–I3) monotonically increases from 3.838(1) to 3.980(1) Å (ΔI1–I3 = 0.142 Å) with elevating temperature, Fig. S11,† consistent with the population of the σ*-LUMO with increasing temperatures. The same scenario is found for the second closest intermolecular I⋯I interaction (I1–I4), Fig. S12,† which increases from 4.374(1) Å to 4.535(1) Å (ΔI1–I4 = 0.161 Å). Notably, instead of the linear growth in intermolecular interatomic distance observed for the other I⋯I interactions, the I3–I3 distances display a parabolic behaviour, Fig. S13,† likely owing to the colinear orientation of the σ-hole relative to the halogen⋯halogen interaction.
Magnetic studies
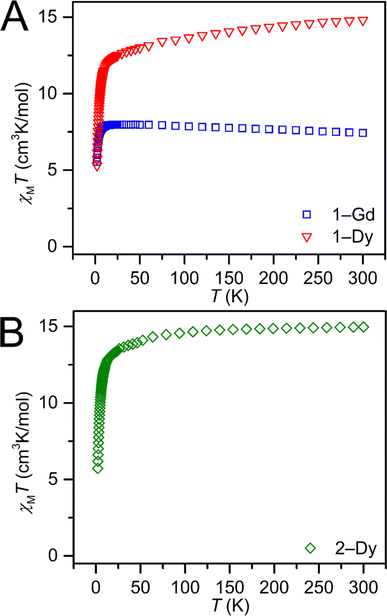
Dc magnetic susceptibility (χM) data for 1-Gd, 1-Dy, and 2-Dy were collected from 2 to 300, Fig. 6 and S36–S38.† At 1.0 T the room temperature χMT values 7.43, 15.27 and 14.96 cm3 K mol−1 for 1-Gd, 1-Dy and 2-Dy, respectively, are in good agreement with the expected values of 7.88 cm3 K mol−1 and 14.14 cm3 K mol−1 for the unperturbed GdIII and DyIII ions, respectively. The higher χMT value for the dysprosium congeners may be attributed to a combination of higher magnetic anisotropy,88 and a slight discrepancy in mass.As the temperature is lowered, a slight decline in χMT is observed until 13.0 and 14.2 K, respectively, for 1-Dy and 2-Dy. At the lowest temperatures, a sharp drop in χMT occurs, in accordance with the depopulation of the Stark sublevels of the DyIII ion.89 The field- and zero-field-cooled magnetic susceptibility data of both 1-Dy and 2-Dy are superimposable, indicating the absence of magnetic blocking. The field-dependent magnetization data of 1-Gd, 1-Dy, and 2-Dy were collected between 2 and 10 K. For the DyIII complexes, magnetic saturation was not reached even at 7 T. At 2 K, the magnetization grows with increasing magnetic field until it reaches a value of 5.82 and 6.09 NμB, slightly higher than the expected saturation magnetization for one DyIII ion (5.23 NμB), suggestive of the presence of significant magnetic anisotropy.90 Similarly, at 2 K the magnetization of 1-Gd grows with increasing applied field until it reaches a value of 7.56 NμB. The reduced magnetization curves (H/T versus M) for 1-Dy and 2-Dy at temperatures ranging from 2 to 10 K are non-superimposable, indicative of thermally accessible excited states, Fig. S50 and S60.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 89
89
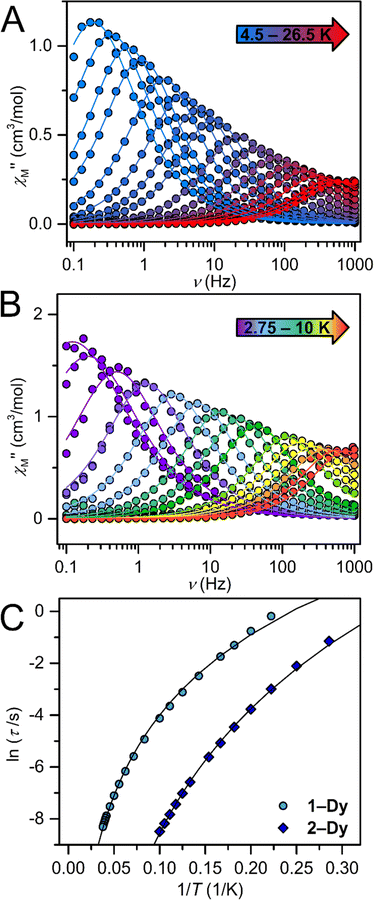
A single DyIII ion is a Kramers' ion and innate to high magnetic anisotropy, which can be augmented by pairing it with an appropriate ligand field, ushering in single-molecule magnet behaviour.91 Multinuclear SMMs featuring real magnetic memory require strong magnetic exchange coupling between multiple lanthanide centres due to the deeply contracted nature of the 4f-orbitals. Strong coupling ensures the emergence of a giant spin which helps suppressing quantum tunnelling of the magnetization (QTM) and thus, engendering slower magnetic relaxation. Several strategies to foster strong coupling has been proven to be successful: (1) metal–metal bonding interactions,92 (2) radical-bridging ligands with diffuse spin orbitals,31,64,66,93 and (3) diamagnetic heavy main group element-containing bridges, also innate to diffuse orbitals, capable of penetrating the core-like 4f-mainfold.94,95 Notably, the inclusion of heavy main-group elements into the primary coordination sphere of a given metal ion influences the zero-field splitting parameter,88,96,97 owing to the ∼Z4 dependence on the spin–orbit coupling Hamiltonian.98 With this in mind, the dynamic magnetic properties of both 1-Dy and 2-Dy were explored under zero dc field, Fig. S39, S40 and S53.†1-Dy displays out-of-phase  components of the ac magnetic susceptibility from 1.8 to 14 K. The position of the signals hinges marginally on temperature and move past 1000 Hz at temperatures above 14 K. Relative to some other neutral, mononuclear SMMs containing a dysprosium metallocene unit,99,100 the
components of the ac magnetic susceptibility from 1.8 to 14 K. The position of the signals hinges marginally on temperature and move past 1000 Hz at temperatures above 14 K. Relative to some other neutral, mononuclear SMMs containing a dysprosium metallocene unit,99,100 the  signals move faster which originates from more prevalent quantum tunnelling of the magnetization (QTM), potentially arising from the asymmetric crystal field imparted by the coordinated TIP ligand relative to that of the neutral ammonia or large [BPh4]− anion. Employing the Cole–Davidson model implemented in CCFit2 to extract relaxation times yielded seemingly satisfactory fits,48,49 however, with large standard deviations attributed to the high frequency
signals move faster which originates from more prevalent quantum tunnelling of the magnetization (QTM), potentially arising from the asymmetric crystal field imparted by the coordinated TIP ligand relative to that of the neutral ammonia or large [BPh4]− anion. Employing the Cole–Davidson model implemented in CCFit2 to extract relaxation times yielded seemingly satisfactory fits,48,49 however, with large standard deviations attributed to the high frequency 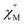 peak position.
peak position.
For 2-Dy, the peak maximum of the out-of-phase 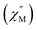 component of the ac magnetic susceptibility resides past the frequency limit of the magnetometer at 2 K and the peak loses intensity with raising temperature up to 10 K, thus precluding the extraction of relaxation times, Fig. S53.†
component of the ac magnetic susceptibility resides past the frequency limit of the magnetometer at 2 K and the peak loses intensity with raising temperature up to 10 K, thus precluding the extraction of relaxation times, Fig. S53.†
The application of an external magnetic field can mitigate these fast relaxation pathways. To determine the optimum field, out-of-phase ac susceptibility 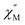 was collected at 2 K under dc fields ranging from 250 to 1500 Oe (1-Dy) and 250 to 1550 Oe (2-Dy), Fig. S42 and S54,† respectively. In both cases, the exposure to external magnetic fields influences the shape of the
was collected at 2 K under dc fields ranging from 250 to 1500 Oe (1-Dy) and 250 to 1550 Oe (2-Dy), Fig. S42 and S54,† respectively. In both cases, the exposure to external magnetic fields influences the shape of the 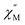 signals. Subjecting to strong magnetic fields decreases substantially the intensity of the peaks positioned at higher frequency, concurrent with the appearance of signals at lower frequency. The optimum dc fields are 1250 Oe for 1-Dy and 1450 Oe for 2-Dy as the high-frequency peak at these fields vanished entirely. Thus, variable-temperature ac susceptibility measurements of 1-Dy and 2-Dy were performed at these dc fields which uncovered much stronger temperature dependences than were apparent under zero dc fields.
signals. Subjecting to strong magnetic fields decreases substantially the intensity of the peaks positioned at higher frequency, concurrent with the appearance of signals at lower frequency. The optimum dc fields are 1250 Oe for 1-Dy and 1450 Oe for 2-Dy as the high-frequency peak at these fields vanished entirely. Thus, variable-temperature ac susceptibility measurements of 1-Dy and 2-Dy were performed at these dc fields which uncovered much stronger temperature dependences than were apparent under zero dc fields.
Temperature-dependent 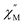 peaks were observed for 1-Dy between 4.5 and 26.5 K under a 1250 Oe applied dc field, Fig. 7A. Using the program CCFit101 the relaxation times (τ) were extracted from a generalized Debye model from the generation of Cole–Cole plots, Fig. S45,† and were subsequently used to construct an Arrhenius plot. A satisfactory fit of the relaxation times was achieved through considering a Raman process utilizing the eqn (2)
peaks were observed for 1-Dy between 4.5 and 26.5 K under a 1250 Oe applied dc field, Fig. 7A. Using the program CCFit101 the relaxation times (τ) were extracted from a generalized Debye model from the generation of Cole–Cole plots, Fig. S45,† and were subsequently used to construct an Arrhenius plot. A satisfactory fit of the relaxation times was achieved through considering a Raman process utilizing the eqn (2)
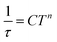 | (2) |
The temperature-dependent out-of-phase 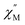 signals of 2-Dy occur between 2.75 and 10 K at 1450 Oe dc field, Fig. 7B. Similarly, through the generation of Cole–Cole plots, Fig. S57,† the relaxation times were extracted using a generalized Debye model as implemented in CCFit2.101 The resulting experimentally determined relaxation times were subsequently fit to a Raman process yielding C = 0.00062(5) s−1 K−n, n = 6.92(4), Fig. 7C.
signals of 2-Dy occur between 2.75 and 10 K at 1450 Oe dc field, Fig. 7B. Similarly, through the generation of Cole–Cole plots, Fig. S57,† the relaxation times were extracted using a generalized Debye model as implemented in CCFit2.101 The resulting experimentally determined relaxation times were subsequently fit to a Raman process yielding C = 0.00062(5) s−1 K−n, n = 6.92(4), Fig. 7C.
The retention of magnetization in the absence of an applied dc magnetic field is a key observable for any SMM. Variable-field magnetization measurements were conducted on 1-Dy at ±7 T from 1.8 to 4 K, Fig. S51 and S52.† At the lowest temperatures, the variable-field magnetization data displays a slightly open butterfly hysteresis loop, where the coercivity of Hc = 0.18 T exceeds the sweep rate of 100 Oe at its largest point. The magnetic hysteresis measurement conducted on 2-Dy lacks coercivity at the lowest temperature measured, Fig. S61.†
Electron paramagnetic resonance (EPR) spectroscopy
Since the introduction of heavy main-group elements into the first coordination sphere of the paramagnetic metal ion impacts the zero-field splitting parameter with respect to the transition metals,88,96,97 we set out to probe the influence of the proximal I-atom on the cw-EPR spectrum of 1-Gd. The spin-only GdIII ion can give rise to well-resolved EPR signals, unlike other paramagnetic lanthanides that oftentimes lead to non-informative EPR peaks that are weak or silent altogether.102 The 8S ground state of the GdIII ion is separated by ∼35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 from the first excited state (6P).103 The EPR spectrum of a well-isolated spin ground state can be described in terms of the following spin Hamiltonian, eqn (3).
000 cm−1 from the first excited state (6P).103 The EPR spectrum of a well-isolated spin ground state can be described in terms of the following spin Hamiltonian, eqn (3).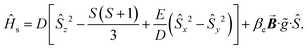 | (3) |
The first term is the zero-field splitting (ZFS) interactions. Here, Ŝμ is the component of the spin operator (μ = x, y, z) and D/E are the axial and rhombic terms of the ZFS, respectively. In cases where S ≥ 2, the spin system may need to be characterized by higher order ZFS terms.104 We have limited the analysis to only second-order terms as not to overparameterize the model. The second term is the electronic Zeeman interaction where βe is the electron Bohr magneton,  is the magnetic field vector,
is the magnetic field vector, ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) is the g-tensor (assumed to be isotropic), and Ŝ represents the electron spin operator.
is the g-tensor (assumed to be isotropic), and Ŝ represents the electron spin operator.
Our best simulations for the spectrum, Fig. 8 and Table S10,† recorded at 5 K of 1-Gd require E/D to be near 1/3 with D = −0.121 cm−1, |E| = 0.039 cm−1 (|E/D| = 0.322), and giso = 1.992. A second spectrum recorded at 100 K required slightly different parameters to simulate. The necessity for different parameters is best appreciated by comparing the ∼2 mT shift in the lowest field resonance (∼0.05 T) and the splitting of the second lowest field feature near 0.09 T. We find that both observations can be reproduced by using D = −0.122, |E| = 0.037 cm−1 (|E/D| = 0.304), and giso = 1.992.
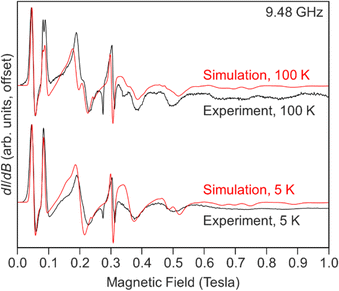 | ||
| Fig. 8 Experimental (black) and simulated (red) X-band EPR spectra of Cp*2Gd(TIP), 1-Gd recorded at 5 (bottom) and 100 (top) K. | ||
These values are very similar to those observed for the metallocenium complex [Cpttt2Gd][B(C6F5)4] (Cpttt = C5H2tBu3-1,2,4) (D = −0.1937 cm−1 and |E| = 0.0148 cm−1) indicative of substantial axial ZFS.105 Notably, the halogenated species, Cpttt2Gd(Cl) yields a more rhombic signal (D = 0.0920 cm−1 and |E| = 0.0239 cm−1).
Electronic absorption spectroscopy
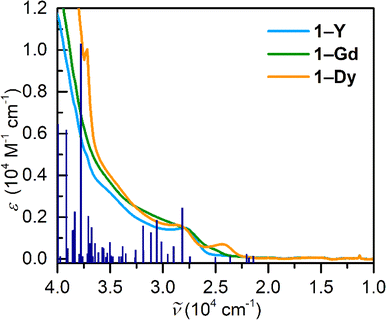
Electronic absorption spectra of 1-RE were taken in dichloromethane, Fig. 9, S34.† The complexation of the tetraiodopyrrole ligand results in the emergence of a band at ∼350 nm. For all compounds, there is minor change in the absorption spectra across the series. Notably, the UV-vis spectrum of the Gd complex features the emergence of a band centred at 411 nm. To gain insight into the electronic absorption spectra of 1-Y, TDDFT calculations were carried out, Table S28.† The most intense band is located at 250 nm and is primarily composed of a MLCT (metal-to-ligand charge transfer) stemming from the metallocene unit to the ancillary TIP ligand. Remarkably, there are multiple transitions ascribed to π–π* transitions of the ancillary TIP ligand, the strongest of which is in the ultraviolet region positioned at 242 nm. The transition in the visible region (345 nm) is attributed to a ligand-to-metal charge transfer (LMCT) arising from a TIP-based molecular orbital to the d-manifold of the central YIII ion. Similarly, the electronic absorption spectra of 2-RE were taken in diethyl ether, Fig. S35,† and feature one transition centred at 350 nm. Owing to the similarity between 2-Y and 2-Dy, this is tentatively assigned as a LMCT band originating from the DMP ligand.Ab inito calculations
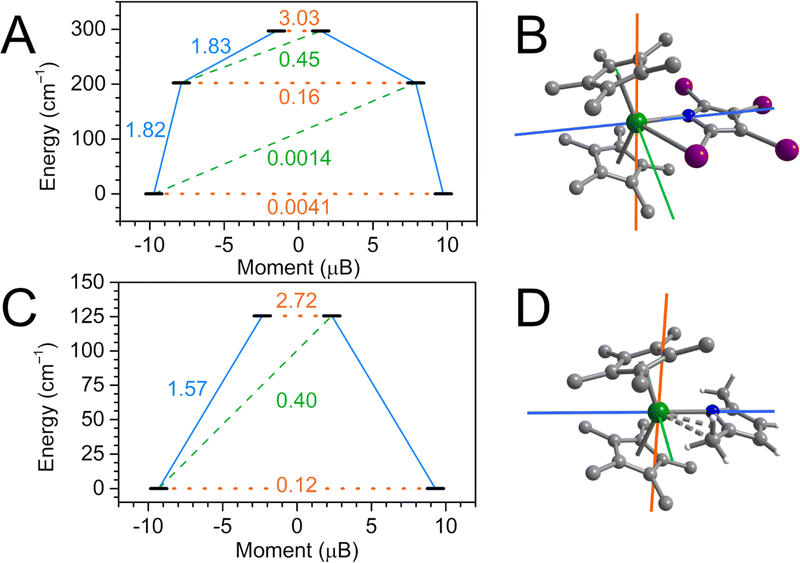
The isolation of the archetypical tetraiodopyrrole complex 1-RE and its temperature dependence in RE–I distance prompted the question whether the relaxation behavior of the DyIII ion in 1-Dy is modulated by Dy–I distance, a feature that could potentially be exploited for temperature-switchable magnetic materials or molecular sensors. To assess the influence of the Dy–I distance on the splitting of the lowest-lying energy spectrum and crystal field parameters, complete active space self-consistent field (CASSCF) calculations were carried out on coordinates obtained from single crystal XRD at 100 K, 200 K and 300 K after optimization of all hydrogen positions. Subsequently, dynamic correlation effects were accounted for via N-electron valence perturbation theory (NEVPT2) under consideration of spin–orbit coupling effects via a quasi-degenerate (QD) approach. These calculations were carried out using the ORCA 5.0.4 software suite.55,106The low-lying energy spectrum for 1-Dy was first assessed for the 100 K structure (Fig. 10). The ground state Kramers doublet (KD1) comprises essentially purely of MJ = |±15/2〉 character, with negligible gx and gy contributions rivalling the predominant gz tensor component. The first excited KD2 is found 202 cm−1 above the ground state, with predominant MJ = |±13/2〉 composition. However, admixture of the higher lying |±9/2〉 MJ state results in considerable reduction of the uniaxiality of this state, manifesting in noticeable transversal gx and gy contributions (0.3 and 0.7, respectively) to the primary gz component (15.8). While the transition dipole moment (TDM) connecting ±KD2 is considerably higher than the KD1 TDM it is not large enough to shortcut the barrier. By contrast, the second excited state KD3 at 297 cm−1 is no longer ascribable to a singular MJ state due to heavy admixture of excited states, with gx = 3.0 and gy = 3.2 concurring with gz = 15.0. Such strong equatorial fields result in the gz axis being tilted by 92° in KD2 compared to the ground state gz orientation, and the TDM crossing the relaxation barrier becoming largest, marking the high end of the estimated relaxation barrier for 1-Dy.
Having identified the maximum KD determining the magnetic relaxation in 1-Dy, we then interrogated the effect of increasing Dy–I distances on the MJ composition of KD1–KD3. Surprisingly, it was found that the relative energy of the three lowest-lying KDs remains essentially unchanged between 100 and 300 K, with a maximum change of ∼1% for KD3. The magnetic moment of KD3 decrease continuously upon increasing temperatures, a manifestation of increased excited state admixture. Similarly, the intra KD3 TDM increases slightly by ∼1% from 100–300 K, reaching a maximum TDM at 200 K ∼2% larger than in the ground KD1. Overall, the considerable Dy–I distance modulation observed in single crystal XRD is not reflected in a modulation of the relaxation dynamics in 1-Dy. Moreover, the calculated crystal field parameters (CFPs) of 1-Dy vary across the temperatures: Inspecting the dominant CFPs, B02 and B22, together attesting for ∼66% weight of the entire crystal field splitting, B02 decreases from −4.04 (100 K) to −4.14 (300 K) while B22 increases from 6.50 (100 K) to 6.79 (300 K).
The observed marginal changes in the low-lying KD composition and associated relaxation dynamics likely arise from the relatively weak Dy–I interaction compared to the Dy–N distance, which experiences a far less pronounced elongation in comparison and therefore dominates the crystal field (Fig. S66†). In this situation, the Dy–I interactions are far too insignificant to meaningfully modulate the relaxation behaviour in 1-Dy when the Dy–N distance remains unchanged.
We conducted ab initio calculations on 2-Dy as well. Here, the formal change of α-substituents from iodine to methyl groups serves as an excellent tool to gauge the impact of lighter or heavier atoms within the vicinity of the Dy site on its relaxation behaviour. Similar to 1-Dy, the ground state KD1 of 2-Dy is strongly uniaxial with predominant MJ = |±15/2〉 character, resulting in a gz = 18.59 and small gx and gy equatorial contributions. Although small, these equatorial contributions are already 26× and 35× higher for gx and gy compared to 1-Dy, respectively, manifesting in a 28× acceleration of the ground state tunnelling TDM, Fig. 10. Looking at the first excited KD2, lying ∼126 cm−1 above KD1, the adversely effect of methyl substitution becomes apparent: the uniaxiality is lost and excited states are strongly admixed, resulting gx and gy of 2.39 and 4.68, respectively. It is therefore not surprising that the crossing transition is dominant already in the second excited state, with TDM = 2.72 being 17× higher than in 1-Dy. This is in excellent qualitative agreement with the experimentally found acceleration in magnetic relaxation from 1-Dy to 2-Dy. While their relaxation behaviour has experienced considerable altercations, the crystal fields remain rather comparable: Similar to 1-Dy, B02 and B22 remain dominant with ∼70% weight, but B22 is larger by 44% to the detriment of B02. A similar study by Mills, Chilton and coworkers on a series of dysprosocenium halobenzene adducts (CptttCp*Dy)(X-Ph)(Al{OC(CF3)}4) (where X = F, Cl, Br),107 where the lighter fluorobenzene was found to accelerate magnetic relaxation most whereas heavier bromobenzene showed slowest relaxation.
The ab initio calculations showed that the presence of α-methyl substitution compared to iodine dramatically impacts the single ion anisotropy of DyIII in a destructive way. It can be hypothesized that the presence of methyl protons close to the DyIII site in 2-Dy induces a multitude of low-energy vibrations that facilitate relaxation of the magnetic moment. By contrast, the weak equatorial Dy–I interaction in 1-Dy barely affects the single ion anisotropy due to the higher atomic weight of iodine vs. hydrogen. One can further hypothesize that the coordination of multiple TIP ligands within the equatorial plane, while simultaneously providing strongly electronegative donor ligands in the axial positions could yield a viable route for future stable high-performance SMMs.
Density functional theory
Taking advantage of the diamagnetic nature of the YIII ion, the electronic structure and bonding situation of 1-Y and 2-Y were readily deduced through density functional theory. A suitable functional was determined through comparing the computed interatomic distances for six different functions each employing the def2-SVP basis set,42,49 with those obtained experimentally. For all optimizations, Grimmes' GD3 empirical dispersion correction was included for all atoms,50,51 as well as a 28 in-core electron pseudopotential for both yttrium and iodine.45 Of the six functionals examined, the TPSSh functional described best the experimentally-determined structure of 1-Y. Thus, a final geometry optimization was performed at the def2-TZVP level of theory, again including the GD3 dispersion correction as well as the aforementioned pseudopotentials for both Y and I. A similar procedure was followed to determine the most appropriate description of 2-Y, Tables S30 and S31.† However, owing to the success of the TPSSh functional in the case of 1-Y, this functional was also used to allow for comparison of the computational data.The frontier orbitals of 1-Y and 2-Y are depicted in Fig. 11 and S74,† respectively. For both, the highest occupied molecular orbital (HOMO) resides predominantly on the pyrrolyl ligand. However, the lowest unoccupied molecular orbital (LUMO) of 1-Y is mainly localized on the TIP ligand, whereas it is centred on the metal in 2-Y. The metal centred LUMO implies that a chemical reduction by one electron will render the highly reducing REII oxidation state accessible.
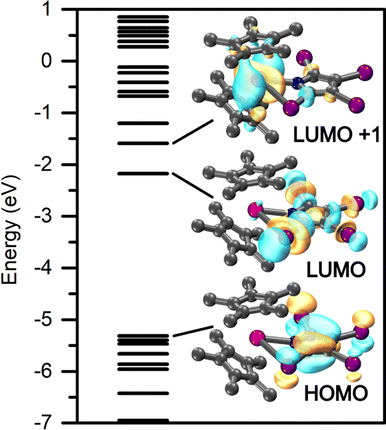 | ||
| Fig. 11 Calculated frontier orbitals of Cp*2Y(TIP), 1-Y, with the TPSSh functional and def2-TZVP basis set. All isovalues were set to 0.4. | ||
Owing to the strongly delocalized structure of 1-Y and 2-Y, the bonding interactions were investigated through a natural localized molecular orbital (NLMO)53 analysis, where the relevant donor/acceptor NLMO interactions are provided in Tables S29 and S32,† respectively. The NLMOs of 1-Y prove the ionic bonding picture between the YIII cation and the [TIP]− and [Cp*]− anionic ligands. A second-order perturbation analysis of the Y–N interactions are strongly localized toward the coordinating N atom (92.8%), representative of a RE–N bonding situation. The Y–I interaction vastly exceeds that for the chelating nitrogen with summed contributions of 93.16 and 31.42 kcal mol−1, respectively, attributable to the augmented negative charge located on the I-substituents of the TIP ligands. This interaction is also strongly localized (90.6–98.4%) toward the donor I atom. The structure of 1-Y additionally benefits from small stabilization energies arising from the C–N molecular orbitals (7.58–1.84 kcal mol−1).
The bonding between the yttrium ion and DMP ligand in 2-Y is most accurately reflected as ionic because the Y–N interactions are similarly polarized toward the N-atom. The strongest interaction arises from the donation of the N lone pair into the d-manifold of the yttrium centre for a summed contribution of impressive 41.12 kcal mol−1, slightly greater than that observed for 1-RE. A small stabilization energy is detected originating from the C–H bonds of the methyl substituent of the dimethylpyrrolyl ligand (22.09 kcal mol−1). The much lower stabilization energy of 2-Y relative to that of 1-Y is allocated to the difference in partial anionic charge on the substituent when comparing iodine to methyl.
Conclusions
Three isostructural mononuclear complexes Cp*2RE(TIP) (1-RE, RE = Y, Gd and Dy; TIP = 2,3,4,5-tetraiodopyrrolyl) were synthesized through a protonolysis reaction from the respective RE allyl complexes. 1-RE were characterized through numerous techniques including crystallography, spectroscopy, magnetometry, and computations. Notably, 1-RE constitute the first compounds installing tetraiodopyrrole as a ligand for any metal. To adequately assess the influence of the I-atom on the electronic properties of the RE metal centre, the analogous 2,5-dimethlpyrrole (DMPH) complex was isolated, Cp*2RE(DMP) (2-RE, RE = Y, Dy; DMP = 2,5-dimethlpyrrolyl). Owing to the difference in acidity of the DMP analogue relative to other pyrrole derivatives, an alternative synthetic route was necessary highlighting the limits of the protonolysis reaction pathway involving Cp*2RE(η3-C3H5). Here, the DMP ligand coordinates in a similar fashion to the TIP ligand rendering it an appropriate comparison. The introduction of the TIP ligand to coordination chemistry represents a promising route to introduce intermolecular halogen bonding interactions between molecules within a crystal lattice. The study of such halogen bonding interactions poses a critical development in the field of quantum information science as these interactions can help prevent pivotal rotations and vibrations which are thought to be responsible for fast magnetic relaxation pathways. The Dy analogue, 1-Dy, is a zero-field single-molecule magnet, where ab initio calculations uncovered the influence of the Dy–I interatomic distance on the electronic structure of the DyIII ion. In comparison, the methyl-substituted complex, 2-Dy exhibits faster magnetic relaxation likely stemming from a combination of decreased donor capacity of the TIP anion relative to DMP and the mitigation of low energy vibrations residing close to the metal centre.In both cases, DFT calculations uncover the bonding situations of both 1-Y, and 2-Y respectively. The introduction of ligand scaffolds bearing covalently bonded I-atoms represent an exciting frontier of research where the intermolecular interactions of these species can potentially mitigate fast, vibrationally activated, relaxation pathways. From a more general perspective, the introduction of tetraiodopyrrole into coordination chemistry may inspire the pursuit of coordination compounds with the entirety of the transition metals that could be relevant for catalysis and small molecule activation.
Data availability
All computational data, spectroscopic data, supplementary figures and tables, and detailed crystallographic information can be found in the ESI.† Crystallographic data are available via the Cambridge Crystallographic Data Centre (CCDC): 2350192–2350216. The data supporting this article have been included as part of the ESI.†Author contributions
F. D. prepared and characterised all compounds. S. J. provided experimental assistance. F. B. performed ab initio calculations. S. M. G. collected and interpreted EPR data. S. D. assisted with data analysis, formulated, and directed the research, and wrote the manuscript with input from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded in part through the National Science Foundation (NSF) Faculty Early Career Development Program (CAREER) CHE-2339595. S.D. is grateful to the Department of Chemistry at Michigan State University (MSU) for generous start-up funds. We are grateful to Dr Rui Huang and Dr Richard Staples (MSU) for assistance with CHN and X-ray diffraction analyses respectively. We thank Ernesto Castellanos for experimental assistance. This work was supported in part through computational resources and services provided by the Institute for Cyber-Enabled Research at MSU. The LANL EPR Lab is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Heavy Element Chemistry Program (2020LANLE372) and the Laboratory Directed Research and Development program at LANL (20230399ER). LANL is managed by Triad National Security, LLC, for the NNSA of the U.S. Department of Energy (contract 89233218CNA000001).Notes and references
- J. C. Vanjak, B. O. Wilkins, V. Vieru, N. S. Bhuvanesh, J. H. Reibenspies, C. D. Martin, L. F. Chibotaru and M. Nippe, J. Am. Chem. Soc., 2022, 144, 17743–17747 CrossRef CAS PubMed.
- A. H. Vincent, Y. L. Whyatt, N. F. Chilton and J. R. Long, J. Am. Chem. Soc., 2023, 145, 1572–1579 CrossRef CAS PubMed.
- X. Sun, L. Münzfeld, D. Jin, A. Hauser and P. W. Roesky, Chem. Commun., 2022, 58, 7976–7979 RSC.
- J. Liu, K. Singh, S. Dutta, Z. Feng, D. Koley, G. Tan and X. Wang, Dalton Trans., 2021, 50, 5552–5556 RSC.
- L. Münzfeld, X. Sun, S. Schlittenhardt, C. Schoo, A. Hauser, S. Gillhuber, F. Weigend, M. Ruben and P. W. Roesky, Chem. Sci., 2022, 13, 945–954 RSC.
- F. Jaroschik, T. Shima, X. Li, K. Mori, L. Ricard, X.-F. Le Goff, F. Nief and Z. Hou, Organometallics, 2007, 26, 5654–5660 CrossRef CAS.
- S.-M. Chen, J. Xiong, Y.-Q. Zhang, Q. Yuan, B.-W. Wang and S. Gao, Chem. Sci., 2018, 9, 7540–7545 RSC.
- P. Evans, D. Reta, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2019, 141, 19935–19940 CrossRef CAS PubMed.
- F.-S. Guo, M. He, G.-Z. Huang, S. R. Giblin, D. Billington, F. W. Heinemann, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Inorg. Chem., 2022, 61, 6017–6025 CrossRef CAS PubMed.
- F. Nief, D. Turcitu and L. Ricard, Chem. Commun., 2002, 1646–1647 RSC.
- E. R. Pugliese, F. Benner and S. Demir, Chem.–Eur. J., 2023, 29, e202302687 CrossRef CAS PubMed.
- L. Knorr, Ber. Dtsch. Chem. Ges., 1884, 17, 2863–2870 CrossRef.
- C. Paal, Ber. Dtsch. Chem. Ges., 1884, 17, 2756–2767 CrossRef.
- T. W. Lyons and M. S. Sanford, Chem. Rev., 2010, 110, 1147–1169 CrossRef CAS PubMed.
- P.-B. Jin, K.-X. Yu, Q.-C. Luo, Y.-Y. Liu, Y.-Q. Zhai and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2022, 61, e202203285 CrossRef CAS PubMed.
- P.-B. Jin, Q.-C. Luo, Y.-Q. Zhai, Y.-D. Wang, Y. Ma, L. Tian, X. Zhang, C. Ke, X.-F. Zhang, Y. Lv and Y.-Z. Zheng, iScience, 2021, 24, 102760 CrossRef CAS PubMed.
- P.-B. Jin, Y.-Q. Zhai, K.-X. Yu, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2020, 59, 9350–9354 CrossRef CAS PubMed.
- J.-M. Lehn, Angew Chem. Int. Ed. Engl., 1988, 27, 89–112 CrossRef.
- P. J. Costa, Phys. Sci. Rev., 2017, 2, 20170136 Search PubMed.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296 CrossRef CAS PubMed.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS PubMed.
- H. Bock and S. Holl, Z. Naturforsch., B: J. Chem. Sci., 2002, 57, 843–858 CAS.
- M. A. Bondarenko, A. S. Novikov, P. A. Abramov, I. F. Sakhapov, M. N. Sokolov and S. A. Adonin, J. Mol. Struct., 2021, 1230, 129931–129936 CrossRef CAS.
- P. M. J. Szell, S. Zablotny and D. L. Bryce, Nat. Commun., 2019, 10, 916–924 CrossRef PubMed.
- G. L. Ciamician and M. Dennstedt, Ber. Dtsch. Chem. Ges., 1882, 15, 2579–2585 CrossRef.
- J. Chang, G. Zhao, X. Zhao, C. He, S. Pang and J. M. Shreeve, Acc. Chem. Res., 2021, 54, 332–343 CrossRef CAS PubMed.
- G. Mínguez Espallargas, L. Brammer, D. R. Allan, C. R. Pulham, N. Robertson and J. E. Warren, J. Am. Chem. Soc., 2008, 130, 9058–9071 CrossRef PubMed.
- A. Forni, P. Metrangolo, T. Pilati and G. Resnati, Cryst. Growth Des., 2004, 4, 291–295 CrossRef CAS.
- W. J. Evans, S. A. Kozimor, J. W. Ziller and N. Kaltsoyannis, J. Am. Chem. Soc., 2004, 126, 14533–14547 CrossRef CAS PubMed.
- L. C. H. Gerber, R. R. Schrock and P. Müller, Organometallics, 2013, 32, 2373–2378 CrossRef CAS.
- S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, J. Am. Chem. Soc., 2012, 134, 18546–18549 CrossRef CAS PubMed.
- W. J. Evans, S. A. Kozimor, J. C. Brady, B. L. Davis, G. W. Nyce, C. A. Seibel, J. W. Ziller and R. J. Doedens, Organometallics, 2005, 24, 2269–2278 CrossRef CAS.
- CrysAlisPro Software System, Rigaku Corporation, Oxford 2020 Search PubMed.
- SCALE3 ABSPACK Empirical Absorption Correction, CrysAlis Pro - Software Package, Rigaku Corporation, Oxford 2020 Search PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3–8 CrossRef PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- H. Bock, S. Holl and V. Krenzel, Z. Naturforsch., B: J. Chem. Sci., 2001, 56, 13–24 CrossRef CAS.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- J. R. Pliego, Chem. Phys. Lett., 2003, 367, 145–149 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, J. Chem. Phys., 2007, 126, 124101 CrossRef PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. B01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- D. G. A. Smith, L. A. Burns, K. Patkowski and C. D. Sherrill, J. Phys. Chem. Lett., 2016, 7, 2197–2203 CrossRef CAS PubMed.
- L. Münzfeld, C. Schoo, S. Bestgen, E. Moreno-Pineda, R. Köppe, M. Ruben and P. W. Roesky, Nat. Commun., 2019, 10, 3135 CrossRef PubMed.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1985, 83, 1736–1740 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- P. M. Zeimentz, S. Arndt, B. R. Elvidge and J. Okuda, Chem. Rev., 2006, 106, 2404–2433 CrossRef CAS PubMed.
- B. M. Day, F.-S. Guo and R. A. Layfield, Acc. Chem. Res., 2018, 51, 1880–1889 CrossRef CAS PubMed.
- M. T. Dumas, T. F. Jenkins, J. C. Wedal, J. W. Ziller, F. Furche and W. J. Evans, Organometallics, 2021, 40, 735–741 CrossRef CAS.
- F. Delano IV, F. Benner, S. Jang and S. Demir, Inorg. Chem., 2023, 62, 14604–14614 CrossRef CAS PubMed.
- S.-S. Liu, S. Gao, J. W. Ziller and W. J. Evans, Dalton Trans., 2014, 43, 15526–15531 RSC.
- M. E. Fieser, T. J. Mueller, J. E. Bates, J. W. Ziller, F. Furche and W. J. Evans, Organometallics, 2014, 33, 3882–3890 CrossRef CAS.
- M. Rupp, R. Korner and I. V. Tetko, Comb. Chem. High Throughput Screening, 2011, 14, 307–327 CrossRef CAS PubMed.
- F. Delano IV, E. Castellanos, J. McCracken and S. Demir, Chem. Sci., 2021, 12, 15219–15228 RSC.
- C. A. Gould, E. Mu, V. Vieru, L. E. Darago, K. Chakarawet, M. I. Gonzalez, S. Demir and J. R. Long, J. Am. Chem. Soc., 2020, 142, 21197–21209 CrossRef CAS PubMed.
- F. Benner and S. Demir, Inorg. Chem. Front., 2023, 10, 4981–4992 RSC.
- F. Benner, L. L. Droitte, O. Cador, B. L. Guennic and S. Demir, Chem. Sci., 2023, 14, 5577–5592 RSC.
- M. R. MacDonald, J. W. Ziller and W. J. Evans, Inorg. Chem., 2011, 50, 4092–4106 CrossRef CAS PubMed.
- C. A. Gould, L. E. Darago, M. I. Gonzalez, S. Demir and J. R. Long, Angew. Chem., Int. Ed., 2017, 56, 10103–10107 CrossRef CAS PubMed.
- E. R. Pugliese, F. Benner, E. Castellanos, F. Delano IV and S. Demir, Inorg. Chem., 2022, 61, 2444–2454 CrossRef CAS PubMed.
- F. Delano IV and S. Demir, Cryst. Growth Des., 2023, 23, 3134–3143 CrossRef CAS.
- F. Delano IV, S. Deshapriya and S. Demir, Inorg. Chem., 2024, 63, 9659–9669 CrossRef CAS PubMed.
- P.-B. Jin, Q.-C. Luo, G. K. Gransbury, I. J. Vitorica-Yrezabal, T. Hajdu, I. Strashnov, E. J. L. McInnes, R. E. P. Winpenny, N. F. Chilton, D. P. Mills and Y.-Z. Zheng, J. Am. Chem. Soc., 2023, 145, 27993–28009 CrossRef CAS PubMed.
- Y. Wang, Q.-C. Luo, Y.-Q. Zhai, P.-B. Jin, Z. Fu, Q. Sun, F.-N. Li and Y.-Z. Zheng, Cryst. Growth Des., 2022, 22, 6398–6404 CrossRef CAS.
- P.-B. Jin, K.-X. Yu, Y.-Q. Zhai, Q.-C. Luo, Y.-D. Wang, X.-F. Zhang, Y. Lv and Y.-Z. Zheng, Chin. J. Chem., 2021, 39, 1635–1640 CrossRef CAS.
- F. Delano, S. Deshapriya and S. Demir, Polyhedron, 2024, 249, 116785 CrossRef CAS.
- Y. Luo and J. Chen, J. Organomet. Chem., 2018, 863, 10–14 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- K. L. M. Harriman, J. L. Brosmer, L. Ungur, P. L. Diaconescu and M. Murugesu, J. Am. Chem. Soc., 2017, 139, 1420–1423 CrossRef CAS PubMed.
- Y.-S. Meng, Y.-Q. Zhang, Z.-M. Wang, B.-W. Wang and S. Gao, Chem.–Eur. J., 2016, 22, 12724–12731 CrossRef CAS PubMed.
- M. Li, H. Wu, Z. Xia, L. Ungur, D. Liu, L. F. Chibotaru, H. Ke, S. Chen and S. Gao, Inorg. Chem., 2020, 59, 7158–7166 CrossRef CAS PubMed.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812 CrossRef CAS PubMed.
- A. Mukherjee, S. Tothadi and G. R. Desiraju, Acc. Chem. Res., 2014, 47, 2514–2524 CrossRef CAS PubMed.
- J. S. Murray, M. C. Concha, P. Lane, P. Hobza and P. Politzer, J. Mol. Model., 2008, 14, 699–704 CrossRef CAS PubMed.
- W. Wang, N.-B. Wong, W. Zheng and A. Tian, J. Phys. Chem. A, 2004, 108, 1799–1805 CrossRef CAS.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189 RSC.
- M. P. Mitoraj and A. Michalak, J. Mol. Model., 2013, 19, 4681–4688 CrossRef CAS PubMed.
- S. V. Rosokha, C. L. Stern and J. T. Ritzert, Chem.–Eur. J., 2013, 19, 8774–8788 CrossRef CAS PubMed.
- M. R. Saber and K. R. Dunbar, Chem. Commun., 2014, 50, 12266–12269 RSC.
- H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1–33 CrossRef CAS.
- O. Kahn, Molecular Magnetism, VCH, 1993 Search PubMed.
- N. F. Chilton, Inorg. Chem., 2015, 54, 2097–2099 CrossRef CAS PubMed.
- C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202 CrossRef CAS PubMed.
- S. Kumar Kushvaha, P. Ravichandran, C. Dan, L. Ungur, N. Suryadevara, M. Ruben and K. Chandra Mondal, Eur. J. Inorg. Chem., 2024, 27, e202300598 CrossRef CAS.
- P. Zhang, F. Benner, N. F. Chilton and S. Demir, Chem, 2022, 8, 717–730 CAS.
- P. Zhang, R. Nabi, J. K. Staab, N. F. Chilton and S. Demir, J. Am. Chem. Soc., 2023, 145, 9152–9163 CrossRef CAS PubMed.
- L. Devkota, D. J. SantaLucia, A. M. Wheaton, A. J. Pienkos, S. V. Lindeman, J. Krzystek, M. Ozerov, J. F. Berry, J. Telser and A. T. Fiedler, Inorg. Chem., 2023, 62, 5984–6002 CrossRef CAS PubMed.
- T. A. Betley and J. C. Peters, Inorg. Chem., 2003, 42, 5074–5084 CrossRef CAS PubMed.
- P. Pyykkö, Annu. Rev. Phys. Chem., 2012, 63, 45–64 CrossRef PubMed.
- S. Demir, J. M. Zadrozny and J. R. Long, Chem.–Eur. J., 2014, 20, 9524–9529 CrossRef CAS PubMed.
- S. Demir, M. D. Boshart, J. F. Corbey, D. H. Woen, M. I. Gonzalez, J. W. Ziller, K. R. Meihaus, J. R. Long and W. J. Evans, Inorg. Chem., 2017, 56, 15049–15056 CrossRef CAS PubMed.
- D. Reta and N. F. Chilton, Phys. Chem. Chem. Phys., 2019, 21, 23567–23575 RSC.
- P. Zhang, M. Perfetti, M. Kern, P. P. Hallmen, L. Ungur, S. Lenz, M. R. Ringenberg, W. Frey, H. Stoll, G. Rauhut and J. van Slageren, Chem. Sci., 2018, 9, 1221–1230 RSC.
- T. P. Gompa, S. M. Greer, N. T. Rice, N. Jiang, J. Telser, A. Ozarowski, B. W. Stein and H. S. La Pierre, Inorg. Chem., 2021, 60, 9064–9073 CrossRef CAS PubMed.
- J. Telser, in eMagRes, John Wiley & Sons, Ltd, 2017, pp. 207–234 Search PubMed.
- C. A. P. Goodwin, D. Reta, F. Ortu, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2017, 139, 18714–18724 CrossRef CAS PubMed.
- Y. Guo, K. Sivalingam, C. Kollmar and F. Neese, J. Chem. Phys., 2021, 154, 214113 CrossRef CAS PubMed.
- S. C. Corner, G. K. Gransbury, I. J. Vitorica-Yrezabal, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, Inorg. Chem., 2024, 63, 9552–9561 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2350192–2350216. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc03786c |
| This journal is © The Royal Society of Chemistry 2024 |