Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
HANNA: hard-constraint neural network for consistent activity coefficient prediction†
Thomas
Specht
 a,
Mayank
Nagda
a,
Mayank
Nagda
 b,
Sophie
Fellenz
b,
Sophie
Fellenz
 b,
Stephan
Mandt
b,
Stephan
Mandt
 c,
Hans
Hasse
c,
Hans
Hasse
 a and
Fabian
Jirasek
a and
Fabian
Jirasek
 *a
*a
aLaboratory of Engineering Thermodynamics (LTD), RPTU Kaiserslautern, Germany. E-mail: fabian.jirasek@rptu.de
bDepartment of Computer Science, RPTU Kaiserslautern, Germany
cDepartment of Computer Science, University of California, Irvine, CA, USA
First published on 31st October 2024
Abstract
We present the first hard-constraint neural network model for predicting activity coefficients (HANNA), a thermodynamic mixture property that is the basis for many applications in science and engineering. Unlike traditional neural networks, which ignore physical laws and result in inconsistent predictions, our model is designed to strictly adhere to all thermodynamic consistency criteria. By leveraging deep-set neural networks, HANNA maintains symmetry under the permutation of the components. Furthermore, by hard-coding physical constraints in the model architecture, we ensure consistency with the Gibbs–Duhem equation and in modeling the pure components. The model was trained and evaluated on 317![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 421 data points for activity coefficients in binary mixtures from the Dortmund Data Bank, achieving significantly higher prediction accuracies than the current state-of-the-art model UNIFAC. Moreover, HANNA only requires the SMILES of the components as input, making it applicable to any binary mixture of interest. HANNA is fully open-source and available for free use.
421 data points for activity coefficients in binary mixtures from the Dortmund Data Bank, achieving significantly higher prediction accuracies than the current state-of-the-art model UNIFAC. Moreover, HANNA only requires the SMILES of the components as input, making it applicable to any binary mixture of interest. HANNA is fully open-source and available for free use.
Introduction
Neural networks (NNs) have recently revolutionized many fields, including image analysis,1 speech recognition,2 predicting protein folding,3,4 and language modeling.5,6 These models are universal and highly flexible function approximators,7 which perform best if they have large amounts of training data. NNs are also gaining more and more attention in chemical engineering8–12 but face two significant challenges preventing them from exploiting their full potential in this field: sparse training data and inconsistent predictions. Like in other fields of science and engineering, data sparsity is ubiquitous in chemical engineering due to the high effort and costs related to experimental data collection, making predictions with purely data-driven NNs difficult. Furthermore, since NNs are a priori agnostic about physical laws and boundaries, there is no guarantee that their predictions obey these rules, frequently leading to physically inconsistent results and predictions.13 This, in turn, is detrimental to the trust in NN-based models and a severe obstacle to their adoption and use in practice.The most promising solution to these challenges is to incorporate explicit physical knowledge into NNs to support their training beyond using only the limited available data. Most prominently, Physics-Informed Neural Networks (PINNs)14 have been successfully applied in different fields,10,13,15–20 primarily to solve partial differential equations (PDE) efficiently. PINNs incorporate the governing physical equation or boundary conditions into the loss function of an NN by adding a term that penalizes solutions deviating from the constraint (e.g., the compliance of a PDE).21 PINNs are inherently soft-constraint methods that do not enforce exact compliance with the given constraints, which is a well-known limitation of penalty methods in general22,23 and has potential drawbacks. Specifically, while approximately complying with physical laws and boundaries might be sufficient in some cases, this is unacceptable in many applications; for instance, thermodynamic models that yield physically inconsistent predictions will not be accepted and used in chemical engineering practice.
Hard-constraint models, which strictly enforce physical relations and constraints in NNs, are generally considered challenging to develop.21,23–26 Thermodynamics is the ideal field for designing such hard-constraint models with its extensive treasure of explicit physical knowledge on the one hand and the high demand for strict compliance of predictive thermodynamic models with physical laws and constraints on the other. In this work, we introduce the first hard-constraint NN-based model for thermodynamic property prediction, which opens up an entirely new way of thermodynamic model development but also holds the promise to advance model development in other fields of chemical engineering and beyond.
Predicting the thermodynamic properties of pure components and mixtures is fundamental in many fields of science and engineering. In chemical engineering, knowledge of thermodynamic properties is the basis for process design and optimization. However, experimental data on thermodynamic properties are scarce. The problem is particularly challenging for mixtures, where missing data are prevalent due to the combinatorial complexity involved.
One of the most critical thermodynamic properties is the activity coefficient of a component in a mixture. Activity coefficients are the key to modeling the chemical potential in liquid mixtures, one of the most central properties in physical chemistry and chemical engineering. Activity coefficients are essential for correctly describing chemical equilibria,27 reaction kinetics,28 phase equilibria,29 and many other properties of mixtures, such as electrochemical properties.30,31 Since activity coefficients cannot be measured directly, they are usually determined indirectly by evaluating phase equilibrium experiments. Since these experiments are time-consuming and expensive, experimental data on activity coefficients are often lacking, and many physical prediction methods have been developed and are widely applied in industry.29
Physical methods for predicting activity coefficients model the molar Gibbs excess energy gE as a function of temperature T and mixture composition in mole fractions x, from which the logarithmic activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi are obtained by partial differentiation.29 The two most widely used gE models are NRTL32 and UNIQUAC.33 These models generalize over state points, i.e., temperature and mole fractions, but cannot extrapolate to unstudied mixtures. In contrast, gE models based on quantum-chemical descriptors, such as COSMO-RS34 and COSMO-SAC,35–37 or group-contribution models, such as the different versions of UNIFAC38,39 (with modified UNIFAC (Dortmund) being the most advanced39,40) also allow to generalize over components and mixtures. However, even though they have been continuously developed and refined for decades, the state-of-the-art models show significant weaknesses for certain classes of components. The consequential inaccuracies in predicting activity coefficients result in wrongly predicted phase equilibria, leading to poor process modeling and simulation.41,42 On the upside, the theoretical foundation of the established physical models allows for good extrapolation performance, and, even more importantly, they exhibit strict compliance with thermodynamic laws, boundaries, and consistency criteria.
γi are obtained by partial differentiation.29 The two most widely used gE models are NRTL32 and UNIQUAC.33 These models generalize over state points, i.e., temperature and mole fractions, but cannot extrapolate to unstudied mixtures. In contrast, gE models based on quantum-chemical descriptors, such as COSMO-RS34 and COSMO-SAC,35–37 or group-contribution models, such as the different versions of UNIFAC38,39 (with modified UNIFAC (Dortmund) being the most advanced39,40) also allow to generalize over components and mixtures. However, even though they have been continuously developed and refined for decades, the state-of-the-art models show significant weaknesses for certain classes of components. The consequential inaccuracies in predicting activity coefficients result in wrongly predicted phase equilibria, leading to poor process modeling and simulation.41,42 On the upside, the theoretical foundation of the established physical models allows for good extrapolation performance, and, even more importantly, they exhibit strict compliance with thermodynamic laws, boundaries, and consistency criteria.
Recently, machine-learning (ML) methods have gained attention for predicting activity coefficients43–45 and other thermodynamic properties.46–52 Even though these models are purely data-driven, they surpassed the physical thermodynamic models in prediction accuracy. However, they were all limited to specific state points and could, e.g., not describe the composition dependence of activity coefficients.
To improve the ML models further, various hybridization approaches53 were developed that combine the flexibility of ML methods with physical knowledge. This was, e.g., done by augmenting the training data with synthetic data obtained from physical prediction methods.42,54 Other recently developed hybridization approaches55–57 have broadened the application range of physical thermodynamic models. In these approaches, an ML method is embedded in a physical thermodynamic model to predict the physical model's parameters. By retaining the framework of the physical models, these hybrid models are intrinsically thermodynamically consistent. On the downside, these models are subject to the same assumptions and simplifications taken during the development of the original model, limiting their flexibility. Consequently, they have a restricted value range of predictable activity coefficients,58 limiting the description of certain phase behaviours.59–62
Rittig et al. recently developed a PINN13 and a hard-constraint approach63 considering the Gibbs–Duhem equation; however, their study was limited to synthetic data and the Gibbs–Duhem equation as only one of the relevant physical boundary conditions. Hybrid models for activity coefficient prediction that fully exploit the flexibility of NNs while guaranteeing consistency with all thermodynamic constraints have not been available until now. This work has addressed this gap.
Specifically, we have developed the first hard-constraint NN model for the Gibbs excess energy gE of a mixture, which allows us to predict activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi in any binary mixture of arbitrary components at any state point. We name our method HArd-constraint Neural Network for Activity coefficient prediction (HANNA) in the following. We restrict ourselves here to binary mixtures. All physical models of mixtures are based on pair interactions, which can, and practically always are, trained on data for binary mixtures. Therefore, predictions for binary activity coefficients obtained from HANNA could be used to fit the parameters of a physical model based on pair-interactions, which can then be used for predictions of multicomponent mixtures. However, it would also be very interesting to study the generalization of HANNA to multicomponent mixtures in future work.
γi in any binary mixture of arbitrary components at any state point. We name our method HArd-constraint Neural Network for Activity coefficient prediction (HANNA) in the following. We restrict ourselves here to binary mixtures. All physical models of mixtures are based on pair interactions, which can, and practically always are, trained on data for binary mixtures. Therefore, predictions for binary activity coefficients obtained from HANNA could be used to fit the parameters of a physical model based on pair-interactions, which can then be used for predictions of multicomponent mixtures. However, it would also be very interesting to study the generalization of HANNA to multicomponent mixtures in future work.
Development of HANNA
HANNA combines a flexible neural network with explicit physical knowledge. At its heart, it predicts the Gibbs excess energy gE of a mixture, from which subsequently the activity coefficients of the mixture components, typically given in the natural logarithm ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi, can be derived. The Gibbs excess energy gE and consequently the activity coefficients ln
γi, can be derived. The Gibbs excess energy gE and consequently the activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi, are typically expressed as functions of temperature T, pressure p, and the composition in mole fractions x of the components. In the following, we will express gE and the activity coefficients ln
γi, are typically expressed as functions of temperature T, pressure p, and the composition in mole fractions x of the components. In the following, we will express gE and the activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi in binary mixtures as functions of T, p, and x1. For liquid mixtures, the influence of the pressure is small and is often neglected, which is also the case for our model. However, for the sake of clarity, all thermodynamic derivations are written here without this assumption.
γi in binary mixtures as functions of T, p, and x1. For liquid mixtures, the influence of the pressure is small and is often neglected, which is also the case for our model. However, for the sake of clarity, all thermodynamic derivations are written here without this assumption.
The predictions of HANNA strictly comply with all relevant thermodynamic consistency criteria, which are listed for binary mixtures as follows.
(1) The activity coefficients of pure components are unity:
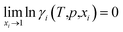 | (1) |
(2) The activity coefficients of the components in a mixture are coupled by the Gibbs–Duhem equation, which reads for the binary mixture:
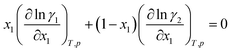 | (2) |
(3) The activity coefficients in a pseudo-binary mixture A + B where A = B are always unity:
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi(T,p,xi) = 0 γi(T,p,xi) = 0 | (3) |
(4) Upon changing the order of the components in the input of a model for predicting the activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ1 and ln
γ1 and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ2 in a binary mixture, the values of the predicted activity coefficients must not change, only their order. Mathematically, this is called permutation-equivariance and can be expressed as:
γ2 in a binary mixture, the values of the predicted activity coefficients must not change, only their order. Mathematically, this is called permutation-equivariance and can be expressed as:
| γ(P(x)) = P(γ(x)) | (4) |
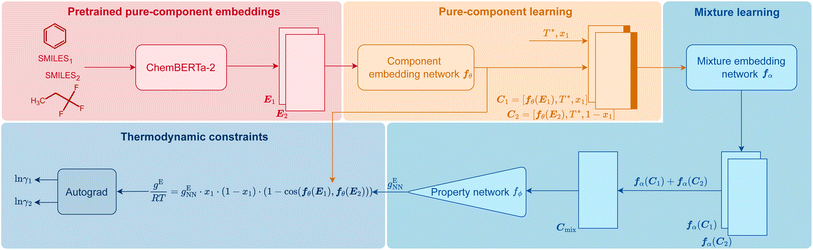
In Fig. 1, we visualize how HANNA strictly enforces these constraints for predicting activity coefficients, leading to the novel class of hybrid NNs developed in this work. The central idea is to learn the molar excess Gibbs energy gE of the mixture rather than the individual activity coefficients (γ1 and γ2) directly. The values of γ1 and γ2 can then be obtained from gE by the laws of thermodynamics, ensuring strict thermodynamic consistency. HANNA consists of four parts:
(1) Pure-component embeddings from pretrained ChemBERTa-2
We use SMILES64 strings to represent the components and preprocess them with ChemBERTa-2,65 a language model pretrained on an extensive database of molecules for learning “pure component embeddings” of the molecules from the respective SMILES.(2) Refining pure-component embeddings for thermodynamic property prediction
Since the embeddings of ChemBERTa-2 were not explicitly trained on thermodynamic properties, we “fine-tune” them to predict thermodynamic properties in a two-step process. We first feed them into a “component embedding network” fθ to get a lower dimensional representation of each component i. Then, the information on the standardized temperature T* (see Section Data splitting, training, and evaluation of the model for the definition) and the composition (here: mole fraction x1 of component 1) are concatenated to each of the component embeddings. The result of this step is a refined embedding for each component i, represented as vector Ci, tailored for thermodynamic mixture property prediction.(3) Learning mixture embeddings and preliminarly prediction
The component embeddings Ci are then individually processed by the “mixture embedding network” fα, whose outputs are then aggregated using the sum operation to yield Cmix. This step guarantees permutation invariance, i.e., independence of the order of the components, an idea inspired by deep-set models,66,67 and ensures that eqn (4) is fulfilled. Subsequently, the sum is fed into another “property prediction” network fϕ whose output gENN is a scalar that can be understood as a preliminary prediction of the molar Gibbs excess energy gE of the mixture.(4) Enforcing all physical consistency criteria
In this step, gENN is further processed to guarantee the compliance of HANNA's predictions with the remaining consistency criteria, cf.eqn (1)–(3). Step 4 basically corrects the preliminary gENN to hard-constrain the final predicted molar Gibbs excess energy gE on physically consistent solutions. Specifically, gE of the mixture of interest is calculated by: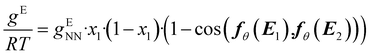 | (5) |
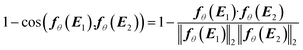 | (6) |
Finally, the logarithmic activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi are derived in a thermodynamically consistent way from gE by partial differentiation, which reads for a binary mixture:29,68
γi are derived in a thermodynamically consistent way from gE by partial differentiation, which reads for a binary mixture:29,68
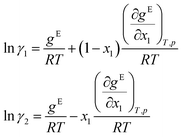 | (7) |
For this purpose, the auto-differentiation function “autograd” from pytorch69 is used to calculate ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi following eqn (7). This last step intrinsically ensures the Gibbs–Duhem consistency of the predicted activity coefficients, cf.eqn (2). Furthermore, since gE is enforced to be permutation-invariant in step 3, the differentiation in eqn (7) always yields permutation-equivariant predictions for ln
γi following eqn (7). This last step intrinsically ensures the Gibbs–Duhem consistency of the predicted activity coefficients, cf.eqn (2). Furthermore, since gE is enforced to be permutation-invariant in step 3, the differentiation in eqn (7) always yields permutation-equivariant predictions for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi.
γi.
HANNA was trained end-to-end and evaluated on 317![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 421 data points for ln
421 data points for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi in 35
γi in 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 012 binary systems from the Dortmund Data Bank (DDB),70cf. Section Data for details. The data set was randomly split system-wise in 80% training, 10% validation, and 10% test set. Technical details on HANNA and the optimization procedure are given in Section Data splitting, training, and evaluation of the model. We also trained and validated a version of HANNA on 100% of the data with the final set of hyperparameters. This version is not discussed or used to evaluate the predictive performance of HANNA in this work but will be provided together with this paper as an open-source version. This final version of HANNA should be used if activity coefficients in any binary mixture need to be predicted. The only inputs needed are the SMILES of the components, their mole fractions, and the temperature.
012 binary systems from the Dortmund Data Bank (DDB),70cf. Section Data for details. The data set was randomly split system-wise in 80% training, 10% validation, and 10% test set. Technical details on HANNA and the optimization procedure are given in Section Data splitting, training, and evaluation of the model. We also trained and validated a version of HANNA on 100% of the data with the final set of hyperparameters. This version is not discussed or used to evaluate the predictive performance of HANNA in this work but will be provided together with this paper as an open-source version. This final version of HANNA should be used if activity coefficients in any binary mixture need to be predicted. The only inputs needed are the SMILES of the components, their mole fractions, and the temperature.
Results
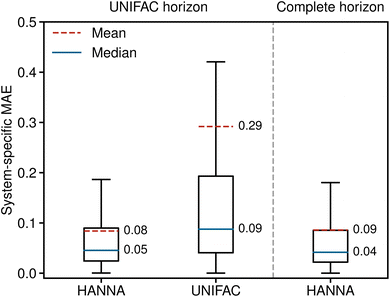
In the following, we discuss the performance of HANNA for predicting activity coefficients from the test set, which were not used for training or hyperparameter optimization. For comparison, we also include the results of modified UNIFAC (Dortmund),39,40 referred to simply as UNIFAC in the following. The UNIFAC training set has not been disclosed. However, since the groups developing UNIFAC and maintaining the DDB are essentially the same, one can assume that a large share of the data considered here was also used for training UNIFAC. Hence, contrary to the results of HANNA, the results obtained with UNIFAC cannot be considered true predictions. This generates a strong bias of the comparison in favor of UNIFAC.We compare the performance of the models using a system-wise error score. Specifically, we calculate system-specific mean absolute errors (MAE) by averaging the absolute deviations of the predicted logarithmic activity coefficients from the experimental data for each system from the test set. This procedure ensures equal weighting of all systems irrespective of the number of data points and prevents overweighting well-studied systems like water + ethanol. All 3502 systems in the test set can be predicted with HANNA, but due to missing parameters, only 1658 can be modeled with UNIFAC. Therefore, both models are compared on the smaller shared horizon, called the “UNIFAC horizon” in the following.
Fig. 2 shows the system-specific MAE of the predicted logarithmic activity coefficients in boxplots; the whisker length is 1.5 times the interquartile range. Outliers are not depicted for improved visibility. The left panel of Fig. 2 shows the results for the UNIFAC horizon, i.e., for the data points that can be predicted with both models. HANNA significantly outperforms UNIFAC, with a mean MAE reduced to approximately a third of UNIFAC's, particularly indicating a reduced number of very poorly predicted data points. Furthermore, the significantly reduced median MAE (from 0.09 to 0.05) indicates higher overall accuracy than UNIFAC. Fig. 2 (right) shows that the performance of our model on all test data (“complete horizon”), including those that cannot be predicted with UNIFAC, is similar to the UNIFAC-horizon performance. In Fig. S.7 in the ESI,† we show the robustness of HANNA over different random seeds for data splitting.
As each data point in the test set corresponds to a binary system, three different cases can occur:
(1) Only the combination of the two components is new, i.e., the respective system was not present in the training or validation data. However, for both components, some data (in other systems) were used for training or validation.
(2) One component is unknown, i.e., only for one of the components, some data (in other systems) were used during training or validation.
(3) Both components are unknown, i.e., no data for any of the components (in any system) were used during training or validation.
While we do not differentiate between these cases in Fig. 2, we demonstrate in Fig. S.6 in the ESI† that HANNA significantly outperforms UNIFAC in extrapolating to unknown components.
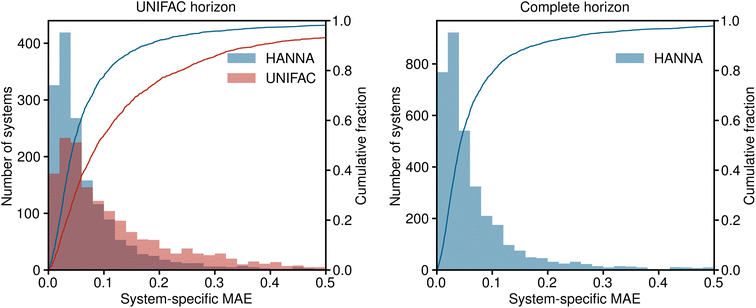
In Fig. 3, the results for the test set are shown in a histogram representation of the system-specific MAE. Furthermore, the cumulative fraction, i.e., the share of all test systems that can be predicted with an MAE smaller than the indicated value, is shown in Fig. 3. Again, in the left panel, the predictions of HANNA are compared to those of UNIFAC on the UNIFAC horizon; in the right panel, the predictions of HANNA for the complete test set are shown. The results underpin the improved prediction accuracy of HANNA compared to UNIFAC, e.g., while approximately 78% of the test systems on the UNIFAC horizon can be predicted with an MAE < 0.1 with HANNA, which is in the range of typical experimental uncertainties for activity coefficients, this is the case for only approximately 54% with UNIFAC.
Fig. 4 shows detailed results for five isothermal systems of the test set. In addition to the predicted activity coefficients as a function of the composition of the mixtures (middle panel), the corresponding Gibbs excess energies are plotted (left panel), which are internally predicted in HANNA, cf.Fig. 1. Furthermore, the respective vapor–liquid phase diagrams obtained with the predicted activity coefficients are shown (right panel), cf. Section Data for computational details. In all cases, HANNA's predictions (lines) are compared to experimental test data (symbols) from the DDB.
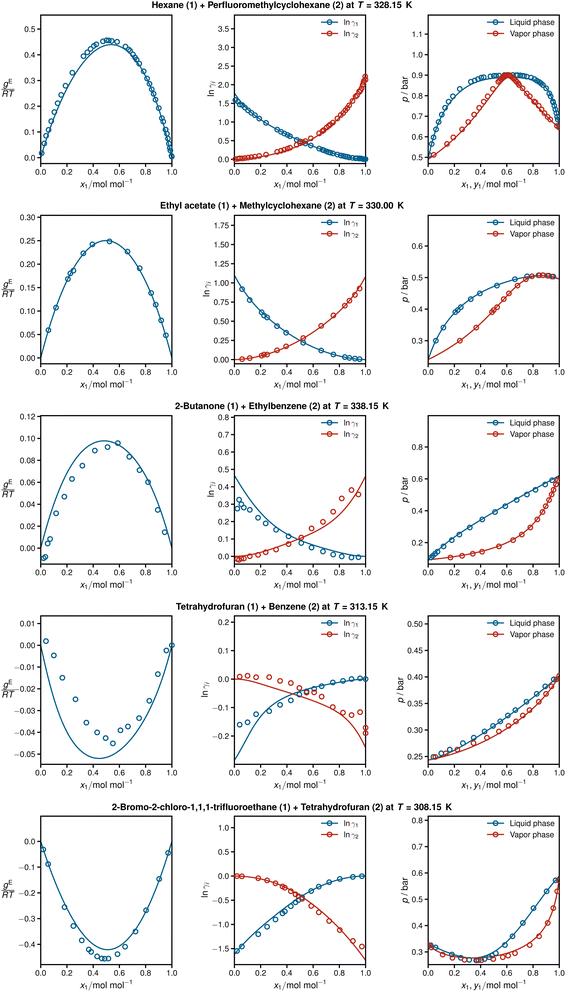 | ||
Fig. 4 From left to right: Gibbs excess energies  resulting logarithmic activity coefficients ln resulting logarithmic activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi, and isothermal vapor–liquid phase diagrams for five systems from the test set plotted as a function of x1 as predicted with HANNA (lines) and comparison to experimental test data from the DDB70 (symbols). No data for any of the depicted systems were used for training or hyperparameter optimization. γi, and isothermal vapor–liquid phase diagrams for five systems from the test set plotted as a function of x1 as predicted with HANNA (lines) and comparison to experimental test data from the DDB70 (symbols). No data for any of the depicted systems were used for training or hyperparameter optimization. | ||
The shown systems were chosen randomly from the test set, aiming to cover various phase behaviours from low-boiling azeotropes (top), through approximately ideal systems (middle), to high-boiling azeotropes (bottom). In all cases, excellent agreement is found between the predictions and the experimental data. The results also demonstrate the thermodynamic consistency of HANNA: gE = 0 and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi = 0 for the pure components, and the Gibbs–Duhem equation is fulfilled throughout.
γi = 0 for the pure components, and the Gibbs–Duhem equation is fulfilled throughout.
In Section Ablation studies in the ESI,† results of ablation studies for which different parts in HANNA have been removed are presented. These results demonstrate the importance of hard-coding physical knowledge in the architecture of HANNA, not only regarding the thermodynamic consistency of the predictions but also regarding the predictive accuracy. Overall, the results clearly underpin the power of the hybrid approach, which combines the strengths of flexible NNs with that of physical knowledge. Given that our space of possible binary mixtures is easily in the millions, even if we only take components with experimental data on activity coefficients into account, it is remarkable that HANNA can generalize well based on only a fraction of about 1% of the binary systems.
Conclusion
This work introduces a novel type of thermodynamic models: a hard-constraint neural network (NN) model combining the flexibility of NNs with rigorous thermodynamics. We demonstrate this for an essential thermodynamic modeling task: predicting activity coefficients in binary mixtures. The new hybrid model, HANNA, incorporates thermodynamic knowledge directly into the NN architecture to ensure strict thermodynamic consistency. HANNA was trained end-to-end on comprehensive data from the Dortmund Data Bank (DDB).HANNA enables thermodynamically consistent predictions for activity coefficients in any binary mixture whose components can be represented as SMILES strings. It is fully disclosed and can be used freely. The predictive capacity of HANNA was demonstrated using test data from the DDB that were not used in model development and training. HANNA clearly outperforms the best physical model for predicting activity coefficients, modified UNIFAC (Dortmund), not only in terms of prediction accuracy but also regarding the range in which it can be applied, which is basically unlimited for HANNA but restricted for UNIFAC by the availability of parameters. Only about 50% of the mixtures in the test data set could be modeled with UNIFAC, while all could be predicted with HANNA.
Now that the path for developing hard-constraint NNs in thermodynamics is clear, many exciting options exist. As the framework presented here is based on the Gibbs excess energy, the Gibbs–Helmholtz equation is implicitly considered so that HANNA can be easily extended to also include excess enthalpies, which is expected to improve the description of the temperature dependence of the activity coefficients. Furthermore, not only enthalpies of mixing could be incorporated, but other types of thermodynamic data could also be used, e.g., activity coefficients determined from liquid–liquid equilibria. The approach described here could also be extended to multicomponent mixtures. However, this can already be achieved by using HANNA to predict the binary subsystems and employing established physical models based on pair interactions for extrapolating to multicomponent mixtures.
Finally, the approach described here for Gibbs excess energy models can also be transferred to other thermodynamic modeling approaches, e.g., equations of state based on the Helmholtz energy. More broadly, it could be adapted to merge physical theory with NNs in other scientific fields.
Methods
Data
Experimental data on vapor–liquid equilibria (VLE) and activity coefficients at infinite dilution in binary mixtures were taken from the Dortmund Data Bank (DDB).70 In preprocessing, data points labeled as poor quality by the DDB were excluded. Furthermore, only components for which a canonical SMILES string could be generated with RDKit71 from mol-files from DDB were considered.From the VLE data, activity coefficients were calculated with extended Raoult's law:
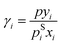 | (8) |
The final data set after preprocessing comprises 317![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 421 data points and covers 35
421 data points and covers 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 012 binary systems and 2677 individual components.
012 binary systems and 2677 individual components.
ChemBERTa-2 embeddings
The numerical embeddings of the components were generated from a pretrained language model called ChemBERTa-2,65 which was trained on a large database of SMILES. We used the “77M-MTR” model that is openly available on Huggingface.72 The “77M-MTR” model used 77 million SMILES to train ChemBERTa-2 in a multiregression task using the CLS token embedding.65 We use the CLS token embedding of the last layer of ChemBERTa-2, which results in a 384-dimensional input vector Ei for each pure component i, cf.Fig. 1. The maximum number of tokens, i.e., the individual SMILES building blocks used by ChemBERTa-2, was set to 512. The tokenization process of the original ChemBERTa-2 was slightly adapted here as explained in detail in Section Improved tokenization of ChemBERTa-2 in the ESI† due to an error in the default tokenizer.Data splitting, training, and evaluation of the model
For training and evaluating the hybrid model HANNA, the data set was split randomly system-wise as follows: all data points for 80% of the binary systems (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 009) were used for training, all data points for another 10% of the systems (3501) were used for validation and hyperparameter optimization, and all data points for the remaining 10% of the systems (3502) were used to test the model. The data split was carried out system-wise, i.e., all data points for an individual system are only present in a single set (training, validation, or test). This procedure ensures a fair evaluation of our model on truly unseen systems in the test set. The splitting of the systems to the different sets was completely random. In Fig. S.7 in the ESI,† we demonstrate the robustness of HANNA for different random splittings of the data set.
009) were used for training, all data points for another 10% of the systems (3501) were used for validation and hyperparameter optimization, and all data points for the remaining 10% of the systems (3502) were used to test the model. The data split was carried out system-wise, i.e., all data points for an individual system are only present in a single set (training, validation, or test). This procedure ensures a fair evaluation of our model on truly unseen systems in the test set. The splitting of the systems to the different sets was completely random. In Fig. S.7 in the ESI,† we demonstrate the robustness of HANNA for different random splittings of the data set.
All models and training and evaluation scripts were implemented in Python 3.8.18 using PyTorch 2.1.2.69 The models were trained on one A40 GPU using the AdamW73 optimizer with an initial learning rate of 0.0005 or 0.001, a learning rate scheduler with a decay factor of 0.1, and a patience of 10 epochs based on the validation loss. The training was stopped if the validation loss (cf. below) was not improving for 30 epochs (early stopping), and the model with the best validation loss was chosen. Typical training times for the model were between 30 and 60 minutes.
The pure-component embedding network fθ and the property network fϕ consist of one hidden layer, whereas the mixture embedding network fα consists of two hidden layers, cf.Fig. 1. In all cases, the Sigmoid Linear Unit (SiLU) function with default PyTorch settings was used as the activation function.
The models are using the same number of nodes in each layer, except for the mixture embedding network fα, where the input size is increased by two to include the standardized temperature and mole fraction of the respective component. Also, the output dimension of the property network fϕ is always one.
The embeddings of ChemBERTa-2 and the temperature in the training set were standardized using the StandardScaler from scikit-learn 1.3.0,74 whereas the mole fractions remained unchanged. The loss function SmoothL1Loss from PyTorch69 was used to mitigate the effect of experimental outliers of the activity coefficients. The hyperparameter β that controls the change between the L2 and L1 loss in the SmoothL1Loss was set to 0.25 and not varied. A batch size of 512 was used. The AdamW optimizer was used to update the NN weights during training. Besides the early stopping, the validation loss was used for hyperparameter tuning. The only varied hyperparameters were the weight decay parameter λ in the AdamW optimizer, the number of nodes in each network, and the initial learning rate, cf. above. Based on the results of the validation set, λ = 0.01 and 96 nodes with an initial learning rate of 0.001 were chosen. In the ESI† in Section Hyperparameter optimization, we discuss the influence of the different hyperparameters and present the validation loss results.
We provide a “final” version of HANNA with this paper that was trained as described above, except that no test set was used, i.e., 90% of all systems were used for training and 10% for validation.
Data availability
All data were taken from the Dortmund Data Bank.70 The final version of HANNA, which was trained and validated on 100% of the data (without using a test set), is available on Github (https://github.com/tspecht93/HANNA) and distributed under the MIT license.Author contributions
Thomas Specht: formal analysis, conceptualization, methodology, software, data curation, validation, writing – original draft, writing – review & editing, visualization. Mayank Nagda: methodology, software. Sophie Fellenz: formal analysis, writing – review & editing, methodology. Stephan Mandt: formal analysis, writing – review & editing, methodology, conceptualization. Hans Hasse: formal analysis, conceptualization, writing – review & editing, supervision, visualization, funding acquisition. Fabian Jirasek: formal analysis, conceptualization, methodology, writing – original draft, writing – review & editing, supervision, visualization, funding acquisition.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors gratefully acknowledge financial support by Carl Zeiss Foundation in the frame of the project “Process Engineering 4.0” (grant number P2018-02-002) and by DFG in the frame of the Priority Program SPP2363 “Molecular Machine Learning” (grant number 497201843). Furthermore, FJ gratefully acknowledges financial support by DFG in the frame of the Emmy-Noether program (grant number 528649696). SM acknowledges support from the National Science Foundation (NSF) under an NSF CAREER Award, award numbers 2003237 and 2007719, by the Department of Energy under grant DE-SC0022331.References
- S. Ravindran, Five ways deep learning has transformed image analysis, Nature, 2022, 609, 864–866, DOI:10.1038/d41586-022-02964-6.
- Y. LeCun, Y. Bengio and G. Hinton, Deep learning, Nature, 2015, 521, 436–444, DOI:10.1038/nature14539.
- J. Jumper, et al., Highly accurate protein structure prediction with AlphaFold, Nature, 2021, 596, 583–589, DOI:10.1038/s41586-021-03819-2.
- J. Abramson, et al., Accurate structure prediction of biomolecular interactions with AlphaFold 3, Nature, 2024, 630, 493–500, DOI:10.1038/s41586-024-07487-w.
- A. M. Bran, et al., Augmenting large language models with chemistry tools, Nat. Mach. Intell., 2024, 6, 525–535, DOI:10.1038/s42256-024-00832-8.
- D. Van Veen, et al., Adapted large language models can outperform medical experts in clinical text summarization, Nat. Med., 2024, 30, 1134–1142, DOI:10.1038/s41591-024-02855-5.
- K. Hornik, M. Stinchcombe and H. White, Multilayer feedforward networks are universal approximators, Neural Network., 1989, 2, 359–366, DOI:10.1016/0893-6080(89)90020-8.
- V. Venkatasubramanian, The promise of artificial intelligence in chemical engineering: Is it here, finally?, AIChE J., 2018, 65, 466–478, DOI:10.1002/aic.16489.
- X. Fang, et al., Geometry-enhanced molecular representation learning for property prediction, Nat. Mach. Intell., 2022, 4, 127–134, DOI:10.1038/s42256-021-00438-4.
- R. Li, et al., Physics-informed deep learning for solving phonon Boltzmann transport equation with large temperature non-equilibrium, npj Comput. Mater., 2022, 8, 29, DOI:10.1038/s41524-022-00712-y.
- X. Zang, X. Zhao and B. Tang, Hierarchical molecular graph self-supervised learning for property prediction, Commun. Chem., 2023, 6, 34, DOI:10.1038/s42004-023-00825-5.
- A. M. Schweidtmann, Generative artificial intelligence in chemical engineering, Nat. Chem. Eng., 2024, 1, 193, DOI:10.1038/s44286-024-00041-5.
- J. G. Rittig, et al., Gibbs–Duhem-informed neural networks for binary activity coefficient prediction, Digital Discovery, 2023, 2, 1752–1767, 10.1039/d3dd00103b.
- M. Raissi, P. Perdikaris and G. Karniadakis, Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, J. Comput. Phys., 2019, 378, 686–707, DOI:10.1016/j.jcp.2018.10.045.
- G. Lin, Y. Wang and Z. Zhang, Multi-variance replica exchange SGMCMC for inverse and forward problems via Bayesian PINN, J. Comput. Phys., 2022, 460, 111173, DOI:10.1016/j.jcp.2022.111173.
- W. Zhu, et al., Neural networks enforcing physical symmetries in nonlinear dynamical lattices: The case example of the Ablowitz–Ladik model, Phys. D, 2022, 434, 133264, DOI:10.1016/j.physd.2022.133264.
- J. P. Molnar and S. J. Grauer, Flow field tomography with uncertainty quantification using a Bayesian physics-informed neural network, Meas. Sci. Technol., 2022, 33, 065305, DOI:10.1088/1361-6501/ac5437.
- A. F. Psaros, K. Kawaguchi and G. E. Karniadakis, Meta-learning PINN loss functions, J. Comput. Phys., 2022, 458, 111121, DOI:10.1016/j.jcp.2022.111121.
- J. Martin and H. Schaub, Physics-informed neural networks for gravity field modeling of the Earth and Moon, Celestial Mech. Dyn. Astron., 2022, 134, 13, DOI:10.1007/s10569-022-10069-5.
- Z. Zhao, et al., Full-field temperature recovery during water quenching processes via physics-informed machine learning, J. Mater. Process. Technol., 2022, 303, 117534, DOI:10.1016/j.jmatprotec.2022.117534.
- G. E. Karniadakis, et al., Physics-informed machine learning, Nat. Rev. Phys., 2021, 3, 422–440, DOI:10.1038/s42254-021-00314-5.
- K. Xu and E. Darve, Physics constrained learning for data-driven inverse modeling from sparse observations, arXiv, 2020, preprint, arXiv:2002.10521, DOI:10.48550/ARXIV.2002.10521.
- Y. Chen, et al., Theory-guided hard constraint projection (HCP): A knowledge-based data-driven scientific machine learning method, J. Comput. Phys., 2021, 445, 110624, DOI:10.1016/j.jcp.2021.110624.
- Y. Chen and D. Zhang, Physics-constrained indirect supervised learning, Theor. Appl. Mech. Lett., 2020, 10, 155–160, DOI:10.1016/j.taml.2020.01.019.
- P. Márquez-Neila, M. Salzmann and P. Fua, Imposing hard constraints on deep networks: promises and limitations, arXiv, 2017, preprint, arXiv:1706.02025, DOI:10.48550/ARXIV.1706.02025.
- L. Lu, et al., Physics-informed neural networks with hard constraints for inverse design, SIAM J. Sci. Comput., 2021, 43, B1105–B1132, DOI:10.1137/21m1397908.
- M. Dyga, A. Keller and H. Hasse, Vapor–liquid equilibria and chemical equilibria in the system (formaldehyde + water + isoprenol), Ind. Eng. Chem. Res., 2021, 60, 4471–4483, DOI:10.1021/acs.iecr.1c00168.
- M. Dyga, A. Keller and H. Hasse, 13C-NMR spectroscopic study of the kinetics of formaldehyde oligomerization reactions in the system (formaldehyde + water + isoprenol), Ind. Eng. Chem. Res., 2021, 61, 224–235, DOI:10.1021/acs.iecr.1c03911.
- J. Gmehling, et al., Chemical thermodynamics for process simulation, John Wiley & Sons, 2nd edn, 2019 Search PubMed.
- N. Hayer and M. Kohns, Thermodynamically rigorous description of the open circuit voltage of redox flow batteries, J. Electrochem. Soc., 2020, 167, 110516, DOI:10.1149/1945-7111/ab9e85.
- J. Heiß and M. Kohns, Open circuit voltage of an all-vanadium redox flow battery as a function of the state of charge obtained from UV-Vis spectroscopy, Energy Adv., 2024, 3, 2597–2603, 10.1039/d4ya00360h.
- H. Renon and J. M. Prausnitz, Local compositions in thermodynamic excess functions for liquid mixtures, AIChE J., 1968, 14, 135–144, DOI:10.1002/aic.690140124.
- D. S. Abrams and J. M. Prausnitz, Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems, AIChE J., 1975, 21, 116–128, DOI:10.1002/aic.690210115.
- A. Klamt, Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena, J. Phys. Chem., 1995, 99, 2224–2235, DOI:10.1021/j100007a062.
- S.-T. Lin and S. I. Sandler, A priori phase equilibrium prediction from a segment contribution solvation model, Ind. Eng. Chem. Res., 2001, 41, 899–913, DOI:10.1021/ie001047w.
- C.-M. Hsieh, S. I. Sandler and S.-T. Lin, Improvements of COSMO-SAC for vapor–liquid and liquid–liquid equilibrium predictions, Fluid Phase Equilib., 2010, 297, 90–97, DOI:10.1016/j.fluid.2010.06.011.
- C.-M. Hsieh, S.-T. Lin and J. Vrabec, Considering the dispersive interactions in the COSMO-SAC model for more accurate predictions of fluid phase behavior, Fluid Phase Equilib., 2014, 367, 109–116, DOI:10.1016/j.fluid.2014.01.032.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, Group-contribution estimation of activity coefficients in nonideal liquid mixtures, AIChE J., 1975, 21, 1086–1099, DOI:10.1002/aic.690210607.
- U. Weidlich and J. Gmehling, A modified UNIFAC model. 1. Prediction of VLE, hE, and γ∞, Ind. Eng. Chem. Res., 1987, 26, 1372–1381, DOI:10.1021/ie00067a018.
- D. Constantinescu and J. Gmehling, Further development of modified UNIFAC (Dortmund): Revision and extension 6, J. Chem. Eng. Data, 2016, 61, 2738–2748, DOI:10.1021/acs.jced.6b00136.
- R. Fingerhut, et al., Comprehensive assessment of COSMO-SAC models for predictions of fluid-phase equilibria, Ind. Eng. Chem. Res., 2017, 56, 9868–9884, DOI:10.1021/acs.iecr.7b01360.
- F. Jirasek, R. Bamler and S. Mandt, Hybridizing physical and data-driven prediction methods for physicochemical properties, Chem. Commun., 2020, 56, 12407–12410, 10.1039/d0cc05258b.
- F. Jirasek, et al., Machine learning in thermodynamics: Prediction of activity coefficients by matrix completion, J. Phys. Chem. Lett., 2020, 11, 981–985, DOI:10.1021/acs.jpclett.9b03657.
- J. Damay, et al., Predicting temperature-dependent activity coefficients at infinite dilution using tensor completion, Chem. Ing. Tech., 2023, 95, 1061–1069, DOI:10.1002/cite.202200230.
- E. I. Sanchez Medina, et al., Graph neural networks for the prediction of infinite dilution activity coefficients, Digital Discovery, 2022, 1, 216–225, 10.1039/d1dd00037c.
- V. V. Santana, et al., PUFFIN: A path-unifying feed-forward interfaced network for vapor pressure prediction, Chem. Eng. Sci., 2024, 286, 119623, DOI:10.1016/j.ces.2023.119623.
- J. Habicht, C. Brandenbusch and G. Sadowski, Predicting PC-SAFT pure-component parameters by machine learning using a molecular fingerprint as key input, Fluid Phase Equilib., 2023, 565, 113657, DOI:10.1016/j.fluid.2022.113657.
- J. Deng, et al., A systematic study of key elements underlying molecular property prediction, Nat. Commun., 2023, 14, 6395, DOI:10.1038/s41467-023-41948-6.
- S. Shilpa, G. Kashyap and R. B. Sunoj, Recent applications of machine learning in molecular property and chemical reaction outcome predictions, J. Phys. Chem. A, 2023, 127, 8253–8271, DOI:10.1021/acs.jpca.3c04779.
- A. R. N. Aouichaoui, et al., Combining group-contribution concept and graph neural networks toward interpretable molecular property models, J. Chem. Inf. Model., 2023, 63, 725–744, DOI:10.1021/acs.jcim.2c01091.
- N. Hayer, F. Jirasek and H. Hasse, Prediction of Henry’s law constants by matrix completion, AIChE J., 2022, 68, e17753, DOI:10.1002/aic.17753.
- O. Großmann, et al., Database for liquid phase diffusion coefficients at infinite dilution at 298 K and matrix completion methods for their prediction, Digital Discovery, 2022, 1, 886–897, 10.1039/d2dd00073c.
- F. Jirasek and H. Hasse, Combining machine learning with physical knowledge in thermodynamic modeling of fluid mixtures, Annu. Rev. Chem. Biomol. Eng., 2023, 14, 31–51, DOI:10.1146/annurev-chembioeng-092220-025342.
- B. Winter, et al., A smile is all you need: Predicting limiting activity coefficients from SMILES with natural language processing, Digital Discovery, 2022, 1, 859–869, 10.1039/d2dd00058j.
- F. Jirasek, et al., Making thermodynamic models of mixtures predictive by machine learning: matrix completion of pair interactions, Chem. Sci., 2022, 13, 4854–4862, 10.1039/d1sc07210b.
- F. Jirasek, et al., Prediction of parameters of group contribution models of mixtures by matrix completion, Phys. Chem. Chem. Phys., 2023, 25, 1054–1062, 10.1039/d2cp04478a.
- B. Winter, et al., SPT-NRTL: A physics-guided machine learning model to predict thermodynamically consistent activity coefficients, Fluid Phase Equilib., 2023, 568, 113731, DOI:10.1016/j.fluid.2023.113731.
- J. Werner, et al., Multiplicities in thermodynamic activity coefficients, AIChE J., 2023, 69, e18251, DOI:10.1002/aic.18251.
- J. Rarey, Extended flexibility for GE models and simultaneous description of vapor-liquid equilibrium and liquid-liquid equilibrium using a nonlinear transformation of the concentration dependence, Ind. Eng. Chem. Res., 2005, 44, 7600–7608, DOI:10.1021/ie050431w.
- A. Marcilla, M. M. Olaya and M. D. Serrano, Liquid-vapor equilibrium data correlation: Part I. Pitfalls and some ideas to overcome them, Ind. Eng. Chem. Res., 2011, 50, 4077–4085, DOI:10.1021/ie101909d.
- A. Marcilla, M. Olaya and J. Reyes-Labarta, The unavoidable necessity of considering temperature dependence of the liquid Gibbs energy of mixing for certain VLE data correlations, Fluid Phase Equilib., 2018, 473, 17–31, DOI:10.1016/j.fluid.2018.05.025.
- A. Marcilla, et al., Procedure for the correlation of normal appearance VLE data, where the classical models dramatically fail with no apparent reason, Fluid Phase Equilib., 2019, 493, 88–101, DOI:10.1016/j.fluid.2019.04.001.
- J. G. Rittig and A. Mitsos, Thermodynamics-consistent graph neural networks, arXiv, 2024, preprint, arXiv:2407.18372, DOI:10.48550/ARXIV.2407.18372.
- D. Weininger, SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36, DOI:10.1021/ci00057a005.
- W. Ahmad, et al., ChemBERTa-2: towards chemical foundation models, arXiv, 2022, preprint, arXiv:2209.01712, DOI:10.48550/ARXIV.2209.01712.
- M. Zaheer, et al., Deep sets, arXiv, 2017, preprint, arXiv:1703.06114, DOI:10.48550/ARXIV.1703.06114.
- K. Hanaoka, Deep neural networks for multicomponent molecular systems, ACS Omega, 2020, 5, 21042–21053, DOI:10.1021/acsomega.0c02599.
- U. K. Deiters and T. Kraska, High-Pressure Fluid Phase Equilibria, Elsevier, 1st edn, 2012 Search PubMed.
- A. Paszke, et al., PyTorch: An imperative style, high-performance deep learning library, arXiv, 2019, preprint, arXiv:1912.01703, DOI:10.48550/ARXIV.1912.01703.
- Dortmund Data Bank, 2023, https://www.ddbst.com/.
- RDKit: Open-source cheminformatics, Last accessed: 04.04.2024, https://www.rdkit.org.
- Huggingface ChemBERTa-2 model, https://huggingface.co/DeepChem/ChemBERTa-77M-MTR, Last accessed: 05.04.2024.
- I. Loshchilov and F. Hutter, Decoupled weight decay regularization, arXiv, 2017, preprint, arXiv:1711.05101, DOI:10.48550/ARXIV.1711.05101.
- F. Pedregosa, et al., Scikit-learn: machine learning in python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc05115g |
| This journal is © The Royal Society of Chemistry 2024 |