DOI:
10.1039/D4SM00751D
(Paper)
Soft Matter, 2024,
20, 8952-8967
Formation of bijels stabilized by magnetic ellipsoidal particles in external magnetic fields
Received
19th June 2024
, Accepted 4th October 2024
First published on 8th October 2024
Abstract
Bicontinuous interfacially-jammed emulsion gels (bijels) are increasingly used as emulsion templates for the fabrication of functional porous materials including membranes, electrodes, and biomaterials. Control over the domain size and structure is highly desirable in these applications. For bijels stabilized by spherical particles, particle size and volume fraction are the main parameters that determine the emulsion structure. Here, we investigate the use of ellipsoidal magnetic particles and study the effect of external magnetic fields on the formation of bijels. Using hybrid Lattice Boltzmann-molecular dynamics simulations, we analyze the effect of the magnetic field on emulsion dynamics and the structural properties of the resulting bijel. We find that the formation of bijels remains robust in the presence of magnetic fields, and that the domain size and tortuosity become anisotropic when ellipsoidal particles are used. We show that the magnetic fields lead to orientational ordering of the particles which in turn leads to alignment of the interfaces. The orientational order facilitates enhanced packing of particles in the interface which leads to different jamming times in the directions parallel and perpendicular to the field. Our results highlight the potential of magnetic particles for fabrication and processing of emulsion systems with tunable properties.
1 Introduction
Mixtures of two or more immiscible liquids commonly form emulsions whose structures can serve as templates for fabrication of porous materials, including porous polymers,1,2 porous ceramics,3,4 synthetic nanoparticles,5 and artificial tissue.6 Emulsion templating provides a facile route to tailoring the properties of porous materials by leveraging processing techniques that offer control over the volume fraction, domain size, and composition of the emulsion.7 Thermodynamic and mechanical stability are essential for processing of emulsion templates, and particle-stabilization has emerged as a viable alternative to surfactant-stabilization while avoiding potentially harmful chemicals. Emulsions stabilized by particles are commonly known as Pickering emulsions,8,9 and a variety of particle types have been used to stabilize emulsions, ranging from polystyrene colloidal particles10 to carbon nanotubes (CNTs).11
Bicontinuous interfacially stabilized emulsion gels (bijels) are a particular class of particle-stabilized emulsions with a bicontinuous domain morphology.12 Bijels emerge when a binary mixture containing particles is quenched rapidly into the phase separating region. Spinodal decomposition leads to formation of large interfaces that sequester the particles while sweeping through the system. During coarsening of the phases, the particles become jammed and arrest the phase-separation, locking in the bicontinuous phase morphology. Bijels were first discovered in simulations13 and subsequently realized in water–lutidine mixtures with silica particles.14,15 A range of robust and versatile formulations of bijels have since been developed.16–18 For example, Haase et al.19 used solvent transfer-induced phase separation (STRIPS) as a versatile and scalable technique that combines separation with an imposed flow that offers control over the formation of droplets and jets. Following these fundamental developments, bijels have gained popularity as emulsion templates for the fabrication of functional porous materials including membranes,19–21 electrodes,22,23 and biomaterials.6,24,25
Anisotropic particles, when adsorbed at liquid interfaces, induce shape-dependent capillary interactions that can have a distinct effect on the microstructure of emulsions.26,27 For instance, Madivala et al.28,29 found that emulsion stability can be significantly enhanced by ellipsoidal particles. Additionally, capillary interactions can lead to direct assembly of anisotropic particles.30–33 Ellipsoidal particles can rotate and migrate on curved surfaces,34 where the interface curvature acts as an external field that controls the orientation and placement of particles.35 Anisotropic particles at fluid interfaces were considered in Monte Carlo simulations by Bresme et al. to test the accuracy of thermodynamic models for the free energy as a function of the particle–fluid interactions, particle size, and orientation.36,37 Harting and co-workers38,39 have performed lattice Boltzmann simulations of anisotropic particles at liquid interfaces and in emulsions. They found that anisotropic particles affect the dynamics of emulsion formation by introducing two additional timescales associated with particle rotation. Following initial adsorption, particles rotate to align their larger cross-section with the interface. When jamming sets in, capillary interactions cause the particle to re-orient in the interface leading to prolonged coarsening at long timescales. Due to the larger aspect ratio, ellipsoidal particles can stabilize a larger interface area leading to smaller domain sizes. Hijnen et al.40 experimentally realized bijels stabilized by colloidal rods and analyzed their effect on the interface and domain morphology. Their experiments confirmed that jamming occurs at lower interface separations than for spherical particles with the same volume fraction. Moreover, they observed that the overall structure remains isotropic and attributed this to the rapid jamming of the rods. Additionally, they found that some rods tilted out of the interface due to the compression induced by domain coarsening.
Particle-stabilized emulsions can be made responsive to external magnetic fields by magnetic particles.41,42 An external field can then be used to control the stability of the emulsion41 and the self-assembly of particles.43,44 The tendency of anisotropic particles to adopt distinct orientations gives rise to an orientation transition when an external field is applied.45–47 Magnetic fields thus offer a means to control the capillary interactions of ellipsoidal particles at an interface. For bijels stabilized by spherical magnetic particles, simulations by Kim et al.48 revealed that magnetic fields do not have a significant effect on the microstructure of bijels. In contrast, Carmack and Millett49 demonstrated that the structure of thin-film bijels stabilized by dielectric particles can change drastically when an external electric field is applied. The dielectric contrast of the particles induces polar interactions that cause liquid domain alignment leading to percolating cylindrical domains in the thin-film bijel. In addition, they found that particle chains can act as nucleation sites for phase separation. This suggests that anisotropic interactions can have a considerable effect on the phase separation and the resulting emulsion morphology and may offer a means to control the size and shape of liquid domains.
In this work, we investigate the effect of external magnetic fields on the formation of bijels stabilized by anisotropic magnetic particles. We performed hybrid Lattice Boltzmann-molecular dynamics simulations of a binary liquid with suspended anisotropic particles that possess a permanent magnetic dipole moment along their symmetry axis. We analyzed the structural properties of bijels that form with oblate, spherical, and prolate particles in magnetic fields at different flux densities. The results show that, while the overall bijel formation is not disrupted by the magnetic field, the resulting domain morphology varies depending on the particle aspect ratio and the magnetic flux density. Notably, the average domain spacing and tortuosity of the bijel become anisotropic. Analysis of the orientational order reveals that the kinetic formation of the bijel is governed by rotation of particles due to the magnetic field, which in turn causes a re-alignment of the liquid domains. The increased orientational order within the interfaces facilitates particle packing and delays the onset of jamming. The resulting interfacial particle arrangement exhibits a higher degree of structural order compared with bijels formed in the absence of a magnetic field. These results demonstrate the potential of magnetic particles in fabricating emulsion systems with tunable domain structure.
2 Methods
2.1 Lattice Boltzmann method for binary mixture
We employed a multicomponent lattice Boltzmann model to simulate an immiscible binary fluid. In the multicomponent lattice Boltzmann method,50–52 each fluid component k is represented by populations fki(x, t) that evolve in discrete timesteps Δt on a cubic lattice with lattice spacing Δx. The populations fki are associated with discrete velocities ci such that ciΔt connects the lattice sites, and fki(x, t) represents the density of fluid k at lattice site x and time t that is moving with velocity ci. In this work, we use the D3Q19 velocity set53 that connects nearest and next-nearest neighbors on the lattice and includes a rest population fk0 associated with c0 = 0. The evolution of the populations is governed by the lattice Boltzmann equation with a BGK collision term54| | 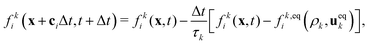 | (1) |
where fk,eqi(ρk, ueqk) denotes an equilibrium distribution that depends on the local fluid density 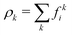 and velocity ueqk (specified below). The equilibrium distribution fk,eqi = feqi is written as a polynomial expansion in the velocity
and velocity ueqk (specified below). The equilibrium distribution fk,eqi = feqi is written as a polynomial expansion in the velocity| | 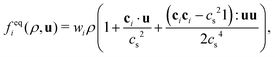 | (2) |
where wi = w|ci| are lattice weights and cs is the (pseudo-)speed of sound. For the D3Q19 model, the weights are 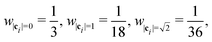 and the speed of sound is
and the speed of sound is 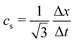 .
.
To incorporate nonideal interactions, we adopt the Shan–Chen model50,55 and introduce momentum transfer between the fluid components in terms of a non-local interaction force
| | 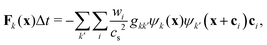 | (3) |
where
ψk(
x) =
ψ(
ρk(
x)) represents the effective density of the fluid component
k taken as the function
| | 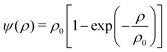 | (4) |
with a reference density
ρ0. The momentum change caused by the force is incorporated in the lattice Boltzmann equation by defining the velocity to be used in the calculation of the equilibrium distribution
fk,eqi as
| | 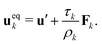 | (5) |
The common velocity
u′ is defined through
| | 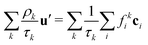 | (6) |
which ensures that in the absence of forces, the total momentum of all components is conserved. The total mass density and momentum of the fluid are given by
51| | 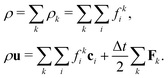 | (7) |
The macroscopic transport equations can be obtained by carrying out a Chapman–Enskog expansion. For the multicomponent model introduced above, it yields the mass and momentum equation for the binary fluid mixture51,56
| | 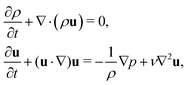 | (8) |
where the pressure
p is given by the nonideal equation of state
| | 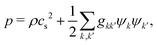 | (9) |
and the kinematic viscosity of the fluid is given by
| | 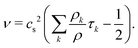 | (10) |
In a binary fluid, the density profile of the components can be described by a single order parameter 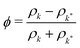 that is governed by a diffusion equation. For an incompressible fluid, we have
that is governed by a diffusion equation. For an incompressible fluid, we have 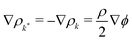 . In this work, we use equal relaxation times τ = τk = τk* for both fluids. We also set the self-interactions to zero gkk = gk*k* = 0 and use a single interaction parameter g = gkk* = gk*k. The diffusion equation for the order parameter simplifies to50
. In this work, we use equal relaxation times τ = τk = τk* for both fluids. We also set the self-interactions to zero gkk = gk*k* = 0 and use a single interaction parameter g = gkk* = gk*k. The diffusion equation for the order parameter simplifies to50
| | 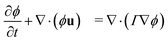 | (11) |
with an order parameter diffusivity
| | 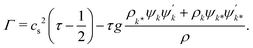 | (12) |
In addition to a non-ideal equation of state, the Shan–Chen force also leads to a surface tension at the interface between two immiscible components. The surface tension σ depends on the interaction parameters gkk* and can formally be obtained from the full pressure tensor P by integrating over a planar interface55,57
| | 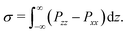 | (13) |
In practice, it is common to determine the value of
σ for a chosen
gkk* by performing a simulation of a spherical droplet and using the Young–Laplace equation to calculate the surface tension from the measured droplet radius and pressure drop across its interface. We have taken this route and report the measured surface tension in Section 2.2.4.
2.2 Suspended colloidal particles
Suspended particles can be coupled to the lattice Boltzmann fluid by the approach pioneered by Ladd58–61 and Aidun.62 The particles are assumed to be rigid bodies that evolve according to Newton's equation of motion| | 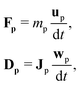 | (14) |
where Fp and Dp are the force and torque acting on the particle, up and ωp are the linear and angular velocity, and mp and Jp the mass and moment of inertia. Eqn (14) can be solved using a standard MD integrator.63 To couple the particles to the LB fluid, the particles are overlayed on the lattice, and sites covered by the particle are marked as solid nodes. LB populations that move along velocities connecting fluid and solid nodes are updated according to a moving bounce-back boundary condition, i.e., if x is a fluid node and x + ciΔt is a solid node, the propagation step is modified to| | 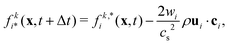 | (15) |
where ci* = −ci and 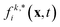 is the post-collision population, and ui = up + ω × ri is the velocity of the particle surface at
is the post-collision population, and ui = up + ω × ri is the velocity of the particle surface at 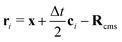 with Rcms the particle's center of mass. The momentum change
with Rcms the particle's center of mass. The momentum change 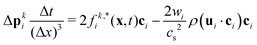 associated with the bounce-back of both fluid components is summed over the surface of the particle to obtain the force and torque on the particle
associated with the bounce-back of both fluid components is summed over the surface of the particle to obtain the force and torque on the particle| | 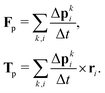 | (16) |
As the particle moves over the lattice, it covers and uncovers individual lattice sites which then turn from fluid into solid nodes and vice versa. When a lattice site x becomes covered, its momentum is transferred to the particle by a force| | 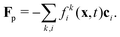 | (17) |
When a lattice site x becomes uncovered, it is filled with the average density of Nf neighboring fluid nodes at x + cif| | 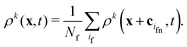 | (18) |
To evaluate the Shan–Chen force (3) at particle surfaces, we use the same expression for assigning a virtual density ρkv(x, t) to the outer shell of solid nodes inside the particle. An additional shift Δρ in the density of either fluid component can be imposed to control the fluid contact angle at the particle surface.64,65
2.2.1 Particles near contact.
For particles close to contact, we add a lubrication force to account for the unresolved hydrodynamics. The lubrication correction is added to particle pairs that are separated by a gap d smaller than a cutoff dc and is given as61,66| | 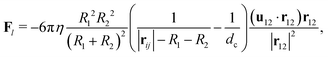 | (19) |
where u12 = u1 − u2 is the relative velocity, r12 is the vector connecting the centers of the particles, and d = |r12| − R1 − R2 is the gap between the particle surfaces with curvature radii R1 and R2. Despite the repulsive nature of the the lubrication forces, particle overlaps can still occur in numerical simulations. To address the possibility of particle contact and overlap, we add a Hertz force FH = −∇ϕH to the particle–particle interactions, which is derived from the Hertz potential| | 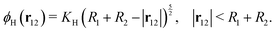 | (20) |
2.2.2 Ansiotropic particles.
The interparticle forces (19) and (20) can be generalized for ellipsoidal particles following Günther et al.38,39 who adopted an approach proposed by Berne et al.67,68 We first rescale the potential and force such that| | 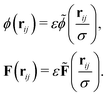 | (21) |
For the lubrication force (19), we choose σ = R1 + R2 and 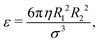 and for the Hertz potential we chose σ = R1 + R2 and ε = KHσ5/2. For two identical, rotationally symmetric ellipsoidal particles with orientations ôi and ôj, we then replace ε and σ by the anisotropic functions
and for the Hertz potential we chose σ = R1 + R2 and ε = KHσ5/2. For two identical, rotationally symmetric ellipsoidal particles with orientations ôi and ôj, we then replace ε and σ by the anisotropic functions| | 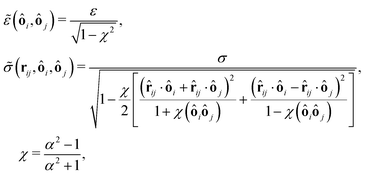 | (22) |
where R‖ is the particle radius along the symmetry axis ô and α = R‖/R⊥ the aspect ratio of the particle. The anisotropic Hertz potential and lubrication force are then defined as| | 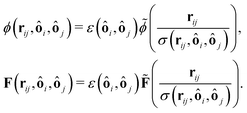 | (23) |
2.2.3 Magnetic particles and magnetic fields.
Particles with a constant magnetic dipole moment m = mô have been considered by Harting and coworkers.46,69–71 The interaction between magnetic particles is modeled by the pairwise potential between two dipoles mi and mj that are separated in space by a vector rij| | 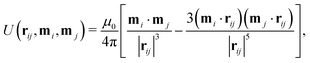 | (24) |
where μ0 is the vacuum permeability. The dipole–dipole force and torque exerted by particle j on particle i are thus| | 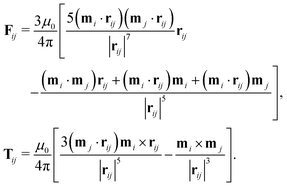 | (25) |
Here it is assumed that the dipole moment of the particles does not change in an external field and that it is oriented along the symmetry axis of ellipsoidal particles, as was observed experimentally in ref. 72 and 73 (cf. Section 2.2.4).
An external magnetic flux density B = μ0H exerts a force and a torque on each dipole
The total magnetic force and torque exerted on the particles are the sums of the dipole–dipole and field contributions.
2.2.4 Model parameters and simulation setup.
The dynamics of the binary fluid mixture is governed by inertial, viscous, and surface tension forces. The relative magnitudes of these forces at a characteristic length scale L and characteristic velocity U are captured by the capillary number 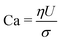 and the Weber number
and the Weber number 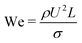 . Here we are primarily interested in spinodal decomposition of the mixture, where we analyze the dynamics after the initial formation of the interfaces and neglect residual diffusion. Hence the Peclet number
. Here we are primarily interested in spinodal decomposition of the mixture, where we analyze the dynamics after the initial formation of the interfaces and neglect residual diffusion. Hence the Peclet number 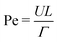 is of lesser importance and we do not consider it when choosing our simulation parameters.
is of lesser importance and we do not consider it when choosing our simulation parameters.
The equations of motion of our model comprise the relevant materials properties: the density ρ, viscosity ν, and surface tension σ of the binary fluid, and the mass mp, size Rp and aspect ratio α, and dipole moment m of the particles. In addition, we can control the particle volume fraction ϕp and magnetic field strength B. These nine quantities involve four unit dimensions (mass, length, time, and charge), hence we can use five dimensionless variables to specify the parameters of the system. These are the particle aspect ratio α, particle volume fraction ϕp, particle vs. fluid density ratio ξ = 3mp/(4πρVp), nominal Weber number Wen = ρσVp1/3/η2, and magnetic Bond number ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = mB/(σAp), where Vp = (4/3)πR‖3/α2 is the particle volume and Ap = max(πR‖2/α, πR‖2/α2) the area of the larger cross-section of the ellipsoidal particles.
= mB/(σAp), where Vp = (4/3)πR‖3/α2 is the particle volume and Ap = max(πR‖2/α, πR‖2/α2) the area of the larger cross-section of the ellipsoidal particles.
For our simulations, we choose units Δx, Δt, Δm, and Δi such that Vp = ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) p(Δx)3,
p(Δx)3, 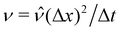 , σ =
, σ = ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) Δm/(Δt)2, and m =
Δm/(Δt)2, and m = ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) Δi(Δx)2. We used Vp = 2000π/3,
Δi(Δx)2. We used Vp = 2000π/3, 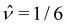 ,
, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) = 0.0267,
= 0.0267, ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) = 1, and a density ratio ξ = 1/
= 1, and a density ratio ξ = 1/![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) . For reference, the values of the model parameters are listed in Table 1. The values of α and
. For reference, the values of the model parameters are listed in Table 1. The values of α and ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) are variable and are reported with the results in Section 3.
are variable and are reported with the results in Section 3.
Table 1 Summary of the parameters of the numerical model and the values used in the simulations
| Parameter |
Value |
|
L
V/Δx |
256 |
|
ρ·(Δx)3/Δm |
0.7 |
|
ν·Δt/(Δx)2 |
1/6 |
|
σ·(Δt)2/Δm |
0.0267 |
|
τ/Δt |
1 |
|
g·Δm(Δt)2/(Δx)5 |
0.08 |
|
ϕ
f
|
0.5 |
|
ϕ
p
|
0.15 |
|
n
p
|
1200 |
|
ρ
p·(Δx)3/Δm |
1 |
|
V
p/(Δx)3 |
2000π/3 |
|
m/(Δi(Δx)2) |
1 |
|
d
c/Δx |
2/3 |
|
K
H·(Δx)1/2(Δt)2/Δm |
100 |
We performed simulations of a binary fluid using the software package LB3D,74 that implements the lattice Boltzmann method described in Section 2. The multicomponent lattice Boltzmann model is solved in a cubic box of size LV = 256Δx with periodic boundary conditions. The simulation box is filled with equal volume fractions ϕf = 0.5 of two fluids, initially homogeneously mixed with a density ρ = 0.7Δm/(Δx)3. The BGK relaxation time is set to τ = Δt and the Shan–Chen interaction strength is set to gkk* = 0.08(Δx)2/(Δm(Δt)2). We performed preliminary simulations of a spherical droplet with these parameters and fitted the pressure difference inside and outside the droplet to the Young–Laplace law, which yielded a surface tension σ = 0.0267Δm/(Δt)2. To study the influence of anisotropic particle shapes on the bijel formation, we performed simulations for particles with three different aspect ratios: α = 1 for spherical particles, α = 2 for prolate ellipsoids, and α = 1/2 for oblate ellipsoids. To match the particle volume fraction ϕp between the different particle shapes, we kept the volume of the particles fixed and used the same number of particles for each aspect ratio. The radius along the symmetry axis of the particles was calculated from Vp = (4/3)πR‖3/α2, yielding R‖ = 7.9Δx for spheres, R‖ = 12.6Δx for prolate ellipsoids, and R‖ = 5Δx for oblate ellipsoids, respectively. Particles were added to the fluid by placing them randomly inside the box. The lubrication cutoff distance was set to the value dc = (2/3)Δx recommended by Ladd,60 and the strength of the Hertz potential was set to KH = 100Δm/((Δx)1/2(Δt)2). We first equilibrated the particle positions and orientations by evolving only the equations of motion of the particles, while the fluid remained in its initial configuration, until the minimum particle distance exceeded 1.2·max(R‖, R‖/α). After the equilibration, the magnetic flux density B = Bẑ was switched on and the full system was evolved for 105 timesteps. In the course of the simulation, the binary mixture undergoes spinodal decomposition. The particles adsorb at the coarsening interface and eventually become jammed, resulting in the bicontinuous phase morphology of the bijel.
It is worth discussing briefly the possible realization of our model in experiments. A common choice for bijel formation in binary liquids is a mixture of water and lutidine.14,15 The surface tension between the phases of a water–lutidine system at 40 °C is around σ = 0.22 mN m−1 and the dynamic viscosity of the lutidine-rich phase is around η = 2.38 mPa s.75 Ellipsoidal particles with various aspect ratios can be formed by mechanically stretching spherical particles.76 Such particles can be magnetically functionalized by e-beam deposition of a Nickel layer. Fei et al.77,78 fabricated coated 4 μm polystyrene particles with a permanent magnetic dipole moment of m ≈ 3 × 10−14 A m2. It was shown that the dipole moment is oriented in the direction parallel to the coated interface,72,73i.e., it can be aligned with the axis of ellipsoidal particles. For the given surface tension, the capillary torque on a particle adsorbed at an interface is approximately 8.8 × 10−16 N m. We thus can estimate that a magnetic flux density of 30 mT is able to exert a magnetic torque that exceeds the capillary torque. We note that under these conditions, the dipole–dipole interaction is on the order of 10−16 J and an order of magnitude smaller than the particle-interface interaction which is of order 10−15 J. For these bijel properties and the parameters given in Table 1, the spatial resolution of our simulations is Δx ≈ 252 nm, and the time step is Δt = 624 ns. This corresponds to a system side length of LV ≈ 64.5 μm and a runtime of T ≈ 62.4 ms.
3 Results
Bijels can be used as emulsion templates for porous materials with applications including drug delivery, water desalination, and battery electrodes.79–82 The transport properties of porous materials depend on the porosity and tortuosity of the void space and can be linked to the phase-separated morphology of the bijel template. Therefore, we study the domain size and tortuosity of the phase morphology of bijels stabilized by anisotropic particles. In particular, we investigate the effect of magnetic particles on the microstructure of bijels that are formed in external magnetic fields. We simulated bijels with a particle volume fraction of ϕp = 0.15 and varied the magnetic flux density such that the Bond numbers varies in the range 0 ≤ ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) ≤ 1. In this work, we use a fixed particle volume fraction and focus on the dependence of the bijel structure on the magnetic field. Bijels with varying particle loading and surface tension and have been studied elsewhere in the literature, e.g., by Hijnen et al.40 and Jansen and Harting.65
≤ 1. In this work, we use a fixed particle volume fraction and focus on the dependence of the bijel structure on the magnetic field. Bijels with varying particle loading and surface tension and have been studied elsewhere in the literature, e.g., by Hijnen et al.40 and Jansen and Harting.65
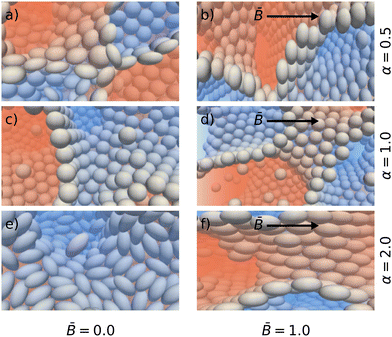
Fig. 1 shows snapshots of the bijel microstructure observed at different times with and without an external magnetic field. The figure illustrates how anisotropic particles align with the direction of the magnetic field. As the particles reorient, they can deform the interface which thus responds by rearrangements including reorientation and domain coalescence or breakup. This results in apparently larger domain sizes for bijel formation in magnetic fields. The quantitative effect on the bijel morphology, and domain size in particular, is analyzed in the following sections.
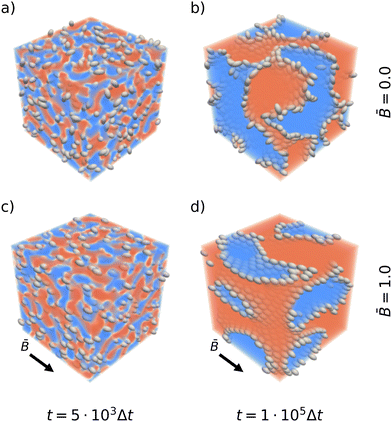 |
| | Fig. 1 Snapshots of emulsion gels stabilized by prolate ellipsoids after t = 5 × 103 timesteps (left) and after 105 timesteps (right). The top row shows the structure forming without a magnetic field. The bottom row shows the structure forming in an applied magnetic field of reduced strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 1.0. The snapshots are colored according to the order parameter ϕ. = 1.0. The snapshots are colored according to the order parameter ϕ. | |
3.1 Structure factor and domain size of magnetically responsive bijels
In LB simulations of spinodal decomposition,83,84 a characteristic length scale can be obtained from the structure factor| | S(k, t) = ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) (k, t) (k, t)![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) (−k, t) (−k, t) | (27) |
where ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) (k, t) is the Fourier transform of the order parameter fluctuations ϕ(x, t) − 〈ϕ〉. A common measure of domain size uses the spherically averaged structure factor
(k, t) is the Fourier transform of the order parameter fluctuations ϕ(x, t) − 〈ϕ〉. A common measure of domain size uses the spherically averaged structure factor| | 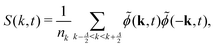 | (28) |
where k = |k| denotes the modulus of k and nk is the number of lattice sites in a shell of radius k and thickness Δ = 2π/LV. The average domain size can then be defined in terms of the n-th moment of the structure factor85| | 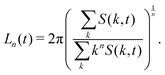 | (29) |
It is worth noting that this definition of average domain size does not necessarily yield values that coincide with the typical domain size observed visually in snapshots such as those shown in Fig. 1. However, in a dynamic scaling regime, different measures of domain size are expected to differ only by a constant ratio. We found that the commonly used measure L1(t) tends to overestimate the observed domain size. Numerically, the calculation of the spherically averaged structure factor is subject to poor statistics in the low k-shells, where the average |k| of the lattice sites differs from the nominal shell radius. Additionally, the measurement of L(t) in simulations with periodic boundary conditions is subject to finite size effects. More importantly, in suspensions of anisotropic particles, we cannot expect that the structure factor is isotropic. Therefore, we also used the 3D structure factor to calculate a lateral domain size in each Cartesian direction from the second moments39,65| | 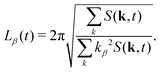 | (30) |
This allows us to compute a domain size parallel (L‖ = Lz) and perpendicular (L⊥ = (Lx + Ly)/2) to the direction of B separately. The average domain size Ld(t) is computed as 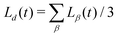 .
.| | 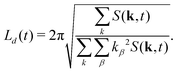 | (31) |
Before calculating the structure factor S(k, t), we first filled the lattice sites covered by particles with the average density at the surrounding lattice sites. We employed an iterative procedure that fills the particles layer by layer, starting at the surface layer and using eqn (18) to approximate the density at solid nodes that have a least one neighboring fluid node. This is repeated until all solid nodes have been filled with fluid. The order parameter ϕ(x, t) was then calculated for the filled density fields ρk(x, t). Filling the lattice sites covered by particles is crucial to avoid spurious oscillations of the structure factor at length scales corresponding to the particle size.
Fig. 2 shows the scaling of the dynamic structure factor S(k,t). The data collapse is good, albeit deviations from dynamic scaling are present at smaller length scales. The decay to the right of the maximum is reasonably well described by Porod's law S(k) ∼ k−4 indicating scattering off a nearly flat interface. These results are in line with the scaling results by Kendon et al.83,84 for spinodal decomposition of binary fluids, which suggests that the formation of bijels is primarily driven by the separation dynamics of the fluids. The effect of the suspended particles only comes into play once larger domains have formed and the coarsening interface reduces the accessible area to the point where the particles start interacting. The onset of particle interactions and subsequent jamming leads to a fairly sudden slow-down of domain growth, as can be observed in the time evolution of the domain size shown in Fig. 3.
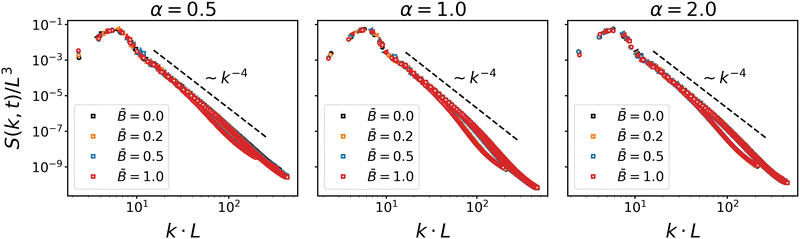 |
| | Fig. 2 Scaling plot of the dynamic structure factor S(k, t) for different particle shapes α and at different magnetic field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . The structure factor is plotted at four different timesteps for each case. The good data collapse shows that the bijel formation is driven by spinodal decomposition. The decay to the right of the peak is reasonably well described by Porod's law S(k) ∼ k−4. . The structure factor is plotted at four different timesteps for each case. The good data collapse shows that the bijel formation is driven by spinodal decomposition. The decay to the right of the peak is reasonably well described by Porod's law S(k) ∼ k−4. | |
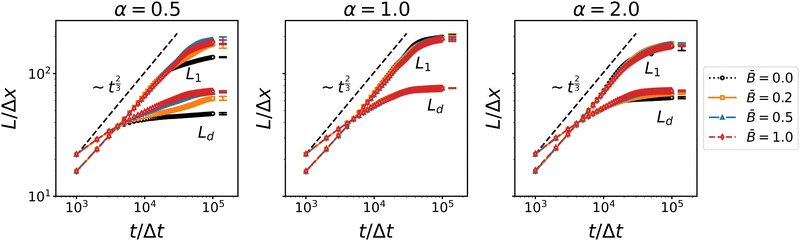 |
| | Fig. 3 Time dependence of the average domain size of the bijel for different particles shapes α and at different magnetic field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . L1 denotes the domain size obtained from the first moment of the spherical average structure factor, and Ld denotes the domain size obtained from the second moment of the 3D structure factor. The increase roughly follows a ∼t2/3 scaling law indicative of the inertial regime of spinodal decomposition. . L1 denotes the domain size obtained from the first moment of the spherical average structure factor, and Ld denotes the domain size obtained from the second moment of the 3D structure factor. The increase roughly follows a ∼t2/3 scaling law indicative of the inertial regime of spinodal decomposition. | |
The domain size L1 obtained from the spherically averaged structure factor initially shows a power law behavior very close to L1 ∼ t2/3. A nonlinear curve fit of the function b(t − t0)a to the interval t ∈ [0, 3 × 105Δx] yields the exponents a = 0.6448 for spherical particles, a = 0.6083 for oblate particles with aspect ratio α = 0.5, and a = 0.652 for prolate ellipsoids with aspect ratio α = 2. These values are in good agreement with the exponent a = 2/3 that is expected in an inertial scaling regime, where the characteristic velocity U = dL/dt scales with the characteristic length scale 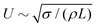 , leading to L ∼ t2/3. After around 30
, leading to L ∼ t2/3. After around 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 40
000 to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time steps, the domain growth starts slowing down and approaches a plateau at L1 ≈ 200Δx for spherical particles, L1 ≈ 180Δx for the prolate particles, and L1 ≈ 170Δx for the oblate particles. Interestingly, the alternative domain size measure Ld obtained from the second moments of the 3D structure factor does not show the same power law behavior. The rate of increase of Ld is substantially smaller than that of L1, with a fitted exponent in the range of 0.12 to 0.20. The increase of Ld levels of earlier and reaches a plateau around Ld ≈ 70Δx for all three particle aspect ratios. While dynamic scaling allows different measures of the characteristic length scale to vary by a prefactor, the deviation from the expected power law of both viscous and inertial scaling indicates that the second moment of the 3D structure factor does not yield a proper characteristic length scale. If one interprets the moments of the structure factor as moments of a probability distribution, then the second moment of the 3D structure factor is equivalent to the ratio of the fourth and second moments of the spherically averaged structure factor (due to the factor k2 in the volume integral). Hence Ld is perhaps better interpreted as describing the shape of the structure factor (similar to kurtosis, but not exactly the same) rather than a characteristic length scale. Nevertheless, the second moments Lβ provide separate measures for the three Cartesian directions and can thus reveal anisotropy of the domain morphology.
000 time steps, the domain growth starts slowing down and approaches a plateau at L1 ≈ 200Δx for spherical particles, L1 ≈ 180Δx for the prolate particles, and L1 ≈ 170Δx for the oblate particles. Interestingly, the alternative domain size measure Ld obtained from the second moments of the 3D structure factor does not show the same power law behavior. The rate of increase of Ld is substantially smaller than that of L1, with a fitted exponent in the range of 0.12 to 0.20. The increase of Ld levels of earlier and reaches a plateau around Ld ≈ 70Δx for all three particle aspect ratios. While dynamic scaling allows different measures of the characteristic length scale to vary by a prefactor, the deviation from the expected power law of both viscous and inertial scaling indicates that the second moment of the 3D structure factor does not yield a proper characteristic length scale. If one interprets the moments of the structure factor as moments of a probability distribution, then the second moment of the 3D structure factor is equivalent to the ratio of the fourth and second moments of the spherically averaged structure factor (due to the factor k2 in the volume integral). Hence Ld is perhaps better interpreted as describing the shape of the structure factor (similar to kurtosis, but not exactly the same) rather than a characteristic length scale. Nevertheless, the second moments Lβ provide separate measures for the three Cartesian directions and can thus reveal anisotropy of the domain morphology.
3.2 Effect of magnetic field on bijel formation
At first glance, the time-dependence of the domain size in Fig. 3 suggests that the domain size is not strongly affected by the external magnetic field. In Fig. 4, we plotted the domain size measure Ld normalized by R, the larger of the two radii of the ellipsoidal particles. The data points represent the domain size measured at the final time step and averaged over three independent simulation runs with the same parameters. The normalization with the particle radius makes it apparent that the ellipsoidal particles reduce the domain size of bijels. This observation is in line with observations by Günther et al.39 and indicates that – relative to their volume – ellipsoidal particles stabilize a larger interface area than spherical particles. This is due to the larger cross-sectional area of ellipsoidal particles at the same volume. Furthermore, steric constraints prevent anisotropic particles to pack less densely in the interface than spherical particles, as we will discuss in more detail below.
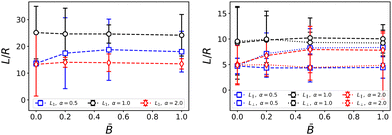 |
| | Fig. 4 Dependence of the average domain size on the magnetic field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . The left plot shows the average domain size L1 obtained from the spherically averaged structure factor. The right plot shows the parallel and perpendicular domain size obtained from the respective second moments of the 3D structure factor. Errorbars indicate the standard deviation taken over three independent simulation runs. For anisotropic particles, the directional domain size becomes more anisotropic with increasing field strength. . The left plot shows the average domain size L1 obtained from the spherically averaged structure factor. The right plot shows the parallel and perpendicular domain size obtained from the respective second moments of the 3D structure factor. Errorbars indicate the standard deviation taken over three independent simulation runs. For anisotropic particles, the directional domain size becomes more anisotropic with increasing field strength. | |
The magnetic field does have an effect on the directional domain size as shown in Fig. 4 where we plotted the domain size in the direction parallel and perpendicular to B separately. We find that for prolate particles, the domain size in the parallel direction increases with the field strength up to approximately three particle radii for the largest field, while the perpendicular domain size stays constant. This trend is reversed for oblate particles for which the domain size in the parallel direction decreases slightly with field strength while the perpendicular domain size increases by approximately four particle radii. Without a field, prolate particles lead to smaller domain size than both spherical and oblate particles, whereas they increase the domain size when the bijel forms under the influence of a magnetic field. The anisotropy is due to the alignment of ellipsoidal particles which leads to a closer packing within the interface akin to nematic ordering. The difference between oblate and prolate particles is caused by the orientation of the magnetic dipole moment m along the symmetry axis of the particles. In our model, m is aligned with the larger axis of prolate ellipsoids, whereas it is aligned with the smaller axis of oblate ellipsoids. Hence m lies in the plane of the larger cross-section of prolate particles while m is perpendicular to the larger cross-section of oblate particles. We thus expect that alignment of the particles with the magnetic field B facilitates closer packing perpendicular to the field for prolate particles, and parallel to the field for oblate particles. The increase/decrease of domain size levels off at intermediate field strength and further increases of the field have no additional effect.
3.3 Tortuosity
The anisotropy of domain size suggests that the magnetic field influences the bijel morphology at the microscale. To investigate whether these structural changes have an effect on macroscopic transport properties, we also characterized the tortuosity of the bijels. Various definitions of tortuosity have been proposed in the literature,86 including geometric, diffusional, and hydraulic tortuosity. Here we use the diffusional tortuosity τ = εD/Deff, i.e., the ratio of the effective diffusivity Deff and the intrinsic diffusivity D. Porous structures were generated from the order parameter field at the last time step of the simulations by binarizing the raw order parameter data using a threshold of zero. We masked the largest connected component representing the percolating domain and then used the Python package taufactor87 to calculate the tortuosity in the three Cartesian coordinate directions. Taufactor determines the tortuosity by comparison of steady-state diffusive flow through a porous medium with the bulk diffusive flow in a control volume of the same size, molecular diffusivity, and driving force.87 We used the PeriodicSolver to employ periodic boundary conditions.
Fig. 5 shows the results for the tortuosity as a function of the applied magnetic flux for the three particle aspect ratios. In the absence a magnetic field, the three aspect ratios lead to a similar tortuosity around τ ≈ 1.5, slightly larger than the tortuosity predicted by the Bruggeman relation τ = ε−0.5 = 1.41 for equal volume fractions ε = 0.5 of the phases.88,89 The observed tortuosity is consistent with simulations of gyroid structures by Luo et al., who found diffusive tortuosities in the range from 1.48 to 1.73.90Fig. 5 shows that in an applied magnetic field, the tortuosity of bijels stabilized by anisotropic particles (α ≠ 1) becomes anisotropic as well. Oblate particles (α = 0.5) lead to an increase of the tortuosity τ‖ in the direction of the magnetic field while the tortuosity in the direction perpendicular to the magnetic field remains around τ‖ ≈ 1.5. Conversely, prolate particles (α = 2) lead to an increase of the tortuosity in the direction perpendicular to the magnetic field, while the tortuosity in the parallel direction slightly decreases with increasing field strength. In both cases, the changes in tortuosity are consistent with the anisotropic domain size and the alignment of particles with the magnetic field. For prolate particles, the longer axis is aligned with the magnetic moment and induces larger domain size and lower tortuosity in this direction. The results show that the magnetic field has a noticeable effect on the tortuosity of the bijel. We observe that the largest change of tortuosity is measured at intermediate field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.5. This suggests that the competition of interfacial and magnetic forces and the resulting alignment of particles and liquid domains induces morphological changes that are more complex than a monotonic increase or decrease. We therefore turn to investigate the microstructural changes within the bijel morphology in more detail.
= 0.5. This suggests that the competition of interfacial and magnetic forces and the resulting alignment of particles and liquid domains induces morphological changes that are more complex than a monotonic increase or decrease. We therefore turn to investigate the microstructural changes within the bijel morphology in more detail.
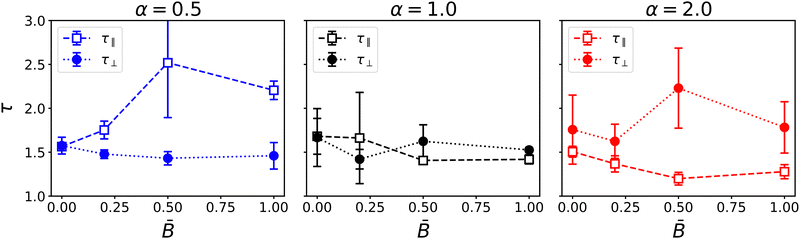 |
| | Fig. 5 Dependence of the tortuosity on the magnetic field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) for different particle shapes α. Different components of the tortuosity tensor show the anisotropy for oblate and prolate particles. for different particle shapes α. Different components of the tortuosity tensor show the anisotropy for oblate and prolate particles. | |
3.4 Kinetics of bijel formation in magnetic fields
To shed light on the mechanisms involved in the coarsening dynamics, we now turn to the kinetics of bijel formation in more detail. The coarsening dynamics can be characterized by a coarsening speed. Here, we use the finite difference of the directional domain size to calculate the components of the coarsening velocity| | 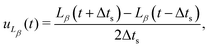 | (32) |
where Δts is the time between simulation snapshots, and β denotes either the direction parallel or perpendicular to the magnetic field.
Fig. 6 shows the coarsening speed in the directions parallel and perpendicular to the applied magnetic field. The data confirms that for spherical particles, domain coarsening remains isotropic. We observe a higher coarsening speed initially which slows at later times when the particles begin to jam. This indicates that the coarsening is subject to different time scales, as reported previously by Harting and co-workers.39 Reeves et al.91 have pointed out that bijel formation hinges on the jamming time in relation to the disruption time, i.e., the time scale at which domain pinch-off events can cause bijel break-up through depercolation. In our simulations, however, we have not observed disruption of bijel formation; stable bijels form for all parameters consistent with simulations by Stratford et al.13 and Jansen et al.65
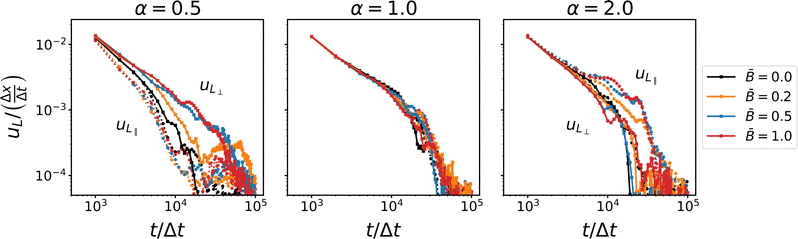 |
| | Fig. 6 Time-dependence of the coarsening velocity uL for different particles shapes α and at different magnetic field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . The different components of the coarsening velocity show that the jamming time is different in the direction parallel and perpendicular to the magnetic field. . The different components of the coarsening velocity show that the jamming time is different in the direction parallel and perpendicular to the magnetic field. | |
For ellipsoidal particles, our data clearly shows that anisotropic domain coarsening arises in magnetic fields. For oblate particles (α = 0.5), the coarsening speed in the direction perpendicular to the field increases with increasing magnetic field strength. Jamming in this direction appears to be delayed compared with the direction parallel to the field. The coarsening speed in the parallel direction remains comparable to the case without an applied magnetic field. This anisotropic behavior of the coarsening speed reverses for prolate particles, where the coarsening speed in the direction parallel to the field increases with increasing field strength, and jamming in this direction is delayed compared with the perpendicular direction. In addition, we observe a shoulder (around 104Δt) where the coarsening speed decays more slowly before jamming sets in. These results suggest that the coarsening near the jamming time is affected by a mechanism that depends on the applied magnetic field and causes the anisotropic behavior. This mechanisms involves the re-orientation of anisotropic particles and their alignment relative to the direction of the magnetic field. To confirm this hypothesis, we analyze the orientational order of the particles and their alignment relative to the magnetic field and the interface, respectively.
3.5 Particle re-orientation and packing
The primary effect of the magnetic field is the torque it exerts on the magnetic dipole of the particles. This torque rotates the particles towards the direction of the magnetic field. The alignment of the particles with the field direction can be clearly observed in the simulation snapshots shown in Fig. 7. While the particles are oriented randomly in the interface in the absence of a magnetic field (![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0), the magnetic field induces orientational order of the magnetic dipoles (shown for
= 0), the magnetic field induces orientational order of the magnetic dipoles (shown for ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 1).
= 1).
 |
| | Fig. 7 Snapshots illustrating the particle packing at the interface for different particle shapes α with (left) and without (right) applied magnetic field ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . The right column shows the alignment of the symmetry axis of the oblate (top row) and prolate (bottom row) particles in the direction of the magnetic field indicated by arrows. . The right column shows the alignment of the symmetry axis of the oblate (top row) and prolate (bottom row) particles in the direction of the magnetic field indicated by arrows. | |
To measure the particle alignment quantitatively, we computed the nematic order tensor92
| | 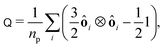 | (33) |
where
ôi is the orientation of the
i-th particles and
np is the number of particles in the system. The largest eigenvalue of
Q yields the nematic order parameter
| | 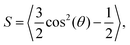 | (34) |
where
θ = arccos(
ôi·
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif)
) is the angle between the particle orientation and the nematic director
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif)
.
Fig. 8 shows the time evolution of the nematic order parameter S for the three different particle aspect ratios α and varying magnetic field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . The onset of orientational order is nearly instantaneous and increases with increasing field strength. For magnetic flux densities
. The onset of orientational order is nearly instantaneous and increases with increasing field strength. For magnetic flux densities ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) ≥ 0.5, the nematic order parameter saturates at S ≈ 1.0 towards the end of the simulation. For the prolate particles (α = 2.0), we observe a shoulder at around 104Δt and an intermittent plateau. The occurrence of this plateau coincides with the slowed decay of the coarsening speed in Fig. 6. This change in the orientational ordering is even more distinct for the oblate particles, where the nematic order decays intermittently before it increases again. The intermittent decay for oblate particles, and the plateau for prolate particles, correlate with the delayed onset of jamming in the direction perpendicular and parallel to the magnetic field, respectively. These observations can be interpreted as follows: the magnetic field aligns the particles with the direction of the magnetic field early during the simulation. Due to this alignment, the steric constraints between particles adsorbed at the interface are reduced which allows further coarsening of the interfacial area. However, during coarsening, the interfaces may re-orient themselves and cause a capillary torque on the particles that competes with the magnetic torque. This competition intermittently perturbs the nematic order of the particles leading to the observed decay and plateau of the nematic order parameter. Accordingly, the decay of S is most pronounced at the weakest magnetic field
≥ 0.5, the nematic order parameter saturates at S ≈ 1.0 towards the end of the simulation. For the prolate particles (α = 2.0), we observe a shoulder at around 104Δt and an intermittent plateau. The occurrence of this plateau coincides with the slowed decay of the coarsening speed in Fig. 6. This change in the orientational ordering is even more distinct for the oblate particles, where the nematic order decays intermittently before it increases again. The intermittent decay for oblate particles, and the plateau for prolate particles, correlate with the delayed onset of jamming in the direction perpendicular and parallel to the magnetic field, respectively. These observations can be interpreted as follows: the magnetic field aligns the particles with the direction of the magnetic field early during the simulation. Due to this alignment, the steric constraints between particles adsorbed at the interface are reduced which allows further coarsening of the interfacial area. However, during coarsening, the interfaces may re-orient themselves and cause a capillary torque on the particles that competes with the magnetic torque. This competition intermittently perturbs the nematic order of the particles leading to the observed decay and plateau of the nematic order parameter. Accordingly, the decay of S is most pronounced at the weakest magnetic field ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.2.
= 0.2.
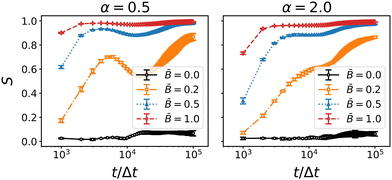 |
| | Fig. 8 Time-dependence of the nematic order parameter S of oblate (α = 0.5) and prolate (α = 2) particles at different field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . Errorbars indicate the standard deviation taken over three independent simulation runs. Nematic order generally increases with applied field strength for all particle geometries. The increase slows down (for prolate particles) or reverses (for oblate particles) around 104 timesteps. . Errorbars indicate the standard deviation taken over three independent simulation runs. Nematic order generally increases with applied field strength for all particle geometries. The increase slows down (for prolate particles) or reverses (for oblate particles) around 104 timesteps. | |
To further corroborate this mechanism, we quantify the orientational order of the interfaces. We computed the interfacial orientation tensor
| | 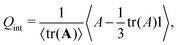 | (35) |
where the local tensor field
A is defined by
The largest eigenvalue of
Q is taken as the interface nematic order parameter
Sint.
The results for the interface nematic order parameter Sint are shown in Fig. 9. The nematic interface alignment increases over time and the rate of increase appears to be higher for larger magnetic field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . In all cases, the final value of Sint is below 0.5 indicating that the tortuous structure of the interface is maintained in the presence of magnetic fields. This confirms that the re-orientation of the particles does not disrupt the bijel structure but leads to partial alignment of the interfaces without changing the general topology of the bicontinuous morphology.
. In all cases, the final value of Sint is below 0.5 indicating that the tortuous structure of the interface is maintained in the presence of magnetic fields. This confirms that the re-orientation of the particles does not disrupt the bijel structure but leads to partial alignment of the interfaces without changing the general topology of the bicontinuous morphology.
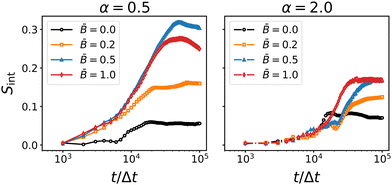 |
| | Fig. 9 Time-dependence of the interface nematic order for oblate (α = 0.5) and prolate (α = 2) particles at different magnetic field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . The interface alignment tends to increase with increasing field strength. The rate of increase becomes larger around 104 timesteps, indicating the alignment of the interfaces due to capillary interactions with the particles. . The interface alignment tends to increase with increasing field strength. The rate of increase becomes larger around 104 timesteps, indicating the alignment of the interfaces due to capillary interactions with the particles. | |
When the particles rotate, the interface exerts a capillary torque on the particles due to the surface tension and the contact angle. If the magnetic torque exceeds the interfacial forces, the particles can potentially overcome the capillary torque and rotate out of the interface. For prolate particles (α = 2) adsorbed at flat interfaces, Davies et al. have shown that a transition between the energetically preferred “flat” orientation and a tilted orientation occurs at a critical field strength of approximately ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.2.36,46,93 In the case of bijels, however, the percolating interfaces are tortuous and thus more mobile. We therefore posit that, rather than tilting out of the interface, rotating particles can “pull” the interface along and thereby align the liquid domains. For anisotropic particles, we expect that the interfaces align along the larger cross-section of the particles, i.e., perpendicular to the symmetry axis of oblate particles and parallel to the symmetry axis of prolate particles. The data for the anisotropic domain size and tortuosity above is consistent with this assumption. To ascertain that the particles remain indeed in their energetically preferred orientation with respect to the interface, we analyzed the angle between the symmetry axis of the particles and the interface normal. To this end, we generated a mesh of the interface using a marching cubes algorithm. For each particle we identified the mesh vertex closest to the particle's position (excluding particles whose distance to the mesh exceeds the radius of the longer particle axis) and computed the angle between the particle orientation vector ôi and the interface normal at the closest vertex. Fig. 10 shows the time-dependence of the average angle ψ between the particle dipole axis and the nearest interface normal.
= 0.2.36,46,93 In the case of bijels, however, the percolating interfaces are tortuous and thus more mobile. We therefore posit that, rather than tilting out of the interface, rotating particles can “pull” the interface along and thereby align the liquid domains. For anisotropic particles, we expect that the interfaces align along the larger cross-section of the particles, i.e., perpendicular to the symmetry axis of oblate particles and parallel to the symmetry axis of prolate particles. The data for the anisotropic domain size and tortuosity above is consistent with this assumption. To ascertain that the particles remain indeed in their energetically preferred orientation with respect to the interface, we analyzed the angle between the symmetry axis of the particles and the interface normal. To this end, we generated a mesh of the interface using a marching cubes algorithm. For each particle we identified the mesh vertex closest to the particle's position (excluding particles whose distance to the mesh exceeds the radius of the longer particle axis) and computed the angle between the particle orientation vector ôi and the interface normal at the closest vertex. Fig. 10 shows the time-dependence of the average angle ψ between the particle dipole axis and the nearest interface normal.
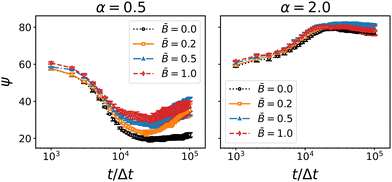 |
| | Fig. 10 Time-dependence of the average angle ψ between the particle axis and the interface normal for oblate (α = 0.5) and prolate (α = 2) particles at different magnetic field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . Errorbars indicate the standard deviation taken over three independent simulation runs. The angle between between the particles and the interface normal generally approaches the energetically preferred value (0° for oblate particls, 90° for prolate particles). The average angle changes most rapidly around 104 timesteps. . Errorbars indicate the standard deviation taken over three independent simulation runs. The angle between between the particles and the interface normal generally approaches the energetically preferred value (0° for oblate particls, 90° for prolate particles). The average angle changes most rapidly around 104 timesteps. | |
For both types of anisotropic particles, the average angle between the particle dipole and the interface normal is initially around ψ ≈ 60°. As the spinodal interface sweeps through the system, particles attach to the interface and alignment due to the capillary torque sets in. For oblate particles, the dipole axis aligns with the interface normal as indicated by the decay of ψ towards zero. For prolate particles, the preferential alignment of the dipole axis is parallel to the interface and hence ψ increases towards 90°. The main variation of ψ occur in a time interval around 104Δt which coincides with the distinct features of the coarsening speed and the particle nematic order observed above. The results thus substantiate the proposed mechanism of particle re-orientation in the magnetic field and the concomitant local alignment of the interface. Once the particles start jamming, the shrinking interfacial area forces some particles out of their preferred alignment with the interface, leading to an increase of ψ for oblate particles and a decrease of ψ for prolate particles. Fig. 10 suggests that the forced tilting is more pronounced for oblate particles than for prolate particles. Due to the larger aspect ratio, the tilting of prolate particles relative to the interface induces deformations that appear to cause a larger capillary torque than the tilting of oblate particles. Hence the prolate particles remain mostly aligned with the interface even in the stronger applied magnetic fields.
As hypothesized above, the alignment of the particle dipole axis with the magnetic field reduces the steric constraints within the interface. To corroborate this idea, we analyzed the radial distribution function (RDF) of the particles
| | 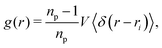 | (37) |
where
np is the number of particles in the volume
V, and 〈·〉 denotes an average over all particles. The radial distribution function was calculated by binning the distance between all particle pairs and normalizing the shells with respect to the distribution 4π
ρr2d
r of an ideal gas. The time-evolution of the RDFs for the three particle shapes and varying magnetic flux density is illustrated in
Fig. 11.
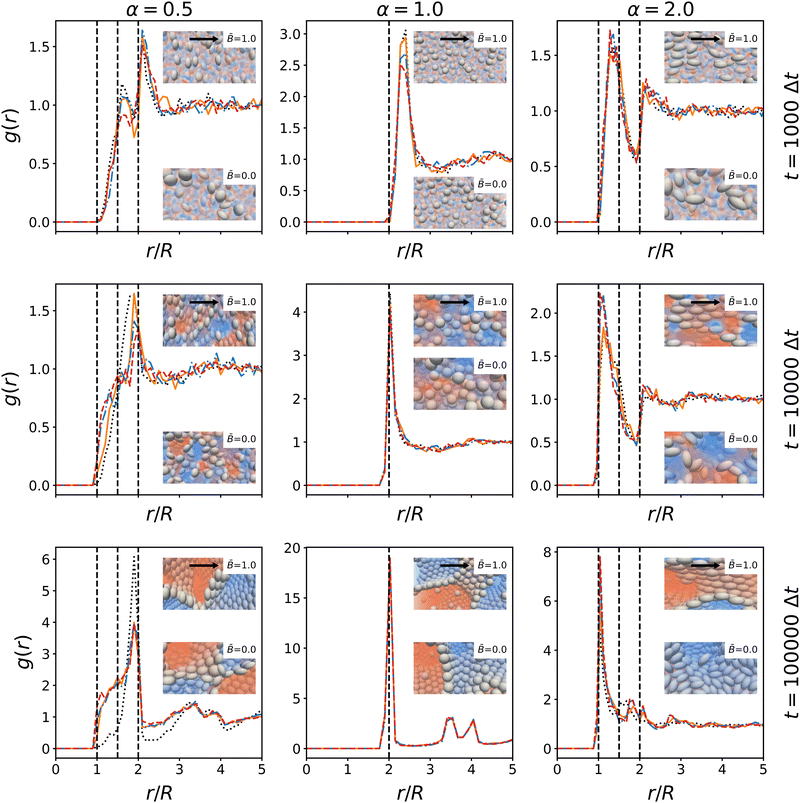 |
| | Fig. 11 Time-evolution of the radial distribution function g(r) of the particles at different magnetic field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . The radial distribution function is shown at 103, 104, and 105 timesteps. The distance r is normalized by the radius R = max(R‖, R⊥) of the larger particle axis. The peaks illustrate the packing of particles in the interface. Dashed lines indicate the side-by-side, tip-to-tip, and side-to-tip configuration of particle pairs. For spherical particles, the three values are identical. The insets show snapshots of the particle arrangement with and without magnetic field at the respective timesteps. The direction of the magnetic field is indicated by arrows. . The radial distribution function is shown at 103, 104, and 105 timesteps. The distance r is normalized by the radius R = max(R‖, R⊥) of the larger particle axis. The peaks illustrate the packing of particles in the interface. Dashed lines indicate the side-by-side, tip-to-tip, and side-to-tip configuration of particle pairs. For spherical particles, the three values are identical. The insets show snapshots of the particle arrangement with and without magnetic field at the respective timesteps. The direction of the magnetic field is indicated by arrows. | |
The radial distribution function is shown at time steps t = 1000Δt, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000Δt, 100
000Δt, 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000Δt. For ellipsoidal particles, the characteristic distances between particles in contact are 2R‖, 2R⊥, and R‖ + R⊥. These distances are marked by dashed lines in Fig. 11. We observe that the largest peak of the RDF coincides with the distance 2R⊥ for both oblate and spherical particles, indicating that oblate particles tend to be in contact at their circumference while prolate particles preferentially align side-by-side. These arrangements lead to closer packing of particles in the interface. The peaks are less pronounced in the early stage of the simulations, where the particles are more randomly oriented. Notably, there is a dip in the RDF of prolate particles at 2R‖ indicating that initially the tip-to-tip configuration occurs more rarely. The growth of the peak height over time shows that the magnetic fields promote this alignment compared to the case without magnetic field. For oblate particles, a shoulder develops around R‖ + R⊥, indicating that some particles tilt out of the interface to reduce the covered interfacial area. For prolate particles, the dip at 2R‖ disappears over time, indicating that more particles align tip-to-tip. This is consistent with alignment of prolate particles with respect to the magnetic field, which facilitates closer packing along both axes of the particles. It further suggests that particles arrange in layers, which can also be observed in the snapshot in Fig. 7. Together with the analysis of nematic order above, these results substantiate the proposed mechanisms that influence the formation of bijels with anisotropic particles in magnetic fields: the magnetic field aligns the particle dipole axis in the field direction, and the particle re-orientation couples to interface alignment due to the capillary interactions. The alignment of particles reduces the steric constraints within the interface, which allows the interface to shrink further and facilitates domain coarsening. In terms of the time-evolution, the rotation of particles due to the magnetic field occurs during the initial stages of the simulation, followed by the local re-alignment of interfaces due to capillary interactions. In the case of prolate particles, we observed the shrinking interface can force particles to tilt out of their preferential alignment to facilitate closer packing. Generally, our results show that when bijels stabilized by anisotropic magnetic particles form under the influence of a magnetic field, the domain size and tortuosity become anisotropic. Additionally, we observe that the particle packing in the interface becomes more ordered due to the alignment effects.
000Δt. For ellipsoidal particles, the characteristic distances between particles in contact are 2R‖, 2R⊥, and R‖ + R⊥. These distances are marked by dashed lines in Fig. 11. We observe that the largest peak of the RDF coincides with the distance 2R⊥ for both oblate and spherical particles, indicating that oblate particles tend to be in contact at their circumference while prolate particles preferentially align side-by-side. These arrangements lead to closer packing of particles in the interface. The peaks are less pronounced in the early stage of the simulations, where the particles are more randomly oriented. Notably, there is a dip in the RDF of prolate particles at 2R‖ indicating that initially the tip-to-tip configuration occurs more rarely. The growth of the peak height over time shows that the magnetic fields promote this alignment compared to the case without magnetic field. For oblate particles, a shoulder develops around R‖ + R⊥, indicating that some particles tilt out of the interface to reduce the covered interfacial area. For prolate particles, the dip at 2R‖ disappears over time, indicating that more particles align tip-to-tip. This is consistent with alignment of prolate particles with respect to the magnetic field, which facilitates closer packing along both axes of the particles. It further suggests that particles arrange in layers, which can also be observed in the snapshot in Fig. 7. Together with the analysis of nematic order above, these results substantiate the proposed mechanisms that influence the formation of bijels with anisotropic particles in magnetic fields: the magnetic field aligns the particle dipole axis in the field direction, and the particle re-orientation couples to interface alignment due to the capillary interactions. The alignment of particles reduces the steric constraints within the interface, which allows the interface to shrink further and facilitates domain coarsening. In terms of the time-evolution, the rotation of particles due to the magnetic field occurs during the initial stages of the simulation, followed by the local re-alignment of interfaces due to capillary interactions. In the case of prolate particles, we observed the shrinking interface can force particles to tilt out of their preferential alignment to facilitate closer packing. Generally, our results show that when bijels stabilized by anisotropic magnetic particles form under the influence of a magnetic field, the domain size and tortuosity become anisotropic. Additionally, we observe that the particle packing in the interface becomes more ordered due to the alignment effects.
4 Conclusions
In this work, we studied the effect of applied magnetic fields on the formation of bijels stabilized by magnetic ellipsoidal particles. We considered oblate, spherical, and prolate particles with a permanent magnetic dipole moment suspended in a symmetric binary liquid. We found that, while the overall formation of a bijel is not disrupted by magnetic interactions, bijels stabilized by oblate or prolate ellipsoids exhibit anisotropic domain size and an anisotropic tortuosity. For oblate particles, the domain size increases in the direction perpendicular to the magnetic field while the tortuosity increases in the parallel direction. Conversely, for prolate particles, the domain size increases in the direction parallel to the magnetic field while the tortuosity increases in the perpendicular direction. Compared with bijels formed in the absence of a magnetic field, we observed changes in domain size up to 30% for non-spherical particles. This effect can be explained by the re-orientation of the particle dipole axis with the magnetic field, which in turn re-aligns the interfaces in the direction of the longer axis of the particles. We further corroborated this mechanisms by analyzing the coarsening speed and the nematic order of the particles and the interfaces. We found that jamming of particles is delayed in the direction of the longer ellipsoidal axis leading to enhanced coarsening in this direction. The timescale of the delayed jamming coincides with a slow-down of the orientational ordering of the particles whereas the alignment of the interfaces increases. We also found that the angle between the particle dipole axis and the interface normal changes at this stage. Additionally, we analyzed the radial distribution function of the particles and found that prolate particles tend to align side by side, while the oblate particles exhibit a less regular arrangement. Based on these findings, we propose that bijel formation in magnetic fields is governed by two coupled effects: during the initial stage, the magnetic torque rotates the particles to align the magnetic dipole moment with the field, and the orientational order of the particles facilitates further coarsening. As coarsening proceeds, the capillary interactions cause the interfaces to align with the longer particle axis. The shrinking interface compresses the particles into ordered arrangements. When jamming sets in, some particles can be forced to tilt out of the interface and this effect is more prominent for oblate particles.
Our results demonstrate the effects of magnetic fields on the structural properties of bijels stabilized by ellipsoidal magnetic particles. This control is desirable in applications where the domain size and tortuosity affect the transport properties. For example, reduced tortuosity can increase the diffusive permeability of bone-like materials.94 Similarly, low tortuosity in lithium electrodes facilitates homogeneous ion transport and uniform lithium deposition, leading to enhanced cyclability of batteries.95,96 Whereas we have considered one particular regime of spinodal decomposition, the viscosity and surface tension of the liquids offer additional parameters that could be leveraged to tune the bijel formation. Moreover, the particle volume fraction is another parameter that is known to affect the formation of particle-stabilized emulsions.40,65 With respect to possible experimental realizations of our simulations, we should emphasize that we have generally considered micron-size particles and have neglected thermal fluctuations. At the nanoscale, thermal fluctuations may in principle play a role, however, Reeves et al.91 have shown that nanoparticles benefit from smaller driving forces towards disruptive curvature and actually lead to more robust bijel formation. Nevertheless, the stability of magnetically-responsive bijels is a relevant question for applications that involve shear flows such as crossflow reactors.97 Aside from particle-size and shape effects, direct interactions between particles are a possible avenue to tune the formation of particle-stabilized emulsions gels, as the recent discovery of bicontinuous intraphase jammed emulsion gels (bipjels) illustrates.98 Another interesting observation arising from our simulations is that the packing order of particles in the interface appears to increase when bijels form under the influence of a magnetic field. While such interfacial ordering effects have been studied on planar interfaces,99–101 they have hitherto not been reported for particle-stabilized emulsion gels. It would be interesting to examine the implications of this ordering on the optical and transport properties of jammed emulsion gels. In conclusion, our simulations provide relevant insights into the formation of magnetic particle-stabilized bijels in the presence of external magnetic fields, and they demonstrate the potential of magnetic particles for fabrication of emulsion systems with tunable and anisotropic particle packing and domain structure.
Author contributions
NK: investigation, data curation, visualization, validation, writing – original draft. UDS: conceptualization, methodology, software, investigation, data curation, formal analysis, visualization, funding acquisition, project administration, supervision, writing – original draft, writing – review & editing.
Data availability
The data and code used to generate the figures in this manuscript are available as an interactive notebook on Code Ocean at https://doi.org/10.24433/CO.6321940.v1. Due to size limitations, the raw simulation data are available for download on request from the authors.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Science Foundation under NSF Awards DMR-1944942, DMR-2414458, and OIA-2346036. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect those of the National Science Foundation. This work used NCSA Delta at the National Center for Supercomputing Applications through allocation PHY220131 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants #2138259, #2138286, #2138307, #2137603, and #2138296. We wish to thank Jens Harting and Alexander Wagner for insightful discussions.
References
- T. Zhang, R. A. Sanguramath, S. Israel and M. S. Silverstein, Macromolecules, 2019, 52, 5445–5479 CrossRef CAS.
- C. Stubenrauch, A. Menner, A. Bismarck and W. Drenckhan, Angew. Chem., Int. Ed., 2018, 57, 10024–10032 CrossRef CAS PubMed.
- B. H. Jones and T. P. Lodge, J. Am. Chem. Soc., 2009, 131, 1676–1677 CrossRef CAS PubMed.
- B. P. Binks, Adv. Mater., 2002, 14, 1824–1827 CrossRef CAS.
- Z. Abbasian Chaleshtari, M. Zhou and R. Foudazi, J. Appl. Phys., 2022, 131, 150902 CrossRef CAS.
- B. Aldemir Dikici and F. Claeyssens, Front. Bioeng. Biotechnol., 2020, 8, 875 CrossRef PubMed.
- M. A. Mudassir, H. Z. Aslam, T. M. Ansari, H. Zhang and I. Hussain, Adv. Sci., 2021, 8, 2102540 CrossRef PubMed.
- W. Ramsden, Proc. R. Soc. London, 1903, 72, 156–164 CAS.
- S. U. Pickering, J. Chem. Soc., Dalton Trans., 1907, 91, 2001–2021 RSC.
- R. Zheng and B. P. Binks, Langmuir, 2022, 38, 1079–1089 CrossRef CAS PubMed.
- A. Menner, R. Verdejo, M. Shaffer and A. Bismarck, Langmuir, 2007, 23, 2398–2403 CrossRef CAS PubMed.
- M. E. Cates and P. S. Clegg, Soft Matter, 2008, 4, 2132–2138 RSC.
- K. Stratford, R. Adhikari, I. Pagonabarraga, J.-C. Desplat and M. E. Cates, Science, 2005, 309, 2198–2201 CrossRef CAS PubMed.
- P. S. Clegg, E. M. Herzig, A. B. Schofield, S. U. Egelhaaf, T. S. Horozov, B. P. Binks, M. E. Cates and W. C. K. Poon, Langmuir, 2007, 23, 5984–5994 CrossRef CAS PubMed.
- E. M. Herzig, K. A. White, A. B. Schofield, W. C. K. Poon and P. S. Clegg, Nat. Mater., 2007, 6, 966–971 CrossRef CAS PubMed.
- J. W. Tavacoli, J. H. J. Thijssen, A. B. Schofield and P. S. Clegg, Adv. Funct. Mater., 2011, 21, 2020–2027 CrossRef CAS.
- M. N. Lee, J. H. J. Thijssen, J. A. Witt, P. S. Clegg and A. Mohraz, Adv. Funct. Mater., 2012, 23, 417–423 CrossRef.
-
J. W. Tavacoli, J. H. J. Thijssen and P. S. Clegg, Particle-Stabilized Emulsions and Colloids: Formation and Applications, The Royal Society of Chemistry, 2014, pp. 129–168 Search PubMed.
- M. F. Haase, K. J. Stebe and D. Lee, Adv. Mater., 2015, 27, 7065–7071 CrossRef CAS PubMed.
- Y. Yabuno, K. Mihara, N. Miyagawa, K. Komatsu, K. Nakagawa, T. Shintani, H. Matsuyama and T. Yoshioka, J. Membr. Sci., 2020, 612, 118468 CrossRef CAS.
- R. Pang, K. K. Chen, Y. Han and W. S. W. Ho, J. Membr. Sci., 2020, 612, 118443 CrossRef CAS.
- J. A. Witt, D. R. Mumm and A. Mohraz, J. Mater. Chem. A, 2016, 4, 1000–1007 RSC.
- J. S. Samdani, T.-H. Kang, C. Zhang and J.-S. Yu, ACS Omega, 2017, 2, 7672–7681 CrossRef CAS PubMed.
- T. J. Thorson, E. L. Botvinick and A. Mohraz, ACS Biomater. Sci. Eng., 2018, 4, 587–594 CrossRef CAS PubMed.
- T. J. Thorson, R. E. Gurlin, E. L. Botvinick and A. Mohraz, Acta Biomater., 2019, 94, 173–182 CrossRef CAS PubMed.
- J. C. Loudet, A. M. Alsayed, J. Zhang and A. G. Yodh, Phys. Rev. Lett., 2005, 94, 018301 CrossRef CAS PubMed.
- J. C. Loudet and B. Pouligny, EPL, 2009, 85, 28003 CrossRef.
- B. Madivala, S. Vandebril, J. Fransaer and J. Vermant, Soft Matter, 2009, 5, 1717 RSC.
- B. Madivala, J. Fransaer and J. Vermant, Langmuir, 2009, 25, 2718–2728 CrossRef CAS PubMed.
- N. Bowden, A. Terfort, J. Carbeck and G. M. Whitesides, Science, 1997, 276, 233–235 CrossRef CAS PubMed.
- E. P. Lewandowski, M. Cavallaro, L. Botto, J. C. Bernate, V. Garbin and K. J. Stebe, Langmuir, 2010, 26, 15142–15154 CrossRef CAS PubMed.
- K. J. Stebe, E. Lewandowski and M. Ghosh, Science, 2009, 325, 159–160 CrossRef CAS PubMed.
- L. Botto, L. Yao, R. L. Leheny and K. J. Stebe, Soft Matter, 2012, 8, 4971–4979 RSC.
- M. Cavallaro, L. Botto, E. P. Lewandowski, M. Wang and K. J. Stebe, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20923–20928 CrossRef CAS PubMed.
- E. M. Furst, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20853–20854 CrossRef CAS PubMed.
- F. Bresme and J. Faraudo, J. Phys.: Condens. Matter, 2007, 19, 375110 CrossRef.
- F. Bresme, Eur. Phys. J. B, 2008, 64, 487–491 CrossRef CAS.
- F. Günther, F. Janoschek, S. Frijters and J. Harting, Comput. Fluids, 2013, 80, 184–189 CrossRef.
- F. Günther, S. Frijters and J. Harting, Soft Matter, 2014, 10, 4977–4989 RSC.
- N. Hijnen, D. Cai and P. S. Clegg, Soft Matter, 2015, 11, 4351–4355 RSC.
- S. Melle, M. Lask and G. G. Fuller, Langmuir, 2005, 21, 2158–2162 CrossRef CAS PubMed.
- J. Zhou, X. Qiao, B. P. Binks, K. Sun, M. Bai, Y. Li and Y. Liu, Langmuir, 2011, 27, 3308–3316 CrossRef CAS PubMed.
- U. Dassanayake, S. Fraden and A. van Blaaderen, J. Chem. Phys., 2000, 112, 3851–3858 CrossRef CAS.
- M. E. Leunissen, H. R. Vutukuri and A. V. Blaaderen, Adv. Mater., 2009, 21, 3116–3120 CrossRef CAS.
- A. R. Morgan, N. Ballard, L. A. Rochford, G. Nurumbetov, T. S. Skelhon and S. A. F. Bon, Soft Matter, 2012, 9, 487–491 RSC.
- G. B. Davies, T. Krüger, P. V. Coveney, J. Harting and F. Bresme, Soft Matter, 2014, 10, 6742–6748 RSC.
- G. B. Davies and L. Botto, Soft Matter, 2015, 11, 7969–7976 RSC.
- E. Kim, K. Stratford and M. E. Cates, Langmuir, 2010, 26, 7928–7936 CrossRef CAS PubMed.
- J. M. Carmack and P. C. Millett, Soft Matter, 2018, 14, 4344–4354 RSC.
- X. Shan and H. Chen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 1815–1819 CrossRef PubMed.
- X. Shan and G. Doolen, J. Stat. Phys., 1995, 81, 379–393 CrossRef.
-
U. D. Schiller and O. Kuksenok, Reviews in Computational Chemistry, John Wiley & Sons, Ltd, vol. 31, 2018, pp. 1–61 Search PubMed.
- Y. H. Qian, D. D'Humières and P. Lallemand, Europhys. Lett., 1992, 17, 479–484 CrossRef.
- P. L. Bhatnagar, E. P. Gross and M. Krook, Phys. Rev., 1954, 94, 511–525 CrossRef CAS.
- X. Shan and H. Chen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 2941–2948 CrossRef CAS PubMed.
- X. Shan and G. Doolen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 3614–3620 CrossRef CAS.
- X. Shan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2008, 77, 066702 CrossRef PubMed.
- A. J. C. Ladd, Phys. Rev. Lett., 1993, 70, 1339–1342 CrossRef CAS PubMed.
- A. J. C. Ladd, J. Fluid Mech., 1994, 271, 285–309 CrossRef CAS.
- A. J. C. Ladd and R. Verberg, J. Stat. Phys., 2001, 104, 1191–1251 CrossRef CAS.
- B. Dünweg and A. J. C. Ladd, Adv. Comput. Simulat. App. Soft Matter Sci. III, 2009, 221, 89–166 Search PubMed.
- C. K. Aidun, Y. Lu and E.-J. Ding, J. Fluid Mech., 1998, 373, 287–311 CrossRef CAS.
-
D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, 2001 Search PubMed.
- S. Schmieschek and J. Harting, Commun. Comput. Phys., 2011, 9, 1165–1178 CrossRef.
- F. Jansen and J. Harting, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2011, 83, 046707 CrossRef PubMed.
- A. J. C. Nguyen and N.-Q. Ladd, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2002, 66, 046708 CrossRef PubMed.
- B. J. Berne and P. Pechukas, J. Chem. Phys., 1972, 56, 4213–4216 CrossRef CAS.
- J. G. Gay and B. J. Berne, J. Chem. Phys., 1981, 74, 3316–3319 CrossRef CAS.
- G. B. Davies, T. Krüger, P. V. Coveney, J. Harting and F. Bresme, Adv. Mater., 2014, 26, 6715–6719 CrossRef CAS PubMed.
- Q. Xie, G. B. Davies and J. Harting, ACS Nano, 2017, 11, 11232–11239 CrossRef CAS PubMed.
- Q. Xie and J. Harting, Adv. Mater., 2021, 33, 2006390 CrossRef CAS PubMed.
- J. Yan, M. Bloom, S. C. Bae, E. Luijten and S. Granick, Nature, 2012, 491, 578–581 CrossRef CAS PubMed.
- J. Yan, S. C. Bae and S. Granick, Soft Matter, 2014, 11, 147–153 RSC.
- S. Schmieschek, L. Shamardin, S. Frijters, T. Krüger, U. D. Schiller, J. Harting and P. V. Coveney, Comput. Phys. Commun., 2017, 217, 149–161 CrossRef CAS.
- C. A. Grattoni, R. A. Dawe, C. Y. Seah and J. D. Gray, J. Chem. Eng. Data, 1993, 38, 516–519 CrossRef CAS.
- S. Trevenen and P. J. Beltramo, J. Colloid Interface Sci., 2021, 583, 385–393 CrossRef CAS PubMed.
- W. Fei, M. M. Driscoll, P. M. Chaikin and K. J. M. Bishop, Soft Matter, 2018, 14, 4661–4665 RSC.
- W. Fei, P. M. Tzelios and K. J. M. Bishop, Langmuir, 2020, 36, 9b03119 CrossRef PubMed.
- V. Vanoli, G. Massobrio, F. Pizzetti, A. Mele, F. Rossi and F. Castiglione, ACS Omega, 2022, 7, 42845–42853 CrossRef CAS PubMed.
- L. Chen, A. He, J. Zhao, Q. Kang, Z.-Y. Li, J. Carmeliet, N. Shikazono and W.-Q. Tao, Prog. Energy Combust. Sci., 2022, 88, 100968 CrossRef.
- T. Lu, Y. Zhu, W. Wang and A. Wang, J. Cleaner Prod., 2020, 277, 124092 CrossRef CAS.
- A. E. Garcia, C. S. Wang, R. N. Sanderson, K. M. McDevitt, Y. Zhang, L. Valdevit, D. R. Mumm, A. Mohraz and R. Ragan, Nanoscale Adv., 2019, 1, 3870–3882 RSC.
- V. M. Kendon, J.-C. Desplat, P. Bladon and M. E. Cates, Phys. Rev. Lett., 1999, 83, 576–579 CrossRef CAS.
- V. M. Kendon, M. E. Cates, I. Pagonabarraga, J.-C. Desplat and P. Bladon, J. Fluid Mech., 2001, 440, 147–203 CrossRef CAS.
- M. Laradji, S. Toxvaerd and O. G. Mouritsen, Phys. Rev. Lett., 1996, 77, 2253–2256 CrossRef CAS PubMed.
- M. T. Q. S. da Silva, M. do Rocio Cardoso, C. M. P. Veronese and W. Mazer, Mater. Today: Proc., 2022, 58, 1344–1349 CAS.
- S. Cooper, A. Bertei, P. Shearing, J. Kilner and N. Brandon, SoftwareX, 2016, 5, 203–210 CrossRef.
- D. A. G. Bruggeman, Ann. Phys., 1935, 416, 636–664 CrossRef.
- B. Tjaden, S. J. Cooper, D. J. Brett, D. Kramer and P. R. Shearing, Curr. Opin. Chem. Eng., 2016, 12, 44–51 CrossRef.
- J.-W. Luo, L. Chen, T. Min, F. Shan, Q. Kang and W. Tao, Int. J. Heat Mass Transfer, 2020, 146, 118837 CrossRef.
- M. Reeves, A. T. Brown, A. B. Schofield, M. E. Cates and J. H. J. Thijssen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2015, 92, 032308 CrossRef CAS PubMed.
- J. A. C. Veerman and D. Frenkel, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 5632–5648 CrossRef PubMed.
- B. J. Newton, K. A. Brakke and D. M. A. Buzza, Phys. Chem. Chem. Phys., 2014, 16, 26051–26058 RSC.
- A. T. Prakoso, H. Basri, D. Adanta, I. Yani, M. I. Ammarullah, I. Akbar, F. A. Ghazali, A. Syahrom and T. Kamarul, Biomedicines, 2023, 11, 427 CrossRef PubMed.
- H. Chen, A. Pei, J. Wan, D. Lin, R. Vilá, H. Wang, D. Mackanic, H.-G. Steinrück, W. Huang, Y. Li, A. Yang, J. Xie, Y. Wu, H. Wang and Y. Cui, Joule, 2020, 4, 938–952 CrossRef CAS.
- M. Ebner, D.-W. Chung, R. E. Garca and V. Wood, Adv. Energy Mater., 2014, 4, 1301278 CrossRef.
- M. A. Khan, A. J. Sprockel, K. A. Macmillan, M. T. Alting, S. P. Kharal, S. Boakye-Ansah and M. F. Haase, Adv. Mater., 2022, 34, 2109547 CrossRef CAS.
- B. Kinkead, R. Malone, G. Smith, A. Pandey and M. Trifkovic, Chem. Mater., 2019, 31, 7601–7607 CrossRef CAS.
- A. Toor, T. Feng and T. P. Russell, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 57 CrossRef PubMed.
- S. Shi and T. P. Russell, Adv. Mater., 2018, 30, 1800714 CrossRef PubMed.
- P. Y. Kim, Y. Gao, Z. Fink, A. E. Ribbe, D. A. Hoagland and T. P. Russell, ACS Nano, 2022, 16, 5496–5506 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b and
Ulf D.
Schiller
b and
Ulf D.
Schiller
 *ab
*ab
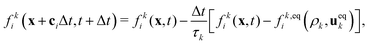
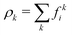 and velocity ueqk (specified below). The equilibrium distribution fk,eqi = feqi is written as a polynomial expansion in the velocity
and velocity ueqk (specified below). The equilibrium distribution fk,eqi = feqi is written as a polynomial expansion in the velocity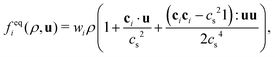
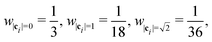 and the speed of sound is
and the speed of sound is 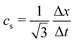 .
.
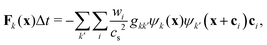
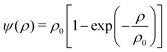
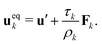
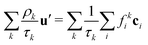
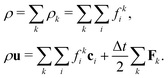
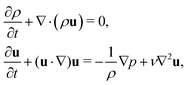
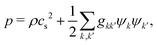
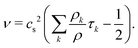
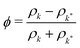 that is governed by a diffusion equation. For an incompressible fluid, we have
that is governed by a diffusion equation. For an incompressible fluid, we have 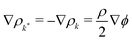 . In this work, we use equal relaxation times τ = τk = τk* for both fluids. We also set the self-interactions to zero gkk = gk*k* = 0 and use a single interaction parameter g = gkk* = gk*k. The diffusion equation for the order parameter simplifies to50
. In this work, we use equal relaxation times τ = τk = τk* for both fluids. We also set the self-interactions to zero gkk = gk*k* = 0 and use a single interaction parameter g = gkk* = gk*k. The diffusion equation for the order parameter simplifies to50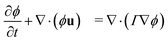
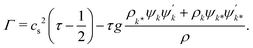
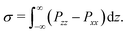
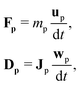
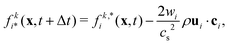
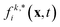 is the post-collision population, and ui = up + ω × ri is the velocity of the particle surface at
is the post-collision population, and ui = up + ω × ri is the velocity of the particle surface at 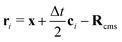 with Rcms the particle's center of mass. The momentum change
with Rcms the particle's center of mass. The momentum change 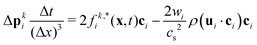 associated with the bounce-back of both fluid components is summed over the surface of the particle to obtain the force and torque on the particle
associated with the bounce-back of both fluid components is summed over the surface of the particle to obtain the force and torque on the particle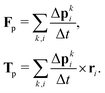
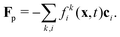
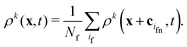
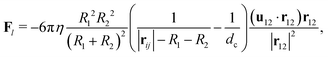
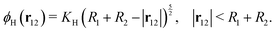
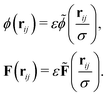
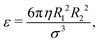 and for the Hertz potential we chose σ = R1 + R2 and ε = KHσ5/2. For two identical, rotationally symmetric ellipsoidal particles with orientations ôi and ôj, we then replace ε and σ by the anisotropic functions
and for the Hertz potential we chose σ = R1 + R2 and ε = KHσ5/2. For two identical, rotationally symmetric ellipsoidal particles with orientations ôi and ôj, we then replace ε and σ by the anisotropic functions
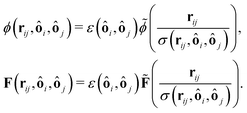
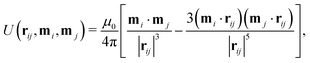
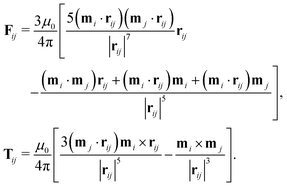
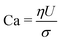 and the Weber number
and the Weber number 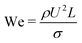 . Here we are primarily interested in spinodal decomposition of the mixture, where we analyze the dynamics after the initial formation of the interfaces and neglect residual diffusion. Hence the Peclet number
. Here we are primarily interested in spinodal decomposition of the mixture, where we analyze the dynamics after the initial formation of the interfaces and neglect residual diffusion. Hence the Peclet number 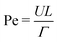 is of lesser importance and we do not consider it when choosing our simulation parameters.
is of lesser importance and we do not consider it when choosing our simulation parameters.
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = mB/(σAp), where Vp = (4/3)πR‖3/α2 is the particle volume and Ap = max(πR‖2/α, πR‖2/α2) the area of the larger cross-section of the ellipsoidal particles.
= mB/(σAp), where Vp = (4/3)πR‖3/α2 is the particle volume and Ap = max(πR‖2/α, πR‖2/α2) the area of the larger cross-section of the ellipsoidal particles.![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) p(Δx)3,
p(Δx)3, 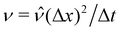 , σ =
, σ = ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) Δm/(Δt)2, and m =
Δm/(Δt)2, and m = ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) Δi(Δx)2. We used Vp = 2000π/3,
Δi(Δx)2. We used Vp = 2000π/3, 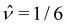 ,
, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) = 0.0267,
= 0.0267, ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) = 1, and a density ratio ξ = 1/
= 1, and a density ratio ξ = 1/![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) . For reference, the values of the model parameters are listed in Table 1. The values of α and
. For reference, the values of the model parameters are listed in Table 1. The values of α and ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) are variable and are reported with the results in Section 3.
are variable and are reported with the results in Section 3.![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) ≤ 1. In this work, we use a fixed particle volume fraction and focus on the dependence of the bijel structure on the magnetic field. Bijels with varying particle loading and surface tension and have been studied elsewhere in the literature, e.g., by Hijnen et al.40 and Jansen and Harting.65
≤ 1. In this work, we use a fixed particle volume fraction and focus on the dependence of the bijel structure on the magnetic field. Bijels with varying particle loading and surface tension and have been studied elsewhere in the literature, e.g., by Hijnen et al.40 and Jansen and Harting.65
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) (k, t)
(k, t)![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) (−k, t)
(−k, t)![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) (k, t) is the Fourier transform of the order parameter fluctuations ϕ(x, t) − 〈ϕ〉. A common measure of domain size uses the spherically averaged structure factor
(k, t) is the Fourier transform of the order parameter fluctuations ϕ(x, t) − 〈ϕ〉. A common measure of domain size uses the spherically averaged structure factor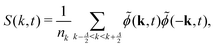
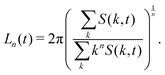
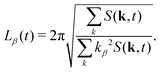
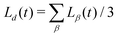 .
.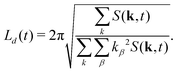
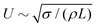 , leading to L ∼ t2/3. After around 30
, leading to L ∼ t2/3. After around 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 40
000 to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time steps, the domain growth starts slowing down and approaches a plateau at L1 ≈ 200Δx for spherical particles, L1 ≈ 180Δx for the prolate particles, and L1 ≈ 170Δx for the oblate particles. Interestingly, the alternative domain size measure Ld obtained from the second moments of the 3D structure factor does not show the same power law behavior. The rate of increase of Ld is substantially smaller than that of L1, with a fitted exponent in the range of 0.12 to 0.20. The increase of Ld levels of earlier and reaches a plateau around Ld ≈ 70Δx for all three particle aspect ratios. While dynamic scaling allows different measures of the characteristic length scale to vary by a prefactor, the deviation from the expected power law of both viscous and inertial scaling indicates that the second moment of the 3D structure factor does not yield a proper characteristic length scale. If one interprets the moments of the structure factor as moments of a probability distribution, then the second moment of the 3D structure factor is equivalent to the ratio of the fourth and second moments of the spherically averaged structure factor (due to the factor k2 in the volume integral). Hence Ld is perhaps better interpreted as describing the shape of the structure factor (similar to kurtosis, but not exactly the same) rather than a characteristic length scale. Nevertheless, the second moments Lβ provide separate measures for the three Cartesian directions and can thus reveal anisotropy of the domain morphology.
000 time steps, the domain growth starts slowing down and approaches a plateau at L1 ≈ 200Δx for spherical particles, L1 ≈ 180Δx for the prolate particles, and L1 ≈ 170Δx for the oblate particles. Interestingly, the alternative domain size measure Ld obtained from the second moments of the 3D structure factor does not show the same power law behavior. The rate of increase of Ld is substantially smaller than that of L1, with a fitted exponent in the range of 0.12 to 0.20. The increase of Ld levels of earlier and reaches a plateau around Ld ≈ 70Δx for all three particle aspect ratios. While dynamic scaling allows different measures of the characteristic length scale to vary by a prefactor, the deviation from the expected power law of both viscous and inertial scaling indicates that the second moment of the 3D structure factor does not yield a proper characteristic length scale. If one interprets the moments of the structure factor as moments of a probability distribution, then the second moment of the 3D structure factor is equivalent to the ratio of the fourth and second moments of the spherically averaged structure factor (due to the factor k2 in the volume integral). Hence Ld is perhaps better interpreted as describing the shape of the structure factor (similar to kurtosis, but not exactly the same) rather than a characteristic length scale. Nevertheless, the second moments Lβ provide separate measures for the three Cartesian directions and can thus reveal anisotropy of the domain morphology.![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.5. This suggests that the competition of interfacial and magnetic forces and the resulting alignment of particles and liquid domains induces morphological changes that are more complex than a monotonic increase or decrease. We therefore turn to investigate the microstructural changes within the bijel morphology in more detail.
= 0.5. This suggests that the competition of interfacial and magnetic forces and the resulting alignment of particles and liquid domains induces morphological changes that are more complex than a monotonic increase or decrease. We therefore turn to investigate the microstructural changes within the bijel morphology in more detail.
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) for different particle shapes α. Different components of the tortuosity tensor show the anisotropy for oblate and prolate particles.
for different particle shapes α. Different components of the tortuosity tensor show the anisotropy for oblate and prolate particles.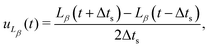
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0), the magnetic field induces orientational order of the magnetic dipoles (shown for
= 0), the magnetic field induces orientational order of the magnetic dipoles (shown for ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 1).
= 1).
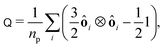
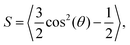
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ) is the angle between the particle orientation and the nematic director
) is the angle between the particle orientation and the nematic director ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) .
.
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . The onset of orientational order is nearly instantaneous and increases with increasing field strength. For magnetic flux densities
. The onset of orientational order is nearly instantaneous and increases with increasing field strength. For magnetic flux densities ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) ≥ 0.5, the nematic order parameter saturates at S ≈ 1.0 towards the end of the simulation. For the prolate particles (α = 2.0), we observe a shoulder at around 104Δt and an intermittent plateau. The occurrence of this plateau coincides with the slowed decay of the coarsening speed in Fig. 6. This change in the orientational ordering is even more distinct for the oblate particles, where the nematic order decays intermittently before it increases again. The intermittent decay for oblate particles, and the plateau for prolate particles, correlate with the delayed onset of jamming in the direction perpendicular and parallel to the magnetic field, respectively. These observations can be interpreted as follows: the magnetic field aligns the particles with the direction of the magnetic field early during the simulation. Due to this alignment, the steric constraints between particles adsorbed at the interface are reduced which allows further coarsening of the interfacial area. However, during coarsening, the interfaces may re-orient themselves and cause a capillary torque on the particles that competes with the magnetic torque. This competition intermittently perturbs the nematic order of the particles leading to the observed decay and plateau of the nematic order parameter. Accordingly, the decay of S is most pronounced at the weakest magnetic field
≥ 0.5, the nematic order parameter saturates at S ≈ 1.0 towards the end of the simulation. For the prolate particles (α = 2.0), we observe a shoulder at around 104Δt and an intermittent plateau. The occurrence of this plateau coincides with the slowed decay of the coarsening speed in Fig. 6. This change in the orientational ordering is even more distinct for the oblate particles, where the nematic order decays intermittently before it increases again. The intermittent decay for oblate particles, and the plateau for prolate particles, correlate with the delayed onset of jamming in the direction perpendicular and parallel to the magnetic field, respectively. These observations can be interpreted as follows: the magnetic field aligns the particles with the direction of the magnetic field early during the simulation. Due to this alignment, the steric constraints between particles adsorbed at the interface are reduced which allows further coarsening of the interfacial area. However, during coarsening, the interfaces may re-orient themselves and cause a capillary torque on the particles that competes with the magnetic torque. This competition intermittently perturbs the nematic order of the particles leading to the observed decay and plateau of the nematic order parameter. Accordingly, the decay of S is most pronounced at the weakest magnetic field ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.2.
= 0.2.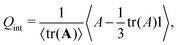
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . In all cases, the final value of Sint is below 0.5 indicating that the tortuous structure of the interface is maintained in the presence of magnetic fields. This confirms that the re-orientation of the particles does not disrupt the bijel structure but leads to partial alignment of the interfaces without changing the general topology of the bicontinuous morphology.
. In all cases, the final value of Sint is below 0.5 indicating that the tortuous structure of the interface is maintained in the presence of magnetic fields. This confirms that the re-orientation of the particles does not disrupt the bijel structure but leads to partial alignment of the interfaces without changing the general topology of the bicontinuous morphology.![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.2.36,46,93 In the case of bijels, however, the percolating interfaces are tortuous and thus more mobile. We therefore posit that, rather than tilting out of the interface, rotating particles can “pull” the interface along and thereby align the liquid domains. For anisotropic particles, we expect that the interfaces align along the larger cross-section of the particles, i.e., perpendicular to the symmetry axis of oblate particles and parallel to the symmetry axis of prolate particles. The data for the anisotropic domain size and tortuosity above is consistent with this assumption. To ascertain that the particles remain indeed in their energetically preferred orientation with respect to the interface, we analyzed the angle between the symmetry axis of the particles and the interface normal. To this end, we generated a mesh of the interface using a marching cubes algorithm. For each particle we identified the mesh vertex closest to the particle's position (excluding particles whose distance to the mesh exceeds the radius of the longer particle axis) and computed the angle between the particle orientation vector ôi and the interface normal at the closest vertex. Fig. 10 shows the time-dependence of the average angle ψ between the particle dipole axis and the nearest interface normal.
= 0.2.36,46,93 In the case of bijels, however, the percolating interfaces are tortuous and thus more mobile. We therefore posit that, rather than tilting out of the interface, rotating particles can “pull” the interface along and thereby align the liquid domains. For anisotropic particles, we expect that the interfaces align along the larger cross-section of the particles, i.e., perpendicular to the symmetry axis of oblate particles and parallel to the symmetry axis of prolate particles. The data for the anisotropic domain size and tortuosity above is consistent with this assumption. To ascertain that the particles remain indeed in their energetically preferred orientation with respect to the interface, we analyzed the angle between the symmetry axis of the particles and the interface normal. To this end, we generated a mesh of the interface using a marching cubes algorithm. For each particle we identified the mesh vertex closest to the particle's position (excluding particles whose distance to the mesh exceeds the radius of the longer particle axis) and computed the angle between the particle orientation vector ôi and the interface normal at the closest vertex. Fig. 10 shows the time-dependence of the average angle ψ between the particle dipole axis and the nearest interface normal.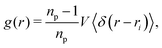
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000Δt, 100
000Δt, 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000Δt. For ellipsoidal particles, the characteristic distances between particles in contact are 2R‖, 2R⊥, and R‖ + R⊥. These distances are marked by dashed lines in Fig. 11. We observe that the largest peak of the RDF coincides with the distance 2R⊥ for both oblate and spherical particles, indicating that oblate particles tend to be in contact at their circumference while prolate particles preferentially align side-by-side. These arrangements lead to closer packing of particles in the interface. The peaks are less pronounced in the early stage of the simulations, where the particles are more randomly oriented. Notably, there is a dip in the RDF of prolate particles at 2R‖ indicating that initially the tip-to-tip configuration occurs more rarely. The growth of the peak height over time shows that the magnetic fields promote this alignment compared to the case without magnetic field. For oblate particles, a shoulder develops around R‖ + R⊥, indicating that some particles tilt out of the interface to reduce the covered interfacial area. For prolate particles, the dip at 2R‖ disappears over time, indicating that more particles align tip-to-tip. This is consistent with alignment of prolate particles with respect to the magnetic field, which facilitates closer packing along both axes of the particles. It further suggests that particles arrange in layers, which can also be observed in the snapshot in Fig. 7. Together with the analysis of nematic order above, these results substantiate the proposed mechanisms that influence the formation of bijels with anisotropic particles in magnetic fields: the magnetic field aligns the particle dipole axis in the field direction, and the particle re-orientation couples to interface alignment due to the capillary interactions. The alignment of particles reduces the steric constraints within the interface, which allows the interface to shrink further and facilitates domain coarsening. In terms of the time-evolution, the rotation of particles due to the magnetic field occurs during the initial stages of the simulation, followed by the local re-alignment of interfaces due to capillary interactions. In the case of prolate particles, we observed the shrinking interface can force particles to tilt out of their preferential alignment to facilitate closer packing. Generally, our results show that when bijels stabilized by anisotropic magnetic particles form under the influence of a magnetic field, the domain size and tortuosity become anisotropic. Additionally, we observe that the particle packing in the interface becomes more ordered due to the alignment effects.
000Δt. For ellipsoidal particles, the characteristic distances between particles in contact are 2R‖, 2R⊥, and R‖ + R⊥. These distances are marked by dashed lines in Fig. 11. We observe that the largest peak of the RDF coincides with the distance 2R⊥ for both oblate and spherical particles, indicating that oblate particles tend to be in contact at their circumference while prolate particles preferentially align side-by-side. These arrangements lead to closer packing of particles in the interface. The peaks are less pronounced in the early stage of the simulations, where the particles are more randomly oriented. Notably, there is a dip in the RDF of prolate particles at 2R‖ indicating that initially the tip-to-tip configuration occurs more rarely. The growth of the peak height over time shows that the magnetic fields promote this alignment compared to the case without magnetic field. For oblate particles, a shoulder develops around R‖ + R⊥, indicating that some particles tilt out of the interface to reduce the covered interfacial area. For prolate particles, the dip at 2R‖ disappears over time, indicating that more particles align tip-to-tip. This is consistent with alignment of prolate particles with respect to the magnetic field, which facilitates closer packing along both axes of the particles. It further suggests that particles arrange in layers, which can also be observed in the snapshot in Fig. 7. Together with the analysis of nematic order above, these results substantiate the proposed mechanisms that influence the formation of bijels with anisotropic particles in magnetic fields: the magnetic field aligns the particle dipole axis in the field direction, and the particle re-orientation couples to interface alignment due to the capillary interactions. The alignment of particles reduces the steric constraints within the interface, which allows the interface to shrink further and facilitates domain coarsening. In terms of the time-evolution, the rotation of particles due to the magnetic field occurs during the initial stages of the simulation, followed by the local re-alignment of interfaces due to capillary interactions. In the case of prolate particles, we observed the shrinking interface can force particles to tilt out of their preferential alignment to facilitate closer packing. Generally, our results show that when bijels stabilized by anisotropic magnetic particles form under the influence of a magnetic field, the domain size and tortuosity become anisotropic. Additionally, we observe that the particle packing in the interface becomes more ordered due to the alignment effects.









