Geometrical impacts of platonic particles on nematic liquid crystal dynamics
Stiven
Villada-Gil
 ab,
Monirosadat
Sadati
ab,
Monirosadat
Sadati
 c,
Juan D.
Ospina-Correa
c,
Juan D.
Ospina-Correa
 bd,
Daniel A.
Olaya-Muñoz
bd,
Daniel A.
Olaya-Muñoz
 be,
Juan P.
Hernández-Ortiz
be,
Juan P.
Hernández-Ortiz
 *bfg and
José A.
Martínez-González
*bfg and
José A.
Martínez-González
 *h
*h
aFacultad de Ciencias y Educación, Politécnico Colombiano Jaime Isaza Cadavid, Medellín, Colombia
bGlobal Health Institute One-Health Colombia, Universidad Nacional de Colombia–Medellín, Colombia. E-mail: jphernandezo@unal.edu.co
cDepartment of Chemical Engineering, College of Engineering and Computing, University of South Carolina, Columbia, SC, USA
dGrupo de Investigación Ingeniar, Facultad de Ingenierías, Corporación Universitaria Remington, Medellín, Colombia
eDepartamento de Materiales y Nanotecnología, Universidad Nacional de Colombia–Medellín, Colombia
fFacultad de Ciencias de la Vida, Universidad Nacional de Colombia–Medellín, Colombia
gPritzker School of Molecular Engineering, University of Chicago, Chicago, IL 60637, USA
hFacultad de Ciencias, Universidad Autónoma de San Luis Potosí, Av. Parque Chapultepec 1570, San Luis Potosí, 78295 SLP, Mexico. E-mail: jose.adrian.martinez@uaslp.mx
First published on 17th October 2024
Abstract
Platonic-solid-like particles in liquid crystals offer intriguing opportunities for engineering complex materials with tailored properties. Inspired by platonic solids’ geometric simplicity and symmetry, these particles possess well-defined shapes such as cubes, tetrahedra, octahedra, dodecahedra, and icosahedra. When dispersed within nematic liquid-crystalline media, these particles interact with the surrounding medium in intricate ways, influencing the local orientational order of liquid crystal molecules. In this work, we implement continuum simulations to study how the combination of particle shape and surface anchoring gives rise to line defects that follow the edges of the particles and how they are affected by the presence of a Poiseuille flow. Platonic-solid-like particles in liquid crystals have shown promise in diverse applications ranging from photonics and metamaterials to colloidal self-assembly and responsive soft materials.
1 Introduction
Liquid crystals (LCs) represent a unique state of matter with properties that bridge the characteristics of conventional liquids and crystalline solids. These materials exhibit anisotropic fluidity and responsiveness to external stimuli, making them valuable in a variety of technological applications.1–13 A nematic liquid crystal (NLC) corresponds to a phase where the molecules tend to align in a preferred direction which is usually denoted by a vector called director (n).Integrating colloidal particles into LC systems presents an intriguing avenue for engineering hierarchical materials with tailored properties. Colloidal particles, typically ranging from nanometers to micrometers in size, interact with the LC medium, influencing its structural, optical, and mechanical characteristics.14–16 Features such as the particle's size and shape, surface chemistry, and anchoring conditions affect the intrinsic structural properties of the LC host. One of the remarkable features of colloidal particles in LCs is their ability to induce topological defects and alter the director field – the local average orientation of LC molecules. These defects arise due to the mismatch between the preferred orientation of LC molecules and the boundary conditions imposed by colloidal particles. For instance, when immersed in a uniformly aligned NLC, a spherical colloid with strong homeotropic anchoring induces a hyperbolic point defect;17,18 another possibility is the formation of the Saturn ring line defect,19,20 leading to a quadrupolar structure of the director field. Conversely, a colloid with planar anchoring causes the formation of two point defects (boojums17) at the poles along n, resulting in a quadrupolar configuration of the LC alignment.
Unlike their spherical counterparts, non-spherical colloidal particles induce intricate distortions in the director field, leading to the formation of point and line defects with distinctive behaviors, as well as anisotropic interactions between particles;21–23 the symmetry breaking induced by their asymmetrical shape modifies the inter-particle interactions as it has been demonstrated for electrostatic24,25 and hydrodynamic fields.26–28
Numerous simulation studies have investigated the nematodynamics of liquid crystals in the presence of colloidal particles and external stimuli, as well as the interaction between disclinations and surfaces. These studies have examined the influence of anchoring conditions on flow behavior,29–31 the dynamics of topological defects around spherical particles under flow,32–35 and the interactions between nanoparticles and disclination lines in nematic and complex nematic phases.36–40 They underscore the critical roles of particle shape, surface anchoring, and external forces in governing the complex behavior of nematic liquid crystals, offering key insights that inform the foundation of our present work. The interaction between disclinations and surfaces plays a critical role in the stability and dynamics of defect structures in liquid crystals. These interactions can result in either attractive or repulsive forces, depending on the distance between the disclination and the surface, as well as the type of surface anchoring.
Previous research showed how hollow colloidal prisms direct the emergence of fractal topological defect states in LCs.41 The shape of colloidal platelet-like particles influence significantly the inter-particle interaction and self-assembly of these colloids.42 In the past two decades, significant advancements in particles synthesis43–45 have resulted in a spectacular variety of anisotropic nanoparticles, including cubes,46,47 rods,48 tetrahedrons,49 octahedrons,47,50,51 icosahedrons,52 nanostars,53,54 tetrapods,55 octapods,56,57 bipyramids,58 and superballs,59,60 among others.52 Computer simulations have shown that the particle's size and shape direct the final packing structure and equilibrium phase behavior of LCs.61–65 When the particle shape is combined with other interactions, it can play a crucial role in the design of materials for self-assembly,59,66via topological defects.
In this paper, we present a computational platform with continuum simulations based on the Landau–de Gennes theory and the Stark and Lubensky formulation for LC hydrodynamics67 to explore how the particle shapes of platonic solid-like colloids, along with their surface anchoring conditions and Poiseuille flow, influence the structural properties of a host NLC. These polyhedra, representing geometric perfection and symmetry, provide a unique platform for elucidating the interplay between particle morphology, confinement, and external stimuli, such as an imposed flow in the emergence of topological defects and phase behavior of LCs. Moreover, they pave the way for diverse applications ranging from photonics and metamaterials to colloidal self-assembly and responsive soft materials.
In this work, we explore the relatively uncharted territory of platonic solid-like particles immersed in nematic liquid crystals (NLCs), with a focus on how their distinct symmetries and sharp edges interact with disclination line configurations under external flow. While previous research has extensively investigated spherical and non-spherical particles in liquid crystals, a comprehensive analysis of how the number of faces of colloidal particles affects defect dynamics remains underexplored. By systematically examining how platonic solid-like particles influence disclination structures, we uncover how confinement and flow collectively govern the behavior of topological defects. Our findings not only enhance the fundamental understanding of defect behavior in NLCs but also pave the way for new possibilities in self-assembly, microfluidics, and the design of advanced materials with tailored properties, expanding the potential applications of colloidal-liquid crystal systems in responsive soft materials and photonic devices.
2 Theoretical model
We analyzed the equilibrium configurations of an NLC in the presence of platonic-solid-like particles with surface homeotropic anchoring, as well as the combined effect that these particles and strong confinement have on the structure of the liquid crystalline host (Fig. 1). We employed a mean-field theoretical approach to model the free energy of the liquid crystal and determine the stablest configurations under strong confinement and in the presence of anisotropic particles. Specifically, we utilized the Landau–de Gennes approach, where the free energy functional is linked to the tensor order parameter, Q, that characterizes the orientational order of LC molecules. This free energy functional captures the underlying physics of LCs, incorporating contributions from various sources: a short-range Landau polynomial expansion in Q to model the isotropic–nematic transition; a long-range functional that penalizes elastic distortions, and a surface contribution imposing a preferred orientation at the boundaries.68 Therefore, we have,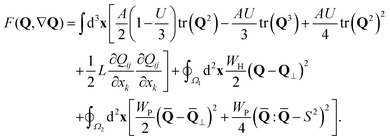 | (1) |
The free energy functional of the LC expressed in eqn (1) incorporates several key parameters. The phenomenological coefficients, A and U, set the overall energy scale and control the isotropic–nematic transition. The elastic constant, L, is associated with the elastic moduli for a uniaxial LC through K = 2LS2. Furthermore, WH represents the strength of homeotropic anchoring over surface region Ω1, while WP denotes the strength of planar anchoring over surface region Ω2. The tensor Q⊥ is the perpendicular tensor preferred at the surface ![[Q with combining macron]](https://www.rsc.org/images/entities/b_char_0051_0304.gif) = Q + Sδ/3 and
= Q + Sδ/3 and ![[Q with combining macron]](https://www.rsc.org/images/entities/b_char_0051_0304.gif) ⊥ = p·
⊥ = p·![[Q with combining macron]](https://www.rsc.org/images/entities/b_char_0051_0304.gif) ·p is the tensor projection on the surface, with p = δ − νν.
·p is the tensor projection on the surface, with p = δ − νν.
Once the equilibrium configurations corresponding to the confined cases were obtained, we continued analyzing the effect of Poiseuille flow on the LC configuration for each studied case. To this end, we employed the Stark and Lubensky (SL) formulation of liquid crystal hydrodynamics, which uses a general Poisson-bracket formalism to obtain a molecular theory for the structure and dynamics of LCs. This formulation considers the hydrodynamics of topological defects based on a full tensorial description of the nematic ordering.67
For the system considered here, we proceed to define an appropriate characteristic length Lc = ξ, where 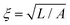 is the nematic coherence length of the LC, and a characteristic time tc. These define a characteristic velocity uc = Lc/tc. Based on this choice of characteristic scales, the dimensionless constitutive equation for the tensor order parameter evolution in the SL model is given by
is the nematic coherence length of the LC, and a characteristic time tc. These define a characteristic velocity uc = Lc/tc. Based on this choice of characteristic scales, the dimensionless constitutive equation for the tensor order parameter evolution in the SL model is given by
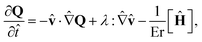 | (2) |
![[v with combining circumflex]](https://www.rsc.org/images/entities/b_char_0076_0302.gif) (
(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) is the velocity field at point
) is the velocity field at point ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) . Er is the Ericksen number used to describe the deformation of the director field underflow, which represents the ratio of viscous force to the elastic force of an NLC:
. Er is the Ericksen number used to describe the deformation of the director field underflow, which represents the ratio of viscous force to the elastic force of an NLC: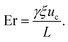 | (3) |
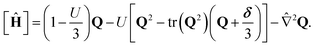 | (4) |
The alignment and rotation of the molecular orientations with velocity gradients occur in the LC dynamics through the fourth-order tensor λ(Q), which was originally derived by Stark and Lubensky.67 The full-flow aligning term is written as
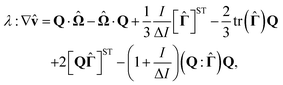 | (5) |
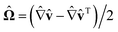 is the vorticity tensor and
is the vorticity tensor and 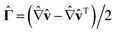 is deformation tensor. I/ΔI is a molecular parameter which will depend on the molecular details of a given LC and the superscript ST implies a symmetric and traceless tensor, i.e., BST = (1/2)(B + BT) − tr(B)δ/3.
is deformation tensor. I/ΔI is a molecular parameter which will depend on the molecular details of a given LC and the superscript ST implies a symmetric and traceless tensor, i.e., BST = (1/2)(B + BT) − tr(B)δ/3.
In this work, we assume that the LC media is incompressible 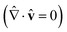 , and since the typical dimensions in experimental systems are on the order of nanometers, inertial effects in the LC are neglected (Re ≈ 10−4). Thus, the dimensionless momentum balance equation of the SL theory takes the form:
, and since the typical dimensions in experimental systems are on the order of nanometers, inertial effects in the LC are neglected (Re ≈ 10−4). Thus, the dimensionless momentum balance equation of the SL theory takes the form:
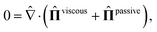 | (6) |
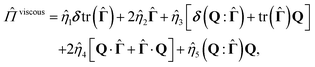 | (7) |
![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) i are viscosity coefficients, which are related to Leslie–Ericksen parameters67,68 and they satisfy the two Onsager relations68 and the Parodi relation.69 The rotational viscosity γ and the viscosities ηi are normalized concerning the Newtonian viscosity η2. The second term is passive stress, normalized by L/ξ2 and is defined as follows:
i are viscosity coefficients, which are related to Leslie–Ericksen parameters67,68 and they satisfy the two Onsager relations68 and the Parodi relation.69 The rotational viscosity γ and the viscosities ηi are normalized concerning the Newtonian viscosity η2. The second term is passive stress, normalized by L/ξ2 and is defined as follows: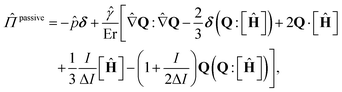 | (8) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) is the pressure field normalized by η2uc/ξ.
is the pressure field normalized by η2uc/ξ.
This study employs a numerical approach to solve the coupled equations governing liquid crystal hydrodynamics, specifically eqn (2) and (6) and the incompressibility condition 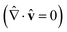 . The spatial domain is discretized using the Galerkin finite element method with optimized quadratic tetrahedral elements, while an implicit Euler scheme handles time evolution. Convergence is ensured through a two-step relaxation process. Initially, the system relaxes with a random order field Q and no flow. Subsequently, the full system is solved under an applied pressure gradient. Mesh optimization70,71 and the SuperLU package library72–74 are utilized for efficient solution. For a detailed methodology, readers are referred to the authors’ prior work.35
. The spatial domain is discretized using the Galerkin finite element method with optimized quadratic tetrahedral elements, while an implicit Euler scheme handles time evolution. Convergence is ensured through a two-step relaxation process. Initially, the system relaxes with a random order field Q and no flow. Subsequently, the full system is solved under an applied pressure gradient. Mesh optimization70,71 and the SuperLU package library72–74 are utilized for efficient solution. For a detailed methodology, readers are referred to the authors’ prior work.35
3 Results
In our simulations, we considered material parameters that were found to suitably model the phase behavior of NLCs. For the Landau–de Gennes free energy functionals, we used A = 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J m−3 and an elastic constant k ≈ 6 pN, which results in a nematic coherence length ξ = 10.0 nm.
000 J m−3 and an elastic constant k ≈ 6 pN, which results in a nematic coherence length ξ = 10.0 nm.
In this work, we use a value of U = 3.165 for all simulations, corresponding to a bulk scalar order parameter S ≈ 0.548. The rotational viscosity is γ = 0.018 Pa s and the Newton viscosity considered here is η2 = 0.02 Pa s, resulting in dimensionless viscosities of η1 = 1 and η3,4,5 = 0.4. A laminar fluid is considered because of the Reynolds number Re ≪ 1.
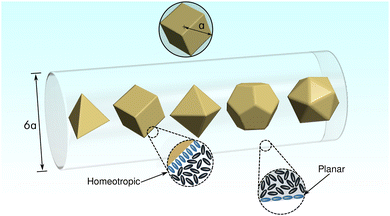
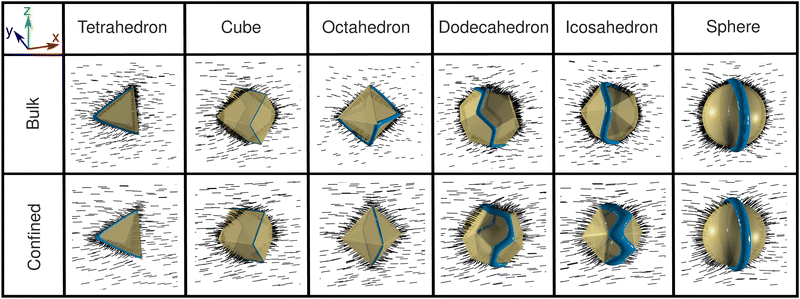
We started by analyzing the equilibrium configurations when platonic-solid-like particles exhibiting homeotropic anchoring are immersed in the bulk of an NLC host – we considered strong anchoring energy with WH = 1 × 10−3 J m−2. These particles were constructed to be circumscribed into a sphere of radius a = 120 nm (see Fig. 1). The simulations started considering an isotropic configuration which, for each particle, evolved in an NLC with the alignment shown in Fig. 2. We obtain that in all the cases, the NLC equilibrates in a configuration where a vertex of the particle coincides with the average director vector. We can also see from the figure that a disclination line was formed at some edges of the particles, and in most cases, a closed line surrounding the particle resembles the Saturn-ring disclination line observed in spherical colloids.
For confinement, we considered a cylindrical channel of R = 6a. The channel's walls exert strong planar anchoring (WP = 1 × 10−3 J m−2) and periodic boundary conditions along the cylindrical axis (x-direction) were applied. The NLC was aligned with its director parallel to the x-axis (see Fig. 1). The platonic-solid-like particles were positioned at the center of the channel, oriented according to the equilibrium configuration found in bulk. Specifically, the director aligns parallel to the channel axis (x-direction), and the particle is oriented with one of its vertices along this x-axis. We observed that confinement facilitates the formation of the “ring” defect in the case of the octahedron-like colloid, while for the other cases, there are no significant differences in the shape of the disclination lines. Given the orientation of the colloids for the nematic host, the disclinations appear to be located at the center (“equators”) of the particles and induce, like in spherical particles, a quadrupolar configuration of the director field of the NLC (see Fig. 2).
Finally, a pressure gradient, Δp, was applied along the x-direction to drive a Poiseuille flow; the largest flow velocity value was achieved at the center of the channel. Table 1 shows the values used in our simulations. Next, we will refer only to the Ericksen numbers.
| Δp (Mpa) | v max (ms−1) | Er |
|---|---|---|
| 0.2 | 0.11 | 2 |
| 0.5 | 0.28 | 5 |
| 4.9 | 2.8 | 50 |
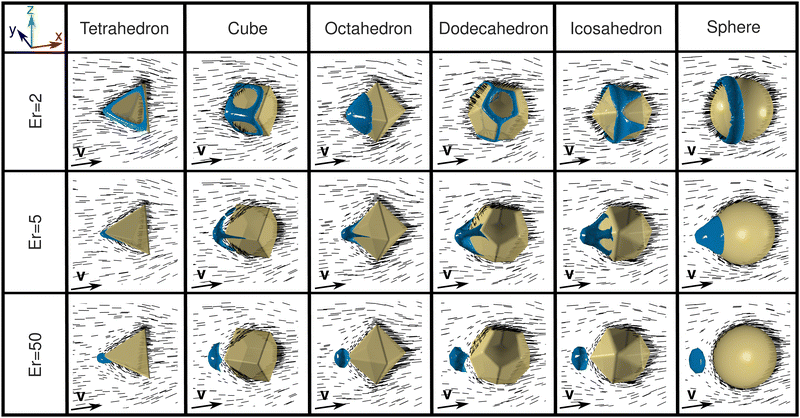
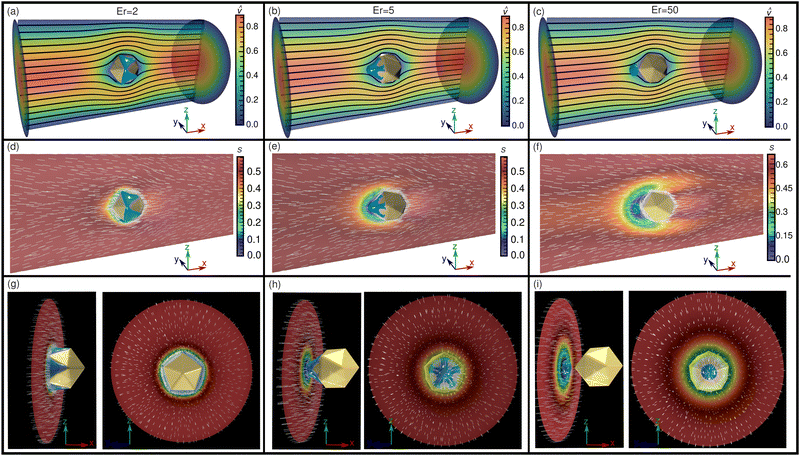
In general, flow can induce alignment or reorientation of liquid crystal molecules; in this case, the Poiseuille flow enhances the alignment of liquid crystal molecules along the flow direction. Starting from the equilibrium configuration shown in Fig. 2 for the confined case of each polyhedron, a pressure gradient was applied. For Er = 2, the flow induces a upstream displacement of the line defect; as a result, for each case, the liquid crystal configuration exhibits a dipole moment (see Fig. 3). The dipole moment grows with Er; for each polyhedron, the line defect moves upstream toward the vertex, exhibiting an octopus-like shape, with several limbs depending on the edges at the vertex. For sufficiently high Er, the defect separates from the particle, and a hyperbolic hedgehog point defect is formed (see Fig. 3). The upstream movement of the defect is consistent with the findings in Gettelfinger et al.34 and Villada et al.,35 where the diverging flow upstream of the particle promotes disorder and attracts the defect to minimize the elastic free energy. In the equilibrium state, disclination lines in tetrahedron, cube, and dodecahedron particles form closed loops that align with some of their edges, as illustrated in Fig. 2. When subjected to flow, these disclination lines are displaced upstream for each polyhedron, stretching toward the vertex in the direction opposite to the flow (see Fig. 3). The interaction between the disclination and the sharp edges of the platonic-like particles is crucial in determining the defect's behavior under flow. These sharp edges act as pinning sites, which influence both the configuration and the movement of the disclination.
Fig. 4 shows additional details of the streamlines and some director field views for the case of the icosahedral colloid. The dipole configuration can be appreciated for the different Er's as shown by the contrast of the color in the scalar order parameter. The 5-limbed octopus shape of the defect achieved when Er = 5 can also be appreciated. The disorder regions shrink when increasing Er, and to visualize the defect regions, we decrease the value of the scalar order parameter, S, used for obtaining the isosurfaces in Fig. 3. In all the cases, we found that once the flow was switched off, the system recovered its initial configuration.
Fig. 5 shows the phase (FLdG), elastic (FE), and surface (FS) contributions to the total free energy density (FT), as given in eqn (1), as a function of the number of flat faces of the polyhedra. Although a sphere can be considered the limit case where the number of faces of a regular polyhedron approaches infinity, we use zero as the number of flat faces associated with the sphere in these plots. The observed kink is simply a result of including the sphere at the origin of the graph. Once this is taken into account, we observe that the free energy exhibits a monotonic trend as a function of the number of faces. As expected, the presence of flow increases each contribution to the free energy except for the elastic one. In this case, the preferred LC alignment is enhanced in the flow direction, thereby reducing the overall elastic distortions. We can also appreciate from the figure that the total free energy increases with the number of flat faces due to the elastic and surface contributions. The sphere, as a limit case, is the one that causes the most distortion in the LC alignment.
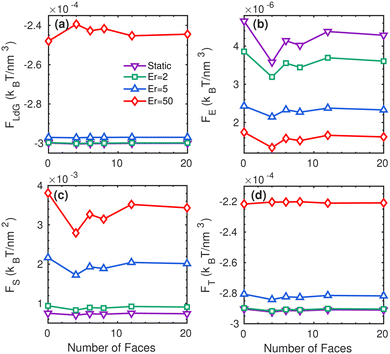 | ||
| Fig. 5 Free energy as a function of the number of flat faces of the polygons for different Ericksen numbers. | ||
4 Conclusions
When asymmetric colloidal particles with homeotropic anchoring are immersed in a uniformly aligned NLC, the presence of edges in the shape of the particles induces significant distortions in the director field. For cubes, octahedra, dodecahedra, and icosahedra, a disclination line that “encircles” the particle is formed, following the edges of each polyhedron at the central part of the particle. Only in the case of tetrahedra, the disclination line is not closed. When Poiseuille flow is applied, the disclination line is displaced towards the opposite direction, thereby inducing a dipole configuration of the NLC alignment. The dipolar moment increases with the Ericksen number. As a result, the disclination line collapses at the particle's vertex opposite to the flow direction, and eventually, it separates from the particle, which results in a hyperbolic hedgehog point defect, which is similar to what is observed in spherical colloids. With its acute vertex angle, the tetrahedron-like colloid exhibits a stronger adherence to the topological defect to the surface.In addition to the specific findings regarding disclination behavior around platonic solid-like particles, our results suggest exciting applications in the field of self-assembly. The controlled manipulation of disclination lines, as demonstrated in our simulations, can be exploited to guide the self-assembly of particles into ordered structures. This is consistent with recent work where disclination networks were used as templates for colloidal assembly.75–78 The tunability of defect configurations – determined by particle shape, confinement, and external flow – offers additional flexibility in designing these self-assembled structures. By fine-tuning these parameters, it may be possible to engineer complex assemblies with tailored optical, mechanical, or topological properties. Our findings, therefore, open new avenues for defect-guided self-assembly processes, presenting exciting potential for the development of advanced materials.
Author contributions
S. V.-G. and J. A. M.-G. designed the project and wrote the manuscript. All the authors analyzed the data, discussed the results, and contributed to the final manuscript.Data availability
The data that support the findings of this study, as well as the models used in our calculations, are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge computer resources by the Global Health Institute One-Health Colombia at Universidad Nacional de Colombia, Medellín, Colombia. S. V.-G. is greatful to Politécnico Colombiano Jaime Isaza Cadavid, located in Medellín, Colombia, for its financial support (No. 2024/00095/001). J. D. O.-C. extends gratitude to the Grupo de Investigación Ingeniar, Facultad de Ciencias Básicas e Ingeniería, Corporación Universitaria Remington, Medellín, Colombia, for financial support (No. 4000000310).Notes and references
- D. Mistry, N. Traugutt, B. Sanborn, R. Volpe, L. Chatham, R. Zhou, B. Song, K. Yu, K. Long and C. Yakacki, Nat. Commun., 2021, 12, 123 CrossRef PubMed.
- R. M. Parker, T. H. Zhao, B. Frka-Petesic and S. Vignolini, Nat. Commun., 2022, 13, 1 Search PubMed.
- Y. Shi, J. Han, C. Li, T. Zhao, X. Jin and P. Duan, Nat. Commun., 2023, 14, 1 Search PubMed.
- X. Sun, S. Chen, B. Qu, R. Wang, Y. Zheng, X. Liu, W. Li, J. Gao, Q. Chen and D. Zhuo, Nat. Commun., 2023, 14, 1 CAS.
- X. Ma, Y. Han, Y.-S. Zhang, Y. Geng, A. Majumdar and J. P. F. Lagerwall, Nat. Commun., 2024, 15, 1 Search PubMed.
- H. M. van der Kooij, D. J. Broer, D. Liu and J. Sprakel, ACS Appl. Mater. Interfaces, 2020, 12, 19927–19937 CrossRef CAS PubMed.
- A. Concellón, Angew. Chem., Int. Ed., 2023, 62, 1 Search PubMed.
- S. A. Oladepo, Molecules, 2022, 27, 1453 CrossRef CAS PubMed.
- Z. Zhang, X. Yang, Y. Zhao, F. Ye and L. Shang, Adv. Mater., 2023, 35, 1 Search PubMed.
- G. Hu, B. Zhang, S. M. Kelly, J. Cui, K. Zhang, W. Hu, D. Min, S. Ding and W. Huang, Addit. Manuf., 2022, 55, 102861 CAS.
- F. Chen, J. Zheng, C. Xing, J. Sang and T. Shen, Displays, 2024, 82, 102632 CrossRef CAS.
- L.-L. Ma, C.-Y. Li, J.-T. Pan, Y.-E. Ji, C. Jiang, R. Zheng, Z.-Y. Wang, Y. Wang, B.-X. Li and Y.-Q. Lu, Light: Sci. Appl., 2022, 11, 1 CrossRef PubMed.
- W. Wu, W. Hu, G. Qian, H. Liao, X. Xu and F. Berto, Mater. Des., 2019, 180, 107950 CrossRef.
- I. Musevic, M. Skarabot, U. Tkalec, M. Ravnik and S. Zumer, Science, 2006, 313, 954–958 CrossRef CAS PubMed.
- V. G. Nazarenko, A. B. Nych and B. I. Lev, Phys. Rev. Lett., 2001, 87, 075504 CrossRef CAS PubMed.
- C. Blanc, D. Coursault and E. Lacaze, Liq. Cryst. Rev., 2013, 1, 83–109 CrossRef CAS.
- P. Poulin and D. A. Weitz, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 626–637 CrossRef CAS.
- P. Poulin, H. Stark, T. C. Lubensky and D. A. Weitz, Science, 1997, 275, 1770–1773 CrossRef CAS PubMed.
- Y. Gu and N. L. Abbott, Phys. Rev. Lett., 2000, 85, 4719–4722 CrossRef CAS PubMed.
- O. Mondain-Monval, J. Dedieu, T. Gulik-Krzywicki and P. Poulin, Eur. Phys. J. B, 1999, 12, 167–170 CrossRef CAS.
- B. I. Lev, S. B. Chernyshuk, P. M. Tomchuk and H. Yokoyama, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 1 CrossRef PubMed.
- D. A. Beller, M. A. Gharbi and I. B. Liu, Soft Matter, 2015, 11, 1078–1086 RSC.
- F. Serra, Liq. Cryst., 2016, 43, 1920–1936 CrossRef CAS.
- D. A. Olaya-Muñoz, J. P. Hernández-Ortiz and M. Olvera de la Cruz, J. Chem. Phys., 2022, 157, 204104 CrossRef PubMed.
- M. Gorman, X. Ruan and R. Ni, Phys. Rev. E, 2024, 109, 034902 CrossRef CAS PubMed.
- L. Botto, E. P. Lewandowski, M. Cavallaro and K. J. Stebe, Soft Matter, 2012, 8, 9957–9971 RSC.
- A. Lefauve and D. Saintillan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 021002 CrossRef PubMed.
- J. de Graaf, H. Menke, A. J. Mathijssen, M. Fabritius, C. Holm and T. N. Shendruk, J. Chem. Phys., 2016, 144, 1 CrossRef PubMed.
- V. M. O. Batista, M. L. Blow and M. M. Telo da Gama, Soft Matter, 2015, 11, 4674–4685 RSC.
- P. Steffen, E. Stellamanns and A. Sengupta, Phys. Fluids, 2021, 33, 072005 CrossRef CAS.
- M. Čopič, M. Vilfan and A. Mertelj, Liq. Cryst., 2013, 40, 1646–1654 CrossRef.
- J. S. Lintuvuori, D. Marenduzzo, K. Stratford and M. E. Cates, J. Mater. Chem., 2010, 20, 10547 RSC.
- S. Čopar, M. Ravnik and S. Žumer, Crystals, 2021, 11, 956 CrossRef.
- B. T. Gettelfinger, J. A. Moreno-Razo, G. M. Koenig Jr, J. P. Hernández-Ortiz, N. L. Abbott and J. J. de Pablo, Soft Matter, 2010, 6, 896 RSC.
- S. Villada-Gil, V. Palacio-Betancur, J. C. Armas-Pérez, J. J. de Pablo and J. P. Hernández-Ortiz, Soft Matter, 2021, 17, 3463–3472 RSC.
- R. B. Meyer, Solid State Commun., 1973, 12, 585–588 CrossRef CAS.
- G. S. Ranganath, J. Phys., Colloq., 1979, 40, C3-87–C3-89 CrossRef.
- R. Zhang, T. Roberts, I. S. Aranson and J. J. de Pablo, J. Chem. Phys., 2016, 144, 084905 CrossRef PubMed.
- J. Jiang, O. I. Akomolafe, X. Wang, Z. Asilehan, W. Tang, J. Zhang, Z. Chen, R. Wang, K. Ranabhat, R. Zhang and C. Peng, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2402395121 CrossRef PubMed.
- Ž. Kos, M. Ravnik and S. Žumer, Liq. Cryst., 2017, 1–11 CrossRef.
- S. M. Hashemi, U. Jagodič, M. R. Mozaffari, M. R. Ejtehadi, I. Muševič and M. Ravnik, Nat. Commun., 2017, 8, 1 CrossRef PubMed.
- C. Jiang, H. Huang, C. Ma, T. He and F. Zhang, J. Colloid Interface Sci., 2013, 411, 53–60 CrossRef CAS PubMed.
- S. Sacanna and D. J. Pine, Curr. Opin. Colloid Interface Sci., 2011, 16, 96–105 CrossRef CAS.
- L. Scarabelli, Pure Appl. Chem., 2018, 90, 1393–1407 CrossRef CAS.
- A. K. Pearce, T. R. Wilks, M. C. Arno and R. K. OReilly, Nat. Rev. Chem., 2020, 5, 21–45 CrossRef PubMed.
- H.-L. Wu, C.-H. Kuo and M. H. Huang, Langmuir, 2010, 26, 12307–12313 CrossRef CAS PubMed.
- M. Eguchi, D. Mitsui, H.-L. Wu, R. Sato and T. Teranishi, Langmuir, 2012, 28, 9021–9026 CrossRef CAS PubMed.
- A. Kuijk, A. van Blaaderen and A. Imhof, J. Am. Chem. Soc., 2011, 133, 2346–2349 CrossRef CAS PubMed.
- D. Doan, J. Kulikowski and X. W. Gu, Part. Part. Syst. Charact., 2021, 38, 1 CrossRef.
- J. Henzie, M. Grünwald, A. Widmer-Cooper, P. L. Geissler and P. Yang, Nat. Mater., 2011, 11, 131–137 CrossRef PubMed.
- S. Yoo, R. Sen, Z. C. Simon, J. H. Smith, K. N. Kunzler, S. Tan and J. E. Millstone, Chem. Mater., 2023, 35, 6274–6282 CrossRef CAS.
- V. Thambi, A. Kar, P. Ghosh, D. Paital, A. R. S. Gautam and S. Khatua, ACS Omega, 2019, 4, 13733–13739 CrossRef CAS PubMed.
- T. Huang, Q. Zhao, J. Xiao and L. Qi, ACS Nano, 2010, 4, 4707–4716 CrossRef CAS PubMed.
- G. A. Vinnacombe-Willson, J. K. Lee, N. Chiang, L. Scarabelli, S. Yue, R. Foley, I. Frost, P. S. Weiss and S. J. Jonas, ACS Appl. Nano Mater., 2023, 6, 6454–6460 CrossRef CAS PubMed.
- M. C. Newton and P. A. Warburton, Mater. Today, 2007, 10, 50–54 CrossRef CAS.
- R. Brescia, K. Miszta, D. Dorfs, L. Manna and G. Bertoni, J. Phys. Chem. C, 2011, 115, 20128–20133 CrossRef CAS.
- K. Miszta, J. de Graaf, G. Bertoni, D. Dorfs, R. Brescia, S. Marras, L. Ceseracciu, R. Cingolani, R. van Roij, M. Dijkstra and L. Manna, Nat. Mater., 2011, 10, 872–876 CrossRef CAS PubMed.
- X. Zhu, H. Jia, X. Zhu, S. Cheng, X. Zhuo, F. Qin, Z. Yang and J. Wang, Adv. Funct. Mater., 2017, 27, 1 Search PubMed.
- L. Rossi, V. Soni, D. J. Ashton, D. J. Pine, A. P. Philipse, P. M. Chaikin, M. Dijkstra, S. Sacanna and W. T. M. Irvine, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5286–5290 CrossRef CAS PubMed.
- Y. Zhang, F. Lu, D. van der Lelie and O. Gang, Phys. Rev. Lett., 2011, 107, 135701 CrossRef PubMed.
- Y. Jiao, F. H. Stillinger and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 1–12 CrossRef PubMed.
- P. F. Damasceno, M. Engel and S. C. Glotzer, ACS Nano, 2012, 6, 609–614 CrossRef CAS PubMed.
- R. D. Batten, F. H. Stillinger and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 1–13 CrossRef PubMed.
- R. Ni, A. P. Gantapara, J. de Graaf, R. van Roij and M. Dijkstra, Soft Matter, 2012, 8, 8826 RSC.
- M. Dijkstra, Adv. Chem. Phys., 2014, 156, 35–71 CrossRef.
- D. Zerrouki, J. Baudry, D. Pine, P. Chaikin and J. Bibette, Nature, 2008, 455, 380–382 CrossRef CAS PubMed.
- H. Stark and T. C. Lubensky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 061709 CrossRef CAS PubMed.
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, Oxford, 2nd edn, 1993 Search PubMed.
- O. Parodi, J. Phys., 1970, 31, 581–584 CrossRef CAS.
- Sandia National Laboratories, Cubit Version 14.1, 2014.
- B. S. Kirk, J. W. Peterson, R. H. Stogner and G. F. Carey, Eng. Comput., 2006, 22, 237–254 CrossRef.
- J. W. Demmel, J. R. Gilbert and X. S. Li, SIAM J. Matrix Anal. Appl., 1999, 20, 915–952 CrossRef.
- J. W. Demmel, S. C. Eisenstat, J. R. Gilbert, X. S. Li and J. W. H. Liu, SIAM J. Matrix Anal. Appl., 1999, 20, 720–755 CrossRef.
- X. S. Li and M. Shao, ACM Trans. Math. Software, 2011, 37, 1–20 CrossRef CAS.
- H. Yoshida, K. Asakura, J. Fukuda and M. Ozaki, Nat. Commun., 2015, 6, 7180 CrossRef CAS PubMed.
- Y. Guo, M. Jiang, S. Afghah, C. Peng, R. L. Selinger, O. D. Lavrentovich and Q.-H. Wei, Giant, 2024, 17, 100228 CrossRef CAS.
- B. Senyuk, Q. Liu, Y. Yuan and I. I. Smalyukh, Phys. Rev. E, 2016, 93, 062704 CrossRef PubMed.
- I. I. Smalyukh, Rep. Prog. Phys., 2020, 83, 106601 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2024 |