Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Osmotic spawning vesicle†
Minoru
Kurisu
 * and
Masayuki
Imai
* and
Masayuki
Imai

Department of Physics, Graduate School of Science, Tohoku University, Japan. E-mail: kurisu@bio.phys.tohoku.ac.jp
First published on 16th September 2024
Abstract
We discovered a cascade vesicle division system driven by osmotic inflation. Binary giant unilamellar vesicles (GUVs) composed of sodium bis(2-ethylhexyl)sulfosuccinate (AOT) and cholesterol (Chol) were subjected to an osmotic pressure difference by encapsulating membrane-impermeable osmolytes (typically sucrose) in an external aqueous solution containing membrane-permeable osmolytes (typically fructose). This simple setup enabled the mother GUVs to repeatedly form small membrane buds and subsequently undergo divisions over several hundred seconds, resulting in the production of approximately 30–300 daughter GUVs from a single mother GUV. The observed morphological change of GUVs is well described by the mechanical balance between membrane bending, membrane tension, and osmotic pressure difference based on the spontaneous curvature model. This “osmotic spawning” behavior of GUVs does not rely on chemical reactions or functional macromolecules. Therefore, this cascade division system is compatible with various chemical systems and has the potential to implement proliferation ability in artificial cells, drug delivery systems, and protocells simply by modifying their membrane compartments and osmolytes.
Introduction
Living cells proliferate by dividing themselves into daughter cells. All contemporary living systems are enclosed by plasma membranes, which undergo deformation and division during the process of cell proliferation. In the field of soft matter physics and biophysics of membranes, the morphologies of cells and their transitions have been described on the basis of membrane elasticity by employing simple model membranes such as giant unilamellar vesicles (GUVs).1–4 GUVs have attracted attention also from the field of the origins of life and artificial cells, as a plausible starting point for the road connecting matter and life. The vesicle membrane separates the internal aqueous solution from the external environment, and thus, chemical reaction networks and functional molecules (e.g., genetic polymers and enzymatic proteins) are encapsulated into this simple membrane compartment. In this context, coupled with the internal molecular synthesis, the mother GUVs should deform and divide to produce daughter GUVs that contain the same functional molecules and chemical reaction networks as their mother, i.e., the proliferation of protocells or artificial cells.1,5–12The reproduction of GUVs by dividing a mother GUV into several daughter GUVs has been one of the main focus points in the field of protocells and artificial cells. For such morphological changes, spherical mother GUVs require excess membrane area against the encapsulated volume, e.g., the increase of membrane area with a constant vesicle volume by the uptake of vesicle-forming amphiphiles or by the thermal expansion of membranes.1,13–18 The mother GUVs with excess membrane area take the shapes that minimize elastic energy of the membranes. In the presence of positive spontaneous curvature of the membranes, the mother GUVs with the increasing membrane area may take the deformation pathway from a sphere to prolate, pear, and then a limiting shape, in which two spherical segments are connected by an infinitesimally narrow neck.1,19–21 Finally, the breaking of the narrow neck results in the formation of two separated GUVs (i.e., division of a mother GUV).1,18,22–24 As an alternative approach, GUVs can generate excess membrane area more easily by osmotically draining water from the GUVs while keeping the membrane area. This osmotic deflation sometimes results in the formation of a multi-sphere vesicle, whereby multiple and similar-sized daughter GUVs are connected to the mother GUV as the inward buds25–30 or the outward buds30–32 depending on the spontaneous curvature of the membranes. If the outward buds were finally separated from the mother GUV, the vesicle division would be completed; however, in most cases, the membrane buds remained stably connected to the mother GUV and did not undergo spontaneous division.
In this study, we report a cascade division behavior of GUVs, which enabled the successful coupling of the recursive formation of the outward membrane buds and their spontaneous separation from the mother GUVs. Remarkably, we observed that a single mother GUV generated tens to a few hundred daughter GUVs over a period of ten minutes to two hours. This cascade vesicle division was driven by the opposite mechanism of the osmotic deflation described above, i.e., the mother GUVs realized division when they took in water from the environment due to the slight osmotic pressure differences, not when they drained water to the environment. Therefore, the total volume of GUVs did not decrease but increased during the divisions. The cascade division of GUVs was easily achieved: binary sodium bis(2-ethylhexyl)sulfosuccinate (AOT) + cholesterol (Chol) GUVs prepared in an aqueous solution containing 5 to 250 mM disaccharides were transferred into another solution containing isomolar monosaccharides and 3.0 mM AOT. After the transfer, the binary AOT + Chol GUVs encapsulated disaccharide molecules, and the external environment contained the same concentration of monosaccharides. The internal disaccharide molecules are hard to permeate the vesicle membrane, whereas the external monosaccharide molecules diffuse into the GUVs more easily. This asymmetric molecular permeation generates a slight but long-term molecular concentration difference across the vesicle membrane, which facilitates the gradual influx of water (i.e., volume growth) and the uptake of additional AOT molecules from the environment into the GUV membrane (i.e., membrane growth) for relaxing membrane tension.17 If the GUVs were composed solely of AOT molecules, which have cylindrical molecular shapes, the mother GUVs also experienced the influx of water and the uptake of AOT molecules, but the GUVs only inflated while keeping their spherical shapes (i.e., no division). The GUVs required the second membrane component, Chol, which has an inverse-cone molecular shape (small head and bulky tail), for the cascade division. The influx of AOT molecules from the external environment into the outer leaflet of the bilayer membrane is likely to induce an asymmetry in the distribution of Chol between the outer and inner monolayers, thereby generating a spontaneous curvature of the membrane. This results in the formation of membrane buds on the mother GUVs, followed by the breaking of the membrane neck connecting the mother and daughter GUVs. The long-term cascade division of binary AOT + Chol GUVs was spontaneously triggered without any external force or manipulations after the initial transfer of the GUVs. Although small portions of encapsulated solutions might leak out by every division event, the macromolecules stored inside the mother GUVs were distributed to the daughter GUVs. These “osmotic spawning vesicles” were analyzed based on the spontaneous curvature model of membrane elasticity theory and the shape equation of (multi-) spherical membranes.4,19–21,33
Results and discussion
Microscopy observations of osmotic spawning vesicles
Fig. 1a provides an overview of the experimental setup, which involves the application of a slight osmotic pressure difference on a giant unilamellar vesicle (GUV) and the incorporation of vesicle-forming molecules into the GUV. Specifically, we prepared binary AOT + Chol (9/1, molar ratio) GUVs in a 20 mM NaH2PO4 solution containing membrane-impermeable sucrose (disaccharide) molecules. These GUVs were then transferred into another 20 mM NaH2PO4 solution containing membrane-permeable molecules (typically monosaccharide fructose) and dispersed vesicle-forming molecules, AOT. The initial concentrations of saccharides in the internal and external aqueous solution were the same, normally 250 mM, and the initial concentration of AOT in the external solution was ∼3.0 mM. In the presence of 20 mM NaH2PO4, the critical vesiculation concentration (cvc) of AOT is ∼1.5 mM;34i.e., roughly half of AOT molecules (∼1.5 mM) form vesicles and the other half (∼1.5 mM) AOT molecules are dispersed in the external solution as monomer state. Due to the difference in membrane permeabilities of mono- and disaccharides, most sucrose molecules will remain inside GUVs while fructose molecules gradually diffuse into the GUVs, continuously generating a slight osmotic pressure difference and water influx.17,35 The increase in encapsulated volume imposes tension on vesicle membranes, but the free AOT molecules in the external aqueous solution will be inserted into the vesicle membrane to relax the tension stress.17,35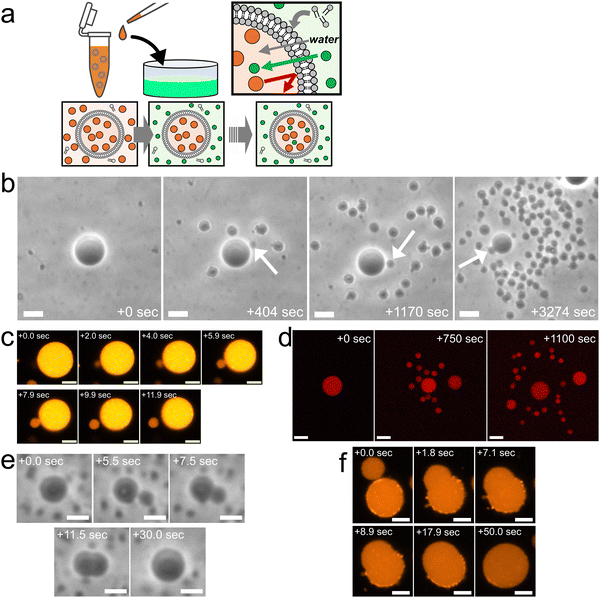 | ||
| Fig. 1 Osmotic spawning of binary AOT + Chol vesicles and their termination. (a) Schematic of the experimental setup and the asymmetric permeation mechanism which triggers water inflow and incorporation of free membrane molecules. Green filled circles represent permeable osmolyte, typically monosaccharide fructose, and orange filled circles represent impermeable osmolyte, disaccharide sucrose. Both internal (orange) and external (green) solutions were prepared by using 20 mM NaH2PO4 solution (pH = 4.3). The initial concentrations of mono- and di-saccharides are the same, typically 250 mM. The monosaccharides solution (green) contains ∼3.0 mM AOT, ∼1.5 mM of which exist as free monomers, playing a role as a reservoir of membrane molecules for relaxing vesicle membrane under osmotic tension stress. (b) Phase contrast microscopy images of binary AOT + Chol (9/1) GUVs during osmotic spawning. The internal and external osmolytes were sucrose and fructose, respectively. The images were taken from Movie S1 (ESI†). White arrows indicate daughter GUVs which were produced at the moment the snapshots were taken. Length of scale bars: 10 μm. (c) Fluorescence microscopy images of binary AOT + Chol (9/1) GUVs labelled with 1.5% (mol) Rhod-PE during the formation of a daughter vesicle. Brightness and contrast of the images were enhanced for clarifying a small membrane bud. Length of scale bars: 5 μm. (d) Confocal fluorescence microscopy images of binary AOT + Chol (9/1) GUVs during osmotic spawning. The initial mother GUV encapsulated 100 μM Dextran Texas-Red (MW = 3000). Length of scale bars: 10 μm. (e) Phase contrast microscopy images of a binary AOT + Chol (9/1) GUV at the end of osmotic spawning. The images were taken from Movie S3 (ESI†). A membrane bud formed on the mother GUV (5.5 s) continued increasing in size and was eventually fused with the mother GUV. No budding was observed thereafter. Length of scale bars: 5 μm. (f) Fluorescence microscopy images of a binary AOT + Chol (9/1) GUVs labelled with 1.5% (mol) Rhod-PE at the end of osmotic spawning. The neck connecting the daughter membrane bud and the mother GUV opened up, and the membrane bud continued to increase in size until it fused with the mother GUV. No budding was observed thereafter. Length of scale bars: 5 μm. | ||
We discovered that the binary AOT + Chol (9/1, mol) GUVs can generate (i.e., spawn) multiple daughter GUVs through the osmotic pressure difference and the uptake of vesicle-forming molecules (Fig. 1b and Movie S1, S2, ESI†). Specifically, several tens of seconds after the GUV transfer (Fig. 1a), the mother GUVs started to repeat the instantaneous formation of membrane buds (indicated by arrows in Fig. 1b) and the subsequent division from the mother GUVs. Focusing on the single spawning event, an initially spherical binary AOT + Chol GUV first formed a small bud on the mother membrane, the process of which was completed within a few seconds (from 0.0 s to 2.0 s in Fig. 1c). The bud grew slightly for several seconds while connected to the mother GUV (from 2.0 s to 7.9 s in Fig. 1c). Then, the neck connecting the bud and the mother GUV was spontaneously broken (from 7.9 s to 11.9 s in Fig. 1c), which formed a separated small daughter GUV. The typical initial concentrations of internal and external saccharides were 250 mM in our experiments, and this spawning behavior was observed even by the increase in concentrations up to 500 mM and the decrease to at least 5 mM, as far as we examined. It should be noted that the maximal Chol content in binary AOT + Chol GUVs is 10%, and we have not succeeded in preparing the GUV with higher Chol content (Chol begins to aggregate). When the initial Chol content was reduced in the binary GUVs, we observed osmotic spawning at least with 1.0% Chol. Under several different conditions, this spawning process was repeated about 30 to 300 times during the observation period of about 10 to 100 minutes, as summarized in no. 1–13 in Table 1. No phase-separated domains were detected in vesicle membranes by fluorescent microscope observations.
| No. | Chol [mol%] | Internal/external osmolyte | C ini [mM] | t obs [s] | R M,ini [μM] | N D | A D,sum | V D,sum | Note |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | Sucrose/fructose | 250 | 5000 | 8.0 | 228 | 7.1 | 1.7 | Contrast of smaller daughter GUVs were unclear. |
| 2 | 10 | Sucrose/fructose | 250 | 1500 | 9.0 | 35 | 3.6 | 1.7 | |
| 3 | 2.5 | Sucrose/fructose | 250 | 900 | 8.2 | 32 | 3.2 | 1.2 | |
| 4 | 2.5 | Sucrose/fructose | 250 | 1100 | 6.7 | 50 | 3.4 | 1.2 | |
| 5 | 1.0 | Sucrose/fructose | 250 | 2200 | 9.1 | 218 | 7.5 | 1.6 | |
| 6 | 1.0 | Sucrose/fructose | 250 | 800 | 5.9 | 98 | 4.3 | 1.5 | |
| 7 | 10 | Sucrose/fructose | 500 | 1500 | 7.3 | 68 | 3.9 | 1.5 | |
| 8 | 10 | Sucrose/fructose | 200 | 5000 | 7.4 | 166 | 7.9 | 2.5 | |
| 9 | 10 | Sucrose/fructose | 5 | 1600 | 12.8 | ≥47 | ≥2.2 | ≥0.5 | |
| 10 | 10 | Sucrose/glucose | 250 | 6000 | 7.8 | 315 | 8.3 | 1.7 | |
| 11 | 10 | Sucrose/glucose | 250 | 1100 | 8.1 | 64 | 4.1 | 1.2 | |
| 12 | 10 | Sucrose/glucose | 250 | 4000 | 8.1 | 86 | 5.7 | 1.8 | |
| 13 | 10 | Sucrose/glucose | 250 | 1500 | 8.9 | 77 | 3.6 | 1.3 | |
| 14 | 0 | Sucrose/fructose | 50–500 | N/A | Slight inflation while keeping spherical shapes. | ||||
| 15 | 10 | Sucrose/glycerol | 50–250 | N/A | Radical inflation and budding-retraction behavior. | ||||
| 16 | 0 | Sucrose/glycerol | 50–250 | N/A | Radical inflation while keeping spherical shapes. | ||||
The neck structure connecting mother and daughter vesicles is known to be normally stable (i.e., not broken spontaneously).1,32 Although the increase of membrane spontaneous curvature may generate a constriction force on the neck,1,21 it should be noted that we utilized another neck destabilization mechanism that couples the Gaussian curvature of the membrane and the local lipid composition at the neck.18,22–24 If binary vesicles are composed of cylindrical shaped molecules (such as AOT) and inverse-cone shaped molecules (such as Chol), the inverse-cone shaped molecules can be expelled from the infinitesimally narrow neck (which has a negative Gaussian curvature) and produce an interface between the neck region and the spherical region of a neck-forming GUV. This interface may reduce the energy barrier to pinch off (i.e., destabilize) the neck, thereby facilitating the vesicle division without extra energy input. The spontaneous neck breaking of binary AOT + Chol GUVs has been previously reported.1,17,34 In phospholipids, the vesicle division by this mechanism was reported using DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine) as cylindrical shaped molecules and DLPE (1,2-dilauroyl-sn-glycero-3-phosphoethanolamine) as inverse-cone shaped molecules.18,22
In the osmotic spawning process, the aqueous solutions initially encapsulated in mother GUVs were also distributed to their daughter GUVs. The fluorescent Dextran Texas-Red molecules (MW = 3000) were encapsulated in mother GUVs. The confocal microscopy observations of the spawning mother GUVs revealed that the fluorescent macromolecules were successfully encapsulated by their daughter GUVs (Fig. 1d), while small portions of the macromolecules may have leaked out with each division event. The distribution of these molecules to the daughter GUVs is an important property for potential applications in the field of artificial cells and drug delivery. In addition, together with the fluorescent microscopy observation which introduced Rhod-PE into the membranes of mother GUVs (Fig. 1c), it was confirmed that both the vesicle membranes and the internal aqueous solution of daughter GUVs originated from the fluorescent mother GUVs, i.e., the daughter GUVs were produced by the deformation and division of the mother GUVs, not by the nucleation of AOT molecules dispersed in the external solution.
At the end of the spawning, we observed that mother GUVs always retracted daughter membrane buds. Fig. 1e shows the typical case, where a mother GUV quickly formed a bud on the membrane as the usual spawning process, but the bud was not stabilized as an independent daughter GUV (see also Movie S3, ESI†). The once-closed (i.e., infinitesimally narrow) neck connecting the mother GUV and the daughter membrane bud opened up in a few seconds, and the bud continued growing in size while keeping the semispherical shape. Finally reaching nearly the mother's size, the daughter bud was fused with the mother GUV. This incomplete division was also observed by fluorescent microscopy where binary AOT + Chol (9/1, mol) GUVs contained fluorescent dye-labeled amphiphile (Rhod-PE) in their membranes (Fig. 1f). Boundaries of phase-separated domains between the mother and daughter segments were not observed. As far as we observed, once mother GUVs showed such budding-and-retraction behaviors after the usual spawning, the GUVs never restarted spawning but instead maintained the spherical shapes. As discussed in the later sections, this spawning and end-of-spawning transition may be governed by the mean curvature required for closing the neck or by the (osmotic) pressure difference.
Vesicle radius and volume-to-area ratio
The radii of mother and daughter GUVs decreased during osmotic spawning. Fig. 2a shows the typical radii changes of a mother GUV (RM) and its generating daughter GUVs (RD) taken from the observation of Fig. 1b. Each data point represents a single spawning event, and the total number of spawning events (i.e., the number of daughter GUVs) is 228. The radii were estimated by approximating the vesicle shape as a sphere. Specifically, the radii of daughter GUVs were measured just after the neck breaking. The daughter GUVs subsequently exhibited a slight increase in size by osmotic inflation, which is not included in Fig. 2a and hereafter. In this observation, the total surface area and volume of the daughter GUVs increased roughly 7.1 times and 1.7 times, respectively, from the initial values of the mother GUV. In all observations of osmotic spawning vesicles, the mother radii decreased monotonically, presumably due to the release of membranes and encapsulated solution in the form of daughter GUVs. Concurrently, the radii of daughter GUVs also decreased.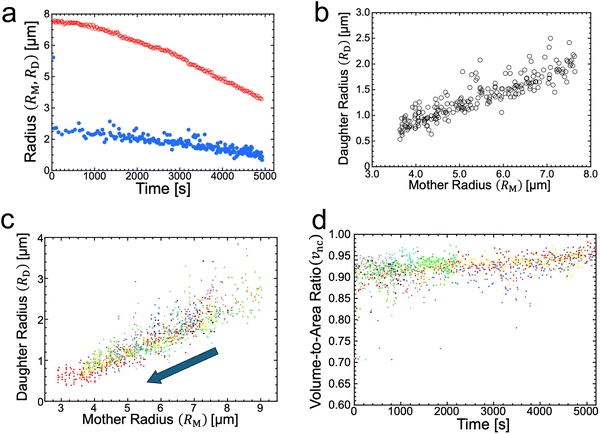 | ||
| Fig. 2 Vesicle radii and volume-to-area ratio during osmotic spawning. (a) Radius change of mother (red open circles) and daughter (blue filled circles) binary AOT + Chol (9/1) GUVs against time, obtained from single observation (Fig. 1b). The radii of daughter GUVs were measured just after separated from their mother, and thereafter the daughter GUVs gradually increased in size from the plotted values by osmotic inflation. (b) Relationship between the radius of mother GUV and the radius of daughter GUVs, obtained from Fig. 2a. (c) Relationship between the radius of mother binary AOT + Chol (9/1) GUV and the radius of daughter GUVs, obtained from ten independent observations using 250 mM sucrose and fructose as internal and external osmolytes, respectively. The data points move from upper right to lower left with the progress of spawning, as indicated by an arrow. Each color represents an independent observation. (d) Time evolution of the volume-to-area ratio of the GUVs when neck closure, vnc, estimated from the radii of mother and daughter GUVs (ten observations). Each color represents and independent observation and corresponds to color code used in Fig. 2c. | ||
Notably, if the radii of mother GUVs were the same, the radii of daughter GUVs also became approximately the same. From the typical observation of Fig. 1b, the daughter-to-mother radius ratio (RD/RM) is obtained, as shown in Fig. 2b. The time-dependent changes in vesicle radius (RD and RM plot; Fig. 2a) did not always coincide with the other observations since the frequency of spawning varied among different observations (see Supplementary Note 1 for two additional observations, ESI†). However, the time-independent RD/RM plot (Fig. 2b) was consistent among different observations, which was confirmed by superimposing the results from ten independent observations, as shown in Fig. 2c. Several data points with upward deviations in the figure came from the fusion of two membrane buds appearing almost simultaneously on the same mother GUV (see Supplementary Note 2 and Movie S4, ESI†). The consistency in the RD/RM ratio indicates that the same size of mother GUVs spawned roughly the same size of daughter GUVs, regardless of variations in the mother's initial radii and the elapsed time.
The formation of a small membrane bud from a spherical mother GUV requires the generation of excess surface area relative to encapsulated volume. In osmotic spawning, the instantaneous micro-pore opening on osmotically tensed mother membranes35–41 is attributed to the generation of the excess surface area. For a given membrane area A of a budding GUV, the vesicle size is characterized by
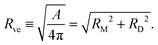 | (1) |
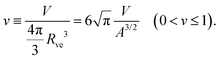 | (2) |
Membrane elasticity model and shape equation
In this section, we introduce a membrane elasticity model that describes morphological changes of GUVs. For bilayer membranes composed of amphiphiles that show fast flip–flop motions between outer and inner monolayers, the equilibrium vesicle shape is described by the spontaneous curvature model (SC model).19–21 In this model, a vesicle takes the shape that minimizes the bending energy given by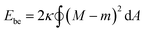 | (3) |
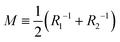 (Ri=1,2: principal radii of curvature) is local mean curvature, m is global spontaneous curvature of the membrane. A spherical vesicle is the special case where the membrane mean curvature is equal to the inverse of the vesicle radius, M = R−1, at any point on the membrane. However, if a vesicle has excess membrane area against vesicle volume, the vesicle morphology will deviate from a sphere, and the values of local mean curvature M will depend on the spontaneous curvature m, the membrane area A, and the vesicle volume V.
(Ri=1,2: principal radii of curvature) is local mean curvature, m is global spontaneous curvature of the membrane. A spherical vesicle is the special case where the membrane mean curvature is equal to the inverse of the vesicle radius, M = R−1, at any point on the membrane. However, if a vesicle has excess membrane area against vesicle volume, the vesicle morphology will deviate from a sphere, and the values of local mean curvature M will depend on the spontaneous curvature m, the membrane area A, and the vesicle volume V.
The coexistence of two different sphere radii (such as “+7.9 s” in Fig. 1c) in a single GUV is explained by the minimization of vesicle free energy. For analytical minimization of eqn (3) with the geometrical constraints of membrane area A and vesicle volume V, the mechanical membrane tension Σ and the pressure difference between the inside and outside of the vesicle ΔP (≡ Pin − Pout) are incorporated into eqn (3) as Lagrange multipliers. Then, one has to minimize
| F = Ebe + ΣA − ΔPV | (4a) |
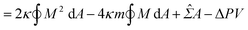 | (4b) |
![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e139.gif) ≡ Σ + 2κm2 is total tension. The two parameters Σ and ΔP are adjusted to achieve the desired A and V. The first variation of eqn (4b) provides an analytical derivation of the relation that should be satisfied for stationary membrane shapes. Especially for spherical membrane segments, the Euler–Lagrange equation of eqn (4b) has the following form:20,33,42–45
≡ Σ + 2κm2 is total tension. The two parameters Σ and ΔP are adjusted to achieve the desired A and V. The first variation of eqn (4b) provides an analytical derivation of the relation that should be satisfied for stationary membrane shapes. Especially for spherical membrane segments, the Euler–Lagrange equation of eqn (4b) has the following form:20,33,42–45ΔP = 2![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e139.gif) Msp − 4κmMsp2, Msp − 4κmMsp2, | (5) |
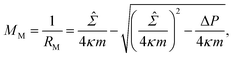 | (6) |
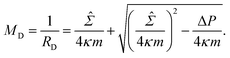 | (7) |
Spontaneous curvature and its origin
The formation of a closed (i.e., infinitesimally narrow) neck connecting mother and daughter spherical segments (such as “+7.9 s” in Fig. 1c) provides information on spontaneous curvature m of the membrane. The mother and daughter spherical segments are characterized by mean curvatures of the membranes, MM (= 1/RM) and MD (= 1/RD), respectively. For the vesicles to close the neck, the analytical and numerical studies based on the SC model have shown that the spontaneous curvature m of the vesicle membrane should have the value of20,21,46–48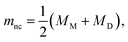 | (8) |
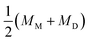 is associated with the mean curvature of the ideal closed neck located between the two spherical segments (MM and MD).21 The neck will remain closed if the spontaneous curvature m exceeds mnc but will open up if m falls below mnc. Assuming that mean curvatures of mother and daughter spherical segments (MM and MD) do not change before and after the neck breaking, the value of m when a spherical membrane bud with a closed neck was formed on a mother GUV can be estimated as mnc from the microscopy observations, as shown in Fig. 3a for the observation of Fig. 1b. The estimated spontaneous curvature mnc of the neck-closed GUVs increased during osmotic spawning due to the increase in mean curvatures (MM and MD), i.e., due to the decrease in radii (RM and RD; Fig. 2a). Since m has a dimension of an inverse length and depends on the vesicle radii, it is convenient to use the reduced (i.e., dimensionless) spontaneous curvature
is associated with the mean curvature of the ideal closed neck located between the two spherical segments (MM and MD).21 The neck will remain closed if the spontaneous curvature m exceeds mnc but will open up if m falls below mnc. Assuming that mean curvatures of mother and daughter spherical segments (MM and MD) do not change before and after the neck breaking, the value of m when a spherical membrane bud with a closed neck was formed on a mother GUV can be estimated as mnc from the microscopy observations, as shown in Fig. 3a for the observation of Fig. 1b. The estimated spontaneous curvature mnc of the neck-closed GUVs increased during osmotic spawning due to the increase in mean curvatures (MM and MD), i.e., due to the decrease in radii (RM and RD; Fig. 2a). Since m has a dimension of an inverse length and depends on the vesicle radii, it is convenient to use the reduced (i.e., dimensionless) spontaneous curvature![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ≡ mRve ≡ mRve | (9) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) nc = mncRve = 2.5 ± 0.5, regardless of the difference in initial vesicle size and elapsed time.
nc = mncRve = 2.5 ± 0.5, regardless of the difference in initial vesicle size and elapsed time.
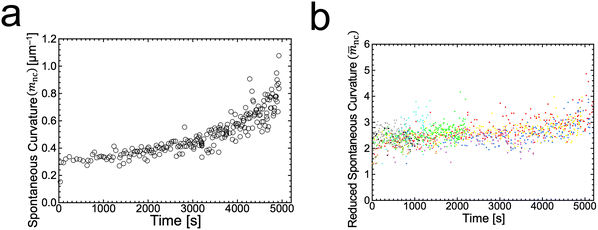 | ||
Fig. 3 Estimated spontaneous curvature. (a) Time evolution of the estimated values of spontaneous curvature 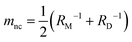 obtained from the radii of mother and daughter GUVs in Fig. 1b. (b) Time evolution of the estimated values of reduced spontaneous curvature obtained from the radii of mother and daughter GUVs in Fig. 1b. (b) Time evolution of the estimated values of reduced spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) nc = mncRve obtained from the radii of mother and daughter GUVs (ten observations). Each color represents an independent observation and corresponds to color code used in Fig. 2c. nc = mncRve obtained from the radii of mother and daughter GUVs (ten observations). Each color represents an independent observation and corresponds to color code used in Fig. 2c. | ||
The SC model enables the comparison of vesicle shapes beyond the size differences by using dimensionless parameters. When we take membrane area A and vesicle volume V as the constraints in the SC model, the bending energy (eqn (3)) depends only on two dimensionless parameters (except for membrane intrinsic bending rigidity κ): the volume-to-area ratio v (eqn (2)) and the reduced spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (eqn (9)).20,21 In our observations, initial vesicle sizes were different, and the vesicle size varied with the progress of spawning. Nevertheless, the dimensionless parameters vnc (Fig. 2d) and
(eqn (9)).20,21 In our observations, initial vesicle sizes were different, and the vesicle size varied with the progress of spawning. Nevertheless, the dimensionless parameters vnc (Fig. 2d) and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) nc (Fig. 3b) took almost consistent values among the observations. This indicates that the osmotic spawning GUVs we observed had approximately the same morphology within the SC model despite the differences in initial vesicle sizes and elapsed time.
nc (Fig. 3b) took almost consistent values among the observations. This indicates that the osmotic spawning GUVs we observed had approximately the same morphology within the SC model despite the differences in initial vesicle sizes and elapsed time.
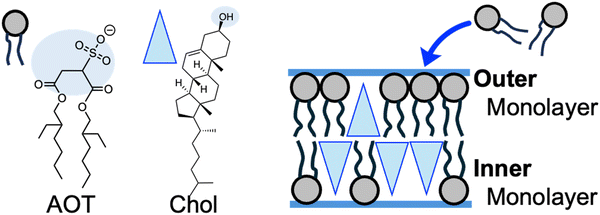
The plausible origin of spontaneous curvature is the asymmetry in cholesterol distribution between outer and inner monolayers of vesicle membranes (Fig. 4). Several techniques are known to impose spontaneous curvature on vesicle membranes.1,21,49,50 In this study, osmotically tensed binary AOT + Chol (9/1, mol) GUVs continuously incorporated AOT molecules from the bulk solution into the membranes to reduce the tension stress (Fig. 1a). AOT has a cylindrical molecular shape with an almost zero molecular spontaneous curvature. In contrast, Chol will act as an inverse-cone shaped molecule with a negative value of molecular spontaneous curvature (∼−0.3 nm−1)1,49,51 in AOT membranes. Although we cannot address the value of flip–flop rate of AOT molecules, Chol molecules are known to have a very fast flip–flop rate (milli-seconds)52 among vesicle-forming amphiphiles. During osmotic spawning (Fig. 4), free AOT molecules are presumably first inserted from bulk solution into the outer monolayer of the vesicle membrane. Subsequently, coupled with the faster flip–flop motions of Chol, AOT molecules will be transferred into the inner monolayer via flip–flop motion. The balance between the accumulation of AOT in the outer monolayer and its transfer into the inner monolayer will determine the asymmetric distribution of Chol in the bilayer (see also Supplementary Note 3 and 4, ESI†). Consequently, through the molecular spontaneous curvature of Chol, the asymmetry of Chol distribution in the bilayer will generate the membrane spontaneous curvature.
Here, we evaluate the asymmetry of cholesterol distribution in bilayers at the beginning and the end of osmotic spawning. According to the observations of binary AOT + Chol (9/1, mol) GUVs employing sucrose and fructose as the internal and external osmolytes, respectively, osmotic spawning tends to occur (i.e., neck closure is observed) with the typical initial spontaneous curvature value of 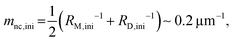 which is estimated from Fig. 2c. To generate this value of spontaneous curvature, only ∼0.3% more abundance of Chol in the inner monolayer against the outer monolayer is required (see Supplementary Note 3, ESI†). Similarly, the maximal value of spontaneous curvature during osmotic spawning is estimated to be mnc,max ∼ 1.2 μm−1, which requires ∼2% asymmetry in Chol distribution (see Supplementary Note 3, ESI†). Compared to the initially required asymmetry (∼0.3%), the estimated maximal value at the end of spawning (∼2%) competes with the Chol content in the bilayer: the initial content of Chol in the bilayer is 10%, but Chol becomes diluted from this value at the later stage of osmotic spawning due to the incorporation of AOT molecules from the external environment and the release of Chol in the form of daughter GUVs. As seen in Fig. 1e and f, once the neck connecting mother and daughter GUVs opened up, the mother GUVs no longer resumed spawning in our observations. Therefore, one of the plausible factors to terminate osmotic spawning is the depletion of Chol in the bilayer, where the spontaneous curvature required for closing the neck (eqn (8)) can no longer be generated by the asymmetry in Chol distribution. It should be noted that the exposure of the inner and outer surfaces of vesicle membranes to different saccharide solutions may also result in the generation of spontaneous curvature, the value of which will be proportional to the saccharide concentration.53 Nevertheless, osmotic spawning was observed across a wide range of saccharide concentrations (5 to 500 mM, see no. 1–13 in Table 1), and reasonable values of spontaneous curvature cannot be consistently estimated for this concentration range by the saccharide asymmetry. Therefore, we concluded that the primary source of spontaneous curvature is the asymmetric distribution of Chol in vesicle bilayers.
which is estimated from Fig. 2c. To generate this value of spontaneous curvature, only ∼0.3% more abundance of Chol in the inner monolayer against the outer monolayer is required (see Supplementary Note 3, ESI†). Similarly, the maximal value of spontaneous curvature during osmotic spawning is estimated to be mnc,max ∼ 1.2 μm−1, which requires ∼2% asymmetry in Chol distribution (see Supplementary Note 3, ESI†). Compared to the initially required asymmetry (∼0.3%), the estimated maximal value at the end of spawning (∼2%) competes with the Chol content in the bilayer: the initial content of Chol in the bilayer is 10%, but Chol becomes diluted from this value at the later stage of osmotic spawning due to the incorporation of AOT molecules from the external environment and the release of Chol in the form of daughter GUVs. As seen in Fig. 1e and f, once the neck connecting mother and daughter GUVs opened up, the mother GUVs no longer resumed spawning in our observations. Therefore, one of the plausible factors to terminate osmotic spawning is the depletion of Chol in the bilayer, where the spontaneous curvature required for closing the neck (eqn (8)) can no longer be generated by the asymmetry in Chol distribution. It should be noted that the exposure of the inner and outer surfaces of vesicle membranes to different saccharide solutions may also result in the generation of spontaneous curvature, the value of which will be proportional to the saccharide concentration.53 Nevertheless, osmotic spawning was observed across a wide range of saccharide concentrations (5 to 500 mM, see no. 1–13 in Table 1), and reasonable values of spontaneous curvature cannot be consistently estimated for this concentration range by the saccharide asymmetry. Therefore, we concluded that the primary source of spontaneous curvature is the asymmetric distribution of Chol in vesicle bilayers.
Control experiments without cholesterol in bilayers support the scenario that asymmetry in cholesterol distribution is the origin of spontaneous curvature. Instead of binary AOT + Chol (9/1, mol) GUVs, we examined single-component AOT GUVs (i.e., 0% Chol) and otherwise the same experimental setup with osmotic spawning (Fig. 5a). In this condition, where only cylindrical-shaped amphiphiles with almost zero molecular spontaneous curvature compose the vesicle membrane, the mother GUVs did not form a membrane bud; instead, the GUVs osmotically inflated by maintaining their spherical shape (Fig. 5b, c and no. 14 in Table 1). Thus, the incorporation of AOT molecules into the outer monolayer cannot be the sole trigger of osmotic spawning, but Chol is also required in the bilayer.
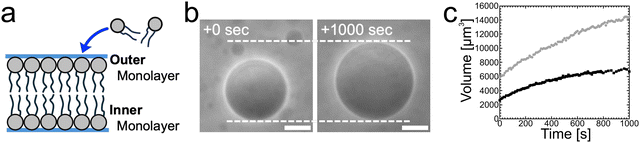 | ||
| Fig. 5 Osmotic inflation of AOT GUVs. (a) Schematic of single-component (i.e., 0% Chol) AOT bilayer, which should be compared with Fig. 4. (b) Phase contrast microscopy images of an osmotically inflating single-component AOT GUV. An AOT GUV prepared in 20 mM NaH2PO4 solution (pH = 4.3) containing 250 mM sucrose was transferred into another 20 mM NaH2PO4 solution containing 250 mM fructose and 3.0 mM AOT (cvc ∼ 1.5 mM). Length of scale bars: 10 μm. (c) Volume increase of AOT GUVs observed in the condition of Fig. 5b. Black filled squares and gray filled circles represent independent observations. The microscopy images in Fig. 5b and the gray filled circles were taken from the same observation. The vesicle volume was estimated from the vesicle radii, approximating vesicle shape as sphere. | ||
Membrane tension and pressure difference
We recall the shape equation (eqn (5)) and its two solutions (eqn (6) and (7)), which are analytically derived based on the SC model and describe the relation between the global parameters (Σ and ΔP) and the local mean curvatures (MM and MD) for stationary spherical membrane segments. Although these equations involve membrane spontaneous curvature m and bilayer bending rigidity κ, the neck closure of budding GUVs provides the values of m as mnc (eqn (8)), and the fluctuation spectroscopy54–56 provides the value of κ (κ ∼ 15kBT for binary AOT + Chol (9/1, mol) membranes, see Supplementary Note 5, ESI†). Therefore, by employing the experimentally obtained mean curvature values of mother and daughter spherical membrane segments (MM = RM−1 and MD = RD−1; Fig. 2c), we can solve eqn (6) and (7) to obtain the values of membrane tension Σ and pressure difference ΔP, as shown in Fig. 6. A power-law relationship between Σ and ΔP came from the almost constant size ratio between mother and daughter GUVs during osmotic spawning (Fig. 2c and d): when we represent MM = αMD with a constant value α (experimentally, MM = 6MD − 0.3 μm−1 is obtained, slightly deviating from the proportional relationship), the power law ΔP ∝ Σ1.5 is obtained from the shape equation (eqn (6) and (7)) and the neck closure condition (eqn (8)). In our typical experimental condition using binary AOT + Chol (9/1) GUVs and 250 mM sucrose and fructose as osmolytes, the membrane tension and pressure difference primarily ranged from Σ ∼ 10−8–10−7 N m−1 and ΔP ∼ 10−3–10−1 N m−2, respectively (Fig. 6). This tension range coincides with the flaccid (i.e., weak tension) regime of vesicle membranes, where microscopic thermal undulations of membranes are not smoothed out by lateral tensions.57,58 The (osmotic) pressure difference values were also in a weak region, e.g., a straightforward conversion using the van’t Hoff relation on osmosis gives a concentration difference of osmolytes between the inside and outside of a GUV as Δc ≲ 0.04 μM (from ΔP ≲ 0.1 N m−2). The micro-pore formation before morphological changes of GUVs, which accounts for the generation of excess membrane area for forming a daughter GUV (v ∼ 0.92), may also be responsible for these weak membrane tension and pressure difference.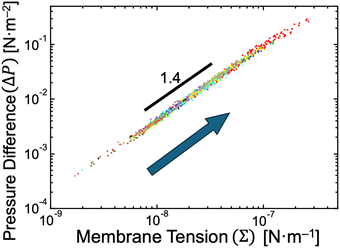 | ||
| Fig. 6 Estimated pressure difference and membrane tension. The relationship between pressure difference and membrane tension when neck closure was obtained based on eqn (6) and (7) by using experimental data presented in Fig. 2c. With the progress of osmotic spawning, the data points move from lower left to upper right, as indicated by an arrow. Each color represents an independent observation and corresponds to color code used in Fig. 2c. | ||
Osmotic spawning will fail in the presence of large pressure differences. The requirements of the neck closure (eqn (8)) and the real-valued mean curvatures (eqn (6) and (7)) read
| ΔP ≤ 4κm3, | (10) |
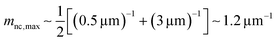 (Fig. 2c) and bending rigidity of binary AOT + Chol (9/1) bilayers κ = 15kBT, resulting in 4κm3 ∼ 0.4 N m−2 relative to the experimentally estimated values of 0.2–0.3 N m−2 (Fig. 6). Thus, with the typical experimental setup in this study (i.e., binary AOT + Chol (9/1) GUVs and 250 mM sucrose and fructose as osmolytes in 20 mM NaH2PO4 solution), the osmotic spawning seems to permit only a small margin of (osmotic) pressure difference in comparison to the upper bound specified by eqn (10). Modifications to the experimental setup for imposing higher pressure differences on mother GUVs may result in the failure of spawning, as described just below.
(Fig. 2c) and bending rigidity of binary AOT + Chol (9/1) bilayers κ = 15kBT, resulting in 4κm3 ∼ 0.4 N m−2 relative to the experimentally estimated values of 0.2–0.3 N m−2 (Fig. 6). Thus, with the typical experimental setup in this study (i.e., binary AOT + Chol (9/1) GUVs and 250 mM sucrose and fructose as osmolytes in 20 mM NaH2PO4 solution), the osmotic spawning seems to permit only a small margin of (osmotic) pressure difference in comparison to the upper bound specified by eqn (10). Modifications to the experimental setup for imposing higher pressure differences on mother GUVs may result in the failure of spawning, as described just below.
A control experiment employing osmolytes with higher membrane permeability resulted in unsuccessful osmotic spawning, presumably due to the significant pressure differences. The typical experimental setup mentioned so far has employed fructose molecules, which have mild permeability (∼10−9 m s−1 for AOT membranes17), as the external osmolyte for mother GUVs (Fig. 1a). However, as a control experiment, when the external osmolyte was replaced by one with much higher permeability such as glycerol (∼10−7 m s−1 for AOT membranes), the daughter membrane buds were formed on the mother GUVs but immediately retracted before being pinched off (Fig. 7 and Movie S5, ESI;† no. 15–16 in Table 1). Specifically, a mother binary AOT + Chol (9/1, mol) GUV first showed an instantaneous bud formation (0–1.6 s in Fig. 7), as the usual osmotic spawning (0–2.0 s in Fig. 1c). Then, in contrast to the usual spawning process, the bud was not pinched off but instead continued to grow (1.6–3.9 s in Fig. 7). The mean curvature of the membrane bud approached to the mother's one, and finally the bud was retracted into the mother GUV (3.9–4.5 s). No successful spawning event was observed in this control condition. The plausible scenario behind this budding-and-retraction behavior is as follows. First, a membrane bud was successfully formed on the mother GUV just after the micro-pore formation (i.e., generation of excess surface area and relaxation of membrane tension and pressure difference), as the usual spawning process. However, due to the much faster membrane permeation of the external osmolytes (glycerol) and the subsequent volume growth by water influx, the pressure difference ΔP did not remain in lower values but instead began to increase rapidly even during the deformation process. If ΔP exceeded the critical value (eqn (10)), the GUV could no longer maintain the neck closure. Furthermore, as the increase in pressure difference ΔP decreases the value under the square root of eqn (6) and (7), the daughter and mother spherical membrane segments began to take the closer values of mean curvature (MD and MM) while connected via the opened neck. Consequently, the use of high permeability osmolytes will result in the retraction of the budded membrane segment.
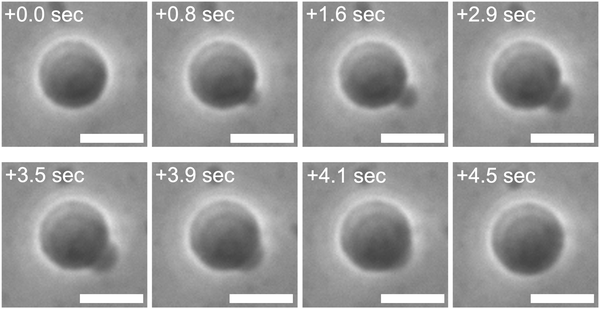 | ||
| Fig. 7 Unsuccessful spawning by using glycerol as external osmolytes. Phase contrast microscopy images of a binary AOT + Chol (9/1, mol) GUV in the high osmotic pressure setup. The images were taken from Movie S5 (ESI†). A GUV prepared in 20 mM NaH2PO4 solution (pH = 4.3) containing 250 mM sucrose was transferred into another 20 mM NaH2PO4 solution containing 250 mM glycerol, which has about 102 times higher permeability than fructose, and 3.0 mM AOT (cvc ∼ 1.5 mM). Length of scale bars: 10 μm. | ||
The retraction of membrane buds observed by using high permeability osmolytes (Fig. 7) is similar to the unsuccessful divisions observed at the end of the usual osmotic spawning (Fig. 1e and f). The higher membrane permeabilities of external osmolytes will facilitate the rapid generation of pressure difference ΔP, as described just above. Moreover, GUVs with smaller radii will also rapidly increase ΔP: the number of osmolyte molecules permeating the membrane (ΔN) is proportional to the vesicle surface area (ΔN ∝ R2; see also Supplementary Note 4, ESI†),35,59 and the vesicle volume, which will contain the permeated molecules, is proportional to R3. Therefore, the concentration increments resulting from the permeation of osmolytes (Δc = ΔN/V ∝ R−1) will be enhanced in the smaller mother GUVs. Accordingly, the scenario for the retraction of membrane buds when high permeability osmolytes (i.e., glycerol) are employed may also be plausible as the scenario terminating the usual osmotic spawning, in addition to the depletion of Chol in bilayer membranes: the decrease in size of a mother GUV due to the progress of osmotic spawning accelerates the increase of ΔP even when mild permeability osmolytes (i.e., fructose) are used. This enables ΔP to reach its upper bound values (eqn (10)) within the timescale of membrane deformations.
Conclusion
This study presents the first report on the cascade vesicle division coupled with osmotic inflation. Disaccharides and monosaccharides were employed as the internal and external osmolytes, respectively, and the osmotic spawning of binary AOT + Chol GUVs occurred due to the uptake of water and AOT molecules from the external solution. After the mother GUVs were exposed to the external solution, the mother GUVs spontaneously produced about 30 to 300 daughter GUVs. The size of the mother and daughter GUVs decreased with the progress of spawning, but the size ratio between the mother and daughter GUVs (i.e., RD/RM ratio and reduced volume v) remained almost constant in our observations. The deformation is presumed to be driven by spontaneous curvature of the bilayer membranes, which is primarily generated by the asymmetric distribution of Chol between the outer and inner monolayers. The membrane tension and pressure difference were estimated to be very small when daughter GUVs were formed on mother GUVs, and the significant osmotic stress resulted in unsuccessful division. In comparison to other vesicle division mechanisms, the most notable feature of osmotic spawning is the sustainability of vesicle division. If either or both the membrane area or encapsulated volume does not increase, such vesicle division mechanisms will soon face a shortage of membrane area or volume to produce daughter vesicles, preventing the division mechanisms from being sustainable. However, by coupling with osmotic inflation, which continuously supplies both the membrane area and volume to the mother GUVs, the osmotic spawning mechanism can successfully sustain the division and produce significantly more daughter GUVs than other division mechanisms.Osmotic spawning has the potential to be a valuable tool in the field of artificial cells and drug delivery systems due to the simplicity of the experimental setup and the non-usage of chemical reactions and functional molecules. The cascade division of binary AOT + Chol GUVs in this study is driven essentially by the mixing of two species of molecules (i.e., disaccharide and monosaccharide) via the vesicle membrane. If a small amount of disaccharide solution, which is not confined within a GUV, is simply dropped into a bulk monosaccharide solution, the di- and monosaccharide molecules will rapidly mix with each other, resulting in an equilibrated (i.e., homogeneous) solution. On the other hand, if the small amount of disaccharide solution is confined by a vesicle membrane, the mixing of di- and monosaccharide molecules proceeds gradually, and the mother GUVs may exploit the free energy of mixing as the work for producing daughter GUVs and for inflating mother and daughter GUVs through osmotic pressure (i.e., W = PΔV). Thus, osmotic spawning is driven by the mixing of osmolytes and does not require chemical reactions or functional macromolecules. For this reason, when osmotic spawning is applied to artificial cells and drug delivery systems, the mother GUVs will be able to produce daughter GUVs without interfering with the encapsulated chemical and molecular functionalities. A variety of existing and future microcompartment systems may be equipped with the proliferation ability by simply replacing their membrane compositions and osmolytes with those suitable for osmotic spawning.
In this paper, we have focused on demonstrating osmotic spawning vesicles and on carrying out a basic analysis rather than exploring possible combinations of membrane compositions and osmolytes. Whether this unique division behavior of vesicles can be realized in other membrane compositions remains an open question. Morphological changes of GUVs coupled with the uptake of water and amphiphiles have been previously reported by using phospholipid GUVs and by inserting fatty acid molecules into the membranes.60,61 However, the mother GUVs did not produce daughter GUVs, and instead they formed multiple tubes or protrusions, which were stably connected to the mother GUVs (i.e., no division). For successful osmotic spawning, the major requirements on membrane compositions are presumed as follows: firstly, the amphiphiles inserted from the external solution into the vesicle membranes should have higher critical aggregation concentrations (cac), such as AOT and fatty acids (cac ∼ mM). Phospholipids, the standard vesicle-forming molecules, normally have very low cac values ranging from nM to μM, which means that the resources of freely dispersed membrane molecules in the external solution are sparse. Therefore, the influx of membrane molecules to the outer monolayer of vesicle membranes will be significantly reduced, resulting in unsuccessful spawning. For the membrane composition of mother GUVs, it seems necessary to include inverse-cone shaped molecules (i.e., molecules with negative values of molecular spontaneous curvatures), which contribute to the generation of membrane spontaneous curvatures coupled with the uptake of membrane molecules into the outer monolayer of vesicle membranes. With regard to osmolytes, our study has focused solely on sucrose as the internal osmolyte of GUVs. However, sucrose will be in principle replaced with various membrane-impermeable molecules. Moreover, the encapsulation of membrane-impermeable functional macromolecules, including DNA, proteins, and drug molecules, may be compatible with osmotic spawning, as demonstrated with the fluorescent dextran in this paper (Fig. 1d). In contrast to the presumed robustness against internal osmolytes, the external osmolytes will require a careful selection. The rapid trans-membrane diffusion of external osmolytes enhances the generation of (osmotic) pressure differences. Although the use of monosaccharide molecules (i.e., fructose and glucose) as the external osmolytes for binary AOT + Chol GUVs was found to result in successful spawning, the use of glycerol, which has a membrane permeability approximately 102 times higher, was confirmed to disturb the formation of membrane buds. The values of membrane permeability vary according to the compositions and thickness of the membranes.59 Therefore, even when the internal and external osmolytes are sucrose and fructose, respectively (which is the successful setup for the spawning of binary AOT + Chol vesicles; the bilayer thickness is ∼2 nm62), phospholipid vesicles might not undergo morphological changes since the permeability of fructose against standard phospholipid membranes (the bilayer thickness is ∼4–5 nm) will be significantly suppressed. It is thus necessary to explore the combination of membrane compositions and external osmolytes in a coordinated manner. Such explorations will not only expand the scope of osmotic spawning but also elucidate the requirements for primitive molecular assemblies to reach the first cell division in the primordial soup on the early Earth.
Methods
Materials
AOT (sodium bis(2-ethylhexyl)sulfosuccinate, >99%, catalogue no. 86139) was purchased from Sigma-Aldrich Japan (Tokyo, Japan). Cholesterol (Chol, ovine wool, >98%, no. 700000) and Rhod-PE (1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (ammonium salt), >99%, no. 810158) were purchased from Avanti Polar Lipids, Inc. (AL, USA). Dextran Texas Red (3000 MW, neutral, no. D3329) was purchased from Thermo Fisher Scientific (OR, USA). Glucose (>99%), fructose (>99%), sucrose (>99%), sodium dihydrogenphosphate (NaH2PO4) dihydrate (>99%), phosphoric acid (>85%), and chloroform (>99%) were purchased from FUJIFILM Wako Pure Chemical Corporation (Osaka, Japan). The amphiphiles were used without further purification and dissolved in chloroform at 100 mM (AOT) or at 10 mM (Chol) and stored at −20 °C as stock solution.Preparation of binary AOT + Chol GUVs
Binary giant unilamellar vesicles (GUVs) composed of AOT and Chol (9/1, molar ratio, 5.0 mM in total, 0.50 mL suspension) were prepared using the gentle hydration method.17,34 First, 22.5 μL chloroform solution of 100 mM AOT, 25.0 μL chloroform solution of 10 mM Chol, and 0.5 mL chloroform were mixed in a 5 mL glass vial, followed by forming a thin AOT + Chol film upon removing chloroform with a nitrogen gas stream under rotation of the vial by hand. For complete removal of chloroform, the AOT + Chol film was put under a high vacuum overnight, while the vial was kept wrapped with aluminium foil. The dried film was hydrated and dispersed at 60 °C for 20 min with 0.5 mL of 20 mM NaH2PO4 solution (pH = 4.3) containing typically 250 mM of sucrose. This resulted in the formation of GUVs with radii around 10 μm. The obtained GUV suspension was used within the day of hydration. It should be noted that the concentration of NaH2PO4 influences the critical vesiculation concentration (cvc) of AOT and that no vesicles are formed in the absence of NaH2PO4. Binary AOT + Chol GUVs with different molar ratios were prepared just by changing the amount of chloroform solution of AOT and Chol in a glass vial. Binary GUVs for the fluorescent microscopy observations were prepared by adding 37.5 μL chloroform solution of 1.0 mM Rhod-PE to the above mentioned 47.5 μL chloroform solution of AOT + Chol before forming a film, resulting in AOT/Chol/Rhod-PE = 9/1/0.15 molar ratio, or by hydrating the above mentioned AOT + Chol film with 20 mM NaH2PO4 solution (pH = 4.3) containing sucrose and 100 μM of Dextran Texas Red.Protocol for osmotic spawning
Binary AOT + Chol GUVs encapsulating sucrose (typically 250 mM) were transferred into an isomolar monosaccharide (typically 250 mM of fructose) solution containing 3.0 mM of AOT. For the preparation of the external solution for binary AOT + Chol GUVs, firstly, 6.65 mg of solid AOT was dissolved in 5.0 mL of 20 mM NaH2PO4 solution (pH = 4.3) containing typically 250 mM of fructose. For complete dispersion of AOT molecules, the solution was heated to 60 °C and then mixed with a vortex mixer for about two minutes, followed by the cool down at room temperature (T ∼ 25 °C). The obtained 20 mM NaH2PO4 solution (pH = 4.3) contains 250 mM fructose and 3.0 mM AOT, and cvc of AOT is ∼1.5 mM,34i.e., ∼1.5 mM of AOT molecules dispersed as free monomers in equilibrium with AOT vesicles. Then, the solution was passed through a 0.2 μm polypropylene filter Puradisc 25 PP (GE Healthcare, UK) for removal of AOT vesicles with observable sizes, and 2.0 mL of the filtrated solution was finally placed in a glass bottom dish D11130H (Matsunami, Japan) as the external solution. For the observation of osmotic spawning, firstly, 120 μL suspension of binary AOT + Chol GUVs encapsulating typically 250 mM of sucrose was dropped in the microscope sample chamber, which is a hole in a silicone rubber sheet placed onto a glass slide. The hole had a diameter of 12 mm and a depth of 1 mm. Then, a small volume containing a few selected GUV was carefully transferred into the glass bottom dish containing 2.0 mL of the external solution with a transfer pipette VacuTipII and Cell Tram Vario (Eppendorf, Germany). The glass bottom dish was quickly covered by a plastic lid to prevent water flow induced by airflow. The transferred GUVs were located at the bottom of the chamber due to the difference in the specific gravity between the encapsulated sucrose solution and the external fructose solution. The initial concentrations of each component were as follows: (inside of the GUVs) 20 mM NaH2PO4 (pH = 4.3), typically 250 mM sucrose; (outside of the GUVs) 20 mM NaH2PO4 (pH = 4.3), typically 250 mM fructose, and ∼3 mM AOT (cvc ∼1.5 mM). Several tens of seconds after the transfer, the drifting flow of the transferred GUVs decayed, and the binary AOT + Chol GUVs began to produce daughter GUVs.In this protocol, where the external solution contains AOT molecules above cvc, the observed membrane growth can be attributed to the incorporation of free AOT molecules, rather than to the fusion with small AOT vesicles. The asymmetry between the inner and outer monolayers (i.e., the difference in Chol distribution) can be generated by inserting free AOT molecules into the outer monolayer of binary AOT + Chol GUVs. In contrast, the membrane growth via the fusion with other AOT vesicles will supply AOT molecules to both the inner and outer monolayers of binary AOT + Chol GUVs,63 which will not result in the generation of the bilayer asymmetry. Moreover, the fusion of vesicles must overcome the two significant free energy barriers: the adhesion of two strongly hydrated (and negatively charged) membranes and the merger of proximal monolayers.64 It can therefore be presumed that the osmotically tensed mother GUVs will preferentially take up free AOT molecules through an equilibrium shift by the tension stress of membranes, rather than through the fusion of vesicles.
Microscope observation of GUVs
The morphological changes of osmotic spawning GUVs and the membrane fluctuations of GUVs were followed by using an Axio Vert A1 FL-LED inverted fluorescence microscope (Carl Zeiss, Germany) with a dry 40× objective (LD A-Plan 40×, NA = 0.55) and a CCD camera (Axiocam 506mono) (Carl Zeiss, Germany) for recording the images. For the transfer of GUVs, the microscope was equipped with a hydraulic micro-manipulator MMO-202 ND (Narishige, Japan).Bending rigidity measurements by fluctuation analysis
Membrane bending rigidities of binary AOT + Chol (9/1) GUVs and DOPC GUVs (for reference) were measured by fluctuation spectroscopy of the thermal undulations of quasi-spherical GUVs.54–56 Membrane fluctuations were recorded by using the Axio Vert A1 FL-LED in the phase-contrast mode equipped with the LD A-Plan 40×. Sequences of 3000–4000 snapshots per GUV were recorded with the Axiocam 506mono at an exposure time of 0.25 ms. The internal and external aqueous solutions contained 250 mM sucrose and 275 mM fructose, respectively, for distinct contrast and optically resolvable fluctuations. The vesicle contour was detected and analyzed with Mathematica (Wolfram Research, version 13.2) homemade computer program. The bending rigidity of binary AOT + Chol (9/1) bilayers was measured to be κ = 14.7 ± 1.8kBT at room temperature (see also Supplementary Note 5, ESI†).Author contributions
M. K. discovered the osmotic spawning behavior of vesicles. M. K. and M. I. conceived the work and wrote the manuscript. M. K. conducted experiments and theoretical analysis.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JST ACT-X (Grant Number JPMJAX23DA), JSPS KAKENHI (grant number JP20H00120, JP22K20346, JP23H00087, and JP23K13070), and Astrobiology Center Program of National Institutes of Natural Sciences (grant number AB0508).References
- M. Imai, Y. Sakuma, M. Kurisu and P. Walde, Soft Matter, 2022, 18, 4823–4849 RSC.
- R. Dimova and C. M. Marques, The Giant Vesicle Book, CRC Press, Boca Raton, 2020 Search PubMed.
- G. Gompper and M. Schick, Soft Matter: Lipid bilayers and red blood cells, Wiley-VCH, Weinheim, vol. 4, 2008 Search PubMed.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- I. A. Chen and P. Walde, Cold Spring Harbor Perspect. Biol., 2010, 2, 1–14 Search PubMed.
- P. Stano and P. L. Luisi, Chem. Commun., 2010, 46, 3639–3653 RSC.
- S. Herianto, P. J. Chien, J. an A. Ho and H. L. Tu, Biomater. Adv., 2022, 142, 213156 CrossRef CAS PubMed.
- Y. Miele, G. Holló, I. Lagzi and F. Rossi, Life, 2022, 12, 841 CrossRef CAS.
- J. A. Vance and N. K. Devaraj, J. Am. Chem. Soc., 2021, 143, 8223–8231 CrossRef CAS PubMed.
- N. J. Gaut and K. P. Adamala, Adv. Biol., 2021, 5, 1–20 Search PubMed.
- S. Tror, S. M. Jeon, H. T. Nguyen, E. Huh and K. Shin, Small Methods, 2023, 7, 2300182 CrossRef CAS.
- Y. Sato, ChemSystemsChem, 2024, 6, e202400021 CrossRef CAS.
- R. Wick, P. Walde and P. L. Luisi, J. Am. Chem. Soc., 1995, 117, 1435–1436 CrossRef CAS.
- K. Takakura and T. Sugawara, Langmuir, 2004, 20, 3832–3834 CrossRef CAS PubMed.
- T. F. Zhu and J. W. Szostak, J. Am. Chem. Soc., 2009, 131, 5705–5713 CrossRef CAS PubMed.
- J. M. Castro, H. Sugiyama and T. Toyota, Sci. Rep., 2019, 9, 165 CrossRef.
- M. Kurisu, R. Katayama, Y. Sakuma, T. Kawakatsu, P. Walde and M. Imai, Commun. Chem., 2023, 6, 56 CrossRef CAS PubMed.
- Y. Sakuma and M. Imai, Phys. Rev. Lett., 2011, 107, 198101 CrossRef.
- W. Helfrich, Z. Naturforsch., C: J. Biosci., 1973, 28, 693–703 CrossRef CAS.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A, 1991, 44, 1182–1202 CrossRef CAS PubMed.
- R. Lipowsky, in The Giant Vesicle Book, ed. R. Dimova and C. M. Marques, Understanding giant vesicles: A theoretical perspective, CRC Press, Boca Raton, 2020, ch. 5, pp. 73–168 Search PubMed.
- T. Jimbo, Y. Sakuma, N. Urakami, P. Ziherl and M. Imai, Biophys. J., 2016, 110, 1551–1562 CrossRef CAS.
- N. Urakami, T. Jimbo, Y. Sakuma and M. Imai, Soft Matter, 2018, 14, 3018–3027 RSC.
- N. Urakami, Y. Sakuma, T. Chiba and M. Imai, Soft Matter, 2021, 17, 8434–8445 RSC.
- A. L. Bernard, M. A. Guedeau-Boudeville, L. Jullien and J. M. Di Meglio, Biochim. Biophys. Acta, Biomembr., 2002, 1567, 1–5 CrossRef CAS PubMed.
- X. Liu, J. Stenhammar, H. Wennerström and E. Sparr, J. Phys. Chem. Lett., 2022, 13, 498–507 CrossRef CAS.
- P. D. Sambre, J. C. S. Ho and A. N. Parikh, J. Am. Chem. Soc., 2024, 146, 3250–3261 CrossRef CAS.
- M. M. A. E. Claessens, F. A. M. Leermakers, F. A. Hoekstra and M. A. C. Stuart, Biochim. Biophys. Acta, Biomembr., 2008, 1778, 890–895 CrossRef CAS PubMed.
- S. Moreno-Flores, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 793–799 CrossRef CAS PubMed.
- W. Zong, Q. Li, X. Zhang and X. Han, Colloids Surf., B, 2018, 172, 459–463 CrossRef CAS.
- T. Bhatia, S. Christ, J. Steinkühler, R. Dimova and R. Lipowsky, Soft Matter, 2020, 16, 1246–1258 RSC.
- H. G. Döbereiner, J. Käs, D. Noppl, I. Sprenger and E. Sackmann, Biophys. J., 1993, 65, 1396–1403 CrossRef.
- H. Wu, Z.-C. Ou-Yang and R. Podgornik, Membranes, 2023, 13, 332 CrossRef CAS.
- M. Kurisu, H. Aoki, T. Jimbo, Y. Sakuma, M. Imai, S. Serrano-Luginbühl and P. Walde, Commun. Chem., 2019, 2, 117 CrossRef.
- M. Mally, P. Peterlin and S. Svetina, J. Phys. Chem. B, 2013, 117, 12086–12094 CrossRef CAS PubMed.
- M. Chabanon, J. C. S. Ho, B. Liedberg, A. N. Parikh and P. Rangamani, Biophys. J., 2017, 112, 1682–1691 CrossRef CAS PubMed.
- K. Oglęcka, P. Rangamani, B. Liedberg, R. S. Kraut and A. N. Parikh, eLife, 2014, 3, e03695 CrossRef.
- S. U. Alam Shibly, C. Ghatak, M. A. Sayem Karal, M. Moniruzzaman and M. Yamazaki, Biophys. J., 2016, 111, 2190–2201 CrossRef CAS PubMed.
- M. Ohno, T. Hamada, K. Takiguchi and M. Homma, Langmuir, 2009, 25, 11680–11685 CrossRef CAS PubMed.
- N. Rodriguez, S. Cribier and F. Pincet, Phys. Rev. E, 2006, 74, 061902 CrossRef PubMed.
- E. Karatekin, O. Sandre, H. Guitouni, N. Borghi, P. H. Puech and F. Brochard-Wyart, Biophys. J., 2003, 84, 1734–1749 CrossRef CAS.
- Z. C. Ou-Yang and W. Helfrich, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 5280–5288 CrossRef CAS.
- B. Božič, G. Gomišček, V. Kralj-Iglič, S. Svetina and B. Žekš, Eur. Biophys. J., 2002, 31, 487–496 CrossRef.
- R. Lipowsky, Faraday Discuss., 2013, 161, 305–331 RSC.
- R. Lipowsky, Adv. Colloid Interface Sci., 2014, 208, 14–24 CrossRef CAS.
- R. Lipowsky, Adv. Colloid Interface Sci., 2022, 301, 102613 CrossRef CAS.
- L. Miao, B. Fourcade, M. Rao, M. Wortis and R. K. P. Zia, Phys. Rev. A, 1991, 43, 6843–6856 CrossRef CAS.
- B. Fourcade, L. Miao, M. Pao and M. Wortis, Phys. Rev. E, 1994, 49, 5276–5287 CrossRef CAS.
- J. Zimmerberg and M. M. Kozlov, Nat. Rev. Mol. Cell Biol., 2006, 7, 9–19 CrossRef CAS.
- R. Lipowsky and R. Dimova, Soft Matter, 2021, 17, 214–221 RSC.
- Z. Chen and R. P. Rand, Biophys. J., 1997, 73, 267–276 CrossRef CAS.
- J. A. Hamilton, Curr. Opin. Lipidol., 2003, 14, 263–271 CrossRef CAS PubMed.
- B. Rózycki and R. Lipowsky, J. Chem. Phys., 2016, 145, 074117 CrossRef.
- J. H. Ipsen, A. G. Hansen and T. Bhatia, Vesicle fluctuation analysis, in The Giant Vesicle Book, ed. R. Dimova and C. M. Marques, CRC Press, Boca Raton, 2020, ch. 14, pp. 333–345 Search PubMed.
- H. A. Faizi, C. J. Reeves, V. N. Georgiev, P. M. Vlahovska and R. Dimova, Soft Matter, 2020, 16, 8996–9001 RSC.
- J. F. Faucon, M. D. Mitov, P. Méléard, I. Bivas and P. Bothorel, J. Phys., 1989, 50, 2389–2414 CrossRef.
- J. R. Henriksen and J. H. Ipsen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 14, 149–167 CrossRef CAS.
- E. Evans, W. Rawicz and B. A. Smith, Faraday Discuss., 2012, 161, 591–611 RSC.
- B. J. Zwolinski, H. Eyring and C. E. Beese, J. Phys. Chem., 1949, 53, 1426–1453 CrossRef CAS.
- P. Peterlin, V. Arrigler, K. Kogej, S. Svetina and P. Walde, Chem. Phys. Lipids, 2009, 159, 67–76 CrossRef CAS.
- J. Dervaux, V. Noireaux and A. J. Libchaber, Eur. Phys. J. Plus, 2017, 132, 1–10 CrossRef CAS.
- I. Grillo, P. Levitz and T. Zemb, Langmuir, 2000, 16, 4830–4839 CrossRef CAS.
- A. Grafmüller, J. Shillcock and R. Lipowsky, Phys. Rev. Lett., 2007, 98, 218101 CrossRef PubMed.
- R. Jahn and H. Grubmüller, Curr. Opin. Cell Biol., 2002, 14, 488–495 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00915k |
| This journal is © The Royal Society of Chemistry 2024 |