Piezochromic effects and low-pressure superconductivity discovered in inorganic halide perovskite RbPbI3†
Siyuan
Zhou‡
ab,
Hao
Tian‡
 c,
Xiaoyu
Kuang
c,
Xiaoyu
Kuang
 b,
Siyu
Jin
b,
Miao
Yu
b,
Jichao
Chen
b and
Aijie
Mao
*ab
b,
Siyu
Jin
b,
Miao
Yu
b,
Jichao
Chen
b and
Aijie
Mao
*ab
aCollege of Physics, Sichuan University, Chengdu 610064, China. E-mail: scu_mij@126.com
bInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
cSchool of Physics and Electronic Engineering, Zhengzhou Normal University, Zhengzhou 450044, China
First published on 28th November 2023
Abstract
The structural phase evolution and superconductivity of perovskite RbPbI3 under pressure have been investigated by employing first-principles calculations. The findings suggest that RbPbI3 undergoes three structural phase transitions from ppPv-Pnma to ppPv-Pnma(I) phases at 4.6 GPa, from ppPv-Pnma(I) to ppPv-Pnma(V) phases at 19 GPa, and from ppPv-Pnma(V) to Pm phases at 69.2 GPa, respectively. Two novel phases ppPv-Pnma(V) and Pm are predicted, differing from previously reported results. Meanwhile, an obvious piezochromic effect appears in the ppPv-Pnma(I) phase due to the change of the band gap under pressure tuning. Quite surprisingly, the electron–phonon coupling calculations reveal that the ppPv-Pnma(V) phase may be a potential low-pressure superconductor with a Tc of 8 K (7.3 K) at 20 GPa, which is slightly higher than those of other similar perovskites or alloys (∼3 K). Our studies further provide theoretical support for exploring high-Tc low-pressure superconductivity and piezochromic effects in halide perovskites.
1 Introduction
Inorganic lead halide perovskites with the chemical formula APbX3 (A = alkali cation and X = halide anion) have aroused extensive interest due to their adjustable band gaps, long carrier diffusion length, high carrier mobility and other excellent photophysical properties.1–3 Especially, CsPbI3 and RbPbI3 are regarded as potential candidate materials to improve the stability replacing organic lead halide perovskites.4–6 Thus, numerous experimental and theoretical methodologies have been investigated to enhance their structural stability and applications.7,8 Even if CsPbI3 possesses a suitable bandgap energy of 1.73 eV for application in solar cells, the structural instability (different phases Pnma, Pm3m, and P4/mbm will appear at different temperatures) further limits its practical application. However, for RbPbI3, an orthorhombic Pnma phase persists in the temperature range from 200 K to 400 K, and no other phase is observed.9 Meanwhile, adding RbI to formamidinium-based perovskites can suppress its “yellow-phase impurity”, and in turn forms RbPbI3 impurities, resulting in an excellent power output.10 Moreover, δ-RbPbI3 has suitable band alignment with TiO2, which aids in carrying out effective electron transfer, enabling it to be regarded as a potential solar cell material.11 Of course, low dimensional RbPbI3 nanowires also present good photoresponsive activity when the absorption wavelength is below 450 nm.12,13 All of the aforementioned merits indicate that RbPbI3 is worth paying attention to, even if it does not have a suitable band gap as CsPbI3 does. Nevertheless, the crystal structure and structural phase transition are the most fundamental issues in understanding and improving their performance. To the best of our knowledge, most experiments and theories have focused on investigating the structure characteristics of CsPbI3via dopants, dimensional reduction, and pressure,14,15 and only few studies have involved RbPbI3, especially at high-pressure.Pressure is regarded as an effective avenue to tune the crystal structures and physical properties of perovskite materials.16 By applying a hydrostatic pressure, all kinds of structural phases (such as Pmn21, Pm, P21/c, P21/m, post-perovskite (pPv), post–post-perovskite (ppPv), I4mm, and so on) emerge.5,6,16,17 More importantly, the pPv structure appeared in MgSiO3 explains satisfactorily the existence of anisotropic features in the D′ layer of Earth, which was discovered in some ABX3 compounds and was transformed from Pv (perovskite structures) under pressure.18 Recent progress on the pressure-induced structure further reveals that a novel stable post–post-perovskite (ppPv) structure has been obtained in a number of ABO3, ABF3, and A2O3 materials under pressure, explaining successfully the “N phase” as discovered in the experiment.19–21 This ppPv structure is composed of a three-dimensional network of edge-sharing oxygen or fluorine octahedra, unlike traditional ABX3 perovskite structures (Pv) which are composed of corner-sharing [BX6 ]4− octahedra, even though they both belong to the same point group Pnma.19 As research progressed, ppPv structures present heterogeneous phases, which can be divided into ppPv-Pnma(I), ppPv-Pnma(II), and ppPv-Pnma(III) according to the connection mode among octahedra or polyhedra.19,22 Meanwhile, the detailed structural characteristic of RbPbI3 in the experiment is along the b direction of the crystal of double rows of edge-sharing PbI6 octahedra, which is consistent with that of the aforementioned ppPv structure.19 Taking the diversity of the ppPv structure into account, it is unknown whether the new ppPv structure or other novel structures will emerge under high pressure for RbPbI3.
Usually, perovskite oxides or perovskite halides function as insulators at ambient temperature and pressure. It is remarkable, however, that the insulator can become a metal by applying pressure in perovskite oxide CaZrO3.22 This offers the possibility for further exploring superconductivity in perovskite materials. To date, research on the superconductivity of hydrides is quite hot due to the higher superconducting transition temperature Tc.23,24 There are also studies involving the superconductivity of anti-perovskites CuNNi3 and Ca3 PN, and the corresponding superconducting transition temperatures of 3.2 K and 4 K are predicted.25,26 Of course, the superconductivity is found in other compounds, such as (Ca1−xSrx)Pd3 P (0.17≤ x ≤ 0.55), PbVSe2 and Ba0.5Sr0.5Pb3.27–29 Regrettably, the superconductivity of perovskite halides has not been reported, and even the superconductivity of perovskite oxide has rarely been reported. Thus, the goal of this work is to predict the novel structural phases of RbPbI3 under pressure, further analyzing the pressure-induced piezochromic effect and superconductivity.
2 Computational details
The pressure-induced piezochromic effect and superconductivity of RbPbI3 were investigated by means of the Vienna ab initio simulation package (VASP) based on density functional theory (DFT) combined with the crystal structure analysis by particle swarm optimization (CALYPSO).30–33 Many of structures of the analogue unit RbPbI3 in 2–4 formula units (f.u.) were searched based on the CALYPSO method.32,33 The initial structures are randomly generated and subsequently optimized. Each generation comprises 30 structures, with 70% generated through particle swarm optimization and the remaining 30% newly generated in a random fashion. The search process encompasses fifty generations. In the all calculations, PBEsol, PBEsol + SOC, and HSE06 functionals based on the generalized gradient approximation (GGA) are adopted, where the HSE06 functional is mainly used for the accurate calculation of band gaps.34 The valence electrons of the atoms considered are: Rb 4s2 4p6 5s1, Pb 5d10 6s2 6p2, and I 5s2 5p5. The k-point grid is sampled along the k-tight Monkhorst–Pack grid,35 with a minimum allowable spacing between k-points set to 0.1 A−1. The k-Monkhorst–pack grid refers to the specified minimum grid density, which is the maximum distance between any two k-points in the grid. Furthermore, a conversion theory was utilized to relate the physical wave function to the auxiliary wave function (projected amplified wave (PAW) method),36 setting the cutoff energy of the wave function to 700 eV. Correspondingly, the convergence thresholds of the energy and Herman Feynman force on any ion were established as 10−8 eV and −10−3 eV A−1 respectively, where the Herman Feynman force refers to the derivative of generalized free energy. Moreover, to ensure structural stability, we use the finite-displacement method for phonon dispersion curve calculations. This involves computing forces in density functional theory (DFT) and determining their derivatives using the finite difference method, as illustrated in Fig. S1 (ESI†). The calculated different crystal structures were visualized using the VESTA software package37 and the space group was determined using the FINDSYM program.38 Finally, electron–phonon coupling is calculated by means of the Quantum-ESPRESSO package based on linear response theory.39,40 Utilizing the standard solid-state pseudopotentials (SSSPs), we employed pseudopotentials tailored for Rb, Pb and I atoms. Pseudopotential approximation involves substituting the coulomb potential in the many-electron system Hamiltonian with a smooth function. The calculation employed a k-point grid of 12 × 16 × 4 for each q-point, with a corresponding q-point grid of 3 × 4 × 1. The superconducting transition temperature was simulated using the Allen–Dynes modified McMillan equation.41 The cutoff energy was set at 100 Ry, and the coulomb pseudopotentials were selected as μ = 0.1 and 0.13, respectively.3 Results and discussion
3.1 Pressure-induced structural phase transitions
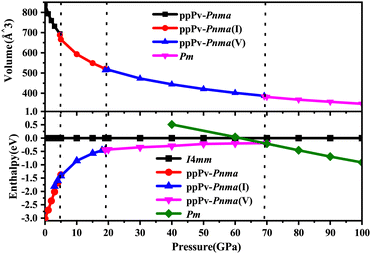
Based on the first principles calculations and CALYPSO method, many structures of RbPbI3 are taken into account under a pressure of 0–100 GPa. The relationships between enthalpies (ΔH = E + PV) and pressures are plotted in Fig. 1 for RbPbI3 with different stable phases. Meanwhile, Fig. 1 also presents the relationship between the volume and the pressure for different stable phases.From Fig. 1, one can see that RbPbI3 undergoes three structural phase transitions from ppPv-Pnma to ppPv-Pnma(I) phases at 4.6 GPa, from ppPv-Pnma(I) to ppPv-Pnma(V) phases at 19 GPa, and from ppPv-Pnma(V) to Pm phases at 69.2 GPa, respectively. Here, to distinguish it from the previous studies, the new post–post-perovskite structure is identified as ppPv-Pnma(V). Of course, the ppPv-Pnma and ppPv-Pnma(I) phases are employed with the same labels as in previous reports.22 Regrettably, ppPv-Pnma(II), ppPv-Pnma(III) and ppPv-Pnma(IV) phases presented in previous studies as well as Pnma, C21/m(I) and C21/m(II) predicted in CsPbI3 are not observed in this work.17,22,42 At the same time, some structures (P4/mmm, C2mm, I4mm, Cm, and so on) predicted in other halide perovskites may be absent or metastable.43,44 Surprisingly, the new crystal phase ppPv-Pnma(V) has never been previously observed in any materials. Moreover, the relationship between the volume and the pressure in Fig. 1 reveals that the phase transitions from ppPv-Pnma to ppPv-Pnma(I) and ppPv-Pnma(V) to Pm belong to a first-order structural phase transition, and the phase transition from ppPv-Pnma(I) to ppPv-Pnma(V) belongs to a second-order structural phase transition. A first-order structural phase transition involves a material undergoing a direct transformation from one crystal structure to another, marked by significant thermodynamic changes such as abrupt jumps in energy, volume, or other physical properties. This results in noticeable discontinuities, distinguishing it from the continuous changes observed in a second-order phase transition.45,46
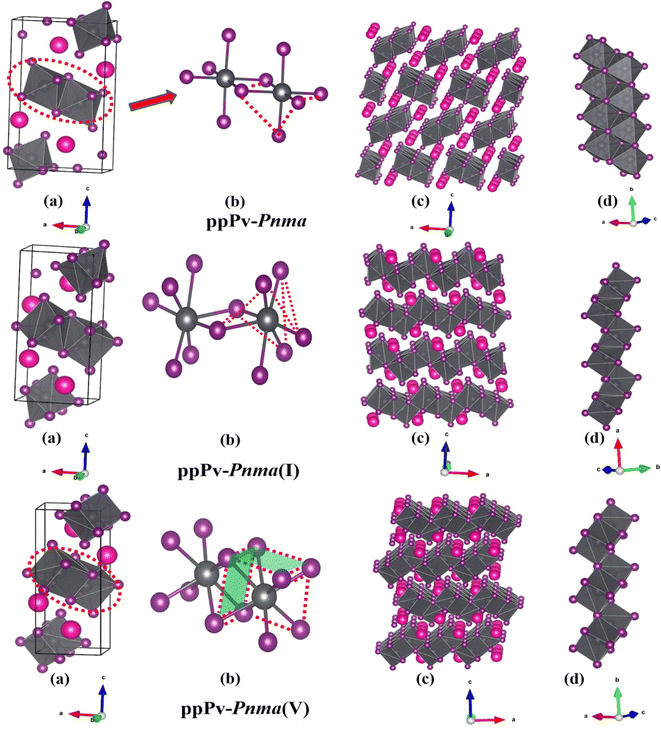
In order to further understand the characteristics of these stable phases, the schematic view of the corresponding structures is shown in Fig. 2, and the corresponding structural parameters are summarized in Table S1 (seen in the ESI†). As revealed in Fig. 1 and 2(a), the ground state of RbPbI3 is the post–post-perovskite structure (ppPv-Pnma) up to about 4.6 GPa. Table S1 (ESI†) indicates that the structural parameters (a = 10.272 Å, b = 4.736 Å, and c = 17.297 Å) of the ground state for the ppPv-Pnma phase are in line with the experimental results (a = 10.276 Å, b = 4.775 Å, and c = 17.382 Å).9 Meanwhile, Fig. 2(a) reveals that the ppPv-Pnma phase can be characterized by any oxygen octahedron connected to other four oxygen octahedra by four common edges. Note that the coordination around each Pb ion in ppPv-Pnma is six I ions due to Pb–I bonds contained two doubly degenerate and other two non-degenerate, and these bonds decrease with the increasing pressure as seen in Table S1 (ESI†) and Fig. 3. On the other hand, the c lattice parameter (17.297 Å) is significantly elongated, while the b lattice parameter (4.736 Å) is significantly shortened relative to the a lattice parameter (10.272 Å), as seen in Table S1 (ESI†). These characteristics of the ppPv-Pnma phase are similar to those of the ppPv-Pnma phase reported by Xu et al., while it is different from the ppPv-Pnma(I) characterized by each oxygen polyhedron connected to other six oxygen polyhedrons by six common edges in previous studies.19,22 Moreover, it is clear that the ground state of RbPbI3 is the post–post-perovskite structure (ppPv-Pnma) and not the perovskite structure (Pnma) appeared commonly in oxygen perovskites and other halide perovskites.19,22,43,44 Of course, in order to further verify the ground state structure, several other possible structures (Pnma, ppPv-Pnma(Cmcm), ppPv-Pnma(III), and Pm3m) appeared in previous reports have also been examined.19,22,43,44,47 The calculated results indicate that the energy values (−35.9172 eV) of ppPv-Pnma is lower than those of Pnma (−35.6253 eV), ppPv-Pnma(Cmcm) (−35.7586 eV), ppPv-Pnma(III) (−34.9954 eV) and Pm3m (−34.4393 eV). Meanwhile, the phonon dispersions of ppPv-Pnma, Pnma and ppPv-Pnma(Cmcm) shown in Fig. S1(a)–(c) (ESI†) indicate that three structures have no negative phonon frequencies and are dynamically stable. These further reveal that ppPv-Pnma is the ground state, which is consistent with the experimental results,9 where Pnma and ppPv-Pnma(Cmcm) phases are possible metastable for RbPbI3.
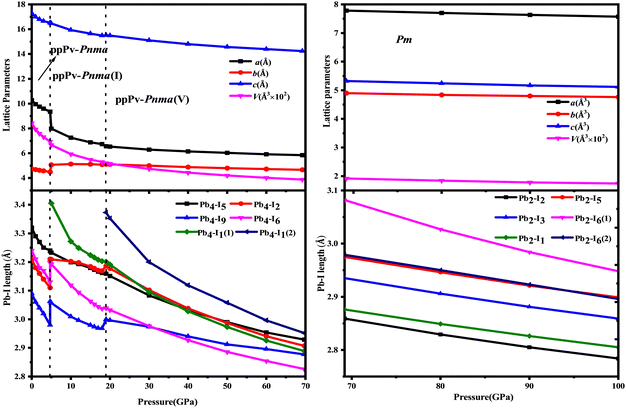 | ||
| Fig. 3 Lattice parameters and Pb–I lengths of Pv-Pnma, ppPv-Pnma(II), ppPv-Pnma(V) and Pm phases of RbPbI3 at a hydrostatic pressure of 0–100 GPa. | ||
As also shown in Fig. 1, RbPbI3 is predicted to undergo a phase transition from a post–post-perovskite structure (ppPv-Pnma) to another post–post-perovskite structure of about 4.6 GPa. Fig. 2(b) clearly presents that any halide polyhedron is connected to six adjacent halide polyhedral by four common edges and two common faces (each face is triangle formed by three common edges) along the a axis, which is similar to the characteristics of the ppPv-Pnma(I) phase in our previous reports.22 For consistency, this post–post-perovskite structure is denoted as ppPv-Pnma(I) in the following, and retains the ground state up to about 19 GPa. Moreover, as indicated in Fig. 3, the lattice parameters a, b, c and V (volume) have a sudden change at a pressure of 4.6 GPa from ppPv-Pnma to ppPv-Pnma(I) phases, which reveals that the phase transition is the first-order structural phase transition. Fig. 3 and Table S1 (ESI†) also indicate that seven Pb–I bonds of polyhedrons in ppPv-Pnma(I) phases exist two doubly degenerate and three non-degenerate bonds, and the varietal tendency of the Pb–I bond with the pressure is the same to that of ppPv-Pnma. Apparently, the coordination of each Pb ion goes from six to seven after phase transition due to adding another non-degenerate Pb–I bond in ppPv-Pnma(I). Interestingly, for a given pressure of 5 GPa (very close to the phase transition pressure 4.6 GPa), one can see that the a (= 7.97 Å) and b (= 5.07 Å) lattice constants of ppPv-Pnma(I) are 14.4% shorter and 13.7% longer than a (= 9.32 Å) and b (= 4.46 Å) lattice constants of ppPv-Pnma, as well as the c (= 16.52 Å) lattice constant of ppPv-Pnma(I) have a very small change relative to the c (= 16.46 Å) lattice constant of ppPv-Pnma. It means that the phase transition from ppPv-Pnma to ppPv-Pnma(I) is associated with an alteration in the crystal's structural shape. Even though ppPv-Pnma and ppPv-Pnma(I) phases have the same space group (no. 62) and the same types of Wyckoff positions, the changes in lattice constants, the coordination number and the structural shape reveal that it is also a reconstructive phase transition.
When the pressure rises to 19 GPa, another post–post-perovskite structure appears and retains lower enthalpies than ppPv-Pnma(I) phases up to 69.2 GPa. Fig. 2(c) reveals that this post–post-perovskite structure differs from other post–post-perovskite structures previously reported.22 We also found that the connection mode among the halide polyhedra in this structure is the same as that of the ppPv-Pnma(III) phase, but there exist some differences (i.e., common faces are almost square formed by four common edges, and are different from the common face is the triangle formed by three common edges in the ppPv-Pnma(III) phase) in detail. For distinction, this post–post-perovskite structure is marked as ppPv-Pnma(V) in this work. As shown in Fig. 2(c) and Table S1 (ESI†), Pb–I bonds of polyhedra in ppPv-Pnma(V) phases are eight contained two doubly degenerate and four non-degenerate bonds. Interestingly, by analyzing Fig. 1 and 3, the sudden change in the lattice parameters a, b, c and V is not observed from ppPv-Pnma(I) to ppPv-Pnma(V) phases, which reveals that the phase transition is the second-order structural phase transition. Meanwhile, the transformation from ppPv-Pnma(I) to ppPv-Pnma(V) results in a change in coordination number from seven to eight only, implying that the phase transition is the isostructural phase transition similar to the transition from ppPv-Pnma(I) to ppPv-Pnma(II) in previous reports.22
To our surprise, the other new phase Pm is predicted successfully at about 69.2 GPa and retains the most stable up to 100 GPa, which completely differs from the post–post-perovskite structure as seen in Fig. 2(a)–(d). As indicated by Fig. 2(b) and (c), any halide polyhedron is connected to other neighboring halide polyhedra via corner sharing along the c axis and edges sharing on different c planes, which is different from the halide octahedra in traditional perovskites via corner sharing each other reported in CsMI3 (M = Pb and Sn) only.48 Moreover, in Fig. 1, 3 and Table S1 (ESI†), sudden changes of the lattice parameters a, b, c and V (volume) are observed at about 69.2 GPa, and the coordination number around Pb retains the same at eight. Meanwhile, the Pm and ppPv-Pnma(V) phases possess the different space groups and the different types of Wyckoff positions as shown in Table S1 (ESI†). The aforementioned discussion further illustrates the transition from ppPv-Pnma(V) to Pm is both a first-order phase transition and a reconstructive phase transition. Of course, by continuing to apply pressure on the ppPv-Pnma(V) phase, the other phase P21/c can be obtained at pressures from 69.2 GPa to 100 GPa. In order to further verify the ground state at this pressure region, we employ the CALYPSO search method by fixing the cell of P21/c or ppPv-Pnma(V) phases to obtain other relative stable phases (Pm, Pmn21, P21/c, P21/m, Cmc2, Cm, Pc and so on). Their enthalpies and the phonon dispersions further reveal that Pm is the most stable at a pressure from 69.2 GPa to 100 GPa compared with other phases. Unfortunately, the Pmn21 phase reported in CsPbI3 is only a metastable phase for RbPbI3.49
3.2 Electric properties and piezochromic effects
Pressure can induce bond length shortening and B–X–B angle increase, which narrows and widens the corresponding band gap, respectively. The “B–X–B angle” refers to the bond angle in a molecule or a compound, with X representing one atom and B/B′ representing another atom or group. It specifically indicates the angle formed when there is a bond between an atom (X) and two other atoms or groups (B and B′) in the molecule. Thus, the pressure is regarded as a good strategy to regulate the band gap. In this work, based on the stable structures obtained above, the electric band structures are predicted by employing functionals PBEsol, HSE06 and PBEsol contained the spin–orbit coupling (SOC) under pressure from 0 to 100 GPa. As depicted in Fig. 4, the energy band gap decreases gradually with the increasing pressure at the corresponding stable phase pressure region. It can also be seen that the variation tendency of the band gap is consistent with the PBEsol or HSE06 functional, which is different from that of PBEsol + SOC. As presented in Fig. 4, the tuning of pressure on the band gap for ppPv-Pnma(I) is very obvious, resulting in the piezochromic effect. That is to say, the band gap of ppPv-Pnma(I) decreases from 2 to 0 eV with the pressure varying from 5 to 18 GPa, and undergoes a transition from an insulator to a metal. Considering the alterations in the band gap and pressure, we calculated the piezochromic effect amplitude of the ppPv-Pnma(I) phase. The amplitude of the piezochromic effect is measured at 0.154 eVGPa−1, surpassing the 0.058 eVGPa−1 piezochromic effect observed in the study of BiFeO3 by Sando et al.,50 indicating the significant piezochromic effect of RbPbI3 under pressure. This piezochromic effect also appeared in ppPv-Pnma(II) for CaZrO3 in previous reports.22 Similarly, this piezochromic effect has also been found in the ppPv-Pnma(IV) phase of RbSnBr3 and the non-Pv-Pnma phase of CsPbX3,17,42 as well as in the experimental study of Cs4MnBi2Cl12 with the Imma phase and Cs2CoCl4 with the Pnma phase. The above discussion further indicates that the piezochromic effect appears in these materials with the same orthorhombic symmetry, which is closely related to the symmetry of structure. To date, one can see that the piezochromic effect is very likely to occur when the crystal structure belongs to the orthorhombic perovskite-like structure. Of course, it needs to be further verified in theory and experiment.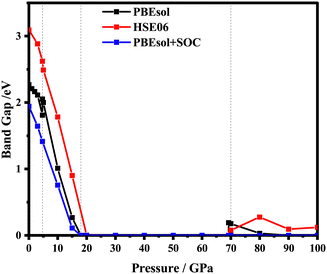 | ||
| Fig. 4 RbPbI3 electronic band gaps calculated by PBEsol, HSE06 and PBEsol + SOC under a hydrostatic pressure of 0–100 GPa. | ||
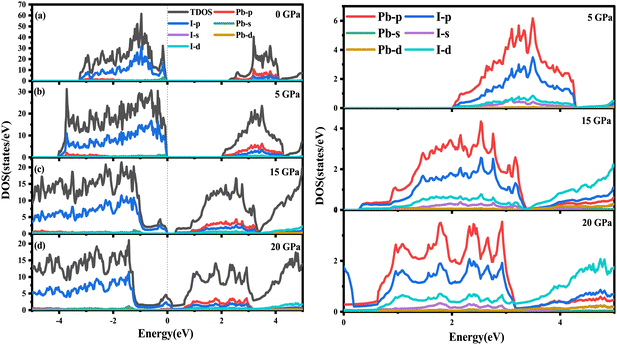
To explore deeper insight into the effect of pressure on the band gap, the atom-resolved density of states for the corresponding stable phases at certain pressures (0 GPa, 5 GPa, 15 GPa, 20 GPa) are displayed in Fig. 5, respectively. As shown in Fig. 5(a), at 0 GPa, the conduction band edge is dominated essentially by p orbitals of I and Pb atoms. Whereas, the valence band edge derives primarily from the p orbital of the I atom with a very small contribution of the s orbital of the Pb atom. When pressure is up to 5 or 15 GPa, the contribution of the orbital on the conduction and valence band edges is similar to that in 0 GPa. In surprise, the contribution of the I-p state on the conduction band is more and more obvious compared with the p orbital of Pb. As the pressure increases, the p orbitals of the I atom shift towards lower energy regions, causing the band gap to decrease. As revealed in Fig. 4, RbPbI3 presents the metallic properties at 18 GPa. When pressure ranges from 0 to 18 GPa, the transition from insulation to semiconductor to metal occurs. Thus, the piezochromic effect appeared in ppPv-Pnma(I) is mainly derived from the p orbital of I, which is different from that in CaZrO3 derived from the d orbital of Zr.
3.3 Superconductivity properties
The aforementioned discussion reveals that RbPbI3 retains metallic with pressure varying from 20 to 100 GPa, implying that it could be a potential superconductor. Superconductivity relies on a substantial density of states (DOS) at the Fermi level and a high symmetrical crystal structure.51,52 DOS, representing the count of allowable electron states at a specific energy level, aids in understanding the overall distribution of states with respect to energy and unveils energy band spacing in semiconductors. In comparison, more electronic states appear near the Fermi level for RbPbI3 with the ppPv-Pnma(V) phase at 20 GPa, revealing that the ppPv-Pnma(V) phase of RbPbI3 possesses a higher superconducting transition temperature. Therefore, we will select the ppPv-Pnma(V) phase of RbPbI3 at 20 GPa to explore its superconductivity. Correspondingly, the electron–phonon interaction parameter λ, the Eliashberg phonon spectral function α2F(ω) and the logarithmic average of the phonon vibration frequency ωlog have been investigated as shown in Fig. 6. Based on eqn (1), a value 1.16 of the electron–phonon interaction parameter λ is estimated.53,54 Where NεF is the density of electronic states at the Fermi level, 〈g2〉 is the average value of the electroacoustic matrix elements near the Fermi level, M is the atomic mass, and 〈ω2〉 is the average value of the square of the vibration frequency. Therefore, it can be seen that λ is positively correlated with DOS near the Fermi level and negatively correlated with the average value of the atomic vibration frequency. Apparently, our calculated parameter λ is higher than some alloys (0.56 for PbVSe2 at 6.4 GPa, 0.46 for SnVSe2 and 0.64 for Ti6Pb4) and slightly lower than some perovskites (1.43 for MgVH6 at 150 GPa).28,55,56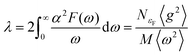 | (1) |
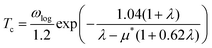 | (2) |
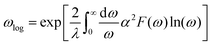 | (3) |
When λ is less than 1.5, the superconducting critical temperature Tc can be calculated by the Allen–Dynes modification of the McMillan formula as seen in eqn (2) and (3). Where μ* represents the shielded anti-superconducting Coulomb pseudopotential. When μ* values are set to 0.1 and 0.13, the corresponding Tc values of ppPv-Pnma(V) in RbPbI3 are about 8 and 7.3 K at 20 GPa, respectively. Meanwhile, we also estimate the Tc of ppPv-Pnma(V) with 3. 8 K at 60 GPa (see Fig. S2, ESI†), which is smaller than that at 20 GPa. It may be attributed to the smaller DOS value at the Fermi level at 60 GPa.
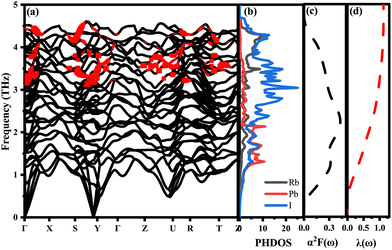
To effectively explain the electronic coupling mechanism on which superconductivity depends, we give PHDOS, and α2F(ω) and λ(ω) are drawn in Fig. 6. Fig. 6(a) shows the phonon spectrum modified by the normalized phonon linewidth. The phonon linewidth is closely associated with the electron–phonon interaction matrix element, describing the scattering probability amplitude of phonons with a wave vector q on the Fermi surface (FS).57 Compared with the cutoff frequency of δ-CsPbI3, the frequency of the largest RbPbI3 is increased by 24%,58 which may be attributed to the high-frequency modes of RbPbI3 contributed mainly by the vibration of the I and Rb atoms. This enhancement is due to the vibration of Rb atoms, proving beneficial for improving Tc. In contrast to low-frequency acoustic modes, high-frequency optical phonons contributed by Rb and I atoms exhibit stronger electroacoustic coupling, driven by their larger phonon linewidth. As revealed in Fig. 6(b), it is not difficult to see that the vibration frequency in the low frequency region (less than 2.5 THz) is mainly contributed by Pb and I atoms, while that in the high frequency region (higher than 2.5 THz) is mainly related to I atoms, and a large number of electrons are transferred from I-p to Pb-p, resulting in the strong hybridization of p–p orbitals. Electron transfer between Pb and I atoms leads to electron scattering in the lattice, which increases electron–phonon coupling. Thus, the superconductivity of RbPbI3 is mainly contributed by the p orbital which is different from Ca3 PN contributed mainly by Ca-d orbitals.26 Near the Fermi energy level, I ions contribute to TDOS of 60.14%, Rb of 20% and Pb of only 19.79%, which is consistent with the contribution to the total λ and is a key factor in enhancing phonon-mediated superconductivity EPC. Regretfully, both Pb and I have large relative atomic masses, which drag down the average value of RbPbI3 atomic vibration frequency, making 〈ω2〉 smaller. These factors lead to a strong electro-acoustic coupling interaction in RbPbI3 and also suggest that the superconductivity of RbPbI3 is mainly contributed by I. Analogously, Na0.2WO3 in the MxWO3 system also has a superconducting transition temperature of 3 K,26,59,60 which is slightly lower than that of RbPbI3 with 8 K at 20 GPa. Our findings may further promote to explore high-temperature low-pressure superconductors and also need further experiment to verify the accuracy of our calculations.
4 Summary
First-principles calculations in conjunction with the particle swarm optimization algorithm were performed to explore the structural evolution, electronic properties, and superconductivity of RbPbI3 at 0–100 GPa. The results indicate that RbPbI3 undergoes a rich structural evolution by tuning the hydrostatic pressure. Two first-order reconstruction phase transitions from ppPv-Pnma to ppPv-Pnma(I) and from ppPv-Pnma(V) to Pm phases as well as a second-order isomorphic phase transition from ppPv-Pnma(I) to ppPv-Pnma(V) were predicted, respectively. Notably, details of structural characteristics indicate that ppPv-Pnma(V) or Pm phases are two novel phases different from the previously reported ppPv-Pnma(I), ppPv-Pnma(II), ppPv-Pnma(III), ppPv-Pnma(IV) or Pm. Consequently, by tuning the pressure from 0 to 18 GPa, the insulator-to-semiconductor-to-metal transitions occur resulting in an obvious piezochromic effect. More importantly, a superconducting transition temperature of 8 K (7.3 K) at 20 GPa of the ppPv-Pnma(V) phase is predicted, implying that RbPbI3 is a potential low-pressure superconducting material. Undoubtedly, the p orbitals in I significantly contribute to the observed piezochromic effects and the emergence of superconductivity. These outstanding properties will stimulate experimental interest, potentially catalyzing additional investigations into novel superconductivity phenomena. Furthermore, this prompts further exploration of high-Tc low-pressure superconductivity of halide perovskites and their potential in scientific applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financially supported by the Central Government Funds of Guiding Local Scientific and Technological Development for Sichuan Province (no. 2021ZYD0026) and the National Natural Science Foundation of China (no. 11874043 and 12104416). H. T. thanks for the support from the Zhengzhou Normal University Young Backbone Teacher Training Project (QNGG-221971).Notes and references
- W. Zhao, R. Su, Y. Huang, J. Wu, C. F. Fong, J. Feng and Q. Xiong, Nat. Commun., 2020, 11, 5665 CrossRef CAS PubMed.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696 CrossRef CAS PubMed.
- H. Zhu, M. T. Trinh, J. Wang, Y. Fu, P. P. Joshi, K. Miyata, S. Jin and X.-Y. Zhu, Adv. Mater., 2017, 29, 1603072 CrossRef PubMed.
- Y. Hu, F. Bai, X. Liu, Q. Ji, X. Miao, T. Qiu and S. Zhang, ACS Energy Lett., 2017, 2, 2219–2227 CrossRef CAS.
- R. J. Sutton, M. R. Filip, A. A. Haghighirad, N. Sakai, B. Wenger, F. Giustino and H. J. Snaith, ACS Energy Lett., 2018, 3, 1787–1794 CrossRef CAS.
- M. Tai, C. F. J. Lau, H. Lin and Z. Wang, Sol. RRL, 2020, 4, 2000495 CrossRef CAS.
- A. K. Jena, A. Kulkarni, Y. Sanehira, M. Ikegami and T. Miyasaka, Chem. Mater., 2018, 30, 6668–6674 CrossRef CAS.
- D. Liu, W. Zha, Y. Guo and R. Sa, ACS Omega, 2020, 5, 893–896 CrossRef CAS.
- C. Abia, C. A. Lopez, J. Gainza, J. E. F. S. Rodrigues, M. M. Ferrer, G. Dalenogare, N. M. Nemes, O. J. Dura, J. L. Martinez, M. T. Fernandez-Diaz, C. alvarez Galvan and J. A. Alonso, Inorg. Chem., 2022, 61, 5502–5511 CrossRef CAS.
- S.-H. Turren-Cruz, M. Saliba, M. T. Mayer, H. Juarez-Santiesteban, X. Mathew, L. Nienhaus, W. Tress, M. P. Erodici, M.-J. Sher, M. G. Bawendi, M. Gratzel, A. Abate, A. Hagfeldt and J.-P. Correa-Baena, Energy Environ. Sci., 2018, 11, 78–86 RSC.
- M.-H. Jung, S. H. Rhim and D. Moon, Sol. Energy Mater Sol. Cells, 2017, 172, 44–54 CrossRef CAS.
- D. Amgar, T. Binyamin, V. Uvarov and L. Etgar, Nanoscale, 2018, 10, 6060–6068 RSC.
- S. Kumavat, D. Singh, Y. Sonvane and S. Gupta, AIP Conf. Proc., 2019, 2115, 030154 CrossRef.
- P. Pansa-Ngat, K. Singh, B. Patel, C. Seriwattanachai, P. Kanjanaboos and O. Voznyy, Chem. Mater., 2023, 35, 271–279 CrossRef CAS.
- D. Andres-Penares, J. Navarro-Arenas, R. I. Sánchez-Alarcón, R. Abargues, J. P. Martínez-Pastor and J. F. Sánchez-Royo, Appl. Surf. Sci., 2021, 536, 147939 CrossRef CAS.
- S. Mitro, M. Saiduzzaman, A. Biswas, A. Sultana and K. M. Hossain, Mater. Today Commun., 2022, 31, 103532 CrossRef CAS.
- X. Wang, H. Tian, X. Li, H. Sang, C. Zhong, J.-M. Liu and Y. Yang, Phys. Chem. Chem. Phys., 2021, 23, 3479–3484 RSC.
- M. Murakami, K. Hirose, K. Kawamura, N. Sata and Y. Ohishi, Science, 2004, 304, 855–858 CrossRef CAS PubMed.
- C. Xu, B. Xu, Y. Yang, H. Dong, A. R. Oganov, S. Wang, W. Duan, B. Gu and L. Bellaiche, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 020101 CrossRef.
- A. C. Garcia-Castro, N. A. Spaldin, A. H. Romero and E. Bousquet, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 104107 CrossRef.
- H. Cheng, A.-J. Mao, X.-R. Cheng, H. Tian, X.-L. Dou, S.-M. Yang and X.-Y. Kuang, J. Phys.: Condens. Matter, 2019, 31, 505406 CrossRef CAS PubMed.
- H. Tian, X.-Y. Kuang, A.-J. Mao, Y. Yang, C. Xu, S. O. Sayedaghaee and L. Bellaiche, Phys. Rev. B, 2018, 97, 020103 CrossRef CAS.
- A. P. Drozdov, M. I. Eremets, I. A. Troyan, V. Ksenofontov and S. I. Shylin, Nature, 2015, 525, 73–76 CrossRef CAS PubMed.
- F. Peng, Y. Sun, C. J. Pickard, R. J. Needs, Q. Wu and Y. Ma, Phys. Rev. Lett., 2017, 119, 107001 CrossRef.
- Z. Hui, X. Tang, D. Shao, H. Lei, J. Yang, W. Song, H. Luo, X. Zhu and Y. Sun, Chem. Commun., 2014, 50, 12734–12737 RSC.
- H. Cheng, A.-J. Mao, S.-M. Yang, H. Tian, S.-Y. Jin, M. Yu and X.-Y. Kuang, J. Mater. Chem. C, 2020, 8, 13072–13078 RSC.
- A. Iyo, H. Fujihisa, Y. Gotoh, S. Ishida, H. Ninomiya, Y. Yoshida, H. Eisaki, H. T. Hirose, T. Terashima and K. Kawashima, Inorg. Chem., 2020, 59, 12397–12403 CrossRef CAS.
- J. Song, Y. Qin, Y. Wang and C. Cao, Phys. Chem. Chem. Phys., 2022, 24, 1770–1778 RSC.
- T. Kong, K. Gornicka, S. Golab, B. Wiendlocha, T. Klimczuk and R. J. Cava, J. Phys. Soc. Jpn., 2018, 87, 074711 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- H. Stokes and D. Hatch, J. Appl. Crystallogr., 2005, 38, 237–238 CrossRef CAS.
- S. Y. Savrasov, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16470–16486 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. B. Allen and R. C. Dynes, Phys. Rev. B: Solid State, 1975, 12, 905–922 CrossRef CAS.
- S. Zhou, X. Kuang, F. Kuang, J. Qiu, M. Yu, J. Chen, J. Ma, Y. Li, F. Tang and A. Mao, J. Phys. Chem. C, 2023, 127, 13346–13355 CrossRef CAS.
- Y. Li, X. Gong, P. Zhang and X. Shao, Chem. Phys. Lett., 2019, 716, 76–82 CrossRef CAS.
- Y. Huang, Z. Hu, K. Li and X. Shao, Comput. Mater. Sci., 2018, 143, 403–410 CrossRef CAS.
- W. C. Kerr, A. M. Hawthorne, R. J. Gooding, A. R. Bishop and J. A. Krumhansl, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 7036–7053 CrossRef.
- N. Ni, S. Nandi, A. Kreyssig, A. I. Goldman, E. D. Mun, S. L. Bud’ko and P. C. Canfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 014523 CrossRef.
- J. Qiu, X. Kuang, M. Yu, Z. Xing, S. Zhou, J. Chen, J. Ma and A. Mao, Phys. Chem. Chem. Phys., 2022, 24, 22038–22045 RSC.
- X.-R. Cheng, X.-Y. Kuang, H. Cheng, H. Tian, S.-M. Yang, M. Yu, X.-L. Dou and A.-J. Mao, RSC Adv., 2020, 10, 12432–12438 RSC.
- F. Ke, J. Yan, S. Niu, J. Wen, K. Yin, H. Yang, N. R. Wolf, Y.-K. Tzeng, H. Karunadasa, I. Y. S. Lee, W. L. Mao and Y. Lin, Nat. Commun., 2022, 13, 7067 CrossRef CAS.
- D. Sando, Y. Yang, E. Bousquet, C. Carretero, V. Garcia, S. Fusil, D. Dolfi, A. Barthelemy, P. Ghosez, L. Bellaiche and M. Bibes, Nat. Commun., 2016, 7, 10718 CrossRef CAS.
- F. Peng, Y. Sun, C. J. Pickard, R. J. Needs, Q. Wu and Y. Ma, Phys. Rev. Lett., 2017, 119, 107001 CrossRef PubMed.
- D. Duan, Y. Liu, F. Tian, D. Li, X. Huang, Z. Zhao, H. Yu, B. Liu, W. Tian and T. Cui, Sci. Rep., 2014, 4, 6968 CrossRef CAS PubMed.
- P. B. Allen and R. C. Dynes, Phys. Rev. B: Solid State, 1975, 12, 905–922 CrossRef CAS.
- W. L. McMillan, Phys. Rev., 1968, 167, 331–344 CrossRef CAS.
- J. Zheng, W. Sun, X. Dou, A.-J. Mao and C. Lu, J. Phys. Chem. C, 2021, 125, 3150–3156 CrossRef CAS.
- X.-W. Yi, Z.-W. Liao, J.-Y. You, B. Gu and G. Su, iScience, 2023, 26, 105813 CrossRef CAS.
- M. Gao, Z.-Y. Lu and T. Xiang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 045132 CrossRef.
- A. Marronnier, H. Lee, B. Geffroy, J. Even, Y. Bonnassieux and G. Roma, J. Phys. Chem. Lett., 2017, 8, 2659–2665 CrossRef CAS PubMed.
- C.-S. Lian, C. Si, J. Wu and W. Duan, Phys. Rev. B, 2017, 96, 235426 CrossRef.
- K. Sano, Y. Nitta and Y. No, J. Phys. Soc. Jpn., 2020, 89, 113704 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc03535b |
| ‡ S.-Y. Z. and H. T. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |