Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaluating spatial material distributions: adopting geospatial entropy definitions into resource management†
Cristina
Moyaert
 a,
Philippe
Nimmegeers
abc,
Bilal
Mellouk
a,
Dimitri
Voordeckers
d,
Paul
De Meulenaere
ef and
Pieter
Billen
*a
a,
Philippe
Nimmegeers
abc,
Bilal
Mellouk
a,
Dimitri
Voordeckers
d,
Paul
De Meulenaere
ef and
Pieter
Billen
*a
aIntelligence in Processes, Advanced Catalysts and Solvents (iPRACS), Faculty of Applied Engineering, University of Antwerp, Groenenborgerlaan 171, 2020 Antwerp, Belgium. E-mail: pieter.billen@uantwerpen.be
bEnvironmental Economics (EnvEcon), Department of Engineering Management, Faculty of Business and Economics, University of Antwerp, Prinsstraat 13, 2000 Antwerp, Belgium
cFlanders Make@UAntwerp, 2000 Antwerp, Belgium
dResearch Group for Urban Development, Faculty of Design Sciences, University of Antwerp, Mutsaardstraat 31, 2000 Antwerp, Belgium
eCoSys-Lab, Faculty of Applied Engineering, University of Antwerp, Groenenborgerlaan 171, 2020 Antwerp, Belgium
fAnsymo/Cosys Core Lab, Flanders Make, 2020 Antwerp, Belgium
First published on 15th January 2024
Abstract
Human activity depends on resources that are often consumed without regard for their future availability. Consequently, resources in the form of raw materials and finished products are widely dispersed across society, creating energetic challenges for resource management, since the processes of procuring materials, purifying and processing them, distributing goods, and collecting waste all require significant amounts of energy. The costs and energy requirements for these activities depend on factors such as the mode of transportation and the distance travelled. Efficient transportation strategies can help reduce the negative environmental impact of human activities and ensure the sustainable use of resources for future generations. Quantifying the impact of this transport requires specific and expert logistics management knowledge. The current approach relies on information that is often not readily available, making it impractical and costly. Fast and quantitative methods to support decision making are especially needed when evaluating different potential circular economy (CE) strategies and business models that aim to reduce environmental impact by keeping materials at a high functionality level by closing material cycles (e.g., through reuse, reparation, refurbishment, remanufacturing, repurposing, recycling or material recovery). As a consequence, in this article, geospatial entropy definitions are studied as novel metrics to quantify the geospatial distribution of resources. The overall goal of this article is to review existing geospatial entropy definitions and evaluate their potential to be applied for assessing resource management strategies in view of a circular economy. In doing so, insight into the decision making behind the location of a value-added activity through a collection and processing of resources is gained, as well as how entropy can be used to support this. To achieve this, we analyse several definitions used in the field of urban sprawling, illustrate how they are calculated using conceptual examples, and translate these to relevant research questions for resource management. This analysis results in several promising definitions, which, in our view, are able to quantify the geospatial distribution of resources accurately. The resulting entropy value can then serve as a proxy for collection efforts. As a result, a viewpoint is presented on how these geospatial entropy definitions can support resource management decisions, such as the appraisal of resource/waste collection schemes and the location of processing and recycling facilities.
Environmental significanceIn the framework of sustainability, resource recovery is paramount. However, there is no easy and accessible method to optimize resource recovery. As a result, research questions about relevant collection schemes and site location decision making are currently performed based on complex (multi-objective) optimization problems, and are time-consuming and energy intensive. As a result, we investigate geospatial entropy definitions as innovative measures for quantifying the geospatial dispersion of resources, allowing for general, unambiguous and easy metrics. We have demonstrated how such geospatial entropy-based metrics can support resource management decisions, such as the evaluation of waste/resource collection schemes and the location of processing/recycling facilities, by elaborating a case study. |
1. Introduction
Since the 1960s, the world has experienced a sharp increase in prosperity.1 Materials and resources have become more affordable, leading to an increase in production. This improvement gave corporations the ability to create their items quickly and cheaply, resulting in the introduction of low-cost production. Instead of repairing products and materials, it became more economical to replace them.2,3 Since time is a more valued asset than most resources, convenience took precedence, and we entered an era of throwaway culture.4,5 Over the past decades, large volumes of products, materials and resources have been routinely consumed by individuals and organizations without sufficient consideration for their future availability or for the full cost of a depleting resource. As a result, these volumes of materials are scattered across our society.6,7Currently, society is becoming increasingly dependent on the use of these resources (i.e. metals, plastics, etc.) to the extent that policymakers and executives are rapidly gaining interest in their sustainability.8–11 As a result, sustainability goals are being set, with a circular economy (CE) being a key factor in the achievement of these goals. For instance, in 2022, the European Union (EU) introduced specific objectives to increase the EU's self-sufficiency on key raw materials needed for the green and digital transitions.12 In addition, the United Nations (UN) have set specific sustainable development goals, which include CE goals such as: ensuring sustainable consumption and production patterns, and ensuring availability and sustainable management of water and sanitation.13 However, achieving a CE comes with many challenges, including poor recycling technologies, a lack of proper resource management infrastructure, and a lack of government legislations and specific implementation guidelines. Lastly, geopolitical dynamics can also have a significant impact on achieving a CE, as geopolitics heavily influence the allocation of resources, environmental policies, the price of resources and their economic progress.
In addition to these challenges, the spread of resources and goods also poses a problem for resource management, as procuring materials, transporting them to facilities for purification and processing, distributing goods, and collecting waste all demand energy for transportation. Since economies of scale are crucial to the profitability of waste collection and waste management businesses,14–17 and the costs and energy requirements of transportation rely largely on the mode of transportation and on the distance travelled,18,19 a method which can easily quantify geospatial distributions is paramount for answering resource management related research questions.
Historically, the 4-step-model, or trip-based model, is the most commonly used aggregate technique for quantifying transportation impacts. More recently, more detailed models such as activity-based models or agent-based models (ABM) and incremental pivot-point models have been adopted.20 In their current states, the transportation impact quantification models require a lot of information, such as detailed logistics data and expert knowledge and insights, all of which incur additional costs. Lamentably, most companies do not have sufficient data and/or insight into the entirety of relevant logistic chains, resulting in an unfeasible impact quantification. In addition, even if the logistics management would be sufficiently advanced, the remaining information required for this assessment would not be readily available. As a result, the current methodology is both impractical, costly, and in certain situations even impossible. Moreover, it is important to calculate the performance of materials rather than the performance of a region or a specific logistics system. Consequently, a need for easily calculated and interpretable methods to quantify transportation impacts arises. We hypothesize that methods which quantify geospatial distributions based on readily available data can support this.6,21–23
We envision that the quantification of distributions holds the key to evaluating transportation impacts, owing to the close relationship between the distribution of materials and the energy required for their retrieval, as established by Gutowski.24 Specifically, the concentration of materials correlates inversely with the energy necessary for their collection: the more concentrated materials are, the less energy required to collect them, while a high degree of dilution leads to a corresponding increase in energy requirements. Notably, the most arduous scenario is the uniform spread, which represents the pinnacle of dilution, and demands the greatest effort for retrieval.
An established approach to quantifying distributions can be found in the field of information theory: statistical entropy (more commonly referred to as Shannon entropy, as it originates from his mathematical theory of communication). Statistical entropy quantifies the average uncertainty on a distributed variable. The higher the statistical entropy, the higher the average uncertainty and the more spread the variable is (with as maximum a uniform distribution). The lower the statistical entropy, the lower the average uncertainty on the variable and the less spread the variable is (with as minimum the ideal case in which the probability that a variable takes a specific value is 100%).25,26
The notion of statistical entropy has been applied widely: from information sciences and computer engineering to describe image randomness27 and to improve the evaluation of cross efficiencies,28 to the field of biology where it can be used to address the parameters of muscle biopotentials29 or to study the expression patterns of genes.30 Moreover, considerable advances have recently been made in the field of circular economy (CE). Several papers have been published directly linking the two concepts. This connection is achieved by interpreting a circular economy as a sustainability approach which aspires to keep entropy levels low, i.e. at a functional state, or at least an approach that allows a high entropic product or material to decrease to a low entropy state with minimum efforts. As a general rule, the maximum degree of functionality should be maintained for materials and products in a CE, whereas processes such as mixing, dilution and contamination should be avoided, since they are regarded as an entropy increasing process.21,31–35
Even though significant advances have been made in the field of CE, the allocation of resources is a new area of interest. While the concept of statistical entropy based on geospatial distributions has been studied extensively in the field of urban sprawling,32,36–39 the distribution used is mainly population based. To the authors' best knowledge, no other studies have been performed on interlinking this concept with resource management.
The goal of this paper is to provide insight into the current entropy definitions used to measure geographical distributions, as well as their possible application to the areas of CE and resource management. This entails (i) providing a clear understanding of the various entropy definitions employed and exploring their nuances, differences and similarities and (ii) assessing the suitability of different entropy definitions in capturing and quantifying geographical distributions, as well as identifying scenarios where certain definitions may be more effective or appropriate, and (iii) assessing the applicability of these definitions for resource management strategies in view of a circular economy.
The main research question of the paper corresponds with the following: how can we make decisions about where to locate a value-added activity through a collection and processing of resources based on a simple calculation that does not require much information? And how can we use entropy for that purpose? In addition to addressing the primary research question, this paper also aims to achieve a secondary goal, namely to bridge the gap between theoretical concepts and practical applications by offering a case study as a practical example. Not only does this offer concrete examples on how entropy definitions can be applied in real-world situations, but it also provides interpretations of results to enhance practical understanding, as well as providing practical recommendations or guidelines for decision-makers in CE and resource management based on the insights derived from the case study.
2. Shannon entropy and its affiliation to circular economy
In 1948, Shannon expanded the concept of entropy and used it in the field of information theory, where he linked entropy to the average level of “information”, “surprise”, or “uncertainty” inherent to a variable's possible outcomes. Shannon's entropy function H(X) is defined by eqn (1), which measures the average uncertainty of a certain event, given a randomly distributed variable X that can take values: Xi. The probability that X = Xi is denoted by p(Xi), or simply put: pi. In particular, given a constant variable (i.e., no uncertainty about the value of the variable, or pi = 1), the minimum Hmin = 0 is obtained, which corresponds with a fully localized probability distribution. The other extreme of H = maximum, is obtained for a uniform distribution.25,32,40H = −∑pi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log2(pi) log2(pi) | (1) |
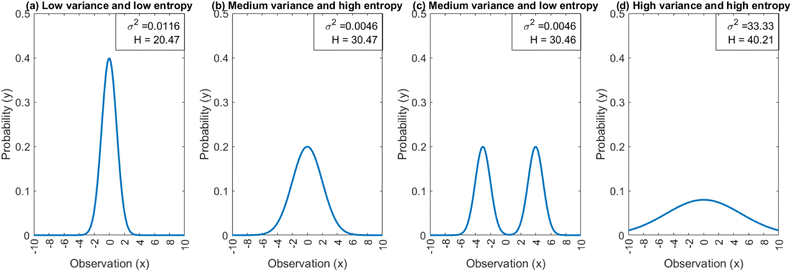
Entropy can in essence be seen as a statistical property of distributions just as a standard deviation and an average. A high entropy corresponds with a high uncertainty and a low entropy with a low uncertainty. As illustrated in the examples in Fig. 1, entropy should not be confused with other dispersion metrics like variance, which are relative to a mean value. The multimodal distribution (Fig. 1c) has a higher variance but a lower entropy than the normal distribution in Fig. 1b.
Entropy has found its use in many different domains including power systems,41 physics,26 finance,42 biology,43 physiology,44 and cardiovascular medicine.45,46 More specifically, recent research into the Shannon entropy has further developed the concept into an assessment methodology suited for several research questions in the domain of circular economy (CE).21,31,47,48 The link between entropy and CE was first developed by Rechberger and Brunner47 in order to examine the distribution of certain compounds in waste-to-energy facilities and later modified for streams of mostly inorganic/metallic components. Parchomenko et al.31 extended the approach, which allows for statistical entropies at different levels, such as component (consisting of multiple substances, e.g., a multilayer) and product (consisting of multiple components, e.g., a drink carton), to evaluate resource effectiveness of CE strategies.
Furthermore, the concept has also been used to quantify the separation complexity of mixed plastic waste streams, as Skelton et al.49 addressed the issue of applying the metric to material mixtures with radically varied origins or compositions. Through their research, a strategy based on statistical entropy and a multi-level material classification system that is extensively applicable to many resource types over the whole life cycle has been developed. Lastly, newly found interest into assessing product recyclability from a design point-of-view is developing. This entails using entropy during the design-phase to assess the recyclability of the product, allowing for recyclability by design choices to be made.21,35 Even though the above contributions have already been made to the domain of CE, the geospatial distribution or resources and products has not been considered.
As previously mentioned, in the search for statistical entropy methods that are not contingent upon specific background systems, Statistical Entropy Analysis (SEA) was devised.47 In recent times, extensions to this approach have been introduced, giving rise to Multilevel SEA (MSEA).31 Some of the already proposed extensions include product level and component level, where the presented methodology has already proven capable of capturing unwanted entropy increases that do not correspond with a clear energy gain in recycling and, thus, likely negatively influence waste management systems.33,35 We propose an extension of this methodology to encompass a geospatial level, as the geospatial dispersion of products can impact their recyclability via numerous factors such as accessibility to recycling infrastructure, market demand for recycled materials, environmental regulations, and cultural attitudes towards recycling. Therefore, this type of distribution, as well as their link to CE will be the central thesis of this paper.
3. Geospatial entropy definitions
One of the fields where the concept of statistical entropy is widely used is the field of geographical research, more specifically urban sprawl. In fact, one of the main focusses of urban sprawl studies is the examination of distributions. Numerous researchers have used the concept of entropy to quantitatively analyse geographical distributions in search for spatial patterns.36,38,50 The word “spatial pattern” can refer to a distribution's form, dispersion, relative location, density, and other properties. Throughout literature, it is proposed that the arrangement of any point pattern in space may be precisely defined, and that many of the features implied by the term pattern or arrangement can be quantitatively examined using statistical entropy definitions.39 Even though the use of entropy in geographical related research fields is extensively studied, the coupling of the concept with sprawling of materials and resources has not been considered. The six most common distribution types and corresponding entropy definitions in the field of geographic studies and urban sprawling are summarized in Table 1. All six definitions are from urban sprawl literature, and are part of the review section. In the next sections, these definitions will be discussed in more detail, and illustrated with conceptual examples.| Distribution type | Probability (pi) | Mathematical formulations | Interpretation | References |
|---|---|---|---|---|
| Area (m2) |
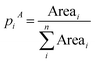 (3) (3) |
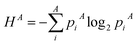 (10) (10) |
How distributed is an area in different sub-areas? How is an area divided among sub-areas? | Chapman (1970),39 Batty (1976)38 |
| Population number |
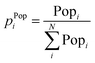 (4) (4) |
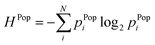 (11) (11) |
How distributed is a population in different areas? Suppose we pick one person from a larger area, what is the probability that person comes from a certain sub-area? | Chapman (1970),39 Batty (1976),38 Liu et al. (2018)36 |
| Population density |
 (5) (5) |
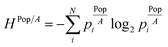 (12) (12) |
How geometrical are spatial systems in terms of population density? | Batty (1976)38 |
| How equal is the distribution of densities over several sub-areas? | ||||
| Population density levels |
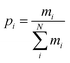 (6) (6) |
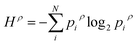 (13) (13) |
How common is this level of occurrence, compared to the total occurrences? | Semple (1970)51 |
| If we pick a random square, what are the chances it has a certain density level? | ||||
“Flows” from one area i to an other area j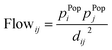 (2) (2) |
P Flow ij = Fract. Flowij (7) |
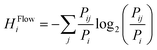 (14) (14) |
Which flow is preferential over other flows? How uniform is the flow pattern between different cities? | Chapman (1970)39 |
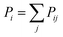 (8) (8) |
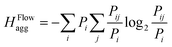 (15) (15) |
|||
| Percentage of land development pixels within buffer zones around |
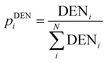 (9) (9) |
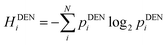 (16) (16) |
How is the distribution of land development densities? | Yeh and Li (2001)37 |
| If we are in a random patch of developed land, what are the chances we are in a specific zone? |
3.1 Area distribution
The first type of entropy definitions that are studied are based on area distribution, indicating how a total studied area (e.g., a province) is distributed over its sub-areas (e.g., a municipality). Hence, it expresses the probability of being in a sub-area i. The entropy in terms of area distribution is low if there is a lot of area clustering. On the contrary, a high entropy corresponds with an even distribution in terms of area size across the subareas. A maximum entropy value is obtained if the area size is uniformly distributed over the different sub-areas. The only data required for this approach, is an overview of the size (in m2) of sub-areas in an overarching area. The illustration of this concept, together with an explanatory case study is elaborated in the ESI.†This type of distribution has been studied by a number of different researchers, most important among them being Chapman39 and Batty.38 The main difference between their area distribution techniques lies in the demarcation of the sub-areas: Batty works with pre-set geographical boundaries (e.g. municipalities) while Chapman works with Thiessen polygons of municipal centres. Thiessen polygons are generated from a set of points such that each polygon defines an area of influence around its sample point. Any location inside the polygon is closer to that point than any of the other sample points. Essentially, it defines an area around a point (in Chapman's case a municipal centre), where every location is nearer to this point than to all the others.52
An alternative method of setting up an area distribution, was proposed by Liu et al. in 2018.36 They stated that the use of Shannon's entropy together with the spatial correlation rule of Tobler's Law, could be used to determine the distribution of populations in an area. Tobler's first law of geography states that “everything is related to everything else, but near things are more related than distant things”.53 Essentially, the law is founded on the idea of distance friction, or how physical separation prevents contact between locations. The difficulty or cost of an interaction increases with the distance between two locations. For instance, walking to the corner store for the groceries is more likely than driving across town for the same groceries.54
3.2 Population distribution
Similarly to an area distribution, population distributions can be used in geospatial entropy, indicating how the total population in a studied area (e.g., a province) is distributed over its sub-areas (e.g., a municipality). A high entropy in terms of population means a highly uniform population pattern. A maximum entropy is achieved when the population is divided uniformly over all the sub-areas. The analysis of population spatial distribution patterns is highly relevant in the field of population ecology, where one of the goals is to find the past mechanisms behind spatial population synchrony, which refers to changes in the affluence of geographically separated populations that occur at the same moment.50In order to establish a population distribution, only data regarding the population of the sub-areas is required, which is relatively simple to acquire. Once the distribution is obtained, this can be converted into probabilities, which form the basis of the entropy calculations. The illustration of this concept, together with an explanatory case study is elaborated in the ESI.†
Liu et al. (2018)36 defined the local spatial entropy method, which essentially consists of pairing the Shannon entropy with the Floating Catchment Area (FCA) method. FCA divides an area into a grid. In doing so, surrounding areas within a threshold distance can be searched. Next, the probability of a point i is then calculated based on the population of the surrounding 8 points in the grid, rendering the equation:
| pi = population of point i/total population of 9 points | (17) |
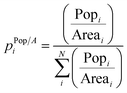
3.3 Population density distribution
The distribution of population density is another possible distribution used to describe urban sprawling. By dividing the population of an area by the size of the area, the population density is obtained. This metric takes both the population and area of a zone into account. Population density essentially normalises population distribution by area so it gives a clearer picture of dense vs. sparse population, than the previous two metrics. By gauging how evenly distributed population densities are throughout various sub-areas, the geometry of spatial systems can be examined. In general, a maximum entropy is obtained when the distribution is equal throughout all sub-areas. Population density is commonly used to describe the location, growth, and migration of many organisms. For this approach, data about both population and size of the studied areas in required. The illustration of this concept, together with an explanatory case study is elaborated in the ESI.†3.4 Population density levels
Another method of looking at population distributions is by categorizing them into population density levels. Depending on the size of the population density distribution, discrete levels are set-up, with the interval of the levels varying in range. Data points can then be classified into these discrete levels, which gives an idea of the uniformity of the population density pattern. This method of quantifying distributions is often used as a way to measure the tendency of a distribution to move towards an ideal, uniform pattern. This approach requires data about the location of different sub-areas and a classification of density levels.The approach is as follows: an overarching area of different cities is scaled down to a field of points, and is then divided into Q equal squares. Each point corresponds with a city or town centre, meaning where the central part, or main business and commercial area of a city or town is located. The size of the squares is crucial: each square should contain at least one point, which means that each square should be larger than the average distance between the points. Next, each square's points are counted to get n levels of density Di, where n < Q. The amount of occurrences for each density level is reported and given the abbreviation mi. Following the above statements, it is discernible that 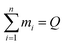 , and the required probabilities pi for the entropy definition can be calculated as: pi = mi/∑mi. The illustration of this concept, together with an explanatory case study is elaborated in the ESI.†
, and the required probabilities pi for the entropy definition can be calculated as: pi = mi/∑mi. The illustration of this concept, together with an explanatory case study is elaborated in the ESI.†
An important feature of this definition is the use of squares. By dividing the total area of the studied case into squares of identical sizes, the resulting entropy is still normalized to area, but the size of the sub-areas as a parameter is redundant. Additionally, since the definition works with levels, it is not the value of the level that is important, but the distribution of the levels. Meaning, an area with levels LMMM will have the same entropy as an area with levels LHHH, since level L has one occurrence and level M/H has three. This is different from the above definitions, where the value of the ‘level’ has an effect on the entropy value of the distribution, except for the case where the distribution is uniform.
3.5 Relative location and “flows” from one area i to an other area j
Another way of quantifying distributions is by looking at flows between areas. In this definition, a flow between two cities is defined as the product of the population numbers of both cities, divided by the distance between them. This equation measures the interaction between two cities, where interaction could be defined as either trade, human interaction, shared resources, etc. A high flow value between two cities means that there is a preferential flow between them, indicating potential to set up an interaction. Similarly, a low value indicates no preferential flows, meaning it would be unprofitable to set up an interaction. Once the flows between all cities are calculated, they are then fractioned by dividing each flow with the total flow of the area. This way, probabilities are obtained, which are then used to calculate entropies. This definition requires more data than the previous ones, namely population, location and distances between sub-areas/cities.The entropy formula for this definition consists of 2 parts: (1) a general entropy part and (2) an entropy aggregation part. The general entropy part quantifies the incoming and outgoing flow of a city in relation to the incoming and outgoing flow of all surrounding cities. In general, it is a measure for the total mobility of a city within an area. The entropy aggregation part can be used to calculate the entropy of an overarching area, like a province. The calculation exists of multiplying the obtained entropy with the total flow of the overarching area, essentially creating a weighted sum. This approach allows us to directly compare different overarching areas.
In order to illustrate this concept, several cases were developed: the cases comprise of 4 cities, and in each instance, the geometric design and the separation between the cities are altered. Starting with 5 alternative patterns and 5 population number options, there is a total of 25 possible choices, which are shown in Fig. 2. The entropy values resulting from these cases are also illustrated in Fig. 2. The values of flowij and the fractional values of the flow Pij are summarized in Table S1 in the ESI.†
 | ||
| Fig. 2 Illustrative overview of the 25 possible combinations for flow from one area i to an other area j. | ||
3.6 Percentage of land development
If data from a Geographic Information System (GIS) is present, one can use this to determine the amount of land development in an area. Land development is referred to as the man-made change of the environment in any number of ways. Often, it alludes to investments and initiatives that make land more accessible to people and that enhance the land's value. This entropy can only be calculated when a complete map of the area and a GIS system are available.The procedure is as follows: buffer zones are constructed around the studied town centres and roads. The width of the buffer zone is arbitrarily chosen depending on the chosen case study (for the particular work read by the authors, the buffer zone was 250 m). With help of a GIS system, a density value is obtained by using a function which determines the percentage of land developed pixels for each buffer zone. The GIS function calculates the percentage of land development by using the colours of the pixels. In doing so, a distribution pattern for land development densities of an area is obtained.
The resulting distribution is interesting for the measurement of urban sprawling, as well as for studying the development and growth of urban regions. Once land development densities are obtained, they can be converted into probabilities, which are obtained by dividing the developed area of a specific buffer, by the total developed area in all the studied buffers. The illustration of this concept, together with an explanatory case study is elaborated in the ESI.†
4. Geospatial entropy for resource management
In the previous section, we looked at the six most prevalent distribution types and corresponding entropy definitions in the field of geographic studies. When relating this to resource management, it is critical to consider the elements that are relevant, namely: collection quantities, transport distances and the possibilities to merge flows.4.1 Area
The distribution of resources within an area is heavily influenced by human activities. For instance, the establishment of infrastructure, urban development, or industrial zones may lead to the concentration of certain resources in specific areas. The concept of entropy can be applied to understand the distribution of resources or activities across different areas. In terms of area distribution, we see two options:In the first option, the probability is defined based on the division of a larger area (e.g. a province) into sub-areas (e.g. municipalities). The probability of landing in a specific sub-area when throwing a dart at the map of the larger area represents the distribution of resources or activities across the municipalities in the province.
When all municipalities have the same surface area, it implies a uniform distribution of resources or activities. The entropy of the reaches a maximum value here. This suggests that resources are evenly distributed across the region, and there is no particular concentration or preference. If there is only one municipality in the province, it implies that all the resources or activities are concentrated in a single location. The entropy reaches a minimum value. This indicates a lack of diversity and a highly centralized distribution.
By quantifying the entropy, you can measure the level of dispersion or concentration of resources or activities across different areas. Higher entropy indicates a more evenly distributed allocation, while lower entropy suggests a more concentrated distribution. Analysing the entropy of area distributions can provide valuable insights into where it makes sense to start a new activity, expand an existing activity, or mine resources.
In the second option, the probability is defined based on the specific activities or raw materials available in an area. For example, determining the probability of growing a certain produce in a region represents the distribution of agricultural activities.
When the area is uniformly distributed in terms of different activities or raw materials, it suggests a balanced allocation of resources, and the entropy reaches a maximum value here. This implies that various activities or raw materials have an equal presence across the region. If there is only one dominant activity or raw material, it indicates a highly specialized or concentrated distribution. As a result, the entropy reaches a minimum value. For instance, if all the area is allocated to growing a certain produce, it implies a lack of diversification in agricultural activities.
By calculating the entropy, we can assess the diversity or concentration of activities or resources across different areas. Higher entropy signifies a more diverse allocation, while lower entropy indicates a more focused or specialized distribution.
In both options, the concept of entropy provides a quantitative measure to understand the distribution patterns of resources, activities, or raw materials across different areas. It can be valuable for identifying regions with potential for new activities, expansion of existing activities, or resource mining, depending on the specific context and goals.
4.2 Population number
The spatial distribution of population plays a vital role in shaping the distribution patterns of resources. Areas with a higher concentration of population tend to have increased resource consumption due to factors such as residential activities, commercial operations, and industrial activities. Consequently, higher population areas often exhibit a scattered distribution of resources.The probability of a particular population number is determined by the scattering of the population across an area. The probability of randomly choosing a person from a specific sub-area over a larger area, represents the distribution of population.
A uniform population distribution is observed when all regions within an area have the same population size. In this case, the entropy reaches its maximum value. This suggests that the population is evenly spread across the entire area, without any specific concentration or preference for particular regions. On the other hand, if the entire population is concentrated in a single location, the entropy reaches its minimum value, namely 0. This indicates a lack of diversity and a highly centralized distribution of population.
By quantifying the entropy, we can assess the level of dispersion or concentration of population across different areas. A higher entropy value indicates a more evenly distributed population, while a lower entropy value suggests a more concentrated distribution. Measuring entropy provides valuable insights into the spatial patterns of population distribution. It helps inform decision-making processes related to resource allocation, urban planning, and policy development, allowing for targeted interventions that address disparities, promote equitable growth, and optimize resource utilization.
4.3 Population density
Population density distribution and resource distribution are closely linked as the spatial arrangement of population density within an area influences the availability, allocation, and utilization of resources. The distribution of population density can affect the generation and distribution of waste and recyclable materials.The entropy pattern for population density closely aligns with the distribution of area and population numbers. High entropy is observed when the population density pattern is uniform, meaning that the density is evenly distributed across the region. This uniformity can be achieved either by the population or the area size. For instance, a small area with a small population can exhibit the same density as a large area with a large population.
Conversely, low entropy is observed when the population density pattern is highly irregular. This can occur when there are extremely concentrated or diluted densities attributed to small populations in large areas or large populations in small areas, respectively. In such cases, the density distribution is uneven and exhibits a significant deviation from uniformity.
The concept of entropy in population density analysis helps us understand the level of variation and dispersion within a region. Higher entropy indicates a more uniform distribution of population density, while lower entropy suggests a more pronounced disparity in density patterns. Analysing population density entropies provides insights into the spatial distribution of population and its concentration within specific areas. This understanding can inform decision-making processes related to urban planning, resource allocation, and the development of policies aimed at addressing inequalities and optimizing resource utilization in different regions.
4.4 Population density levels
Population density distribution and resource distribution are closely linked as the spatial arrangement of population density within an area influences the availability, allocation, and utilization of resources. By incorporating density levels, the data points can be categorized into distinct levels, simplifying the classification into density categories and facilitating the analysis of resource-related consequences.The entropy pattern for population density levels closely mirrors that of population density. The only distinction lies in the introduction of levels to represent different ranges of population density. High entropy in population density levels is observed when the distribution of population density across the regions is relatively uniform, regardless of the specific density values. This indicates a balanced and even distribution of population density across the area, without significant concentration or disparity in density levels. Conversely, low entropy in population density levels occurs when the distribution of population density exhibits a significant skewness or disparity among different regions. This can manifest as highly concentrated or diluted population density levels, where certain areas have notably higher or lower densities compared to others.
The introduction of density levels provides a structured and systematic framework for analysing the relationship between population density and resource distribution. This classification enables us to identify distinct density ranges and examine their specific impacts on resource distribution in a more granular manner. By studying density thresholds or ranges, we can gain insights into how different levels of population concentration influence resource availability, access, and long-term sustainability.
By considering the specific density levels, decision-makers and planners can develop targeted strategies and policies to address the unique challenges and opportunities associated with each density category. This approach aids in optimizing resource allocation, promoting sustainable development, and ensuring equitable access to resources across regions with varying population densities.
4.5 Relative location and “flows” from one area i to an other area j
This definition is of particular interest for translation towards resource management, due to several reasons: on the one hand, this definition allows for a representation of the number of products or people present in assessed cities of a studied area. On the other hand, the distance between the cities is also quantified. The combination of these gives a measure of the potential towards exchange, which can be used as an output to objectively measure where the greatest potential lies for, e.g., a collection hub.The entropy definition is based on the fractional flow of the cities, which portrays the share of each city separately in the total mobility of the area. This mobility can be interpreted as mobility of people, but also as the mobility of goods, which is where the opportunity for resource management arises from. This mobility of goods can be translated to the localization of recycling plants and/or centralized collection hubs.
The entropy definition, translated to products and materials, quantifies the entropy of expected material flows. In other words, it is capable of expressing how concentrated or dispersed material flows are. This feature of the definition can aid in assessing future logistic problems, as described above, but can also aid in the assessment of new products. The definition is capable of assessing the energy impact connected to the spread of new products, which is also dependent on the market penetration. This assessment is namely achieved by a very generic prediction of the logistic efforts required to recollect them, which is exactly what this definition is capable of quantifying.
As already mentioned, the calculated flow between two cities says something about the interaction between these cities, with interaction possibly being general trade, population interaction, shared resources, etc. A high flow value means there is a lot of potential to set up an interaction between the cities, whilst a low value means there is little potential and it is not worth setting up an interaction. Based on this, it is then possible to compare cities to one another in terms of interaction potential (or interaction possibilities/opportunities).
In addition to being a representation of interaction potential, the flow values of cities also indicate where it would make the most sense to localise collection centres. Since this definition also takes distance into account, it can be used on its own as a valuable parameter for resource management, but it can also be used as a proxy for the required energy to bridge this distance. In general, if things are close to each other and there is a large potential, it would be interesting to merge the flows/potential of the analysed cities. If the cities are very apart in distance, and have a low interaction, then it would be more efficient to keep them separated. In terms of waste management, this definition can be used to decide where it makes sense to start clustering or whether it is more useful to treat waste together or separately.
In essence, this definition takes several crucial elements into account: on the one hand, the flow of a resource, where we wish to gather huge amounts at the same collecting sites. On the other hand, the flow's entropy. The ideal location for a collection centre would be the place where both the flow and the entropy is the highest. The flow should be high because you want to transport as many resources as possible to the same spot, either in large amounts or across short distances. In addition, a high entropy also indicates that the flow from all surrounding sites to the analysed area is (near) equal, implying that no preferential flows exist inside the zone. In most cases there will be a trade-off between high entropy and high flow, and the most optimal choice will essentially rely on distance versus quantity.
4.6 Percentage of land development
This method requires a GIS analysis of a map, which determines the amount of developed land in a predefined buffer zone around a town centre. This value of developed land can then be converted to a percentage of land development, by dividing the area of developed land, by the total area of the buffer. Since the same zone size is used to calculate the land development, the actual zone size of the studied areas will not affect the entropy value. This makes it possible to directly compare differently sized areas with each other, since only the buffer around the town centre is of importance.This definition is of particular interest for the collection of natural resources, since GIS data is available for most of them. In addition, GIS data is also available for e.g. the location of different companies and different manufacturing industries, which would prove very interesting for a localisation research question on for example a processing plant.
In the field of urban sprawling, this entropy value is used to examine whether land development is dispersed or compact. In general, the rule of thumb for land development in urban sprawling studies is the following: the density of land development decreases as the distance from roads or the town centre increases. Since the amount of land development can be directly linked to a compact or dispersed urban settlement, it can also be used as a proxy for determining the required energy values necessary to recollect the products and resources. Evidently, a compact settlement requires less collection energy than a dispersed settlement. In addition, it is a valuable tool to gauge the rationale to recollect resources or treat waste in either central or spatially distributed hubs, especially when researching natural resources such as lignocellulose biomass.
Similarly to the previous definitions, a high entropy is achieved when the land development across buffer zones evenly distributed, with a maximum value achieved when the distribution is uniform. A lower entropy is obtained when the land development across buffer zones is irregularly distributed, meaning some buffer zones are very developed, whilst others are not. A minimum possible entropy of 0 is obtained when the land development is concentrated in only 1 buffer zone.
5. Illustrative case study: location of collection centre for the recycling of mattresses
To enhance the comprehension of the various definitions, an illustrative case study is presented. The objective of this case study is to employ an entropy definition to gain insight in the optimal locations for recycling centres for mattresses. The use of three different entropy-based approaches is illustrated: (i) population number, (ii) floating catchment area (also based on population numbers) and (iii) flow-based entropies.5.1 A population number-based entropy approach
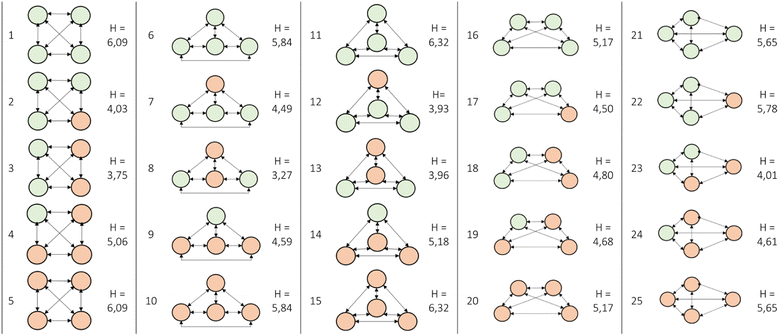
The province of Antwerp was divided into a grid of 25 km2 squares. The population within each square was then estimated by using data capturing the number of inhabitants per occupied address point. Next, within each square the number of inhabitants per address point were added up, giving an approximation of the number of inhabitants per square.The results of this approach are presented by Fig. 3: in total, the province of Antwerp has been divided into 145 squares. The colour of the square represents the population number: the deeper the shade of red, the higher the population.
 | ||
| Fig. 3 Overview of the grid overlay for the province of Antwerp. The deeper the shade of red, the higher the population. | ||
Entropies can be derived from the aforementioned data using a straightforward methodology: the procedure involves dividing the population count of each square by the total population of the province of Antwerp, thereby establishing population probabilities. These probabilities provide insight into the likelihood of randomly selecting an inhabitant from a specific square. Subsequently, the calculated probabilities can be transformed into entropies utilizing eqn (11). To ensure fairness in the analysis, squares situated on the province's border, which are frequently incomplete, are excluded. Once the entropies have been calculated, the squares with the highest and lowest entropy values were highlighted on the map. The results of these calculations are set out in Fig. 4.
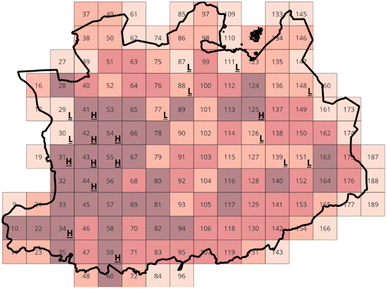 | ||
| Fig. 4 Overview of the highest and lowest population entropies for a grid of the province of Antwerp. | ||
The entropies reflect the level of dispersion or concentration of the population across different sub-regions within that area. It provides insights into the variations in population density. A high entropy indicates a greater likelihood of finding an inhabitant of the province within that square. In other words, if you were to randomly choose an inhabitant of Antwerp, there would be a higher probability that the selected individual resides in a square with a dense population and thus exhibits a high entropy. In contrast, a low entropy means there is a small chance of finding an inhaitant of the province within that square, since it is not densely populated.
The entropies of the squares can also be summarized over the region, where it would give an insight into the degree of heterogeneity or homogeneity across the whole province area. Once aggregated, a higher statistical entropy suggests a more evenly dispersed population across the sub-regions within the area. This indicates a relatively balanced distribution of population density, with no significant concentration or preference for specific sub-areas. Conversely, a lower statistical entropy in population distribution implies a higher degree of concentration or disparity in population density among the sub-regions within the area.
When considering the localization of a recycling centre, it is advantageous to place it in an area surrounded by high entropy squares. This is because squares with high entropy indicate a dense population, which correlates with a higher quantity of mattresses in need of recycling. By locating the recycling centre near such areas, it ensures that the centre is in close proximity to the highest concentration of waste, reducing transportation costs and minimizing the distance that waste needs to travel for recycling purposes.
Despite its simplicity, this methodology lacks crucial attributes necessary for the localization of a recycling centre, specifically the consideration of distance and interaction with the neighboring environment. Due to this inherent limitation, the existing methodology proves to be overly simplistic in its approach, failing to align with the desired outcome of this case study. Consequently, it becomes imperative to modify and enhance the methodology to facilitate a more comprehensive and in-depth analysis.
5.2 A floating catchment area-based entropy approach
The enhancement of the methodology can be achieved through the incorporation of Floating Catchment Analysis (FCA) into the framework. By introducing FCA, the analysis incorporates the crucial aspect of interaction with the neighboring environment. The revised methodology closely resembles its predecessor, with the exception lying in the definition of the probability calculations: instead of dividing the population of each square by the total population of the province, it is now divided by the total population of its catchment area. The catchment area of a square encompasses the square itself as well as the eight surrounding squares. For instance, in Fig. 3, the catchment area of square 90 is composed of squares 77, 78, 79, 89, 90, 91, 101, 102, and 103.In order to implement the FCA method, the preceding approach was once again employed for the province of Antwerp. However, a prerequisite for the successful application of FCA was to delimit the largest possible rectangle within the province. This step was necessary as the FCA method requires a defined rectangular or square shape for its successful application. Once the rectangle was outlined, a FCA analysis was performed for every square inside the rectangle. This analysis generated FCA population probabilities specific to each square. Utilizing eqn (11), these probabilities were further transformed into entropies. The entropies obtained were then visually represented in Fig. 5, with the lowest and highest entropy values being prominently depicted.
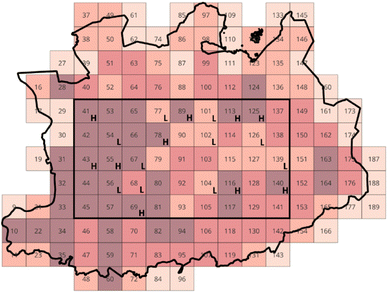 | ||
| Fig. 5 Overview of the highest and lowest population entropies for a grid of the province of Antwerp using the FCA method. | ||
The calculation of entropies based on a floating catchment area implies that their meaning is specific to that catchment area. Therefore, the value of the entropies provides information about how the population of a particular square relates to its immediate surrounding squares. A high entropy signifies that the population distribution is localized within that specific square. This means that the probability of finding a person from the catchment area is highest in this square, indicating a higher concentration of population in that area. On the other hand, a low entropy suggests the opposite scenario within the catchment area, where the population in the square is comparatively diluted compared to the rest of the squares. In this case, the chances of encountering a person are higher in the other squares of the catchment area.
When considering the placement of a recycling centre, it is logical to choose a square with a high entropy that is surrounded by other squares with high entropy. By doing so, the centre is strategically located in an area with a dense population that generates a significant amount of mattress waste. This facilitates the efficient collection and reprocessing of materials since the centre is situated in close proximity to the source of waste. By reducing travel distances and associated costs, concentrating the recycling efforts in a high entropy area offers logistical advantages and enhances the overall effectiveness of the recycling process.
This adjustment to the approach enables a more precise estimation of the population probabilities within the context of the specific catchment areas. However, despite the introduction of the floating catchment area, the methodology still fails to account for a fundamental aspect of localization problems: distance. Furthermore, while the floating catchment area permits a more granular estimation at a local level, it overlooks interactions and considerations on a larger scale. As a result, the current methodology remains insufficient in addressing the comprehensive requirements necessary for an effective analysis in this context.
5.3 A flow-based entropy approach
To address the limitations of the previous approach and account for both distance and interaction, definition 3.5 is introduced into our analysis. This definition incorporates flows between distinct areas, thereby providing a more holistic approach. The significance of the flow lies in its sensitivity to the distance between two given points, i and j. Given the paramount importance of accurately identifying the optimal location for a recycling/collection centre, distances are a crucial factor that must be taken into careful consideration.The updated methodology, featuring definition 3.5, is displayed for the geographical province of Antwerp, Belgium, which has 69 smaller municipalities and a total area of 2.9 km2. The sectioning of an area into different squares is no longer required, since the method of quantifying flows between areas takes the distance between geographical town or city centres into consideration. The geographical centre of an area is defined as the centre of gravity of the surface, or that point on which the surface of the area would balance if it were a plane of uniform thickness.
The approach is as follows: first, population statistics for the entire country of Belgium as well as the 69 smaller cities in the province of Antwerp are gathered from the federal government database.55 The total number of mattresses introduced into the Belgian market each year is also obtained, which corresponds to 930.000 matrasses each year. Since a distinction must be made between single and double mattresses, the number of mattresses is converted into ‘laying surfaces’, using data obtained from Valumat, which is the producer responsibility organisation for mattresses in Flanders. Each year, Valumat is required to report annual data on the purchase and disposal of mattresses to the regulatory authorities.
Laying surfaces are defined as the area of a mattress suited to accommodate one person, meaning a double mattress has two laying surfaces, and a single matrass has just one.
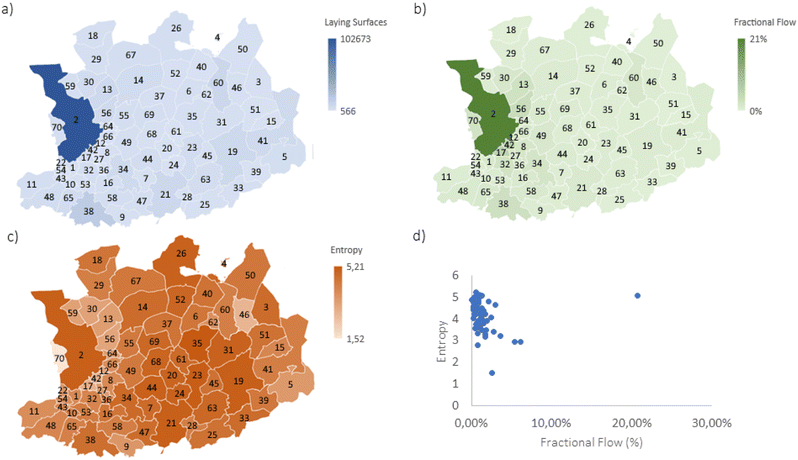
Next, to translate the obtained population data per city/town into mattresses data, the total population of Belgium is divided by the total amount of ‘laying surfaces’ sold each year, resulting in a scaling index of 5.061 (inhabitants. year/laying surfaces). This scaling index can then be used to translate the population of each town or city into a ‘laying surface’ value, visualised in Fig. 6a. To summarize, the distribution of mattresses is derived from population distribution data, and the population number is tailored to ‘laying surfaces' using Valumat data.
Once the amount of ‘laying surfaces’ is obtained, the flow between all the cities Flowij can be calculated using eqn (2) from Table 1. Instead of population numbers, ‘laying surfaces’ numbers are used to make the translation towards mattresses. Lastly, the fractional flow Fract. Flowij is calculated by dividing each flow with the total flow of the province (i.e. the sum of all the flows). The result of this translation from population to ‘laying surfaces’ per city/small town in the province of Antwerp is illustrated in Fig. 3b (as fractional flows) and Fig. 6 left in the ESI† (as normal flows). The flow probabilities PFlowij and Pi are then calculated (according to eqn (7) and (8) in Table 1), and the resulting entropy can be obtained by implementing the values in eqn (14). The overall result of these calculations, namely the entropy flow values per city/town is plotted in Fig. 3c, and Fig. 6 right in the ESI.† A detailed excel-file with the values of the Flowij and the fractional values of the flow Pij is provided with the ESI.†
In terms of collection placement, the following guidelines are suggested: on the one hand, areas with high flows are preferred, since this entails, that people, resources or even products, will move naturally towards that area. This makes these areas interesting locations for central collection centres, since this is already a naturally occurring mobility hub. An essential aspect to consider is that for this case study we assume equal thermodynamic efficiency among each transportation type, which is evidently not the case in reality. On the other hand, maximum entropy is also desired, so that the flow from different locations is equal in size. A maximum entropy means that the flows from other municipalities into the studied municipality are equal in size, meaning no preferential flow is present. We prefer this over a preferential flow (which would have a low entropy), because this would mean a municipality will have a higher potential interaction with a preferred other municipality, and therefore will have lower flows to the surrounding municipalities. For the case of a central processing location, a uniform flow pattern is preferred, since this entails the highest flows from all surrounding areas, and not just one. In theory, this point of maximum flow and entropy is the ideal point to place collection or sorting plants. However, in reality, the values will stray from this ideal point, and we will opt for the area closest to this (meaning highest flow and entropy).
To illustrate this with data from the case study, a graph (see Fig. 6d) is created with the entropy on one axis and the total flow of each region on the other. The area closest to the ideal point (the upper right hand corner), is chosen as the optimal location (in this case the city of Antwerp). The result of this analysis is shown in Fig. 6d.
To finalize this section, it is crucial to reiterate the primary objective of the study, which is to investigate and determine the optimal approach for determining the most suitable location for a recycling centre or waste collection facility. Through a process of experimentation and evaluation, it became evident that definition 3.5 best aligns with the study's objectives. This particular definition was chosen as it takes into account both neighbouring interactions and direct distances, two critical properties that were absent in the previously considered definitions. By adopting definition 3.5, the study aims to provide a comprehensive analysis that encompasses all relevant factors for effective decision-making regarding the placement of recycling centres or waste collection facilities. However, it is crucial to acknowledge that our assertion does not imply that the entropy of flows is universally regarded as the superior metric for localizing collection centres. Rather, it reflects our subjective opinion that, based on the study's specific objectives and considerations, the entropy of flows aligns most effectively with our research goals. It is important to recognize that, while the entropy of flows provides valuable insights into the dynamics and interactions within a given area, different metrics may be more appropriate or relevant depending on the specific context, and alternative viewpoints and approaches should be considered in the overall decision-making process. To provide a comprehensive overview of the various definitions and their capacity to address the research question, a summarized comparison has been compiled and presented in Table 2.
| Distribution type | Relevant research questions for resource management | Required data | Sufficiently useful to support decisions around the localisation of a value-added activity around resources? |
|---|---|---|---|
| Area (m2) | How is area spread throughout our society? | Size and location of sub-areas | No: area solely refers to areas and areas as a proxy for quantities. It is only beneficial if we have limited data and if area is proportionate to quantities. Nevertheless, this definition only applies to the distribution of amounts and not to distances or flows |
| Population number | How is population spread throughout our society? | Population and location of sub-areas | No: more realistic assessment when looking at resource quantities than area, but again, this definition only applies to the distribution of amounts and not to distances or flows |
| Population density | How is population density spread throughout our society? | Size and population of sub-areas | No: distribution is hard to interpret, and does not provide clear enough information to serve as a proxy |
| Population density levels | How is are population density levels spread throughout our society? | Location and either population or sub-area amounts | No: not very useful since values rely heavily on how the levels are defined. In doing so, you can inflate or diminish entropies depending on how you define your levels. From this point of view, it doesn't convey much, and it's not directly useful |
| Relative location and “flows” | How are flows between areas spread throughout our society? | Population, location and distance of sub-areas/cities | Yes: this definition takes several crucial elements into account, namely the flow of a resource, and the resource flow's entropy. This definition allows for the trade-off relationship between high entropy and high flow to be studied |
| Percentage of land development | How is land development spread throughout our society? | Complete map of the area and GIS system | Yes: GIS data is accessible for a wide range of resources, and for the location of various organizations, industrial sectors, and so on. This availability allows for the research questions such as the localisation of processing plants. Thus, both in terms of availability of natural resources and localisation research, it is a useful definition |
6. Discussion
6.1 Multi-objective optimization and decision making
Finding the optimal location of a site is a problem that has been studied in the field of logistics and supply chain management. Weber (1989) was the first to develop the notion of warehouse site selection by situating a warehouse such that the total distance traversed between the warehouse and the clients is minimized. Since then, numerous studies have been published on this subject.56–59The selection of a warehouse site from a set of alternatives is a multi-objective optimization and multi-criteria decision-making problem that includes both quantitative and qualitative decision variables. Most decisions about warehouse localisation are taken depending on 5 criteria: movement flexibility, average distance to suppliers, average distance to shops, stock holding capacity and unit price.60,61 Alternatively, the flow-based entropies and the flow calculations could serve as criteria (in the ideal case both maximum) for locating the optimal site location (e.g., warehouse or collection centre), hence reducing the number of objective functions from 5 to 2. As such the dimensionality and complexity of the multi-objective optimization problem and the multi-criteria decision making problem would be reduced.
6.2 Economies of scale
When choosing the location of a recycling centre, economies of scale are vital as they have a substantial impact on the centre's cost-effectiveness and profitability. By strategically situating a recycling centre near a large population or a high concentration of resources, it can benefit from economies of scale through greater volume of materials processed. Moreover, EoS can have a substantial influence on the number of centres: in general, the average cost per unit of output decreases as production increases, owing to a variety of factors. As a result, businesses must carefully assess the ideal size and scale of their operations while minimizing excessive expenditures. Depending on the available budget, this could translate into several smaller centres, rather than 1 big centre, or vice versa.By considering economies of scale when locating recycling centres, decision-makers can estimate the optimal amount of centres, as well as ensure the centre's financial viability, cost-effectiveness, and profitability, while also maximizing the volume of materials processed and contributing to the circular economy.
6.3 Geographical variability and contextual considerations
The definitions discussed in Section 3 apply universally to any geographical variability (e.g., urban versus rural areas). However, their interpretation should be specific to the geographical context of the studied area. The translation from entropy to energy requirements involves geographical and infrastructural considerations such as terrain type, topography, transportation nodes and infrastructure. For example, even though in the case study Antwerp comes out as the ideal location, the impracticality of siting a sorting plant in Antwerp's bustling centre highlights the significance of considering contextual factors. Placing a sorting plant in a city centre poses challenges like space constraints, noise, pollution, and traffic issues. This underscores the importance of contextual awareness in our analysis across all geographical areas.6.4 Adaptability & versatility
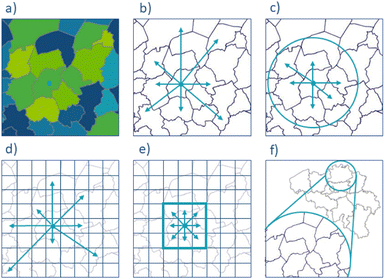
An important aspect to highlight is the versatility and adaptability of the proposed method. In the ideal case, resource and geographical context-specific data are available through Geographical Information Systems (GIS). However, this is often not (yet) the case, requiring assumptions or simplified versions of the methodology that are less data-intensive. In fact, the mattresses case study is such a case in which already two key simplifying assumptions were made: (i) population distribution data were available at the level of postal codes, not at the level of a fine spatial grid and (ii) population distribution data were extrapolated to the geospatial distribution of mattresses using a conversion factor that was obtained from communication with VALUMAT. Finer and coarser geospatial grids could be implemented in the methodology, aggregating data at different levels depending on the case that is evaluated, available information/data and the decisions that need to be taken. While, for instance, deciding where to locate a refining facility in a developing country, and screening feasibility of resource recovery for different types of resources (e.g., biomass, steel scrap) and geographical context (e.g., woodlands, desert), would be more complicated using traditional methods with the limited (or even inexistent) infrastructure and data, the proposed geospatial entropy method allows to on-the-fly support this type of decisions.Several simplified approaches, which cater to different levels of complexity and data resolution, are illustrated in Fig. 7. The most straightforward method involves assigning quantities to municipalities based on the highest concentration (a). Another simplified method involves an analysis with reduced data resolution, focusing on the distribution of items relative to a central point, typically a municipality centre. In addition entropy is only calculated based on the quantity of mattresses, removing the need for distances (b). A more nuanced approach introduces a maximum collection distance of 200 km, delineating catchment areas around each municipality centre. Within each province, the catchment areas are assessed to determine the number of mattresses present. This allows for the identification of maximum entropy and flow values within each catchment area, revealing the areas where mattress concentration and distribution are most pronounced. Since a catchment area is introduced, the resolution of data is lowered and less data and analysis is required (c). An alternative approach would be to reduce the geographical area to a square grid, thus reducing the complexity of distance data, since all distances are easily calculated mathematically (d). Another, even simpler approach considers only the 8 neighbouring municipalities of this grid and the centre municipality, narrowing the approach down to only 9 municipalities. This approach inherently acknowledges the disadvantage of municipalities without neighbours (e). A last approach could be to tackle the analysis with a multiresolution approach. One could first analyse the area on a higher aggregation level and reduce the resolution of the approach as you go to lower aggregation levels. This way, the required amount of data and data processing effort are reduced (f).
6.5 Future work
A next step would be to conduct a thorough analysis of Belgium's mattresses waste stream. This would entail expanding this analysis to the whole country of Belgium, as well as bridging geospatial and product entropy levels together, since mattresses differ significantly in terms of types and their material composition. In addition, future work on the topic would also entail the inclusion of multi-objective optimisation problem formulations, multi-criteria decision making methods and the development of algorithms to support decisions based on flow-based entropy and flow values as objective functions. This integration is contingent on GIS compatibility, requiring alignment with platforms like QGIS or Python commonly used in spatial analysis, and data alignment to ensure coherence with existing resource management datasets. Geospatial entropy values can serve as objective functions in optimization algorithms, prompting the need for careful integration into existing frameworks. Nonetheless, a validation against state-of-the-art optimization problems in logistics and supply chain management would be required. The exact methodologies and applications and the evaluation of their efficiency and accuracy compared with traditional approaches require further research through dedicated studies. The inclusion of different constraints, such as the capacities of collection centres or the area capacity for locating a collection centre, would enhance the model's practicality and robustness in real-world resource management scenarios.7. Conclusions
In this study, the primary goal was to provide perspective on the current landscape of geospatial entropy definitions and their potential applications to support the evaluation of and resource management and circular economy strategies. This study resulted in a nuanced understanding of how geospatial entropy metrics can be used to quantify geographical distributions for this purpose, exemplified on conceptual examples and a more specific case study. It is illustrated that geospatial entropy calculations require little data and expertise, contrary to the current alternative methods, which require data, methods, and expertise from different fields. Moreover, the integration of geospatial entropy calculations with existing frameworks and methods, its adaptability, and versatility have been discussed.For the specific case of localising recycling centres, our research points to flow-based statistical entropy as the most promising method. The case study focusing on Antwerp demonstrated that the ideal location for such centres is where both entropy and flow are maximised. However, the impracticality of localising a recycling centre in Antwerp underscores the importance of considering the geographical variability of a region in interpreting results and making informed decisions.
We recognise geospatial entropy as a valuable proxy for estimating the energy requirements associated with material recollection and transport. Beyond this application, our method can answer additional research questions, such as the determination of the most effective resource collection methods and the optimal localisation of waste processing plants. The flexibility of the employed methodology makes it an elegant tool for addressing a spectrum of research questions within the broader field of resource management.
Nomenclature
List of Symbols
| X i /i | statistical event, for this specific paper a city or town |
| H | Statistical entropy (or Shannon entropy) |
| N | Amount of statistical events |
| p i | Probability of event i |
| Areai | Area of event i |
| Popi | Population of event i |
| m i | Number of occurrences for each level of density i |
| p pop i | Population number for event i |
| d ij | Distance between events i and j (in km) |
| Fract. Flowij | Flow between events i and j, normalised to sum = 1 for all flows |
| DENi | Density of event i |
| Q | Number of squares |
| D i | Level of density |
List of abbreviations
| CE | Circular economy |
| EU | European Union |
| UN | United Nations |
| TEA | Techno-economic analysis |
| LCA | Life cycle assessment |
| SEA | Statistical entropy analysis |
| MSEA | Multilevel statistical entropy analysis |
| FCA | Floating catchment area |
| GIS | Geograhphical information system |
| PWSS | Public warehouses selection support |
| QFD | Quality function deployment |
| AHP | Analytic hierarchy process |
| ABM | Agent based model |
| EoS | Economies of scale |
Author contributions
Cristina Moyaert: writing – original draft, writing – review & editing, conceptualization, methodology, software, data curation, formal analysis, validation, visualization. Philippe Nimmegeers: writing – original draft, writing – review & editing, conceptualization, methodology, software, data curation, formal analysis, validation, visualization, supervision. Bilal Mellouk: conceptualization, methodology, formal analysis. Dimitri Voordeckers: writing – review & editing, conceptualization, methodology, formal analysis. Paul De Meulenaere: writing – review & editing, conceptualization, methodology. Pieter Billen: writing – review & editing, conceptualization, validation, resources, supervision. All have read and agreed to the published version of the manuscript.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationship that could have appeared to influence the work reported in this paper.Acknowledgements
Philippe Nimmegeers holds a FWO senior postdoctoral fellowship (grant number: 1215523N) granted by FWO Vlaanderen/Research Foundation Flanders. This research is also part of the RESTEP FWO junior fundamental research project funded by the Research Foundation − Flanders − Grant No. G027122N. Support was also received from the Special Research Fund of the University of Antwerp (BOF) for the BOF-KP RePUSE (grant number: 46224).Notes and references
- J. Midgley, Growth, redistribution, and welfare: Toward social investment, Soc. Serv. Rev., 1999, 73, 3–21 CrossRef.
- J. McCollough, Consumer discount rates and the decision to repair or replace a durable product: a sustainable consumption issue, J. Econ. Issues, 2010, 44, 183–204 CrossRef.
- K. A. Scott and S. T. Weaver, To repair or not to repair: What is the motivation, J. Res. Consum., 2014, 26, 43–44 Search PubMed.
- K. L. McDermott, Plastic Pollution and the Global Throwaway Culture: Environmental Injustices of Single-Use Plastic, 2016 Search PubMed.
- N. Whiteley, Toward a throw-away culture. Consumerism,'style obsolescence'and cultural theory in the 1950s and 1960s, Oxf. Art J., 1987, 10, 3–27 CrossRef.
- How We Created A Throwaway Culture, https://www.sustainabledesign.studio/resources/blog-post-title-three-5r852 Search PubMed.
- G. George, S. J. Schillebeeckx and T. L. Liak, The Management of Natural Resources: an Overview and Research Agenda, Managing Natural Resources, 2018 Search PubMed.
- R. Costanza, Three general policies to achieve sustainability, Investing in Natural Capital: the Ecological Economics Approach to Sustainability, 1994, pp. 392–407 Search PubMed.
- I. Figueira, A. R. Domingues, S. Caeiro, M. Painho, P. Antunes, R. Santos, N. Videira, R. M. Walker, D. Huisingh and T. B. Ramos, Sustainability policies and practices in public sector organisations: The case of the Portuguese Central Public Administration, J. Cleaner Prod., 2018, 202, 616–630 CrossRef.
- J. Zuo, G. Zillante, L. Wilson, K. Davidson and S. Pullen, Sustainability policy of construction contractors: a review, Renewable Sustainable Energy Rev., 2012, 16, 3910–3916 CrossRef.
- K. L. Larson, D. D. White, P. Gober, S. Harlan and A. Wutich, Divergent perspectives on water resource sustainability in a public–policy–science context, Environ. Sci. Policy, 2009, 12, 1012–1023 CrossRef.
- F. Simon, EU to introduce targets for raw materials self-sufficiency, 2022 Search PubMed.
- U. SDG, Sustainable development goals, The Energy Progress Report. Tracking SDG, 2019, vol. 7 Search PubMed.
- S. J. Callan and J. M. Thomas, Economies of scale and scope: A cost analysis of municipal solid waste services, Land Econ., 2001, 77, 548–560 CrossRef.
- P. Llanquileo-Melgarejo and M. Molinos-Senante, Evaluation of economies of scale in eco-efficiency of municipal waste management: An empirical approach for Chile, Environ. Sci. Pollut. Res., 2021, 28, 28337–28348 CrossRef CAS PubMed.
- X. Wu, G. H. Huang, L. Liu and J. Li, An interval nonlinear program for the planning of waste management systems with economies-of-scale effects—a case study for the region of Hamilton, Ontario, Canada, Eur. J. Oper. Res., 2006, 171, 349–372 CrossRef.
- P. Carvalho, R. C. Marques and B. Dollery, Is bigger better? An empirical analysis of waste management in New South Wales, Waste Manage., 2015, 39, 277–286 CrossRef PubMed.
- W. Cheng, Y. Zhang and P. Wang, Effect of spatial distribution and number of raw material collection locations on the transportation costs of biomass thermal power plants, Sustain. Cities Soc., 2020, 55, 102040 CrossRef.
- B. Sahin, H. Yilmaz, Y. Ust, A. F. Guneri and B. Gulsun, An approach for analysing transportation costs and a case study, Eur. J. Oper. Res., 2009, 193, 1–11 CrossRef.
- S. Or, T. Piernicki and A. Wiegel, The quick e-Guide to Transportation Modeling: Mastering sustainability, safety, and efficiency in mobility For mobility and transport planners, 2022 Search PubMed.
- C. Roithner, O. Cencic and H. Rechberger, Product design and recyclability: How statistical entropy can form a bridge between these concepts-A case study of a smartphone, J. Cleaner Prod., 2022, 331, 129971 CrossRef.
- Circular Economy: critics and challenges, https://www.circular.academy/circular-economy-critics-and-challenges/ Search PubMed.
- A. Bahraini, The 5 Common Obstacles in Implementing Circular Economy, 2021 Search PubMed.
- T. G. Gutowski, S. Sahni, J. M. Allwood, M. F. Ashby and E. Worrell, The energy required to produce materials: constraints on energy-intensity improvements, parameters of demand, Philos. Trans. Royal Soc. A, 2013, 371, 20120003 CrossRef PubMed.
- A. Lesne, Shannon entropy: a rigorous notion at the crossroads between probability, information theory, dynamical systems and statistical physics, Math. Struct. Comput. Sci., 2014, 24, e240311 CrossRef.
- C. E. Shannon, A mathematical theory of communication, The Bell system technical journal, 1948, 27, 379–423 CrossRef.
- Y. Wu, Y. Zhou, G. Saveriades, S. Agaian, J. P. Noonan and P. Natarajan, Local Shannon entropy measure with statistical tests for image randomness, Inf. Sci., 2013, 222, 323–342 CrossRef.
- M. Song, Q. Zhu, J. Peng and E. D. S. Gonzalez, Improving the evaluation of cross efficiencies: A method based on Shannon entropy weight, Comput. Ind. Eng., 2017, 112, 99–106 CrossRef.
- V. Eskov, V. Eskov, Y. V. Vochmina, D. Gorbunov and L. Ilyashenko, Shannon entropy in the research on stationary regimes and the evolution of complexity, Mosc. Univ. Phys. Bull., 2017, 72, 309–317 CrossRef.
- J. Schug, W.-P. Schuller, C. Kappen, J. M. Salbaum, M. Bucan and C. J. Stoeckert, Promoter features related to tissue specificity as measured by Shannon entropy, Genome Biol., 2005, 6, 1–24 CrossRef PubMed.
- A. Parchomenko, D. Nelen, J. Gillabel, K. C. Vrancken and H. Rechberger, Evaluation of the resource effectiveness of circular economy strategies through multilevel Statistical Entropy Analysis, Resour. Conserv. Recycl., 2020, 161, 104925 CrossRef.
- P. Cabral, G. Augusto, M. Tewolde and Y. Araya, Entropy in urban systems, Entropy, 2013, 15, 5223–5236 CrossRef.
- P. Nimmegeers, A. Parchomenko, P. De Meulenaere, D. R. D’hooge, P. H. Van Steenberge, H. Rechberger and P. Billen, Extending multilevel statistical entropy analysis towards plastic recyclability prediction, Sustainability, 2021, 13, 3553 CrossRef CAS.
- P. Nimmegeers and P. Billen, Quantifying the separation complexity of mixed plastic waste streams with statistical entropy: a plastic packaging waste case study in Belgium, ACS Sustain. Chem. Eng., 2021, 9, 9813–9822 CrossRef CAS.
- C. Moyaert, Y. Fishel, L. Van Nueten, O. Cencic, H. Rechberger, P. Billen and P. Nimmegeers, Using Recyclable Materials Does Not Necessarily Lead to Recyclable Products: A Statistical Entropy-Based Recyclability Assessment of Deli Packaging, ACS Sustain. Chem. Eng., 2022, 10, 11719–11725 CrossRef CAS.
- L. Liu, Z. Peng, H. Wu, H. Jiao, Y. Yu and J. Zhao, Fast identification of urban sprawl based on K-means clustering with population density and local spatial entropy, Sustainability, 2018, 10, 2683 CrossRef.
- A. G.-O. Yeh and X. Li, Measurement and monitoring of urban sprawl in a rapidly growing region using entropy, Photogramm. Eng. Remote Sens., 2001, 67, 83–90 Search PubMed.
- M. Batty, Entropy in spatial aggregation, Geogr. Anal., 1976, 8, 1–21 CrossRef.
- G. Chapman, The application of information theory to the analysis of population distributions in space, Econ. Geogr., 1970, 46, 317–331 CrossRef.
- A. Namdari and Z. Li, A review of entropy measures for uncertainty quantification of stochastic processes, Adv. Mech. Eng., 2019, 11, 1687814019857350 CrossRef.
- Z. He, Y. Cai and Q. Qian, A study of wavelet entropy theory and its application in power system, 2004 International Conference on Intelligent Mechatronics and Automation, 2004. Proceedings., 2004, pp. 847–851 Search PubMed.
- P. M. Robinson, Consistent nonparametric entropy-based testing, Rev. Econ. Stud., 1991, 58, 437–453 CrossRef.
- A. Sabatini, Analysis of postural sway using entropy measures of signal complexity, Med. Biol. Eng. Comput., 2000, 38, 617–624 CrossRef CAS PubMed.
- S. M. Ross, J. J. Kelly, R. J. Sullivan, W. J. Perry, D. Mercer, R. M. Davis, T. D. Washburn, E. V. Sager, J. B. Boyce and V. L. Bristow, Stochastic Processes, Wiley, New York, 1996 Search PubMed.
- L. A. Fleisher, S. M. Pincus and S. H. Rosenbaum, Approximate entropy of heart rate as a correlate of postoperative ventricular dysfunction, Anesthesiology, 1993, 78, 683–692 CrossRef CAS PubMed.
- G. Dawes, M. Moulden, O. Sheil and C. Redman, Approximate entropy, a statistic of regularity, applied to fetal heart rate data before and during labor, J. Obstet. Gynecol., 1992, 80, 763–768 CAS.
- H. Rechberger and P. H. Brunner, A new, entropy based method to support waste and resource management decisions, Environ. Sci. Technol., 2002, 36, 809–816 CrossRef CAS PubMed.
- J. Tanzer and H. Rechberger, Complex system, simple indicators: Evaluation of circularity and statistical entropy as indicators of sustainability in Austrian nutrient management, Resour. Conserv. Recycl., 2020, 162, 104961 CrossRef.
- M. Skelton, S. Huysveld, S. De Meester, K. M. Van Geem and J. Dewulf, Statistical entropy of resources using a categorization tree for material enumeration: Framework development and application to a plastic packaging case study, Resour. Conserv. Recycl., 2022, 181, 106259 CrossRef.
- O. N. Bjørnstad, R. A. Ims and X. Lambin, Spatial population dynamics: analyzing patterns and processes of population synchrony, Trends Ecol. Evol., 1999, 14, 427–432 CrossRef PubMed.
- R. K. Semple and R. Golledge, An analysis of entropy changes in a settlement pattern over time, Econ. Geogr., 1970, 46, 157–160 CrossRef.
- K. E. Brassel and D. Reif, A procedure to generate Thiessen polygons, Geogr. Anal., 1979, 11, 289–303 CrossRef.
- H. J. Miller, Tobler's first law and spatial analysis, Ann. Am. Assoc. Geogr., 2004, 94, 284–289 CrossRef.
- M. Marsh and P. S. Alagona, AP Human Geography 2008, Barron's Educational Series, 2008, pp. 91–92 Search PubMed.
- Bevolkingscijfers op 1 januari, 2020.
- F. Y. Partovi, An analytic model for locating facilities strategically, Omega, 2006, 34, 41–55 CrossRef.
- G. Colson and F. Dorigo, A public warehouses selection support system, Eur. J. Oper. Res., 2004, 153, 332–349 CrossRef.
- M. Vlachopoulou, G. Silleos and V. Manthou, Geographic information systems in warehouse site selection decisions, Int. J. Prod. Econ., 2001, 71, 205–212 CrossRef.
- G. H. Tzeng and Y. W. Chen, The optimal location of airport fire stations: a fuzzy multi-objective programming and revised genetic algorithm approach, Transp. Plan. Technol., 1999, 23, 37–55 CrossRef.
- T. Demirel, N. Ç. Demirel and C. Kahraman, Multi-criteria warehouse location selection using Choquet integral, Expert Syst. Appl., 2010, 37, 3943–3952 CrossRef.
- T. Özcan, N. Çelebi and Ş. Esnaf, Comparative analysis of multi-criteria decision making methodologies and implementation of a warehouse location selection problem, Expert Syst. Appl., 2011, 38, 9773–9779 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3va00166k |
| This journal is © The Royal Society of Chemistry 2024 |