Open Access Article
Open Access ArticleIndustrial biomass waste as an economical, potential adsorbent for removing the Bismarck Brown R dye and zinc metal ions from effluents†
Sivamani
Sivalingam
 *a and
Sowmiya
A.
b
*a and
Sowmiya
A.
b
aDepartment of Chemical Engineering, Rajalakshmi Engineering College, Thandalam, Tamilnadu 602105, India. E-mail: sivamchem@gmail.com; sivamani.s@rajalakshmi.edu.in
bDepartment of Chemical Engineering, Sriram Engineering College, Thiruvallur, Tamilnadu 602024, India
First published on 26th March 2024
Abstract
In this research, activated carbon (AC) was prepared from date seed (DS) biomass using a chemical activation method for the removal of the Bismarck Brown R (BBR) dye and zinc metal ions from water. As-prepared AC was characterized using thermogravimetric analysis (TGA), scanning electron microscopy (SEM), and Brunauer–Emmett–Teller (BET) analysis for understanding the porous carbon surface and pore structure, which are essential properties for removing organic and inorganic pollutants. DSs are complex and were selected to prepare AC as they can yield hard activated carbon and perform better in packed-bed and fluidized-bed adsorption columns. AC samples were prepared at different soaking temperatures, specifically at 45 °C, 55 °C, and 65 °C, and subsequently tested for the removal of both the BBR dye and Zn ions. Various parameters were studied to complete the batch adsorption process, including solution pH, initial concentration (BBR: 100–500 mg L−1; Zn ions: 10–50 mg L−1), contact time (0–240 min), and temperature (30–60 °C). The maximum monolayer adsorption capacity for BBR and Zn metal ions were found to be 192.31 mg g−1 and 15.55 mg g−1, respectively. The data was most accurately described by the pseudo-second-order and Elovich kinetics models. Analysis using the particle diffusion model indicated that both film-diffusion and pore-diffusion mechanisms governed adsorption. Thermodynamic assessments revealed the endothermic behavior of BBR dye adsorption and the exothermic behavior of Zn metal ion adsorption.
Environmental significanceThe rapid expansion of industry presents environmental degradation as a critical global concern. All living organisms face health risks owing to the widespread issue of water pollution, which has become an urgent global challenge today. Substantially, industries such as textile, electroplating, mining, pharmaceutical, and chemical industries are discharging wastewater containing organic and inorganic pollutants. The frequent detection of these persistent and harmful dyes and excess heavy metals in wastewater discharges have raised worldwide concern about their potential long-term consequences on aquatic life and human well-being and their adverse impact on the broader ecosystem. Date seeds, often overlooked and considered waste in the date fruit industry, have been recognized as a valuable resource in the pursuit of sustainability. Their utilization reduces agricultural waste and offers a unique advantage for yielding hard-type activated carbon, which is ideally suited for adsorption applications. Removing the Bismarck Brown R dye and zinc metal ions from wastewater represents a significant research area due to their environmental, health, and regulatory aspects, particularly ecosystem health and water quality. The Bismarck Brown R dye and zinc metal ions can harm aquatic ecosystems deeply. Moreover, these pollutants can disrupt the balance of aquatic life, affecting various species' survival and reproductive abilities. Removing these pollutants would improve the quality of water bodies, making them safer for aquatic organisms and preserving the biodiversity of natural ecosystems. Eliminating these pollutants from wastewater would also help prevent bioaccumulation and the transfer of toxins through the food chain. Proper wastewater treatment can safeguard worker health. Recovering these metals through appropriate treatment processes supports resource efficiency and circular economy principles. Here highlighing the potential of agricultural byproducts, such as date seeds, in contributing to sustainable wastewater treatment solutions. As we pursue sustainability, innovative approaches such as date seed-based activated carbon showcase the power of nature-inspired solutions to safeguard our planet's precious water resources. The adsorption of these hazardous compounds by activated carbon presents a promising approach for effectively eliminating dyes and toxic metal contaminants from wastewater, minimizing their release into natural water bodies and supporting sustainable development goals. |
1. Introduction
Wastewater is generated from diverse sources and can directly affect the environment and living microorganisms. For instance, textile industries generate highly colored wastewater containing organic and inorganic pollutants and removing dyes from these industrial effluents is essential since they pollute the environment.1,2 Discharging highly colored wastewater into the ecosystem can cause environmental problems, such as aesthetic pollution (even if a tiny amount of dye is apparent) and harm to aquatic life. Wastewater generated by textile and tanning industries contains many exhausted dyes and pigments. It has been estimated that about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 dyes and pigments are produced and about 7 × 105 tons are used in different industries, such as textile, rubber, paper, and cosmetic industries. Among these various industries, the textile industry uses the most dyes.3,4
000 dyes and pigments are produced and about 7 × 105 tons are used in different industries, such as textile, rubber, paper, and cosmetic industries. Among these various industries, the textile industry uses the most dyes.3,4
Bismarck Brown R (BBR) is a cationic basic diazo dye commonly known as Basic Brown 4. It is used in coloring paper, pulp, wool, leather, and other materials. Both the short-term and prolonged contact of the dye with the eyes and skin can cause severe irritation and redness at the contact site.5,6 Upon ingestion, it can cause gastrointestinal irritation with nausea, vomiting, diarrhea, soreness, and redness of the mouth and throat, while its inhalation can irritate the throat and cause a feeling of tightness in the chest and even coughing and wheezing. It is also carcinogenic to humans and aquatic organisms.7,8 It is therefore considered necessary to develop an easy, efficient, and economical process for the removal of this hazardous dye.
Zinc is widely used in many industries, such as galvanization, paint, battery, smelting, fertilizer, pesticide, fossil fuel combustion, pigment, and polymer stabilizer industries, and the wastewater from these industries is polluted with large quantities of zinc.8,9 The World Health Organization (WHO) recommends a maximum acceptable concentration of zinc of 3 mg L−1 in drinking water, as mentioned in the WHO's Guidelines for Drinking-water Quality set up in Geneva, 1993). Therefore, removing the BBR dye and Zn metals from wastewater is imperative. There are various methods available for the removal of heavy metals such as Zn and dyes such as BBR from aqueous solutions, including chemical precipitation, oxidation/reduction, electrochemical treatment, evaporative recovery, filtration, ion exchange, and membrane technologies, which may sometimes be ineffective or cost-expensive, especially when the metal ion concentrations in solution are in the range of 1–100 mg L−1.10–12
Adsorption is often a more promising method than other water treatment techniques.11,13–15 In the past few years, scientists have endeavored to develop waste materials as potential adsorbents for the removal of different types of pollutants from wastewater, and indeed many adsorbents have been employed for wastewater treatment.11,12,16,17 Activated carbons are known to be very effective adsorbents due to their highly developed porosity, large surface area, variable characteristics of surface chemistry, and high degree of surface reactivity.4,15 Activated carbon (AC) is a common term for carbon-based materials with well-developed internal pore structures. AC is produced from various carbonaceous-rich materials, such as wood, coal, lignite, and coconut shells.18,19 The high surface area, large porosity, well-developed internal pore structure consisting of micro-, meso-, and macropores, and a broad spectrum of functional groups present on the surface of AC make it a versatile material with numerous applications in the environmental field.20 The production of activated carbon from carbonaceous source materials can be achieved by physical reactivation and chemical activation methods.21–23 Activated carbon is used in many areas, including air purification, gold purification, metal extraction, water purification, medicine, sewage treatment, air filters in gas masks and respirators, filters in compressed air, and metal finishing fields. This has led to increasing research interest in producing activated carbon from renewable and cheaper precursors.11,24
Date seeds (DSs) are often used to prepare activated carbon since they are complex in nature.25,26 When the activated carbons are softer, they might break down into tiny particles that are unsuitable for packed-bed and fluidized-bed adsorption processes.19,27 For instance, when small particles are used in a packed bed: (1) the available pores will decrease in continuous fluid flow, (2) channeling may take place, or (3) the fluid path may be blocked, increasing the pressure drop.25 These can decrease the contact between the adsorbent and adsorbate, resulting in poor adsorption.28,29 In fluidized-bed adsorption, entrainment of the particles may occur, which would result in the loss of adsorbate particles. Hence, the main objective of the present study was to produce activated carbon from hard materials, like DSs, by a chemical activation method by changing the activation process conditions. As-prepared activated carbon samples were analyzed with techniques like TGA, SEM, and BET, and also used to remove Bismarck Brown R (BBR) dye and zinc ions from water. Several key aspects contribute to the uniqueness of this research, including the utilization of date seed biomass, the use of comprehensive characterization techniques, adsorption process optimization, and the incorporation of isotherm and kinetic and thermodynamic analyses.
2. Raw materials and characterization
The materials and reagents used in this study were purified for use. The raw material selection, procedure for preparing activated carbon, characterization methods for the synthesized material, preparation of adsorbate solution, and batch adsorption experiments are also explained.2.1. Reagents
The required reagents phosphoric acid, Bismarck Brown R dye, potassium iodate, potassium iodide, boric acid, and methanol were supplied by Central Drug House (P) Ltd, India. Iodine was supplied by Rankem India Ltd. Hydrochloric acid was obtained from MERCK Chemicals, India. Sodium thiosulphate, soluble starch, and sodium hydroxide were supplied by SRL Chem (P) Ltd, India. Zinc sulfate and zincon were provided by Sisco Research Laboratories (P) Ltd. All the reagents used for analysis were of analytical grade, and distilled water was used for preparing all the adsorbate solutions. The dye was calibrated by visible spectrophotometry to determine the relationship between the absorbance and concentration for the BBR dye samples obtained after the adsorption experiments. The maximum wavelength of BBR dye was 468 nm. First, 1000 mg L−1 stock solution was prepared by dissolving 1.0 g of the dye in 1000 mL of distilled water. Desired samples of different concentrations were prepared by dilution of the stock solution and then used for the adsorption experiments. The concentrations of Zn were found by forming a complex with zincon and observed at 620 nm by visible spectrophotometry. Also, 1000 mg L−1 stock solution was prepared by dissolving 4.4 g of ZnSo4·7H20 in 1000 mL of distilled water. Samples of different concentrations were prepared by dilution of the stock solution, and the absorbance of the corresponding concentrations were noted.2.2. Selection of the biomass for preparation of the activated carbon
As softer activated carbons might break into tiny particles that would be unsuitable for packed-bed and fluidized-bed adsorption processes, activated carbon that is harder in nature was aimed for as a better candidate. In this study, date seeds (DSs) were used to produce activated carbon because of their hard nature. The chemical activation method was also applied here, using an acid (phosphoric acid) to produce activated carbon by a different methodology. A textile dye (Bismarck Brown R), an organic pollutant, and metal ion (zinc), an inorganic pollutant, were selected for the removal experiments. Since date seeds are very hard, the activation process required a high temperature for carbonization (around 850 °C).Date seeds were first collected, washed, and dried under sunlight. These were then broken into an average particle size of 5 mm and heated in a hot-air oven until constant weight was reached. The weight ratio of acid to seeds varied as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3
1, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 4
1, and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the samples were named as 1
1 and the samples were named as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 AC, 2
1 AC, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 AC, 3
1 AC, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 AC, and 4
1 AC, and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 AC, respectively. The seeds were soaked in phosphoric acid at 55 °C for 4 h and at room temperature for 20 h. To find the optimum temperature for soaking at which the development of pores was the best, the soaking temperature range was varied between 45 °C and 65 °C. The activated carbons produced under different soaking temperatures of 45 °C, 55 °C, and 65 °C were named AC 45, AC 55, and AC 65, respectively. Then, the seeds were carbonized without draining the acid at 500 °C for 1 h. The obtained products were washed with hot distilled water to pH 6 to 7.
1 AC, respectively. The seeds were soaked in phosphoric acid at 55 °C for 4 h and at room temperature for 20 h. To find the optimum temperature for soaking at which the development of pores was the best, the soaking temperature range was varied between 45 °C and 65 °C. The activated carbons produced under different soaking temperatures of 45 °C, 55 °C, and 65 °C were named AC 45, AC 55, and AC 65, respectively. Then, the seeds were carbonized without draining the acid at 500 °C for 1 h. The obtained products were washed with hot distilled water to pH 6 to 7.
2.3. Characterization techniques
Thermogravimetric analysis (TGA; 500 V20.10 Build 36) was performed to find the raw material's moisture content, and for a proximate analysis, including the volatile matter, ash content, and fixed carbon content, and to know the decomposition characteristic during carbonization. After the evacuation of the test chamber, the analysis process was started. The initial and final temperatures were chosen as 30 °C and 950 °C while the heating rate was 10 °C min−1. SEM analysis was performed to study the surface morphology of the produced activated carbons. BET analysis was conducted to measure the surface area, average pore radius, and total pore volume of the prepared activated carbons. Also, the methylene blue number and iodine number of the prepared activated carbons were determined. The yield of the produced activated carbons was calculated from the following equation,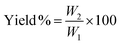 | (1) |
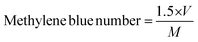 | (2) |
In the process, 10 mL of 5 wt% hydrochloric acid solutions was added to the carbon and boiled for 30 s on a hot plate. Next, 100 mL of 0.1 N iodine solution was added, and the mixture was then vigorously shaken for 1 min, and filtered. The first 20 to 30 mL of the filtrate was discarded, while the remaining filtrate was collected in another beaker. Then, 50 mL was taken in a flask and titrated against standardized 0.1 N sodium thiosulphate. The volume of sodium thiosulphate used was noted.
| A = (N2) (12693.0) | (3) |
| B = (N1) (126.93) | (4) |
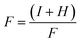 | (5) |
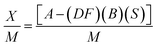 | (6) |
2.4. Point of zero charge (pHPZC)
The determination of pHPZC was conducted through acid–base titration, following the methodology outlined previously.33 Initially, 50 mL aliquots of 0.01 M NaCl solution were prepared in individual flasks. The pH of these solutions underwent systematic adjustment from pH 2 to pH 12 via incremental additions of 0.01 M solution of NaOH or HCl. Upon reaching a stable pH value, indicating equilibrium, 0.1 g of the DS-AC was introduced into each flask. Subsequently, the sealed flasks were placed on a shaker for 3 days to ensure thorough equilibration. To account for potential CO2 influence on the pH measurements, blank tests were performed without the DS-AC sample. Following the equilibration period, the final pH values were recorded. The pHPZC value was determined by plotting the pH against the point of zero charge to identify the point of intersection with the line, representing the pH at which the surface charge of DS-AC becomes neutral, thereby indicating the pHPZC value. This method offers a reliable approach for discerning the point of zero charge of the DS-AC samples, thereby enhancing comprehension of their surface chemistry and adsorption properties.2.5. Batch adsorption experiments
A stock solution of the dye of 1000 mg L−1 was prepared by dissolving 1 g of the dye (BBR) in 1000 mL of distilled water. From the stock solution, working concentrations of adsorbate solution, i.e., from 100 to 500 mg L−1, were obtained by successive dilution. A stock solution of 1000 mg L−1 metal was also prepared by dissolving 4.4 g of ZnSO4·7H20 in 1000 mL of distilled water. From the stock solution of 1000 mg L−1, samples of different concentrations, such as 10 to 50 mg L−1, were prepared by dilution. The concentrations of BBR dye and Zn metal were found using a UV-visible spectrophotometer at maximum wavelengths of 468 nm and 620 nm, respectively. BBR dye is typically found at higher concentrations in water due to its prevalent use in various industries, such as textiles, printing, and dyeing; while Zn ions are commonly present in wastewater from industrial processes, mining activities, and the corrosion of galvanized materials.Batch adsorption tests were conducted by mixing a known weight of AC (0.1 g) with 50 mL of the adsorbate solution at pH 6. The mixture was agitated in a shaker (Orbital, Scigenics) at 180 rpm. Samples were taken at prescribed time intervals; the solutions were centrifuged and analyzed for the final concentration using a UV-visible spectrophotometer (Shimadzu Model UV-2100S). The batch adsorption studies were carried out for the adsorptions of BBR and Zn on the DS-AC samples. To find the time required to reach equilibrium, adsorption studies were carried out for a dye concentration of 500 mg L−1 and metal ion concentration of 50 mg L−1 and the contact time was varied from 0 to 240 min. The % removal could be found from the following equation:
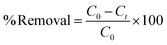 | (7) |
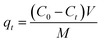 | (8) |
2.6. Adsorption isotherms
To optimize the design of an adsorption system to remove pollutants, it is essential to establish the most appropriate correlations for the equilibrium data for each system. The operational parameters here included pH 6, contact time of 120 min, agitation at 180 rpm, and temperature of 30 °C. Four isotherm models were tested in the present study: Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich isotherms. The isotherm parameters were calculated. The theoretical Langmuir isotherm is valid for the adsorption of a solute from a liquid solution as monolayer adsorption on a surface containing a finite number of identical sites. The Langmuir isotherm model assumes uniform adsorption energies onto the surface without transmigration of the adsorbate in the surface plane. The linear form of the Langmuir isotherm is given by the following equation:35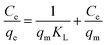 | (9) |
The Freundlich adsorption model stipulates that the ratio of solute adsorbed to the solute concentration is a function of the solution. The empirical model was consistent with an exponential of active centers, characteristic of heterogeneous surfaces. The amount of solute adsorbed is related to the equilibrium concentration of the solute in the solution. The linear form of Freundlich isotherm is given by the following equation:36
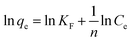 | (10) |
qe = B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A + B A + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce Ce | (11) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qm − K ε2 qm − K ε2 | (12) |
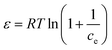 | (13) |
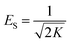 | (14) |
2.7. Adsorption kinetics
Adsorption kinetic studies are significant since they provide valuable insights into reaction pathways and describe the solute uptake rate, which in turn controls the residence time of a sorbate at the solid–liquid interface. Here, the operational setup included pH level held constant at 6, contact duration spanning from 0 to 120 min, agitation maintained at 180 rpm, temperature set at 30 °C, and BBR concentrations varying between 100 and 500 mg L−1, alongside Zn ion concentrations ranging from 10 to 50 mg L−1. To investigate the adsorption mechanism and determine the rate-controlling step, various kinetic models, such as pseudo-first-order (PFO), pseudo-second-order (PSO), Elovich, and intraparticle diffusion models, are generally used to test the experimental data.39,40 The PFO kinetic model is represented by the following equation41| ln(qe − qt) = ln(qe) − K1t | (15) |
The PSO model assumes that adsorption follows a second-order mechanism. So, the occupation rate of the adsorption sites is proportional to the square of the number of unoccupied sites, and can be given as:42
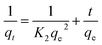 | (16) |
The rate constants, qe, and regression values for PSO kinetics for different concentrations were calculated.
Elovich's equation, initially presented in 1939, is suitable for chemical adsorption processes and for systems with heterogeneous adsorbing surfaces,14 and is given by:
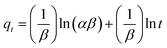 | (17) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t) against the amount adsorbed (qt). The intercept and slope of the plot give the initial adsorption rate σ and desorption constant β, respectively.
t) against the amount adsorbed (qt). The intercept and slope of the plot give the initial adsorption rate σ and desorption constant β, respectively.
The most commonly used technique for identifying the mechanism involved in the adsorption process is fitting the experimental data into an intraparticle diffusion plot.43,44 This model can be expressed as follows:1,4
| qt = Kidt0.5 + C | (18) |
2.8. Thermodynamic studies
The effect of temperature was tested to find the optimum temperature at which the maximum adsorption occurs. Adsorption tests were carried at different temperatures 30 °C, 40 °C, 50 °C, and 60 °C. The thermodynamic parameters, such as standard Gibbs free energy (ΔG°), enthalpy (ΔH°), and entropy change (ΔS°) of adsorption were evaluated using the equations below:ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc Kc | (19) |
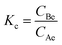 | (20) |
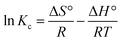 | (21) |
2.9. Regeneration study
Regeneration of the DS-AC after adsorption of BBR dye and Zn metal ions involved removing the adsorbed contaminants and restoring the adsorption capacity of the material. To desorb the DS-AC from the BBR adsorbed material, 0.1 g of the adsorbent was introduced into 50 mL of 0.5 M hydrochloric acid (HCl) solution for BBR and 0.5 M ammonium chloride (NH4Cl) solution for Zn ions, with these acting as chelating agents. The solution was continuously stirred for 60 min to aid the desorption of the contaminants from the DS-AC surface, with the stirring duration adjusted based on the adsorption capacity and affinity of the contaminants. Once desorption was complete, the regenerated DS-AC was separated from the solution, typically achieved through filtration. The regenerated DS-AC was then thoroughly rinsed with deionized water to eliminate any residual regeneration solution and contaminants. Following regeneration, excess moisture was removed from the DS-AC by utilizing a hot-air oven at 80 °C. Once dried, the regenerated DS-AC was stored in a clean, dry container or sealed bag to prevent recontamination and to preserve its adsorption capacity until further use. Subsequently, sample aliquots of the solution were subjected to UV spectroscopy analysis to determine the concentration of the desorbed contaminants.3. Results and discussions
3.1. Characterization of the raw date seeds
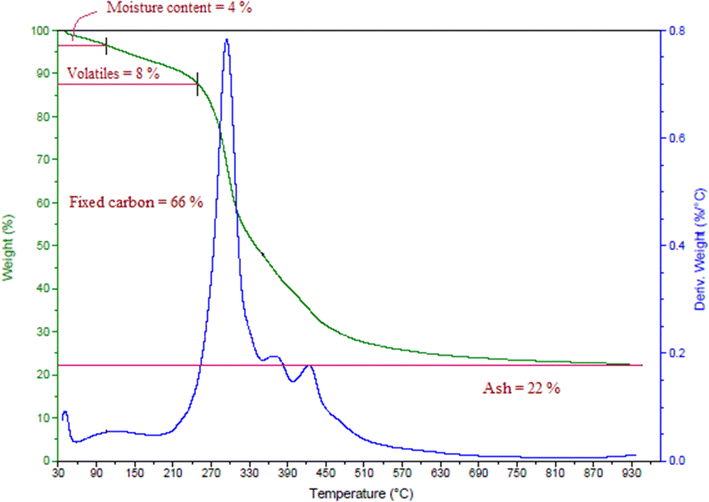
Proximate analysis of a biomass includes its moisture content, volatile content, ash content, and fixed carbon content, found here by thermogravimetric analysis, as shown in Fig. 1. The fixed carbon content, ash content, moisture content, and volatile content of the date seeds were calculated and the results are presented in Table 1.| Properties | Weight % |
|---|---|
| Moisture content | 4 |
| Volatile content | 8 |
| Ash content | 22 |
| Fixed carbon content | 66 |
The effects of the methylene blue number, iodine number, and percentage yield were studied for changing the activated carbon production method, the acid to seed weight ratio, and the soaking temperature. The weight ratio of phosphoric acid to date seed was varied as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3
1, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 4
1, and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
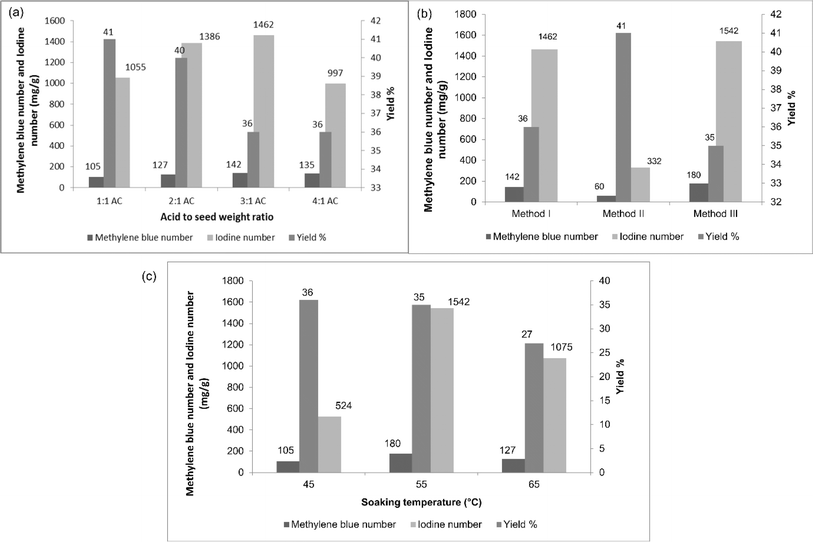
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 respectively. From Fig. 2(a), it could be observed that an increase in the weight of the acid of up to 3 times increase both the methylene blue and iodine numbers. After that, both decreased, indicating that the amount of phosphoric acid used affected the pore formation and development process. When the amount of acid increased, the formation of new micropores and widening of the pores occurred. The decrease in methylene blue and iodine numbers for the 4
1 respectively. From Fig. 2(a), it could be observed that an increase in the weight of the acid of up to 3 times increase both the methylene blue and iodine numbers. After that, both decreased, indicating that the amount of phosphoric acid used affected the pore formation and development process. When the amount of acid increased, the formation of new micropores and widening of the pores occurred. The decrease in methylene blue and iodine numbers for the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio may be caused by the degeneration of the porous structures of the activated carbon due to excessive dehydration. It could also be seen from the figure that the yield percentage slightly decreased when increasing the weight ratio.
1 ratio may be caused by the degeneration of the porous structures of the activated carbon due to excessive dehydration. It could also be seen from the figure that the yield percentage slightly decreased when increasing the weight ratio.
Therefore, the maximum methylene blue and iodine numbers were observed for AC31, indicating the better formation of micropores and mesopores. This weight ratio was thus chosen for the further studies. When the seeds were soaked at room temperature, there was a poor formation of micropores and mesopores, which could be explained by the low iodine and methylene blue numbers, respectively, as represented in Fig. 2(b). When soaked at higher temperature, the methylene blue and iodine numbers increased over soaking at room temperature. This might have happened because when the hard material (DS) was subjected to higher temperature during soaking, the acid penetrated well into the seed and loosened the organic content present in the seed, meaning the organics could escape easily during the carbonization process, resulting in the formation of more and wider pores.
Moreover, when the carbonization was done after draining the acid in the soaking process, higher methylene blue and iodine numbers were obtained than when carbonized with the acid, as shown in Table 2. Excess acid (during carbonization) might have deposited on the surface of the seed, preventing the phosphate molecules and organic matter from escaping from the surface, resulting in poor pore formation. To find the optimum soaking temperature for better pore formation, the seeds were soaked at 3 different temperatures (45 °C, 55 °C, and 65 °C and named respectively as AC 45, AC 55, and AC 65) and the methylene blue number, iodine number, and yield percentage were determined and are presented in Table 3 and Fig. 2(c). AC 45 showed low methylene blue and iodine numbers, whereas AC 55 and AC 65 had higher methylene blue and iodine numbers. So both micropores and mesopores were better developed in AC 55 and AC 65 than in AC 45. Hence, AC 55 and AC 65 were chosen for the removal of BBR dye and zinc metal ions. Further increasing the soaking temperature could result in a better pore formation, but when it comes to yield, increasing the temperature decreased the yield percentage, as shown in Table 2 and Fig. 2(c).
| Results | Soaking temperature | ||
|---|---|---|---|
| 45 °C | 55 °C | 65 °C | |
| Methylene blue number (mg g−1) | 105 | 180 | 127 |
| Iodine number (mg g−1) | 524 | 1542 | 1075 |
| Surface area (mg g−1) | 723.08 | 996.12 | 877.6 |
| Average pore radius (A0) | 8.82 | 9.45 | 10.44 |
| Total pore volume (cc g−1) | 0.318 | 0.471 | 0.458 |
| Yield (%) | 36 | 35 | 27 |
| Isotherm model | Parameters | BBR | Zn metal ions | ||
|---|---|---|---|---|---|
| AC 55 | AC 65 | AC 55 | AC 65 | ||
| Langmuir | q m (mg g−1) | 138.88 | 192.31 | 15.55 | 13.11 |
| K L (L mg−1) | 0.023 | 0.036 | 0.378 | 0.022 | |
| R 2 | 0.9751 | 0.9756 | 0.9972 | 0.9539 | |
| Freundlich | K F ((mg g−1) (L mg−1) (1/n)) | 17.18 | 24.85 | 5.03 | 0.42 |
| 1/n | 0.36 | 0.38 | 0.38 | 0.74 | |
| n (g L−1) | 2.77 | 2.62 | 2.63 | 1.35 | |
| R 2 | 0.9316 | 0.9987 | 0.9599 | 0.9894 | |
| Temkin | A (L mg−1) | 0.32 | 0.55 | 4.31 | 0.27 |
| B | 27.37 | 36.30 | 3.28 | 2.46 | |
| R 2 | 0.9527 | 0.9629 | 0.9852 | 0.9774 | |
| Dubinin–Radushkevich | q m (mg g−1) | 104.58 | 130.32 | 12.46 | 5.11 |
| K ((mol K kJ−1)2) | 40.94 | 5.62 | 0.32 | 9.57 | |
| E s (kJ mol−1) | 0.11 | 0.298 | 1.25 | 0.228 | |
| R 2 | 0.9053 | 0.7812 | 0.8983 | 0.8852 | |
The textural properties of the activated carbon determined by N2 adsorption method are given in Table 2. The surface area, average pore radius, and total pore volume of AC 45, AC 55, and AC 65 were found by this method. Table 2 shows that the surface area of AC 55 was comparatively higher than that of AC 45 and AC 65. This can be explained from the high iodine number of AC 55, from its micropores. The average pore radius of AC 65 was slightly greater than in AC 55; which was slightly greater than in AC 45. This might be due to widening of the pores with the higher soaking temperature. Table 2 shows that both the methylene blue number and iodine number were higher for AC 55 than AC 45 and AC 65. This might be due to the high pore volume of AC 55. Overall, the surface area and total pore volume of AC 55 and AC 65 were comparatively higher than for AC 45. Hence AC 55 and AC 65 were chosen for dye and metal ion removal.
Fig. 3(a)–(c) show the SEM images of AC 45 at magnifications of 2500×, 3500×, and 6500×, respectively. Some substances sticking on the surface of the carbon and pores were not visible. It was likely that when the organic content in the seed tried to escape from the surface during carbonization, it formed a thick layer on the surface, resulting in poor pore formation. Fig. 3(d)–(f) show the SEM images of AC 55 at magnifications of 2500×, 3500×, and 6500×, respectively. The pores are visible, and pores of various sizes could be seen at 2500× magnification. Deeper and longitudinal pores could be seen at 3500× magnification. Fig. 3(g)–(i) displays the SEM images of AC 65 at magnifications of 2500×, 3500×, and 6500×, respectively. The glossy appearance of AC 65 may be due to the deposition of substances formed during carbonization. Significantly larger pores and smaller pores were visible at 2500× magnification.
3.2. Batch adsorption experiments
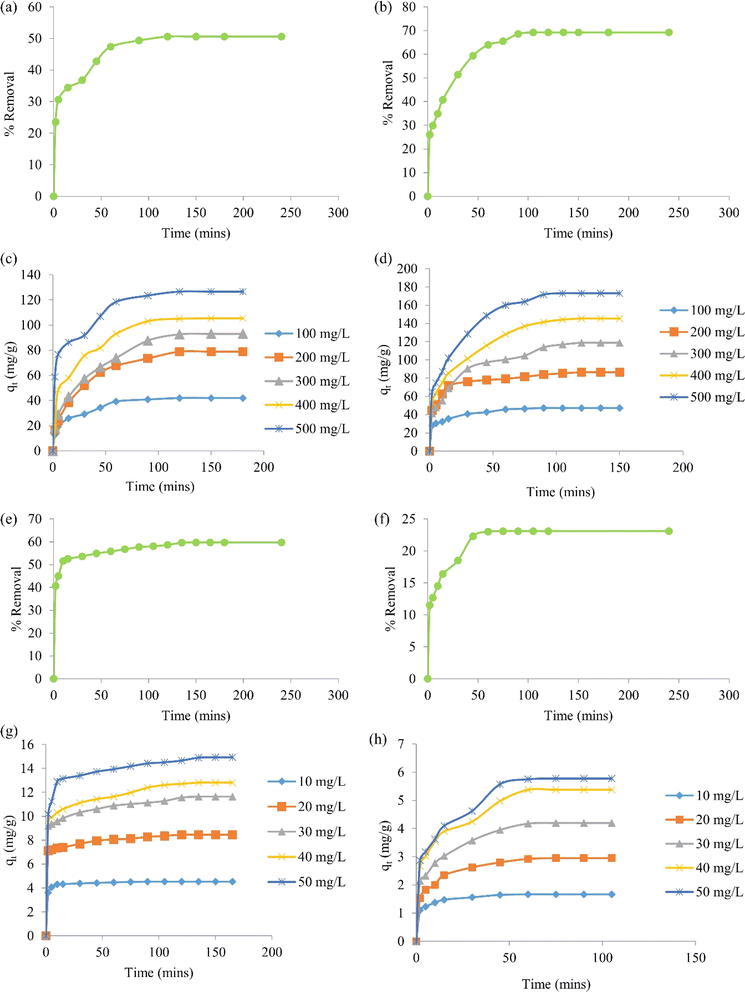
Batch adsorption experiments of BBR and Zn metal ions on the ACs were conducted in a shaker (Orbital, Scigenics) at 180 rpm by mixing 0.1 g of AC to 50 mL of adsorbate solution. The effects of the contact time and initial concentration of the dye and metal ions were studied in the adsorption process with AC 55 and AC 65. The adsorption studies for the dye were done by mixing 0.1 g of AC 55 in 50 mL of BBR dye and 0.1 g of AC 65 in 50 mL of BBR dye. The batch adsorptions of the metal ions were done by mixing 0.1 g of AC 55 in 50 mL of Zn solution and 0.1 g of AC 65 in 50 mL of Zn solution.Adsorption studies were carried out for a dye concentration of 500 mg L−1 and the contact time was varied from 0 to 240 min to find the time at which equilibrium was attained. The % removal was calculated using eqn (7). Fig. 4(a) and (b) illustrate the impact of the contact time on the attainment of equilibrium, revealing that equilibrium was reached within 120 min for the adsorption of BBR on AC 55 and within 105 min for the adsorption of BBR on AC 65. Hence for further adsorption studies, the time was reduced from 240 min, but still to ensure equilibrium conditions contact times of 180 min and 150 min were selected for the adsorption of BBR on AC 55 and BBR on AC 65, respectively. Five different initial concentrations of BBR dye (100, 200, 300, 400, and 500 mg L−1) were taken and the adsorption was carried out for each concentration. The adsorption capacity (qt) for each concentration was calculated using eqn (8) and a graph of qtvs. time was plotted.
The results demonstrate the impact of the initial dye concentration on the adsorption capacity of AC 55 and AC 65 for BBR dye. The experimental findings, as depicted in Fig. 4(c) and (d), revealed notable trends in the adsorption behavior of these activated carbon materials. First, it was evident that as the initial dye concentration increased, the adsorption capacity of both AC 55 and AC 65 rose accordingly. This trend suggests that higher initial dye concentrations provide more available dye molecules for adsorption onto the activated carbon surfaces, resulting in increased adsorption capacities. This phenomenon is consistent with the Langmuir isotherm model, where higher initial concentrations typically lead to higher adsorption capacities until a saturation point is reached.
Furthermore, the equilibrium time required for adsorption to reach the maximum capacity varied slightly between AC 55 and AC 65. In the case of AC 55, equilibrium was achieved within the range of 120–180 min for all initial dye concentrations tested. Conversely, for AC 65, equilibrium was attained within the range of 90–150 min. This difference in equilibrium time may be attributed to variations in the surface properties and pore structures of the activated carbon materials. Moreover, the increase in adsorption capacity with higher initial dye concentrations was substantial. For instance, the adsorption capacity of AC 55 increased from 41.93 to 126.55 mg g−1, while that of AC 65 increased from 47.3 to 173.07 mg g−1, as the initial dye concentration was raised from 100 to 500 mg L−1. This significant enhancement in adsorption capacity underscores the effectiveness of both AC 55 and AC 65 in removing BBR dye from aqueous solutions, particularly at higher dye concentrations. Overall, these results highlight the importance of considering the initial dye concentration when designing adsorption processes using DS-AC. Understanding the influence of the initial concentration on the adsorption capacity is crucial for optimizing the process parameters and ensuring the efficient removal of BBR dye from wastewater.
Fig. 4(e)–(h) show the results of the study into the intricate dynamics of the adsorption kinetics and the impact of the initial metal ion concentration on the adsorption capacity of AC 55 and AC 65 for Zn ions. First, the investigation began by exploring the effect of the contact time on Zn adsorption. By varying the contact time from 0 to 240 min, the study aimed to ascertain the equilibrium time required for adsorption on both AC 55 and AC 65. The findings, as depicted in Fig. 4(e) and (f), revealed interesting nuances in the adsorption process. It was observed that equilibrium was reached at different time intervals for AC 55 (135 min) and AC 65 (75 min), indicating variations in the adsorption kinetics of the materials. The selection of the contact times of 165 min for AC 55 and 105 min for AC 65 for the subsequent studies aimed to ensure that adsorption occurs under equilibrium conditions, providing reliable data for further analysis. Subsequently, the study explored the effect of the initial metal ion concentration on the adsorption capacity. Five different concentrations of Zn ion solutions, ranging from 10 to 50 mg L−1, were employed to understand how variations in the concentration influence the adsorption behavior. The calculated adsorption capacities in Fig. 4 illustrate the relationship between the initial concentration and adsorption contact time.
A detailed analysis of Fig. 4(g) and (h) gave some intriguing insights into the adsorption process. For AC 55, equilibrium was achieved at 90 min for lower concentrations (10 mg L−1), while higher concentrations of 20–50 mg L−1 required slightly longer equilibrium times (120–165 min). In contrast, AC 65 exhibited a shorter equilibrium time across all concentrations, ranging from 60 to 105 min. This disparity in equilibrium times underscores the distinct adsorption kinetics of the materials, possibly attributed to variations in their surface properties and pore structures. Moreover, the increase in adsorption capacity with higher initial Zn ion concentrations was noteworthy. The significant enhancement in adsorption capacity from 10 to 50 mg L−1 highlights the favorable adsorption behaviors of both AC 55 and AC 65 toward Zn ions. Overall, these results provide valuable insights into the adsorption kinetics and capacity of DS-AC for Zn ion removal. The findings contribute to a deeper understanding of the factors influencing adsorption processes and hold implications for the development of efficient wastewater-treatment strategies utilizing activated carbon materials.
3.3. Adsorption isotherms
Adsorption isotherm studies are significant as they can provide crucial insights into the behavior of adsorbate molecules on adsorbent surfaces, and can help determine the equilibrium relationship between the concentration of adsorbate in the solution and its concentration on the surface of the adsorbent. Understanding adsorption isotherms aids in characterizing the surface properties of adsorbents and predicting their adsorption capacities under different conditions. The most widely used isotherm models for solid–liquid adsorption that describe the equilibrium data are the Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich isotherm models. The isotherm study was carried out in an Orbital shaker at 180 rpm, pH 6, with 150 min contact time for BBR and 105 min for Zn. The concentrations used were 100 mg L−1 for BBR and 10 mg L−1 for Zn. The isotherms parameters and constants for each model were calculated and are given in Table 3. The Langmuir isotherm is given in eqn (9). The values of qm and KL were calculated from the slope and intercept, respectively, of a plot of Ce/qevs. Ce, as shown in Fig. S4(a)–(d).† The Freundlich isotherm is given in eqn (10). The values of KF and n were calculated from the intercept and slope of a plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qevs. ln
qevs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce, as shown in Fig. S4(e)–(h).† The Temkin isotherm is given in eqn (11). The values of A and B were calculated from the intercept and slope of a plot of qevs. ln
Ce, as shown in Fig. S4(e)–(h).† The Temkin isotherm is given in eqn (11). The values of A and B were calculated from the intercept and slope of a plot of qevs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce, respectively, as shown in Fig. S5(a)–(d).† The Dubinin–Radushkevich isotherm is given in eqn (12).17 The values of K and qm were calculated from the slope and intercept, respectively, from the plot of ln
Ce, respectively, as shown in Fig. S5(a)–(d).† The Dubinin–Radushkevich isotherm is given in eqn (12).17 The values of K and qm were calculated from the slope and intercept, respectively, from the plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qevs. ε2, as shown in Fig. S5(e)–(h).†
qevs. ε2, as shown in Fig. S5(e)–(h).†
Table 3 provides valuable insights into the adsorption mechanisms governing the interaction between the dye and metal ions and AC 55 and AC 65. The results indicate that the Langmuir and Temkin isotherm models exhibited good fittings for both types of adsorbates on both activated carbons. This suggests that the adsorption process followed a monolayer adsorption behavior and accounted for the interaction between adsorbate molecules on the adsorbent surface. Furthermore, the Freundlich isotherm model demonstrated a good fit for the adsorption of metal ions on both ACs and the adsorption of dye on AC 65. This model indicates multilayer adsorption and considers the heterogeneity of the adsorbent surface, providing insights into the adsorption mechanism.
However, it could be noted that the fitness of the Dubinin–Radushkevich model was slightly lower compared to the other models, as evidenced by the R2 values presented in Table 3. The Dubinin–Radushkevich model is typically used to characterize microporous adsorbents and provides information on the energetics of the adsorption process. Interpretation of the regression coefficient (R2) values reveals crucial insights into the dominant adsorption mechanisms. A higher R2 value indicates a better fit of the model to the experimental data. When the R2 value for the Langmuir model is higher than that of the Freundlich model, it suggests that chemical adsorption predominates in the adsorption process. Conversely, if the R2 value for the Freundlich model is higher, it indicates that physisorption behavior is dominant. From Table 3, it could be inferred that the adsorption of dye and metal ions on AC 55 was predominantly through chemisorption, while the adsorption of these species on AC 65 leaned toward physisorption. This distinction in adsorption mechanisms between the two activated carbons highlights the importance of their surface properties and pore structures in influencing their adsorption behavior.
The maximum monolayer adsorption capacity (qm) calculated from the Langmuir isotherm model for the adsorption of dye on AC 65 was 192.31 mg g−1, which was greater than the adsorption on AC 55, which was 138.88 mg g−1. The maximum monolayer adsorption capacity for AC 55 for the adsorption of metal ions was 15.55 mg g−1, which was comparably higher than that for AC 65, which was 13.11 mg g−1. The sorption constant, KL, followed the same trend as that of qm. A higher KF value describes the adsorption capacity related to the bonding energy for multilayer adsorption. It is evident from Table 3 that KF was higher for the adsorption of the dye on AC 65 than on AC 55. Table 3 shows that KF was higher for metal ions adsorption on AC 55 than on AC 65, as already proven by the qm values.
In the Freundlich isotherm, the value 1/n is a parameter of the adsorption intensity or surface heterogeneity and nF is a measure of the deviation from the linearity of adsorption. When 0 < 1/n < 1, adsorption is favorable; when 1/n greater than 1, adsorption is unfavorable; and when 1/n is closer to unity, it represents the heterogeneity of adsorption. Further, when n equals 1, the adsorption is linear; n < 1 the adsorption happens by chemical means; and when n > 1, the adsorption favors the physical process. From the results obtained, it could be found that 1/n was less than 1, as shown in Table 3, which indicates the favorability of the adsorption of the dye and metal ions on both ACs. The value of n was greater than 1 for both the adsorption of the dye and metal ions on both AC 55 and AC 65, which explains the physical nature of the adsorption process.
The binding constant A and constant related to the heat of adsorption B calculated using the Temkin isotherm were higher for BBR dye adsorption on AC 65 than on AC55 and higher for Zn adsorption on AC 55 than on AC 65. The values of ES calculated using the D–R model were below 1 kJ mol−1, indicating that the physico-sorption process plays a significant role in the adsorption of BBR and Zn on both ACs. The maximum adsorption capacity calculated from this model was lower than from the Langmuir model.
3.4. Adsorption kinetics
The kinetic study was carried out in an Orbital shaker at 180 rpm, pH 6, with a contact time of 0 to 150 min for BBR and 0 to 105 min for Zn, and concentrations of 100–500 mg L−1 for BBR and 10–50 mg L−1 for Zn. The pseudo-first-order kinetics model is represented in eqn (15). The values of qe,calculated and K1 could be found from a plot of ln(qe − qt) vs. t. The rate constants, qe,calculated, and regression values for the pseudo-first-order kinetics for different concentrations of the aqueous adsorbate solutions were also calculated. Fig. S6(a) and (b)† show the kinetics plots for BBR adsorption on AC 55 and AC 65 and Fig. S6(c) and (d)† illustrate Zn adsorption on AC 55 and AC 65 for the five different concentrations. The values qe,calculated and K1 were found from the plots of ln(qe − qt) vs. t. The rate constants, qe,calculated, and regression values for the pseudo-first-order kinetics for different concentrations of the BBR dye solution on AC 55 and AC 65 are presented in Tables 4 and 5 and for Zn metal ion solution adsorption on AC 55 and AC 65 in Tables 6 and 7, respectively. To determine the validity of the pseudo-first-order model, the plot of ln(qe − qt) vs. t should be linear. It could be observed from the plots that the data needed to be better represented by the model. This could also been seen from the poor regression co-efficients obtained, and also as the values of qe,calc did not match with the experimental qe,exp values. Hence, the assumption that the adsorption kinetics follows first-order kinetics does not apply.The pseudo-second-order model was given by ref. 46, and is represented in eqn (16). The value of qe,calculated and K2 could be determined from a plot of t/qt against t.
The rate constants, qe, and regression values for the pseudo-second-order kinetics for different concentrations were calculated. Fitting of the pseudo-second-order kinetics model to the experimental data obtained for the adsorption of BBR dye on AC 55 and AC 65 of different concentrations (100–500 mg L−1) is shown in Fig. S6(e) and (f),† respectively. Fig. S6(g) and (h)† demonstrate the pseudo-second-order kinetics model for Zn ion adsorption on AC 55 and AC 65 of different concentrations (10–50 mg L−1). The values of qe,calculated and K2 were determined from the plots of t/qt against t, as shown. It could be observed from the plots that the experimental data were well represented by the pseudo-second-order kinetics model for all five concentrations of both dyes and metal ions. Also it can be seen from Tables 4–7 that the correlation co-efficients were very high and close to unity, and also, the values of the calculated qe were almost equal to the values obtained from the experiments.
The Elovich equation is given in eqn (17), and satisfies chemical adsorption processes and is suitable for systems with heterogeneous adsorbing surfaces.47 The Elovich model can be explained by plotting the logarithmic time (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t) against the amount adsorbed (qt), as can be seen in Fig. S7(a)–(d).† The intercept and slope of the plot gives the initial adsorption rate σ and desorption constant β, respectively. The regression values and Elovich model constants are listed in Tables 4–7. It can be seen from these tables that the Elovich model gave a reasonably good fit to the experimental data (Fig. S7(a)–(d)†). Though the Elovich equation does not give any idea of the adsorption mechanism, it seems well suited for heterogeneous systems.48 It could also be observed that the initial adsorption rate α was always higher than the value of β, which is the desorption constant. This indicates that the rate of adsorption was larger than the rate of desorption. This was seen for all five dye and metal ion concentrations for adsorption on both AC 55 and AC 65.
t) against the amount adsorbed (qt), as can be seen in Fig. S7(a)–(d).† The intercept and slope of the plot gives the initial adsorption rate σ and desorption constant β, respectively. The regression values and Elovich model constants are listed in Tables 4–7. It can be seen from these tables that the Elovich model gave a reasonably good fit to the experimental data (Fig. S7(a)–(d)†). Though the Elovich equation does not give any idea of the adsorption mechanism, it seems well suited for heterogeneous systems.48 It could also be observed that the initial adsorption rate α was always higher than the value of β, which is the desorption constant. This indicates that the rate of adsorption was larger than the rate of desorption. This was seen for all five dye and metal ion concentrations for adsorption on both AC 55 and AC 65.
The intraparticle diffusion model can be found in eqn (18).49 The intraparticle diffusion kinetics were studied by plotting the amount adsorbed (qt) against the square root of the adsorption time (t0.5). The intraparticle diffusion rate constants were calculated and are presented in Tables 4–7. Fig. S7(e) and (f)† show the intraparticle kinetic plots for BBR dye adsorption on AC 55 and AC 65, and Fig. S7(g) and (h)† display the same for Zn adsorption on AC 55 and AC 65, respectively. It could be seen in these figures that increasing the initial adsorbate concentration increased the intraparticle diffusion rate constant and integral constant.50,51 These results suggest that diffusion through the pores increased with concentration. Moreover, the film diffusion resistance increased with the initial concentration, since the thickness of the boundary layer also increased. Hence the adsorption process was controlled by both film diffusion and pore diffusion.
3.5. Thermodynamic studies of BBR dye and Zn metal ions
The temperature involved in the adsorption of BBR dye and Zn metal ions on AC 65 and AC 55 can be explained through thermodynamic principles. For the adsorption of BBR dye on AC 65, the temperature increased from 30 °C to 60 °C, while the adsorption capacity of BBR dye on AC 65 also increased, as depicted in Fig. S8(a).† This increase in adsorption capacity with temperature suggests an endothermic nature of the adsorption process. Endothermic adsorption occurs when the adsorbate molecules are more energetically favored to bind to the adsorbent surface at higher temperatures. The rise in temperature provides more kinetic energy to the system, facilitating the movement of dye molecules from the solution onto the surface of AC 65. Additionally, higher temperatures may disrupt intermolecular forces within the dye molecules, making them more susceptible to adsorption onto the activated carbon surface. The increase in adsorption capacity observed herein from 86.54 mg g−1 to 94.62 mg g−1 indicates that the adsorption process was favored at elevated temperatures, reflecting the endothermic nature of the interaction between BBR dye and AC 65 (Table 8).| Adsorbate | Adsorbent | ΔG0 (kJ mol−1) | ΔH0 (kJ mol−1) | ΔS0 (kJ mol−1 K−1) | |||
|---|---|---|---|---|---|---|---|
| 303 K | 313 K | 323 K | 333 K | ||||
| BBR dye | 65 AC | −2.95 | −3.59 | −4.67 | −6.01 | 28.05 | 0.102 |
| Zinc metal ions | 55 AC | −1.38 | −1.01 | −0.51 | −0.08 | −14.75 | −0.044 |
For the adsorption of Zn metal ions on AC 55, the temperature increased from 30 °C to 60 °C, while the adsorption capacity of Zn metal ions on AC 55 decreased, as illustrated in Fig. S8(b).† This decrease in adsorption capacity with temperature suggests an exothermic nature of the adsorption process. Exothermic adsorption occurs when the adsorbate molecules are less energetically favored to bind to the adsorbent surface at higher temperatures. The reduction in adsorption capacity may be attributed to thermally induced changes in the adsorbate–adsorbent interaction. Here, at higher temperatures, the affinity between Zn metal ions and the AC 55 surface weakened, leading to decreased adsorption. Additionally, elevated temperatures could result in an increased desorption of previously adsorbed metal ions from the AC 55 surface, further reducing the overall adsorption capacity. The decrease in adsorption capacity from 11.64 mg g−1 to 10.09 mg g−1 suggests that the adsorption process was less favored at higher temperatures, indicating the exothermic nature of the interaction between Zn metal ions and AC 55. The thermodynamic parameters, such as standard Gibbs free energy (ΔG°), enthalpy (ΔH°), and entropy change (ΔS°) of adsorption were evaluated using eqn (21). ΔH° and ΔS° were obtained from the slope and intercept of the plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kcvs. 1/T, as shown in Fig. S8(c) and (d).†
kcvs. 1/T, as shown in Fig. S8(c) and (d).†
The thermodynamic study here could indicate the feasibility and spontaneous nature of dye and metal ion adsorption. For dye adsorption, free energy decreased with the increase in temperature, which shows that when the temperature increased, the spontaneous nature also increased, resulting in more dye adsorption. For metal ions, the spontaneity decreased with the increase in temperature, hence adsorption decreased with temperature. The endothermic nature of the dye adsorption could be confirmed by the positive value of the change in enthalpy (ΔH0 = 28.05 kJ mol−1). In contrast, the positive value of the change in entropy (ΔS0 = 0.102 kJ mol−1 K−1) exhibited increased randomness in the dye adsorption. The exothermic nature of metal ions was confirmed by the negative value of enthalpy change (ΔH0 = −14.75 kJ mol−1); while a negative value of entropy (ΔS0 = −0.044 kJ mol−1 K−1) indicated a decrease in randomness of adsorption.
3.6. Mechanism of BBR dye and Zn ions removal
To elucidate the possible mechanism of BBR dye and Zn ions removal using DS-AC, several adsorption mechanisms and interactions between the adsorbent and the adsorbates were considered. In considering the mechanism, it is known that BBR dye and Zn ions undergo physical adsorption onto the surface of DS-AC through weak van der Waals forces/electrostatic interactions.52,53 The porous structure of DS-AC provides a large surface area and numerous adsorption sites for the adsorbates to adhere. Chemical adsorption involves the formation of chemical bonds between the adsorbate molecules and functional groups on the surface of DS-AC. Oxygen-containing functional groups, such as hydroxyl (–OH), carboxyl (–COOH), and carbonyl (–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) groups, present on DS-AC may participate in chemical interactions with BBR dye and Zn ions. BBR dye molecules are typically negatively charged, while zinc ions are positively charged in solution. Consequently, the presence of charged functional groups on DS-AC, as well as the point of zero charge (pHPZC), influences the electrostatic interactions between DS-AC and the adsorbates. When the pH is below the pHPZC of DS-AC, the surface may be positively charged, facilitating the adsorption of anionic BBR dye molecules. Conversely, when the pH is above the pHPZC, the surface may be negatively charged, favoring the adsorption of cationic zinc ions. Zn ions may form complexes with functional groups on DS-AC, such as carboxyl groups, through coordination bonds. Ion-exchange processes may also occur, where Zn ions replace other ions present on the surface of DS-AC, depending on the relative affinities of the ions for the adsorbent surface. BBR dye molecules and Zn ions may enter the pores of DS-AC through pore-filling mechanisms, particularly for mesoporous and microporous materials. Surface diffusion allows the adsorbates to migrate along the surface of DS-AC and into its pores, thereby enhancing the overall adsorption capacity.
O) groups, present on DS-AC may participate in chemical interactions with BBR dye and Zn ions. BBR dye molecules are typically negatively charged, while zinc ions are positively charged in solution. Consequently, the presence of charged functional groups on DS-AC, as well as the point of zero charge (pHPZC), influences the electrostatic interactions between DS-AC and the adsorbates. When the pH is below the pHPZC of DS-AC, the surface may be positively charged, facilitating the adsorption of anionic BBR dye molecules. Conversely, when the pH is above the pHPZC, the surface may be negatively charged, favoring the adsorption of cationic zinc ions. Zn ions may form complexes with functional groups on DS-AC, such as carboxyl groups, through coordination bonds. Ion-exchange processes may also occur, where Zn ions replace other ions present on the surface of DS-AC, depending on the relative affinities of the ions for the adsorbent surface. BBR dye molecules and Zn ions may enter the pores of DS-AC through pore-filling mechanisms, particularly for mesoporous and microporous materials. Surface diffusion allows the adsorbates to migrate along the surface of DS-AC and into its pores, thereby enhancing the overall adsorption capacity.
3.7. Comparison study
Table 9 provides a comprehensive comparison of various adsorbents utilized for the remediation of BBR dye and Zn ions from wastewaters. Notably, the current study findings showcase remarkable efficacy for both dye and heavy metal removal. Specifically, the prepared DS-AC adsorbent demonstrated good adsorption capacities, achieving impressive removal efficiencies of 192.31 mg g−1 for BBR dye and 15.55 mg g−1 for zinc ions. These results underscore the exceptional effectiveness of DS-AC in adsorbing BBR dye and Zn ions, which were equally impressive. The attained adsorption capacities highlight DS-AC's potential as a highly promising adsorbent for wastewater treatment applications, offering superior performance for the removal of both organic dyes and heavy metal contaminants.| Pollutant | Adsorbent | Adsorption capacity (mg g−1) | References |
|---|---|---|---|
| Bismarck Brown R (BBR) dye | Multiwall carbon nanotubes | 32.15 | 8 |
| Activated carbon from raw Ziziphusspina-christi | 35.88 | 7 | |
| Adsorbent hen feather | 21.52 | 5 | |
| Activated carbons from rubberwood sawdust | 1111 | 30 | |
| Biosorbent | 17.59 | 54 | |
| DS-AC | 192.31 | Present study | |
| Zinc ion | Activated carbon from Hevea brasiliensis | 22.03 | 9 |
| Adsorbent from brewed tea waste | 1.163 | 55 | |
| Magnetic MnFe2O4 spinel ferrite nanoparticles | 454.5 | 56 | |
| Magnetic CoFe2O4 spinel ferrite nanoparticles | 384.6 | 56 | |
| Magnetic modified chitosan | 32.16 | 57 | |
| Magnetite/carbon nanocomposites | 48.45 | 58 | |
| DS-AC | 15.55 | Present study |
3.8. Regeneration and reuse
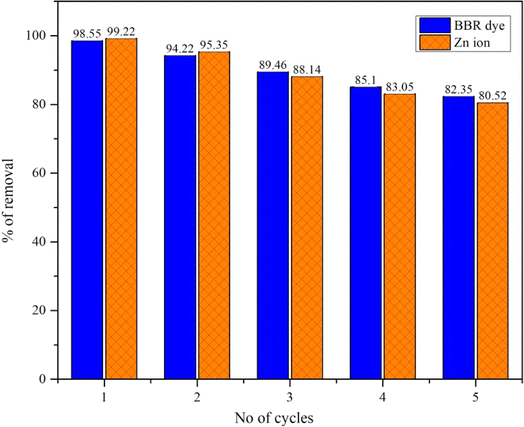
Fig. 5 shows the regeneration and reuse of DS-AC materials in five consecutive cycles for BBR dye and Zn ion removal. In the first cycle, the DS-AC adsorbent could effectively remove the contaminants from the solution, with efficiencies for BBR dye and Zn metal ions removal of 98.55% and 99.22%, respectively. After the first cycle, the DS-AC was regenerated to apply it for further cycles. Although some loss in adsorption capacity may occur during regeneration, the material still demonstrated the efficient removal of contaminants. In the second cycle, the removal efficiencies for BBR dye and Zn metal ions were observed to be 94.22% and 95.35%, respectively. In each successive cycle, the removal efficiencies for both contaminants gradually decreased, indicating a gradual loss in adsorption capacity. Despite the decrease in removal efficiencies, the DS-AC continued to demonstrate significant adsorption capabilities, retaining its effectiveness in removing contaminants from the solution. The decrease in removal efficiencies over successive cycles could be attributed to factors such as gradual fouling of the adsorbent surface, saturation of active sites, and structural changes in the DS-AC material. After five cycles, the removal efficiencies for BBR dye and Zn metal ions decreased to 82.35% and 80.52%, respectively. Therefore, the regeneration and reuse of DS-AC materials show the promise of such materials for sustainable pollutant removal.4. Conclusions
Low-cost efficient activated carbons were prepared from date seeds that are hard in nature, which aided producing hard-based activated carbons. A chemical activation method was adopted for preparation of the activated carbon. Low methylene blue and iodine numbers were obtained for the activated carbons produced under room temperature with soaking. When the soaking temperature was increased to higher temperature, the activated carbons produced high methylene blue and iodine numbers. These results suggested that both micropores and mesopores were present and were better formed in high-temperature soaking than at room temperature. The soaking temperature was varied as 45 °C, 55 °C, and 65 °C to find the optimum soaking temperature for better pore development. The maximum BET surface area obtained was 996.12 m2 g−1, comparable to the usual chemical activation methods. The AC 55 and AC 65 samples had better pore formation than AC 45, which could be explained by the methylene blue number, iodine number, SEM images, and BET surface area. Hence AC 55 and AC 65 were chosen for BBR dye (bigger size molecule) and Zn metal ion (smaller in size) removal from aqueous solutions, in which metal ion adsorption was better in AC 55 and dye adsorption was better in AC 65. The Langmuir isotherm fitted well for the adsorption on AC 55, whereas the Freundlich isotherm fitted better for the adsorption on AC 65. The maximum monolayer adsorption capacity calculated from the Langmuir isotherm for dye removal was 192.31 mg g−1 and for metal ion removal was 15.55 mg g−1. Among the various kinetic models, the pseudo-second-order and Elovich models fitted well for the adsorption of both the dye and metal ions on DS-AC. In the thermodynamic studies, it was found that increasing the temperature resulted in more dye adsorption, whereas metal ion adsorption decreased with the increase in temperature. Therefore, this adsorbent was more efficient at eliminating toxic dyes and heavy metals, but could also be used further for other kinds of organic pollutants removal from water.Author contributions
Sivamani Sivalingam: conceptualization, methodology, supervision, writing – original draft, writing – review & editing. Sowmiya A.: investigation, validation and visualization, and data curation.Conflicts of interest
The authors declare herewith that they do not have any conflict of interest with any organization or individual.Acknowledgements
The authors would like to acknowledge their sincere thanks to Sriram Engineering College, Perumalpattu, Chennai and Rajalakshmi Engineering College (Autonomous), Thandalam, Chennai for the support.References
- J. Leonard, S. Sivalingam, R. Venkata and S. Mishra, Environmental Chemistry and Ecotoxicology Efficient removal of hexavalent chromium ions from simulated wastewater by functionalized anion exchange resin: process optimization, isotherm and kinetic studies, Environ. Chem. Ecotoxicol., 2023, 5(December 2022), 98–107, DOI:10.1016/j.enceco.2023.03.001.
- S. Sivalingam and V. Gopal, Efficient removal of magenta dye from water by both natural and chemical coagulants, Rasayan J. Chem., 2023, 16(1), 307–311 CrossRef CAS.
- S. Dutta, B. Gupta, S. K. Srivastava and A. K. Gupta, Recent advances on the removal of dyes from wastewater using various adsorbents: a critical review, Mater. Adv., 2021, 2(14), 4497–4531, 10.1039/d1ma00354b.
- S. Dawood, Synthesis and characterization of biomass and clay mineral based adsorbents for the removal of cationic dye and metal ion from wastewater by adsorption, PhD thesis, Curtin University, 2018, https://espace.curtin.edu.au/handle/20.500.11937/69346.
- J. Mittal, V. Thakur and A. Mittal, Batch removal of hazardous azo dye Bismark Brown R using waste material hen feather, Ecol. Eng., 2013, 60, 249–253, DOI:10.1016/j.ecoleng.2013.07.025.
- J. Cheng, C. Zhan and J. Wu, et al., Highly Efficient Removal of Methylene Blue Dye from an Aqueous Solution Using Cellulose Acetate Nanofibrous Membranes Modified by Polydopamine, ACS Omega, 2020, 5(10), 5389–5400, DOI:10.1021/acsomega.9b04425.
- A. Koohmareh and G. H. V. Khah, Enhanced removal of Bismark Brown (BB) dye from aqueous solutions using activated carbon from raw Ziziphusspina-christi (ZSAC) Equilibrium, thermodynamic and kinetics, J. Phys. Theor. Chem., 2012, 14(3), 237–249 Search PubMed.
- A. M. Kamil, F. H. Abdalrazak, A. F. Halbus and F. H. Hussein, Adsorption of Bismarck Brown R Dye Onto Multiwall Carbon Nanotubes, J. Environ. Anal. Chem., 2014, 1(1), 1–8, DOI:10.1209/0295-5075/101/10000.
- H. Kalavathy, B. Karthik and L. R. Miranda, Removal and recovery of Ni and Zn from aqueous solution using activated carbon from Hevea brasiliensis: batch and column studies, Colloids Surf., B, 2010, 78(2), 291–302, DOI:10.1016/j.colsurfb.2010.03.014.
- U. O. Aigbe, K. E. Ukhurebor and R. B. Onyancha, et al., A Facile Review on the Sorption of Heavy Metals and Dyes Using Bionanocomposites, Adsorpt. Sci. Technol., 2022, 2022, 1–36, DOI:10.1155/2022/8030175.
- S. Afroze and T. K. Sen, A Review on Heavy Metal Ions and Dye Adsorption from Water by Agricultural Solid Waste Adsorbents, Water, Air, Soil Pollut., 2018, 229(7), 1–50, DOI:10.1007/s11270-018-3869-z.
- M. A. Islam, I. A. W. Tan, A. Benhouria, M. Asif and B. H. Hameed, Mesoporous and adsorptive properties of palm date seed activated carbon prepared via sequential hydrothermal carbonization and sodium hydroxide activation, Chem. Eng. J., 2015, 270, 187–195, DOI:10.1016/j.cej.2015.01.058.
- S. Sivalingam, T. Kella, M. Maharana and S. Sen, Efficient sono-sorptive elimination of methylene blue by fly ash-derived nano-zeolite X: process optimization, isotherm and kinetic studies, J. Cleaner Prod., 2019, 208, 1241–1254, DOI:10.1016/j.jclepro.2018.10.200.
- S. Sivalingam and S. Sen, Sono-assisted Adsorption of As(V) from Water by Rice-Husk-Ash-Derived Iron-Modified Mesoporous Zeolite Y: A Cradle-to-Cradle Solution to a Problematic Solid Waste Material, Ind. Eng. Chem. Res., 2019, 58(31), 14073–14087, DOI:10.1021/acs.iecr.9b01785.
- E. I. Ugwu and J. C. Agunwamba, A review on the applicability of activated carbon derived from plant biomass in adsorption of chromium, copper, and zinc from industrial wastewater, Environ. Monit. Assess., 2020, 192, 240, DOI:10.1007/s10661-020-8162-0.
- S. Sivalingam and S. Sen, Efficient removal of textile dye using nanosized fly ash derived zeolite-x: kinetics and process optimization study, J. Taiwan Inst. Chem. Eng., 2019, 96, 305–314, DOI:10.1016/j.jtice.2018.10.032.
- S. Mopoung, P. Moonsri, W. Palas and S. Khumpai, Characterization and Properties of Activated Carbon Prepared from Tamarind Seeds by KOH Activation for Fe(III) Adsorption from Aqueous Solution, Sci. World J., 2015, 2015, 1–9, DOI:10.1155/2015/415961.
- J. Aguilar-Rosero, M. E. Urbina-López, B. E. Rodríguez-González, S. X. León-Villegas, I. E. Luna-Cruz and D. L. Cárdenas-Chávez, Development and Characterization of Bioadsorbents Derived from Different Agricultural Wastes for Water Reclamation: A Review, Appl. Sci., 2022, 12(5), 1–27, DOI:10.3390/app12052740.
- J. Andas, M. L. A. Rahman and M. S. M. Yahya, Preparation and Characterization of Activated Carbon from Palm Kernel Shell, Fac. Pure Appl. Sci. LAUTECH, Print Niger Prep., 2012, 17(2), 188–197, DOI:10.1088/1757-899X/226/1/012156.
- K. Rambabu, F. Banat, G. S. Nirmala, S. Velu, P. Monash and G. Arthanareeswaran, Activated carbon from date seeds for chromium removal in aqueous solution, Desalin. Water Treat., 2019, 156(April 2018), 267–277, DOI:10.5004/dwt.2018.23265.
- R. Chen, L. Li and Z. Liu, et al., Preparation and characterization of activated carbons from tobacco stem by chemical activation, J. Air Waste Manage. Assoc., 2017, 67(6), 713–724, DOI:10.1080/10962247.2017.1280560.
- T. Subramani and P. K. Revathi, Production Of Activated Carbon From Agricultural Raw Waste, IOSR J. Eng., 2015, 5(5), 54–63 Search PubMed.
- M. S. Reza, C. S. Yun and S. Afroze, et al., Preparation of activated carbon from biomass and its' applications in water and gas purification, a review, Arab J. Basic Appl. Sci., 2020, 27(1), 208–238, DOI:10.1080/25765299.2020.1766799.
- K. Y. Foo and B. H. Hameed, Preparation of activated carbon from date stones by microwave induced chemical activation: application for methylene blue adsorption, Chem. Eng. J., 2011, 170(1), 338–341, DOI:10.1016/j.cej.2011.02.068.
- F. Bouhamed, Z. Elouear and J. Bouzid, Adsorptive removal of copper(II) from aqueous solutions on activated carbon prepared from Tunisian date stones: equilibrium, kinetics and thermodynamics, J. Taiwan Inst. Chem. Eng., 2012, 43(5), 741–749, DOI:10.1016/j.jtice.2012.02.011.
- J. M. Salman, V. O. Njoku and B. H. Hameed, Bentazon and carbofuran adsorption onto date seed activated carbon: kinetics and equilibrium, Chem. Eng. J., 2011, 173(2), 361–368, DOI:10.1016/j.cej.2011.07.066.
- A. R. Hidayu, M. Z. Sukor and N. F. Mohammad, et al., Preparation of activated carbon from palm kernel shell by chemical activation and its application for β-carotene adsorption in crude palm oil, J. Phys.: Conf. Ser., 2019, 1349(1), 2–8, DOI:10.1088/1742-6596/1349/1/012103.
- V. K. Gupta, S. Khamparia, I. Tyagi, D. Jaspal and A. Malviya, Decolorization of mixture of dyes: a critical review, Global J. Environ. Sci. Manage., 2015, 1(1), 71–94, DOI:10.7508/gjesm.2015.01.007.
- W. Zhang, H. Liu, Q. Xia and Z. Li, Enhancement of dibenzothiophene adsorption on activated carbons by surface modification using low temperature oxygen plasma, Chem. Eng. J., 2012, 209, 597–600, DOI:10.1016/j.cej.2012.08.050.
- B. G. P. Kumar, L. R. Miranda and M. Velan, Adsorption of Bismark Brown dye on activated carbons prepared from rubberwood sawdust (Hevea brasiliensis) using different activation methods, J. Hazard. Mater., 2005, 126(1–3), 63–70, DOI:10.1016/j.jhazmat.2005.05.043.
- M. Kisan, S. Sangathan, J. Nehru and S. G. Pitroda, Activated Carbons, Powdered and Granular — Methods of Sampling and Test, Bureau of Indian Standards, 1990, 2, pp. , pp. 1–7, https://law.resource.org/pub/in/bis/S02/is.877.1989.pdf Search PubMed.
- ASTM, Standard Test Method for Determination of Iodine Number of Activated Carbon 1, ASTM Int., 2006, 94(Reapproved), 1–5 Search PubMed . http://compass.astm.org.acces.bibl.ulaval.ca/download/D4607.6656.pdf.
- O. E. A. Adam, Removal of Resorcinol from Aqueous Solution by Activated Carbon : Isotherms , Removal of Resorcinol from Aqueous Solution by Activated Carbon : Isotherms , Thermodynamics and Kinetics, Am. Chem. Sci. J., 2016, 16(August), 1–13, DOI:10.9734/ACSJ/2016/27637.
- B. H. Hameed, J. M. Salman and A. L. Ahmad, Adsorption isotherm and kinetic modeling of 2,4-D pesticide on activated carbon derived from date stones, J. Hazard. Mater., 2009, 163(1), 121–126, DOI:10.1016/j.jhazmat.2008.06.069.
- I. Langmuir, The adsorption of gases on plane surfaces of glass, mica and platinum, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- H. M. F. Freundlich, Over the adsorption in solution, J. Phys. Chem., 1906, 57, 385–471 CAS.
- M. Temkin and V. Pyzhev, Recent Modifications to Langmuir Isotherms, Acta Phys.-Chim. Sin., 1940, 12, 217–222 Search PubMed.
- M. Ghaedi, A. Ansari, M. H. Habibi and A. R. Asghari, Removal of malachite green from aqueous solution by zinc oxide nanoparticle loaded on activated carbon: kinetics and isotherm study, J. Ind. Eng. Chem., 2014, 20, 17–28 CrossRef CAS.
- S. G. Muntean, A. Todea, S. Bakardjieva and C. Bologa, Removal of non benzidine direct red dye from aqueous solution by using natural sorbents: beech and silver fir, Desalin. Water Treat., 2017, 66, 235–250, DOI:10.5004/dwt.2016.0154.
- S. G. Muntean, M. A. Nistor, A. A. Andelescu, M. E. Radulescu-Grad and R. Ianos, Magnetite Nanocomposites , Application for Decontamination of Wastewaters, Chem. Bull., 2016, 61(75), 66–71 CAS.
- S. K. Lagergren, About the Theory of So-Called Adsorption of Soluble Substances, Sven. Vetenskapsakad. Handingarl, 1898, 24, 1–39 Search PubMed.
- Y. S. Ho and G. Mckay, Sorption of dyes from aqueous solution by peat, Chem. Eng. J., 1998, 70, 115–124 CrossRef CAS.
- O. M. Paska, C. Pəcurariu and S. G. Muntean, Kinetic and thermodynamic studies on methylene blue biosorption using corn-husk, RSC Adv., 2014, 4(107), 62621–62630, 10.1039/c4ra10504d.
- S. G. Muntean, A. Todea, M. E. Radulescu-Grad and A. Popa, Decontamination of colored wastewater using synthetic sorbents, Pure Appl. Chem., 2014, 86(11), 1771–1780, DOI:10.1515/pac-2014-0805.
- A. El Nemr, A. Khaled, O. Abdelwahab and A. El-Sikaily, Treatment of wastewater containing toxic chromium using new activated carbon developed from date palm seed, J. Hazard. Mater., 2008, 152(1), 263–275, DOI:10.1016/j.jhazmat.2007.06.091.
- Y. S. Ho and G. McKay, Pseudo-second order model for sorption processes, Process Biochem., 1999, 34, 451–465, DOI:10.1016/S0032-9592(98)00112-5.
- C. Aharoni and F. C. Tompkins, Kinetics of Adsorption and Desorption and the Elovich Equation, Adv. Catal., 1970, 21(C), 1–49, DOI:10.1016/S0360-0564(08)60563-5.
- Y. S. Ho and G. Mckay, Kinetic Models for the Sorption of Dye from Aqueous Solution by Wood, Process Saf. Environ. Prot., 1998, 76(2), 183–191 CrossRef CAS.
- G. McKay, M. S. Otterburn and J. A. Aga, Intraparticle diffusion process occurring during adsorption of dyestuffs, Water, Air, Soil Pollut., 1987, 36(3–4), 381–390, DOI:10.1007/BF00229680.
- T. Senthilkumar and L. R. Miranda, Adsorption of anionic and cationic dyes on chemically modified pomegranate peel: a isotherms and kinetics studies, Asian J. Chem., 2015, 27(9), 3267–3276, DOI:10.14233/ajchem.2015.18533.
- M. H. El-Naas, S. Al-Zuhair and M. A. Alhaija, Removal of phenol from petroleum refinery wastewater through adsorption on date-pit activated carbon, Chem. Eng. J., 2010, 162(3), 997–1005, DOI:10.1016/j.cej.2010.07.007.
- Z. Raji, A. Karim, A. Karam and S. Khalloufi, Adsorption of Heavy Metals: Mechanisms, Kinetics, and Applications of Various Adsorbents in Wastewater Remediation—A Review, Waste, 2023, 1(3), 775–805, DOI:10.3390/waste1030046.
- F. H. Hussein, A. F. Halbus, A. J. Lafta and Z. H. Athab, Preparation and characterization of activated carbon from iraqi khestawy date palm, J. Chem., 2015, 2015, 295748, DOI:10.1155/2015/295748.
- G. Bharathidasan, N. Mani, G. Vishnuvardhanaraj and K. M. Faizal, Removal of Bismark Brown R Dye from Aqueous Solution by Laplap Purpureus Plant Stems Utilized as Biosorbent, J. Adv. Sci. Res., 2020, 11(2), 201–208 CAS . http://www.sciensage.info/journal/1359303580JASR_3006121.pdf.
- H. Celebi, G. Gok and O. Gok, Adsorption capability of brewed tea waste in waters containing toxic lead(II), cadmium (II), nickel (II), and zinc(II) heavy metal ions, Sci. Rep., 2020, 10(1), 1–12, DOI:10.1038/s41598-020-74553-4.
- R. Asadi, H. Abdollahi, M. Gharabaghi and Z. Boroumand, Effective removal of Zn (II) ions from aqueous solution by the magnetic MnFe2O4 and CoFe2O4 spinel ferrite nanoparticles with focuses on synthesis, characterization, adsorption, and desorption, Adv. Powder Technol., 2020, 31(4), 1480–1489, DOI:10.1016/j.apt.2020.01.028.
- L. Fan, C. Luo, Z. Lv, F. Lu and H. Qiu, Preparation of magnetic modified chitosan and adsorption of Zn2+ from aqueous solutions, Colloids Surf., B, 2011, 88(2), 574–581, DOI:10.1016/j.colsurfb.2011.07.038.
- A. Andelescu, M. A. Nistor, S. G. Muntean and M. E. Rădulescu-Grad, Adsorption studies on copper, cadmium, and zinc ion removal from aqueous solution using magnetite/carbon nanocomposites, Sep. Sci. Technol., 2018, 53(15), 2352–2364, DOI:10.1080/01496395.2018.1457696.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3va00314k |
| This journal is © The Royal Society of Chemistry 2024 |