Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optimizing direct air capture under varying weather conditions†
H. M.
Schellevis
 ,
J. D.
de la Combé
and
D. W. F.
Brilman
,
J. D.
de la Combé
and
D. W. F.
Brilman
 *
*
University of Twente, Faculty of Science and Technology, PO Box 217, 7500AE Enschede, The Netherlands. E-mail: d.w.f.brilman@utwente.nl
First published on 27th May 2024
Abstract
CO2 from adsorption with supported-amine sorbents using steam-assisted temperature-vacuum swing adsorption is a technology to capture CO2 from the atmosphere (direct air capture). This process has many operational parameters and, on top of that, is heavily influenced by the ambient temperature and relative humidity. Identifying the minimum cost of direct air capture becomes a multi-dimensional problem in which climate conditions has to be incorporated as well. This study aims to evaluate the cost of direct air capture for year-round operation and to relate this to climate conditions. An optimization framework was developed with the ambient conditions as input parameters. This framework is able to find the minimum cost of direct air capture for a given fixed bed DAC facility and provides the corresponding operational parameters. These results were coupled to year-round weather data to find the total costs for continuous operation. We showed that the cost of CO2 capture from air correlates well with the average annual temperature, with a high average temperature being more beneficial. Furthermore, climates with strong variation in weather conditions over the seasons require dynamic process control in order to operate at minimum cost of DAC. Overall, the presented optimization framework is an excellent tool to identify suitable locations for direct air capture and provide the operational parameters to minimize its cost.
Introduction
Direct air capture (DAC) is a technology that provides a sustainable carbon source in the form of CO2, harvested from the atmosphere. Alternatively, when combined with permanent storage, it can compensate fossil-based CO2 emissions to achieve net-zero operation or act as negative emission technology. Due to the low concentration, a very selective separation method is required to separate CO2 from air. Adsorption with supported-amine sorbents was shown to be suitable due to the affinity of the basic amine groups with the acidic CO2.1–4Temperature-vacuum swing adsorption (TVSA) is a common practise for DAC,1,5 exemplified by its application in Climeworks’ Orca facility, present day's largest DAC facility in operation.6,7 A steam purge can be applied as well to enhance the desorption rate resulting in steam-assisted temperature vacuum swing adsorption or (S-)TVSA.8,9 A complete optimization of such process is not straightforward due to the many operational parameters present in the process. A returning complexity was the interrelation between these parameters.9–12 It is not possible to optimize the process by assessing each parameter individually. A multi-dimensional optimization is required including an economic analysis to find the most optimal operating point of this DAC process.13
Constantly changing ambient conditions generate additional complexity to the process.14 Amine-based sorbents possess affinity towards H2O.15–18 Several studies show that there is no competitive adsorption between the physisorption of H2O and chemisorption of CO2. In fact, the presence of H2O showed a beneficial effect for CO2 adsorption especially for low CO2 partial pressure.12,16,19 At high relative humidity, H2O co-adsorption could become a dominant factor.19 Moreover, reaction kinetics and CO2 equilibrium capacity depend heavily on temperature and relative humidity. Consequently, performance of the DAC process, in terms of energy duty, system productivity and cost of DAC, will depend on the ambient conditions. Additionally, each weather condition will have a specific set of optimal operational parameters.
In this study, we evaluate how climate conditions influence the cost of DAC for year-round operation. For this, we developed an optimization framework to determine the optimal operational parameters for a minimum cost of DAC (€/tCO2) of an S-TVSA process. First, we introduce the optimization framework to determine the most optimal operating point for a fixed combination of temperature and relative humidity. Then, this framework is used to optimize a fixed bed adsorption column for DAC that has been described in a previous study.20 These results are presented in terms of cost of DAC, key performance indicators and operational parameters for each different weather conditions. Finally, the average cost of DAC for year-round production in various climates can be determined.
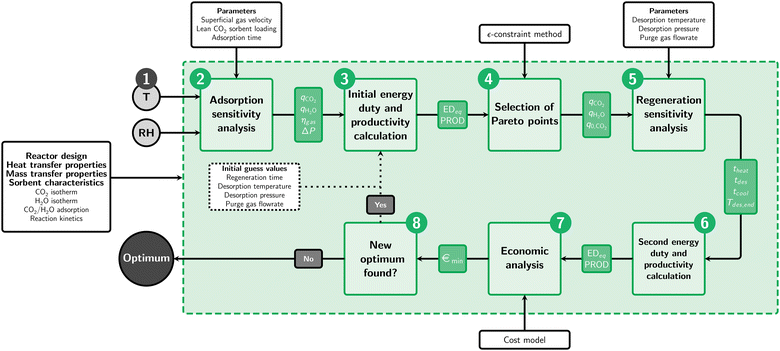
Optimization framework
This chapter explains the features of the optimization framework that is developed to find the minimum cost of DAC. We briefly describe the numerical model that forms basis of the framework. The optimization framework is specific for an S-TVSA process for the capture of CO2 from air. This is a cyclic process, which can be split into five phases: adsorption, evacuation, heating, desorption and cooling. Adsorption of CO2 on the supported-amine sorbent occurs at ambient conditions, whereas desorption takes place at elevated temperature and reduced absolute pressure. A steam purge is applied during the desorption phase to enhance the desorption rate. During the evacuation phase, the pressure is reduced to the desired desorption pressure. This phase is very short compared to the other phases and therefore this phase will be neglected in this optimization study.Numerical model
An accurate numerical model of the complete adsorption-regeneration cycle is essential for process optimization. The model consists of separate 1-dimensional, dynamic models for adsorption, heating, desorption and cooling in a fixed bed adsorption column (ESI1†). These are solved consecutively and for several successive adsorption-regeneration cycles. For a more detailed explanation of the (S-)TVSA model and its validation we refer to a previous study.10 That study also shows sensitivity analyses of operational parameters to identify the parameters that have the largest impact on the system performance.Sorbent characteristics
The performance of an (S-)TVSA process for DAC are highly dependent on the sorbent characteristics. Therefore, detailed descriptions of adsorbent properties are essential input for the model. In this study, optimization is showcased for a commercially available supported-amine sorbent, Lewatit® VP OC 1065, that is also used in the model validation study.10 The required characterisations of this sorbent are available from previous studies with the relevant correlations introduced in ESI1.†The pure component CO2 equilibrium capacity is described by the Tóth isotherm. Isotherm parameters are obtained from literature, where they were fitted to a wide range of experimental data.10,21 The temperature ranged from 0 °C to 140 °C and CO2 partial pressure from 10 Pa to 0.8 bar. The pure component H2O equilibrium capacity is fitted by the GAB isotherm from a data set spanning from 8 °C to 33 °C and 0% to 95% relative humidity.19 The effect of relative humidity on the CO2 equilibrium capacity is accounted for via a two-parameter empirical correlation. The fitting procedure and experimental data set are available in literature.19 Other essential sorbent characteristics are reaction kinetics21 and heat and mass transfer properties on particle and bed level are needed.21,22
Operational parameters
Many operational parameter influence the performance of an (S-)TVSA process (ESI2†). These are:1. Ambient temperature
2. Ambient relative humidity,
3. Superficial gas velocity during adsorption,
4. Adsorption time,
5. Desorption temperature,
6. Desorption pressure,
7. Purge gas flowrate and
8. Desorption time.
The ambient temperature and relative humidity are fixed input parameters. These cannot be chosen, but are a given depending on the climate. Two parameters are relevant for the adsorption phase: the superficial gas velocity and the adsorption time. Four parameters are relevant for the desorption phase: desorption temperature (or temperature of the heat transfer medium to be more precise), desorption pressure, purge gas flowrate and desorption time. The combination of adsorption time and desorption time results in a certain CO2 (and H2O) working capacity. This approach requires an initial guess for the CO2 sorbent loading in the first adsorption step after which a steady-state will develop after several cycles. We use a slightly different approach in this study. Instead of the desorption time, we define a certain bed average lean CO2 sorbent loading at the start of adsorption as input parameter for the adsorption phase. Then, the desorption time to reach this loading is obtained from the desorption model. Therefore, each S-TVSA cycle runs between fixed lean and saturated CO2 sorbent loadings. This will lead to a steady-state situation within a single cycle, since separate simulations showed that different initial sorbent loading profiles throughout the bed does not significantly influence the results for a given bed average sorbent loading.
Optimization algorithm
The optimal operating parameters and minimum cost of DAC are obtained for a certain set of ambient conditions via an optimization algorithm (Fig. 1). This algorithm consists of eight steps and will be elaborated in this section. ESI3† gives a more extensive overview, including intermediate results for one of the evaluations as example.Step 1 of the optimization algorithm is to set the ambient temperature and relative humidity. With the here presented algorithm, the minimum cost of capture and accompanying operational parameters at these ambient conditions are found. Optimization is performed for ambient temperatures from 0 to 40 °C combined with relative humidities from 0 to 100%.
The adsorption sensitivity analysis (step 2) is performed with varying adsorption time, superficial gas velocity and lean CO2 sorbent loading. The adsorption model and the regeneration (heating, desorption and cooling) model are solved independently. In principle, these are linked via the axial CO2 loading profile being exchanged between the models. Starting point for adsorption is the CO2 loading profile at the end of regeneration, that by itself will depend on the regeneration conditions. However, it was found that using a uniform CO2 loading profile, set at the average sorbent loading, resulted in nearly identical results. The same holds for the initial CO2 loading profile of the regeneration stage. Consequently, the models only require the average CO2 (and H2O) sorbent loading regardless of the adsorption or regeneration conditions. In addition, the cooling phase has a pre-defined final average temperature of 40 °C. Hence, each adsorption simulation (for each weather condition) starts with this temperature and can be solved completely independent from the regeneration model.
Table 1 shows the minimum and maximum input values for each parameter. The maximum adsorption time for each simulation is set at 20 hours and the performance indicators are evaluated at a time interval of 10 minutes. Since the adsorption and desorption models are completely independent, it is not necessary to perform separate cyclic simulations for each adsorption time.
| Parameter | Minimum value | Maximum value |
|---|---|---|
| Superficial gas velocity (mg3 mr−2 s−1) | 0.05 | 0.3 |
| Lean CO2 sorbent loading (molCO2 kgs−1) | 0.01 | 0.3 |
| Adsorption time (h) | 0 | 20 |
| Desorption temperature (°C) | 120 | 120 |
| Desorption pressure (mbar) | 15 | 150 |
| Purge gas flowrate (gpurge kgs−1 min−1) | 0.5 | 6 |
Step 3 uses the results of each combination of adsorption time, superficial gas velocity and lean CO2 sorbent loading to calculate two performance indicators as described in a previous study:20 energy duty (in MJ kgCO2−1) and productivity (in kgCO2 kgs−1 day−1). The relevant simulation results consist of the final CO2 and H2O sorbent loading, fraction of ingoing CO2 that is captured (gas efficiency) and the pressure drop. However, calculating the total energy duty and productivity requires operational conditions during regeneration. Therefore, an initial guess of these parameter is made. An iteration step is applied later on to validate these guesses. When evaluating a series of weather condition, the optimal parameters of an evaluation with similar weather conditions could be used as initial estimation.
The adsorption sensitivity analysis results in an extensive amount of data points. Therefore, the desorption sensitivity analysis is limited in step 4 to those data points that potentially contain the optimal operating point, based on the energy duty and productivity. This is a multiple objective optimization problem since the energy duty is preferably as low as possible and the productivity is preferably as high as possible. As a result, a Pareto front is created and we use the ε-constraint method to find the non-dominated points on this front.23,24 In this method, one objective function is optimized (productivity), while the other is constraint (energy duty). From this, only a very selective set of combinations of superficial gas velocity, lean CO2 sorbent loading and adsorption time are selected.
For this approach to be valid, a lower energy duty must always be beneficial. However, the total energy duty is the sum of thermal energy and electrical energy. The price of these energy sources depends on the actual sources of energy, but most likely are not equal. Therefore, a higher energy duty does not necessarily correspond to a higher energy cost. Somehow, these different energy sources must be translated to an ‘equivalent’ energy duty. In this study, the thermal energy is assumed to be generated via a high temperature heat pump with a COP of 1.7.25
Step 5 is a sensitivity analysis, using the regeneration model, for each of the selected Pareto points. This involves the desorption temperature, desorption pressure and purge gas flowrate, within the specified ranges in Table 1. The desorption temperature (referring to the temperature of the heating medium) is fixed at the highest possible value. A previous studies concluded that it is beneficial for both energy duty and productivity to operate at the highest possible temperature.10
The regeneration model combines sub-models for the heating, desorption and cooling steps. In the heating step, heating is continued until a pre-defined temperature of 50 °C. Initial conditions for the desorption step are the CO2 and H2O sorbent loadings that resulted from the adsorption optimization and correspond to the Pareto points.
The energy duty and productivity are calculated for each simulation (step 6), combining results from adsorption and regeneration. Therefore, these are now determined for the complete (S-)TVSA cycle without guess values. The original Pareto front of step 4 is thereby updated, and the optimum will be located somewhere on the new Pareto front.
The overall objective is to find the minimum cost of capture. An economic evaluation is needed to solve the trade-off between energy duty and productivity (step 7). We use a rather simple cost model proposed by Sinnott and Towler.26 The capital costs are based on a novel (2020) 0.5 tpa DAC pilot unit.20 The total ISBL capital investment of this pilot unit is estimated and scaled up to a capacity of 10 kton per annum. For this, we assume an economy of scale factor 0.6 following the “six-tenth rule”. The operational costs include costs of sorbent, labour, maintenance, energy and additional fixed costs. Table 2 lists the assumptions used in the economic analysis.
| Parameter | Value |
|---|---|
| CAPEX of DAC pilot unit (€2020) | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Full scale capacity (tCO2 year−1) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Economy of scale (−) | 0.6 |
| Depreciation time (year) | 10 |
| Sorbent lifetime (year) | 2 |
| Sorbent costs (€ kgs−1) | 30 |
| Working hours (h year−1) | 8400 |
| Salary costs (€ year−1) | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Maintenance costs | 4% of CAPEX |
| Additional fixed costs | 2% of CAPEX |
| Solar energy price (€ kW h−1)27 | 0.03 |
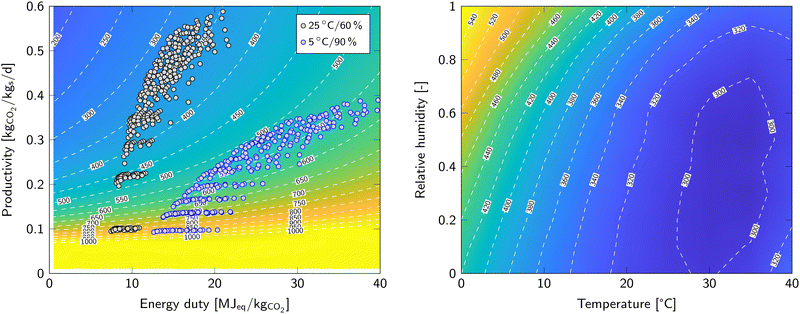
Remember that the cost of capture is only evaluated for the initial Pareto points. However, these were obtained in step 3 using guess values for the regeneration phase. Therefore, iteration is required (step 8) using the optimal desorption parameters to calculate the energy duty and productivity for the adsorption sensitivity analysis in step 3. Iteration is then continued until no new optimum is found in step 7. Fig. 2 (left) shows the energy duty and productivity of the data points along the Pareto front obtained after the final iteration of step 8. The contour lines and colour map show the cost of DAC as function of productivity and energy duty.
Optimization results
The optimization algorithm is able to find the minimum cost of DAC for a fixed set of ambient conditions; temperature and relative humidity. Feasible ambient conditions for DAC are in the temperature range of 0 to 40 °C. At sub-zero temperatures, handling of condensed water may become problematic, whereas above 40 °C cooling becomes limiting since the adsorption phase starts at this temperature. There is no limitation in the relative humidity range, hence it will be evaluated from completely dry to completely saturated. The optimization algorithm provides the minimum cost of DAC, together with the corresponding operational parameters and additional key performance indicators at this optimum.Key performance indicators
Minimizing the cost of DAC is the main objective. Fig. 2 (left) already shows the result of the optimization algorithm for two sets of ambient conditions. By extending this for condition throughout the feasible operating range, we map the cost of DAC as function of temperature and relative humidity (Fig. 2, right). The operating condition with the lowest costs is found at 35 °C and 50% RH with an estimated price of 290 €/tCO2. In contrast, at 0 °C and 100% RH, when it is most expensive, the estimated price is 555 €/tCO2. These values for the cost of DAC depend on the assumptions and estimations made regarding, for example, capital investment and sorbent lifetime. Moreover, it is valid for this specific sorbent. Literature values for the cost of DAC vary widely, most likely due to these assumptions.1,28–34It is unmistaken that high temperatures are beneficial for Lewatit® VP OC 1065, with an optimum between 30 and 35 °C, depending on the relative humidity. Additionally, a lower relative humidity is generally preferred, especially at low temperature. Therefore, a high relative humidity and low temperatures are preferably avoided. The influence of relative humidity on the cost of DAC seems smaller than the influence of temperature. However, a strong increase is observed towards high relative humidity at very low temperature. This is related to the pore condensation regime of the H2O adsorption isotherm resulting in a very high H2O equilibrium capacity. Experimental data to support these high H2O co-adsorption values are however scarce or absent and therefore these conditions require special attention in follow up studies. An optimization study by Wiegner et al.13 concludes opposing trends with beneficial operation at low temperature and high humidity. This is directly related to the properties of the investigated sorbent. In that case, the sorbent has a very high CO2 equilibrium capacity at cold, humid conditions. Combined with an adsorption rate that is independent of temperature resulted in a different beneficial climate for that sorbent. Hence, these optimization algorithms are excellent tools to match the appropriate sorbents to a certain climate.
The cost of DAC is calculated directly from the values for the productivity and energy duty. It may not be a surprise that these follow the same general trend as the cost of DAC (Fig. 3). Important performance indicators to determine the energy duty and productivity are CO2 and H2O working capacity, cycle time, gas efficiency, pressure drop and purge gas ratio. These values are provided in ESI4† for each combination of ambient condition. At low temperature the slow kinetics cause a low adsorption rate, and thus low productivity. A higher relative humidity causes a higher H2O sorbent loading, which results in a longer desorption time. The CO2 equilibrium capacity decreases with increasing temperature. At high temperature, when reaction kinetics are fast, the CO2 equilibrium capacity can become limiting. Such a trade-off is observed at high temperature and low relative humidity, where the productivity has a maximum when varying temperature.
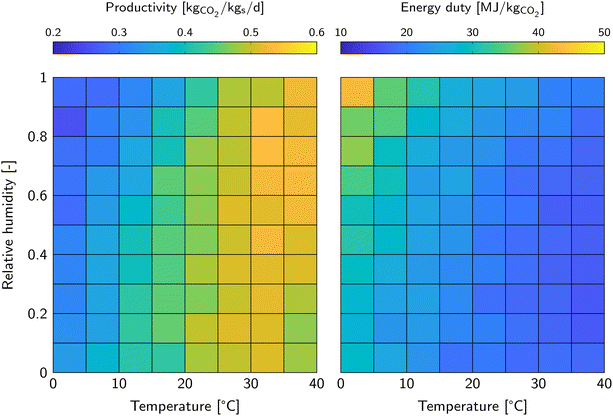 | ||
| Fig. 3 Productivity (left) and energy duty (right) corresponding to the minimum cost of DAC for the varying ambient conditions. | ||
The energy duty is in general relatively high in this study. The lowest value is 16 MJ kgCO2−1 at 35 °C and 30% RH, whereas the highest value is 45 MJ kgCO2−1 at 0 °C and 100% RH (Fig. 3). Note that this is not the lowest possible energy duty, but the energy duty that corresponds to the lowest cost of DAC as visualized in Fig. 2 (left). The corresponding productivity is relatively high as well. It shows that, with the prevailing assumptions for the economic analysis, achieving a high productivity is more important than achieving a low energy duty. Interestingly, studies on DAC tend to put more emphasis on a low energy duty, but neglect to mention the corresponding productivity. Both, cost of sorbent renewal and initial capital investment, have a significant impact on the cost of DAC.
This optimization is based on the characteristics of a DAC pilot unit developed in a previous study.20 That study included several suggestions for scaling-up regarding design and operation of the technology. These were not yet implemented in this optimization study. Therefore, further improvement of productivity, reduction of energy consumption and thus reduction of the cost of DAC is definitely possible via advances in the design of both the gas–solid contactor and the process operating conditions.
Operational parameters
The minimum cost of DAC for each weather condition calculated in the previous section corresponds to a certain set of operational parameters. Obviously, this set of operational parameters has to be applied to be able to operate at minimum cost. As a result, with varying ambient conditions (seasonal and/or diurnal) a dynamic process control strategy could be necessary. The complexity of process control is affected by the spread in optimal operational parameters on one side and the spread in ambient conditions at the particular location on the other side. The spread and trends in operational parameters will be covered in this section.Fig. 4 shows all operational parameters that result in the minimum cost of DAC for the relevant temperature and relative humidity combinations. The superficial gas velocity, lean CO2 loading and adsorption are relevant for the adsorption phase, whereas the desorption pressure and purge gas flowrate are relevant for the desorption phase. The sixth operational parameter is the desorption temperature. Its value was fixed at 120 °C for all evaluations and is therefore not shown in the figure. Using the lean CO2 sorbent loading as parameter was proven to be very convenient for modelling steady-state adsorption-regeneration cycles. For process control on the other hand, it difficult to monitor and act upon. The combination of lean CO2 sorbent loading and adsorption time results in a certain desorption time. That is easy to control and is therefore shown in Fig. 4 as well.
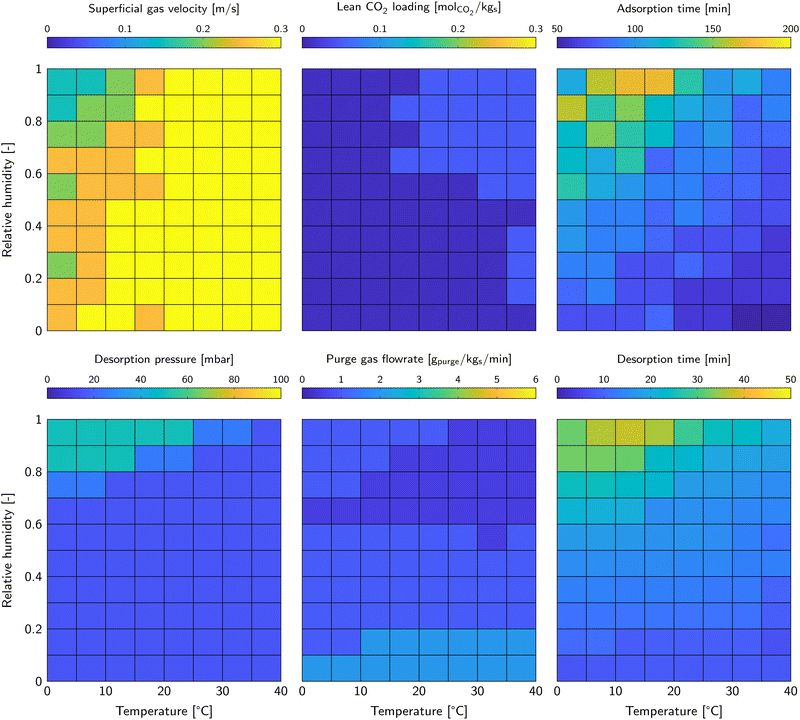 | ||
| Fig. 4 Operational parameters that result in the minimum cost of DAC for each combination of temperature and relative humidity. The colour scheme corresponds to the colourbar above the figures. | ||
The superficial gas velocity is preferably high. Above 20 °C it has a value of 0.3 m s−1, which is the highest superficial gas velocity considered in the evaluation. Flexible boundaries of the operational parameters were not implemented in this algorithm, but is a potential improvement in future studies. It is a result of the preference for a high productivity over a low energy duty. The superficial gas velocity decreases at lower temperature. Then, reaction kinetics limit the adsorption rate, reducing the need for a high CO2 supply rate. The lean CO2 sorbent loading is low for all conditions. As it appears, the longer desorption time to reach such a low CO2 sorbent loading pays off in terms of the higher adsorption rate at the start of the adsorption phase. The adsorption time varies widely from a very short adsorption phase of only 50 minutes for hot, dry conditions and up to three hours for humid conditions at moderate temperature. High relative humidity asks for a longer adsorption time to suppress the H2O co-adsorption costs by increasing the CO2 working capacity. In that case, both H2O and CO2 sorbent loadings are relatively high, which shows in a very similar trend regarding the desorption time.
The desorption pressure is as low as possible for the majority of the ambient conditions. Only at a combination of low temperature and high relative humidity, less vacuum is more beneficial. This is likely due to the large amounts of co-adsorbed H2O that is processed by the vacuum pump. Moreover, fast desorption is not crucial, since the adsorption time dominates the cycle length anyway. Adsorption is fast at low relative humidity and high temperature, which calls for fast desorption. Therefore, the desorption pressure as well as the purge gas flowrate is set to enhance the desorption rate.
Effect of climate conditions
The analysis from the previous chapter does not provide us with the actual cost of year-round DAC. It only gives a value at a certain moment in time depending on the ambient conditions. This introduces a climate dependency, which will be assessed in this section. Here, we determine the actual cost of DAC for year-round operation for various locations around the world.Fig. 5 visualises the chosen approach for two locations with a completely different climate: Amsterdam and Bonaire. The contour lines established in Fig. 2 form the basis of the analysis as they represent the cost of DAC at that certain ambient condition. The data points are the average temperature and relative humidity over a six-hour period for the complete year of 2021.35 Each of these data points correspond to a certain cost of DAC in that time period and is obtained via linear interpolation of the contour lines, i.e. the minimum cost of DAC as determined with the optimization algorithm. The cost of DAC at that location is than the average of all data points. Note that the scope of this study is to assess the effect of climate on the cost of DAC and not of other aspects that are location dependent, such as cost of labour and cost of capital. Moreover, the choice and cost of the energy source will depend on the availability of renewable energy sources at that location.
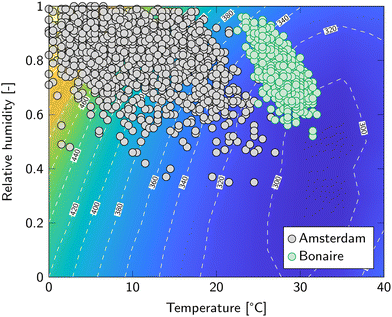 | ||
| Fig. 5 Cost of DAC analysis for Amsterdam and Bonaire. The contour represents the cost of DAC and is identical to Fig. 2. Data points are six-hour averages of temperature and relative humidity in 2021.35 | ||
Amsterdam has an oceanic climate, which is classified as type Cfb in the widely used Köppen climate classification.36 It is characterized by cool summers and mild winters with frequent precipitation. This generally means a high relative humidity and moderate to low temperature (Fig. 5). The average year-round cost of DAC is then 433 €/tCO2. Bonaire, on the other hand, has a hot semi-arid climate (type BSh) with uniform hot, humid weather and little precipitation. This is characterized by a narrow temperature zone of 25 to 30 °C and a relative humidity only a little lower than Amsterdam (Fig. 5). From the previous section is became already evident that temperature has a significant impact on the cost of DAC. For Bonaire, the year-round average cost of DAC is 317 €/tCO2, which is 27% lower compared to Amsterdam.
Temperatures above 40 °C and below 0 °C were deemed unsuitable for DAC. Amsterdam, however, experienced sub-zero temperatures during 4% of the year 2021. For other places, such as Reykjavik (Iceland) or Ulaanbaatar (Mongolia), this even approached 50%. In this analysis, these data points are simply ignored when averaging the average cost of DAC. To incorporate this more accurately, the amount of operating hours should be decreased in the economic analysis of the optimization algorithm. However, this level of detail falls outside the scope of the current study.
The same analysis to determine the cost of DAC is applied to many other world cities and is captured in Fig. 6. ESI5† provides the climate data per city for the selected set. Dubai shows the lowest cost of DAC of all evaluated cities (307 €/tCO2), closely followed by other cities in hot climates. In contrast, Reykjavik has the highest cost of DAC at 460 €/tCO2, although other cold, humid cities are not far behind. The cost of DAC is mostly influenced by the temperature, since the average temperature gives a good correlation with the cost of DAC (Fig. 7). On the other hand, no clear trend is visible with the relative humidity.
 | ||
| Fig. 6 The average cost of DAC for world cities grouped by the Köppen climate classification.36 The dashed lines separate subgroups within the main climate group, except for the continental group. The errorbars represent the standard deviation of the cost of DAC. | ||
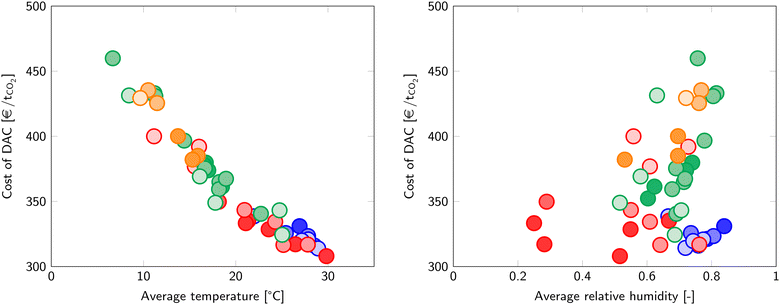 | ||
| Fig. 7 The effect of temperature (left) and relative humidity (right) on the cost of DAC. Marker colours refer to the Köppen climate classification in Fig. 6. | ||
These costs of DAC are only valid when the process operates under optimal conditions during the whole year. Therefore, operational conditions will change based on the ambient conditions. Fig. 4 showed that some parameters depend strongly on climate conditions, which could result in a complex control strategy. The error margins in Fig. 6 represent the standard deviation of the cost of DAC within a year. The standard deviation is directly related to the spread in ambient conditions and thereby complexity of operation. In other words, a low standard deviation results in a more static process operation. The tropical and hot dry climates have little variation in their cost of DAC over the year. Temperate climates show more variation already due to their distinct seasons and continental climates show the largest deviation in cost of DAC.
Conclusions
In this study, the effect of climate conditions on a DAC process was assessed via multi-dimensional optimization of an S-TVSA process. An optimization algorithm was developed to find the optimum operational parameter settings to achieve the minimum cost of DAC at a given combination of ambient temperature and relative humidity. Subsequently, the location specific weather conditions over the full year of 2021 were evaluated for a set of geographical locations covering all climates, to investigate the influence of climate conditions on DAC costs.Results of this optimization study show that climates with a high average temperature are most attractive for DAC. In a cold, humid climate, the cost of DAC is approximately 40% higher. Tropical and dry, hot climates have an additional advantage of relatively constant year-round conditions, which results in easier process operation. The varying seasonal weather conditions of temperate and continental climates require dynamic process control to operate at minimum cost of DAC throughout the year.
We focused only on effect of the climate and did not address all other location specific aspects that are relevant for the cost of DAC. Elements to consider can include accessibility of sustainable energy sources, availability of waste heat and labour costs. This would allow for a more accurate, location specific, estimation of the cost of DAC. Furthermore, downtime of the system at very low or very high temperature is not considered. Climates with a low temperature will then become even more unfavourable then reported in this work. Moreover, it could even be more beneficial to temporarily shut down operation above a certain cost of DAC, even though it is within the technological feasibility window. The presented results are therefore only the tip of the iceberg regarding the information this optimization algorithm can provide. Such as sensitivity studies and more in-depth insight on the variations in the operation and performance of a DAC process.
Overall, it can be concluded that the DAC process for harvesting CO2 from air, a sustainable carbon source that is available everywhere around the world, cannot be considered location independent in terms of performance and operation. For a location with significant variation in ambient conditions, active process control can significantly reduce the costs and the developed optimization framework can help in this, as well as in identifying the more beneficial locations for DAC.
Author contributions
Conceptualization: H. M. S., J. D. C., D. W. F. B.; methodology: H. M. S., J. D. C., D. W. F. B; software: H. M. S., J. D. C.; formal analysis: H. M. S.; investigation: H. M. S., J. D. C.; writing – original draft: H. M. S.; writing – review & editing: J. D. C., D. W. F. B.; visualization: H. M. S.; supervision: D. W. F. B.; project administration: H. M. S., D. W. F. B; funding acquisition: D. W. F. B.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by NORTH-WEST EUROPE INTERREG, grant number NWE 639 as part of the IDEA project (Implementation and Development of Economic viable Algae-based value chains in North-West Europe).References
- M. Erans, E. S. Sanz-Pérez, D. P. Hanak, Z. Clulow, D. M. Reiner and G. A. Mutch, Energy Environ. Sci., 2022, 15, 1360 RSC.
- G. Leonzio, P. S. Fennell and N. Shah, Appl. Sci., 2022, 12, 2618 CrossRef CAS.
- M. Low, L. V. Barton, R. Pini and C. Petit, Chem. Eng. Res. Des., 2023, 189, 745 CrossRef CAS.
- X. Shi, H. Xiao, H. Azarabadi, J. Song, X. Wu, X. Chen and K. S. Lackner, Angew. Chem., Int. Ed., 2020, 59, 6984 CrossRef CAS PubMed.
- M. Gholami, T. R. Van Assche and J. F. Denayer, Curr. Opin. Chem. Eng., 2023, 39, 100891 CrossRef.
- Orca: the first large-scale plant, https://climeworks.com/plant-orca, (accessed: December 2023).
- J. A. Wurzbacher, C. Gebald, S. Brunner and A. Steinfeld, Chem. Eng. J., 2016, 283, 1329 CrossRef CAS.
- M. Bos, S. Pietersen and D. Brilman, Chem. Eng. Sci., 2019, 2, 100020 CAS.
- V. Stampi-Bombelli, M. van der Spek and M. Mazzotti, Adsorption, 2020, 26, 1183 CrossRef CAS.
- H. M. Schellevis, T. N. van Schagen and D. W. F. Brilman, Int. J. Greenhouse Gas Control, 2021, 110, 103431 CrossRef CAS.
- A. Luukkonen, J. Elfving and E. Inkeri, Chem. Eng. J., 2023, 471, 144525 CrossRef CAS.
- J. Young, E. García-Díez, S. Garcia and M. van der Spek, Energy Environ. Sci., 2021, 14, 5377 RSC.
- J. F. Wiegner, A. Grimm, L. Weimann and M. Gazzani, Ind. Eng. Chem. Res., 2022, 61, 12649 CrossRef CAS.
- F. Kong, G. Rim, M. Song, C. Rosu, P. Priyadarshini, R. P. Lively, M. J. Realff and C. W. Jones, Korean J. Chem. Eng., 2022, 39, 1 CrossRef CAS.
- C. Gebald, J. A. Wurzbacher, A. Borgschulte, T. Zimmermann and A. Steinfeld, Environ. Sci. Technol., 2014, 48, 2497 CrossRef CAS PubMed.
- R. Veneman, N. Frigka, W. Zhao, Z. Li, S. Kersten and W. Brilman, Int. J. Greenhouse Gas Control, 2015, 41, 268 CrossRef CAS.
- C. Drechsler and D. W. Agar, Energy, 2020, 192, 116587 CrossRef CAS.
- J. M. Kolle, M. Fayaz and A. Sayari, Chem. Rev., 2021, 121, 7280 CrossRef CAS PubMed.
- H. M. Schellevis, PhD thesis, University of Twente, 2023.
- H. M. Schellevis and D. W. F. Brilman, React. Chem. Eng., 2024, 9, 910 RSC.
- M. J. Bos, T. Kreuger, S. R. A. Kersten and D. W. F. Brilman, Chem. Eng. J., 2019, 377, 120374 CrossRef CAS.
- R. T. Driessen, S. R. A. Kersten and D. W. F. Brilman, Ind. Eng. Chem. Res., 2020, 59, 6874 CrossRef CAS.
- M. Laumanns, L. Thiele and E. Zitzler, Eur. J. Oper. Res., 2006, 169, 932 CrossRef.
- M. Mesquita-Cunha, J. R. Figueira and A. P. Barbosa-Povoa, Eur. J. Oper. Res., 2023, 306, 286 CrossRef.
- C. Arpagaus, F. Bless, M. Uhlmann, J. Schiffmann and S. S. Bertsch, Energy, 2018, 152, 985 CrossRef CAS.
- G. Towler and R. Sinnott, Chemical Engineering Design, Butterworth-Heinemann, Oxford, 2020 Search PubMed.
- IRENA, Renewable Power Generation Costs in 2021, International Renewable Energy Agency, Abu Dhabi, 2022.
- M. Fasihi, O. Efimova and C. Breyer, J. Cleaner Prod., 2019, 224, 957 CrossRef CAS.
- N. McQueen, P. Psarras, H. Pilorgé, S. Liguori, J. He, M. Yuan, C. M. Woodall, K. Kian, L. Pierpoint, J. Jurewicz, J. M. Lucas, R. Jacobson, N. Diech and J. Wilcox, Environ. Sci. Technol., 2020, 54, 7542 CrossRef CAS PubMed.
- A. Sinha, L. A. Darunte, C. W. Jones, M. J. Realff and Y. Kawajiri, Ind. Eng. Chem. Res., 2017, 56, 750 CrossRef CAS.
- R. P. Wijesiri, G. P. Knowles, H. Yeasmin, A. F. A. Hoadley and A. L. Chaffee, Processes, 2019, 7, 503 CrossRef CAS.
- N. McQueen, K. V. Gomes, C. McCormick, K. Blumanthal, M. Pisciotta and J. Wilcox, Prog. Energy, 2021, 3, 032001 CrossRef.
- F. Sabatino, A. Grimm, F. Gallucci, M. van Sint Annaland, G. J. Kramer and M. Gazzani, Joule, 2021, 5, 2047 CrossRef CAS.
- P. Viebahn, A. Scholz and O. Zelt, Energies, 2019, 12, 3443 CrossRef CAS.
- World Temperatures – Weather Around The World, https://www.timeanddate.com/weather, (accessed: December 2023).
- H. E. Beck, N. E. Zimmermann, T. R. McVicar, N. Vergopolan, A. Berg and E. F. Wood, Sci. Data, 2018, 5, 180214 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00200h |
| This journal is © The Royal Society of Chemistry 2024 |