Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the effect of gas generation on heat transfer during thermal runaway of pouch cells
Niklas
Weber
 *a,
Sebastian
Schuhmann
b,
Robert
Löwe
c,
Jens
Tübke
b and
Hermann
Nirschl
a
*a,
Sebastian
Schuhmann
b,
Robert
Löwe
c,
Jens
Tübke
b and
Hermann
Nirschl
a
aInstitute of Mechanical Process Engineering and Mechanics, Karlsruhe Institute of Technology, Straße am Forum 8, 76131 Karlsruhe, Germany. E-mail: niklas.weber@kit.edu
bFraunhofer Institute for Chemical Technology ICT, Joseph-von-Fraunhofer-Straße 7, 76327 Pfinztal, Germany
cInstitute for Applied Materials – Energy Storage Systems, Karlsruhe Institute of Technology, Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
First published on 7th June 2024
Abstract
Lithium-ion batteries produce a vast amount of gases during decomposition reactions and thermal runaway. While the amount and composition of these gases has been investigated in the past, little is known about their impact on thermal transport inside the battery cell. Especially for pouch cells, which do not have a rigid housing, this becomes even more important in multi-cell scenarios since thermal propagation is governed by heat transfer. In this work, a simulation framework is presented that enhances the chemical single cell model by accounting for these thermal transport changes in gas producing pouch cells. It is validated by performing two battery cell propagation experiments in an autoclave. Besides the temperature measurement, the propagation time between the cells and the gas composition are analyzed and compared between simulation and experiment. Further, it is investigated how the application of an external pressing force impacts the heat transfer and thus the propagation behavior. In the given setup, the propagation time decreased from 37.2 s to 16.8 s with increasing pressing force.
1 Introduction
Li-ion batteries have become a key technology for energy storage. A major safety concern for the application of Li-ion batteries is the thermal runaway. It is characterized by self-accelerating uncontrolled decomposition reactions of the cell components such as anode and cathode active material and electrolyte.1–3 Thermal runaway can be triggered by thermal abuse, mechanical abuse which disintegrates the structure of the cell or electrical abuse like a short circuit or overcharge.4–6 It usually results in quick generation of vast amounts of heat and gases and potentially even fire and explosion.7,8In systems with multiple battery cells, further safety issues arise from thermal propagation. This term describes the thermal triggering of battery cell by heat transfer from its neighbour cell which underwent thermal runaway itself. In large packs, that creates the most severe incidents and therefore, several authors have investigated thermal propagation and strategies to prevent or mitigate it.9–12 This has lead into modelling approaches which are composed of a model for heat generation caused by thermal runaway reactions coupled with a thermal simulation13–15 and venting models.16
In our previous publication, we presented a chemical model consisting of ten decomposition reactions.17 It was used to predict the heat and gas generation of Li-ion batteries during thermal runaway triggered by heating with a constant ramp. Due to these decomposition reactions, thermally abused lithium-ion batteries start producing a significant amount of gas at about 90 °C.18 In opposition to cylindrical and prismatic cells, pouch cells do not have a rigid housing. Therefore, the gas generation causes inflation of the pouch bags. Huang et al. have shown that this affects the heat transfer within the battery cell19 by using a thermal resistance network model. Since thermal propagation is governed by heat transfer, there is a need to investigate how it is impacted by these effects in multi-cell arrangements or even large battery packs.
Thus, in this work, a model for heat transfer within gas producing pouch cells is developed. The previously developed model17 allows the thermal resistance of the battery to be directly coupled with the amount of produced gases, calculated during the chemical reaction simulation. A 3D thermal model is then applied for the full computation of the propagation behavior. Several stages are considered in order to take cell swelling, bursting and the rapid thermal runaway itself into account. The model is validated in an experimental thermal propagation setup with two pouch cells. This further allows to evaluate the impact of the heat transfer model on thermal propagation processes and its ability to predict propagation times. Since in applications pouch cells are usually tightly confined with high external pressing forces,20 it is further investigated how that impacts thermal transport and propagation time.
2 Experimental setup
2.1 Pouch cell assembly and preparation
For the experiments, pouch cells with a nominal 1C-capacity of about 12 Ah and a nominal voltage of 3.7 V were assembled. Double-sided coated and calendered graphite anodes and NMC622 cathodes as well as an Al2O3 particle supported non-woven polyethylene terephthalate separator are used. After the cell assembly, it is filled with LP30 electrolyte (1 M LiPF6 in EC/DMC 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt%), to which 3 wt% vinylene carbonate were added, and sealed under reduced pressure. The assembly of the battery cells including the process conditions are described in greater detail by Smith et al.21
50 wt%), to which 3 wt% vinylene carbonate were added, and sealed under reduced pressure. The assembly of the battery cells including the process conditions are described in greater detail by Smith et al.21
During the formation step, three cycles were executed. Initial charging utilized a constant current (CC) at C/10 until reaching a voltage of 4.2 V. The C-rate is defined as the current in ampere divided by the nominal capacity in ampere-hours. This is followed by charging at constant voltage (CV) until the current fell below C/20. Subsequently, the discharge was carried out using a CC of C/2, followed by two full cycles using C/2 during charge (CC–CV) and discharge (CC). Finally, the cells were charged to 3.64 V (equivalent to 20% State of Charge (SOC)) for storage until the thermal runaway tests were conducted. The produced pouch cells have dimensions of 230 mm × 176 mm × 3 mm and weigh 282 g.
For electrochemical characterization of the produced pouch cells, discharge rate tests were conducted at various C-rates ranging from C/20 to 3C. For these trials, the cells were first charged to 100% SOC with a CC–CV protocol. Then, the cells were discharged with a constant current until the cut-off voltage of 3 V is reached. The C-rate dependent capacity of the cells is displayed in Table 1. In order to check reproducibility, each test was repeated three times.
| Discharge current | Discharge capacity [Ah] |
|---|---|
| C/20 | 12.54 ± 0.01 |
| C/5 | 12.50 ± 0.01 |
| C/2 | 12.28 ± 0.01 |
| 1C | 11.97 ± 0.01 |
| 2C | 11.45 ± 0.01 |
| 3C | 10.84 ± 0.05 |
In order to prevent that any aging effects influence the thermal runaway experiments, the electrochemical characterization was conducted with identically built cells instead of the ones that were used for the propagation experiments.
Immediately before the propagation experiments, each cell is charged back to 100% SOC. For this, the cells are first charged with a C-rate of 0.5 until a voltage of 4.2 V is reached. Then, this voltage is kept constant until the current undercuts C/100 which marks the end of the charging process.
2.2 Test rig for propagation experiments
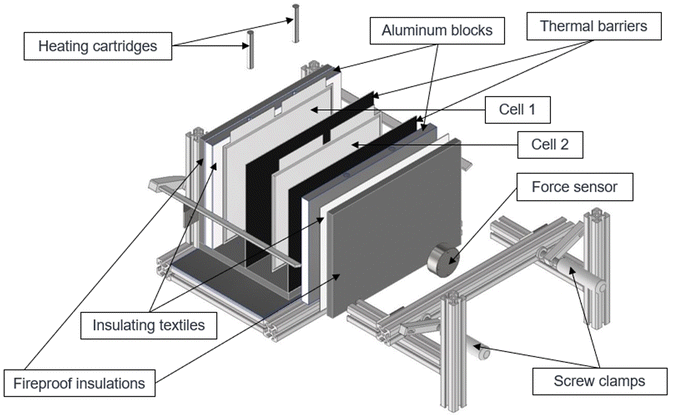
The thermal runaway battery experiments are carried out in a 125 L autoclave with an internal diameter of approximately 400 mm (DN400). For the tests, two cells are placed next to each other in a specially developed setup and separated from each other by thermal barriers. The cells are placed between two aluminum blocks, whereby one aluminum block can be heated with two heating cartridges with 300 W power each (total power of 600 W). In the following, the cell next to the heater will be referred to as cell 1 and the cell next to the unheated aluminum block will be called cell 2 as it is also shown in Fig. 2. As described in Section 2.3, different external pressing forces are applied. This is set by using two F-clamps and the pressing force is measured using a force sensor. The heating aluminum block is wrapped again with a thermal textile made of glass fiber so that the temperature between the aluminum block and the cells can be differentiated and to reduce heat loss to the outside. Furthermore, gypsum fiber plates were installed as fire protection boards on the outside to further insulate the test stand. For the tests, the aluminum block was heated with a linear temperature ramp of 4 K min−1, so that initially the heat input was only transferred to the first cell. The temperature ramp is maintained until the first cell goes into thermal runaway. The heating controller is then switched off and the system waits until the neighboring cell also enters thermal runaway.During the experiment, the temperatures are determined at different positions with type K thermocouples (Fig. 1):
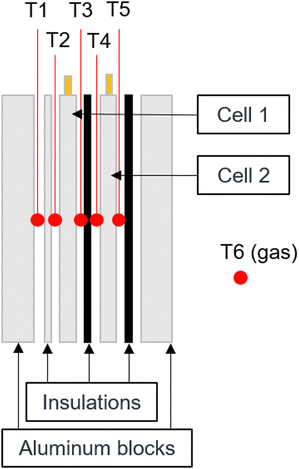 | ||
| Fig. 1 Schematic drawing of the test rig showing the thermocouple positions. They are placed in the middle between each layer. | ||
• T1: Heated aluminium block
• T2: Cell 1 left side (heater side)
• T3: Cell 1 right side (heater averted side)
• T4: Cell 2 left side (heater side)
• T5: Cell 2 right side (heater averted side)
• T6: Gas temperature
The cell voltage and gas pressure are also measured. 10 minutes after the first thermal runway, a gas sample is taken from a 1 L Tedlar bag and analyzed using a gas chromatograph (GC) with a flame ionization detector (FID) and a thermal conductivity detector (TCD).
2.3 Conducted trials
A total of seven experiments has been conducted with the procedure described in Section 2.2 in order to test the effect of various heat shields and different pressing forces on thermal propagation behavior. The first experiment can be seen as a reference experiment. No heat shield was placed between the two battery cells in this trial. In experiments 2, 3 and 4 two types of heat shields were investigated. One type is made of rigid mica and is tested in two different thicknesses, 0.2 mm and 1 mm. The other type is a compound material in which mica is combined with compressible fibre core. These first four experiments have been conducted with a low external pressing force of 50 N. The effect of a variation of the pressing force has been investigated in experiments 5, 6 and 7. An initial force of 450 N, 1170 N and 2150 N was applied respectively in these three tests.Table 2 summarizes the conducted experiments, listing the used heat shields and the initially applied pressing forces. All battery cells under testing were assembled and prepared according to Section 2.1.
| Label | Heat shield | Force [N] |
|---|---|---|
| 1 | None | 50 |
| 2 | Rigid mica sheet, 0.2 mm | 50 |
| 3 | Mica compound material, 1 mm | 50 |
| 4 | Rigid mica sheet, 1 mm | 50 |
| 5 | Rigid mica sheet, 1 mm | 450 |
| 6 | Rigid mica sheet, 1 mm | 1170 |
| 7 | Rigid mica sheet, 1 mm | 2150 |
3 Model description
3.1 Chemical model
The decomposition of the battery cell components during thermal runaway is represented by ten chemical reactions which are listed in Table 3. The anode main reaction R1 describes the reaction of intercalated lithium with electrolyte solvent, forming lithium carbonate on the anode surface.22,23 On the anode side, reaction R1 is main contributor to heat release. The main species on the anode surface at elevated temperatures are lithium fluoride and lithium oxide.24 Thus reactions R2 and R3 are included, which are the further reactions of lithium carbonate to the named lithium salts.24,25 LiF formation is enabled by the decomposition of the electrolyte's conductive salt LiPF6 (reaction R6),26,27 which creates fluor-containing species such as PF5 as a product. Reaction R6 further is the main fluor-containing species, found in the liberated gases.28 Besides the conductive salt, the electrolyte solvent is prone to degradation as well. For ethylene carbonate, the main reaction is the ring opening and polymerization under CO2 release as shown in reaction R7.29,30 Apart from decomposing, ethylene carbonate also evaporates (reaction R8).31,32 Both, reactions R7 and R8, contribute to the depletition of electrolyte solvent which limits the main heat generating reactions.33| No. | Description | Chemical equation | Reaction enthalpy | Ref. |
|---|---|---|---|---|
| R1 | Anode main reaction | 2LiC6 + C3H4O3 → Li2CO3 + C2H4 + 2C6 | −281.4 kJ mol−1 | 33 |
| R2 | LiF formation | Li2CO3 + PF5 → 2LiF + POF3 + CO2 | −77.1 kJ mol−1 | 33–35 |
| R3 | Li2O formation | Li2CO3 → Li2O + CO2 | 222.6 kJ mol−1 | 33 and 36 |
| R4 | Cathode, full oxidation | 5MO2 + C3H4O3 → 5MO + 3CO2 + 2H2O | −201.5 kJ mol−1 | 37 and 38 |
| R5 | Cathode, partial oxidation | 5MO2 + 3C3H4O3 → 5MO + 6CO + 4H2 + 3CO2 + 2H2O | −105.5 kJ mol−1 | 37 and 38 |
| R6 | Salt decomposition | LiPF6 → LiF + PF5 | 84.27 kJ mol−1 | 35 |
| R7 | Solvent decomposition | nC3H4O3 → (CH2CH2O)n + nCO2 | ||
| R8 | Solvent evaporation | C3H4O3 (l) → C3H4O3 (g) | 60.8 kJ mol−1 | 33 |
| R9 | HF formation | POF3 + 3H2O → 3HF + H3PO4 | −123.4 kJ mol−1 | 34 and 39 |
| R10 | Water gas shift | CO + H2O ⇌ CO2 + H2 | −41.2 kJ mol−1 | 34 |
For the cathode side, reactions R4 and R5 both describe oxygen release due to phase transition of the metal oxide. In both chemical equations M stands for the cathode metal which is Ni0.6Mn0.2Co0.2 in this work. The released oxygen reacts with organic electrolyte solvent in a full or partial oxidation reaction.38 While reactions R4 and R5 are among the main contributors to heat release, they are also important to include in the model for the production of the gaseous products CO2, H2O, CO and H2 which they majorly contribute to. For an accurate prediction of the release gas composition we further include water gas shift and HF formation reactions (reactions R9 and R10).28,40,41
Table 3 further includes the enthalpy of reaction for each reaction. Note that for reaction R7, a reaction enthalpy of 0 was assumed since this reaction does not significantly contribute to heat release and no literature values could be found for the undefined polymeric product. For a more detailed explanation of the used chemical reaction model we refer to our previous paper17 where it was first described.
The reaction rates ri are calculated by the power law (eqn (1)) where ki, xj and aj,i are the temperature dependent reaction constant of reaction i the mass fraction of species j and the according exponent for reaction i.
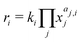 | (1) |
For all reactions except for the anode main reaction, ki is determined by using the Arrhenius law:
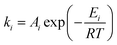 | (2) |
A i is the pre-exponential factor of reaction i, Ei the activation energy and R the universal gas constant. For the computation of the anode main reaction rate, we take inhibition caused by the deposition of lithium salts, especially lithium fluoride, on the anode surface into account. This inhibitive effect is considered by an exponential term exp(−z) where z is a modelling variable which is directly coupled with the current amount of LiF.17
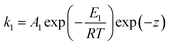 | (3) |
Using a modelling approach presented by Shurtz et al.,33z is limited to a critical value zcrit. This limits the described inhibition and the reaction kinetic becomes Arrhenius like once zcrit is reached. With the reaction rates calculated, the mass fraction of each species changes according to eqn (4). νi,j are the stoichiometric coefficients of species j in reaction i.
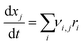 | (4) |
As an input for the chemical model, the initial mass fractions for each species is needed. These are computed viaeqn (5), using the individual volume Vi and density ρi of the species.
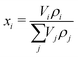 | (5) |
The results of the initial composition of the used battery cells is listed in Table 4 For the electrode and separator components, the volume Vi is calculated by the number ni, thickness si and porosity εi of the sheets:
| Vi = nisiAi(1 − εi) | (6) |
| Symbol | Value |
|---|---|
| λ B,⊥ | 0.5740 W m−1 K−1 |
| λ B,‖ | 23.39 W m−1 K−1 |
| ρ B | 2855 kg m−3 |
| c p,B | 1300 J kg−1 K−1 |
| h | 5 W m−2 K−1 |
| ε | 0.5 |
| x Anode | 0.1592 |
| x Cathode | 0.2762 |
| x Solvent | 0.1703 |
| x Salt | 0.0232 |
| x inert | 0.3711 |
3.2 Thermal model
The described chemical model is coupled with a thermal simulation. For both, the software OpenFOAM is applied. For the calculation of the temperature distribution a three-dimensional Fourier equation for heat conduction is used:15,42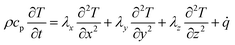 | (7) |
ρ and cp are density and heat capacity, λj is the thermal conductivity in direction j and ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) is the volumetric heat source. Eqn (7) is solved for each part of the test rig as it is described in Section 2. For the battery cells we use a homogenized thermal model. This means that the layers (e.g. electrode sheets) and their thermal properties are not modeled individually, but averages over all battery components are used. For this reason, the cell's thermal conductivity is to be considered anisotropic. In direction perpendicular to the sheets, which we define as x-direction, it can be determined as follows:43
is the volumetric heat source. Eqn (7) is solved for each part of the test rig as it is described in Section 2. For the battery cells we use a homogenized thermal model. This means that the layers (e.g. electrode sheets) and their thermal properties are not modeled individually, but averages over all battery components are used. For this reason, the cell's thermal conductivity is to be considered anisotropic. In direction perpendicular to the sheets, which we define as x-direction, it can be determined as follows:43
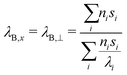 | (8) |
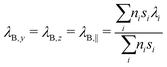 | (9) |
The volumetric heat source in the battery cell regions equals the heat released by chemical reactions as described in Section 3.1. With the reaction rates rk, determined by eqn (1), where ΔHr,k is the reaction enthalpy of reaction k.
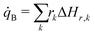 | (10) |
In the other regions, namely the insulations, the aluminum blocks and the heater rods, the thermal conductivity is isotropic and thus λx = λy = λz. The insulating textiles are considered thermally thin and thus, they are regarded in the boundary condition between the two adjacent blocks. Their heat capacity is neglected.
Except for the heater rods, there are no further heat sources. The volumetric heating power of the rods ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) H is controlled to conserve the given heating rate of 4 K min−1. The heat flux
H is controlled to conserve the given heating rate of 4 K min−1. The heat flux ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) BC to the surroundings is governed by a mixed convective and radiative heat transfer boundary condition:44
BC to the surroundings is governed by a mixed convective and radiative heat transfer boundary condition:44
![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) BC = h(TBC − Ts) + σε(TBC4 − Ts4) BC = h(TBC − Ts) + σε(TBC4 − Ts4) | (11) |
h is the convective heat transfer coefficient, ε and σ the emissivity and the Stefan–Boltzmann constant. TBC and Ts are the temperatures of the test rig on the boundary and the surroundings respectively. Table 4 lists the calculated thermal data of the battery cells and the parameters of the boundary condition.
3.3 Thermal resistance due to gas generation
As mentioned, the inflation of the pouch bag due to gas generation heavily impacts the total thermal resistance of the cell.19 The total thermal resistance Rtot is composed of the thermal resistance of the battery stack RB and of the produced gases Rgas. RB is composed of the thermal resistances of the electrode and separator sheets, the current collectors and the pouch bag. As a simple modelling approach, we assume that the gas forms layers with uniform thickness inside the battery cell. Perpendicular to the sheets, these thermal resistances are connected serially and the total resistance can be calculated according to eqn (12).| Rtot = RB + Rgas | (12) |
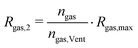
For modelling thermal resistance of the pouch cell during thermal runaway caused by external heating we can divide the process in four stages as follows:
 | (13) |
This model contains three unknown parameters: the maximum thermal resistance of the gases immediately before the first venting event Rgas,max, the amount of gas produced up to that point ngas,Vent and the gas thermal resistance in stage 3 Rgas,3. These parameters cannot directly be obtained from the experiments. Therefore, they are fitted with the temperature curves from experiments 1 to 4. As benchmarks, the time of the first venting event tVent and the temperature difference between the left and right side of cell 1, right before (ΔTVent) and right after (ΔT3) the first venting event are used. The three modelling parameters are fitted to minimize the root mean square error of these benchmarks over experiments 1 to 4. For this purpose, the simulations were repeatedly performed and the root mean square error was calculated with regard to the experimental data. The modelling parameters were then adjusted for the next simulation. This iterative process was repeated until the minimum of the root mean square error was found with an accuracy of four digits for the three modelling parameters. The root mean square errors of the three benchmarks in the final iteration step are listed in Table 5. Only experiments 1 to 4 are used for fitting since the objective of experiments 5 to 7 is to investigate the impact of the pressing forces on the parameters of this heat transfer model.
| Benchmark | Root mean square error |
|---|---|
| t Vent | 2.11 min |
| ΔTVent | 4.23 K |
| ΔT3 | 2.21 K |
4 Results and discussion
4.1 Thermal barrier tests
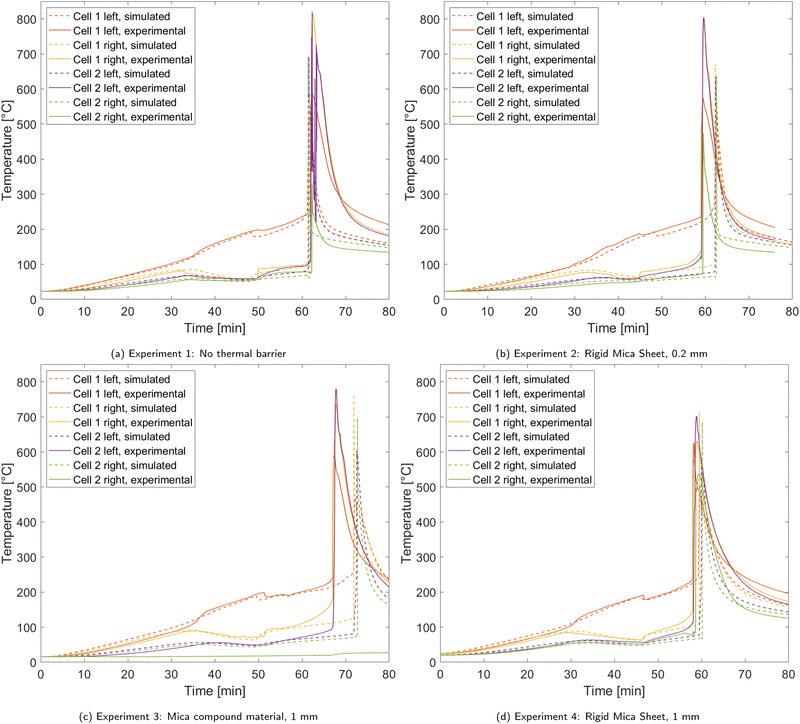
To analyze the thermal and chemical processes during the heat propagation experiments, the temperature curves are discussed first. Fig. 3 displays the temperatures of the two battery cells, measured on both sides of each cell, during experiments 1 to 4 in comparison with the according simulations.In the first 30 min of the experiments the cells are heated until cell 1 reaches about 100 °C. Starting at that point, the amount of gas produced inside cell 1 becomes notable in the temperature curves, causing a rise in temperature difference between the two thermocouples placed on cell 1 until the first venting event occurs. In this moment, there is a sudden drop in the temperature of cell 1 measured on the heater side and a jump of the temperature measured on the heater averted side. In literature, the Joule–Thomson effect is named as the reason for these temperature jumps at the first venting event.41,45–47 However, as this effect is not included in the model presented in this work, this agreement between experiment and simulation on the temperature jumps imply that the Joule–Thomson effect is not the only reason, but sudden changes in thermal transport properties affect this temperature jump as well. It has to be taken into account, that in references41,46,47 cylindrical cells have been under testing rather than pouch cells. Since cylindrical cells inflate less and the gas flow at the venting event has a much higher velocity, the Joule–Thomson effect is likely contribute to the temperature drop than in pouch cell experiments. Thus, dependent on the set-up, it is important to consider various potential reasons for this behavior. After the breakage of the pouch bag, the cells are steadily heated by the cartridges until self-heating sets in due to the decomposition reactions. When the first cell has gone into thermal runaway, the second cell is quickly heated to its own onset temperature because of the massive temperature difference between the cells. Thermal runaway then also occurs in the second cell. After both cells have reached their peak temperature due to the depletion of reactants, the cells cool down via heat transfer to the aluminum blocks, insulations and the surrounding gas.
The comparison between the four trials reveals that the initial heating stage, the swelling of the cell and the first venting event take place similarly, regardless of which thermal barrier is used. However, even in these early stages of the trials, the influence of the thicker thermal barriers in experiments 3 and 4 already manifests in a bigger temperature difference between the two cells. Some deviations among the trials occur in terms of thermal runaway time. Overall, the onset of rapid thermal runaway happens after about one hour after the start of the heating ramp. In experiment 3, it is delayed by some minutes due to a brief malfunction of the heater. Further, some artifacts in the experiments temperature curves can be observed during rapid thermal runaway due to the extreme conditions.
With the data of the four experiments, the amount of gas that is produced before the first venting event is fitted to ngas,Vent = 0.1473 mol kg−1. Note that it is normed to the total mass of the battery cell. For the entire cell, this equals 41.5 mmol which is about 3.1% of the gas generated during the entire simulation. The thermal resistance of the gases at the time of the first venting event is fitted to Rgas,max = 0.1686 m2 KW−1 and the gas thermal resistance in stage 3 to Rgas,3 = 0.0564 m2 KW−1.
With these parameters, the simulation model is able to describe the swelling and venting behavior of the cells during the heating ramp very well. The onset temperature of rapid thermal runaway is also met with adequate accuracy in all four cases which further proves validity of the chemical model. However, in rapid thermal runaway, some deviations between simulation and experiment occurs which are likely to be caused by thermal transport phenomenons. Thus, that will be further discussed in the following.
For a more detailed analysis of the thermal transport inside the battery cell, Fig. 4 further shows the temperature difference between the heater side and the heater averted side of battery cell 1. The data is taken from experiment 4 as an example and compared with the simulation. In the first stage, until significant amount of gases are produced, the temperature difference curve shows a slight, linear increase up to 9 °C after 27 min. After that, when gas is generated, it creates further thermal resistance in the cell which increases over time. For this reason, the increase in temperature difference is much steeper than in the gas free heating stage before until the local maximum is reached at 130 °C. The deviation of the experimental data from the simulation between around 30 and 35 min is caused by the compression of the insulating textile between battery cell and heater block which lowers its thermal resistance. This effect is not modelled in the simulations. When the pouch seam breaks, a sudden drop of the temperature difference from about 130 °C to 100 °C is observed. As mentioned above, this can be attributed to the quick release of gas from the pouch bag, causing the cell's total thermal resistance to drop as well.
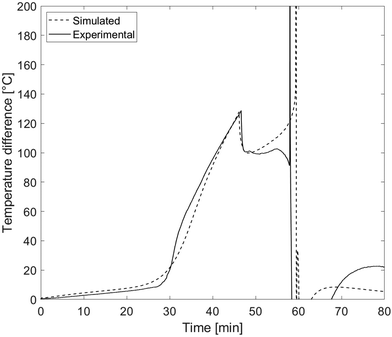 | ||
| Fig. 4 Temperature difference between the heater side and the heater averted side of cell 1 in experiment 4. | ||
In the next heating stage, the most significant difference between experimental and simulation occurs. In the simulation, the temperature difference steadily increases until the transition into rapid thermal runaway. In the experiment on the other hand, there is a short decrease before the onset of rapid thermal runaway is reached. The most likely reason for this behavior is the rising gas production rate. While the total amount of gas within the pouch bag is assumed to be constant in this stage, the increasing gas flow rate inside the cell causes convection to become a non-negligible thermal transport mechanism in the minutes before rapid thermal runaway. Convective heat transport is also the reason for differences between simulations and experiments during the rapid thermal runaway itself. Especially the temperature distribution between the two sides of each cell deviates substantially, because no gas movement is simulated.
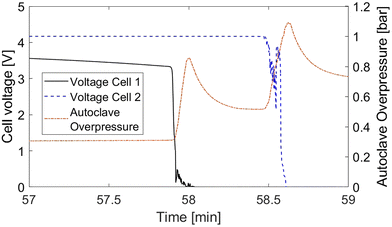
As a further measure for the model validity, we investigate the propagation time between the two cells due to its importance in applications. It is defined as the interval between the thermal runaway of cell 1 and cell 2. There are several options to obtain propagation time from experimental data, such as cell voltage, cell temperature and autoclave pressure. The analysis of temperature curves reveals that due to the interference of thermal transport processes, the cell temperature is not eligible for the determination of the thermal runaway time.
Fig. 5 shows the voltage curves for both cells and the autoclave overpressure as potential thermal runaway indicators. Again, the data is taken from experiment 4 as an example. For cell 1 the voltage drops suddenly at the beginning of rapid thermal runaway, which is marked in the diagram by the steep increase in autoclave pressure. The voltage of the second cell however displays a noisy signal around the rapid thermal runaway which makes it difficult to clearly define the runaway time. For this reason, we choose the autoclave pressure as thermal runaway indicator for the propagation time evaluation. Over all trials, the overpressure proved to be the most assessable and reliable measure.
Table 6 shows the comparison of propagation times between experiments and simulations. In the reference trial without any thermal barrier between the two cells, thermal propagation takes 18.1 s and 16.6 s in experiment and simulation respectively. The thin 0.2 mm mica barrier is barely able to delay the thermal runaway of the second cell in the given setup. Both 1 mm barriers however prolong the propagation time notably. In the experiments, the delay is 32.9 s for the mica compound sheet and 37.2 s for the rigid mica sheet. While the simulations are able to predict propagation times in experiments 1, 2 and 4 within a small margin, an overprediction of 15.3 s is found in experiment 3 with the compressible mica compound sheet. A probable reason for this deviation is the compressibility of the thermal barrier used in this trial. The mechanical stress on barrier caused by thermal runaway of the nearby battery cell compresses it which decreases its thermal resistance resulting in a lower propagation time than in the simulation.
| Experiment | Heat shield | Exp. propagation time [s] | Sim. propagation time [s] |
|---|---|---|---|
| 1 | None | 18.1 | 16.6 |
| 2 | Rigid mica sheet, 0.2 mm | 18.6 | 17.7 |
| 3 | Mica compound material, 1 mm | 32.9 | 48.2 |
| 4 | Rigid mica sheet, 1 mm | 37.2 | 41.0 |
4.2 Tests under elevated pressing forces
In experiments 5 to 7 a higher external pressing force was applied to the test rig compared to experiments 1 to 4 as displayed in Table 2. A 1 mm thick rigid mica barrier was used between the two cells like in experiment 4, which we therefore use as a reference experiment in this section. Fig. 6 shows the temperature curves of experiments 5 to 7 in comparison with the simulations. In all three experiments, some major differences to the reference experiment 4 occur. The temperature difference between the two sides of cell 1 before and after the first venting event are much lower. This is directly linked to a lower gas thermal resistance caused by the external pressing force. The lower thermal resistance of cell 1 also leads into higher temperatures at cell 2 before the onset of rapid thermal runaway. In experiments 6 and 7, this causes a notable inflation of cell 2, which is marked in the temperature curves by a rising temperature difference between the two thermocouples placed on cell 2. Furthermore, the first venting event and the rapid thermal runaway happen earlier than in reference experiment.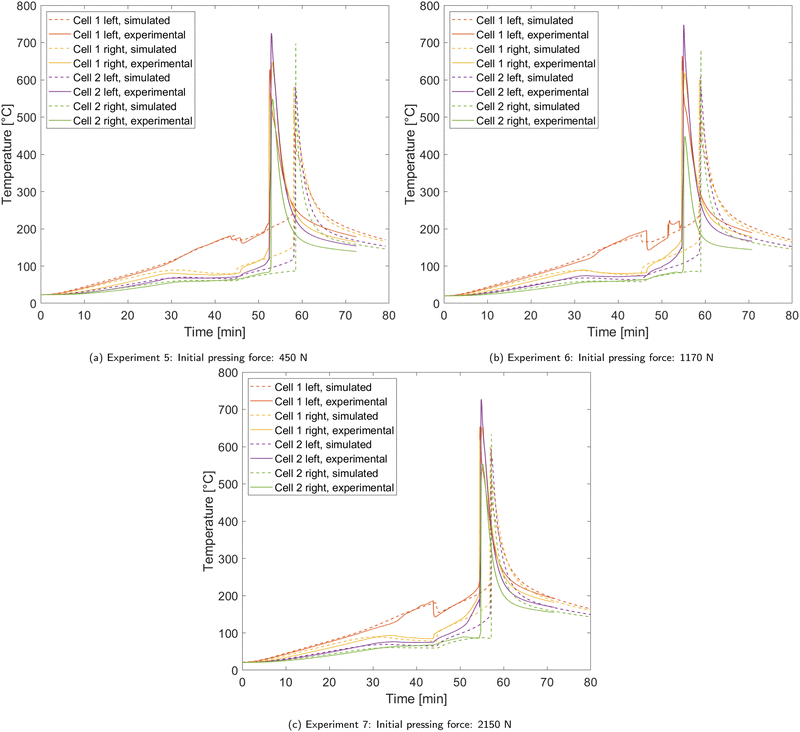 | ||
| Fig. 6 Comparison of temperature curves between experiments 5 to 7 and the according simulations. Temperature is measured on both sides of each cell. | ||
These differences also reflect in the parameters of the gas thermal resistance model. Table 7 displays the fitted parameters for experiments 5 to 7. It shows that in these three trials the maximum thermal resistance of the gases Rgas,max is about 37% lower on average compared to the cases with 50 N initial pressing force, but among experiments 5 to 7 the difference is low and there is no clear trend with the further rising initial pressing force. However, for the gas thermal resistance after the first venting event Rgas,3, a steady trend with increasing pressing force can be observed. The external force leads into a decrease of Rgas,3 due to lower thickness of the gas forming layers inside the cell.
| Experiment | Initial pressing force [N] | n gas,Vent [mol kg−1] | R gas,max [m2 KW−1] | R gas,3 [m2 KW−1] |
|---|---|---|---|---|
| 5 | 450 | 0.1473 | 0.1045 | 0.0219 |
| 6 | 1170 | 0.1473 | 0.1140 | 0.0135 |
| 7 | 2150 | 0.1473 | 0.1017 | 0.0090 |
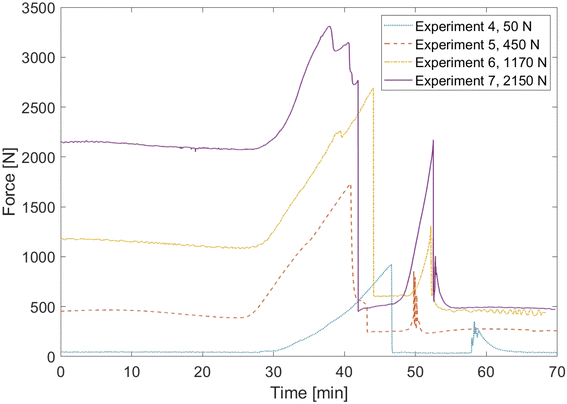
It is further notable that there is no need to adjust the parameter ngas,Vent for the simulations with increased pressing force since the deviation of the time of the first venting event is well within the error that was observed in the first four cases as well. This means that the amount of gas produced before the breakage of the pouch bag is independent of the externally applied pressing force. This finding is supported by results of the force sensor which are shown in Fig. 7. During all experiments, the measured force is approximately constant in the first 30 min until cell 1 starts swelling due to gas production. Then the force rises until the first venting event which results in a sudden drop of the measured force. The difference between the maximum force and the initial pressing force is between 900 N and 1500 N in each experiment and there is no clear dependence on the initial pressing force. This shows that the rise in pressing force compared to the initial state is an indicator for the breakage of the pouch seam rather than the absolute pressing force measured. The force curves also show that cell 2 produces an increasing amount of gas with higher pressing forces before rapid thermal runaway occurs.
The external pressing force also affects the propagation time of thermal runaway. Table 8 displays the experimental and simulated propagation times of experiments 5 to 7. In the given setup, a higher external pressing force leads into a lower propagation time, decreasing from 37.2 s at 50 N to 16.8 s at 2150 N in the experiments. The main reason for this behavior is reduction of the thermal resistance of gases inside cell 1. As described above, this causes cell 2 to preheat more before the occurrence of rapid thermal runaway, which largely affects the propagation time. The simulations capture this effect well, showing a decrease from 41 s at 50 N to 14.4 s at 2150 N. This proves that the changes in propagation time under different pressing forces are mostly governed by the heat transfer processes.
| Experiment | Initial pressing force [N] | Exp. propagation time [s] | Sim. propagation time [s] |
|---|---|---|---|
| 5 | 450 | 25.7 | 23.6 |
| 6 | 1170 | 21.6 | 17.9 |
| 7 | 2150 | 16.8 | 14.4 |
4.3 Analysis of liberated gases
In all experiments, gas analyses were performed as described in Section 2.2. For comparison with the simulation results, the main released species CO2, CO, H2 and short-chain hydrocarbons41 are taken into account and assessed relative to each other. Since the chemical model cannot cover the variant emerging hydrocarbon species, their amount is evaluated in a lump. The experimental and simulated gas compositions are shown in Fig. 8. It is apparent that the experimental data scatters a lot more than the simulated data. This phenomenon has been observed by other authors in the past, Koch et al. have reported similar scattering behavior for the gas composition in their large series of thermal runaway experiments on cells with similar composition.48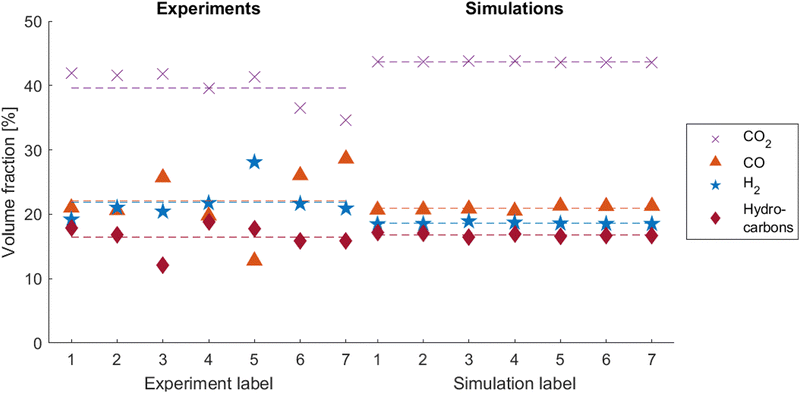 | ||
| Fig. 8 Experimental (left) and simulated (right) gas compositions. Dashed lines represent the average values. | ||
In all experiments and simulations, CO2 is the main component, averaging at 39.6% in the experiments and 43.7% in the simulations. It evolves from various decomposition reactions on both, the anode and the cathode side, as well as from the solvent polymerization reaction (see Table 3). CO and H2, both originating from the partial oxidation reaction of the solvent on the cathode side, are found with 22.1% and 21.9% on average respectively in the experimental gas analyses. In the simulations, the released gas contains 20.9% CO and 18.6% H2. Hydrocarbons primarily emerge from the anode main decomposition reaction. They are found with 16.4% in the experiments and 16.8% in the simulations.
In Table 9, these results are compared with the average gas composition of single cell tests, published in our previous paper.17 In both, simulations and experiments, some trends can be observed. In the two cell tests, a higher fraction of hydrocarbons but a lower fraction of CO is produced, compared to the single cell tests. Since the chemistry and the inner build-up of the cells is the same, the consistency of these trends proves that the composition of released gases is not only dependent on the cell itself, but also on the heating conditions. In addition, this also shows that the simulation framework is able to predict these trends in the gas composition caused by different testing setups. Therefore, the shown results in two-cell setups add further confidence to our previously published gas generation model by adding more validation data and predicting the trends caused by the different experimental setup.
| CO2 | CO | H2 | Hydrocarbons | ||
|---|---|---|---|---|---|
| Single cell | Simulated | 41.4% | 27.0% | 17.4% | 14.2% |
| Experimental | 40.8% | 30.0% | 18.8% | 10.2% | |
| Two cells | Simulated | 43.7% | 20.9% | 18.6% | 16.8% |
| Experimental | 39.6% | 22.1% | 21.9% | 16.4% |
It is further possible to extract in-depth information on the reasons for these composition shifts from the simulations which are hardly accessible with experimental techniques. Especially in the hydrocarbon fraction, there is a significant difference between the gases released from cell 1 and cell 2 in the two cell simulations, which causes the difference between one and two cell trials. Over the seven trials, the average content of short-chain hydrocarbons is 15.3% in the first cell and 18.0% in the second cell. Since hydrocarbons evolve from the anode main reaction (R1 in Table 3), we can conclude that this reaction progresses further in cell 2 than in cell 1. The reason for this is that less solvent is consumed in other reactions and especially due to evaporation. Due to slower heating, in cell 1 there is much longer time span between the first venting event and rapid thermal runaway in which solvent evaporates. Cell 2 is heated much faster by heat transfer from its neighbour cell and thus, more solvent is available for the anode main reaction.
5 Conclusion and outlook
In this work, a thermal transport model for 3D simulations of gas producing pouch cells is presented. It couples the thermal resistance of the battery with the amount of produced gases, obtained from a chemical model. This approach is applied on a setup with two pouch cells in order to investigate thermal propagation processes since these are highly dependent on heat transfer. Experimental validation is done by performing heat ramp trials with two cells, heated from one side. With this, we can prove that the simulations are able to predict the thermal behavior of the cells during different stages of the heating process, including the cell swelling, the first venting event and the onset of rapid thermal runaway, within a reasonable margin. Further, it is shown that the simulations are able to gain further insight on the thermal transport mechanisms. The findings are summarized in the following:• The total thermal resistance of the emerging gases inside the pouch rises linearly with the amount of produced gases up to the first venting event. After that, it can be considered constant until shortly before the onset of rapid thermal runaway.
• Few minutes before the onset of rapid thermal runaway and especially during rapid thermal runaway itself, the gas production rate becomes so high, that convective heat transfer via the outflowing gas has a notable impact on the temperature distribution inside the battery cell.
• Temperature drops, measured on the cell surface when the first venting event occurs, are often reported to be caused by the Joule–Thomson effect. Simulation results in this paper imply that a sudden change in thermal resistance of the cell is at least another reason for that. Dependent on the setup, it can potentially even become the main reason.
For applying the presented models on real battery systems, a correct prediction of propagation times is highly important. For this reason, various heat shields are tested experimentally and numerically. The simulation model is able to predict the propagation time between the two cells with a low deviation.
Further propagation experiments are conducted and modelled under elevated external pressing forces in order to investigate their influence on the thermal transport. The modeling results imply that the amount of gases produced until the cell bursts does not depend on the pressing force which is supported by the results of the force sensor. The thermal resistance before the first venting event and between the venting event and rapid thermal runaway however are notably diminished by the application of an external pressing force. Especially the latter also causes the propagation time between the two cells to be substantially reduced with increasing pressing force. We can conclude that the thermal behavior of gas producing pouch cells is not only dependent on the cell itself but also on external mechanical conditions which still leaves room for further investigation.
Finally, gas analyses are performed in all trials. The major components found are CO2 with 39.6% on average, CO (22.1%), H2 (21.9%) and short-chain hydrocarbons (16.4%). Comparing these results with single cell experiments that we previously published17 shows that the heating condition has a significant impact on the composition of the released gases. The most notable trends are an increase in hydrocarbon content and a decrease in CO content. These trends are in accordance with the simulation results, which underlines the validity of the chemical model. Moreover, it is pointed out how further in-depth knowledge on the reasons for changing gas composition can be obtained from the simulations by evaluating cell-by-cell gas release and detailed reaction progress. This helps to gain insight on information that is hard to access experimentally.
Abbreviations
| CC | Constant current |
| CV | Constant voltage |
| DMC | Dimethyl carbonate |
| EC | Ethylene carbonate |
| FID | Flame ionization detector |
| GC | Gas chromatograph |
| NMC622 | LixNi0.6Mn0.2Co0.2O2 |
| SOC | State of charge |
| TCD | Thermal conductivity detector |
Symbols
| A | Surface, pre-exponential factor in the Arrhenius equation |
| a | Reaction exponent |
| c p | Heat capacity |
| E | Activation energy |
| h | Heat transfer coefficient |
| H r | Reaction enthalpy |
| k | Reaction constant |
| n | Number, moles |
![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif)
| Heat flux |
| R | Thermal resistance, ideal gas constant |
| r | Reaction rate |
| s | Thickness |
| T | Temperature |
| t | Time |
| V | Volume |
| x | Mass fraction |
| z | Modelling variable for the inhibition of reaction R1 |
| Δ | Difference |
| ε | Porosity, emissivity |
| λ | Thermal conductivity |
| ν | Stoichiometric coefficients |
| ρ | Density |
| σ | Stefan–Boltzmann constant |
Subscripts
| B | Battery |
| BC | Boundary condition |
| gas | Gas related |
| i, j, k | Counting variables |
| max | Maximum |
| s | Surroundings |
| tot | Total |
| Vent | At the first venting event |
| x, y, z | Space variables |
| 1,2,3,4 | In stage 1,2,3,4 |
| ⊥ | Perpendicular |
| ‖ | Parallel |
Author contributions
Niklas Weber: conceptualization, investigation, methodology, software, visualization, writing – original draft, writing – review & editing. Sebastian Schuhmann: Conceptualization, investigation, methodology, validation, writing – original draft, writing – review & editing. Robert Löwe: investigation, validation, writing – original draft, writing – review & editing. Jens Tübke: funding acquisition, resources, supervision, writing – review & editing. Hermann Nirschl: funding acquisition, resources, supervision, writing – review & editing.Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Baden-Württemberg Ministry of Science, Research and the Arts within the project ‘AgiloBat’ (grant number 32-7533-4-161.2/9/12) as part of the Innovation Campus Mobility of the Future. The research was also supported by the state of Baden-Württemberg through bwHPC. We would further like to thank Michael Abert and Kevin Gneupel (both Fraunhofer ICT) for performing the gas analyses as well as Olivia Wiegand (KIT, IAM-ESS) for the assembly of the pouch cells.Notes and references
- H. Li, Q. Duan, C. Zhao, Z. Huang and Q. Wang, J. Hazard. Mater., 2019, 375, 241–254 CrossRef CAS PubMed.
- D. H. Doughty, E. P. Roth, C. C. Crafts, G. Nagasubramanian, G. Henriksen and K. Amine, J. Power Sources, 2005, 146, 116–120 CrossRef CAS.
- L. Huang, T. Lu, G. Xu, X. Zhang, Z. Jiang, Z. Zhang, Y. Wang, P. Han, G. Cui and L. Chen, Joule, 2022, 6, 906–922 CrossRef CAS.
- C. Essl, A. W. Golubkov and A. Fuchs, J. Electrochem. Soc., 2020, 167, 130542 CrossRef CAS.
- V. Ruiz, A. Pfrang, A. Kriston, N. Omar, P. Van den Bossche and L. Boon-Brett, Renewable Sustainable Energy Rev., 2018, 81, 1427–1452 CrossRef CAS.
- L. Huang, G. Xu, X. Du, J. Li, B. Xie, H. Liu, P. Han, S. Dong, G. Cui and L. Chen, Adv. Sci., 2021, 8, 2100676 CrossRef CAS PubMed.
- Q. Wang, B. Mao, S. I. Stoliarov and J. Sun, Prog. Energy Combust. Sci., 2019, 73, 95–131 CrossRef.
- Q. Wang, P. Ping, X. Zhao, G. Chu, J. Sun and C. Chen, J. Power Sources, 2012, 208, 210–224 CrossRef CAS.
- S. Gao, X. Feng, L. Lu, M. Ouyang, N. Kamyab, R. E. White and P. Coman, J. Electrochem. Soc., 2019, 166, A1653 CrossRef CAS.
- D. Becher, M. Bauer, H. Döring, O. Böse, B. Friess and M. A. Danzer, J. Energy Storage, 2021, 42, 103057 CrossRef.
- P. V. Chombo and Y. Laoonual, J. Power Sources, 2020, 478, 228649 CrossRef CAS.
- V. Talele, U. Moral, H. Najafi Khaboshan, M. S. Patil, S. Panchal, R. Fraser and M. Fowler, Int. Commun. Heat Mass Transfer, 2024, 155, 107527 CrossRef CAS.
- P. T. Coman, E. C. Darcy and R. E. White, J. Electrochem. Soc., 2022, 169, 040516 CrossRef CAS.
- X. Feng, X. He, M. Ouyang, L. Lu, P. Wu, C. Kulp and S. Prasser, Appl. Energy, 2015, 154, 74–91 CrossRef CAS.
- X. Feng, L. Lu, M. Ouyang, J. Li and X. He, Energy, 2016, 115, 194–208 CrossRef CAS.
- J. K. Ostanek, W. Li, P. P. Mukherjee, K. Crompton and C. Hacker, Appl. Energy, 2020, 268, 114972 CrossRef CAS.
- N. Weber, S. Schuhmann, J. Tübke and H. Nirschl, Energy Technol., 2023, 11, 2300565 CrossRef CAS.
- B. Lei, W. Zhao, C. Ziebert, N. Uhlmann, M. Rohde and H. J. Seifert, Batteries, 2017, 3, 14 CrossRef.
- Z. Huang, H. Wang, T. Yang, W. Tian, T. Dong and J. Wu, Appl. Therm. Eng., 2022, 217, 119255 CrossRef.
- J. Cannarella and C. B. Arnold, J. Power Sources, 2014, 245, 745–751 CrossRef CAS.
- A. Smith, P. Stüble, L. Leuthner, A. Hofmann, F. Jeschull and L. Mereacre, Batteries Supercaps, 2023, 6, e202300080 CrossRef CAS.
- R. Spotnitz and J. Franklin, J. Power Sources, 2003, 113, 81–100 CrossRef CAS.
- J. C. Hewson, H. Zhou, M. Parmananda, R. C. Shurtz and P. P. Mukherjee, MRS Bull., 2021, 46, 402–409 CrossRef CAS.
- O. Haik, S. Ganin, G. Gershinsky, E. Zinigrad, B. Markovsky, D. Aurbach and I. Halalay, J. Electrochem. Soc., 2011, 158, A913 CrossRef CAS.
- C. Forestier, S. Grugeon, C. Davoisne, A. Lecocq, G. Marlair, M. Armand, L. Sannier and S. Laruelle, J. Power Sources, 2016, 330, 186–194 CrossRef CAS.
- J. Jiang and J. Dahn, Electrochim. Acta, 2004, 49, 4599–4604 CrossRef CAS.
- H. Yang, G. V. Zhuang and P. N. Ross, J. Power Sources, 2006, 161, 573–579 CrossRef CAS.
- F. Larsson, S. Bertilsson, M. Furlani, I. Albinsson and B.-E. Mellander, J. Power Sources, 2018, 373, 220–231 CrossRef CAS.
- J. Lamb, C. J. Orendorff, E. P. Roth and J. Langendorf, J. Electrochem. Soc., 2015, 162, A2131 CrossRef CAS.
- Y. Yu, J. Wang, P. Zhang and J. Zhao, J. Energy Storage, 2017, 12, 37–44 CrossRef.
- F. Baakes, M. Lüthe, M. Gerasimov, V. Laue, F. Röder, P. Balbuena and U. Krewer, J. Power Sources, 2022, 522, 230881 CrossRef CAS.
- E. P. Roth and C. J. Orendorff, Electrochem. Soc. Interface, 2012, 21, 45 CrossRef CAS.
- R. C. Shurtz, J. D. Engerer and J. C. Hewson, J. Electrochem. Soc., 2018, 165, A3878 CrossRef CAS.
- M. M. Ghahremanpour, P. J. Van Maaren, J. C. Ditz, R. Lindh and D. Van der Spoel, J. Chem. Phys., 2016, 145, 114305 CrossRef.
- K. Gavritchev, G. Sharpataya, A. Smagin, E. Malyi and V. Matyukha, J. Therm. Anal. Calorim., 2003, 73, 71–83 CrossRef CAS.
- G. K. Johnson, R. T. Grow and W. N. Hubbard, J. Chem. Thermodyn., 1975, 7, 781–786 CrossRef CAS.
- R. C. Shurtz, J. Electrochem. Soc., 2020, 167, 140544 CrossRef CAS.
- R. C. Shurtz and J. C. Hewson, J. Electrochem. Soc., 2020, 167, 090543 CrossRef CAS.
- NIST Chemistry WebBook database, https://webbook.nist.gov/cgi/, Accessed: 2022-06-25.
- C. Schultz, S. Vedder, B. Streipert, M. Winter and S. Nowak, RSC Adv., 2017, 7, 27853–27862 RSC.
- A. W. Golubkov, D. Fuchs, J. Wagner, H. Wiltsche, C. Stangl, G. Fauler, G. Voitic, A. Thaler and V. Hacker, RSC Adv., 2014, 4, 3633–3642 RSC.
- S. Chen, C. Wan and Y. Wang, J. Power Sources, 2005, 140, 111–124 CrossRef CAS.
- D. Oehler, J. Bender, P. Seegert and T. Wetzel, Energy Technol., 2021, 9, 2000722 CrossRef CAS.
- P. Taheri, M. Yazdanpour and M. Bahrami, J. Power Sources, 2013, 243, 280–289 CrossRef CAS.
- R. Zhao, J. Liu and J. Gu, Appl. Energy, 2016, 173, 29–39 CrossRef CAS.
- P. T. Coman, S. Mátéfi-Tempfli, C. T. Veje and R. E. White, J. Electrochem. Soc., 2017, 164, A1858 CrossRef CAS.
- D. P. Finegan, M. Scheel, J. B. Robinson, B. Tjaden, I. Hunt, T. J. Mason, J. Millichamp, M. Di Michiel, G. J. Offer, G. Hinds, D. J. L. Brett and P. R. Shearing, Nat. Commun., 2015, 6, 6924 CrossRef CAS PubMed.
- S. Koch, A. Fill and K. P. Birke, J. Power Sources, 2018, 398, 106–112 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |