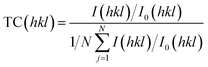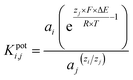A new compact potentiometric electrode for pH monitoring built upon a glass substrate with a Ce-doped SnO₂ layer

Abstract

A novel compact potentiometric electrode specifically designed for pH monitoring, featuring a good construction on a glass substrate coated with a cerium-doped tin oxide (Ce-doped SnO₂) layer. The Ce-doped SnO₂ thin film was created by spray-pyrolysis it on a glass substrate. Field emission scanning electron microscopy (FESEM) and X-ray diffraction (XRD) were used to characterize the deposited metal oxide coating. As a miniature potentiometric electrode, the synthesized Ce-doped SnO₂/glass substrate was utilized to measure a broad pH range (pH 2–12) in aqueous solutions. The electrode had a perfect near-Nernstian response (slope of −58.6 ± 0.7 mV per decade), high potential stability, mechanical durability, and great selectivity towards some common interfering cations and anions. These characteristics made it ideal for quality control and assurance purposes. The electrode's performance parameters and validation measurements were assessed using established procedures. The Ce-doped SnO₂-based electrode satisfactorily monitored the pH of several genuine water, drink, and fruit juice samples, and the data compared well with those obtained using a traditional pH glass electrode. The integration of Ce-doped SnO₂ as the active material marks a significant advancement, providing enhanced electrochemical stability, improved sensitivity, and a wider pH detection range compared to conventional electrodes. The compact design not only reduces the sensor's footprint but also facilitates its application in miniaturized and portable pH monitoring devices, making it highly suitable for advanced analytical and environmental sensing applications.

---

1 Introduction

Electrochemical pH sensors are popular because they respond quickly (less than 10 seconds), can measure pH levels from 2 to 12, are sensitive (near the Nernstian response of 59.12 mV pH⁻¹), are easy to attach to wearable or flexible materials, are biocompatible, and don't cost much to make. They are used in many areas, such as food processing, health monitoring, agriculture, and nuclear power. Ion-sensitive metal oxides (MO_x) with micro- and nanostructured shapes have received a lot of attention because they could be used in many scientific fields, such as electrochemistry and biomedical sciences. Their unique electrical, electrochemical, and biocompatible qualities demonstrate their value in the creation of sensors for use in industrial settings, wearable medical devices, and food and water quality monitoring, among other uses. MO_x increases catalytic activity, and sensitivity due to its high surface-to-volume ratio. Furthermore, MO_x is an excellent choice for the upcoming wave of online monitoring and wireless sensing applications because of their quick response time and extended lifespan in a variety of environmental situations. One of the main uses of MO_x among the different types of sensors in these applications is the creation of electrochemical pH sensors. MO_x is at the forefront of materials research due to the importance of pH in a variety of sectors, such as chemistry, agriculture, food processing, pharmaceuticals, environmental science, and chemical and biomedical engineering applications.^1–8 The measurement and regulation of hydrogen ion concentration—expressed in terms of the pH value-is crucial for many chemical and biological interactions. The pH level can significantly impact a person's physiological, biochemical, and medical conditions.^9–14

Advancements in pH sensing technology, using appropriate sensitive materials, have primarily focused on improving sensitivity, operational life, biocompatibility, rapid response in wider pH ranges, cost-effectiveness, and mobility. Recently, researchers have described several MO_x materials for the development of pH sensors in expanding fields such as flexible and wearable systems,^{1,3,5,15–20} biological and food quality applications,^10,21 and pollution monitoring.^22–24Fig. 1 shows a few instances of recently created pH sensors based on MO_x that are essential for our everyday lives. Given that several factors, including the rise of MO_x as a crucial component for the development of these sensors, determine a pH sensor's performance, this comprehensive evaluation of the MO_x-based pH sensor will be beneficial for future advancements in both fabrication and application. Examining the ionic exchange between sensitive nanomaterials and electrolytes is essential. The electrochemical characteristics of an aqueous solution, such as its pH level and ionic content, can drastically alter the electrodes' capacitance, impedance, and electrochemical potential.

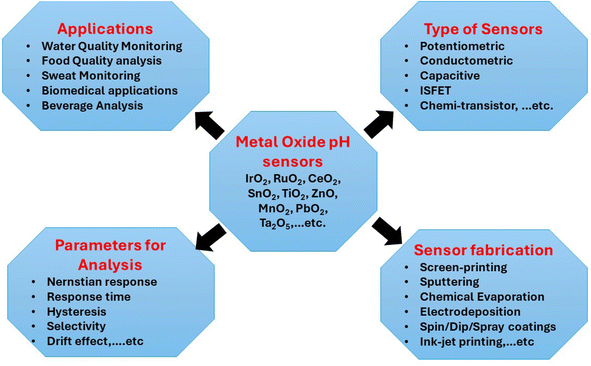Fig. 1 Different metal oxide-based pH sensors including essential techniques for fabricating sensors and preparing electrode materials, types of sensors, parameters for analysis, and applications.

Conventional glass-based sensors have been widely used to monitor pH. However, their deployment in new fields like wearable systems is hampered by their mechanical fragility and lack of flexibility and bendability. Moreover, their employment in industrial applications such as pollution monitoring is restricted due to their instability in performance at high temperatures and pressures and their durability. The limitations of glass-based sensors have prompted researchers to investigate pH-sensing methods that are not glass-based. Of these, MO_x-based pH sensors have garnered a lot of interest because of their near-Nernstian sensitivity, quick response time (<10 s), extended lifespan (>1 year), ease of miniaturization, and stability in a variety of environments, and the biocompatibility of most MO_x.

The choice of material composition and the deposition technique have a significant impact on the MO_x pH sensor's sensitivity because they can affect the material's microstructure, porosity, surface uniformity, and crystalline structure. This causes the electrodes' sensitivity to vary. Typically, we use the Nernstian response to express the sensitivity of pH sensors. If the sensitivity factor approaches the optimal Nernstian response of 59.14 mV pH⁻¹ at 25 °C, as calculated from the Nernst equation, the sensor should perform exceptionally well.

Ruthenium oxide (RuO₂) and iridium oxide (IrO₂), distinguished by their exceptional sensitivity to hydrogen ions and great accuracy, are the most well-known and frequently used oxides for the creation of pH sensors. For use as pH sensors, we can also tell the difference between these oxides: tantalum(V) oxide Ta₂O₅, titanium dioxide TiO₂, SnO₂, CeO₂, WO₃, and PbO₂, and mixed oxides Bi₂O₃–Nb₂O₅, IrO₂–TiO₂, and RuO₂–TiO₂. Furthermore, bismuth and antimony-based metal/MO_x-based pH sensors have been the subject of some research. The redox equilibrium between the metal/MO_x phases (e.g., Sb–Sb₂O₃) is believed to be the source of the pH sensitivity in these couples.^25,26 A comparison was made between the observed and theoretical sensitivity of several MO_x, namely IrO₂,^27,28 RuO₂,^23,29–33 TiO₂,^31,33,34 SnO₂,^29,35 Ta₂O₅,^23,36 WO₃,^37,38 CeO₂,³⁹ PbO₂,⁴⁰ MnO₂,⁴¹ and CoO₂.⁴²Table 1 compares the analytical properties of MO_x-based sensors, such as the pH measurement range, calibration curve slope, and response time.

Table 1 Metal oxide-based pH sensors—metal oxides as sensing components

Sensing material	Slope [mV pH^−1]	pH range	Time response, s	Ref.
RuO2	55.64	1–13	—	30
RuO2–TiO2	56.03	2–12	—	34
RuO2–Ni	52	1.5–12.5	—	31
RuO2–nanotubes	55	2–12	<40	32
RuO2–Ta2O5	56	2–12	<8	23
RuO2–SnO2	56.5	2–12	<5	29
IrO2	63.5	2–10	60	27
IrO2–TiO2	59.1	1–13	120	28
Ta2O5	58–59	2–12	0.3	36
SnO2	58.1	2–12	—	35
TiO2	58.73	1–11	—	33
WO3	44.85	1–7	—	37
WO3–nanotubes	41	2–12	<90	38
CeO2	38	7.2–10.8	—	39
PbO2	64.82	1.5–12.5	<1	40
MnO2	78.3	2–12	5	41
CoO2	54.9	1–12	<60	42

---

This work introduces a novel compact potentiometric electrode specifically designed for pH monitoring, featuring a groundbreaking construction on a glass substrate coated with a cerium-doped tin oxide (Ce-doped SnO₂) layer. The integration of Ce-doped SnO₂ as the active material marks a significant advancement, providing enhanced electrochemical stability, improved sensitivity, and a wider pH detection range compared to conventional electrodes. The compact design not only reduces the sensor's footprint but also facilitates its application in miniaturized and portable pH monitoring devices, making it highly suitable for advanced analytical and environmental sensing applications. This study represents a critical step forward in the development of next-generation pH sensors, combining innovative materials science with practical engineering solutions.

2 Experimental

2.1 Chemicals and reagents

Tin(IV) chloride (SnCl₄), cerium(III) chloride heptahydrate (CeCl₃·7H₂O) and all other chemicals were of the highest purity, purchased from Sigma-Aldrich (St. Louis, MO, USA) and used as received. Deionized distilled water was used throughout the present work. Britton–Robinson (BR) buffer solutions were prepared with pH ranging from 2 to 12. The buffer was prepared by dissolving 0.04 mol of H₃PO₄, H₃BO₃ and CH₃COOH in one liter of deionized water. The pH of the buffer solution was adjusted to 4.0 using 1.0 M NaOH, resulting in an ionic strength of approximately 0.044 M, which was counterbalanced by the concentrations of [H₂PO₄⁻], [CH₃COO⁻], and [H⁺]. This consideration is crucial for accurate determination of the selectivity coefficients.

2.2 Apparatus

All electrochemical measurements were carried out using a PalmSens4 (Bi)Potentiostat/Galvanostat/Impedance Analyzer [PalmSens BV, Houten, Netherland]. The data are collected using PSTrace 5 software (version 5.10). The electrochemical cell volume in all experiments was 10 mL, and all measurements were performed at room temperature. The pH of the solutions was measured using an Orion (Cambridge, MA, USA) Model STAR A211 pH mV⁻¹ m⁻¹. X-ray diffraction (XRD) (Bruker AXS-D8, Germany) and CuKα radiation (λ = 1.5406 Å) were used to study the synthesized undoped and Ce-doped SnO₂ thin films in the 2θ range of 10° to 90°. In addition, the surface morphology of the fabricated thin films was characterized, and the elemental composition was measured using an energy dispersive X-ray spectroscopy (EDS) instrument (QUANTA FEG 250 FE-SEM with an EDAX system, Netherlands) at 450 °C. The thickness of the undoped and Ce-doped SnO₂ thin films was measured using a UVISEL Plus ellipsometer (HORIBA Scientific, Japan).

2.3 Electrode fabrication

Non-phosphate detergents, deionized water, and isopropanol were used under sonication to clean the glass substrates and to make sure that no unwanted absorption—such as lipids—had taken place. Using a homemade pulsed spray pyrolysis (PSP) apparatus with a revolving heater, Ce-doped SnO₂ films are formed on glass substrates.^43,44 The Ce-doped SnO₂ layer was deposited after heating the substrate to a constant temperature of 450 °C. The distance between the substrate and nozzle is set at 30 cm. The system operates in an ON/OFF mode for 5 seconds at a time—1 second of ON and 4 seconds of OFF—with a total deposition duration of 20 min. To atomize the solution across the heated glass substrates at a flow rate of 2.5 mL min⁻¹, compressed dry air is delivered at a pressure of 2.5 bars. Fig. 2 illustrates the method of applying a handmade pulsed spray pyrolysis (PSP) apparatus to deposit the Ce-doped SnO₂ coating on the glass substrate.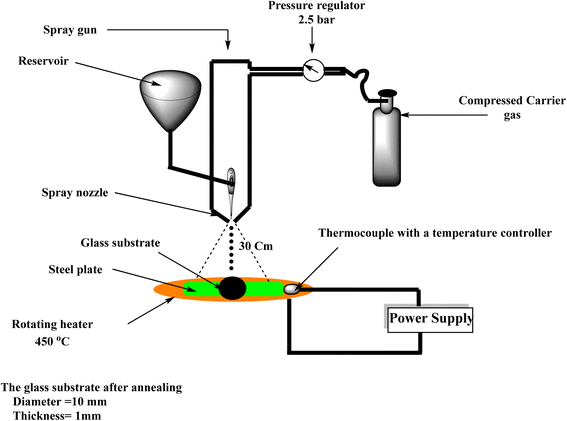

Fig. 2 An illustration shows the steps involved in applying a homemade pulsed spray pyrolysis (PSP) system to deposit a Ce-doped SnO₂ coating on a glass substrate.

2.4 Sensor assembly

After the spraying of the tin and cerium chloride solution onto the glass substrate (aluminosilicate glass), the coated glass was subjected to a thermal annealing process at 450 °C for 20 min, facilitating the conversion of the metal chlorides into their respective oxides. This process ensured the formation of a uniform Ce-doped SnO₂ layer on the glass substrate. Post-annealing, the glass disk with the oxide coating was cut into smaller pieces of 10 mm × 10 mm, ensuring that each piece had a uniform oxide coating on one face. To create a low-resistance contact, the aluminosilicate glass was coated with polyaniline (PANI), a conductive polymer with significantly lower resistivity than glass. Polyaniline provides a stable, conductive surface that reduces the overall resistance between the coated and uncoated faces of the glass substrate, which is crucial for potentiometric and impedance measurements. With PANI's resistivity in the range of 10⁰ to 10⁻¹ Ω cm, it ensures that the total resistance is indeed significantly lower than a gigaohm. A thin layer of silver epoxy paste, applied to the uncoated side of the glass slide, served to securely attach a thin copper wire. To minimize resistance, the epoxy was applied uniformly, and the connection was thoroughly tested for electrical continuity. We encapsulated the entire assembly to protect it from contact with the solution during measurements. Preliminary tests indicated that the electrical resistance of the connection was significantly lower than a gigaohm, ensuring that potentiometric and impedance measurements remain feasible. To prevent direct exposure of the electrical connections to the solution, the sensor was coated with a thin, chemically inert protective layer, leaving only the Ce-doped SnO₂ surface exposed to the solution.

2.5 Potential measurements

Using conventional potentiometric techniques, the potential response of the Ce-doped SnO₂/glass electrodes was measured. In conjunction with an Ag/AgCl/KCl 3.5 M double-junction reference electrode that was loaded with 10% (w/v) KNO₃, the Ce-doped SnO₂/glass electrode was used as an indicator electrode. The pH range of the Britton–Robinson buffer solutions was used to generate the calibration curve. After stabilizing to approximately ±1 mV, we took the potential readings and plotted the electromotive force (EMF) against the pH of the solutions.

For optimal performance, the Ce-doped SnO₂ sensors were soaked in deionized water for approximately 24 hours to ensure proper hydration of the surface and stabilization of the sensor's response. This soaking process allows the sensor to reach a steady-state potential, which is crucial for accurate pH measurements. After the initial conditioning, the sensors can be dried and reused without significant degradation in performance.

The fabricated pH electrode was subjected to a range of pH solutions, from 2 to 12, to investigate the response time. The potential corresponding to each pH was monitored for two minutes. Utilizing the two-solution method (TSM),⁴⁵ the pH electrode's selectivity coefficients against various interfering ions were determined. The glass substrate was subjected to electrochemical impedance spectroscopy (EIS) experiments in both undoped SnO₂ and Ce-doped SnO₂ membrane-based sensors. Using a pH 6 Britton–Robinson buffer, the Nyquist plot (−Z′′vs. Z′) was obtained under the open circuit potential with a frequency range of 100 kHz to 1.0 Hz.

3 Results and discussion

3.1 XRD analysis

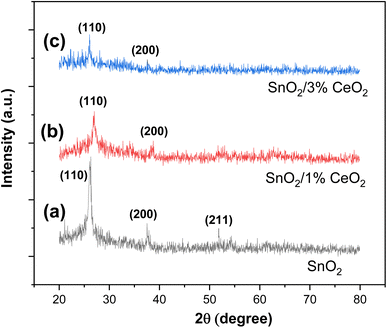
The XRD patterns of undoped and Ce-doped SnO₂ thin films are displayed in Fig. 3. The SnO₂ film that is not doped has a polycrystalline structure. The diffraction peaks at Θ = 26.12°, 37.69°, and 51.88° are in the (110), (200), and (211) planes, according to JCPDS card 41-1445. They are linked to the tetragonal phase of SnO₂ (space group P4₂/mnm). This finding indicates that a tetragonal phase is present in the undoped SnO₂ thin film. Fig. 3b and c show how the XRD patterns of undoped and Ce-doped thin films change structurally as the concentration of Ce varies. Peak intensity varies in response to an increase in Ce concentration. Ce concentrations up to 3 wt% still exhibit the tetragonal phase. Another important finding from the XRD study is that there are no peaks for other phases, like Ce₂O₃. This means that Ce³⁺ ions have replaced Sn⁴⁺ ions in the SnO₂ lattice.

Fig. 3 XRD spectra of (a) undoped, (b) 1% and (c) 3% Ce-doped SnO₂ thin films.

The XRD results (Fig. 3) indicate that the production of distortions and dislocations in the SnO₂ lattice most likely causes the decrease in peak intensity of the tetragonal phase with increasing doping concentration. These limitations are caused by the different ionic radii of Sn⁴⁺ (0.069 nm) and Ce⁴⁺ (0.088 nm), as well as the influence of doping during the nucleation process, which can either accelerate or impede the formation of SnO₂ crystallites.

Since the intensity of the (110) plane is higher, the (110) peak for the tetragonal phase has the strongest and greatest intensity. As a result, we can acknowledge that there may have been a preferred growth along this direction (110). Using the following formula to calculate the texture coefficient TC (hkl), a quantitative investigation of variations in preference orientation was carried out.⁴⁶

where N represents the reflection number, n denotes the order of peaks, I(hkl) represent the measured relative intensity of the plane (hkl), and I₀(hkl) represents the standard relative intensity of the plane (hkl) as determined from JCPDS data.

Table 2 summarizes the computed TC (hkl) for the elaborated samples for the (110), (200), and (211) planes. The texture coefficient must be greater than unity to define the desired growth orientation. For all SnO₂ tetragonal phase samples, the (110) plane dominates in intensity. Another noteworthy observation pertains to the differences detected between the TC (200) and TC (211) of the tetragonal phase and the TC (110) of the same phase. These data suggest that the axis (110) is the preferred growth direction for SnO₂ crystallites in the tetragonal phase.

Table 2 The crystallite sizes, lattice parameters, TC (hkl), and microstrains of undoped and Ce-doped SnO₂ thin films

Ce (wt%)	0%	1%	3%
Average crystallite size (nm)	21.43	24.62	27.52
Lattice parameters (Å)	a = 4.7339	a = 4.7356	a = 4.7321
	c = 3.1974	c = 3.1961	c = 3.1924
TC (hkl)	(110) 1.80	(110) 1.85	(110) 1.41
	(200) 0.55	(200) 0.69	(200) 0.65
	(211) 0.63	(211) 0.44	(211) 0.0.42
Microstrain (ε × 10^−5)	166	135	123
Cell volume (Å^3) (at^2 × ct)	71, 65	71, 67	71, 48

---

Using the following formulae, the lattice parameters of elaborated SnO₂ thin films were computed from the XRD pattern data to assess the impact of Ce doping on the volume of the crystalline SnO₂ cell.^47,48

2d sin θ = nλ

and

1/d_hkl² = h²/a² + k²/bc² + l²/c²

for the tetragonal phase.

The average sizes of crystallites were calculated using the Scherrer formula⁴⁹

D = 0.9λβ cos θ

where θ is the Bragg angle, β is the whole width at half maximum of the diffraction peak, D is the crystallite size, and λ the X-ray wavelength.

The results found are listed in Table 2. For the undoped sample, the calculated lattice parameters of the tetragonal phase are a = b = 4.7339 Å and c = 3.1974 Å, whereas the standard ones are a = b = 4.7382 Å, and c = 3.1871 Å for the tetragonal phase. It was noted that the tetragonal phase's lattice parameters slightly increase as the Ce concentration increases from 0 to 3 wt%. Given the large difference in ionic radius between Ce³⁺ and Sn⁴⁺, we hypothesize that the lattice distortions of SnO₂ caused by Ce doping are the reason for this shift in lattice parameters.

Table 2 shows the microstrains for the tetragonal phase, as well as the average size of SnO₂ crystallites. The estimated crystallite size and the microstrains in the tetragonal phase agree. It is evident that films with a larger crystallite size and reduced stress result from doping with 3 wt% Ce. The inverse relationship between microstrains and average crystallite sizes supports the generation of larger SnO₂ crystallites as the defect amount decreases, ultimately leading to the production of high-quality films with an average thickness of 986 nm which was obtained using ellipsometry.

The scanning electron microscopy (SEM) images depict the surface morphology of pure SnO₂ and Ce-doped SnO₂ thin films deposited on glass substrates via the spray pyrolysis technique (Fig. 4). The SEM image of the pure SnO₂ film shows a relatively smooth and uniform surface, with some agglomeration of particles, characteristic of nanostructured films. The grain size appears to be consistent across the surface, which is typical for films deposited using spray pyrolysis, indicating a controlled growth process. In contrast, the Ce-doped SnO₂ film exhibits a more heterogeneous structure with a slight increase in surface roughness. The incorporation of Ce into the SnO₂ matrix seems to have influenced the film's morphology by promoting the formation of larger and more defined grains, which can be attributed to the effect of Ce ions on the nucleation and growth dynamics during deposition. This modified surface morphology is likely to affect the electrical and sensing properties of the doped films, making them potentially more responsive in sensor applications.

Fig. 4 SEM images for (A) Ce doped SnO₂ and (B) SnO₂ films.

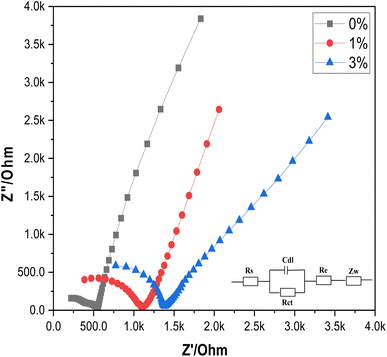
3.2 Electrochemical impedance spectroscopy (EIS) measurements

EIS is employed to study the impedance characteristics of both undoped and Ce-doped SnO₂ thin films as shown in Fig. 5. The impedimetric responses of these films provide insights into the underlying electrochemical processes, including charge transfer resistance and diffusion. The measurements reveal that both diffusion and charge transfer processes dominate the impedance behavior, which is consistent with the expectation for materials used in electrochemical applications. The experimental data were fitted using the traditional Randles' circuit model, a well-established approach for analyzing impedance data. In this model, R_s represents the solution resistance, R_ct is the charge transfer resistance, C_dl denotes the double layer capacitance, R_e represents the added high-resistance component, and Z_w represents the Warburg impedance, which is associated with the diffusion of electroactive species. The fitting of the data to this model allows for the quantification of these key electrochemical parameters. The analysis shows a significant difference in the charge transfer resistance between the undoped and Ce-doped SnO₂ thin films. The undoped SnO₂ exhibits a relatively low R_ct value of 349.8 Ω, indicating efficient charge transfer. However, when SnO₂ is doped with cerium, the R_ct values increase to 714.7 Ω and 578.8 Ω for 1% and 3% doping levels, respectively. This increase suggests that the introduction of cerium atoms into the SnO₂ lattice affects the charge transfer process, potentially due to changes in the electronic structure or surface chemistry of the doped films, which correlates with better electrochemical reactivity of the surface. This allows for more efficient electron exchange during protonation/deprotonation at the surface, a fundamental process for potentiometric pH sensing. In addition, the introduction of Ce into the SnO₂ matrix enhances surface activity by increasing the density of oxygen vacancies, which acts as active sites for the adsorption of H⁺ ions, essential for the potentiometric response. The reduction in R_ct combined with increased surface capacitance (C_dl) from the EIS data highlights enhanced surface charging behavior, crucial for a quick response to pH changes. This could be due to the increased surface area or more active sites provided by the doped SnO₂ films, which facilitate the accumulation of charge carriers. This suggests a trade-off between charge transfer efficiency and charge storage capability. This dual effect of doping is crucial for optimizing the performance of SnO₂-based electrodes in their potentiometric response. In conclusion, Ce-doping is introduced into the SnO₂ matrix to address specific limitations of pure SnO₂ in pH sensing. SnO₂ alone suffers from lower surface conductivity and limited sensitivity to pH changes due to fewer available surface sites for proton exchange. As evidenced by the EIS results, Ce doping reduces the overall impedance and enhances the conductive pathways for charge transport across the electrode surface. In addition, Ce-doped SnO₂ exhibits higher resistance to corrosion and chemical degradation under varying pH conditions, ensuring a longer sensor lifetime and consistent performance. The data presented in Table 3 further corroborate these observations and provide a quantitative basis for evaluating the impact of cerium doping on the electrochemical performance of SnO₂ thin films.

Fig. 5 Nyquist plot of both undoped and Ce-doped SnO₂ thin films using a pH 6 Britton–Robinson buffer; the Nyquist plot (−Z′′ vs. Z′) was obtained under the open circuit potential with a frequency range of 100 kHz to 1.0 Hz. The Nyquist plot includes data fitting based on an updated equivalent circuit model with an additional high-resistance element (R_e), accounting for the increased impedance due to Ce doping. This revised model reflects the higher resistance at the interface and accurately captures the electrochemical response of the Ce-doped SnO₂ film.

Table 3 Calculated data obtained from the Nyquist plot of both undoped and Ce-doped SnO₂ thin films

Electrode	R s (Ω)	R ct (Ω)	C dl (μF)
Undoped SnO2	187.2	349.8	41.4
Ce-doped SnO2 (1%)	379.7	714.7	60.2
Ce-doped SnO2 (3%)	772.9	578.8	62.6

---

The EIS results show that the Ce-doped SnO₂ sensor exhibits a significant change in charge transfer resistance (R_ct) and double-layer capacitance (C_dl) compared to undoped SnO₂. These impedance characteristics directly influence the potentiometric response of the sensor. Specifically, the increased R_ct observed in Ce-doped SnO₂ correlates with a slower charge transfer process, which impacts the sensor's sensitivity and response time. Conversely, the higher C_dl values are associated with improved capacitive effects, enhancing the sensor's ability to detect pH changes more accurately.

3.3 Potentiometric measurements

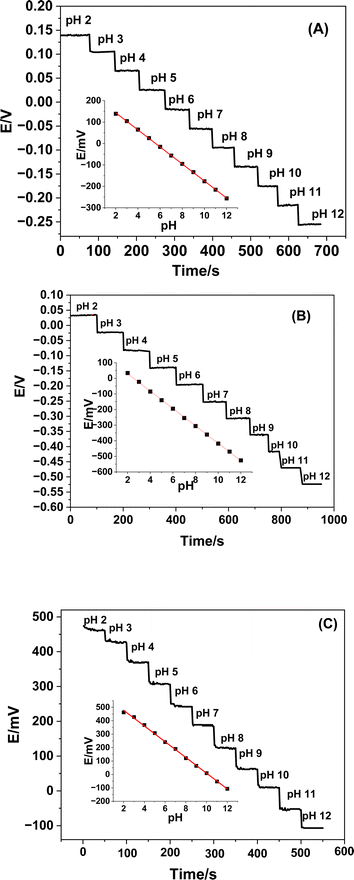
At ambient temperature, the potentiometric responses of both undoped and Ce-doped SnO₂ thin film-based sensors were assessed and tested in relation to pH changes. The fabricated sensors were submerged in Britton–Robinson buffer solutions in each scenario, which ranged in pH from 2 to 12, from the most acidic to the most alkaline. The pH of the solution under examination determines each sensor's potential, as Fig. 6 illustrates. Table 4 confirms that, despite differences in each plot's Nernstian slope, all plots are linear.

Fig. 6 Time responses of (A) the undoped Ce–SnO₂ based sensor and Ce-doped SnO₂ thin films-based sensors with (B) 1% doping and (C) 3% doping. [Inset: potential response of the proposed sensors versus pH of buffered solutions ranging from 2 to 12].

Table 4 Potentiometric performance characteristics of the fabricated pH sensors

Parameter	Undoped SnO2	Ce-doped SnO2 (1%)	Ce-doped SnO2 (3%)
Slope, mV per decade	−39.8 ± 0.2	−55.8 ± 0.3	−58.6 ± 0.7
Linear response range, pH	2–12	2–12	2–12
Correlation coefficient, r^2	0.9998	0.9997	0.9986
Average response time, s	∼15	∼13	∼10
Precision, (%)	1.1	0.9	0.7
Accuracy (recovery), (%)	99.2	99.4	99.2
Trueness, (%)	99.1	99.3	99.2

---

By immersing the electrodes in buffer solutions with pH ranges of 2 to 12 and monitoring the potential corresponding to each pH for two minutes, the response times of the manufactured sensors were assessed. Compared to un-doped Ce–SnO₂ based sensors, it was observed that Ce-doped SnO₂-based sensors require less time to reach the equilibrium state (Fig. 5). This is most likely the result of the sensors' distinct response mechanisms. The electrodes manufactured at doping percentages of 0.0, 1.0, and 3.0% exhibited average reaction times of 15, 13, and 10 s, respectively.

The near-Nernstian slopes observed for both the RuO₂–SnO₂ (ref. 29) and bare SnO₂ (ref. 35) sensors, as well as for the Ce-doped SnO₂ sensors, indicate that these materials are effective in providing a predictable and reliable potentiometric response over a wide pH range (pH 2 to 12). The fact that the 1% and 3% Ce-doped SnO₂ sensors exhibit near-Nernstian slopes (−55.8 mV pH⁻¹ and −58.6 mV pH⁻¹, respectively) similar to RuO₂–SnO₂ and bare SnO₂ highlights their potential as robust pH sensors. Although the Ce-doped sensors show similar pH ranges and slopes to the other sensors listed in Table 1, one of the unique aspects of the Ce-doped SnO₂ sensors is their improved sensitivity at lower doping levels. The 1% Ce-doped sensor, with a slope of −55.8 mV pH⁻¹, maintains high sensitivity while potentially offering advantages in stability and selectivity due to the incorporation of cerium. The 3% Ce-doped sensor further enhances this sensitivity, achieving a slope of −58.6 mV pH⁻¹, which is very close to the ideal Nernstian response. In contrast, the undoped SnO₂ sensor exhibits a significantly lower slope (−39.8 mV pH⁻¹), indicating a less efficient response in terms of sensitivity. This improvement in sensitivity with Ce doping suggests that cerium incorporation enhances the electrochemical properties of SnO₂, possibly by increasing the density of active sites or improving the electron transfer characteristics of the material.

Another critical attribute of the Ce-doped sensors is the potential improvement in stability and selectivity, which is not solely reflected in the calibration slopes but also in their operational robustness. Cerium doping is known to stabilize the SnO₂ structure and reduce the impact of interfering ions, which could explain the stable performance of the Ce-doped sensors across a wide pH range. While RuO₂–SnO₂ (ref. 29) and bare SnO₂ (ref. 35) sensors perform well, the introduction of cerium offers an additional layer of material stability and potentially enhances the long-term operational stability of the sensor.

3.4 Sensors' selectivity

To demonstrate the selective efficiency of the pH sensors in various matrices, the selectivity of the manufactured sensors towards some of the common interfering ions has been investigated. The selectivity coefficient values (K^pot) were computed using the following formula and assessed using the two solution method (TSM):⁵⁰
where a_i, z_i, a_j and z_j are the activities and the charges of the primary and the interfering ions, respectively. ΔE is the difference between the electrode potentials in a solution which contains both the primary (a_i) and the interfering (a_j) ions and solution which contains only the primary ion (a_i), knowing that (a_i) is the same in both solutions. Potentiometric measurements were conducted at a concentration of 0.1 M for the interfering ions, with an H⁺ ion activity of approximately 1.0 × 10⁻⁴ M at pH 4.0. The concentrations of all interfering ions are adjusted according to the appropriate activity coefficients (gamma) as per the Davies equation [the gamma value of 0.76 is correct for monovalent and of 0.6 for divalent interfering ions]. This activity reflects the reduced effective concentration of ions, which is critical for accurate K_A,_Bpot calculations, as outlined in IUPAC guidelines. Table 5 contains a tabulation of the selectivity coefficients. The product a_j × K_ij ≪ a_i indicates that the pH sensors exhibit good selectivity for H⁺ ions over the interfering ions, while accuracy is influenced by other factors such as drift and hysteresis. The determined constants reflect both the effects of the counterions and any resulting pH shifts, as well as the interference from the targeted ions.

Table 5 Selectivity coefficients of the fabricated pH sensors^a

Interfering ion	Log K^potij
	Undoped SnO2	Ce-doped SnO2 (1%)	Ce-doped SnO2 (3%)
a All anions and cations were in the form of sodium and chloride salts, respectively.
Na^+	−3.01	−3.24	−3.43
K^+	−3.13	−3.22	−3.31
Li^+	−3.43	−3.62	−3.87
NH4^+	−3.56	−3.74	−3.91
Ca^2+	−4.97	−5.02	−5.11
Mg^2+	−4.77	−5.00	−5.01
Ba^2+	−4.73	−4.87	−5.02
Cl^−	−3.02	−3.16	−3.19
NO3^−	−3.40	−3.51	−3.57
I^−	−3.40	−3.48	−3.67
SCN^−	−3.66	−3.72	−3.81
CH3COO^−	−4.12	−4.36	−4.44
PO4^3−	−5.32	−5.39	−5.43
NO2^−	−3.78	−3.88	−4.01

---

The impedance measurements provide insight into the sensor's selectivity towards different ions. The higher R_ct observed in Ce-doped SnO₂ films suggests a reduced interaction with interfering ions, enhancing the sensor's selectivity. The impedance data support the observed selectivity by indicating that the doped films have a more stable response to pH changes while minimizing interference from ions such as Na⁺ and K⁺.

3.5 Potential drift

Potential drift refers to the gradual change in the electrode's potential over time when it is immersed in a solution of constant pH. It reflects the stability of the electrode's response. To evaluate it, the electrode is immersed in a buffer solution of pH 7. The potential (mV) was recorded over a full day. The potential at regular intervals (e.g., every 15 minutes) was measured. From the slope of the potential versus time plot, it was found that the drift of the undoped SnO₂, Ce-doped SnO₂ (1%) and Ce-doped SnO₂ (3%) based sensors was 0.32, 0.12, and 0.08 mV h⁻¹, respectively. The drift rate of a standard glass pH electrode was 0.3 mV h⁻¹.

3.6 Sensing mechanism

The sensing mechanism of pH sensors based on MO_x has been the subject of extensive research. (i) Simple ion exchange in a surface layer containing –OH groups; (ii) a redox equilibrium between two different solid phases; (iii) a redox equilibrium involving only one solid phase whose hydrogen content can be continuously varied by passing current through the electrode; (iv) single phase “oxygen intercalation” of the electrode; and (v) steady-state corrosion of the electrode material are the five different mechanisms that Fog and Buck⁵¹ considered to explain the pH sensitivity of MO_x. Researchers have discovered that “oxygen intercalation” provides the most plausible explanation for the mechanism behind pH sensitivity.⁵² According to Fog and Buck's⁵¹ explanation, Mihell and Atkinson,^53,54 have also suggested that ion exchange in the surface layer containing eOH groups could potentially trigger the pH response. Dissociative adsorption of water causes hydroxide groups to generally blanket the MO_x surface when the sensor comes into contact with a solution. A potential difference between the sensing electrode (SE) and reference electrode (RE) may arise from the oxide sites created by proton release, which may lead to the production of a few higher- and lower-valency MO_x. Site-binding theory^33,55,56 says that when most oxides are placed in water, they form the surface groups –OH⁻, –OH, and –OH₃⁺, as seen in Fig. 7a. Protons and hydroxide ions from the solution attract oxygen ions from the MO_x crystal lattice and the surface cations, respectively. As a result of this, hydroxide groups cover MO_x. The formed metal hydroxide groups can either absorb a proton from the solution, transforming into a positive surface group, or donate a proton to the solution, producing a negative surface group.^33,55,57,58 As seen in Fig. 6b, the charged surface groups at the MO_x-solution interface form an electrical double layer (edl) structure. The edl is composed of the diffuse layer (Stern layer) and the Helmholtz layer (compact layer). As seen in Fig. 7b, the Helmholtz layer consists of the inner Helmholtz plane (IHP) and the outer Helmholtz plane (OHP). The IHP contains the charged surface groups, which chemically link to the MO_x surface to form a strong adhesion. In the OHP, coulombic contact draws the ions from the solution to the surface charge. Ions in the solution flow freely into the diffuse layer as a result of thermal or electrical forces.^29,55,56 Ions can cause these reactions by diffusing, adhering, or combining with ion adsorption at the MO_x surface.^29,57 Changes in the pH of a solution can affect the MO_x surface's equilibrium state, which could lead to changes in the SE's electrical properties and surface potential (Ψ).^{29,33,59–61} The kind of electrode material and its chemical reactivity at the solution interface determine how the electrical characteristics of the edl vary. In order to look into how pH ISFETs work, Liao et al.³³ did a lot of experiments and theoretical work based on site binding theory at the point of zero charge pH_PZC and the surface potential of a tin oxide gate ISFET. The alterations of MO_x³³ are described in the following way:

2.303(pH_PZC − pH) = qϕ/kT + sinh⁻¹[qϕ/kTβ]

where β reflects the sensitivity of the gate insulators and depends on the surface density of hydroxyl groups.

β = 2q²N_s(K_aK_b)¹²/kTC_dl

N_s represents the total number of surface sites per unit area, and the dissociation constants K_a and K_b correspond to acidic and basic equilibrium. When N_s is greater, the response is more linear, and the pH sensitivity is higher. The material's crystalline structure affects the N_s value. The Gouy–Chapman–Stern model is the source of double layer capacitance, also known as C_dl.

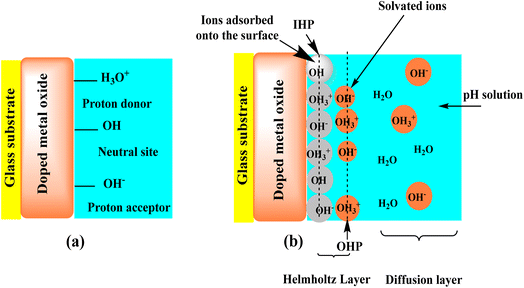Fig. 7 Schematic of the site-binding theory of a MO_x-based pH sensor (a) and the adsorption of potential determining ions on the surface and the resulting edl structure (b).

The EIS analysis reveals key aspects of the sensing mechanism. The observed increase in R_ct in Ce-doped SnO₂ is a consequence of the more complex charge transfer mechanism induced by the incorporation of cerium ions into the SnO₂ lattice. The Ce doping introduces oxygen vacancies, which significantly influence both electronic and ionic conductivity. Oxygen vacancies act as shallow donors, contributing to the electron density in the conduction band of SnO₂. However, they also introduce localized states that can trap charge carriers, leading to an increase in R_ct. The oxygen vacancies increase the availability of active sites for H⁺ ion adsorption, which is essential for the pH response. The charge transfer mechanism at the sensor-electrolyte interface is dominated by protonation and deprotonation reactions involving these vacancies. However, the presence of Ce introduces a second effect: the cerium ions can exist in mixed oxidation states (Ce³⁺/Ce⁴⁺), which participate in reversible redox reactions. This redox behavior creates an additional pathway for electron exchange, complicating the charge transfer process at the electrode surface. The involvement of the Ce³⁺/Ce⁴⁺ couple adds a layer of complexity to the electron transfer, contributing to the observed higher R_ct. Several studies have demonstrated that dopants, such as Ce, can modify the defect chemistry of metal oxides, leading to altered charge transport mechanisms. According to Xu et al. (2024),⁶² Ce doping can lead to the formation of deep-level traps, which act as recombination centers for charge carriers, thus increasing the charge transfer resistance in electrochemical measurements. This is consistent with the increase in R_ct observed in our EIS results, indicating that the charge transfer mechanism is no longer a simple electron conduction process, but involves additional ionic and redox pathways. Furthermore, the literature on Ce-doped oxides^63,64 suggests that the interaction between Ce and oxygen vacancies enhances the material's chemical stability and catalytic activity, which is beneficial for pH sensing. However, this also leads to more complex surface chemistry, as the cerium ions contribute to both the generation of oxygen vacancies and the electron trapping processes that increase R_ct.

The increased R_ct does not negatively affect the sensor's pH sensitivity. In contrast, the oxygen vacancies and the Ce redox couple contribute to enhanced surface reactivity. The increased number of active sites for H⁺ adsorption improves the sensor's ability to rapidly respond to pH changes, even though the overall charge transfer mechanism becomes more complex. In fact, the higher R_ct reflects the enhanced surface interactions between the electrode and the electrolyte, which are crucial for accurate and stable pH measurements.

3.7 Analytical applications

The pH of tap water, bottled drinking water, seawater, beverages, and fruit juices was measured using the developed pH sensors. Three replicates' averages were compared to those obtained from using the commercial glass electrode. The results are summarized in Table 6. The doped Ce–SnO₂-based sensors displayed pH values that were comparable to or close to those found in the traditional glass electrode, whereas the undoped SnO₂-based sensor had the least sensitivity to pH. The pH unit variations ranged from 0.06 to 0.3. The outcomes show how well the doped Ce–SnO₂-based sensors work to measure the pH of various environmental, clinical, and industrial samples.

Table 6 Application of the fabricated pH sensors to measure the pH values of different natural samples

Sample type	Orion™ based glass membrane electrode	The fabricated sensors
		Undoped SnO2	Ce-doped SnO2 (1%)	Ce-doped SnO2 (3%)
a Calibration buffers used: – pH 4 (Britton–Robinson buffer, with NaCl added to simulate seawater conditions) – pH 7 (Britton–Robinson buffer) – pH 10 (Britton–Robinson buffer).
Sea water, Zallaq, Bahrain	8.04 ± 0.07	7.98 ± 0.05	8.02 ± 0.02	8.05 ± 0.01
Tap water, University of Bahrain	8.38 ± 0.01	8.12 ± 0.1	8.27 ± 0.07	8.31 ± 0.03
Drinking bottled water (Areef)	7.79 ± 0.05	7.45 ± 0.3	7.81 ± 0.04	7.83 ± 0.02
Drinking bottled water (Adhari)	7.81 ± 0.07	7.52 ± 0.2	7.75 ± 0.06	7.76 ± 0.1
Soft drink, citrus	3.01 ± 0.02	2.86 ± 0.1	3.07 ± 0.04	3.02 ± 0.06
Soft drink, pomegranate	2.51	2.76 ± 0.07	2.67 ± 0.02	2.62 ± 0.07
Mix fruit juice, Suntop, Binzagr Limited Co., KSA	3.18	3.33 ± 0.09	3.09 ± 0.06	3.07 ± 0.03
Peach juice (Awal Dairy Co., Bahrain)	3.64	3.42 ± 0.04	3.60 ± 0.03	3.55 ± 0.04
Mango juice (Awal Dairy Co., Bahrain)	3.96	4.16 ± 0.06	3.99 ± 0.02	3.87 ± 0.03
Orange juice (Sunkist, Food Refreshments Co., Kuwait)	3.07	3.24 ± 0.07	3.17 ± 0.05	3.09 ± 0.02

---

4 Conclusion

Using the spray pyrolysis method, undoped and Ce-doped SnO₂ thin films were deposited on a glass substrate for 20 min. at 450 °C. The deposited films' surface shape and crystalline structure were described. The synthesized undoped and Ce-doped SnO₂ based membrane was utilized to create a compact, selective, and sensitive planar electrode for measuring pH across a broad range (2–12). The electrode demonstrated a fast reaction time, steady readings, high selectivity, and a near-Nernstian slope of −58.6 ± 0.7 mV per decade. The electrode was effectively employed to measure the pH of a few natural samples, and the findings were comparable to those of the conventional glass electrode. This study successfully demonstrates the design and fabrication of a compact potentiometric electrode for pH monitoring, utilizing a glass substrate and a cerium-doped tin oxide (Ce-doped SnO₂) layer. The incorporation of Ce-doped SnO₂ has been shown to significantly enhance the electrode's performance, offering superior sensitivity, stability, and a broad pH detection range compared to traditional pH sensors. The compact form factor, coupled with the robust electrochemical properties of Ce-doped SnO₂, makes this electrode a promising candidate for integration into portable and miniaturized pH monitoring systems. This work not only contributes to the advancement of pH sensor technology but also opens new avenues for the development of high-performance sensors in various analytical and environmental applications.

Data availability

Data will be made available on request.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflicts of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgements

The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through the Large Groups Project under grant number (RGP.2/282/45). The potentiometric measurements carried out using a PalmSens4 potentiostat were supported by grant number (2/2023) funded by the Deanship of Scientific Research, University of Bahrain.

References

1. T. Guinovart, G. Valdés-Ramírez, J. R. Windmiller, F. J. Andrade and J. Wang, Electroanalysis, 2014, 26, 1345–1353.
2. S. Zhuiykov, Sens. Actuators, B, 2012, 161, 1–20.
3. L. Manjakkal, C. G. Núñez, W. Dang and R. Dahiya, Nano Energy, 2018, 51, 604–612.
4. A. J. Bandodkar, V. W. S. Hung, W. Jia, G. Valdés-Ramírez, J. R. Windmiller, A. G. Martinez, J. Ramírez, G. Chan, K. Kerman and J. Wang, Analyst, 2013, 138, 123–128.
5. W. Dang, L. Manjakkal, W. T. Navaraj, L. Lorenzelli, V. Vinciguerra and R. Dahiya, Biosens. Bioelectron., 2018, 107, 192–202.
6. J. Kim, T. N. Cho, G. Valdés-Ramírez and J. Wang, Talanta, 2016, 150, 622–628.
7. K. Paek, H. Yang, J. Lee, J. Park and B. J. Kim, ACS Nano, 2014, 8, 2848–2856.
8. H. Cao, V. Landge, U. Tata, Y.-S. Seo, S. Rao, S.-J. Tang, H. F. Tibbals, S. Spechler and J.-C. Chiao, IEEE Trans. Biomed. Eng., 2012, 59, 3131–3139.
9. P. P. Ravi, J. Lindner, H. Oechsner and A. Lemmer, Bioresour. Technol., 2018, 247, 96–102.
10. W. Lonsdale, M. Wajrak and K. Alameh, Talanta, 2018, 180, 277–281.
11. Y. Lian, W. Zhang, L. Ding, X. Zhang, Y. Zhang and X. Wang, in Novel Nanomaterials for Biomedical, Environmental and Energy Applications, Elsevier, 2019, pp. 241–273.
12. J. Han, D. Cui, Y. Li, H. Zhang, Y. Huang, Z. Zheng, Y. Zhu and X. Li, Sens. Actuators, B, 2000, 66, 203–204.
13. D. H. Kohn, M. Sarmadi, J. I. Helman and P. H. Krebsbach, J. Biomed. Mater. Res., 2002, 60, 292–299.
14. J. Srivastava, D. L. Barber and M. P. Jacobson, Physiology, 2007, 22, 30–39.
15. L. Manjakkal, B. Sakthivel, N. Gopalakrishnan and R. Dahiya, Sens. Actuators, B, 2018, 263, 50–58.
16. W. Dang, L. Manjakkal, L. Lorenzelli, V. Vinciguerra and R. Dahiya, in 2017 IEEE SENSORS, IEEE, 2017, pp. 1–3.
17. L. Manjakkal, W. Dang, N. Yogeswaran and R. Dahiya, Biosensors, 2019, 9, 14.
18. S. Nakata, T. Arie, S. Akita and K. Takei, ACS Sens., 2017, 2, 443–448.
19. S. Anastasova, B. Crewther, P. Bembnowicz, V. Curto, H. M. D. Ip, B. Rosa and G.-Z. Yang, Biosens. Bioelectron., 2017, 93, 139–145.
20. H. Lee, T. K. Choi, Y. B. Lee, H. R. Cho, R. Ghaffari, L. Wang, H. J. Choi, T. D. Chung, N. Lu and T. Hyeon, Nat. Nanotechnol., 2016, 11, 566–572.
21. A. M. Gibson, N. Bratchell and T. A. Roberts, Int. J. Food Microbiol., 1988, 6, 155–178.
22. R. Martínez-Máñez, J. Soto, E. García-Breijo, L. Gil, J. Ibáñez and E. Gadea, Sens. Actuators, A, 2005, 120, 589–595.
23. L. Manjakkal, K. Zaraska, K. Cvejin, J. Kulawik and D. Szwagierczak, Talanta, 2016, 147, 233–240.
24. M. Simić, G. M. Stojanović, L. Manjakkal and K. Zaraska, in 2016 24th Telecommunications Forum (TELFOR), IEEE, 2016, pp. 1–4.
25. L. Manjakkal, D. Szwagierczak and R. Dahiya, Prog. Mater. Sci., 2020, 109, 100635.
26. N. Lenar, R. Piech, C. Wardak and B. Paczosa-Bator, Membranes, 2023, 13, 876.
27. S. A. M. Marzouk, S. Ufer, R. P. Buck, T. A. Johnson, L. A. Dunlap and W. E. Cascio, Anal. Chem., 1998, 70, 5054–5061.
28. R. Karimi Shervedani, H. R. Zare Mehrdjardi and S. H. Kazemi Ghahfarokhi, J. Iran. Chem. Soc., 2007, 4, 221–228.
29. L. Manjakkal, K. Cvejin, J. Kulawik, K. Zaraska, D. Szwagierczak and G. Stojanovic, J. Electroanal. Chem., 2015, 759, 82–90.
30. Y.-H. Liao and J.-C. Chou, Sens. Actuators, B, 2008, 128, 603–612.
31. G. M. Da Silva, S. G. Lemos, L. A. Pocrifka, P. D. Marreto, A. V Rosario and E. C. Pereira, Anal. Chim. Acta, 2008, 616, 36–41.
32. B. Xu and W.-D. Zhang, Electrochim. Acta, 2010, 55, 2859–2864.
33. Y.-H. Liao and J.-C. Chou, Mater. Chem. Phys., 2009, 114, 542–548.
34. L. A. Pocrifka, C. Gonçalves, P. Grossi, P. C. Colpa and E. C. Pereira, Sens. Actuators, B, 2006, 113, 1012–1016.
35. C.-N. Tsai, J.-C. Chou, T.-P. Sun and S.-K. Hsiung, IEEE Sens. J., 2006, 6, 1243–1249.
36. D.-H. Kwon, B.-W. Cho, C.-S. Kim and B.-K. Sohn, Sens. Actuators, B, 1996, 34, 441–445.
37. J.-L. Chiang, S.-S. Jan, J.-C. Chou and Y.-C. Chen, Sens. Actuators, B, 2001, 76, 624–628.
38. W.-D. Zhang and B. Xu, Electrochem. Commun., 2009, 11, 1038–1041.
39. S. Betelu, K. Polychronopoulou, C. Rebholz and I. Ignatiadis, Talanta, 2011, 87, 126–135.
40. H. Razmi, H. Heidari and E. Habibi, J. Solid State Electrochem., 2008, 12, 1579–1587.
41. L. Telli, B. Brahimi and A. Hammouche, Solid State Ionics, 2000, 128, 255–259.
42. L. Qingwen, L. Guoan and S. Youqin, Anal. Chim. Acta, 2000, 409, 137–142.
43. S. S. M. Hassan, M. A. Fathy, I. Moussa, M. Obaida and A. H. Kamel, Sens. Actuators, B, 2023, 380, 133397.
44. M. Obaida, I. Moussa, S. Hassan, H. Afify and A. Abouelsayed, Egypt. J. Chem., 2020, 63, 2331–2344.
45. C. Maccà, Electroanalysis, 2003, 15, 997–1010.
46. Dislocations in Crystals, Dislocations in Solids, ed. P. Paufler and F. R. N. Nabarro, North-Holland Publ. Co., Amsterdam, 1979, vol. 2, p. 94.
47. R. J. D. Tilley, Perovskites: Structure-Property Relationships, John Wiley & Sons, 2016.
48. A. S. Reddy, N. M. Figueiredo and A. Cavaleiro, Appl. Surf. Sci., 2012, 258, 8902–8907.
49. B. D. Cullity, Adv. X-Ray Anal., 1976, 20, 259–271.
50. Y. Umezawa, P. Bühlmann, K. Umezawa, K. Tohda and S. Amemiya, Pure Appl. Chem., 2000, 72, 1851–2082.
51. A. Fog and R. P. Buck, Sens. Actuators, 1984, 5, 137–146.
52. H. N. McMurray, P. Douglas and D. Abbot, Sens. Actuators, B, 1995, 28, 9–15.
53. J. A. Mihell and J. K. Atkinson, Sens. Actuators, B, 1998, 48, 505–511.
54. S. Trasatti, Electrochim. Acta, 1991, 36, 225–241.
55. S. Al-Hilli and M. Willander, Sensors, 2009, 9, 7445–7480.
56. D. E. Yates, S. Levine and T. W. Healy, J. Chem. Soc., Faraday Trans. 1, 1974, 70, 1807–1818.
57. M. Chen, Y. Jin, X. Qu, Q. Jin and J. Zhao, Sens. Actuators, B, 2014, 192, 399–405.
58. P. Kurzweil, J. Power Sources, 2009, 190, 189–200.
59. E. Gill, K. Arshak, A. Arshak and O. Korostynska, Microsyst. Technol., 2008, 14, 499–507.
60. M. Kosmulski, J. Colloid Interface Sci., 2002, 253, 77–87.
61. E. Tombácz, Period. Polytech., Chem. Eng., 2009, 53, 77–86.
62. T. Xu, R. Chu, X. Chen, Y. Wei, G. Li and Z. Xu, J. Mater. Sci.: Mater. Electron., 2024, 35, 446.
63. L. Yang and Y. Guo, Separations, 2023, 10, 560.
64. R. Patel, A. K. Mishra, J. Singh and I. Mukhopadhyay, J. Solid State Electrochem., 2024, 1–12.

---