EigenRF: an improved metabolomics normalization method with scores for reproducibility evaluation on importance rankings of differential metabolites†
Chencheng
Tang
ab,
Dongfang
Huang
a,
Xudong
Xing
 *a and
Hua
Yang
*a and
Hua
Yang
 *a
*a
aState Key Laboratory of Natural Medicines, China Pharmaceutical University, Nanjing 211198, China. E-mail: mrxing_xudong@126.com; yanghuacpu@126.com
bSchool of Science, China Pharmaceutical University, Nanjing 211198, China
First published on 8th November 2024
Abstract
Screening differential metabolites is of great significance in biomarker discovery in metabolomics research. However, it is susceptible to unwanted variations introduced during experiments. Previous normalization methods have improved the accuracy of inter-group classification by eliminating systematic errors. Nonetheless, the classification ability of differential metabolites obtained through these methods still requires further enhancement, and the reproducibility evaluation on importance rankings of differential metabolites is often disregarded. The EigenRF algorithm was developed as an improvement over the previous metabolomics normalization method referred to as EigenMS, which aims to normalize metabolomics data. Furthermore, scoring metrics, including the local consistency (LC) and overall difference (OD) scores, were introduced to evaluate the reproducibility of importance rankings of differential metabolites from a dual perspective. After conducting validation on three publicly accessible datasets, the EigenRF method has demonstrated enhanced classification ability of differential metabolites as well as improved reproducibility. In summary, EigenRF enhances the reliability of differential metabolites in metabolomics research, benefiting the further exploration of molecular mechanisms underlying biological alterations in complex matrices. The EigenRF algorithm was implemented in an R package: https://www.github.com/YangHuaLab/EigenRF.
Introduction
The rapid advancements in untargeted metabolomics techniques have enabled researchers to analyze variations in large-scale metabolomics data, thereby discovering valuable biological information. Meanwhile, it also poses challenges as the variations in metabolomics data are typically complex and subject to biases. Precisely, the total variation in the data consists of biological variations of interest and unwanted variations.1 The biological variations of interest refer to the changes in metabolites that are directly related to the research topic, providing crucial insights into understanding specific biological processes or disease states.2 Unwanted variations include both biologically uninteresting variations and errors during the experimental process, known as experimental errors. Primarily, biologically uninteresting variations mainly arise from changes in the concentration of biological fluids, cell size differences, and sample weight or volume.3 Besides, the experimental errors primarily result from the susceptibility of chromatographic or ionization processes of metabolites to external influences. Therefore, obtaining reproducible results is nearly impossible, even if dedicated operators adhere to standard operating procedures within the same laboratory and using the same instruments.4 This is also the result of the combined effects of numerous factors. For instance, deviations in sample preparation and storage procedures, disparities among laboratories and instruments, and the execution of large-scale, inter-temporal, and multi-batch analyses within the same laboratory and using the same instruments can introduce experimental errors. Specifically, the experimental errors can generally be categorized into two main types: random errors and systematic errors. Systematic errors are primarily associated with batches or injection sequences.5–7 A batch of samples refers to a group of samples collected within the same laboratory, using the same instrument, and during an uninterrupted time interval in the mass spectrometry data acquisition process,8i.e., samples from the same batch should be simultaneously placed in the same injection box. Different batches of samples may exhibit systematic errors caused by changes in laboratory temperature, column performance, or instrument instability, such as fluctuations in mass spectrometry sensitivity, etc. Therefore, a generic approach is needed to address experimental errors and improve the reproducibility and reliability of the results.Due to the inherent unpredictability and irreducibility of random errors, whereas systematic errors exhibit regular patterns and are amenable to reduction or elimination, the process of eliminating experimental errors primarily involves addressing systematic errors induced by batch effects or injection sequences,9,10 also known as “signal drift correction” or “quality control (QC) sample correction” since QC samples can be utilized for signal drift correction. Researchers often refer to integrating this procedure with data standardization as “normalization”, as these two processes are complementary. Certain signal drift correction methods can even substitute the standardization process,3 enabling data to be scaled to a comparable level while eliminating batch effects. The normalization process in metabolomics data processing has evolved from a traditional concept of simple data scaling to a more focused approach to eliminating batch effects and correcting signal drift. Currently, there are four main types of normalization methods applied to metabolomics: (1) QC sample-based methods, (2) internal standard (IS)-based methods, (3) biological sample-based methods, and (4) combinations thereof.11 Therein, biological sample-based methods identify and estimate systematic errors directly from the signal expression matrix of biological samples without the assistance of internal standards or QC samples. Karpievitch et al. formed the EigenMS algorithm by incorporating the singular value algorithm (SVA) and initially applying it to proteomics,12,13 later extending it to metabolomics in 2014.14 Like SVA, EigenMS captures systematic errors through singular value decomposition and subtracts them from the original data to obtain normalized data. Compared to EigenMS, the SVA requires surrogate variables to predict trends in systematic deviations and includes them as covariates in downstream statistical inference. EigenMS exhibited high accuracy and reproducibility.15 However, it assumes a linear relationship between the biological variations of interest and sample groups, disregarding their potential nonlinear nature. Consequently, this limitation may result in some biological variations of interest being delimited into the residual matrix and eliminated as systematic errors.
Hence, we have improved the EigenMS method and proposed it as EigenRF. EigenRF comprises two steps in the normalization process. Initially, EigenMS is utilized to estimate and eliminate systematic errors from the data. Subsequently, a random forest regression model is employed to estimate the nonlinear biological variations of interest, which are reintegrated into the data. Random forest, a decision tree-based algorithm, excels at capturing nonlinearities in data,16,17 complementing the linear model employed in EigenMS. Furthermore, novel metrics were introduced to evaluate the reproducibility of importance rankings of differential metabolites in group discrimination, including two scores: the local consistency (LC) score, which evaluates the consistency of local rankings of differential metabolites, and the overall difference (OD) score, which evaluates the difference in overall rankings of differential metabolites. We applied EigenRF to three datasets, and the results demonstrated improved accuracy and reproducibility, thereby emphasizing its superiority over other methods.
Materials and methods
Datasets
To evaluate the performance of EigenRF, it was compared with EigenMS and ten other commonly used normalization methods (Table S1†) across three publicly accessible datasets with distinct characteristics. This comparison serves to validate the generalizability of EigenRF.BCPUM: a urine metabolomics study of the bladder cancer population.18 The dataset consists of 982 features and 311 samples, representing high dimensionality with a relatively small sample size. It includes 128 biological samples from the TG, 120 from the CG, and 63 QC samples. The samples were run in 12 batches, each containing approximately 5 QC samples (with a 5-biological-sample interval) and 20 biological samples, with the two groups of biological samples randomly ordered. Features with missing values exceeding 20% in QC samples and exceeding 50% in both groups of biological samples were removed. Afterwards, 661 features remained, and missing values were imputed with the mean values of each group.
GCPPM: a plasma metabolomics study of gastric cancer population.4 The dataset comprises 354 features (including 6 internal standards) and 615 samples, representing low dimensionality with a relatively large sample size. It includes 60, 197, and 240 biological samples from groups A, B, and C, respectively, and 120 QC samples. The samples were run in 7 batches, each containing approximately 17 QC samples (with a 5-biological-sample interval) and 70 biological samples, with the three groups of biological samples randomly ordered. The column and injector were adjusted by injecting adjusted QC samples and blank samples at the beginning of each batch to minimize systematic errors.
ACPPM: a plasma metabolomics study of adenocarcinoma population.19 The dataset consists of 6402 features and 729 samples, representing high dimensionality, a large sample size, and an imbalance in the number of samples. It includes 571 and 73 biological samples from CRC and CE, respectively, and 85 QC samples. The samples were run in 4 batches, each containing approximately 25 QC samples (with an 8-biological-sample interval) and 192 biological samples, with the two groups of biological samples randomly ordered.
EigenRF implementation
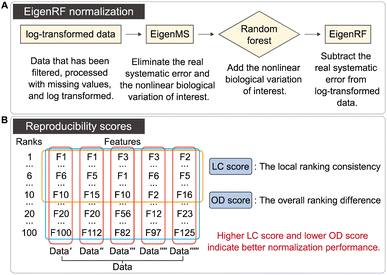
As shown in Fig. 1A, the EigenRF algorithm represents an improvement over EigenMS. The procedures of EigenMS involve estimating the biological variations of interest by fitting a linear model with groups as the independent variable and the signal value of the feature (peak intensity or peak area) as the dependent variable and generating a residual matrix. Singular value decomposition is then performed on the residual matrix to estimate the systematic errors, which are subsequently subtracted from the raw data to derive normalized data. Following this process, a random forest model is employed to estimate the nonlinear biological variations of interest and reintegrate them into the data. EigenRF is implemented in R 4.2.1 with core dependency packages including “parallel” and “randomForest”. The parameters for the random forest regression model are set to ntree = 500, mtry = floor(sqrt(ncol(x))), replace = TRUE, sampsize = nrow(x), nodesize = 1.The detailed procedures of EigenRF are as follows:
First, we assume that an additive model can represent the log-transformed feature signal values:
| yi = Xlβli + WEi + εi, | (1) |
Next, the linear model of the EigenMS algorithm is employed to fit the biological variations of interest and obtain a residual matrix:
| R = Y − lm(G), | (2) |
Subsequently, singular value decomposition is performed on the residual matrix R, like that of EigenMS:
| R = UDV′, | (3) |
| R = BV0 + ε, | (4) |
Further, the estimated systematic errors matrix WE is the estimated value of BV0:
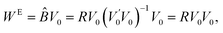 | (5) |
| WEi = Xni + Wri, | (6) |
A random forest regression model is employed to fit the nonlinear biological variations of interest:
| Xni ∼ Φi(G,I−i), | (7) |
Finally, the systematic errors are eliminated from the feature, that is, subtract the systematic errors captured by EigenMS, and add the nonlinear component of the biological variations of interest estimated by the random forest regression model, then the normalized value is obtained:
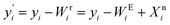 | (8) |
Evaluation metrics
The distribution of the relative standard deviation (RSD) and the median RSD of each batch are used to represent the systematic errors in the data. Subsequently, batch effects are further represented using run plots and batch-based principal component analysis (PCA) plots, while the biological variations of interest are represented by group-based PCA plots and group-based orthogonal partial least squares discriminant analysis (OPLS-DA) score plots. Then, the accuracy of differential metabolites screening is evaluated using a support vector machine (SVM) classifier with ten-fold cross-validation to obtain the receiver operating characteristic (ROC) curve and the mean area under curve (AUC) value. For the imbalanced dataset, the precision-recall (PR) curve and the corresponding AUC value are additionally included for evaluation.20 The SVM classifier is trained using a polynomial kernel function with parameters set to gamma = 0.1 and degree = 2. Finally, the reproducibility scores for the importance rankings of differential metabolites are calculated. These evaluation metrics indicate the ability of the normalization method to eliminate systematic errors and preserve the biological variations of interest, as well as the impact on the accuracy and reproducibility of differential metabolite screening. The calculation of the reproducibility scores for the importance rankings of differential metabolites is described below, and the other evaluation metrics are described in Note S1.†Two scores are proposed here to evaluate the reproducibility of the screened differential metabolites, as shown in Fig. 1B. First, the new dataset is extracted by stratified sampling at a ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 from the normalized dataset. This process is repeated five times with replacement in the same ratio, resulting in five new datasets. For each new dataset, differential metabolites are screened according to the criteria of variable importance in projection (VIP) ≥1 and false discovery rate (FDR)-adjusted p-value <0.05. These metabolites are then ranked primarily in descending order of VIP and in ascending order of the p-value when VIPs are the same. The top 100 metabolites from each of the five new datasets are selected, and the LC score and the OD score are calculated as follows:
1 from the normalized dataset. This process is repeated five times with replacement in the same ratio, resulting in five new datasets. For each new dataset, differential metabolites are screened according to the criteria of variable importance in projection (VIP) ≥1 and false discovery rate (FDR)-adjusted p-value <0.05. These metabolites are then ranked primarily in descending order of VIP and in ascending order of the p-value when VIPs are the same. The top 100 metabolites from each of the five new datasets are selected, and the LC score and the OD score are calculated as follows:
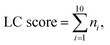 | (9) |
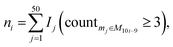 | (10) |
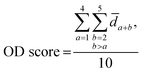 | (11) |
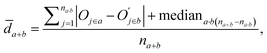 | (12) |
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) a+b denotes the average rank difference of metabolites in the union of the top 100 differential metabolites between dataset a and dataset b, which are present in both datasets; na·b denotes the number of metabolites in the intersection of the top 100 differential metabolites in both datasets, and mediana·b denotes the median rank difference of metabolites in the intersection, while na+b denotes the number of metabolites in the union. Oj∈a and
a+b denotes the average rank difference of metabolites in the union of the top 100 differential metabolites between dataset a and dataset b, which are present in both datasets; na·b denotes the number of metabolites in the intersection of the top 100 differential metabolites in both datasets, and mediana·b denotes the median rank difference of metabolites in the intersection, while na+b denotes the number of metabolites in the union. Oj∈a and 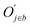 denote the 10i-th metabolite's rank in dataset a and dataset b, respectively.
denote the 10i-th metabolite's rank in dataset a and dataset b, respectively.
The LC score measures the consistency of local rankings, and the OD score measures the difference of overall rankings. The higher the LC score and the lower the OD score, the higher the reproducibility is.
Results
Method comparison on datasets with the characteristics of different dimensionality and sample size
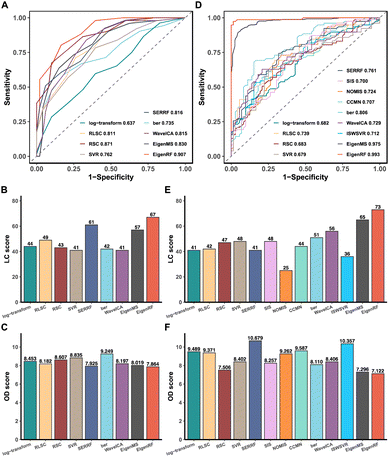
A comparative analysis was conducted on the high-dimensional and relatively small sample size BCPUM dataset, comparing EigenRF with EigenMS and six other normalization methods (Table S1†), which include four QC sample-based methods and two biological sample-based methods. Compared to the original log-transformed data, RLSC, RSC, SERRF, WaveICA, EigenMS and EigenRF decreased the RSDs of QC samples (Fig. S1A†) and the median RSD of each batch of QC samples (Fig. S1B†), indicating that these methods have an excellent ability to fit signal drift across samples. In contrast, SVR exhibited sharply rising median RSDs across batches 6–12, revealing relatively poor stability. The performance of ber was also inferior to the log-transformed data regarding the median RSD of each batch of QC samples. To evaluate the classification accuracy of the normalized data, we performed PCA and OPLS-DA to visualize the classification performance. Except for ber and WaveICA, the normalized data obtained from the other methods exhibited no significant signal drift (Fig. S2A†) or within-batch clustering tendencies (Fig. S2B†). In the group-based PCA plots (Fig. S2C†), only EigenMS and EigenRF significantly improved upon the log-transformed data, enabling a clear distinction among the QC, TG, and CG samples. Similarly, the group-based OPLS-DA score plots indicate that only EigenMS and EigenRF can effectively classify the TG and CG samples (Fig. S2D†). Regarding the ROC curves depicted in Fig. 2A, the mean AUC values obtained from log-transform, RLSC, RSC, SVR, SERRF, ber, WaveICA, EigenMS, and EigenRF were 0.637, 0.811, 0.871, 0.762, 0.816, 0.735, 0.815, 0.830, and 0.907, respectively, demonstrating that EigenRF outperformed other methods in terms of classification accuracy for the selected features. Furthermore, the LC and OD scores were calculated to evaluate the reproducibility of the methods. Based on Fig. 2B and C, we can observe that normalization methods had significant influences on the reproducibility of importance rankings of differential metabolites. Overall, RLSC, SERRF, EigenMS, and EigenRF increased the LC score of the log-transformed data, while RSC, SVR, ber, and WaveICA decreased the LC score. Similarly, RLSC, SERRF, WaveICA, EigenMS, and EigenRF decreased the OD score of the log-transformed data, whereas RSC, SVR, and ber increased the OD score. Among them, EigenRF achieved the highest LC score of 67, followed by SERRF with an LC score of 61, and EigenMS with an LC score of 57. Likewise, EigenRF had the lowest OD score of 7.864, with SERRF following at 7.925 and EigenMS at 8.019. Consequently, the accuracy and reproducibility of EigenRF were improved in comparison to other methods.EigenRF was further compared with EigenMS and ten other normalization methods (Table S1†) on the low-dimensional and relatively large sample size GCPPM dataset. These ten common normalization methods include four QC sample-based methods, three IS-based methods, two biological sample-based methods, and one combination method. All methods decreased the RSDs of QC samples compared to the original log-transformed data (Fig. S3A†), and except for RLSC and ber, the median RSD of each batch of QC samples was also decreased by the remaining methods (Fig. S3B†). Moreover, except for the RSC method, the normalized data obtained from the other methods exhibited no significant signal drift (Fig. S4A†) or within-batch clustering tendencies (Fig. S4B†). EigenMS and EigenRF demonstrated slightly superior performance to the other methods in the run plots and the batch-based PCA plots. In the group-based PCA plots (Fig. S4C†), most methods could not effectively distinguish the QC, A, B, and C samples, except for EigenMS and EigenRF, which provided clear distinctions among these groups. Similarly, in the group-based OPLS-DA score plots (Fig. S4D†), the performance of the other methods was suboptimal, with only EigenMS and EigenRF being able to fully distinguish among the A, B, and C samples. Based on the ROC curves depicted in Fig. 2D, the mean AUC values obtained from log-transform, RLSC, RSC, SVR, SERRF, SIS, NOMIS, CCMN, ber, WaveICA, ISWSVR, EigenMS, and EigenRF were 0.682, 0.739, 0.683, 0.679, 0.761, 0.700, 0.724, 0.707, 0.806, 0.729, 0.712, 0.975, and 0.993, respectively. EigenRF demonstrated superior classification performance, surpassing EigenMS and significantly outperforming ber, which performed best among the other ten normalization methods. However, the remaining methods demonstrated no significant effect. The reproducibility scores illustrated in Fig. 2E and F indicate that, with the exception of SERRF, NOMIS, and ISWSVR, all other methods improved the LC score over the log-transformed data. On the other hand, all methods except SERRF, CCMN, and ISWSVR showed a decrease in the OD score over the log-transformed data. The EigenRF method achieved the highest LC score of 73 and the lowest OD score of 7.122, outperforming EigenMS with an LC score of 65 and an OD score of 7.296, and also significantly higher than the subsequent LC score of 56 for WaveICA and lower than the subsequent OD score of 7.506 for RSC. In general, EigenRF outperformed other methods in eliminating systematic errors and preserving biological variations of interest, and its reproducibility in differential metabolites screening was also excellent.
Method comparison on the imbalanced dataset
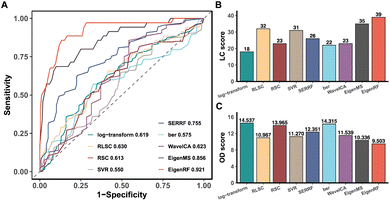
EigenRF was applied to address the challenges posed by high dimensionality, a large sample size, and an imbalanced distribution in the ACPPM dataset, and was compared with EigenMS and six other normalization methods (Table S1†), which include four QC sample-based methods and two biological sample-based methods. Afterwards, several improvements were observed.All methods exhibited overall lower RSDs of QC samples compared to the original log-transformed data (Fig. 3A). However, RLSC and ber performed poorly in terms of median RSDs across almost all batches of QC samples, while the median RSD of each batch of QC samples for the other methods was considerably lower than that of the log-transformed data (Fig. 3B). Among them, EigenRF exhibited slight improvements in both RSD metrics compared to EigenMS. The signal drift manifested in the run plots was moderately reduced through normalization (Fig. 4A and S5A†), as the feature signals of the QC, CRC, and CE samples became relatively smooth after being normalized. Additionally, there were no apparent within-batch clustering tendencies in QC, CRC, and CE samples after normalization of EigenMS and EigenRF (Fig. 4B and S5B†). SERRF demonstrated slightly lower effectiveness in eliminating batch effects than EigenMS and EigenRF. In contrast, other methods only achieved satisfactory results across certain sample groups. For instance, ber and WaveICA showed distinct batch clustering effects in QC samples, while RLSC, RSC, and SVR exhibited such effects in CRC samples, and RLSC and RSC illustrated clear batch clustering in CE samples. Furthermore, the group-based PCA plots (Fig. 4C and S5C†) showed that the classification trends were only fully apparent after normalization with EigenMS and EigenRF, clearly distinguishing the QC, CRC, and CE samples. Other methods did not separate these three groups of samples. This indicates that the batch effects and signal drift present in the original data introduced deviations in PCA, which could be effectively eliminated through normalization with EigenMS and EigenRF. The OPLS-DA score plots of the CRC and CE samples also reflected changes in classification trends before and after normalization of EigenRF and other methods (Fig. 4D and S5D†), highlighting the advantages of EigenRF. Differentiated metabolites between the CRC and CE samples were examined to investigate the impact of normalization on feature selection. As shown in Fig. 5A, the mean AUC values obtained from different normalization methods differed from each other as well as from that of the log-transformed data, indicating that normalization methods can affect the results of feature selection. Among the methods evaluated, EigenMS and EigenRF significantly improved classification accuracy, achieving mean AUC values of 0.856 and 0.921, respectively. The remaining methods did not show substantial improvement compared to the log-transformed data. In fact, the mean AUC values of several normalization methods were lower than that of the log-transformed data, such as RSC, SVR, and ber. This indicates that EigenRF not only considerably outperformed the other methods but also enhanced performance based on EigenMS. Considering the imbalanced nature of the dataset, the PR curve was utilized as an additional evaluation metric (Fig. S6†). The results indicate that the log-transformed data exhibited poor classification performance for CE samples, with a mean AUC value of 0.183, suggesting that it struggled to identify CE samples accurately. Furthermore, methods such as RLSC, RSC, SVR, ber, and WaveICA showed little to no improvement overall. SERRF showed a moderate improvement, with a mean AUC value of 0.350. In contrast, EigenRF demonstrated significant enhancement for log-transformed data, effectively identifying CE samples with a mean AUC value of 0.812, surpassing the mean AUC value of EigenMS at 0.624, as well as other methods. In the reproducibility score plots from Fig. 5B and C, the LC scores for RLSC, SVR, SERRF, EigenMS, and EigenRF were markedly higher than that of the log-transformed data, with EigenRF achieving the highest score of 39, followed by EigenMS with a score of 35. In comparison, RSC, ber, and WaveICA only slightly increased the LC score above that of the log-transformed data. Regarding OD scores, RSC and ber were only slightly lower than the log-transformed data, while RLSC, SVR, SERRF, and WaveICA showed a moderate decrease. Notably, EigenMS and EigenRF significantly decreased the OD score of the log-transformed data, with scores of 10.336 and 9.503, respectively. As a result, the reproducibility of differential metabolites screening has been substantially improved with EigenRF.
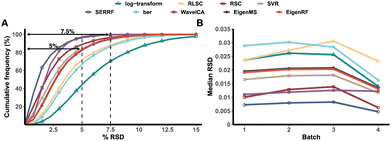 | ||
| Fig. 3 Cumulative frequency distribution of the RSDs of QC samples (A) and the median RSD of each batch of QC samples (B) in the ACPPM dataset. | ||
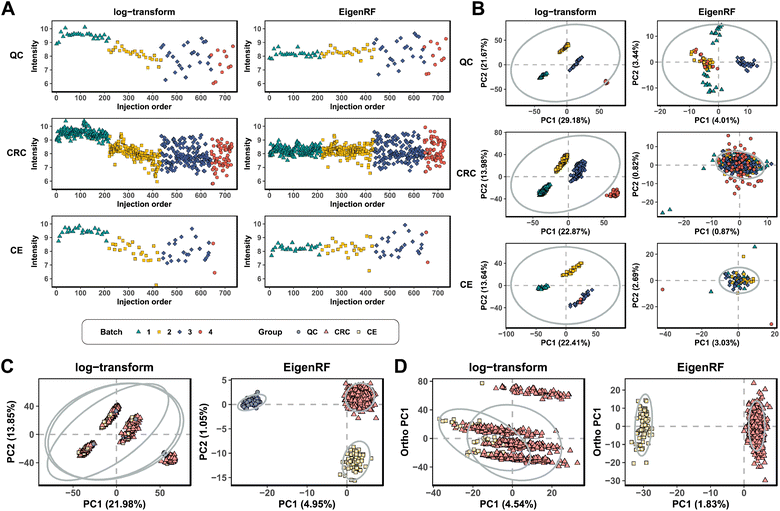 | ||
| Fig. 4 Run plots of the first feature (A), batch-based PCA plots of the QC, CRC, and CE samples (B), group-based PCA plots (C), and group-based OPLS-DA score plots (D) in the ACPPM dataset. | ||
In summary, the EigenRF normalization method can effectively eliminate batch effects and signal drift in original data and improve the accuracy and reproducibility of the feature selection within the imbalanced dataset.
Discussion
Normalization is essential in metabolomics research to eliminate systematic errors introduced by batch effects and signal drift. While eliminating errors, it should also preserve the biological variation of interest as much as possible.21 However, in the actual metabolomics data, the relationship between biological variations and groups may not be linear; it could be nonlinear. The SVA involved in EigenMS is a linear model that can only capture the linear component of biological variations. Consequently, some nonlinear variations are incorrectly treated as systematic errors and eliminated. To overcome this limitation, EigenRF integrates random forest regression, a nonlinear model, to complement the linear model used in EigenMS. EigenRF addresses the issue of removing nonlinear biological variations wrongly identified as systematic errors by EigenMS. The advanced EigenRF algorithm demonstrated superior normalization capabilities, including improved classification accuracy and reproducibility.EigenRF was extensively tested and evaluated on the high-dimensional and relatively small sample size BCPUM dataset, as well as the low-dimensional and relatively large sample size GCPPM dataset, in comparison with EigenMS and other commonly used normalization methods. The results indicate that EigenRF exhibited significant advantages over EigenMS and other normalization methods in terms of AUC values and reproducibility scores (Fig. 2A–F). This suggests that EigenRF is capable of identifying features that are truly relevant to biological questions from the raw data while ensuring result reproducibility, thereby enhancing the reliability of the findings. It provided substantial evidence for the existence of nonlinear variation and non-negligible impact on biological variations of interest. From a visual perspective, the run plots generated by EigenRF showed the most compact and stable signal values (Fig. S2A and S4A†). Compared to EigenMS, EigenRF exhibited slightly different signal value levels, indicating that EigenRF successfully captured the component of nonlinear biological variations, which was an intuitive manifestation of the enhanced effects. EigenRF outperformed other normalization methods in PCA and OPLS-DA score plots (Fig. S2B–D and S4B–D†), indicating superior utility. Furthermore, the PCA and OPLS-DA score plots of EigenRF were fairly similar to those of EigenMS, which reflects the limitations of such traditional metrics used to evaluate normalization algorithms due to the nature of the linear dimensionality reduction technique. The EigenRF algorithm has been applied to the high-dimensional, large-sample, and imbalanced ACPPM dataset, and it has continued to maintain a leading advantage over other methods in various aspects, including AUC values of ROC and PR curves (Fig. 5A and S6†), as well as reproducibility scores (Fig. 5B and C). This further validates its broad applicability and robust normalization capability when handling complex datasets.
In this study, we observed differences in the performance of the EigenRF method across various datasets. These discrepancies may arise from several factors: (1) Dimensionality and sample size of the dataset: EigenRF demonstrated advantages when handling the low-dimensional and relatively large sample size GCPPM dataset compared to the high-dimensional and relatively small sample size BCPUM dataset. This can be attributed to the fact that the number of features in the BCPUM dataset far exceeds the number of samples, leading the model to be more susceptible to noise in the high-dimensional space, making batch effects more pronounced. Additionally, the insufficient sample size makes it difficult to accurately capture the overall distribution of the data, thereby affecting the normalization effectiveness. In contrast, the relatively large sample size of the GCPPM dataset allows for a better reflection of the true data structure, facilitating easier identification and elimination of batch effects. (2) Imbalance in the dataset: In the ACPPM dataset, the imbalance in sample distribution may have impacted the performance of EigenRF. When dealing with such imbalanced data, EigenRF might struggle due to insufficient data for certain groups, which could hinder the effectiveness of normalization methods across different groups and reduce classification ability. However, since the total sample size of ACPPM is large, its performance across various metrics remains satisfactory. (3) Types and degrees of systematic errors: Different datasets may be influenced by various systematic errors, including sample handling and storage discrepancies, laboratory differences, and instrument variations. The superior performance of EigenRF on certain datasets may be due to its effective identification and correction of these specific systematic errors. (4) Algorithm adaptability: The EigenRF algorithm integrates both linear and nonlinear models, enabling it to adapt to the characteristics of different datasets. In some datasets, the prominence of nonlinear patterns may be more pronounced, thus favoring the advantages offered by EigenRF in those contexts. Overall, the differences in the performance of the EigenRF method across various datasets reflect its adaptability and flexibility in addressing different types and complexities of systematic errors. These findings underscore the importance of selecting appropriate normalization methods in metabolomics research.
Normalization can significantly alter the numerical values of the original data, potentially affecting downstream analysis results. Evaluating the performance of normalization methods using different evaluation metrics aims to assess their capabilities comprehensively. Typically, metrics such as RSD and run plots are used to evaluate the performance of normalization methods.4 Theoretically, the signal values of QC samples should be identical for a given feature. In general, higher RSD values of QC samples indicate more unwanted variations introduced during the experimental process and lower reproducibility of the results.22 To identify the systematic errors caused by batch and injection order, it is more appropriate to calculate the median RSD for each batch and compare the values. In our calculations across three datasets, we found that log transformation is sufficient to decrease the RSD of QC samples. This reflects both the good quality of the original data and the limitation of RSD as an indicator to demonstrate the ability of normalization methods to eliminate batch effects. Run plots provide a more intuitive visualization method to showcase batch effects and signal drift in the data, facilitating comparisons among different normalization methods. As demonstrated by the run plots generated on three datasets, the trend of feature signal values of QC samples normalized by EigenRF concentrates around a horizontal line, indicating its superior stability compared to other methods. Although RSD and run plots are widely used metrics for evaluating normalization method performance, they primarily focus on internal variability and fall short of comprehensively assessing the impact of normalization on result reproducibility. Furthermore, a lower RSD of QC samples does not necessarily indicate that a normalization method is optimal. Effective normalization methods should not only mitigate systematic errors but also preserve biologically relevant variations associated with the biological questions of interest. Some normalization methods may effectively decrease the RSD of QC samples but could excessively smooth the data, leading to the loss of critical biological variations of interest. In such cases, while the RSD of QC samples might be low, the actual analytical outcomes could be inaccurate.
Considering that normalization methods could significantly impact downstream analysis involving classification visualization and feature selection, we evaluated the performance of normalization methods by classification accuracy and reproducibility of feature selection. An excellent normalization method should preserve the biological variations of interest and maintain high reproducibility of feature selection while ensuring high classification accuracy. Classification accuracy is commonly used to evaluate the ability of normalization methods to preserve the biological variations of interest since preserving these variations allows the data to exhibit the inherent classification trends of biological samples. However, there is currently no universally recognized metric to evaluate the reproducibility of the results. To address this issue, we proposed the metrics to evaluate the reproducibility of importance rankings of differential metabolites for group discrimination. Specifically, the LC score was used to evaluate the consistency of local rankings and the OD score was used to evaluate the difference of overall rankings. Including reproducibility evaluation metrics is necessary as low reproducibility can undermine the reliability of research findings, even if accuracy is high. Our findings indicate that the LC and OD scores can provide deeper insights. The LC score reveals the effectiveness of normalization methods in preserving key biological variations of interest by evaluating the consistency of local rankings, while the OD score reflects the normalization method's ability to maintain the overall structure of feature importance data by measuring the difference of overall rankings. EigenRF effectively decreased the RSD of log-transformed data, though it was not the method with the lowest RSD among all normalization methods (Fig. S1A, B, S3A, B, 3A and B†). However, EigenRF demonstrated optimal reproducibility scores (Fig. 2B, C, E, F, 5B and C). Conversely, while significantly reducing RSD, some methods such as RSC, SERRF, WaveICA, and ISWSVR exhibited poor reproducibility scores on certain datasets, indicating a loss of experimental result reliability that could mislead conclusions. This suggests that reproducibility scores can evaluate the performance of normalization methods more comprehensively, especially for complex biomedical data. Therefore, we recommend considering LC and OD scores alongside RSD when assessing normalization methods for a more accurate and multi-perspective performance assessment.
Conclusions
The improved method, EigenRF, leverages the EigenMS method to capture systematic errors and employs a random forest to capture the nonlinear component of the biological variations of interest. Through validation on three distinct datasets, it has been demonstrated that EigenRF eliminated systematic errors significantly, effectively preserved the biological variations of interest, and maintained high reproducibility. EigenRF exhibited clear advantages over EigenMS and the ten commonly used normalization methods. The systematic errors captured by EigenMS may contain the nonlinear component of the biological variations of interest, as evidenced by the obvious improvement in accuracy. This improvement is attributed to the capability of the random forest regression model in EigenRF to compensate for this component of variations. Besides, EigenRF is a biological sample-based normalization method without the requirement for QC samples and internal standards, effectively mitigating certain operational pressure in experimental procedures. In addition, we proposed novel reproducibility metrics, including the LC score to evaluate the consistency of local rankings and the OD score to evaluate the difference of overall rankings. These metrics quantify the reproducibility of feature selection results from two distinct calculations, serving as a novel perspective to evaluate the capability of normalization algorithms more comprehensively.Data availability
This study was carried out using publicly available data from the published sources (BCPUM: https://doi.org/10.1021/acs.jproteome.1c00392; GCPPM: https://doi.org/10.1021/acs.analchem.1c05502; ACPPM: https://doi.org/10.1016/j.aca.2019.02.010). The code for EigenRF can be found at https://www.github.com/YangHuaLab/EigenRF.Author contributions
C. T.: conceptualization, formal analysis, methodology, software, validation, visualization, writing – original draft. D. H.: conceptualization, data curation, investigation, validation. X. X.: funding acquisition, project administration, writing – review & editing. H. Y.: funding acquisition, project administration, resources, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the National Key R&D Program of China, 2022YFC3500302 and National Natural Science Foundation of China, 82173963 and 82404831.References
- T. Kim, O. Tang, S. T. Vernon, K. A. Kott, Y. C. Koay, J. Park, D. E. James, S. M. Grieve, T. P. Speed, P. Yang, G. A. Figtree, J. F. O'Sullivan and J. Y. H. Yang, Nat. Commun., 2021, 12, 4992 CrossRef PubMed
.
- J. T. Leek, R. B. Scharpf, H. C. Bravo, D. Simcha, B. Langmead, W. E. Johnson, D. Geman, K. Baggerly and R. A. Irizarry, Nat. Rev. Genet., 2010, 11, 733–739 CrossRef PubMed
.
- A. M. De Livera, G. Olshansky, J. A. Simpson and D. J. Creek, Metabolomics, 2018, 14, 54 CrossRef PubMed
.
- X. Ding, F. Yang, Y. Chen, J. Xu, J. He, R. Zhang and Z. Abliz, Anal. Chem., 2022, 94, 7500–7509, DOI:10.1021/acs.analchem.1c05502
.
- B. Drotleff and M. Lämmerhofer, Anal. Chem., 2019, 91, 9836–9843 CrossRef PubMed
.
- M. Giordan, Stat. Biosci., 2014, 6, 73–84 CrossRef
.
- R. Molania, J. A. Gagnon-Bartsch, A. Dobrovic and T. P. Speed, Nucleic Acids Res., 2019, 47, 6073–6083 CrossRef
.
- W. Han and L. Li, Mass Spectrom. Rev., 2022, 41, 421–442 CrossRef PubMed
.
- N. Bararpour, F. Gilardi, C. Carmeli, J. Sidibe, J. Ivanisevic, T. Caputo, M. Augsburger, S. Grabherr, B. Desvergne, N. Guex, M. Bochud and A. Thomas, Sci. Rep., 2021, 11, 5657 CrossRef
.
- M. Chen, R. S. P. Rao, Y. Zhang, C. X. Zhong and J. J. Thelen, Springerplus, 2014, 3, 439 CrossRef
.
- J. Fu, Y. Zhang, Y. Wang, H. Zhang, J. Liu, T. Tang, Q. Yang, H. Sun, W. Qiu, Y. Ma, Z. Li, M. Zheng and F. Zhu, Nat. Protoc., 2022, 17, 129–151 CrossRef CAS
.
- J. T. Leek and J. D. Storey, PLoS Genet., 2007, 3, 1724–1735 Search PubMed
.
- Y. V. Karpievitch, T. Taverner, J. N. Adkins, S. J. Callister, G. A. Anderson, R. D. Smith and A. R. Dabney, Bioinformatics, 2009, 25, 2573–2580 CrossRef PubMed
.
- Y. V. Karpievitch, S. B. Nikolic, R. Wilson, J. E. Sharman and L. M. Edwards, PLoS One, 2014, 9, e116221 CrossRef PubMed
.
- M. S. R. Abid, H. Qiu, B. A. Tripp, A. D. L. Leite, H. E. Roth, J. Adamec, R. Powers and J. W. Checco, Sci. Rep., 2022, 12, 8289 CrossRef PubMed
.
- G. Biau, J. Mach. Learn. Res., 2012, 13, 1063–1095 Search PubMed
.
- S. Fan, T. Kind, T. Cajka, S. L. Hazen, W. H. W. Tang, R. Kaddurah-Daouk, M. R. Irvin, D. K. Arnett, D. K. Barupal and O. Fiehn, Anal. Chem., 2019, 91, 3590–3596 CrossRef
.
- I. V. Plyushchenko, E. S. Fedorova, N. V. Potoldykova, K. A. Polyakovskiy, A. I. Glukhov and I. A. Rodin, J. Proteome Res., 2022, 21, 833–847, DOI:10.1021/acs.jproteome.1c00392
.
- K. Deng, F. Zhang, Q. Tan, Y. Huang, W. Song, Z. Rong, Z. Zhu, K. Li and Z. Li, Anal. Chim. Acta, 2019, 1061, 60–69, DOI:10.1016/j.aca.2019.02.010
.
- T. Saito and M. Rehmsmeier, PLoS One, 2015, 10, e0118432 CrossRef PubMed
.
- P. Cuevas-Delgado, D. Dudzik, V. Miguel, S. Lamas and C. Barbas, Anal. Bioanal. Chem., 2020, 412, 6391–6405 CrossRef PubMed
.
- H. M. Parsons, D. R. Ekman, T. W. Collette and M. R. Viant, Analyst, 2009, 134, 478–485 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ay01569j |
| This journal is © The Royal Society of Chemistry 2025 |