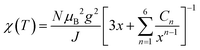Two new tellurite compounds ACu₃Te₂O₈ (A = Ca, Cd) with ferromagnetic spin-1/2 kagomé layers

Abstract

Two new tellurite compounds ACu₃Te₂O₈ (A = Ca, Cd) have been synthesized by a typical hydrothermal method, exhibiting a similar 2D layered structure in the trigonal system of space group R3̄m, where Cu²⁺ ions construct a spin-1/2 regular kagomé lattice via corner-sharing. Magnetic measurements confirmed that ACu₃Te₂O₈ (A = Ca, Cd) possesses antiferromagnetic ordering at low temperature, while exchange interactions between magnetic ions within layers are ferromagnetic.

---

Two-dimensional (2D) kagomé compounds composed of 3d transition-metal ions have been a subject of intense research in material sciences and condensed matter physics due to their unique structural features and exotic magnetic phenomena.^1–6 For kagomé antiferromagnets, many compounds such as ZnCu₃(OH)₆Cl₂,⁷ Cu₃V₂O₇(OH)₂·2H₂O,⁸ CdCu₃(OH)₆(NO₃)₂·H₂O,⁹ BaNi₃(VO₄)₂(OH)₂,¹⁰ and KFe₃(SO₄)₂(OH)₆¹¹ with a 2D kagomé structure have been found to show a possible spin-liquid state,¹² orbital switching,¹³ fractional magnetization plateaus,⁹ spin-glass,¹⁰ and spin-chirality behaviors,¹¹ respectively. However, the current interest is mainly focused on the exploration of spin-1/2 perfect kagomé antiferromagnets, which are considered as the most ideal candidates for the realization of a quantum spin-liquid state, because a synergistic effect of strong spin-fluctuation and geometrical-frustration could prevent the appearance of a long-range magnetic order at low temperature.¹⁴

On the other hand, kagomé ferromagnets are also found to exhibit various interesting physical properties. For example, Fe₃Sn₂,¹⁵ Co₃Sn₂S₂,¹⁶ and LiMn₆Sn₆¹⁷ were confirmed to show an anomalous Hall effect, while UCo_0.8Ru_0.2Al was observed to have a colossal anomalous Nernst effect.¹⁸ Moreover, Li₉Cr₃(P₂O₇)₃(PO₄)₂ was found to have a large magnetocaloric effect at low temperature.¹⁹ Furthermore, kagomé metal CsV₃Sb₅ was also found to exhibit a superconducting ground state.^20,21 Generally, both kagomé antiferromagnetic and kagomé ferromagnetic compounds have given many exciting topics, and the exploration of kagomé compounds is still a great challenge.

It is well-known that the Se⁴⁺ and Te⁴⁺ ions with stereochemically active lone-pair electrons can usually form SeO₃ and TeO₃ trigonal pyramids in the oxygen-coordination environments, which often act as “chemical scissors” to introduce a low-dimensional structural framework, resulting in the formation of many novel materials. In our previous works, we have successfully synthesized many kagomé-related selenite or tellurite compounds, including M₃(TeO₃)(SO₄)(OH)₂·2H₂O (M = Ni, Co) with a distorted striped kagomé lattice,²² A₂Cu₅(TeO₃)(SO₄)₃(OH)₄ (A = Na, K) with a 1D kagomé strip lattice,²³ BiOCu₂(XO₃)(SO₄)(OH)·H₂O (X = Te, Se) with an octa-kagomé lattice,²⁴ Co₃(SeO₃)(SO₄)(OH)₂ with a distorted kagomé lattice,²⁵ K₂Ni₉(TeO₃)₄(MoO₄)₄(OH)₄ with a capped-kagomé lattice,²⁶ and Pb(OF)Cu₃(SeO₃)₂(NO₃) with a breathing-kagomé lattice.²⁷ In this work, we have recently obtained two new Cu²⁺-based tellurite compounds of ACu₃Te₂O₈ (A = Ca, Cd) with a trigonal system of space group R3̄m, exhibiting a regular kagomé lattice built by magnetic Cu²⁺ ions. Surprisingly, magnetic measurements indicate that ACu₃Te₂O₈ (A = Ca, Cd) both possess an antiferromagnetic (AFM) ordering at low temperature with ferromagnetic (FM) interactions in the kagomé layers.

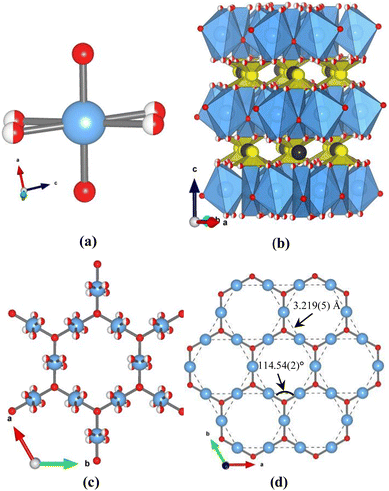
Single crystals of ACu₃Te₂O₈ (A = Ca, Cd) were synthesized by a conventional hydrothermal reaction. The experimental details can be seen in the ESI.† Both compounds are found to crystallize in the trigonal system with a space group of R3̄m. Since they are isostructural, CaCu₃Te₂O₈ is selected as a representative for the descriptions of their structural features. There is one Cu site, one Te site, one Ca site, and two O sites (O1 and O2) in an asymmetric unit. The O2 atoms occupy two crystallographically equivalent sites with 1/2 atom occupancy for each site (Fig. 1a). Such cases of disordered oxygen atoms are also seen in many kagomé compounds such as β-BaCu₃V₂O₈(OH)₂,²⁸ CdCu₃(OH)₆(NO₃)₂·H₂O,⁹ YCu₃(OH)₆Cl₃,²⁹ KMn₃O₂(Ge₂O₇),³⁰ and YCa₃(MnO)₃(BO₃)₄ series.^31,32 Moreover, all Cu²⁺ ions are equivalent and coordinated by four O atoms, forming a CuO₄ square plaquette (Fig. S8, ESI†). The Cu–O bond lengths of the CuO₄ square plaquettes range from 1.913(2) to 1.991(8) Å. Te atoms are coordinated by three oxygen atoms, forming TeO₃ trigonal pyramids with bond lengths of 1.890(8) Å.

Fig. 1 (a) The oxygen-coordination environments of Cu²⁺ ions. (b) The layered structure of CaCu₃Te₂O₈ viewed along the c-axis with (c) the linkage of CuO₄ square plaquettes, and (d) a regular kagomé layer viewed on the a–b plane. Color codes: Ca, black; Cu, blue; Te, yellow; O, red.

Fig. 1b shows a typical layer-structure of CaCu₃Te₂O₈ running along the c-axis, in which the layers are separated by TeO₃²⁻ groups and Ca²⁺ cations. The shortest distance of Cu–Cu in neighbouring layers is 5.879(3) Å. The CuO₄ square plaquettes are interconnected via corner-sharing (O1) to form the layers (Fig. 1c), and each TeO₃²⁻ group connects with three CuO₄ square plaquettes via corner-sharing (O2) (Fig. S4, ESI†). It is worth noting that a typical kagomé lattice with a unique planar arrangement of corner-sharing triangles constructed by magnetic Cu²⁺ ions can be seen on the a–b plane, when nonmagnetic Ca²⁺ and TeO₃²⁻ groups of CaCu₃Te₂O₈ are removed from the structural framework. Fig. 1d clearly shows the ideal kagomé topological structure of Cu²⁺ ions, in which the distance between the Cu²⁺ ions is 3.219(5) Å and the angle of Cu–O1–Cu is 114.54(2)°. It is also noted that the Cu–Cu distances and the angles of the Cu–O1–Cu pathways in CdCu₃Te₂O₈ are close to those in CaCu₃Te₂O₈, due to quite similar radii of Ca²⁺ and Cd²⁺ ions situated between the layers. As a result, the replacement of Ca²⁺ by Cd²⁺ shows a slight impact on the kagomé layers.

It is instructive to compare the structure of ACu₃Te₂O₈ (A = Ca, Cd) with regular kagomé compound Zn_xCu_4−x(OH)₆Cl₂ (0 ≤ x ≤ 1) (Fig. S8 and Table S6, ESI†).^33,34 Although all these compounds are superexchanged by equatorial Cu–O bonds, there are significant differences between them. Zn_xCu_4−x(OH)₆Cl₂ (0 ≤ x ≤ 1) is coordinated by four equatorial O atoms and two axial Cl atoms, with all four O atoms in the facet involved in superexchange interactions. However, in ACu₃Te₂O₈ (A = Ca, Cd) since each Cu ion is surrounded by two close equatorial O1 ligands (1.913(2) Å) and two distant equatorial O2 ligands (1.991(8) Å) (Fig. S8, ESI†), only O1 is involved in the superexchange interactions between Cu ions. It is noted that O2 is situated outside the kagomé layers without participating in the superexchange interaction (Fig. S8, ESI†), and thus the disordered O2 sites seem to have a negligible effect on the kagomé layers.²⁸ Moreover, it must be noted that the shortest distance (∼4.7 Å) between the Cu²⁺ ions and the angle (∼180°) of Cu–O–Cu for kagomé compound Cu₃(CO₃)₂(x)₃·2ClO₄ (MOF-x) are much larger than those (∼3.2 Å and ∼114°) in ACu₃Te₂O₈ (A = Ca, Cd), where the exchange interactions within the kagomé layers are also ferromagnetic in nature.³⁵

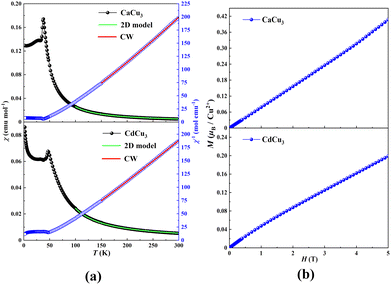
Fig. 2a shows the temperature dependence of magnetic susceptibility (χ) and the corresponding reciprocal one (χ⁻¹) of ACu₃Te₂O₈ (A = Ca, Cd) measured at 0.1 T. The susceptibilities increase with decreasing temperature, while a sharp peak is observed at ∼38 K for CaCu₃Te₂O₈ and ∼47 K for CdCu₃Te₂O₈, confirming the onset of antiferromagnetic (AFM) ordering. Such AFM transition was further confirmed by the specific heat data with zero field (Fig. S5, ESI†), showing a λ-type peak around 38 K for CaCu₃Te₂O₈ and 47 K for CdCu₃Te₂O₈. These are in good agreement with the interlayer interactions of ACu₃Te₂O₈ (A = Ca, Cd), where the interlayer distance of CdCu₃Te₂O₈ is shorter than that of CaCu₃Te₂O₈ (Table S6, ESI†). Moreover, the Curie upturn below 25 K in CdCu₃Te₂O₈ may be attributed to the contribution from free spins due to the crystal defect. Also, it is noted that the plot of χ⁻¹versus T can be fitted well to the Curie–Weiss law above 150 K, giving the Curie constant C = 1.423 emu K mol⁻¹ and Weiss temperature θ = 49.6 K for CaCu₃Te₂O₈ and C = 1.442 emu K mol⁻¹ and θ = 45.1 K for CdCu₃Te₂O₈. The calculated effective magnetic moment of Cu²⁺ for CaCu₃Te₂O₈ is 1.947μ_B and for CdCu₃Te₂O₈ is 1.961μ_B, slightly larger than the theoretical spin value of 1.732μ_B for Cu²⁺ (S = 1/2, g = 2). The positive Weiss temperature suggests a dominant ferromagnetic (FM) interaction exchange between neighbouring Cu²⁺ ions in the layers. Fig. 2b displays the isothermal magnetization (M) as a function of the applied field (H) at 2 K. The magnetization increases linearly with increasing field, which is consistent with an AFM ground state.

Fig. 2 (a) Magnetic susceptibility (χ) and the corresponding reciprocal one (χ⁻¹) of ACu₃Te₂O₈ (A = Ca, Cd) at 0.1 T. The red line shows Curie–Weiss fitting and the green line is fitted by the 2D Heisenberg model. (b) The isothermal magnetization (M) as a function of magnetic field at 2 K.

The mean field theory θ_CW = −zJS(S + 1)/3k_B (z is the number of neighbouring magnetic atoms around a magnetic atom) can be used to estimate the intralayer exchange coupling |J| = ∼49.6 K for CaCu₃Te₂O₈, and |J| = ∼45.1 K for CdCu₃Te₂O₈. Furthermore, the χ(T) from 100–300 K (Fig. 2a) can be well-fitted to the two-dimensional (2D) Heisenberg model, which is expressed as follows:³⁶

where x = k_BT/JS(S + 1), N is the number of spins in the lattice and C_n is the coefficient provided by lines. The fit gives J = 76.3 K, g = 2.06 for CaCu₃Te₂O₈, and J = 60.1 K, g = 2.17 for CdCu₃Te₂O₈. The results are consistent with those estimated from the mean field theory. It must be noted that ACu₃Te₂O₈ (A = Ca, Cd) show the FM interactions inside the kagomé layers and AFM interactions between the neighbouring layers, therefore the geometrical spin-frustration effect cannot be observed in the systems.

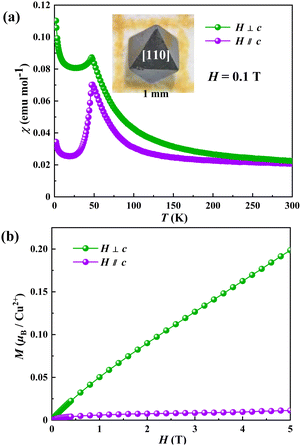
Since CdCu₃Te₂O₈ single crystals obtained here are large enough to further investigate the anisotropic behaviors, we measured magnetic susceptibilities (χ_‖ and χ_⊥) of CdCu₃Te₂O₈ under an applied field H = 0.1 T parallel and perpendicular to the c-axis using a single crystal sample (Fig. 3a). We note that an obvious divergence between χ_‖ and χ_⊥ reveals magnetic anisotropy in the system. The rapid decrease of χ_‖ below 47 K is indicative of the easy magnetic c-axis. As shown in Fig. S6 (ESI†), the reciprocal susceptibilities (H_‖c and H_⊥c) at high temperature can be fitted by the Curie–Weiss law with the Weiss temperature θ_‖ = −39.4 K and θ_⊥ = 27.3 K, showing an AFM interaction between the Cu²⁺ ions along the c-axis, while a FM interaction is seen between the Cu²⁺ ions perpendicular to the c-axis. Fig. 3b illustrates the magnetization curves (M_‖ and M_⊥) at 2 K with applied magnetic fields parallel and perpendicular to the c-axis, both showing an almost linear increase with increasing magnetic field. The differences between M_‖ and M_⊥ also confirmed strong magnetic anisotropy in the system. The above findings support FM interactions inside the layers and AFM interactions between the neighbouring layers.

Fig. 3 (a) Magnetic susceptibilities (χ) of CdCu₃Te₂O₈ measured under the applied field (H) parallel and perpendicular to the c-axis. The inset shows a single crystal sample with natural crystal planes. (b) The magnetization (M) curves at 2 K measured with applied fields (H) parallel and perpendicular to the c-axis.

It is well known that the Hamiltonian for exchange interaction between any two spins (S1 and S2) can be expressed as H = −2JS1S2, where the magnitude and the sign of the exchange constant J are determined by the bonding geometry according to the Goodenough rules.^37–39 Although the superexchange pathways of Cu–O1–Cu in the kagomé layers of ACu₃Te₂O₈ (A = Ca, Cd) with the coupling distance of ∼3.2 Å and the coupling angle of ∼114° (Fig. 1d) look to be an antiferromagnetic interaction according to the Goodenough rules,^37–39 the microscopic structure with Cu–O–Te–O–Cu pathways may strongly affect the formation of Cu-centered polyhedra and further change the coupling exchange, leading to FM interactions in the kagomé layers.⁴⁰ A similar behavior is also observed in breathing kagomé compound Pb(OF)Cu₃(SeO₃)₂(NO₃) with coupling angles of Cu–O1–Cu (∼113°) and Cu–F1–Cu (∼116°), showing FM interactions in the kagomé layers. Furthermore, the exchange pathways of the Cu–O–Cu bonds with the coupling angles (>110°) in Cu₃Bi(SeO₃)₂O₂X (X = Cl, Br) (CBSX) have been confirmed to be FM interactions using neutron experiments.^41,42 More surprisingly, the exchange pathways with the coupling angle of ∼180° in Cu₃(CO₃)₂(x)₃·2ClO₄ (MOF-x) are also FM interactions.³⁵ Also, it must be noted that ACu₃Te₂O₈ (A = Ca, Cd) and CBSX have a similar structural feature, in which the Cu atoms are coordinated to four O atoms to form CuO₄ square plaquettes and such plaquettes are connected to each other via corner-sharing. To further understand the nature of the magnetic behaviors of ACu₃Te₂O₈ (A = Ca, Cd), neutron experiments and theoretical calculations may be required to provide a deeper explanation.

In summary, two new tellurite compounds ACu₃Te₂O₈ (A = Ca, Cd) were successfully synthesized by means of a conventional hydrothermal method, exhibiting a similar 2D layered structure in the trigonal system of space group R3̄m, where magnetic Cu²⁺ ions construct a spin-1/2 regular kagomé lattice via corner-sharing. Our results of magnetic and specific heat measurements confirmed the appearance of an AFM ordering at ∼38 K for CaCu₃Te₂O₈ and ∼47 K for CdCu₃Te₂O₈, respectively, where the positive Weiss temperatures suggest the FM exchange interactions of the Cu–O1–Cu pathways in the kagomé layers. Also, magnetic anisotropy was observed using a single crystal sample of CdCu₃Te₂O₈, showing the easy magnetic c-axis. The results further support FM interactions inside the layers and AFM interactions between the neighbouring layers. We envisage that the present study will further enrich the chemical and physical contents of kagomé systems, which may stimulate the exploration of various interesting kagomé compounds.

This work was financially supported by the National Natural Science Foundation of China (NSFC) (no. 22175173).

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. L. Balents, Nature, 2010, 464, 199–208.
2. C. Broholm, R. J. Cava, S. A. Kivelson, D. G. Nocera, M. R. Norman and T. Senthil, Science, 2020, 367, 263.
3. J. R. Chamorro, T. M. McQueen and T. T. Tran, Chem. Rev., 2021, 121, 2898–2934.
4. M. R. Norman, Rev. Mod. Phys., 2016, 88, 041002.
5. D. G. Nocera, B. M. Bartlett, D. Grohol, D. Papoutsakis and M. P. Shores, Chem. – Eur. J., 2004, 10, 3850–3859.
6. A. Harrison, J. Phys.: Condens. Matter, 2004, 16, S553–S572.
7. M. P. Shores, E. A. Nytko, B. M. Bartlett and D. G. Nocera, J. Am. Chem. Soc., 2005, 127, 13462–13463.
8. Z. Hiroi, M. Hanawa, N. Kobayashi, M. Nohara, H. Takagi, Y. Kato and M. Takigawa, J. Phys. Soc. Jpn., 2001, 70, 3377.
9. R. Okuma, D. Nakamura, T. Okubo, A. Miyake, A. Matsuo, K. Kindo, M. Tokunaga, N. Kawashima, S. Takeyama and Z. Hiroi, Nat. Commun., 2019, 10, 1229.
10. D. E. Freedman, R. Chisnell, T. M. McQueen, Y. S. Lee, C. Payen and D. G. Nocera, Chem. Commun., 2012, 48, 64–66.
11. D. Grohol, K. matan, J.-H. Cho, S.-H. Lee, J. W. Lynn, D. G. Nocera and Y. S. Lee, Nat. Mater., 2005, 4, 323–327.
12. T.-H. Han, J. S. Helton, S. Chu, D. G. Nocera, J. A. Rodriguez-Rivera, C. Broholm and Y. S. Lee, Nature, 2012, 492, 406–420.
13. H. Yoshida, J. Yamaura, M. Isobe, Y. Okamoto, G. J. Nilsen and Z. Hiroi, Nat. Commun., 2012, 3, 860.
14. S. M. Yan, D. A. Huse and S. R. White, Science, 2011, 332, 1173–1176.
15. K. I. A. Khan, R. S. Yadav, H. Bangar, A. Kumar, N. Chowdhury, P. K. Muduli and P. K. Muduli, Nanoscale, 2022, 14, 8484–8492.
16. Q. Wang, Y. Xu, R. Lou, Z. Liu, M. Li, Y. Huang, D. Shen, H. Weng, S. Wang and H. Lei, Nat. Commun., 2018, 9, 3681.
17. D. Chen, C. Le, C. Fu, H. Lin, W. Schnelle, Y. Sun and C. Felser, Phys. Rev. B, 2021, 103, 144410.
18. T. Asaba, V. Ivanov, S. M. Thomas, S. Y. Savrasov, J. D. Thompson, E. D. Bauer and F. Ronning, Sci. Adv., 2021, 7, eabf1467.
19. A. Magar, V. Singh, J. J. Abraham, Y. Senyk, A. Alfonsov, B. Büchner, V. Kataev, A. A. Tsirlin and R. Nath, Phys. Rev. Appl., 2022, 18, 054076.
20. B. R. Ortiz, S. M. L. Teicher, Y. Hu, J. L. Zuo, P. M. Sarte, E. C. Schueller, A. M. M. Abeykoon, M. J. Krogstad, S. Rosenkranz, R. Osborn, R. Seshadri, L. Balents, J. He and S. D. Wilson, Phys. Rev. Lett., 2020, 125, 247002.
21. K. Jiang, T. Wu, J.-X. Yin, Z. Wang, M. Z. Hasan, S. D. Wilson, X. Chen and J. Hu, Natl. Sci. Rev., 2023, 10, 199.
22. Y. Tang, W. Guo, S. Zhang, M. Yang and Z. He, Cryst. Growth Des., 2014, 14, 5206–5211.
23. Y. Tang, W. Guo, H. Xiang, S. Zhang, M. Yang, M. Cui, N. Wang and Z. He, Inorg. Chem., 2016, 55, 644–648.
24. Y. Tang, C. Peng, W. Guo, J. F. Wang, G. Su and Z. He, J. Am. Chem. Soc., 2017, 139, 14057–14060.
25. M. Zhang, Y. Song, Z. Zhao, J. Li, W. Zhang, Y. Xie, X. Huang, X. Huang and Z. He, Inorg. Chem., 2020, 59, 8054–8060.
26. W. Zhang, Z. He, Y. Xie, M. Cui, S. Zhang, S. Chen, Z. Zhao, M. Zhang and X. Huang, Inorg. Chem., 2020, 59, 2299–2307.
27. M. Zhang, Z. Zhao, W. Zhang, J. Li, X. Huang and Z. He, Chem. Commun., 2020, 56, 11965–11968.
28. H. Yoshida, Y. Michiue, E. Takayama-Muromachi and M. Isobe, J. Mater. Chem., 2012, 22, 18793–18796.
29. A. Zorko, M. Pregelj, M. Gomilšek, M. Klanjšek, O. Zaharko, W. Sun and J. X. Mi, Phys. Rev. B, 2019, 100, 144420.
30. M. S. Williams, J. P. West and S.-J. Hwu, Chem. Mater., 2014, 26, 1502–1504.
31. R. Li and C. Greaves, Phys. Rev. B:Condens. Matter Mater. Phys., 2003, 68, 172403.
32. C.-H. Wang, M. Avdeev, B. J. Kennedy, M. Küpers and C. D. Ling, Inorg. Chem., 2016, 55, 7535–7541.
33. Z. Hiroi, H. Yoshida, Y. Okamoto and M. Takigawa, J. Phys. Conf. Ser., 2009, 145, 012002.
34. R. H. Colman, A. Sinclair and A. S. Wills, Chem. Mater., 2010, 22, 5774–5779.
35. S. A. Ivko, K. Tustain, T. Dolling, A. Abdeldaim, O. H. J. Mustonen, P. Manuel, C. Wang, H. Luetkens and L. Clark, Chem. Mater., 2022, 34, 5409–5421.
36. M. E. Lines, J. Phys. Chem. Solids, 1970, 31, 101–116.
37. J. B. Goodenough, John Wiley and Sons, Magnetism and the Chemical Bond, New York, p. 1963.
38. J. B. Goodenough, Phys. Rev., 1955, 100, 564–573.
39. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
40. J. Deisenhofer, R. M. Eremina, A. Pimenov, T. Gavrilova, H. Berger, M. Johnsson, P. Lemmens, H. A. Krug von Nidda, A. Loidl, K. S. Lee and M. H. Whangbo, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 74, 174421.
41. M. Pregelj, O. Zaharko, A. Günther, A. Loidl, V. Tsurkan and S. Guerrero, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 144409.
42. H. C. Wu, K. D. Chandrasekhar, J. K. Yuan, J. R. Huang, J. Y. Lin, H. Berger and H. D. Yang, Phys. Rev. B, 2017, 95, 125121.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, crystal pictures, PXRD patterns, EDS, and additional magnetic data. CCDC 2371102 and 2370923. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cc03756a

---