Single crystal diffraction study of Ba[H₄C₄O₁₀][H₃C₄O₁₀][H₂CO₃][HCO₃], a hydrous mixed sp²/sp³-carbonate

Abstract

We have synthesized the first hydrous sp³-carbonate by laser-heating Ba[CO₃], CO₂ and H₂O in a diamond anvil cell at 40(3) GPa. The crystal structure of Ba[H₄C₄O₁₀][H₃C₄O₁₀][H₂CO₃][HCO₃] was determined by synchrotron single crystal X-ray diffraction. The experiments were complemented by DFT-based calculations. This compound is the first example of a carbonate containing both trigonally-coordinated carbon in [CO₃]²⁻-groups and tetrahedrally coordinated carbon in [CO₄]⁴⁻-groups. The [CO₄]⁴⁻-groups polymerize by corner-sharing to form pyramidal [C₄O₁₀]⁴⁻-groups, which can bind three or four hydrogen atoms. As the pyramidal [C₄O₁₀]⁴⁻-groups are a constituent of several anhydrous sp³-carbonates, we now expect that further high-pressure hydrous carbonates can be obtained.

---

In the last decade there has been a significant expansion of our understanding of the crystal chemistry and the structures of carbonates, mainly triggered by high-pressure single crystal structure determinations. In earlier textbooks (e.g. Okrusch and Frimmel¹ or Reeder), “conventional” carbonates were defined by the presence of trigonal, nearly planar [CO₃]²⁻-groups, and a limited number of structure types were known, of which the trigonal calcite- and dolomite-type, and the orthorhombic aragonite-type structures are the most important ones. Especially the phase diagrams of Ca[CO₃] (calcite/aragonite) and (Ca,Mg)[CO₃]₂ (dolomite) have been studied in great detail, as they account for >90% of the carbonates present in the Earth's crust.^2–4 In these carbonates sp²-hybrid orbitals are present on the central carbon atom in the [CO₃]²⁻-group.

A profound expansion took place when it was shown that at high pressures carbonates can be formed in which the carbon is tetrahedrally coordinated, i.e. where sp³-hybridization was induced by high pressure. Structure solutions from powder data at very high pressures typically rely on assumptions, so initial studies such as Ono et al.⁵ (CaCO₃-C222₁) or Boulard et al.⁶ new (Mg₃[C₃O₉]-C2/m) relied on comparisons to density functional theory (DFT) based predictions. Later, the results of a single crystal study of Mg₂Fe₂[C₄O₁₃]-C2/c unambiguously showed that at very high pressures carbonates may contain carbon in tetrahedral coordination.⁷ This was exciting, not only because a new building block had been discovered, but also because the tetrahedrally coordinated [CO₄]⁴⁻-groups can polymerize by corner-sharing an oxygen atom, to form groups, rings, and clusters (see summary in Spahr et al.⁸). However, as initially the sp³-carbonates were only formed by polymorphic transitions or dissociation at very high pressures of ≈70 GPa, only a limited number of systems were experimentally investigated.

A next milestone was then reached when sp³-carbonates were obtained at much lower pressures by reactions, and when it was shown that some of them are recoverable to ambient pressure.^8–11 Further noticeable progress was the recent synthesis of inorganic anhydrous pyrocarbonates, in which flexible [C₂O₅]²⁻-groups are the defining structural units.^12–16 Mixed carbonate, with both trigonal [CO₃]²⁻-groups and [C₂O₅]²⁻-groups have also been obtained.^17,18 Here, we will denote carbonates with either [CO₄]⁴⁻ or [C₂O₅]²⁻-groups as “novel carbonates”. It is, worthwhile to note that even for the conventional carbonates, syntheses at high pressures have achieved substantial advances. For example, the recent single crystal structure determination of Al₂[CO₃]₃ has shown for the first time that it is possible to form a chemically simple anhydrous carbonate with a single type of trivalent metal cation which can be recovered to ambient conditions.¹⁷

An efficient route for the synthesis of novel carbonates is to either react carbonates with oxides or CO₂, or to react oxides with CO₂.^8–18 We have constructed a cryogenic diamond anvil cell (DAC) loading system which is optimized to condense CO₂ into a pre-cooled DAC.¹³ With the synthesis of the hydrous lithium pyrocarboante Li[HC₂O₅] we demonstrated that this set-up can also be employed to co-condense H₂O ice into the gasket hole in order to obtain hydrous carbonates.¹⁶ To the best of our knowledge, there have neither been structure prediction studies of novel hydrous carbonates nor any experimental report of a novel hydrous carbonate except for the synthesis of Li[HC₂O₅]. This is surprising, as about 2/3 of the known ambient pressure carbon-bearing minerals are hydrous or hydrated.¹⁹

Here, we describe the synthesis and characterization of barium hydrogen carbonate Ba[H₄C₄O₁₀][H₃C₄O₁₀][H₂CO₃][HCO₃]. It was obtained by CO₂-laser heating a cold-compressed mixture of a Ba[CO₃] crystal, CO₂ and H₂O at 40(3) GPa (Fig. S1, in the ESI†). The synthesis was performed in a similar manner to that described for the synthesis of Ba[C₂O₅] at 30 GPa.¹⁴ In an earlier study we described that heating Ba[CO₃] in CO₂ at 30 GPa results in the formation of a pyrocarbonate, hexagonal Ba[C₂O₅]-P6/m.¹⁴ Unexpectedly, Ba[C₂O₅] is structurally quite distinct from the monoclinic and isostructural pyrocarbonates Sr[C₂O₅]-P2₁/c and Pb[C₂O₅]-P2₁/c.^12,13 Initial structure predictions in the barium carbonate system failed to anticipate the Ba[C₂O₅] phase, and later structure prediction calculations failed to correctly predict the space group and the substantial twist of the [C₂O₅]²⁻-groups.^20,21 In the present experiments, we have observed that heating Ba[CO₃] together with CO₂ and H₂O results in the formation of a novel hydrous carbonate. We assume that small amounts of H₂O-ice unintentionally co-condensed with the CO₂ through the gas jet.¹⁶

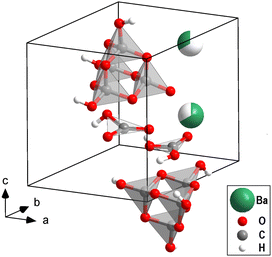
The structure of one of the phases with Ba[H₄C₄O₁₀][H₃C₄O₁₀][H₂CO₃][HCO₃] composition (Fig. 1), has been solved on a temperature-quenched sample by single crystal X-ray diffraction at 40(3) GPa in combination with DFT-based calculations (see ESI†). The structure is triclinic (P1) with a = 6.346(2) Å, b = 6.377(2) Å, c = 8.191(2) Å, α = 89.77(2)°, β = 89.66(2)° and γ = 60.72(4)°. It shows a P3̄ pseudo-symmetry. The structure refinement is strongly biased by the heavy barium atoms (I_hkl ∝ Z²). In addition to the barium positions, the presence and locations of both [CO₃]²⁻-groups and [C₄O₁₀]⁴⁻-groups could reliably be established from the analysis of the X-ray diffraction data. After locating the barium atoms (Z_Ba = 56), the [CO₃]²⁻-and the [C₄O₁₀]⁴⁻-groups (Z_C = 6, Z_O = 8), hydrogen atoms (Z_H = 1) were required in order to obtain charge balancing. The locations of these hydrogen atoms cannot be reliably derived experimentally due to the limited access to reciprocal space imposed by the metallic body of the DAC and the presence of much stronger scatterers. The analysis of the experimental data resulted in a triclinic structure, where the one Ba atom was distributed over two sites.

Fig. 1 Content of one unit cell of the mixed sp²/sp³-barium hydrogencarbonate Ba[H₄C₄O₁₀][H₃C₄O₁₀][H₂CO₃][HCO₃] at 40 GPa. The partial site occupancies of the two Ba-positions are indicated by partially filled spheres.

In order to better understand structure–property relations and to better constrain the hydrogen positions, DFT-based atomistic model calculations have been carried out. There are several approaches to approximate structures with partially occupied sites in atomistic modelling approaches based on the use of periodic boundary conditions. Conceptually the most straight forward is to generate a very large supercell, in order to mimic the disorder. This is computationally expensive. Alternatively, the “virtual crystal approximation” (VCA) can be employed (e.g. Winkler et al.²²), which is computationally much less demanding, but which can neither be used with perturbation theory-based approaches nor with finite difference methods to compute phonon dispersion curves. Also, in the VCA local relaxations are not described correctly.

Here, we note that simply fully occupying either of the two barium sites leads to lattice parameters and atomic coordinates for the non-hydrogen atoms which are in very good agreement with the experiment when the barium is on 0.81,0.75,0.38 (“option 1”), while a slightly worse agreement results if the barium is located on 0.80,0.74,0.86 (“option 2”), after geometry optimization. For both options, the structures can be fully relaxed and the lattice dynamics at the Γ-point and Raman spectra have been obtained (Fig. S6, in the ESI†). The computation of a full set of phonon dispersion curves was not feasible with the limited available computational resources. As there were no modes with imaginary frequencies the structure is at least stable with respect to translationengleiche phase transitions. At 40 GPa the enthalpy difference favors “option 1” over “option 2” by ≈0.5 eV per unit cell, which contains one formula unit. This is fully consistent with the preferred occupation found experimentally. Table S1 (in the ESI†) shows the experimentally obtained structural data in comparison to the “option 1” DFT calculations. The lattice parameters of both structural models agree within the expected uncertainties.

The positions of barium, oxygen and carbon atoms in the relaxed DFT structures were in very good agreement with our single crystal data, even if the completeness of the data collection was limited. Hence, we conclude that our general structural model is accurate. As the experimental structure is an average structure, and as the experimental positions of the hydrogen atoms are somewhat uncertain, there are some close Ba–H–O contacts in the experimental structure. However, as mentioned above, due to the limitations imposed by the data collection in a DAC, the diffraction data are not expected to be sensitive to the hydrogen position. In contrast, it has been long established that DFT model calculations can reliably predict hydrogen positions.²³ Hence, we decided to introduce and constrain the hydrogen positions from the DFT calculations in the experimental structural model. Geometry optimizations at 40 GPa gave hydrogen positions which resulted in covalent O–H bonds having bond distances d(O–H) ranging from 0.98–1.05 Å. The hydrogen bond distances d(H⋯O) range from 1.42–1.70 Å and have, as expected²⁴ much lower Mulliken bond populations of 0.1–0.2 e⁻ Å⁻³ than the covalent O–H bonds, which have bond populations of about 0.6 e⁻ Å⁻³. Tables S2 and S3 (in the ESI†) lists interatomic distances and angles between the barium atom and the oxygen/hydrogen and nearest Ba–H contacts in the DFT-based structural model.

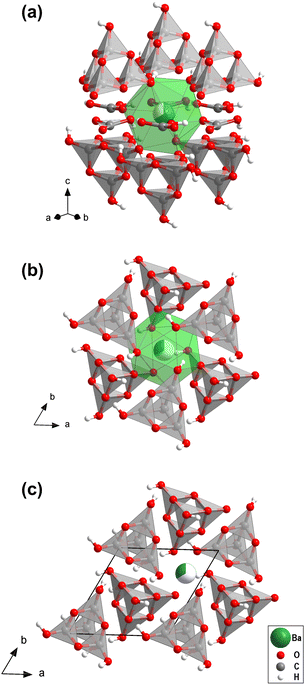
We then carried out supercell calculations up to 2 × 2 × 2, where one Ba atom was on the “option 2” position, while all others were located on the “option 1” position, thus mimicking increasing disorder (Fig. S3, in the ESI†). On both atomic positions the barium atoms are nearly spherical coordinated with 12 oxygen atoms (Fig. 2a and b). Supercells larger than 2 × 2 × 1 have enthalpies per formula unit lower than the “option 1” structure, i.e. disordering the barium over the two available sites actually stabilizes the structure. However, due to the substantial computational resources required for these calculations, the effect of short-range and long-range ordering could not be determined quantitatively.

Fig. 2 (a) and (b) Coordination of the two different barium positions with 12 oxygen atoms in the mixed sp²/sp³-barium hydrogencarbonate. (c) Alternating directions of the [H₄C₄O₁₀]- and [H₃C₄O₁₀]⁻-groups. Partially filled spheres indicate partial site occupancies.

A comparison of the experimentally determined and computed structure is given in Fig. S2 (in the ESI†). In Fig. 1 the experimental structure with refined hydrogen positions derived from DFT calculations is shown. The location of the hydrogen atoms depends on the distribution of the Ba-atoms over the available sites in the model calculations. This implies that in the actual structure there will be an appreciable disorder of the hydrogen atoms. However, it is beyond the currently available experimental techniques to locate the hydrogen positions experimentally in order to benchmark the models.

Fig. S3 (in the ESI†) shows that Ba[H₄C₄O₁₀][H₃C₄O₁₀][H₂CO₃][HCO₃] consists of layers. In the first layer [H₄C₄O₁₀]- and [H₃C₄O₁₀]⁻-groups point in alternating directions (Fig. 2c). The second type of layer contains [H₂CO₃]- and [HCO₃]⁻-groups. There is an intricate network of hydrogen bonds both within the two types of layers and between them. The individual structural units of the mixed sp²/sp³-barium hydrogencarbonate are shown in Fig. 3.

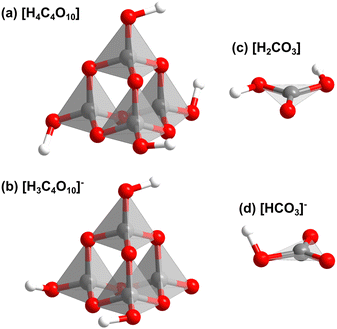Fig. 3 Structrual units of the mixed sp²/sp³-barium hydrogencarbonate Ba[H₄C₄O₁₀][H₃C₄O₁₀][H₂CO₃][HCO₃] from DFT-based calculations: (a) [H₄C₄O₁₀], (b) [H₃C₄O₁₀]⁻, (c) [H₂CO₃] and (d) [HCO₃]⁻.

While at high pressures van der Waals (vdW) interactions don’t contribute significantly, they become relevant at lower pressures. This can be inferred from the DFT calculations by of results for calculations with and without vdW-interactions. When a vdW-correction scheme is applied at high pressures, the results of the geometry optimizations change only slightly with respect to the uncorrected calculations. Specifically, when a Tkatchenko–Scheffler dispersion correction is applied,²⁵ the molar volume at 40 GPa changes by less than 1.5%. At low pressures, however, the effects are significant and at 0 GPa the molar volumes between dispersion-corrected and uncorrected models differ by 11%. Hence, the compression behavior was studied with a vdW-corrected approach.²⁵ As expected from the structural features, Ba[H₄C₄O₁₀][H₃C₄O₁₀][H₂CO₃][HCO₃] is a very compressible compound with a bulk modulus of K₀ = 14(2) GPa with K_p= 8.2(8) (see Fig. S4, in the ESI†). We found that the compression mechanism is very anisotropic (see Fig. S5, in the ESI†). The structure is highly compressible along the c-axes (≈25% between 0–40 GPa), caused by the reduction of the space between the alternating layers of the [H₄C₄O₁₀]-/[H₃C₄O₁₀]⁻-groups and [H₂CO₃]-/[HCO₃]⁻-groups. In contrast, within the layers along the b-axes the compressibility is significantly lower (≈5%).

In the framework of the current study, due to the limited beam time available, it was not possible to elucidate the stability field of Ba[H₄C₄O₁₀][H₃C₄O₁₀][H₂CO₃][HCO₃] experimentally. It was also not feasible to derive the stability field by DFT calculations, as this would involve calculations of disordered ice-VII,²⁶ which would have been beyond the available computational resources. Here, further experiments and calculations are therefore required.

In conclusion, by combining the synchrotron single crystal X-ray diffraction data with DFT calculations for the location of the hydrogen atoms, we now have a robust model of a new carbonate structure type, the first structure which has both trigonal [CO₃]²⁻-groups with sp²-hybridized bonds and [C₄O₁₀]⁴⁻-groups with sp³-hybridized bonds (Fig. 1). Also, this is the first hydrous high-pressure sp³-carbonate. Hence, this synthesis enlarges the family of novel carbonates substantially. The [C₄O₁₀]⁴⁻-group in Ba[H₄C₄O₁₀][H₃C₄O₁₀][H₂CO₃][HCO₃] is a constituent of several sp³-carbonates, including Mn₂[C₄O₁₀]-Fd3̄m or Ca₂[C₄O₁₀]-I4̄2d.^11,27 Ca₂[C₄O₁₀]-I4̄2d has been suggested as a carbonate host in the Earth's lower mantle and may contribute to the seismic anomalies of the Earth's mantle.^11,28 This seems to imply that sp³-carbonates may serve as a carrier of both carbon and hydrogen into the Earth's mantle. Also, due to the structural similarities to other novel carbonates we think it should be facile to replace the Ba-atoms in order to obtain further new hydrous high-pressure carbonates, and such experiments are currently in progress.

We gratefully acknowledge funding from the DFG (projects WI1232, BA4020, FOR2125/CarboPaT and BY101/2-1). BW is grateful for support by the Dassault Systemes Ambassador program. We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at PETRA III, beamline P02.2 under proposal I-20230653.

Data availability

All study data are included in the article and/or in the ESI.† Structural models had been deposited at the CCDC: 2332909 (exp.), 2332910 (DFT) and 2332910 (DFT, 2 × 2 × 2).

Conflicts of interest

There are no conflicts to declare.

References

1. M. Okrusch and H. Frimmel, Mineralogy: An Introduction to Minerals, Rocks, and Mineral Deposits, Springer-Verlag, Berlin, 2020.
2. R. J. Reeder, Carbonates: Mineralogy and Chemistry, De Gruyter, Berlin, Boston, 1983.
3. L. Bayarjargal, C.-J. Fruhner, N. Schrodt and B. Winkler, Phys. Earth Planet. Inter., 2018, 281, 31–45.
4. J. Binck, S. Chariton, M. Stekiel, L. Bayarjargal, W. Morgenroth, V. Milman, L. Dubrovinsky and B. Winkler, Phys. Earth Planet. Inter., 2020, 299, 106403.
5. S. Ono, T. Kikegawa and Y. Ohishi, Am. Mineral., 2007, 92, 1246–1249.
6. E. Boulard, A. Gloter, A. Corgne, D. Antonangeli, A.-L. Auzende, J.-P. Perrillat, F. Guyot and G. Fiquet, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5184–5187.
7. M. Merlini, M. Hanfland, A. Salamat, S. Petitgirard and H. Müller, Am. Mineral., 2015, 100, 2001–2004.
8. D. Spahr, J. König, L. Bayarjargal, P. N. Gavryushkin, H.-P. Liermann, V. Milman and B. Winkler, Inorg. Chem., 2021, 60, 14504–14508.
9. J. Binck, D. Laniel, L. Bayarjargal, S. Khandarkhaeva, T. Fedotenko, A. Aslandukov, K. Glazyrin, V. Milman, S. Chariton, V. B. Prakapenka, N. Dubrovinskaia, L. Dubrovinsky and B. Winkler, Am. Mineral., 2022, 107, 336–342.
10. D. Spahr, J. König, L. Bayarjargal, R. Luchitskaia, W. Morgenroth, D. Comboni, V. Milman and B. Winkler, Inorg. Chem., 2021, 60, 5419–5422.
11. J. König, D. Spahr, L. Bayarjargal, P. N. Gavryushkin, V. Milman, H.-P. Liermann and B. Winkler, Earth Space Chem., 2022, 6, 73–80.
12. D. Spahr, J. König, L. Bayarjargal, V. Milman, A. Perlov, H.-P. Liermann and B. Winkler, J. Am. Chem. Soc., 2022, 144, 2899–2904.
13. D. Spahr, J. König, L. Bayarjargal, R. Luchitskaia, V. Milman, A. Perlov, H.-P. Liermann and B. Winkler, Inorg. Chem., 2022, 61, 9855–9859.
14. D. Spahr, L. Bayarjargal, E. Haussühl, R. Luchitskaia, A. Friedrich, V. Milman, E. Fedotenko and B. Winkler, Chem. Commun., 2023, 59, 11951–11954.
15. D. Spahr, L. Bayarjargal, M. Bykov, L. Brüning, T. H. Reuter, V. Milman, H.-P. Liermann and B. Winkler, Dalton Trans., 2024, 53, 40–44.
16. D. Spahr, L. Bayarjargal, M. Bykov, L. Brüning, P. L. Jurzick, V. Milman, N. Giordano, M. Mezouar and B. Winkler, Angew. Chem., Int. Ed., 2024, e202409822.
17. L. Bayarjargal, D. Spahr, V. Milman, J. Marquardt, N. Giordano and B. Winkler, Inorg. Chem., 2023, 62, 13910–13918.
18. D. Spahr, L. Bayarjargal, M. Bykov, L. Brüning, Y. Jurzick, P. L. Wang, V. Milman, K. Refson, M. Mezouar and B. Winkler, Commun. Chem., 2024, 7, 238.
19. R. M. Hazen, R. T. Downs, A. P. Jones and L. Kah, Rev. Mineral. Geochem., 2013, 75, 7–46.
20. P. N. Gavryushkin, D. N. Sagatova, N. Sagatov and K. D. Litasovc, Earth Space Chem., 2021, 5, 1948–1957.
21. D. N. Sagatova, P. N. Gavryushkin, N. E. Sagatov and M. V. Banaev, J. Comput. Chem., 2023, 44, 2453–2460.
22. B. Winkler, C. Pickard and V. Milman, Chem. Phys. Lett., 2002, 362, 266–270.
23. V. Milman and B. Winkler, Z. Kristallogr., 2001, 216, 99–104.
24. B. Winkler, M. Hytha, C. Pickard, V. Milman, M. Warren and M. Segall, Eur. J. Mineral., 2001, 13, 343–349.
25. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
26. K. Yamashita, K. Komatsu, S. Klotz, O. Fabelo, M. T. Fernández-Díaz, J. Abe, S. Machida, T. Hattori, T. Irifune, K. Sugiyama, T. Kawamata and H. Kagi, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2208717119.
27. S. Chariton, PhD thesis, University of Bayreuth, 2020.
28. H. Wang, L. Liu, Z. Gao, L. Yang, G. Naren and S. Mao, Nat. Commun., 2024, 15, 755.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and computational details, crystallographic data and X-ray single crystal measurements. CCDC 2332909–2332911. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cc04674a

---