The effect of a distorted MO₆ octahedral unit on the activity and stability for the oxygen evolution reaction

Abstract

Metal oxides have garnered significant attention in the oxygen evolution reaction (OER), where a distorted MO₆ octahedral unit has a marked impact on their performance. This study introduces the distortion coefficient to quantify the MO₆ distortion composed of its volume and shape, and reports the effect of MO₆ distortion on the activity and stability in rutile metal oxides for the OER. This provides a fundamental understanding for designing effective MO₆ active units for the OER.

---

Hydrogen (H₂) fuel has emerged as a potential solution to the prevailing energy conundrum.¹ The H₂ generation via water electrolysis is an exceptionally meritorious and efficient modality;² however, its industrial application remains limited by the shortage of effective catalysts for the oxygen evolution reaction (OER).³ Metal oxides have garnered significant attention for the OER due to their modifiability and easy availability,⁴ such as nickel,⁵ manganese,⁶ cobalt,⁷ ruthenium and iridium oxides.⁸ Nonetheless, with the exception of precious iridium-based oxides, most of them are largely impeded in industry due to their undesirable activity or stability, particularly under harsh acidic conditions. It is strongly desired to develop efficient and inexpensive metal oxide catalysts for the OER.

Metal octahedral units (MO₆) are typical active structures that are preferentially exposed on the surface of metal oxides.⁹ A slight structural change of the MO₆ unit (i.e., octahedral distortion) has a significant effect on the OER activity and stability of the corresponding catalysts.¹⁰ Modifying the MO₆ unit has become an effective strategy for designing high-performance metal oxide catalysts for the OER, for which various approaches have been proposed. For instance, the incorporation of Na and Ho into SrRuO₃ and Y₂RuO₇ can weaken the octahedral distortion of the RuO₆ unit, which in turn enhances the strength of the Ru–O bond, thus optimizing the adsorption energy of key oxygen-containing intermediates and facilitating the OER.¹¹ The Ru incorporation into the SnO₂ matrix introduces tensile strain in the RuO₆ unit, which results in a weakened Ru–O bond, thereby significantly improving the long-term stability.¹² Similarly, the distortions of CoO₆ and IrO₆ octahedrons have been reported for their effects on the OER.¹³ Obviously, the OER activity and stability of the MO₆ active units in metal oxides are usually related to their distortion degree. Despite these findings, there is no comprehensive understanding of the relations between the distortion degree of the MO₆ unit and the OER activity or stability. Therefore, one fundamental question is necessarily answered: How do different MO₆ units distort to influence their OER activity and stability?

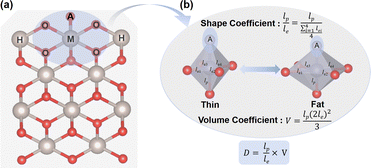
Aiming to address the above issue, we selected the representative non-iridium metal (M = Co, Ni, Ru) sites incorporated in different rutile metal oxides as the basic research objects, which are generally used as the active site models for the OER.^13b,14 We introduced the distortion coefficient (D), which is composed of its volume and shape, to quantify MO₆ distortion and help explore the effect of such distortion on the OER activity and stability of the MO₆ unit. Accordingly, we uncovered the tuning role of the MO₆ distortion in rutile metal oxides for the OER, and gave some suggestions for designing effective MO₆-incorporated metal oxide catalysts for the OER. This work provides a fundamental insight into the structural dependence of MO₆ active units for the OER, and may facilitate the design of metal oxide catalysts to some extent.

Before exploring the effect of the MO₆ distortion on the OER, we constructed a doping model to delineate the varying degrees of the MO₆ distortion, as shown in Fig. 1a, in which the metal active sites (M = Co, Ni, Ru) substitute a five-coordinated metal site on the (110) surface of some rutile metal oxides (CrO₂, MnO₂, RhO₂, RuO₂, IrO₂). These metal oxides have different lattice sizes: MnO₂ < CrO₂ < RhO₂ < IrO₂ < RuO₂, which can give rise to diverse modifications in the octahedral structure of the MO₆ unit, involving either longitudinal contraction/extension or volumetric changes. The distortion of the MO₆ octahedron typically manifests as changes in both volume and shape, as shown in Fig. 1b. To illustrate the distortion degree of the MO₆ active unit, we have introduced a distortion coefficient (D, Fig. 1b), defined as D = V × (l_p/l_e). Here, l_p and l_e represent the average M–O bond lengths in the polar and equatorial directions, respectively. The ratio of l_p and l_e (i.e., l_p/l_e) represents the shape of the MO₆ octahedron. l_p/l_e < 1 (or > 1) is indicative of a flat (or leptosomic) type of MO₆ octahedron. V is the volume of the MO₆ octahedron, given by [(2l_e)²l_p]/3, which represents the size of the MO₆ unit.

Fig. 1 (a) Construction of the MO₆ octahedron by doping M into different rutile metal oxide (110) surfaces. A, O, M and H represent the adsorbed oxygen-containing intermediates, oxygen atom, doped metal site and metal atoms in the host rutile metal oxides, respectively. (b) Scheme of the illustration of distortion coefficient (D).

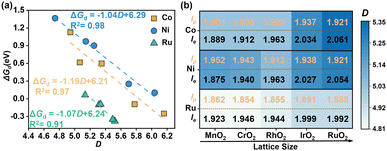
Based on the above models, we first explored the electrochemical stabilities of different MO₆ units incorporated in different rutile metal oxides, by calculating the dissolution free energy (ΔG_d) at the working conditions (pH = 0, U = 1.5 V vs. SHE, see the detail in Note S2, ESI†). A more positive ΔG_d means better stability of the M site. Interestingly, after scaling ΔG_d with the distortion coefficient (D) of the MO₆ octahedron, there are very good linear relationships between D and ΔG_d for these MO₆ units (Fig. 2a). This suggests that D could be the effective indicator for describing the stability of MO₆. Specifically, the incorporation of NiO₆ and CoO₆ octahedrons into different rutile metal oxides results in a significant variation in the value of D, which changes in a wide range of about 4.745 < D < 6.038 and 4.944 < D < 6.160 (see the blue and orange lines in Fig. 2a), respectively; only as D increases to a certain extent (> ∼6.0 for NiO₆ and CoO₆), ΔG_d becomes negative, implying the instability of NiO₆ and CoO₆ octahedrons. This illustrates that the structural tunability of the NiO₆ and CoO₆ octahedrons for stability is considerable, which may be suitably modified to design more stable Ni-based and Co-based oxide catalysts for the acidic OER. For RuO₆ in different rutile metal oxides, its relationship changes in a small range of about 5.136 < D < 5.521, implying its limited structural tunability; at the same time, ΔG_d for the RuO₆ unit is generally less than zero in this range (see the green line in Fig. 2a), implying the poor stability of the RuO₆ active unit in the OER as reported in the experiment.¹⁵ Therefore, it is anticipated that the modification for the stability of NiO₆ and CoO₆ could be relatively easier compared to that of RuO₆.

Fig. 2 (a) Relationship of the dissolution free energy (ΔG_d) of the metal site as a function of the distortion coefficient (D) of the MO₆ octahedron (M = Co, Ni, Ru). (b) Variation trends of the polar (l_p, orange) and equatorial (l_e, black) M–O bonds in different MO₆ octahedrons.

All these relationships in Fig. 2a have negative slopes, illustrating that ΔG_d increases with the decrease of D, implying that the small D could contribute to the electrochemical stability of the MO₆ unit. To further understand the origin of the better stabilized MO₆ with small D, we performed structural and electronic analysis. Structurally, the reduction in D of the MO₆ octahedron significantly extrudes the equatorial M–O bonds of MO₆ (l_e, indicated by black values in Fig. 2b) and strengthens these equatorial M–O bonds, while the polar M–O bonds (l_p, indicated by orange values in Fig. 2b) undergo relatively small changes. The shorter equatorial M–O bond indicates the stronger bond strength, resulting in better stability, as shown by the relationship between ΔG_d and l_p/l_e (Fig. S1, ESI†). Consequently, the central M site can be better stabilized by the equatorial O atoms as MO₆ has a relatively small D, inhibiting its dissolution. Combining with the changes of l_e and the lattice parameter of different rutile metal oxide substrates, we can find that the small lattice parameter, which compresses the octahedral structure of MO₆ in the equatorial direction, corresponds to the shorter l_e (Fig. 2b). Hence, for a given MO₆, incorporating it into a rutile metal oxide with a relatively smaller lattice parameter can stabilize it in the OER. Furthermore, the charge density difference (CDD) analysis of CoO₆, NiO₆ and RuO₆ units incorporated in different metal oxides was carried out. As shown in Fig. S2 (ESI†), it can be found that there are good linear relationships between ΔG_d and electron transfer (Δq) from the metal center to the surrounding O atoms within the MO₆ unit; their positive slopes show that with the increase of Δq, which strengthens the M–O bond in MO₆, ΔG_d becomes more positive, thus improving the stability of MO₆ with relatively small D.

In addition to the stability of the MO₆ unit, its catalytic activity stands as a pivotal determinant in its suitability in the OER. Here, we first calculated the adsorption free energies (G_i) of key oxygen-containing intermediates (*OH, *O and *OOH) involved in the OER by using the computational hydrogen electrode method¹⁶ (see the detailed calculation method in Note S3, ESI†), and examined the change trend of the theoretical overpotential η. As a consequence of the distortion of MO₆ upon incorporation into different rutile metal oxides, we can find a deviation from the dependence with a smaller slope of 0.85 (G_[*OOH] = 0.85G_[*OH] + 3.06, R² = 0.95) compared to the universal scaling relation of G_[*OOH] = G_[*OH] + (3.2 ± 0.2) observed in standard MO₆ in rutile or perovskite oxides¹⁷ (Fig. 3a). This indicates that the scaling limitation for the standard MO₆ octahedron on rutile metal oxides has been broken through. Based on this scaling relationship between G_[*OH] and G_[*OOH], a universal 3D volcanic map was constructed to describe the OER activity of these MO₆ units incorporated in different rutile metal oxides (Fig. 3b).

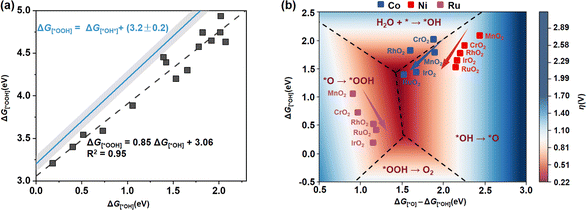Fig. 3 (a) Scaling relationship between G_[*OOH] and G_[*OH] on MO₆ incorporated in different rutile metal oxides (black dashed line), and the universal relationship between G_[*OOH] and G_[*OH] observed in standard MO₆ of rutile or perovskite metal oxides (blue line). (b) 3D volcanic map of theoretical overpotential η for MO₆ in different rutile metal oxides as a function of G_[*O]–G_[*OH] and G_[*OH], in which the blue, red and purple points represent CoO₆, NiO₆ and RuO₆ units, respectively. The discussion for the boundary between the four rate-determining steps can be seen in Fig. S4 (ESI†), and the detailed overpotentials (η) are listed in Table S3 (ESI†).

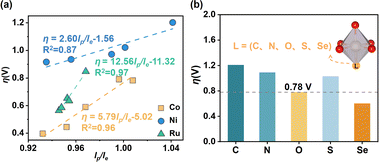
The 3D activity map in Fig. 3b shows that for each MO₆ unit, η can gradually approach the optimum region in a certain pattern. To further understand the specific effect of the MO₆ distortion on the OER activity, we proceeded to fit the relationship between the overpotential η and D. For all CoO₆, NiO₆ and RuO₆ units, there are poor relationships between η and D (see Fig. S3a, ESI†). According to the definition of D = (l_p/l_e) × V, we further scaled the relationships of η as a function of volume (V) and shape coefficient (l_p/l_e), respectively. The distribution of η as a function of V remains relatively chaotic (Fig. S3b, ESI†), and the unique relationships between them have a relatively low R². Interestingly, there are very good linear relationships between η and l_p/l_e for CoO₆, NiO₆ and RuO₆ units, as illustrated in Fig. 4a. This implies that in the MO₆ distortion, the shape of MO₆ (flat or leptosomic) could be the predominant factor influencing its OER activity.

Fig. 4 (a) Relationships of the overpotential η as a function of l_p/l_e of the MO₆ octahedron (M = Co, Ni, Ru). (b) Overpotential η for the OER of CoO₆ with different ligand heteroatoms (C, N, S, Se) incorporated.

The positive slopes of their relationships in Fig. 4a illustrate that η generally decreases as l_p/l_e decreases, meaning that the small l_p/l_e (i.e., the fat MO₆ unit) could be more favourable for the OER. The slopes (α) of the relationships for the MO₆ units decrease in the following order: RuO₆(α = 12.56) > CoO₆(α = 5.79) > NiO₆(α = 2.60). A larger α means that the shape of the MO₆ unit has a better sensitivity to the overpotential η (i.e., OER activity). The slopes of the relationships for RuO₆ and CoO₆ units are much larger than that for the NiO₆ unit, implying their greater shape sensitivities to η compared with the NiO₆ unit, especially the CoO₆ unit. In addition, the intercepts (β) of the relationships for η, which illustrate the intrinsic activity of the MO₆ unit for the OER, decrease with the order: NiO₆(β = −1.56) > CoO₆(β = −5.02) > RuO₆(β = −11.32). A lower β means a better intrinsic activity. Thus, the RuO₆ unit possesses the best intrinsic OER activity, and is widely demonstrated and used in experiments; the intrinsic OER activity for the NiO₆ unit is the worst. Therefore, the activity regulatory effect of the RuO₆ (or NiO₆) unit for the OER is the greatest (or worst).

Specifically, as demonstrated by the activity map in Fig. 3b, NiO₆ units incorporated into different rutile metal oxides are distant from the optimal range, indicating the relatively poor activity in these rutile metal oxides. For RuO₆, although the RuO₆ unit has the optimal activity sensitivity (i.e., larger α) and the best intrinsic activity (i.e., lowest β), its incorporation into these rutile metal oxides has a relatively small distortion degree compared with NiO₆ or CoO₆ units, thus leading to the relatively small change of the overpotential η for the OER. Hence, rutile metal oxides may not be suitable as a substrate for modifying RuO₆, unless metal oxides that differ greatly from RuO₂ lattice size are used. The CoO₆ unit can locate near the optimum range (Fig. 3b), and CoO₆ cooperated in IrO₂ or RuO₂ can reach an overpotential η as low as 0.44 V and 0.39 V, respectively. This illustrates the excellent structural tunability of CoO₆ for activity, which could be a more viable option for the OER.

Scaling the adsorption free energies of *OH, *O and *OOH on these MO₆ units incorporated in different rutile metal oxides with l_p/l_e, as shown in Fig. S5 (ESI†), we can find that the decrease of l_p/l_e leads to the strengthened adsorption of the intermediates *O, *OH and *OOH to different extents. For CoO₆ and NiO₆, the promotion of *O adsorption is greater, contributing to the rate-determining *OH → *O step and thus facilitating the OER. For RuO₆, decreasing l_p/l_e changes *OOH more visibly compared to *O, thereby promoting the rate-determining *O → *OOH step and facilitating the OER. In general, the OER activity of the MO₆ unit incorporated in rutile metal oxide is inversely proportional to its shape (i.e., l_p/l_e). Decreasing the M–O bond lengths in the polar direction (l_p) or increasing the M–O bond lengths in the equatorial direction (l_e) can effectively improve the OER activity of the corresponding MO₆ unit in rutile metal oxide.

In terms of structure, the polar M–O bond (l_p) of the MO₆ unit is directly related to the interaction of the O-containing intermediate on the M site, and the shorter l_p means stronger adsorption strength of the intermediate in the polar direction. In addition, according to the bond order conservation principles, the longer l_e (i.e., the weaker equatorial M–O bond) can also strengthen the adsorption in the polar direction on the M site.¹⁸ Therefore, decreasing l_p/l_e can enhance the adsorption of the O-containing intermediate, facilitating the OER on the MO₆ unit incorporated in rutile metal oxide.

Based on the above analysis of the distortion of MO₆ in terms of stability and OER activity, we can obtain the tuning rule of the MO₆ active unit incorporated in rutile metal oxides for the OER. The M–O bond length (i.e., strength) in MO₆ plays a key role in its stability and OER activity. A reduction in the M–O bond strength of MO₆, especially the equatorial one, results in enhanced stability. However, for the OER activity, the fat MO₆ (i.e., a lower l_p/l_e) could be favourable, in which a longer l_e or shorter l_p is required. In general, controlling the MO₆ active unit with a relatively short l_e (i.e., strong equatorial M–O bond) and low l_p/l_e value at the same time could be effective for designing a MO₆ unit in rutile metal oxide for the OER, which can simultaneously maintain the high activity and stability. The above analysis of the change trends of M–O bonds in MO₆ shows that MO₆ incorporated in different rutile metal oxides primarily mainly affects the changes in the equatorial M–O bonds, with a comparatively minor impact from changes in the polar M–O bond. The change trends of the equatorial M–O bond strength and l_p/l_e of MO₆ in rutile metal oxides could be consistent. In other words, to achieve the good stability of MO₆, the short l_e, i.e., strong equatorial M–O bond, is required, but this may mean a large l_p/l_e value, which is detrimental to the OER activity. Therefore, breaking this inherent distortion limitation of MO₆ for stability and activity is necessary for designing rutile metal oxide catalysts for the OER.

According to the above discussion, for the stable MO₆ in rutile metal oxides, which has a strong equatorial M–O bond, the directional enhancement of the polar M–O bond could be effective in improving its OER activity. The CoO₆ unit has excellent structural tunability for OER activity and good stability as discussed above, and MnO₂ as a substrate has been widely used in the OER due to its superior stability and low cost.¹⁹ Accordingly, the CoO₆ unit incorporated into MnO₂, which has superior stability in the OER (ΔG_d = 2.29 eV), was chosen as the basic object to verify this idea. Here, the oriented doping engineering was adopted to directly modify the polar Co–O bond strength in CoO₆, in which several ligand heteroatoms (e.g., C, N, S, Se) were introduced into the polar O position (Fig. 4b). One can see that the Se incorporation into CoO₆ units in MnO₂ can achieve a low overpotential η of 0.60 V compared with the original η = 0.78 V of the pure CoO₆ in MnO₂. Compared with the O and S atoms, the introduction of the Se atom results in more overlap between the Co 3d of the Co site and O 2p orbitals of O-containing species adsorbed on the Co site, significantly promoting the key *O adsorption and thereby facilitating the OER (see the detailed discussion in Fig. S6 and S7, ESI†). This result verifies the feasibility of our strategy, which may be worth experimenting with in the future.

In summary, this work investigated the effect of the distortion of MO₆ octahedrons in rutile metal oxide, which generally involves the change in volume and shape of the MO₆ unit, on the activity and stability for the OER through the introduction of a distortion coefficient (D). The results show that the M–O bond length (i.e., strength) and shape of MO₆ are the key factors in the stability and OER activity. The shorter M–O bond of MO₆, especially the equatorial one, promotes its stability due to more electron transfer between the M center and the adjacent O atoms, which strengthens the M–O bond and thus stabilizes the M center. The MO₆ unit with a fat shape (i.e., small l_p/l_e value) has a higher OER activity. However, the short l_e of MO₆ with superior stability generally results in a large l_p/l_e value, which is not conducive to the OER activity. It is therefore evident that breaking this cooperative limitation resulting from the structural distortion of the MO₆ unit in rutile metal oxides on the stability and activity is necessary. Accordingly, the oriented doping engineering was proposed to modify the MO₆ unit, directing the proposal of a cost-effective Se-doped CoO₆ unit incorporated into MnO₂ for the OER. This work provides a fundamental understanding of the effect of the MO₆ octahedral distortion on the activity and stability in the OER, promoting the rational design of metal oxide catalysts.

This work was financially supported by the National Natural Science Foundation of China (22472053 and 22239001), Science and Technology Commission of Shanghai Municipality (23ZR1416800 and 22ZR1416400), and Innovation Program of Shanghai Municipal Education Commission (E00014).

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. J. A. Turner, Science, 2004, 305, 972.
2. (a) X. Wang, S. Xi, P. Huang, Y. Du, H. Zhong, Q. Wang, A. Borgna, Y.-W. Zhang, Z. Wang, H. Wang, Z. G. Yu, W. S. V. Lee and J. Xue, Nature, 2022, 611, 702; (b) X. X. Zou and Y. Zhang, Chem. Soc. Rev., 2015, 44, 5148.
3. N. Suen, S. Hung, Q. Quan, N. Zhang, Y. Xu and H. Chen, Chem. Soc. Rev., 2017, 46, 337.
4. (a) D. Yan, Y. Li, J. Huo, R. Chen, L. Dai and S. Wang, Adv. Mater., 2017, 29, 1606459; (b) S. Lee, Y. J. Lee, G. Lee and A. Soon, Nat. Commun., 2022, 13, 3171.
5. N. Zhang, X. Feng, D. Rao, X. Deng, L. Cai, B. Qiu, R. Long, Y. Xiong, Y. Lu and Y. Chai, Nat. Commun., 2020, 11, 4066.
6. M. Huynh, D. K. Bediako and D. G. Nocera, J. Am. Chem. Soc., 2014, 136, 6002.
7. H. Jia, N. Yao, C. Yu, H. Cong and W. Luo, Angew. Chem., Int. Ed., 2023, 62, 202313886.
8. (a) P. Ping, R. J. Nielsen and W. A. GoddardIII, J. Am. Chem. Soc., 2017, 139, 149; (b) Y. H. Fang and Z. P. Liu, J. Am. Chem. Soc., 2010, 132, 18214.
9. (a) J. Druce, H. Téllez, M. Burriel, M. D. Sharp, L. Fawcett, S. N. Cook, D. Mcphail, T. Ishihara, H. H. Brongersma and J. A. Kilner, Energy Environ. Sci., 2014, 7, 3593; (b) D. K. Bediako, B. Lassalle-Kaiser, Y. Surendranath, J. Yano, V. K. Yachandra and D. G. Nocera, J. Am. Chem. Soc., 2012, 134, 6801.
10. (a) B. Kim, A. Oh, M. K. Kabiraz, Y. Hong, J. Joo, H. Baik, S. Choi and K. Lee, ACS Appl. Mater. Interfaces, 2018, 10, 10115; (b) J. Yan, J. Zhu, D. Chen, S. Liu, X. Zhang, S. Yu, Z. Zeng, L. Jiang and F. Du, J. Mater. Chem. A, 2022, 10, 9419.
11. (a) N. Zhang, C. Wang, J. Chen, C. Hu, J. Ma, X. Deng, B. Qiu, L. Cai, Y. Xiong and Y. Chai, ACS Nano, 2021, 15, 8537; (b) Y. Xu, Z. Mao, J. Zhang, J. Ji, Y. Zou, M. Dong, B. Fu, M. Hu, K. Zhang, Z. Chen, S. Chen, H. Yin, P. Liu and H. Zhao, Angew. Chem., Int. Ed., 2024, 63, e202316029.
12. F. Yang, J. Xie, D. Rao, X. Liu, J. Jiang and X. Lu, Nano Energy, 2021, 85, 106020.
13. (a) W. Sun, Y. Song, X. Gong, L. Cao and J. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 820; (b) L. Sun, Z. Dai, L. Zhong, Y. Zhao, Y. Cheng, S. Chong, C. Guanjun, C. Yan, X. Zhang, H. Tan, L. Zhang, K. N. Dinh, S. Li, F. Ma and Q. Yan, Appl. Catal., B, 2021, 297, 120477.
14. (a) Z. Wu, F. Chen, B. Li, S. Yu, Y. Z. Finfrock, D. M. Meira, Q. Yan, P. Zhu, M. Chen, T. Song, Z. Yin, H. Liang, S. Zhang, G. Wang and H. Wang, Nat. Mater., 2023, 22, 100; (b) J. Wang, Y. Ji, R. Yin, Y. Li, Q. Shao and X. Huang, J. Mater. Chem. A, 2019, 7, 6411.
15. J. Chen, Y. Ma, T. Huang, T. Jiang, S. Park, J. Xu, X. Wang, Q. Peng, S. Liu, G. Wang and W. Chen, Adv. Mater., 2024, 36, e2312369.
16. A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, Energy Environ. Sci., 2010, 3, 1311.
17. M. Bajdich, M. García-Mota, A. Vojvodić, J. K. Nørskov and A. T. Bell, J. Am. Chem. Soc., 2013, 135, 13521.
18. L. Zhang, H. Yuan, L. Wang, H. Zhang, Y. Zang, Y. Tian, Y. Wen, F. Ni, H. Song, H. Wang, B. Zhang and H. Peng, Sci. China Mater., 2020, 63, 2509.
19. C. Lin, J.-L. Li, X. Li, S. Yang, W. Luo, Y. Zhang, S.-H. Kim, D.-H. Kim, S. S. Shinde, Y.-F. Li, Z.-P. Liu, Z. Jiang and J.-H. Lee, Nat. Catal., 2021, 4, 1012.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cc04992f

‡ These authors contributed equally to this work.

---