Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nonadiabatic ab initio chemical reaction dynamics for the photoisomerization reaction of 3,5-dimethylisoxazole via the S1 electronic state†
Mizuki
Kimura
a and
Shinkoh
Nanbu
 *b
*b
aGraduate School of Science and Technology, Sophia University, Japan, Chiyoda, Tokyo 102-8554, Japan. E-mail: m-kimura-0o3@eagle.sophia.ac.jp
bFaculty of Science and Technology, Sophia University, Chiyoda, Tokyo 102-8554, Japan
First published on 20th November 2024
Abstract
Nonadiabatic ab initio molecular dynamics simulations were performed to explore the photoisomerization pathway from isoxazole (iso-OXA) to oxazole (OXA), considering four electronic states. The XMS-CASPT2 and SA4-CASSCF theories were employed to describe these electronic structures, which were caused by 12 electrons in 11 orbitals with the cc-pVDZ + sp diffuse basis set; the Gaussian s- and p-type diffuse functions were extracted from Dunning's aug-cc-pVDZ function. The potential energy and its gradient at each time step were computed on-the-fly at these levels in the time evolution of the classical trajectory. When the two electronic states were close to each other, the trajectory surface hopping (TSH) judgment between the two adjacent states was carried out by the anteater procedure based on the Zhu–Nakamura formula (ZN-TSH). The two different excited state lifetimes were found to exist in the first electronic state (S1), estimated at 10.77 and 119.81 fs. Upon photoexcitation, the N–O bond breaks and energetically relaxes to the ground state (S0). In the pathway leading to the main product, azirine formation, the 5-membered ring retains a planar structure while undergoing a non-adiabatic transition with an increasing N–O bond distance. Furthermore, it was verified that a 1,2-shift takes place in the pathway that results in the production of ketenimine, causing a nonadiabatic transition.
Introduction
The five-membered heterocyclic compound isoxazole is shown in Fig. 1(a). In organic synthesis, this kind of molecule is mostly employed as an inhibitor and finds utility in agrochemistry, anti-corrosion compounds, and medicines.1–9 Since the 1960s, isoxazole's photochemical reactions have been researched. It is well known that the reaction is initiated by breaking the weak N2–O1 bond in the five-membered ring. The bond is broken to form a diradical, which is isomerized to 2H-azirine, and then the C3–C4 bond in the three-membered ring of 2H-azirine is broken to form oxazole.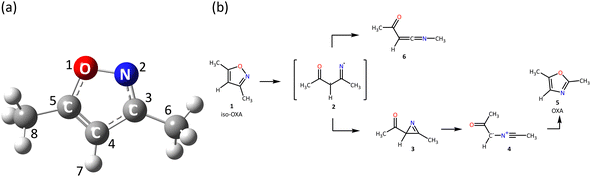 | ||
| Fig. 1 (a) The equilibrium geometry of 3,5-dimethylisoxazole in the S0 state at the XMS-CASPT2/cc-pVDZ + sp level and its label-number and (b) the isomerization process proposed by Nunes et al.10 | ||
Wakefield and Wright11 pioneered the physicochemical characterisation of isoxazole and oxazole, together with the synthetic pathway, several reactions with electrophiles or nucleophiles, and the photolysis, thermal decomposition, fragmentation by electron impact, reductive bond-cleavage and so on were discussed in their paper. Furthermore, they summarised the quantum yield (%) of azirine derivatives based on the combination of functional groups located at R3, R4 and R5. Specifically, when R3 is a methyl group, R4 is hydrogen and R5 is a methyl group, the quantum yield is 14%;12 when R3 is a phenyl group, R4 is hydrogen and R5 is an amino group, the quantum yield is 42%;13 when R3 is a para-chlorophenyl group, R4 is hydrogen and R5 is an amino group, the quantum yield is 28%;14 when R3 is a methyl group, R4 is hydrogen and R5 is a phenyl group, the quantum yield is 25%;15 and it is 18%16 when R3 is a phenyl group, R4 is a methyl group and R5 is an amino group. The quantum yield of azirine derivatives depends on the structure of the functional group. The n–π* electronic transition of azirine causes C3–C4 (N2–C4) bond-breaking and cyclization to oxazole (isoxazole).
In light of the experimental facts, a theoretical study was conducted in 1980. Tanaka et al.17 clarified the energetics for the photoisomerization mechanism of isoxazole, with the photochemistry of 2H-azirine intermediate by ab initio MO–CI calculations. They found that the N2–O1 bond tends to loosen in the first singlet electronically excited state (S1) upon the isomerization to 2H-azirine, and N2 and O1 have a negative net charge and lone electron pair, respectively, and repel each other due to electrostatic force. The subsequential internal conversion (IC) to the ground state (S0) results in the formation of a biradical on the N2–C3–C4 bond of the vinyl nitrene structure, which forms a new N2–C4 bond and obtains 2H-azirine. However, the N2–C4 dissociation of 2H-azirine proceeds by delocalising the electron density from the C atom of C5![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1, which has accumulated charge density to the antibonding orbital of the three-membered ring in S1, ultimately causing the backward reaction to isoxazole. Furthermore, in the 2H-azirine to oxazole pathway, the removal of an electron from the non-bonding orbital of N promotes an increase in the C4–N2–C3 bond angle by changing the sp2 hybridization orbitals to the sp hybrid. They also pointed out that this pathway to oxazole formation could occur in a single step, without any intermediates, when the intersystem crossing (ISC) between S1 and the triplet state (T1) happened.
O1, which has accumulated charge density to the antibonding orbital of the three-membered ring in S1, ultimately causing the backward reaction to isoxazole. Furthermore, in the 2H-azirine to oxazole pathway, the removal of an electron from the non-bonding orbital of N promotes an increase in the C4–N2–C3 bond angle by changing the sp2 hybridization orbitals to the sp hybrid. They also pointed out that this pathway to oxazole formation could occur in a single step, without any intermediates, when the intersystem crossing (ISC) between S1 and the triplet state (T1) happened.
Ab initio molecular dynamics (MD) simulations on 2-formyl-2H-azirine and isoxazole were performed by Cao for the first time in this story of isoxazole photochemistry,18 in which Tully's fewest-switches surface hopping (FSSH) algorithm was employed.19 One hundred classical trajectories were taken into account in the three-state-averaged complete active space (CAS) SCF (SA3-CASSCF) level with 12 electrons in 10 orbitals (12e, 10o) and a 6-31G* basis set, assuming two photoexcitations to S1 and S2. As a result, the forty trajectories in the 100 initiated isoxazole to S1 produced 2-formyl-2H-azirine, and the nine trajectories converted to the minor product of 3-formylketenimine. Four trajectories of isoxazole were also found to dissociate back to the original isoxazole, and since the result was almost the same as the case when isoxazole was excited to the S2 state, it is concluded that isomerization from isoxazole to oxazole does not occur. Other findings included the following: the lifetime of S1 was determined to be 82.4 fs by fitting to a single exponential function, and the isomerization started at 2-formyl-H-azirine to oxazole was found only when excited to S2.
In order to understand the ultrafast dynamics for ring-opening in heterocyclic systems, Geng et al.20 using time-resolved photoelectron spectroscopy, which was supported by nonadiabatic ab initio MD simulation of isoxazole and oxazole in 2020. In their study, the molecules were excited by laser pulses at 200 nm, and the excited molecular dynamics were probed by those at 267 nm, while the ADC2 (the second-order algebraic-diagrammatic configuration scheme) theory was employed for their ab initio simulation with the aug-cc-pVDZ basis set. In particular, nonadiabatic transitions were taken into account through a surface hopping algorithm based on the Landau–Zener formula in their simulation. The simulation time was up to 100 fs after photoexcitation. Their measured ring-opening time of isoxazole was 35 fs, and their simulations also supported their own experimental result, with 80% of the trajectories undergoing N2–O1 dissociation within 100 fs. They also pointed out that the reaction rate initiated from oxazole was approximately two times slower and less efficient than the ring-opening product due to the presence of a small barrier after the photoexcitation.
On the other hand, Nunes et al.10,21,22 investigated the photochemistry of 3,5-dimethylisoxazole matrix-isolated in argon at 15 K by the tunable UV-laser irradiation at 222 nm and infrared spectroscopy, with the theoretical support at the B3LYP/6-311++G(d,p) level. The existence of nitrile ylide was confirmed for the first time, and moreover, the reaction pathways were proposed as shown in Fig. 1(b). In their experiments, two different irradiation times were conducted for (a) 1 and (b) 80 minutes; each product was then isolated, and FTIR spectra were measured to confirm the azirine 3 and ketenimine 6 in the (a) case, while 3, nitrile ylide 4, and 6 in (b). It is also found that 3,5-dimethylisoxazole to 2,5-dimethyloxazole isomerization remains a minor event, but the oxazole 5 was produced by the subsequent irradiation to 4 at 340 nm light. The other isomerization process to 6 appeared involving the [1,2]-methyl shift. The mechanism of this 1,2-shift was discussed in 2002 by Wilsey et al.23 at the CASSCF/6-31G* level; the shift of the vinylic hydrogen or carbon atom from the alkene to the carbene structure is attributed to the presence of a conical intersection between two electronic states. Carbene formation occurs directly from the π–π* state. However, the proposed reaction mechanism from isoxazole 1 to oxazole 5 was later disproved by Su24 in 2016; the singlet potential energy surface (PES) was explored at the CASSCF and MP2-CAS (OVB-MP2, orthogonal valence bond Møller–Plesset second-order perturbation) level with the 6-311G(d) basis set. Three different pathways correlated with 5 were found from the Franck–Condon region of 1, but the direct mechanism to 5 through the single conical intersection was concluded to be the most likely pathway from the viewpoint of both energetics and kinetics. They also performed experiments using Xe-matrix and found that the triplet ground state (T1) was not involved in this isomerization mechanism.
In the present paper, non-adiabatic ab initio MD simulations were performed to explore the photoisomerization pathway from 3,5-dimethylisoxazole (iso-OXA) to 2,5-dimethyloxazole (OXA), considering the four lowest singlet electronic states (S0, S1, S2, and S3). In particular, the classical trajectory surface hopping (TSH) method based on the Zhu–Nakamura formula25 was employed to take into account the nonadiabatic transitions. Two different ab initio methodologies were employed to obtain the potential energy and its gradient for the staying state of classical trajectory; one was the SA4-CASSCF method, and the other was the extended multi-state (XMS-) CASPT2 theory26 to account for dynamical electron-correlation energy. For our basis sets, the Dunning cc-pVDZ + sp basis set27 was mainly used, which is based on the cc-pVDZ function with diffusion functions for s-type and p-type orbitals widely used in aug-cc-pVDZ. Our simulations were performed up to 500 femtoseconds after photoexcitation. The three hundred classical trajectories evolved in time at the SA4-CASSCF level, while the fifty-two trajectories evolved at the XMS-CASPT2 level, and then these trajectories were analysed. The results successfully reproduced the various processes that have been discussed so far. In addition, the 1,2-shift transition process due to methyl groups was dynamically captured. Non-adiabatic transitions were identified as the cause of these methyl group shifts.
Methodology
The method for the ab initio electronic excited state calculation
We chose eleven molecular orbitals (MOs) in the active space at C1 symmetry as shown in eqn (1) and used an active space that packs twelve electrons into it. In addition, the four electronic states were optimized with even weight in the SA4-CAS(12e, 11o)-SCF.| [(21a) (22a) (23a) (24a) (25a) (26a) (27a) (28a) (29a) (30a) (31a)] | (1) |
| Electronic state | Primary electronic config. At the XMS-CASPT2 level | Theory | Exp. | TDM2/a02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
|||
|---|---|---|---|---|---|---|---|
| XMS-CASPT2/cc-pVDZ + sp | SA4-CASSCF/cc-pVDZ + sp | SAC-CI/aug-cc-pVDZ | SAC-CI/cc-pVTZ | ||||
| a The electronic configuration is different from XMS-CASPT2, see Table S1(a) (ESI). b Calculated at the XMS-CASPT2 level. | |||||||
| S1 | Ryd ← (πNO + πCCC)* | 6.53 | 6.73 | 6.26 | 5.93 | 5.77 (222 nm) | 0.139 |
| S2 | πNO* + πCCC* ← (πNO + πCCC)* | 6.78 | 6.89 | 6.50 | 6.33 | — | 0.074 |
| S3 | πCONC* ← (πCO + πCCN)* | 7.14 | 7.54a | 6.95 | 6.59 | — | 0.376 |
Nonadiabatic ab initio molecular dynamics simulation
Ab initio MD simulations were carried out, based on two different quantum chemical calculation methods, SA4-CASSCF and XMS-CASPT2 methods. The Wigner distribution functions30,31 were used for initial coordinates and momenta given by the normal modes of molecular vibration in S0; the vibrational frequencies were determined using harmonic oscillator analysis. In the simulations, for each case of SA4-CASSCF and XMS-CASPT2, these initial structures and momenta were generated using uniform random variables in the range of 0 to 1, resulting in three hundred and fifty-two different molecular configurations, respectively. The obtained initial structures and momenta were vertically excited from S0 to S1 following the Franck–Condon principle. The classical trajectories initiated with these initial conditions were propagated in time using a Velocity-Verlet integrator with a 0.25 fs time step. At each time step, the potential energy and its gradient were obtained by the direct ab initio calculation. On the way, when two potential energies are found to be lying closely to each other, the Zhu–Nakamura trajectory surface hopping (ZN-TSH) algorithm25,32 is applied to make a nonadiabatic transition decision between the two electronic states; the non-adiabatic vector is obtained, and the transition along the vector is determined probabilistically at the pseudo-crossing by the ZN formula; the shapes of the two curvatures are evaluated, and the transition probability (p) is obtained from the crossing velocity. A random number (z) is generated between 0 and 1, and if the random number is less than the transition probability (z ≦ p), the running trajectory should hop to the other state. There are two different types of the non-adiabatic transitions, vertical hopping (VH) and non-vertical hopping (non-VH).33,34 If the surface-hopping would happen, the momenta of the next step was adjusted following the ZN-TSH theory. In our ZN-TSH method, if the potential energy curves given by the sequential on-the-fly ab initio electronic state calculations generates an energy gap of 0.001Eh = 0.02721 eV = 219.5 cm−1 or more at each time step, we abort the ab initio MD run under those calculation conditions. The active space and the number of electronic states to be averaged were readjusted, and the entire simulation calculation was performed from the beginning. The final optimal active space and number of electronic states were 12 electrons and 11 orbitals, and 4 states. Regarding crashes during the simulation, one trajectory was observed in XMS-CASPT2 and two trajectories in SA4-CASSCF, but these trajectories were not counted, and these lost trajectories (one for XMS-CASPT2 and two for SA4-CASSCF) were compensated for by increasing the number of trajectories. This computational algorithm was repeated until the desired time was reached; our simulations were performed up to 500 fs after photoexcitation.Results and discussion
Electronic state transition due to vertical excitation
The active MOs, which are also natural orbitals from SA4-CASSCF calculation in the S0 equilibrium structure, are shown in Fig. S1 (ESI†). The 26a MO could correspond to a HOMO-like orbital for this system in CASSCF theory. In particular, the MOs of 24a to 29a are the key orbitals to describe the electronically excited states in SA4-CASSCF and XMS-CASPT2. The orbital properties are described below,24a: anti-bonding orbital consisting of an out-of-plane bonding orbital composed of C5–O1 together with an out-of-plane bonding orbital of C4–C3–N2, (πCO + πCCN)*
25a: in-plane non-bonding orbital of N2 with a five-membered ring composed of C3–C4–C5–O1, (nN + σCC+CO)*
26a (HOMO-like orb.): anti-bonding orbital consisting of an out-of-plane bonding orbital of N2–O1 with an out-of-plane bonding orbital of C3–C4–C5, (πNO + πCCC)*
27a (LUMO-like orb.): anti-bonding orbital consisting of an out-of-plane anti-bonding orbital of N2–C3 with an out-of-plane anti-bonding orbital of C5–O1, (πNC* + πCO*)*
28a: Rydberg orbital around the C5 carbon atom, Ryd.
29a: anti-bonding orbital consisting of an out-of-plane bonding orbital of N2–O1 with an out-of-plane anti-bonding orbital of C3–C4–C5, (πNO + πCCC*)*where the atom labels are shown in Fig. 1(a).
Furthermore, Table S2(a) (ESI†) presents the expansion-coefficients of configuration state functions (CSFs) obtained at the XMS-CASPT2 level, whereas Table S2(b) (ESI†) shows those at SA4-CASSCF. The CI-coefficients for the S0, S1, and S2 states had similar values and the same electron configuration at both levels, except S3, which is of the single excitation of 24a → 27a at the XMS-CASPT2 level, but of 25a → 27a at SA4-CASSCF. The single excitation of 26a → 28a for S1 results in a photoinduced electron transfer (PET) process from the bonding orbital of N2–O1 to the Rydberg orbital around the C5–carbon atom, which would be similar to the Rydberg orbital that appeared in the excited states of quinazoline,35 but this PET process is not expected to be the direct cause of N2–O1 bond dissociation in the heterocyclic five-membered ring. The subsequent conformational change is thought to cause the electrons ionized in the cationic five-membered ring to transfer to the antibonding orbital and break the N2–O1 bond. We will discuss more detail on these mechanics later. The theoretical values for each vertical electronic excitation energy are listed for S1, S2, and S3 in Table 1 and Table S1 (ESI†), where the experimental data was estimated from the experimental conditions by Nunes et al.
Nonadiabatic ab initio molecular dynamics with the ZN-TSH approach
The theoretical product ratios (%) are listed in Table 2, which also represent the dependency upon two different ab initio methodologies of SA4-CASSCF and XMS-CASPT2. As shown in the table, our theoretical results are in agreement with the experimental results.10 The formation of 6 was found to be low. This was because the classical trajectories that produced 6 did not remain in the stable structure of 6 and the methyl group bond to C2 was broken, causing dissociation. The data for the two comparisons were selected based on the criteria of experimental and theoretical conditions (gas phase), that are analogous to those employed in our own calculations.| Compound | ||||||||
|---|---|---|---|---|---|---|---|---|
| Theory | 1 | 3 | 4 | 5 | 6 | Othera | Excited stateb | Total number of trajectories |
| a Trajectories that break the bond with isomers other than those described by Nunes et al. in Fig. 1(b). b Trajectories that remain in the excited state beyond 500 fs. | ||||||||
| XMS-CASPT2 | 9.6 | 55.8 | 3.8 | 1.9 | 3.8 | 11.5 | 13.5 | 52 |
| SA4-CASSCF | 3.7 | 56.3 | 0.7 | 0.0 | 3.3 | 33.0 | 3.0 | 300 |
| Cao18 | 4.0 | 40.0 | 0.0 | 0.0 | 9.0 | 47.0 | — | 100 |
| Nunes et al.10 | Major | Minor | Minor | Minor | ||||
The acquired relaxation times of the decay process are shown in Fig. 2(a) and (b). The fraction of trajectories was determined by the ratio of the number of trajectories staying in S1 to the total number of trajectories. The theoretical lifetime was determined through the regression curve fitting of the relaxation data.36 Initially, a single exponential function had been attempted, but it did not converge. Therefore, a bi-exponential function, eqn (2), was eventually utilized.
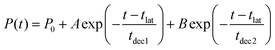 | (2) |
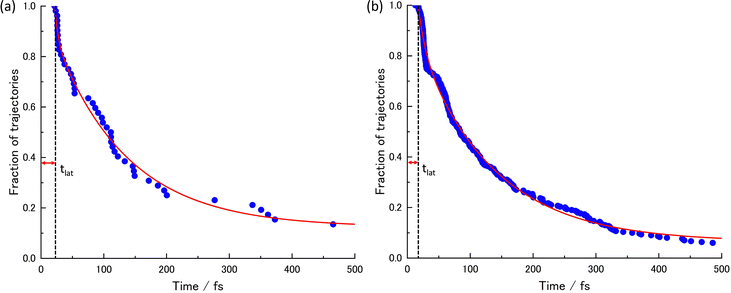 | ||
| Fig. 2 The lifetimes of the S1 state and the decay curves given by the regression curve fitting at (a) XMS-CASPT2 for 52 trajectories and (b) SA4-CASSCF for 300 trajectories. | ||
| t lat | t dec1 | t dec2 | P 0 | A | B |
|---|---|---|---|---|---|
| (a) at XMS-CASPT2 level | |||||
| 21.50 | 4.89 | 115.65 | 0.10 | 0.15 | 0.75 |
| t lat | t dec1 | t dec2 | P 0 | A | B |
|---|---|---|---|---|---|
| (b) at SA4-CASSCF level | |||||
| 14.70 | 10.77 | 119.81 | 0.01 | 0.19 | 0.80 |
Due to some trajectories trapped in excited states for a long time, the lifetime would become longer. When transitions to S2 or S3 happen, some did not reach the final product within 500 fs; P0 is the ratio of the staying trajectories in excited states to the total trajectories. In the XMS-CASPT2 method, seven trajectories stay in the excited state even at 500 fs, in the SA4-CASSCF method, seventeen trajectories stay in the excited state. From this lifetime analysis, it was predicted that the S1 → S0 transition could be classified into two categories, indicating the existence of two different decay processes.
Just after photoexcitation to S1, the other transitions to S2 frequently occurred at 36 of 52 trajectories, 33 VHs and 3 non-VHs in XMS-CASPT2, and 157 of 300 trajectories, 130 VHs and 27 non-VHs in SA4-CASSCF. These transitions occur because S1 and S2 could be in close vicinity around the Frank–Condon region. Some trajectories transitioned to S3 or were trapped in S2, but most quickly returned to the adjacent S1 state and relaxed to S0. The 143 of 300 trajectories hopped from S1 to S0 without going through S2, all of which were VHs.
S1 → S0 transition mapping: nonadiabatic coupling homology in the Coulomb matrix framework
The relationship between the structures of VHs from S1 to S0 and the non-adiabatic transition probabilities was described using Coulomb matrices. The used data consisted of 300 classical trajectories in SA4-CASSCF, and the 366 structures and their probabilities that occurred within these trajectories were analysed based on machine learning by M. Rupp et al., which dealt with modelling molecular atomization energies.37Usually, Cartesian coordinates are used for MD simulations, but when treating molecular structure characteristics, Cartesian coordinates pose a problem; the same structure described after translation or rotation appears as a different structure. Therefore, Cartesian coordinates are transformed into the Coulomb matrix M defined by eqn (3) where {RI} is the Cartesian coordinate and {ZI} is
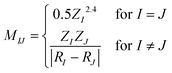 | (3) |
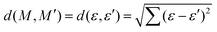 | (4) |
The following two types of analysis were carried out.
(i) a comparison by brute force of structures with non-adiabatic transitions
290
C
2 = 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905 possible ways
905 possible ways
(ii) optimized structure in S0 in contrast to non-adiabatic transition-undergoing structures
1 × 290 = 290 possible ways
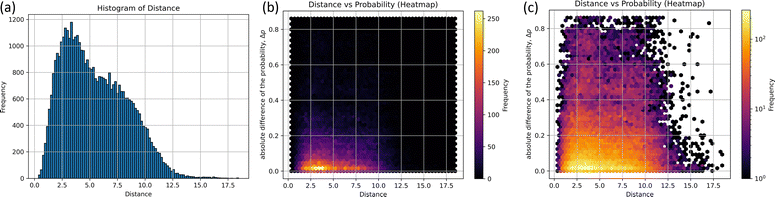
The histograms on structural similarity (frequency) and heatmaps for differences in non-adiabatic transition probabilities (Δp) of different structures are shown in Fig. 3, where Δp is the absolute difference between the non-adiabatic transition probabilities of the two structures, and 97% of non-adiabatic transition probability-data have a probability greater than 0.4, as shown in Fig. 3(b).
The two peaks appear as clearly seen in the histogram. The maximum frequency of bin is 1179 at the distance d = 3.16, which implies that certain pairs of the structures corresponding to 3.16 exhibit the most probable pair in 290 non-adiabatic transitions. In particular, the five pairs of structures are illustrated in Table S3 (ESI†); the random.sample(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) )38 function was utilized to extract 1179 arbitrary combinations of five. The subsidiary peak was observed at d = 6.79 with the frequency of 797. It is also found that Δp is close to zero at d = 3.16 and 6.79 in Fig. 3(b). In other words, similar structures taking similar distances could take similar probabilities. However, it not easy to see the two peaks around d = 3.16 and 6.79 due to overlapping with other cases. To see the differences around d = 3.16 to 6.79, the heatmap of Δp scaled by the logarithm is drawn in Fig. 3(c). Δp at d = 3.16 is found to be scattered to 0.8, which means that some of them have the same distance but have different probabilities. The non-adiabatic transition probability is determined by including the potential gradient and the crossing speed at the pseudo-crossing of the two potentials, so it cannot be easily determined from the coordinates alone. However, the Δp distribution would suggest that there are two correlations at d = 3.16 and 6.79 between the structure of non-adiabatic transitions and transition probabilities.
)38 function was utilized to extract 1179 arbitrary combinations of five. The subsidiary peak was observed at d = 6.79 with the frequency of 797. It is also found that Δp is close to zero at d = 3.16 and 6.79 in Fig. 3(b). In other words, similar structures taking similar distances could take similar probabilities. However, it not easy to see the two peaks around d = 3.16 and 6.79 due to overlapping with other cases. To see the differences around d = 3.16 to 6.79, the heatmap of Δp scaled by the logarithm is drawn in Fig. 3(c). Δp at d = 3.16 is found to be scattered to 0.8, which means that some of them have the same distance but have different probabilities. The non-adiabatic transition probability is determined by including the potential gradient and the crossing speed at the pseudo-crossing of the two potentials, so it cannot be easily determined from the coordinates alone. However, the Δp distribution would suggest that there are two correlations at d = 3.16 and 6.79 between the structure of non-adiabatic transitions and transition probabilities.
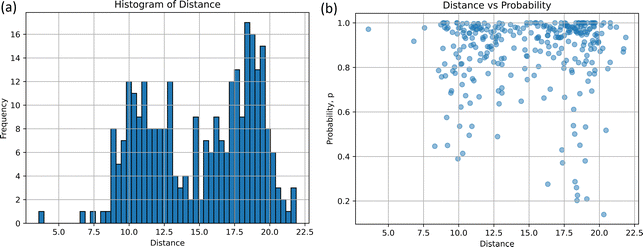
The comparison-(ii) of the optimized structure in S0 to the non-adiabatic structure provides the histogram and scatter plot presented in Fig. 4(a) and (b), respectively. Two peaks can be seen from the histogram result. The distance d at the highest frequency is 18.03 and the frequency at that time is 17, which indicates that the non-adiabatic transition occurred most frequently at d = 18.03 from the stable structure. The five arbitrarily selected structures at this distance are listed in Table S4(a) and (b) (ESI†). Another peak in Fig. 4(a) is observed around d = 9.98, with the frequency of 12; the non-adiabatic transitions occur in the regions closer than 18.03. In terms of probability, p, as depicted in Fig. 4(b), for d = 9.98 and 18.03, most probabilities are localized at 1.0 for both distributions, while the distribution at d = 18.03 extends to p = 0.20. Table S4(c) (ESI†) shows the results of the time-resolved histograms every 50 fs (or 100 fs).
In the S1 → S0 non-adiabatic transition, these two types of emerged molecular structures could suggest the existence of two different lifetimes and two different conical crossings. Although there are exceptions in our classical trajectories, the shorter lifetime process corresponds to the lower peak (d = 9.98), while the longer lifetime process is associated with the higher peak (d = 18.03).
Trajectories back to the reactant/initial structure, isoxazole
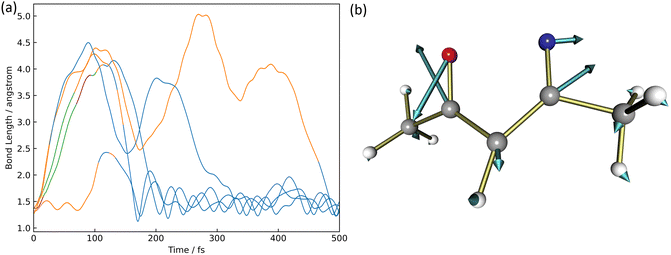
There were five trajectories where the return process to the reactant occurred in the XMS-CASPT2 calculation. This happening would be slightly larger than the 4 trajectories out of 100 trajectories in the paper by Cao18 considering three electronic states, S0, S1, and S2. The time variation of the N2–O1 binding distance is shown in Fig. 5(a). The orange, blue, green, and purple lines correspond to trajectories staying in S0, S1, S2, and S3, respectively.In four of the five trajectories, the bonding distance was greatly extended to 4.5 Å in the excited states by 200 fs, except in one trajectory, the N2–O1 bonding distance was not extended much. One of these four is deactivated to S0 at 26 fs but continues to oscillate with large amplitude after 200 fs up to 300 fs. This motion is caused by the azirine structure it goes through. In addition to this trajectory, large amplitude vibrations are observed in the N2–O1 bond up to 5.0 Å in S1. Finally, at 500 fs, all 5 trajectories become isoxazole structures and continue to oscillate stably. The S1 → S0 non-adiabatic transition vector is shown in Fig. 5(b). This non-adiabatic vector indicates the N2–O1 bond direction, which contributes to N2–O1 bond formation and produces 1.
The isomerization pathway to the azirine product
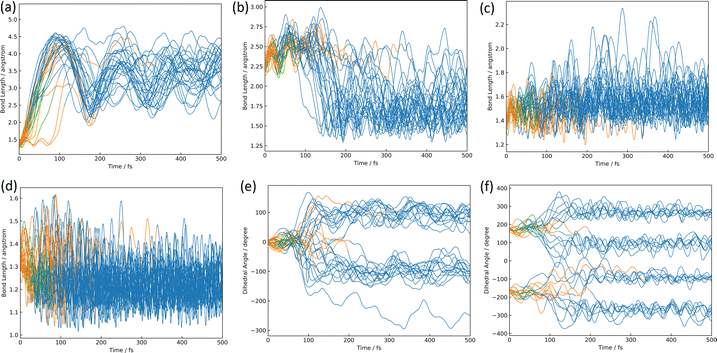
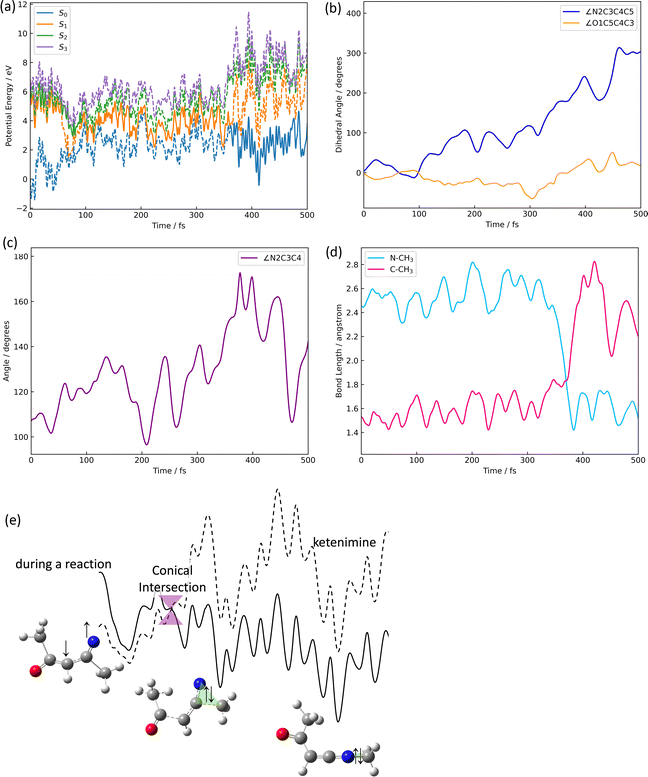
The azirine structure is shown in compound 3 in Fig. 1(b). This structure is the main product of the photoisomerization reaction of isoxazole. As mentioned above, isoxazole 1 is known to have two lifetimes. The estimated half-lives for the respective lifetimes are 24.89 fs and 101.66 fs at XMS-CASPT2. Here, the two classical trajectories with transitions at the times corresponding to these two half-lives are taken up in Fig. 6; the time variations for the potential energies and CI-coefficients shown along the classical trajectory where the nonadiabatic transition occurred at 23.50 fs are shown in Fig. 6(a) and (b), while those variations for the trajectory where the transition occurred at 104.75 fs are shown in Fig. 6(c) and (d). Time profiles up to 100 fs for the complexes in Fig. 6(b) and (d) are shown in Fig. S2(a) and S3(b) (ESI†). These two classical trajectories with the non-adiabatic transitions close to each other are typical phenomena. In the case of the transition at 23.50 fs, the electronic state immediately after photoexcitation is unstable as three electronic states can exist in close proximity, and within the first few fs the dominant electronic configuration becomes a single electron excitation of 26a → 28a, which involves the excitation from a HOMO-like orbital to a Ryd.-like orbital (or non-bonding orbital of C5–carbon, see Fig. S2, ESI†) (the blue line in Fig. 6(b), which is not unclear in this figure see Fig. S2(a) for an enlarged image, ESI†). However, this electron-rearrangement quickly happened due to a single-electron excitation from the HOMO-like orbital to the LUMO-like orbital (the orange line in Fig. 6(b)). The MOs of 26a, 27a, and 28a at 0 fs and 10 fs are listed in Table S5(a) (ESI†). This single electron excitation from the N2–O1 bonding orbital to the N2–O1 anti-bonding orbital leads to an unstable electron configuration and ultimately a longer N2–O1 bond distance at S1. This dissociation of the N2–O1 bond causes the S0 state to rise and a nonadiabatic transition between S1 and S0 occurs at 23.50 fs. After the transition, in S0, the single excitation of 26a → 27a became the main configuration drawn by the orange line. This configuration kept this main structure until about 100 fs, and then (after 100 fs) the electronic structure started to be fully occupied up to the HOMO-like orbital drawn by the purple line. Furthermore, the time series of the MOs of 26a and 27a along the purple line of CI-coefficients in Fig. 6(b) in this period (18.75 fs to 250 fs) are shown in Table S5(b) (ESI†). After the non-adiabatic transition, the parent molecule (isoxazole) can no longer maintain a planar structure. The 1,3-diradical electronic structure appears on this time scale, which was proposed by Nunes et al.10 In their study, open-shell singlet vinylnitrene 2 was assumed to be an intermediate molecule, and the photochemistry of isoxazole produced 3 and keteneimine 6. Thus, the evidence for 1,3-diradical was also found in our simulation, 3,5-dimethylisoxazole 1. Additionally, a typical classical trajectory for the second lifetime eventually experiences a non-adiabatic transition from S1 to S0 at 104.75 fs. However, prior to that, there are transitions from S1 to S2 at 15.5 fs, S2 to S1 at 68.25 fs, S1 to S2 at 69.75 fs, and S2 to S1 at 74.75 fs. Finally, at 79.5 fs, the trajectory relaxes from S1 to S0, but it suddenly returns to S1 at 86.50 fs. The CI-coefficients show a mixture of many electronic states up to 100 fs in Fig. 6(d) (for more details, see Fig. S2(b), ESI†). Table S5(c) (ESI†) lists the MOs of 24a, 25a, 26a, 27a, and 28a until the final non-adiabatic transition occurs. Comparing these CI-coefficients with Fig. 6(d), the main electron configuration in the first few fs, as seen in the first trajectory, is a single electron excitation of 26a → 28a, involving the excitation from a HOMO-like orbital to a Ryd.-like (or C5–carbon non-bonded) orbital (blue line in Fig. 6(d)) moving to S2 at 15.5 fs. Then, the CSF of 26a → 27a replaces the main configuration, which is a single electron excitation from the bonding orbital of N2–O1 to the antibonding orbital. As a result, the N2–O1 bond breaks. Unlike the trajectory hopping at 23.50 fs, although the transition to S2 is also involved, this trajectory hopping at 104.75 fs leads to the involvement of 25a → 27a and 24a → 27a, which further elongates the N2–O1 bond length and distorts the planar structure. When the final non-adiabatic transition from S1 to S0 occurs at 104.75 fs, the structure is distorted from the planar structure and the N2–O1 bond length is larger than in the previous case. Within 50 fs after the final non-adiabatic transition, all electrons begin to be packed up to 26a as the main electronic configuration, and isomerization to azirine occurs quickly. These two structures appeared at the nonadiabatic transitions highlighting the similar trends to the trajectories classified by the Coulomb matrix, and the structural difference is thought to shorten the time of isomerization between the relaxation to S0 and the formation of 3. Furthermore, the dynamic processes of the molecular structure associated with this isomerization are shown in Fig. 7(a)–(f) in terms of bond distances and dihedral angles. Fig. 7(a) clearly shows the dissociation of the N2–O1 bond immediately after photoexcitation. Multiple trajectories have similar directions of the N2–O1 bond dissociation and oscillate with similar periodicity to each other. Immediately after photoexcitation, the parent molecule undergoes a memorised molecular vibration in S0 according to the Frank–Condon principle. This corresponds to vibrations up to R(N2–O1) = 1.5 Å and within 100 fs, indicated by the orange line, but as it undergoes a non-adiabatic transition to S0, R(N2–O1) stretches to about 4.5 Å with a transition to the blue line, indicating a transition to S0. This means that the parent molecule, 3,5-dimethylisoxazole 1, which maintains the N2–O1 bond in S0, loses this memory in the excited state and begins to vibrate with a high amplitude between N2 and O1. On the other hand, as shown in Fig. 7(b), after 100 fs, a corresponding vibration appears around R(C4–N2) = 1.7 Å, giving rise to a new C4–N2 bond; as there are multiple large-amplitude motions in the C4–N2 bond, the shape of the azirine triangle is not very stable, affecting the motion of the C5–C4 bond shown in Fig. 7(c). Precisely, it can be read that the distance between the C5–C4 bonds shrinks in S1, but when hopping to S0, the distance between the C5–C4 bonds increases and the stretching motion is more facilitated. This is because, in the stable structure of 3,5-dimethylisoxazole, this bond exhibits the properties of a double bond at S0, but the N2–O1 bond dissociates at S1 following the transition to S0, thus weakening the properties of the C5–C4 bond, accompanied by a change in the dihedral angle. Nevertheless, while the aforementioned three stretching vibrations (N2–O1, C4–N1, C5–C4) are correlated, the C5–O1 vibration shown in Fig. 7(d), appears to oscillate stably like a spectator once the azirine molecule is formed. The C5–O1 bond is a type of resonance bond due to the five-membered ring on S0. However, upon the N2–O1 bond cleavage during photoisomerization, a sp2 hybridization of the C5–O1 bond emerges due to the bond being a fully double bond. The radical on the oxygen atom moves onto the carbon atom (C4) after the 1,3-diradical appears on the nitrogen and oxygen atoms.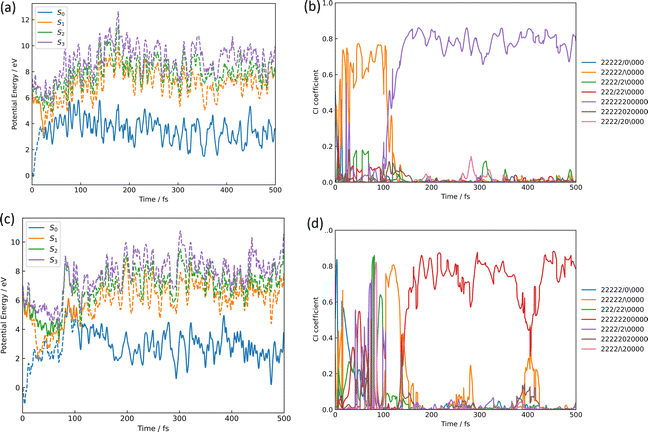 | ||
| Fig. 6 The isomerization pathways to azirine by the two typical trajectories causing the S1 → S0 transition at 23.50 fs for (a) and (b), while at 104.75 fs for (c) and (d); (a) and (c) are the potential energies of S0, S1, S2, and S3 over time-evolution, furthermore (b) and (d) are CI-coefficients over the same time. The legends used in (b) and (d) show how the 11 orbitals in the active space for CASSCF are packed with 12 electrons, with two “2” indicating two electrons occupied, the slash-symbol “/” indicating an alpha spin electron and the backslash-symbol “\” indicating a beta spin electron are packed, while zero “0” means an empty orbital, where the order of MOs in the active space is seen in eqn (1). Time profiles up to 100 fs for the complexes (b) and (d) are shown in Fig. S2(a) and (b) (ESI†). | ||
Fig. 7(e) and (f) show the characteristics of the two dihedral angles that correlate mainly with the formation process of the azirine isomer of 3. The dihedral angle of ∠C5C4C3N2 in Fig. 7(e) starts at almost 0° and remains in the molecular plane of isoxazole until the transition to S0, after which the nitrogen atom moves out of the plane and becomes metastable at about 100°, giving rise to 3. As in the previous discussion, the 1,3-diradical structure described by the single excitation of 26a → 27a after hopping to S0 causes isomerization to 3, a 3-membered ring. This photoisomerization finally produces diastereomers (syn- and anti-) and enantiomers (R- and S-) for 3.
In our 500 fs simulations, the ratio of syn- to anti-form was eight to nineteen, with the anti-form being the major product. The experimental data is 58 to 42, which differs from our ratio, but it is noted that this ratio depends on the buffer gas used in the measurements.14
The time variation of the ∠N2C3C4H7 dihedral angle correlated to the mirror isomer is shown in Fig. 7(f); the dihedral angles are around 180° and −180° in S1, but the angle shifts significantly from 180° to 100°, 260°, −100° and −260° after the relaxation in S0. This conformational change occurs before the formation of the three-membered ring and determines which of the two pathways is the R- or S-conformational pathway. There is no bias towards either pathway, the ratio being approximately one to one.
The isomerization pathway to the products of nitrile ylide and oxazole
The structures of nitrile ylide and oxazole are shown in Fig. 1(b), nitrile ylide 4 and oxazole 5. Immediately after the formation of azirine 3, the dissociation of the C3–C4 bond gives rise to 4. These three trajectories are referred to here as the i-, j-, and k- trajectories, whereas two of the three trajectories (i and j) are products of the trapped nitrile ylide up to 500 fs. It is well known that 4 is easily formed from the syn-conformation of 3 with the further isomerization to 5, because of the lower potential energy barrier than the anti-conformation.10,24 The time profile of the potential energy for the i-trajectory is shown in Fig. S3(a) (ESI†). In addition, its CI-coefficients are shown in Fig. S3(b) (ESI†).In one of the two trajectories producing nitrile ylide (i), the N2–O1 bond was dissociated immediately after photoexcitation, and the 1,3-diradical structure appeared (see Fig. 8(a)). The electronic structure mixing was quite like the previous discussion; the mixed configurations arose between the single excitation of 26a → 27a and the fully closed-shell structure until 100 fs (see Fig. S3(b), ESI†). Conversely, a commonality among the three trajectories is that the N2–O1 bond is dissociated following the transition to S1. After the N2–O1 bond stretching, the C3–C4 bond also stretches (see Fig. 8(b)) as it begins to isomerize to 3, forming 4, which means that it does not spend much time staying in 3, but soon becomes 4. In other words, the time spent in azirine is not very long, and isomerization to nitrile ylide occurs immediately. The molecular orbitals of 26a, 27a, and 28a related to this process at 0.00 fs, 4.75 fs, 7.25 fs, and 7.50 fs are shown in Table S6(a) (ESI†). The main electronic structure is of a single electron excitation of 26a → 27a until the nonadiabatic transition to S0 at 21.50 fs, but the structure changed to the single excitation of 26a → 28a from 4.75 fs to 7.25 fs, although it was very tiny period. This exchange of the 28a to 27a orbitals on the electronic transition indicates the S2 state lying closely to S1; the single-electron excitation of the HOMO-like orbital, 26a, to the Ryd-like orbital is dominant around the Franck–Condon region. While, at 7.50 fs, when the single electron excitation of 26a → 27a returns as the primary character, this Ryd-like orbital disappears and is replaced by the single electron excitation to the N2–O1 anti-bonding π orbital. It follows that the N2–O1 bonding distance increases; the transition to S0 shows that the main electronic configuration features filling all MOs up to the HOMO-like 26a by two electrons, however the CI coefficient of a single electron excitation to 27a is also large up to around 100 fs. Therefore, the N2–O1 part of the 26a orbital looks like an out-of-plane bonding π orbital, whereas 27a is an anti-bonding π orbital, so the N2–O1 distance is considered to leave without bonding. Furthermore, this bond-breaking would widen the C5–C4–C3 angle, which would result in the formation of a bonding orbital of C4–N2, as can be read from the MOs at 76.00 fs; the MOs of 26a and 27a at 21.50 fs and 76.00 fs are shown in Table S6(b) (ESI†). As described above, 3 arose as an intermediate through the cyclization. However, after this cyclization, the C3–C4 bond was broken, resulting in the formation of 4; this bond elongation began at around 175 fs in S0. The time variation of MOs for 26a on the isomerization of 3 to 4 are shown in Table S6(c) (ESI†). In the process of nitrile ylide formation, the excess energy obtained in photoexcitation would be concentrated on the motion of the three-membered ring albeit of the energy redistribution to all motions of the molecule. Thus, the main pathway seems to have been in the direction of cleavage of the C3–C4 bond. The three trajectories (i, j, k) constitute a nitrile ylide, which then adopts both syn- and anti- forms as illustrated in Fig. 8(c) by the dihedral angle ∠N2C3C4C5. Subsequently, one of the nitrile ylide (j) adopts the anti-forms (∠N2C3C4C5 ≈ 180°), while the other and the oxazole former (i, k) adopt the syn-forms (∠N2C3C4C5 ≈ 360°).
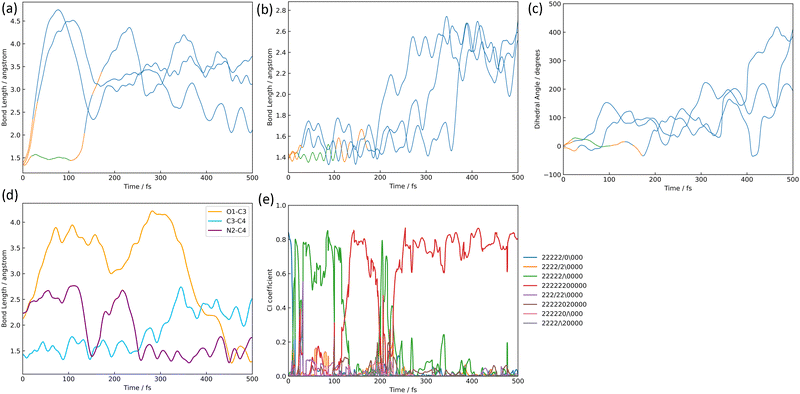 | ||
| Fig. 8 The isomerization pathways to nitrile ylide and oxazole; (a) the bond length of N2–O1, (b) the bond length of C3–C4, (c) the dihedral angle of ∠N2C3C4C5 where the color lines correspond to the electric state mentioned in the figure caption of Fig. 7, (d) the bond length's alternation, and (e) the CI coefficients (the legends mentioned in Fig. 6) are shown over time-evolution. | ||
Only one trajectory led to the isomerization from one of the three trajectories that formed 4 to 5. As mentioned above, compound 4 has two isomers, the anti- and syn-form, in our simulation. Su also reported that two isomers could appear in the ab initio calculation;16 it was stated that the only isomerized species to the syn-form would be isomerized to oxazole 5. In our work, three trajectories of nitrile ylide were formed, and two of three trajectories were stable in the anti- and the syn-forms, respectively. One last trajectory underwent isomerization to oxazole after going through the syn-form. The trajectory that isomerized to 5 gave rise to a non-adiabatic transition from S1 to S0 at 31.75 fs, after which it formed azirine 3. Thereafter, the C3–C4 bond begins to break after about 300 fs, while retaining the N2–C4 bond. When forming 3, the conformation becomes a syn-form and maintains a syn-form when isomerized to 4. The C4–O1 bond is formed immediately afterward, with a bond distance of 1.5 Å at 450 fs and stabilizes to 5. The N2–C4, C3–C4, and O1–C4 bond distances are summarised as a function of time in Fig. 8(d), and the time variation of the CI-coefficients is shown in Fig. 8(e), where the coefficient of single-electron excitation of 26a → 27a increases once at around 350 fs. Furthermore, the MOs from 350 fs to 425 fs from the formation of 4 to that of 5 are shown in Table S6(d) (ESI†). The single-electron excitation from the non-bonding orbital of C4 to the anti-bonding orbital of N2–C4 becomes dominant at this moment. Therefore, the C3–N2–C4 bond angle is expected to be distorted afterward. Finally, the main electron configuration is predominantly two electrons occupied up to 26a, and the bond between O1 and C4 is considered to stabilize.
The methyl migration to the product of 3-acetyl-N-methyl ketenimine
The product ratio of 3-acetyl-N-methylketenimine 6 is 3.8% in the XMS-CASPT2-based simulation, which is a minor event in terms of probability, but methylketenimine formation was found. In addition, a single other trajectory was observed in which the methyl group migrates once to form 6 as an intermediate, but the methyl group is subsequently cleaved off. In photoisomerization simulations of isoxazole, which is the backbone molecule of 3,5-dimethylisoxazole 1, the formation of 6 has also been reported.8 In that case, it was formed by a [1,2]-hydrogen shift. However, in our case, the methyl-group shift occurred at a smaller probability. On the trajectory for this pathway shown in Fig. 9(a), the hopping of the electronic state is roughly as follows; quickly after the photoexcitation, the molecule excited to S1 at 0 fs made a non-adiabatic transition to S2 at 16.75 fs and returned to S1 again at 28.25 fs. It then transitioned again to S2 at 55.75 fs and again to S1 at 92.50 fs; the S1 state lasted longer and transitioned to S0 at 361.75 fs; the frequent switching between the S1 and S2 states is due to the proximity of the two states of 3,5-dimethylisoxazole 1 as mentioned before. In other words, vinylnitrene 2 does not undergo a nonadiabatic transition while it is close to S0 at about 100 fs, but it does conduct several nonadiabatic transitions at the S2–S1 pseudo-crossing after it appears. When deactivated to S0 in this structure of 2, an azirine 3 is formed. In conclusion, the bifurcation points between 3 (→ nitrile ylide 4 → oxazole 5) and 6 depends on whether a nonadiabatic transition from the structure of 2 to S0 occurs. The structural change of the molecule was also traced (see Fig. 9(b)). Immediately after excitation, the two dihedral angles (∠O1C5C4C3 and ∠N2C3C4C5), which define the five-membered ring of the isoxazole skeleton, are near 0° until 100 fs, indicating that the five-membered ring structure was preserved. However, the five-membered ring structure gradually begins to collapse on S1 after about 150 fs. At around 180 fs, cis–trans isomerization occurred in S1; the dihedral angle of ∠O1C5C4C3 (∠N2C3C4C5) began to increase (decrease), reaching around 100° (−100°) in S1, resulting in a trans isomer. As soon as the ∠N2C3C4 bond shown in Fig. 9(c), the angle of the trans isomer, approaches 180° (or a linear shape), the MOs showing the methyl group and the N2–C3 bond easily interact, and the S1 state comes close to S0, resulting in a [1,2]-methyl shift as shown in Fig. 9(d), with a nonadiabatic transition to S0, yielding 6. In Table S7(a) (ESI†), the MOs associated with the formation of 6 are drawn at various time steps. Furthermore, the main electron configurations are listed in Table 4, together with the actual value of the coefficient for the CSF. Upon returning to S1 at 92.50 fs, the electronic state is a single-electron excitation from the non-bonding orbital of oxygen (nO) to the non-bonding orbital of nitrogen (nN). This electronic configuration significantly differs from the configuration during the formation of 3 discussed in the previous section, because the azirine formation involves a one-electron excitation from the non-bonding orbital of carbon (nC) to nN. As mentioned above, in 3, the two radicals on the N2 and O1 atoms moved onto the N2 and C4 atoms after a non-adiabatic transition from S1 to S0. On the other hand, in the pathway to ketenimine formation, there is a bi-radical on N2 and C4 atoms in the excited state, but they gradually start to move, and the bi-radical gather on the triangle formed by N2–C3–CH3. Here, the migration structure on the triangle becomes the non-adiabatic geometry at the conical intersection as well and then a non-adiabatic transition occurs smoothly. The change in the molecular structure at this nonadiabatic transition to S0 is as shown in Fig. 9(b); the ∠O1C5C4C3 is around 180° and the ∠N2C3C4C5 is around 0°, which indicates that the O1's dihedral angle opens further to 180° from 100° at trans isomer and the N2's dihedral angle returns from −100° to around 0°. Furthermore, a methyl shift starts to occur at this moment, resulting in a single electron excitation of 26a → 27a, which features the single electron excitation of πN–C4* to σC3–Me. After the transition to S0, the electronic state becomes a ground state occupied with two electrons each up to 26a. There are two of fifty-two trajectories at XMS-CASPT2 with a methyl shift, both of which are in S1 and undergo non-adiabatic transitions after the ∠O1C5C4C3 dihedral angle reaches around 180°. The MO after the transition is shown in Table S7(b) (ESI†). The N–CH3 bonding orbital becomes larger as it moves towards the N2–CH3 stable structure after the transition.| Time/fs | Single excitations | CI coefficients |
|---|---|---|
| 0.00 | 26a → 28a | 0.93164482 |
| 16.75 | 24a → 27a, 26a → 28a | 0.45397086, 0.33661073 |
| 28.25 | 26a → 27a | 0.55543761 |
| 55.75 | 26a → 27a | 0.84249959 |
| 65.00 | 26a → 28a, 25a → 27a | 0.51832320, 0.44864707 |
| 92.50 | 25a → 27a | −0.46944657 |
| 361.75 | 26a → 27a | −0.79529092 |
In order to understand the mechanism of the [1,2]-methyl shift associated with a nonadiabatic transition, the minimum energy structure for the conical intersection in S1 was explored by using the trajectory-based geometry that actually caused the nonadiabatic transition along with the [1,2]-methyl shift. The optimized geometry at SA4-CASSCF shown in Fig. S4(a) (ESI†) was finally obtained in Cs symmetry; the bond distances for N2–CH3 and C3–CH3 are 2.107 Å and 1.699 Å, respectively. Thus, the bond distance to carbon (C3) is closer than that to nitrogen (N2) at the optimized structure for the conical intersection. The 26a, 27a, and 28a orbitals at this geometry are listed in Fig. S4(b) (ESI†), where the main electron configuration for S1 is of the single-electron excitation of 26a → 27a. Since the 27a orbital features the σ antibonding orbital of N2–CH3 (πN–CH3*), the σ bonding orbital of N2–CH3 (σN–CH3) has not appeared in S1, yet. On the other hand, the coefficient of single electron excitation of 26a → 28a is also large; the 28a features the πC3–N* orbital, suggesting the possibility of the radical appearance on the top of nitrogen.
To clarify how the methyl group moves, the geometry when the carbon of the methyl group and the C3 and N2 atoms took a triangular structure was extracted from the data of classical trajectories with methyl shifts, and the MOs of 4a, 10a, 15a, 17a, and 24a, at that time are listed in Fig. S4(c) (ESI†). Besides, the MOs for the methyl radical alone are shown in Fig. S4(d) (ESI†). The ground state configuration for the methyl radical is as follows;
| (1a)2(2a)2(3a)2(4a)2(5a)1. |
The other products
The other complex products of 11.5% for XMS-CASPT2 and 33.0% for SA4-CASSCF were found, as present in Table 2. The complex products consisted of isomers and fragments resulting from the dissociation process. The four main complex products are listed in Table S8 (ESI†). To distinguish them from compounds 1–6, fragments are designated 7, 8, 9 and 10. As has been discussed above, all trajectories, except the two trajectories in the SA4-CASSCF method, undergo N2–O1 bond breaking immediately after photoexcitation. The subsequent dissociations happened in 7, where the methyl group on the O side was cleaved (C5–C8); in 8, where the methyl group on the N side was cleaved (C3–C6); in 9, where acetonitrile was formed (C3–C4); and in 10, where biradicals were formed (C4–C5). Table 5 gives details of the formation ratios together with Cao's results, and although there were few dissociation pathways in our simulation similar to Cao's results, methyl groups dissociated, and other isomers were identified.There are two types of methyl group dissociation at both theoretical levels. One is that the ketenimine 6 formed but was not stable and then the methyl group was cleaved, while the other is that the methyl group dissociated directly. For example, at the SA4-CASSCF level, 6 was formed but was not stable, and in total eight trajectories involve methyl bond dissociation; five happened within 50 fs and three happened after 100 fs, 300 fs, and 400 fs, respectively. It is the S1 state lying closely to S0, which caused the instability of 6. On the other hand, there are 16 trajectories at SA4-CASSCF, in which the direct dissociation happened just after the nonadiabatic transition to S0. In other words, this conical intersection can also lead to the direct dissociation, as mentioned by Sarah et al. Furthermore, three trajectories show the direct dissociation in S1 without hopping but then relax to S0. The former is of the bond-cleavage in the ground state (D0), but the latter is in D1 and then hopping to D0.
Conclusions
In this study, we conducted non-adiabatic ab initio molecular dynamics simulations using the trajectory surface hopping method to elucidate the complex reaction dynamics in the photoisomerization of 3,5-dimethylisoxazole. We assumed photoexcitation from S0 to S1 due to zero-point vibrations and employed two different theoretical methods, XMS-CASPT2 and SA4-CASSCF, with the cc-pVDZ + sp basis set.The isomerization pathway followed the route pointed out by Nunes et al. in their experiments, where the five-membered ring undergoes ring-opening after excitation to S1 and subsequently undergoes non-adiabatic transition to S0. After hopping to S0, we identified pathways leading to the regeneration of isoxazole 1, as well as the formation of azirine 3, nitrile ylide 4, oxazole 5, and ketenimine 6. Additionally, we calculated their quantum yields, revealing that 3 was the major product with a yield of 56%, successfully reproducing the experimental results.
By analyzing the time evolution of CI coefficients and molecular orbitals during the formation of 3, we found that the bonding orbital between N2 and C4 emerges after hopping to the ground state, leading to the formation of the three-membered ring. In the case of 6 formation, we observed that the non-adiabatic transition occurs in a structure where the methyl group begins to shift, which corresponds to the 1,2-shift mechanism proposed by Wilsey et al., successfully capturing this mechanism dynamically.
Notably, our theoretical simulations provide new insights into the excited-state lifetimes. For the XMS-CASPT2 method, two lifetimes of 4.89 and 115.65 fs were observed, while for the SA4-CASSCF method, lifetimes of 10.77 and 119.81 fs were identified. This revealed the existence of two distinct non-adiabatic transitions. Furthermore, using the Coulomb matrix, a tool frequently applied in machine learning, to analyze the S1–S0 non-adiabatic transition structures, we observed significant structural changes not only in comparison to the S0 equilibrium structure but also under more forced conditions. Two distinct peak groups were discovered, suggesting that the non-adiabatic transition structures can be classified into two processes.
The findings of this study deepen our understanding of the photoisomerization mechanism of 3,5-dimethylisoxazole and provide new insights into non-adiabatic phenomena.
Author contributions
Mizuki Kimura: conceptualization, data curation, formal analysis, investigation, methodology, project administration, software, validation, visualization, writing – original draft. Shinkoh Nanbu: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing – review & editing.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request. Additionally, the datasets generated and/or analyzed during the current study are available in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Sophia University Special Grant for Academic Research, with Faculty of Science and Technology Proposal-based Research Fund.References
- X. Wang, Q. Hu, H. Tang and X. Pan, Pharmaceuticals, 2023, 16, 228 CrossRef CAS PubMed.
- L. Zhou, Y. Zhang, R. Fang and L. Yang, Mol. Catal., 2018, 460, 27–35 CrossRef CAS.
- A. Khutorianskyi, B. Chalyk, P. Borysko, A. Kondratiuk and P. K. Mykhailiuk, Eur. J. Org. Chem., 2017, 3935–3940 CrossRef CAS.
- M. A. Erteeb, F. Mahmoud and A. S. Kareem, Int. Res. J. Pure Appl. Chem., 2022, 23, 16–22 CrossRef.
- A. Roua, A. Ameziane, E. Hassani, A. Fitri, A. T. Benjelloun, M. Benzakour, M. Mcharfi and K. Tanji, J. Mol. Model., 2024, 30, 193 CrossRef CAS PubMed.
- E. Elqars, A. Oubella, M. E. Hachim, S. Byadi, A. Auhmani, M. Guennoun, A. Essadki, A. Riahi, A. Robert, M. Y. A. Itto and T. Nbigui, J. Mol. Liq., 2022, 347, 0167–7322 CrossRef.
- T. Morita, S. Yugandar, S. Fuse and H. Nakamura, Tetrahedron Lett., 2018, 59, 1159–1171 CrossRef CAS.
- J. Zhu, J. Mo, H. Lin, Y. Chen and H. Sun, Bioorg. Med. Chem., 2018, 26, 3065–3075 CrossRef CAS PubMed.
- M. Majirská, M. B. Pilátová, Z. Kudlicková, M. Vojtek and C. Diniz, Drug Discovery Today, 2024, 29, 104059 CrossRef PubMed.
- C. M. Nunes, I. Reva and R. Fausto, J.Org. Chem., 2013, 78, 10657–10665 CrossRef CAS PubMed.
- B. J. Wakefield and D. J. Wright, in Advances in Heterocyclic Chemistry, ed. A. R. Katritzky and A. J. Boulton, Elsevier Science, Amsterdam, 1981, vol. 25, ch. 4, pp. 1293–1298 Search PubMed.
- T. Sato and K. Saito, J. Chem. Soc., Chem. Commun., 1974, 19, 781–782 RSC.
- T. Nishiwaki, A. Nakano and H. Matsuoka, J. Chem. Soc. C, 1970, 1825 RSC.
- T. Nishiwaki and T. Saito, J. Chem. Soc. C, 1971, 3021 RSC.
- B. Singh, A. Zweig and J. B. Gallivan, J. Am. Chem. Soc., 1972, 94, 1199 CrossRef CAS.
- T. Nishiwaki, T. Saito, S. Onomura and K. Kondo, J. Chem. Soc. C, 1971, 2644 RSC.
- H. Tanaka, Y. Osamura, T. Matsushita and K. Nishimoto, Bull. Chem. Soc. Jpn., 1981, 54, 1293–1298 CrossRef CAS.
- J. Cao, J. Chem. Phys., 2015, 142, 244302 CrossRef.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- T. Geng, J. Ehtmaier, O. Schalk, G. W. Richings, T. Hansson, G. Worth and R. D. Thomas, J. Phys. Chem. A, 2020, 24, 3984–3992 CrossRef PubMed.
- C. M. Nunes, I. Reva, T. M. V. D. Pinho e Melo, R. Fausto, T. Solomek and T. Bally, J. Am. Chem. Soc., 2011, 133, 18911–18923 CrossRef CAS.
- C. M. Nunes, I. Reva, T. M. V. D. Pinho e Melo and R. Fausto, J. Org. Chem., 2012, 77, 8723–8732 CrossRef CAS PubMed.
- S. Wilsey and K. N. Houk, J. Am. Chem. Soc., 2002, 124, 11182–11190 CrossRef CAS PubMed.
- M. Su, J. Phys. Chem. A, 2015, 119, 9666–9669 CrossRef CAS PubMed.
- T. Ishida, S. Nanbu and H. Nakamura, Int. Rev. Phys. Chem., 2017, 36, 229–285 Search PubMed.
- T. Shiozaki, W. Győrffy, P. Celani and H. Werner, J. Chem. Phys., 2011, 135, 081106 CrossRef.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- H.-J. Werner, P. J. Knowles, P. Celani, W. Györffy, A. Hesselmann, D. Kats, G. Knizia, A. Köhn, T. Korona, D. Kreplin, R. Lindh, Q. Ma, F. R. Manby, A. Mitrushenkov, G. Rauhut, M. Schütz, K. R. Shamasundar, T. B. Adler, R. D. Amos, J. Baker, S. J. Bennie, A. Bernhardsson, A. Berning, J. A. Black, P. J. Bygrave, R. Cimiraglia, D. L. Cooper, D. Coughtrie, M. J. O. Deegan, A. J. Dobbyn, K. Doll, M. Dornbach, F. Eckert, S. Erfort, E. Goll, C. Hampel, G. Hetzer, J. G. Hill, M. Hodges, T. Hrenar, G. Jansen, C. Köppl, C. Kollmar, S. J. R. Lee, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, B. Mussard, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. A. Peterson, K. Pflüger, R. Pitzer, I. Polyak, P. Pulay, M. Reiher, J. O. Richardson, J. B. Robinson, B. Schröder, M. Schwilk, T. Shiozaki, M. Sibaev, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, J. Toulouse, M. Wang, M. Welborn and B. Ziegler, MOLPRO, version 2023.2, a package of ab initio programs, see https://www.molpro.net.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- E. Wigner, Phys. Rev., 1932, 40, 749–759 CrossRef CAS.
- E. J. Heller, J. Chem. Phys., 1978, 68, 2066–2075 CrossRef CAS.
- The software is archived in “https://pweb.cc.sophia.ac.jp/nanbu_lab/downloads.html” with tar and gzip archive of “zntsh.tgz.”.
- H. Nakamura, Nonadiabatic Transition Concepts, Basic Theories and Applications, World Scientific, Singapore, 2012 Search PubMed.
- C. Zhu, K. Nobusada and H. Nakamura, J. Chem. Phys., 2001, 115, 3031–3044 CrossRef CAS.
- M. Motoyama, T.-H. Doan, P. Hibner-Kulicka, R. Otake, M. Lukarska, J.-F. Lohier, K. Ozawa, S. Nanbu, C. Alayrac, Y. Suzuki and B. Witulski, Chem. – Asian J., 2021, 16, 2087 CrossRef CAS.
- Origin(Pro), Version 2024. OriginLab Corporation, Northampton, MA, USA.
- M. Rupp, A. Tkatchenko, K. Muller and O. A. Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- Python Software Foundation. “random.sample.” Python 3.10 Documentation, 2024, https://docs.python.org/3/library/random.html.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03137g |
| This journal is © the Owner Societies 2025 |