Intermolecular interaction potential maps from energy decomposition for interpreting reactivity and intermolecular interactions

Abstract

The electrostatic potential (ESP) has been widely used to visualize electrostatic interactions about a molecule. However, electrostatic effects are often insufficient for capturing the entirety of an interaction or a reaction of interest. In this investigation, intermolecular interaction potential maps (IMIPs), constructed from the potentials derived from energy decomposition analysis (EDA) using density functional theory, were developed and applied to provide unique insight into molecular interactions and reactivity. To this end, rather than constructing a potential map from probe point charge interactions, IMIPs were constructed from probe interactions with small molecular fragments, including CH₃⁺, CH₃⁻, benzene, and atomic probes including alkali metals, transition metals, and halides. The interaction potentials are further decomposed producing IMIPs for each interaction component using EDA (electrostatic, orbital, steric, etc.). The IMIPs are applied to the study of various interactions including cation–π and anion–π interactions, electrophilic and nucleophilic aromatic substitution, Lewis acid activation, π-stacking, endohedral fullerenes, and select organometallics which reveal fundamental insight into the positional preferences and physical origins of the interactions that otherwise would be difficult to uncover through other surface analyses.

---

Introduction

Molecular surfaces reflecting defined properties are often used to predict locations of greater interaction or reactivity within a molecule. The most applied surface properties for predicting interactions is the molecular electrostatic potential (MESP).^1–4 MESP surfaces reflect the interaction of the system with a point charge at a designated constant electron density surrounding the molecule and have been applied for describing a wide range of interactions.^3,4 While the MESP has proven to be a valuable property for analysis, which is also directly observable, it loses some of its utility in application to weaker dispersion type interactions and orbital based interactions, particularly with unoccupied orbitals, which are not represented by the MESP. Furthermore, the electrostatic interaction is only one component of the total interaction energy, and often is not the strongest. To address these limitations in part, extensions to the MESP that include polarization, from perturbation theory, and empirical dispersion effects have been developed^5,6 and applied to anion–π interactions.^6–8 It would be useful if molecular surfaces representing all components of the interaction, in addition to the electrostatic, were readily accessible at the QM level. The application and production of such surfaces that reflect all components of the interaction energy with atoms and small molecules of interest have been the focus of this investigation.

The MESP belongs to a broader category of molecular surface property approaches (MSPA) that can be used to capture intermolecular interactions indirectly through rigorous manipulation of the wave function or electron density.⁹ These additional methods include the average local ionization energy (AIE)^10,11 and the local electron attachment energy (LEAE).^12,13 The AIE gives insight into electron rich sites in a molecule, particularly characterized as Lewis basic or nucleophilic. It accounts for the electron density contributions from all occupied orbitals, with greater weighting given to contributions from higher energy orbitals. In contrast, the LEAE gives a sense of electron deficient regions of the system, particularly those that can be characterized as Lewis acidic or electrophilic, with a similar expression to that of the AIE. These surfaces have been applied to non-covalent interactions,^13,14 organic substitution and addition reactions,^15–17 and nanoparticles and surfaces.^18,19 Related approaches include Fukui index surfaces²⁰ that reflect the most favorable sights within the HOMO and LUMO, orbital overlap distance,²¹ and through visualization of non-covalent interactions (NCIs) through various NCI analysis approaches^22,23 including the electron localization function (ELF).^24,25 While these approaches have been used to correlate with reactivity and intermolecular interactions, these correlations are indirect in part by excluding reacting or interacting components of interest, thereby missing some components of the total interaction, and many of these approaches are typically insufficient for capturing both weak and steric interactions in particular.

Conversely, intermolecular interactions can be directly captured through calculating probe interactions which can be mapped on a grid producing molecular interaction fields (MIFs). An MIF is a field of points of interaction around a target molecule with a probe.²⁶ The interaction between the probe and molecule is typically evaluated classically through a Coulomb potential to capture electrostatic interactions and a Lennard-Jones potential to capture steric interactions. Recent efforts have been undertaken for the construction of DFT based MIFs with some success in describing protein–ligand interactions.^27,28 MIFs have been used extensively as descriptors for the development of quantitative structure–activity relationship (QSAR) predictive models for drug design,^29,30 as well as in asymmetric catalysis using machine learning.³¹ While MIFs have found success in predictive modeling, they have generally not been applied for interpretation or rationalization of intermolecular interactions nor for electronic structure analysis.

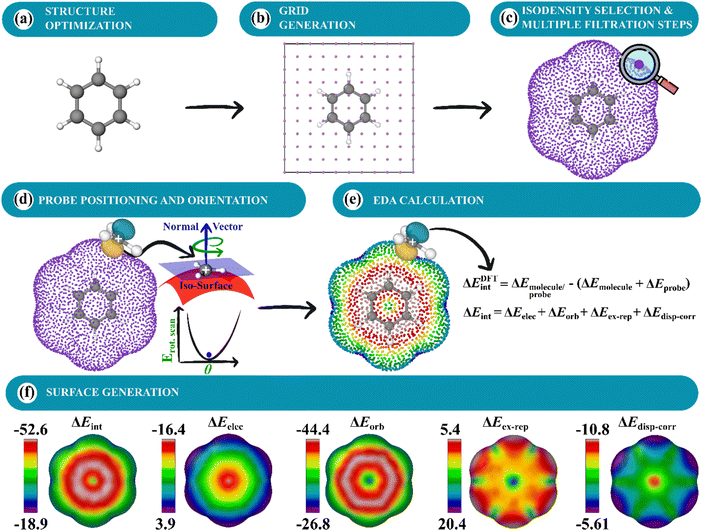
In this work, we sought to construct molecular surfaces that can be used for characterizing both weak and strong intermolecular interactions that expand the predictive capacity of MIFs and the MSPA by mapping relevant probe interactions on an isodensity surface (Fig. 1). This approach required judicious orientations for molecular probes about the isosurface. In particular, a planar CH₃⁺ probe is positioned tangentially to the isodensity surface using its norm vector with planarity restricted (Fig. 1). These probe interactions are then further decomposed into contributions from electrostatic, orbital, steric, and dispersion interactions using energy decomposition analysis (EDA), which are mapped on an isodensity surface that can be used to uncover physical insight into the nature of the interactions and positional preferences. These intermolecular interaction potential maps (IMIPs) are then shown to capture interactions important in describing reactivity in electrophilic aromatic substitution, nucleophilic aromatic substitution, and organometallics as well as intermolecular interactions including cation–π, anion–π, and π–π stacking with appropriate probe selection. While this IMIP approach is computationally more costly, as each probe interaction represents an independent wave function determination, it can be used to better reflect these interactions, furnishing deeper insight into the nature of the interaction while also imparting information about the electronic structure.

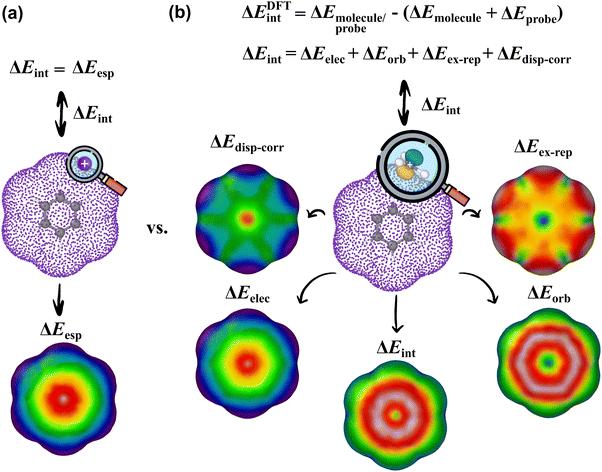Fig. 1 (a) MESP surface for benzene. (b) IMIP surfaces from probe interaction energies between benzene and a CH₃⁺ probe, further decomposed using EDA.

Computational methods

The IMIPs are generated using atomic or small molecule probes, from which interaction energies are calculated. EDA is used to further decompose these energies to generate EDA-IMIPs. EDA methods within Orca 5.1,³² Turbomole 7.7,^33,34 and xTB 6.6.0³⁵ have been implemented in the code for molecular surface generation. The Python code for generating IMIP surfaces is hosted on GitHub.

EDA methods

Multiple EDA methods are used for surface generation which include the LMO-EDA³⁶ as implemented in Turbomole, Grimme Group's xTB-IFF,³⁷ and the ETS-NOCV³⁸ schemes as implemented in ORCA. All of the results discussed here are based on the LMO-EDA method for its available implementation in Turbomole and its applications in describing various non-covalent interactions, some considered here.³⁹ The resulting surfaces are shown to be qualitatively similar surfaces constructed using the ETS-NOCV scheme (Fig. S1, ESI†). Details on the NOCV-ETS and xTB-IFF EDA methods and their respective surfaces are available in the ESI† (Fig. S1). The LMO-EDA method uses a supramolecular approach to obtain the interaction energies of two interacting fragments. The interaction energy (ΔE_int) is decomposed into electrostatic (ΔE_elec), exchange (ΔE_ex), repulsion (ΔE_rep), polarization (ΔE_orb), dispersion (ΔE_disp), and correlation (ΔE_corr) energies (eqn (1)). Furthermore, the exchange and repulsion, and the dispersion and correlation terms are combined to construct terms for the repulsive (ΔE_ex–rep) and van der Waals like attractive (ΔE_disp–corr) interactions, respectively.

ΔE_int = ΔE_elec + ΔE_ex + ΔE_rep + ΔE_orb + ΔE_corr + ΔE_disp (1)

Probe selection

The interpretation of the IMIFs is dependent on the probe structure. For the assessment of the varied interactions discussed here, many probe types are explored (Fig. S2, ESI†) including alkali cations, alkali earth cations, transition metals, halides, CH₃⁺, CH₃⁻, and C₆H₆. Where main-group metals, transition metals, and halide probes are suitable for studying systems where metal–ligand interactions, cation–π, or anion–π interactions are of interest, while C₆H₆ can be used to probe systems for regions where π-stacking interactions exist. The CH₃⁺ probe is well-suited for capturing electron-rich regions susceptible to electrophilic attack, while CH₃⁻ is appropriate for exploring electron-deficient regions susceptible to nucleophilic attack. Finally, probes like CO and PR₃ are ideal for studying unsaturated transition metal complexes. Additional probes can be readily implemented for IMIP construction.

Surface generation

Molecular surfaces are constructed by generating a grid surrounding a target molecule. An EDA calculation is performed at each grid point between the probe and molecule. Grid generation, probe placement, positioning, orientation, and visualization are described in Fig. 2 (expanded in Fig. S4, ESI†).

Fig. 2 Overview for IMIP map generation (a), structure optimization (b), grid generation (c), isodensity selection and multiple filtration steps (d), probe positioning and orientation (e), EDA calculation and (f) surface generation (units: kcal mol⁻¹).

Grid generation method

Cubic (Fig. 2) or spherical (Fig. S3, ESI†) grid methods can be used for grid construction. The present study utilizes a cubic grid generation method. The surfaces generated are based on user-defined electron isodensity values. First, a sparse cubic grid is generated around the molecule (Fig. 2a and b). An isodensity range is then set to filter off points. Subsequently, a volume element is created for each remaining grid point, and within this volume, a finer grid is constructed and filtered. This refined grid selects grid points within a narrow electron density range of 0.01% (Fig. 2c and Fig. S4, ESI†). A more detailed illustration of this method is provided in the ESI† (Fig. S4).

The cubic initial grid is typically dense; conducting EDA calculations for probes at each grid point would be computationally demanding, therefore grid filtering is necessary. A K-means clustering algorithm⁴⁰ is used to filter grid points (Fig. 2c).

Probe positioning and orientation

After grid generation and filtration, probes are positioned at each grid point. Single-atom probes are positioned without ambiguity while the alignment of molecular probes is determined by vectors normal to the tangential plane of the molecular surface (Fig. 2d) based typically on the preferred orbital directionality of the probes. The normal vectors are computed using the Open3D Python library.⁴¹ Open3D estimates the normal vectors on the surface by statistical analysis of neighboring grid points.⁴² By combining this approach with a rigid rotor scan using GFN2-xTB (Fig. 2d), the lowest energy orientation of the probe is determined within reasonable computational cost. EDA calculations are then conducted on the grid points; their corresponding energy values are stored as extended XYZ files and are subsequently used to construct surfaces using Ovito Pro (Fig. 2e and f).⁴³ Coupling the GFN2-xTB scan with DFT interaction energies produces surfaces that are qualitatively indistinguishable from surfaces produced from a full DFT scan coupled with DFT interaction energies (Fig. S6, ESI†), thus validating the use of the GFN2-xTB scan at substantially lower computational cost.

Structure optimization and EDA

Quantum mechanical (QM) and semi-empirical methods were employed depending on the size of the system under investigation. For larger systems biomolecule or supramolecular systems, the GFN2-xTB⁴⁴ method was utilized for geometry optimizations. For all other cases, DFT with the r2SCAN⁴⁵ functional, def2-SVP^46,47 basis set, D4 dispersion correction,^48–50 and resolution of identity (RI) approximation^51,52 was used with a full grid and radial grids sizes set to 7 and 5, respectively^45,53,54 and SCF convergence was set to 10⁻⁶ for EDA calculations and 10⁻⁷ for geometry optimization. The r2SCAN functional combined with the D4 dispersion correction was chosen as a proven cost-effective all-purpose method capable of describing a broad range of chemistry^54–56 determined to be suitable for the applications covered in this investigation. BSSE corrections were not employed here, although surfaces for select molecules were constructed with a larger basis set (def2-TZVPP) and were shown to be qualitatively very similar (Fig. S5, ESI†).

Isodensity value selection

Isodensity selection for surface generation was based on two approaches (methods A and B). In method A, the isodensity is selected based on a restricted scan along a coordinate approximately normal to the surface, at a site of interest to the interaction, to locate the maximum interaction strength. This method was used for comparing the same molecule with different probes. In method B, isodensities were determined from exploratory work on weak and strong interactions. For weak interactions a smaller isodensity of 1.0 × 10⁻⁶ was used, and a larger isodensity of 6.0 × 10⁻⁵ was used for stronger interactions. Method B was applied to compare different structures with the same probe.

Results and discussion

Cation–π interactions

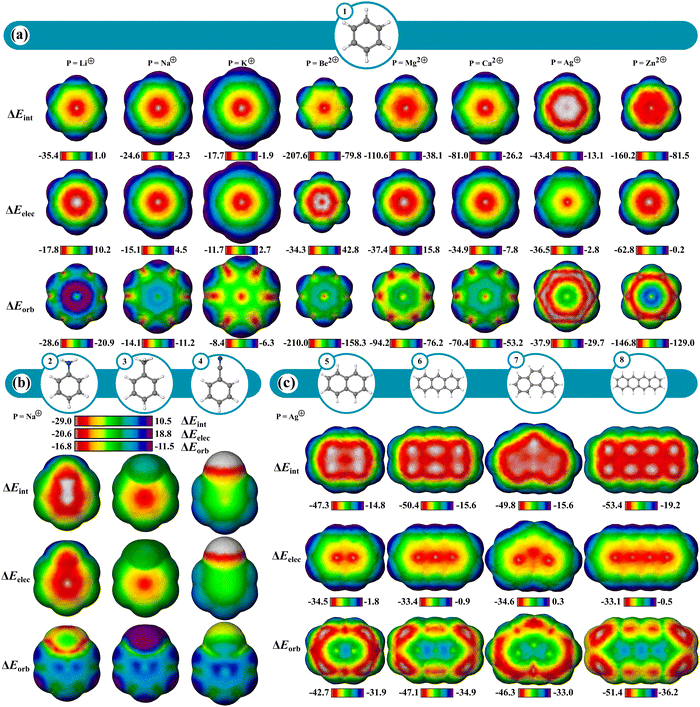
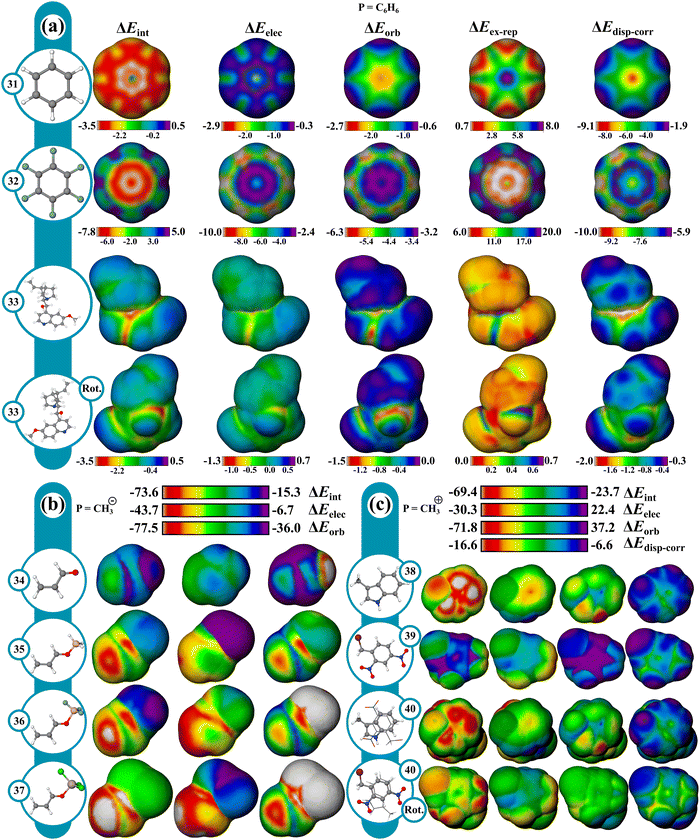
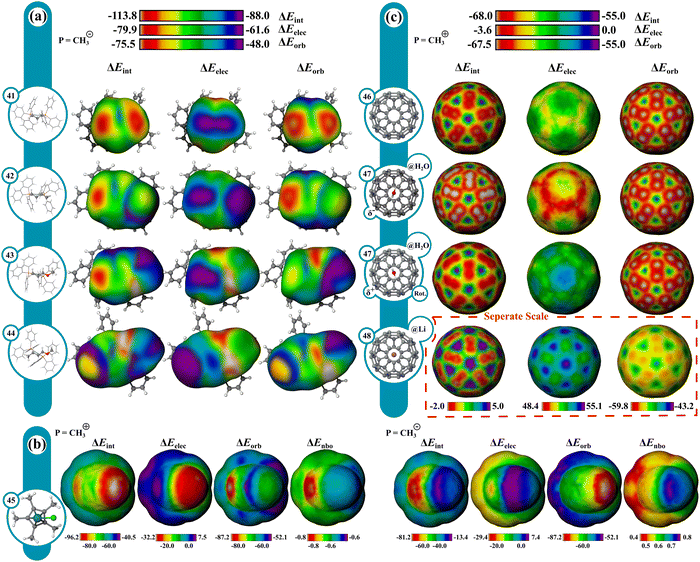
The cation–π interaction is defined as occurring between a metal cation and an aromatic π-surface^57,58 and influences the physical and chemical properties of various systems across fields including biology,^58–60 organic chemistry,^58,60–62 and materials chemistry.⁶⁰ IMIP surfaces can be used to better understand the magnitude and positional preference for cation–π interactions across various systems. In this study, a series of aromatic hydrocarbons with the probes Li⁺, Na⁺, K⁺, Mg²⁺, Be²⁺, Ca²⁺, Ag⁺, and Zn²⁺ were investigated (Fig. 3a). This selection encompasses a broad spectrum of interactions within aromatic systems.

Fig. 3 ΔE_int, ΔE_elec, and ΔE_orb (top to bottom) IMIP's of (a) benzene with Li⁺, Na⁺, K⁺, Mg²⁺, Be²⁺, Ca²⁺, Ag⁺, and Zn²⁺ probes (left to right). (b) Aniline, toluene, and benzonitrile (probe = Na⁺) (c) naphthalene, anthracene, phenanthrene, and tetracene (Ag⁺ probe). Isodensities (method A; benzene centroid): Be²⁺: 3.15 × 10⁻³, Mg²⁺: 5.49 × 10⁻⁴, Ca²⁺: 1.32 × 10⁻⁴, Li⁺: 7.52 × 10⁻⁴, Na⁺: 9.15 × 10⁻⁵, K⁺: 8.21 × 10⁻⁶, Zn²⁺: 5.49 × 10⁻⁴, Ag⁺: 1.93 × 10⁻⁴.

ΔE_int surfaces reveal that for all cations, the most favorable interactions occur over the center of the benzene (1) π-system. Divalent cations exhibit stronger total interaction energies with benzene than monovalent cations, manifested in both ΔE_orb and ΔE_elec. ΔE_int decreases for probes along a periodic group. This reduction in ΔE_int is predominantly attributed to decreased ΔE_orb, as there is little variation in ΔE_elec, consistent with poorer orbital overlap with the carbon π system (as probe size increases) resulting in reduced covalent character. This transition in bonding character is further highlighted by the ratio of ΔE_elec to ΔE_orb at the ring center. For Be²⁺, Mg²⁺ and Ca²⁺, the ratios are 1 : 8.5, 1 : 2.4, 1 : 2, respectively, which suggests a more covalent bonding character. In contrast, Li⁺, Na⁺, and K⁺ have 1 : 1.4, 1 : 0.8, and 1 : 0.7 ratios, indicating a shift towards more ionic-like character. Other theoretical investigations have shown this shift in ionic to covalent character between the alkali and alkaline earth metals.^63,64 The maximum in ΔE_elec is centered over the π-system for all probes excluding Be²⁺, where the maximum is shifted slightly outward ∼10 kcal mol⁻¹ relative to the center. Conversely, ΔE_orb is strongest at the center for Be²⁺, with a ∼27 kcal mol⁻¹ difference between these points and where the electrostatic interaction is maximal. It is the dominant ΔE_orb that drives the ΔE_int to the center, not the ΔE_elec for Be²⁺, whereas for Mg²⁺ and Ca²⁺, ΔE_elec is more important for central probe preference.

The surfaces of mono-substituted benzenes (2–4) with a Na⁺ probe reveal interesting trends in substituent influence on the interaction (Fig. 3b; Fig. S51, ESI†). While the interaction is strongest with donating groups (NH₂) and weakest with withdrawing groups (CN), the variation in ΔE_int tracks with the variation in ΔE_elec, while only a small variation is observed in ΔE_orb (Table S3 and Fig. S52, ESI†). These trends indicate that the substituent influence on the cation–π interaction is primarily an electrostatic effect. Similar observations were made regarding substituent influence on cation–π interactions by Wheeler and Houk.^65–67

The transition metals Zn²⁺ and Ag⁺ show a notable increase in ΔE_int compared to metals with similar ionic radii (Mg²⁺ and K⁺, respectively; Fig. 3a). Like non-transition metal probes, ΔE_int is most prominent at the center of the π-system. The increase in ΔE_int stems from both ΔE_elec and ΔE_orb terms. The enhanced ΔE_orb for the transition metals can be rationalized based on more favorable interaction with their higher energy occupied s and p orbitals with some back-bonding from their occupied d orbitals.

As polyaromatic cyclic hydrocarbon (PAH) size increases, ΔE_int increases with increasing number of fused rings, driven largely by ΔE_orb, translating to increased partial covalent character in the interactions (Fig. 3c; Fig. S7–S14, ESI†), which is in agreement with prior theoretical studies.^68–70 Furthermore, ΔE_orb reveals that alkali and alkaline earth metals mainly engage around the center of rings of the π-systems, whereas transition metals (eq. Ag⁺) are drawn to terminal rings, engaging in isolated π bonding. Notably, larger rings enhance orbital interactions at their peripheries, where the interacting probe can localize electron density most while maintaining delocalization and aromaticity in the unbound rings. This effect is more pronounced when contrasting anthracene and phenanthrene (Fig. 3c; Fig. S7 and S14, ESI†). This also clarifies why the outer rings of anthracene exhibit enhanced orbital interactions over its center. In contrast, carbons at ring junctions interact less favorably, where probe association results in reduced aromaticity. This behavior is most noticeable with transition metals. These effects are largely orbital based as reflected in the ΔE_orb surfaces.

Anion–π interactions

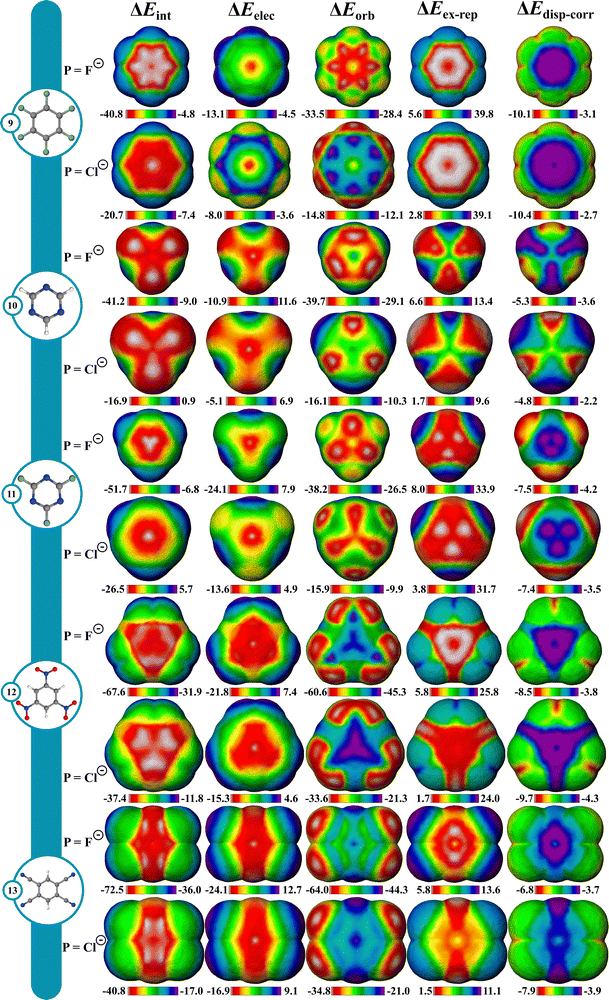
Favorable interactions can occur between anions and electron deficient π systems called anion–π interactions.⁷¹ They are thought to operate in some biological and supramolecular systems, and more recently in small molecule catalysis,^72,73 but are not as well understood as cation–π interactions. To give a better understanding of these interactions, IMIP surfaces are used to examine how different anionic probes engage with various electron-deficient π systems. Finding stable anion–π complexes is both experimentally and computationally challenging due to the propensity for Meisenheimer^74,75 complex formation, therefore our focus is not necessarily on systems where anion–π interactions are experimentally verified, but rather on identifying regions in molecules where these interactions may be relevant.

The molecules shown in Fig. 4 were selected for studying anion–π interactions as they have been extensively examined previously.^76–80 The halide probes explored include F⁻, Cl⁻, Br⁻ and I⁻. It is shown that ΔE_int decreases as the halide probe size decreases, (Fig. 4; Fig. S52–S56, ESI†). For Cl⁻, Br⁻, and I⁻ probes, the minimum ΔE_int is over the hexafluorobenzene (9) center. However, with F⁻, the most favorable site shifts to between the π bonds. This shift for F⁻ is attributed to preferences in ΔE_orb which is likely reflecting favorable F⁻(2p) overlap with the π* orbitals resulting in an energetic preference of ∼2.3 kcal mol⁻¹ compared to the center. Within the π system, steric repulsion is reduced with the probe nonconcentric. Conversely, ΔE_elec is most favorable at the ring center, but ΔE_orb and ΔE_ex–rep shift the ΔE_int preference off-center. This trend is less pronounced with larger probes like Cl⁻, Br⁻, and I⁻ and is ascribed to weaker ΔE_orb than that with F⁻.

Fig. 4 ΔE_int, ΔE_elec, ΔE_orb, ΔE_ex–rep and ΔE_disp–corr IMIP's (left to right) of hexafluorobenzene, triazine, trifluoroazine, trinitrobenzene, and tetracyanobenzene (top to bottom), with F⁻ and Cl⁻ probes. Isodensities (method A; center of ring system): F⁻ = 5.62 × 10⁻⁵ and Cl⁻ = 1.22 × 10⁻⁶.

With azines, trifluoro-triazine (11) interacts stronger with all halide probes than triazine (10) which is largely attributed to ΔE_elec since ΔE_orb is similar in magnitude between the two. Since the fluorine substituents are both inductively withdrawing and π-donating,⁸¹ these effects are partially cancelled out, leading to a small difference in ΔE_orb. The heightened electrostatic interactions in 11 can be rationalized by considering the sum of the ion–dipole (C–F bond dipoles) interactions. This helps account for the observed decrease in ΔE_elec as the probe size increases, since ion–dipole interactions are more pronounced with denser F⁻ ion than with Cl⁻. In both azines, ΔE_elec is most favorable in the center, with some reduced preference near the C–H bonds in triazine. Additionally, the ΔE_ex–rep surfaces reveal that the minimum repulsions are located around the C–H bonds for 10 whereas in 11, the maximum repulsions are around the C–F bonds. This combined steric and electrostatic effect results in different favorable energy landscapes between the molecules.

The most favorable interaction for compounds with strong π-withdrawing groups, trinitrobenzene (12) and tetracyano-benzene (13), is shifted off-center, driven by ΔE_orb and ΔE_ex–rep with the center still being favored by ΔE_elec. The shift off-center is a result of enhanced ΔE_orb (where the LUMO is localized) with slight reinforcement from ΔE_ex–rep (Fig. 4 and Fig. S52–S56, ESI†). While both systems show similar ΔE_int at their center, their most favorable sites differ by ∼4.8 kcal (F⁻) and ∼3.3 kcal (Cl⁻), with 13 being stronger given the extra π-withdrawing group.

From the surfaces provided, it is apparent that increasing the number of π-withdrawing substituents leads to increased overall interaction. Moreover, π-withdrawing groups enhance the anion–π interaction more effectively than σ-withdrawing groups (cf.9, 12, and 13). Lastly, while the probe interaction is not strongly influenced by ΔE_disp–corr, the proportion to ΔE_int increases with increasing probe size.

EAS reactivity

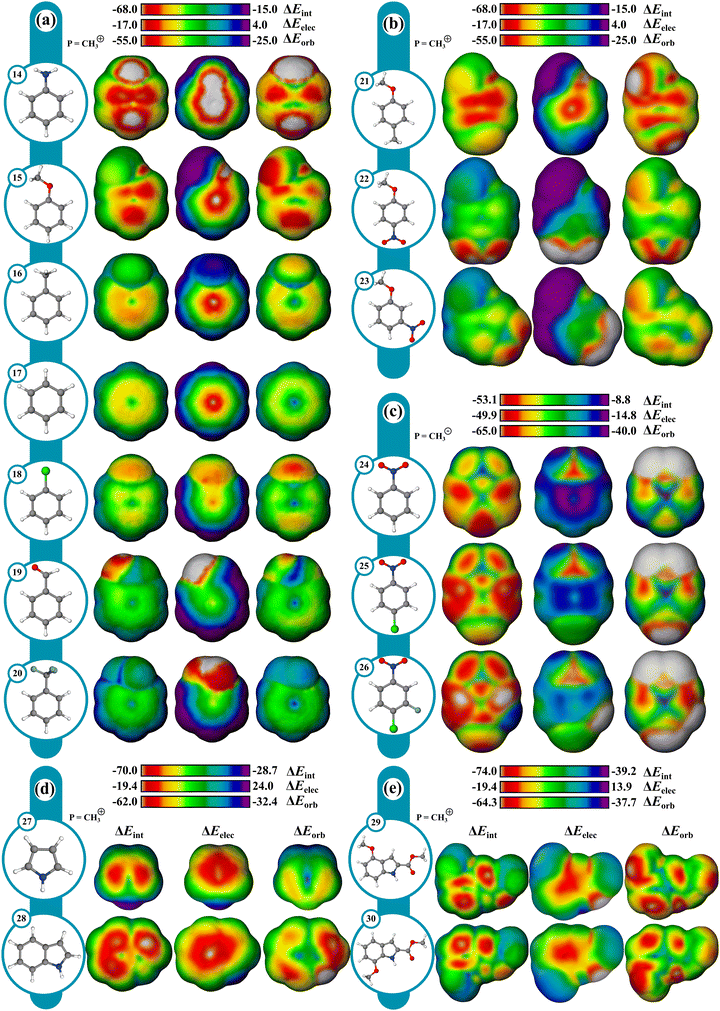
Reactivity can often be interpreted through analysis of reactant structure, particularly through the use of FMO theory. In cases where the electronic structure of the reactant is useful for assessing reactivity, typically where substantial nuclear rearrangement has not occurred in the TS, the resulting IMIP surfaces may be useful.

While ESP maps have been used to qualitatively assess relative rates of substituted aromatics in EAS, these surfaces are much less useful for understanding selectivity concepts pertaining to orbital overlap which influences chemical reactivity.^21,82–84 IMIP surfaces can be particularly useful for revealing the electronic structure of π-surfaces with variable substitution, which strongly affects rates and selectivity in EAS reactions. The IMIP surfaces of various benzene derivatives were generated using the CH₃⁺ probe, which can be used to pinpoint the most reactive sites for electrophilic addition. Benzene derivatives with substituents of –NH₂, –OCH₃, –CH₃, –Cl, –H, –CHO, and –CF₃ (14–20) have been compared. This list spans most of the electronic spectrum as supported by substituent constants including Hammett sigma values reflecting inductive and π-donating and withdrawing effects.⁸⁵ Shown in Fig. 5a, the ΔE_int surface clearly highlights enhanced interaction at the ortho and para positions, which is dominated by orbital interactions as illustrated in the ΔE_orb surfaces. The most favorable ΔE_orb within the π system correlates with relative reactivity patterns observed in EAS reactions.⁸⁶ The reactivity order follows NH₂ > OCH₃ > CH₃ > Cl > H > CHO > CF₃ and correlates with Hammett σ⁺ constants which are known to reflect EAS reactivity (Fig. 6; Table S1, ESI†).^87,88 This level of analysis is less readily extracted from ESP surfaces alone.

Fig. 5 From left to right ΔE_int, ΔE_elec, and ΔE_orb IMIP's of (a) mono-, (b) di-subsituted benzene derivatives (probe = CH₃⁺), and (c) surfaces generated with CH₃⁻ probe for benzene derivatives. Surfaces for (d) pyrrole, indole, and (e) indole derivatives (probe = CH₃⁺); isodensity: 6.00 × 10⁻⁵; method B.

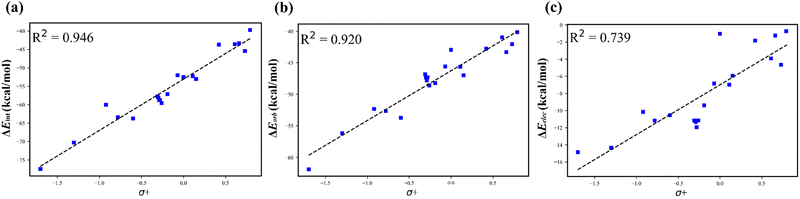Fig. 6 Hammet plot of (a) ΔE_intvs. σ⁺, (b) ΔE_orbvs. σ⁺, and (c) ΔE_elecvs. σ⁺. Energies are obtained at the para-position.

The orbital surface for chloro-benzene (18) shows that the strongest probe interaction is directed to the ortho and para positions consistent with EAS selectivity with halogens, which is greater than the maximum orbital interaction in benzene (17). However, the orbital surface analysis does not capture the complete reactivity profile as 18 is deactivated relative to 17. The ΔE_elec surface reveals that 18 is electrostatically deactivated relative to 17. The electrostatic deactivation in 18 offsets its orbital activation rendering it overall deactivating as reflected in the ΔE_int surface. With meta-directing deactivating groups, like –CHO (19) and –CF₃ (20), the ΔE_int surfaces show significantly weaker interactions consistent with their reduced reactivity.^88,89 Selectivity in poly-substituted benzenes (21–23; Fig. 5b) with meta and ortho–para directors (OMe vs. NO₂) or competing ortho–para directors (OMe vs. Me) is readily visualized through the ΔE_int and ΔE_orb surfaces, and is in agreement with experiment.^90,91

Moreover, useful reactivity patterns can be discerned with heteroaromatics in EAS (Fig. 5d). ΔE_int and ΔE_orb surfaces (Fig. 5d) for pyrrole (27) clearly show the 2-position to be the most reactive, while the ΔE_elec surface shows little difference between the positions. For indole (28), the surfaces show the most reactive position to be closer to the 3-position than the 2-position, consistent with experimental patterns. Also, ΔE_int between indole and pyrrole reveals indole to be more reactive, reflected mostly in ΔE_orb, consistent with experimental nucleophilicity parameters.^92,93 Regioselectivity in substituted indoles can also be assessed. For example, 29 shows an experimental preference for the 7 and 5 positions at an 85 : 15 ratio towards EAS. For 30, experiments also show the 4 and 6 positions to be reactive towards EAS at 80 : 20 ratio.⁹⁴ The ΔE_int and ΔE_orb surfaces for both 29 and 30 are qualitatively consistent with the experimental site preferences.

S_NAr reactivity

While EAS reactivity was probed using a CH₃⁺ probe, nucleophilic aromatic substitution (NAS) can likewise be probed with an anionic CH₃⁻ probe. Using nitrobenzene (24) as a reference in the absence of a leaving group, the most reactive sites are the ortho and para positions with ∼2.1 kcal mol⁻¹ difference between sites favoring the para as determined from ΔE_int. para substitution shifts the preference to ortho. Computational and experimental findings revealed that nucleophiles add to unsubstituted ortho positions more rapidly than at the halogenated para positions.⁹⁵ However, only addition at the halogenated para positions leads to the desired substitution product, while other additions result in transient adducts without productive outcomes, which the surfaces can readily highlight.

To assess the influence of multiple leaving groups on reactivity, 1-chloro-4-nitrobenzene (25) and the 3-fluoro (26) analogue were compared. For both compounds the ortho positions are identified as the most reactive. Notably, 26 displays enhanced reactivity at both the ortho and para positions with energy differences of approximately 3–4 kcal mol⁻¹ and 5–6 kcal mol⁻¹, respectively, when compared to 25. This enhancement is driven largely by the ΔE_elec component, which favors the ortho and para positions by 1 kcal mol⁻¹ and 3 kcal mol⁻¹ respectively. The ΔE_orb component also contributes to the enhancement in 26, though to a lesser extent. The surfaces highlight the preference for nucleophilic attack at the p-chloro position over the m-fluoro position despite fluoro being more active in NAS.

π-stacking

The IMIP surfaces can be used to gain insight into weaker non-covalent interactions including π–π type interactions (Fig. 7a). Benzene can be used as a probe to generate surfaces revealing favorable π–π interactions which may include sandwich, T-shaped, and slip-stacking arrangements as well as cation–π, anion–π, and polar–π interactions. The ΔE_int surface for stacked benzene (31) is unfavorable at the centroid (∼1.2 kcal mol⁻¹), contrasted by favorable interaction encircling the centroid (∼−3.0 to −3.5 kcal mol⁻¹). There is also favorable interaction at the ring periphery leading to T-shaped and edge-to-face interactions (∼−2.3 kcal mol⁻¹). ΔE_elec and ΔE_orb surfaces mark the central region as having favorable interactions with each contributing ∼2.3 kcal mol⁻¹ stabilization. ΔE_disp–corr provides ∼9 kcal mol⁻¹ of stabilization in this region. ΔE_ex–rep surface reveals that maximal repulsions (∼15 kcal mol⁻¹) occur when the rings are directly stacked, suggesting at close distances sterics drives the preference for a slipped arrangement (∼15 kcal mol⁻¹vs. ∼4 kcal mol⁻¹). The total energy surfaces for hexaflourobenzene (32) follow a similar trend, where the slip-stacked arrangement is still the most favored, as steric repulsion at the center is more unfavorable. The trends at sites of maximum interaction are summarized in Fig. 8.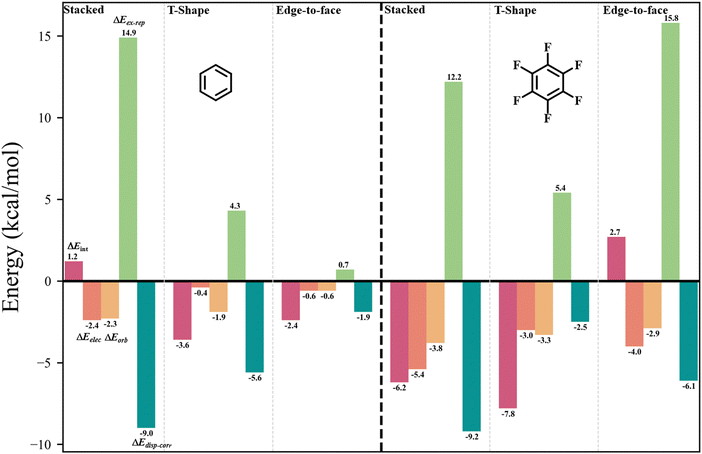

Fig. 7 IMIPs: (a) benzene, hexafluorobenzene, cinchona alkaloid (probe = C₆H₆); (b) acrolein, –BH₃, –BF₃, and –AlCl₃ coordinated acrolein (probe = CH₃⁺); (c) methylindole, 2,4-dinitrobenzyl bromide, EDA complex (probe = CH₃⁺). Isodensity: benzene, cinchona alkaloids, hexafluorobenzene (method B; 1.00 × 10⁻⁶), acrolein systems (method B; 6.00 × 10⁻⁵), and EDA complex (method B; 6.00 × 10⁻⁵).

Fig. 8 Plots of (a) C₆H₆ (left) and (b) C₆F₆ (right) sites of maximum interaction, ΔE_int (red), ΔE_elec (orange), ΔE_orb (yellow), ΔE_disp–corr (light green), and ΔE_ex–rep (dark green); probe = C₆H₆.

The positional preference for the π–π interactions is controlled mostly by ΔE_disp–corr and ΔE_ex–rep consistent with the general understanding that dispersion interactions are important for describing π-stacking. Furthermore, despite the stabilizing roles of ΔE_elec, ΔE_orb, and ΔE_disp–corr, it is ΔE_ex–rep that often overrides these stabilizing effects, emphasizing its importance in determining molecular stacking arrangements. These results are in agreement with recent theoretical findings,^96,97 which propose that at typical π-stacking and CH⋯π distances the traditional electrostatic model may not accurately capture the nature of these interactions.

Furthermore, complex π-type interactions can be isolated in larger molecules from these IMIPs. Using quinine (33) as an example, four types of favorable π interaction regions can be identified which include the interaction of the nitrogen lone pair on the quinoline ring (n → π*), the oxygen lone pair from the hydroxyl group (n → π*), the hydroxyl proton (polar–π), and the π-face interactions (π–π stacking).

Lewis acid-activated acrolein

The influence of Lewis acids on unsaturated carbonyls was explored using a nucleophilic CH₃⁻ probe, with focus on 1,2 vs. 1,4-addition to acrolein (Fig. 7b). Starting with unactivated acrolein (34), ΔE_int surfaces show a favorable interaction with a probe at both the carbonyl carbon and β carbons, with the β carbon displaying a greater preference for nucleophilic attack. Under Lewis acid activation, the magnitude of ΔE_int max increases, following the reactivity trend of unactivated (−46.2 kcal) < BH₃ (−71.2 kcal, 35) < BF₃ (−73.6 kcal, 36) < AlCl₃ (−87.1 kcal, 37). The ΔE_orb term more strongly influences this reactivity trend than ΔE_elec. While the carbonyl carbon exhibits stronger ΔE_elec, the ΔE_orb term at the β carbon dominates. This orbital preference for the β-carbon is consistent with the known preference of soft nucleophiles favoring conjugate addition. Interestingly, BH₃ increases the ΔE_orb term at both sites more than BF₃. BF₃ offsets this disparity through increased ΔE_elec. These surfaces uniquely reveal the enhanced activation of BF₃ over BH₃ which is explained as an electrostatic influence rather than an orbital influence and is in agreement with recent theoretical findings.^98,99

Electron donor–acceptor complexes

The electron donor–acceptor (EDA) complex (40) formed by 3-methylindole and 2,4-dinitrobenzyl bromide¹⁰⁰ was investigated using a CH₃⁺ probe to capture electron transfer effects (Fig. 7c). Comparison of the surfaces of the individual fragments (38 and 39) with the complex (40) shows a stronger total interaction near the acceptor and a weaker interaction near the donor, reflecting charge transfer from 38 to 39 manifested mostly in ΔE_orb and to a lesser extent in ΔE_elec. The probe interaction change is greater in 38, since the CH₃⁺ interaction near 39 induces further electron transfer from 38, and probe interaction near 38 reduces charge transfer to 39.

Organometallic complexes

Reactivity in select organometallic complexes is next shown in Fig. 9 using CH₃⁻ and CH₃⁺ probes. The regioselectivity of nucleophilic attack on allyl–Pd complexes generally favors the less substituted position with standard phosphine ligands but can be reversed in the presence of strong cation stabilizing groups like OMe.^101,102 Analysis of the corresponding reactant allyl–Pd complexes reproduces these trends (Fig. 9a and Fig. S58, ESI†). With methyl substitution, (42), the largest probe interaction favors the unsubstituted allyl carbon by 5.4 kcal mol⁻¹ in ΔE_int, which is favored by both ΔE_orb and ΔE_elec. Substitution of the methyl group for a methoxy group (43) reverses the most favored probe interaction site to the more substituted allyl carbon by 5.2 kcal mol⁻¹ in ΔE_int, driven primarily by a preference in ΔE_elec (ca. 12.1 kcal mol⁻¹). The preference for the methoxy position is enhanced further with methoxy and methyl substitution on each allyl carbon (44), (ΔΔE_int = 23.4 kcal mol⁻¹). The unsubstituted (41) reference system is also shown, where no such preference exists, with only slight differences based on ligand conformation.

Fig. 9 IMIPs: (a) substituted Pd(PPh₃)₃(allyl) complexes (probe = CH₃⁻); (b) Cp*RuCl complex (CH₃⁺ and CH₃⁻ probes); (c) fullerene and endohedral fullerenes@H₂O, @Li⁺ (probe = CH₃⁺). Isodensity: 6.00 × 10⁻⁵.

CpRuX (X = halogen) complexes can be used to catalyze an array of transformations and are particularly useful for effecting trans-selective hydrogenation and hydrometalation.¹⁰³ The surfaces for CpRuCl highlight its ambiphilic donating and accepting behavior (45). ΔE_orb for the CH₃⁺ and CH₃⁻ probes shows favorable orbital interactions at the metal, being −87 kcal mol⁻¹ and ∼−60 kcal mol⁻¹, respectively. ΔE_elec for CH₃⁺ demonstrates unfavorable interactions (∼7 kcal mol⁻¹), stemming from the electropositive metal. CH₃⁻ interacts favorably at −27 kcal mol⁻¹. Favorable ΔE_orb and unfavorable ΔE_elec indicate charge donation from the metal to the probe. Favorable ΔE_orb and ΔE_elec suggest donation from the probe to the metal indicating that the complex is a stronger donor than acceptor. These results are further corroborated by comparing surfaces constructed from NBO charge transfer values, which give charge transfers of ∼−0.8e with CH₃⁺ and ∼+0.5e with CH₃⁻ (Fig. 9b).

Endohedral fullerenes & host guest effects

Endohedral fullerenes were also investigated to uncover the electronic influence of the guest on the C₆₀ surface (Fig. 9c). With a CH₃⁺ probe, the interaction is strongest at the 6-membered rings, comprising mostly ΔE_orb. With an H₂O guest (47), the C₆₀ surface becomes polarized, which is mostly attributed to a change in ΔE_elec induced by the H₂O dipole moment. With a Li⁺ guest (48), the probe interaction is substantially weakened uniformly throughout. ΔE_elec becomes highly repulsive with minor reduction in ΔE_orb while the symmetry of the surface remains unchanged. The scale is adjusted for Li⁺@C₆₀ (48) to provide contrast. The IMIP surfaces readily convey the effects of guests on the C₆₀ electronic structure.

Conclusions

In this investigation, the development and application of IMIP maps towards rationalizing reactivity and intermolecular interactions for a variety of systems in an intuitive way has been presented that is not readily achieved through other surface analyses. Within cation–π interactions, the surfaces demonstrate the ring center to be the site of maximum interaction, controlled by ΔE_elec. They also reveal that for alkali metals, the reduction in the interaction along a periodic group is attributed to a decreasing orbital interaction. With transition metal probe examples including Zn²⁺ and Ag⁺, the interaction positional preference is shifted off-center on account of favorable π-bonding as indicated in ΔE_orb.

The IMIP maps revealed unique positional preferences in anion–π interactions with halide probes. In C₆F₆, the positional preference is for the π bonds as revealed by the ΔE_orb surface using an F⁻ probe, whereas larger halide probes exhibit preferential binding at the center on account of weaker π bonding interactions. The preference shifts for the triazines and stronger π-withdrawing groups.

EAS and NAS reactivity and selectivity were readily demonstrated from analysis of the surfaces with a CH₃⁺ probe. The ortho/para selectivity was clearly highlighted from π-donating groups to halogens, which is reflected by ΔE_orb, with ΔE_elec modulating the level of activation from benzene. Selectivity for multiply substituted rings can be predicted from the inspection of the ΔE_int and ΔE_orb surfaces. Similar predictions can be made for more complex heteroaromatics including pyrrole and substituted indoles. Strong correlation between ΔE_int and σ⁺ was demonstrated which is dominated by ΔE_orb with lower correlation with ΔE_elec.

The origins of positional preferences in weaker π–π type interactions were revealed through inspections of the IMIP surfaces using a C₆H₆ probe. The preference for the slipped-stack arrangement was shown to be determined by reduced ΔE_exp–rep despite all favorable interactions favoring direct stacking, including the most favorable term, ΔE_disp–corr. The C₆F₆⋯C₆H₆ interaction still favored a slipped-stack arrangement, but shifted closer to direct stacking largely driven by reduced ΔE_ex–rep interactions. More complex π interactions were also probed in quinine.

Furthermore, Lewis acid activation on acrolein was inspected using a CH₃⁻ probe which revealed enhanced reactivity and enhanced site selectivity at the β carbon driven by ΔE_orb. Interestingly, while it is shown that BF₃ is more activating than BH₃, the increased activation is electrostatic in origin as BH₃ enhances ΔE_orb more than BF₃. Insight into interactions involved in select organometallics, endohedral fullerenes, and an EDA complex were also gained through the analysis of the IMIP surfaces.

The demonstrations of the utility of IMIP surfaces for the interactions discussed here are just a small subset of their potential applications. We predict these surfaces to have broader applicability and work into expanding their utility is ongoing.

Author contributions

A. K. and W. Z. contributed equally to this work. The manuscript was written through contributions of all authors. All authors have approved the final version of the manuscript.

Data availability

The Python code for generating IMIP surfaces has been made accessible at https://github.com/lwolflab/IMIP. All QM calculations were performed using Turbomole 7.7 (https://turbomole.org). Molecular probe scans and xTB-IFF EDA calculations were performed using the xTB package (https://github.com/grimme-lab/xtb). Multiwfn 3.8 (https://sobereva.com/multiwfn/) was used for extracting electron densities. All visualization was done using Ovito (https://ovito.org). Computational data including detailed methods, additional IMIP surfaces images, plots, tables, molecular Cartesian coordinates, and field files are available in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful for partial financial support from the National Science Foundation (CHE-2305006). The authors thank the Massachusetts Green High-Performance Computing Center (MGHPCC) and the MIT SuperCloud and Lincoln Laboratory Supercomputing Center for providing computational resources.

Notes and references

1. M. Orozco and F. J. Luque, J. Comput. Chem., 1993, 14, 587–602.
2. E. B. Wilson, Jr., J. Chem. Phys., 1962, 36, 2232–2233.
3. J. S. Murray and P. Politzer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 153–163.
4. C. H. Suresh, G. S. Remya and P. K. Anjalikrishna, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1601.
5. F. J. Luque and M. Orozco, J. Comput. Chem., 1998, 19, 866–881.
6. D. Escudero, A. Frontera, D. Quiñonero, A. Costa, P. Ballester and P. M. Deyà, J. Chem. Theory Comput., 2007, 3, 2098–2107.
7. C. Estarellas, A. Frontera, D. Quiñonero and P. M. Deyà, J. Chem. Theory Comput., 2008, 4, 1981–1989.
8. C. Estarellas, A. Bauzá, A. Frontera, D. Quiñonero and P. M. Deyà, Phys. Chem. Chem. Phys., 2011, 13, 5696–5702.
9. T. Brinck and J. H. Stenlid, Adv. Theory Simul., 2019, 2, 1800149.
10. P. Sjoberg, J. S. Murray, T. Brinck and P. Politzer, Can. J. Chem., 1990, 68, 1440–1443.
11. F. A. Bulat, M. Levy and P. Politzer, J. Phys. Chem. A, 2009, 113, 1384–1389.
12. B. Ehresmann, B. Martin, A. H. C. Horn and T. Clark, J. Mol. Model., 2003, 9, 342–347.
13. T. Brinck, P. Carlqvist and J. H. Stenlid, J. Phys. Chem. A, 2016, 120, 10023–10032.
14. J. H. Stenlid, A. J. Johansson and T. Brinck, Crystals, 2017, 7, 222.
15. J. J. Brown and S. L. Cockroft, Chem. Sci., 2013, 4, 1772–1780.
16. M. Liljenberg, T. Brinck, B. Herschend, T. Rein, G. Rockwell and M. Svensson, J. Org. Chem., 2010, 75, 4696–4705.
17. J. H. Stenlid and T. Brinck, J. Org. Chem., 2017, 82, 3072–3083.
18. J. H. Stenlid and T. Brinck, J. Am. Chem. Soc., 2017, 139, 11012–11015.
19. J. Du, X. Cheng, X. Zhou, M. Shi, G. Jiang and D. Chen, J. Phys. Chem. A, 2024, 128, 9587–9595.
20. R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050.
21. A. Mehmood, S. I. Jones, P. Tao and B. G. Janesko, J. Chem. Inf. Model., 2018, 58, 1836–1846.
22. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
23. R. Laplaza, F. Peccati, R. A. Boto, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-García, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1497.
24. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
25. A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832.
26. P. J. Goodford, J. Med. Chem., 1985, 28, 849–857.
27. D. Hayakawa, N. Sawada, Y. Watanabe and H. Gouda, J. Mol. Graphics Modell., 2020, 96, 107515.
28. D. Hayakawa, Y. Watanabe and H. Gouda, J. Chem. Inf. Model., 2024, 64, 6003–6013.
29. R. D. Cramer, D. E. Patterson and J. D. Bunce, J. Am. Chem. Soc., 1988, 110, 5959–5967.
30. G. Klebe, U. Abraham and T. Mietzner, J. Med. Chem., 1994, 37, 4130–4146.
31. A. F. Zahrt, S. V. Athavale and S. E. Denmark, Chem. Rev., 2020, 120, 1620–1689.
32. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
33. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. Van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
34. Y. J. Franzke, C. Holzer, J. H. Andersen, T. Begušić, F. Bruder, S. Coriani, F. Della Sala, E. Fabiano, D. A. Fedotov, S. Fürst, S. Gillhuber, R. Grotjahn, M. Kaupp, M. Kehry, M. Krstić, F. Mack, S. Majumdar, B. D. Nguyen, S. M. Parker, F. Pauly, A. Pausch, E. Perlt, G. S. Phun, A. Rajabi, D. Rappoport, B. Samal, T. Schrader, M. Sharma, E. Tapavicza, R. S. Treß, V. Voora, A. Wodyński, J. M. Yu, B. Zerulla, F. Furche, C. Hättig, M. Sierka, D. P. Tew and F. Weigend, J. Chem. Theory Comput., 2023, 19, 6859–6890.
35. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493.
36. P. Su, Z. Tang and W. Wu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1460.
37. S. Grimme, C. Bannwarth, E. Caldeweyher, J. Pisarek and A. Hansen, J. Chem. Phys., 2017, 147, 161708.
38. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
39. N. Kumar, S. Saha and G. N. Sastry, Phys. Chem. Chem. Phys., 2021, 23, 8478–8488.
40. J. B. MacQueen, L. M. Le Cam and J. Neyman, Proceedings of the fifth berkeley symposium on mathematical statistics and probability, 1967.
41. Q.-Y. Zhou, J. Park and V. Koltun, arXiv, 2018, preprint DOI:10.48550/arXiv.1801.09847.
42. M. Pauly, In Point primitives for interactive modeling and processing of 3D-geometry, 2003 DOI:10.3929/ethz-a-004612876.
43. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012.
44. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
45. J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215.
46. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
47. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057.
48. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 15122.
49. E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112.
50. E. Caldeweyher, J.-M. Mewes, S. Ehlert and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512.
51. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124.
52. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290.
53. G. Santra and J. M. L. Martin, Molecules, 2022, 27, 141.
54. S. Ehlert, U. Huniar, J. Ning, J. W. Furness, J. Sun, A. D. Kaplan, J. P. Perdew and J. G. Brandenburg, J. Chem. Phys., 2021, 154, 061101.
55. M. Bursch, J.-M. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735.
56. S. Spicher, E. Caldeweyher, A. Hansen and S. Grimme, Phys. Chem. Chem. Phys., 2021, 23, 11635–11648.
57. J. C. Ma and D. A. Dougherty, Chem. Rev., 1997, 97, 1303–1324.
58. D. A. Dougherty, Acc. Chem. Res., 2013, 46, 885–893.
59. J. P. Gallivan and D. A. Dougherty, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9459–9464.
60. A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2013, 113, 2100–2138.
61. R. R. Knowles, S. Lin and E. N. Jacobsen, J. Am. Chem. Soc., 2010, 132, 5030–5032.
62. C. R. Kennedy, S. Lin and E. N. Jacobsen, Angew. Chem., Int. Ed., 2016, 55, 12596–12624.
63. X. Jian Tan, W. Liang Zhu, M. Cui, X. Min Luo, J. De Gu, I. Silman, J. L. Sussman, H. Liang Jiang, R. Yun Ji and K. Xian Chen, Chem. Phys. Lett., 2001, 349, 113–122.
64. W. Zhu, X. Tan, J. Shen, X. Luo, F. Cheng, P. C. Mok, R. Ji, K. Chen and H. Jiang, J. Phys. Chem. A, 2003, 107, 2296–2303.
65. S. E. Wheeler and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 3126–3127.
66. R. K. Raju, J. W. G. Bloom, Y. An and S. E. Wheeler, ChemPhysChem, 2011, 12, 3116–3130.
67. S. E. Wheeler, Acc. Chem. Res., 2013, 46, 1029–1038.
68. D. Vijay and G. N. Sastry, Phys. Chem. Chem. Phys., 2008, 10, 582–590.
69. J. R. Premkumar, D. Vijay and G. N. Sastry, Dalton Trans., 2012, 41, 4965–4975.
70. T. C. Dinadayalane, A. Hassan and J. Leszczynski, Theor. Chem. Acc., 2012, 131, 1131.
71. B. L. Schottel, H. T. Chifotides and K. R. Dunbar, Chem. Soc. Rev., 2008, 37, 68–83.
72. Y. Zhao, Y. Cotelle, L. Liu, J. López-Andarias, A.-B. Bornhof, M. Akamatsu, N. Sakai and S. Matile, Acc. Chem. Res., 2018, 51, 2255–2263.
73. D.-X. Wang and M.-X. Wang, Acc. Chem. Res., 2020, 53, 1364–1380.
74. K. Hiraoka, S. Mizuse and S. Yamabe, J. Phys. Chem., 1987, 91, 5294–5297.
75. K. Hiraoka, S. Mizuse and S. Yamabe, J. Chem. Phys., 1987, 86, 4102–4105.
76. D. Quiñonero, C. Garau, C. Rotger, A. Frontera, P. Ballester, A. Costa and P. M. Deyà, Angew. Chem., Int. Ed., 2002, 41, 3389–3392.
77. D. Quiñonero, C. Garau, A. Frontera, P. Ballester, A. Costa and P. M. Deyà, Chem. Phys. Lett., 2002, 359, 486–492.
78. I. Alkorta, I. Rozas and J. Elguero, J. Am. Chem. Soc., 2002, 124, 8593–8598.
79. B. Han, J. Lu and J. K. Kochi, Cryst. Growth Des., 2008, 8, 1327–1334.
80. M. Mascal, A. Armstrong and M. D. Bartberger, J. Am. Chem. Soc., 2002, 124, 6274–6276.
81. T. X. Carroll, T. D. Thomas, H. Bergersen and K. J. Børve, J. Org. Chem., 2006, 71, 1961–1968.
82. K. Fukui, Science, 1982, 218, 747–754.
83. R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1982, 21, 711–724.
84. G. Klopman, J. Am. Chem. Soc., 1968, 90, 223–234.
85. C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195.
86. B. Galabov, S. Ilieva, D. Cheshmedzhieva, V. Nikolova, V. A. Popov, B. Hadjieva and H. F. Schaefer, ACS Omega, 2022, 7, 8199–8208.
87. G. A. Olah, S. J. Kuhn and S. H. Flood, J. Am. Chem. Soc., 1961, 83, 4571–4580.
88. L. M. Stock and H. C. Brown, in Advances in Physical Organic Chemistry, ed. V. Gold, Academic Press, 1963, vol. 1, pp. 35–154.
89. P. W. Robertson, P. B. D. De La Mare and B. E. Swedlund, J. Chem. Soc., 1953, 782–788.
90. L. M. Stock and H. C. Brown, J. Am. Chem. Soc., 1960, 82, 1942–1947.
91. J. G. Hoggett, Nitration and Aromatic Reactivity, Cambridge University Press, 1971.
92. B. Kempf, N. Hampel, A. R. Ofial and H. Mayr, Chem. – Eur. J., 2003, 9, 2209–2218.
93. S. Lakhdar, M. Westermaier, F. Terrier, R. Goumont, T. Boubaker, A. R. Ofial and H. Mayr, J. Org. Chem., 2006, 71, 9088–9095.
94. N. Roué, T. Delahaigue and R. R. Barret, Heterocycles, 1996, 43, 263.
95. K. Błaziak, W. Danikiewicz and M. Mąkosza, J. Am. Chem. Soc., 2016, 138, 7276–7281.
96. K. Carter-Fenk and J. M. Herbert, Chem. Sci., 2020, 11, 6758–6765.
97. K. Carter-Fenk and J. M. Herbert, Phys. Chem. Chem. Phys., 2020, 22, 24870–24886.
98. L. J. Duarte, W. E. Richter, R. E. Bruns and P. L. A. Popelier, J. Phys. Chem. A, 2021, 125, 8615–8625.
99. A. Thayyil and P. C. Parambil, ChemPhysChem, 2023, 24, e202200761.
100. G. E. M. Crisenza, D. Mazzarella and P. Melchiorre, J. Am. Chem. Soc., 2020, 142, 5461–5476.
101. F. Delbecq and C. Lapouge, Organometallics, 2000, 19, 2716–2723.
102. N. Vicart, B. Cazes and J. Goré, Tetrahedron Lett., 1995, 36, 535–538.
103. A. Fürstner, J. Am. Chem. Soc., 2019, 141, 11–24.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03237c

‡ These authors contributed equally to this work.

---