Open Access Article
Open Access ArticleA critical review on Li-ion transport, chemistry and structure of ceramic–polymer composite electrolytes for solid state batteries†
Sara Catherine
Sand
 a,
Jennifer L. M.
Rupp
a,
Jennifer L. M.
Rupp
 *abcd and
Bilge
Yildiz
*abcd and
Bilge
Yildiz
 *ae
*ae
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: jrupp@tum.de; byildiz@mit.edu
bDepartment of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
cDepartment of Chemistry, Technical University of Munich, München, Germany
dTUM.int. Energy Research, 85748 Garching, Germany
eDepartment of Nuclear Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 18th November 2024
Abstract
In the transition to safer, more energy-dense solid state batteries, polymer–ceramic composite electrolytes may offer a potential route to achieve simultaneously high Li-ion conductivity and enhanced mechanical stability. Despite numerous studies on the polymer–ceramic composite electrolytes, disagreements persist on whether the polymer or the ceramic is positively impacted in their constituent ionic conductivity for such composite electrolytes, and even whether the interface is a blocking layer or a highly conductive lithium ion path. This lack of understanding limits the design of effective composite solid electrolytes. By thorough and critical analysis of the data collected in the field over the last three decades, we present arguments for lithium conduction through the bulk of the polymer, ceramic, or their interface. From this analysis, we can conclude that the unexpectedly high conductivity reported for some ceramic–polymer composites cannot be accounted for by the ceramic phase alone. There is evidence to support the theory that the Li-ion conductivity in the polymer phase increases along this interface in contact with the ceramic. The potential mechanisms for this include increased free volume, decreased crystallinity, and modulated Lewis acid–base effects in the polymer, with the former two to be the more likely mechanisms. Future work in this field requires understanding these factors more quantitatively, and tuning of the ceramic surface chemistry and morphology in order to obtain targeted structural modifications in the polymer phase.
1. Introduction
Solid state battery (SSB) electrolytes offer the possibility for high density and safe energy storage as compared to traditional liquid-electrolytes in Li-ion batteries (LIBs). By nature, solid state Li-ion electrolytes are non-flammable but also are more chemically stable and improve battery safety. They often reduce shuttling of other “cross-over” ions in the electrolyte which ultimately increases efficiency.1,2 Some solid state electrolyte chemistries have shown lithium dendrite suppression, indicating that they have the potential for stable operation with lithium metal anodes, which could increase gravimetric energy density by 35%.3,4 Current research on solid state electrolytes typically investigates two primary classes of materials—polymer-lithium salt matrices and ceramic electrolytes—which each have benefits and drawbacks.Ceramic electrolytes have the benefit of having relatively high ionic conductivities, with sulfide materials such as Li10GeP2S12 (LGPS) reaching about 10−2 S cm−1 at room temperature, and oxide materials such as Li7La3Zr2O12 [LLZO] and LLTO (LiLaTiO4) reaching 10−3 and 10−4 S cm−1, respectively.1,4,5 Additionally, ceramics are single-ion conductors, with several, including LLZO and LLTO, having transference numbers very close to unity.6–8 Several ceramic electrolytes, including Li-garnet-type oxides [LLZO] and LixPOyNz [LiPON], have an electrochemical stability window sufficient to operate with lithium metal and have practically been shown to operate with high voltage cathodes.1,9,10 The relatively high shear modulus of ceramics compared to polymers allows them to be more resistant against lithium dendrite formation,11 although other factors such as imperfect contact or electronic conductivity at grain boundaries must be also addressed. Despite these benefits, ceramic electrolytes tend to be brittle with Young's moduli ranging up to 140–200 GPa in oxide-based lithium-conducting solids, causing delamination of the electrode from the electrolyte surface or even cracking as the electrodes expand and contract during cycling.1,3,12,13 Ceramics tend to form interfacial chemistries that can either benefit through stable sub-oxide formation,14 or that can lead to more resistive interfaces.15–17 Lastly, ceramics are typically more difficult and expensive to fabricate, when compared with either liquid or polymer electrolytes, with the exception of some sulfide synthesis techniques.5 Ceramics often require high fabrication temperatures ranging from approximately 500 to 700 °C for crystalline thin films or over 1000 °C for pellets and tapes to assure crystallization and densification.18–22 Despite these challenges, the ionic conductivity approaching those of liquid electrolytes, and their electrochemical stability with lithium make ceramics of particular interest for SSBs.18,23,24
Polymer-lithium salt matrices are another major class of materials as solid electrolytes. Polyethylene oxide [PEO], polyacrylonitrile [PAN], and polyvinylidene fluoride [PVDF] are the most prominently used polymers for these applications with the addition of lithium salts such as LiClO4 or LiTFSI.1,25,26 The ionic conductivities of polymer electrolytes remain relatively low, with values around 10−7–10−5 S cm−1 at room temperature.27,28 Unfortunately, polymer electrolytes are also generally not single ion conductors with the anion of the lithium salt typically being conducted at similar rates to that of the lithium ion, having transference numbers close to 0.5.12 In contrast to the ceramic electrolytes, mechanical flexibility of the polymer electrolytes is their key advantage and allow them to tolerate the expansion and contraction of the electrodes without delamination or cracking. Due to the viscoelastic nature of these polymer materials, a direct numerical comparison of their moduli to that of ceramics is not possible, but the Young's storage modulus does not typically exceed 1 GPa.12,29 Understanding how the viscoelasticity of the polymers impacts both the electrode contact and the dendrite propagation during cycling is an open area of research.30 At the same time, the low shear modulus, with the shear storage modulus ranging between 0.1 and 1 GPa, presents a challenge, as the polymer electrolytes appear to have less ability to deter Li-dendrite formation.2,31,32 Electrochemical stability windows are difficult to compare between the classes of electrolytes as they can vary significantly particularly among ceramic materials. While oxidation potentials are often improved for polymer electrolytes over ceramics, with PEO:LiTFSi being 4.77 V as compared to LLZO 2.91 V or LATP 4.21 V, reduction potentials are less clear: PEO:LiTFSi being 1.2 V, LLZO being 0.05 V, and LATP being 2.17 V.33,34 However, a clear advantage of polymer electrolytes is that, they are nearly as simple to fabricate as liquid electrolytes, because they can be produced through solution-based processing with a low-temperature drying below 100 °C. We summarize typical ionic conductivity values of polymer and ceramic electrolytes in Table 1.
| Material class | Material | Conductivity at RT (S cm−1) | Ref. |
|---|---|---|---|
| Ceramic | LLZO | 3 × 10−5–3 × 10−4 | 35–37 |
| LLTO | 4 × 10−5–9 × 10−4 | 35,38,39 | |
| LATP | 3 × 10−6–7 × 10−4 | 35,40,41 | |
| LGPS | 2 × 10−3–2 × 10−2 | 5,42 | |
| LRAP | 1 × 10−2–1 − 10−1 | 5,43 | |
| Polymer | PEO:LiTFSI | 6 × 10−6–2 × 10−5 | 44,45 |
| PAN:LiClO4 | 3 × 10−7–6 × 10−6 | 46,47 | |
| PVDF:LiClO4 | 6 × 10−5–4 × 10−4 | 27,48 |
Polymer–ceramic composite solid electrolytes have been explored as a material class to leverage the advantages of each phase – high ionic conductivity of the ceramic and the mechanical flexibility of the polymer. However, composites have shown unexpectedly high ionic conductivity in experiments, with conductivity increasing by an order of magnitude with the ceramic fraction being below the percolation threshold or with non-lithium conducting ceramics. The reasons for such high conductivity in polymer–ceramic composites are currently under debate and benefit from further discussion.27,49–51
Composite solid electrolytes have been fabricated using inert—non-lithium conducting—and active—lithium conducting—ceramic fillers in structures ranging from nanoparticles to wires and aerogels.46,50 Such composite Li-ion electrolytes have been able to reach high ionic conductivities, often up to 10−4 S cm−1 and in one study up to 10−3 S cm−1.27 The achieved ionic conductivities were much higher than can be expected based on volume fraction of each phase; typically with less than 20 vol% of the ceramic filler phase, which allows them to maintain much of the good interfacial contact of polymer electrolyte with cathode or anode.52 For example, Sivaraj et al. combined 30 wt%, or approximately 20 vol% of LLTO with PVDF polymer electrolyte.27 If each phase carries bulk-like conductivity values in this composite (as we have calculated by the values given in this paper), then the composite Li-ion conductivity would be 1 × 10−4 S cm−1, calculated as a weighted average of the conductivity of the two materials based on volume fractions. However, the measured conductivity was more than one order of magnitude greater, 2.7 × 10−3 S cm−1.27 The non-linear dependence of Li-ion conductivity on ceramic filler fraction in such composite electrolytes is intriguing. Despite research on polymer–ceramic Li-composite electrolytes for three decades, the primary conduction pathway or structural interface characteristics in such composites is still not proven.
Beyond these conductivity results, there have been other promising results with initial implementation into full batteries. Several works have implemented these materials composite electrolytes into full battery cells, most commonly using LiFePO4 and Li metal electrodes. While these have not been significantly optimized with thickness of electrolyte or amount of active material, promising capacity and cyclability have been demonstrated. For example, Cheng et al. fabricated electrolytes of PEO:LiClO4 with dispersed Li6.4La3Zr1.4Ta0.6O12 (LLZTO) and achieved a specific capacity of 140 mA h g−1 and retain 83% of this capacity over 500 cycles at 60 °C.4 Similarly, Li et al. found that when LATP nanowires were added to a PEO:LiTFSI electrolyte they improved capacity retention from approximately 65% with the polymer alone to 99.5% for the composite over 100 cycles.53 They theorize that the nanofibers assisted in stabilizing the PEO but the exact mechanism of this effect has not been established. More cycling data is presented in Table S1 (ESI†).54–61 The majority of studies on composite electrolytes have thickness on approximate of 100 μm.48,62–65 Recent approximation of solid-state battery with Li metal anode could achieve an energy density of 350 W h kg−1 (slightly higher than commercial energy density) with an solid electrolyte of approximately 25 μm.66 This thickness should be achievable through standard cast methods of many of these studies, but more work is necessary to determine capacity and cycling with thicknesses optimization. Not only has the thickness of the electrolyte not been optimized but the cells precented have large excess of lithium. Therefore, beyond the conductivity questions on which this review will focus, there remain several other questions as to the optimization of the composite electrolytes for stability with the electrodes, dendrite suppression, and energy density.
In spite of these promising cycling results, many questions remain about composite electrolytes with electrode stability and dendrite penetration. For example, we do not fully understand how dispersed ceramic particles of a reduced electrochemical stability window compared to the polymer matrix impacts the composite's stability window. Additionally, the varying mechanical properties of the polymer and ceramic raises many questions: whether good contact can be maintained due to the polymer, whether the high shear modulus of the ceramic can reduce dendrite growth is helpful in a composite, and whether the interface between the two phases can be a point for dendrite propagation. More knowledge is required to know the limits of these materials.
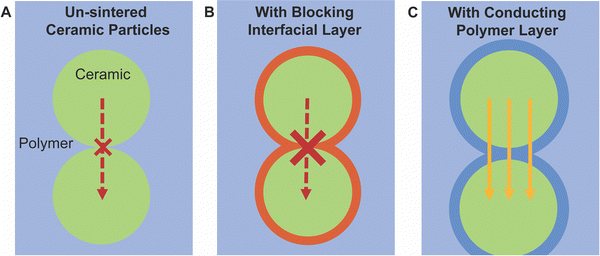
Identification of the primary conduction mechanism and the modification of the materials at the interface will assist in knowledgeable optimization of conductivity with consideration of the other properties required. In general, three possible main conduction pathways have been proposed in such composites as seen in Fig. 1: (i) through the polymer phase, (ii) through the ceramic phase, (iii) along the interface between the two constituent phases. Additionally, a combination of multiple pathways may be significant, with polymers perhaps bridging conduction between ceramic particles. We will consider both questions: which is the primary ionic conduction pathway, and which pathway is the primarily modified phase when put in the composite? In our review, we focus on the potential mechanisms that can give rise to changes in either phase or at the interface, and their dependence on the material chemistry and structure.
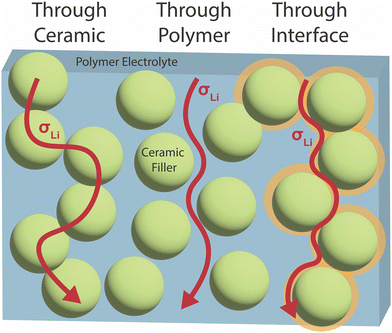 | ||
| Fig. 1 Three possible Li ion conduction pathways have been proposed in polymer–ceramic composite electrolytes: through the polymer phase, through the ceramic phase, or through an interfacial region between the two phases. There is also the potential for ion conduction through a combination of these pathways.52 | ||
2. Composite electrolyte microstructures
2.1. Scope of this review
Before beginning our discussion, we will first define its scope, due to the many parameters to analyze in this field. For our analysis of the field, particularly our statistical analysis as shown in Fig. 2 and 3, we will limit the scope in four ways. First, we have set a cutoff at a maximum of 60 vol% of ceramic phase in the polymer–ceramic composite as composites with higher ceramic phase fraction have a more clear conduction pathway (i.e. defined primarily by the ceramic), and do not benefit from the mechanical properties of the polymer. Second, we will discuss “active” fillers as lithium conducting ceramics in contrast to “inert” fillers that are non-lithium conducting. Because active fillers can have a wide range of conductivities, we categorize all lithium-containing ceramics of a composite to be so-called “active” fillers, even if only minorly ion conducting.67 Third, we do not consider composites, which include gel-type polymer electrolytes with liquid electrolyte, or composites with polymers that contain additional plasticizers, as these often make it more difficult to understand the direct impact of the ceramic filler.68 Such gel-type or plasticized polymer electrolytes may additionally behave more as viscous liquids or still contain flammable liquid electrolyte, limiting their benefits as compared to more rigid, solid electrolytes.68 Lastly, layered structures of ceramic sandwiched between polymer will be discussed in terms of their contribution to understanding the interface, but they are not included in the conductivity data of the field as shown in Fig. 2 and 3 because the conductivity measured is highly dependent on thickness of each layer and there is only one possible pathway through the material.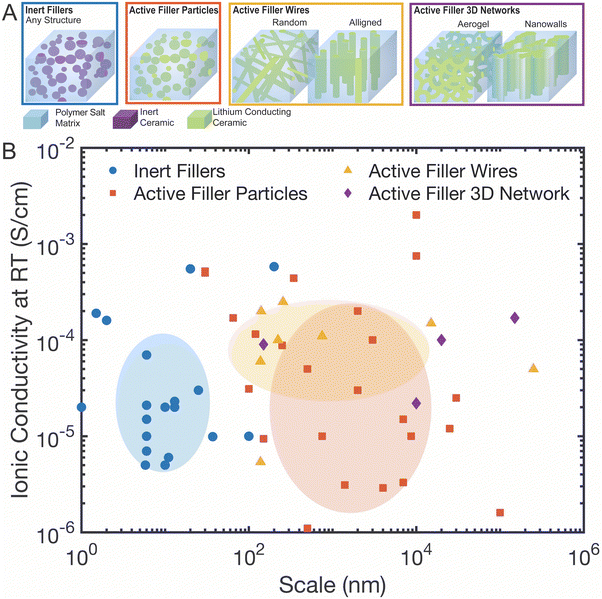 | ||
| Fig. 2 (A) Categories of composite electrolytes as used in 2b and Fig. 3: inert fillers, active filler particles, active filler wires, and active filler 3D networks (B) the ionic conductivity observed in various studies as compared to the scale of the dimensions of the nanoparticle, nanowire, or other structures used. The positions and sizes of the shaded circles are based on average values and standard deviation for that category of the scale and conductivities, respectively. These values are presented in Table 2. This is not displayed for active filler 3D networks as there are only four studies to consider in this category. These structures are split into four categories as illustrated in Fig. 2A. References for this figure are in Table S2 (ESI†). | ||
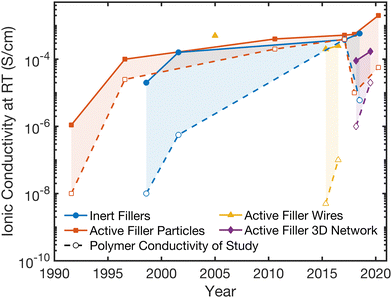 | ||
| Fig. 3 Tracking of record composite electrolyte conductivities in each category and presenting the corresponding conductivity of the polymer electrolyte alone which was used in that study. The solid lines represent the record conductivity values over the years for each of the four composite categories, while the dashed lines show the polymer electrolyte conductivity alone that was shown in that study (if presented in the study).27,28,48–50,64,69–77 | ||
2.2. Categories of composite electrolytes
A wide range of composite polymer–ceramic electrolytes have been fabricated over the past three decades. In Fig. 2A, we illustrate four categories of polymer–ceramic composite electrolytes: (i) inert fillers of any structure, (ii) active filler particles, (iii) active filler wires, either random or aligned, and (iv) active filler three-dimensional connected structures. Here the term filler always refers to the ceramic phase in the composite.Inert fillers are classified as any ceramic material that is not Li-ion conducting, primarily Al2O3, SiO2, and TiO2 dispersed in a polymer salt matrix. These can provide an interesting reference as they eliminate the possibility for ion conduction through the ceramic phase. In contrast, active filler particles are randomly dispersed Li-ion conducting ceramic particles within the polymer ceramic matrix. These include a wide range of lithium conductors but have been primarily the following: LiAl2O, LATP, LAGP, LLZO, and LLTO. Depending on volume fraction and percolation level, these active filler particles represent a potential additional pathway for Li-ion conduction. The majority of studies discuss active filler particles randomly dispersed in the polymer matrix.27,63 Several recent studies have explored the use of active filler wires in the polymer matrix and even more complex 3D-structures including nanowalls—vertically aligned, roughly planar surfaces of ceramic materials—and aerogels.
2.3. Filler characteristic size can impact the Li ion conductivity of the composite
In this field, so many properties—polymer chemistry, ceramic chemistry, filler size and structure, ceramic fabrication method—vary between studies that comparison across the field is difficult. We analyzed over 70 studies in order to understand what parameters have the largest impact on ionic conductivity (all of the found studies that meet the scope of our analysis are listed in Table S2 with details, ESI†).78–91 In Fig. 2B, we plotted all of the conductivity values of these studies against the size of the nanoparticles, nanowires, or 3D structure.‡ The ovals shown represent different types of fillers, and are centered at the average values and have radii of the standard deviation values for both the length scales and the conductivities. The averages and standard deviations across all these studies are shown in Table 2. We can quickly see that no one category shows statistically significantly higher conductivity than the others.| Type of ceramic filler in the composite | Average particle or wire diameter (log10(nm)) | Average conductivity (log10(S cm−1)) |
|---|---|---|
| Inert | 1.0 ± 0.6 | −4.7 ± 0.7 |
| Active particles | 3.2 ± 1.0 | −4.7 ± 1.0 |
| Active wires | 2.9 ± 1.2 | −4.1 ± 0.5 |
The length scales of the ceramic particle or wires in these four categories of polymer–ceramic composites can vary widely throughout the field from 10 s of nanometers to several micrometer scale as seen in Fig. 2B. Within individual studies, when looking at inert fillers, it has been shown that ionic conductivity improves much more, when fillers have at least one dimension below 100 nm due to two primary phenomena.92,93 First, smaller dimensional fillers are more readily dispersed between individual chains and disrupt the packing of the chains, increasing the free volume and decreasing the crystallinity in the polymer. Second, when volume fraction is held constant, the increased interface area due to smaller particulate size can increase interfacial effects, such as the Lewis acid–base effect that can allow increased lithium salt dissociation. If there was a strong correlation with filler size and conductivity, we would have expected to see a positive trend line, but none is observed in our analysis of Fig. 2B. Therefore, from this study, we cannot confirm a correlation between a filler size and Li-conductivity within any category of filler type. As we will present later in more detail, this data also shows that the composite conductivities obtained by either active or inert ceramic fillers are not discernibly different on average in the field.
2.4. Composite electrolytes throughout the decades
In Fig. 3, we present the record Li ion conductivity obtained in the past 30 years for the four, previously designated categories in Section 2.2. The dashed lines in this figure present ionic conductivity of the polymer electrolyte used in this composite (if no such data point is shown, the data for the polymer alone was not presented in the study). In each of the four structure categories, the composites show improved ionic conductivity compared to reference samples of polymer electrolyte alone, except in one inert study in which the polymer had 2 percent higher conductivity than the composite.It is important to assess whether the increased conductivity of the composite arises through the improvement of an individual phase. To address this, two key observations can be made from Fig. 3. First, the Li-ion conductivity of the composites and of the polymer reference have been increasing over time, and the improvement in ionic conductivity of the composites largely tracks with the improvement in the conductivity of the polymer electrolyte utilized (though there are exceptions). The trend indicates that while some improvements have been made in the composite structure, many of the benefits may simply originate from an individual phase, the polymer. This correlation concludes that the polymer phase properties are critical for the primary conduction pathway in the composite. Second is that, all the composite conductivities seem to have approached the same order of magnitude in the last five years, regardless of whether the filler ceramic phase is inert or active. This is consistent with the fact that, the ionic conductivities obtained in composites with inert or with active fillers do not differ statistically significantly on average, as noted on Fig. 2B and Table 2. These key observations indicate that, the polymer phase is the component that is being affected and improved in the composite.
2.5. Inert ceramic fillers in polymer improve Li ion conductivity
Research in composite polymer–ceramic electrolytes began in the 80s by utilizing inert alumina particles to improve the mechanical stability and reduce viscoelastic creep in polymer–salt matrices.94 Initially, these studies focused on PEO-NaI electrolytes with Al2O3 particles and PEO-LiClO4 electrolytes containing LiAlO2 particles to show improved cyclability but additionally observed increased ionic conductivity.95,96 In 1998, Scrosati et al. utilized both Al2O3 and TiO2 to optimize ionic conductivity in Li-ion conducting polymers. Subsequent studies in the area of inert fillers continued to study Al2O3, SiO2, TiO2 and even clay, primarily to alter mechanical properties for the composites, but additionally showed improvement in conductivity over the polymer electrolyte alone.73,74,93,97 This trend is well reflected in Fig. 3 and it is widely observed that inert ceramic fillers improve ionic conductivity of ceramic–polymer composites. That is an intriguing conclusion, since the inert ceramic phase itself cannot contribute to Li-ion conduction. Additionally, connected networks of inert fillers as seen in Fig. 4A show some of the highest ionic conductivities, around 5 × 10−4 S cm−1, indicating the importance of a continuous near-interface region.69,98 This has led to the inquiry of potential mechanisms that arise from a change in the polymer structure or chemistry near the interface with the ceramic fillers.75,99,100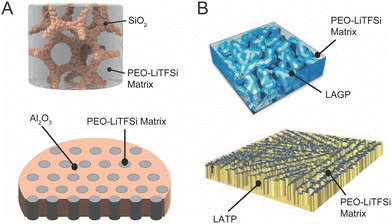 | ||
| Fig. 4 (A) Structures of three dimensional networks of non-lithium conducting inert fillers which can create continuous conduction pathways of modified polymers, reproduced with permission from ref. 98 and 69. B) Three dimensional structures of an active filler aerogel and ice-templated active filler nanowalls which either create fast conduction through the ceramic directly or through direct pathways of modified polymer structure, reproduced with permission from ref. 28 and 64. | ||
2.6. Active Li conducting ceramic filler particles improve Li ion conductivity
Studies of active ceramic filler also began in the early 1990s, although polymers had been used as binders for ceramic ion conductors previously. In 1991, Capuano et al. created one of the first composite materials with lithium conducting fillers for the ceramic phase.50,67 This electrolyte was fabricated through the simple dispersion of γ-LiAlO2 powder (exhibiting a low ionic conductivity of 10−9 S cm−1), with particles on the scale of hundreds of nanometers, in the polymer solution before casting, which resulted in a 3 orders or magnitude increased ionic conductivity around 10−6 S cm−1 at room temperature.50 Due to the low bulk ionic conductivity of γ-LiAlO2 and evidence of suppressed glass transition temperature of the polymer in the composite, the increased ionic conductivity was hypothesized to be due to a modified structure in the polymer. In 1994, Kumar et al. found that with less than 50 vol% Li3N, ionic conductivity of the ceramic–polymer composite could be improved by an order of magnitude over the polymer alone while improving interfacial resistances with electrodes.101,102 In reviewing the field in this study, Kumar et al. stated that the choice between active and passive filler was often quite arbitrary but argued that evidence was starting to support that active fillers were likely preferential for both ionic conductivity and transference number.102 What we are deducing from the data shown in Fig. 2 and 3 is in contrast to this argument. In the last decade, highly Li-conductive fillers such as LATP, LLTO, or LLZO have been studied extensively at concentrations below 60 vol%.27,28,46,49,103–107 These represent most of the data points as seen in Fig. 2B and similarly, Fig. 3 indicates no significant improvement in conductivity introduced by active fillers over inert fillers in the polymer. This lack of difference in the effect of inert or active fillers on average across the field leads us to conclude that the polymer phase is being altered structurally or chemically to provide an improved and dominant conduction pathway in the composite.2.7. Active Li ceramic filler wires create continuous interfacial pathways
In 2005, Wang et al. produced the first composites using ceramic wires and woven matts to reach increased ionic conductivity at around 5 × 10−4 S cm−1 with 20 wt% LLTO in PEO-LiN(SO2CF2CF3)2.77 Unfortunately, this study did not publish the ionic conductivity of polymer electrolyte alone as a reference, making the clarification on the role of constituent phases difficult. A decade later, a major shift occurred in 2015 when the Cui group published a work utilizing active ceramic wires, namely 15 wt% LLTO in a PAN:LiClO4 polymer matrix, and was able to reach a room temperature ionic conductivity of 10−4 S cm−1.49 While this conductivity was not as high as record conductivities for nanoparticle systems (as seen in Fig. 3), the resulting Li-conductivity of the composite in this study is about two orders of magnitude higher than that of nanoparticle dispersions in a polymer keeping ceramic volume fraction and polymer and ceramic chemistries constant.49 Therefore, this was the first clear evidence of the benefits of wires over particles and prompted much more research in a wide range of structures. This benefit is likely because wire type fillers create a continuous pathway of higher conducting polymer along the wire's surface. The wires used in this process were made through electrospinning. This technique was subsequently utilized by several studies including a study by the same research group, which fabricated aligned nanowire composites in 2017, observing improvement in conductivity with more direct pathways along aligned wires.46,106,1082.8. Active Li ceramic filler with a 3D network structure in polymer matrices
The fabrication of 3D networks has greatly expanded in recent years. In the category of inert ceramic fillers, Lin et al. created a silica aerogel that reinforced a PEO electrolyte and Cui et al. fabricated Al2O3 pellets with vertical nanochannels, ranging from 40 to 200 nm in diameter (with concentrations between 34 and 56 vol% of ceramic), into which PEO/LiTFSI was infiltrated.69,98 Xie et al. utilized cellulose as a template to create an LLZO interconnected nanofiber network with diameters under 100 nm,109 while Wang et al. used ice as a template to fabricate vertical, 10 μm-thick, Li1.5Al0.5Ge1.5(PO4)3 [LAGP], wall-like structures,64 as shown in Fig. 4B. Bae et al. made LLTO hydrogel, which was subsequently dried and heat treated before being infiltrated with PEO, resulting in a ceramic interconnected framework, also shown in Fig. 4B.28 Though the precise fabrication procedures of these structures vary, they are typically heat treated to create a sintered 3D structure before infiltrating the polymer.64,110,111 Such sintering is not possible with dispersed ceramic particles in the polymer. We can see that as compared to active filler particles and wires, 3D networks do not show particularly large improvements over the ionic conductivity of their respective polymer reference samples and they do not show the highest overall conductivities in the field. This is inconsistent with our understanding, as seen in inert fillers, that the 3D network can create continuous pathways on conductive, modified polymer material. However, with low volume fraction that are less dispersed, these systems generally have lower ceramic surface area, perhaps decreasing the total, modified polymer volume.3. Discussion of each possible ion conduction pathway and their chemical and structural changes
Within this section, we present the various possible conduction pathways and the arguments for each. Within the first two subsections, we discuss the ceramic and polymer phases in turn and how their structure may be altered by proximity to the polymer–ceramic interface. We will finish this discussion by analyzing the contradictions in the field which argue for either a highly conductive or highly resistive interface.3.1. Why the ceramic phase is unlikely to dominate ion conduction in the composite
As seen in Table 1, the Li-conductivity of ceramic electrolytes are often two orders of magnitude higher than that of polymer electrolytes.64,71 Many studies have not considered, however, the lack of connectivity between the ceramic particles within the composite. We will begin by presenting the arguments for the ceramic being the primary conduction pathway, and continue by presenting evidence to the contrary.Many studies have looked to utilize the percolation pathway of ceramic particles that allow to optimize ionic conductivity of the composite with a fraction of active ceramic filler. The majority of such studies have revealed a non-monotonic, volcano type dependence of conductivity or activation energy on the filler concentration, with the peak of conductivity at 4–20 vol% of ceramic nanoparticles in polymer matrix, as seen in Fig. 5A.27,63,70,112,113 Often this is interpreted as a percolation threshold with additional effects due to increased agglomeration at increased concentration.70,112 Though percolation threshold varies with the dimensions of the system, the percolation threshold for spheres in a 3D network is 15 vol% and 30 vol% in two different studies.114,115 Several studies show a volcano type trend of the conductivity relative to concentrations of phase constituents with values of maximum conductivity at either 2, 6, 10 or 20 vol% of ceramic.27,65,112,113,116 These values at or below the percolation threshold might be explained by agglomeration of the particles as they reach the percolation threshold. However, two studies show a continuous decrease in conductivity with the addition of ceramic particles throughout the whole concentration range, as shown in Fig. 5B.51,103
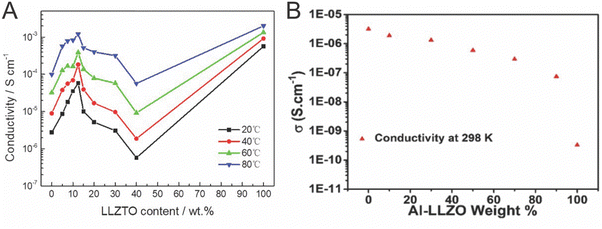 | ||
| Fig. 5 These figures illustrate the variation in conductivity with varying concentrations of conductive ceramic fillers. (A) Lu et al. provides evidence of a volcano like behavior with the addition of LLZTO and compares with the conductivity of a sintered pellet (100%), reproduced with permission from ref. 117. (B) Waidha et al. did a similar study but found a continuous decrease in conductivity with the addition, with 100% being a non-sintered pellet, illustrating that with a small addition of polymer in the ceramic pellet, the polymer could bridge conduction between particles, reproduced with permission from ref. 51. | ||
Additionally, the arguments considered for more connected and sintered networks cannot so simply be applied to dispersed particle systems. Generally, bulk ceramic electrolytes must be sintered in order to gain grain-connectivity in densification and minimize surface energy to form successful neck growth at the grains interfaces. Because the active filler particles have not been sintered to have enough connection, a percolation pathway through modified polymer structure affecting the conductivity is more likely to dominate rather than through the ceramic pathway with connection bottle-necks. The polymer must act at least as a conducting bridge between ceramic nanoparticles. Two recent papers have provided evidence to this point. Waidha et al. utilized non-sintered ceramic particles as their comparison to their composite electrolytes, as seen in Fig. 5A.51 They found that when a small amount of polymer electrolyte was added to a green pellet (non sintered pellet, creating 90 wt% LLZO), the conductivity increased by two orders of magnitude and reduced the activation energy by approximately 0.5 eV, as shown in Fig. 5B. Chen et al. showed the same effect in Li ion conductivity by coating ceramic particles in a conjugated polymer layer, which reduced grain boundary resistance between ceramic particles and increased ionic conductivity.118 The authors provide NMR data and DFT calculations to support the conclusion that lithium ions are transferring between the ceramic and the polymer phases. These studies argue for a conduction pathway through ceramic particles with polymer bridges between these non-sintered particles, as we have illustrated in Fig. 6.
Our analysis of the field has determined that there is no appreciable difference in the Li ion conductivity between composites with inert and with active fillers. However, some individual studies have shown a more increased conductivity with active fillers, but these studies were not well-controlled keeping all other factors the same. For example, Choi et al. showed that while dispersed Al2O3 particles improved ionic conductivity of a PEO–LiClO4 matrix by roughly one order of magnitude, LLZO increased the over-all ionic conductivity of the composite by two orders of magnitude.113 However, this study did not keep particle size consistent between the Al2O3 (approximately 100 nm diameter) and LLZO (between 500 and 1000 nm diameter). Even though the weight fraction was held constant, this results in a higher volume fraction of Al2O3 as compared to LLZO, making comparison difficult. Wang et al. similarly showed that a one order of magnitude increase between composites with LATP fillers and with inert SiO2 or TiO2 particles with the same weight percent and different particle sizes.63 Based on the limitations of these studies, and the lack of a field-wide variation between inert and active particles as presented in Fig. 2B and 3, this is not a compelling argument for predominant conduction through the ceramic.
In analysis of composite electrolyte conduction, it is often presumed that the conductivity of the ceramic is equivalent to that of the highly optimized and high temperature sintered pellets. However, one should consider the crucial role of processing techniques in developing highly conductive ceramic electrolytes. In general, sintering increases the density of a ceramic and reduces the resistance caused by pores or by imperfect contacts and in some of the phases also assures the high ionic conductive phases. Within wires and connected 3D networks, some high temperature treatments are possible, for example Liu et al. calcined their LLTO nanowires at 800 °C for 2 hours and Wang et al. sintered their LAGP nano walls at 800 °C for 5 hours.46,64 However, this high temperature processing does not guarantee that the conductivity is as high as optimized bulk conductivity. Generally, it should not be presumed that low temperature synthesized or nanowire/nanowall structures have comparable Li conductivity to a microcrystalline and high temperature sintered ceramic pellet. In dispersed ceramic particles within polymer matrices, even when a percolation threshold is reached remain loose as such. Hence, the ionic conductivity within each particle may be similar to that of single grain contributions in a bulk sample, but the overall composite likely has appreciably lower conductivity in the assembly due to unsintered boundaries between particles and missing neck growth. With these considerations, evidence indicates that ceramic particles without neck growth are insufficient to account for the high conductivity in the composite even when they are percolated in the composite electrolytes.
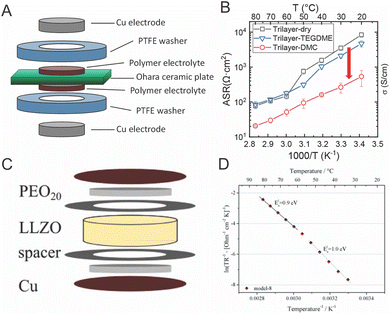
Additionally, given the fact that the percolation is not reached and that particles are typically not sintered, it must be considered that polymers must play a role in bridging ceramic particles if the ceramic were to be an important path for ion conduction. However, several papers have argued that the polymer–ceramic interface is too resistive to allow for such behavior. This conclusion was primarily based on trilayer studies,52,119 which found resistive interfaces between the phases when measuring electrochemical impedance spectroscopy, or based on a continuous decline in conductivity with increasing ceramic content.103 Such a resistive interface would block any possible bridging effects as shown schematically in Fig. 6B. Whether such bridging effects are possible may highly depend on the particular chemistries utilized. Therefore, we will present the theories for such an interface which may block a polymer-bridged ceramic pathway. Namely, Gupta et al. identified two possible chemical variations occurring at or near the surface of the ceramic, when studying layered structures of PEO–LiTFSI and Ta-doped LLZO.52 These layered structures were fabricated by depositing PEO electrolyte on each side of an LLZO pellet, such that the impedance was measured through both phases and their connecting interfaces. The first chemical variation is the formation of a lithium carbonate layer on the surface of the LLZO due to air exposure before deposition of the polymer layers.52 They showed that heat treatment of the LLZO to remove lithium carbonates reduces the interfacial resistance between the LLZO and PEO surface by two orders of magnitude, as illustrated in Fig. 7. The phase change on the surface was confirmed by X-ray diffraction analysis. Although this may be a significant factor when utilizing LLZO fillers, it should be noted that not all ceramic fillers are prone to formation of such secondary phases at their surface when exposed to air.120
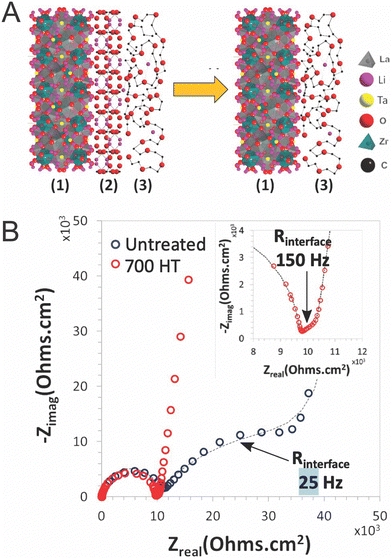 | ||
| Fig. 7 (A) Illustration of interface between LLZTO (1) and PEO–LiTFSI (3) and the reduction of the lithium carbonate impurity layer (2) through heat treatment (B) Nyquist plot of Au|PEO–LiTFSI|LLZTO|PEO–LiTFSI|Au symmetric cell untreated and with a 700 °C heat treatment for removal of lithium carbonate layer and reduction of interfacial resistance, reproduced with permission from ref. 52. | ||
Second, Gupta et al.52 also pointed out that, in their system and in many composite systems, there is significant difference between the lithium concentration between the two phases; i.e., higher in the ceramic phase and low in the polymer phase. The authors proposed that this variation in concentration (and the corresponding lithium chemical potential) could kinetically limit lithium ion diffusion from the ceramic to the polymer. Gupta et al. found that increasing the lithium concentration of the polymer phase could decrease interface resistance by one order of magnitude. For instance, with an ethylene oxide to lithium ion ratio [EO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li+] of 27
Li+] of 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 interfacial resistance was 1.48 kΩ cm−2 and with a ratio of 15
1 interfacial resistance was 1.48 kΩ cm−2 and with a ratio of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 it was 0.44 kΩ cm−2. By making the lithium activity in the polymer phase closer to that in ceramic phase, they were able to limit the effects of ions having to move against a concentration gradient. Both of these effects create more resistive layers and reduce ion conduction across the ceramic–polymer interface. With these considerations, evidence indicates that ceramic particles alone are insufficient to account for the high conductivity in composite electrolytes.
1 it was 0.44 kΩ cm−2. By making the lithium activity in the polymer phase closer to that in ceramic phase, they were able to limit the effects of ions having to move against a concentration gradient. Both of these effects create more resistive layers and reduce ion conduction across the ceramic–polymer interface. With these considerations, evidence indicates that ceramic particles alone are insufficient to account for the high conductivity in composite electrolytes.
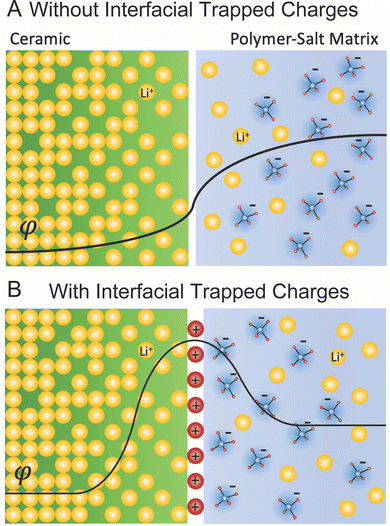
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is constant throughout the material.121 When considering this mechanism for a polymer–ceramic interface in a composite, this can create a delithiated layer in the ceramic—the initially higher lithium concentration phase—and consequently an increased lithiation layer in the polymer. Second, the interface can trap a net charge due to preferential accumulation or depletion of charged species at the interface plane. We have provided the example of positive charges trapped at the interface plane, which create a lithium depletion region on both sides of the interface as illustrated in Fig. 8B. The thickness and concentration variance in these two layers depend on the dielectric constant, the material and phase specific Debye length defining the width of space charge, the concentration of charged species, and the difference in chemical potential within the two materials.121 Debye length in ion conductors depends inversely on the concentration of charge carriers due to screening effects, and it is typically very small (order of nm)123,124 given the high concentration of charge carriers in good ion conductors. It is to be noted that in both examples, Fig. 8A and B, we consider solely the majority lithium ionic carriers, however, those are balanced also by minority electronic carriers (i.e. in the ceramic phase) accordingly. This is rather relevant as it is often the minority electronic carriers in any pure ceramic Li-ionic system that define important properties such as reduction towards lithium and ultimately critical current density.
is constant throughout the material.121 When considering this mechanism for a polymer–ceramic interface in a composite, this can create a delithiated layer in the ceramic—the initially higher lithium concentration phase—and consequently an increased lithiation layer in the polymer. Second, the interface can trap a net charge due to preferential accumulation or depletion of charged species at the interface plane. We have provided the example of positive charges trapped at the interface plane, which create a lithium depletion region on both sides of the interface as illustrated in Fig. 8B. The thickness and concentration variance in these two layers depend on the dielectric constant, the material and phase specific Debye length defining the width of space charge, the concentration of charged species, and the difference in chemical potential within the two materials.121 Debye length in ion conductors depends inversely on the concentration of charge carriers due to screening effects, and it is typically very small (order of nm)123,124 given the high concentration of charge carriers in good ion conductors. It is to be noted that in both examples, Fig. 8A and B, we consider solely the majority lithium ionic carriers, however, those are balanced also by minority electronic carriers (i.e. in the ceramic phase) accordingly. This is rather relevant as it is often the minority electronic carriers in any pure ceramic Li-ionic system that define important properties such as reduction towards lithium and ultimately critical current density.
In attempting to explain highly conductive space charge regions near the ceramic–polymer interface, Li et al. investigated these regions experimentally and computationally with Monte Carlo simulations, but with an inert polymer that did not contain lithium salts as seen in Fig. 9A.125 Therefore, the space charge region was only modeled in the lithium-containing ceramic, LLZO. They found that the ion concentration only varied by a maximum of 70% and only within 5 nm of the interface, as seen in Fig. 9B.125 They argue that the space charge layer model, when combined with a random resistor model, shows good agreement with their experimental results.46,125 However, this 70% increase of Li-ion concentration within a few nanometers is unlikely to account for the orders of magnitude increase in Li ion conductivity seen in other studies.27,46
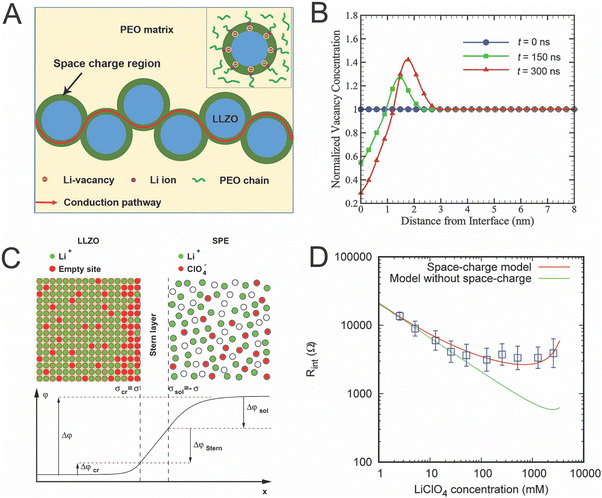 | ||
| Fig. 9 (A) Illustration of the possible conduction pathway through the space charge region in dispersed LLZO particles, as reproduced with permission from ref. 125. (B) Plot of computationally determined this vacancy concentrations as a function of distance from the interface at three different time scales, also reproduced with permission from ref. 125. (C) Illustration of charge carrier concentration at the interface of LLZO as illustrated by Brogioli et al. (D) Experimental data (shown in blue) as compared to computational data of the interfacial resistance between LLZO and PEO/LiClO4 with and without consideration of space charge regions.126 Both (C) and (D) are reproduced with permission from ref. 126. | ||
Alternatively, Brogioli et al. attempted to understand why the interface is highly resistive and investigated the variation in concentration of Li-ion that may be created in both phases with the consideration of a stern, or core, layer between the two materials.126 They calculated that the PEO phase could have nearly two orders of magnitude decrease in concentration of Li-ion while the LLZO only changed by approximately two fold increase or decrease, though both varied with the applied potential. Additionally, based on the values provided in this work, we calculated that the width of the effected region as approximated by the Debye length, would be 2 nm or less for each phase.126 While these two studies had very different assumptions, the space charge regions associated with their samples had similar orders of magnitude in length scales and charge carrier concentration. Ultimately, Brogioli et al. determined that the resistivity originates from the activation energy required to move across the core of the interface directly between the two phases, as the interfacial resistance cannot be accounted for by the space charge layers created. This is shown in Fig. 9D through comparison of their experimental data and computational data which includes consideration of space charge regions and computational data that does not consider space charge regions. Both of these studies show fairly minimal effects of the space charge regions as they are thin and the maximum variation shown is twofold in the LLZO. In either case, the minimal effects seen indicate that space charge regions do not explain the high Li ion conductivities seen in composite electrolytes.
Lastly, Bonilla et al. studied ion redistribution computationally using molecular dynamics and Monte Carlo simulations. They found that the lithium cations and oxygen anions form an amorphous layer on the surface of the garnet.127 On either side of this interface layer with trapped charges, there is a depletion of lithium ions, similar to that shown in Fig. 8B. Surprisingly, they additionally concluded that lithium in the polymer transfers into the garnet while no lithium transfers from the garnet into the polymer. This is contrary to the chemical concentration of Li in both phases. The authors state that this indicates a large energy barrier for diffusion from the ceramic to the polymer and requires further study. Because no explanation is given for this asymmetry and the authors state that it requires further study, this evidence for lithium diffusion into ceramic should be considered preliminary. They did not provide diffusion constant in this amorphous layer on the surface of the garnet, but still concluded that there was reduced diffusion along the interface largely due to the rigidity of the polymer in this layer.
Based on these three studies summarized above, we find no evidence that the presence of space charge layers increases the ionic conductivity along the surface of ceramic or the polymer sufficiently to account for the ionic conductivity of composites. Alternatively, we will present the potential for charge redistribution effects in the polymer more thoroughly in the next section.
3.2. Li-ion conductivity of the polymer–salt matrices increases with proximity to the ceramic fillers
Despite the fact that polymers have significantly lower ionic conductivity, several groups have hypothesized that the polymer is the primary phase being affected in the composite, becoming the primary conduction pathway when put into the composite.49,51,52,92,100 Therefore, whether the polymer is the predominant conduction path hinges on how it is impacted by the presence of the ceramic phase, and whether it increases conductivity sufficiently to become the most significant conduction path.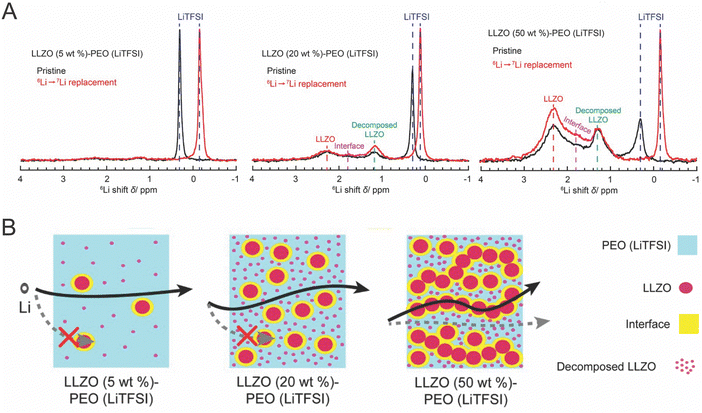 | ||
| Fig. 10 (A) The 6Li I spectra of various concentrations of composite electrolyte in which peaks can be assigned to the ceramic, the interface, decomposed ceramic, and the polymer (B) illustrates the conduction pathway measured for each of these concentrations, reprinted with permission.128 | ||
Croce et al. described these effects for Al2O3 in PEO:LiTFSI and measured that by utilizing more acidic alumina they were able to increase both ionic conductivity and Li transference number, as shown in Fig. 11A and B respectively.99 Similarly, Wang et al. illustrated this mechanism for Al2O3 in a PAN/LiClO4 matrix.132 Surface acid groups, such as protons on the Al2O3 particles’ surface have great affinity for the anions, releasing the lithium cations to be free ions, as we illustrated in Fig. 12A. On the other hand surface basic groups, or the oxygen anions, have electrostatic attraction to the lithium cations, as illustrated in Fig. 12B. Wang et al. theorized that during Li-ion conduction, these weak bonds allow for Li to migrate along the surface of the filler particles,132 but there is no quantification of the O–Li bonds being weak at the interface. While these basic effects were theorized to increase ionic conductivity, it is unlikely that such a thin affected layer, just the very interface plane, would have a substantial impact on the composite electrolyte ionic conductivity unless this was many orders of magnitude more conducting than the surrounding phases. Additionally, there is no reasoning or quantification provided as to why the lithium ions on the surface would be more mobile than those within the polymer. In contrast, Croce et al. showed that composite electrolyte with basic Al2O3 particle surfaces had lower conductivity than neutral Al2O3 particle surfaces, as seen in Fig. 12B, illustrating that basic surface groups attracting lithium ions was not an effective transport mechanism.99
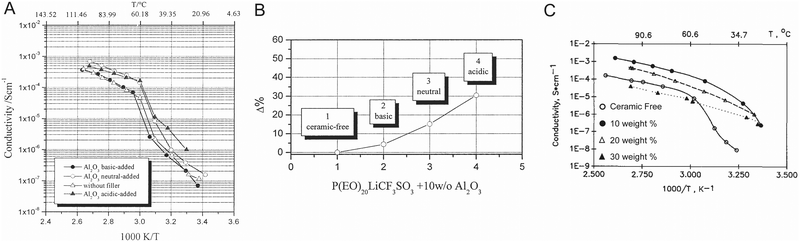 | ||
| Fig. 11 (A) Temperature dependence of Li ion conductivity of PEO:LiCF3SO3 electrolyte containing no filler as well as acidic, basic, and neutral Al2O3 particles, illustrating that acidic surface groups provide more improvement in ionic conductivity due to their increase in lithium salt dissociation (B) change in transference number as compared to ceramic free material for basic, neutral, and acidic Al2O3 particles in PEO-based electrolytes.99 (A) and (B) are both reproduced with permission from ref. 99. (C) Temperature dependence of Li ion conductivity of (PEO)8LiClO4 with γ-LiAlO2 fillers, which illustrates the variation of conductivity of the composite, particularly at low temperatures, as reproduced with permission from ref. 50. | ||
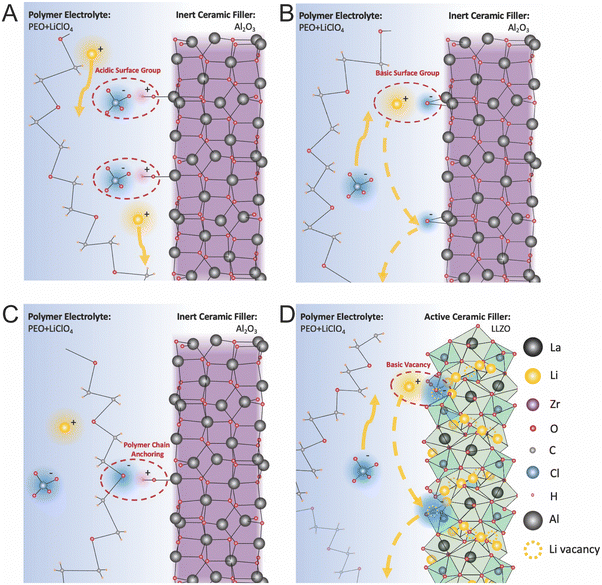 | ||
| Fig. 12 Illustrates the possible chemical interactions at the interface of ceramic fillers and PEO:LiClO4 as an example of a polymer electrolyte. (A) the effect of acidic surface groups on alumina which can pin the anion in the lithium salt and increase both conductivity and transference number (B) basic surface groups can attract lithium ions but the effect on conduction is not well understood. It has been hypothesized only increase movement of the anion or lithium ions may be able to hop along the surface of the alumina.99 However, this would be very thin layer to appreciably impact conductivity and lithium ions may be similarly tightly bound to the surface as to the polymer or even anions. (C) The last possible effect is that charged surface groups may pin the polymer chain which may additionally prevent polymer rearrangement and increase free volume and decrease crystallinity. For example, the electronegative oxygen in PEO can be attracted to an acidic surface group. (D) Similar effects are possible in active fillers, such as LLZO. It has been hypothesized that lithium vacancies may act as basic groups and could attract lithium ions possibly allowing more anion conductivity or lithium hoping along the surface of the ceramic.106 However, as with the inert fillers, this would be a very thin layer of to produce a large increase in conductivity and is therefore unlikely to have an appreciable effect. | ||
Surface chemistry of the ceramic can also affect the structure of the surrounding polymer. As mentioned previously, polymer chains used in polymer electrolytes, typically have a more highly electronegative atom in the polymer chain in order to assist in lithium salt dissolution. This electronegative atom, oxygen in the case of PEO in Fig. 12C, can be attracted to acidic surface groups, creating anchor points of the polymer on the surface of the ceramic and limiting the polymer's ability to rearrange. Croce et al. describes how these anchor points can prevent polymer chains from rearranging, and but also creating a more disordered polymer structure with more free volume near the interface.99 While this could result in a more rigid polymer chain at the interface, the increased disorder and free volume could still result in higher Li ion conductivity.
Unfortunately, the Lewis acid–base theory for conducting ceramic fillers has been less thoroughly described for other metal oxide ceramics than for alumina specifically. However, Sivaraj et al. hypothesizes that these effects are the mechanism through which their PVDF-LiClO4 matrix with dispersed LLTO particles reached an ionic conductivity of 2 × 10−3 S cm−1.27 This study utilized density functional theory calculations to track the changes in bonding in the polymer matrix with and without LLTO, and to analyze infrared spectra. These calculations showed that without the LLTO filler, the lithium ion remained bound to the anions with a long Li–O bond within the lithium salt, meaning lithium could not conduct freely. In contrast, with the addition of LLTO to the electrolyte, a PVDF, LLTO, and ClO4 cluster is formed around a central La and created free lithium cations, which consequently improved lithium mobility.27 Yang et al. briefly speculates as to the Lewis acid–base effects of LLZO. LLZO is typically doped with Al or Ta in order to have high lithium vacancy concentrations and to phase stabilize the high ionic conducting polymorphs. As pointed out by Yang et al., these negatively charged vacancy sites could act as strong Lewis base centers.106
With consideration of these two studies, we speculate about several possible mechanisms for Lewis acid–base effects to impact polymer conductivity. We have utilized LLZO ceramics as an example for this structure but the general theory can translate to many active fillers. Possible acidic groups in this structure are Li+, La3+, Zr4+, and O vacancies (with positive charge), which could affect both the polymer structure through anchoring and could bind to anions and dissociate Li ions in the polymer. On the other hand, possible basic groups would include O2− ions and Li+ vacancies (with negative charge). Generally, we can theorize that the charged defects would have higher partial charges and therefore more appreciable effects in the polymer's conductivity.
However, we know that these ions with varied binding strengths within the LLZO structure would likely have varied effects on the surface, which are yet to be quantified.133 Based on this understanding, the high defect concentration in lithium ion conductors would produce either highly acidic or basic surfaces which would more significantly impact the ionic conductivity, perhaps explaining higher conductivity with active fillers rather than inert fillers seen in a few individual studies. However, these speculations require quantification for any conclusions to be made. We must also note that this remains a simplified picture as LLZO readily forms carbonates on its surface, so these possible charged defects in LLZO may not truly be in contact with the polymer.
Several studies have provided data to approximate the thickness and the ionic conductivity of the modified polymer layer as a result of Lewis effects. Zhang et al. fabricated an Al2O3 pellet with 500 nm columnar holes which were filled with polymer electrolyte.69,134,135 They assumed a region of modified polymer near the edges of each column with a thickness that decreases with increasing temperature, following the Vogel–Tammann–Fulcher model, which is used to describe a viscous liquid's behavior with temperature and is similarly used to characterize a polymer's Li ionic conductivity above the glass transition temperature. Non-linear fitting of conductivity's dependence on temperature was applied and no statistics were provided on the accuracy of this fit. The extracted thickness of the modified layer thickness is approximately 5 nm with little dependence on temperature, and the ionic conductivity of this layer is 5 × 10−3 S cm−1, two orders of magnitude higher than the bulk polymer electrolyte alone. In addition to this estimate, we have done calculations of the Debye length for PEO:LiClO4 polymer electrolytes with the relative dielectric constant of 20 and charge carrier concentration of 0.001 mol cm−3, resulting in a Debye length on the order of 0.2 nm.71,126 Therefore, we conclude that Lewis acid–base effects likely occur on nanometer or smaller scales, which means they are likely not the dominant reason in altering the polymer matrix conductivity in the composites.
Two types of changes can take place in the polymer structure when in composite or contact with a ceramic, and increase the conductivity in the polymer. These are the decrease of the overall crystallinity of the polymer, and increase of its free volume.92,100 Here, three possible mechanisms have been discussed for such changes in structure of the polymer: (i) particles may disrupt the packing of the polymers, thus increasing the free volume and decreasing crystallinity, (ii) the presence of particles may block polymer chain rearrangement and therefore decrease the possibility for crystallization kinetically, and (iii) the particles can form cross-linking centers which reduce the packing of the chains, increasing free volume.92,137 Perhaps the largest piece of evidence to confirm the increase in ionic conductivity of the polymer phase is that even when non-conducting filler particles are added to the polymer matrix (as discussed previously in Fig. 2B when comparing inert and active filler), ionic conductivity increases as shown by Croce et al. in 1998, who suggested that fillers kinetically inhibit crystallization.75 The authors showed that activation energy did not increase below the glass transition temperature when inert fillers were added. Capuano et al. confirmed a similar effect with conducting fillers as shown in Fig. 11C.50,75 Lastly, Mohapatra et al. also provided evidence of the reduction of crystallization through differential scanning calorimetry.100 As previously mentioned, Yang et al. performed an NMR study on LLZO wire and PAN–LiClO4 matrix composites in which they observed a shifted PAN peak associated with a modified polymer structure. They approximated the fraction of the modified polymer volume to be 37% of the overall polymer.106 From this value and the overall ionic conductivity, we calculated the thickness of this modified layer to be on the order of 70 nm and have a Li-ion conductivity on the order of 10−4 S cm−1, or 3 orders of magnitude higher than the bulk PAN electrolyte. Because PAN is amorphous regardless of ceramic fillers, this could not be associated with a shift from crystalline to amorphous. This length scale is comparable to the length scales of polymer confinement studied through thin films or through nano gratings. For example, Zhang et al. showed a complete suppression of crystallinity in PEO:LiTFSI matrices in nanogratings of 110 nm,94 and Massa et al. showed non-linear increases in crystal growth rate from in thin films increasing from 10 to 1000 nm.134,135 Both of these studies represent strong evidence that increased free volume and higher amorphous phase fractions in the polymers could be induced in the composites and could substantially impact the ionic conductivity of a polymer–ceramic composite.
Polymer confinement effects have been seen in features on the order of 10–100 nm, several orders of magnitude larger than the relevant length scales for Lewis acid–base effects (0.2–5 nm).134,135 Wang et al. attempts to fit data to calculate a thickness and ionic conductivity.63 However, this study specified the thickness of the modified layer relative the radius of the particle, although various particle sizes were not measured. The thickness of the interfacial layer is calculated to be 1 to 2 times the radius of the particle, meaning a thickness of approximately 100 nm. This corresponds to an ionic conductivity of 2 × 10−4 S cm−1, or two orders of magnitude higher than the bulk nominal polymer. These length scales of structural effects seem reasonable as the radius of gyration of the polymer, or the distance between the two ends of the polymer chain, is typically on the order of 100 nm, if assuming an ideal polymer, and crystallites in PEO are on the order of 100 μm.138 The thickness of both chemical and structural affects are likely dependent on many particular factors—polymer crystallinity, temperature, surface chemistry of fillers, and binding energies. However, we can reasonably conclude that the structural effects occur at much larger length scales compared to the Lewis effects on the polymer, and therefore are more likely to have appreciable effects on Li ion conductivity.
The argument of reduced polymer conductivities in composites have been supported by trilayer studies. Chen et al. and Langer et al. both performed impedance on trilayer samples as shown in Fig. 13.119,141 They showed that the interfacial resistance originated in the polymer near the interface by seeing the dependence of conductivity on the plasticizer addition and temperature. Dougnac et al. and Buvana et al., among others, have theorized that fillers improve ionic conductivity by reducing segmental motion and kinetically reducing packing, and thus allowing more free volume in the final polymer. This theory could rectify the reduced segmental motion seen in neutron scattering, but does not clarify the large interfacial resistance seen in the trilayer study.92,137,142
 | ||
| Fig. 13 (A) Trilayer system studied by Chen et al., as reproduced with permission from ref. 141. (B) Temperature dependence of the resistance of this trilayer system with and without plastizing additives also reproduced with permission from ref. 141. (C) Trilayer system studied by Langer et al.119 (D) Temperature dependence of the interfacial resistance in this trilayer system. Bother (C) and (D) are reproduced with permission from ref. 119. | ||
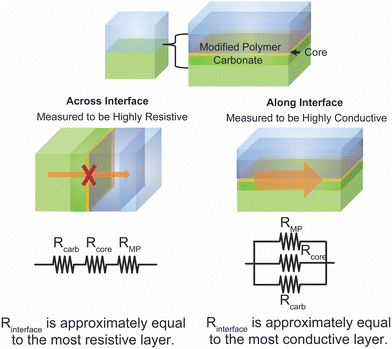
3.3. Resolving the contradictions of a blocking or conductive interface by considering interface layers
As presented in the preceding sections, there is contradiction within literature over whether the polymer–ceramic interfaces represent a highly resistive or highly conductive portion of composite. The contradiction between these two arguments may be resolved through an understanding of the various effects—increased free-volume in the polymer, space charge regions or Lewis acid base effects, core of the interface, and carbonates on some ceramics. Each of these effects impacts different spatial regions at or near the interface as illustrated in Fig. 14. Therefore, when measuring across the interface, the most blocking layer has the dominant effect, as the various layers act as resistors in series. Contrastingly, the most conductive layer has the largest effect when measured along, or in parallel to, the interface. This way the interface could simultaneously have a blocking and a conductive effect in directions both across and parallel to the interface, respectively.Two effects could contribute directly between the two phases that would exemplify this contrast in across versus along configurations: an interfacial core and interfacial contact voids. The interfacial core is a thin layer—approximated on the order of 0.5 to 2 nm depending on the materials—between two phases which, due to these length scales, would require extremely high conductivity to appreciably impact the overall conductivity of a composite.123,126 However, as concluded by Brogioli et al., this layer can be a source of high resistance across the interface (rather than due to space charge layers).126 Similarly, interfacial voids or gaps at the interface can decrease the interfacial contact region and therefore increase interfacial resistance, but may have little impact on the efficiency of the ion conduction pathways parallel to the interface.143
While limited computational studies have been done to model these dispersed particle systems—to our knowledge only two have modeled these systems of dispersed particles with a single interfacial layer, one of which is shown in Fig. 15.144 We have illustrated in Fig. 14 that considering this complex interface as a single layer is inaccurate. The “interface” has several distinct regions either in the ceramic or polymer portion, or directly in between, and considering these distinct regions complementarily in a combined model can resolve contradictions in the field.
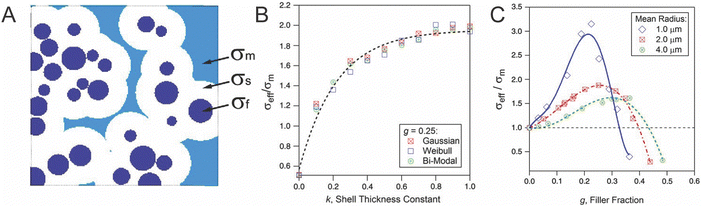 | ||
| Fig. 15 (A) Illustration of conductivity of three regions considered by Kalnaus et al. in which a conductivity was assigned to three portions of the materials: σf of the filler or the ceramic, σm of the matrix or polymer, and σs of the shell or interface (B) dependence on conductivity of the composite over that of the polymer matrix, σeff/σm, on the interfacial thickness with three different distributions of particle size. (C) Dependence of conductivity on filler concentration with three different particle mean sizes through random resistor model.144 These figures are reproduced with permission from ref. 144. | ||
4. Conclusions
With increasing needs for high energy and power density batteries in transportation, the grid, and portable devices, there is a growing need for scalable and high performance solid Li-ion conductors. Composite electrolytes made of ceramic and polymer materials offer the possibility for leveraging both good mechanical properties and high ionic conductivity, but the interactions of the two phases and the resulting effects on Li-ion conductivity are not well understood. In this article, we have critically reviewed how the ceramic and polymer phases could be impacted in such composites as a function of the type of ceramic filler phase, including whether they are inactive (not lithium containing) or active (lithium containing), their structure and characteristic size scale.On a field wide scale, the conductivities obtained in composites that have active ceramic fillers or inert fillers have a wide distribution, and do not differ statistically significantly from each other. There has also been no chemical or structural variation identified in the ceramic phase of a composite that would increase its ionic conductivity. These two observations point to the importance of the polymer phase in conduction rather than the ceramic filler. We also observe that the space charge regions and interfacial cores are unlikely to significantly increase ionic conductivity of the composite. As a result, we analyze that the most likely mechanisms at play for the improved Li-ion conductivity in ceramic–polymer composite electrolytes arise from structural confinement effects that reduce crystallinity and increase free volume in the polymer.
In addition to the challenges required to understand ion conduction, extensive work is still required to effectively implement these materials into full battery setups. A primary concern in the field of solid state batteries is the suppression of lithium dendrite growth. While the high shear modulus of the ceramic have been shown to allow some suppression of dendrites, polymers flexibility can assist in maintaining good contact. Several studies have shown improved cyclability of composites over polymer alone, leading to theories that the ceramic provides support to the polymer electrolyte.53 Several studies have therefore considered layered systems to provide this support with good electrode contact and placing stable materials against each electrode.53 However, such a layered system often introduces more resistive layers and interfaces. Therefore, more optimization is needed to consider how thin these materials can effectively be and how contact of a particular phase against the electrode—whether in a full layer or some nanoparticles in contact with the electrode—impacts the final performance of the battery. Electrode material amount will also require optimization for maximal energy density.
While both polymer and ceramic electrolytes are thriving fields individually, composites of these two phases present an even more fertile ground for exploration, however require more work to understand the governing mechanisms of ion conduction. The areas of research to consider in the future of this field include the following:
(1) Studies of composite materials should provide ionic conductivity and transference number measurements of each phase individually, as consistently-made reference samples in the same investigation.
(2) Controlling the polymer structure (crystallinity, density, free volume) in simplified geometries can help to reveal the role of the interface more clearly. The current composite electrolytes present a microstructure that makes it difficult to deconvolute the effect on structure and the effect on chemistry unequivocally. This may include advanced neutron scattering and X-ray scattering techniques to reveal more about the amorphous structure.
(3) More analysis of the very surface chemistry of ceramic fillers is needed to understand how they may impact polymer chemistry and structure differently than inert fillers. Controlling and understanding the role of surface chemistry, such as surface acidity, carbonate formation and degree of lithiation, as well as surface microstructure, without affecting the bulk ion conductivity, is crucial for determining the nature of these interfaces and how they impact the polymer phase.
(4) Multi-scale simulations, hand-in-hand with interface and near-interface sensitive analytical tools, are needed to help resolve the governing mechanisms arising from charge redistribution or structural changes, in both the polymer and the ceramic side of the interface. We have additionally discussed works by Bonilla et al. and Li et al. to simulate lithium ion movement at nanoscales using molecular dynamics and Monte Carlo simulations but more work is needed in this area.125,127
(5) In addition to conductivity studies, more study is needed to understand how these electrolytes would function in a battery. Particularly in how the structure—nanoparticles, nanowires, or more complex structures—impact the electrochemical stability window in terms of interfacial reactions with electrodes or dendrite growth through the electrolyte. By implementing more composites into full battery systems and working to optimize these systems, we can understand other limitations of these systems.
Once the governing mechanisms are quantitatively understood, the field can leverage those physical principles to optimize the composite electrolyte's Li-ion conductivity, electrochemical stability, and mechanical properties, and advance the development of solid state electrolytes for batteries in wide-ranging technologies.
Data availability
The data presented in this article is included in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation Graduate Research Fellowship Program under Grant Number (2141064) and the MIT Energy Initiative. J. L. M. R. acknowledges support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2089/1 – 390776260 and support by the project “Industrialisierbarkeit von Festkörperelektrolytzellen” funded by the Bavarian Ministry of Economic Affairs, Regional Development and Energy.References
- J. Janek and W. G. Zeier, A solid future for battery development, Nat. Energy, 2016, 1(9), 16141 CrossRef
.
- X. B. Cheng, R. Zhang, C. Z. Zhao and Q. Zhang, Toward Safe Lithium Metal Anode in Rechargeable Batteries: A Review, Chem. Rev., 2017, 117(15), 10403 CrossRef CAS PubMed
.
- K. J. Kim, M. Balaish, M. Wadaguchi, L. Kong and J. L. M. Rupp, Solid-State Li–Metal Batteries: Challenges and Horizons of Oxide and Sulfide Solid Electrolytes and Their Interfaces, Adv. Energy Mater., 2021, 11(1), 2002689 CrossRef CAS
.
- C. Bauer, S. Burkhardt, N. P. Dasgupta, L. A. W. Ellingsen, L. L. Gaines and H. Hao,
et al., Charging sustainable batteries, Nat. Sustainability, 2022, 5(3), 176 CrossRef
.
- K. J. Kim, M. Balaish, M. Wadaguchi, L. Kong and J. L. M. Rupp, Solid-State Li–Metal Batteries: Challenges and Horizons of Oxide and Sulfide Solid Electrolytes and Their Interfaces, Adv. Energy Mater., 2021, 11(1), 2002689 CrossRef CAS
.
- S. Furusawa, H. Tabuchi, T. Sugiyama, S. Tao and J. Irvine, Ionic conductivity of amorphous lithium lanthanum titanate thin film, Solid State Ionics, 2005, 176(5–6), 553 CrossRef CAS
.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke and M. Wilkening,
et al., Structure and dynamics of the fast lithium ion conductor “Li7La3Zr2O12, Phys. Chem. Chem. Phys., 2011, 13(43), 19378 RSC
.
- M. Kotobuki and M. Koishi, Effect of Li salts on the properties of Li1.5Al0.5Ti1.5(PO4)3 solid electrolytes prepared by the co-precipitation method, J. Asian Ceram. Soc., 2019, 7(4), 426 CrossRef
.
- J. van den Broek, S. Afyon and J. L. M. Rupp, Interface-Engineered All-Solid-State Li-Ion Batteries Based on Garnet-Type Fast Li+ Conductors, Adv. Energy Mater., 2016, 6(19), 1600736 CrossRef
.
- J. Li, C. Ma, M. Chi, C. Liang and N. J. Dudney, Solid Electrolyte: the Key for High-Voltage Lithium Batteries, Adv. Energy Mater., 2015, 5(4), 1401408 CrossRef
.
- J. H. Cho, K. Kim, S. Chakravarthy, X. Xiao, J. L. M. Rupp and B. W. Sheldon, An Investigation of Chemo-Mechanical Phenomena and Li Metal Penetration in All-Solid-State Lithium Metal Batteries Using In Situ Optical Curvature Measurements, Adv. Energy Mater., 2022, 12(19), 2200369 CrossRef CAS
.
- F. Lv, Z. Wang, L. Shi, J. Zhu, K. Edström and J. Mindemark,
et al., Challenges and development of composite solid-state electrolytes for high-performance lithium ion batteries, J. Power Sources, 2019, 441 Search PubMed
.
- H. Liu, X. B. Cheng, J. Q. Huang, H. Yuan, Y. Lu and C. Yan,
et al., Controlling Dendrite Growth in Solid-State Electrolytes, ACS Energy Lett., 2020, 5(3), 833 CrossRef CAS
.
- S. Wenzel, T. Leichtweiss, D. Krüger, J. Sann and J. Janek, Interphase formation on lithium solid electrolytes—An in situ approach to study interfacial reactions by photoelectron spectroscopy, Solid State Ionics, 2015, 278, 98–105 CrossRef CAS
.
- G. Vardar, W. J. Bowman, Q. Lu, J. Wang, R. J. Chater and A. Aguadero,
et al., Structure, Chemistry, and Charge Transfer Resistance of the Interface between Li7La3Zr2O12 Electrolyte and LiCoO2 Cathode, Chem. Mater., 2018, 30(18), 6259 CrossRef CAS
.
- Y. Kim, I. Waluyo, A. Hunt and B. Yildiz, Avoiding CO 2 Improves Thermal Stability at the Interface of Li7La3Zr2O12 Electrolyte with Layered Oxide Cathodes, Adv. Energy Mater., 2022, 2102741 CrossRef CAS
.
- Y. Kim, D. Kim, R. Bliem, G. Vardar, I. Waluyo and A. Hunt,
et al., Thermally Driven Interfacial Degradation between Li7La 3Zr2O12 Electrolyte and LiNi0.6Mn0.2Co0.2O2 Cathode, Chem. Mater., 2020, 32(22), 9531 CrossRef CAS
.
- Z. D. Hood, Y. Zhu, L. Miara, W. S. Chang, P. Simmons and J. L. M. Rupp, A Sinter-Free Future for Solid-State Battery Designs, Energy Environ. Sci., 2022, 15, 2927–2936 RSC
.
- D. H. A. Choi, N. Donnelly, T. Holme, W. Hudson, S. Iyer and O. Karpenko, US Pat., 20170179522A1, 2019 Search PubMed.
- E. Kazyak, K. H. Chen, A. L. Davis, S. Yu, A. J. Sanchez and J. Lasso,
et al., Atomic layer deposition and first principles modeling of glassy Li3BO3–Li2CO3 electrolytes for solid-state Li metal batteries, J. Mater. Chem. A, 2018, 6(40), 19425 RSC
.
- R. Pfenninger, M. Struzik, I. Garbayo, E. Stilp and J. L. M. Rupp, A Low Ride on Processing Temperature for a Fast Li Conduction in Garnet Solid State Battery Films, Nat. Energy, 2019, 4(6), 475 CrossRef CAS
.
- Y. Zhu, M. Chon, C. V. Thompson and J. L. M. Rupp, Time-Temperature-Transformation (TTT) Diagram of Battery-Grade Li-Garnet Electrolytes for Low-Temperature Sustainable Synthesis, Angew. Chem., Int. Ed., 2023, 62(45), e202304581 CrossRef CAS PubMed
.
- R. Mahbub, K. Huang, Z. Jensen, Z. D. Hood, J. L. M. Rupp and E. A. Olivetti, Text mining for processing conditions of solid-state battery electrolytes, Electrochem. Commun., 2020, 121, 106860 CrossRef CAS
.
- J. Irvine, J. L. M. Rupp, G. Liu, X. Xu, S. Haile and X. Qian,
et al., Roadmap on inorganic perovskites for energy applications, J. Phys. Energy, 2021, 3(3), 031502 CrossRef CAS
.
- A. Panday, S. Mullin, E. D. Gomez, N. Wanakule, V. L. Chen and A. Hexemer,
et al., Effect of Molecular Weight and Salt Concentration on Conductivity of Block Copolymer Electrolytes, Macromolecules, 2009, 42(13), 4632 CrossRef CAS
.
- D. T. Hallinan and N. P. Balsara, Polymer Electrolytes, Annu. Rev. Mater. Res., 2013, 43(1), 503 CrossRef CAS
.
- P. Sivaraj, K. P. Abhilash, B. Nalini, P. Perumal, K. Somasundaram and P. C. Selvin, Performance Enhancement of PVDF/LiCIO4 Based Nanocomposite Solid Polymer Electrolytes via Incorporation of Li0.5La0.5TiO3 Nano Filler for All-Solid-State Batteries, Macromol. Res., 2020, 28, 739–750 CrossRef CAS
.
- J. Bae, Y. Li, J. Zhang, X. Zhou, F. Zhao and Y. Shi,
et al., A 3D Nanostructured Hydrogel-Framework-Derived High-Performance Composite Polymer Lithium-Ion Electrolyte, Angew. Chem., Int. Ed., 2018, 57(8), 2096 CrossRef CAS PubMed
.
- X. Su, K. Guo, T. Ma, P. A. Tamirisa, H. Ye and H. Gao,
et al., Deformation and Chemomechanical Degradation at Solid Electrolyte–Electrode Interfaces, ACS Energy Lett., 2017, 2(8), 1729 CrossRef CAS
.
- D. Grazioli, V. Zadin, D. Brandell and A. Simone, Electrochemical-mechanical modeling of solid polymer electrolytes: Stress development and non-uniform electric current density in trench geometry microbatteries, Electrochim. Acta, 2019, 296, 1142 CrossRef CAS
.
- E. Glynos, L. Papoutsakis, W. Pan, E. P. Giannelis, A. D. Nega and E. Mygiakis,
et al., Nanostructured Polymer Particles as Additives for High Conductivity, High Modulus Solid Polymer Electrolytes, Macromolecules, 2017, 50(12), 4699 CrossRef CAS
.
- G. Nikolakakou, C. Pantazidis, G. Sakellariou and E. Glynos, Ion Conductivity–Shear Modulus Relationship of Single-Ion Solid Polymer Electrolytes Composed of Polyanionic Miktoarm Star Copolymers, Macromolecules, 2022, 55(14), 6131 CrossRef CAS
.
- C. F. N. Marchiori, R. P. Carvalho, M. Ebadi, D. Brandell and C. M. Araujo, Understanding the Electrochemical Stability Window of Polymer Electrolytes in Solid-State Batteries from Atomic-Scale Modeling: The Role of Li-Ion Salts, Chem. Mater., 2020, 32(17), 7237 CrossRef CAS
.
- Y. Zhu, X. He and Y. Mo, Origin of Outstanding Stability in the Lithium Solid Electrolyte Materials: Insights from Thermodynamic Analyses Based on First-Principles Calculations, ACS Appl. Mater. Interfaces, 2015, 7(42), 23685 CrossRef CAS
.
- M. Balaish, J. C. Gonzalez-Rosillo, K. J. Kim, Y. Zhu, Z. D. Hood and J. L. M. Rupp, Processing thin but robust electrolytes for solid-state batteries, Nat. Energy, 2021, 6(3), 227 CrossRef CAS
.
- D. Rettenwander, One Step Closer to Realizing Solid-State Batteries with Cubic Li7La3Zr2O12 Garnets, Chem, 2019, 5(7), 1695 CAS
.
- Y. Ren, Y. Shen, Y. Lin and C. W. Nan, Direct observation of lithium dendrites inside garnet-type lithium-ion solid electrolyte, Electrochem. Commun., 2015, 57, 27–30 CrossRef CAS
.
- C. L. Li, B. Zhang and Z. W. Fu, Physical and electrochemical characterization of amorphous lithium lanthanum titanate solid electrolyte thin-film fabricated by e-beam evaporation, Thin Solid Films, 2006, 515(4), 1886 CrossRef CAS
.
- Y. Zhu, X. He and Y. Mo, First principles study on electrochemical and chemical stability of solid electrolyte–electrode interfaces in all-solid-state Li-ion batteries, J. Mater. Chem. A, 2016, 4(9), 3253 RSC
.
- Q. Ling, Z. Yu, H. Xu, G. Zhu, X. Zhang and Y. Zhao,
et al., Preparation and electrical properties of amorphous Li-Al-Ti-P-O thin film electrolyte, Mater. Lett., 2016, 169, 42 CrossRef CAS
.
- A. Mei, X. L. Wang, J. L. Lan, Y. C. Feng, H. X. Geng and Y. H. Lin,
et al., Role of amorphous boundary layer in enhancing ionic conductivity of lithium–lanthanum–titanate electrolyte, Electrochim. Acta, 2010, 55(8), 2958 CrossRef CAS
.
- X. Tao, Y. Liu, W. Liu, G. Zhou, J. Zhao and D. Lin,
et al., Solid-State Lithium–Sulfur Batteries Operated at 37 °C with Composites of Nanostructured Li7La3Zr2O12/Carbon Foam and Polymer, Nano Lett., 2017, 17(5), 2967 CrossRef CAS PubMed
.
- H. Fang and P. Jena, Li-rich antiperovskite superionic conductors based on cluster ions, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(42), 11046 CrossRef CAS PubMed
.
- Q. Pan, Y. Zheng, S. Kota, W. Huang, S. Wang and H. Qi,
et al., 2D MXene-containing polymer electrolytes for all-solid-state lithium metal batteries, Nanoscale Adv., 2019, 1(1), 395–402 RSC
.
- J. W. Fergus, Ceramic and polymeric solid electrolytes for lithium-ion batteries, J. Power Sources, 2010, 195(15), 4554 CrossRef CAS
.
- W. Liu, S. W. Lee, D. Lin, F. Shi, S. Wang and A. D. Sendek,
et al., Enhancing ionic conductivity in composite polymer electrolytes with well-aligned ceramic nanowires, Nat. Energy, 2017, 2(5), 17035 CrossRef CAS
.
- W. Jia, Z. Li, Z. Wu, L. Wang, B. Wu and Y. Wang,
et al., Graphene oxide as a filler to improve the performance of PAN-LiClO4 flexible solid polymer electrolyte, Solid State Ionics, 2018, 315, 7–13 CrossRef CAS
.
- X. Zhang, T. Liu, S. Zhang, X. Huang, B. Xu and Y. Lin,
et al., Synergistic Coupling between Li6.75La3Zr1.75Ta0.25O12 and Poly(vinylidene fluoride) Induces High Ionic Conductivity, Mechanical Strength, and Thermal Stability of Solid Composite Electrolytes, J. Am. Chem. Soc., 2017, 139(39), 13779 CrossRef CAS PubMed
.
- W. Liu, N. Liu, J. Sun, P. C. Hsu, Y. Li and H. W. Lee,
et al., Ionic Conductivity Enhancement of Polymer Electrolytes with Ceramic Nanowire Fillers, Nano Lett., 2015, 15(4), 2740 CrossRef CAS PubMed
.
- F. Capuano, Composite Polymer Electrolytes, J. Electrochem. Soc., 1991, 138(7), 1918 CrossRef CAS
.
- A. I. Waidha, T. Ferber, M. Donzelli, N. Hosseinpourkahvaz, V. Vanita and K. Dirnberger,
et al., Compositional Dependence of Li-Ion Conductivity in Garnet-Rich Composite Electrolytes for All-Solid-State Lithium-Ion Batteries—Toward Understanding the Drawbacks of Ceramic-Rich Composites, ACS Appl. Mater. Interfaces, 2021, 13(26), 31111 CrossRef CAS PubMed
.
- A. Gupta and J. Sakamoto, Controlling Ionic Transport through the PEO-LiTFSI/LLZTO Interface, Electrochem. Soc. Interface, 2019, 28(2), 63 CrossRef CAS
.
- D. Li, L. Chen, T. Wang and L. Z. Fan, 3D Fiber-Network-Reinforced Bicontinuous Composite Solid Electrolyte for Dendrite-free Lithium Metal Batteries, ACS Appl. Mater. Interfaces, 2018, 10(8), 7069 CrossRef CAS PubMed
.
- W. Zhou, S. Wang, Y. Li, S. Xin, A. Manthiram and J. B. Goodenough, Plating a Dendrite-Free Lithium Anode with a Polymer/Ceramic/Polymer Sandwich Electrolyte, J. Am. Chem. Soc., 2016, 138(30), 9385 CrossRef CAS PubMed
.
- Y. Zhao, C. Wu, G. Peng, X. Chen, X. Yao and Y. Bai,
et al., A new solid polymer electrolyte incorporating Li10GeP2S12 into a polyethylene oxide matrix for all-solid-state lithium batteries, J. Power Sources, 2016, 301, 47–53 CrossRef CAS
.
- S. H. S. Cheng, K. Q. He, Y. Liu, J. W. Zha, M. Kamruzzaman and R. L. W. Ma,
et al., Electrochemical performance of all-solid-state lithium batteries using inorganic lithium garnets particulate reinforced PEO/LiClO4 electrolyte, Electrochim. Acta, 2017, 253, 430 CrossRef CAS
.
- C. Z. Zhao, X. Q. Zhang, X. B. Cheng, R. Zhang, R. Xu and P. Y. Chen,
et al., An anion-immobilized composite electrolyte for dendrite-free lithium metal anodes, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(42), 11069 CrossRef CAS PubMed
.
- P. Yao, B. Zhu, H. Zhai, X. Liao, Y. Zhu and W. Xu,
et al., PVDF/Palygorskite Nanowire Composite Electrolyte for 4 V Rechargeable Lithium Batteries with High Energy Density, Nano Lett., 2018, 18(10), 6113 CrossRef CAS PubMed
.
- H. Huo, B. Wu, T. Zhang, X. Zheng, L. Ge and T. Xu,
et al., Anion-immobilized polymer electrolyte achieved by cationic metal-organic framework filler for dendrite-free solid-state batteries, Energy Storage Mater., 2019, 18, 59–67 CrossRef
.
- Z. Sun, Y. Li, S. Zhang, L. Shi, H. Wu and H. Bu,
et al., g-C3N4 nanosheets enhanced solid polymer electrolytes with excellent electrochemical performance, mechanical properties, and thermal stability, J. Mater. Chem. A, 2019, 7(18), 11069 RSC
.
- W. Tang, S. Tang, X. Guan, X. Zhang, Q. Xiang and J. Luo, High-Performance Solid Polymer Electrolytes Filled with Vertically Aligned 2D Materials, Adv. Funct. Mater., 2019, 29(16), 1900648 CrossRef
.
- L. Chen, W. Li, L. Fan, C. Nan and Q. Zhang, Intercalated Electrolyte with High Transference Number for Dendrite-Free Solid-State Lithium Batteries, Adv. Funct. Mater., 2019, 29(28), 1901047 CrossRef
.
- W. Wang, E. Yi, A. J. Fici, R. M. Laine and J. Kieffer, Lithium Ion Conducting Poly(ethylene oxide)-Based Solid Electrolytes Containing Active or Passive Ceramic Nanoparticles, J. Phys. Chem. C, 2017, 121(5), 2563 CrossRef CAS
.
- X. Wang, H. Zhai, B. Qie, Q. Cheng, A. Li and J. Borovilas,
et al., Rechargeable solid-state lithium metal batteries with vertically aligned ceramic nanoparticle/polymer composite electrolyte, Nano Energy, 2019, 60, 205 CrossRef
.
- Y. Zhao, Z. Huang, S. Chen, B. Chen, J. Yang and Q. Zhang,
et al., A promising PEO/LAGP hybrid electrolyte prepared by a simple
method for all-solid-state lithium batteries, Solid State Ionics, 2016, 295, 65–71 CrossRef CAS
.
- X. Wu, K. Pan, M. Jia, Y. Ren, H. He and L. Zhang,
et al., Electrolyte for lithium protection: From liquid to solid, Green Energy Environ., 2019, 4(4), 360 CrossRef
.
- D. Wohlmuth, V. Epp, P. Bottke, I. Hanzu, B. Bitschnau and I. Letofsky-Papst,
et al., Order vs. disorder—a huge increase in ionic conductivity of nanocrystalline LiAlO2 embedded in an amorphous-like matrix of lithium aluminate, J. Mater. Chem. A, 2014, 2(47), 20295 RSC
.
- D. Zhou, D. Shanmukaraj, A. Tkacheva, M. Armand and G. Wang, Polymer Electrolytes for Lithium-Based Batteries: Advances and Prospects, Chem, 2019, 5(9), 2326 CAS
.
- X. Zhang, J. Xie, F. Shi, D. Lin, Y. Liu and W. Liu,
et al., Vertically Aligned and Continuous Nanoscale Ceramic–Polymer Interfaces in Composite Solid Polymer Electrolytes for Enhanced Ionic Conductivity, Nano Lett., 2018, 18(6), 3829 CrossRef CAS PubMed
.
- J. Zhang, X. Zang, H. Wen, T. Dong, J. Chai and Y. Li,
et al., High-voltage and free-standing poly(propylene carbonate)/Li6.75La3Zr1.75Ta0.25O12 composite solid electrolyte for wide temperature range and flexible solid lithium ion battery, J. Mater. Chem. A, 2017, 5(10), 4940 RSC
.
- K. Fu, Y. Gong, J. Dai, A. Gong, X. Han and Y. Yao,
et al., Flexible, solid-state, ion-conducting membrane with 3D garnet nanofiber networks for lithium batteries, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(26), 7094 CrossRef CAS PubMed
.
- J. Kumar, S. J. Rodrigues and B. Kumar, Interface-mediated electrochemical effects in lithium/polymer-ceramic cells, J. Power Sources, 2010, 195(1), 327 CrossRef CAS
.
- H. W. Chen and F. C. Chang, The novel polymer electrolyte nanocomposite composed of poly(ethylene oxide), lithium triflate and mineral clay, Polymer, 2001, 7 Search PubMed
.
- F. Croce, R. Curini, A. Martinelli, L. Persi, F. Ronci and B. Scrosati,
et al., Physical and Chemical Properties of Nanocomposite Polymer Electrolytes, J. Phys. Chem. B, 1999, 103(48), 10632 CrossRef CAS
.
- F. Croce, G. B. Appetecchi, L. Persi and B. Scrosati, Nanocomposite polymer electrolytes for lithium batteries, Nature, 1998, 394, 456 CrossRef CAS
.
- K. Nairn, M. Forsyth, H. Every, M. Greville and D. R. MacFarlane, Polymer-ceramic ion-conducting composites, Solid State Ionics, 1996, 86–88, 589 CrossRef CAS
.
- C. Wang, X. W. Zhang and A. J. Appleby, Solvent-Free Composite PEO-Ceramic Fiber/Mat Electrolytes for Lithium Secondary Cells, J. Electrochem. Soc., 2005, 152(1), A205 CrossRef CAS
.
- G. B. Appetecchi and F. Croce, Composite Polymer Electrolytes with Improved Lithium Metal Electrode Interfacial Properties, J. Electrochem. Soc., 1998, 8 Search PubMed
.
- G. B. Appetecchi, F. Croce, F. Ronci, B. Scrosati, F. Alessandrini and M. Carewska,
et al., Electrochemical characterization of a composite polymer electrolyte with improved lithium metal electrode interfacial properties, Ionics, 1999, 5(1–2), 59–63 CrossRef CAS
.
- F. Croce, Nanocomposite polymer electrolytes and their impact on the lithium battery technology, Solid State Ionics, 2000, 135(1–4), 47–52 CrossRef CAS
.
- S. H. Chung, Y. Wang, L. Persi, F. Croce, S. G. Greenbaum and B. Scrosati,
et al., Enhancement of ion transport in polymer electrolytes by addition of nanoscale inorganic oxides, J. Power Sources, 2001, 97–98, 644 CrossRef CAS
.
- Y. Ikeda, T. Kitade, S. Kohjiya, A. Hayashi, A. Matsuda and M. Tatsumisago,
et al., Ion
conducting composites from Li2S-SiS2-Li4SiO4 oxysulide glass and poly(oxyethylene)s, Polymer, 2001, 4 Search PubMed
.
- A. Hayashi, T. Kitade, Y. Ikeda, S. Kohjiya, A. Matsuda and M. Tatsumisago,
et al., Preparation and Characterization of Lithium Ion Conducting Glass–Polymer Composites, Chem. Lett., 2001, 814 CrossRef CAS
.
- S. Kohjiya, T. Kitade, Y. Ikeda, A. Hayashi, A. Matsuda and M. Tatsumisago,
et al., Solid electrolyte composed of 95(0.6Li2S:0.4SiS2)Á5Li4SiO4 glass and high molecular weight branched poly(oxyethylene), Solid State Ionics, 2002, 6 Search PubMed
.
- Y. Ikeda, Ionic conductivity of lithium chloroboracite/polyethylene glycol composites, Solid State Ionics, 2004, 175(1–4), 261 CrossRef CAS
.
- Y. C. Jung, S. M. Lee, J. H. Choi, S. S. Jang and D. W. Kim, All Solid-State Lithium Batteries Assembled with Hybrid Solid Electrolytes, J. Electrochem. Soc., 2015, 162(4), A704 CrossRef CAS
.
- D. Safanama and S. Adams, Flexible Light-Weight Lithium-Ion-Conducting Inorganic–Organic Composite Electrolyte Membrane, ACS Energy Lett., 2017, 2(5), 1130 CrossRef CAS
.
- X. Ban, W. Zhang, N. Chen and C. Sun, A High-Performance and Durable Poly(ethylene oxide)-Based Composite Solid Electrolyte for All Solid-State Lithium Battery, J. Phys. Chem. C, 2018, 122(18), 9852 CrossRef CAS
.
- F. Chen, W. Zha, D. Yang, S. Cao, Q. Shen and L. Zhang,
et al., All-Solid-State Lithium Battery Fitted with Polymer Electrolyte Enhanced by Solid Plasticizer and Conductive Ceramic Filler, J. Electrochem. Soc., 2018, 165(14), A3558–65 CrossRef CAS
.
- X. Li, D. Wang, H. Wang, H. Yan, Z. Gong and Y. Yang, Poly(ethylene oxide)–Li10SnP2S12 Composite Polymer Electrolyte Enables High-Performance All-Solid-State Lithium Sulfur Battery, ACS Appl. Mater. Interfaces, 2019, 11(25), 22745 CrossRef CAS PubMed
.
- Z. Huang, W. Pang, P. Liang, Z. Jin, N. Grundish and Y. Li,
et al., A dopamine modified Li6.4La3Zr1.4Ta0.6O12/PEO solid-state electrolyte: enhanced thermal and electrochemical properties, J. Mater. Chem. A, 2019, 7(27), 16425 RSC
.
- C. Wolf, H. Angellier-Coussy, N. Gontard, F. Doghieri and V. Guillard, How the shape of fillers affects the barrier properties of polymer/non-porous particles nanocomposites: A review, J. Membr. Sci., 2018, 556, 393–418 CrossRef CAS
.
- M. A. K. L. Dissanayake, P. A. R. D. Jayathilaka, R. S. P. Bokalawala, I. Albinsson and B. E. Mellander, Effect of concentration and grain size of alumina filler on the ionic conductivity enhancement of the (PEO)9LiCF3SO3:Al2O3 composite polymer electrolyte, J. Power Sources, 2003, 119–121, 409 CrossRef CAS
.
- J. Weston and B. Steele, Effects of inert fillers on the mechanical and electrochemical properties of lithium salt-poly(ethylene oxide) polymer electrolytes, Solid State Ionics, 1982, 7(1), 75 CrossRef CAS
.
- F. Croce, B. Scrosati and G. Mariotto, Electrochemical and spectroscopic study of the transport properties of composite polymer electrolytes, Chem. Mater., 1992, 4(6), 1134 CrossRef CAS
.
- F. Croce and B. Scrosati, Interfacial phenomena in polymer-electrolyte cells: lithium passivation and cycleability, J. Power Sources, 1993, 43(1–3), 9–19 CrossRef CAS
.
- L. Fan, Effect of modified SiO2 on the properties of PEO-based polymer electrolytes, Solid State Ionics, 2003, 164(1–2), 81 CrossRef CAS
.
- D. Lin, P. Y. Yuen, Y. Liu, W. Liu, N. Liu and R. H. Dauskardt,
et al., A Silica-Aerogel-Reinforced Composite Polymer Electrolyte with High Ionic Conductivity and High Modulus, Adv. Mater., 2018, 30(32), 1802661 CrossRef PubMed
.
- F. Croce, L. Persi, B. Scrosati, F. Serraino-Fiory, E. Plichta and M. A. Hendrickson, Role of the ceramic fillers in enhancing the transport properties of composite polymer electrolytes, Electrochim. Acta, 2001, 46(16), 2457 CrossRef CAS
.
- S. R. Mohapatra, M. G. Nair and A. K. Thakur, Synergistic effect of nano-ceria dispersion on improvement of Li + ion conductivity in polymer nanocomposite electrolytes, Mater. Lett., 2018, 221, 232 CrossRef CAS
.
- S. Skaarup, Mixed phase solid electrolytes, Solid State Ionics, 1988, 28–30, 975 CrossRef
.
- B. Kumar and L. G. Scanlon, Polymer-ceramic composite electrolytes, J. Power Sources, 1994, 52(2), 261 CrossRef CAS
.
- J. Zagorski, L. Buannic and A. Llordes, Garnet−Polymer Composite Electrolytes: New Insights on Local Li- Ion Dynamics and Electrodeposition Stability with Li Metal Anodes, ACS Appl. Energy Mater., 2019, 15 Search PubMed
.
- J. Zhao, J. Zhang, T. Zhou, X. Liu, Q. Yuan and A. Zhang, New understanding on the reaction pathways of the polyacrylonitrile copolymer fiber pre-oxidation: online tracking by two-dimensional correlation FTIR spectroscopy, RSC Adv., 2016, 6(6), 4397 RSC
.
- M. Keller, G. B. Appetecchi, G. T. Kim, V. Sharova, M. Schneider and J. Schuhmacher,
et al., Electrochemical performance of a solvent-free hybrid ceramic–polymer electrolyte based on Li7La3Zr2O12 in P(EO)15 LiTFSI, J. Power Sources, 2017, 353, 287 CrossRef CAS
.
- T. Yang, J. Zheng, Q. Cheng, Y. Y. Hu and C. K. Chan, Composite Polymer Electrolytes with Li7La3Zr2O12 Garnet-Type Nanowires as Ceramic Fillers: Mechanism of Conductivity Enhancement and Role of Doping and Morphology, ACS Appl. Mater. Interfaces, 2017, 9(26), 21773 CrossRef CAS PubMed
.
- K. Karthik and R. Murugan, Lithium garnet based free-standing solid polymer composite membrane for rechargeable lithium battery, J. Solid State Electrochem., 2018, 22(10), 2989 CrossRef CAS
.
- K. Fu, Y. Gong, J. Dai, A. Gong, X. Han and Y. Yao,
et al., Flexible, solid-state, ion-conducting membrane with 3D garnet nanofiber networks for lithium batteries, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(26), 7094 CrossRef CAS PubMed
.
- H. Xie, C. Yang, K. K. Fu, Y. Yao, F. Jiang and E. Hitz,
et al., Flexible, Scalable, and Highly Conductive Garnet-Polymer Solid Electrolyte Templated by Bacterial Cellulose, Adv. Energy Mater., 2018, 8(18), 1703474 CrossRef
.
- Z. Li, W. X. Sha and X. Guo, Three-Dimensional Garnet Framework-Reinforced Solid Composite Electrolytes with High Lithium-Ion Conductivity and Excellent Stability, ACS Appl. Mater. Interfaces, 2019, 11(30), 26920 CrossRef CAS PubMed
.
- X. Fu, Y. Li, C. Liao, W. Gong, M. Yang and R. K. Y. Li,
et al., Enhanced electrochemical performance of solid PEO/LiClO4 electrolytes with a 3D porous Li6.28La3Zr2Al0.24O12 network, Compos. Sci. Technol., 2019, 184, 107863 CrossRef CAS
.
- L. Chen, Y. Li, S. P. Li, L. Z. Fan, C. W. Nan and J. B. Goodenough, PEO/garnet composite electrolytes for solid-state lithium batteries: From ceramic-in-polymer to polymer-in-ceramic, Nano Energy, 2018, 46, 176 CrossRef CAS
.
- J. H. Choi, C. H. Lee, J. H. Yu, C. H. Doh and S. M. Lee, Enhancement of ionic conductivity of composite membranes for all-solid-state lithium rechargeable batteries incorporating tetragonal Li7La3Zr2O12 into a polyethylene oxide matrix, J. Power Sources, 2015, 274, 458 CrossRef CAS
.
- H. Scher and R. Zallen, Critical Density in Percolation Processes, J. Chem. Phys., 1970, 53(9), 3759 CrossRef CAS
.
- C. D. Lorenz and R. M. Ziff, Precise determination of the critical percolation threshold for the three-dimensional “Swiss cheese” model using a growth algorithm, J. Chem. Phys., 2001, 114(8), 3659 CrossRef CAS
.
- F. Chen, D. Yang, W. Zha, B. Zhu, Y. Zhang and J. Li,
et al., Solid polymer electrolytes incorporating cubic Li7La3Zr2O12 for all-solid-state lithium rechargeable batteries, Electrochim. Acta, 2017, 258, 1106 CrossRef CAS
.
- J. Lu, Y. Liu, P. Yao, Z. Ding, Q. Tang and J. Wu,
et al., Hybridizing poly(vinylidene fluoride-co-hexafluoropropylene) with Li6.5La3Zr1.5Ta0.5O12 as a lithium-ion electrolyte for solid state lithium metal batteries, Chem. Eng. J., 2019, 367, 230 CrossRef CAS
.
- W. P. Chen, H. Duan, J. L. Shi, Y. Qian, J. Wan and X. D. Zhang,
et al., Bridging Interparticle Li+ Conduction in a Soft Ceramic Oxide Electrolyte, J. Am. Chem. Soc., 2021, 143(15), 5717 CrossRef CAS PubMed
.
- F. Langer, M. S. Palagonia, I. Bardenhagen, J. Glenneberg, F. La Mantia and R. Kun, Impedance Spectroscopy Analysis of the Lithium Ion Transport through the Li7La3Zr2O12/P(EO) 20 Li Interface, J Electrochem Soc., 2017, 164(12), A2298 CrossRef CAS
.
- S. Chandra, Y. Kim, D. Vivona, I. Waluyo, A. Hunt and C. Schlueter,
et al., Thermally-driven reactivity of Li0.35La0.55TiO3 solid electrolyte with LiCoO2 cathode, J. Mater. Chem. A, 2022, 10(7), 3485 RSC
.
- N. J. J. de Klerk and M. Wagemaker, Space-Charge Layers in All-Solid-State Batteries; Important or Negligible?, ACS Appl. Energy Mater., 2018, 1, 5609–5618 CAS
.
-
J. Maier, Physical chemistry of ionic materials: ions and electrons in solids, Wiley, Chichester, Hoboken, NJ, 2004, p. 537 Search PubMed
.
- H. Tuller, Ionic conduction in nanocrystalline materials, Solid State Ionics, 2000, 131(1–2), 143 CrossRef CAS
.
- J. Maier, Enhancement of the Ionic Conductivity in Solid-Solid-Dispersions by Surface Induced Defects, Ber. Bunsenges Für Phys. Chem., 1984, 88(11), 1057 CrossRef CAS
.
- Z. Li, H. M. Huang, J. K. Zhu, J. F. Wu, H. Yang and L. Wei,
et al., Ionic Conduction in Composite Polymer Electrolytes: Case of PEO:Ga-LLZO Composites, ACS Appl. Mater. Interfaces, 2019, 11(1), 784 CrossRef CAS PubMed
.
- D. Brogioli, F. Langer, R. Kun and F. La Mantia, Space-Charge Effects at the Li 7La3Zr2O12/Poly(ethylene oxide) Interface, ACS Appl. Mater. Interfaces, 2019, 11(12), 11999 CrossRef CAS PubMed
.
- M. R. Bonilla, F. A. García Daza, P. Ranque, F. Aguesse, J. Carrasco and E. Akhmatskaya, Unveiling Interfacial Li-Ion Dynamics in Li7La3Zr2O12/PEO(LiTFSI) Composite Polymer-Ceramic Solid Electrolytes for All-Solid-State Lithium Batteries, ACS Appl. Mater. Interfaces, 2021, 13(26), 30653 CrossRef CAS PubMed
.
- J. Zheng and Y. Y. Hu, New Insights into the Compositional Dependence of Li-Ion Transport in Polymer–Ceramic Composite Electrolytes, ACS Appl. Mater. Interfaces, 2018, 10(4), 4113 CrossRef CAS PubMed
.
- J. Zheng, H. Dang, X. Feng, P. H. Chien and Y. Y. Hu, Li-ion transport in a representative ceramic–polymer–plasticizer composite electrolyte: Li7La3Zr2O12 –polyethylene oxide–tetraethylene glycol dimethyl ether, J Mater Chem A, 2017, 5(35), 18457 RSC
.
- J. Zheng, M. Tang and Y. Y. Hu, Lithium Ion Pathway within Li7La3Zr2O12-Polyethylene Oxide Composite Electrolytes, Angew. Chem., Int. Ed., 2016, 55(40), 12538 CrossRef CAS PubMed
.
- W. Wieczorek, Z. Florjanczyk and J. R. Stevens, Composite polyether based solid electrolytes, Electrochim. Acta, 1995, 40(13–14), 2251 CrossRef CAS
.
- Z. Wang, X. Huang and L. Chen, Understanding of Effects of Nano-Al2O3 Particles on Ionic Conductivity of Composite Polymer Electrolytes, Electrochem. Solid-State Lett., 2003, 6(11), E40 CrossRef CAS
.
- Y. Zhu, Z. D. Hood, H. Paik, P. B. Groszewicz, S. Emge and F. N. Sayed, Highly Disordered Amorphous Li-Battery Electrolytes, Matter, 2023, 7(2), 500–522 CrossRef
.
- M. V. Massa, K. Dalnoki-Veress and J. A. Forrest, Crystallization kinetics and crystal morphology in thin poly(ethylene oxide) films, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 11(2), 191 CrossRef CAS PubMed
.
- Z. Zhang, J. Ding, B. M. Ocko, J. Lhermitte, J. Strzalka and C. H. Choi,
et al., Nanoconfinement and Salt Synergistically Suppress Crystallization in Polyethylene Oxide, Macromolecules, 2020, 53(4), 1494 CrossRef CAS
.
- R. Chen, W. Qu, X. Guo, L. Li and F. Wu, The pursuit of solid-state electrolytes for lithium batteries: from comprehensive insight to emerging horizons, Mater. Horiz., 2016, 3(6), 487–516 RSC
.
- P. Buvana, K. Vishista, D. Shanmukaraj and R. Murugan, Lithium garnet oxide dispersed polymer composite membrane for rechargeable lithium batteries, Ionics, 2017, 23(3), 541 CrossRef CAS
.
- R. Abdullah, S. Aziz, S. Mamand, A. Hassan, S. Hussein and M. Kadir, Reducing the Crystallite Size of Spherulites in PEO-Based Polymer Nanocomposites Mediated by Carbon Nanodots and Ag Nanoparticles, Nanomaterials, 2019, 9(6), 874 CrossRef PubMed
.
- X. C. Chen, R. L. Sacci, N. C. Osti, M. Tyagi, Y. Wang and M. J. Palmer,
et al., Study of segmental dynamics and ion transport in polymer–ceramic composite electrolytes by quasi-elastic neutron scattering, Mol. Syst. Des. Eng., 2019, 4(2), 379 RSC
.
- V. Aravindan, J. Gnanaraj, S. Madhavi and H. K. Liu, Lithium-Ion Conducting Electrolyte Salts for Lithium Batteries, Chem. – Eur. J., 2011, 17(51), 14326 CrossRef CAS PubMed
.
- X. C. Chen, X. Liu, A. Samuthira Pandian, K. Lou, F. M. Delnick and N. J. Dudney, Determining and Minimizing Resistance for Ion Transport at the Polymer/Ceramic Electrolyte Interface, ACS Energy Lett., 2019, 4(5), 1080 CrossRef CAS
.
- V. N. Dougnac, R. Alamillo, B. C. Peoples and R. Quijada, Effect of particle diameter on the permeability of polypropylene/SiO2 nanocomposites, Polymer, 2010, 51(13), 2918 CrossRef CAS
.
- W. E. Tenhaeff, K. A. Perry and N. J. Dudney, Impedance Characterization of Li Ion Transport at the Interface between Laminated Ceramic and Polymeric Electrolytes, J. Electrochem. Soc., 2012, 159(12), A2118 CrossRef CAS
.
- S. Kalnaus, A. S. Sabau, S. Newman, W. E. Tenhaeff, C. Daniel and N. J. Dudney, Effective conductivity of particulate polymer composite electrolytes using random resistor network method, Solid State Ionics, 2011, 199–200, 44–53 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cs00214h |
| ‡ Here, we utilize the term ionic conductivity rather than Li-ion conductivity because in the case of polymer electrolytes, many conductivity measurements do not exclude the conduction of anions in the material. While all of the materials discussed are lithium-ion electrolytes, the conductivity measured is not purely lithium ion conduction and in many cases. |
| This journal is © The Royal Society of Chemistry 2025 |