 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
MatFold: systematic insights into materials discovery models' performance through standardized cross-validation protocols†
Matthew D.
Witman
 *a and
Peter
Schindler
*a and
Peter
Schindler
 *b
*b
aSandia National Laboratories, Livermore, California 94551, USA. E-mail: mwitman@sandia.gov
bNortheastern University, Boston, Massachusetts 02115, USA. E-mail: p.schindler@northeastern.edu
First published on 9th December 2024
Abstract
Machine learning (ML) models in the materials sciences that are validated by overly simplistic cross-validation (CV) protocols can yield biased performance estimates for downstream modeling or materials screening tasks. This can be particularly counterproductive for applications where the time and cost of failed validation efforts (experimental synthesis, characterization, and testing) are consequential. We propose a set of standardized and increasingly difficult splitting protocols for chemically and structurally motivated CV that can be followed to validate any ML model for materials discovery. Among several benefits, this enables systematic insights into model generalizability, improvability, and uncertainty, provides benchmarks for fair comparison between competing models with access to differing quantities of data, and systematically reduces possible data leakage through increasingly strict splitting protocols. Performing thorough CV investigations across increasingly strict chemical/structural splitting criteria, local vs. global property prediction tasks, small vs. large datasets, and structure vs. compositional model architectures, some common threads are observed; however, several marked differences exist across these exemplars, indicating the need for comprehensive analysis to fully understand each model's generalization accuracy and potential for materials discovery. For this we provide a general-purpose, featurization-agnostic toolkit, MatFold, to automate reproducible construction of these CV splits and encourage further community use in model benchmarking.
Introduction
Understanding and quantifying the generalizability, improvability, and uncertainty of machine learning (ML)-based materials discovery models is critical, especially in applications where downstream experimental validation (synthesis, characterization, and testing) is often time- and cost-intensive. Careful, and sometimes extensive, cross-validation (CV) is required to both avoid erroneous conclusions regarding a model's capabilities and to fully understand its limitations.1 Withholding randomly selected test data is often insufficient for quantifying a model's performance as this sub-set is drawn from the same distribution that potentially suffers from data leakage. This in-distribution (ID) generalization error is typically minimized during model training and hyperparameter tuning to avoid over/underfitting. Model prediction uncertainties can be assessed utilizing model ensembling (e.g., for bagged regressor ML models2,3 and deep neural networks4,5) and/or through nested (“double”) CV.6 However, the out-of-distribution (OOD) generalization error constitutes a more useful performance metric for assessing a model's true ability to generalize to unseen data—an especially critical factor when models are used to discover materials with exceptional target properties (i.e., outliers).7 This error originates from either lack of knowledge (e.g., imbalance in data, or poor data representation) or sub-optimal model architecture and is referred to as being epistemic.4 Evaluating OOD generalization, however, requires more careful considerations during data splitting.One approach to constructing OOD test sets is to utilize unsupervised clustering with a chosen materials featurization and then conduct leave-one-cluster-out CV (LOCO-CV). For example, on compositional models for superconducting transition temperatures, LOCO-CV revealed how generalizability and expected accuracy are drastically overestimated due to data leakage in random train/test splits.8 Omee et al. have investigated the performance of OOD prediction tasks on MatBench9 datasets (refractive index, shear modulus, and formation energy) utilizing structure-based graph neural network (GNN) models and LOCO-CV (k-means clustering and t-distributed stochastic neighbor embedding).10 Hu et al. similarly have utilized LOCO-CV to study the improvement of OOD generalizability of various domain adaptation algorithms during materials property predictions (experimental band gaps and bulk metallic glass formation ability).11
Quantifying distribution shifts in materials databases over time and identifying whether specific samples are OOD have been shown critical for developing databases and models that promote greater robustness and generalizability.12 To quantify whether data points are OOD can be assessed based on their distance to training data in feature space (e.g., via kernel density estimates2). Data bias arising from uneven coverage of materials families may also be mitigated by entropy-targeted active learning.13
Alternative methods for defining OOD splits without relying on the feature space include using (i) target property ranges, (ii) time or date thresholds when data was added, or (iii) general materials information, such as structure, chemistry, or prototype/class. Splits based on target-property-sorted data14 can facilitate the discovery of materials with extraordinary target properties7 and has also been used in “k-fold forward CV”.15 Splitting datasets based on when data points were added mimics acquiring new, unseen data that may be realistically considered OOD.14,16,17 Lastly, the OOD generalization has recently been studied for formation energy models with structural and chemical hold-outs.18
To further encourage standardized reporting of these types of detailed insights into generalization performance and limitations of ML-based models in the materials sciences, here we provide “MatFold” as a featurization-agnostic programmatic tool for automatically generating CV splits for arbitrary materials datasets and model architectures, such as structure-based19 or composition-based20 models. Specifically, we propose a standardized series of CV splits based on increasingly difficult chemical/structural hold-out criteria, dataset size reduction, nested vs. non-nested splits, and others. By assessing model performance across various combinations of MatFold splitting criteria, one could, for example, more fairly compare the performance of differing approaches with the same modeling objectives. This approach allows for a better understanding of how well models' predictions generalize with increasingly difficult chemical or structural hold-out criteria. Additionally, it can determine the expected model improvement with continued data acquisition and assess whether this improvement depends on the splitting criteria used for OOD generalization. Furthermore, the method evaluates whether nested CV ensembles enhance OOD predictions and quantifies the extent of this improvement. It also examines the reliability of uncertainty estimates derived from nested CV ensembles and whether this reliability varies based on the splitting criteria used for assessing generalization.
For practically demonstrating the utility of insights derived from MatFold, we select ML exemplars from our previous work (modeling vacancy formation energies21 and surface work functions22). These are examples in structure-based ML where data leakage can be very problematic since multiple training examples are derived from the same base crystal structure. For example, many structures may contain vacancy sites that are determined to be unique but are in fact nearly identical because they are only slightly above the symmetry tolerance. Similarly, Miller surfaces from the same base crystal structure may be extremely similar. In either exemplar, the expected model error for inference (i.e., materials screening) can vary by factors of 2–3, depending on the splitting criteria. For comparison we additionally include a standard benchmarking exemplar from MatBench9 (bulk modulus). Through detailed insights into expected model performance in these exemplars and how it compares/differs across various splitting criteria, dataset sizes, and the exemplars themselves, we motivate MatFold as an easy-to-use, lightweight, and open-source tool for the materials ML community to enable the generation of reproducible data splits that deliver greater insights into model generalizability, improvability, and uncertainty.
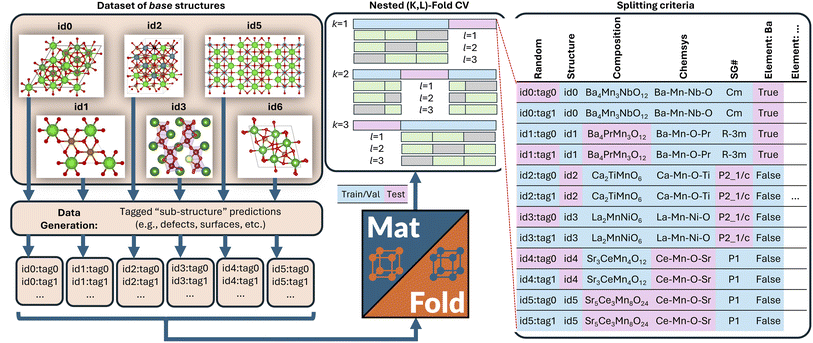
MatFold procedure
MatFold serves as a convenient and automated tool to process a user's materials data and systematically generate increasingly difficult CV splits to test a modeling approach's generalizability (Fig. 1). This lightweight, pip-installable Python package requires minimal data preparation and ensures reproducible dataset splits. When generating splits, MatFold creates a JSON file (see ESI Fig. 9†) that allows users to recreate identical splits from the same dataset, at a later time or by different users. This feature makes it easy to share splitting protocols, promoting consistent and reproducible benchmarking. MatFold offers two split methods, S = {K-fold or nested (K, L)-fold}, where K and L are integers chosen by the user. If the user sets K or L to zero then the value is determined by MatFold and is set to be equal to the number of unique split labels (i.e., the created folds are then leave-one-out (LOO)). Outer K-folds can be split on a variety of criteria, CK = {Random, Structure, Composition, Chemical system = Chemsys, Element, Periodic table (PT) group, PT row, Space group number = SG#, Point group, or Crystal system}, while inner L-folds can be split either randomly or utilizing the same split criteria as the outer splits (CL = {Random, CK}). We note that for datasets where each target label corresponds to a unique bulk crystal structure (e.g., Materials Project ID, mpid) the splitting strategies “Random” and “Structure” coincide (which is the case for the log(KVRH) dataset but not for the ΔHV and ϕ datasets considered in this work). As shown in Table 1, MatFold provides functionality to artificially reduce the dataset size by a fractional amount D (which applies to the entire dataset before splitting is performed). Furthermore, materials with a specified number of unique chemical elements can be assigned to the training set by default thereby exempting them from the split criteria. This could be, for example, whether the automatic assignment of all binary compounds to the training data is performed, T = {None or Binary} (the motivation for which is discussed in the next section). For the case where T = Binary and the outer splitting criteria holds out the element Fe, for example, then binary materials like FeO or FeAl would still be included in the training set, even though they would otherwise be placed in the test set under the hold-out criteria. Split labels which make up a small or large fraction of the entire dataset can also be excluded from the test set by specifying lower or upper limits within MatFold, respectively. This can be utilized to avoid skewed test sets.Based on the user's choices of D, T, K, L, and CK, MatFold can typically create thousands of splits. The feasibility of training this many models may depend on the dataset size and modeling approach and may be less feasible, for example, in the training of recently developed universal ML potentials.23–26 However, dataset and model sizes are often small enough for more specialized ML-based materials discovery models to perform splits across at least some subset of the criteria summarized in Table 1. Subsequent exemplars based on our previous work (modeling vacancy defect formation energies21 and surface work functions22) and a standard MatBench example (modeling bulk modulus9), we are able to train thousands of model splits generated by MatFold to obtain improved insights into our models' generalizability and limitations. An overview of the ΔHV, ϕ, and log(KVRH) datasets and the chosen MatFold split protocols for each are listed in Table 2. Model hyperparameters are fixed at the optimal conditions as determined in the respective previous work.9,21,22
| Vacancy formation energy (ΔHV) | Work function (ϕ) | Bulk modulus log(KVRH) | |
|---|---|---|---|
| # Data points | 1670 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 332 332 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 574 574 |
| # Of unique: | |||
| Structures | 250 | 3716 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 574 574 |
| Compositions | 230 | 3623 | 9321 |
| Chemsys | 114 | 2832 | 6946 |
| Space groups | 35 | 62 | 173 |
| Elements | 18 | 77 | 78 |
| 〈target〉 | 5.8 eV | 3.92 eV | 1.88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(GPa) log(GPa) |
| σ(target) | 3.5 eV | 0.86 eV | 0.37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(GPa) log(GPa) |
| Model type | dGNN | RF | {CGCNN,RF} |
| D | {0.1, 0.25, 0.5, 0.75, 1.0} | {0.05, 0.1, 0.25, 0.5, 1.0} | 1.0 |
| T | {None, binary} | None | None |
| S | {K, (K, L)} | {K, (K, L)} | (K, L) |
| C K | |||
| Random | K = 10, L = 10 | K = 10, L = 10 | — |
| Structure | K = 10, L = 10 | K = 10, L = 10 | K = 5, L = 5 |
| Composition | K = 10, L = 10 | K = 10, L = 10 | — |
| Chemsys | K = 10, L = 10 | K = 10, L = 10 | — |
| Elements | K = LOO, L = 10 | K = LOO, L = LOO | K = {LOO, 5}, L = 5 |
| PT group | — | K = LOO, L = LOO | — |
| Space group | K = 10, L = 10 | K = 10, L = 10 | K = 5, L = 5 |
| Point group | — | K = LOO, L = LOO | — |
| Crystal Sys | — | K = LOO, L = LOO | — |
| C L | Random | C K | Random |
| # Total splits | 7480 | 4046 | 930 |
To evaluate the model performances, we denote the mean absolute error of an outer test set MAE = 1/Nk∑i|![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) i − pi|, where Nk is the number of samples in the outer fold k,
i − pi|, where Nk is the number of samples in the outer fold k, ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) i is the model prediction of sample i, and pi the truth value. The expected model performance is given as the ensemble average over the set of all K folds, 〈{MAE}K〉. For non-nested CV, i.e., K-fold,
i is the model prediction of sample i, and pi the truth value. The expected model performance is given as the ensemble average over the set of all K folds, 〈{MAE}K〉. For non-nested CV, i.e., K-fold, ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) i in the kth test set is predicted by a single model trained on the kth train set. For nested CV, i.e., (K, L)-fold, the final prediction is the ensemble average over the set of inner model predictions on the outer test set, 〈{
i in the kth test set is predicted by a single model trained on the kth train set. For nested CV, i.e., (K, L)-fold, the final prediction is the ensemble average over the set of inner model predictions on the outer test set, 〈{![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) i}L〉. The deviation of that ensemble average prediction from the true value is referred to as residuals, calculated as |pi − 〈{
i}L〉. The deviation of that ensemble average prediction from the true value is referred to as residuals, calculated as |pi − 〈{![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) i}L〉|. Importantly, nested CV also yields an uncertainty metric via the standard deviation over the set of inner model predictions on the outer test set, σ({
i}L〉|. Importantly, nested CV also yields an uncertainty metric via the standard deviation over the set of inner model predictions on the outer test set, σ({![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) i}L).
i}L).
We note that for datasets with strong imbalances in splitting labels (e.g., an element present in almost the entire dataset vs. another element being present only in a tiny fraction of the dataset) the MAE and its standard deviation may be affected by the random seed during split generation. This can be mitigated in MatFold by specifying a minimum and maximum threshold of split label prevalence that determines whether that label is considered during the CV procedure or is always enforced to be in the training set. For example, if oxygen is present in 90% of structures in the dataset and the user specifies a maximum threshold of 0.9, then oxygen-containing structures will be part of the training set by default during CV.
Vacancy formation energy exemplar
Recently we developed a defect GNN (dGNN) modeling approach to directly predict relaxed vacancy formation energies, ΔHV, from their respective bulk crystal structures.21 The accompanying open-source dataset27 specifically computes neutral cation and oxygen vacancies in ∼200 compounds, to which we added the neutral oxygen vacancy formation energies for ∼50 more structures from the work by Wexler et al.28 in this study (self-consistency between these two datasets was previously determined21). Now, we use MatFold to generate ∼7480 possible splits and train/test our model performance, as summarized in Fig. 2 and 4, to better understand the modeling approach's generalizability, improvability, and uncertainty.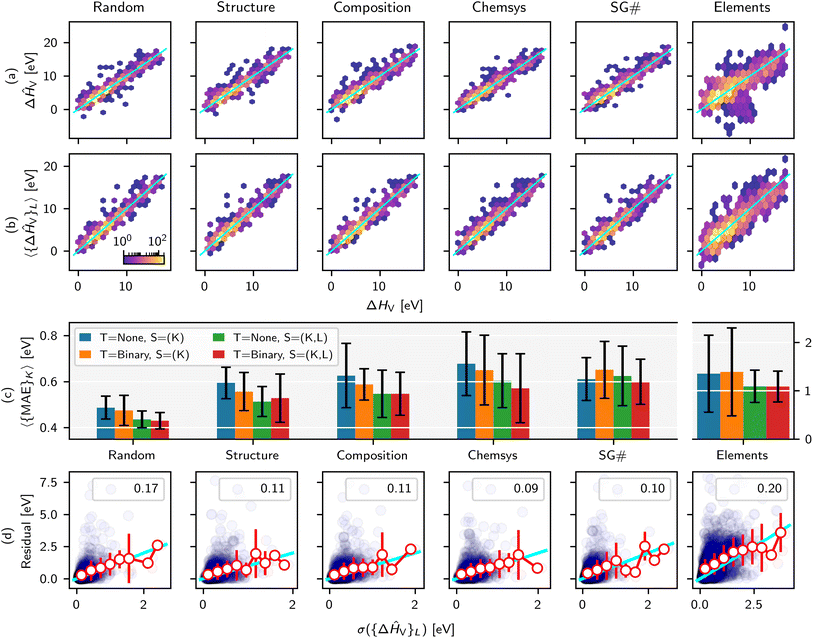 | ||
| Fig. 2 ΔHV test set parity plots for D = 1.0 and various CK criteria for (a) T = None and S = (K) and (b) T = Binary and S = (K, L). (c) Expected MAE for various split criteria and combinations of other MatFold options such as T = {None, Binary} and S = {K, (K, L)}. Quartile box plot of MAE and R2 values are shown in ESI Fig. 5.† (d) Correlation of residual vs. standard deviation of ensemble predictions (purple circles), with R2 shown in the inset. Additionally, within individual bins for σ({ΔĤV}L), the average and standard deviation of residuals in that bin are shown with white circles and red error bars, respectively. The cyan line represents y = x. | ||
Fig. 2a shows density parity plots of all outer test set predictions for CK = {Random, Structure, Composition, Chemsys, SG#, Elements} and D = 1.0, T = None, and S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) K-fold, while Fig. 2b shows the same but for T = Binary and S
K-fold, while Fig. 2b shows the same but for T = Binary and S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (K, L)-fold. The color code is on a logarithmic scale with respect to the number of predictions at that grid point. Note that for this dataset, we are able to compute all ΔHV for at least one of each binary oxide in the chemical space of interest, motivating the investigation of automatically assigning binaries to the training data. Immediately noticeable in Fig. 2b is the mitigation of over-fitting for some of the largest outliers observed in Fig. 2a. Additional analysis in the ESI,† applicable only to this exemplar, investigates the CK = Elements parity plots at a more granular level and further reveals insights into the generalization capabilities of dGNN.
(K, L)-fold. The color code is on a logarithmic scale with respect to the number of predictions at that grid point. Note that for this dataset, we are able to compute all ΔHV for at least one of each binary oxide in the chemical space of interest, motivating the investigation of automatically assigning binaries to the training data. Immediately noticeable in Fig. 2b is the mitigation of over-fitting for some of the largest outliers observed in Fig. 2a. Additional analysis in the ESI,† applicable only to this exemplar, investigates the CK = Elements parity plots at a more granular level and further reveals insights into the generalization capabilities of dGNN.
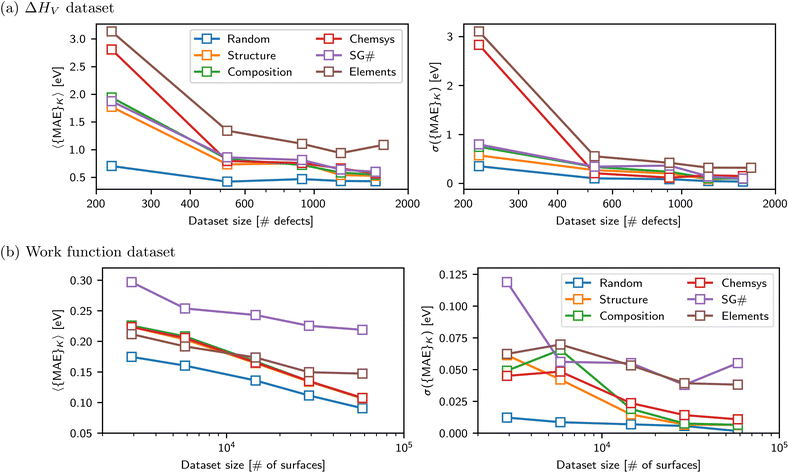
Fig. 2c further quantifies the dependence of the expected model error as a function of T, S, and CK and highlights key conclusions. The expected MAE is strongly influenced by the splitting criteria and generally increases with Random < Structure < Composition < Chemsys < SG# ≪ Elements, where error bars correspond to σ({MAE}K). Several key conclusions arise. For this particular dataset and model, using a single training model for inference (blue bars) generally produces an expected MAE ∼10–20% higher than using the ensemble of models from nested CV (green bars) across all CK. From a different perspective, one would overestimate the expected MAEs by ∼10–20% if using the ensemble of non-nested K-fold models to perform inference for materials screening exercises, compared to the MAEs calculated by nested (K, L)-folds. Further assigning all binaries to the train set generally helps but has less of an impact than model ensembling.
More importantly, the choice of CK has a very strong influence on the expected MAE. The goal of this and many other specialty ML models for materials discovery, trained on small-to medium-sized datasets (∼100s–1000s of examples), is to screen properties of structures that represent entirely new compositions, or even chemical systems, that are outside the training data. For this use case, performing a purely random split introduces substantial data leakage which leads to a ∼30% underestimation of the expected MAE when, for example, predicting defects in a structure that represents an unseen chemical system in the training data. As an even more extreme example, CK = Elements reveals a ∼2.5 times higher expected MAE than a purely random split, although ensembling can reduce expected MAE by ∼30% relative to a non-ensemble prediction.
Fig. 2d confirms that the standard deviation of predictions over model ensembles is a useful uncertainty metric29,30 in this modeling application, but with some limitations. The individual residuals for any given test prediction (blue circles) are only very weakly correlated with σ({ΔĤV}L). However, computing the average and standard deviation of residuals within a given bin of σ({ΔĤV}L) (red markers and error bars, respectively) collapses the data onto the y = x parity line (cyan). Therefore, on average a low σ({ΔĤV}L) is correlated with a low residual, but there is a non-negligible probability of individual predictions with very large residuals despite low uncertainty.
The final key insight from the MatFold analysis stems from the dependence of expected MAE on both CK and D. Fig. 4 plots expected MAE for D = {0.1, 0.25, 0.5, 0.75, 1.0}, expressed on the x-axis in units of number of defect examples in the training data. Data leakage and underestimation of expected MAE are even more pronounced for the smallest dataset, and the rapid plateauing of the expected MAE with increasing data is potentially indicative of the absolute accuracy limit of the model. For more realistic screening criteria, i.e., CK = {Composition, Structure, Chemsys}, large accuracy gains are and will continue to be obtained with increasing data collection. Interestingly (and perhaps intuitively), for CK = Chemsys the improvement qualitatively appears to be saturating before the other criteria, but will only be confirmed with additional data collection. Finally, CK = Elements reveals that additional data collection does not increase the accuracy during inference on compounds containing unseen elements. In fact, the error slightly increased intermittently with additional data collection because it may have introduced compounds with new test set elements which are even more difficult to extrapolate to from the elements contained in the train set (see ESI† for more details).
Surface work function exemplar
To gain insights into generalization error trends for a different type of dataset and ML model, we utilize MatFold on our dataset of 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 332 work functions, ϕ, of surfaces (generated from 3716 bulk crystals that have a zero band gap) calculated by density functional theory (DFT).22 On average, each unique bulk crystal structure has ∼15 derived surfaces. The dataset contains work functions of elemental (261), binary (14
332 work functions, ϕ, of surfaces (generated from 3716 bulk crystals that have a zero band gap) calculated by density functional theory (DFT).22 On average, each unique bulk crystal structure has ∼15 derived surfaces. The dataset contains work functions of elemental (261), binary (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 623), and ternary (43
623), and ternary (43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448) crystalline surfaces. The ML model trained on this dataset was based on a random forest (RF) model and a physics-motivated custom featurization of the top-most three atomic surface layers considering their electron affinities, atomic radii, ionization energy, Mendeleev number as well as structural information in the form of area packing fraction and interlayer spacing (details explained in our previous work22). The final RF model trained with 15 features has a test-MAE of 0.09 eV utilizing a random 90/10 split and 5-fold CV for hyperparameter optimization. This MAE is about 4–5 times better than the best benchmarking model and more than six times better than the random baseline. The model enabled the discovery of surfaces with extreme work functions for thermionic energy conversion31 and high-brightness photocathodes.32,33 Studying this dataset with MatFold is especially interesting as it significantly differs from the defect dataset in size, classes of materials, and model architecture.
448) crystalline surfaces. The ML model trained on this dataset was based on a random forest (RF) model and a physics-motivated custom featurization of the top-most three atomic surface layers considering their electron affinities, atomic radii, ionization energy, Mendeleev number as well as structural information in the form of area packing fraction and interlayer spacing (details explained in our previous work22). The final RF model trained with 15 features has a test-MAE of 0.09 eV utilizing a random 90/10 split and 5-fold CV for hyperparameter optimization. This MAE is about 4–5 times better than the best benchmarking model and more than six times better than the random baseline. The model enabled the discovery of surfaces with extreme work functions for thermionic energy conversion31 and high-brightness photocathodes.32,33 Studying this dataset with MatFold is especially interesting as it significantly differs from the defect dataset in size, classes of materials, and model architecture.
We utilize similar split possibilities as for the defect dataset (see Table 2), except we do not automatically assign binary compounds to the training set (i.e., here we use only T = None). Moreover, for the LOO splits we excluded labels that make up less than 5% or more than 40% of the whole dataset to avoid unbalanced test set sizes (the user can specify these thresholds in MatFold). A total of 4046 unique splits were generated. As discussed in the previous section and Fig. 2 for the defect dataset, Fig. 3a and b show density parity plots of all outer test set (D = 1.0) predictions for CK = {Random, Structure, Composition, Chemsys, SG#, Elements} for non-nested S = K-fold and nested S = (K, L)-fold, respectively.
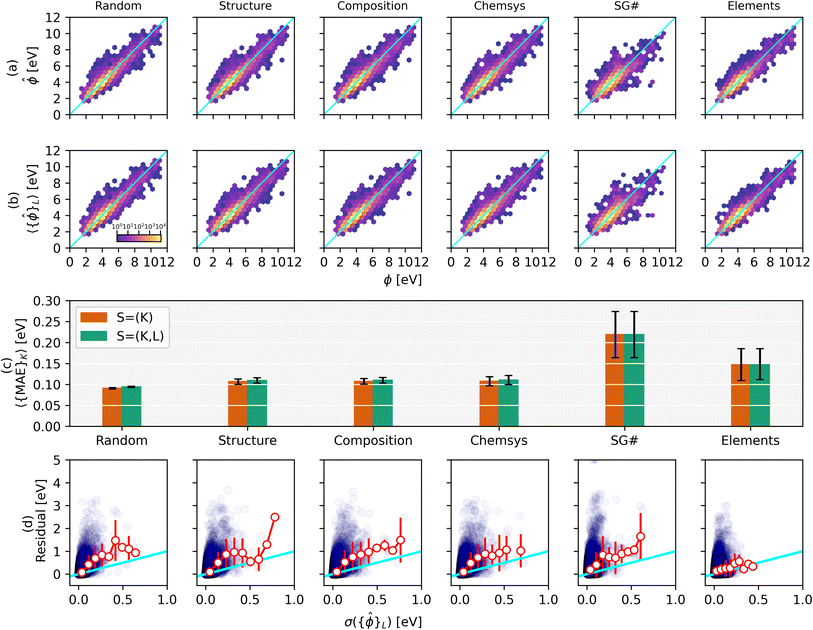 | ||
Fig. 3 Parity plots of DFT-calculated vs. ML-predicted work functions are shown for (a) K-fold and (b) nested (K, L)-fold splits for different splitting strategies. The color scale is on a logarithmic scale w.r.t. the number of structures at that grid point. The corresponding MAEs are displayed in (c) for K-fold and nested (K, L)-fold splits in green and orange, respectively. Quartile box plot of MAE and R2 values are shown in ESI Fig. 7.† The residuals, |ϕ − 〈{![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) }L〉|, are plotted vs. the standard deviation of the work function predictions (nested K-fold) in (d) alongside the average and standard deviation of residuals in 9 bins (white circles and red error bars, respectively). The individual residuals and corresponding standard deviations exhibit a negative R2 value for all splitting strategies. All units are in eV and the x = y line is highlighted in cyan. }L〉|, are plotted vs. the standard deviation of the work function predictions (nested K-fold) in (d) alongside the average and standard deviation of residuals in 9 bins (white circles and red error bars, respectively). The individual residuals and corresponding standard deviations exhibit a negative R2 value for all splitting strategies. All units are in eV and the x = y line is highlighted in cyan. | ||
Fig. 3c summarizes the MAEs for the parity plots displayed in (a) and (b). Unlike the defect dataset, the MAEs and their standard deviations for the work function dataset are very similar between the non-nested and nested splitting strategies. This likely stems from the GNN-based model being more prone to overfitting compared to the 15-feature RF model. Hence, the GNN model benefits more from statistical averaging during nested splitting. Like the defect dataset, the MAEs increase in the order Random < Structure < Composition < Chemsys < Elements. However, an interesting difference is that the SG# split exhibits the highest MAE, less than the MAE for the Elements split (219 and 149 meV, respectively for nested splits). Compared to the MAE of the random split this is an increase of 133% and 59%, respectively. This agrees well with the RF model features being largely comprised of elemental properties (e.g., electron affinity) while containing little structural information. The work function model generalizes better outside the elemental training distribution and worse outside the structural training distribution. Among all splits that leave one element out, the MAEs are significantly larger for holding out F, H, O, or Cl (1178, 959, 708, 657 meV, respectively; cf. periodic table heat map in ESI Fig. 8†). These elements typically exhibit complex chemical behavior that may not be well captured in other chemistries. Compared to random splitting the MAE (94 meV) increases by only ∼17% for structural, compositional, and chemical systems splitting (all three have an MAE of ∼110 meV for nested splits). This surprisingly small increase in MAE may be explained by the work function strongly depending on the element present in the topmost surface layer – hence, as long as an element is present in any chemical system (or composition) in the train set, the RF model is able to learn the elemental trend for the work function and can then extrapolate well for an unseen chemical system. The average MAE increases (218 meV) by holding out groups of the periodic table compared to holding out just Elements (149 meV). Similarly, the MAEs increase by holding out point groups (227 meV) and crystal systems (272 meV) compared to just holding out space groups (219 meV). ESI Fig. 6† displays the parity plots, MAE trends, and residuals for these additional hold-out strategies.
Similar to Fig. 2d, the residuals |ϕ – 〈{![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) L}〉| are plotted against the standard deviation of the work function predictions over model ensembles in Fig. 3d. Interestingly, the averages of the residuals within a given bin of σ({
L}〉| are plotted against the standard deviation of the work function predictions over model ensembles in Fig. 3d. Interestingly, the averages of the residuals within a given bin of σ({![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) }L) (red markers) tend to have a slightly greater slope than the x = y parity line (cyan). The overconfidence of this bootstrapped uncertainty metric appears to be typical of tree-based models using hand-engineered features and therefore requires re-calibration3 such that the expectation value of the residual for a given σ bin is closer to parity.
}L) (red markers) tend to have a slightly greater slope than the x = y parity line (cyan). The overconfidence of this bootstrapped uncertainty metric appears to be typical of tree-based models using hand-engineered features and therefore requires re-calibration3 such that the expectation value of the residual for a given σ bin is closer to parity.
Fig. 4b shows the dataset size dependence of the MAEs and their standard deviations for the work function dataset. A roughly linear decrease in the MAEs is observed with a logarithmic increase in the dataset size for splitting strategies CK = {Random, Structure, Composition, and Chemsys}. The standard deviations of the MAEs typically decrease with increasing dataset size. However, for splitting strategies CK = {SG#, Elements}, the MAEs start to plateau with increasing data size, indicating that additional data may no longer improve the RF model's capability to infer OOD samples accurately.
MatBench bulk modulus exemplar
The ΔHV and ϕ exemplars (1) contain relatively small datasets in terms of unique structures, (2) represent local property prediction tasks (i.e., multiple target values exist per unique structure), and (3) require specialty modeling approaches via the aforementioned GNN and RF works, respectively. Meanwhile, the Voigt–Reuss–Hill averaged bulk modulus, KVRH MatBench9 dataset represents a global property prediction task (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mapping between ≈10
1 mapping between ≈10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 unique structures and their target property) that can be generally modeled by either structure-based models (e.g., GNN) or compositionally-derived feature models (e.g., RF). MatFold-automated CV can readily be applied to this standard benchmarking MatBench dataset, where data exists in larger quantities and contains materials with elements spanning nearly the entire periodic table.
000 unique structures and their target property) that can be generally modeled by either structure-based models (e.g., GNN) or compositionally-derived feature models (e.g., RF). MatFold-automated CV can readily be applied to this standard benchmarking MatBench dataset, where data exists in larger quantities and contains materials with elements spanning nearly the entire periodic table.
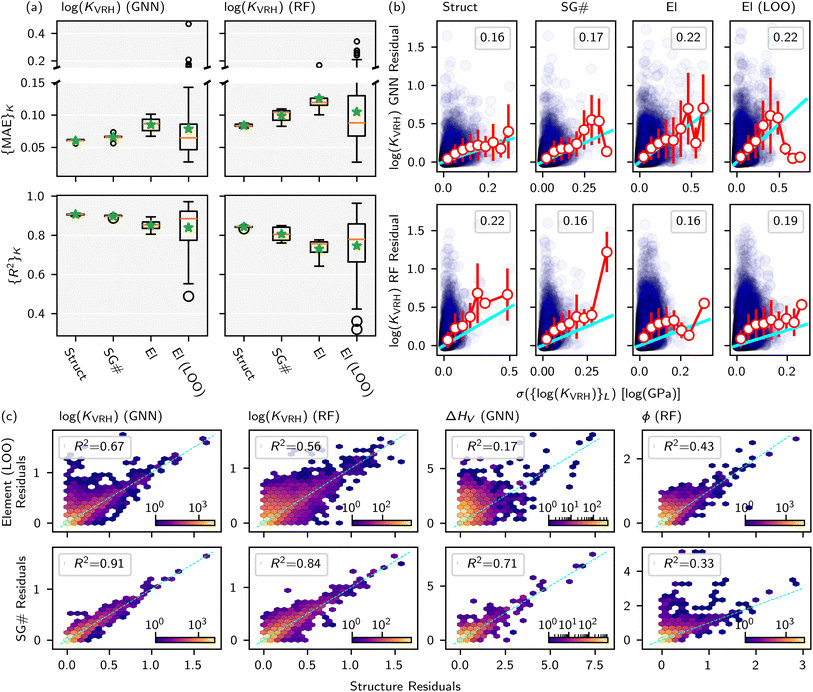
Fig. 5 shows (K = 5, L = 5)-fold test set predictions for CK = {Structure, SG#, Elements} and (K = LOO, L = 5)-fold test predictions for CK = {Elements}. Fig. 5a and b show the difference in performance between a GNN approach (using a crystal graph convolutional neural network, CGCNN) and an RF approach (using Magpie features), as detailed in MatBench.9 Compared to the CK = Structure baseline, the GNN generalizes much better to unseen structural motifs (CK = SG#) than unseen elements (CK = Elements) with a 9% vs. 41% increase, respectively, which is qualitatively consistent with observations in the ΔHV exemplar. The RF model shows an even larger 18% MAE increase for CK = SG# compared to its own CK = Structure baseline. For either modeling approach, the CK = Elements (LOO) have an 〈{MAE}K〉 that is notably larger than the CK = Structure baseline, but the median test set error is comparable, driven by a very large skew for some elemental test sets that are very poorly predicted.
Fig. 5b demonstrates that inner nested ensembles of structure-based models (GNN) produce an uncertainty metric that is close to parity with the residual on average (i.e., 〈Residual|σ〉 ≈ σ). While for a composition-based model, this metric tends to be overconfident (i.e., 〈Residual|σ〉 > σ). Interestingly, this observation is consistent with the previous exemplars, despite the significant differences between all three ΔHV, ϕ, and log(KVRH) datasets and modeling tasks. Nonetheless the uncertainty metric remains only very weakly correlated with the individual residuals (cf. R2 values stated in the respective Figures).
Finally, Fig. 5c presents a parity plot of the residuals from CK = {Element (LOO), SG#} vs. the residuals from CK = Structure for each dataset and models corresponding to D = 1.0, T = None, and S = (K, L). Notably, there can be strong correlations (R2 > 0.7) between them: many large prediction errors are simply because the structure itself is OOD with respect to all other structures in the dataset and does not specifically arise from being OOD with respect to the stricter splitting criteria. However, models/datasets with the lowest R2 values arise because the test set residuals for CK = Element (LOO) or CK = SG# are much larger than the residuals for CK = Structure. Here the stricter splitting criteria is enforcing the OOD test prediction, which otherwise is trivial because the structure is too similar to another in the dataset.
Discussion
MatFold provides an automated, easy-to-use tool for generating CV splits of materials data and ultimately enables deeper insights into a data-driven modeling approach's generalizability, uncertainty, and improvability. By computing expected error as a function of the splitting criteria in MatFold, one can both estimate OOD performance (via material featurization-agnostic CV splits) and readily and systematically decouple the expected generalization performance of a given modeling approach from its training dataset size. This can be combined with nested CV and bootstrapped model ensembles to ascertain the potential to mitigate over-fitting of high error outliers and the fidelity of uncertainty estimates. Finally, combining all of the above with fractional data hold-out indicates whether continued data collection is beneficial, and most importantly, how it depends on the OOD inference task probed by the different splitting criteria.Some intuitive similarities and differences in MatFold CV trends can be observed between different modeling approaches and data domains, as demonstrated in our three exemplars. As expected in these exemplars, purely random splits provide the most biased underestimation of expected MAE, but the evolution of expected MAE with increasingly strict splitting criteria is heavily dependent on the modeling approach and data domain. For GNN's predictions of ΔHV (a direct crystal structure input model), the expected MAE on structures with unseen elements is nearly double that of structures with unseen space groups. Yet the opposite is true for RF predictions of ϕ (a hand-engineered feature input model). Therefore these ΔHV GNN models generalize better to unseen structural motifs than unseen chemistry, the exact opposite of the ϕ RF models. Trained on smaller datasets and even more sensitive to local structural features (e.g., when a vacancy defect site itself corresponds to the held out element), these local property models' expected error showed higher sensitivity to the splitting criteria than a global property model trained on a much larger dataset (the MatBench bulk modulus). This further highlights the need for performing the comprehensive and automated CV splitting analysis enabled by MatFold in any given study to gain a detailed and unbiased perspective on a materials discovery model's generalization limitations.
The ΔHV GNN predictions also benefit substantially from bootstrapped model ensembling to reduce over-fitting and mitigate outliers in test set prediction parity, while no benefit is observed in the ϕ RF models. Consequently, we observed the need to re-calibrate the bootstrapped uncertainty metric derived for the ϕ RF models, but not for the ΔHV GNN models. This observation also holds true for both GNN vs. RF models trained for the same global property log(KVRH) modeling task. It should be noted that re-tuning the hyperparameters during model ensembling could further reduce over-fitting but comes at a large computational cost (e.g., tuning 2 hyperparameters with 10 possible values each would already require training 100 times more models). Finally, in both ΔHV and ϕ exemplars, we generally observe continued improvement in model performance with more training data for moderately difficult OOD inference (e.g., structure, composition, or chemsys splits). However, for their weakest inference task (Elements for ΔHV GNN and SG# for ϕ RF models), neither is likely to improve further with additional data indicating fundamental limitations of the respective model architectures.
We anticipate that the splitting criteria and other functionality introduced by MatFold will lower the bar for better and more automated CV of data-driven materials models. Practitioners will have a better understanding of their expected accuracy for materials discovery in increasingly difficult OOD inference, regardless of their modeling approach because MatFold CV splits are only material dependent and entirely material featurization-agnostic. This will also enable deeper insights of materials discovery performance spanning differing modeling approaches and data domains and, if widely adopted, provide more grounded evidence for which modeling approaches may be more appropriate in various materials discovery situations.
Code availability
The code is available open-source on GitHub (at https://github.com/d2r2group/MatFold) and can be installed by pip. A frozen version of the code is permanently accessible on Zenodo via this link: https://doi.org/10.5281/zenodo.13147391.Data availability
The work function database is available for download at https://doi.org/10.5281/zenodo.10381505. The ΔHV data,21,28 is available for download from its original source at https://doi.org/10.5281/zenodo.808787127 and https://doi.org/10.1021/jacs.1c05570. We summarize the data in supplementary_files_defects.zip file that contains all CIF files and a CSV file with the corresponding structure name, index of the vacancy defect, and vacancy formation energy.Author contributions
M. D. W. performed writing – original draft (lead); review and editing (equal); software (equal); methodology (equal); visualization (lead); investigation (equal); data curation (equal); conceptualization (lead); supervision (equal); resources (equal). P. S. performed writing – original draft (supporting); review and editing (equal); software (equal); methodology (equal); visualization (supporting); investigation (equal); data curation (equal); conceptualization (supporting); supervision (equal); resources (equal).Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors gratefully acknowledge research support from the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Fuel Cell Technologies Office through the HydroGEN Consortium. This work was supported by the Laboratory Directed Research and Development (LDRD) program at Sandia National Laboratories. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly-owned subsidiary of Honeywell International Inc., for the U.S. Department of Energy's National Nuclear Security Administration (DOE/NNSA) under contract DE-NA0003525. This written work is authored by an employee of NTESS. The employee, not NTESS, owns the right, title and interest in and to the written work and is responsible for its contents. Any subjective views or opinions that might be expressed in the written work do not necessarily represent the views of the U.S. Government. The publisher acknowledges that the U.S. Government retains a non-exclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this written work or allow others to do so, for U.S. Government purposes. The DOE will provide public access to results of federally sponsored research in accordance with the DOE Public Access Plan. P. S. gratefully acknowledged the start-up funds from Northeastern University, Department of Mechanical and Industrial Engineering.References
- D. Morgan and R. Jacobs, Opportunities and Challenges for Machine Learning in Materials Science, Annu. Rev. Mater. Res., 2020, 50, 71–103 CrossRef.
- R. Jacobs, L. E. Schultz, A. Scourtas, K. J. Schmidt, O. Price-Skelly, W. Engler, I. Foster, B. Blaiszik, P. M. Voyles and D. Morgan, Machine Learning Materials Properties with Accurate Predictions, Uncertainty Estimates, Domain Guidance, and Persistent Online Accessibility, arXiv, 2024, preprint, DOI:10.48550/arXiv.2406.15650.
- G. Palmer, S. Du, A. Politowicz, J. P. Emory, X. Yang, A. Gautam, G. Gupta, Z. Li, R. Jacobs and D. Morgan, Calibration after bootstrap for accurate uncertainty quantification in regression models, npj Comput. Mater., 2022, 8, 115 CrossRef.
- S. Jiang, S. Qin, R. C. Van Lehn, P. Balaprakash and V. M. Zavala, Uncertainty quantification for molecular property predictions with graph neural architecture search, Digital Discovery, 2024, 3(8), 1534–1553, 10.1039/D4DD00088A.
- J. Gawlikowski, C. R. N. Tassi, M. Ali, J. Lee, M. Humt, J. Feng, A. Kruspe, R. Triebel, P. Jung, R. Roscher, M. Shahzad, W. Yang, R. Bamler and X. X. Zhu, A survey of uncertainty in deep neural networks, Artif. Intell. Rev., 2023, 56, 1513–1589 CrossRef.
- D. Baumann and K. Baumann, Reliable estimation of prediction errors for QSAR models under model uncertainty using double cross-validation, J. Cheminf., 2014, 6, 1–19 Search PubMed.
- S. K. Kauwe, J. Graser, R. Murdock and T. D. Sparks, Can machine learning find extraordinary materials?, Comput. Mater. Sci., 2020, 174, 109498 CrossRef.
- B. Meredig, E. Antono, C. Church, M. Hutchinson, J. Ling, S. Paradiso, B. Blaiszik, I. Foster, B. Gibbons, J. Hattrick-Simpers, A. Mehta and L. Ward, Can machine learning identify the next high-temperature superconductor? Examining extrapolation performance for materials discovery, Mol. Syst. Des. Eng., 2018, 3, 819–825 RSC.
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, Benchmarking materials property prediction methods: the Matbench test set and Automatminer reference algorithm, npj Comput. Mater., 2020, 6, 138 CrossRef.
- S. S. Omee, N. Fu, R. Dong, M. Hu and J. Hu, Structure-based out-of-distribution (OOD) materials property prediction: a benchmark study, npj Comput. Mater., 2024, 10, 144 CrossRef.
- J. Hu, D. Liu, N. Fu and R. Dong, Realistic material property prediction using domain adaptation based machine learning, Digital Discovery, 2024, 3, 300–312 RSC.
- K. Li, B. DeCost, K. Choudhary, M. Greenwood and J. Hattrick-Simpers, A critical examination of robustness and generalizability of machine learning prediction of materials properties, npj Comput. Mater., 2023, 9, 1–9 CrossRef.
- H. Zhang, W. Chen, J. M. Rondinelli and W. Chen, ET-AL, Entropy-targeted active learning for bias mitigation in, Appl. Phys. Rev., 2023, 10(2), 021403 Search PubMed.
- Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing and V. Pande, MoleculeNet: a benchmark for molecular machine learning, Chem. Sci., 2018, 9, 513–530 RSC.
- Z. Xiong, Y. Cui, Z. Liu, Y. Zhao, M. Hu and J. Hu, Evaluating explorative prediction power of machine learning algorithms for materials discovery using k-fold forward cross-validation, Comput. Mater. Sci., 2020, 171, 109203 CrossRef.
- R. P. Sheridan, Time-Split Cross-Validation as a Method for Estimating the Goodness of Prospective Prediction, J. Chem. Inf. Model., 2013, 53, 783–790 CrossRef PubMed.
- K. Li, D. Persaud, K. Choudhary, B. DeCost, M. Greenwood and J. Hattrick-Simpers, Exploiting redundancy in large materials datasets for efficient machine learning with less data, Nat. Commun., 2023, 14, 1–10 Search PubMed.
- K. Li, A. N. Rubungo, X. Lei, D. Persaud, K. Choudhary, B. DeCost, A. B. Dieng and J. Hattrick-Simpers, Probing out-of-distribution generalization in machine learning for materials, arXiv, 2024, preprint, arxiv:2406.06489, DOI:10.48550/arXiv.2406.06489.
- T. Xie and J. C. Grossman, Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties, Phys. Rev. Lett., 2018, 120, 145301 CrossRef PubMed.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A general-purpose machine learning framework for predicting properties of inorganic materials, npj Comput. Mater., 2016, 2, 16028 CrossRef.
- M. D. Witman, A. Goyal, T. Ogitsu, A. H. McDaniel and S. Lany, Defect graph neural networks for materials discovery in high-temperature clean-energy applications, Nat. Comput. Sci., 2023, 3, 675–686 CrossRef.
- P. Schindler, E. R. Antoniuk, G. Cheon, Y. Zhu and E. J. Reed, Discovery of Stable Surfaces with Extreme Work Functions by High-Throughput Density Functional Theory and Machine Learning, Adv. Funct. Mater., 2024, 2401764, 1–12 Search PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals, Chem. Mater., 2019, 31, 3564–3572 CrossRef.
- K. Choudhary, B. DeCost, L. Major, K. Butler, J. Thiyagalingam and F. Tavazza, Unified graph neural network force-field for the periodic table: solid state applications, Digital Discovery, 2023, 2, 346–355 RSC.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling, Nat. Mach. Intell., 2023, 5, 1031–1041 CrossRef.
- I. Batatia, et al., A foundation model for atomistic materials chemistry, arXiv, 2023, preprint, arXiv:2401.00096, DOI:10.48550/arXiv.2401.00096.
- M. Witman, A. Goyal, T. Ogitsu, A. H. McDaniel and S. Lany, A database of vacancy formation enthalpies for materials discovery (0.0.1) [dataset], Zenodo, 2023, DOI:10.5281/zenodo.8087871.
- R. B. Wexler, G. S. Gautam, E. B. Stechel and E. A. Carter, Factors Governing Oxygen Vacancy Formation in Oxide Perovskites, J. Am. Chem. Soc., 2021, 143, 13212–13227 CrossRef PubMed.
- H.-J. Lu, N. Zou, R. Jacobs, B. Afflerbach, X.-G. Lu and D. Morgan, Error assessment and optimal cross-validation approaches in machine learning applied to impurity diffusion, Comput. Mater. Sci., 2019, 169, 109075 CrossRef.
- V. Agrawal, S. Zhang, L. E. Schultz and D. Morgan, Accelerating Ensemble Error Bar Prediction with Single Models Fits, arXiv, 2024, preprint, arxiv:2404.09896, DOI:10.48550/arXiv.2404.09896.
- P. Schindler, D. C. Riley, I. Bargatin, K. Sahasrabuddhe, J. W. Schwede, S. Sun, P. Pianetta, Z.-X. Shen, R. T. Howe and N. A. Melosh, Surface Photovoltage-Induced Ultralow Work Function Material for Thermionic Energy Converters, ACS Energy Lett., 2019, 4, 2436–2443 CrossRef PubMed.
- E. R. Antoniuk, P. Schindler, W. A. Schroeder, B. Dunham, P. Pianetta, T. Vecchione and E. J. Reed, Novel Ultrabright and Air-Stable Photocathodes Discovered from Machine Learning and Density Functional Theory Driven Screening, Adv. Mater., 2021, 33, 2104081 CrossRef PubMed.
- E. R. Antoniuk, Y. Yue, Y. Zhou, P. Schindler, W. A. Schroeder, B. Dunham, P. Pianetta, T. Vecchione and E. J. Reed, Generalizable density functional theory based photoemission model for the accelerated development of photocathodes and other photoemissive devices, Phys. Rev. B, 2020, 101, 235447 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: The ΔHV dataset is provided in the supplementary_files_defects.zip. Additional CV analysis showing inference performance for additional hold-out strategies. MAE heatmaps and parity plots for leave-one-element-out splits. Quartile boxplots of model performance metrics. See DOI: https://doi.org/10.1039/d4dd00250d |
| This journal is © The Royal Society of Chemistry 2025 |

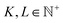
![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif)