A multi-robot–multi-task scheduling system for autonomous chemistry laboratories

Abstract

We present a multi-robot–multi-task scheduling system designed for autonomous chemistry laboratories to enhance the efficiency of executing complex chemical experiments. Building on the herein formulated and developed scheduling algorithms and employing a constraint programming approach, the scheduling system optimizes task allocation across three robots and 18 experimental stations, facilitating the coordinated and concurrent execution of experiments. The system allows for dynamic task insertion during ongoing operations without significant disruption, enhancing laboratory efficiency and flexibility while providing a scalable solution for high-throughput experimentation. In real-world applications involving four diverse chemical experiments with varied step counts, step durations, and sample throughputs, the system demonstrated its ability to reduce total execution time by nearly 40% compared to sequential execution of individual experiments, where in-experiment tasks were already optimized for concurrency. Our multi-robot–multi-task system represents a timely and significant advancement in autonomous chemistry, enabling automated laboratories to conduct experiments with greater efficiency and versatility. By reducing the time and resources required for experimentation, it accelerates the pace of scientific discovery and offers a robust framework for developing more sophisticated autonomous laboratories capable of handling increasingly complex and diverse scientific tasks.

---

Main

In recent years, the fields of chemistry and materials science have experienced a profound transformation driven by advances in laboratory automation and robotics.^1–17 The rapid development of sophisticated automation systems, including high-throughput platforms, dexterous robotic arms, mobile robots, and automated experimental stations, is propelling the continuous evolution of autonomous chemistry laboratories. These advancements not only significantly shorten the time from hypothesis formation to experimental validation but also expand researchers' perspectives and experimental boundaries. They provide powerful tools for addressing complex scientific problems, enabling research in chemistry and materials science to advance at unprecedented speed and scale.

In recent years, several notable initiatives have emerged in the field of autonomous chemistry laboratories, also referred to as self-driving laboratories. These initiatives encompass a wide range of technological advancements, from programmable Chemputers for molecular synthesis^6,7 to mobile robotic chemists capable of conducting multi-step material synthesis, characterization, and testing.^1,5 Additionally, advancements include autonomous reaction optimization driven by large language models (LLMs)³ and AI-coordinated self-driving labs that facilitate asynchronous, cloud-based, and delocalized closed-loop discovery of functional molecules.⁸ These automated systems, which typically operate in a “single-robot–single-task” mode, have demonstrated significant efficacy and efficiency in achieving their intended goals.

Research in chemistry and materials science often involves complex experimental demands, requiring the execution of multiple diverse and intricate operations within individual tasks, as well as the ability to conduct various tasks in parallel. Single-robot systems and single-task scheduling strategies can struggle to meet these challenges effectively. To address these limitations, researchers have turned to multi-robot collaborative systems and multi-task parallelization strategies. For example, Lunt et al. developed a system using three different types of robots to collaboratively execute a complex 12-step workflow, showcasing the ability to integrate various robotic capabilities within a single task.⁹ Similarly, Strieth-Kalthoff et al. created a decentralized automated laboratory by deploying robots across four geographically separated sites, enabling the collaborative discovery of functional materials.⁸ Furthermore, Fei et al. designed a general-purpose software framework that implements the parallel execution of diverse workflows composed of modular tasks using a greedy algorithm.¹⁵ Meanwhile, Yoo et al. proposed a closed-packing algorithm, which, under the premise of the greedy algorithm, optimizes idle resource utilization, improving resource efficiency in multi-task parallel experiments.¹⁶ These examples of “multi-robot–single-task”, “distributed-system-single-task”, and “single-robot–multi-task” setups demonstrate the significant potential of automated laboratories to handle complex experimental tasks more efficiently.

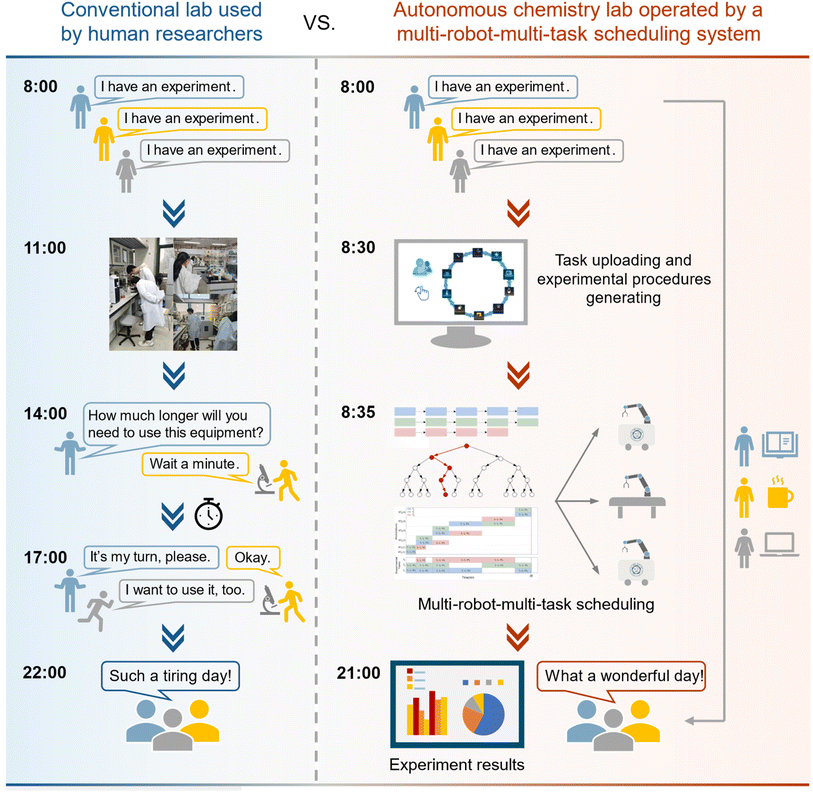
In conventional chemistry laboratories (Fig. 1), it is common for multiple researchers to conduct various experiments simultaneously. This “multi-researcher–multi-task” approach is a core characteristic of laboratory work, as it relies on the division of experimental resources and cooperation among researchers to optimize resource utilization. Reproducing this collaborative effort in an autonomous chemistry laboratory—achieving effective and efficient collaboration in a “multi-robot–multi-task” scenario—is crucial for advancing chemistry automation. However, it remains a significant challenge, and to the best of our knowledge, no direct demonstration of such capability has been reported. For autonomous chemistry laboratories to handle the parallel execution of diverse experimental tasks with complex constraints in a coordinated manner, they must possess strategies and capabilities to autonomously plan the sequence and timing of specific experimental steps, resolve resource conflicts between tasks from a global perspective, ensure rational resource allocation and efficient utilization, and allocate tasks to multiple robots to guarantee the successful completion of all tasks. Additionally, these systems must be flexible enough to accommodate new tasks and adapt existing ones as they run.

Fig. 1 Conceptual diagram of the herein developed multi-robot–multi-task system.

Multi-robot–multi-task scheduling has been a focal research area in the industrial sector, demonstrating significant value in fields such as logistics, warehousing, autonomous driving, and intelligent workshops.^18–35 In logistics and warehousing, research and applications of multi-robot–multi-task scheduling primarily focus on structured tasks such as pickup and delivery,^18,19 with multi-agent path finding as a central component. Methods like Conflict-Based Search (CBS)^21–24 cleverly address path conflict issues that may arise when multiple robots move simultaneously between locations. This approach provides robust theoretical and practical support for efficient, conflict-free task execution in complex environments and has received widespread recognition in the industry. In intelligent workshops, multi-task scheduling is crucial due to the complexity of mixed assembly lines and the high demand for diverse components. Workshops must sequence the production processes of different parts based on multiple production goals and environmental conditions, optimizing one or more performance metrics to enhance overall production efficiency and resource utilization. The Job-shop Scheduling Problem (JSP)^25–30 and its derivatives—such as the Flexible Job-shop Scheduling Problem (FJSP)^{25,27,31–33} and the Flexible Job-shop Scheduling Problem with machines having Batch-processing capacity (FJSP-B)^34,35—provide a solid theoretical foundation for solving multi-task scheduling problems in workshops. These frameworks allow for the consideration of constraints such as machine resources and production deadlines, ensuring that scheduling is both efficient and adaptable to changing demands.

In autonomous chemistry laboratories, the challenge of parallel scheduling for various experimental tasks is analogous to the FJSP-B scenario. Chemical experiments often involve numerous constraints, such as reaction temperature, stirring speed, and reaction time, which add layers of complexity beyond those typically encountered in machining environments. In this work, we propose a multi-robot–multi-task scheduling system based on the FJSP-B framework that incorporates additional constraints specific to chemical experiments. Our system employs a constraint programming approach to generate scheduling schemes capable of handling multiple experimental tasks concurrently, ensuring that all constraints are met and that resources are optimally utilized. We consider the transfer of experimental samples in autonomous chemistry laboratories using mobile robots, which places high demands on transfer efficiency and requires effective resolution of route conflicts. To tackle this issue, we apply the CBS algorithm, which efficiently resolves path conflicts in multi-robot environments, to ensure that each experimental sample is delivered to its designated location accurately and on time, facilitating seamless integration of the experimental process.

Our multi-robot–multi-task scheduling system provides end-to-end automation for parsing, scheduling, and executing concurrent experimental tasks. By assessing the laboratory's current resources, the system efficiently processes a variety of tasks submitted by researchers, generating optimal scheduling plans. Tasks are dynamically assigned to multiple robots in real time, enabling efficient parallel processing. With an interactive graphical interface, researchers can input tasks, which are then translated into algorithm-parsable formats, optimized, and executed by robots. This approach offers a viable solution for achieving intelligent scheduling, automation, and simultaneous execution of multiple chemical experiments in autonomous chemistry laboratories.

In summary, the innovations of this paper are as follows:

- We propose the FESP-B model, which is the first to model chemical experimental tasks with complex constraints as a global optimization problem. The model aims to minimize the overall makespan as the objective function and guides the optimization process through a series of constraints. This global perspective enables FESP-B to effectively handle dependencies across tasks, resource limitations, and complex synchronization requirements, thereby generating the optimal task scheduling solution.

- Based on the FESP-B model, we further developed a multi-robot–multi-task scheduling algorithm and successfully implemented the corresponding scheduling system. By combining the optimization results of FESP-B with the multi-robot scheduling algorithm, our system can automate the entire chemical experimental process, significantly improving the efficiency and accuracy of laboratory operations.

Results

Multi-task scheduling

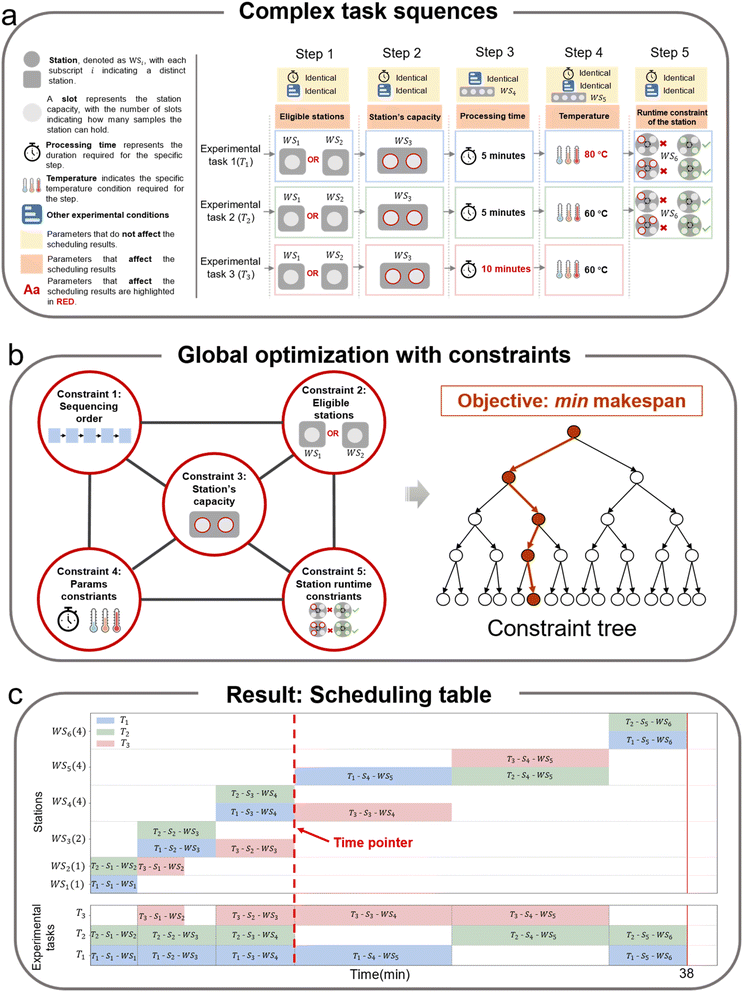
Completing a chemical experimental task involves sequentially passing an experimental sample through specific stations for operations such as synthesis, characterization, and testing. Each operation contributes to the “assembly” of the final product or result and completing all operations marks the task's completion. Incorporating batch-processing stations, like magnetic stirring stations with parallel processing capabilities, is essential for high-throughput experimentation. A sample requiring magnetic stirring station, for example, can be processed at any available station, and each station can stir multiple samples in the same batch if the parameters—stirring time, temperature, and rotation speed—are identical. Moreover, chemical experimental tasks often involve multiple parameter constraints; for example, drying operations are constrained by time and temperature, while centrifugation is constrained by time and rotation speed. The flexibility in choosing stations for samples, combined with the requirement to meet these constraints, adds significant complexity to the multi-task scheduling problem for chemical experiments. To address this, we formulate the problem as a Flexible Experiment Scheduling Problem with Batch-processing capabilities (FESP-B), drawing inspiration from the FJSP-B in intelligent workshops. This problem formulation is described in detail below.

Consider a laboratory with a total of m stations, represented as WS = {WS₁, WS₂,⋯, WS_m}, where each station has a corresponding maximum working capacity. Some stations have specific runtime constraints (e.g., a centrifuge station requires samples to be placed symmetrically to ensure balance, which imposes constraints on the number of samples it can process in a batch). Assume there are n experimental tasks to be conducted in the laboratory, represented as T = {T₁, T₂, ⋯, T_n}. Each specific experimental task T_i essentially consists of a series of ordered operation steps with specific parameters. The parameters for each operation step include the expected processing time for the step, a list of eligible stations where the step can be executed, and experimental conditions other than processing time, such as temperature settings for drying or speed settings for magnetic stirring. The constraints that must be satisfied during the experimental process are:

(1) Operation steps within the same experimental task must be processed in sequence.

(2) At any given time, an experimental sample can only be processed by one station.

(3) At any given time, the number of experimental samples processed by a station must not exceed its maximum capacity.

(4) At any given time, only experimental samples with identical processing times and experimental conditions can be handled by the same station.

(5) Each station must meet the corresponding runtime constraints while performing the operational steps.

The goal of solving the problem is to schedule the tasks for each station to determine the start time and end time for each step in each experimental task, with the objective of minimizing the maximum completion time of all experimental tasks. To solve this optimization problem, we adopted the constraint programming approach for the FJSP-B^35,36 and adapted it to yield a new constraint programming approach specifically for FESP-B. Details of the algorithm are provided in the ESI.†

Fig. 2 outlines the scheduling process of a multi-task scheduling problem involving three chemical experimental tasks with different parameters, as an illustrative example. Fig. 2a shows the initial sequence of these tasks and highlights the differences between them. After analysis, Fig. 2b depicts the scheduling process using a constraint programming algorithm, and Fig. 2c shows the final scheduling results. The following describes how contraints in Fig. 2b affect the scheduling outcomes in Fig. 2c:

Fig. 2 An illustrative example of a multi-task scheduling problem involving three chemical experimental tasks and their scheduling process. (a) The initial sequence derived by analysing the task sequence and laboratory resources: tasks 1 and 2 have five steps each, while task 3 has four steps. Identical parameters for the first steps allow tasks to be performed on either WS₁ or WS₂, highlighting the role of redundant resources. The second steps, which can only be done on WS₃ with a capacity of 2, illustrate the impact of station capacity. For the third steps, tasks 1 and 2 differ in time from task 3, while other parameters match. In the fourth steps, tasks 2 and 3 have different temperatures compared to task 1. These variations demonstrate the influence of processing time and experimental conditions. The fifth step of tasks 1 and 2 must be done on WS₆, requiring an specific number of samples (i.e., 2 or 4) for balance, illustrating runtime constraints. (b) Solving the FESP-B problem with a constraint programming algorithm involves adding constraints based on task sequences, constructing them into a tree, and using heuristic search to find optimal solutions. (c) Scheduling results for an illustrative example, consisting of a station scheduling table and an experimental task scheduling table, use rectangles to represent task steps, with labels T_i–S_j–WS_k indicating assignments: i-th experimental task's j-th step, conducted on the WS_k station. Start and end times are shown on the rectangle's edges, with overlapping rectangles indicating parallel operations. The end time of the last step represents the makespan. The station scheduling table's vertical axis lists stations with capacities in brackets, while the experimental task scheduling table's vertical axis shows tasks, with dashed lines distinguishing steps. A time pointer traverses the scheduling table, guiding task execution.

(1) Sequence constraints within an experimental task. This constraint ensures that the sequence of experimental steps within each task remains unchanged. Thus, from the perspective of each task in the scheduling table, although there may be time gaps between steps due to other constraints, the order of the steps is always fixed and will not be disrupted.

(2) Allocation of eligible stations. This involves listing candidate stations for each step of a specific experimental task. The first step of all three tasks can be processed on either WS₁ or WS₂. As WS₁ and WS₂ are single-capacity stations, each can process only one sample (i.e., one step of a task) at a time. However, WS₁ and WS₂ can process different samples, from two different tasks, in parallel. According to the scheduling tables, step 1 of tasks 1 and 2 are processed simultaneously on WS₁ and WS₂, while step 1 of task 3 follows.

(3) Station capacity limitation. This parameter specifies the number of operations a station can handle simultaneously. For instance, WS₃ has a maximum capacity of 2, so step 2 of the three tasks cannot be processed at the same time, despite being identical. Thus, step 2 of tasks 1 and 2 are processed first, followed by step 2 of task 3.

(4) Processing time of current step. This parameter indicates the estimated processing time of the current step. For instance, for the third step of the three tasks, the processing time for task 3 differs from tasks 1 and 2, although other parameters remain the same. Only steps with the same processing time and experimental conditions can be assigned to the same station for parallel processing. Although WS₄ can process up to four samples simultaneously, the discrepancy in processing time prevents simultaneous processing of all three tasks. Therefore, step 3 of tasks 1 and 2 are processed first, followed by step 3 of task 3.

(5) Experimental conditions other than processing time. Specific conditions are set according to each step and each station's specification, such as temperature for drying stations, and temperature and rotation speed for stirring stations. In the fourth step of the three tasks, all parameters match except temperature. Samples from tasks 2 and 3 can be processed in the same batch due to matching temperature parameters, while the sample from step 4 of task 1 is processed separately.

(6) Runtime constraints of stations. Some stations have specific runtime constraints. For example, the centrifuge station (WS₆) requires a specific number of samples to be placed symmetrically to maintain balance. Therefore, although step 4 of task 1 finishes before that of task 2, it waits until task 2 is ready so both can be processed together, satisfying the runtime constraint of WS₆.

In the illustrative example shown in Fig. 2, by considering and addressing all constraints, the final completion time for conducting all tasks concurrently is optimized to 38 minutes. In comparison, performing the same three tasks sequentially requires a total of 84 minutes.

Since most existing multi-task scheduling algorithms are based on greedy strategies and lack the ability to handle runtime constraints of stations, it is difficult to make a comprehensive comparison between the performance of FESP-B and these algorithms. However, ESI, Fig. S1† presents a simple example where all tasks have no complex synchronization requirements, allowing the greedy algorithm to execute smoothly following a “first-come-first-served” principle without violating any critical constraints. This example demonstrates the advantage of FESP-B's global optimization through its objective function, reducing the experimental time by 45% compared to the local optimization of the greedy algorithm. This indicates that even in relatively simple task environments, FESP-B can significantly improve experimental efficiency through its global optimization capability, showing a clear advantage over traditional methods.

Multi-robot–multi-task scheduling

The scheduling table provides a clear execution plan for multiple experimental tasks, with robots acting as executors. When executing tasks according to the scheduling table, a time pointer traverses from the left end, guiding task execution. Robots must retrieve samples from their stations when the operation step's end time equals the time pointer and place samples into stations when the start time equals the time pointer. Since operation steps within a task are sequential, a sample must complete the current step before beginning the next. Therefore, at the time indicated by the time pointer, robots first remove all samples that need to be taken out and then place samples that need to start their next step into the corresponding stations.

In Fig. 2c, at the time point indicated by the time pointer, for example, the robot first removes the sample of experimental task 3 from WS₃ and the samples of tasks 1 and 2 from WS₄, then places the sample of task 3 into WS₄ and the sample of task 1 into WS₅. If there is only one mobile robot, it must sequentially remove samples from WS₃ and WS₄, and then place them into WS₄ and WS₅. With two mobile robots, robot 1 can take the sample from WS₃ while robot 2 takes samples from WS₄, allowing robot 1 to place its sample into WS₄ while robot 2 places its sample into WS₅. This approach halves the sample transfer time compared to a single-robot scenario. At any given time point, samples to be removed are categorized by their respective stations, and all samples from the same station are assigned to the same robot. If the number of robots matches the number of station categories, each robot is assigned to a designated station to retrieve samples. If there are fewer robots than station categories, those handling fewer samples are assigned additional stations. If there are more robots than station categories, some robots remain idle. Samples that need to be placed into stations are handled by the robot carrying them. In case of conflicts where multiple robots need access to the same station, they will take turns placing the samples.

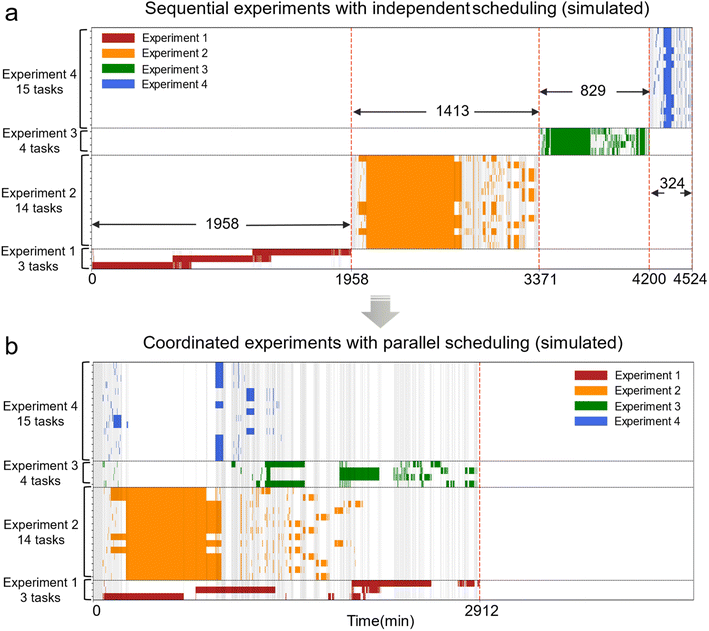
The impact of multi-robot–multi-task scheduling was assessed through simulations involving four types of chemical experiments, each with different setups. Experiment 1 consisted of 3 tasks, each with 11 steps; experiment 2 included 14 tasks, each with 12 steps; experiment 3 comprised 4 tasks, each with 23 steps; and experiment 4 involved 15 tasks, each with 6 steps. Together, these tasks utilized 18 different stations, with capacities ranging from 1 to 20, and individual step processing times varying from 3 to 720 minutes. Fig. 3 presents optimized task scheduling tables for four types of chemical experiments, comprising a total of 36 tasks (i.e., samples), using two mobile robots in the laboratory. Two scenarios are considered: (1) the four different types of experiments are conducted sequentially with multi-robot–multi-task scheduling applied only within each experiment (Fig. 3a); (2) a full parallel multi-robot–multi-task scheduling is applied to all tasks across the four experiments (Fig. 3b). In the first scenario, the sequential execution requires 1958 minutes for experiment 1 (3 tasks), 1413 minutes for experiment 2 (14 tasks), 829 minutes for experiment 3 (4 tasks), and 324 minutes for experiment 4 (15 tasks), totalling 4524 minutes. In contrast, the full parallel scheduling requires only 2912 minutes, reducing the total execution time to 64% of that needed for sequential experiments and achieving significant time efficiency improvements.

Fig. 3 Simulated multi-robot–multi-task scheduling tables for four experiments using 2 mobile robots. Grey vertical lines indicate the estimated sample transfer time, and each colour other than grey represents a different type of experiment. Each tick on the vertical axis represents an experimental task (i.e., sample), while the horizontal axis depicts the timeline. Both scheduling tables share the same timeline. (a) Scheduling table for individual experiments conducted sequentially, with tasks within each experiment scheduled together. (b) Scheduling table for parallel execution of the different types of experiments, with all tasks scheduled concurrently.

Fig. 4 illustrates the positive impact of increasing the number of mobile robots and using cross-experiment parallel scheduling to reduce the makespan of experiments. Simulation results show that deploying more robots in the lab improves the efficiency of sample transfers, thereby shortening the makespan. However, this time reduction effect diminishes as the number of robots increases for three main reasons. First, pure experimental times—the time required for each experiment itself—remain unchanged, regardless of any efficiency gains in sample transfers. ESI, Fig. S2a† shows that the essential total duration of the four experiments, excluding sample transfer times, is 1928 minutes. Thus, even with zero transfer time, the minimum experimental duration is still 1928 minutes. Second, adding more robots does not proportionally enhance sample transfer efficiency. In the scenario depicted in ESI, Fig. S2b,† at a given time step, two samples require transfer with different starting and ending points. With one robot, two transfers are needed. With two robots, each robot handles one sample, halving the transfer time. However, with three robots, only two samples need transfer, leaving the third robot idle, and the transfer time remains the same as with two robots. Finally, if the experimental process is dominated by a long-duration step, the transfer time of short-duration steps during this phase, although influenced by the number of robots, will not affect the overall experimental process. As shown in the grey rectangle of ESI, Fig. S2c,† the time required for short-duration steps may vary with the number of robots, but this variation does not impact the total completion time due to the lengthy waiting period for the long-duration step that follows. These factors create a saturation point for optimization, beyond which adding more robots provides diminishing returns in improving time efficiency.

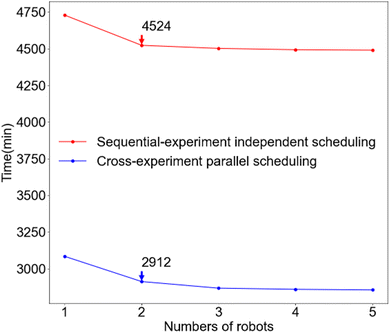Fig. 4 Simulated scenarios of using 1 to 5 robots to automate the four experiments shown in Fig. 3. Comparison of the overall completion time between cross-experiment parallel scheduling and sequential-experiment independent scheduling of the four different types of experiments, considering varying numbers of mobile robots. The vertical axis represents the total time to complete all four experiments, while the horizontal axis represents the number of robots.

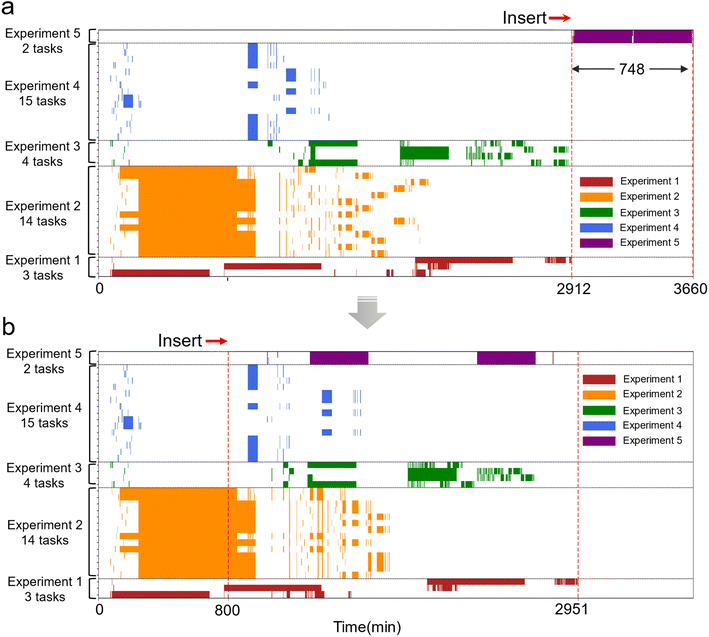
Importantly, our multi-robot–multi-task scheduling system can dynamically handle the insertion of new tasks during the operation of existing ones. Fig. 5a illustrates the simulated scenario of conducting a new experiment 5 after completing the initial four experiments, which were scheduled concurrently using the cross-experiment parallel scheduling approach shown in Fig. 3b. In this case, experiment 5 took 748 minutes to finish, resulting in a total completion time of 3660 minutes for all five experiments. For comparison, Fig. 5b presents a simulated scenario where the scheduling system dynamically handled the insertion of experiment 5 into the ongoing parallel execution of the initial four experiments after the 800th minute. When a new experiment is inserted, a task rescheduling strategy is triggered, and the unfinished task steps from ongoing experiments are combined with the newly added experiment for constraint evaluation and optimization, generating a new task scheduling table. During this process, completed task steps are excluded from optimization, and their scheduling status remains unchanged. Therefore, as shown in Fig. 5a and b, the scheduling plan before the 800th minute remains unchanged. After the 800th minute, the unfinished task steps from the original schedule were rescheduled along with the newly added experiment 5, resulting in changes to the task scheduling plan. Tasks from experiment 5 began in parallel with the other experiments shortly after their insertion, utilizing available resources as they became free. As a result, the overall makespan increased by only 39 minutes, just 5.2% of the increase in the scenario without dynamic handling capability. This demonstrates that efficient task rescheduling significantly improves resource utilization and overall efficiency.

Fig. 5 Dynamic rescheduling upon insertion of new tasks in simulation. (a) A new experiment 5 was inserted and started after completing the initial four experiments, adding 748 minutes to the total time. (b) The same new experiment 5 was inserted after the 800th minute and began running in parallel with the four ongoing experiments, adding only 39 minutes to the original makespan.

Notably, the computation time for rescheduling tasks after an insertion does not significantly impact the experimental process. The speed of generating the task schedule depends on the scale of variables, the complexity of constraints, and the optimality of the solution. During rescheduling, completed tasks are excluded from optimization, which significantly reduces the number of variables and the search space. On the laboratory computing platform (i9-12900H), scheduling the mixed execution of four experiments takes 20 seconds, while rescheduling after the insertion of experiment 5 takes only 2 seconds.

Deploying the multi-robot–multi-task scheduling system

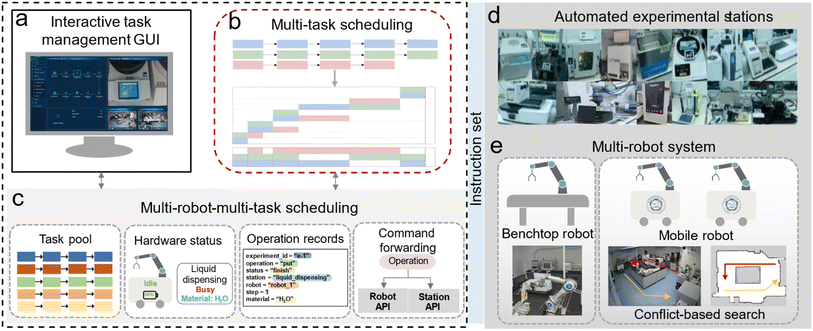
To achieve a seamless transition from user-specified experiments to the precise execution of multiple tasks in multiple steps using multiple robots and various experimental stations, the cross-experiment parallel multi-robot–multi-task scheduling system is deployed as depicted in Fig. 6. To start, researchers submit various chemical experiments via an interactive graphical user interface (GUI) for task management (Fig. 6a). These tasks are added to the task pool and processed by the multi-task scheduling module (Fig. 6b), which optimizes the task sequence into a scheduling table based on task interdependencies and constraints. The multi-robot–multi-task scheduling system uses this scheduling table, along with real-time status updates of robots, stations, and operation records (Fig. 6c), to assess status and progress for each task, assigning the next steps to appropriate robots and stations.

Fig. 6 Multi-robot–multi-task scheduling system deployed in our autonomous chemistry laboratory. (a) Interactive graphical user interface for task management. (b) Multi-task scheduling module, optimizing and organizing task flows into a scheduling table. (c) Multi-robot–multi-task scheduling module, managing the task pool and monitoring the runtime status of tasks, stations, and robots, providing scheduling decisions and hardware commands. (d) Automated experimental stations. (e) Multi-robot system, comprising two mobile robots and one benchtop robot, facilitating sample transfer between stations and coordinating with them to complete experiments.

Throughout task execution, a time pointer manages task progression, incrementing with time to indicate each step from start to completion. Task runtime status, along with system status from the automated experimental stations (Fig. 6d) and the multiple robots (Fig. 6e), is dynamically monitored by the scheduling system. When robots need to transfer samples between stations, the CBS algorithm is employed to plan conflict-free optimal paths for navigation. The interactive task management GUI maintains real-time communication with the scheduling system, allowing users to view task status, robot status, station status, and operation records in real-time.

Multi-robot–multi-task scheduling system in action: real chemical experiments

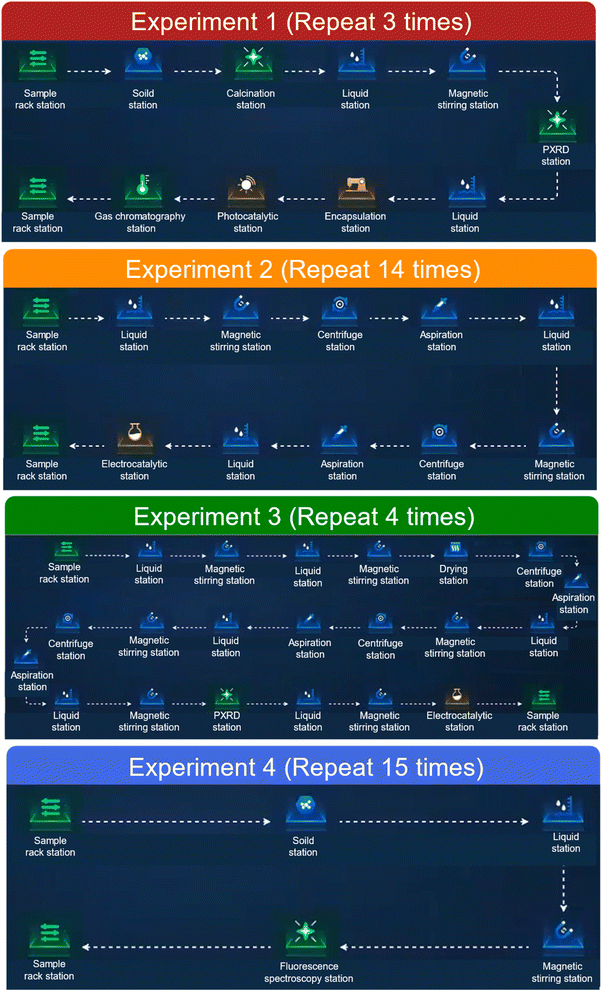
To evaluate the performance of our multi-robot–multi-task scheduling system in practical applications within autonomous chemistry laboratories, we used it to orchestrate four different types of experiments with distinct objectives and procedures. The first experiment involved preparing graphitic carbon nitride (g-C₃N₄) using the thermal polycondensation method with dicyandiamide as a precursor under varying synthetic temperatures. Calcination temperatures were set at 500, 550, and 600 °C, each with a holding time of 5 hours, including heating and cooling for a total duration of approximately 10 hours, resulting in three tasks for synthesizing g-C₃N₄ samples. This experiment also included characterizing the g-C₃N₄ samples and assessing their photocatalytic hydrogen production performance, as shown in ESI, Fig. S3.† The second experiment focused on synthesizing quinary metal–organic high-entropy catalysts (MO-HECs) for electrocatalytic oxygen evolution reactions. Fourteen MO-HECs were synthesized by adjusting the ratios of metal ions—Co, Cu, Fe, Mn, and Ni—while maintaining a constant total metal feedstock of 0.434 mol. The overpotential for each synthesized MO-HEC was measured, with results given in ESI, Fig. S4.†

In the third experiment, we investigated the performance of four binary layered double hydroxides (LDHs) with varying Ni²⁺/Fe²⁺ ratios, exploring their potential for urea oxidation. The X-ray diffraction patterns and electrocatalytic urea oxidation properties of the LDHs were measured, as shown in ESI, Fig. S5–S9.† The final experiment explored the aggregation-induced emission (AIE) properties of berberine chloride (BBR), assessing AIE luminescence of BBR solutions at concentrations of 5, 10, 15, 20, and 25 mM within solvents containing tetrahydrofuran volume fractions of 30%, 60%, and 90%. This resulted in 15 tasks, with photoluminescence spectra measured for each BBR solution, as illustrated in ESI, Fig. S10.† These experiments were scheduled in our autonomous chemistry laboratory, equipped with two mobile robots, one benchtop robot, and 18 automated experimental stations. The workflows for these experiments were input and visualized in the interactive task management GUI, as depicted in Fig. 7.

Fig. 7 Workflows of four chemical experiments visualized in the interactive task management GUI. Experiment 1 included 11 steps across 3 tasks; experiment 2 included 12 steps across 14 tasks; experiment 3 included 23 steps across 4 tasks; and experiment 4 included 6 steps across 15 tasks.

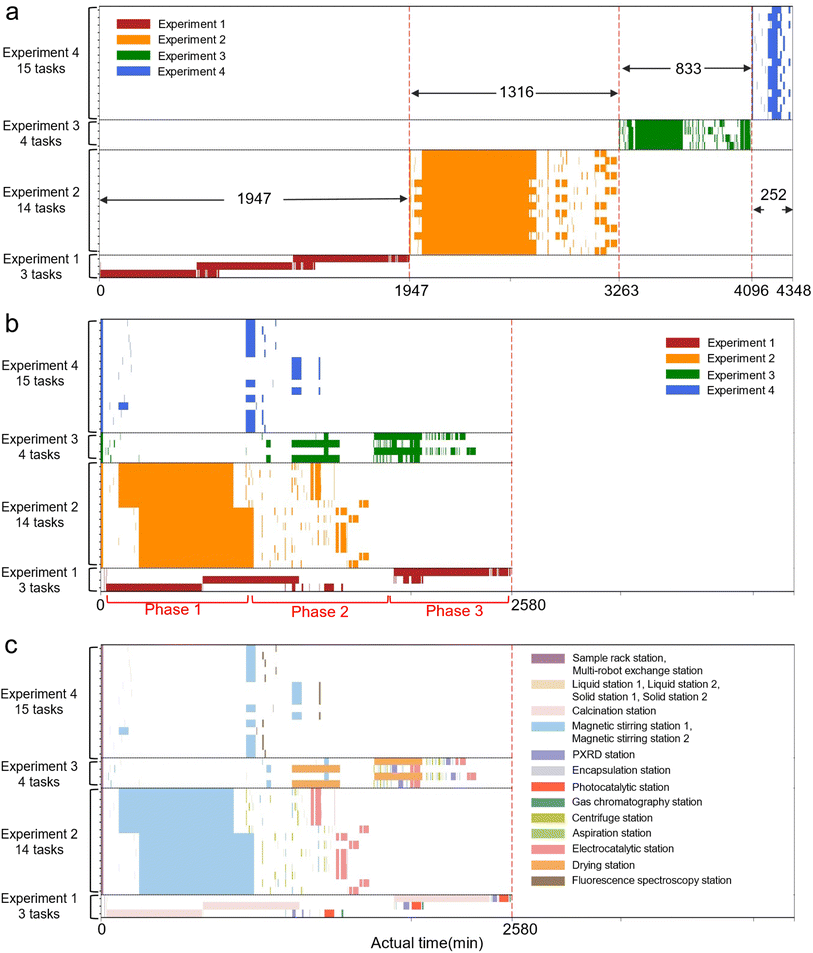
Fig. 8 illustrates the optimized scheduling results and execution times for the four experiments based on the task scheduling table. We performed two actual executions of the four experiments using two approaches, sequentially conducted and concurrently conducted, to demonstrate the capability of our multi-robot–multi-task scheduling algorithm. The individual execution times were 1947 minutes for experiment 1, 1316 minutes for experiment 2, 833 minutes for experiment 3, and 252 minutes for experiment 4. These experiments exhibited significant overlap in their requirements for the experimental stations: experiments 2, 3, and 4 all required the magnetic stirring stations; all four experiments required the liquid stations; experiments 1 and 3 both needed the PXRD station; and experiments 2 and 3 required the aspiration station, centrifuge station, and electrocatalytic station. When the four experiments were conducted sequentially, in conjunction with in-experiment multi-robot–multi-task scheduling, the total cumulative time reached 4348 minutes (Fig. 8a). In contrast, when multi-robot–multi-task scheduling was done fully across the four experiments, the total execution duration reduced to 2580 minutes, achieving nearly a 40% time saving compared to executing the experiments sequentially.

Fig. 8 Scheduling results for the four real chemical experiments. Each scheduling table features a vertical axis where each tick represents an experimental task and a horizontal axis indicating the precise start and end times of each step, which are the actual time recordings during the execution of the chemical experiments in our autonomous chemistry laboratory. (a) Scheduling table for individual experiments conducted sequentially, with tasks within each experiment scheduled together. (b) Scheduling table for parallel execution of the different experiments, with all tasks scheduled concurrently. (c) The same scheduling table as in (b) but viewed from the perspective of the experimental stations' utility during the execution of all the experiments and their tasks.

Among the experiments, 1 and 3 involved fewer tasks, while 2 and 4 handled a larger number of tasks. In terms of duration, experiments 1 and 2 had a long initial phase (Fig. 8b, phase 1); however, experiment 1 had relatively fewer subsequent steps, whereas experiment 2's later part comprised numerous short steps. Experiment 3 began with medium-duration steps followed by short ones, similar to experiment 2. Experiment 4 had relatively few steps, each with a short processing time. The algorithm identified experiments 1 and 2, with their long-duration steps, as key factors limiting overall completion speed. To maximize time efficiency, it prioritized the 10 hour calcination step for experiment 1 and the 12 hour magnetic stirring step for experiment 2. The scheduling also considered other factors, such as the single-capacity calcination station requiring experiment 1's samples to be processed one at a time, while the magnetic stirring station, with two units accommodating up to 10 samples each, fully met the needs of experiment 2. As a result, the 14 samples for experiment 2 were batch-processed in the two magnetic stirring stations, each processing 6 and 8 samples, respectively (Fig. 8c). In the second phase, only experiments 1 and 3 had long-duration steps remaining. Since the calcination station used for experiment 1 and the drying station used for experiment 3 did not conflict with the station needs of other experiments, parallel execution was unaffected. As shown in the scheduling table, the second phase achieved a high level of parallelism, with experiments 4 and 2 fully completed. In the third phase, experiments 1 and 3 continued in parallel until all tasks were completed.

Building on the discussion in Fig. 4, Table 1 reveals a significant imbalance in the workload between the two mobile robots in both the sequential-experiment (Fig. 8a) and concurrent-experiment (Fig. 8b) scenarios. The benchtop robot was assigned to fewer experimental stations, which were less frequently required by the four experiments. In contrast, the two mobile robots served similar purposes and were treated equivalently by the scheduling algorithms. This indicates that, for these specific experiments, the demand for sample transfers at any given time was relatively low, potentially underutilizing the multi-robot system's capabilities. The findings suggest that further efficiency gains could be realized in scenarios involving a larger number of short-duration steps, where the benefits of a multi-robot setup are more pronounced. By optimizing task allocation to better leverage the capabilities of multiple robots, particularly in experiments with high-frequency transfers or overlapping steps, the system could achieve even greater throughput and efficiency.

Table 1 Utilization statics of the multi-robot system

	Sequentially conducted;^a total duration: 4348 minutes				Concurrently conducted;^b total duration: 2580 minutes
	Experiment 1 (3 samples)	Experiment 2 (14 samples)	Experiment 3 (4 samples)	Experiment 4 (15 samples)	Experiments 1–4 (36 samples)
a Statistics of the experiments shown in Fig. 8a.b Statistics of the experiments shown in Fig. 8b.c Time lapsed when at least one experimental step was being executed.d Time lapsed when not a single experimental step was being executed; for example, all samples were being or waiting to be transferred.
Total time (min)	1947	1316	833	252	2580
Time spent on experiments^c (min)	1914	1052	622	132	2472
Time spent on non-experiment operations^d (min)	33	264	211	120	108
Mobile robot 1's operations/total number of operations	42/72 (58.33%)	304/364 (83.52%)	162/208 (77.88%)	122/210 (58.10%)	604/854 (70.73%)
Mobile robot 2's operations/total number of operations	18/72 (25.00%)	4/364 (1.10%)	14/208 (6.73%)	28/210 (13.33%)	90/854 (10.54%)
Benchtop robot's operations/total number of operations	12/72 (16.67%)	56/364 (15.38%)	32/208 (15.38%)	60/210 (28.57%)	160/854 (18.74%)

---

Table 2 compares the actual execution time of four experiments (Fig. 8) with the simulation time (Fig. 3), revealing differences closely related to the logic of multi-robot–multi-task scheduling. The execution of multi-robot–multi-task scheduling involves two steps: first, the task flows are optimized into a task scheduling table; second, the task scheduling table is used to guide the robots in transferring samples and instructing workstation operations.

Table 2 Comparison between the simulated and real schedules

	Sequentially conducted				Concurrently conducted
	Experiment 1 (3 samples)	Experiment 2 (14 samples)	Experiment 3 (4 samples)	Experiment 4 (15 samples)	Experiments 1–4 (36 samples)
Simulation; total time (min)	1958	1413	829	324	2912
Real; total time (min)	1947	1316	833	252	2580

---

In the first step of computing the task scheduling table, the multi-task scheduling algorithm requires estimated processing time parameters for each experimental step, which is a crucial condition. Some stations, such as the magnetic stirring station, only require timed placement and retrieval of samples, so the actual experimental time closely aligns with the estimated processing time. However, other stations that involve operations, such as liquid stations, lack inherent time parameters, necessitating estimated times based on equipment actions. This results in some discrepancies between the actual experimental time and the estimated processing time used for calculating the task scheduling table. The simulation experiment adopts slightly relaxed time settings—estimated processing times that most operations in the actual experiment will not exceed. The purpose of these relaxed settings is to provide users with a maximum acceptable experimental duration.

During sample transfer operations in the simulation experiment, the transfer time for a single sample is modeled by assigning a fixed value for a robot's motion to a single station to perform one retrieval or placement operation. In actual experiments, sample transfer time varies due to differences in robotic arm movements at each station and the robot travel time between stations. Similarly, the simulated sample transfer time is set to be more relaxed than the actual time.

The simulation results are based on the generated task scheduling table, using the estimated processing experimental time and the robot's simulated sample transfer time; while the actual experiments are conducted strictly according to the logical sequence of tasks planned in the generated scheduling table, using the actual experimental time and the actual sample transfer time to calculate the actual experimental results. In summary, the discrepancies between the simulation results and the actual experimental results primarily stem from two sources: (1) differences between the actual experimental time and the estimated processing time for operational stations, and (2) differences between the robot's actual sample transfer time and the transfer time estimated by the simulation program. Due to the relatively relaxed estimated processing times in the task scheduling algorithm and the robot transfer time in the simulation, the actual experimental time is shorter than the simulated time in most cases.

Discussion

In this work, we have developed and implemented a multi-robot–multi-task scheduling system for autonomous chemistry laboratories, which enables the efficient execution of complex chemical experiments. Our system seamlessly integrates multiple robots and numerous experimental stations, allowing for the coordinated and concurrent execution of diverse experimental tasks. Through real-world application—comprising four experiments with varied step counts, step durations, sample throughputs, and other differing aspects—we demonstrated the system's ability to significantly reduce total execution time, achieving nearly a 40% time saving compared to sequential execution. This efficiency gain was realized even when the tasks within the individual experiments were already optimized for concurrent execution during the experiments' sequential execution.

This work offers several key contributions to the field of autonomous chemistry. We have adapted and expanded the Flexible Job-shop Scheduling Problem with Batch-processing capabilities (FJSP-B) framework to address the unique constraints of chemical experiments, resulting in the development of the Flexible Experiment Scheduling Problem with Batch-processing capabilities (FESP-B) framework. This framework can be readily deployed in other autonomous chemistry laboratories. Building on FESP-B and employing a constraint programming approach, we have formulated and developed a robust multi-robot–multi-task scheduling system capable of optimizing task allocation across multiple robots and numerous stations. Furthermore, we have demonstrated the system's dynamic handling capability, which allows for the insertion of new tasks during ongoing operations without substantial disruption, thereby enhancing laboratory efficiency and flexibility.

Future improvements could focus on refining the scheduling algorithms to handle a broader range of experimental conditions and constraints. Expanding the system to incorporate more advanced robotic technologies and sensor networks could further enhance its capabilities. Additionally, our results highlight the importance of tailoring scheduling strategies to the specific requirements of each experimental setup. Adjusting the balance of workloads among robots and ensuring that tasks are distributed in a way that maximizes the utilization of available resources could lead to more efficient operations. Future experiments could focus on dynamically adjusting robot roles based on real-time demands, thus optimizing the deployment of robotic resources in response to varying experimental conditions.

Overall, our work represents a timely advancement toward highly efficient autonomous chemistry laboratories, highlighting a new direction in multi-robot–multi-task coordination for future developments in the field. By enhancing the flexibility and scalability of such systems, they open new avenues for scientific exploration and innovation, paving the way for more sophisticated autonomous laboratories capable of handling increasingly complex and diverse scientific tasks. Our system enables chemists to conduct high-throughput experiments with greater efficiency and versatility, thereby accelerating the pace of scientific discovery. By reducing the time and resources required for experimentation, our approach facilitates rapid iteration of experiments, allowing for quicker hypothesis testing and validation. Looking ahead, this approach could significantly advance autonomous chemistry by integrating artificial intelligence (AI) to further enhance scheduling and decision-making processes. For instance, AI algorithms could predict experimental outcomes based on available data and dynamically adjust schedules to prioritize tasks with the greatest potential impact.

Methods

Interactive task management GUI

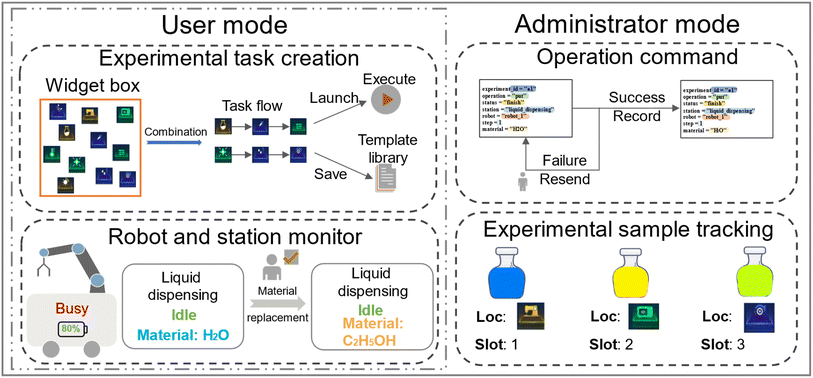
The interactive task management GUI acts as the interface bridge between the multi-robot–multi-task scheduling system and research users, providing an intuitive platform for experimental task management. As shown in Fig. 9 of the Appendix, the interactive GUI is designed with a dual-permission mode, comprising user mode and administrator mode, to accommodate users at different levels.

In user mode, the GUI offers a convenient task design platform. Users can easily construct experimental step sequences through simple drag-and-drop operations of various station widgets, visually representing the tasks' logical order by connecting components with lines. Once the task flow is created, users can initiate experiment execution with a single click. Additionally, users can save frequently used workflows as templates for quick deployment in future experiments. The GUI integrates real-time monitoring of station and robot statuses, allowing users to view the global status of all equipment at any time. Users can also adjust the material information of each station according to current experimental needs to ensure the smooth execution of experiments.

Administrator mode provides system administrators with comprehensive monitoring and control capabilities. In this mode, administrators can access the task execution status of the entire system, including task progress, station usage, and operation command records. Administrators can also track the real-time location of each experimental sample and take timely measures, such as restarting stations or resending operation commands, to maintain system stability when experimental operations encounter faults.

Multi-robot–multi-task scheduling module

As shown in Fig. 6c, the multi-robot–multi-task scheduling module is the core data processing hub of the scheduling system, responsible for maintaining and managing global data while ensuring real-time updates and accurate information transmission. Its main functions include:

(1) Task pool management: the scheduling module maintains a global task pool where all task sequences submitted by users through the interactive GUI are injected. Completed tasks are removed from the pool, and all task information in the pool is sent to the multi-task scheduling module for scheduling. The tasks in the task pool encoded in JSON format are shown in ESI, Fig. S36.†

(2) Robot and station status management: the module periodically polls robots and stations to monitor their real-time operational status. When equipment is idle, the polling frequency is typically 0.1 Hz. Upon completing an instruction, robots or stations immediately report their status. This status information is also sent to the multi-task scheduling module for scheduling purposes. We use JSON format data to manage and transmit the status of robots and stations, with key information including station capacity, material information, and the samples (bottles) in stations and carried by robots. The station capacity and material information will influence which station an operation step will be assigned to for processing, while the bottle location information will determine which robot will pick up or place the sample. The detailed arrangement of the information format is shown in ESI, Fig. S34 and S35.†

(3) Operation records management: the module maintains a detailed list of operation records from task submission to completion, logging each experimental step (ESI, Fig. S37†), including experiment name, operation start and end times, completion status, and the station or robot involved. The multi-task scheduling module updates the task progress pointer based on these records, controlling overall task progress. Administrators can view operation records (ESI, Fig. S33†) to troubleshoot and resolve issues during experiments.

(4) Instruction forwarding function: serving as a communication bridge between the multi-task scheduling module and the stations and robots, the module maintains IP addresses and operation instruction API lists for all equipment. By forwarding scheduling instructions (ESI, Tables S2 and S3†), it reduces the burden on the multi-task scheduling module, allowing it to focus on core scheduling tasks.

Automated experimental stations

As shown in Fig. 6d, the automated experimental stations are a key component of the multi-robot–multi-task scheduling system, responsible for executing specific experimental operations. As illustrated in Fig. 10 of the Appendix, each station is equipped with a Raspberry Pi embedded device that responds fully to standardized system instructions. With precise parameter settings and automated control, these stations can independently perform specific experimental steps without manual intervention. This standardization ensures consistent operation and reliable results, minimizing errors and inconsistencies typically associated with manual operations. Additionally, some stations are designed with high-throughput parallel processing capabilities, allowing them to handle multiple experimental samples simultaneously, which significantly enhances throughput and efficiency. All station control commands are structured as modular programming interfaces, facilitating the quick integration of new stations into the system.

Multi-robot system

As shown in Fig. 6e, the multi-robot system consists of two mobile robots and one benchtop robot, which are crucial for sample transfer during the experimental process. The system optimizes the collaboration and division of labour among different types of robots to enhance the overall efficiency of task execution. The benchtop robot handles sample transfer and auxiliary experimental operations on the high-throughput platform, performing efficiently in high-density environments, as depicted in Fig. 11 of the Appendix. Meanwhile, the mobile robots are responsible for transferring samples between various locations within the laboratory, facilitating transfers over a wider range and connecting different phases of the experimental process.

Multi-agent path finding algorithm

The smooth transfer of experimental samples between different stations relies on mobile robots. The Multi-Agent Path Finding (MAPF) algorithm addresses path planning problems in multi-robot systems, providing collision-free paths for a group of robots in a shared environment while minimizing total movement time. We use the classic Conflict-Based Search (CBS) algorithm to solve MAPF problems. This algorithm constructs a hierarchical search tree to resolve potential conflicts among robots step-by-step, generating collision-free path planning solutions. By applying the CBS algorithm, the multi-robot system can achieve intelligent obstacle avoidance and path optimization during sample transfer tasks, ensuring the safe transfer of experimental samples between stations while minimizing waiting time and movement distance. This approach significantly improves the efficiency and smoothness of the entire experimental process.

Data availability

The authors declare that the data supporting the findings of this study are available within the paper and its ESI† file. Open-sourced codes include minimal implementations of multi-agent path finding algorithms and scheduling algorithms, designed to be hardware-agnostic, as well as scripts to reproduce the simulation results for the various scheduling scenarios discussed in the manuscript. These codes are available at https://github.com/pic-ai-robotic-chemistry/multi-bot-coordinator, which have been deposited at https://doi.org/10.5281/zenodo.14597765. The GUI is not open-sourced, as it is an integral part of the broader AI robotic chemist operating system (OS) designed for uses extending beyond the scope of this research, such as integration into other academic autonomous chemistry laboratories and commercial deployment. Furthermore, the GUI plays an auxiliary role in providing a user-friendly interface for visualizing experiment progress and laboratory status, and it does not constitute the central innovation or primary objective of this study.

Author contributions

J. J., W. S., and F. Z. conceived the project, conceptualized the design of the multi-robot–multi-task scheduling system. J. Z. carried out all the technical development and implementation of the scheduling system, which was overseen by J. J., W. S., F. Z., and L. C. M. L., Q. Z., and S. J. provided essential support to the design of the chemical experiments and during their execution by the autonomous chemistry laboratory orchestrated by the scheduling system, which was overseen by J. J. and L. C. J. J., L. C., and W. S. led the preparation of the manuscript, with contributions from all other authors.

Conflicts of interest

The authors declare no competing interests.

Appendix

Fig. 9 Architecture of the interactive task management GUI. The GUI includes two permission modes: user mode and administrator mode. In user mode, users can view information about the laboratory's robots and stations and submit experimental tasks. Administrator mode is primarily used for the maintenance and management of the experimental process. Administrators can track the location of each experimental sample, view historical operation records, and use the command resending function to restore experimental progress in case of any issues.

Fig. 10 Control structure for automated experimental stations. The multi-robot–multi-task scheduling module can fully control station operations through Raspberry Pi embedded devices, achieving a high level of automation.

Fig. 11 High-throughput platform. (a) Real scene. (b) Grid map.

Acknowledgements

J. J., and W. S. acknowledge the Strategic Priority Research Program of the Chinese Academy of Sciences for funding (Grant XDB0450302). J. J. acknowledges the National Natural Science Foundation of China (Grants 22025304, 22033007) and the CAS Project for Young Scientists in Basic Research (Grant YSBR-005) for funding. W. S. acknowledges the National Natural Science Foundation of China for funding through Grants U22A2056. Q. Z. acknowledges the National Key R&D Program of China (2024YFB3817302) and National Natural Science Foundation of China (22103076) and Anhui Provincial Natural Science Foundation (2108085QB63) and Henan Provincial Natural Science Foundation (242300421138) and Joint Fund of Henan Province Science and Technology R&D Program (235200810107) and USTC Research Funds of the Double First-Class Initiative (YD9990002032).

References

1. B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai and X. Wang, et al., Nature, 2020, 583, 237–241.
2. N. J. Szymanski, B. Rendy, Y. Fei, R. E. Kumar, T. He and D. Milsted, et al., Nature, 2023, 624, 86–91.
3. D. A. Boiko, R. MacKnight, B. Kline and G. Gomes, Nature, 2023, 624, 570–578.
4. M. Abolhasani and E. Kumacheva, Nat. Synth., 2023, 2, 483–492.
5. Q. Zhu, Y. Huang, D. Zhou, L. Zhao, L. Guo and R. Yang, et al., Nat. Synth., 2024, 3, 319–328.
6. S. H. M. Mehr, M. Craven, A. I. Leonov, G. Keenan and L. Cronin, Science, 2020, 370, 101–108.
7. S. Rohrbach, M. Šiaučiulis, G. Chisholm, P. A. Pirvan, M. Saleeb and S. H. M. Mehr, et al., Science, 2022, 377, 172–180.
8. F. Strieth-Kalthoff, H. Hao, V. Rathore, J. Derasp, T. Gaudin and N. H. Angello, et al., Science, 2024, 384, eadk9227.
9. A. M. Lunt, H. Fakhruldeen, G. Pizzuto, L. Longley, A. White and N. Rankin, et al., Chem. Sci., 2024, 15, 2456–2463.
10. T. Ha, D. Lee, Y. Kwon, M. S. Park, S. Lee, J. Jang and B. Choi, et al., Sci. Adv., 2023, 9, eadj0461.
11. A. G. Kusne and A. McDannald, Matter, 2023, 6, 1880–1893.
12. Q. Zhu, F. Zhang, Y. Huang, H. Xiao, L. Zhao and X. Zhang, et al., Natl. Sci. Rev., 2022, 9, nwac190.
13. H. Fakhruldeen, G. Pizzuto, J. Glowacki and A. I. Cooper, 2022 IEEE International Conference on Robotics and Automation (ICRA), 2022, pp. 6013–6019.
14. X. Jiang, S. Luo, K. Liao, S. Jiang, J. Ma and J. Jiang, et al., Cell Rep. Phys. Sci., 2024, 5, 102049.
15. Y. Fei, B. Rendy, R. Kumar, O. Dartsi, H. P. Sahasrabuddhe and M. J. McDermott, et al., Digital Discovery, 2024, 3, 2275–2288.
16. H. J. Yoo, K. Y. Lee, D. Kim and S. S. Han, Nat. Commun., 2024, 15, 9669.
17. M. Sim, M. G. Vakili, F. Strieth-Kalthoff, H. Hao, R. J. Hickman and S. Miret, et al., Matter, 2024, 7, 2959–2977.
18. J. Li, A. Tinka, S. Kiesel, J. W. Durham, T. K. S. Kumar and S. Koenig, Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), 2021, vol. 35, pp. 11272–11281.
19. H. Ma, W. Honig, T. K. S. Kumar, N. Ayanian and S. Koenig, Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), 2019, vol. 33, pp. 7651–7658.
20. Y. Zhang, H. Zhu, D. Tang, T. Zhou and Y. Gui, Robot. Comput.-Integr. Manuf., 2022, 78, 102412.
21. G. Sharon, R. Stern, A. Felner and N. Sturtevant, Artif. Intell., 2015, 219, 40–66.
22. E. Boyarski, A. Felner, R. Stern, G. Sharon, O. Betzalel and D. Tolpin, et al., Proceedings of the International Symposium on Combinatorial Search(SoCS), 2015, vol. 6, pp. 223–225.
23. M. Barer, G. Sharon, R. Stern and A. Felner, Proceedings of the International Symposium on Combinatorial Search(SoCS), 2014, vol. 5, pp. 19–27.
24. J. Li, W. Ruml and S. Koenig, Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), 2021, vol. 35, pp. 12353–12362.
25. H. Xiong, S. Shi, D. Ren and J. Hu, Comput. Oper. Res., 2022, 142, 105731.
26. C. Zhang, W. Song, Z. Cao, J. Zhang, P. S. Tan and C. Xu, Advances in neural information processing systems(NeurIPS), 2020, vol. 33, pp. 1621–1632.
27. J. Zhang, G. Ding, Y. Zou, S. Qin and J. Fu, J. Intell. Manuf., 2019, 30, 1809–1830.
28. D. Y. Sha and C. Y. Hsu, Comput. Ind. Eng., 2006, 51, 791–808.
29. M. Gen, Y. Tsujimura and E. Kubota, Proceedings of IEEE International Conference on Systems, Man and Cybernetics, 1994, vol. 2, pp. 1577–1582.
30. R. Nakano and T. Yamada, Proceedings of the Fourth International Conference on Genetic Algorithms (ICGA), 1991, vol. 91, pp. 474–479.
31. W. Song, X. Chen, Q. Li and Z. Cao, IEEE Trans. Ind. Inf., 2022, 19, 1600–1610.
32. M. Nouiri, A. Bekrar, A. Jemai, S. Niar and A. C. Ammari, J. Intell. Manuf., 2018, 29, 603–615.
33. K. Gao, Z. Cao, L. Zhang, Z. Chen, Y. Han and Q. Pan, IEEE-CAA J. Automatica Sin., 2019, 6, 904–916.
34. B. Ji, S. Zhang, S. S. Yu, X. Xiao, C. Chen and G. Zheng, Comput. Oper. Res., 2024, 161, 106442.
35. A. M. Ham and E. Cakici, Comput. Ind. Eng., 2016, 102, 160–165.
36. P. Laborie, J. Rogerie, P. Shaw and P. Vilím, Constraints, 2018, 23, 210–250.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00313f

‡ These authors contributed equally.

---