 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantitative evaluation of anharmonic bond potentials for molecular simulations†
Paul J.
van Maaren
and
David
van der Spoel
 *
*
Department of Cell and Molecular Biology, Uppsala University, Uppsala, Sweden. E-mail: david.vanderspoel@icm.uu.se
First published on 13th February 2025
Abstract
Most general force fields only implement a harmonic potential to model covalent bonds. In addition, in some force fields, all or a selection of the covalent bonds are constrained in molecular dynamics simulations. Nevertheless, it is possible to implement accurate bond potentials for a relatively small computational cost. Such potentials may be important for spectroscopic applications, free energy perturbation calculations or for studying reactions using empirical valence bond theory. Here, we evaluate different bond potentials for diatomic molecules. Based on quantum-chemical scans around the equilibrium distance of 71 molecules using the MP2/aug-cc-pVTZ level of theory as well as CCSD(T) with the same basis-set, we determine the quality of fit to the data of 28 model potentials. As expected, a large spread in accuracies of the potentials is found and more complex potentials generally provide a better fit. As a second and more challenging test, five spectroscopic parameters (ωe, ωexe, αe, Be and De) predicted based on quantum chemistry as well as the fitted potentials are compared to experimental data. A handful of the 28 potentials tested are found to be accurate. Of these, we suggest that the potential due to Hua (Phys. Rev. A, 42 (1990), 2524) could be a suitable choice for implementation in molecular simulations codes, since it is considerably more accurate than the well-known Morse potential (Phys. Rev., 34 (1929), 57) at a very similar computational cost.
1 Introduction
Prediction of molecular properties can be done, in principle, through theoretical models based on physics or by models based directly on data.1 Both ways involve approximations and require thorough validation based on experimental data. Importantly, though there has been great progress in data-based models,2 the laws of physics remain valid.3 Data and physics-based models share the need for high-quality reference data, and we have recently presented an overview of available quantum-chemistry databases for this purpose.4 Here, we aim to design parts of a force field for molecular dynamics (MD) simulation, for which empirical potentials are needed that reproduce data from high-quality quantum chemistry or experiments. This means that the fundamental physics should be followed as much as possible without making the potentials impractically complicated.5 Systematic design of force fields6 is needed to determine which functions are suitable for predicting properties.7 By careful design of the data set it is possible to break down the complex empirical potential for molecules into simpler parts. We have, for instance, studied noble gases to evaluate potential forms for exchange and dispersion interactions8 and found that the 14-7 potential due to Halgren9 as well as the generalized Buckingham due to Werhahn et al.10 were sufficiently flexible to reproduce both gas-phase and condensed phase data. On the other hand, the popular Lennard-Jones 12-6 potential11 was the poorest contender. We obtained similar results in an earlier study of alkali-halides,12 where multiple potentials were parameterised in exactly the same manner, allowing apples-to-apples comparisons of their predictive power. There we found that the 12-6 potential had three times higher deviation from experimental observables than a modified Buckingham potential.13In this paper, we address potentials for covalent bonds by studying diatomic molecules. The study of diatomic molecules has a long history, with famous old papers such as those by Heitler and London,14 Morse,15 Rydberg16 and Pöschl and Teller.17 Systematic comparisons of potentials with experimental data have been done, for instance by Royappa et al.,18 and by others,19,20 usually focused on reproduction of vibrational modes. It should be noted that many of these potentials are “related” to each other21,22 but we will not discuss this here. Instead, we refer the reader to a recent review by Araújo et al. covering 100 years of history of analytical potentials to fit diatomic energy curves.23 The development of methods for accurate yet affordable prediction of vibrational spectra has been an active research field for a long time24–26 and the choice of a potential for covalent bonds is a step towards force field based prediction of vibrational spectra.27,28
When addressing the question what bond potential is best suitable for molecular simulation, it is important to realize that “best” by necessity involves a compromise between accuracy (deviation from experimental data or high-level quantum chemistry) and computational efficiency. A further consideration is that a potential should be simple to parameterize, which favors functions with fewer parameters. It should be noted that many classical force fields use a simple harmonic function to model chemical bonds although, for instance, the MM3 force field can employ a Morse function instead.29 In what follows, we consider the root mean square deviation (RMSD) from the reference data as the “accuracy” of the potential. For comparison with earlier studies, we also provide the least-squares Z-score introduced by Murrell and Sorbie.30 As we have shown in our study on noble gases, it is often advantageous or even necessary to introduce an energy threshold for fitting potentials. The magnitude of such a threshold is important quantitatively, but often not qualitatively.8 The size of the RMSD changes with energy threshold used for training, but the ranking of potentials does not change much. We discuss the effect of different thresholds on different potential functions below. Finally, we evaluate the quantum chemistry data and a number of empirical potentials by computing spectroscopic parameters and comparing them to experimental data.
2 Methods
2.1 Energy calculations
71 diatomic molecules were selected, consisting of first and second row atoms plus sulfur, halogens and alkali halides. The dataset therefore consists of both covalently bound molecules and ion-pairs. Ion-pairs are included because there is a lot of experimental data available to compare fitted potentials to, including spectroscopic data, allowing to test our scripts and the generality of the potentials. In MD simulations, one would not use a covalent potential for ion pairs but rather a combination of Coulomb and van der Waals potentials.12 For each of these molecules respectively ion pairs, a scan of the energy as a function of distance was made at two levels of theory. First, Møller–Plesset 2nd order (MP2) perturbation theory31 with the correlation-consistent basis-set aug-cc-pVTZ32 and second, coupled clusters33 with singlets and doublets and perturbative triples, or CCSD(T), with the same basis-set. Iodine and iodide were modeled using the aug-cc-pwCVTZ-PP basis set34 while for potassium, calcium, cesium and rubidium the def2-TZVPP basis set was employed,35 all downloaded from the basis-set exchange.36 For singlet molecules a restricted Hartree–Fock procedure was used.37 Initially, unrestricted Hartree–Fock calculations were performed for the radicals, but in particular for the MP2 method this led to significant spin contamination. For this reason, restricted open-shell Hartree–Fock38 calculations were used instead, and these were well-behaved.A list of molecules, their charge, multiplicity and the range of distances used for quantum calculations is provided in Table S1.† The range of distances used in the quantum calculations was based on the equilibrium distance re by dividing it by 1.2 and multiplying it by 1.2 to get the lower and upper limits respectively (Table S1†). The distance between scanning points was 0.5 pm. Calculations were performed with the Psi4 software suite.39 Experimental data for the subset of 14 molecules used by Royappa et al.18 were used for fitting here as well. References to experimental data for these molecules are given in Fig. S9–S13, S25, S28, S30, S39, S43, S48–S50, S58 and S59, in the ESI.† Experimental data on frequencies were collected from the database of spectroscopic constants of diatomic molecules40,41 and the National Institute of Standards Webbook.42 We note that the database contained several errors and omissions that we corrected based on the original data collection due to Huber and Herzberg,43 which itself also contained some errors. Corrected files are provided on Zenodo.44
2.2 Data processing
Energies were stored as text files and processed with a curve-fitting script based on Scientific Python.45 28 functions were used to fit the energy curves, 21 of which were evaluated by Royappa et al. previously.18 In addition, we use a harmonic potential, potentials due to Lennard-Jones,11 Buckingham,46 Cahill,47 Tang & Toennies,48 Xie et al.49 and Wang et al.13 Numerical curve-fitting was extremely tedious. First, a careful shifting of the quantum chemical energy curves to have their minimum energy level at zero was needed. Despite tuning of tolerances, the energies produced by geometry optimization were incompatible with single point calculations. Therefore, we located the position and depth of the energy minimum by implementing a bisection algorithm using single point calculations with exactly the same settings as used in the distance scan. Then, manual curating of the starting values was required, using visual inspection of the fitted curves to validate the correctness of the fit. Unfortunately, the Levenberg–Marquardt algorithm50,51 used in Scientific Python45 simply is not fool-proof. Unless starting parameters are close to the correct ones, it cannot be guaranteed that the best solution will be found, in particular since we used some highly non-linear potentials with a relatively small number of correlated data points. The total number of fits to be checked in this manner was well over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. This suggests that, as much as we would like it to, the era of digital discovery has not yet fully started. Even though the curve fitting applied here only requires a small number of parameters to be determined, we are not aware of any guaranteed error-free solution. More elaborate algorithms like Monte Carlo search in parameter space coupled with simulated annealing might help, but any such algorithm can get stuck in a local minimum as well. A further possibility would be the algorithm due to Ho and Rabitz for generating a molecular energy surface from quantum chemistry calculations.52,53 Finally, for fitting the data a number of different energy thresholds were employed: either all data was used, or just the data points with energy of at most 1000 cm−1 respectively 5000 cm−1.
000. This suggests that, as much as we would like it to, the era of digital discovery has not yet fully started. Even though the curve fitting applied here only requires a small number of parameters to be determined, we are not aware of any guaranteed error-free solution. More elaborate algorithms like Monte Carlo search in parameter space coupled with simulated annealing might help, but any such algorithm can get stuck in a local minimum as well. A further possibility would be the algorithm due to Ho and Rabitz for generating a molecular energy surface from quantum chemistry calculations.52,53 Finally, for fitting the data a number of different energy thresholds were employed: either all data was used, or just the data points with energy of at most 1000 cm−1 respectively 5000 cm−1.
Fitting and evaluation of the goodness of fit was done using the Z-score30
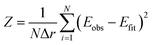 | (1) |
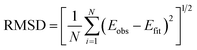 | (2) |
| Function | M | Z | ΔZ | RMSD |
|---|---|---|---|---|
| Sun54 | 8 | 534 | −1264 | 29 |
| Murrell–Sorbie30 | 5 | 3300 | −1158 | 66 |
| Hulburt–Hirschfelder55 | 5 | 4050 | −1154 | 76 |
| Tietz II56 | 5 | 9521 | −1696 | 144 |
| Rafi57 | 5 | 9985 | −45762 | 137 |
| Levine58 | 4 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517 517 |
−18734 | 150 |
| Noorizadeh59 | 5 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 447 447 |
−4086 | 129 |
| Wei Hua60 | 4 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707 707 |
−1127 | 174 |
| Pöschl–Teller17 | 4 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 749 749 |
−61372 | 175 |
| Frost–Musulin61 | 4 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 581 581 |
−1434 | 223 |
| Morse15 | 3 | 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 826 826 |
−1641 | 282 |
| Varshni62 | 3 | 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 698 698 |
−1431 | 315 |
| Rosen–Morse63 | 4 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 451 451 |
−94393 | 349 |
| Rydberg16 | 3 | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734 734 |
−1406 | 357 |
| Pseudo-Gaussian64 | 3 | 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 717 717 |
−1148 | 352 |
| Linnett65 | 4 | 107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 285 285 |
−28842 | 489 |
| Deng–Fan66 | 3 | 154![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 247 247 |
−2646 | 577 |
| Tietz I56 | 5 | 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811 811 |
−60007 | 596 |
| Valence-state67 | 4 | 205![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 072 072 |
−3700 | 625 |
| Kratzer68 | 2 | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 424 424![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 629 |
−6825 | 2283 |
| Lippincott69 | 3 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132 132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 095 095 |
−18092 | 3330 |
| Function | M f | M sim | CCSD(T) | MP2 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Non-covalent (26) | Covalent (45) | Non-covalent (26) | Covalent (45) | |||||||
| Z | RMSD | Z | RMSD | Z | RMSD | Z | RMSD | |||
| Sun54 | 8 | 8 | 0.0 | 0.5 | 0.0 | 0.1 | 0.0 | 0.1 | 0.0 | 0.1 |
| Hulburt–Hirschfelder55 | 5 | 5 | 0.0 | 0.9 | 0.0 | 0.1 | 0.0 | 0.4 | 0.0 | 0.2 |
| Tietz II56 | 5 | 4 | 0.1 | 2.5 | 0.0 | 0.5 | 0.1 | 2.0 | 0.1 | 1.5 |
| Wei Hua60 | 4 | 4 | 0.1 | 2.7 | 0.0 | 0.5 | 0.1 | 2.2 | 0.2 | 2.2 |
| Cahill47 | 6 | 6 | 0.0 | 0.4 | 0.0 | 0.3 | 3.8 | 9.4 | 0.9 | 4.9 |
| Rafi57 | 5 | 4 | 0.1 | 1.8 | 0.1 | 2.1 | 0.1 | 1.7 | 0.5 | 4.8 |
| Murrell–Sorbie30 | 5 | 5 | 0.1 | 2.7 | 0.2 | 2.7 | 0.2 | 3.0 | 0.4 | 3.6 |
| Frost–Musulin61 | 4 | 3 | 0.6 | 5.6 | 0.2 | 3.7 | 0.6 | 5.6 | 1.0 | 5.0 |
| Pöschl–Teller17 | 4 | 3 | 0.6 | 5.8 | 0.2 | 3.7 | 0.7 | 5.9 | 1.1 | 5.1 |
| Valence-state67 | 4 | 4 | 0.6 | 5.0 | 0.3 | 4.3 | 0.5 | 4.6 | 1.2 | 5.4 |
| Rosen–Morse63 | 4 | 3 | 0.9 | 7.0 | 0.4 | 3.8 | 0.9 | 7.0 | 1.2 | 5.4 |
| Morse15 | 3 | 3 | 0.9 | 7.3 | 0.4 | 4.2 | 1.1 | 7.3 | 1.6 | 6.1 |
| Rydberg16 | 3 | 3 | 1.2 | 8.3 | 0.4 | 4.3 | 1.3 | 8.4 | 1.7 | 6.3 |
| Levine58 | 4 | 4 | 0.2 | 3.5 | 0.4 | 5.6 | 4.2 | 10 | 5.8 | 17 |
| Linnett65 | 4 | 3 | 0.6 | 5.7 | 0.5 | 4.6 | 0.6 | 5.6 | 1.5 | 6.4 |
| Pseudo-Gaussian64 | 3 | 3 | 1.9 | 11 | 0.6 | 5.0 | 2.0 | 11 | 1.7 | 6.5 |
| Tietz I56 | 5 | 4 | 1.0 | 6.9 | 0.8 | 6.5 | 1.0 | 6.6 | 4.9 | 9.4 |
| Varshni62 | 3 | 3 | 1.5 | 9.5 | 2.1 | 8.0 | 3.7 | 12 | 4.2 | 10 |
| Deng–Fan66 | 3 | 3 | 0.7 | 6.0 | 5.1 | 13 | 4.8 | 11 | 10 | 18 |
| Wang–Buckingham13 | 3 | 3 | 8.3 | 22 | 9.9 | 20 | 9.1 | 22 | 13 | 21 |
| Tang (2003)48 | 6 | 6 | 17 | 26 | 44 | 29 | 1.0 | 6.7 | 98 | 43 |
| Buckingham46 | 3 | 3 | 4.7 | 16 | 44 | 48 | 5.1 | 16 | 56 | 53 |
| Noorizadeh59 | 5 | 4 | 23 | 29 | 273 | 78 | 22 | 29 | 217 | 69 |
| Kratzer68 | 2 | 2 | 578 | 176 | 380 | 101 | 483 | 166 | 365 | 93 |
| Lippincott69 | 3 | 3 | 1753 | 307 | 1471 | 196 | 1554 | 294 | 1409 | 186 |
| Xie (2005)49 | 4 | 3 | 1747 | 299 | 1818 | 213 | 1512 | 284 | 1767 | 203 |
| Harmonic | 3 | 2 | 3848 | 452 | 3648 | 314 | 3506 | 438 | 3531 | 302 |
| Lennard-Jones11 | 2 | 2 | 5487 | 532 | 9044 | 523 | 5690 | 534 | 9287 | 529 |
3 Results & discussion
3.1 Experimental reference data
To validate our Python code, we attempted to reproduce the data included in the paper by Royappa et al.18 The curve-fitting script reproduces Fig. 2–5 from that paper. We found lower average Z-scores for all of the potentials (Table 1), likely in part because of the manual curation of the data. It is also possible, however, that in some cases a better fit was obtained because the fitting algorithm switched places between the attractive and repulsive part of the potentials. For example, in the potential due to Linnett65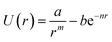 | (3) |
3.2 Quantum chemical reference data
Since quantum chemistry for diatomics is relatively cheap it was possible to include 71 diatomic molecules. The quantum chemistry curves are plotted in Fig. S1–S71† and, where available, experimental data are plotted as well. Statistics of the potentials when fitted using an energy threshold of 1000 cm−1 are given in Table 2. As expected, simple functions like Lennard-Jones11 and the harmonic function represent the quantum chemistry data poorly. The ab initio model due to Xie et al.49 was not accurate for the molecules studied here either, likely due to the fact that most molecules studied here are not just bonded by s-valence electrons, like in the original paper.49 The well-known Tang–Toennies potential,48 that reproduces high-level quantum chemistry interaction functions for noble gases extremely well,8 is not among the top contenders either. Table S2† gives the corresponding data for a fit with an energy threshold of 5000 cm−1 and Table S3† without any energy threshold. No significant difference with Table 2 is found, the potentials with the ten or so best fits to the quantum chemistry data are just shuffled in a somewhat different order. For the best performing functions, it seems somewhat easier to reproduce the CCSD(T) data than the MP2 data (Tables 2 and S2†). It can also be noted that some potentials, like the ones due to Rafi57 or Levine,58 are more accurate for non-covalent interactions than covalent bonds. For the purpose of this paper we are mainly interested in potentials that model covalent bonds well, so we will not investigate this further.3.3 Spectroscopic parameters
Based on the quantum-chemical data, the vibrational harmonic frequency, the first anharmonic correction and other vibrational parameters24 were computed by second order vibrational perturbation theory using the Psi4 software39 (Table S4†). It should be noted that slightly more accurate vibrational constants may be computed by directly solving the 1D Schrödinger equation26,70,71 but vibrational perturbation theory is accurate enough to distinguish the accuracy of the potentials under evaluation here. Fig. 1 displays the residual (quantum chemistry minus experiment) of the vibrational harmonic frequency ωe for the 71 molecules studied here. Despite some outliers, the overall trend is that the frequencies are reproduced well when using CCSD(T), but with considerably more noise for MP2. These results can be compared to results from a machine learning study by Ibrahim and co-workers, who built models to predict spectroscopic constants of diatomic molecules based on atomic and molecular properties.72 Their best model produced vibrational harmonic frequencies ωe of similar accuracy to the ones from CCSD(T) (Fig. 1).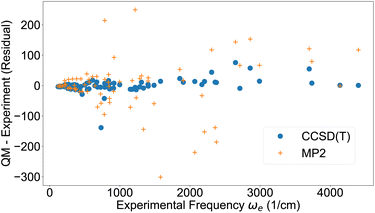 | ||
| Fig. 1 Vibrational harmonic frequency ωe from experimental data42,43 and residual from quantum chemistry. | ||
The first anharmonic correction ωexe, is overestimated by both the MP2 and CCSD(T) methods (Fig. 2). These results are corroborated by a summary of statistics in Table 3, showing the deviation from either experiment or CCSD(T). MP2 has almost three times higher deviation from experiment than CCSD(T) for ωe and ωexe, however for the other parameters the difference is smaller.
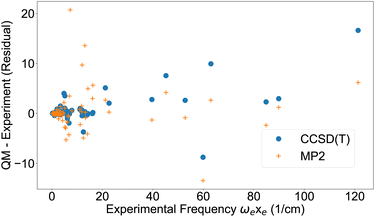 | ||
| Fig. 2 First anharmonic correction ωexe from experimental data42,43 and residual from quantum chemistry. | ||
| Reference | Experiment | CCSD(T) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | ω e | ω e x e | B e | α e | D e | ω e | ω e x e | B e | α e | D e |
| CCSD(T) | 2.92 | 18.64 | 2.77 | 14.12 | 26.92 | |||||
| MP2 | 6.65 | 45.47 | 2.47 | 20.34 | 28.21 | 6.33 | 41.80 | 2.13 | 18.15 | 9.37 |
| Sun54 | 2.92 | 18.24 | 2.77 | 14.16 | 26.92 | 0.01 | 0.58 | 0.00 | 0.09 | 0.03 |
| Hulburt–Hirschfelder55 | 2.92 | 18.07 | 2.77 | 14.07 | 26.92 | 0.01 | 0.67 | 0.00 | 0.13 | 0.03 |
| Cahill47 | 2.92 | 18.85 | 2.77 | 14.13 | 26.92 | 0.02 | 2.28 | 0.00 | 0.17 | 0.03 |
| Wei Hua60 | 2.92 | 17.61 | 2.77 | 13.89 | 26.92 | 0.04 | 1.68 | 0.00 | 0.77 | 0.08 |
| Tietz II56 | 2.93 | 18.10 | 2.77 | 13.85 | 26.92 | 0.05 | 2.55 | 0.00 | 0.93 | 0.11 |
| Rafi57 | 2.94 | 17.46 | 2.77 | 13.85 | 26.93 | 0.08 | 2.63 | 0.00 | 1.19 | 0.16 |
| Murrell–Sorbie30 | 2.92 | 20.33 | 2.77 | 14.13 | 26.92 | 0.08 | 7.78 | 0.00 | 1.00 | 0.17 |
| Levine58 | 2.93 | 18.01 | 2.77 | 13.76 | 26.93 | 0.14 | 6.34 | 0.01 | 2.15 | 0.30 |
| Deng–Fan66 | 2.93 | 19.47 | 2.77 | 16.68 | 26.94 | 0.15 | 9.49 | 0.04 | 8.80 | 0.36 |
| Morse15 | 2.92 | 19.74 | 2.77 | 14.05 | 26.94 | 0.15 | 9.02 | 0.01 | 2.09 | 0.32 |
| Rydberg16 | 2.91 | 21.33 | 2.77 | 14.00 | 26.95 | 0.17 | 10.71 | 0.01 | 2.24 | 0.36 |
| Tietz-I56 | 2.97 | 18.86 | 2.77 | 14.53 | 26.93 | 0.18 | 10.23 | 0.01 | 2.74 | 0.39 |
| Frost–Musulin61 | 2.93 | 18.50 | 2.77 | 14.04 | 26.95 | 0.19 | 7.70 | 0.01 | 2.14 | 0.39 |
| Pöschl–Teller17 | 2.93 | 18.87 | 2.77 | 14.05 | 26.95 | 0.19 | 8.20 | 0.01 | 2.14 | 0.40 |
| Valence-state67 | 2.98 | 16.04 | 2.77 | 14.34 | 26.93 | 0.19 | 8.96 | 0.01 | 2.15 | 0.40 |
| Varshni62 | 2.90 | 22.51 | 2.77 | 14.74 | 26.96 | 0.20 | 11.60 | 0.02 | 4.99 | 0.42 |
| Tang (2003)48 | 2.92 | 21.49 | 2.76 | 17.32 | 26.94 | 0.20 | 15.19 | 0.06 | 14.69 | 0.40 |
| Pseudo-Gaussian64 | 2.89 | 23.89 | 2.77 | 13.89 | 26.96 | 0.21 | 13.43 | 0.01 | 2.74 | 0.44 |
| Rosen–Morse63 | 2.91 | 22.51 | 2.77 | 14.04 | 26.96 | 0.22 | 12.53 | 0.01 | 2.20 | 0.45 |
| Linnett65 | 2.93 | 22.89 | 2.77 | 14.20 | 26.94 | 0.22 | 14.12 | 0.01 | 2.04 | 0.44 |
| Noorizadeh59 | 2.94 | 42.83 | 2.75 | 36.21 | 26.94 | 0.37 | 40.52 | 0.14 | 34.52 | 0.45 |
| Buckingham46 | 2.98 | 69.91 | 2.78 | 22.85 | 26.97 | 0.59 | 59.92 | 0.16 | 21.71 | 1.24 |
| Wang–Buckingham13 | 2.90 | 60.73 | 2.77 | 15.03 | 27.01 | 0.60 | 52.84 | 0.02 | 6.29 | 1.22 |
| Kratzer68 | 3.32 | 63.09 | 2.96 | 50.86 | 26.92 | 0.81 | 63.64 | 0.32 | 50.07 | 0.76 |
| Lippincott69 | 3.06 | 100 | 3.09 | 100 | 27.01 | 0.97 | 90.31 | 0.61 | 100 | 2.40 |
| Xie (2005)49 | 3.69 | 87.13 | 3.09 | 100 | 26.92 | 1.47 | 87.41 | 0.58 | 100 | 1.38 |
| Harmonic | 3.80 | — | — | — | — | 1.66 | — | — | — | — |
| Lennard-Jones11 | 5.02 | 100 | 2.89 | 100 | 27.41 | 4.69 | 100 | 1.65 | 100 | 4.15 |
The potentials, fitted to CCSD(T) with a threshold of 1000 cm−1, were used to compute vibrational parameters as well (Table 3). The five best potentials from Table 2 are the best here as well. All of these seem to reproduce the CCSD(T) energy curves faithfully as they sport the same deviation from experiment as CCSD(T) and low deviation from the CCSD(T) frequencies as well. The deviation for frequencies ωe from experiment for the harmonic potential are comparable to other potentials, however the deviation from CCSD(T) is high and the other spectroscopic parameters are zero by definition.
Table S5† shows that without energy threshold for fitting the analytical potentials to CCSD(T), the top ranking ones are the same as fitted with an energy threshold (Table 3). It could be suspected that using a larger energy threshold of 5000 cm−1 when fitting the potentials, would be advantageous, since the ground state vibration of molecular hydrogen, at 4401.21 cm−1 (ref. 43) would fall well inside this energy range. However, Table S6† shows that the deviation of frequencies from experiment in fact is larger than that fitted with a lower threshold (Table 3). Finally, it is possible to fit potentials directly on experimental data. Table S7† shows the RMSD from experimental frequencies for the 14 molecules from Table 1. The deviation for both ωe and ωexe is somewhat larger than for the fits to the CCSD(T) potential, likely since the ground state vibrations are determined mainly by the shape of the potential close to the minimum. Therefore, fitting a potential to an accurate quantum chemistry calculation may be sufficient if the purpose is to reproduce the vibrational properties listed in Table 3.
4 Conclusions
An evaluation of 28 analytical potentials to reproduce quantum chemistry data for 71 diatomic molecules is presented. Several of these potentials fit the quantum chemical reference data excellently (Table 2) and also produce vibrational parameters on par with the CCSD(T) ones (Table 3). The potential due to Hua is both accurate and relatively simple and therefore it may be a good choice for implementation in molecular simulation codes. It is given by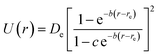 | (4) |
Anharmonicity in the frequencies is not reproduced very well by the quantum chemical methods employed here (Fig. 2 and Table 3) and this is reflected in the analytical potentials. Simply stated, these potentials are not better than the reference data, in this case CCSD(T)/aug-cc-pVTZ. Although this is perhaps a trivial conclusion, it applies to both science-driven1 (like in this work) and data-driven model building, and a careful evaluation of training data is therefore crucial in any machine learning endeavor.4 A data-science problem that needs to be addressed in both schools of modeling is the range of energies incorporated. We have shown previously8,73 as well as here that the choice of energy threshold can affect predictive power of models trained on the data. A high threshold, or including a large range of energies, requires complex models to get good results, and simpler models may not be able to compete. A smaller threshold could lead to more complex potentials being underdetermined, but we find rather the opposite, that frequencies are reproduced better when a limited threshold is used (compare Tables 3 and S6†). Finally, it should be noted that the frequencies produced from the MP2 calculations are much less accurate than those from CCSD(T). However, before disregarding MP2 as a basis for systematic design of force fields,6 studies with larger compounds are needed.
Data availability
All code and data for this article can be found at: https://github.com/AlexandriaChemistry/BondPotentials/. With permanent DOI here: https://doi.org/10.5281/zenodo.13997971.Author contributions
PvM designed the study, implemented the code to evaluate potentials on quantum chemistry and experimental data and, contributed to analysis and writing. DvdS wrote the first version of the manuscript, contributed to implementations and analysis of the results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by AI4Research at Uppsala University, Sweden, by the Swedish Research Council (grant 2020-05059) and by eSSENCE – The e-Science Collaboration (Uppsala-Lund-Umeå, Sweden). Computer resources were provided by the National Academic Infrastructure for Supercomputing Sweden at the national supercomputing center, partially funded by the Swedish Research Council through (grant 2022-06725). Experimental data reproduced with kind permission of Dr Jorge Luque.Notes and references
- J. T. Margraf, Angew. Chem., Int. Ed. Engl., 2023, 62, e202219170 CrossRef CAS PubMed
.
- A. Aspuru-Guzik, R. Lindh and M. Reiher, ACS Cent. Sci., 2018, 4, 144–152 CrossRef CAS PubMed
.
- O. Willcox, K. E. Ghattas and P. Heimbach, Nat. Comput. Sci., 2021, 1, 166–168 CrossRef PubMed
.
- K. Kříž, L. Schmidt, A. T. Andersson, M.-M. Walz and D. van der Spoel, J. Chem. Inf. Model., 2023, 63, 412–431 CrossRef PubMed
.
- A. Hagler, J. Comput.-Aided Mol. Des., 2019, 33, 205–264 CrossRef CAS PubMed
.
- D. van der Spoel, Curr. Opin. Struct. Biol., 2021, 67, 18–24 CrossRef CAS PubMed
.
- L. Wang, P. K. Behara, M. W. Thompson, T. Gokey, Y. Wang, J. R. Wagner, D. J. Cole, M. K. Gilson, M. R. Shirts and D. L. Mobley, J. Phys. Chem. B, 2024, 128, 7043–7067 CrossRef CAS PubMed
.
- K. Kříž, P. J. van Maaren and D. van der Spoel, J. Chem. Theory Comput., 2024, 20, 2362–2376 CrossRef PubMed
.
- T. A. Halgren, J. Am. Chem. Soc., 1992, 114, 7827–7843 CrossRef CAS
.
- J. C. Werhahn, E. Miliordos and S. S. Xantheas, Chem. Phys. Lett., 2015, 619, 133–138 CrossRef CAS
.
- J. E. Jones, Proc. R. Soc. London, Ser. A, 1924, 106, 463–477 CAS
.
- M. M. Walz, M. M. Ghahremanpour, P. J. van Maaren and D. van der Spoel, J. Chem. Theory Comput., 2018, 14, 5933–5948 CrossRef CAS PubMed
.
- L.-P. Wang, J. Chen and T. V. Voorhis, J. Chem. Theory Comput., 2013, 9, 452–460 CrossRef CAS PubMed
.
- W. Heitler and F. London, Z. Phys., 1927, 44, 455–472 CrossRef CAS
.
- P. M. Morse, Phys. Rev., 1929, 34, 57–64 CrossRef CAS
.
- R. Rydberg, Z. Phys., 1932, 73, 376–385 CrossRef CAS
.
- G. Pöeschl and E. Teller, Z. Phys., 1933, 83, 143–151 CrossRef
.
- A. T. Royappa, V. Suri and J. R. McDonough, J. Mol. Struct., 2006, 787, 209–215 CrossRef CAS
.
- G.-D. Zhang, J.-Y. Liu, L.-H. Zhang, W. Zhou and C.-S. Jia, Phys. Rev. A, 2012, 86, 062510 CrossRef
.
- R. K. Pingak, A. Z. Johannes, Z. S. Ngara, M. Bukit, F. Nitti, D. Tambaru and M. Z. Ndii, Results Chem., 2021, 3, 100204 CrossRef CAS
.
- G. A. Natanson, Phys. Rev. A, 1991, 44, 3377–3378 CrossRef CAS PubMed
.
- C.-S. Jia, Y.-F. Diao, X.-J. Liu, P.-Q. Wang, J.-Y. Liu and G.-D. Zhang, J. Chem. Phys., 2012, 137, 014101 CrossRef PubMed
.
- J. P. Araújo and M. Y. Ballester, Int. J. Quantum Chem., 2021, 121, e26808 CrossRef
.
- J. L. Dunham, Phys. Rev., 1932, 41, 721–731 CrossRef CAS
.
- M. Miotto and L. Monacelli, npj Comput. Mater., 2024, 10, 240 CrossRef CAS
.
- L. K. McKemmish, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1520 CAS
.
- H. Henschel, A. T. Andersson, W. Jespers, M. Mehdi Ghahremanpour and D. van der Spoel, J. Chem. Theory Comput., 2020, 16, 3307–3315 CrossRef CAS PubMed
.
- H. Henschel and D. van der Spoel, J. Phys. Chem. Lett., 2020, 11, 5471–5475 CrossRef CAS PubMed
.
- R. J. Shannon, B. Hornung, D. P. Tew and D. R. Glowacki, J. Phys. Chem. A, 2019, 123, 2991–2999 CrossRef CAS PubMed
.
- J. Murrell and K. Sorbie, J. Chem. Soc., Faraday Trans., 1974, 70, 1552–1556 RSC
.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef
.
- T. H. Dunning Jr and K. A. Peterson, J. Chem. Phys., 2000, 1113, 7799–7808 CrossRef
.
- J. Čížek, J. Chem. Phys., 1966, 45, 4256–4266 CrossRef
.
- K. A. Peterson and K. E. Yousaf, J. Chem. Phys., 2010, 133, 174116 CrossRef PubMed
.
- F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef CAS
.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed
.
- J. A. Pople and R. K. Nesbet, J. Chem. Phys., 1954, 22, 571–572 CrossRef CAS
.
- C. C. J. Roothaan, Rev. Mod. Phys., 1960, 32, 179–185 CrossRef
.
- J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. D. Sherrill and T. D. Crawford, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 556–565 Search PubMed
.
- X. Liu, S. Truppe, G. Meijer and J. Pérez-Ríos, J. Cheminf., 2020, 12, 31 CAS
.
- Y. Wang, D. Julian, M. A. Ibrahim, C. Chin, S. Bhattiprolu, E. Franco and J. Pérez-Ríos, J. Mol. Struct., 2023, 398, 111848 CAS
.
-
P. J. Linstrom and W. G. Mallard, NIST Chemistry WebBook, NIST, Standard Reference Database Number 69, 2011, http://webbook.nist.gov Search PubMed
.
-
K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure, Springer-Verlag, Berlin, Germany, 1979 Search PubMed
.
-
P. J. van Maaren and D. van der Spoel, Bond potentials software package and data repository, 2025, DOI:10.5281/zenodo.14842997
.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed
.
- R. A. Buckingham, Proc. R. Soc. London, Ser. A, 1938, 168, 264–283 CAS
.
- K. Cahill and V. A. Parsegian, J. Chem. Phys., 2004, 121, 10839–10842 CrossRef CAS PubMed
.
- K. T. Tang and J. P. Toennies, J. Chem. Phys., 2003, 118, 4976–4983 CrossRef CAS
.
- R.-H. Xie and J. Gong, Phys. Rev. Lett., 2005, 95, 263202 CrossRef PubMed
.
- K. Levenberg, Q. Appl. Math., 1944, 2, 164–168 CrossRef
.
- D. W. Marquardt, J. Soc. Ind. Appl. Math., 1963, 11, 431–441 CrossRef
.
- T. Ho and H. Rabitz, J. Chem. Phys., 1996, 104, 2584–2597 CrossRef CAS
.
- W. Hwang, S. L. Austin, A. Blondel, E. D. Boittier, S. Boresch, M. Buck, J. Buckner, A. Caflisch, H.-T. Chang, X. Cheng, Y. K. Choi, J.-W. Chu, M. F. Crowley, Q. Cui, A. Damjanovic, Y. Deng, M. Devereux, X. Ding, M. F. Feig, J. Gao, D. R. Glowacki, J. E. Gonzales II, M. B. Hamaneh, E. D. Harder, R. L. Hayes, J. Huang, Y. Huang, P. S. Hudson, W. Im, S. M. Islam, W. Jiang, M. R. Jones, S. Käser, F. L. Kearns, N. R. Kern, J. B. Klauda, T. Lazaridis, J. Lee, J. A. Lemkul, X. Liu, Y. Luo, A. D. MacKerell Jr, D. T. Major, M. Meuwly, K. Nam, L. Nilsson, V. Ovchinnikov, E. Paci, S. Park, R. W. Pastor, A. R. Pittman, C. B. Post, S. Prasad, J. Pu, Y. Qi, T. Rathinavelan, D. R. Roe, B. Roux, C. N. Rowley, J. Shen, A. C. Simmonett, A. J. Sodt, K. Töpfer, M. Upadhyay, A. van der Vaart, L. I. Vazquez-Salazar, R. M. Venable, L. C. Warrensford, H. L. Woodcock, Y. Wu, C. L. Brooks III, B. R. Brooks and M. Karplus, J. Phys. Chem. B, 2024, 128, 9976–10042 CrossRef CAS PubMed
.
- W. Sun, Mol. Phys., 1997, 92, 105–108 CrossRef CAS
.
- H. Hulburt and J. Hirschfelder, J. Chem. Phys., 1941, 9, 61–69 CrossRef
.
- T. Tietz, Can. J. Phys., 1971, 49, 1315 CrossRef CAS
.
- F. M. Rafi, Phys. Lett. A, 1995a, 205, 383–387 Search PubMed
.
- I. Levine, J. Chem. Phys., 1966, 45, 827–828 CrossRef
.
- S. Noorizadeh and G. Pourshams, J. Mol. Struct., 2004, 678, 207–210 CrossRef CAS
.
- W. Hua, Phys. Rev. A, 1990, 42, 2524–2529 CrossRef CAS PubMed
.
- A. Frost and B. Musulin, J. Chem. Phys., 1954, 22, 1017–1020 CrossRef CAS
.
- Y. Varshni, Can. J. Chem., 1988, 66, 763–766 CrossRef CAS
.
- N. Rosen and P. Morse, Phys. Rev., 1932, 42, 210–217 CrossRef CAS
.
- M. Sage, Chem. Phys., 1984, 87, 431–439 CrossRef CAS
.
- J. Linnett, Trans. Faraday Soc., 1940, 36, 1123–1134 RSC
.
- Z. H. Deng and Y. P. Fan, Shandong Univ. J., 1957, 7, 162 Search PubMed
.
- D. Gardner and L. von Szentpály, J. Phys. Chem. A, 1999, 103, 9313–9322 CrossRef CAS
.
- A. Kratzer, Z. Phys., 1920, 3, 289–307 CrossRef CAS
.
- E. Lippincott, J. Chem. Phys., 1953, 21, 2070–2071 CrossRef CAS
.
- R. J. Le Roy, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 167–178 CrossRef CAS
.
- S. N. Yurchenko, L. Lodi, J. Tennyson and A. V. Stolyarov, Comput. Phys. Commun., 2016, 202, 262–275 CrossRef CAS
.
- M. A. E. Ibrahim, X. Liu and J. Pérez-Ríos, Digital Discovery, 2024, 3, 34–50 RSC
.
- K. Kříž and D. van der Spoel, J. Phys. Chem. Lett., 2024, 15, 9974–9978 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional tables and figures. See DOI: https://doi.org/10.1039/d4dd00344f |
| This journal is © The Royal Society of Chemistry 2025 |
