Quenching-induced lattice modifications endowing Li-rich layered cathodes with ultralow voltage decay and long life†
Lingcai
Zeng‡
ab,
Haoyan
Liang‡
a,
Yaqian
Wang
a,
Xiaolong
Ying
a,
Bao
Qiu
 *ac,
Jiajie
Pan
b,
Yibin
Zhang
a,
Wen
Wen
d,
Xuechun
Wang
e,
Qingwen
Gu
a,
Junhao
Li
b,
Kaixiang
Shi
*ac,
Jiajie
Pan
b,
Yibin
Zhang
a,
Wen
Wen
d,
Xuechun
Wang
e,
Qingwen
Gu
a,
Junhao
Li
b,
Kaixiang
Shi
 b,
Yanbin
Shen
e,
Quanbing
Liu
b,
Yanbin
Shen
e,
Quanbing
Liu
 *b and
Zhaoping
Liu
*b and
Zhaoping
Liu
 *ac
*ac
aNingbo Institute of Materials Technology and Engineering (NIMTE), Chinese Academy of Sciences (CAS), Ningbo 315201, PR China. E-mail: qiubao@nimte.ac.cn; liuzp@nimte.ac.cn
bGuangzhou Key Laboratory of Clean Transportation Energy Chemistry, Guangdong Provincial Key Laboratory of Plant Resources Biorefinery, School of Chemical Engineering and Light Industry, Guangdong University of Technology, Guangzhou 510006, China. E-mail: liuqb@gdut.edu.cn
cCenter of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
dShanghai Synchrotron Radiation Facility, Chinese Academy of Sciences, Zhangjiang High-Tech. Park, Pudong New Area, Shanghai, China
ei-Lab, Suzhou Institute of Nano-Tech and Nano-Bionics (SINANO), Chinese Academy of Sciences, Suzhou 215123, China
First published on 22nd November 2024
Abstract
While bringing high capacity, oxygen redox in Li-rich layered oxides has also led to severe voltage decay, hindering their practical applications. To break through this bottleneck, we herein propose a general and versatile strategy, brine quenching, to address this issue. Combining with multiple-scale characterizations, theory calculation and electrochemical performance, the underlying mechanism of voltage decay suppression by brine quenching is distinctly revealed. The quenching process can generate local bulk-compatible distortion, which can adjust the whole lattice oxygen framework to mitigate the disorder, and modulate the intrinsic redox properties of the material. The resulting LLO will maintain the ordered structure after long-term cycling, thus mitigating the voltage decay. Additionally, a robust surface can be established through the ion exchange to restrict oxygen release. Therefore, lattice oxygens both in the bulk and surface are stabilized. Benefiting from the synergistic effect, the 1.6 Ah full cell based on the magnesium–nitrate-solution-quenched sample exhibits over 80% retention after 2159 cycles and an ultra-long lifespan of 3200 cycles with a negligible voltage decay rate of 0.091 mV per cycle. This research provides a potential direction for designing next-generation cathode materials that combine long-life and ultralow voltage decay.
Broader contextLi-rich layered oxides (LLOs) that utilize both cation and anion redox can significantly increase battery energy density. However, due to the unstable honeycomb structure of Li2MnO3, the reduced reversibility of the O2−/O2 redox process and O2 loss together lead to structural damage during cycling and thus voltage decay, which remains an obstacle to its practical application. Here, we propose a general strategy, brine quenching, to accurately build a robust surface-bulk structure. The underlying mechanism is revealed for the differences in capacity and voltage stability using different brines. First, brine quenching is accompanied by the formation of a partial “Li–O–M” configuration, in which the appropriate electronegativity of Mn+ induces an electron transfer that lowers the top of the unhybridized O 2p (UO2p) energy band, leading to a decrease in the TM–O covalency. Furthermore, the quenching process produces localized bulk-compatible lattice distortions, which adjust the entire lattice oxygen framework and modulate the intrinsic redox reversibility of the material due to activated lattice oxygen. As a result, the quenched samples achieved unprecedented capacity and voltage cycling stability. This study provides a potential direction for the design of next-generation commercial cathode materials that combine long life and negligible voltage decay. |
Introduction
Developing high-energy-density cathode materials is critical for high-performance Li-ion batteries (LIBs) for portable devices, electric vehicles, and energy storage devices.1 Li-rich layered oxides (LLOs) have been considered as a promising candidate via the utilization of both cation and anion redox, thus providing an ultra-high capacity of over 300 mAh g−1.2–4 Nevertheless, the activation of lattice oxygen also leads to detrimental structure evolution, such as surface-oxygen release and transition-metal migration.5–7 These structure degradations will accumulate during the continuous cycles, leading to voltage decay, which causes energy loss and challenges the battery management system.With the deepening of the research, there is a growing consensus on this issue that voltage decay is more intrinsic.8,9 When charged to high voltage, the lattice oxygen is activated, and the structure of LLOs reaches a highly metastable state. Therefore, the LLOs are bound to make it a stable structure upon the multiple cycling.10 The O2− in the surface will be oxidized to O2 and released. In the bulk, the oxidation of O2− results in the redistribution of charges in the form of oxygen vacancies, O–O peroxo-like dimer or trapped O2, which remains a mystery. Either way, the evolution makes it easy to generate structure transformation, such as lattice distortion and stacking faults, which can be defined to disordered structures. Therefore, the key to suppressing voltage decay should decrease the local disorder at high voltages to stabilize the structure during cycling. In addition, a common phenomenon for LLOs is that the voltage decay is always more significant in the initial stage. With the increase of cycles, the voltage exhibits a gradual stabilization trend. This is because the accumulated disordered transitions of long cycles can increase the overall structural flexibility, which contributes to suppressing the voltage decay. Then, if this process can be accelerated or pre-treated, a smaller voltage decay can be achieved at the beginning of the cycle.
So far, numerous efforts have been put into seeking valid solutions to mitigate voltage decay. Surface modifications are conducted to reduce oxygen release, through surface coating and oxygen vacancies construction.11,12 Unfortunately, such measures have no effect on the bulk, so the results of suppressing voltage decay are hardly satisfactory. Doping with foreign ions is a common method used to stabilize the bulk structure due to the strong bonding of M–O, at the expense of sacrificing partial capacity, accordingly.13–15 In addition, defect engineering aims to pre-embed a series of disordered and defective structures, such as stacking faults, lattice distortions and dislocations into the original LLO bulk structure, which exhibits unexpected effects on voltage decay.16 In our previous work,17 we argued that embedding disorder into the host structure to a certain amount favors structure stability, without damage to the capacity. Based on the pinning effect, this pre-constructed disordered structure prevents the occurrence of TM migration and phase transitions in the already distorted structure, and maintains excellent structural stability. More importantly, the pre-introduced disordered structure acts as a buffer to coordinate the activated structural domains and the ordered lattice framework, which regulates the intrinsic redox properties of the material during the cycling process. Hence, this unusual strategy might be the right direction to mitigate the voltage decay of LLOs.
Inspired by traditional steel manufacturing, researchers have developed a quenching method in the modification of functional materials, particularly in the battery field.18 It was reported that Wang et al.19 generated a Co3O4-like spinel coating on the surface of LiCoO2 by quenching in salt solution, which realized an effective improvement in the cycling performance of LiCoO2. In addition, Zhang et al.20 achieved oxygen vacancy construction and Li/Ti cation redistribution on a Li4Ti5O12 anode by ice-water quenching, obtaining a reversible specific lithium storage capacity exceeding its theoretical value. It is noteworthy that the adjustment of the bulk structure of electrode materials by brine quenching is often neglected regarding brine quenching, especially with salt solution as the medium. Benefiting from a rapid thermal exchange, the quenching method has been proven to be a unique strategy to regulate the lattice structure. Vacancies, distortion and stacking faults are successfully induced into the bulk of the materials. Meanwhile, metal doping can also be achieved by quenching with salt-solution, thus a robust surface has been constructed.21 Therefore, the brine quenching is supposed to generate a synergistic effect on the modification of LLOs.
Herein, modification of LLOs using a brine quenching strategy is systematically elaborated. The experimental results indicate the construction of localized disorder in the bulk and remodeling layer on the surface. Combined with DFT+U calculations, the underlying mechanism has been revealed and the electronegativity of metal-ion in the brine is closely connected to the macro-properties. In addition, results from atomic-scale spherical aberration-corrected scanning transmission electron microscopy (AC-STEM), synchrotron X-ray absorption (XAS), time-of-flight secondary ion mass spectrometry (TOF-SIMS) and Operando electrochemical mass spectrometry (DEMS) demonstrate the validity of the combined surface-bulk structure design. Consequently, the assembled half-cell and full-cell both display an excellent electrochemical performance. Wherein, the pouch cell with magnesium nitrate-treated LLO shows a negligible voltage decay rate of 0.091 mV per cycle and an ultra-long lifespan of more than one year. This study provides a potential methodology to solve the voltage decay issue and may inspire innovation in the development of LLOs in the future.
Results and discussion
Structure characterizations of LLOs quenched in different brines
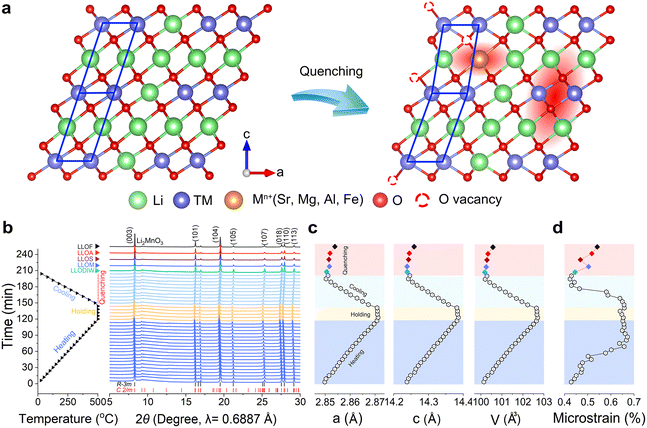
Samples are successfully prepared using a brine-quenching method (see details in the Experimental section). As mentioned in the introduction, the expected result is that localized distortions are created in the long-range ordered lattice and the original surface gets re-constructed turning into a solid-stable surface after brine quenching (Fig. 1a). Defined by the quenching solution (magnesium nitrate, strontium nitrate, aluminum nitrate and ferric nitrate), the samples are denoted as LLOM, LLOS, LLOA and LLOF, respectively. Moreover, a sample quenched in deionized water is also prepared under the same condition and denoted as LLODIW. The rapid thermal exchange does not destroy the original LLO particles, yet brings a more consistent surface, according to scanning electron microscopy (SEM) images (Fig. S1, ESI†). Inductively coupled plasma optical emission spectrometry (ICP-OES) was also performed to analyze the chemical composition of the quenching-treated samples (Table S1, ESI†). The result shows that metal ions enter the lattice as a replacement with Li+, not involving the transition metal ions of Ni, Co and Mn. More importantly, the quenched reaction filtrates of LLODIW and LLOA were subjected to elemental analysis. As shown in Table S2 (ESI†), minimal Li and TM elements were detected in the reaction filtrate after quenching in deionized water lacking Al3+. In contrast, an alarming amount of Li was detected in the LLOA, as high as 357.899 μg mL−1. This observation suggests that the quenching in aluminum nitrate occurs as a result of the Li+/Al3+ ion exchange process, leading to the loss of Li. It is noteworthy that trace amounts of Li and TM ions were detected in the quench reaction filtrates of LLODIW and LLOA, respectively, which were mainly due to the infiltration of a small number of microscopic filtrate particles during the filtrate extraction process. Interestingly, the degree of the replacement differs upon the used brine. Considering the same driver, thermal exchange, we here speculate that the self-property of the Mn+ is the reason causing differential results, specifically the ionic radius and electronegativity.To reveal the evolution of the lattice structure during quenching, we conducted variable-temperature in situ synchrotron X-ray diffraction (SXRD). The temperature variation simulates the heating and holding process, and the natural-cooling process serves as a contrast to the quenching process. The characteristics of LLO are maintained in all the XRD patterns during the temperature variation, indicating heat treatment would not cause substantial damage, even under a quenching process (Fig. 1b). The SXRD Rietveld refinements are conducted using a single rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase in GSAS-II (Fig. S2 and Table S3, ESI†).22 The lattice parameters of all samples indicate a typical positive thermal expansion behavior (Fig. 1c). However, the brine quenched samples show variability in lattice parameters and microstrain, compared with natural-cooling and quenching in deionized water (Fig. 1c and d). This phenomenon can be attributed to Li+/Mn+ replacement during the quenching process. The hypothesis can be proved by the results of ICP-OES. When the Li site is occupied by high-valence and different-radius ions, the coulomb force alters the distance between the Li slab and TM slab, resulting in a change in lattice parameters.
m phase in GSAS-II (Fig. S2 and Table S3, ESI†).22 The lattice parameters of all samples indicate a typical positive thermal expansion behavior (Fig. 1c). However, the brine quenched samples show variability in lattice parameters and microstrain, compared with natural-cooling and quenching in deionized water (Fig. 1c and d). This phenomenon can be attributed to Li+/Mn+ replacement during the quenching process. The hypothesis can be proved by the results of ICP-OES. When the Li site is occupied by high-valence and different-radius ions, the coulomb force alters the distance between the Li slab and TM slab, resulting in a change in lattice parameters.
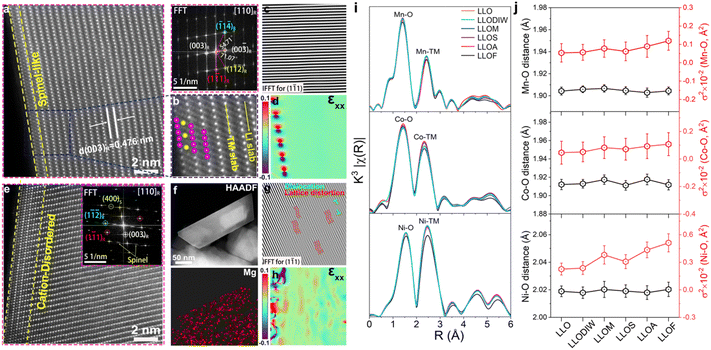
Spherical aberration-corrected scanning transmission electron microscopy (AC-STEM) was used to investigate the lattice structure at the atomic level. The representative images (Fig. 2 and Fig. S3, ESI†) of LLO and quenched samples are acquired along the [110] axis. It is well known that heavy atoms (Mn, Co, Ni) are present as bright spots because their contrast is proportional to Z1.7 (Z is the atomic number) in the high-angle annular dark-field (HAADF) images.23 All images indicate a feature of layered structure and the few spinel-like layers on the surface of the pristine sample are caused by the evaporation of lithium carbonate (Fig. 2a).24 Combined with EDS mapping analysis, it confirms the insertion of the Mn+ (Fig. 2f and Fig. S3b, f and j, ESI†). A cation-disordered layer was found on the surface of the quenched samples to different extents (5 nm). We suggest that the near-surface Li+/H+ exchange that occurs during quenching in acidic nitrate solution forms a large number of Li vacancies on the surface of the material, and the formation of Li vacancies accelerates the anionic and cationic rearrangements on the surface: On one hand, the quenching process is thermally driven by the highly inhomogeneous temperature field to promote the doping of Mg2+ from the salt solution into the Li vacancies for charge compensation. On the other hand, the generation of Li vacancies will further induce the generation of oxygen vacancies. In addition, cation migration in a highly inhomogeneous temperature field is favorable and will facilitate the occurrence of Li/Ni miscibility.25 Since Mg2+ and Ni2+ have a similar atomic number, it is difficult to accurately determine the occupancy position of the surface-doped Mg by STEM, and thus we define it as a cationic remodeling layer, as observed by STEM. In addition, inverse fast Fourier transform (IFFT) and geometric phase analysis (GPA) were conducted to evaluate the micro-strain of the lattice. Wherein, the lattice of the pristine is uniform and uninterrupted, indicating a perfectly ordered layer (Fig. 2c and d). After the brine quenching, in contrast, the lattice fringes become twisted, indexing the formation of dislocation and lattice distortions (Fig. 2g, h and Fig. S3c–d, g–h and k–l, ESI†). This phenomenon corroborates the refined microstrain of the SXRD pattern. Notably, there are significant differences in the as-prepared samples quenched in different brines, observed in the IFFT and GPA plots. The LLOF sample has the greatest extent of lattice distortion and dislocation, while the LLOS sample has the least. This result agrees well with the refinement result of the microstrain. As discussed above, the distortion and dislocation are the consequence of Li+/Mn+ replacement, and the more Mn+ substitute, the more disordered structure it will generate. It is noteworthy that the lattice distortions and dislocations in the brine-quenched sample LLOM are not limited to the surface of this particle, but are also observed inside the bulk. The lattice distortions and dislocations near the surface mainly arise from the cationic disordered structure induced by Li+/Mn+ ion exchange and the generation of oxygen vacancies, as well as from the freezing of the expanded lattice during quenching. In addition, HRTEM images of the quenched sample LLODIW in deionized water were used to investigate the causes of the formation of bulk lattice distortions and dislocations. Compared to brine quenching, the lattice distortions and micro stresses in LLODIW are mainly distributed at the lattice edges and less in the bulk (Fig. S4, ESI†). This is mainly attributed to the fact that quenching in deionized water does not involve ion exchange and has less effect on the bulk lattice. At the same time, the surface lattice edges preferentially come into contact with deionized water during quenching, and heat transfer occurs to balance the inhomogeneous temperature fields of the surface and bulk lattices. The smaller temperature difference in the grains increases the tendency of the bulk-expanded lattice to regain orderliness. Therefore, the formation of bulk lattice distortions and dislocations after brine quenching is mainly attributed to bulk Mn+ doping achieved by ion exchange during the quenching process. This bulk Mn+ doping impedes the recovery of expanded lattice orderliness and increases bulk cation disorder.
The local coordination of Ni, Co and Mn in different quenched samples is analyzed by X-ray absorption spectroscopy (XAS).26 According to X-ray absorption near-edge structure (XANES) spectra, the Mn K-edge shifts towards a low energy in samples of LLOA and LLOF, indicating a partial reduction during the quenching process (Fig. S5, ESI†).27 To further reveal the change in local environment brought by the insertion of Mn+, k3-weight Fourier-transformed extended X-ray absorption fine structure (EXAFS) spectra of the quenched samples and the pristine sample are compared (Fig. 2i). The result shows a similar pattern of the nearest neighbor TM–O bond (the first shell) and TM–TM bond (the second shell),28 except for a slight deviation in the strength of the TM–O coordination in the LLOA and LLOF samples. Furthermore, the EXAFS fitting analysis was employed on the first two coordination shells to elucidate more details of the quenched samples (Fig. S6 and Table S4, ESI†). Examining the evolution of the TM–O shell layer is especially crucial because the local structural changes are intimately linked to the TMO6 octahedra.29,30 The quenching process makes a difference to the TM–O bonds, indexing a deformation of the original TMO6 octahedra (Fig. 2i). Additionally, previous studies have suggested that the structural distortion can be reflect by the deviation of absorbing atoms from their equilibrium positions.31 Thus, the Debye–Waller factor (σ2) was proposed to represent the degree of local disorder, and they are positively correlated in theory. After the quenching process, all samples exhibit increased σ2 of Mn–O, Co–O and Ni–O, indicating the generation of a disordered structure (Fig. 2j). In addition, the dramatic increase in σ2Mn–O and σ2Ni–O suggests that distortions prefer to occur in the neighborhood of Mn and Ni atoms. Wherein, the samples of LLOA and LLOF display a larger degree of change, meaning more disordered domains are generated. The XAS further proves the existence of local disordered structures generated by the quenching process.
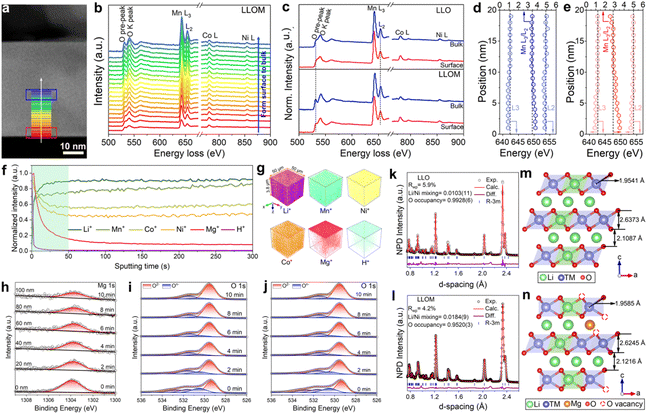
As the bulk structure has already been analyzed in detail, it is time to discuss the influence of the quenching process on the surface structure. The electron energy loss spectroscopy (EELS) technique was used mainly to collect TM and O chemical valence states (Fig. 3a–e and Fig. S7, ESI†). The well-defined O K-edge pre-peak is located at 531 eV, which is closely related to the hybridization of the O 2p state with the highly localized TM 3d state.32 After the quenching process, the samples show a reduced intensity of O K-edge pre-peak and broadening of the O K-edge peak on the surface compared to the bulk, while this phenomenon did not occur in the pristine LLO (Fig. 3c and Fig. S7m–p, ESI†). According to previous studies, the quenching process can inhibit oxygen extraction during the natural cooling process and generate oxygen vacancies in the oxides, thus endowing them with new properties.20 This result suggests the formation of oxygen vacancies and a reduced covalency of the neighboring TM–O, which will alleviate the changes in the O 2p band and therefore inhibit the release of oxygen.33 The formation of oxygen vacancies is also confirmed by electron paramagnetic resonance (EPR), which is sensitive to unpaired electrons and therefore can be used in their detection.34 The spectra show a sharp g value of around 2.004, in accordance with the characteristic response of oxygen vacancies (Fig. S8, ESI†). Besides, the intensity of the quenched samples is significantly higher than that of the pristine sample, indicating more vacancies generated. In the case of the Mn L-edge, the peak of the quenched samples shifted to a higher energy loss and the ratio of L3/L2 decreased from the surface to the bulk (Fig. 3e). Typically, the Mn L3 and L2 edge peaks are the result of the transition from 2p3/2 and 2p1/2 to 3d, respectively. Furthermore, their energy position and peak area ratio L3/L2 are sensitive indicators of Mn chemical valence state.35 Therefore, there is a lower valence state of Mn on the surface of the quenched samples, mainly because of the formation of oxygen vacancies.36 A similar pattern was not found in the pristine one, indicating the stable valence state of Mn (Fig. 3d). Considering the reduction of Mn at the surface, the formation of cation-disordered layers is promoted in the quenched samples, which is consistent with the results of AC-STEM.
In order to reveal more intuitively the spatial distribution of Li+/H+ substitution and Li+/Mn+ substitution in the particles and their intrinsic connection during the brine quenching process, time-of-flight secondary ion mass spectrometry (TOF-SIMS) was employed to determine the chemical species that make up the particles of the pristine and brine-quenched samples and their distribution from the surface to bulk. Depth profiles showed that the normalized intensities of Mg+, Co+, and Ni+ in the LLOM particles gradually decreased with increasing sputtering time, while Li+ and Mn+ gradually increased (Fig. 3f). The signals all remained unchanged after 50 seconds of sputtering time. This indicates that Mg+, Co+ and Ni+ are enriched on the surface of the LLOM particles, corresponding to a gradual increase in Li+ and Mn+. This is related to the formation of a near-surface spinel phase and cation mixed disorder structure (Fig. S9, ESI†). In addition, the 3D depth images further clearly show the loss of Li and enrichment of Mg+ signals at the surface and the weakening of Mg+ signals in the bulk with increasing depth (Fig. 3g), which further validates the occurrence of Li+/Mg2+ ion exchange. Similarly, Fig. S10 (ESI†) shows the TOF-SIMS depth profiles and 3D depth images of Li+, Ni+, Co+, Mn+ and Mn+ species in pristine LLO, LLOS, LLOA and LLOF particles. The results show that LLOS, LLOA and LLOF exhibit subtle differences in surface Li+ loss and Mn+ enrichment. Among them, Sr+ in LLOS mainly aggregates on the particle surface with negligible bulk compared to LLOM, while LLOA exhibits more pronounced surface enrichment and gradient distribution of Al3+. Notably, the most pronounced normalized Fe3+ signal was detected in LLOF particles from the surface to the bulk. This observation suggests that the most pronounced Li+/Fe3+ ion exchange occurs in LLOF, which is consistent with the above HRTEM and ICP-OES results. The above TOF-SIMS results further demonstrate that different brine quenches exhibit differential levels of Li+/Mn+ ion exchange. However, the detected H+ species were predominantly enriched near the surface of the particles and showed lower levels compared to the Mn+ species signals. Thus, Li+/H+ substitution during brine quenching occurs mainly near the particle surface, whereas Li+/Mn+ substitution can diffuse into the bulk. This discrepancy mainly originates from the effect of Mn+ ions in the quench solution. Specifically, during the quenching process, a stable vapor film is first formed on the particle surface under a highly inhomogeneous temperature field, which allows the evaporation of near-surface moisture, leading to metal salt bias on the material surface and thermally driven Li+/Mn+ substitution with the material.37 Towards the end of the quenching process, the temperature difference between the quenching solution and the material is balanced by heat transfer effects causing the vapor film on the particle surface to rupture. While at the same time, the H+ in solution undergoes a near-surface Li+/H+ ion exchange driven by residual heat.
Meanwhile, the X-ray photoelectron spectroscopy (XPS) reveals the detailed change of electronic structure and elemental composition induced by the quenching process. The results confirm the insertion of Mn+ after the quenching process and present a trend of gradient doping based on the surface etching technique (Fig. 3h and Fig. S11, ESI†). Despite all gradient trends, there is a slight discrepancy among the inserted ions, which verifies the results of ICP-OES and AC-STEM. The states of oxygen in the LLOM and pristine samples were also investigated by XPS from the surface to the bulk. A characteristic O 1s peak at 529.5 eV represents the typical TM–O (O2−) in layered oxide materials, while the weaker peak located at 531.5 eV can be attributed to the characteristic peak of the oxygen vacancy.38–40 With the etching time prolonged, both peaks exhibit negligible change in the pristine sample (Fig. 3i). In contrast, there is an apparent alteration in the intensity of the LLOM sample. Specifically, the intensity of the O2− peak increases, while the one for the oxygen vacancy peak decreases gradually (Fig. 3j). In summary, the XPS technique discloses the modification of brine quenching on the surface of LLO. The unstable O2− on the surface of LLO was removed and a new surface was re-constructed with cation disorder, thus contributing to no irreversible oxygen release and harmful phase transformation. More directly, the focused ion beam-scanning electron microscopy (FIB-SEM) was used to perform mapping/energy dispersive X-ray spectrometry (EDS) and cross-sectional SEM of LLOM to visually analyze the distribution of pristine Mg from the surface to the bulk. As shown in Fig. S12 and S13 (ESI†), the EDS mapping, line scan and point scan all show surface Mg enrichment and gradient doping of Mg in the bulk. This is in agreement with the TOF-SIMS results mentioned above, indicating that brine quenching undergoes ion exchange to realize the surface Mg enrichment and shows a gradient-decreasing trend in the bulk.
SXRD/NPD joint Rietveld refinement was conducted to determine all the information regarding the crystal structure after the quenching process such as lattice oxygen, using a single rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase (Fig. 3k, l and Fig. S14, ESI†). Depending on the detailed structural parameters, the decrease in the oxygen occupancy, 99.28% of LLO to 95.20% of LLOM, proves the formation of an oxygen vacancy (Tables S5 and S6, ESI†). At the same time, the occupancy of TM in the Li3a site increases, meaning the anti-site is prevailing in LLOM, which is beneficial to suppressing phase transition and voltage decay.41 Additionally, refinement using the monoclinic C2/m phase model further verifies that brine quenching introduces H protons into lithium octahedral vacancies via Li+/H+ substitution (Table S7, ESI†), which is consistent with previous reports.42 The corresponding crystal structures of LLO and LLOM are found based on the results of joint Rietveld refinement, from which we can clearly see the changes in TM-slab and Li-slab distance (Fig. 3m and n). Typically, the slab distance is calculated from eqn (1) and (2),43
m phase (Fig. 3k, l and Fig. S14, ESI†). Depending on the detailed structural parameters, the decrease in the oxygen occupancy, 99.28% of LLO to 95.20% of LLOM, proves the formation of an oxygen vacancy (Tables S5 and S6, ESI†). At the same time, the occupancy of TM in the Li3a site increases, meaning the anti-site is prevailing in LLOM, which is beneficial to suppressing phase transition and voltage decay.41 Additionally, refinement using the monoclinic C2/m phase model further verifies that brine quenching introduces H protons into lithium octahedral vacancies via Li+/H+ substitution (Table S7, ESI†), which is consistent with previous reports.42 The corresponding crystal structures of LLO and LLOM are found based on the results of joint Rietveld refinement, from which we can clearly see the changes in TM-slab and Li-slab distance (Fig. 3m and n). Typically, the slab distance is calculated from eqn (1) and (2),43
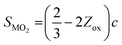 | (1) |
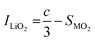 | (2) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure, respectively.
m structure, respectively.
Based on the experimental results above, such changes in the lattice parameters after the quenching process can be explained from two aspects as follows: (1) the inhomogeneous temperature field generates residual stress aggregation resulting in lattice expansion during the quenching process; (2) the thermally driven near-surface Li+/H+ exchange during the quenching process is accompanied by the formation of vacancies and insertion of Mg2+, which breaks the original charge distribution and induces electrostatic interactions, leading to the expansion of the Li slab and shrinking of the TM slab. Together with the extension of the TM–O bond in the TM slab, the lattice distortion is formed and leads to the increase in lattice parameters. The increase in the thickness of the Li slab will lower the energy barrier required for Li+ diffusion, which facilitates the rapid intercalation and de-intercalation of Li+ in the lattice structure. More importantly, the brine-quenched LLOM sample has a more stable structure than the LLO sample, which is beneficial to the cycling stability of the Li-rich cathode material.
Theoretical calculation of LLOs quenched in different brines
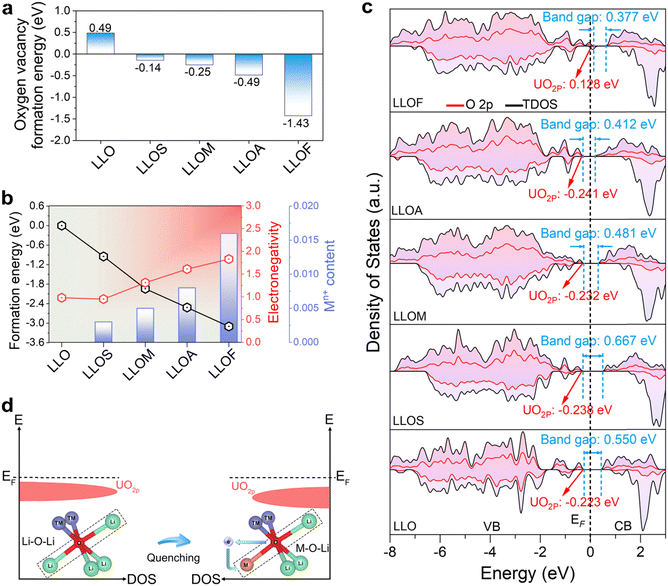
To elucidate the underlying mechanism of using different brine quenching, the first-principles calculations were performed to investigate the local electronic properties (see details in the Experimental section). Firstly, the formation energies for the possible occupations of the Mg element were verified by DFT calculations using LLOM as an example. LLOMs doped with Mg atoms at different Li and TM positions were considered, and the corresponding configurations are shown in Fig. S15a and S16 (ESI†). The Li position substitution has a lower formation energy compared to the TM (Ni, Co, Mn) position substitution (Fig. S15b, ESI†). In particular, the lowest formation energy of −1.94 eV is obtained when Mg substitutes the LiLi4 site in the Li layer, further verifying that Li+/Mg2+ ion exchange occurs upon brine quenching. Thus, the sample structure model for Li+/Mn+ ion exchange after different brine quenches is shown in Fig. S17 (ESI†).The results in the former section have shown that there are oxygen vacancies generated by the quenching process. It is well known that the formation and diffusion of oxygen vacancies during anion redox processes in LLO accompanied by irreversible oxygen release and TM ion migration alters the chemical coordination environment and disrupts the crystal structure, leading to electrochemical performance degradation.44 However, with a deeper understanding of the oxygen-involved reactions and their induced structural evolution in LLO, active introduction strategies of oxygen vacancies have been proposed and validated in recent years to improve structural stability and electrochemical reversibility and mitigate voltage decay and hysteresis.45 For example, Xu et al.46 proposed that doping Gd in LLO can significantly reduce the formation energy of oxygen vacancies in Li2MnO3. Due to the construction of oxygen vacancies, LLO exhibits a more stable oxygen framework and lattice structure. Therefore, the models of quenched samples are constructed with oxygen vacancy and Li+/Mn+ replacement, and the pristine LLO is considered as a perfect crystal (Fig. S17, ESI†). We calculate the formation energy of oxygen vacancies, and it is all negative in quenched samples, which indicates the formation of oxygen vacancies is thermodynamically favorable during the quenching process (Fig. 4a). Previous studies have demonstrated that preliminary oxygen extraction can enhance the electrochemical performance of Li-rich cathodes, due to the removal of unstable lattice oxygen.46 Moreover, quenching in ferric nitrate seems to be more beneficial to the formation of oxygen vacancy, indicating there is a higher degree of reconstruction in the LLOF sample. This result agrees well with the experimental results of EPR. In the last section, based on the ICP-OES and AC-STEM results, we determined the amount of inserted content during different brine-quenching processes, and that there are also differences in the doping gradient and the degree of lattice disorder. Generally, the smaller the ion radius is, the more it inserts. Nevertheless, this rule seems not to work in the situation of LLOA and LLOF (0.535 Å for Al3+ and 0.645 Å for Fe3+). Meanwhile, there is a relationship between inserted content and electronegativity, so the formation energy of the Li+/Mn+ replacement is calculated and plotted with electronegativity and Mn+ content (Fig. 4b). The formation energy represents the difficulty of replacing Li+ with Mn+. The energy of all quenched samples is negative, suggesting the insertion is easily completed, wherein the LLOF is the easiest one. More importantly, the plots show a positive correlation between Mn+ content and electronegativity, and a negative correlation between formation energy and electronegativity. These results make it clearly intelligible that the electronegativity is the key to determining the insertion content of Mn+ under the same driving force during the quenching process.
Based on previous studies, electronegativity is the primary factor used to determine the ionic or covalent character of metal–ligand bonding, which will affect the anion redox reaction structurally and compositionally.47 A low electronegativity will allow oxygen atoms to attract more electrons, thus leading to the reduced covalency character of the TM–O bond. This reduction will decrease the gap between bonding and antibonding orbitals, increasing the redox potential of lattice oxygen.48 For this purpose, DFT calculations are adopted to calculate the partial density of states (p-DOS) and the total density of states (t-DOS) of the samples before and after the quenching process (Fig. 4c). The band gap between the valence band maximum (VBM) and the conduction band minimum (CBM) reflects the electronic conductivity of the material. When the band gap decreases, the excited electron will more easily transition to the conduction band.49 As calculated, the samples of LLOM, LLOA and LLOF show a smaller band gap than that of the pristine LLO, and the reduction degree agrees with the electronegativity of the Mn+ in brines. In the case of LLOS, the band gap gets broadened due to the smaller electronegativity of Sr (0.95) compared with that of the replaced Li (1.0). The results of the conductivity tests of the samples at different pressures also proved the above calculations (Fig. S18, ESI†), with the brine-quenched samples exhibiting higher conductivity at different pressures. Besides, the result shows that the occupied states of electrons in the LLOF sample are near the Fermi level, indicating the metallic character. This is mainly attributed to the introduced impurity energy levels brought by the Fe substitution within the system. As a result, the sample undergoes spin polarization separated from the conduction band valence band, inducing ferromagnetism, making it easier for electrons to jump from the valence band to the conduction band.
Furthermore, the presence of strong covalency of TM–O bands or reactive Li–O–Li configurations facilitates the generation of electron holes in O 2p bands and leads to the oxidation of the lattice oxygen (O2−→ On−), which leads to charge compensation at high de-lithiation states.50 Therefore, reducing TM–O covalency or reactive Li–O–Li configurations would mitigate the changes in the O 2p band, which significantly improves oxygen stability at high voltage in continuous cycling.41 After the quenching process, the increase in Li–O–M configurations has lowered the top of the unhybridized O 2p (UO2p) energy band, which decreases the electron density of oxygen due to the high electronegativity of the doped Mn+ (Fig. 4d). This suggests that the redox activity of lattice oxygen is partially suppressed by the introduction of oxygen vacancies and Li+/Mn+ replacement. Therefore, the voltage and capacity stability are strengthened.
Electrochemical measurement of LLOs quenched in different brines
The electrochemistry of the pristine LLO and quenched samples was measured in half-cells using galvanostatic charge/discharge tests in the voltage window of 2.0–4.8 V. By comparing the first charging–discharging curves of all samples, it can be seen that the brine quenching can significantly increase the specific capacity (Fig. 5a). Wherein, the LLOF sample displays a decreased charge capacity and large electrochemical polarization. This is mainly attributed to the fact that the higher electronegativity induces a large amount of Fe substitution, which decreases the electron transfer for O, thus inhibiting the oxygen redox activity and increasing the oxygen redox potential. As for LLODIW, it was mentioned above that the effect on the bulk is small since the quenching process does not involve ion exchange (Fig. S4, ESI†). As a result, LLODIW has similar electrochemical properties to LLO (Fig. S19, ESI†). Notably, the higher capacity contribution of LLODIW is due to the cationic disordered layer of oxygen-containing vacancies on the surface, which improves the reversibility of oxygen anion redox. To further investigate the underlying reasons for the differential electrochemical properties exhibited by different brine quenches, potassium nitrate, chromium nitrate and copper nitrate–brine quenches were extended for comparison. As shown in Fig. S20a (ESI†), all samples exhibit differential polarisation increases, with LLOCr, LLOFe and LLOCu showing the most pronounced ones. Fig. S20b (ESI†) shows the distribution of capacity provided by cationic redox (CR) and capacity provided by oxygen redox (OR) for all samples in relation to the electronegativity difference of M–O. Among them, the OR capacity shows a tendency to increase and then decrease with the decrease in M–O electronegativity difference. This phenomenon is mainly related to the nature of valence bonding in the M–O–Li configuration resulting from ion exchange during brine quenching, and it is directly determined by the average electronegativity and electronegativity difference of M–O (Fig. S20c, ESI†).51 Thus, when the nature of the M–O valence bond is ionically dominated (LLOk–LLOM), the covalency of the M–O–Li configuration gradually increases, resulting in a gradual decrease in the covalency of the TM–O, which improves the reversibility of the anionic redox chemistry and activates more OR capacity (Fig. S20b, ESI†). When a significant change in the nature of the M–O valence bond transitions to covalency dominance (LLOA–LLOCu), this will result in a significant reduction in the electron cloud density around oxygen. Excessive electron loss inhibits anion redox chemistry, thus hindering the OR capability. Furthermore, the gradual decrease in CR from LLOK to LLOCu is attributed to the Li+/Mn+ ion exchange that occurs during brine quenching. This builds a cationic mixed structure with many oxygen vacancies and spinel-like phases on the surface of the material, leading to the reduction of the material TM, and consequently to the loss of CR.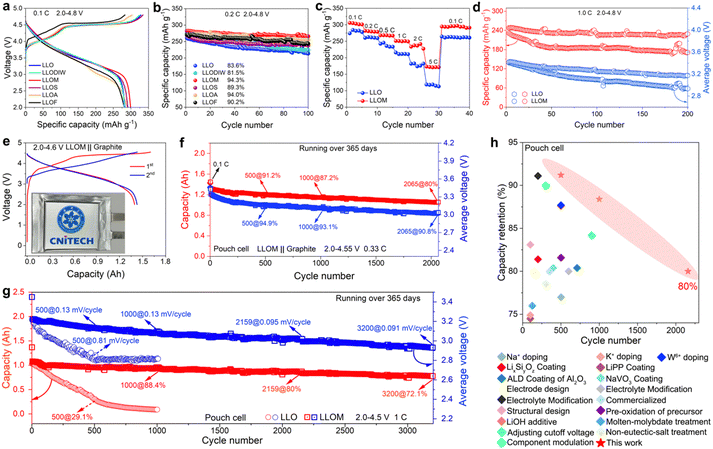 | ||
| Fig. 5 Electrochemical performance of the pristine and quenched LLO in half and pouch cells. (a) Comparison of the initial charge–discharge curves at 0.1 C. (b) Cycling performance at 0.2 C. (c) Rate capacity at various current densities of LLO and LLOM. (d) Cycling performance at 1C of LLO and LLOM. (e) Charge–discharge profiles of the LLOM‖graphite pouch cell in the window of 2.0–4.6 V. (f) The cyclic stability of the Ah-level LLOM‖graphite pouch full cell within 2.0–4.55 V (equal to 4.6 V vs. Li/Li+) under 0.33 C. (g) Cycling performance of LLO‖graphite and LLOM‖graphite pouch cell at 1 C and 2.0–4.5 V (equal to 4.55 V vs. Li/Li+) with 0.1 C for the first three cycles. (h) Comparison of the capacity retention of the rechargeable intercalation-type Li-rich cathode pouch cells (references in Table S10, ESI†). | ||
The cycling performances of all samples are also compared at the current density of 0.2 C (Fig. 5b and Fig. S21, ESI†). The capacity and voltage stability of the samples are significantly enhanced after the brine quenching process. More importantly, the retention shows a trend of increasing initially and decreasing afterward, along with the increase of Mn+ electronegativity in brine. This trend is consistent with the structural characterization of AC-STEM and SXRD refinement. This enhancement is associated with the design of disordered domains in the bulk and robust surface. When the electronegativity is significantly increased, the severe distortion and deformation of TMO6 octahedra will squeeze the neighboring tetrahedra, thus inevitably affecting the intercalation and de-intercalation of Li+. It explains the anomalous phenomenon of LLOA and LLOF samples. The results indicate that the robust surface and disordered domain in the bulk introduced by brine quenching are beneficial to the electrochemical performance within an appropriate degree. By comparing the electrochemical data of all quenched samples comprehensively, we find that the LLOM sample displays the highest capacity retention of 94.3% after 100 cycles, together with the mitigated voltage decay and discharge voltage close to the pristine LLO (Fig. 5b and Fig. S21h, ESI†). Therefore, the LLOM sample was selected for further analysis in the later part of the discussion. The LLOM sample also exhibits an improved rate capability and superior capacity recovery (Fig. 5c and Fig. S22, ESI†). The galvanostatic intermittent titration technique (GITT) was conducted to analyze the difference in kinetics between the LLOM and LLO samples, and the lithium diffusion coefficient (DLi+) was calculated based on Fick's second law (Fig. S23, ESI†).52 The result shows that LLOM exhibits a higher DLi+ than LLO, which can be attributed to the disordered domains and oxygen vacancies. The disordered domain caused by the rapid cooling rate during the quenching process has increased the Li slab thickness, resulting in the fast Li+ transportation. On the other hand, the oxygen vacancies can construct more active sites on the surface to participate in Li+ storage and promote kinetics. The cycling stability was evaluated for 200 cycles at a current density of 1 C (Fig. 5d). It is observed that the retention of capacity and discharge voltage is enhanced after the quenching process. Specifically, the LLOM sample retains more than 229.1 mAh g−1 of discharge capacity after 200 cycles (92.3% retention), which is much higher than that of LLO with only 170.9 mAh g−1 remaining (73.8% retention). The same result can also be obtained under other current densities (Fig. S24, ESI†). This excellent cycling stability is comparable to the majority of the reported LLO (Table S8, ESI†). The in situ electrochemical impedance spectroscopy (EIS) was adopted to analyze the structural stability during cycling (Fig. S25, ESI†). Based on the constructed equivalent circuit, the charge transfer resistance (Rct) and surface CEI film resistance (Rsf) are simulated, respectively. The calculation shows that the LLOM sample exhibits smaller and more stable Rct and Rsf, indicating a stabilized electrode/electrolyte interface and the inhibition of side reactions. The differential electrochemical mass spectrometry (DEMS) indicates that there is less oxygen release of LLOM in the first cycle, which further confirms a robust surface was constructed successfully (Fig. S26, ESI†). More importantly, LLOM showed a suppressed voltage decay rate compared to LLO during 200 cycles (1.21 mV per cycle vs. 2.36 mV per cycle). The differential capacity (dQ/dV) curves of the oxygen reduction peak also prove the reversibility of the oxygen reaction in the LLOM sample (Fig. S27, ESI†). The suppressed voltage decay is attributed to the disordered domain induced by the quenching process, which drives the structure flexibility to harmonize the conflicts between oxygen redox and ordered lattice. Hence, the migration of TM and oxygen vacancies can be prevented, so the structural stability is maintained to suppress voltage decay.
Additionally, an Ah-grade pouch cell was assembled with pristine LLO and LLOM as the cathode and graphite as the anodes to evaluate the effectiveness of the brine quenching strategy (see the Experimental section and Table S9, ESI† for details). The LLOM/graphite pouch cell delivers an initial discharge capacity of 1.4 Ah with a high coulombic efficiency of 87.1% at a current density of 0.1 C (160 mA g−1, Fig. 5e). The lifespan of long-term cycling was appraised at the discharging current density of 0.33C and 1 C (Fig. 5f and g). Typically, the cycle life is defined as the cycle number when the battery reaches 80% of the capacity retention.53 Strikingly, the LLOM/graphite pouch cell achieved a cycle life of 2065 cycles at 0.33 C between 2–4.55 V (equivalent to 4.6 V vs. Li/Li+ in the half cell), and 2159 cycles at 1 C between 2–4.5 V (equal to 4.55 V vs. Li/Li+) (Fig. 5f and g). However, the capacity and voltage retention of the pristine LLO‖graphite after 500 cycles at 0.33C were 48.9% and 89.2%, respectively (Fig. S28b, ESI†), much lower than that of the LLOM‖graphite at 91.2% and 94.5%. Surprisingly, the LLOM‖graphite pouch cell lasted for more than a year at 1 C and retained more than 72% of its capacity, while the LLO‖graphite cell had only 29.1% of its capacity remaining after 500 cycles. Additionally, the LLOM/graphite pouch cell has more significant voltage retention, with a negligible voltage decay of 0.091 mV per cycle after 3200 consecutive cycles. In contrast, the pristine LLO‖graphite exhibited a sharp voltage decay of 0.81 mV per cycle after 500 cycles. The LLOM‖graphite pouch cell is quite competitive compared to others reported in the literature to date (Fig. 5h and Table S10, ESI†). Finally, in order to more visually represent the overall performance of the surface-bulk joint structure design achieved by brine quenching, we tested the fast charging (under 1 C charging and 2 C discharging), high-voltage (2.0–4.75 V, equal to 4.8 V vs. Li/Li+), and high-temperature (50 °C) cycling stability of the brine-quenched LLOM‖graphite pouch cell. The results show that LLOM exhibits an excellent fast charging performance (Fig. S29a, ESI†). Moreover, compared with LLO, LLOM exhibits more excellent high-temperature and high-voltage tolerance (Fig. S29b and c, ESI†). The above results indicate that the robust cationic disordered surface structure and bulk-compatible disordered domains constructed by the brine quenching process positively affect the overall performance of LLOM.
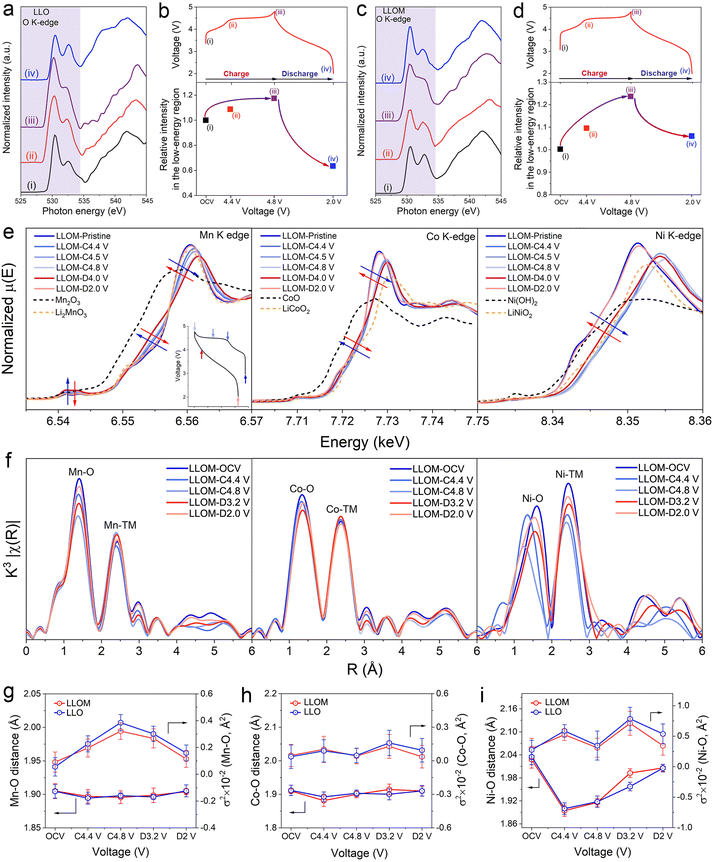
Mechanism of structure evolution during the electrochemical process
X-ray absorption spectroscopy (both hard and soft) was adopted to investigate the structure evolution in detail. The soft X-ray absorption spectroscopy (sXAS) was used to record a wide energy range from 520 to 552 eV, covering energies well below and above the sample absorption. The ex situ sXAS of the O K-edge in the first cycle was collected for both LLO and LLOM samples (Fig. 6a and c) at the different voltage of open circuit voltages: OCV (i), 4.4 V (ii), 4.8 V (iii) and 2.0 V (iv). The spectroscopy can be divided into two regions in the boundary of 534 eV. The high-energy region is associated with transitions from O 1s to the TM 4sp band mixed with O 2p states, while the low-energy region is attributed to transitions from the O 1s to empty TM 3d orbitals hybridized with O 2p orbitals.54 The low-energy region illustrates the charge compensation of TM and O, which is widely used in the fundamental study of LLO.55 Since the Mn element is the main component, the two peaks in the low-energy region are the contribution of the Mn–O hybridization states.56 Here, we follow established procedures for normalizing sXAS spectra and plotting them using relative intensity fits between low-energy regions to assess the extent of the response (Fig. 6a and c).57 The combined integrated intensity relative to the original LLO and LLOM at different charges, which is a measure of the increase in the density of hole states above the Fermi level, is plotted as shown in Fig. 6b and d. The anion/cation redox reactions in different regions were quantified based on the integrated intensity changes. Fig. 6b and d show similar evolutionary behavior of LLO and LLOM, with the relative intensity increasing during charging and decreasing during discharging. However, by subtracting the integrated intensity under sXAS from the integrated intensity under spectrum ii in the shaded region from the integrated intensity under spectrum i of the pristine material, the difference gives additional unoccupied states associated with the Ni4+ eg and Co4+ t2g orbitals. The results show that the spectral integral intensities of LLO and LLOM increase by 9.2% and 8.8%, respectively, before 4.4 V (Fig. 6b and d). This is in general agreement with the previously reported 8.6% amount of additional sXAS transition from Ni2+ oxidation to Ni4+ and Co3+ oxidation to Co4+ when the pristine Li1.2[Ni0.132+Co0.133+Mn0.544+] spectra were charged to 4.4 V.58,59 Thus, the increase in relative integrated strength at voltages below 4.4 V is mainly due to the oxidation of Ni and Co.60 In addition, spectrum iii in Fig. 6a and c shows the O K-edge sXAS spectra after charging to 4.8 V. As expected, the density of the unoccupied state of both increases significantly. The difference in integrated intensity under spectrum iii and ii for LLO and LLOM is about 8.0% and 12.8% of the additional unoccupied state, respectively (Fig. 6b and d). This additional unoccupied state is mainly related to anionic redox, demonstrating that more oxygen redox chemistry occurs in the LLOM sample, which is consistent with the first charge–discharge curve above exhibiting a higher plateau capacity (Fig. 5a).61 More importantly, when discharging to 2.0 V, the relative integrated intensity of the LLOM sample returns closer to that of the pristine state, which indicates the reversible oxygen redox. In contrast, there is a severe irreversible oxygen loss in the LLO sample confirmed by the results of DEMS above.The evolution of TM in the first cycle was also explored by hard-XAS in LLO and LLOM samples (Fig. 6e and Fig. S30, ESI†). Both TM K-edge XANES spectra exhibit similar behaviors during charging and discharging states. When the cathode is charged from the open circuit voltage to 4.4 V, the Ni2+ and Co3+ are oxidized to higher valence, which means the quenching process would not influence the charge compensation provided by TM-ion. Wherein, the absorption edge of the Ni K-edge XANES spectra shifts to higher energy, corresponding to the oxidation of Ni2+ to Ni4+.62 In contrast, the Co K-edge XANES spectra show negligible changes in absorption edge and shape, because of the small change in valence. When the voltage is charged to more than 4.4 V, the Ni and Co cannot be oxidized to higher valence anymore, so the shape of the curves shows only a little shift, which might be ascribed to the changes in the local coordination caused by the activation of lattice oxygen.63 In the discharging stage, Ni and Co spectra both shift to lower energy and return to their pristine position nearby. This recovery is due to the reduction of Ni4+ and Co4+ to Ni2+ and Co3+, respectively. In the case of Mn, no significant changes mean the Mn4+ does not participate in the redox process during the whole cycle. However, the maximum of the absorption edge shifts in one direction, whereas the edge moves towards the other direction. This suggests the evolution of the local environment around Mn, which is caused by alteration of the electron distribution between Mn and O, accompanying the oxidation of Ni2+.64,65 In summary, the TM K-edge XANES spectra of LLOM have a higher overlap with the pristine state at the end of discharge compared to LLO, suggesting that LLOM has a higher activity and reversibility of the oxygen reduction reaction.
Generally, the severe deformation of the TMO6 octahedron has been considered to be the fundamental driver of TM migration during the de-lithiation of LLO.66 The ex situ EXAFS spectra were obtained to determine details regarding the local structural evolution. The first coordination layer shows TM–O interactions, while TM–TM interactions are related in the second coordination layer (Fig. 6f and Fig. S31, ESI†). In the charging stage, the Ni–O distance shortens below 4.4 V and remains stable when the lattice oxygen is activated (voltage >4.4 V). The Co–O distance follows similar trends as those for the Ni–O distance. The only distinction is that the Co–O distance decreases to a smaller extent, because the Co is oxidized from Co3+ to Co4+ and Ni2+ to Ni4+. The Mn–O distance almost stays the same during the first cycle. The results agree with the charge compensation process revealed by the XANES spectra above. It should be emphasized that the intensity of the TM–O peak in the first coordination shell in LLOM does not change significantly after the first cycle, whereas a significant decrease in intensity is observed in LLO, suggesting more severe structural disorder and deterioration of the local coordination environment.
The EXAFS spectra were fitted and the Debye–Waller factor was calculated (Fig. 6g–i, Fig. S32 and Tables S11–S13, ESI†). The uncertainty in the Ni–O bond length below 4.4 V roots from the deformation of the NiO6 octahedron, because of the strong Jahn–Teller effect of Ni3+.67 Upon charging above the 4.4 V plateau, Ni4+ does not possess the Jahn–Teller effect, thus the σ2Ni–O values of both samples return to the initial state. The local structural change of Ni ions during the discharging stage is essentially the inverse of the charging stage, demonstrating the high reversibility of Ni ion coordination. Furthermore, the strength of the first coordination shell layer of the TM–O peak in LLOM did not change significantly after one cycle, indicating that LLO experienced more severe structural disorder and localized coordination environment degradation.68 Similarly, the trend of σ2Co–O evolution for both samples is almost identical to that of Ni–O. However, the σ2Mn–O values of both samples show a continuous increase during the charging process, which is attributed to the oxygen evolution. Although Mn4+ is not directly involved in the redox reaction, its neighboring lattice oxygen will be involved in the charge compensation. Thus, the positional migration of the lattice oxygen will happen, leading to the increased uncertainty of the Mn–O bond length. It is noteworthy that at the end of the discharge, the σ2TM–O value of LLO cannot be restored to the initial stage, while LLOM can basically return to the initial value. The results of the calculated σ2TM–O values indicate the brine quenching process has constructed a flexible structure, which can mitigate the distortion of TMO6 octahedra during the charging–discharging stage. In addition, the evolution of the Mn–TM coordination number in the second coordination shell of the samples during the first charging/discharging process is used to reveal the reversibility of the structural evolution before and after brine quenching. The coordination numbers of low-content Ni and Co could not be accurately obtained for the coordination number evolution of Ni–TM and Co–TM in the second coordination shell due to the large analytical error caused by the coupling of distortion factors and coordination numbers in a single coordination shell.28 As shown in Fig. S33 and Table S14 (ESI†), LLO and LLOM exhibit similar Mn–TM coordination number evolution. Notably, the initial LLOM exhibits a smaller Mn–TM coordination number compared to LLO, which is mainly attributed to the reduction of the intrinsic Li–O–Li configuration by the Mg–O–Li configuration constructed by ion exchange occurring in brine quenching. Similarly, at the end of the discharge, LLOM has a Mn–TM coordination number closer to the initial state, suggesting that LLOM has a more reversible Mn ion-localized structure evolution. This is mainly attributed to the fact that the bulk defect state disordered structure constructed by brine quenching mitigates the conflict between activated lattice oxygen and ordered crystals, significantly improving the activity and reversibility of the oxygen reduction reaction. After long-term cycling, the extent of accumulated defects will be slighter than in the pristine one. In consequence, higher reversibility of oxygen redox is achieved and the voltage decay is successfully suppressed.
Structure stability after long-term cycling
To prove the reliability of the brine quenching strategy, the XRD, Raman, SEM and TEM characterizations are adopted to analyze the structural and chemical information of cycled cathodes. Previous articles suggest that there will be an irreversible phase transition induced by TM migration after long-term cycling.69 Therefore, the XRD and Rietveld refinement were used to analyze the phase composition of 200-cycle cathodes (Fig. S34a–b and Table S15, ESI†). Although the diffraction peaks of both cathodes can be indexed to typical layered structures, the decrease in peak intensity and increase in FWHM indicate severe structural degradation in cycled LLO. The greater Li/Ni mixing degree also proves the integrality of LLOM after long-term cycling. Raman spectra and fitting results are also employed to confirm the stability of the LLOM cathode (Fig. S34c and d, ESI†). The Raman spectra can be deconvoluted into four peaks. The peaks located at 590 cm−1 and 490 cm−1 are assigned to the symmetric stretching A1g and bending vibrations Eg of the hexagonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry, respectively.40 And the shoulder peak located at 650 cm−1 is associated with polyhedral distortions in the TM–O stretching vibrations of MnO6 octahedra in the spinel phase. Generally, the composition of the layer structure can be reflected by comparing the detected intensity of vibrational signals in the layer (IL) and spinel (IS) structures.70 The higher IL/IS ratio of the LLOM cathode suggests that the undesired phase transition is inhibited due to the enhanced TM–O interactions after brine quenching.
m symmetry, respectively.40 And the shoulder peak located at 650 cm−1 is associated with polyhedral distortions in the TM–O stretching vibrations of MnO6 octahedra in the spinel phase. Generally, the composition of the layer structure can be reflected by comparing the detected intensity of vibrational signals in the layer (IL) and spinel (IS) structures.70 The higher IL/IS ratio of the LLOM cathode suggests that the undesired phase transition is inhibited due to the enhanced TM–O interactions after brine quenching.
The morphology characterization was employed to investigate the structural change in particles after cycling (Fig. S35, ESI†). The SEM images show that there are apparent cracks in the secondary particle of LLO, while the LLOM particle maintains the spherical morphology after 200 cycles. The robust layer constructed by the quenching process can effectively prevent the surface from undergoing side reactions, and the disordered domain in the bulk can mitigate the TM transition and avoid further dissolution. Meanwhile, the bare LLO suffers side reactions and deteriorates during continuous cycling. The local structural evolution in the bulk was also characterized by STEM and IFFT after cycling (Fig. S36, ESI†). The HRTEM image and SAED pattern index the generation of spinel phase in the surface of LLO after 200 cycles, while the LLOM primely maintains the layered structure. In the bulk, numerous lattice distortions were observed in the LLO sample, while there is only a small amount of disordered structure in the LLOM sample. The distinction originates from the pre-constructed disordered domain by the quenching process, which makes the structure accommodate the dramatic changes brought by the activation of lattice oxygen. Benefiting from this advantage, the LLOM sample shows outstanding capacity retention and suppressed voltage decay after long-term cycling.
Conclusions
In summary, we developed a wise strategy of a quenching process with different brines on a Li-rich layered cathode with mitigated voltage decay. The underlying mechanism is revealed for the differences in capacity and voltage stability using different brines. The brine quenching process was accompanied by Li+/Mn+ substitution, and a partial “Li–O–M” configuration was formed. Appropriate electronegativity induces the electron transfer and lowers the top of the O 2p energy band, leading to the reduction in the TM–O covalency, thus significantly improving the stability of the oxygen at high voltage during continuous cycling. Meanwhile, the structural stability is improved by creating a robust surface through near-surface Li+/H+ substitution to limit the release of oxygen and the occurrence of phase transitions. More importantly, the quenching process generates locally moderate bulk-compatible distortions, adjusting the whole lattice oxygen framework. This mitigates the conflict between the activated lattice oxygen and the ordered lattice, thereby modulating the reversibility of the inherent redox in the material brought about by the activated lattice oxygen. As a result, the magnesium–nitrate-solution-quenched sample achieved unprecedented capacity stability and almost negligible voltage decay. Our study not only unravels a profound ingredient in understanding the voltage decay of Li-rich materials and their suppression strategies, but also reveals the role of brine quenching strategies on the structural design of the material bulk structure, which provides guidance for the design of novel energy materials with long lifetimes and ultralow voltage decay.Author contributions
L. Z. and H. L. conceived the project. B. Q., Q. L. and Z. L. supervised the project. L. Z., B. Q. and H. L. performed the mechanism analysis. L. Z. and Q. G. performed the synthesis work. L. Z. and W. W. performed Rietveld refinement about X-ray characterization and neutron diffraction. L. Z., Y. W. and X. Y. performed the electrochemical test. Y. Z. performed the AC-STEM characterization. J. P. performed the DFT calculations. X. W. and Y. S. helped with the ToF-SIMS experiment. L. Z. and H. L. prepared the initial draft of the manuscript. Y. W., X. Y., J. L., and K. S., helped revise the manuscript. B. Q., Q. L. and Z. L. organized the work and helped with the draft of the manuscript. All the authors discussed the results and approved the final version of the manuscript.Data availability
The data supporting this article have been included as part of the ESI.† The authors confirm that the data supporting the findings of this study are available within the article [and/or its ESI†].Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
L. Z. and H. L. contributed equally to this work. This work was financially supported by National Key R&D Program of China (Grant No. 2021YFB3803002), the National Natural Science Foundation of China (Grant No. 52272253, 52472266), the External Cooperation Program of Chinese Academy of Sciences (Grant No.181GJHZ2024126MI), “Lingyan” Research and Development Plan of Zhejiang Province (Grant No. 2022C01071), Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ22B030013), Zhongke Hangzhou Bay Institute (Ningbo) New Materials Co. Ltd. (Grant No. NIMTE-61-2024-2), the Natural Science Foundation of Ningbo (Grant No. 2024QL041) and the Youth Innovation Promotion Association of Chinese Academy of Sciences (Grant No. 2022299). The authors thank the beam time from beamline BL14B (SSRF), beamline BL11B (SSRF), and the beam time at GPPD granted from China Spallation Neutron Source (CSNS) for providing the beam time and help during experiments. The authors are grateful for the technical support for Nano-X from Suzhou Institute of Nano-Tech and Nano-Bionics, Chinese Academy of Sciences (SINANO).Notes and references
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed
.
- D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS
.
- N. Yabuuchi, M. Nakayama, M. Takeuchi, S. Komaba, Y. Hashimoto, T. Mukai, H. Shiiba, K. Sato, Y. Kobayashi, A. Nakao, M. Yonemura, K. Yamanaka, K. Mitsuhara and T. Ohta, Nat. Commun., 2016, 7, 13814 CrossRef CAS
.
- B. Qiu, M. Zhang, Y. Xia, Z. Liu and Y. S. Meng, Chem. Mater., 2017, 29, 908–915 CrossRef CAS
.
- M. Sathiya, A. M. Abakumov, D. Foix, G. Rousse, K. Ramesha, M. Saubanère, M. L. Doublet, H. Vezin, C. P. Laisa, A. S. Prakash, D. Gonbeau, G. VanTendeloo and J. M. Tarascon, Nat. Mater., 2015, 14, 230–238 CrossRef CAS
.
- D. Qian, B. Xu, M. Chi and Y. S. Meng, Phys. Chem. Chem. Phys., 2014, 16, 14665–14668 RSC
.
- Z. Sun, L. Xu, C. Dong, H. Zhang, M. Zhang, Y. Ma, Y. Liu, Z. Li, Y. Zhou, Y. Han and Y. Chen, Nano Energy, 2019, 63, 103887 CrossRef CAS
.
- P. Yan, A. Nie, J. Zheng, Y. Zhou, D. Lu, X. Zhang, R. Xu, I. Belharouak, X. Zu, J. Xiao, K. Amine, J. Liu, F. Gao, R. Shahbazian-Yassar, J.-G. Zhang and C.-M. Wang, Nano Lett., 2015, 15, 514–522 CrossRef CAS PubMed
.
- L. Zeng, H. Liang, B. Qiu, Z. Shi, S. Cheng, K. Shi, Q. Liu and Z. Liu, Adv. Funct. Mater., 2023, 33, 2213260 CrossRef CAS
.
- P. Yan, J. Zheng, Z.-K. Tang, A. Devaraj, G. Chen, K. Amine, J.-G. Zhang, L.-M. Liu and C. Wang, Nat. Nanotechnol., 2019, 14, 602–608 CrossRef CAS
.
- D. Luo, H. Zhu, Y. Xia, Z. Yin, Y. Qin, T. Li, Q. Zhang, L. Gu, Y. Peng, J. Zhang, K. M. Wiaderek, Y. Huang, T. Yang, Y. Tang, S. Lan, Y. Ren, W. Lu, C. M. Wolverton and Q. Liu, Nat. Energy, 2023, 8, 1078–1087 CrossRef CAS
.
- J. Zheng, M. Gu, J. Xiao, B. J. Polzin, P. Yan, X. Chen, C. Wang and J.-G. Zhang, Chem. Mater., 2014, 26, 6320–6327 CrossRef CAS
.
- S. Liu, Z. Liu, X. Shen, W. Li, Y. Gao, M. N. Banis, M. Li, K. Chen, L. Zhu, R. Yu, Z. Wang, X. Sun, G. Lu, Q. Kong, X. Bai and L. Chen, Adv. Energy Mater., 2018, 8, 1802105 CrossRef
.
- H. Wu, J. Dong, Y. Zhang, L. Lin, G. Gao, T. Li, X. Yi, B. Sa, J. Wang, L. Wang, J. Li, K. Amine, D.-L. Peng and Q. Xie, Adv. Funct. Mater., 2023, 33, 2303707 CrossRef CAS
.
- C. Yin, X. Wen, L. Wan, Z. Shi, Z. Wei, X. Li, Q. Gu, B. Qiu and Z. Liu, J. Power Sources, 2021, 503, 230048 CrossRef CAS
.
- H. Guo, Z. Wei, K. Jia, B. Qiu, C. Yin, F. Meng, Q. Zhang, L. Gu, S. Han, Y. Liu, H. Zhao, W. Jiang, H. Cui, Y. Xia and Z. Liu, Energy Storage Mater., 2019, 16, 220–227 CrossRef
.
- Y. Zhou, H. Cui, B. Qiu, Y. Xia, C. Yin, L. Wan, Z. Shi and Z. Liu, ACS Mater. Lett., 2021, 3, 433–441 CrossRef CAS
.
- N. Kozlov and O. Keßler, Int. J. Therm. Sci., 2016, 101, 133–142 CrossRef
.
- C. Zhang, X. Shen, X. Li, Q. Liu, Z. Liu, Y. Huang, Y. Gao, Z. Hu, J.-M. Chen, Y. Yang, J. Ma, S.-C. Haw, X. Wang, R. Yu, Z. Wang and L. Chen, Chem. Mater., 2023, 35, 6692–6701 CrossRef CAS
.
- Z. Su, S. Li, L. Ma, T. Liu, M. Li, T. Wu, Q. Zhang, C. Dong, C. Lai, L. Gu, J. Lu, F. Pan and S. Zhang, Adv. Mater., 2023, 35, 2208573 CrossRef CAS
.
- B. Liu, K. Cheng, S. Nie, X. Zhao, H. Yu, J. Yu, A. Fujishima and K. Nakata, J. Phys. Chem. C, 2017, 121, 19836–19848 CrossRef CAS
.
- B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS
.
- Z. Ding, C. Zhang, S. Xu, J. Liu, C. Liang, L. Chen, P. Wang, D. G. Ivey, Y. Deng and W. Wei, Energy Storage Mater., 2019, 21, 69–76 CrossRef
.
- Z. Hao, H. Sun, Y. Ni, G. Yang, Z. Yang, Z. Hao, R. Wang, P. Yang, Y. Lu, Q. Zhao, W. Xie, Z. Yan, W. Zhang and J. Chen, Adv. Mater., 2024, 36, 2307617 CrossRef CAS
.
- S. Li, H. Zhang, H. Li, S. Zhang, B. Zhu, S. Wang, J. Zheng, F. Liu, Z. Zhang and Y. Lai, ACS Appl. Mater. Interfaces, 2021, 13, 39480–39490 CrossRef CAS PubMed
.
- E. Hu, X. Yu, R. Lin, X. Bi, J. Lu, S. Bak, K.-W. Nam, H. L. Xin, C. Jaye, D. A. Fischer, K. Amine and X.-Q. Yang, Nat. Energy, 2018, 3, 690–698 CrossRef CAS
.
- B. J. Hwang, Y. W. Tsai, D. Carlier and G. Ceder, Chem. Mater., 2003, 15, 3676–3682 CrossRef CAS
.
- C. Yin, Z. Wei, M. Zhang, B. Qiu, Y. Zhou, Y. Xiao, D. Zhou, L. Yun, C. Li, Q. Gu, W. Wen, X. Li, X. Wen, Z. Shi, L. He, Y. Shirley Meng and Z. Liu, Mater. Today, 2021, 51, 15–26 CrossRef CAS
.
- X. Li, Q. Gu, B. Qiu, C. Yin, Z. Wei, W. Wen, Y. Zhang, Y. Zhou, H. Gao, H. Liang, Z. He, M. Zhang, Y. S. Meng and Z. Liu, Mater. Today, 2022, 61, 91–103 CrossRef CAS
.
- Y. W. Tsai, B. J. Hwang, G. Ceder, H. S. Sheu, D. G. Liu and J. F. Lee, Chem. Mater., 2005, 17, 3191–3199 CrossRef CAS
.
- X. Yu, Y. Lyu, L. Gu, H. Wu, S.-M. Bak, Y. Zhou, K. Amine, S. N. Ehrlich, H. Li, K.-W. Nam and X.-Q. Yang, Adv. Energy Mater., 2014, 4, 1300950 CrossRef
.
- L. Li, E. C. Self, D. Darbar, L. Zou, I. Bhattacharya, D. Wang, J. Nanda and C. Wang, Nano Lett., 2020, 20, 2756–2762 CrossRef CAS PubMed
.
- W. Zuo, M. Luo, X. Liu, J. Wu, H. Liu, J. Li, M. Winter, R. Fu, W. Yang and Y. Yang, Energy Environ. Sci., 2020, 13, 4450–4497 RSC
.
- M. Tang, A. Dalzini, X. Li, X. Feng, P.-H. Chien, L. Song and Y.-Y. Hu, J. Phys. Chem. Lett., 2017, 8, 4009–4016 CrossRef CAS
.
- B. Qiu, M. Zhang, L. Wu, J. Wang, Y. Xia, D. Qian, H. Liu, S. Hy, Y. Chen, K. An, Y. Zhu, Z. Liu and Y. S. Meng, Nat. Commun., 2016, 7, 12108 CrossRef CAS
.
- Q. Shao, P. Gao, C. Yan, M. Gao, W. Du, J. Chen, Y. Yang, J. Gan, Z. Wu, C. Zhang, G. Chen, X. Zheng, Y. Lin, Y. Jiang, W. Sun, Y. Liu, M. Gao and H. Pan, Adv. Mater., 2022, 34, 2108543 CrossRef CAS
.
- L. H. Pizetta Zordão, V. A. Oliveira, G. E. Totten and L. C. F. Canale, Int. J. Heat Mass Transfer, 2019, 140, 807–818 CrossRef
.
- L. Zeng, K. Shi, B. Qiu, H. Liang, J. Li, W. Zhao, S. Li, W. Zhang, Z. Liu and Q. Liu, Chem. Eng. J., 2022, 437, 135276 CrossRef CAS
.
- C. Zhang, B. Wei, M. Wang, D. Zhang, T. Uchiyama, C. Liang, L. Chen, Y. Uchimoto, R. Zhang, P. Wang and W. Wei, Energy Storage Mater., 2022, 46, 512–522 CrossRef
.
- Z. Shi, Q. Gu, L. Yun, Z. Wei, D. Hu, B. Qiu, G. Z. Chen and Z. Liu, J. Mater. Chem. A, 2021, 9, 24426–24437 Search PubMed
.
- Q. Li, D. Ning, D. Zhou, K. An, D. Wong, L. Zhang, Z. Chen, G. Schuck, C. Schulz, Z. Xu, G. Schumacher and X. Liu, J. Mater. Chem. A, 2020, 8, 7733–7745 Search PubMed
.
- J. Wu, X. Zhang, S. Zheng, H. Liu, J. Wu, R. Fu, Y. Li, Y. Xiang, R. Liu, W. Zuo, Z. Cui, Q. Wu, S. Wu, Z. Chen, P. Liu, W. Yang and Y. Yang, ACS Appl. Mater. Interfaces, 2020, 12, 7277–7284 CrossRef CAS
.
- A. Rougier, P. Gravereau and C. Delmas, J. Electrochem. Soc., 1996, 143, 1168 Search PubMed
.
- Q. Li, H. Wang, G. Wang, F. Xia, W. Zeng, H. Peng, G. Ma, A. Guo, R. Dong and J. Wu, Small, 2024, 20, 2307419 CrossRef CAS
.
- X. Liu, J. Cheng, Y. Guan, S. Huang and F. Lian, Mater. Chem. Front., 2023, 7, 3434–3454 RSC
.
- J. Xu, J. Wan, W. Zhang, Y. Li, F. Cheng, Z. Cheng, Y. Xu, S. Sun, Q. Li, C. Fang and J. Han, Adv. Funct. Mater., 2023, 33, 2214613 CrossRef CAS
.
- S. Jia, E. Yao, R. Peng, A. Jonderian, M. Abdolhosseini and E. McCalla, Chem. Mater., 2022, 34, 11047–11061 CrossRef CAS
.
- B. C. Melot and J. M. Tarascon, Acc. Chem. Res., 2013, 46, 1226–1238 CrossRef CAS PubMed
.
- D. Mao, Z. Fan, L. Song, P. Zhang, J. Xie, S. Su, G. Liu, H. Wang and W. Chu, Nano Energy, 2024, 121, 109231 CrossRef CAS
.
- S. Liu, Z. Liu, X. Shen, X. Wang, S.-C. Liao, R. Yu, Z. Wang, Z. Hu, C.-T. Chen, X. Yu, X. Yang and L. Chen, Adv. Energy Mater., 2019, 9, 1901530 CrossRef
.
- W. B. Jensen, J. Chem. Educ., 1995, 72, 395 CrossRef CAS
.
- A. Nickol, T. Schied, C. Heubner, M. Schneider, A. Michaelis, M. Bobeth and G. Cuniberti, J. Electrochem. Soc., 2020, 167, 090546 CrossRef CAS
.
- Z. Yu, P. E. Rudnicki, Z. Zhang, Z. Huang, H. Celik, S. T. Oyakhire, Y. Chen, X. Kong, S. C. Kim, X. Xiao, H. Wang, Y. Zheng, G. A. Kamat, M. S. Kim, S. F. Bent, J. Qin, Y. Cui and Z. Bao, Nat. Energy, 2022, 7, 94–106 CrossRef CAS
.
- K. Luo, M. R. Roberts, R. Hao, N. Guerrini, D. M. Pickup, Y.-S. Liu, K. Edström, J. Guo, A. V. Chadwick, L. C. Duda and P. G. Bruce, Nat. Chem., 2016, 8, 684–691 CrossRef CAS
.
- Q. Li, D. Zhou, L. Zhang, D. Ning, Z. Chen, Z. Xu, R. Gao, X. Liu, D. Xie, G. Schumacher and X. Liu, Adv. Funct. Mater., 2019, 29, 1806706 CrossRef
.
- K. Luo, M. R. Roberts, N. Guerrini, N. Tapia-Ruiz, R. Hao, F. Massel, D. M. Pickup, S. Ramos, Y.-S. Liu, J. Guo, A. V. Chadwick, L. C. Duda and P. G. Bruce, J. Am. Ceram. Soc., 2016, 138, 11211–11218 CrossRef CAS
.
- B. Gilbert, B. H. Frazer, A. Belz, P. G. Conrad, K. H. Nealson, D. Haskel, J. C. Lang, G. Srajer and G. De Stasio, J. Phys. Chem. A, 2003, 107, 2839–2847 CrossRef CAS
.
- F. M. F. de Groot, M. Grioni, J. C. Fuggle, J. Ghijsen, G. A. Sawatzky and H. Petersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 5715–5723 CrossRef CAS PubMed
.
- W.-S. Yoon, M. Balasubramanian, X.-Q. Yang, Z. Fu, D. A. Fischer and J. McBreen, J. Electrochem. Soc., 2004, 151, A246 CrossRef CAS
.
- Z. Wei, Z. Shi, X. Wen, X. Li, B. Qiu, Q. Gu, J. Sun, Y. Han, H. Luo, H. Guo, Y. Xia, C. Yin, P. Cai and Z. Liu, Mater. Today Energy, 2022, 27, 101039 Search PubMed
.
- S. Hy, W.-N. Su, J.-M. Chen and B.-J. Hwang, J. Phys. Chem. C, 2012, 116, 25242–25247 CrossRef CAS
.
- M. G. Kim, N. E. Sung, H. J. Shin, N. S. Shin, K. S. Ryu and C. H. Yo, Electrochim. Acta, 2004, 50, 501–504 CrossRef CAS
.
- W.-S. Yoon, K. Y. Chung, J. McBreen, D. A. Fischer and X.-Q. Yang, J. Power Sources, 2007, 174, 1015–1020 CrossRef CAS
.
- H. Koga, L. Croguennec, M. Ménétrier, K. Douhil, S. Belin, L. Bourgeois, E. Suard, F. Weill and C. Delmas, J. Electrochem. Soc., 2013, 160, A786 CrossRef CAS
.
- H. Koga, L. Croguennec, M. Ménétrier, P. Mannessiez, F. Weill, C. Delmas and S. Belin, J. Phys. Chem. C, 2014, 118, 5700–5709 CrossRef CAS
.
- Y. Gao, X. Wang, J. Ma, Z. Wang and L. Chen, Chem. Mater., 2015, 27, 3456–3461 CrossRef CAS
.
- W. Lee, S. Muhammad, T. Kim, H. Kim, E. Lee, M. Jeong, S. Son, J.-H. Ryou and W.-S. Yoon, Adv. Energy Mater., 2018, 8, 1701788 CrossRef
.
- K. Zhang, J. Qi, J. Song, Y. Zuo, Y. Yang, T. Yang, T. Chen, X. Liu, L. Chen and D. Xia, Adv. Mater., 2022, 34, 2109564 CrossRef CAS
.
- J. Wang, X. He, E. Paillard, N. Laszczynski, J. Li and S. Passerini, Adv. Energy Mater., 2016, 6, 1600906 CrossRef
.
- L. Bao, L. Wei, N. Fu, J. Dong, L. Chen, Y. Su, N. Li, Y. Lu, Y. Li, S. Chen and F. Wu, J. Energy Chem., 2022, 66, 123–132 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee02511c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |