Automated Dynamic Inlet Microfluidics (ADIM) system: cost-effective biaxial nanoliter droplet on demand generation platform and its application in agglutination assays†
Abdul Basit
Zia
 * and
Ian G.
Foulds
* and
Ian G.
Foulds

School of Engineering, The University of British Columbia, Okanagan Campus, Kelowna, BC, Canada. E-mail: abdulbasit.zia@ubc.ca; Tel: +01 250 8998710
First published on 15th November 2024
Abstract
The paper demonstrates an adaptation of a Prusa Mini+ 3D printer through the integration of 3D printed modules, creating a system capable of producing varied droplets from multiple Eppendorf tubes. Building upon our previous model, this system enhances calibration methodology enabling any fused deposition modeling (FDM) printer to produce mono-disperse droplets (coefficient of variance (CV%) <2% for train of 100 droplets) with 6900 assays per hour rate. The cost of the developed system is 85% lower than that of existing droplet generation solutions on the market, and 30% more economical than the previous iteration of the system. Additionally, the system's utility in quantification of agglutination assays is highlighted using image analysis, capable of distinguishing between agglutinated and non-agglutinated samples. By offering significant savings and ease of use, this system aims to lower the barriers to entry for microfluidic research, potentially broadening the scope of scientific exploration and application in this field.
1 Introduction
Droplet microfluidics is a branch of microfluidics where one fluid is suspended within another immiscible fluid in microchannels. Droplet microfluidics leverages the unique capabilities of droplets in dual-phase systems as micro-reactors for a variety of applications, from chemical synthesis to biochemical assays.1–6 Droplets (dispersed phase) in dual-phase microfluidics are isolated from each other and the tubing walls because of the immiscibility and encapsulation of the droplet with a thin film of the continuous phase.4 The generation of a droplet of an analyte with the required composition and volume is the first step in droplet microfluidics,7 followed by droplet manipulation and then quantification. Generally, the droplet generation is designed for continuous operation yielding high throughput achieved through structures like a T junction,8–10 co-flow,11–13 or flow focusing14–16 channels operating in squeezing or dripping in configurations.In comparison to continuous operation, droplet-on-demand (DoD) systems utilize external forces or mechanisms to offer precise control over the number, size, and timing of droplet generation of droplets. DoD systems allow for more complex droplet manipulation like fusion, mixing, sorting, and splitting as compared to continuous systems. DoD systems can be fabricated using lithography (micro-fabrication), 3D-printed, or macro system.
Traditional DoD systems in microfluidics often involve microfabricated devices and techniques like lithography to create SU-8 molds to create PDMS chips,17,18 offering tight control over droplet size and easy integration of the control mechanism. However, a cleanroom is required for photo-lithography, which significantly raises expenses, making it cost-prohibitive for the researchers lacking cleanroom facilities.
The advent of 3D printing technology has allowed an alternative method to fabricate droplet generation DoD systems. 3D printing is predominantly used for crafting PDMS molds19 or for direct fabrication of microfluidic devices.20 Projection micro stereo-lithography 3D printing technology allows a feature size of a few microns, e.g. Junyi Chen et al.21 who developed a 3D printed modular microfluidic chips with a feature size of 10 mm. The resulting microfluidic system, with droplet generation, is versatile but the equipment required incurs a high cost (approx. $180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 USD).
000 USD).
The prevalent method for generating droplets in droplet on demand (DoD) systems typically involves using a valve to control the disperse phase, controlled pneumatically22 or electrically. These systems are designed to create droplets with nanoliter or picoliter volume precisely,23 yet they depend on complex and costly setups, such as specialized flow controllers.24 There's less emphasis on generating droplets through electrical actuation in literature,25e.g. using alternating current (AC) electrical field26,27 or microwave-induced heating or AC fields.28
Several companies offer microfluidic kits for easy setup of droplet generation systems, such as the Elveflowl' starter pack.29 Designed for straightforward use, these kits include essential components like pressure controllers but require users to familiarize themselves with the accompanying custom software.
Interest in the development of microfluidics systems with the capability of movements in three dimensions (X–Y–Z) has grown lately. In these systems, either the inlet or controlling mechanism is moving in Cartesian coordinates to generate and manipulate droplets. An example of systems moving the controlling mechanism is work by Xuyang Hu et al. on the latest version of DropLab, where the system controls magnets in magnetic digital microfluidic (MDM) technology.30 Alternatively, the system can move the inlet of the microfluidic system and generate droplets from a variety of analytes, they can be referred to as automated dynamic inlet microfluidic systems (ADIM systems). Research identifies two primary categories of automated dynamic inlet microfluidic (ADIM) systems: those that modify existing liquid handling systems31,32 and those creating new platforms.
Helena Zec et al. devised a microfluidic setup using a serial sampling loading (SSL) mechanism, integrating an automated vertical (Z) axis with manually controlled horizontal (X–Y) axes.33 This design facilitates the creation of extensive sample libraries linked to microfluidic devices and is capable of generating 150 nL droplets. The droplet is formed by moving the inlet from its starting position above the analyte, lowering it into the liquid, and then pulling it back up. Its key strength lies in its scalability, permitting analysis of numerous samples against multiple reagents (N samples against M reagents (N × M)) without complicating the system's design. Fabrice Gielen et al. developed a platform tailored for nanoliter-scale assays,34 which evolved into the Mitos Dropix sampler through collaboration with dolomite microfluidic.35 This device enables digital programming for generating sequences from up to 24 distinct reagents, and its compatibility with dolomite's microfluidic chips enhances functionality for droplet manipulation. Despite Mitos Dropix's broad capabilities, its market price is approximately $15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Wen-Bin Du et al. designed DropLab, an automated microfluidic platform for droplet-based reactions and screenings at nanoliter scales, achieving picoliter precision.36 It can mix components to create composite droplets and conduct assays in droplet arrays, minimizing sample and reagent use. The system, devoid of complex microchannels, can assemble droplets varying in size, composition, and sequence, with volumes as small as 20 pL.
000. Wen-Bin Du et al. designed DropLab, an automated microfluidic platform for droplet-based reactions and screenings at nanoliter scales, achieving picoliter precision.36 It can mix components to create composite droplets and conduct assays in droplet arrays, minimizing sample and reagent use. The system, devoid of complex microchannels, can assemble droplets varying in size, composition, and sequence, with volumes as small as 20 pL.
Using an XYZ movement platform for droplet generation provides several advantages over complex microfluidic chips. It offers greater flexibility and reconfigurability since inlets or control mechanisms can be easily repositioned without redesigning the microfabricated microchannels. This approach simplifies the overall system and reduces costs by avoiding complex microfabrication. Additionally, XYZ platforms can handle various analytes and scale up more easily, making the system a versatile, cost-effective solution for high-throughput droplet-based applications. It allows for the generation of droplet trains from small sample sizes without dead volume.
In response to the need for an accessible, cost-effective microfluidic system, our study modifies a Prusa MINI+ 3D printer with a 3D printed nozzle replacement module, converting it into an ADIM system: a low-cost biaxial nanoliter droplet on demand generation platform. The overall bill of materials, including the syringe pump, 3D printer, and all chemicals brings the total cost to approximately $1700 USD. The goal of this initiative is to make microfluidic research more accessible by offering a system that is both user-friendly and precise, allowing for broader adoption in the scientific community. Similar to the DropLab and Mitos Dropix, our platform also creates droplets by moving the inlet from a position below the analyte upward and then back down, but it does so more affordably while maintaining a similar level of accuracy in droplet formation.
In our previous iteration of the ADIM droplet generation platform,37 the Prusa Mini+ is modified to generate droplets from a top-down mechanism, similar to the SSL system. However, the system required extensive mathematical modeling and calibration procedures to generate mono-disperse droplet libraries. The latest iteration of our developed system simplifies the setup and achieves higher accuracy at a lower cost. A comparison of all the similar works is summarized in Table 1.
| Mitos Dropix34 | Helena Zec33 | Elveflow | Previous system37 | This study | |
|---|---|---|---|---|---|
| a The throughput has been inferred from the least valve opening times in Fig. 4 of ref. 33. | |||||
| Smallest droplet | 1 nL | 3.8 nL | 0.5 nL | 1 μL | 12 nL |
| Coefficient of variance | 4% | Unknown | <3% | 3% | 2% |
| Number of analytes | 24 | 96 | 2 | 96+ | 15 |
| Throughput (per hour) | 1000 | 6000a | 32 × 106 | 6900 | 6900 |
| Microfluidic chips use | Yes | No | Yes | Yes | Yes |
| Setup difficulty | Low | High | Medium | Medium | Low |
| Clean room required | No | Yes | No | No | No |
| Droplet library storage | Yes | No | No | Yes | Yes |
| Cost (USD) | ≈$15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Unknown | ≈$9000 USD | ≈2500 USD | ≈1700 USD |
2 Methods and materials
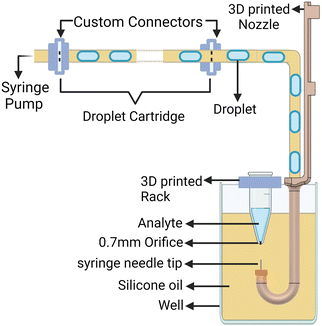
The developed system is shown in Fig. 1, with the modified Prusa Mini+, which has the nozzle head replaced with a 3D-printed nozzle with a J bend at the bottom to allow the tubing to be inserted through and connected to the syringe needle tip (gauge 20 Ga). A 0.7 mm orifice is drilled at the bottom of the Eppendorf tube to move the needle tip from the oil into the tube. The needle tip is chosen to allow for smooth movement in and out of the tube without touching it. The print head is removed from the X-axis carriage but remains electrically connected to the main circuit board of the printer. This allows the 3D printer to be used without requiring any changes to its firmware. The well is fabricated using 3D-printed base and acrylic sheets for walls. The well is filled with silicone oil (XIAMETER PMX-200 100 cSt, The Dow Chemical Company), and a 3D printed rack is placed on the top of the well to house Eppendorf tubes (1.5 mL Eppendorf tube) with analytes. The 3D printer moves in the Z axis to move the needle tip from its resting position in the oil (continuous phase) into the analyte inside the Eppendorf tube (disperse phase) and then back into the oil to create droplets.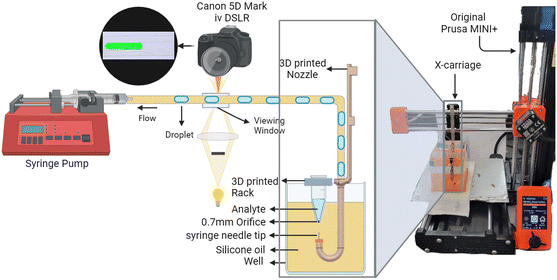 | ||
| Fig. 1 The system diagram: setup of the system with modified Prusa Mini (3D printer) and the modified 3D printed nozzle with J bend. | ||
For the system to generate droplets from different analytes the 3D-printed rack houses multiple Eppendorf tubes. The number of different analytes available depends on the bed size of the printer and the oil well constructed. For the proof of concept in this study, an oil well measuring 85 mm by 55 mm and 64 mm in height is constructed, alongside a 3D-printed rack designed to accommodate five distinct analytes.
The tubing passes through the J bend of the 3D-printed nozzle, then through a viewing window under a microscope with a Canon 5D Mark IV camera for evaluation. After the viewing window, the tubing transfers the droplets into the syringe pump (New Era Systems NE-1000), which applies constant negative pressure on the system. The droplets collected in the syringe are disposed of after each run. The viewing window is created by casing the tubing in PDMS. The tubing type and length can vary depending on the application, while microfluidic chips and sensors can be connected in line with the mentioned setup.
The 3D printer can be operated in three modes, primary mode uses a G-code file via USB disk to run the 3D printer and generate a train of droplets. The G-code is generated using MATLAB script with the start and end point of the needle tip, and the flow rate as input parameters to calculate the delay required in the analyte to generate the desired volume of droplets and generate the G-code for the 3D printer. The second mode to use the system is through a host software such as Printrun to run the generated G-code. Thirdly, a MATLAB script runs the printer in real time by sending G-code commands. This allows sensors, e.g. flow sensors, to be incorporated into the system, providing instantaneous flow rate values for the script to calculate the required delay.
2.1. Calibration
The first step is to evaluate the 3D printer and its movements. The movement in the Z axis is the most important as it is responsible for droplet generation. The maximum feedrate for the three axes are X = Y = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mm min−1, and Z = 720 mm min−1. These speeds have to be tested. Moreover, the main time the syringe needle spends in the analyte is the delay between moving up into the analyte and moving down out of the analyte. The G4 command in the G-code allows the user to enter the delay in milliseconds (P) or seconds (S). For instance, G4 P250 gives a delay of 250 ms between commands while G4 S250 gives a delay of 250 seconds. Both axes' movements and the delay can be evaluated by analyzing the movement of the syringe needle tip captured in a video.
000 mm min−1, and Z = 720 mm min−1. These speeds have to be tested. Moreover, the main time the syringe needle spends in the analyte is the delay between moving up into the analyte and moving down out of the analyte. The G4 command in the G-code allows the user to enter the delay in milliseconds (P) or seconds (S). For instance, G4 P250 gives a delay of 250 ms between commands while G4 S250 gives a delay of 250 seconds. Both axes' movements and the delay can be evaluated by analyzing the movement of the syringe needle tip captured in a video.
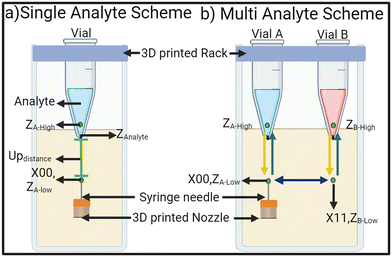
Once the system is set up like in Fig. 1, the system should be calibrated and a few important set-points values have to be evaluated before the system is used. The first step is to align the syringe needle to the 0.7 mm orifice of the Eppendorf tube. Fig. 2 shows all the important set-points to be evaluated for single-analyte and multi-analyte schemes. In the single analyte scheme, an initial point is selected to be the origin point for the X, Y, and Z axis (X00, Y00, Z00). ZAnalyte is the point at which the syringe needle tip touches the analyte in the Eppendorf tube.
The difference between the origin and ZAnalyte is denoted Updistance. It can be as small as 1 mm but for this study Updistance is set at 2.5 mm. The Updistance will affect the throughput of the system. The needle must move beyond ZAnalyte and transverse into the analyte for better droplet generation. Distances between 0.5 mm to 2 mm were tested and we found that the best practice is to have ZA-high at 1.5 mm. The MATLAB script moves the syringe needle tip from oil (origin) up into the analyte to ZA-high taking tup ms, wait for the calculated delay (tdelay) and then take tdown ms to bring the tip back down into the oil (origin) to generate a droplet. Due to the negative pressure, the syringe needle pulls the oil and analyte interface down when descending from the analyte into the oil. This means ZAnalyte differs for the needle ascending and descending. If this interface hysteresis is extensive, it can lead to analyte leakage from the orifice.
| VDroplet = (tup + tdelay + tdown + tsystem) × Flowrate | (1) |
Eqn (1) presents the formula for determining the volume of the produced droplet. The difference between ZAnalyte and ZA-high remains fixed for both ascending and descending motions (1.5 mm respectively) within the analyte. This duration is derivable through the Z-axis feed-rate (720 mm min−1), resulting in a calculated time of 250 ms (tup + tdown). The parameter tsystem encompasses all the dynamics of the system; such as the built-in delay of the 3D printer or interface hysteresis. Two other variables are tdelay and flow rate. Given a fixed flow rate, the MATLAB script can easily calculate the required tdelay to generate the droplet of the desired volume and generate G-code.
In a multi-analyte scheme, the movements of the 3D printer are a bit more complicated than a single-analyte scheme. A low point in the Z axis is selected for each Eppendorf tube, ZA-Low and ZB-Low, which is zero. The 3D printed rack is designed to house each tube 11.5 mm apart. After the syringe needle is aligned with the first Eppendorf tube and X00, ZA-low is set, the next Eppendorf is at X = X00 + 11.5 mm. Due to variations in the manufacturing of the tubes and the placement of the drill hole at the bottom, the user manually aligns each tube, but it is usually a few 0.1 mm steps off. Once the coordinates for all the tubes are aligned and recorded in the program, the assay can be run multiple times.
The high-point of each Eppendorf tube has to be selected 1.5 mm above the ZAnalyte. The leveling of the printer's bed, the well, and the rack is very important. Any imbalance might result in the high points of the two Eppendorf tubes, (ZA-High and ZB-High), being different. As long as the high point is 1.5 mm above the ZAnalyte, the size of droplets will remain the same, however, the gap between the two consecutive droplets in a train will differ slightly.
The 3D printer moves the syringe needle tip from X00, ZA-Low to X00, ZA-High, rests for the calculated delay, and then comes back to X00, ZA-Low, generating a droplet of analyte A, before moving to X11, ZB-Low. Then the printer moves up into the analyte B, to ZB-High, rests, and returns to ZB-Low. Hence a droplet of analyte A is generated followed by a droplet from analyte B. The delay between the movement from X00, ZA-Low to X11, ZB-Low determines the gap between the droplets.
Use of eqn (1), without factoring in tsystem, a target of 1 μL at a flow rate of 35 μL min−1 leads to droplets averaging around 0.7 μL, although uniformly sized. To achieve the target volume, tdelay can be adjusted easily. Moreover, our previous droplet generation system's calibration methodology allows for an empirical relationship between tsystem and flow rate, which requires generating calibration droplets at different flow rates for system dynamics analysis.37 For systems integrated with microfluidic components or sensors, in line with the system in Fig. 1, calculating tsystem is crucial for precision.
The syringe pump exhibits a lag in reaching the designated flow rate, and the lead screw introduces further fluctuations. For shorter tubing length (≈1 m) and short droplet train, this can be managed by turning the pump on 5 minutes before conducting experiments to ensure a stable flow. For longer or narrower tubing, the flow rate will differ from the syringe pump settings. The addition of microfluidic chips and sensors in line with the system in Fig. 1 will also affect the flow rate. For such cases, the methodology for calibration presented in section 2.2 of the previous iteration37 of the system has to be followed to give results with high accuracy.
2.2. Methodology
The developed system is used to generate trains of droplets in different configurations with dyed water to show the functionality and capabilities of the system as a proof of concept. The uniformity of the droplet series produced is assessed by calculating the coefficient of variation (CV%), which is the standard deviation of droplet volumes divided by their mean volume. This serves as an indicator of their uniformity. Consequently, a model protein assay will be implemented using the developed system to show its utility in immunoassays.Agglutination is a biological process where particles clump together, often in response to a probe-target reaction (e.g. antigen–antibody). In medical diagnostics, this method is used to detect the presence of target molecules in body fluids by observing the visible aggregation of particles, such as red blood cells or bacteria, when specific probes like antibodies are present. A common method in biochemical experiments to study protein interactions utilizes the strong affinity between biotin and Streptavidin to capture, detect, quantify, or purify specific proteins.38
The developed system is used to generate 10 droplets from 30 μl analyte (Vector Laboratories 10 mg VECTB2007 biotinylated bovine serum albumin (BSA) and Dynabeads M-270 Streptavidin, Invitrogen) in the concentration range of 2.5 μg mL−1 to 40 μg mL−1. The control consists of Dulbecco's phosphate buffered saline (Sigma-Aldrich) supplemented with 1% non-biotinylated BSA (Sigma-Aldrich) and 1% Tween (Sigma-Aldrich). The non-biotinylated BSA at this concentration ensures that the detected signal is not attributed to non-specific binding. The evaluation of agglutination will demonstrate the developed platform's capability to generate droplet libraries for immunoassay applications.
3 Results
3.1. Calibration
3D printer's movements are recorded in a video (1280 × 720p, 120 fps) to be analyzed for movements in X, Y, and Z axis by focusing on the syringe needle tip. The delay commands are scripted for incremental delays from no delay to 500 ms. The results of the analysis are presented in Table 2. The delay commands are passed to the 3D printer through a G-code file via USB or Pronterface. In our previous work, MATLAB communicated the delay commands to the printer. Compared to previously reported differences between programmed and actual delays, the actual delay is longer in both cases (G-code file and Pronterface). The largest difference between programmed and actual delay can be seen for the Pronterface. However, the utility of Pronterface and G-code file is that it does not overload the cache of the printer which can happen with MATLAB. When the cache is overloaded some commands fail to execute. On the other hand, MATLAB script can incorporate the instantaneous reading of sensors (e.g. flow sensor) therefore it is more robust to changes in the system. The video analysis for the Z-axis movements showed that it moves with 720 mm min−1 speed.| 3D printer G-command | Programmed delay (ms) | Actual delay (ms) [previously reported37] | Actual delay (ms) Pronterface | Actual delay (ms) G-code file |
|---|---|---|---|---|
| No delay | 0 | 20.0 | 8.3 | 8.3 |
| G4 P0 | 0 | — | 125.0 | 116.6 |
| G4 P1 | 1 | 106.6 | 108.0 | 116.6 |
| G4 P10 | 10 | 113.4 | 141.6 | 133.33 |
| G4 P50 | 50 | 153.4 | 158.3 | 166.67 |
| G4 P100 | 100 | 213.4 | 225.0 | 225.0 |
| G4 P150 | 150 | 260.0 | 275.0 | 266.67 |
| G4 P250 | 250 | 300.0 | 375.0 | 375.0 |
| G4 P500 | 500 | 608.0 | 616.67.0 | 625.0 |
The Eppendorf tube is positioned only a few millimeters into the oil, which causes the oil to enter the Eppendorf tube via the bottom orifice. A minimum volume of the analyte has to be maintained in the tube, depending on the tube's position, to ensure that the analyte weight pushes the silicone oil out. For this study, the minimum analyte volume limit is 30 mL. If the analyte volume falls below this limit the oil starts to fill the Eppendorf tube moving the interface and leading to an error in droplet volume, as shown in Fig. S1.†
3.2. Train of droplets with constant volume of single analyte
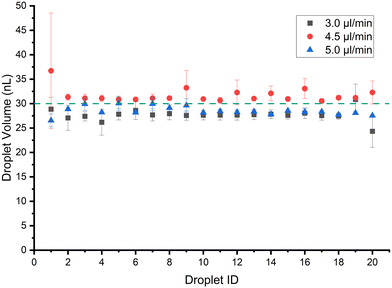
The sizes of the droplets in a train are characterized using the droplet morphometry and velocimetry (DMV) MATLAB plugin.39 The system in Fig. 1 is set up using 70 cm of Tygon tubing (0.508 mm I.D.) with a viewing window at around 30 cm from the point of droplet generation. The syringe pump is used with a 3 mL B.D syringe. Fig. 3 shows the result of generating 1 μL droplets at 35 μL min−1 flow rate in 3 separate runs with the error bars representing absolute error from the mean. The mean CV% achieved for trains of 20 droplets of 1 μL volume is 6.4%. The minimum volume possible at 35 μL min−1 flow rate is 0.3 μL with CV% of 6.3% when the system is calibrated as described in section 2.1, with no tdelay. Note that if experiments are conducted using the G4 P0 command it introduces a 125 ms delay between the up and down commands instead of 8.3 ms, as per Table 2. The extra ≈100 ms leads the minimum volume achieved at 35 μL min−1 to be 0.4 μL rather than 0.3 μL, as shown in Fig. S2.†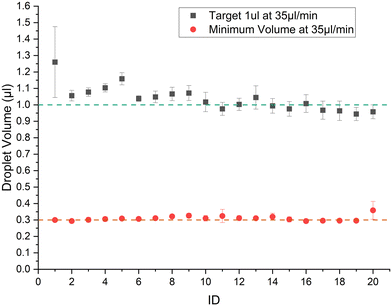 | ||
| Fig. 3 Train of 20 droplets generated at 35 μl min−1 with a target volume of 1 μL and the minimum possible volume (0.3 μL) that can be generated at this flow rate. | ||
The first droplet seems to vary in volume the most compared to the rest of the train. In all the experiments in this study, the last droplet does not show the variance like the first droplet. The reason for variation in the first droplet might be due to changes to hydrodynamic resistances as droplets are added to the tubing. On the other hand, the oil–analyte interface is stable for the first droplet while subsequent droplets face less variation due to insufficient time for the interface to fully stabilize between droplets. SSL system by Helen Zec33 also shows variation in the first and last droplet due to valve actuation sequence. The percentage difference in volume from the mean volume is just above 5% which would make the train of droplets generated mono-disperse. Using this scheme a train of 100, 1 μL droplets is generated with a CV of 1.76%, and a mean volume of 0.98 mL. The resultant volumes of the droplet train and flow rate are shown in Fig. S3,† illustrating the high accuracy achievable with this platform.
3.3. Train of droplets with variable volume of single analyte
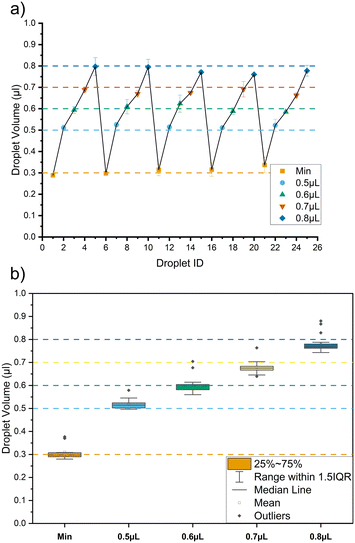
The utility of the modified 3D printer is its ability to be programmed. The system can generate a train of droplets where each droplet in a single train has a different volume. This is useful in particular with concentration gradient generation via droplet merging.8Fig. 5 shows the results for a train of droplets at 35 μL min−1 where the sequence of 0.3 μL (minimum), 0.5 μL, 0.7 μL, and 0.8 μL is repeated 5 times. Fig. 5a shows the mean value of each target volume and the error bars represent mean absolute error for multiple measurements (n = 3). A mean CV% achieved is 5.75%. Fig. 5b shows the boxplot illustrating the variation for each target volume in the train of droplets. The highest CV% of 10.7% is observed for a target volume of 0.3 mL. Due to the CV% achievable and the limitation of the 3D printer chosen, the minimum volume difference discernible is 0.1 μL with the delay change of 100 ms. Fig. S6 in section 4 of the ESI† provides more detail.3.4. Train of droplets with constant volume of multiple analytes
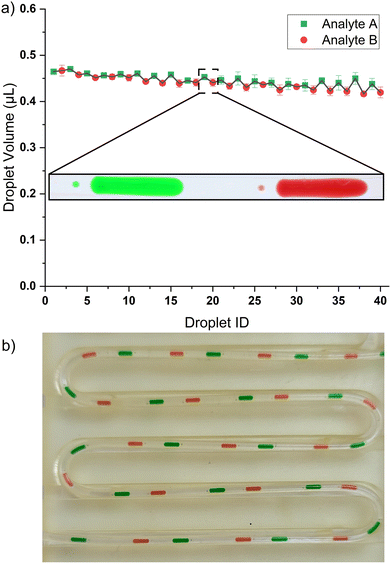
The 3D printer's adaptability stems from its programmable movements along the X–Y and Z axes. This system employs Z-axis motion to create sequences of droplets from a well, with volumes that can be either uniform or varied. Meanwhile, the X–Y axis movement is used to select an Eppendorf tube from a 3D-printed rack atop the well to produce droplet sequences. Currently, the rack can house 5 Eppendorf tubes, with two being used as proof of concept in this study. The setup can be expanded to include more Eppendorf tubes in line within a larger oil bath, depending on the print bed size of the 3D printer. Each Eppendorf tube is set roughly 11 mm apart (from its center point) which means that Prusa Mini+ can hold around 15 Eppendorf tubes with a bed size of 180 mm by 180 mm. A fused deposition modeling (FDM) printer with a bigger print bed can hold more Eppendorf tubes. The 3D printer movements required to generate droplets from multi-analytes are shown in Fig. 2 of section 2.1 (droplet generation videos in ESI†).Fig. 6 shows a train of 20 droplets where the system alternates between two Eppendorf tubes of the analyte. Fig. 6b is a picture of the train of droplets from two (2) different analytes each with constant volume, where the tubing is placed in a 3D printed holder. The inset droplet image in Fig. 6 shows daughter droplets. At a higher flow rate, there is an increased shear force on the analyte–oil interface leading to instability resulting in daughter droplets. At a lower flowrate (e.g., 10 μL min−1) daughter droplets are not formed.
The 3D printed Eppendorf tube places the Eppendorf tube 11 mm apart in the X axis. The distance from the low point to the high point is 4 mm for each Eppendorf tube in the Z axis. The maximum speed of Prusa Mini+ is 12 mm s−1 for the Z-axis, while for the X-axis, it is 200 mm s−1. Accordingly, this means it takes 1.33 seconds for the Z-axis and 0.055 seconds for X-axis movements. The minimum time between the generation of two (2) droplets from adjacent Eppendorf tubes is 1.385 seconds. The interval between droplet formations will extend if the Eppendorf tubes are spaced further apart. Nonetheless, a MATLAB script is capable of determining the interval for droplets originating from the most distant Eppendorf tubes and can introduce delays for those nearer to each other, ensuring a uniform droplet sequence.
3.5. Streptavidin beads tests
The single analyte scheme, section 2.1, is used to generate 10 droplets of a premixed solution consisting of streptavidin microbeads and biotinylated bovine serum albumin (bBSA). The study utilizes Dynabeads M-270 polystyrene microbeads, supplied by Thermo Scientific Pierce, with each bead measuring approximately 2.8 mm in diameter. For the experiments, these beads are suspended in a phosphate-buffered saline solution at varying concentrations, specifically at 2.5, 5, 10, 20, and 40 micrograms per milliliter (μg mL−1). Non-biotinylated BSA in PBS buffer is used as the negative control. Droplet trains are captured by Canon 5D Mark IV mounted on a Zeiss microscope, at 120 fps, 1280 × 720 px in a bright field configuration.Agglutination tests usually yield semi-quantitative results, indicating whether agglutination has occurred or not in a particular range of concentrations, akin to assessing C-reactive protein (CRP) levels where values above 3.0 mg mL−1 suggest a higher risk for cardiovascular issues.
Image analysis is a critical tool for quantifying agglutination processes in various fields such as virology,41,42 blood typing,43–46 and microbiology.47,48 Ana Ferraz et al. underscore the application of image processing techniques for detecting agglutination reactions.49 A dominant part of the literature focuses on hemagglutination43,46 or fluorescently35,50,51 labeled biomarkers. Yi Luo et al. used image processing to quantify C-reactive protein (CRP) in a concentration range of 10 to 500 μg mL−1 with the help of deep learning models.52 Morphological analysis also looked at the particle area of agglutination assay. Huet et al. used image analysis to monitor and quantify hemagglutination using correlation and variance-based indicators for blood typing.43 More details on image analysis can be found in our other research work.53
Subsequent sections will describe the image processing steps taken before quantifying the level of agglutination by two methods, the first is based on variance of gray scale values and the second method measures particle size within droplets.
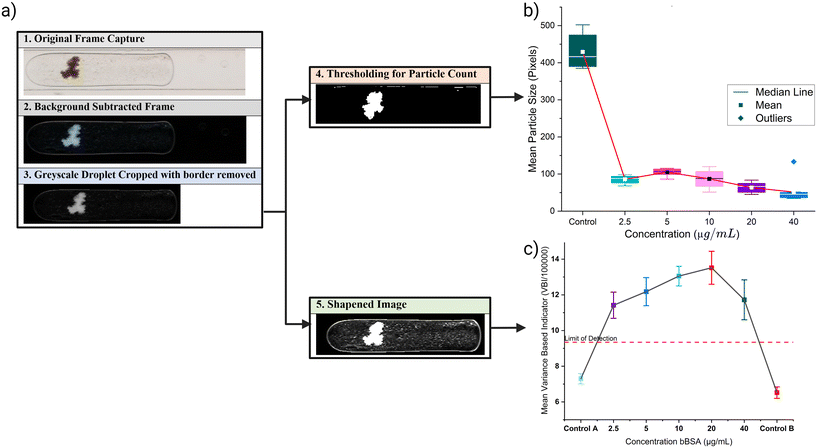
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 194) and their quantification. The first step is to isolate the video frame containing the droplet. This is done using MATLAB script which checks the front and end region of the frame and it should be similar to the background image (the first frame). The middle region's standard deviation must differ from other regions (front and end). The script allows the user to select a region of interest (ROI) for the droplet detection to reduce the amount of computation. If the droplet is detected in a frame then the frame is subtracted from the background image and only the subtracted ROI is stored. A second MATLAB script carries out this function, binarizing each image using MATLAB's auto-threshold function and applying the sharpness filter described in eqn (2) to create sharpened images, binarized and sharpened images are stored in separate folders. The binarized image is used for particle counting (Fig. 7b), while the sharpened image is used to calculate variance-based indicator for agglutination (Fig. 7c).
194) and their quantification. The first step is to isolate the video frame containing the droplet. This is done using MATLAB script which checks the front and end region of the frame and it should be similar to the background image (the first frame). The middle region's standard deviation must differ from other regions (front and end). The script allows the user to select a region of interest (ROI) for the droplet detection to reduce the amount of computation. If the droplet is detected in a frame then the frame is subtracted from the background image and only the subtracted ROI is stored. A second MATLAB script carries out this function, binarizing each image using MATLAB's auto-threshold function and applying the sharpness filter described in eqn (2) to create sharpened images, binarized and sharpened images are stored in separate folders. The binarized image is used for particle counting (Fig. 7b), while the sharpened image is used to calculate variance-based indicator for agglutination (Fig. 7c). | (2) |
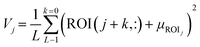 | (3) |
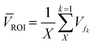 | (4) |
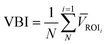 | (5) |
Fig. 7c shows the results of VBI for different concentrations. All images of each droplet for all concentrations are included in this evaluation. This is partly why there is so much variation in each concentration, as the agglomerate's movements within the droplet are influenced by the droplet's inner vortices. The limit of detection is calculated as per the standard.54 Control A is the train of droplets run before running any positive assay, consequently, assays of increasing concentration are generated. Control B is the control assay run after the highest concentration (40 μg mL−1). The four concentrations are clearly above the level of detection (LOD), allowing for qualitative results for agglutinated and non-agglutinated.
4 Discussion
The variance-based indicator and particle size measurement can distinguish between agglutinated and non-agglutinated droplets for the complete concentration range. In our previous experiments,55,56 the concentration range of 0.0128 μg mL−1 to 5000 μg mL−1 of biotinylated BSA was investigated using an off-the-shelf line break sensor (LBS) and deep learning models. Both show that the zone of equivalence for streptavidin and bBSA is between 0.32 μg mL−1 and 200 μg mL−1. It is difficult to distinguish between them since all the concentrations fall within the zone of equivalence. On the other hand, the experiments show the application of the developed system in agglutination assays. This study is calibrated for Prusa Mini+ however the user can use any 3D printer to implement the developed ADIM system. If the user uses a different 3D printer or generates droplet volumes beyond the volumes outlined in the manuscript, section 9 in the ESI† material outlines the methodology for this.4.1. Application of droplet generation platform
Droplet library generators are advancing experimental methodologies in droplet microfluidics toward greater efficiency, affordability, and precision across diverse research areas. Zhang et al.'s study demonstrates this by using manual pipetting from a well plate to carry out oligonucleotide amplification assays with a 192-sequence library.57 A droplet library generator can significantly enhance the throughput of their system, showcasing the utility of droplet library generators.Moreover, Wen-Bin Du et al. showcase the droplet library generator's application through the creation of DropLab.36 The application of DropLab is highlighted in a β-galactosidase inhibition assay, producing 2 nL droplets with varied concentrations of enzyme, substrate, and inhibitor to establish an inhibition curve and determine the IC50 value of the inhibitor. Additionally, the system is employed to assess and optimize crystallization conditions for lysozyme, a standard protein, using an array of 50, 12 nL droplets.
In the previous iteration of the system, custom connectors were designed to create a droplet cartridge, a self-contained droplet library.37 The connectors are crafted with complementary male and female Luer locks, ensuring precise alignment during the assembly of the modules. The tubing passes through the connector openings, where it is meticulously aligned and securely fastened together, preventing any direct contact between the fluids and the 3D-printed surface. Both connector ends feature a groove encircling the opening, designed to accommodate a silicone O-ring (sourced from amazon.ca) with a 3 mm inner diameter and a 2 mm thickness, ensuring a snug fit. Upon assembling the connectors, the tubing ends are pressed together, compressing the O-ring to create a tight seal that precludes any fluid leakage. Additionally, Teflon tape is applied to the male Luer lock's grooves to enhance the sealing efficiency. The connector orifice can be adjusted to accommodate various tubing sizes, offering versatility in system setup.
The system developed can theoretically utilize connectors to form a droplet cartridge that houses a library of droplets, as illustrated in Fig. 8. In the previous iteration of the system, the syringe needle had to descend through the oil into the analyte from above in a 96-well plate, which interfered with the refilling process. The current design facilitates movement from below the Eppendorf tube up into the analyte, allowing the user to refill the Eppendorf tube from its open top, thereby enabling extensive droplet trains.
 | ||
| Fig. 8 Schematic of how a droplet cartridge can be installed in the system to generate droplet libraries. | ||
The developed system is versatile in its setup as sensors and microfluidic chips can be incorporated in place of the droplet cartridge in Fig. 8 to expand the system's application.
4.2. Analyte selection
If the density of the analyte is comparable to or higher than the silicone oil (0.97 g cm−3) used in this study, the analyte can leak from the orifice in the Eppendorf tube and sink to the bottom of the well. The water density is comparable to the density of the silicone oil but the surface tension and capillary forces keep the water in the Eppendorf tube. The issues that can arise with different analyte selections are discussed in detail in section 7 of the ESI† material. If the analyte's density is around or above 0.97 g cm−3, then the user can select oil like Fluorinert FC-40 (ref. 34, 33, 31, 35, 54, 58 and 59) from Sigma-Aldrich with a density of 1.870 g cm−3 or HFE-7500 oil (3M)17,24,60–64 with 1.614 g cm−3 density. Oil with higher density would result in the analyte in the Eppendorf tube not leaking through its orifice at the bottom. Both oils are extensively used in literature related to droplet microfluidics.5 Conclusion
This study addresses the need for an affordable, low-cost microfluidic system by modifying a FDM 3D printer (Prusa MINI+) capable of generating droplets from 15 different analytes. The newly developed system, an automated dynamic inlet microfluidic system, demonstrates the ability to consistently create monodisperse droplets of various sizes and compositions, with limitations stemming from the printer's bed size and speed to house the oil well with analytes. This system distinguishes itself by leveraging the automation and standard equipment of a 3D printer, diverging from traditional microfluidic approaches. Setting up this system is straightforward, requiring less than a day's work. All necessary custom components, such as the 3D-printed nozzle with J bend, can be prepared using the same printer before its modification. Additionally, the printer's original functionality can be easily reinstated by reattaching the print head. Compared to existing methods documented in the literature, this system is user-friendly, eliminating the need for a clean room to produce microfluidic chips for droplet generation and avoiding the complexities of valve-operated droplet-on-demand mechanisms.This ADIM system demonstrates accuracy (CV < 2%) comparable to DropLab and Mitos Dropix while maintaining lower cost, making it suitable for enzyme or protein assays. The limitations of the developed platform related to analyte selection, and Tygon tube fouling are discussed and solutions are presented to give researchers a better understanding of the developed platform. Furthermore, the platform's efficacy in agglutination assays is highlighted, demonstrating the ability to distinguish between agglutinated and non-agglutinated samples through the mean particle size of agglomerates and a variance-based indicator. The system introduced offers a cost advantage, being 5.2 times more affordable than Elveflow's droplet generation starter pack and 8.8 times more economical than the Mitos Dropix. In addition, this version of our system improves upon its predecessor by being 1.5 times more cost-efficient and streamlining the previously complex calibration process.
Data availability
The data that support the findings of this study are openly available in Borealis at https://doi.org/10.5683/SP3/MSLKM4 as part of UBC Research Data Collection.Author contributions
I. G. F. (Ian G. Foulds) and A. B. Z. (Abdul Basit Zia) worked on the original conceptualization. A. B. Z. designed, performed the experiments, analyzed data, and wrote the manuscript. I. G. F. reviewed, proofread, and approved the manuscript. The work was done under the supervision of I. G. F.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Natural Sciences and Engineering Research Council of Canada through the Discovery Grant Program.Notes and references
- C. W. Shields IV, C. D. Reyes and G. P. López, Lab Chip, 2015, 15, 1230–1249 RSC.
- R. Seemann, M. Brinkmann, T. Pfohl and S. Herminghaus, Rep. Prog. Phys., 2011, 75, 016601 CrossRef PubMed.
- C. Parent, K. R. Melayil, Y. Zhou, V. Aubert, D. Surdez, O. Delattre, C. Wilhelm and J.-L. Viovy, Lab Chip, 2023, 5139–5150 RSC.
- G. K. Kurup and A. S. Basu, Biomicrofluidics, 2012, 6, 22008–2200810 CrossRef CAS PubMed.
- S.-C. Chang and Y.-C. Su, Microfluid. Nanofluid., 2010, 10, 1165–1174 CrossRef.
- D. Liu, M. Sun, J. Zhang, R. Hu, W. Fu, T. Xuanyuan and W. Liu, Analyst, 2022, 147, 2294–2316 RSC.
- W. Han and X. Chen, J. Braz. Soc. Mech. Sci. Eng., 2021, 43, 247 CrossRef.
- X. Chen and C. L. Ren, RSC Adv., 2017, 7, 16738–16750 RSC.
- S. G. Sontti and A. Atta, Ind. Eng. Chem. Res., 2020, 59, 3702–3716 CrossRef CAS.
- J. Yao, F. Lin, H. Kim and J. Park, Micromachines, 2019, 10, 808 CrossRef PubMed.
- J. Guerrero, Y.-W. Chang, A. A. Fragkopoulos and A. Fernandez-Nieves, Small, 2019, 16, 1904344 CrossRef PubMed.
- J. Zhang, W. Xu, F. Xu, W. Lu, L. Hu, J. Zhou, C. Zhang and Z. Jiang, J. Food Eng., 2021, 290, 110212 CrossRef CAS.
- A. Dewandre, J. Rivero-Rodriguez, Y. Vitry, B. Sobac and B. Scheid, Sci. Rep., 2020, 10, 21616 CrossRef CAS PubMed.
- A. Lashkaripour, C. Rodriguez, N. Mehdipour, R. Mardian, D. McIntyre, L. Ortiz, J. Campbell and D. Densmore, Nat. Commun., 2021, 12, 25 CrossRef CAS PubMed.
- N. A. Filatov, A. A. Evstrapov and A. S. Bukatin, Micromachines, 2021, 12, 662 CrossRef PubMed.
- Z. Yin, Z. Huang, X. Lin, X. Gao and F. Bao, Micromachines, 2020, 11, 8 CrossRef PubMed.
- F. Ahmadi, K. Samlali, P. Q. Vo and S. C. Shih, Lab Chip, 2019, 19, 524–535 RSC.
- H. Babahosseini, T. Misteli and D. L. Devoe, Lab Chip, 2019, 19, 493–502 RSC.
- C. Wu, J. Sun and B. Yin, Micromachines, 2023, 14, 1302 CrossRef PubMed.
- M. Boaks, C. Roper, M. Viglione, K. Hooper, A. T. Woolley, K. A. Christensen and G. P. Nordin, Micromachines, 2023, 14, 1589 CrossRef PubMed.
- J. Chen, S. Huang, Y. Long, K. Wang, Y. Guan, L. Hou, B. Dai, S. Zhuang and D. Zhang, Biosensors, 2022, 12, 1085 CrossRef CAS PubMed.
- F. Nalin, M. C. Tirelli, P. Garstecki, W. Postek and M. Costantini, Lab Chip, 2024, 24, 113–126 RSC.
- X. Sun, K. Tang, R. D. Smith and R. T. Kelly, Microfluid. Nanofluid., 2013, 15, 117–126 CrossRef CAS PubMed.
- K. Totlani, J. W. Hurkmans, W. M. Van Gulik, M. T. Kreutzer and V. Van Steijn, Lab Chip, 2020, 20, 1398–1409 RSC.
- D. Kim, A. Echelmeier, J. C. Villarreal, S. Gandhi, S. Quintana, A. Egatz-Gomez and A. Ros, Anal. Chem., 2019, 91, 9792–9799 CrossRef CAS PubMed.
- S. Zeng, B. Li, X. Su, J. Qin and B. Lin, Lab Chip, 2009, 9, 1340–1343 RSC.
- A. J. Teo, M. Yan, J. Dong, H. D. Xi, Y. Fu, S. H. Tan and N. T. Nguyen, Microfluid. Nanofluid., 2020, 24, 1–9 CrossRef.
- W. Cui, G. Yesiloz and C. L. Ren, Anal. Chem., 2021, 93, 1266–1270 CrossRef CAS PubMed.
- Elveflow, Microfluidics starter pack, 2024, https://www.elveflow.com/microfluidics-application-packs/microfluidics-packs/starter-pack/ Search PubMed.
- X. Hu, X. Gao, S. Chen, J. Guo and Y. Zhang, Microsyst. Nanoeng., 2023, 9, 10 CrossRef CAS PubMed.
- A. Waldbaur, J. Kittelmann, C. P. Radtke, J. Hubbuch and B. E. Rapp, Lab Chip, 2013, 13, 2337–2343 RSC.
- T. W. Murphy, Y.-P. Hsieh, B. Zhu, L. B. Naler and C. Lu, Anal. Chem., 2020, 92, 2519–2526 CrossRef CAS PubMed.
- H. Zec, T. D. Rane and T. H. Wang, Lab Chip, 2012, 12, 3055–3062 RSC.
- F. Gielen, L. van Vliet, B. T. Koprowski, S. R. Devenish, M. Fischlechner, J. B. Edel, X. Niu, A. J. deMello and F. Hollfelder, Anal. Chem., 2013, 85, 4761–4769 CrossRef CAS PubMed.
- L. D. Van Vliet, F. Gielen, A. Sinha, B. T. Koprowski, J. B. Edel, X. Niu, A. J. De Mello and F. Hollfelder, 18th International Conference on Miniaturized Systems for Chemistry and Life Sciences, MicroTAS 2014, 2014, pp. 1214–1216 Search PubMed.
- W.-B. Du, M. Sun, S.-Q. Gu, Y. Zhu and Q. Fang, Anal. Chem., 2010, 82, 9941–9947 CrossRef CAS PubMed.
- A. B. Zia, J. Farrell and I. G. Foulds, Lab Chip, 2024, 24, 3015–3026 RSC.
- L. Berg Luecke and R. L. Gundry, J. Proteome Res., 2020, 20, 1153–1164 CrossRef PubMed.
- A. S. Basu, Lab Chip, 2013, 13, 1892–1901 RSC.
- D. Castro, PhD thesis, King Abdullah University of Science and Technology Thuwal, Kingdom of Saudi Arabia, 2018 Search PubMed.
- J. L. Arias-Arias, E. Corrales-Aguilar and R. Mora-Rodríguez, Viruses, 2021, 13, 1193 CrossRef CAS PubMed.
- A. Petkidis, V. Andriasyan and U. F. Greber, Microscopy, 2023, 72, 204–212 CrossRef CAS PubMed.
- M. Huet, M. Cubizolles and A. Buhot, High-Throughput, 2018, 7, 10 CrossRef PubMed.
- S.-W. Nam, D.-G. Jeon, Y.-R. Yoon, G. H. Lee, Y. Chang and D. I. Won, Biosensors, 2023, 13, 733 CrossRef CAS PubMed.
- S. Ding, S. Duan, Y. Chen, J. Xie, J. Tian, Y. Li and H. Wang, Talanta, 2022, 252, 123856 CrossRef PubMed.
- A. A. Sklavounos, J. Lamanna, D. Modi, S. Gupta, A. Mariakakis, J. Callum and A. R. Wheeler, Clin. Chem., 2021, 67, 1699–1708 CrossRef PubMed.
- A. Brown, B. Morris, J. K. Kamau, A. A. Alshudukhi, A. Jama and H. Ren, Arch. Microbiol. Immunol., 2023, 7(3), 178–187 Search PubMed.
- H. Jeckel and K. Drescher, FEMS Microbiol. Rev., 2020, 45(4), fuaa062 CrossRef PubMed.
- A. Ferraz, J. Machado and V. Carvalho, Proc. 2015 IEEE 4th Portuguese Meeting on Bioengineering (ENBENG), 2015, pp. 1–6 Search PubMed.
- F. Dinter, M. Burdukiewicz, P. Schierack, W. Lehmann, J. Nestler, G. Dame and S. Rödiger, Anal. Bioanal. Chem., 2019, 411, 7725–7735 CrossRef CAS PubMed.
- M. Ouyang and D. D. Carlo, Biosens. Bioelectron., 2019, 132, 162–170 CrossRef CAS PubMed.
- Y. Luo, H.-A. Joung, S. Esparza, J. Rao, O. Garner and A. Ozcan, Lab Chip, 2021, 21, 3550–3558 RSC.
- A. B. Zia, J. Farrell and I. G. Foulds, Sens. Actuators, A, 2024 DOI:10.2139/ssrn.4940936.
- D. A. Armbruster and T. Pry, Clin. Biochem. Rev., 2008, 29(Suppl 1), S49–S52 Search PubMed.
- J. Farrell, A. B. Zia and I. G. Foulds, IEEE Sens. Lett., 2023, 7, 1–4 Search PubMed.
- H. Juberi, A. B. Zia, J. Farrell and I. G. Foulds, IEEE Sens. Lett., 2024, 8, 1–4 Search PubMed.
- J. Q. Zhang, C. A. Siltanen, A. Dolatmoradi, C. Sun, K.-C. Chang, R. H. Cole, Z. J. Gartner and A. R. Abate, Sci. Rep., 2021, 11, 4351 CrossRef CAS PubMed.
- A. Shahid, S. Chong, J. Mahony, M. J. Deen and P. R. Selvaganapathy, Micromachines, 2017, 8, 353 CrossRef PubMed.
- M. Chabert, K. D. Dorfman, P. de Cremoux, J. Roeraade and J.-L. Viovy, Anal. Chem., 2006, 78, 7722–7728 CrossRef CAS PubMed.
- B. Ahn, K. Lee, H. Lee, R. Panchapakesan and K. W. Oh, Lab Chip, 2011, 11, 3956 RSC.
- L. Nan, M. Y. Lai, M. Y. Tang, Y. K. Chan, L. L. Poon and H. C. Shum, Small, 2019, 16, 1902889 CrossRef PubMed.
- V. Bussiere, A. Vigne, A. Link, J. McGrath, A. Srivastav, J.-C. Baret and T. Franke, Anal. Chem., 2019, 91, 13978–13985 CrossRef CAS PubMed.
- H. Zhang, A. R. Guzman, J. A. Wippold, Y. Li, J. Dai, C. Huang and A. Han, Lab Chip, 2020, 20, 3948–3959 RSC.
- L. Xu, H. Lee, R. Panchapakesan and K. W. Oh, Lab Chip, 2012, 12, 3936–3942 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00643g |
| This journal is © The Royal Society of Chemistry 2025 |