High-throughput, combinatorial droplet generation by sequential spraying

Abstract

Advancements in bulk and microfluidic emulsion methodologies have enabled highly efficient, high-throughput implementations of biochemical assays. Spray-based techniques offer rapid generation, droplet immobilization, and accessibility, but remain relatively underutilized, likely because they result in random and polydisperse droplets. However, the polydisperse characteristic can be leveraged; at sufficiently high droplet numbers, sequential sprays will generate mixed droplets which effectively populate a combinatorial space. In this paper, we present a method involving the sequential spraying and mixing of solutions encoded with fluorophores. This generates combinatorial droplets with quantifiable concentrations that can be imaged over time. To demonstrate the method's performance and utility, we use it to investigate synergistic and antagonistic pairwise antibiotic interactions.

---

1. Introduction

The discretization of bulk liquids into smaller reaction volumes has been a key development in biochemical research. Conventional manual pipetting into tubes or microtiter plates is simple, accessible, and allows easy tracking of reactions. However, it is labor intensive and restricted in its miniaturization, limiting high-throughput investigation. In contrast, bulk emulsions are high throughput and relatively simple to generate. Bulk emulsions are typically composed of aqueous droplets suspended in a continuous oil phase, traditionally produced through bulk homogenization or injection.¹ Bulk emulsions can generate 10⁵ to 10¹⁰ samples with lower time and reagent costs per reaction than pipetting. They have been employed for single-cell microbial isolation^1,2 and antibiotic susceptibility screening,³ as well as more involved protocols such as emulsion polymerase chain reaction (PCR)⁴ and sequencing.⁵ However, manipulation of bulk emulsions is limited as controlled droplet merging is difficult, hindering their application in combinatorial studies. In addition, droplets are polydisperse, which could introduce biases, and are not fixed in space, requiring instrumentation to immobilize and track droplets over time.

Emulsion microfluidics, which use microfluidic techniques to generate emulsion droplets, has many advantages over bulk emulsions, such as the rapid production of monodisperse droplets and reduced sample and reagent consumption.⁶ Microfluidic emulsion techniques have been widely adopted for various applications, including droplet digital PCR⁷ and single-cell sequencing.^8,9 Several studies have utilized optical (such as fluorescence encoding) or bead indexing^10,11 to track reactions to capture dose-dependent responses¹² and to perform combinatorial investigations, such as antibiotic synergism and antagonism assays.¹³ However, many high-throughput droplet microfluidics techniques require skilled fabrication and involve multiple devices for droplet generation, recovery, and readout. While some techniques from bulk emulsions have been implemented to simplify droplet production,¹⁴ their use in multi-component studies has been limited due to persisting challenges in droplet manipulation and tracking. Templated emulsions in bulk¹⁵ are useful for associating nucleic acid sequences with each other for single-cell genomics but are less immediately applicable to encoding different compositions across continuous combinatorial concentration spaces. Alternatively, stationary platforms such as microdroplet arrays¹⁶ offer spatial discretization and ease of manipulation, but often require intensive, specialized fabrication.¹⁷ The trade-off between precise component mixing and ease of droplet generation makes high-throughput, combinatorial experimentation inaccessible to many laboratories.

Spraying-based stationary methods provide a promising alternative, where droplets are deposited from a spray nozzle onto a substrate. Adoption of spray-based methods dates to the mid-20th century¹⁸ but has been confined mainly to one-component systems.¹⁹ However, we noted that higher order component spaces are readily available through spraying. We propose using sequential sprays to create random droplets which, in sufficient numbers, will tile a desired combinatorial space. By coupling component concentration to fluorescent intensity, and measuring the fluorescence after merging, we obviate the need for precisely controlled merging mechanisms. We present an accessible, high-throughput protocol which leverages sequential sprays to rapidly perform combinatorial experiments. We also demonstrate its utility for biochemical experimentation by performing checkerboard analyses for antibiotic pairs.

2. Results and discussion

2.1 Method overview

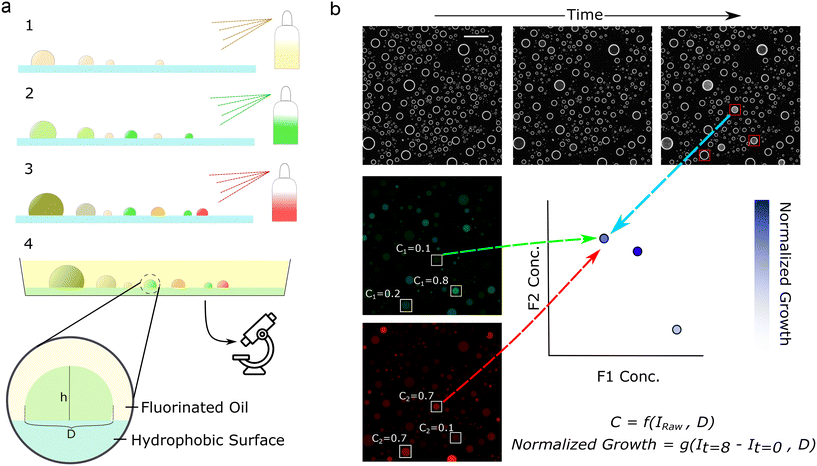
The core of this workflow involves spraying optically encoded solutions onto a substrate for efficient, high-throughput generation of combinatorial droplets. These droplets are optically interrogated, allowing for determination of the input component concentrations. The droplets are also monitored over time with a functional readout.

2.2 Implementation

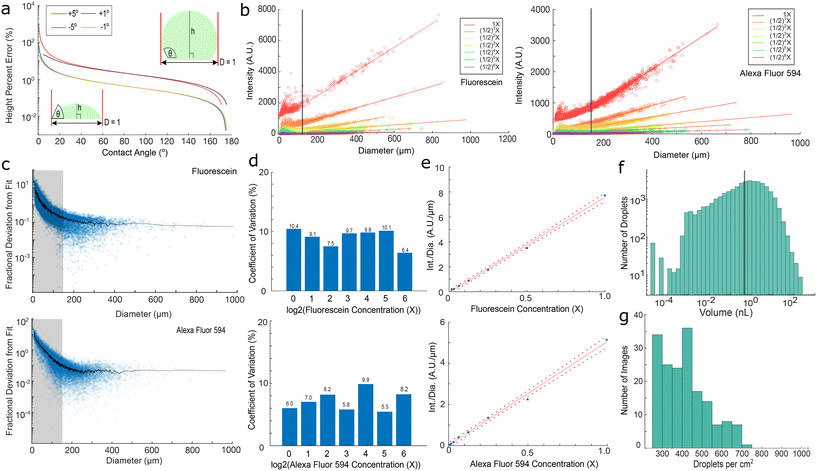
In our implementation, we first prepared the reaction components. We then mixed all but one of the reaction components with a distinct, inert fluorophore at a known concentration. We then sprayed one of these solutions on a treated surface, generating droplets of variable sizes. Next, we then sprayed a second solution, which generated more droplets, a portion of which coalesced with existing droplets to create random mixtures (Fig. 1a). This process was repeated for the chosen number of solutions to form droplets of differing sizes and random concentrations. Then, we immersed the droplets in oil to prevent evaporation (Fig. 1a and Video S1†), immobilizing the droplets on the substrate over the time course of an experiment.

Fig. 1 Components are encoded with fluorophores and sprayed sequentially, forming droplets with random concentrations. Fluorescence imaging enables the calculation of concentrations while darkfield enables phenotypic readout. (a) Schematic of droplet generation procedure, where components are sequentially sprayed on slides treated with FOTS, then immersed in FC-40 oil. (b) Schematic of analysis procedure, where fluorescence images (middle left, bottom left) encode component concentrations while darkfield images (top) encode microbial growth. Fluorescence intensities are normalized by the projected droplet diameter, D, to obtain concentrations, C. The change in darkfield intensity is normalized by droplet diameter to calculate normalized growth. Concentrations and growth are mapped to interrogate parameter spaces. Scale bar represents 500 μm. Fluorescence images are contrast-enhanced for viewing.

This procedure generates many droplets of differing concentrations, which tile a combinatorial space. It is essential to accurately obtain the component concentrations. Here, we use a method that relies on assuming a spherical cap geometry and a constant droplet contact angle. Under these assumptions, droplet geometries are similar, and we can calculate the droplet height – the length of the light path – from the projected droplet diameter (Fig. 1b and 2a). Knowing the droplet height, and assuming that concentration is proportional to fluorescence, we calculate each component's concentration from their respective fluorescence intensity. Here we used concentrations within the linear range. At very low fluorophore concentrations, the intensities reach the noise floor of the imaging setup, while at high concentrations, the linearity breaks due to the inner filter effect. Both effects can be seen in Fig. S1.† Future work could apply alternative curve-fitting methods to nonlinear regions, provided the function remains one-to-one, expanding the range of detectable concentrations.

Fig. 2 The workflow was validated for precision, dynamic range, throughput, and volume distribution. (a) Assuming spherical cap geometry, we calculated the expected droplet height across a range of assumed contact angles. Then, we calculated the droplet height if the assumed contact angle was off by ±1° and ±5°. Plotting theoretical percent deviation in calculated height against contact angle demonstrates that higher contact angles are more robust to noise. (b) For chosen fluorophores at chosen concentrations, intensity varies linearly with diameter. 1× is defined as 10 mg ml⁻¹ fluorescein and 1 mg ml⁻¹ Alexa Fluor 594. (c) Fractional deviation from the line of best fit from (b), with moving averages of 50 samples. Errors are larger at lower diameters, leading us to impose a cut-off at 150 μm. (d) Coefficient of variation of each concentration from (b), using a threshold diameter of 150 μm. Fluorescein has an average CV of 9.0%, while Alexa Fluor 594 has an average CV of 7.2%. (e) For chosen fluorophores at chosen concentration ranges, intensity normalized by diameter varies proportionally with concentration. Each point is derived from the slopes in (b). Dashed lines represent 95% confidence intervals. (f) Distribution of droplet volume, computed from diameter. The vertical line represents the volume associated with the threshold at 150 μm. (g) Throughput distribution for one experiment, displaying all droplets that pass the image analysis pipeline, except for the size filter.

Next, we calculated the error associated with this method if the contact angle is not constant (Fig. 2a). Droplets on non-ideal surfaces typically exhibit some variation in contact angle due to hysteresis.²⁰ From simple geometric considerations we can see that a higher contact angle is more robust against the effects of hysteresis, as evidenced by the small associated error in volume when noise is introduced (Fig. 2a). Thus, we screened for oils, surfaces, and surface treatments that provided high, consistent contact angles, were compatible with the fluorophores, effectively prevented droplet evaporation, and kept droplets immobilized on the surface (Table S1†). After screening through multiple oil-surface-treatment combinations, we found that glass silanized with trichloro(1H,1H,1H,2H,2H-perfluorooctyl)silane (FOTS) and the fluorinated oil Fluorinert FC-40 provided a consistent contact angle. This consistency is reflected in the linear relationship between fluorescence intensity and the measured droplet diameter for fluorophores at constant concentration, which was used to normalize intensity in subsequent experiments (Fig. 2b). We also confirmed that the normalized intensity was proportional to concentration (Fig. 2e). Finally, we validated that the FOTS and FC-40 combination produced droplets that do not shrink or move for at least 12 hours (Video S2†). Other oil-surface treatment combinations did lead to shrinking (Video S3 and Table S1†), as did insufficient oil volume (Video S4 and Table S1†). Lastly, high-throughput experiments need corresponding high-throughput readouts. Here, we used time course darkfield imaging to quantify microbial growth (Fig. 1b). This system allowed easy measurement of phenotypic responses to multicomponent combinations.

2.3 Method performance

We assessed the method for concentration readout precision and accuracy, ease of use, throughput, and dynamic range. First, we evaluated the precision of this method experimentally by generating single-component droplets of known fluorophore concentrations. Here, we show the fractional deviation from fit (Fig. 2c and S2†), calculated from the data in Fig. 2b. This metric is calculated by taking the difference between a droplet's measured intensity and its theoretical intensity (predicted from the diameter-based line of best fit), and then dividing this difference by the theoretical intensity. This metric allows us to visualize the error associated with each droplet. Plotting the fractional deviation from fit against diameter, we see that errors are largest for small diameter droplets, leading us to establish a cut-off where droplets below 150 μm diameter are omitted from analysis (Fig. 2c and S2†). Using larger droplets also mitigates the impact of any volume loss, which happens before the droplets are immersed in oil (Methods, Videos S5 and S6†). Establishing a size cut-off is a balance between the number of droplets sampled and the expected error in concentration for the smaller droplets; a lower threshold has higher sampling with higher error, and vice versa.

After establishing the cut-off, we calculated the coefficient of variation (CV, the standard deviation divided by the mean) of intensity/diameter for each concentration. As a summary statistic, the CV is commonly used to quantify precision in volume or concentration of liquid handling methods. For droplets above the threshold, we obtained an average CV of 9.0% for fluorescein and 7.2% for Alexa Fluor 594 (Fig. 2d and S3–S5†). This is comparable to other widely-used liquid handling methods; CVs for manual pipetting average 5.7% for 10 μL volumes,²¹ and are above 10% for volumes <1 μL,²² while CVs for robotic pipetting have been measured at around 10.5% for 3 μL volumes.²³ There are low-volume methods for generating multiple concentrations that are more precise—such as robotic pipettors capable of precise nanoliter handling (5% CV for 50 nL,²⁴ 5.5% CV for 10 μL²⁵), and certain microfluidic systems (3.6% CV for dilutions in 1 μL droplets²⁶). However, these options often come with significant cost and equipment demands. In contrast, spray droplet generation offers a more accessible alternative.

The required precision for any experiment should be considered when selecting the liquid handling method. CVs in this range indicate that the inferred concentration of most droplets will fall within several percent of expected. Classically, the histogram of deviations often follows a classic bell-shaped curve, as is the case here (Fig. S4 and S5†). This error profile has occasional droplets with much higher deviations. In many assays, other sources of noise (e.g. biological noise) will dominate the noise in the final assay, and better liquid handling precision is not required. In cases where more precision is required, including replicates can average out noise associated with liquid handling (and other) noise sources. This method makes it easy to generate a large number of droplets, which can be used for averaging when needed. Potential strategies to further reduce the CV are covered in alternative implementations.

Next, we interrogated accuracy. We demonstrate that normalized intensities correlate linearly with concentration within this range (Fig. 2e). The linearity, representative of the concentration readout accuracy, allows us to read out concentrations from known intensity and diameter in subsequent experiments. In addition, we wanted to ensure that the method could rapidly perform high-throughput experiments and could cover a wide range of concentrations. The generation of droplets took less than ten seconds, underscoring the method's ability to increase throughput (Video S1†). We generated an average of 442 droplets per square centimeter (Fig. 2g). After the size-based filtering, the average droplet volume was 6.74 nL (Fig. 2f). This density and average volume can easily be manipulated by changing the distance between the spray and the substrate, while throughput can be increased simply by imaging a larger area. Therefore, one can easily capture tens or hundreds of thousands of reactions per experiment. The dynamic range of the platform is defined by two key factors: the range of concentrations present after sequential spraying and the ability to measure the concentrations. While the latter is a function of the fluorophore concentration and the imaging system, the former depends on the number of droplets sampled and the droplet size distribution from the spray. Droplets have a volume range spanning several orders of magnitude (Fig. 2f), permitting a large dynamic range from merged droplet combinations. Due to the random merging process, the dynamic range can be increased simply by increasing sampling. These metrics demonstrate that the spray method allows for examination of combinatorial spaces at high resolution.

2.4 Capability for biotic experimentation

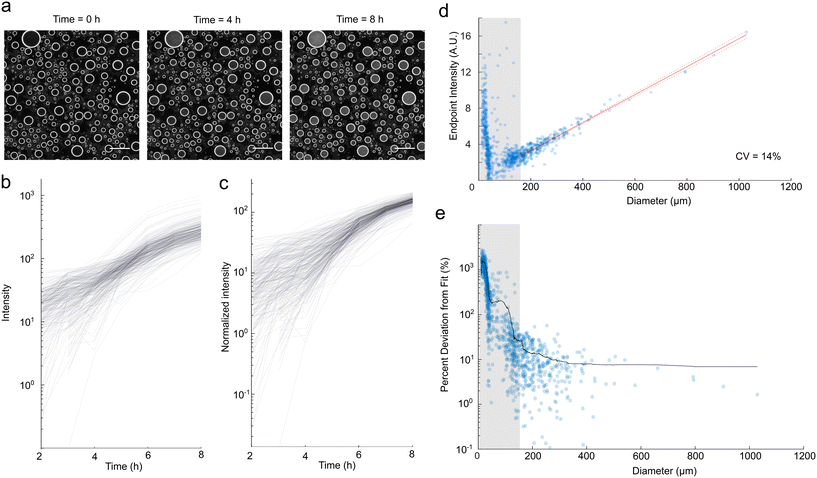
Previous spray droplet methods have primarily been limited to systems without living cells. Therefore, we wanted to confirm our method's compatibility with biotic experimentation and assess whether the polydispersity of droplets resulted in biological biases. To do so, we inoculated media with Escherichia coli and generated droplets. We used darkfield imaging to monitor microbial growth, quantified by an increase in intensity of scattered light (Fig. 3a).

Fig. 3 Darkfield imaging enables the monitoring of microbial growth in spray droplets. Scale bar represents 500 μm. (a) Darkfield imaging over time demonstrates increased turbidity indicative of microbial growth. (b) Change in darkfield intensity over eight hours. (c) Change in darkfield intensity, normalized by droplet size. (d) Growth at t = 8 hours demonstrates a linear relationship with diameter for droplets above 150 μm cut-off, with a CV of 14% in intensity/diameter for droplets in this region. (e) Percent deviation from the line of best fit from (c), with a moving average of window size 50.

We first discuss cell loading into droplets. Assuming the spray solution is well mixed, the number of starting cells in each droplet should follow a Poisson distribution. A feature of Poissonian loading is that the exact number of cells in any droplet is not known and the fractional uncertainty in cell count increases as the average number of cells per droplet goes down. We loaded a concentration of 1.32 × 10⁷ cells per ml which corresponds to 89 cells per droplet for droplets of average volume and 17 cells per droplet for the smallest droplets at the 150 μm size threshold. Thus we would expect a standard deviation of 9.4 cells, or 10% of the number of cells in the average droplet, and 4.1, or 24% of the number of cells in the small droplets. In applications that are sensitive to the concentration of cells, cells should be loaded at a high enough density to ensure a high enough count for a sufficiently consistent starting concentration, or cells should be experimentally counted within each droplet to ensure the target concentrations are reached.

To quantify the noise in our data, we created growth curves for each droplet, which display clear growth over eight hours (Fig. 3b). As expected, the growth curves plotted from raw darkfield intensity were variable for polydisperse droplets (Fig. 3b). To compensate for this variability, we normalized darkfield intensity by droplet diameter (Fig. 3c), following how we normalized fluorescence intensity. We observe high variation in normalized intensity at earlier time points (Fig. 3c) and for smaller droplets (Fig. 3e and S6†). This variability is the result of several factors, including variation in volume as quantified in Fig. 2 and variation due to Poissonian loading of cells, as covered above. Additionally, growth characteristics (lag times and growth rates)^27–29 of individual cells are known to vary substantially, such that small collections of cells are likely to display variability in their growth kinetics. Furthermore, imaging of smaller and lower intensity droplets is more susceptible to noise. The masking procedure calculates intensity using a smaller droplet mask with a proportionally reduced diameter relative to the measured diameter. As a result, smaller droplets at lower intensities are more susceptible to edge effects, leading to increased variability, particularly at earlier time points.

Despite the initial variability, we observe significantly reduced variation in normalized intensity as the microbes exit exponential growth and reach saturation, depicted in the non-linear plateau region in Fig. 3c. Similar findings hold for longer experiments (Fig. S7†). The normalized change in intensity over eight hours of growth against droplet diameter showed a strong linear relationship (Fig. 3d), indicating that cells reached a similar final concentration. In addition, we examined the influence of droplet size on the deviation from this proportionality (Fig. 3e). Similar to our findings with fluorescent controls, the typical deviation was higher for small droplets, motivating a size threshold, for which here we chose 150 μm. This resulted in a CV of 14% for the normalized endpoint intensity for droplets in this region, which is of the same order of magnitude as the percent errors associated with the fluorophores (Fig. 2b and c). As a result, we determined that for sufficiently large droplets, polydispersity introduces minimal biases in final cell concentration with this approach. We proceeded to use this normalization method for subsequent assays. It is possible to tune the average number of E. coli per droplet by changing the spraying parameters and the concentration of E. coli. Lower cell concentrations result in higher stochasticity in initial cell concentration, while higher cell concentrations can require higher concentrations of antibiotics to inhibit growth.^30,31

2.5 Antibiotic synergism and antagonism assay

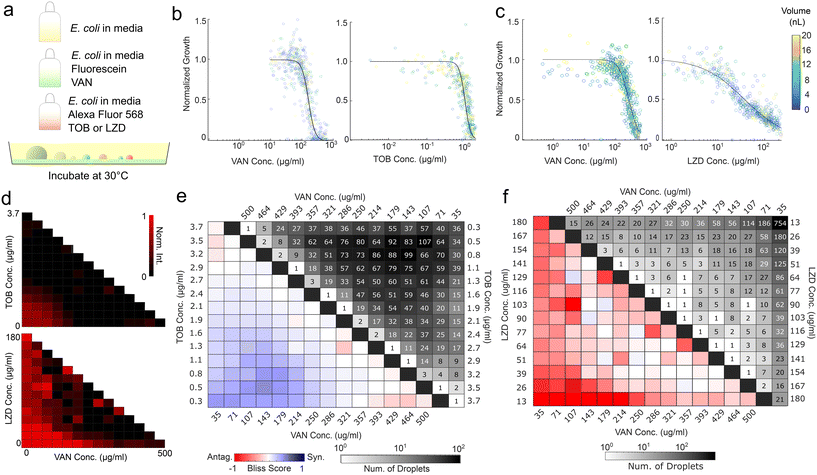
Antibiotic combination therapies are promising for multi-resistant and severe infections³² and are the clinical standard of care for tuberculosis^33,34 and enterococcal infections.³⁵ Combination therapies not only reduce the probability of the emergence of multi-drug resistant strains by targeting multiple mechanisms but can also exhibit synergism. Antibiotic combinations are synergistic if their combined efficacy exceeds the additive efficacies of their constituents. However, some antibiotics can act antagonistically and reduce each other's efficacies. To facilitate the screening of effective combination therapies, we performed synergism and antagonism assays as a proof-of-concept for the proposed method.

Antibiotic pairs were chosen following a preliminary well plate screen, selecting for understudied, water-soluble antibiotic pairs. E. coli strains have demonstrated synergism between vancomycin and tobramycin, though the exact mechanism of action is unknown.³⁶ Vancomycin and linezolid have demonstrated antagonism in Gram-positive microbes, hypothesized due to the bactericidal activity of vancomycin being inhibited by the bacteriostatic mechanism of linezolid.³⁷ Well plate screens confirmed synergism between vancomycin and tobramycin, as well as antagonism between vancomycin and linezolid (Fig. S8†).

In the spray implementation of the synergism and antagonism assays, the vancomycin concentration was encoded with fluorescein, while tobramycin and linezolid concentrations were encoded with Alexa Fluor 594 (Fig. 4a). Cells were added at a fixed initial concentration to all components to ensure comparable initial cell concentrations across droplets. Microbial growth was monitored by darkfield microscopy and normalized by droplet height. Individual dose–response curves were generated for each antibiotic by combining the singular antibiotic spray and the inoculated media spray, the latter acting as a dilution agent. The dose–response curves demonstrated agreement across runs, as evidenced by the vancomycin curves (Fig. 4b and c). In addition, we examined whether antibiotic efficacies were impacted by droplet size, which would undermine the validity of growth normalization. The average dose response does not demonstrate dependency on droplet size (Fig. 4b and c and S9†).

Fig. 4 Spray droplets facilitate pairwise antibiotic synergism–antagonism assays. (a) Schematic of the experimental method. (b) Individual dose–response curves for the synergism and (c) antagonism assays, colored by droplet volumes. Individual points represent one droplet each, while the curve is a fitted Hill equation. (d) Checkerboard of normalized intensity for synergism (top) and antagonism (bottom) assays. (e) Checkerboard analysis of pairwise synergism and (f) antagonism assays. Colors indicate Bliss scores, blue representing synergism and red representing antagonism. Grayscale indicates counts per bin.

The synergism and antagonism assays revealed distinct pairwise isophenotypic contours, with concavity indicative of their respective interactions (Fig. 4d).^36,37 Bliss scores of vancomycin and tobramycin displayed clear dose-dependent synergism, while Bliss scores of vancomycin and linezolid demonstrate sub-inhibitory antagonism (Fig. 4e and f). Both are reflected in well plate results and previous literature (Fig. S8†).^36,37 The produced droplets demonstrated sufficient coverage of the three-component space to a resolution of 1/14 for both the antagonism and synergism assays. While the coverage profiles for the two assays are different due to the stochasticity of the spray process, they both successfully detect the interaction. The resulting data contain over 5000 independent droplets surveyed. This experiment demonstrates that the setup can accurately capture individual antibiotic dose responses and assess the synergism or antagonism contours.

2.6 Alternative implementations

While this sample workflow uses fluorescent dyes to encode concentration and darkfield intensity to track microbial growth, the core method of sequential spraying can be adapted to numerous encoding strategies and readouts. For example, discrete (e.g. beads) or a colorimetric encoding are alternatives to fluorescent dyes, while a wide range of optical techniques could be implemented for the readout, including absorbance or morphological measurements. In addition, the method to calculate droplet height can be changed, especially in solution combinations which exhibit more hysteresis. One potential method is to encode one dye or particle at constant concentration relative to all components. Then, one could assume the intensity of fluorescence of the constant component is proportional to the length of the light path (confirmed experimentally, Fig. 2b), and use it to calibrate the height of the droplet. This, coupled with fluorescence intensities in other channels, would enable the calculation of other fluorophore concentrations for each droplet. However, this method increases the number of fluorophores and the degree of spectral overlap, making translation to higher order search spaces more technically challenging. Finally, there are many spray mechanisms that can be implemented. A more controlled mist system may produce more replicable concentration and droplet size distributions. The degree of spray overlap, the droplet size distribution, and other parameters can be tuned to achieve a different final concentration distributions and sampling density. The droplet size cut-off can be changed correspondingly to balance the number of droplets sampled and the expected error in concentration readouts.

3. Materials and methods

3.1 Glass surface treatment

Glass slides (2.5 cm by 2.5 cm) were cleaned with acetone and water, followed by baking for 10 minutes at 80 °C. The slides were then plasma treated for three minutes (Harrick Plasma). After cleaning, the slides were silanized by vapor deposition, by incubating glass in a vacuum with 100 μl of trichloro(1H,1H,1H,2H,2H-perfluorooctyl)silane (FOTS, Sigma-Aldrich) overnight at room temperature. The slides were baked for 2 hours at 80 °C to remove excess silane.

3.2 E. coli and reagent preparation for proof-of-concept experiment

First, 15 mL of Luria Broth media (RPI Research Products) was inoculated with an E. coli W3110 colony and incubated overnight. The resulting culture was diluted to an OD₆₀₀ of 0.0165. Next, three solutions were prepared, and each was loaded into an individual spray bottle. Solution 1 contained only the inoculated media. Solution 2 contained inoculated media with 10 mg mL⁻¹ fluorescein sodium salt (Sigma-Aldrich) and 500 μg mL⁻¹ vancomycin hydrochloride (VWR). For the synergism assay, solution 3 contained inoculated media with 1 mg mL⁻¹ Alexa Fluor 594 carboxylic tris(triethylammonium) salt (Invitrogen) and 3.7 μg mL⁻¹ tobramycin (RPI Research Products). For the antagonism assay, tobramycin was replaced with 180 μg mL⁻¹ (S)-N-((3-(3-fluoro-4-morpholinophenyl)-2-oxooxazolidin-5-yl)methyl)acetamide (linezolid, AmBeed). Antibiotics were introduced immediately before loading into a sterilized 3 mL spray bottle (Benecreat) and spraying.

3.3 Droplet generation and imaging

First, we loaded an OmniTrayplate™ with 30 mL of FC-40 (Sigma-Aldrich) and adhered double-sided tape to the non-treated side of each slide. The tape can also be adhered to to OmniTray™ if desired. Six spray scenarios were conducted in parallel, each on a separate treated glass slide: (i) the positive control, which involved only the use of solution 1, (ii, iii) the fluorescence calibration, using only solution 2 or only solution 3, (iv, v) single antibiotic dose response, using either solution 1 and 2 or solution 1 and 3, and (vi) the synergism/antagonism assays, which involved the use of all three solutions (solution 1, 2, and 3). The solutions were sequentially sprayed onto treated glass; each glass piece was sprayed four times from an approximate distance of 20 cm. The number of times each component was sprayed was equal for all components, except for the synergism and antagonism assay where solution 1 was sprayed twice, facilitating the sampling of different dilutions. After spraying, each slide was gently loaded into the oil and adhered to the OmniTray™ with tweezers. The capillary forces between the droplets and the silanized glass prevent droplet movement (Video S1†). Droplets within the desired size range experience less than 10% reduction in volume during the initial 40 seconds at 19 °C and 65% relative humidity, during which one can easily generate three-component droplets and immerse them in oil (Video S5†). The working time can be lengthened by introducing a cooled plate below the sample (Video S6†) or increasing the relative humidity at room temperature. Finally, we placed the lid on the OmniTray™ and secured it on our microscope stage (Nikon Eclipse Ti2) with foam tape to further prevent movement. Fluorescence images were captured using mCherry and GFP filter sets. We did not image droplets around the edge of glass slide because the edges are a less ideal surface, exhibiting more variable contact angles. Initial darkfield images were obtained immediately after droplet generation at chosen positions. Droplets were incubated at 30 °C and imaged at specified positions using darkfield every hour for 8 hours to monitor bacterial growth.

3.4 Image analysis

The image analysis protocol utilized droplet masks generated from the t = 0 darkfield images to measure fluorescence and darkfield intensities. Initial darkfield images were converted into droplet masks using manually selected intensity thresholds. The mask underwent size-based filtering (diameter greater than 150 μm) and circularity filtering (circularity greater than 0.99). The mask was used to assign droplet identification number and measure droplet diameter. The droplet diameter was converted into droplet height by assuming a constant contact angle of 116 degrees. To minimize the effect of aberrations at droplet edges, the droplet mask was modified by reducing droplet radius by 10%. The modified mask was then applied to fluorescence images to calculate average fluorescence intensity for each droplet. The background fluorescence values were obtained using the negative control. The background-subtracted fluorescence intensity values obtained in fluorescence calibration droplets were plotted against droplet height to generate reference curves, with one curve for each fluorophore. The reference curves were used to convert background-subtracted fluorescence intensity of experimental droplets into antibiotic concentrations. The background-subtracted droplet fluorescence intensities were normalized by the droplet diameter and the concentration was inferred by linear interpolation from the reference data.

The modified mask was also applied to time course darkfield images. Since the droplets remain stable over time, the same mask may be used over the entire time course to read out darkfield intensity. The positive control sample (without any antibiotic or fluorophore) was used to generate a reference curve, which plotted the change in darkfield intensity against droplet height. Normalized growth was calculated as the endpoint change in droplet intensity divided by the corresponding endpoint change in intensity of the positive control at the same diameter (Fig. S10†). All analyses were conducted in MATLAB 2021a.

3.5 Antibiotic assays

Dose–response curves were generated from the single antibiotic droplets (comprising either solution 1 and 2 or solution 1 and 3) by fitting Hill equations to the normalized growth plotted against the corresponding antibiotic concentration. We used the Hill function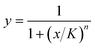 , where x are the calculated antibiotic concentrations and y are the measured normalized intensities. We fit the half-max concentration (K) and the Hill coefficient (n) to our experimental data. The fitted Hill curves were used to calculate hypothetical percent inhibition of combined antibiotics assuming that the antibiotics perform independently; these values are known as the Bliss rate. The synergism/antagonism assays produced data for percent inhibition at different pairwise concentrations; these values were subtracted by the corresponding Bliss rate to generate Bliss scores, a commonly used synergism metric where negative values indicate antagonism and positive values indicate synergism.³⁸

Conclusions

We have developed a rapid, accessible high-throughput platform for combinatorial experimentation and demonstrated its use in detecting antibiotic synergism and antagonism. Unlike many existing microfluidic workflows, this method does not require any specialized equipment for droplet generation. Accessibility can be further enhanced by replacing fluorescence microscopy with color filter sheets and LED excitation or using colorimetric encodings, while throughput can be improved by using a larger glass slide and increasing the number of images per slide. The method can be applied to a variety of combinatorial experiments in materials science, chemistry, and microbiology.

Data availability

Data for this article, including fluorescent and darkfield microscopy images, are available at Zenodo (further details, including links, are provided in a separate document in the ESI†). Supporting MALAB scripts are available on GitHub at https://github.com/RenaFukuda99/High-throughput-combinatorial-droplet-generation-by-sequential-spraying.

Author contributions

Rena Fukuda: conceptualization, methodology, data curation, formal analysis, investigation, visualization, validation, writing – original draft. Nate J. Cira: conceptualization, funding acquisition, project administration, supervision, resources, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

National Science Foundation Graduate Research Fellowship Program (NSF-GRFP, DGE – 2139899).

Notes and references

1. J. Lederberg, A simple method for isolating individual microbes, J. Bacteriol., 1954, 68(2), 258–259.
2. C. A. Salles, A method for the titration of non-viable or slow-growing cultures of bacteria, Rev. Inst. Med. Trop. Sao Paulo, 1964, 6(3), 89–92.
3. C. Ryan, B. T. Nguyen and S. J. Sullivan, Rapid assay for mycobacterial growth and antibiotic susceptibility using gel microdrop encapsulation, J. Clin. Microbiol., 1995, 33(7), 1720–1726.
4. R. Williams, S. G. Peisajovich, O. J. Miller, S. Magdassi, D. S. Tawfik and A. D. Griffiths, Amplification of complex gene libraries by emulsion PCR, Nat. Methods, 2006, 3(7), 545–550.
5. A. D. Griffiths and D. S. Tawfik, Miniaturising the laboratory in emulsion droplets, Trends Biotechnol., 2006, 24(9), 395–402.
6. T. Thorsen, R. W. Roberts, F. H. Arnold and S. R. Quake, Dynamic pattern formation in a vesicle-generating microfluidic device, Phys. Rev. Lett., 2001, 86(18), 4163.
7. B. J. Hindson, K. D. Ness, D. A. Masquelier, P. Belgrader, N. J. Heredia, A. J. Makarewicz, I. J. Bright, M. Y. Lucero, A. L. Hiddessen, T. C. Legler and T. K. Kitano, High-throughput droplet digital PCR system for absolute quantitation of DNA copy number, Anal. Chem., 2011, 83(22), 8604–8610.
8. A. M. Klein, L. Mazutis, I. Akartuna, N. Tallapragada, A. Veres, V. Li, L. Peshkin, D. A. Weitz and M. W. Kirschner, Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells, Cell, 2015, 161(5), 1187–1201.
9. E. Z. Macosko, A. Basu, R. Satija, J. Nemesh, K. Shekhar, M. Goldman, I. Tirosh, A. R. Bialas, N. Kamitaki, E. M. Martersteck and J. J. Trombetta, Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets, Cell, 2015, 161(5), 1202–1214.
10. R. Wilson, A. R. Cossins and D. G. Spiller, Encoded microcarriers for high-throughput multiplexed detection, Angew. Chem., Int. Ed., 2006, 45(37), 6104–6117.
11. R. E. Gerver, R. Gómez-Sjöberg, B. C. Baxter, K. S. Thorn, P. M. Fordyce, C. A. Diaz-Botia, B. A. Helms and J. L. DeRisi, Programmable microfluidic synthesis of spectrally encoded microspheres, Lab Chip, 2012, 12(22), 4716–4723.
12. O. J. Miller, A. E. Harrak, T. Mangeat, J. C. Baret, L. Frenz, B. E. Debs, E. Mayot, M. L. Samuels, E. K. Rooney, P. Dieu and M. Galvan, High-resolution dose–response screening using droplet-based microfluidics, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(2), 378–383.
13. A. Kulesa, J. Kehe, J. E. Hurtado, P. Tawde and P. C. Blainey, Combinatorial drug discovery in nanoliter droplets, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(26), 6685–6690.
14. Z. He, H. Wu, X. Yan and W. Liu, Recent advances in droplet microfluidics for microbiology, Chin. Chem. Lett., 2022, 33(4), 1729–1742.
15. I. C. Clark, K. M. Fontanez, R. H. Meltzer, Y. Xue, C. Hayford, A. May-Zhang, C. D'Amato, A. Osman, J. Q. Zhang, P. Hettige and J. S. Ishibashi, Microfluidics-free single-cell genomics with templated emulsification, Nat. Biotechnol., 2023, 41(11), 1557–1566.
16. W. Feng, E. Ueda and P. A. Levkin, Droplet Microarrays: From Surface Patterning to High-Throughput Applications, Adv. Mater., 2018, 30(20), 1706111.
17. J. Wu, Z. He, Q. Chen and J. M. Lin, Biochemical analysis on microfluidic chips, TrAC, Trends Anal. Chem., 2016, 80, 213–231.
18. B. Rotman, Measurement of activity of single molecules of β-D-galactosidase, Proc. Natl. Acad. Sci. U. S. A., 1961, 47(12), 1981–1991.
19. C. Danielson, G. Pappas, L. Phelps, A. T. Melvin and K. Park, Static microdroplet array generated by spraying and analyzed with automated microscopy and image processing, Anal. Biochem., 2019, 587, 113452.
20. R. H. Dettre and R. E. Johnson Jr, Contact angle hysteresis. IV. Contact angle measurements on heterogeneous surfaces1, J. Phys. Chem., 1965, 69(5), 1507–1515.
21. G. Lippi, G. Lima-Oliveira, G. Brocco, A. Bassi and G. L. Salvagno, Estimating the intra-and inter-individual imprecision of manual pipetting, Clin. Chem. Lab. Med., 2017, 55(7), 962–966.
22. S. Shiri, M. J. Qazi, S. Tan, J. Albo, A. Chen, R. Fukuda, M. S. Jain, M. Menesses, N. Nchinda, G. Ahmed and A. Gallegos, Surface Patterned Omniphobic Tiles (SPOTs): a versatile platform for scalable liquid handling, bioRxiv, 2024, preprint,  DOI:10.1101/2024.01.17.575712.
23. L. Bessemans, V. Jully, C. de Raikem, M. Albanese, N. Moniotte, P. Silversmet and D. Lemoine, Automated gravimetric calibration to optimize the accuracy and precision of TECAN freedom EVO liquid handler, J. Lab. Autom., 2016, 21(5), 693–705.
24. E. E. Councill, N. B. Axtell, T. Truong, Y. Liang, A. L. Aposhian, K. G. Webber, Y. Zhu, Y. Cong, R. H. Carson and R. T. Kelly, Adapting a low-cost and open-source commercial pipetting robot for nanoliter liquid handling, SLAS Technol., 2021, 26(3), 311–319.
25. L. P. Bheemavarapu, M. I. Shah, R. Ramanathan and M. Sivaprakasam, Intelligent pipetting system towards automatic liquid handling applications, in 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), IEEE, 2018, pp. 1–6.
26. W. Postek, T. S. Kaminski and P. Garstecki, A precise and accurate microfluidic droplet dilutor, Analyst, 2017, 142(16), 2901–2911.
27. G. W. Niven, J. S. Morton, T. Fuks and B. M. Mackey, Influence of environmental stress on distributions of times to first division in Escherichia coli populations, as determined by digital-image analysis of individual cells, Appl. Environ. Microbiol., 2008, 74(12), 3757–3763.
28. A. Métris, Y. Le Marc, A. Elfwing, A. Ballagi and J. Baranyi, Modelling the variability of lag times and the first generation times of single cells of E. coli, Int. J. Food Microbiol., 2005, 100(1–3), 13–19.
29. I. Levin-Reisman, O. Gefen, O. Fridman, I. Ronin, D. Shwa, H. Sheftel and N. Q. Balaban, Automated imaging with ScanLag reveals previously undetectable bacterial growth phenotypes, Nat. Methods, 2010, 7(9), 737–739.
30. T. Artemova, Y. Gerardin, C. Dudley, N. M. Vega and J. Gore, Isolated cell behavior drives the evolution of antibiotic resistance, Mol. Syst. Biol., 2015, 11(7), 822.
31. W. Postek, P. Gargulinski, O. Scheler, T. S. Kaminski and P. Garstecki, Microfluidic screening of antibiotic susceptibility at a single-cell level shows the inoculum effect of cefotaxime on E. coli, Lab Chip, 2018, 18(23), 3668–3677.
32. J. W. Chow and L. Y. Victor, Combination antibiotic therapy versus monotherapy for gram-negative bacteraemia: a commentary, Int. J. Antimicrob. Agents, 1999, 11(1), 7–12.
33. World Health Organization, Global Tuberculosis Report 2013, World Health Organization, 2013.
34. M. Cokol, N. Kuru, E. Bicak, J. Larkins-Ford and B. B. Aldridge, Efficient measurement and factorization of high-order drug interactions in Mycobacterium tuberculosis, Sci. Adv., 2017, 3(10), e1701881.
35. R. C. Moellering Jr, Rationale for use of antimicrobial combinations, Am. J. Med., 1983, 75(2), 4–8.
36. A. Zhou, T. M. Kang, J. Yuan, C. Beppler, C. Nguyen, Z. Mao, M. Q. Nguyen, P. Yeh and J. H. Miller, Synergistic interactions of vancomycin with different antibiotics against Escherichia coli: trimethoprim and nitrofurantoin display strong synergies with vancomycin against wild-type E. coli, Antimicrob. Agents Chemother., 2015, 59(1), 276–281.
37. C. Jacqueline, J. Caillon, V. Le Mabecque, A. F. Miègeville, P. Y. Donnio, D. Bugnon and G. Potel, In vitro activity of linezolid alone and in combination with gentamicin, vancomycin or rifampicin against methicillin-resistant Staphylococcus aureus by time–kill curve methods, J. Antimicrob. Chemother., 2003, 51(4), 857–864.
38. C. I. Bliss, The calculation of microbial assays, Bacteriol. Rev., 1956, 20(4), 243–258.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00656a

---