Open Access Article
Open Access ArticleLattice thermal conductivity and phonon properties of polycrystalline graphene
Kunwar
Abhikeern
 and
Amit
Singh
and
Amit
Singh
 *
*
Department of Mechanical Engineering, IIT Bombay, Mumbai, Maharashtra, India 400076. E-mail: kunwarabhikeern@iitb.ac.in; amit.k.singh@iitb.ac.in
First published on 6th December 2024
Abstract
Using the spectral energy density method, we predict the phonon scattering mean lifetimes of polycrystalline graphene (PC-G) having polycrystallinity only along the x-axis with seven different misorientation (tilt) angles at room temperature. Contrary to other studies on PC-G samples, our results indicate a strong dependence of the thermal conductivity (TC) on the tilt angles which we attribute to careful preparation of our grain boundaries-based samples without introducing any local strains and ensuring periodic boundary conditions for the supercells along the x and y axes. We also show that the square of the group velocity components along x and y axes and the phonon lifetimes are uncorrelated and the phonon density of states are almost the same for all samples with different tilt angles. Further, a distribution of the group velocity component along x or y axis as function of normal frequency is found to be exponentially decaying whereas that of the phonon lifetime showed piecewise constant function behavior with respect to the frequency. We provide parameters for these distribution functions and suggest another measure of the TC based on these distributions. Finally, we perform a size-dependent analysis for two tilt angles, 21.78° and 32.20°, and find that bulk TC components decrease by around 34% to 62% in comparison to the bulk TC values of the pristine graphene. Our analysis reveals intriguing insights into the interplay between grain orientation, phonon scattering and thermal conductivity in graphene.
1 Introduction
The computational and experimental thermal conductivity (TC) of single and bilayer graphene systems has received significant attention over the years.1 However, one crucial aspect often overlooked is the influence of grain boundaries (GBs) on the TC of polycrystalline graphene (PC-G), with some notable exceptions.Experimentally, it has been found that the TC of PC-G increases with increases in grain size. Ma et al.2 reported that the TC exponentially increased from almost 610 to 5230 W m−1 K−1 at room temperature as the grain size increased from almost 200 nm to 10 μm. Similarly, Woomin Lee et al.3 found the in-plane TC in the temperature range from 320 K to 510 K to be 680–340, 1890–1020 and 2660–1230 W m−1 K−1 for average grain sizes of 0.5, 2.2, and 4.1 μm, respectively. Dongmok Lee et al.4 measured significantly smaller TCs (412–572 W m−1 K−1) for PC-G samples with reduced grain sizes of less than 1 μm. They also showed almost no dependence on misorientation (tilt) angles of GBs for the TCs of PC-G samples whereas there was strong dependence on misorientation angles for bicrystalline graphene (BC-G) samples.
Numerically, one of the earliest studies to investigate the GB effect on the TCs of PC-G samples was done by Bagri et al.,5 who performed reverse nonequilibrium molecular dynamics simulations with a modified Tersoff interatomic potential on tilt GBs-based graphene samples with misorientation angles 5.5°, 13.2° and 21.7°, and estimated the bulk TCs to be around 2220, 2380 and 2380 W m−1 K−1, respectively, thereby showing a very weak dependence on the misorientation angles. They also calculated boundary conductance (inverse of Kapitza resistance) which decreased with increase in misorientation angles. Following a nonequilibrium Green's function approach, Serov et al.6 showed a strong increasing dependence of the TCs of PC-G samples on grain sizes ranging from close to 1 nm to 1000 nm at room temperature, for which the TCs vary from close to 100 W m−1 K−1 to 550 W m−1 K−1. However, the dependence on the misorientation angle was found to be negligible. In another study, using a REBO potential for the interatomic potential and the Green–Kubo method for the calculation of the TC, Mortazavi et al.7 prepared PC-G samples with average grain sizes from 1 nm to 5 nm and found the TCs of PC-G samples to be one order of magnitude smaller than that of pristine graphene. With the same REBO potential and approach-to-equilibrium molecular dynamics simulations, Hahn et al.8 estimated the bulk TC of PC-G with an average grain size of 1 nm as 26.6 W m−1 K−1 at 300 K, which was almost 3% of the crystalline sample. The presence of GBs significantly decreased the estimated mean free path from 451 nm for crystalline graphene to around 30 nm for PC-G, which suggested increased scattering of phonons with GBs. With the help of the Green–Kubo method and optimized Tersoff potential, Liu et al.9 showed that the TC decreases exponentially with increasing GB energy for PC-G samples.
With the help of the nonequilibrium molecular dynamics (NEMD) method,10 another set of computational works11–13 on BC-G samples show strong dependence of the tilt angle and average density defects along the GB on the Kapitza resistance. In a detailed comprehensive NEMD based study, Fox et al.14 performed simulations on bicrystalline graphene nanoribbons (bi-GNR)† for a wide range of tilt angles (θ) under arbitrary in-plane thermal loading directions (ϕ). They showed that the TCs decrease from 0° to 32.2° tilt angles and then increase almost symmetrically up to 60° tilt angles. Having done the size-dependent analysis for ϕ = 10°, they calculated the bulk TCs for θ = 9.4°, 32.2°, 44.8° and found them to be close to 416, 312 and 476 W m−1 K−1, respectively. This dependence on misorientation angles is similar to the experimental work done by Dongmok Lee et al.4 for BC-G samples. Using a similar NEMD method, another study found that 10.98° BC-G displays anomalous higher TC compared to other misorientation angles,15 which was not observed by Fox et al.14 In both works, it has been established that the TC is inversely proportional to the dislocation density of the GB. In a recent NEMD based work done by Tong et al.,16 where the heat flux was calculated with the incorrect thermostat work done method,1 which overestimates the TC value in comparison to that obtained by a more consistent Irving–Kirkwood based calculation of heat flux, the TCs of BC-G samples were found to first decrease with the tile angle from 0° to 13.18°, but then contrary to Fox et al.14 was shown to have increased for the 21.78° tilt angle.
These works mostly focus upon the calculation of the TCs of PC-G or BC-G samples using Green–Kubo or NEMD approaches10,17 and show that the TCs increase with increasing grain size. The TC of BC-G depends upon the misorientation angle,4,9,14,15 however, the dependence has been found to be weak for PC-G samples.5,6 The NEMD-based works also explore the effect of GBs and misorientation angles on the Kapitza conductance and some studies have also been able to capture the dependence on GB energy and dislocation density, however, none of these works investigate the microstructural properties of the TC of PC-G samples such as phonon mean lifetimes and group velocities of different phonon modes in detail. We found only one study done by Tong et al.16 which discusses the contribution of phonon lifetimes and group velocities, obtained from the Spectral Energy Density (SED) method and the lattice dynamics, respectively, for the GBs with three different misorientation angles, θ = 4.41°, 13.18°, 21.78°, however, the treatment and the discussion remain brief. Moreover, the sample preparation does not seem to have followed proper procedures to maintain stable dislocation core structure.18 The study also adopts the alternative phonon SED Φ′19 approach for the extraction of spectral phonon relaxation times which does not involve eigenvectors and, therefore, does not represent the phonon spectral energy19 accurately. Further, the calculation of phonon lifetimes and group velocities has been performed for polycrystalline samples because the SED method assumes periodicity along all three coordinate axes, however, they have been cited as supporting evidences for the TCs of B-CG samples obtained by the NEMD method.
In the present work, we study the thermal transport in polycrystalline graphene samples with polycrystallinity only along the x-axis (xPC-G samples) with the help of the robust and consistent normal mode decomposition (NMD) analysis-based SED method.1,20 These samples cannot be categorized under the categories of BC-G samples or randomly oriented PC-G samples in the references cited above. First, almost similar size samples with seven different symmetric misorientation angles and stable dislocation cores are prepared and then the phonon properties and the TC tensor components, kxx and kyy, are calculated for each sample. A pristine graphene sample of the same size is also studied for comparison. This is followed by a size-dependent analysis of thermal transport for pristine graphene and xPC-G samples with two different misorientation angles, 21.78° and 32.2°, so that bulk TCs of graphene with GBs of different misorientations can be compared. Contrary to other works on PC-G samples cited above, our work establishes a strong dependence of the TCs of xPC-G samples on misorientation angles. It might be the case that Bagri et al.5 and Serov et al.6 found weak dependence of the TCs on misorientation angles because the grains in their samples might have been experiencing local strains. We ensure that our samples do not have any local strains for the commensurate grain boundaries generated by the centroidal Voronoi tessellation (CVT) based algorithm.21 The local strain can change the behavior of the thermal transport in 2D materials and appropriate strains and disorders can be chosen to decrease the TC of any system.22–24 We also ensure that the supercells of all our samples satisfy the periodic boundary conditions, which might not be the case for some of these previous studies.5,6
The structure of the paper is as follows. Section 2 describes the sample preparation method for the xPC-G samples with different misorientation angles. In Section 3, we perform the MD simulations necessary for the SED analysis. We discuss the results in Section 4 after calculating the phonon group velocities with the help of the harmonic lattice dynamics-based GULP package and phonon lifetimes by fitting the SED curves to the Lorentzian function. In this section, we also obtain the bulk TCs of three graphene systems with the SED method. Finally, we conclude in Section 5 with a summary and suggestions for any future work.
2 Sample preparation
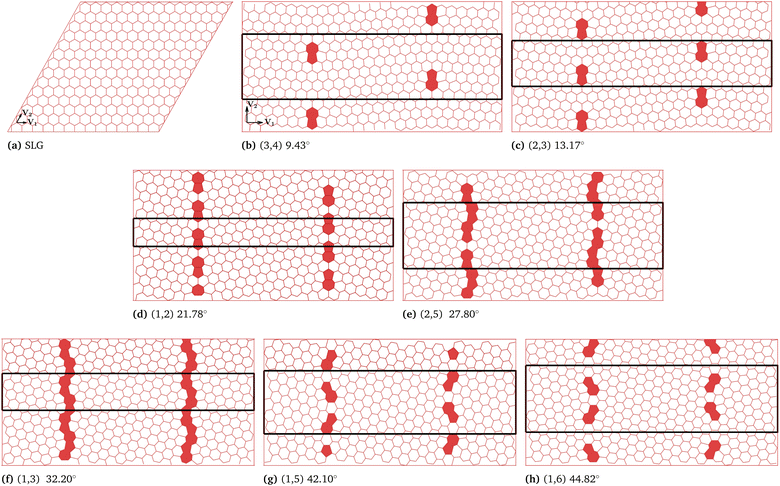
We follow the CVT based algorithm proposed by Ophus et al.21 to generate symmetric GBs in graphene. We prepare xPC-G samples with seven different misorientation angles, where each misorientation angle θ = θL + θR can be defined through translation vectors (nL, mL) and (nR, mR) corresponding to the left and the right domains along the GB, respectively.25 For symmetric GBs, we have nL = nR = n, mL = mR = m,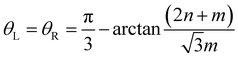 and n and m are integers.21,25 The corresponding periodic length along the GB direction is
and n and m are integers.21,25 The corresponding periodic length along the GB direction is 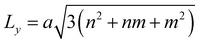 , where the average C–C bond length a = 1.397 Å. Following Yazyev and Louie,26 the simulation supercell for the SED method, involving two parallel equally spaced GBs, is rectangular of length Lx and width Ly in order to satisfy periodic boundary conditions (PBCs). This means the unit cell vectors, V1 = Lxî and V2 = Lyĵ, of the supercell are orthogonal to each other, where î and ĵ are unit vectors in the Cartesian plane. Although close to Lx = 4 nm is sufficient to maintain stable GB structures, since this significantly reduces the influence of elastic interactions due to neighbouring GBs,18,26 we have taken Lx = 6 nm for all our samples. Thus, two neighbouring GBs are separated by 3 nm, which also becomes the grain size along x-axis. The superunit cells for (n, m) xPC-G samples with different misorientation angles θ have been shown in Fig. 1b–h. The primitive unit cell of the pristine graphene (1, 1) sample is created by two planar lattice vectors
, where the average C–C bond length a = 1.397 Å. Following Yazyev and Louie,26 the simulation supercell for the SED method, involving two parallel equally spaced GBs, is rectangular of length Lx and width Ly in order to satisfy periodic boundary conditions (PBCs). This means the unit cell vectors, V1 = Lxî and V2 = Lyĵ, of the supercell are orthogonal to each other, where î and ĵ are unit vectors in the Cartesian plane. Although close to Lx = 4 nm is sufficient to maintain stable GB structures, since this significantly reduces the influence of elastic interactions due to neighbouring GBs,18,26 we have taken Lx = 6 nm for all our samples. Thus, two neighbouring GBs are separated by 3 nm, which also becomes the grain size along x-axis. The superunit cells for (n, m) xPC-G samples with different misorientation angles θ have been shown in Fig. 1b–h. The primitive unit cell of the pristine graphene (1, 1) sample is created by two planar lattice vectors 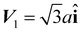 and
and 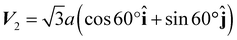 , as shown in Fig. 1a.
, as shown in Fig. 1a.
3 Computational details
Now we reiterate some basic principles of the SED method which has been explained in details in Abhikeern and Singh.1 Based on the Fourier's law and the phonon Boltzmann transport equation (BTE) under the relaxation time approximation, the TC tensor of a system is given by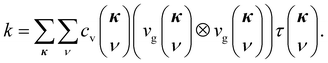 | (1) |
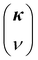 is denoted by wavevector κ and dispersion branch ν. Moreover,
is denoted by wavevector κ and dispersion branch ν. Moreover, 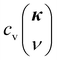 ,
, 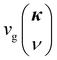 and
and 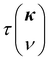 are the mode specific volumetric specific heat, group velocity and phonon lifetime, respectively. We now explain how we calculate these three physical quantities. We take
are the mode specific volumetric specific heat, group velocity and phonon lifetime, respectively. We now explain how we calculate these three physical quantities. We take 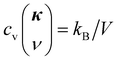 20 for all modes for classical MD simulations, where kB is the Boltzmann's constant and V is the volume of the simulation box. The group velocity
20 for all modes for classical MD simulations, where kB is the Boltzmann's constant and V is the volume of the simulation box. The group velocity 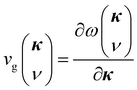 is obtained by using finite difference method over a fine grid of wavevectors around the given mode
is obtained by using finite difference method over a fine grid of wavevectors around the given mode 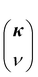 . The GULP package27 is used for calculating the normal mode frequencies
. The GULP package27 is used for calculating the normal mode frequencies 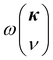 and the corresponding eigenvectors. The phonon lifetime for a mode is calculated by fitting a Lorentzian function over the SED curve, which is determined by the normal mode decomposition method by projecting the equilibrium MD simulation-based atomic positions and velocities onto the normal mode coordinates.1
and the corresponding eigenvectors. The phonon lifetime for a mode is calculated by fitting a Lorentzian function over the SED curve, which is determined by the normal mode decomposition method by projecting the equilibrium MD simulation-based atomic positions and velocities onto the normal mode coordinates.1
We describe the simulation details below. The primitive superunit cell for the (n, m) structure is repeated Nx and Ny times along x and y axes, respectively, to construct a sample of the required size. To ensure the lowest possible energy state for the GB, we first perform energy minimization over this structure with PBCs along all axes, where the C–C interactions are modeled by the original REBO potential.28 The equilibrium MD simulation is then performed with multiple MD runs where MD time step was taken as ΔtMD = 0.2 fs. In the first run, atoms are simulated under NPT ensemble conditions with zero pressure and 300 K temperature for 2 × 105 MD steps. The next run is performed under NVT conditions with 300 K for 2 × 105 MD steps. The Nosé–Hoover chain thermostats are used for these NPT and NVT runs. The final run is performed for another 216 MD time steps under NVE conditions to ensure steady-state conditions without any corrupting influence of thermostats. The package LAMMPS29 is used for all MD simulations and energy minimization. For a given sample, the SEDs are calculated for all allowable1,20 normal modes in the first BZ. Five different MD simulations with different initial atomic velocities are considered so that an average of SEDs for all simulations can be taken for the extraction of the phonon lifetime for a given mode. Then, we consider only the first quadrant of the hexagonal BZ for SLG and rectangular BZ for xPC-G samples to exploit both the symmetry of the BZ and the simplicity in the discretization of the BZ.1,30 The SEDs of the allowable modes in the first quadrant of the first BZ and its symmetric copies in other quadrants are finally averaged over.
4 Results and discussion
Using the primitive superunit cells defined above, we prepare same-size pristine graphene and seven xPC-G samples with different θ corresponding to (n, m) translation vectors. In order to achieve an approximate size of 180 × 32 Å2, the number of unit cells required along x and y axes, Nx and Ny, respectively, for different (n, m) samples has been listed in Table 1. The table also mentions the superunit cell length Ly along y-axis and the number of atoms per superunit cell for each sample.| θ | (n, m) | L y (Å) | Unit cell atoms | (Nx, Ny) |
|---|---|---|---|---|
| 0 | (1, 1) | 2.10 | 2 | (73, 14) |
| 9.43 | (3, 4) | 14.71 | 344 | (3, 2) |
| 13.17 | (2, 3) | 10.55 | 248 | (3, 3) |
| 21.78 | (1, 2) | 6.40 | 152 | (3, 5) |
| 27.80 | (2, 5) | 15.11 | 356 | (3, 2) |
| 32.20 | (1, 3) | 8.72 | 204 | (3, 4) |
| 42.10 | (1, 5) | 13.47 | 320 | (3, 2) |
| 44.82 | (1, 6) | 15.86 | 372 | (3, 2) |
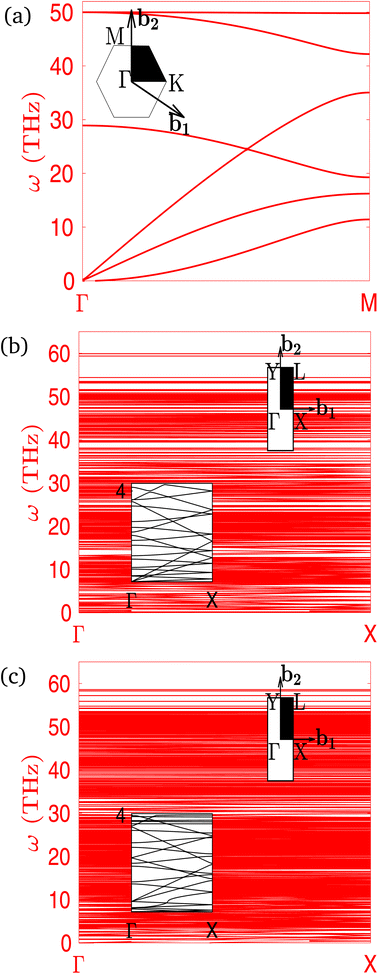
Based on their respective primitive unit and superunit cells, we first show the phonon dispersion curves in Fig. 2 for the pristine (1, 1) graphene and (1, 2) and (1, 3) xPC-G samples with 21.78° and 32.20° misorientation angles. In Fig. 2a we show the dispersion curve for the pristine SLG sample, whereas the dense dispersion curves in Fig. 2b and c reflect a large number of unit cell atoms, 152 and 204, respectively, for 21.78° and 32.20° xPC-G samples. In order to improve clarity, insets in Fig. 2b and c show the zoomed-in area of the same dispersion curves with the upper limit of frequency constrained to 4 THz. Similar to Diery et al.,31 we also obtain some high-frequency flat phonon branches. We also show the respective BZs in another set of insets in Fig. 2a–c, where the shaded area refers to the first quadrant used for discretization of the BZs so that symmetry of the BZs can be exploited.1,30
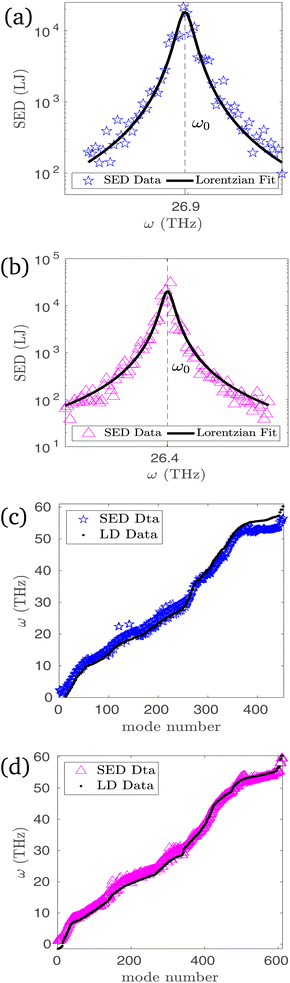
For all our samples, we obtain excellent Lorentzian fits for the SED curves. We particularly show the Lorentzian curve fitting over the SED data in Fig. 3a and b for 21.78° and 32.20° xPC-G samples respectively for a chosen wavevector κ = [π/6a, 0, 0] and one of the optical dispersion branches. The fitting provides not only the phonon lifetime τ but also the anharmonic frequency ω0 as the center of the Lorentzian fit over the SED curve. These anharmonic frequencies match closely with the harmonic lattice dynamics (GULP) based frequencies. For illustration, we provide excellent match for all available modes for a given wavevector κ around the “X” point as shown in Fig. 3c and d for 21.78° and 32.20° angles, respectively. Hence, it is established that the harmonic frequencies are a good approximation for the vibrational modes at room temperature.
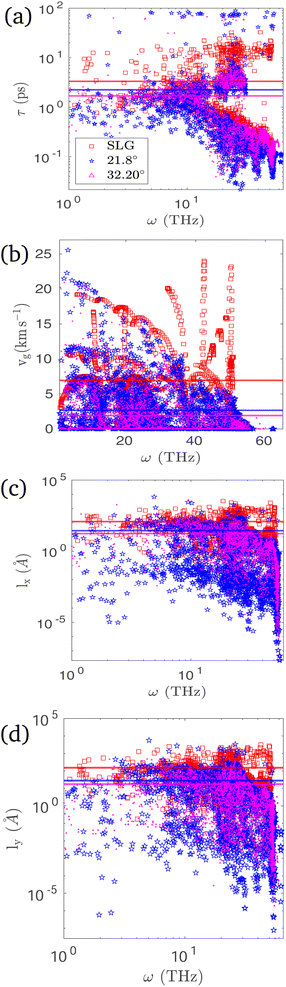
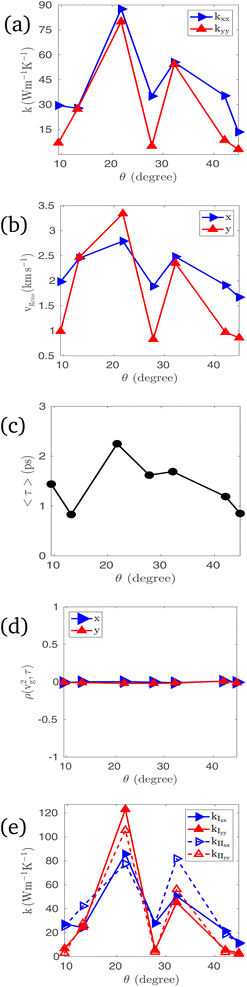
The phonon lifetimes (τ), group velocities 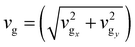 and mean free paths along x and y axes, lx = vgxτ and ly = vgyτ, obtained for the allowable modes in the first quadrant of the first BZs of pristine graphene and two xPC-G samples with θ = 21.78° and 32.20° have been shown in Fig. 4. With a total of 1533, 1710 and 1836 modes for these three systems, respectively, it makes more sense to talk about root mean square (rms) of group velocities vgrms, average of phonon lifetimes 〈τ〉 and average of mean free paths, 〈lx〉 and 〈ly〉, rather than individual acoustic or optical modes, where the average is taken over all available modes in the first quadrant of the first BZ. We obtain 〈τ〉 = 3.33, 2.25, 1.69 ps, vgrms = 6.93, 2.67, 1.91 km s−1, 〈lx〉 = 121.1, 27.7, 17.3 Å and 〈ly〉 = 152.1, 28.0, 17.5 Å, respectively, for three systems shown in Fig. 5 with solid horizontal lines. Later, we also show x and y components of vgrms in Fig. 5b and 〈τ〉 in Fig. 5c for all angles. We note that average mean free paths are less than the grain size along x-axis (30 Å) for xPC-G samples. We also observe that around 90% of the phonon modes have mean free paths less than 30 Å along both x and y axes for all seven different misorientation angles. This was expected for lx since phonons would scatter at the GBs, however, ly also showing similar trend is an interesting result.
and mean free paths along x and y axes, lx = vgxτ and ly = vgyτ, obtained for the allowable modes in the first quadrant of the first BZs of pristine graphene and two xPC-G samples with θ = 21.78° and 32.20° have been shown in Fig. 4. With a total of 1533, 1710 and 1836 modes for these three systems, respectively, it makes more sense to talk about root mean square (rms) of group velocities vgrms, average of phonon lifetimes 〈τ〉 and average of mean free paths, 〈lx〉 and 〈ly〉, rather than individual acoustic or optical modes, where the average is taken over all available modes in the first quadrant of the first BZ. We obtain 〈τ〉 = 3.33, 2.25, 1.69 ps, vgrms = 6.93, 2.67, 1.91 km s−1, 〈lx〉 = 121.1, 27.7, 17.3 Å and 〈ly〉 = 152.1, 28.0, 17.5 Å, respectively, for three systems shown in Fig. 5 with solid horizontal lines. Later, we also show x and y components of vgrms in Fig. 5b and 〈τ〉 in Fig. 5c for all angles. We note that average mean free paths are less than the grain size along x-axis (30 Å) for xPC-G samples. We also observe that around 90% of the phonon modes have mean free paths less than 30 Å along both x and y axes for all seven different misorientation angles. This was expected for lx since phonons would scatter at the GBs, however, ly also showing similar trend is an interesting result.
Having obtained all phonon properties, we use eqn (1) to obtain the TC tensor components kxx ≈ 87, 29, 28, 88, 35, 56, 25, 14 W m−1 K−1 and kyy ≈ 80, 7, 27, 80, 5, 54, 9, 3 W m−1 K−1 for pristine graphene and seven different misorientation angles listed in Table 1 in increasing order. With respect to the pristine graphene, the maximum reduction in the TCs is found in the last sample with 44.82° angle, almost 84% and 96% reduction for kxx and kyy, respectively. As reflected in the values and also shown in Fig. 5a, the TCs strongly depend upon the misorientation angles. We also note that except for samples with 13.17° and 32.2° tilt angles, there exists strong anisotropy along x and y axes in the TCs for other angles. Also, the TC for the 21.78° sample is the highest among all xPC-G samples. These trends in TCs can be explained in terms of the trends in the group velocities and the phonon lifetimes, which were found to be uncorrelated for all xPC-G samples. Since 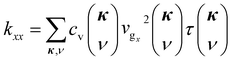 , and we have taken
, and we have taken 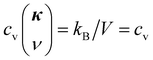 for all modes, hence, the average of kxx over all n modes in the first BZ can be written as
for all modes, hence, the average of kxx over all n modes in the first BZ can be written as 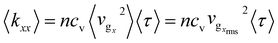 , provided that correlation coefficient ρ of vgx2 and τ for all modes is close to zero. The similar argument holds for 〈kyy〉. The averages of the TCs defined in this way are denoted as 〈kxx〉I and 〈kyy〉I. We calculate ρ(vgx2, τ) and ρ(vgy2, τ) and plot them for all angles in Fig. 5d. All correlation coefficients were found to be in the range of 0.2–1.9%, i.e. they are close to zero. This suggests that group velocities and phonon lifetimes are uncorrelated for all xPC-G samples. We obtain 〈kxx〉I ≈ 27, 24, 86, 28, 50, 21, 12 W m−1 K−1 and 〈kyy〉I ≈ 7, 25, 123, 5, 45, 6, 3 W m−1 K−1 for the seven different angles in increasing order. They are also plotted in Fig. 5e and we observe that the values closely match with actual kxx and kyy values reported earlier, except for 21.78° sample for which 〈kyy〉I = 123 W m−1 K−1 whereas kyy = 80 W m−1 K−1, i.e. an increase of around 54% is found. This deviation can be attributed to the 21.78° sample having a slightly higher ρ(vgy2, τ) and the highest
, provided that correlation coefficient ρ of vgx2 and τ for all modes is close to zero. The similar argument holds for 〈kyy〉. The averages of the TCs defined in this way are denoted as 〈kxx〉I and 〈kyy〉I. We calculate ρ(vgx2, τ) and ρ(vgy2, τ) and plot them for all angles in Fig. 5d. All correlation coefficients were found to be in the range of 0.2–1.9%, i.e. they are close to zero. This suggests that group velocities and phonon lifetimes are uncorrelated for all xPC-G samples. We obtain 〈kxx〉I ≈ 27, 24, 86, 28, 50, 21, 12 W m−1 K−1 and 〈kyy〉I ≈ 7, 25, 123, 5, 45, 6, 3 W m−1 K−1 for the seven different angles in increasing order. They are also plotted in Fig. 5e and we observe that the values closely match with actual kxx and kyy values reported earlier, except for 21.78° sample for which 〈kyy〉I = 123 W m−1 K−1 whereas kyy = 80 W m−1 K−1, i.e. an increase of around 54% is found. This deviation can be attributed to the 21.78° sample having a slightly higher ρ(vgy2, τ) and the highest 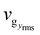 . But in general, we can assert that 〈kxx,yy〉 = 〈kxx,yy〉I ≈ kxx,yy and it can be emphasized that an average phonon mode can be defined whose group velocity components along the x and y axes are the rms of group velocity components of all phonon modes and whose lifetime is the average of all phonon lifetimes. Therefore, anisotropy in the TC components is largely the outcome of anisotropy in the group velocities, since lifetimes remain the same for both xx and yy components of the TC. The maxima and minima of the TC components across all angles, however, have to explained both in terms of the maxima and minima of x and y components of vgrms and also those of 〈τ〉.
. But in general, we can assert that 〈kxx,yy〉 = 〈kxx,yy〉I ≈ kxx,yy and it can be emphasized that an average phonon mode can be defined whose group velocity components along the x and y axes are the rms of group velocity components of all phonon modes and whose lifetime is the average of all phonon lifetimes. Therefore, anisotropy in the TC components is largely the outcome of anisotropy in the group velocities, since lifetimes remain the same for both xx and yy components of the TC. The maxima and minima of the TC components across all angles, however, have to explained both in terms of the maxima and minima of x and y components of vgrms and also those of 〈τ〉.
Next, we express group velocity and phonon lifetime as distribution functions of normal mode frequencies so that the TC components can also be written as distribution functions of frequencies. This can potentially help in the semi-analytical and numerical solutions of the BTE.32 For that, we first show the phonon density of states (DOS) in Fig. 6a, where DOS(ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dω represents the number of modes lying between ω and ω + dω. We observe that the DOS remains almost the same for all GB angles.11 This is followed by calculating the sum of vgrms along x axis for all modes lying in the frequency range [ω, ω + dω) and then dividing by the total number of modes in the same range, which we denote as
dω represents the number of modes lying between ω and ω + dω. We observe that the DOS remains almost the same for all GB angles.11 This is followed by calculating the sum of vgrms along x axis for all modes lying in the frequency range [ω, ω + dω) and then dividing by the total number of modes in the same range, which we denote as 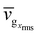 . Similarly, we define
. Similarly, we define 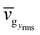 and
and 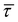 for vgrms along y axis and τ, respectively. Basically, they are distribution functions of ω and can be treated as average properties of phonons in [ω, ω + dω). For any given angle, we find that natural semi-log plots of
for vgrms along y axis and τ, respectively. Basically, they are distribution functions of ω and can be treated as average properties of phonons in [ω, ω + dω). For any given angle, we find that natural semi-log plots of 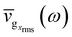 and
and 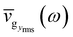 can be fitted with straight lines as shown in Fig. 6b and c, respectively, and the natural semi-log plot of
can be fitted with straight lines as shown in Fig. 6b and c, respectively, and the natural semi-log plot of 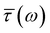 can be fitted with a piecewise constant function in Fig. 6d. Therefore, we can write,
can be fitted with a piecewise constant function in Fig. 6d. Therefore, we can write,
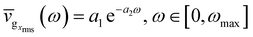 | (2a) |
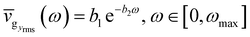 | (2b) |
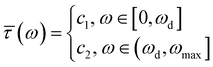 | (2c) |
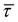 emerges and ωmax is the maximum frequency beyond which the phonon properties can be assumed as zero. Interestingly, we find that ωd = 32 THz and ωmax = 52 THz are the same for all xPC-G samples. The values of the constants appearing in eqn (4) for different misorientation angles are provided in Table 2. Based on this, we calculate another measure of the TC components as
emerges and ωmax is the maximum frequency beyond which the phonon properties can be assumed as zero. Interestingly, we find that ωd = 32 THz and ωmax = 52 THz are the same for all xPC-G samples. The values of the constants appearing in eqn (4) for different misorientation angles are provided in Table 2. Based on this, we calculate another measure of the TC components as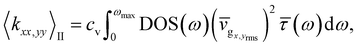 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6 kxx,yy.
0.6 kxx,yy.
 | ||
Fig. 6 (a) DOS of different misorientation angles (θ in degrees). Semi-log plot of (b) 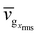 , (c) , (c) 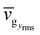 , (d) , (d) 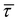 for all xPC-G samples of size close to 180 × 32 Å2. for all xPC-G samples of size close to 180 × 32 Å2. | ||
| θ | a 1 | a 2 | b 1 | b 2 | c 1 | c 2 |
|---|---|---|---|---|---|---|
| 9.43 | 2.182 | 0.033 | 0.554 | 0.012 | 1.704 | 0.311 |
| 13.17 | 3.360 | 0.035 | 2.020 | 0.012 | 1.170 | 0.171 |
| 21.78 | 2.735 | 0.027 | 2.534 | 0.010 | 2.654 | 0.259 |
| 27.80 | 2.094 | 0.040 | 0.605 | 0.019 | 2.298 | 0.260 |
| 32.20 | 3.031 | 0.035 | 1.992 | 0.016 | 2.550 | 0.205 |
| 42.10 | 2.282 | 0.045 | 0.768 | 0.023 | 1.624 | 0.197 |
| 44.82 | 1.699 | 0.033 | 0.663 | 0.023 | 1.115 | 0.222 |
The TCs obtained through the SED method are size-dependent.1 A size-dependent analysis is performed for xPC-G samples with θ = 21.78° and 32.20° by increasing the number of primitive superunit cells along the y-axis, Ny, but keeping Nx same because we reason that the x-axis length, around 18 nm, is too large to significantly affect the TC components if we further increase Nx. In ref. 1, we calculated the TC for SLG up to 50 Å in length along the x-axis, and the TC deviated from the bulk value by only 10%. We chose these two angles because they have the least number of basis atoms in comparison to the xPC-G samples with other misorientation angles, specifically, 152 for 21.78° and 204 for 32.20°, which makes the computation more tractable. We take Ny = 5, 6, 7, 8 and 9 for the 21.78° samples and Ny = 4, 6, 7 and 8 for the 32.20° samples. The results for TC components kxx and kyy are shown in Fig. 7. Following ref. 1, we perform a linear fit between kxx,yy and 1/Ny and then extrapolate the linear curve to obtain the bulk TC (kxx,yy∞). We calculate kxx∞ = 369 and 320 W m−1 K−1, and kyy∞ = 488 and 327 W m−1 K−1 for θ = 21.78° and 32.20°, respectively. The bulk TC values for 32.20° match closely with Fox et al.14 who calculated around 312 W m−1 K−1 for 32.20° BC-G samples with the NEMD method. For the pristine graphene studied here, kxx∞ = 563 and kyy∞ = 863 W m−1 K−1. Therefore, kxx∞ decreased by 34% and 43% and kyy∞ decreased by 43% and 62%, respectively, for the two angles with respect to the pristine graphene. We also note that the 32.20° sample does not show much anisotropy in the bulk TC components whereas the 21.78° sample shows strong anisotropy.
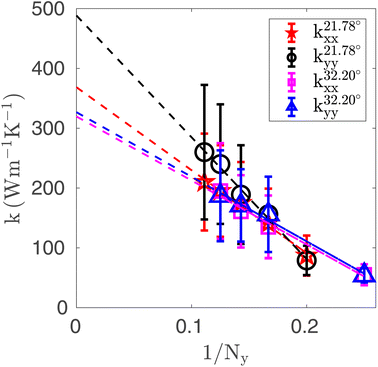 | ||
| Fig. 7 Size dependency of the TCs of the xPC-G samples with θ = 21.78° and θ = 32.20°. The dashed lines are showing the extrapolation to the y-axis to obtain the bulk TC. | ||
5 Conclusion
In conclusion, we predict the phonon properties of xPC-G samples with seven different misorientation angles with equilibrium MD simulations and the SED method. Our work concludes that the TCs of xPC-G samples strongly depend upon misorientation angles. We also find that the square of the group velocity components along x and y axes and the phonon lifetimes are uncorrelated for all samples, which allows for the calculation of TCs in terms of an average phonon mode whose group velocity components are the rms of group velocity components of all phonon modes and lifetime is the mean of all phonon lifetimes. We explain anisotropy in the TC components for some angles with the difference in the rms of group velocity components of all phonon modes along x and y axes. Further, the DOS for all xPC-G samples are found to be independent of the misorientation angles. Based on the DOS, distribution functions of phonon properties have been calculated and plotted as semi-log plots against the phonon normal frequencies. The distributions of group velocity components are found to be exponentially decaying whereas the distributions of phonon lifetimes showed piecewise constant function behavior with respect to frequency. This is reflected in the distribution of the TC components, which also show exponentially decaying behavior against frequency. We provide the parameters for the exponential and piecewise constant functions for the group velocity components and lifetimes, respectively. We provide another measure of the TC based on these functions and estimate that their values are within ±60% range of the actual TC values. Finally, we perform the size-dependent analysis for two angles, 21.78° and 32.20°, and calculated their bulk TC components, which are found to have decreased by 34% to 62% in comparison to the bulk TC values of the pristine graphene. We end with a suggestion that the frequency dependent distribution functions suggested for the rms of group velocity components and the phonon lifetime can be used in multiscale semi-analytical and numerical solutions for the solutions of the BTE.Data availability
The NMD codes for this article are available on GitHub at https://github.com/k-abhikeern/Paper02_GB/tree/master, which are used to calculate the thermal conductivity of a polycrystalline graphene sample.Author contributions
Kunwar Abhikeern: conceptualization, methodology, visualization, software, investigation, and writing – original draft. Amit Singh: conceptualization, methodology, project administration, supervision, and writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Department of Science & Technology, India under the SERB grant MTR/2021/000550. Authors gratefully acknowledge the financial supports and the computing resources of IIT Bombay. Views expressed in this paper are those of the authors and neither of their affiliated institution nor of the funding agencies.Notes and references
- K. Abhikeern and A. Singh, J. Appl. Phys., 2023, 134, 224305 CrossRef CAS.
- T. Ma, Z. Liu, J. Wen, Y. Gao, X. Ren, H. Chen, C. Jin, X.-L. Ma, N. Xu and H.-M. Cheng, Nat. Commun., 2017, 8, 14486 CrossRef CAS.
- W. Lee, K. D. Kihm, H. G. Kim, S. Shin, C. Lee, J. S. Park, S. Cheon, O. M. Kwon, G. Lim and W. Lee, Nano Lett., 2017, 17, 2361–2366 CrossRef CAS.
- D. Lee, S. Lee, B.-S. An, T.-H. Kim, C.-W. Yang, J. W. Suk and S. Baik, Chem. Mater., 2017, 29, 10409–10417 CrossRef CAS.
- A. Bagri, S.-P. Kim, R. S. Ruoff and V. B. Shenoy, Nano Lett., 2011, 11, 3917–3921 CrossRef CAS PubMed.
- A. Y. Serov, Z.-Y. Ong and E. Pop, Appl. Phys. Lett., 2013, 102, 033104 CrossRef.
- B. Mortazavi, M. Potschke and G. Cuniberti, Nanoscale, 2014, 6, 3344–3352 RSC.
- K. R. Hahn, C. Melis and L. Colombo, Carbon, 2016, 96, 429–438 CrossRef CAS.
- H. Liu, Y. Lin and S. Luo, J. Phys. Chem. C, 2014, 118, 24797–24802 CrossRef CAS.
- A. Singh and E. B. Tadmor, J. Comput. Phys., 2015, 299, 667–686 CrossRef CAS.
- A. Cao and J. Qu, J. Appl. Phys., 2012, 111, 053529 CrossRef.
- Y. Zhang, Y. Cheng, Q. Pei, C. Wang and Y. Xiang, Phys. Lett. A, 2012, 376, 3668–3672 CrossRef CAS.
- K. Azizi, P. Hirvonen, Z. Fan, A. Harju, K. R. Elder, T. Ala-Nissila and S. M. V. Allaei, Carbon, 2017, 125, 384–390 CrossRef CAS.
- A. Fox, U. Ray and T. Li, J. Appl. Phys., 2019, 125, 015101 CrossRef.
- T.-H. Liu, S.-C. Lee, C.-W. Pao and C.-C. Chang, Carbon, 2014, 73, 432–442 CrossRef CAS.
- Z. Tong, A. Pecchia, C. Yam, T. Dumitrică and T. Frauenheim, Adv. Sci., 2021, 8, 2101624 CrossRef CAS.
- A. Singh and E. B. Tadmor, J. Appl. Phys., 2015, 117, 185101 CrossRef.
- X. Blase, K. Lin, A. Canning, S. Louie and D. Chrzan, Phys. Rev. Lett., 2000, 84, 5780 CrossRef CAS PubMed.
- J. Larkin, J. Turney, A. Massicotte, C. Amon and A. McGaughey, J. Comput. Theor. Nanosci., 2014, 11, 249–256 CrossRef CAS.
- A. J. McGaughey and J. M. Larkin, Annu. Rev. Heat Transfer, 2014, 17, 49–87 CrossRef.
- C. Ophus, A. Shekhawat, H. Rasool and A. Zettl, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 205402 CrossRef.
- J. He, C. Yu, S. Lu, S. Shan, Z. Zhang and J. Chen, Nanotechnology, 2024, 35, 025703 CrossRef CAS.
- W. Ren, S. Lu, C. Yu, J. He, Z. Zhang, J. Chen and G. Zhang, Appl. Phys. Rev., 2023, 10, 041404 CAS.
- W.-J. Ren, S. Lu, C.-Q. Yu, J. He and J. Chen, Rare Met., 2023, 42, 2679–2687 CrossRef CAS.
- J. Zhang and J. Zhao, Carbon, 2013, 55, 151–159 CrossRef CAS.
- O. V. Yazyev and S. G. Louie, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 195420 CrossRef.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, J. Phys.: Condens. Matter, 2002, 14, 783 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- B. Qiu, H. Bao, X. Ruan, G. Zhang and Y. Wu, Heat Transfer Summer Conference, 2012, pp. 659–670 Search PubMed.
- W. Diery, E. A. Moujaes and R. Nunes, Carbon, 2018, 140, 250–258 CrossRef CAS.
- C. Hua and A. J. Minnich, J. Appl. Phys., 2015, 117, 175306 CrossRef.
Footnote |
| † Although they write polycrystalline but their simulation details suggest bi-GNR samples because periodicity along the x-axis is not present. |
| This journal is © The Royal Society of Chemistry 2025 |