Concealable physical unclonable function generation and an in-memory encryption machine using vertical self-rectifying memristors†
Jea Min
Cho
,
Seung Soo
Kim
,
Tae Won
Park
,
Dong Hoon
Shin
,
Yeong Rok
Kim
,
Hyung Jun
Park
,
Dong Yun
Kim
,
Soo Hyung
Lee
,
Taegyun
Park
* and
Cheol Seong
Hwang
 *
*
Department of Materials Science and Engineering and Inter-University Semiconductor Research Center, Seoul National University Gwanak-ro 1, Gwanak-gu, Seoul 08826, Republic of Korea. E-mail: tagyun@snu.ac.kr; cheolsh@snu.ac.kr
First published on 7th November 2024
Abstract
The importance of hardware security increases significantly to protect the vast amounts of private data stored on edge devices. Physical unclonable functions (PUFs) are gaining prominence as hardware security primitives due to their ability to generate true random digital keys by exploiting the inherent randomness of the physical devices. Traditional approaches, however, require significant data movement between memory units and PUF generation circuits to perform encryption, presenting considerable energy efficiency and security challenges. This study introduces an innovative approach where PUF key generation and encryption are accomplished in the same vertically integrated resistive random access memory (V-RRAM), alleviating the data movement issue. The proposed V-RRAM encryption machine offers concealable PUFs, high area efficiency, and multi-thread data handling using parallel XOR logic operations. The encryption machine is compared with other machines, demonstrating the highest spatiotemporal cost-effectiveness.
New conceptsThis study proposes a hardware security primitive that utilizes vertically stacked resistive random access memory (V-RRAM) to generate concealable physically unclonable function (PUF) keys and perform stateful logic-based parallel XOR encryption directly within the V-RRAM. Unlike most studies, which employ two-dimensional memristive arrays and sequential logic for encryption, this study utilizes the three-dimensional (3D) V-RRAM array and parallel stateful logic. The 3D structure enhances the area efficiency and introduces significant device-to-device variations and minimal cycle-to-cycle variations in the high resistance state due to its fabrication process, which is beneficial for generating concealable keys. In addition, the stackable nature of V-RRAM allowed for a key selection process with minimal area overhead, facilitating the generation of concealable PUF keys with a low bit-error rate (BER). Furthermore, parallel logic operations among the resistance states of the generated keys and the data stored in the V-RRAM were performed to enable efficient data encryption. The results demonstrated the lowest spatiotemporal costs compared to prior studies, emphasizing the potential of the V-RRAM as an effective security hardware solution. |
Introduction
With the advancement of big data, the Internet of Things, and artificial intelligence, large amounts of private data are being generated, collected, and transmitted through edge devices. Therefore, hardware security is gaining attention to protect edge devices with critical information from attackers, where the role of digital keys in information encryption is crucial. The data security may mean on-device security or is related to telecommunication. The former refers to protecting information such as personal data in a cellular phone, while the latter does secure data transport to large-scale cloud servers via the communication network. This work focuses on the former case, where generating a random key and its concealment for data encryption and decryption are crucial. Recent works report the physical unclonable function (PUF) that can effectively generate digital keys in physical devices having intrinsic randomness or stochasticity.1–5 Such an approach showed merits over the pseudo-random keys based on software algorithms. However, it often lacks concealable keys, which are critical for more secure data protection.Device-to-device (D-t-D) variation in large-scale integrated circuit fabrication is a source of complication in semiconductor chip production. However, it might be a helpful feature in the hardware security field when used in the PUF as a device fingerprint. When applying the inputs (challenges) to a specific device, the unique outputs (responses) can be obtained from the property of the specific device, which forms a specific challenge–response pair (CRP). The CRP can be used as the device fingerprint.
Memristors exhibit useful stochasticity for generating random keys and advantages such as low-cost fabrication and excellent scalability.6–9 There have also been studies on memristor devices with high stability and durability, which are crucial characteristics in terms of key reliability.10,11 These characteristics have led to extensive research into the security application of memristors for PUFs and true random number generators.12–17 Moreover, in-memory computing using memristors, such as stateful logic and sequential logic, can calculate and store the results of Boolean operations within the memory.18–22 The XOR operation, one of the Boolean operations, is helpful for data encryption and can be readily achieved by memristor logic circuits.23,24 Therefore, exploring in-memory computing with memristors holds the potential for generating PUF keys and performing encryption directly within the memristor array. Xu et al. demonstrated the feasibility of Boolean logic with TiN/Ta2O5/SiO2/Ta2O5/TiN memristors, showing that encryption can be performed through XOR operations in the passive memristor array.25 The XOR-based in-memory computing can address the energy and security issues associated with key movement and data privacy.26–29 Still, the sequential operation of the memristive in-memory circuit raises issues of slow operation and significant peripheral overhead.
In this regard, exploring the parallel memristive logic operation holds significance. Park et al. demonstrated the feasibility of performing highly parallel logic operations using self-rectifying memristors in a vertically integrated resistive switching random access memory (V-RRAM) array.30 This method may solve the low operation speed issue by adopting parallel XOR operations. At the same time, the D-t-D-related variation of memristors offers encryption capability with high area efficiency and low operation current. Therefore, V-RRAM is a promising encryption hardware for processing large amounts of information in edge devices.31,32
However, several challenges remain due to the disparate requirements of PUF key generation and in-memory logic computing. The PUF key generation requires a relatively high variation to generate a unique key, whereas the logic operation requires a low variation for high accuracy. Storing the PUF key in different locations may solve the issue, but it increases the data path, inducing memory bottlenecks. Furthermore, the co-location of data and PUF keys in the same memory space within in-memory computing systems allows attackers to access the PUF keys easily since memory space has frequent data transmission. Consequently, it is necessary to incorporate a concealable characteristic that reveals the PUF key only during the operation and conceals it when not used.
This work proposes a method to resolve this complication and demonstrates homogeneous security hardware using V-RRAM. A concealable PUF key is generated by the voltage division effect between the high resistance state (HRS) of Pt/Ta2O5/Al-doped HfO2/TiN (PTHT) memristors in the V-RRAM and the added series resistance. In addition, the PTHT memristors in the V-RRAM offer high density, low operation current with negligible sneak component, and forming-free characteristics. Through the stackability of V-RRAM, key selection processes could be conducted with minimal area loss, enabling the generation of the PUF key with a low bit-error rate. The parallel XOR operations in the V-RRAM array also readily achieved data encryption and decryption.
Results and discussion
Key generation and encryption in the V-RRAM encryption machine
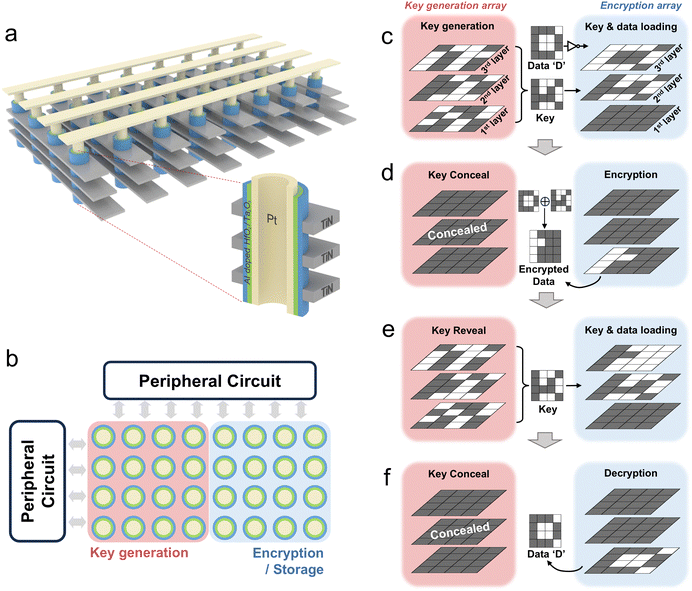
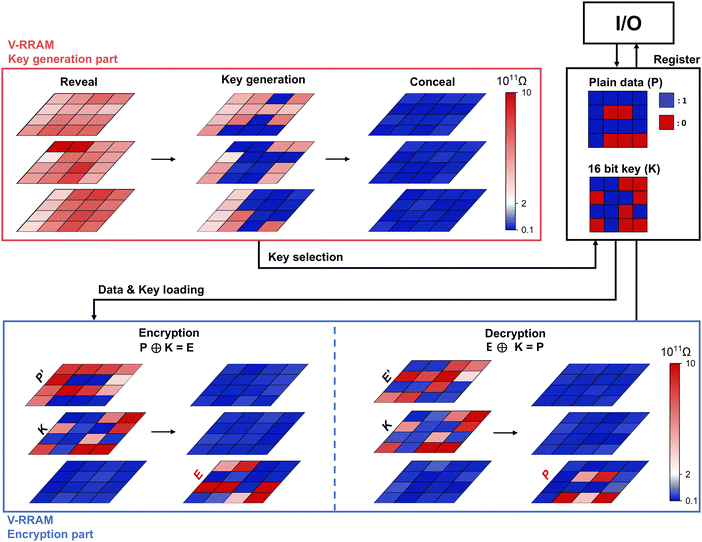
Fig. 1 provides an overview of how the V-RRAM array is utilized as a key generation and encryption/decryption machine. Fig. 1a shows a schematic diagram of a three-layered stacked 4 × 8 V-RRAM array and a cross-section of the memory hole structure. The hole-type V-RRAM was fabricated by etching the multi-layered stack of TiN and SiO2, which serve as the bottom electrodes (BE) and interlayer dielectric layers. SiO2 is not shown in Fig. 1a for clarity. After forming the hole structure, the bi-layered resistive switching (RS) layers of 10-nm-thick Al-doped HfO2 (Al:HfO2) and 10-nm-thick Ta2O5 were deposited using the atomic layered deposition (ALD) method. Then, the Pt layer is deposited for the top electrode (TE). Since the TE and BE intersection has the RS layers, three RRAM devices are formed within a single hole. The Method section provides a more detailed description of the fabrication process.Fig. 1b illustrates that the array is separated into the key generation area (red background, half of V-RRAM) and the encryption area (blue background, remaining half of V-RRAM). Fig. 1c and d show the encryption method within the V-RRAM array, while Fig. 1c shows the methods for loading the key and data. A 16-bit key is generated from the key generation array, the details of which are discussed later, and transferred to the second (middle) layer of the encryption array. This relocation makes the key selection process more efficient, as discussed in Fig. S6 (ESI†), and fully utilizes the parallelism of encryption operations. The data to be encrypted are passed through an inverter and stored in the third (top) layer of the encryption array. The devices in the first layer of the encryption array are initially set to ‘1’ (low resistance state (LRS)). Then, the XOR encrypted data are generated using the in-memory logic operations between the inverted data in the third layer and the generated key in the second layer. The encrypted data are then stored in the encryption array's first (bottom) layer, as shown in Fig. 1d. The key generation array is concealed after the key generation to minimize the key exposure risk.
Fig. 1e and f show the decryption method, while Fig. 1e shows the key and data loading process for the decryption. Since the key generation array is previously concealed, the 16-bit key must be regenerated and loaded to the second layer of the encryption array. The small cycle-to-cycle (C-t-C) variation of the PTHT memristor allows the keys to be recovered. The encrypted data previously stored in the first layer of the encryption array are inverted and loaded into the third layer. Subsequently, the devices in the first layer of the encryption array are initialized to ‘1’. Fig. 1f shows that the logic operations between the encrypted data in the third layer and the regenerated key in the second layer result in the plain data stored in the first layer. Subsequently, the key generation array is concealed again. Details about key generation methods, key concealing, and the XOR logic operation are discussed in the subsequent sections.
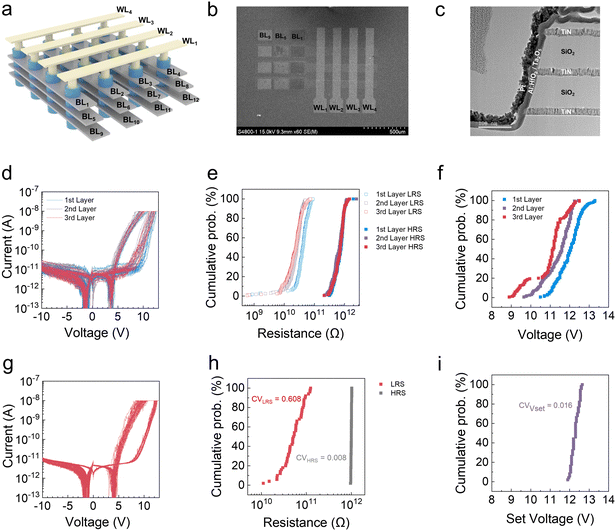
Fig. 2a shows a schematic diagram of the three-layered 4 × 4 V-RRAM arrays fabricated to demonstrate the feasibility of the V-RRAM encryption machine described above. In this structure, TE and BE correspond to the word lines (WLs) and the bit lines (BLs), respectively. Fig. 2b presents the V-RRAM array's top-view scanning electron microscopy (SEM) image, showing BLs, WLs, and their respective contact pads. Fig. 2c shows a cross-section transmission electron microscopy (TEM) image of the three-layered V-RRAM hole structure, revealing layers of TiN, SiO2, Al:HfO2, Ta2O5, and Pt. Consequently, PTHT devices are formed on the etched sidewalls of the first, second, and third layer BEs. Fig. S2 (ESI†) shows the energy-dispersive X-ray spectroscopy (EDS) results of the chemical composition mapping profiles for the three-layered vertical structure. This analysis indicates that the PTHT stack was formed according to the design. However, it can be readily anticipated that the characteristics of the memristors in the different layers are slightly different (D-t-D variation) when seeing the memory hole's slanted and slightly corrugated etching profiles. Although such non-uniformity is undesirable for standard memory applications, it can be used to generate the PUF. Also, the cycle-to-cycle (C-t-C) switching variation of a given memristor cell can affect the characteristics of the random key. In contrast to the large D-t-D for efficient key generation, C-t-C must be small for the key regeneration. Therefore, D-t-D and C-t-C properties are examined in detail.
Fig. 2d shows the current–voltage (I–V) curves of 48 devices in the three-layered 4 × 4 V-RRAM array, showing common electrical characteristics with a sufficient memory window to ensure appropriate operation. The memristors show self-rectifying properties with a low operation current and a high forward-reverse ratio.33,34Fig. 2e shows D-t-D variations of the resistance values of the LRS (RLRS) and HRS (RHRS) at a read voltage of 6 V from 576 devices in twelve V-RRAM arrays. The coefficient of variation (CoV) values, defined as the fraction of standard deviation to mean, are 0.32, 0.43, and 0.55 for RLRS, and 0.33, 0.41, and 0.34 for RHRS, for the first, second, and third layers, respectively. Fig. 2f illustrates the cumulative curves of the set (switching from a HRS to a LRS) voltage (VSET), showing relatively small D-t-D variations with CoV values of 0.05, 0.06, and 0.08 for the first, second, and third layers, respectively.
Fig. 2g shows I–V curves obtained from 50 switching cycles from a single device in the first layer. Fig. 2h and i depict C-t-C variations in RLRS (CoV = 0.608), RHRS (CoV = 0.008), and VSET (CoV = 0.016). The much smaller CoV of RHRS than RLRS is attributed to stable oxygen vacancies generated by Al in Al-doped HfO2, resulting in deeper trap sites that stabilize the HRS. The Poole–Frenkel mechanism through the deep traps mediated the electrical conduction in the HRS.31,35–37 Among these variations, the high CoV of D-t-D and the low CoV of C-t-C for RHRS are the essential requirements for the concealable PUFs, as discussed in subsequent sections. Fig. S3 in the ESI† shows the retention of the VRRAM device, demonstrating its stability over 103 seconds. Fig. S4 (ESI†) presents the measurement results of the interlayer leakage current in the three-layered V-RRAM device. The leakage current is sufficiently low, ensuring that it does not pose any issues for the key generation and logic operations discussed in the following sections.
Key generation in V-RRAM
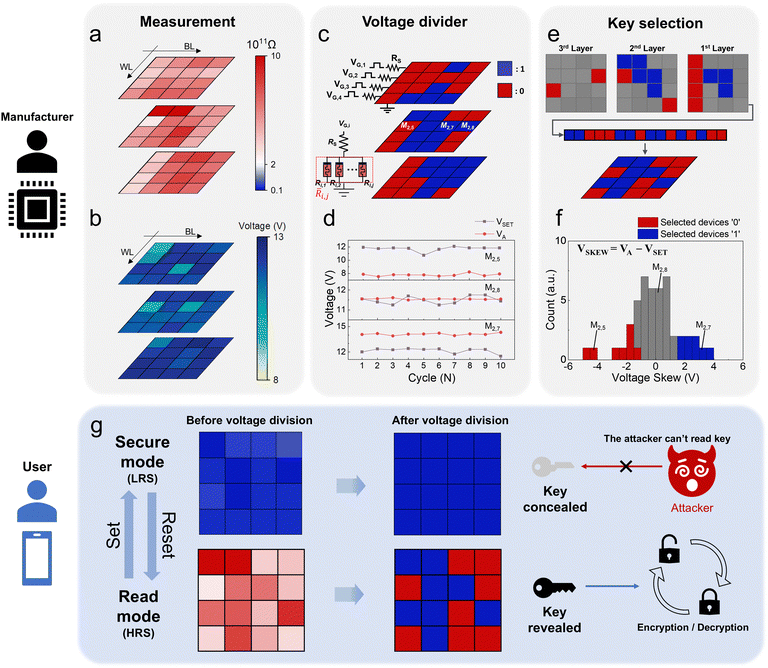
The memristor's RHRS variations (with large D-t-D and small C-t-C variations) in the V-RRAM array are used to generate the concealable PUF keys. Once each memristor is fabricated, its property does not vary with the repeated reset (switching from a LRS to a HRS) operation, resulting in a small C-t-C variation. Fig. 3 shows the basic ideas for generating the PUF keys and encryption processes. The PUF keys can be generated by the three stages of measurement, voltage divider, and key selection. In the measurement stage, one cycle of I–V measurement is conducted for all devices in the V-RRAM array to obtain the D-t-D distribution of HRS and VSET. Since the C-t-C variation is relatively small (0.008) compared to the D-t-D variation (0.33 (1st layer), 0.41 (2nd layer), and 0.34 (3rd layer)), the one cycle measurement is used to represent the D-t-D variation in Fig. 2e. Fig. 3a and b show the RHRS and VSET distribution diagram for all devices in the V-RRAM array, respectively.Next, in the voltage divider stage, the appropriate series resistors are connected to each WL for the key generation using the voltage division effect, as shown in Fig. 3c. This work sets the series resistance (Rs) to 700 GΩ. When the generation voltage (VG,i) is applied to the i-th WL, connected with RS, the voltage drop by the device at the i-th WL and j-th BL (VA,i,j) is defined using eqn (1).
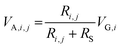 | (1) |
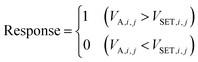 | (2) |
Utilizing the parallel configuration of the voltage dividers, as shown in the inset of Fig. 3c, the appropriate VG,i can be selected to ensure that half of the 12 devices along the i-th WL (a single WL contacts four devices on each layer) have 1s and the other half have 0s. Thus, VG,i can be calculated as shown in eqn (3).
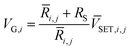 | (3) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i,j and
i,j and ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) SET,i,j are the median of the RHRS and VSET of the devices along the i-th WL, respectively. The voltage division process can be performed in parallel by applying bias to multiple WLs with the selected BL grounded, as shown in Fig. S5 (ESI†). This voltage division for all devices yields a 48-bit key matrix, where half of the components have a 1 (RLRS) value, and the other half have a 0 (RHRS) value, as shown in Fig. 3c. The small CoV of VSET (=0.06) makes the voltage division and the PUF key generation reliable. However, not all these 48-bit key values are used, but 16-bits are selected in the key selection step, as shown in Fig. 3e, to secure the key concealment and regeneration. The key concealment is accomplished by switching all the cells into the LRS, and key regeneration is done by applying Vreset to all cells and repeating the voltage division step, described in Fig. 3c. At this key regeneration step, the successful regeneration depends on the difference between VA,i,j and VSET,i,j. Fig. 3d shows the variations of VA,i,j and VSET,i,j for three devices (M2,5, M2,7 and M2,8) in the second layer as a function of the switching cycle number. Although the difference between VA,i,j and VSET,i,j remained almost constant in each device due to small C-t-C variations, the difference values differ significantly due to large D-t-D variations. Among these three devices, device M2,5 will remain at the HRS (VA,2,5 < VSET,2,5) while device M2,7 will switch to the LRS (VA,2,7 < VSET,2,7), and, thus, these devices will regenerate the original data during the second voltage division step. However, the device M2,8 has similar VA,2,8 and VSET,2,8 values, so it is not guaranteed that this device will regenerate its original key during the key regeneration step. Therefore, these devices should not be included in the final key, which is composed of devices with a substantial difference between VA,i,j and VSET,i,j values. This process is referred to as key selection.
SET,i,j are the median of the RHRS and VSET of the devices along the i-th WL, respectively. The voltage division process can be performed in parallel by applying bias to multiple WLs with the selected BL grounded, as shown in Fig. S5 (ESI†). This voltage division for all devices yields a 48-bit key matrix, where half of the components have a 1 (RLRS) value, and the other half have a 0 (RHRS) value, as shown in Fig. 3c. The small CoV of VSET (=0.06) makes the voltage division and the PUF key generation reliable. However, not all these 48-bit key values are used, but 16-bits are selected in the key selection step, as shown in Fig. 3e, to secure the key concealment and regeneration. The key concealment is accomplished by switching all the cells into the LRS, and key regeneration is done by applying Vreset to all cells and repeating the voltage division step, described in Fig. 3c. At this key regeneration step, the successful regeneration depends on the difference between VA,i,j and VSET,i,j. Fig. 3d shows the variations of VA,i,j and VSET,i,j for three devices (M2,5, M2,7 and M2,8) in the second layer as a function of the switching cycle number. Although the difference between VA,i,j and VSET,i,j remained almost constant in each device due to small C-t-C variations, the difference values differ significantly due to large D-t-D variations. Among these three devices, device M2,5 will remain at the HRS (VA,2,5 < VSET,2,5) while device M2,7 will switch to the LRS (VA,2,7 < VSET,2,7), and, thus, these devices will regenerate the original data during the second voltage division step. However, the device M2,8 has similar VA,2,8 and VSET,2,8 values, so it is not guaranteed that this device will regenerate its original key during the key regeneration step. Therefore, these devices should not be included in the final key, which is composed of devices with a substantial difference between VA,i,j and VSET,i,j values. This process is referred to as key selection.
In the key selection step, 16 devices are selected for defining a 16-bit key based on the voltage skew (VSKEW), which is the difference between VA,i,j and VSET,i,j. The 48 devices were divided into groups with ‘1’ and ‘0’ key values. Eight devices with the largest absolute value of VSKEW were selected from each group for the 16-bit key generation. The selected 16 devices are rearranged based on their original positions in the array to generate a 16-bit key matrix, as shown in Fig. 3e, corresponding to the key matrix in Fig. 1c and e. The positions of the selected devices are stored as a lookup table. Fig. 3f shows the selected devices through key selection from the VSKEW distribution. Even with this key selection process, the chip size does not increase due to the area efficiency of V-RRAM. Then, the 16-bit key matrix is transferred to the corresponding encryption area for in-memory computing, as shown in Fig. 1c. Fig. 3g shows how a user utilizes the V-RRAM PUF. The 4 × 4 matrix in Fig. 3g represents the analog (left panels) and digital codes (middle panels) of the 16-bit key. As previously described, when the key is not in use, all devices in the V-RRAM array are set to the LRS to conceal it. Consequently, even after voltage division, all bit in the key is read as ‘1’, rendering it inaccessible to potential attackers. This state is referred to as secure mode. All cells are reset, and voltage division is performed again to utilize the key. The revealed key is then used for data encryption or decryption. V-RRAM maintains a consistent HRS value even after repeated cycles, thereby possessing a concealable feature and ensuring the system's security.
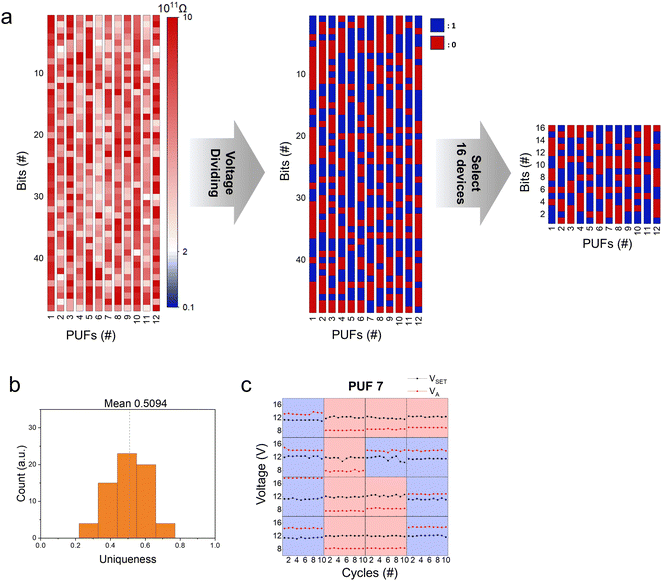
The fabricated 12 three-layered 4 × 4 V-RRAM are used to generate 12 16-bit keys simultaneously. Fig. 4a illustrates how to convert analog HRS distributions obtained from 12 V-RRAM PUFs into 16-bit PUF keys through voltage division and key selection based on the measured HRS distribution. The left, middle, and right panels of Fig. 4a display the distribution of analog HRS values, digitization results through voltage division, and 16-bit PUF keys obtained by the key selection process, respectively, of the 12 PUFs. These 16-bit keys are used for encryption. Fig. 4b shows the uniqueness of distribution among the generated 16-bit keys. Uniqueness can be calculated based on the hamming distance between different keys, indicating whether they have sufficient randomness. The hamming distance is the number of positions where the corresponding values in two equal-length vectors differ. Therefore, uniqueness is a metric that indicates how dissimilar distinct keys are. The optimum uniqueness is 0.5, corresponding to the case where half of the key bits differ. For V-RRAM PUFs, the mean uniqueness value is 0.509, indicating that the HRS and set voltages have sufficiently random distributions. The 12 generated 16-bit keys have equal portions of 1s and 0s, complicating the prediction efforts and enhancing security. Fig. 4c shows the verification results of whether bit errors occur during the conceal and reveal process of a selected 16-bit key from the 7th V-RRAM array. Each voltage–cycle graph represents the 16 selected devices, with the black and red points within each box corresponding to VSET and VA measured across 10 cycles of set and reset operation. It was observed that, even after performing conceal and reveal operations, the selected 16 devices consistently revealed the same key value (1 for the blue background and 0 for the red background) since the VSET and VA values do not overlap. The criteria for the PUF key metrics are summarized in Fig. S7 (ESI†). The additional criteria are discussed in Fig. S8 (ESI†) for the PUF's reliability.
XOR encryption in V-RRAM
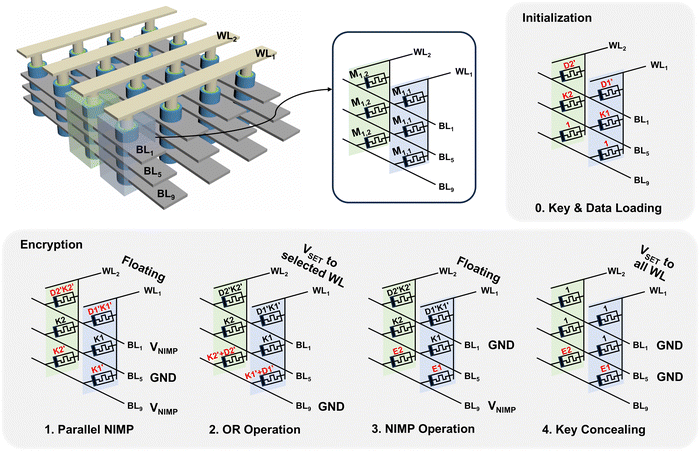
The XOR operation is a crucial function in cryptographic systems because the same XOR operation can be used for encryption and decryption. In this work, the cascading of NIMP operations in V-RRAM is used to implement XOR operations between the generated PUF keys and stored input data. Fig. S9 (ESI†) shows the implementation of the NIMP operations in V-RRAM, while Fig. S9a (ESI†) shows the bias configuration required for the NIMP operation. The bias configuration between two BL nodes, BL1 and BL2, is represented as 〈BL1 (V1), BL2 (V2)〉, where V1 and V2 are the applied voltages. For instance, the NIMP operation between two nodes, N1,1 and N1,2, can be realized when 〈BL1 (VNIMP), BL2 (0 V)〉 is applied, where the VNIMP is the applied voltage for NIMP operation, set to 5 V. By applying VNIMP between the BL nodes, two PTHT memristors (M1,1 and M1,2) are connected in anti-serial configuration. The voltage drop of M1,1 between two memristors is determined by the voltage divider following eqn (4).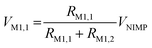 | (4) |
When the two inputs of the NIMP operation, p and q, are defined as the two initial resistance states of the memristors, M1,1 and M1,2, the final resistance state of M1,1 indicates the output of the NIMP operation. Fig. S9b (ESI†) shows the truth table of the NIMP operation that summarizes four input cases. The ra is the output of the NIMP operation, and the subscript ‘a’ denotes the resistance state after the logic operation. Fig. S9c (ESI†) demonstrates NIMP operation with a read voltage of 6 V. The 12 measurements were conducted for each case. By selecting the logical ‘0’ as the resistance state smaller than the reference resistance of 200 GΩ and vice versa for the ‘1’, the NIMP operation can be defined.
The hole size of V-RRAM is modulated (changing the switching area) to control +RHRS, which is the RHRS at the forward bias direction, to optimize the NIMP operation. Since the memristor in the reversed bias direction (M1,1) in anti-serial configuration has a much larger resistance than that in the forward bias direction (M1,2) due to the Schottky barrier of the PTHT stack, the switching area is reduced to 0.094 μm2 to increase +RHRS not to induce most of the voltage applied to the reverse-biased memristor. Furthermore, for stable NIMP operation, the compliance current (ICC) was increased to 50 nA to amplify the difference between +RLRS and +RHRS. As a consequence, the resistive state of M1,1 can be changed only for cases 2 and 4 when most of the voltage drop occurs at the reverse-biased memristor and remains the same when M1,2 is in +RHRS (cases 1 and 3 in Fig. 5b). The reset occurs around −3.7 V, as shown in Fig. S10d (ESI†). Thus, the stable NIMP operation can be implemented by setting the VNIMP to 5 V. The increased window between +RLRS and +RHRS ensures that the voltage drop occurs as intended despite the D-t-D variation in the LRS and HRS. Fig. S10 (ESI†) explains the further details of the NIMP operation. The NIMP operation can be parallelly operated along the BL, as shown in the dotted lines in Fig. 5(a). The number of parallel operations equals the number of WLs (NWL).
 | ||
| Fig. 5 Schematic diagram of the combination of NIMP and OR operations for the XOR encryption process. The corresponding truth table for each step is shown in Table 1. D, K, and D′ represent the original data, generated key, and inversion of data. | ||
Two NIMP operations are combined with the OR operation for the parallel XOR operations, as shown in Fig. 5. First, the generated PUF keys, K1 and K2, and the original data, D1 and D2, are loaded to the four memristors initialized to 1 in complementary form using inverters. The inverted resistance states are denoted with an apostrophe (′). Then, parallel NIMP operations are implemented by 〈BL1(VNIMP), BL9 (VNIMP), BL5 (ground)〉, resulting in D1′K1′, K1′, D2′K2′, and K2′ (where D1′K1′ indicates the AND operation between D1′ and K1′). Utilizing the voltage driver used in the data loading, the OR operation to K1′ and K2′ can be implemented by applying 〈WL1 (VOR,D′), BL9 (ground)〉, resulting in K1′ + D1′ and K2′ + D2′. Then, the final XOR operations can be achieved by the NIMP operations by applying 〈BL9 (VNIMP), BL1 (ground)〉 since (K1′ + D1′)(D1′K1′)′ and (K2′ + D2′)(D2′K2′)′ are equivalent to the K1′D1 + K1D1′ and K2′D2 + K2D2′, which are the XOR operations, described in Table 1. Two parallel XOR operations using two generated keys are shown for simplicity, but more parallel operations can be performed along the WLs. In addition, the key can be concealed by initializing the memristors, which can be recovered by the same PUF generation machine. The decryption follows the same process as encryption since the same XOR operations can be used. Encrypted data are loaded to the same voltage driver circuit of the original data bit, and the rest of the methods are the same as the encryption process. Fig. S12 (ESI†) illustrates the decryption process diagram. Utilizing parallelism, the number of data processed per operation increases as the array size increases.
| Case | Step 0 | Step 1 | Step 2 | Step 3 | |||
|---|---|---|---|---|---|---|---|
| D | K | D′ | K′ | D′K′ | K′ + D′ | (K′ + D′)(D′K′)′ | |
| I | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| II | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| III | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| IV | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
Fig. 6 shows the integrated key generation and encryption process in V-RRAM, performed continuously, where the three-layered 4 × 4 V-RRAMs are used for both the key generation and encryption. The key and data are also represented as 4 × 4 matrices. First, the upper panel of Fig. 6 illustrates the process in the key generation part of the V-RRAM array, where an analog HRS is converted into digital bits, and the selected 16-bit key is temporarily stored in registers. After the key is stored in the register, all the devices in the key generation part of the V-RRAM array are set to the LRS to conceal the key. The simple latch circuit can comprise the registers, which can be integrated into the peripheral circuit of the V-RRAM chip. This configuration can alleviate the data transport with the host processors. The lower panel of Fig. 6 displays the read resistances of the key and data ‘P’ after XOR encryption and decryption operations. The result of the XOR operation is ultimately stored in the first layer of the V-RRAM encryption part, and it can be observed that the data ‘P’ are recovered through two XOR operations. During encryption, the data and, during decryption, the encrypted data are temporarily stored in the resistor before being written, and the data stored in the register are immediately cleared after the OR operation in XOR logic. Fig. S13 (ESI†) shows the system for performing these integrated operations. Data movement between memory and processing units is unnecessary in the suggested key generation and encryption methods. Thus, it eliminates the memory bottlenecks, reduces power consumption, and makes it immune to threatening side-channel attacks in CMOS.
Table 2 shows the summary of several works on PUF utilizing variations in memristors. B. Gao et al. reported generating concealable keys by comparing the HRS current of devices using a sense amplifier, which requires high-performance converter circuits when using low-operating current devices.12 In contrast, this work presents a structure that enables key generations even using the voltage divider with the series resistors, simplifying the conversion circuit to generate keys. Furthermore, by utilizing a 3D structure, area efficiency and capability of performing encryption operations are achieved, which presents a significant advantage. Some studies demonstrated the feasible encryption by conducting in-memory computing on memristor passive arrays or one transistor–one resistor (1T1R) structures. These studies showed that XOR encryption can be achieved within three steps when using non-stateful logic. However, the use of non-stateful logic in these studies presents certain limitations: parallel computations are not feasible, necessitating either a significantly large area by employing diagonal cells in passive arrays for simultaneous logic operations or performing computations one cell at a time, increasing the number of operations proportionally with the data size. In contrast, this work demonstrates that NIMP and OR operations possess parallelism, enabling the efficient processing of massive data. To quantify this efficiency, Table 2 presents the spatiotemporal cost, calculated by multiplying the array size, cell size, and the number of operations required to encrypt M (number of WLs) × N (number of BLs) bits of data and key. The results indicate that while other studies show a cost proportional to M2 × N2, V-RRAM encryption achieves a cost proportional to M × N2 due to its parallelism.
| Reference | B. Gao et al.12 | L. Xu et al.25 | L. Yang et al.26 | K. S. Woo et al.27 | This work |
|---|---|---|---|---|---|
| Memristor type | TiN/TaOx/HfOx/TiN | TiN/Ta2O5/SiO2/Ta2O5/TiN | Ti/HfO2/TiN | CuxTe1−x/HfO2/Pt | Pt/Ta2O5/Al:HfO2/TiN |
| Technology | 1T1R | Passive array | 1T1R | Passive array | Passive array |
| Entropy source | R HRS variations | R HRS variations | Subthreshold slope variation of transistor | V SET variations | R HRS variations |
| Uniqueness | 50.52 | — | 49.95 | 50.62 | 50.94 |
| Uniformity | 50.3 | — | 49.71 | — | 50 |
| BER | 0 | — | 5.06 | 1.88 | 0 |
| Feasibility of encryption | X | O | O | O | O |
| Array size for M × N bit encryption (A) | — | M 2 × N2 | M × N | M 2 × N2 | M × N |
| Unit cell size (B) | — | 4F2 | 6F2 | 4F2 | 4F2 |
| Number of operations for M × N bit encryption (C) | — | 2 | M × N | 3 | N × 5 |
| Spatiotemporal cost for M × N bit encryption (A × B × C) | — | 8F2 × M2 × N2 | 6F2 × M2 × N2 | 12F2 × M2 × N2 | 20F2 × M × N2 |
| Spatiotemporal cost for M × N bit encryption (M, N = 100, unit = F2) | — | 8 × 108 | 6 × 108 | 12 × 108 | 2 × 107 |
| Necessity of converter for encryption | — | O | O | O | X |
| 3D structure | X | X | X | X | O |
Consequently, for M > 4, the spatiotemporal cost of encryption using V-RRAM is the lowest, and the spatiotemporal efficiency of V-RRAM encryption further increases as the array size increases. Furthermore, since other studies utilize non-stateful logic, they require converters to transform resistance, representing data or keys, into voltage. These converters burden peri-circuits and require additional operation time. Moreover, the V-RRAM can potentially increase area efficiency through additional stacking, where the key selection process can be achieved with minimal area cost and effectively suppressing the bit-error rate. The use of self-rectifying memristors also decreases power consumption.
Conclusions
This study demonstrated key generation and encryption/decryption in a three-layered V-RRAM array. The V-RRAM PUF utilizes the intrinsic stochasticity of RHRS based on process variation to generate keys. The D-t-D variation of RHRS exhibited random behavior, demonstrating excellent uniqueness. Additionally, by utilizing the area efficiency of V-RRAM, bit errors can be filtered out to increase uniformity by selecting 16 devices in the array in PUF key generation without significant area overhead. Due to the small C-t-C variation of RHRS, the PUF keys can be concealed and regenerated, increasing the data and key security. Furthermore, the feasibility of NIMP operation and its parallel operations in V-RRAM are demonstrated in V-RRAM to handle multiple data in the XOR encryption. Consequently, the suggested V-RRAM-based PUF machine presents a high potential for new hardware security for edge computing with low spatiotemporal cost.Methods
Device fabrication
A three-layered 4 × 4 V-RRAM array was fabricated as follows. A 30-nm-thick TiN layer was deposited on a SiO2/Si substrate by radio frequency (RF) sputtering using a Ti target under a nitrogen atmosphere (Sorona, SRN 120). Over this layer, a 100-nm-thick SiO2 layer was deposited as a cell separation layer via plasma-enhanced chemical vapor deposition (PECVD, Oxford Instruments, PlasmaPro System100). This deposition sequence was repeated three times to construct a three-layered V-RRAM structure. Photolithography was performed using a maskless lithography system (NanoSystem Solutions, Inc., DL-1000 HP). The multi-layered stack was structured into line patterns, each with a width and space of 100 μm, utilizing dry etching (GIGALANE, NeoS-MAXIS 200L). Residual byproducts from etching were cleared using a photoresist asher (plasma finish, V15-G). To enable electrical contact with the bottom electrodes of various layers, the TiN layer in the contact pad regions was removed using dry etching (Oxford Instruments, PlasmaPro System100 Cobra), and the SiO2 layer in the pad contact regions was etched using a buffered oxide etchant (BOE), creating stepped contact pad structures. Subsequently, a 60-nm-thick SiO2 passivation layer was deposited using PECVD to prevent device formation on the sidewalls. Memory holes, each 1 μm in diameter, were then patterned using photolithography and dry etching (GIGALANE, NeoS-MAXIS 200L). Then, a 10-nm-thick layer of Al:HfO2 was deposited at 280 °C by thermal atomic layer deposition (ALD, CN1, custom-made ALD cluster system) using Hf(NCH3C2H5)4 and ozone (O3), with aluminum doping achieved by co-deposition using Al(CH3)3, maintaining a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 ALD cycle ratio of Al2O3 to HfO2. Subsequently, a 10-nm-thick layer of Ta2O5 was deposited at 200 °C using plasma-enhanced ALD (PEALD, CN1, Atomic Premium plus 200) with (CH3)3CNTa(N(C2H5)2) and plasma-activated H2O. A 50-nm-thick Pt top electrode was deposited by the electron-beam evaporation method (SRN-200, SORONA) and patterned via the lift-off process. Finally, the resistive switching layers above the contact pads were removed by dry etching to reveal the SiO2 passivation layer, which was then wet-etched with BOE. Fig. S1 of the ESI† presents a schematic diagram of the V-RRAM fabrication process.
9 ALD cycle ratio of Al2O3 to HfO2. Subsequently, a 10-nm-thick layer of Ta2O5 was deposited at 200 °C using plasma-enhanced ALD (PEALD, CN1, Atomic Premium plus 200) with (CH3)3CNTa(N(C2H5)2) and plasma-activated H2O. A 50-nm-thick Pt top electrode was deposited by the electron-beam evaporation method (SRN-200, SORONA) and patterned via the lift-off process. Finally, the resistive switching layers above the contact pads were removed by dry etching to reveal the SiO2 passivation layer, which was then wet-etched with BOE. Fig. S1 of the ESI† presents a schematic diagram of the V-RRAM fabrication process.
Electrical characterization
The V-RRAM array's electrical measurements were performed using a semiconductor parameter analyzer (SPA, HP4155A). A bias voltage was applied to the TE during the measurements while the BE was grounded.PUF generation
The process of PUF generation was conducted experimentally. The subsequent key selection was determined by software based on the measurement results. Afterward, the selected keys were mapped to the encryption array. The PUF metrics were calculated using Python.Author contributions
J. M. Cho designed and conducted the experiments and wrote the manuscript. S. S. Kim and T. W. Park performed morphological characterization of the devices. D. H. Shin, Y. R. Kim, H. J. Park, D. Y. Kim, and S. H. Lee provided methodology support. All authors reviewed the manuscript. T. Park and C. S. Hwang supervised the whole research and manuscript preparation.Data availability
Raw data are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (Grant No. 2020R1A3B2079882).References
- Y. Gao, S. F. Al-Sarawi and D. Abbott, Nat. Electron., 2020, 3, 81–91 CrossRef.
- R. Pappu, B. Recht, J. Taylor and N. Gershenfeld, Science, 2002, 297, 2026–2030 CrossRef CAS.
- U. Ruhrmair, J. Solter, F. Sehnke, X. Xu, A. Mahmoud, V. Stoyanova, G. Dror, J. Schmidhuber, W. Burleson and S. Devadas, IEEE Trans. Inf. Forensics Secur., 2013, 8, 1876–1891 Search PubMed.
- D. E. Holcomb, W. P. Burleson and K. Fu, Initial SRAM state as a fingerprint and source of true random numbers for RFID tags, in Proc. Conf. RFID Security 2, 2007.
- F. Tehranipoor, N. Karimian, K. Xiao and J. Chandy, Proceedings of the 25th edition on Great Lakes Symposium on VLSI, ACM, Pittsburgh Pennsylvania USA, 2015, pp. 15–20.
- R. Waser, R. Dittmann, G. Staikov and K. Szot, Adv. Mater., 2009, 21, 2632–2663 CrossRef CAS.
- Z. Wang, H. Wu, G. W. Burr, C. S. Hwang, K. L. Wang, Q. Xia and J. J. Yang, Nat. Rev. Mater., 2020, 5, 173–195 CrossRef CAS.
- S. Yu, X. Guan and H.-S. P. Wong, 2011 International Electron Devices Meeting, IEEE, Washington, DC, USA, 2011, pp. 17.3.1–17.3.4.
- R. Degraeve, A. Fantini, N. Raghavan, L. Goux, S. Clima, B. Govoreanu, A. Belmonte, D. Linten and M. Jurczak, Microelectron. Eng., 2015, 147, 171–175 CrossRef CAS.
- Y. Pei, L. Yan, Z. Wu, J. Lu, J. Zhao, J. Chen, Q. Liu and X. Yan, ACS Nano, 2021, 15, 17319–17326 CrossRef CAS PubMed.
- X. Yan, X. Jia, Y. Zhang, S. Shi, L. Wang, Y. Shao, Y. Sun, S. Sun, Z. Zhao, J. Zhao, J. Sun, Z. Guo, Z. Guan, Z. Zhang, X. Han and J. Chen, Nano Energy, 2023, 107, 108091 CrossRef CAS.
- B. Gao, B. Lin, Y. Pang, F. Xu, Y. Lu, Y.-C. Chiu, Z. Liu, J. Tang, M.-F. Chang, H. Qian and H. Wu, Sci. Adv., 2022, 8, eabn7753 CrossRef PubMed.
- R. Zhang, H. Jiang, Z. R. Wang, P. Lin, Y. Zhuo, D. Holcomb, D. H. Zhang, J. J. Yang and Q. Xia, Nanoscale, 2018, 10, 2721–2726 RSC.
- B. Gao, B. Lin, X. Li, J. Tang, H. Qian and H. Wu, IEEE Trans. Electron Devices, 2022, 69, 536–542 CAS.
- R. Liu, H. Wu, Y. Pang, H. Qian and S. Yu, 2016 IEEE International Symposium on Hardware Oriented Security and Trust (HOST), IEEE, McLean, VA, USA, 2016, pp. 13–18.
- K. S. Woo, J. Kim, J. Han, J. M. Choi, W. Kim and C. S. Hwang, Adv. Intell. Syst., 2021, 3, 2100062 CrossRef.
- K. S. Woo, A. Zhang, A. Arabelo, T. D. Brown, M. Park, A. A. Talin, E. J. Fuller, R. S. Bisht, X. Qian, R. Arroyave, S. Ramanathan, L. Thomas, R. S. Williams and S. Kumar, Nat. Commun., 2024, 15, 4656 CrossRef CAS PubMed.
- J. Borghetti, G. S. Snider, P. J. Kuekes, J. J. Yang, D. R. Stewart and R. S. Williams, Nature, 2010, 464, 873–876 CrossRef CAS.
- N. Xu, T. Park, K. J. Yoon and C. S. Hwang, Phys. Status Solidi RRL, 2021, 15, 2100208 CrossRef CAS.
- N. Xu, T. G. Park, H. J. Kim, X. Shao, K. J. Yoon, T. H. Park, L. Fang, K. M. Kim and C. S. Hwang, Adv. Intell. Syst., 2020, 2, 1900082 CrossRef.
- N. Xu, K. J. Yoon, K. M. Kim, L. Fang and C. S. Hwang, Adv. Electron. Mater., 2018, 4, 1800189 CrossRef.
- Y.-X. Zhou, Y. Li, Y.-T. Su, Z.-R. Wang, L.-Y. Shih, T.-C. Chang, K.-C. Chang, S.-B. Long, S. M. Sze and X.-S. Miao, Nanoscale, 2017, 9, 6649–6657 RSC.
- X. Wang, H. Deng, W. Feng, Y. Yang and K. Chen, 2016 35th Chinese Control Conference (CCC), IEEE, Chengdu, China, 2016, pp. 5847–5851.
- Y. Song, Q. Wu, X. Wang, C. Wang and X. Miao, IEEE Electron Device Lett., 2021, 42, 1398–1401 CAS.
- L. Xu, R. Yuan, Z. Zhu, K. Liu, Z. Jing, Y. Cai, Y. Wang, Y. Yang and R. Huang, Adv. Mater. Technol., 2019, 4, 1900212 CrossRef CAS.
- L. Yang, L. Cheng, Y. Li, H. Li, J. Li, T.-C. Chang and X. Miao, Adv. Electron. Mater., 2021, 7, 2001182 CrossRef CAS.
- K. S. Woo, J. Han, S. Yi, L. Thomas, H. Park, S. Kumar and C. S. Hwang, Nat. Commun., 2024, 15, 3245 CrossRef CAS PubMed.
- M. Ma, Y. Zhu, Z. Zhu, R. Yuan, J. Liu, L. Xu, Y. Yang and Y. Wang, IEEE Nanotechnol. Mag., 2022, 16, 24–C3 Search PubMed.
- R. Wang, S. Wang, Y. Xin, Y. Cao, Y. Liang, Y. Peng, J. Feng, Y. Li, L. Lv, X. Ma, H. Wang and Y. Hao, Small Sci., 2023, 3, 2200082 CrossRef CAS.
- T. Park, S. S. Kim, B. J. Lee, T. W. Park, H. J. Kim and C. S. Hwang, Nanoscale, 2023, 15, 6387–6395 RSC.
- S. S. Kim, S. K. Yong, J. Kim, J. M. Choi, T. W. Park, H. Y. Kim, H. J. Kim and C. S. Hwang, Adv. Electron. Mater., 2023, 9, 2200998 CrossRef CAS.
- Q. Huo, R. Song, D. Lei, Q. Luo, Z. Wu, Z. Wu, X. Zhao, F. Zhang, L. Li and M. Liu, IEEE Electron Device Lett., 2020, 41, 497–500 CAS.
- J. H. Yoon, S. J. Song, I. Yoo, J. Y. Seok, K. J. Yoon, D. E. Kwon, T. H. Park and C. S. Hwang, Adv. Funct. Mater., 2014, 24, 5086–5095 CrossRef CAS.
- J. H. Yoon, S. Yoo, S. J. Song, K. J. Yoon, D. E. Kwon, Y. J. Kwon, T. H. Park, H. J. Kim, X. L. Shao, Y. Kim and C. S. Hwang, ACS Appl. Mater. Interfaces, 2016, 8, 18215–18221 CrossRef CAS PubMed.
- E. Perez, A. Grossi, C. Zambelli, P. Olivo, R. Roelofs and C. Wenger, IEEE Electron. Dev. Lett., 2017, 38, 175–178 CAS.
- S. Roy, G. Niu, Q. Wang, Y. Wang, Y. Zhang, H. Wu, S. Zhai, P. Shi, S. Song, Z. Song, Z.-G. Ye, C. Wenger, T. Schroeder, Y.-H. Xie, X. Meng, W. Luo and W. Ren, ACS Appl. Mater. Interfaces, 2020, 12, 10648–10656 CrossRef CAS.
- S. Yu, B. Gao, H. Dai, B. Sun, L. Liu, X. Liu, R. Han, J. Kang and B. Yu, Electrochem. Solid-State Lett., 2009, 13, H36 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nh00420e |
| This journal is © The Royal Society of Chemistry 2025 |