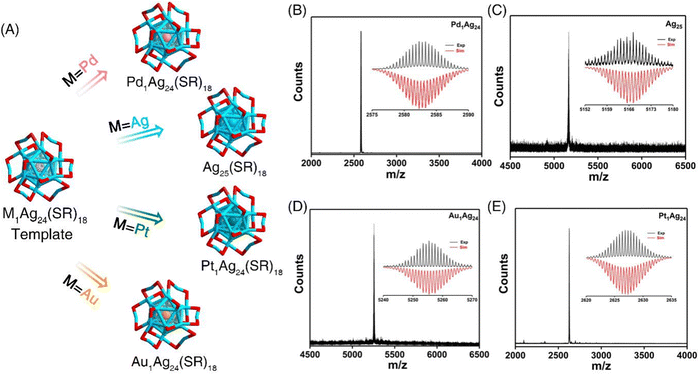
Record-high hyperpolarizabilities in atomically precise single metal-doped silver nanoclusters

Abstract

Recent developments in optical imaging techniques, particularly multi-photon excitation microscopy that allows studies of biological interactions at a deep cellular level, have motivated intensive research in developing multi-photon absorption fluorophores. Biological tissues are optically transparent in the near-infrared region. Therefore, fluorophores that can absorb light in the near-infrared (NIR) region by multi-photon absorption are particularly useful in bio-imaging. For instance, photoluminescence from ligand-protected gold nanoclusters has drawn extensive research interest in the past decade due to their bright, non-blinking, stable emission and tunability from the blue to the NIR emission. In this work, using the control of single metal doping on silver nanoclusters (Ag₂₅ protected by thiolate SR = 2,4-dimethylbenzenethiol (DMBT) ligand), we aim to explore the effects of metal doping on the (photo)stability and nonlinear optical response of liganded nanoclusters. We study two-photon excited photoluminescence and the second harmonic response upon excitation in the NIR (780–950 nm) range. Particular emphasis is placed on the effect of metal doping on the second-order nonlinear optical scattering properties (first hyperpolarizability, β(2ω)) of Ag₂₅ nanoclusters. In addition, β(2ω) values are one order higher than the one reported for Au₂₅ nanoclusters and represent the largest values ever reported for ligand-protected nanoclusters. Such enhanced hyperpolarizability leads to a strong second harmonic response and renders them attractive targets in bioimaging.

---

New concepts

In this work, we aim at opening a new route to controlling and tuning the desired nonlinear optical (NLO) properties for multi-photon absorption using metal nanoclusters. In previous work, it was difficult to achieve fluorophores that can absorb light in the NIR region by multi-photon absorption and display large multiphoton excited fluorescence and second harmonic generation, particularly useful in bio-imaging. Using the control of single metal doping on Ag₂₅ nanoclusters, we aimed at rationally exploring the effects of metal doping on the (photo)stability and nonlinear optical response of metal-doped liganded nanoclusters. We reported large multiphoton excited fluorescence brightness upon excitation in the NIR range. Particular emphasis is placed on the effect of metal doping to boost the second-order nonlinear optical scattering properties (first hyperpolarizability, β(2ω)) of Ag₂₅ nanoclusters. In particular, β(2ω) values are one-order higher than the one reported for Au₂₅ nanoclusters and represent the largest values ever reported. The trends observed in the hyperpolarizability values were further corroborated by quantum mechanical calculations evidencing resonance effects. The basic concepts presented here open a new route to controlling and tuning the desired NLO properties for biological molecular reporters using metal NCs.

Introduction

With the increasing application of femtosecond laser technology, nonlinear optical (NLO) imaging using a femtosecond pulsed laser as a light source has attracted much interest from researchers.¹ The nonlinear imaging methods that have attracted much attention include two-photon excited photoluminescence (2PEPL) imaging, coherent anti-Stokes Raman (CARS) imaging, and second harmonic generation (SHG) imaging.² Usually SHG, a second-order nonlinear effect, uses excitation light in the near-infrared region (700–1300 nm). NLO-phores capable of a high second harmonic (SH) response, can be found with organic molecules. In particular, molecules with electronic push–pull systems, which give rise to π-electron delocalization, present large optical hyperpolarizabilities.^3,4

Ligand-protected metal nanoclusters are an emerging class of quantum materials connecting the gap between atoms and bulk metallic materials.⁵ Owing to their “molecule-like” behavior, they display some analogy with push–pull molecules regarding their nonlinear optical response (coined as ligand-core NLO-phores).^6,7 Antoine et al. reported the first-hyperpolarizability, β(2ω), of glutathione-protected nanoclusters (Au₁₅ and Au₂₅) measured using the hyper-Rayleigh scattering (HRS) technique (with excitation at ∼800 nm).⁸ Further other reports demonstrate the interest of low-nuclearity gold nanoclusters as SH-active targets,^9–11 but first hyperpolarizability values were limited to hundreds of 10⁻³⁰ esu, which is at least one order of magnitude lower than the β(2ω) value of best push–pull systems.^3,12 It was found that both the number of metal atoms in the nanoclusters and their symmetry played a significant role in the first hyperpolarizabilities. In the quantum regime (“quantum clusters”), the highest hyperpolarizabilities were reported for the smallest nanoclusters, first outlined in ref. 8 and further demonstrated by Barbosa-Silva et al.¹³ Two critical parameters are the quantum confinement effect and asymmetry of the nanocluster geometry for nanoclusters with less than 10–15 atoms. Knoppe et al. further pushed the concept of symmetry-breaking by using chiral ligands and metal-doping of nanoclusters.⁹ However, the reported first hyperpolarizabilities were still limited to hundreds of 10⁻³⁰ esu, and metal doping did not enhance the hyperpolarizability of nanoclusters. The same conclusion was raised in our recent investigation on the effect of single platinum atom doping on the SH response of Ag₂₉ nanoclusters.¹⁴

In this work, using atomically precise nanochemistry and combining the quantum regime of small nanoclusters and metal doping strategies, we aim to explore the effect of single metal doping on the second-order nonlinear optical scattering properties of Ag₂₅ nanoclusters. A previous study has demonstrated that the single-atom substitution of the innermost Ag kernel in Ag₂₅(SR)₁₈ (SR = 2,4-dimethylbenzenethiol (DMBT)) by Au/Pd/Pt generated three M₁Ag₂₄(SR)₁₈ (M = Au/Pd/Pt) cluster derivatives with a maintained framework, rendering such a cluster series an ideal platform for investigating the structure–property correlations.¹⁵ However, other metals were difficult to incorporate into the cluster framework or would result in template-altered cluster products. In this context, the doping effects in this work were investigated based on Pd, Pt, and Au heteroatoms. The first hyperpolarizabilities of heteroatom-doped Ag₂₅ nanoclusters upon excitation at 800, 900, and 950 nm are reported. The results were confronted with quantum mechanical calculations. The nature of the metal dopant significantly affects the SH response of nanoclusters. In addition, β(2ω) values are one-order higher than the one reported for un-doped Au₂₅ nanoclusters and represent the largest values ever reported.

Results and discussion

Low nuclearity 25-atom silver and single metal doped silver nanoclusters protected by the 2,4-dimethylbenzenethiol (DMBT) ligand were synthesized using previously reported methods.^16–18 ESI-MS measurements were conducted to determine the identity and purity of the M₁Ag₂₄(SR)₁₈ nanoclusters (M = Pd Ag/Au/Pt, SR = 2,4-dimethylbenzenethiol (DMBT)) (Fig. 1). The presence of a single peak in the mass spectra and the perfect match between the experimental and simulated isotopic patterns of these clusters demonstrate the successful preparation of such M₁Ag₂₄(SR)₁₈ clusters at atomic precision.

Fig. 1 (A) Structural anatomy of M₁Ag₂₄(SR)₁₈ nanoclusters with different innermost kernels. The thiolate ligand SR used in this work is the DMBT ligand (simplified to SR for the sake of clarity). Color codes: red, S; dark blue, kernel Ag; orange, kernel Au; magenta, kernel Pd; purple, kernel Pt; and grey, C. For clarity, all H atoms were omitted. ESI-MS results of (B) Pd₁Ag₂₄(SR)₁₈, (C) Ag₂₅(SR)₁₈, (D) Au₁Ag₂₄(SR)₁₈, and (E) Pt₁Ag₂₄(SR)₁₈ nanoclusters. Spectra are recorded in the negative mode of ionization and show a −1 charge state for Ag₂₅(SR)₁₈, and Au₁Ag₂₄(SR)₁₈ and a −2 charge state for Pt₁Ag₂₄(SR)₁₈ and Pd₁Ag₂₄(SR)₁₈ nanoclusters. Insets: simulated (red lines) and experimental (black lines) isotope patterns matched well, demonstrating the successful preparation of such M₁Ag₂₄(SR)₁₈ clusters.

We then explore the stability of nanoclusters in organic solvents. DMF was used because nanoclusters presented the best stability over time. Nanoclusters also present good stability in CH₂Cl₂ and CHCl₃ (see Fig. S1, ESI†). However, these solvents are either toxic or present very low boiling points avoiding NLO experiments to be conducted. Nanoclusters present moderate stability in THF (degradation observed after 1 day) and poor stability in DMSO (see Fig. S1, ESI†). Photostability under laser irradiation was conducted on nanoclusters with visible and NIR light (see Fig. S2, ESI†). As displayed in Fig. S2 (ESI†), the photostability of M₁Ag₂₄(SR)₁₈ under laser excitation in the NIR region (under an 800 nm femtosecond laser) is much better than that in the visible part (under cw visible lasers), which makes it possible to investigate the NLO properties with a NIR laser. In Fig. S2 (ESI†), we show the photostability of Ag₂₅(SR)₁₈. Ag₂₅(SR)₁₈ loses the characteristic absorption after 473 nm and 532 nm laser irradiation, while absorption features remain similar after 800 nm and 950 nm laser irradiation. Actually, the photostability issue at different excitation wavelengths is related to the absorption of nanoclusters at this excitation wavelength. As the absorption spectra of M₁Ag₂₄(SR)₁₈ shown in Fig. S3 (ESI†), for all 4 nanoclusters, the laser excitation at 473 nm and 532 nm is close to the strongest absorption band located at 450–500 nm. On the other hand, the laser excitation at 800–950 nm is located beyond the first absorption band located at 600–700 nm. Thus, laser excitation in the NIR region leads to better photostability of nanoclusters than that in the visible part.

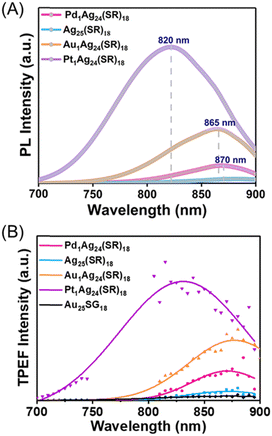
Optical spectra, in particular, specific narrow bands of absorption, excitation, and emission spectra were recorded, to further confirm the homogeneity of the nanoclusters. Replacing the central Ag atom with Au/Pt/Pd causes a notable change in the electronic structure of Ag₂₅(SR)₁₈,^15,19,20 as testified by UV-vis-NIR spectra recorded in DMF solvent (see Fig. S3, ESI†). In UV-vis absorption spectra (Fig. S3, ESI†), the first absorption bands originate from the core electronic states, and the significant blue shift in absorption bands is related to metal core alloying as a consequence of tuning the geometric and electronic structures, as confirmed by previous HOMO–LUMO calculations.²¹ The one-photon excited luminescence spectra of nanoclusters are reported in DMF (Fig. 2A), demonstrating that the emission intensity sequence is as follows: Pt₁Ag₂₄(SR)₁₈ > Au₁Ag₂₄(SR)₁₈ > Pd₁Ag₂₄(SR)₁₈ > Ag₂₅(SR)₁₈ (as already observed by Liu et al. with nanoclusters in acetonitrile).¹⁵ The two-photon excited photoluminescence spectra of nanoclusters (excited at 780 nm) are also reported in DMF (Fig. 2B). The same trend is observed in one-photon excited luminescence spectra for the emission intensity sequence (both in the band position and maximum intensity). Of note, the two-photon excited luminescence brightness of M₁Ag₂₄(SR)₁₈ clusters is also much higher than those of Au₂₅SG₁₈ (in particular for the Pt₁Ag₂₄(SR)₁₈ nanocluster, as depicted in Fig. S4, ESI†).

Fig. 2 (A) Photoluminescence spectra of M₁Ag₂₄(SR)₁₈ nanoclusters (with SR = DMBT) in DMF (excited at 490 nm). (B) 2PEPL spectra of the synthesized M₁Ag₂₄(SR)₁₈ nanoclusters in DMF with excitation at 780 nm and a final concentration of 10 μM, with a comparison of Au₂₅SG₁₈ (SG for glutathione).

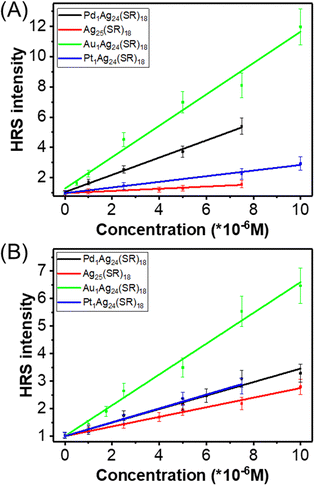Fig. 3 A plot of the HRS intensity of M₁Ag₂₄(SR)₁₈ nanoclusters (with SR = DMBT) as a function of concentration, recorded upon 900 nm (A) and 950 nm (B) laser excitation.

In addition to the multi-photon excited fluorescence dependence on nanoclusters, the effect of chemical substitution-based metal doping on the hyperpolarizability (β(2ω)) value of Ag₂₅ nanoclusters protected by a thiolate ligand (SR) was evaluated. This hyperpolarizability is a molecular measure for the efficiency of second-order nonlinear scattering or frequency-doubling at the molecular level. The Ag₂₅(SR)₁₈ cluster is composed of a centered icosahedral Ag₁₃ core, capped by six Ag₂(SR)₃ dimeric staples (outer shell), as shown in Fig. 1. Monodoped M₁Ag₂₄(SR)₁₈ retains the framework Ag₂₅(SR)₁₈ with the core Ag atom substituted by the Pd/Pt/Au atom in the central position.¹⁵ Ag₂₅(SR)₁₈ has an identical geometry to its Au counterpart, Au₂₅(SR)₁₈. A basic requirement is the absence of centro-symmetry in the molecular structure.

Hyperpolarizabilities in the range of 100–200 × 10⁻³⁰ esu were reported for Au₂₅(SR)₁₈ nanoclusters (see Table S1, ESI†), with different ligands, chiral (amino-acids) or achiral ligands (MBA ligands). For Ag₂₅(SR)₁₈, β(2ω) can reach more than 500 × 10⁻³⁰ esu upon 950 nm laser excitation (see Table S1, ESI†). Clearly, even if Au₂₅(SR)₁₈ or Ag₂₅(SR)₁₈ are quite symmetric clusters, the orientation of ligands in staple motifs in solution may induce symmetry-breaking. Finally, Jahn–Teller effects leading to distortion of the Au₁₃ core were evidenced in Au₂₅(SR)₁₈ nanoclusters.²² For metal-doped nanoclusters, the change in superatomic electronic configuration from 8-electron [Au₂₅]⁻ to 6-electron [PtAu₂₄]⁰ would lead to the splitting of the 1P orbital accompanying a Jahn–Teller-like distortion of the PtAu₁₂ core.²³

It was observed that reduced hyperpolarizability values of (82 ± 30) × 10⁻³⁰ esu and (58 ± 12) × 10⁻³⁰ esu for Pt₁Ag₂₈ nanoclusters protected by BDT and DHLA, respectively, at an excitation wavelength of 800 nm.¹⁴ Also, we measured in this work a similar hyperpolarizability value of 118 × 10⁻³⁰ esu for Pt₁Ag₃₀ nanoclusters protected by glutathione. However, the β(2ω) value of Ag₂₅ doped by a single platinum atom is dramatically enhanced by one order of magnitude (1001 × 10⁻³⁰ esu, see Table 1).

Table 1 Hyperpolarizability values for single Pt doping on silver nanoclusters at 800 nm excitation. Plots of the hyper-Rayleigh scattering (HRS) intensity for Pt₁Ag₂₄(SR)₁₈ and Pt₁Ag₃₀SG₁₉ nanoclusters as a function of concentration are given in Fig. S10 (ESI)

Nanoclusters	Excitation wavelength [nm]	β(2ω) [10^−30 esu]	Optical gap [nm]	Solvent	Ref.
Pt1Ag24(SR)18	800	1001	760	DMF	This work
Pt1Ag28DHLA12	800	58	610	Water	14
Pt1Ag28BDT12	800	82	625	DMF	14
Pt1Ag30SG19	800	118	700	Water	This work

---

Strictly, the first hyperpolarizability β(2ω) of a compound is independent of the intensity and concentration unless higher-order nonlinear processes set in or spurious phenomena like aggregation and degradation occur. The HRS intensity, in contrast, is indeed dependent on the intensity and concentration. Hence, further control experiments were carried out to ensure that the experimental conditions were suitable to determine the nanoclusters' first hyperpolarizability β(2ω) correctly. We operated concentration-dependence and power-dependence measurements to determine the first hyperpolarizability β(2ω) absolute values. Besides, we also performed measurements with another solvent, namely tetrahydrofuran (THF). Furthermore, we worked at moderate irradiation powers, limited to 500 mW, and with moderate nanocluster concentrations, limited to 10 μM, to avoid photo-degradation and other nonlinear processes like nonlinear absorption, nonlinear refraction, etc.

With regard to the solvent, our nanoclusters have limited stability in organic solvents other than DMF. They are however stable in chloroform but this solvent is toxic if inhaled or swallowed and our laser lab is not equipped for manipulating this kind of solvent. DCM is too volatile and would require working with a sealed cuvette and also under a fume hood (not available in the laser lab on the cuvette holder). The nanoclusters also have a short time stability in THF. Nevertheless, we successfully measured the hyperpolarizability value of THF with the known reference of water and it was found to be (0.20 ± 0.03) × 10⁻³⁰ esu at 800 nm. We already tried in our previous study¹⁴ to determine the hyperpolarizability of Pt-doped Ag₂₉ nanoclusters with THF as the solvent but unstable signals were observed. Unfortunately, unstable signals were likewise observed with metal-doped Ag₂₅ NCs preventing measurements in THF.

To better understand the key ingredients leading to changes in second-order nonlinear optical scattering properties, we further explore the single metal doping effect on the hyperpolarizability of mono-doped M₁Ag₂₄(SR)₁₈ nanoclusters. The effect of chemical substitution-based metal doping on the hyperpolarizability (β(2ω)) value of Ag₂₅ nanoclusters was evaluated at three excitation wavelengths (800 nm, 900 nm and 950 nm) in DMF. Unfortunately, due to the fact that the excitation wavelength at 800 nm is very close to the first absorption band of the nanoclusters, some photostability issues were observed. However, as already observed for Ag₂₉ nanoclusters, single Pt doping of Ag₂₅ nanoclusters significantly increases their (photo)stability. Thus it was possible to measure the hyperpolarizability (β(2ω)) values of Pt₁Ag₂₄(SR)₁₈ nanoclusters at 800 nm, 900 nm and 950 nm (see Table 2). A decrease in the hyperpolarizability (β(2ω)) values is observed from 800 nm to 950 nm and can be simply explained by resonance effects. Indeed, at 950 nm, the energy difference between the excitation photon energy (ω) and absorption bands is larger than those at 800 nm, and thus hyperpolarizability (β(2ω)) values are reduced (see Table 2). Of note, the hyperpolarizability (β(2ω)) value of Pt₁Ag₂₄(SR)₁₈ at 800 nm ((1001 ± 100) × 10⁻³⁰ esu) is much higher than that reported for Pt₁Ag₂₈ nanoclusters ((82 ± 30) × 10⁻³⁰ esu). Since the single platinum doping atom is located at the center of the Ag kernel for silver nanoclusters (and thus would not affect the symmetry), the difference in (β(2ω)) values may be attributed to resonance effects. Indeed, optical gaps for Pt₁Ag₂₈ and Pt₁Ag₃₀ nanoclusters are blue-shifted as compared to Pt₁Ag₂₄(SR)₁₈ nanoclusters (increasing the energy difference between the excitation photon energy (ω) and absorption bands for Pt silver nanoclusters, see Table 1). Of note, the experimental value for the hyperpolarizability of Pt₁Ag₂₄(SR)₁₈ at 800 nm is, in comparison with other silver and gold nanoclusters, the largest value ever reported (see Table S1, ESI†).^8,13,24 At the excitation wavelengths of 900 and 950 nm, all nanoclusters displayed enough photostability to allow hyper-Rayleigh scattering experiments to be conducted, and thus hyperpolarizability (β(2ω)) values were obtained for all M₁Ag₂₄(SR)₁₈ nanoclusters (see Table 2). Clearly, single metal doping on Ag₂₅(SR)₁₈ nanoclusters strongly affects the hyperpolarizability (β(2ω)) values. For instance, doping with gold increases the hyperpolarizability of nanoclusters by a factor close to 2 as compared to bare Ag₂₅(SR)₁₈ nanoclusters. These hyperpolarizability values have to be compared with those reported for typical organic molecules with push–pull structures. As a reference, the hyperpolarizability value of a standard nonlinear optical compound used in our group,²⁵ namely 4-(4-dihexadecylaminostyryl)-N-methylpyridinium (DiA) dispersed in methanol, is (1760 ± 53) × 10⁻³⁰ esu.

Table 2 Hyperpolarizability values for single metal doping on Ag₂₅ nanoclusters protected by SR = DMBT at 800 nm, 900 nm and 950 nm excitation. HRS measurements on nanoclusters were done in DMF solution (the hyperpolarizability values for DMF were measured with the known reference of water and were found to be 0.35 × 10⁻³⁰ esu at both 800, 900 and 950 nm). Plots of the HRS intensity for nanoclusters as a function of concentration (recorded at 800 nm and 950 nm laser excitation) are given in Fig. 3

Nanoclusters	Hyperpolarizability β (10^−30esu)	Hyperpolarizability β (10^−30esu)	Hyperpolarizability β (10^−30esu)
	Excitation: 800 nm	Excitation: 900 nm	Excitation: 950 nm
Ag25(SR)18		316 ± 50	516 ± 50
Au1Ag24(SR)18		1310 ± 130	933 ± 90
Pd1Ag24(SR)18		1007 ± 100	615 ± 60
Pt1Ag24(SR)18	1001 ± 100	563 ± 90	611 ± 90

---

To gain a basic understanding of the origin of hyperpolarizability, one can consider a 2-state system (see Scheme S1, ESI†). If the incident light is close to being one-photon resonant with the first excited state (E₁ − E₀ ∼ ω) and two-photon resonant with a higher electronic state (E₂ − E₀ ∼ 2ω), which is the case with the two first absorption bands in M₁Ag₂₄(SR)₁₈ nanoclusters and using photons at excitation wavelengths of 800–950 nm (see Fig. S5, ESI†), then the dominant contribution to the HRS is:²⁶

where Γ corresponds to an energy-broadening term that can be related to the finite lifetime of the excited state. Clearly, if the excitation energy is close to the first and/or the second excited states, resonance effects occur enhancing hyperpolarizability values (denominator of eqn (1)). 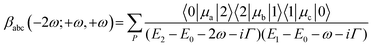Also, the charge transfer character of excitation leads to large transition dipole moments, also contributing to large hyperpolarizability values (numerator of eqn (1)).

We anticipate that single metal doping will affect the charge transfer capability of nanoclusters. Also, since optical gaps strongly depend on the nature of the metal dopant, we expect to observe strong effects on the hyperpolarizability values. To better evaluate these effects, we plotted the correlation between hyperpolarizability (β(2ω)) values and some relevant properties leading to charge transfer and resonance effects (see Fig. S6, ESI†). We found a correlation between hyperpolarizability (β(2ω)) values, charge transfer capability and resonance factor (e.g., the denominator in eqn (1)). Also, a qualitative trend is observed for charge effects such as natural population analysis (NPA). A high NPA charge value means a high affinity to the delocalized electrons of bonding sulfur. The same qualitative trend is observed for electron affinity and bond length, probing the capability of attracting electrons and charge transfer.²²

The importance of the above-mentioned effects on the hyperpolarizability values was further corroborated by quantum mechanical calculations. The calculated first hyperpolarizability β(2ω) values for the lower-energy M₁Ag₂₄(SR)₁₈ structures are presented in Table S2 (ESI†) and are in qualitative agreement with the experimental values. The trends are reproduced, in particular, the evolution of hyperpolarizability (β(2ω)) values as a function of excitation wavelength, demonstrating resonance effects. The fact that first absorption bands in calculated spectra (in the gas phase) are significantly blue-shifted (see Fig. S7, ESI†) as compared to experimental ones (in the solution phase) may explain that only a qualitative agreement is observed for such β(2ω) values at the measured excitation wavelengths (800–950 nm). In order to gain insights into different linear absorption for the Au₁Ag₂₄(SR)₁₈ presented in this work from the previously published one (see ref. 21), additional theoretical characterization was necessary to address structure–property relationships of the electronic transitions. Fig. S9 (ESI†) presents the difference in metal core and staple motifs for DFT optimized geometries of Au₁Ag₂₄(SR)₁₈ (ref. 21 and 27) and Au₁Ag₂₄(SR)₁₈ (this work). Distortions presented in Fig. S9 (ESI†) could result in a more symmetric metallic core and overall structure, which would explain the blue-shifted spectra. Further doping with various elements, as well as considering the effect of ligand reorganization in solvents has a noticeable influence on hyperpolarizabilities. Another important point is that taking fully explicit ligands (instead of SCH₃ simplistic ligands) leads to a strong enhancement in calculated β(2ω) values, demonstrating that asymmetry of ligands on the surface of the nanoclusters is also responsible for large hyperpolarizabilities. Finally, we point out that the β(2ω) values are calculated in the gas phase. Accurately calculating frequency-dependent β(2ω) values for molecular systems in liquid environments remains challenging due to the need for a detailed description of all involved compounds. A particularly useful computational approach for simulating the behavior of nanoclusters in solution is the implicit polarizable continuum model (PCM). PCM incorporates the effects of a polarizable solvent continuum, defined by its dielectric constant, to mimic the solvent surrounding the solute molecule. This method is especially practical for estimating solvent effects on molecular properties such as electronic structure, optical characteristics, and response properties like frequency-dependent β(2ω) values.²⁸

In this study, the TD-DFT one-photon absorption and hyperpolarizabilities of Ag₂₅(SR)18 and M₁Ag₂₄(SR)₁₈ in the absence and presence of organic solvents were calculated (Fig. S7 and S8, ESI†). The solvent effect was modeled using the polarizable continuum model (PCM) within the TD-DFT framework (presented in Table S2, ESI†). Note the significantly elevated values of the calculated frequency-dependent hyperpolarizabilities of nanoclusters in solvents. The discrepancy between the calculated and experimental β(2ω) values may partially stem from the lack of a detailed and explicit solvent description. Accurately modeling the solvent environment requires complex calculations, as it involves accounting for the dynamic interactions between the solvent molecules and the solute. The TD-DFT calculated absorption wavelengths of Ag₂₅(SR)₁₈ and M₁Ag₂₄(SR)₁₈ with the addition of a polar solvent is slightly shifted to a longer wavelength (red shift) mainly due to solvatochromism arising from the interaction between the solvent and the solute molecule. The polarity and dielectric properties of a solvent can affect hyperpolarizability by influencing the spatial distribution of electron density, altering linear and nonlinear optical properties thereby modifying its behavior in response to an electric field.²⁹

Conclusions

In this work, single metal doping on Ag₂₅ nanoclusters obtained at atomic precision allows for a confident exploration of the effect of metal doping on the second-order nonlinear optical scattering properties. Single metal doped nanoclusters, with Au, Pd and Pt as dopants present enhanced hyperpolarizability values upon excitation located in the NIR window and we report record-high hyperpolarizabilities in molecule-like nanoclusters. Such enhanced hyperpolarizability leads to a strong second harmonic response and renders them attractive targets in the field of bioimaging. However, to be attractive, such nanoclusters should be more photostable, biocompatible and water-soluble. To render such NCs attractive for bioapplications, encapsulation or micellization strategies³⁰ should be explored. Following the trends for large hyperpolarizabilities reported in this work, we can provide some guidelines to further enhance the nonlinear optical properties through the design of metal nanoclusters. On the one hand, by increasing the core size, we expect to decrease optical gaps, thereby shifting the resonance effects towards SWIR light (an appealing property for bio-applications). On the other hand, decreasing the size of the core will lead to lower symmetry structures and thus would further enhance hyperpolarizabilities.⁸ In addition, metal doping strategies might be further explored. By doping more than one heterometal atom, the asymmetry of the cluster kernel will be increased.³¹ Finally, ligand strategies can be explored with molecules with more delocalized electrons (e.g. push–pull thiolated molecules) increasing polarizable effects. Work on these lines is currently underway in our lab.

Experimental section

Materials

All the following reagents were purchased from Sigma-Aldrich and used without further purification, including silver nitrate (AgNO₃, 99%), tetrachloroauric(III) acid (HAuCl₄·4H₂O, 99% metal basis), hexachloroplatinic(IV) acid (H₂PtCl₆·6H₂O, 99% metal basis), palladium chloride acid (H₂PdCl₄, 99% metal basis), 2,4-dimethylbenzenethiol (HSPhMe₂, 97%, DMBT), tetraphenylphosphonium bromide (PPh₄Br, 98%), sodium borohydride (NaBH₄, 99%), fluorescein, methanol (MeOH, HPLC grade), dichloromethane (CH₂Cl₂, HPLC grade), n-hexane (HPLC grade), N,N-dimethylformamide (DMF), and tetrahydrofuran (THF).

Synthesis of M₁Ag₂₄(SR)₁₈ nanoclusters

Ag₂₅(SR)₁₈, Au₁Ag₂₄(SR)₁₈, Pd₁Ag₂₄(SR)₁₈, and Pt₁Ag₂₄(SR)₁₈ nanoclusters (with SR = DMBT) were prepared by using previously reported methods.^16–18

Characterization

The optical absorption spectra of nanoclusters were recorded using an Agilent 8453 diode array spectrometer with the same optical density of 0.1 of the cluster samples. Photoluminescence (PL) spectra were measured using an FL-4500 spectrofluorometer with the same optical density of 0.1 of the cluster samples. Electrospray ionization mass spectrometry (ESI-MS) measurements were performed using a Waters XEVO G2-XS QTof mass spectrometer. The sample was directly infused into the chamber at 5 μL min⁻¹. For preparing the ESI samples, the nanoclusters were dissolved in CH₂Cl₂ (1 mg mL⁻¹) and diluted (v/v = 1 : 1) with CH₃OH.

Non-linear optics (NLO) characterization

Two-photon fluorescence measurements were performed with a customized confocal microscope (TE2000-U, Nikon Inc.) in which the excitation light entrance has been modified to allow free-space laser beam input, instead of the original optical-fiber light input. The luminescence was excited at 780 nm with a mode-locked frequency-doubled femtosecond Er-doped fiber laser (C-Fiber 780, MenloSystems GmbH). The output power of the femtosecond laser was 62 mW. The laser spectrum was bounded by two filters (FELH0750 and FESH0800, Thorlabs Inc.). The laser beam was focused using a Nikon CFI Plan Apo VC objective (20×/0.75 NA) on a sample containing NCs. The emitted signal was collected in the epifluorescence illumination mode at 50 μm from the bottom of the sample holder. The two-photon fluorescence emission was separated from the incident light through a dichroic mirror (NFD01-785, IDEX Health & Science LLC) and an FESH0750 filter to obtain the visible range, and an FELH0800 to obtain an NIR range. The two-photon fluorescence emission spectra were recorded using an iHR320 spectrometer equipped with a 53 024 grating from Horiba Jobin Yvon and detected using a −30 °C cooled photomultiplier tube (R943-02, Hamamatsu Photonics). Two-photon excited photoluminescence (2PEPL) cross-sections were measured, extracted and calculated using a reference method according to the following equation:
where σ_2PEFL is the two-photon excited fluorescence cross-section, c is the concentration, and I is the fluorescence intensity. Fluorescein (10 μM) was used as a reference solution. At 780 nm, the σ^ref₂ value of the fluorescein is 33.3 GM.³²

For hyper-Rayleigh scattering, the output of a femtosecond Ti–sapphire laser (Chameleon Ultra I, Coherent) with a pulse duration of about 140 fs centered at wavelengths of 800, 900 and 950 nm was used to generate incoherent second harmonic scattered light from the sample cell. The optical cell was made from fused silica and had an optical path of 5 mm. The HRS light was then detected with a photomultiplier tube working in the single photon counting regime. The first hyperpolarizability of the different nanoclusters was obtained using the internal reference method, where the output scattered harmonic intensity is recorded as a function of the nanocluster concentration in DMF. The first hyperpolarizability of DMF was obtained using the external reference method, where the output scattered harmonic intensity is recorded as a function of the input power of the fundamental intensity and plotted as a function of the square root of this fundamental intensity. Linear plots were thus obtained, and slopes were compared to a reference (see Fig. S11, ESI†). Here, we used ultrapure water (resistivity of 18.2 MΩ) as the reference, the first hyperpolarizability of which is taken as 0.087 × 10⁻³⁰ esu.³³

Computational studies

Density functional theory (DFT) and time-dependent density functional theory (TD-DFT) have been used to investigate the structural and optical properties of M₁Ag₂₄(SR)₁₈ as well as the Au, Pt, and Pd doped liganded silver NCs, as implemented in Gaussian computational chemistry software.³⁴ The structural and optical properties were calculated for liganded nanoclusters with fully explicit ligands – DMBT and with ligands replaced with SCH3 in order to gain insight into the ligand effect on properties. For all calculations, the SVP atomic orbital (AO) basis set³⁵ was used for Ag, Pt, Pd, Au and S atoms, together with the relativistic effective core potential (RECP) of the Stuttgart group.³⁶ For ligands, the 3-21G split-valence basis set³⁷ was used. The PBE functional^38,39 was employed for the structural optimizations. The initial structures were taken from crystal structures^15,16 and were reoptimized using the above-described methodology. TD-DFT calculations of linear (one-photon) absorption spectra were done for all the structures (with full ligands and with SCH₃ ligands) using the Coulomb attenuated version of Becke's three-parameter non-local exchange functional together with the Lee–Yang–Parr gradient-corrected correlation functional (CAM-B3LYP).⁴⁰ The relativistic effective core potential (RECP) of the Stuttgart group³⁵ was employed for metal atoms. TD-DFT calculations of frequency-dependent hyperpolarizabilities were obtained within Gaussian computational chemistry software.^34,41

For the theoretical investigation of the dichloromethane (DCM) solvent effect on the absorption spectra and frequency-dependent hyperpolarizabilities of liganded nanoclusters with fully explicit ligands, the implicit polarizable continuum method (PCM) was used and implemented in Gaussian as the integral equation formalism variant (IEFPCM).⁴²

Author contributions

Hao Yuan: investigation, methodology, formal analysis, writing – original draft, and writing – review & editing; Isabelle Russier-Antoine: investigation, methodology, formal analysis, and writing – review & editing; Christophe Moulin: investigation and writing – review & editing; Pierre-François Brevet: writing – review & editing and methodology; Željka Sanader Maršić: methodology and formal analysis; Martina Perić Bakulić: investigation, methodology, formal analysis, and writing – review & editing; Xi Kang: conceptualization, investigation, methodology, and writing – review & editing; Rodolphe Antoine: conceptualization, writing – original draft, writing – review & editing, funding acquisition, and supervision; and Manzhou Zhu: conceptualization, funding acquisition, and supervision.

Data availability

The data supporting this article have been included as part of the ESI.† All other relevant data are available from the corresponding authors upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

H. Y. is grateful for the PhD scholarship from the China Scholarship Council (CSC, No. 202206140023). R. A. acknowledges the Higher Education Institution Academic Discipline Innovation and Talent Introduction Plan for visiting the School of Chemistry and Chemical Engineering of Anhui University. Ž. S. M. and M. P. B. acknowledge computational facilities of the HPC computer within the University Computing Center in Zagreb, Croatia. This research was partially supported by the project STIM—REI, Contract Number: KK.01.1.1.01.0003, funded by the European Union through the European Regional Development Fund—the Operational Programme Competitiveness and Cohesion 2014–2020 (KK.01.1.1.01). M. Z. and X. K. acknowledge the financial support from the NSFC (22371003 and 22201001).

Notes and references

1. Y. Zeng, Q. Sun and J. Y. Qu, in Handbook of Photonics for Biomedical Engineering, ed. A. H.-P. Ho, D. Kim and M. G. Somekh, Springer Netherlands, Dordrecht, 2017, pp. 461–501 DOI:10.1007/978-94-007-5052-4_9.
2. M. Sun, X. Mu and R. Li, in Linear and Nonlinear Optical Spectroscopy and Microscopy, ed. M. Sun, X. Mu and R. Li, Springer Nature Singapore, Singapore, 2024, pp. 1–7 DOI:10.1007/978-981-99-3637-3_1.
3. S. R. Marder, L.-T. Cheng, B. G. Tiemann, A. C. Friedli, M. Blanchard-Desce, J. W. Perry and J. Skindhøj, Science, 1994, 263, 511–514.
4. T. Verbiest, S. Houbrechts, M. Kauranen, K. Clays and A. Persoons, J. Mater. Chem., 1997, 7, 2175–2189.
5. R. C. Jin, C. J. Zeng, M. Zhou and Y. X. Chen, Chem. Rev., 2016, 116, 10346–10413.
6. V. Bonacic-Koutecky and R. Antoine, Nanoscale, 2019, 11, 12436–12448.
7. J. Olesiak-Banska, M. Waszkielewicz, P. Obstarczyk and M. Samoc, Chem. Soc. Rev., 2019, 48, 4087–4117.
8. I. Russier-Antoine, F. Bertorelle, M. Vojkovic, D. Rayane, E. Salmon, C. Jonin, P. Dugourd, R. Antoine and P.-F. Brevet, Nanoscale, 2014, 6, 13572–13578.
9. N. Van Steerteghem, S. Van Cleuvenbergen, S. Deckers, C. Kumara, A. Dass, H. Häkkinen, K. Clays, T. Verbiest and S. Knoppe, Nanoscale, 2016, 8, 12123–12127.
10. S. Knoppe, M. Vanbel, S. van Cleuvenbergen, L. Vanpraet, T. Bürgi and T. Verbiest, J. Phys. Chem. C, 2015, 119, 6221–6226.
11. S. Knoppe, Q.-F. Zhang, X.-K. Wan, Q.-M. Wang, L.-S. Wang and T. Verbiest, Ind. Eng. Chem. Res., 2016, 55, 10500–10506.
12. J. L. Liu, C. B. Ouyang, F. Y. Huo, W. Q. He and A. C. Cao, Dyes Pigm., 2020, 181, 108509.
13. R. Barbosa-Silva, M. L. Silva-Neto, D. Bain, L. Modesto-Costa, T. Andrade-Filho, V. Manzoni, A. Patra and C. B. de Araújo, J. Phys. Chem. C, 2020, 124, 15440–15447.
14. H. Fakhouri, E. Salmon, X. Wei, S. Joly, C. Moulin, I. Russier-Antoine, P.-F. Brevet, X. Kang, M. Zhu and R. Antoine, J. Phys. Chem. C, 2022, 126, 21094–21100.
15. X. Liu, J. Yuan, C. Yao, J. Chen, L. Li, X. Bao, J. Yang and Z. Wu, J. Phys. Chem. C, 2017, 121, 13848–13853.
16. C. P. Joshi, M. S. Bootharaju, M. J. Alhilaly and O. M. Bakr, J. Am. Chem. Soc., 2015, 137, 11578–11581.
17. M. S. Bootharaju, C. P. Joshi, M. R. Parida, O. F. Mohammed and O. M. Bakr, Angew. Chem., Int. Ed., 2016, 55, 922–926.
18. X. Kang, S. Chen, S. Jin, Y. Song, Y. Xu, H. Yu, H. Sheng and M. Zhu, ChemElectroChem, 2016, 3, 1261–1265.
19. F. Alkan, P. Pandeya and C. M. Aikens, J. Phys. Chem. C, 2019, 123, 9516–9527.
20. Z. Liu, M. Zhou, L. Luo, Y. Wang, E. Kahng and R. Jin, J. Am. Chem. Soc., 2023, 145, 19969–19981.
21. A. Pniakowska, K. Kumaranchira Ramankutty, P. Obstarczyk, M. Perić Bakulić, Ž. Sanader Maršić, V. Bonačić-Koutecký, T. Bürgi and J. Olesiak-Bańska, Angew. Chem., Int. Ed., 2022, 61, e202209645.
22. M. A. Tofanelli, K. Salorinne, T. W. Ni, S. Malola, B. Newell, B. Phillips, H. Häkkinen and C. J. Ackerson, Chem. Sci., 2016, 7, 1882–1890.
23. K. Kwak, W. Choi, Q. Tang, M. Kim, Y. Lee, D.-e Jiang and D. Lee, Nat. Commun., 2017, 8, 14723.
24. I. Russier-Antoine, F. Bertorelle, R. Hamouda, D. Rayane, P. Dugourd, Ž. Sanader, V. Bonačić-Koutecký, P.-F. Brevet and R. Antoine, Nanoscale, 2016, 8, 2892–2898.
25. G. Revillod, J. Duboisset, I. Russier-Antoine, E. Benichou, G. Bachelier, C. Jonin and P.-F. Brevet, J. Phys. Chem. C, 2008, 112, 2716–2723.
26. Z. Hu, J. Autschbach and L. Jensen, J. Chem. Phys., 2014, 141, 124305.
27. K. R. Krishnadas, L. Sementa, M. Medves, A. Fortunelli, M. Stener, A. Fürstenberg, G. Longhi and T. Bürgi, ACS Nano, 2020, 14, 9687–9700.
28. B. Mennucci, J. Tomasi, R. Cammi, J. R. Cheeseman, M. J. Frisch, F. J. Devlin, S. Gabriel and P. J. Stephens, J. Phys. Chem. A, 2002, 106, 6102–6113.
29. R. Cammi, B. Mennucci and J. Tomasi, J. Am. Chem. Soc., 1998, 120, 8834–8847.
30. X. Kang, X. Wei, P. Xiang, X. Tian, Z. Zuo, F. Song, S. Wang and M. Zhu, Chem. Sci., 2020, 11, 4808–4816.
31. X. Liu, E. Wang, M. Zhou, Y. Wan, Y. Zhang, H. Liu, Y. Zhao, J. Li, Y. Gao and Y. Zhu, Angew. Chem., Int. Ed., 2022, 61, e202207685.
32. M. A. Albota, C. Xu and W. W. Webb, Appl. Opt., 1998, 37, 7352–7356.
33. J. Duboisset, G. Matar, I. Russier-Antoine, E. Benichou, G. Bachelier, C. Jonin, D. Ficheux, F. Besson and P. F. Brevet, J. Phys. Chem. B, 2010, 114, 13861–13865.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016.
35. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
36. M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1989, 90, 1730–1734.
37. J. S. Binkley, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102, 939–947.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
39. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
40. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
41. J. E. Rice and N. C. Handy, Int. J. Quantum Chem., 1992, 43, 91–118.
42. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.

---

Footnote

† Electronic supplementary information (ESI) available: Additional figures and data. See DOI: https://doi.org/10.1039/d4nh00454j

---