Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Membrane-mediated interactions between arc-shaped particles strongly depend on membrane curvature
Francesco
Bonazzi
and
Thomas R.
Weikl
 *
*
Max Planck Institute of Colloids and Interfaces, Am Mühlenberg 1, 14476 Potsdam, Germany. E-mail: thomas.weikl@mpikg.mpg.de
First published on 17th February 2025
Abstract
Besides direct molecular interactions, proteins and nanoparticles embedded in or adsorbed to membranes experience indirect interactions that are mediated by the membranes. Membrane-mediated interactions between curvature-inducing proteins or nanoparticles can lead to assemblies of particles that generate highly curved spherical or tubular membrane shapes, but have mainly been quantified for planar or weakly curved membranes. In this article, we systematically investigate the membrane-mediated interactions of arc-shaped particles adsorbed to a variety of tubular and spherical membrane shapes with coarse-grained modelling and simulations. These arc-shaped particles induce membrane curvature by binding to the membrane with their inner, concave side akin to N-BAR domain proteins. We determine both the pairwise interaction free energy, which includes entropic contributions due to rotational entropy loss at close particle distances, and the pairwise interaction energy without entropic components from particle distributions observed in the simulations. For membrane shapes with small curvature, the membrane-mediated interaction free energies of particle pairs exceed the thermal energy kBT and can lead to particle ordering and aggregation. The interactions strongly decrease with increasing curvature of the membrane shape and are minimal for tubular shapes with membrane curvatures close to the particle curvature.
Introduction
The intricately curved shapes of biological membranes are generated by protein assemblies.1–4 BAR (BIN/amphiphysin/Rvs) domain proteins, for example, generate curvature by imposing their arc-like shape on membranes upon binding5–8 and can induce membrane tubules9 covered by dense protein coats10–12 or by less dense protein arrangements,13,14 depending on the protein type and concentration. While the assembly of proteins or particles in solution is typically driven by direct molecular interactions,15–18 assemblies of membrane-associated proteins or membrane-adsorbed particles can also result from indirect interactions that are mediated by the membrane.19–23 Simulations and numerical approaches with a variety of different models24,25 indicate that such indirect interactions play a role in the tubulation of membranes by assemblies of arc-shaped proteins and particles,26–32 can lead the cooperative wrapping of spherical33–43 and elongated particles37,38, and can result in assemblies of membrane-adsorbed Janus particles,44–50 elastic particles,51 and hinge-like particles.52–54 Membrane-mediated interactions and assembly of spherical particles55–61 as well as the cooperative wrapping of spherical virus-like particles62 and rod-like particles63 by membranes have also been observed in experiments.These membrane-mediated interactions result from a change of the membrane curvature induced by the particles or proteins and, therefore, can be expected to depend on the equilibrium curvature or shape of the membranes. However, membrane-mediated pair interactions have mainly been quantified for curvature-inducing model proteins or particles that are adsorbed to or embedded in initially planar or weakly curved membranes.44,45,64–76 Recent exceptions are the pair interactions of spherical Janus particles,46,48 which have been found to depend on whether the particles adsorb to the inside or outside of the vesicles, and the pair interactions of spherical particles adsorbed to vesicles with different sizes.77 The pair interaction energies between curvature-inducing particles or proteins have been determined based on minimum-energy shapes of membranes45,64,68,69,72,74,76 and vesicles46,70 with two embedded or adsorbed particles, or from simulations with constraints on the distance of particle pairs.44,48
In this article, we determine the effective membrane-mediated pair interactions of arc-shaped particles on tubular and spherical membrane vesicles from pair distributions of the particles observed in Monte Carlo simulations. In our coarse-grained model of membrane shaping, the membrane is described as a triangulated elastic surface, and the particles as segmented arcs that induce membrane curvature by binding to the membrane with their inner, concave side.31 In previous work, we found that the vesicle shapes induced by the particles are determined by the arc angle and membrane coverage of the particles, and that membrane tubulation is induced by the particles above a threshold coverage of roughly 50%,31,32 in agreement with experimental observations for amphiphysin N-BAR domains.14 In this work, in contrast, the vesicle shape is fixed by the volume-to-area ratio of the vesicles, and the particle coverage in our simulations is adjusted to relatively small values between 5% and 20% to identify the particles’ pair interactions and the dependence of these pair interaction on the membrane curvature of the spherical and tubular vesicle shapes. We determine the membrane-curvature-dependent effective pair interaction free energy of the particles by comparing pair distributions of the particles obtained from simulations to ideal distributions of non-interacting particles. These interaction free energies include entropic components from the loss of rotational entropy of the arc-shaped particles at close distances due to steric hindrance, besides the curvature-mediated interaction energies. In addition, we determine the effective pair interaction energies of the particles by comparing the pair distributions obtained from simulations to hard-core pair distributions of ‘flattened’ particles with the same shape, to quantify the curvature-mediated interaction of the particles without entropic components. We find that both the interaction free energies and the interaction energies strongly decrease with increasing curvature of the membrane shape and are minimal for tubular shapes with membrane curvatures close to the particle curvature.
Results
Conformations of arc-shaped particles on tubular and spherical vesicles
Fig. 1 and 2 illustrate simulation conformations of closed tubular and spherical membranes with bound arc-shaped particles. In our simulation model, the membranes are dynamically triangulated surfaces composed of 2000 triangles with a constrained total area A (see Methods). The volume V enclosed by the membrane is constrained to different values in the simulations, which results in the different membrane shapes shown in Fig. 1 and 2. The constrained volume-to-area ratio of the membrane can be quantified by the reduced volume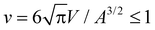 , which adopts its maximum value of 1 for an ideal sphere. In our simulations of spherical membranes, we constrain the reduced volume to v = 0.95 to allow for small variations and fluctuations around the overall spherical shape and to prevent shape changes that occur already at small particle coverages in the absence of such volume constraints.31 In our simulations of spherocylindrical, tubular membranes, the reduced volume is fixed to v = 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, or 0.65. The tubular membrane shapes are metastable, because the stable membrane shape is an oblate ellipsoid for 0.592 ≲ v ≲ 0.652 and a stomatocyte for 0 < v ≲ 0.592.78,79 The metastable tubular shapes are protected against transformations into the stable membrane shapes by an energy barrier that depends on the bending rigidity κ.79 To ensure a sufficiently large energy barrier, we use the relatively large bending rigidity value κ = 30kBT from the range of typical bending rigidities of lipid membranes between about 10 and 40kBT.80,81
, which adopts its maximum value of 1 for an ideal sphere. In our simulations of spherical membranes, we constrain the reduced volume to v = 0.95 to allow for small variations and fluctuations around the overall spherical shape and to prevent shape changes that occur already at small particle coverages in the absence of such volume constraints.31 In our simulations of spherocylindrical, tubular membranes, the reduced volume is fixed to v = 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, or 0.65. The tubular membrane shapes are metastable, because the stable membrane shape is an oblate ellipsoid for 0.592 ≲ v ≲ 0.652 and a stomatocyte for 0 < v ≲ 0.592.78,79 The metastable tubular shapes are protected against transformations into the stable membrane shapes by an energy barrier that depends on the bending rigidity κ.79 To ensure a sufficiently large energy barrier, we use the relatively large bending rigidity value κ = 30kBT from the range of typical bending rigidities of lipid membranes between about 10 and 40kBT.80,81
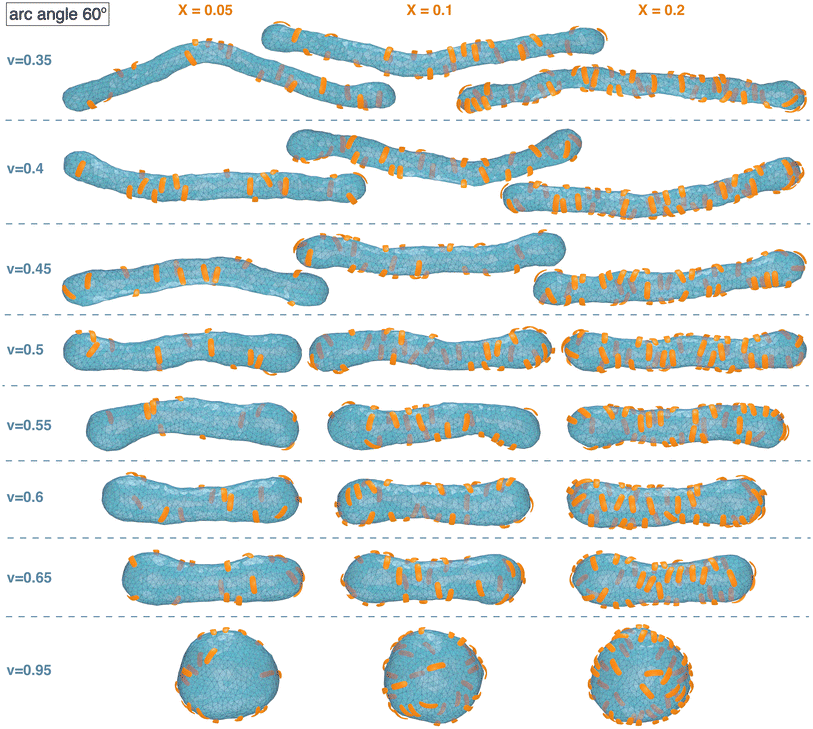 | ||
| Fig. 1 Exemplary simulation conformations for particles with arc angle 60° at different area coverages X and reduced volume v of the membrane. | ||
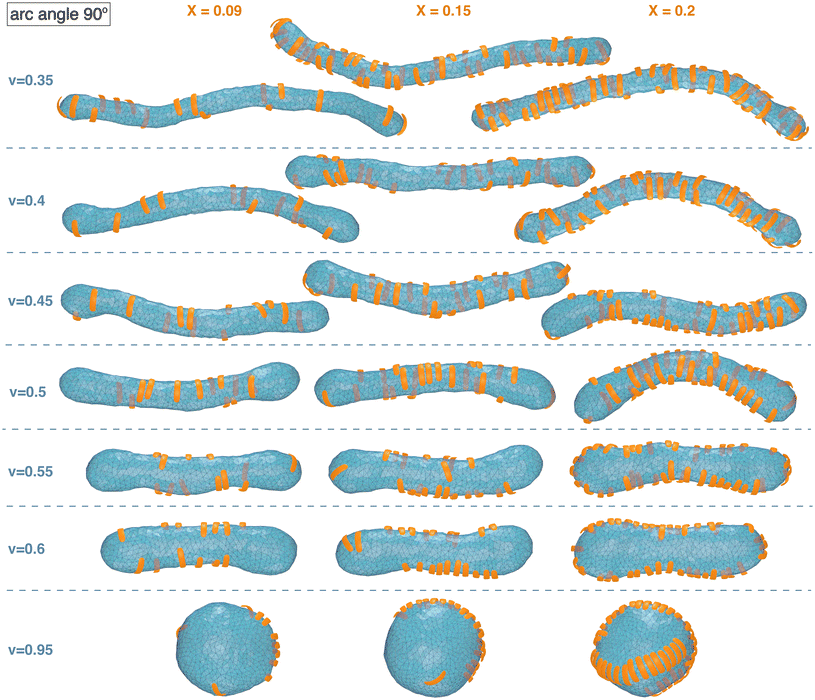 | ||
| Fig. 2 Exemplary simulation conformations for particles with arc angle 90° at different area coverages X and reduced volume v of the membrane. | ||
The arc-shaped particles of our model are composed of either 3 or 4 quadratic segments with side length ap and an angle of 30° between adjacent segments. The arc angle of the particles, i.e. the angle between the terminal segments, thus is 60° for particles composed of 3 segments, and 90° for particles composed of 4 segments. The particles bind to the membrane with their inner, concave sides. A particle segment is bound to the triangulated membrane of our model if its distance to the closest membrane triangle is within a given range, and if the particle segment and membrane triangle are nearly parallel with an angle that is smaller than the cutoff angle 10° (see Methods for details). The relative area of the particle segments and membrane triangles is chosen such that a particle segment can only be bound to a single membrane triangle. The particles can bind to and unbind from the membranes in the simulations. The equilibrium fraction of membrane-bound particles depends on the adhesion energy U per particle segment and on the total number of particles in the simulation box with volume Vbox ≃ 3 × 105am3, which is 64 times as large as the volume of a perfect sphere with the area A0 of the membrane vesicle.31 In our simulations, the area fraction X of the membrane covered by bound particles is kept at a constant value between 5% and 20% by dynamically adjusting the adhesion energy U per particle segment for a total particle number of 400 that greatly exceeds to number of bound particles at all values of X.
The simulation conformations in Fig. 1 and 2 illustrate a tendency of the particles to align side by side that increases with increasing reduced volume v of the membrane and with increasing arc angle of the particles. At the reduced volume v = 0.95, particles with arc angle 90° form linear aggregates on the spherical membranes (see Fig. 2). This alignment and aggregation of the particles is driven by membrane-mediated interactions, because the direct particle–particle interactions are purely repulsive in our model (see Methods).
Interaction free energies
The membrane-mediated pair interactions of the particles can be quantified by two-dimensional interaction free energies, which we obtain from the two-dimensional pair distributions P(x,y) of the particles observed in our simulations. These interaction free energies reflect the highly anisotropic interactions of a particle along its side (x-direction) and along its tip (y-direction) to a neighboring particle, and are two-dimensional generalizations of the one-dimensional potential of mean force.82 More precisely, the interaction free energies are effective pair interactions because our approach neglects multi-body interactions of the particles and takes the particle distributions observed in our simulations to result from pair interactions between the particles. These effective pair interactions can be seen to approximate the two-body interactions of the particles if their dependence on the area coverage X of the particles is small. The effective two-dimensional pair interaction free energies are calculated asF(x,y) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[P(x,y)/Pid] ln[P(x,y)/Pid] | (1) |
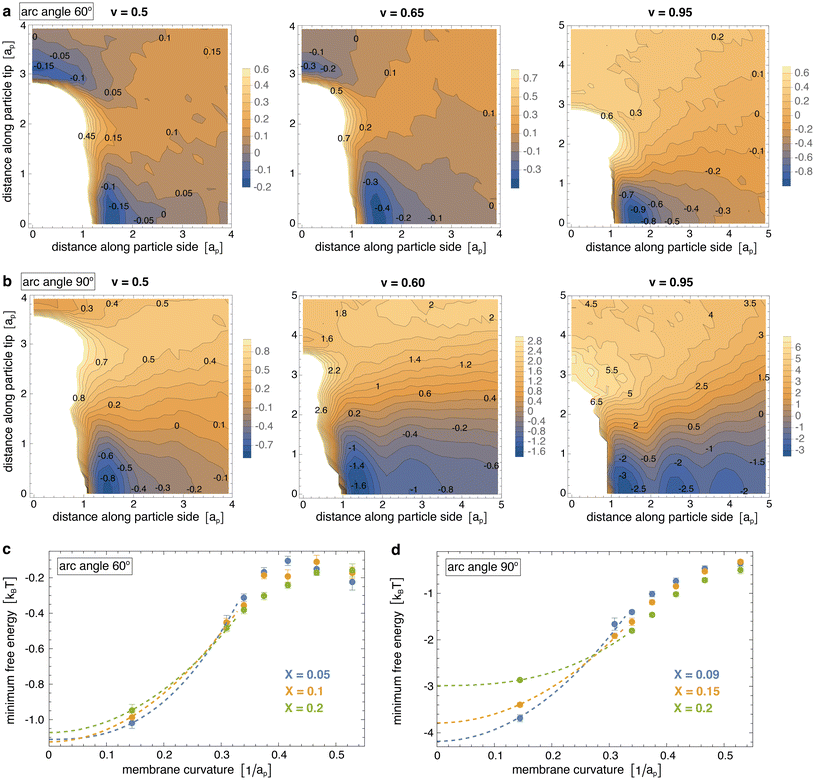
Fig. 3(a) and (b) display the resulting two-dimensional interaction free energies of the simulated particles with arc angle 60° and 90° at three different values of the reduced volume v of the vesicles for intermediate particle coverages of 10% and 15%, respectively. At the small value v = 0.5, the vesicles adopt elongated, thin tubular shapes (see Fig. 1 and 2). At this value of v, the two-dimensional free energy of particles with arc angle 60° exhibits two minima with nearly equal depth of about −0.15kBT for pair conformations in which the particles are oriented side-to-side and tip-to-tip, respectively (see Fig. 3(a)). At the intermediate value v = 0.65 at which the vesicles adopt thicker tubular shapes, the depths of the minima increases to about −0.45kBT for side-to-side alignment of particles with arc angle 60°, and to about −0.3kBT for tip-to-tip alignment. At v = 0.95, the vesicles adopt spherical shapes, and the depth of the minimum for side-to-side alignment of the particles further increases to nearly −1.0kBT, whereas tip-to-tip alignment of the particles is no longer energetically favourable.
For particles with arc angle 90°, the free-energy minima for pair conformations in which the particles are oriented side-to-side are clearly deeper compared to particles with arc angle 60°, while free-energy minima for tip-to-tip alignment of the particles no longer occur (see Fig. 3(b)). These deeper free-energy minima for side-to-side orientation of the particles indicate clearly stronger curvature-mediated interactions of the particles, because the rotational entropy loss in side-to-side conformations is larger for the longer particles with arc angle 90°, compared to particles with arc angle 60°. At the reduced vesicle volume v = 0.5, the free-energy minimum for side-to-side alignment of the particles has a depth of about −0.85kBT. At the larger values v = 0.6 and v = 0.95, several minima in side-to-side direction of the particles appear, which reflects the tendency of the particles to form linear chains with side-to-side orientation in the simulations at these values of v (see Fig. 2). The minimum at the smallest distance along the particle side reflects the interaction free energy of nearest neighbours and has a depth of about −1.6kBT for v = 0.6 and −3.4kBT for v = 0.95.
Fig. 3(c) and (d) illustrate how the interaction free-energy minima for side-to-side alignment of the particles depend on the curvature of the membrane at the three different particle coverages considered in our simulations. For tubular membrane shapes, the membrane curvature here is calculated as the curvature for the tubular section of an ideal spherocylinder with the same area A as the membrane in our simulations. For spherical shapes, the membrane curvature is calculated as the curvature of an ideal sphere with the same area A as the membrane in our simulations. For particles with arc angle 60°, the interaction is weakest at membrane curvatures of about 0.45/ap, with a minimum interaction free energy of about −0.15kBT. These membrane curvature roughly corresponds to the induced curvature of the particles, which can be estimated from the equation c = θ/L for the curvature c of a circular arc with angle θ and arc length L. For the average induced angle of 52.5° between membrane triangles bound to the terminal segments of a particle31 and the particle arc length L ≃ 2ap between the centers of these terminal segments with side length ap, we obtain c ≃ 0.46/ap. The interaction is strongest for spherical vesicles with a curvature of about 0.15/ap, with a minimum interaction free energy of about −1kBT. The dashed lines in Fig. 3(c) are extrapolations to planar membranes with curvature 0 and suggest pair interaction free-energy minima of about −1.2kBT in planar membranes.
For particles with arc angle 90°, the interaction is weakest at the largest considered membrane curvature of about 0.53/ap obtained for the thinnest simulated tubules with reduced volume v = 0.35 (see Fig. 3(d)). The interaction free-energy minima at this largest curvature range from about −0.45 to −0.5kBT, depending on the particle coverage X of the membranes. For particles with arc angle 90°, the induced curvature is about c = θ/L ≃ 0.48/ap for an average induced angle θ ≃ 82.6° (ref. 31) and arc length L ≃ 3ap and, thus, slightly larger than for particles with arc angle 60°. The interaction is again strongest for spherical vesicles with a curvature of about 0.15/ap, with a minimum interaction free energy in the range from −2.9 to −3.7kBT.
Side-to-side interaction energy
Besides effective interaction free energies of the particles, curvature-induced effective pair interaction energies without entropic components from rotational entropy losses can be obtained by comparing pair distributions p obtained from our simulations to hard-core distributions phc of the particles in the absence of attractive interactions. We approximately determine these hard-core distributions at closer particle distances for ‘flattened’ particles with the same shape in a quadratic planar area (see Methods). Our focus now is on one-dimensional radial distributions and on the curvature-induced interaction energies for side-to-side aligned particle pairs, which are reflected by energetic minima at small separations that the particles can only achieve in side-to-side alignment. We calculate the one-dimensional, distance-dependent interaction energy of the particles as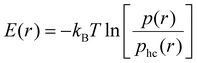 | (2) |
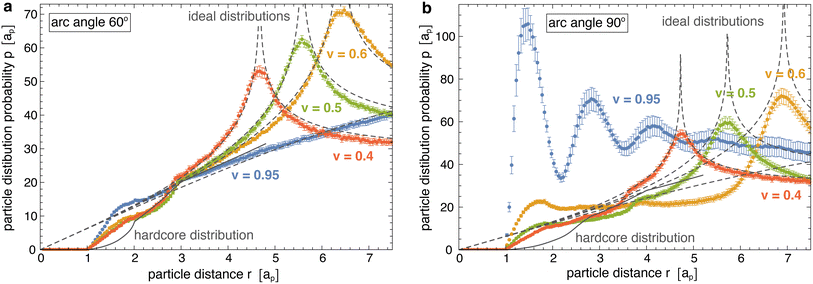
Fig. 4 illustrates the radial distributions p(r) obtained from our simulations at different reduced vesicle volumes v (coloured data points) as well as the hard-core distributions phc(r) of the particles with arc angle 60° and 90° (full grey lines), and compares these distributions to the ideal distributions of non-interacting particles on cylinders for v ≤ 0.6 and spheres for v = 0.95 (dashed grey lines). The distributions p(r) and phc are 0 at particle distances r < ap that are prevented by the hard-core interactions of the particles. At distances r > ap, the hard-core distributions phc(r) gradually increase and exhibit two kinks at distances r at which the particles acquire more rotational freedom. For particles composed of 3 segments, the first kink of phc(r) occurs at the distance r = 2ap above which a particle that is located at the side of another particle gains full rotational freedom. The second kink occurs at the distance r = 3ap above which a particle located at the tip of another particle has full rotational freedom. For particles composed of 4 segments, these kinks occur at corresponding, larger distances r. The curvature-mediated interaction of the particles is reflected by clearly larger values of the distributions p(r) at close distances ap < r < 2ap compared to the hard-core distributions phc(r). For particles with arc angle 60° and tubular vesicles with v ≤ 0.6, the radial distributions p(r) approach the hard-core distributions phc(r) at distances 2ap < r < 3ap and exhibit a kink around r = 3ap, which validates our approach to determine the hard-core distributions phc(r) at closer distances for ‘flattened’ particles in a plane. At larger distances r > 3ap, the radial distributions of the particles with arc angle 60° approach the ideal distributions of non-interacting particles on cylinders and spheres, respectively. For particles with arc angle 90°, the tendency of the particles to form linear chains for reduced vesicle volume v ≳ 0.5 (see Fig. 2) leads to more global deviations from hard-core and ideal distributions, and to multiple maxima of p(r) for spherical vesicles with v = 0.95.
Fig. 5 illustrates the interaction energy profiles E(r) and minimum interaction energies obtained from eqn (2) for the distributions p(r) obtained from our simulations and the numerically determined hard-core distributions phc(r) at the corresponding particle coverages X (see Methods for details). For particles with arc angle 60°, the interaction energy profiles E(r) tend to values close to 0 at larger distances r > 3ap at which the distributions approach each other (see Fig. 5(a, b) and 4(a)). Our main aim is to determine the minima of E(r) at short distances r that reflect the curvature-mediated interaction energy of the particles in side-to-side alignment. These interaction energy minima strongly depend on the membrane curvature (see Fig. 5(c)). As in Fig. 3(c), the interaction is weakest at membrane curvatures of about 0.45/ap with minimum values from −1.25 to −1.6kBT, depending on the particle coverage X. The interaction is strongest at the curvature of about 0.15/ap of our spherical vesicles with minimum values from −2.0 to −2.2kBT. The minimum values of the interaction energies are roughly 1kBT lower than the minima of the interaction free energies in Fig. 3(c) at corresponding curvatures. This difference of about 1kBT can be seen as the free-energy contribution from the loss of rotational entropy of the particles in the minimum-energy side-to-side pair conformations.
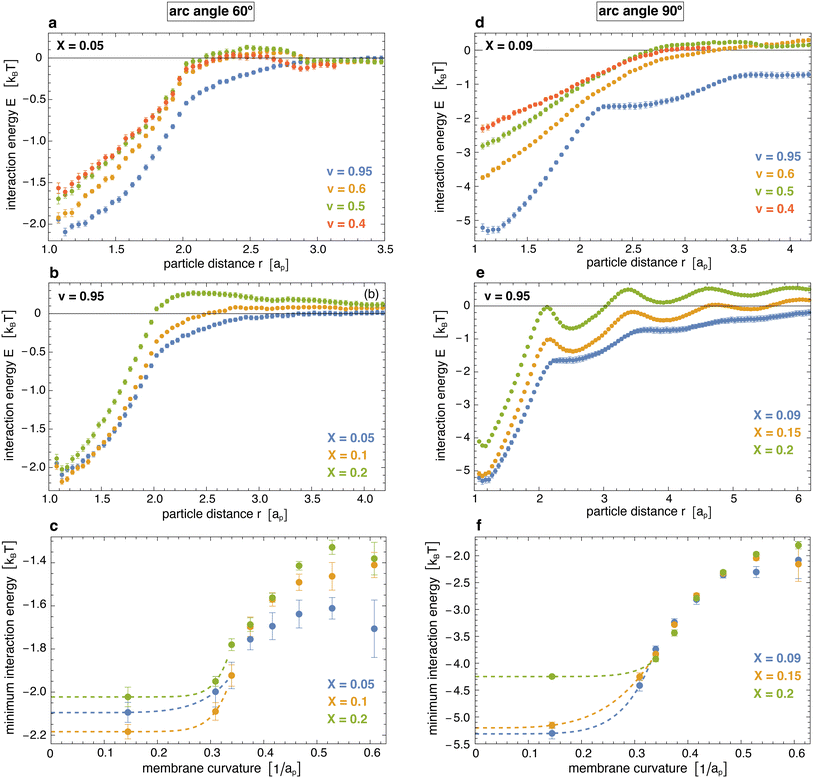 | ||
| Fig. 5 (a) and (b) Interaction energy profiles of pairs of arc-shaped particles with arc angle 60° at different values of the reduced volume v of vesicles and of the coverage X of the particles. (c) Minima of the interaction energy profiles versus membrane curvature for particles with arc angle 60° at coverages of X = 0.05, 0.1, and 0.2. The membrane curvature here is calculated as in Fig. 3, and the dashed extrapolation lines to curvature 0 are guides for the eye. (d) and (e) Interaction energy profiles of pairs of arc-shaped particles with arc angle 90° at different values of v and X. (f) Minima of the interaction energy profiles versus membrane curvature for particles with arc angle 90°. The shown errors have been estimated as error of the mean obtained for a subdivision of the simulation data into 10 contiguous data blocks. | ||
For particles with arc angle 90°, the minima of the interaction energy profiles E(r) at short distances r are clearly lower than for particles with arc angle 60° (see Fig. 5(d)–(f)). For spherical vesicles with v = 0.95, the linear chains of particles observed in the simulations lead to multiple minima of E(r) at the larger particle coverages X = 0.15 and 0.20, and to more global deviations from the hard-core distributions. The global minimum values of the interaction energies are roughly 1 to 2kBT lower than the minima of the interaction free energies in Fig. 3(c) at corresponding curvatures (see Fig. 3(d) and 5(f)), which reflects a slightly larger energy loss of rotational entropy for the longer particles with arc angle 90°, compared to particles with arc angle 60°.
Discussion and conclusions
In this article, we have presented a general methodology to obtain effective membrane-mediated pair interaction free energies and pair interaction energies of anisotropic curvature-inducing particles from distributions observed in simulations at relatively low membrane coverages of the particles. In this methodology, the two-dimensional interaction free energies F(x,y) are calculated in comparison to ideal distributions of non-interacting particles, as generalization of the one-dimensional potential of mean force. For a given particle, the two coordinates x and y describe whether a neighbouring particle is positioned at the side (for y = 0) or tip (for x = 0) of the particle, or in between these two directions (for nonzero x and y). In principle, a third coordinate to completely describe the relative position of two particles on the membrane surface is the angle enclosed by the two particle directions. In our approach, this third coordinate is averaged out in the two-dimensional interaction free energies F(x,y), which leads to a rotationally entropic contribution to F(x,y) because of the steric constraints at close particle distances. At the closest possible distances, the particles need to be positioned side-to-side and in parallel because of these steric constraints.Our methodology implies that the observed particle distributions result from effective pair interactions between the particles. For particles with arc angle 60°, the minima of the effective pair interaction free energy shown in Fig. 3(c) depend rather weakly on the membrane coverage X of the particles, which appears to indicate that multibody interactions are indeed negligible in magnitude compared to the pair interactions, at least in the range from X = 0.05 to 0.2 of our simulations. The effective pair interactions obtained from our analysis then approximate the actual pair interactions in the particle system. For particles with arc angle 90° on spherical vesicles, which form linear aggregates (see Fig. 2), the effective pair interaction free energies and pair interaction energies depend more strongly on the membrane coverage X of the particles and decrease with X (see data points in Fig. 3(d) and 5(f) at the membrane curvature 0.144/ap of our vesicles). This decrease of the effective two-body interactions indicates that the actual two-body interactions in the limit of small coverages X are counterbalanced by multi-body interactions, which become more pronounced at larger membrane coverages X. In general, membrane-mediated interactions can lead to strong multi-body interactions,73,76 in particular in systems with hexagonally packed aggregates of curvature-inducing particles61 because of the larger number of neighbouring particles in these aggregates, compared to linear aggregates. For curvature-inducing spherical particles trapped in membrane-adhesion zones, a counterbalance of attractive two-body interactions by multi-body interactions in hexagonally ordered particle aggregates has been quantified in an energy-miminization approach.61 In such membrane-mediated particle aggregates, the sum of the actual two-body interactions appears to overestimate the overall interaction energies because of screening effects, i.e. because of a reduction of the attractive interactions between next-nearest-neighbour particles by the nearest neighbours, which is reflected in repulsive multi-body interactions.
Our main aim was to determine the dependence of the particles’ interaction free energy on the overall curvature to the membrane, which we adjusted by the reduced volume v of membrane vesicles, from values of v = 0.35 for thin tubular vesicles to v = 0.95 for spherical vesicles (see Fig. 1 and 2). The constraints on the area and volume of the vesicle in our simulations to adjust the reduced volume v are essential for this aim. Without volume constraints, particle coverages between X = 0.05 and 0.20 only lead to spherical vesicle shapes with reduced volume of about v = 0.95 for particles with arc angle 60°, and to faceted shapes with reduced volume v between about 0.8 and 0.9 for particles with arc angle 90°.31 We found that the pair interaction is smallest for tubular vesicles with a curvature close to the particle curvature, with free energy minima of around −0.2kBT and −0.5kBT for particles with arc angle 60° and 90°, respectively. The pair interaction is largest for spherical vesicles with free energy minima of around −1kBT and −3kBT for the two types of particles. We believe that the interaction free energies of our particles with arc angle 60° are realistic for BAR domain proteins such as the Arfaptin BAR domain and the endophilin and Bin1 N-BAR domains, (i) because the induced average angle 52.5° of these particles31 roughly corresponds to the angle enclosed by these BAR domain proteins,83 and (ii) because the electron tomography images of membrane tubules induced by Bin1 N-BAR domains proteins show a rather loose protein arrangement with only short-ranged order,13 similar to the tubular morphologies induced by the particles in our simulations.31,32 In general, the pair interaction free energy can be expected to depend also on the coupling between the particles and the membrane, which is determined by the particle–membrane interaction potential in our model (see Methods).
Besides interaction free energies, we determined the effective pair interaction energies of the particles without rotationally entropic component from the distributions observed in our simulations and numerically determined hard-core distributions of ‘flattened’ particles with the same shape. The minima of the interaction energy profiles are located at short particle distances at which the particles are aligned side-by-side and exhibit the same dependence on membrane curvature as the minima of the interaction free energies. However, the interaction energy minima are about −1kBT and between −1 to −2kBT lower compared to the free energy minima obtained for the particles with arc angle 60° and 90°, respectively. These differences between the minima of the interaction energies and interaction free energies result from the rotational entropy loss of the particles at close contact and can be seen to quantify the free energy contribution of this entropy loss. Our results for the rotationally entropic repulsion with a magnitude of about 1kBT at particle contact agree with previous results for this entropic repulsion based on minimum-energy calculations for two BAR-domain shaped inclusions embedded in initially planar membranes at different distances and orientations.72 However, these minimum-energy calculations led to attractive curvature-mediated interaction energies of tens of kBT, which are much larger than the attractive interaction energies of about 2kBT for our particles with arc angle 60° on weakly curved spherical membrane vesicles. We speculate that this stronger curvature-mediated attraction results from a stronger coupling of the BAR-domain shaped inclusions via boundary conditions to the membrane and a finer membrane discretization in the energy minimizations,72 compared to the weaker membrane coupling of the adsorbed particles and to the membrane triangulation in our model. For a typical BAR domain length of about 20 nm,83 the edge length of our membrane triangles is of the order of 5 nm, so of the order of the membrane thickness. Coarse-grained molecular simulations of lipid membranes indicate that this discretization length, or ‘cutoff length’, of 5 nm for bending modes of lipid membranes is realistic.19,84 The weakly ordered arrangements of our particles with arc angle 60° on membrane tubules, which result from the curvature-mediated interactions quantified in this article, are in line with the short-range order of Bin1 N-BAR domains on membrane tubules observed in tomography images.13 Thermal membrane shape fluctuations, which are present in our simulations, are known to lead to fluctuation-induced attractions of adsorbed particles that locally suppress the shape fluctuations. In principle, these fluctuation-induced attractions are included in the membrane-mediated interaction energies obtained in our approach, but likely small compared to the thermal energy kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 and, thus, small compared to the curvature-mediated attraction in our model. The clearly stronger membrane-mediated interactions for particles with arc angle 90° in our model, compared to particles with arc angle 60°, also indicate a predominance of curvature-mediated interactions.
19 and, thus, small compared to the curvature-mediated attraction in our model. The clearly stronger membrane-mediated interactions for particles with arc angle 90° in our model, compared to particles with arc angle 60°, also indicate a predominance of curvature-mediated interactions.
Methods
Model and simulations
We model the membrane as a dynamically triangulated, closed surface. The membrane model is based on a standard discretization33,85 of the bending energy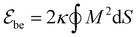 of closed fluid membranes86 with bending rigidity κ and local mean curvature M. Our discretized membranes are composed of nt = 2000 triangles. In our Monte Carlo (MC) simulations, the edges of the triangulated membrane are flipped to ensure membrane fluidity (dynamic triangulation), and the vertices of the triangulation are displaced to allow local changes of the membrane shape. The edge lengths of the triangles are kept within an interval
of closed fluid membranes86 with bending rigidity κ and local mean curvature M. Our discretized membranes are composed of nt = 2000 triangles. In our Monte Carlo (MC) simulations, the edges of the triangulated membrane are flipped to ensure membrane fluidity (dynamic triangulation), and the vertices of the triangulation are displaced to allow local changes of the membrane shape. The edge lengths of the triangles are kept within an interval 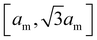 to limit triangle distortions. The vertex displacements occur in MC steps in which a randomly selected vertex of the triangulated membrane is translated along a random direction by a distance that is randomly chosen from an interval between 0 and 0.1am. We impose an overall tubular or spherical membrane shape by constraining both the membrane area A and the enclosed volume V of the membrane via harmonic constraining potentials. The volume-to-area ratio of the membrane therefore is fixed in our simulations.
to limit triangle distortions. The vertex displacements occur in MC steps in which a randomly selected vertex of the triangulated membrane is translated along a random direction by a distance that is randomly chosen from an interval between 0 and 0.1am. We impose an overall tubular or spherical membrane shape by constraining both the membrane area A and the enclosed volume V of the membrane via harmonic constraining potentials. The volume-to-area ratio of the membrane therefore is fixed in our simulations.
The discretized, arc-shaped particles of our model are linear chains of 3 or 4 identical planar quadratic segments with a side length ap and with an angle of 30° between neighboring segments that share a quadratic edge.31,87 The arc angle of the particles, i.e. the angle between the first and last segment, then adopts the values 60° and 90° for particles composed of 3 and 4 segments, respectively. Each planar segment of a particle interacts with the nearest triangle of the membrane via the particle–membrane adhesion potential31
| Vpm = −Ufr(r)fθ(θ) | (3) |
Here, r is the distance between the center of the segment and the center of the nearest triangle, θ is the angle between the normals of the particle segment and this membrane triangle, and U > 0 is the adhesion energy per particle segment. The distance-dependent function fr is a square-well function that adopts the values fr(r) = 1 for 0.25am < r < 0.75am and fr(r) = 0 otherwise. The angle-dependent function fθ is a square-well function with values fθ(θ) = 1 for |θ| < 10° and fθ(θ) = 0 otherwise. By convention, the normals of the membrane triangles are oriented outward from the enclosed volume of the membrane, and the normals of the particle segments are oriented away from the center of the particle arc. The particles thus bind with their inward curved, concave surface to the membrane. The overlapping of particles is prevented by a purely repulsive hard-core interaction that only allows distances between the centres of the planar segments of different particles that are larger than ap. The hard-core area of a particle segment thus is πap2/4. We choose the value ap = 1.5am for the side length of the planar and quadratic particle segments. The particle segments then are slightly larger than the membrane triangles with minimum side length am, which ensures that different particle segments bind to different triangles.
The positions and orientations of the particles are varied by particle translations and rotations in our simulations.31 In a particle translation, a randomly selected particle is translated in random direction by a random distance between 0 and am. In a particle rotation, a randomly selected particle is rotated around a rotation axis that passes through the central point along the particle arc. For particles that consist of 3 segments, the rotation axis runs through the center of the central segments. For particles composed of 4 segments, the rotation axis runs through the center of the edge that is shared by the two central segments. The rotation axis is oriented in a random direction. The random rotations are implemented using quaternions88,89 with rotation angles between 0 and a maximum angle of about 2.3°. Our simulations thus consist of two types of MC steps for the membrane, vertex translations and edge flips, and two types of MC steps for translating and rotating the particles. The different types of MC steps occur with equal probabilities for single membrane vertices, edges, or particles.31
In each simulation, the area fraction X of the membrane covered by bound particles is kept at a constant value between 5% and 20% by dynamically adjusting the adhesion energy U per particle segment. The total number of particles in the system is N = 400. The area of the membrane is constrained to A0 ≃ 0.677ntam2. The strength of the harmonic constraining potential is chosen such that the fluctuations of the membrane area are limited to less than 1%. The simulations are run in a cubic box with periodic boundary conditions and volume Vbox ≃ 3 × 105am3. The simulation box volume is 64 times as large as the volume of a perfect sphere with area A0. After initial relaxation of the simulations until a steady state of bound particles is reached, the simulation frames from which the particle distributions are determined are extracted from the simulations at time intervals of 100 Monte Carlo steps per vertex. For particles with arc angle 60°, the total number of analysed conformations for tubular vesicles with reduced volume v ≤ 0.65 is about 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for the membrane coverage X = 5%, 145
000 for the membrane coverage X = 5%, 145![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for X = 10%, and 100
000 for X = 10%, and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for X = 20%. For spherical vesicles with reduced volume v = 0.95, the total number of conformations is 150
000 for X = 20%. For spherical vesicles with reduced volume v = 0.95, the total number of conformations is 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 85
000, 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and 61
000, and 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 at X = 5%, 10%, and 20%, respectively. For particles with arc angle 90°, the total number of analysed conformations for tubular vesicles with reduced volume v ≤ 0.65 is about 155
000 at X = 5%, 10%, and 20%, respectively. For particles with arc angle 90°, the total number of analysed conformations for tubular vesicles with reduced volume v ≤ 0.65 is about 155![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for the membrane coverage X = 9%, 125
000 for the membrane coverage X = 9%, 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for X = 15%, and 90
000 for X = 15%, and 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for X = 20%. For spherical vesicles with reduced volume v = 0.95, the total number of conformations is 150
000 for X = 20%. For spherical vesicles with reduced volume v = 0.95, the total number of conformations is 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 88
000, 88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and 59
000, and 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 at X = 9%, 15%, and 20%, respectively.
000 at X = 9%, 15%, and 20%, respectively.
Interaction free energy
We determined the two-dimensional interaction free energies of Fig. 3 from two-dimensional pair distributions of the particles obtained from our simulations. These two-dimensional pair distributions reflect the distributions of neighbouring particles around a particle on the surface of the spherical or tubular membranes. For spherical membrane shapes, we determine the position of a neighbouring particle j relative to a particle i based on an angle ϕ between two planes P and Q. Plane P runs through the centres of the two terminal segments of particle i and through the center of mass of the spherical membrane and, thus, reflects the orientation of particle i on the membrane sphere. Plane Q runs through the centre of particle i, the center of particle j, and the center of mass of the spherical membrane. For particles with arc angle 60°, which are composed of three segments, the particle center simply is the center of the central particle segment. For particles with arc angle 90°, which are composed of four segments, the particle center is the center of mass of the two central particle segments. The value ϕ = 0 for the angle between planes P and Q indicates that the center of particle j is located at the tip of particle i, and ϕ = π/2 indicates that the center of particle j is located at the side of particle i. The two-dimensional particle distributions then are calculated from the two coordinates x = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ and y = r
ϕ and y = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ of all particle pairs where r is the distance of the particle centres. To determine these distributions, we discretize the plane of the coordinates x and y into squares with side length ap/5 and count the total number M(x,y) of particle pairs with coordinate values in the square centered at (x,y) for all conformations. The probability for finding a neighboring particle in the square centered at (x,y) can then be determined as P(x,y) = M(x,y)/(4NcNb(Nb − 1)) where Nc is the number of conformations and Nb is the average number of bound particles in a conformation. The factor 4 takes into account that the angle 0 ≤ ϕ ≤ π/2 is limited to one of the four angular quadrants because of the particle symmetry, and Nb(Nb − 1) is the average number of particle pairs per conformation that is considered in this calculation. For ideal, non-interacting particles, the probability of finding a neighboring particle in square (x,y) is Pid = As/A where As = (ap/5)2 is the area of a discrete square and A = A0 is the membrane area. The two-dimensional interaction free energy then follows as,
ϕ of all particle pairs where r is the distance of the particle centres. To determine these distributions, we discretize the plane of the coordinates x and y into squares with side length ap/5 and count the total number M(x,y) of particle pairs with coordinate values in the square centered at (x,y) for all conformations. The probability for finding a neighboring particle in the square centered at (x,y) can then be determined as P(x,y) = M(x,y)/(4NcNb(Nb − 1)) where Nc is the number of conformations and Nb is the average number of bound particles in a conformation. The factor 4 takes into account that the angle 0 ≤ ϕ ≤ π/2 is limited to one of the four angular quadrants because of the particle symmetry, and Nb(Nb − 1) is the average number of particle pairs per conformation that is considered in this calculation. For ideal, non-interacting particles, the probability of finding a neighboring particle in square (x,y) is Pid = As/A where As = (ap/5)2 is the area of a discrete square and A = A0 is the membrane area. The two-dimensional interaction free energy then follows as,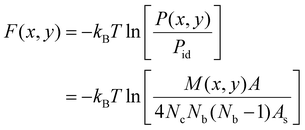 | (4) |
For tubular membrane conformations, we define a central, tubular membrane segment of area A = A0/2 based on the distance of the membrane triangles from the center of mass of the membrane, and focus on particle pairs i and j in which at least one particle is bound to the central membrane segment. Pairs of particles that are both bound to a spherical membrane end are, thus, excluded from the analysis. We next define the tubular axis of a conformation based on a singular value decomposition of the positions of all particles bound to the membrane in this conformation, and project the particle centres on an ideal cylinder with radius rcyl around this tubular axis. For each particle pair, we determine the angle ψ between the tubular axis and the vector that connects the projected particle centres, and define two coordinates as x = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ and y = r
ψ and y = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ where r is the distance of the (unprojected) particle centres. Because the particles are oriented on average perpendicular to the tubular axis, the value ψ = 0 corresponds to a side-to-side orientation of a particle pair, and the value ψ = π/2 corresponds to a tip-to-tip orientation. We discretize the plane of the two coordinates x and y as described above for spherical conformations, and determine the two-dimensional free energy F(x,y) from eqn (4) after rescaling the total number of particle pairs M(x,y) by the factor
ψ where r is the distance of the (unprojected) particle centres. Because the particles are oriented on average perpendicular to the tubular axis, the value ψ = 0 corresponds to a side-to-side orientation of a particle pair, and the value ψ = π/2 corresponds to a tip-to-tip orientation. We discretize the plane of the two coordinates x and y as described above for spherical conformations, and determine the two-dimensional free energy F(x,y) from eqn (4) after rescaling the total number of particle pairs M(x,y) by the factor 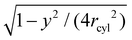 to account for the cylindrical curvature in y-direction. For tubular conformations, Nb in eqn (4) corresponds to the average number of particles bound to the central tubular membrane segments. In this calculation, the tubular radius rcyl of the particle layer around the membrane is obtained from the maximum of the one-dimensional distributions shown in Fig. 4.
to account for the cylindrical curvature in y-direction. For tubular conformations, Nb in eqn (4) corresponds to the average number of particles bound to the central tubular membrane segments. In this calculation, the tubular radius rcyl of the particle layer around the membrane is obtained from the maximum of the one-dimensional distributions shown in Fig. 4.
Interaction energy
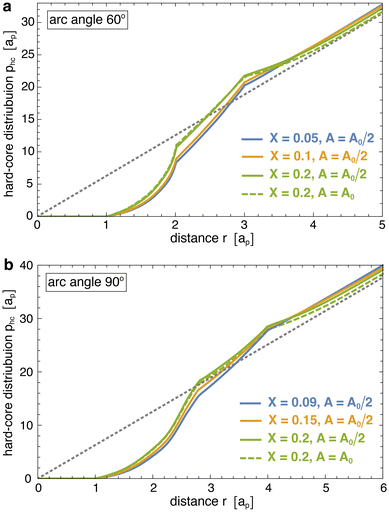
The one-dimensional interaction energies of Fig. 5 were calculated based on eqn (2). To determine the rescaled distribution p(r) of the membrane-bound particles in this equation, we first determine the number of particle pairs M(r) with a distance of the particle centres within the shell r ± dr/2 with width dr = ap/10. The rescaled distribution then follows as p(r) = M(r)/(drNcNb(Nb − 1)/A) where Nc is the number of simulation conformations and Nb is the average number of bound particles in the considered membrane area A. For tubular membrane conformations, the area A is the area A0/2 of the central tubular segment in which at least one of the bound particles in a pair needs to be located (see above). For spherical membrane conformations, the area A is the total area A0 of the membrane.The hard-core distributions phc(r) in eqn (2) are determined for ‘flattened’ particles with an angle of 0 between the quadratic segments of side length ap, rather than the angle of 30° of the curved, membrane-bound particles. To obtain these distribution, we first generate a large number Nc of non-overlapping conformations of Nb ‘flattened’ particles in a quadratic area A. Here, Nb is the average number of membrane-bound particles and A is the membrane area in the corresponding membrane simulation system, in which p(r) has been determined. The hard-core distributions phc(r) then are calculated from the number Mhc(r) of particle pairs with a distance of the particle centres within the shell r ± dr/2 as phc(r) = Mhc(r)/(drNcNb(Nb − 1)/A). We determine Mhc(r) for standard periodic boundaries of the considered quadratic area A, i.e. we take the distance r as the minimum distance among all periodic particle images. The hard-core distributions slightly depend on the area coverage X = NbAp/A of the particles where Ap = nsap2π/4 is the hard-core area of a single particle, which is composed of either ns = 3 or 4 segments. The hard-core distributions phc(r) shown in Fig. 6 slightly increase with area coverage X at close distances r < nsap smaller than the particle length, because of an increase of the pressure in the particle gas with X. This pressure pushes the particles together, against their entropic repulsion at distances r < nsap. Because of the normalization implied by the definition of the distributions, higher values of phc(r) at small distances r < nsap lead to lower values at large distances. The hard-core distributions exhibit two kinks at distances r at which the particles acquire more rotational freedom. For particles composed of 3 segments, the first kink of phc(r) occurs at the distance r = 2ap above which a particle that is located at the side of another particle gains full rotational freedom. The second kink occurs at the distance r = 3ap above which a particle located at the tip of another particle has full rotational freedom. For particles composed of 4 segments, these kinks occur at corresponding, larger distances r.
Data availability
The Monte Carlo data of this study and the Mathematica 13 notebooks used in the data analysis are available in the open research data repository Edmond at https://doi.org/10.17617/3.DIF595.The reference for this dataset is:
Bonazzi, Francesco; Weikl, Thomas, 2024, “Pair distributions and membrane-mediated interactions of arc-shaped particles on spherical and tubular vesicles”, https://doi.org/10.17617/3.DIF595, Edmond, V1.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Max Planck Society and from the Deutsche Forschungsgemeinschaft (DFG) via the International Research Training Group 1524 “Self-Assembled Soft Matter Nano-Structures at Interfaces” is gratefully acknowledged. Open Access funding provided by the Max Planck Society.References
- Y. Shibata, J. Hu, M. M. Kozlov and T. A. Rapoport, Annu. Rev. Cell Dev. Biol., 2009, 25, 329–354 CrossRef CAS PubMed.
- M. M. Kozlov, F. Campelo, N. Liska, L. V. Chernomordik, S. J. Marrink and H. T. McMahon, Curr. Opin. Cell Biol., 2014, 29, 53–60 CrossRef CAS PubMed.
- H. T. McMahon and E. Boucrot, J. Cell Sci., 2015, 128, 1065–1070 CrossRef CAS PubMed.
- T. Baumgart, B. R. Capraro, C. Zhu, S. L. Das, S. R. Leone, P. S. Cremer, J. T. Groves and M. A. Johnson, Annu. Rev. Phys. Chem., 2011, 62, 483–506 CrossRef CAS PubMed.
- B. J. Peter, H. M. Kent, I. G. Mills, Y. Vallis, P. J. G. Butler, P. R. Evans and H. T. McMahon, Science, 2004, 303, 495–499 CrossRef CAS PubMed.
- Y. Rao and V. Haucke, Cell. Mol. Life Sci., 2011, 68, 3983–3993 CrossRef CAS PubMed.
- C. Mim and V. M. Unger, Trends Biochem. Sci., 2012, 37, 526–533 CrossRef CAS PubMed.
- M. Simunovic, E. Evergren, A. Callan-Jones and P. Bassereau, Annu. Rev. Cell Dev. Biol., 2019, 35, 111–129 CrossRef CAS PubMed.
- K. Takei, V. I. Slepnev, V. Haucke and P. De Camilli, Nat. Cell Biol., 1999, 1, 33–39 CrossRef CAS PubMed.
- A. Frost, R. Perera, A. Roux, K. Spasov, O. Destaing, E. H. Egelman, P. De Camilli and V. M. Unger, Cell, 2008, 132, 807–817 CrossRef CAS PubMed.
- C. Mim, H. Cui, J. A. Gawronski-Salerno, A. Frost, E. Lyman, G. A. Voth and V. M. Unger, Cell, 2012, 149, 137–145 CrossRef CAS PubMed.
- J. Adam, N. Basnet and N. Mizuno, Sci. Rep., 2015, 5, 15452 CrossRef CAS PubMed.
- B. Daum, A. Auerswald, T. Gruber, G. Hause, J. Balbach, W. Kühlbrandt and A. Meister, J. Struct. Biol., 2016, 194, 375–382 CrossRef CAS PubMed.
- A.-L. Le Roux, C. Tozzi, N. Walani, X. Quiroga, D. Zalvidea, X. Trepat, M. Staykova, M. Arroyo and P. Roca-Cusachs, Nat. Commun., 2021, 12, 6550 CrossRef CAS PubMed.
- B. A. Shoemaker and A. R. Panchenko, PLoS Comput. Biol., 2007, 3, e42 CrossRef PubMed.
- J. A. Marsh, H. Hernández, Z. Hall, S. E. Ahnert, T. Perica, C. V. Robinson and S. A. Teichmann, Cell, 2013, 153, 461–470 CrossRef CAS PubMed.
- Y. Min, M. Akbulut, K. Kristiansen, Y. Golan and J. Israelachvili, Nat. Mater., 2008, 7, 527–538 CrossRef CAS PubMed.
- M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591–3605 CrossRef CAS PubMed.
- T. R. Weikl, Annu. Rev. Phys. Chem., 2018, 69, 521–539 CrossRef CAS PubMed.
- L. Johannes, W. Pezeshkian, J. H. Ipsen and J. C. Shillcock, Trends Cell Biol., 2018, 28, 405–415 CrossRef CAS PubMed.
- C. A. Haselwandter and R. Phillips, Europhys. Lett., 2013, 101, 68002p1–68002p6 CrossRef PubMed.
- T. Idema and D. J. Kraft, Curr. Opin. Colloid Interface Sci., 2019, 40, 58–69 CrossRef CAS.
- J. Gao, R. Hou, L. Li and J. Hu, Front. Mol. Biosci., 2021, 8, 811711 CrossRef CAS PubMed.
- A. E. Hafner, J. Krausser and A. Saric, Curr. Opin. Struct. Biol., 2019, 58, 43–52 CrossRef CAS PubMed.
- G. Kumar, S. C. Duggisetty and A. Srivastava, J. Membr. Biol., 2022, 255, 757–777 CrossRef CAS PubMed.
- M. Simunovic, A. Srivastava and G. A. Voth, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20396–20401 CrossRef CAS PubMed.
- N. Ramakrishnan, P. B. S. Kumar and J. H. Ipsen, Biophys. J., 2013, 104, 1018–1028 CrossRef CAS PubMed.
- H. Noguchi, Sci. Rep., 2016, 6, 20935 CrossRef CAS PubMed.
- H. Noguchi and J.-B. Fournier, Soft Matter, 2017, 13, 4099–4111 RSC.
- A. D. Olinger, E. J. Spangler, P. B. S. Kumar and M. Laradji, Faraday Discuss., 2016, 186, 265–275 RSC.
- F. Bonazzi and T. R. Weikl, Biophys. J., 2019, 116, 1239–1247 CrossRef CAS PubMed.
- J. Gao, R. Hou, W. Hu, T. R. Weikl and J. Hu, J. Phys. Chem. B, 2024, 128, 4735–4740 CrossRef CAS PubMed.
- A. H. Bahrami, R. Lipowsky and T. R. Weikl, Phys. Rev. Lett., 2012, 109, 188102 CrossRef PubMed.
- A. Saric and A. Cacciuto, Phys. Rev. Lett., 2012, 109, 188101 CrossRef PubMed.
- T. Yue and X. Zhang, ACS Nano, 2012, 6, 3196–3205 CrossRef CAS PubMed.
- M. Raatz, R. Lipowsky and T. R. Weikl, Soft Matter, 2014, 10, 3570–3577 RSC.
- M. Raatz and T. R. Weikl, Adv. Mater. Interfaces, 2017, 4, 1600325 CrossRef.
- K. Xiong, J. Zhao, D. Yang, Q. Cheng, J. Wang and H. Ji, Soft Matter, 2017, 13, 4644–4652 RSC.
- H. Tang, H. Ye, H. Zhang and Y. Zheng, Nanotechnology, 2018, 29, 405102 CrossRef PubMed.
- Z. Yan, Z. Wu, S. Li, X. Zhang, X. Yi and T. Yue, Nanoscale, 2019, 11, 19751–19762 RSC.
- S. Zuraw-Weston, D. A. Wood, I. K. Torres, Y. Lee, L.-S. Wang, Z. Jiang, G. R. Lazaro, S. Wang, A. A. Rodal, M. F. Hagan, V. M. Rotello and A. D. Dinsmore, Nanoscale, 2019, 11, 18464–18474 RSC.
- E. J. Spangler and M. Laradji, J. Chem. Phys., 2021, 154, 244902 CrossRef CAS PubMed.
- T. Chen, Y. Zhang, X. Li, C. Li, T. Lu, S. Xiao and H. Liang, J. Chem. Theory Comput., 2021, 17, 7850–7861 CrossRef CAS PubMed.
- B. J. Reynwar, G. Illya, V. A. Harmandaris, M. M. Müller, K. Kremer and M. Deserno, Nature, 2007, 447, 461–464 CrossRef CAS PubMed.
- B. J. Reynwar and M. Deserno, Soft Matter, 2011, 7, 8567–8575 RSC.
- A. H. Bahrami and T. R. Weikl, Nano Lett., 2018, 18, 1259–1263 CrossRef CAS PubMed.
- A. Bahrami and A. H. Bahrami, Nanotechnology, 2019, 30, 345101 CrossRef CAS PubMed.
- Y. Zhu, A. Sharma, E. J. Spangler and M. Laradji, Soft Matter, 2022, 18, 4689–4698 RSC.
- Y. Zhu, A. Sharma, E. J. Spangler, J.-M. Y. Carrillo, P. B. S. Kumar and M. Laradji, Soft Matter, 2023, 19, 2204–2213 RSC.
- A. Sharma, Y. Zhu, E. J. Spangler, T. B. Hoang and M. Laradji, ACS Nano, 2024, 18, 12957–12969 CrossRef CAS PubMed.
- J. Midya, T. Auth and G. Gompper, ACS Nano, 2023, 17, 1935–1945 CrossRef CAS PubMed.
- B. Li and S. M. Abel, Soft Matter, 2022, 18, 2742–2749 RSC.
- B. Li and S. M. Abel, J. Chem. Phys., 2024, 160, 194901 CrossRef CAS PubMed.
- N. Nambiar, Z. A. Loyd and S. M. Abel, J. Chem. Theory Comput., 2024, 20, 1732–1739 CrossRef CAS PubMed.
- I. Koltover, J. Rädler and C. Safinya, Phys. Rev. Lett., 1999, 82, 1991–1994 CrossRef CAS.
- C. van der Wel, A. Vahid, A. Saric, T. Idema, D. Heinrich and D. J. Kraft, Sci. Rep., 2016, 6, 32825 CrossRef CAS PubMed.
- R. Sarfati and E. R. Dufresne, Phys. Rev. E, 2016, 94, 012604 CrossRef PubMed.
- C. van der Wel, D. Heinrich and D. J. Kraft, Biophys. J., 2017, 113, 1037–1046 CrossRef CAS PubMed.
- E. Lavagna, Z. P. Güven, D. Bochicchio, F. Olgiati, F. Stellacci and G. Rossi, Nanoscale, 2021, 13, 16879–16884 RSC.
- A. Azadbakht, B. Meadowcroft, J. Májek, A. Šarić and D. J. Kraft, Biophys. J., 2024, 123, 307–316 CrossRef CAS PubMed.
- A. Azadbakht, T. R. Weikl and D. J. Kraft, ACS Nano, 2024, 18, 23067–23076 CrossRef CAS PubMed.
- R. Groza, K. V. Schmidt, P. M. Müller, P. Ronchi, C. Schlack-Leigers, U. Neu, D. Puchkov, R. Dimova, C. Matthaeus, J. Taraska, T. R. Weikl and H. Ewers, Nat. Commun., 2024, 15, 2767 CrossRef CAS PubMed.
- S. van der Ham, J. Agudo-Canalejo and H. R. Vutukuri, ACS Nano, 2024, 18, 10407–10416 CrossRef CAS PubMed.
- M. Goulian, R. Bruinsma and P. Pincus, Europhys. Lett., 1993, 22, 145–150 CrossRef CAS.
- M. Goulian, R. Bruinsma and P. Pincus, Europhys. Lett., 1993, 23, 155–155 CrossRef.
- J. M. Park and T. C. Lubensky, J. Phys. I, 1996, 6, 1217–1235 CrossRef CAS.
- R. R. Netz, J. Phys. I, 1997, 7, 833–852 CrossRef CAS.
- T. R. Weikl, M. M. Kozlov and W. Helfrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 6988–6995 CrossRef CAS.
- K. S. Kim, J. Neu and G. Oster, Biophys. J., 1998, 75, 2274–2291 CrossRef CAS PubMed.
- P. Dommersnes, J. Fournier and P. Galatola, Europhys. Lett., 1998, 42, 233–238 CrossRef CAS.
- P. G. Dommersnes and J. B. Fournier, Eur. Phys. J. B, 1999, 12, 9–12 CrossRef CAS.
- Y. Schweitzer and M. M. Kozlov, PLoS Comput. Biol., 2015, 11, e1004054 CrossRef PubMed.
- C. Yolcu and M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031906 CrossRef PubMed.
- J.-B. Fournier and P. Galatola, Eur. Phys. J. E, 2015, 38, 86 CrossRef PubMed.
- O. Kahraman, R. Langen and C. A. Haselwandter, Sci. Rep., 2018, 8, 16383 CrossRef PubMed.
- P. Galatola and J.-B. Fournier, Soft Matter, 2023, 19, 6157–6167 RSC.
- A. Vahid, A. Šarić and T. Idema, Soft Matter, 2017, 13, 4924–4930 RSC.
- U. S. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A, 1991, 44, 1182–1202 CrossRef CAS PubMed.
- A. H. Bahrami and G. Hummer, ACS Nano, 2017, 11, 9558–9565 CrossRef CAS PubMed.
- R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS PubMed.
- J. F. Nagle, Faraday Discuss., 2013, 161, 11–29 RSC.
- D. Chandler, Introduction to modern statistical mechanics, Oxford University Press, 1987 Search PubMed.
- B. Qualmann, D. Koch and M. M. Kessels, EMBO J., 2011, 30, 3501–3515 CrossRef CAS PubMed.
- R. Goetz, G. Gompper and R. Lipowsky, Phys. Rev. Lett., 1999, 82, 221–224 CrossRef CAS.
- F. Jülicher, J. Phys. II, 1996, 6, 1797–1824 CrossRef.
- W. Helfrich, Z. Naturforsch., C: J. Biosci., 1973, 28, 693–703 CrossRef CAS PubMed.
- F. Bonazzi, C. K. Hall and T. R. Weikl, Soft Matter, 2021, 17, 268–275 RSC.
- D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, Academic Press, San Diego, 2nd edn, 2002, vol. 1 Search PubMed.
- F. J. Vesely, J. Comput. Phys., 1982, 47, 291–296 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |