Origin of ¹³C NMR chemical shifts elucidated based on molecular orbital theory: paramagnetic contributions from orbital-to-orbital transitions for the pre-α, α, β, α-X, β-X and ipso-X effects, along with effects from characteristic bonds and groups

Abstract

¹³C NMR chemical shifts (δ(C)) were analysed via MO theory, together with the origin, using σ^d(C), σ^p(C) and σ^t(C), where C⁴⁻ was selected as the standard for the analysis since σ^p(C: C⁴⁻) = 0 ppm. An excellent relationship was observed between σ^d(C) and the charges on C for (C⁴⁺, C²⁺, C⁰, C²⁻ and C⁴⁻) and (C⁴⁻, CH₂²⁻, CH₃⁻ and CH₄). However, such a relationship was not observed for the carbon species other than those above. The occupied-to-unoccupied orbital (ψ_i→ψ_a) transitions were mainly employed for the analysis. The origin was explained by the pre-α, α, β, α-X, β-X and ipso-X effects. The pre-α effect of an approximately 20 ppm downfield shift is theoretically predicted, and the observed α and β effects of approximately 10–15 ppm downfield shifts are well reproduced by the calculations, as are the variations in the α-X, β-X and ipso-X effects. Large downfield shifts caused by the formation of ethene (∼120 ppm), ethyne (∼60 ppm) and benzene (∼126 ppm) from ethane and carbonyl (∼146 ppm) and carboxyl (∼110 ppm) groups from CH₃OH are also reproduced well by the calculations. The analysis and illustration of σ^p(C) through the ψ_i→ψ_a transitions enables us to visualize the effects and to understand the δ(C) values for the C atoms in the specific positions of the species. The occupied-to-occupied orbital (ψ_i→ψ_j) transitions are also examined. The theoretical investigations reproduce the observed results of δ(C). The origin for δ(C) and the mechanism are visualized, which allows us to image the process in principle. The role of C in the specific position of a compound in question can be more easily understood, which will aid in the development of highly functional compounds based on NMR.

---

Introduction

NMR spectroscopy is one of the most important tools in current chemical and biological science research. ¹H and ¹³C NMR spectra are commonly measured and analysed on a daily basis to determine the structures and/or follow up the reactions.^1–4 Lots of ¹H and ¹³C NMR data have been reported thus far. The shift values spread over 20 and 300 ppm, respectively. NMR spectra, other than those above, are also measured on a daily basis.^5–8 The NMR chemical shifts of the atoms in the 3rd and higher periods, such as ³¹P, ⁷⁷Se and ¹²⁵Te, are predominantly controlled by the paramagnetic terms, whereas those in the 1st period of ¹H are controlled by the diamagnetic terms. In the case of the atoms of the 2nd period, such as ¹⁵N, ¹⁷O and ¹⁹F, the chemical shifts are controlled both by the two terms; therefore, the mechanisms are more complex.^5–8 The relativistic effect cannot be avoided when considering those in the 5th and higher periods, whereas the effect can be treated as (much) smaller for the atoms in the 4th and lower periods.

Our research interest lies in establishablishing the plain rules founded in theory for the origin and mechanism of the NMR chemical shifts of nuclei N [δ(N)]. The mechanism of the origin will help experimental chemists understand the role of N at a specific position in the species over the empirical rules,^5,6 which are usually employed in assigning the spectra. The plain rules, which are established based on the theory, must be simple, easily imaged and easily understood for experimental scientists who are not specialists in this field. In our work, this purpose is given more importance than the usual NMR parameter calculations, which accurately predict the shift values of target compounds.

Scheme 1 illustrates the pre-α, α, β, γ and δ effects on δ(C), which are often employed to understand δ(C) uniformly. The typically encountered α, β and γ effects are 12–16 ppm (downfield shifts), 5–9 ppm (downfield shifts) and −2 ppm (upfield shifts), respectively, with the δ effect being negligibly small. The “pre-α effect” has been proposed to establish plain rules and understand the mechanisms for δ(Se) in a unified form.⁹ Scheme 1 contains the α-X, β-X and ipso-X (i-X) effects, where X stands for atoms or groups other than H and Me. The pre-α, α, and β effects are analysed based on the MO theory. The effects are calculated per unit group (per Me or H) and are discussed using the average values, if suitable. The effects of the characteristic bonds and groups are also examined.

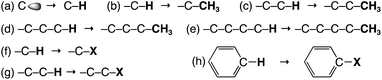Scheme 1 The pre-α (a), α (b), β (c), γ (d), δ (e), α-X (f), β-X (g) and ipso-X (i-X) (h) effects, which are discussed in this paper.

The chemical shifts of the respective structures can be theoretically calculated with satisfactory accuracy. The total absolute magnetic shielding tensor (σ^t) is used for the analysis. As shown in eqn (1), σ^t is decomposed into the contributions from the diamagnetic shielding tensors (σ^d) and the paramagnetic shielding tensors (σ^p) under the DFT levels.^10–12 The magnetic shielding tensors consist of three components: σ^m_xx, σ^m_yy and σ^m_zz, (m = d, p and t). Eqn (2) shows the relationship. As shown in eqn (3), σ^d is simply expressed as the sum of the contributions over the occupied orbitals (ψ_i, so is ψ_j), where the contribution from each ψ_i to σ^d (σ^d_i) is proportional to the average inverse distance of electrons from the nuclei in ψ_i, 〈r_i⁻¹〉 (eqn (4)).¹³ σ^p is evaluated by the coupled Hartree–Fock (CPHF) method. σ^p can be decomposed into contributions from the occupied orbitals or the orbital-to-orbital transitions,¹⁴ under the DFT levels. σ^p is shown in eqn (5), although the contributions from the occupied-to-occupied orbital transitions are neglected.^9,13 The process to evaluate σ^p is highly complex; therefore, σ^p is discussed based on the approximate image derived from eqn (6),¹⁴ where (ε_a − ε_i)⁻¹ is the reciprocal orbital energy gap, ψ_k is the k-th orbital function, and L̂_z,N is the orbital angular momentum around the resonance nucleus N, and r_N is the distance of electrons from N. The origin for δ(C) can be elucidated based on MO theory.

σ^t = σ^d + σ^p (1)

σ^m = (σ^m_xx + σ^m_yy + σ^m_zz)/3 (m = d, p and t) (2)

σ^d = Σ^occ_i σ^d_i (3)

σ^d_i = (μ_oe²/12πm_e)〈r_i⁻¹〉 (4)

σ^p = Σ^occ_i σ^p_i = Σ^occ_i × Σ^unocc_a × σ^p_i→a (5)

σ^p_zz = –(μ_oe²/2m_e²)Σ^occ_iΣ^unocc_a(ε_a − ε_i)⁻¹ × {〈ψ_i|L̂_z|ψ_a〉〈ψ_a|L̂_z,Nr_N⁻³|ψ_i〉 + 〈ψ_i|L̂_z,Nr_N⁻³|ψ_a〉〈ψ_a|L̂_z|ψ_i〉} (6)

The interpretation of NMR chemical shifts based on the empirical rules has traditionally been achieved by considering the distribution of electrons of molecules through the inductive and resonance effects, which has been developed in the theory of reactivity, such as the Hammett plots.¹⁵ Indeed, this treatment has achieved a lot of success, but it does not eliminate the gap arising from the differences in the mechanisms controlling the energy and electromagnetic terms. The ¹H NMR chemical shifts could be essentially explained based on the inductive and resonance effects, if the magnetic anisotropic effect is suitably evaluated. However, the effect on the ¹³C NMR chemical shifts would be complexly distributed in the σ^d and σ^p terms as shown by eqn (3)–(6). Therefore, the effects will not discuss in this paper.

Here, we report the analysis of ¹³C NMR chemical shifts, based on the molecular orbital (MO) theory. It is intended to establish the plain rules founded in theory. The origin and mechanisms for δ(C) are discussed based on the MO theory for the effects shown in Scheme 1, together with the effects of ethene, ethyne, benzene and carbonyl and carboxyl groups. Similar investigations on δ(O), reported very recently,¹⁶ with early investigations on δ(Se),⁹ will aid in an easier understanding of δ(C).

Methodological details in the calculations

The calculations were optimized for various carbon species via the Gaussian 09 program package, including GaussView.¹⁷ No specific conditions, such as the long-range interactions, were considered, unless otherwise noted. Optimizations were performed with opt = tight. The threshold (cutoff) values are 0.000015 au, 0.000010 au, 0.000060 au and 0.000040 au for the maximum force, the root mean square (RMS) force, the maximum displacement and the RMS displacement, respectively, where the predicted change in energy seems around 10⁻¹⁰ au. The structural optimizations were performed at the various DFT levels of B3LYP,^18–21 CAM-B3LYP,²² PBE,²³ PBE0,²⁴ LC-ωPBE²⁵ and ωB97X-D²⁶ (L1) and MP2 (L2),^27–29 employing the 6–311++G(3df,3pd) (6D10F) basis set (BSS-A) (L/BSS-A where L = L1 + L2). HOMO and LUMO of the species, together with other MOs, were drawn using GaussView with an isovalue of 0.04 au. The gauge-independent atomic orbital (GIAO) method^30–34 was applied to calculate the absolute magnetic shielding tensors of C [σ*(C: * = d, p and t)], employing the same method as that used in the optimizations (L_a/BSS-A//L_a/BSS-A, where L_a stands for each level of L). The solvent effect was not considered in the discussion. The charge on C (Q(C)) was obtained via natural population analysis (NPA).³⁵ A utility program³⁶ was applied to evaluate the contributions from each ψ_i and/or ψ_i→ψ_a transition. The procedure is explained in the Appendix of the ESI.†

Results and discussion

Selection of standard and suitable level for the analysis of ¹³C NMR chemical shifts based on σ^d(C), σ^p(C) and σ^t(C)

The σ^t(C) values of some carbon species (S) [σ^t(C: S)] were calculated with the GIAO method under B3LYP/BSS-A, for instance, as were the σ^d(C: S) and σ^p(C: S) values. The σ^t(C) values were similarly calculated with MP2/MSS-A, where σ^d(C: S) and σ^p(C: S) are not obtained at the MP2 level. Table 1 lists the calculated σ^m(C: S) (m = d, p and/or t) values for S = C⁴⁺, C²⁺, C⁰, C²⁻ and C⁴⁻. The σ^t(C) values for C⁴⁺, C²⁺ and C⁴⁻, calculated with the two levels, were very close to each other. Among them, C⁴⁻ is taken as the standard for the analysis in this work. The reason is as follows: σ^p(C: C⁴⁻) = 0.0 ppm, which is very favourable for our purpose, although σ^p(C: C²⁺) and σ^p(C: C⁴⁺) are also 0.0 ppm, as shown in Table 1. The electronic ¹S_o state of C⁴⁻ with eight valence electrons according to the octet rule and its spherical electron distribution are also favourable for this purpose.

Table 1 Absolute shielding tensors for ¹³C* (* = 4+, 2+, 0, 2− and 4−) in the singlet state^a

Nuclear	Configoration	σ^dB3LYP(C: 1s)	σ^dB3LYP(C: 2s)	σ^dB3LYP(C: 2p)	σ^dB3LYP(C)	σ^pB3LYP(C)	σ^tB3LYP(C)	σ^tMP2(C)
a Calculated by applying the GIAO method under B3LYP/BSS-A and MP2/BSS-A.
C^4+	(2s)^0(2p)^0	201.71	0.00	0.00	201.71	0.00	201.71	201.77
C^2+	(2s)^2(2p)^0	200.65	37.58	0.00	238.23	0.00	238.23	238.09
C^0	(2s)^2(2p)^2	200.40	32.63	27.19 (×1)	260.22	3986.91	4247.13	2980.47
C^2−	(2s)^2(2p)^4	200.42	31.40	18.74 (×2)	269.23	4542.23	4811.46	3316.42
C^4−	(2s)^2(2p)^6	274.39	31.72	14.08 (×3)	274.39	0.00	274.39	276.12

---

It is necessary to determine the suitable level in this work, next. The σ^t(C: S) values were calculated for the 40 neutral carbon species (54 plots) at the DFT levels of B3LYP,^18–21 CAM-B3LYP,²² PBE,²³ PBE0,²⁴ LC-ωPBE²⁵ and ωB97X-D²⁶ (L1) with BSS-A, together with σ^d(C: S) and σ^p(C: S). The MP2 level (L2) is also applied to obtain the σ^t(C: S) values. The basis set of def2TZVP^37,38 was also applied at the B3LYP level (B3LYP/def2TZVP). The results are collected in Tables S1–S7 and S9 of the ESI.†

The calculated σ^t(C: S) values are very close with each other. The −Δσ^t(C: S) values calculated at the L (= L1 + L2) levels are plotted versus the corresponding δ(C: S), respectively. The plot for S of the 40 neutral carbon species (54 plots) at B3LYP is drawn in Fig. S1 of the ESI.† The plot is analysed assuming the linear relationship (y = ax + b: R_c² (the square of the correlation coefficient)), where (a, b, R_c²) = (1.05, 1.90, 0.998). (The plot is very similar to Fig. 3 for the neutral and charged 75 carbon species). Similar treatments were performed at L = L1 + L2. Table 2 collects the results. The correlations were very similar with each other. The R_c² values at the B3LYP, PBE and ωB97X-D levels (0.998) seem slightly better than others, therefore, the B3LYP level is selected for the calculations. The B3LYP level is most popularly accepted also by the experimental researchers, which is significant for our purposes.

Table 2 Correlations in the plots of calculated –Δσ^t(¹³C: S) versus observed δ(¹³C: S) for the species.^a,b

Entry	Level (L)	a	b	Rc^2	N
a Calculated with the GIAO method under L/BSS-A.b Observed data are used for the corresponding species in the plot.c Under the solvent effect of CHCl3.d Calculated with B3LYP/def2TZVP.
1	B3LYP	1.049	1.90	0.998	54
2	CAM-B3LYP	1.075	0.00	0.997	54
3	PBE	1.037	2.18	0.997	54
4	PBE0	1.056	0.31	0.997	54
5	LC-ωPBE	1.102	−1.55	0.998	54
6	ωB97X-D	1.058	0.46	0.998	54
7	MP2	1.017	1.89	0.995	54
8^c	B3LYP	1.053	2.44	0.997	54
9^d	B3LYP	1.036	1.37	0.997	54

---

Conformational and solvent effects on ¹³C NMR chemical shifts

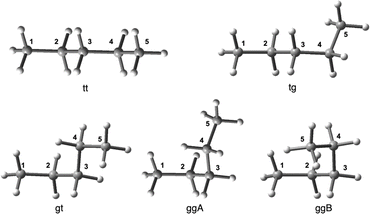
It is an important issue to examine the conformational effect on σ^t(C) in the calculations. The effect is examined exemplified by n-pentane. Five conformers of the different energies are optimized, which are called tt, tg, gt, gg_A and gg_B, together with the topological isomers of tg, where t and g stand for the trans and gauche conformations, respectively. Fig. 1 shows the structures of tt, tg, gt, gg_A and gg_B. The calculated σ^t(C_i: i = 1–5) values are collected in Table S10 of the ESI,† together with the observed values. The energies of tg, gt, gg_A and gg_B from tt are also given in the Table, which are 3.7, 7.2, 6.8 and 14.3 kJ mol⁻¹, respectively. The σ^t(C_i: i = 1–5)_calcd values are plotted versus the δ(C_i: i = 1–5)_obsd values for the five conformers. Fig. 2 shows the plots, which are also analysed assuming the linear relationship. Table 3 collects the (a, b, R_c²) values, which are also given in Fig. 2.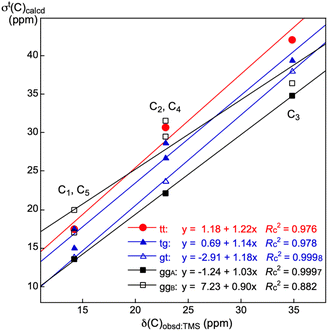

Fig. 1 Optimized conformers for n-pentane with B3LYP/BSS-A.

Fig. 2 Plots of −Δσ^t(C_i: i = 1–5)_calcd:TMS versus δ(C_i: i = 1–5)_obsd:TMS for five conformers in n-pentane.

Table 3 Correlations in the plots of –Δσ^t(C)_calcd:TMS versus δ(C)_obsd for the optimized conformers of n-pentane.^a,b

Entry	Conformer	a	b	Rc^2	N
a Calculated with the GIAO method under B3LYP/BSS-A.b −Δσ^t(C)calcd:TMS = −[σ^t(C: pentane)calcd − [σ^t(C: TMS)calcd].
1	tt	1.22	1.18	0.976	5
2	tg	1.14	0.69	0.978	5
3	gt	1.18	−2.91	0.9998	5
4	ggA	1.03	−1.24	0.9997	5
5	ggB	0.90	7.23	0.882	5

---

As shown in Table 3, the correlation seems excellent for gt and gg_A, good for tt, and moderate for gg_B. The gt and/or gg_A conformers seem most suitable for the purpose, at first glance, however, they are less stable than tt by about 7 kJ mol⁻¹. Judging comprehensively, the tt conformer should also be recommended as the suitable one. The extended conformers would be recommended as the nice ones for the long-chained species in the calculations, since it is inferred that they would be less three-dimensionally crowded than other conformers. The selection of the extended conformers would not damage so much on our discussion, judging from the above discussion. However, other conformers must also be considered for the better discussion since other conformers contribute depending on their populations among the conformers.

The solvent effect of chloroform was also examined with the polarizable continuum model (PCM).³⁹ The calculated results are collected in Table S8 of the ESI† and the plot is contained in Fig. S8 of the ESI.† The correlation is shown in Table 2 (entry 8). The correlation seems very similar to (but very slightly poorer than) that without the solvent effect (entry 1). Therefore, the solvent effect is not considered in this work.

Calculated σ^t(C) and observed δ(C) values

Table 4 lists the σ^m(C: S), Δσ^m(C: S) [ =σ^m(C: S) − σ^m(C: C⁴⁻): Δσ^p(C) (=σ^p(C)) since σ^p(C: C⁴⁻) = 0 ppm] and Δσ^m(C: S)_e (m = d, p and t) values, calculated with B3LYP/BSS-A for various carbon species of 1–56, together with the Q(C) values. The Δσ^m(C: S)_e values are explained later. The values are similar calculated for the carbon species of S1–S20 and S21–S70. The calculated values are provided in Tables S11 and S12, respectively, of the ESI.†

Table 4 The σ^m(C: S), Δσ^m(C: S) and Δσ^m(C: S)_e (m = d, p and t) for various species of 1–56, along with the pre-α, α, β, γ, δ, α-X, β-X and ipso-X (i-X) effects and the effects from the characteristic bonds and groups,^a,b together with the Q(C) values

Species (nos: sym)	Q(C)	σ^d(C)	Δσ^d(C)	σ^p(C)^c	σ^t(C)	Δσ^t(C)	Δσ^d(C)e^d	Δσ^p(C)e^d	Δσ^t(C)e^d	Effect
a Calculated with the GIAO-DFT method under B3LYP/BSS-A.b Δσ^m(C: S) = σ^m(C: S) − σ^m(C: C^4−) (m = d, p and t).c Δσ^p(C) = σ^p(C), since σ^p(C: C^4−) = 0 ppm.d Δσ^m(C: S)e = (1/n)(Δσ^m(C: S) − Δσ^m(C: Se)); see the text for n, S and Se.e The effect not being defined.f From C2H6.
C^4− (1: Oh)	−4.000	274.39	0.00	0.00	274.39	0.00	0.00	0.00	0.00	—
HC^3− (2: C∞v)	−1.815	264.04	−10.35	1807.41	2071.45	1797.06	−10.35	1807.41	1797.06	Pre-α
H2C^2− (3: C2v)	−2.156	261.96	−12.43	137.46	399.42	125.03	−6.22	68.73	62.51	Pre-α
H3C^− (4: C3v)	−1.400	249.53	−24.87	−2.26	247.26	−27.13	−8.29	−0.75	−9.04	Pre-α
CH4 (5: Td)	−0.805	238.98	−35.42	−49.66	189.32	−85.08	−8.85	−12.42	−21.27	Pre-α
CH3H2C^– (6: Cs)	−1.000	250.87	−23.53	−98.55	152.32	−122.08	1.34	−96.29	−94.95	α
EtH2C^− (7: Cs)	−0.915	248.89	−25.51	−82.29	166.59	−107.80	−1.98	16.26	14.28	β
i-PrH2C^− (8: C1)	−0.923	236.54	−37.85	−94.11	142.43	−131.96	−7.16	2.22	−4.94	β
t-BuH2C^− (9: Cs)	−0.985	236.18	−38.22	−62.01	174.16	−100.23	−4.90	12.18	7.28	β
n-PrH2C^− (10: Cs)	−0.990	260.85	−13.54	−87.90	172.96	−101.44	11.97	−5.61	−5.61	γ
n-BuH2C^− (11: Cs)	−0.938	262.85	−11.55	−88.82	174.03	−100.37	1.99	−0.92	1.07	ε
CH3CH3 (12: D3d)	−0.571	238.60	−35.80	−65.21	173.39	−101.00	−0.38	−15.55	−15.92	α
CH3CH2CH3 (13a: C2v)	−0.568	232.81	−41.58	−68.71	164.10	−110.30	−5.79	−3.51	−9.29	β
CH3CH2CH3 (13b: C2v)	−0.382	251.23	−23.17	−91.12	160.10	−114.29	6.12	−20.73	−14.61	α
Me2CHCH3 (14a: C3v)	−0.565	230.20	−44.20	−73.87	156.33	−118.06	−4.20	−4.33	−8.53	β
Me3CH (14b: C3v)	−0.232	267.54	−6.85	−114.35	153.19	−121.21	9.52	−21.56	−12.04	α
t-BuCH3 (15: Td)	−0.563	229.82	−44.58	−78.63	151.19	−123.20	−2.93	−4.47	−7.40	β
CH3CH2CH2CH3 (16a: C2h)	−0.565	236.01	−38.38	−70.67	165.34	−109.05	3.20	−1.96	1.24	γ
CH3CH2CH2CH3 (16b: C2h)	−0.377	244.34	−30.06	−93.60	150.74	−123.66	−6.89	−2.48	−9.37	β
n-BuCH3 (17a: C2v)	−0.375	233.25	−41.15	−67.69	165.55	−108.84	−2.77	2.98	0.21	δ
n-PrMeCH2 (17b: C2v)	−0.564	252.13	−22.27	−99.81	152.32	−122.08	7.79	−6.21	−6.21	γ
i-PrMeCH2 (18a: C1)	−0.372	247.55	−26.84	−102.18	145.37	−129.02	−1.84	−5.53	−7.37	β
EtMe2CH (18b: C1)	−0.225	265.39	−9.01	−118.76	146.63	−127.77	−2.15	−4.41	−6.56	β
t-BuMeCH2 (19: Cs)	−0.371	251.79	−22.60	−112.21	139.58	−134.81	0.19	−7.03	−6.84	β
n-BuMeCH2(20: C2h)	−0.374	243.63	−30.77	−101.29	142.33	−132.06	−8.50	−1.48	−9.98	δ
i-PrMe2CH (21: C2h)	−0.219	259.35	−15.04	−118.14	141.21	−133.18	−4.10	−1.89	−5.99	β
t-BuMe2CH (22: Cs)	−0.215	265.19	−9.20	−127.39	137.80	−136.60	−0.78	−4.35	−5.13	β
n-PrMe2CH (23: C1)	−0.224	274.83	0.43	−128.33	146.50	−127.90	9.44	−9.57	−9.57	γ
n-BuMe2CH (24: C1)	−0.223	276.20	1.80	−128.65	147.55	−126.84	1.37	−0.31	1.06	ε
H3C^+ (25: C3v)	0.362	240.45	−33.94	−467.68	−227.23	−501.62	^e	^e	^e	^e
MeH2C^+ (26: Cs)	−0.215	242.18	−32.21	−219.86	22.32	−252.08	1.73	247.82	249.55	α
EtH2C^+ (27: Cs)	−0.256	242.53	−31.87	−140.46	102.07	−172.33	0.35	79.40	79.75	β
i-PrH2C^+ (28: C1)	−0.472	256.69	−17.70	−139.73	116.96	−157.44	7.26	40.07	47.32	β
t-BuH2C^+ (29: C1)	−0.489	270.61	−3.79	−149.75	120.85	−153.54	9.48	23.37	32.84	β
Me2HC^+ (30: C2)	0.396	247.98	−26.42	−400.37	−152.39	−426.79	3.76	33.66	37.42	α
EtMeHC^+ (31: C1)	0.366	256.56	−17.84	−396.76	−140.20	−414.59	256.56	−396.76	−140.20	β
i-PrMeHC^+ (32: C1)	0.174	268.19	−6.21	−284.57	−16.39	−290.78	134.09	−142.29	−8.19	β
t-BuMeHC^+ (33: C1)	−0.327	293.49	19.10	−182.60	110.89	−163.50	97.83	−60.87	36.96	β
Me3C^+ (34: C1)	0.536	242.28	−32.12	−411.12	−168.84	−443.23	0.61	18.86	19.46	α
EtMe2C^+ (35: C1)	0.540	242.21	−32.19	−414.36	−172.15	−446.55	−0.07	−3.24	−3.31	β
i-PrMe2C^+ (36: C1)	0.544	242.44	−31.95	−404.51	−162.07	−436.46	0.08	3.30	3.39	β
t-BuMe2C^+ (37: C1)	0.537	242.76	−31.63	−402.64	−159.88	−434.27	0.16	2.83	2.99	β
CH3OH (38: Cs)	−0.191	232.16	−42.24	−104.67	127.49	−146.90	−6.82	−55.01	−61.82	α-X
CH3SH (39: Cs)	−0.692	243.86	−30.54	−73.63	170.23	−104.16	4.88	−23.97	−19.09	α-X
CH3SeH (40: Cs)	−0.737	240.42	−33.97	−66.34	174.08	−100.31	1.45	−16.68	−15.23	α-X
CH3SSMe (41: C2)	−0.709	241.38	−33.02	−85.75	155.63	−118.77	2.40	−36.09	−33.69	α-X
CH3F (42: C3v)	−0.066	232.99	−41.40	−126.01	106.99	−167.41	−5.98	−76.35	−82.33	α-X
CH3Cl (43: C3v)	−0.529	243.61	−30.79	−93.19	150.42	−123.98	4.63	−43.53	−38.90	α-X
CH3Br (44: C3v)	−0.601	241.70	−32.69	−83.06	158.65	−115.75	2.73	−33.40	−30.67	α-X
CH3I (45: C3v)	−0.719	236.32	−38.08	−56.17	180.15	−94.24	−2.66	−6.51	−9.17	α-X
CH3CO2Me (46: Cs)	−0.666	248.04	−26.36	−87.22	160.82	−113.58	9.06	−37.56	−28.50	α-X
CH3CN (47: C3v)	−0.677	220.25	−54.14	−38.56	181.70	−92.70	−18.72	11.10	−7.62	α-X
CH3NH2 (48: CS)	−0.360	229.80	−44.60	−79.79	150.01	−124.39	−9.18	−30.13	−39.31	α-X
CH3NO2 (49: Cs)	−0.410	231.58	−42.82	−114.08	117.50	−156.90	−7.40	−64.42	−71.82	α-X
CH3CH2OH (50a: Cs)	−0.016	225.96	−48.44	−108.36	117.60	−156.80	−12.64	−43.15	−55.79	α-X
CH3CH2OH (50b: Cs)	−0.587	245.33	−29.07	−81.19	164.14	−110.26	6.73	−15.98	−9.25	β-X
H2C=CH2 (51: D2h)	−0.365	246.91	−27.49	−194.83	52.08	−222.31	8.31	−129.62	−121.31	C2H4^f
HC≡CH (52: D∞h)	−0.225	255.62	−18.77	−145.56	110.06	−164.34	17.03	−80.35	−63.33	C2H2^f
C6H6 (53: D6h)	−0.106	239.66	−34.73	−192.70	46.96	−227.43	1.07	−127.49	−126.43	C6H6^f
C6H5OH (54: Cs)	0.449	258.53	−15.87	−243.01	15.52	−258.88	18.86	−50.31	−31.45	i-X
H2C=O (55: C2v)	0.307	245.20	−29.19	−263.64	−18.44	−292.83	13.05	−158.97	−145.93	C=O
H(HO)C=O (56: Cs)	0.675	245.49	−28.90	−228.53	16.97	−257.43	13.34	−123.86	−110.53	OC=O

---

The Δσ^m(C: S)_e values are defined by Δσ^m(C: S)_e = (1/n)[Δσ^m(C: S) − Δσ^m(C: S_e)], for the pre-α, α, β, γ and δ effects, together with the α-X, β-X and i-X effects, where S_e are the starting species for the effects and n is the factor used to make Δσ^m(C: S)_e per unit group. Scheme 2 explains the method used to calculate the effects, exemplified by the pre-α, α and β effects. The effects are calculated according to the definition. In the case of the β effect from CH₃CH₂CH₃ to (CH₃)₂CHCH₂CH₃, (CH₃)₂CHCH₂CH₃, CH₃CH₂CH₃ and 2 correspond to S, S_e and n, respectively. The difference in Δσ^t(C: S) between S_e = CH₃CH₂CH₃ (σ^t(C) = 160 ppm) and S = (CH₃)₂CHCH₂CH₃ (145 ppm) is −15 ppm, which corresponds to the 2β effect. The Δσ^t(C: S) values are abbreviated as Δ in Scheme 2. Therefore, the β effect in this process is evaluated as −8 ppm (=Δ/2), for example. The Δσ^d(C: S)_e and Δσ^p(C: S)_e values for the effect are calculated similarly. Scheme 3 summarizes the pre-α, α, β, γ and δ effects, together with the α-X, β-X and i-X effects and the effects of the characteristic bonds and groups. The Δσ^d(C)_e, Δσ^p(C)_e and Δσ^t(C)_e values are also shown in Scheme 3.

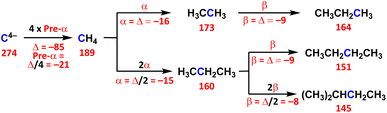Scheme 2 Evaluation of the pre-α, α and β effects. The σ^t(C: S) values in ppm are given in red bold, and the differences between the two values are Δ.

Scheme 3 Pre-α, α, β, γ and δ effects calculated in alkanes and the related species (a) and the α-X, β-X and i-X effects and the effects from the characteristic bonds and groups (b) calculated with the GIAO method under B3LYP/BSS-A.

Fig. 3 shows the plots of δ(C: S)_obsd:TMS versus –Δσ^t(C: S)_calcd:TMS for the various species of 1–56 shown in Table 4 and S21–S70 in Table S12 of the ESI,† although the species are limited for those of the available δ(C: S)_obsd:TMS values. The −Δσ^t(C: S)_calcd:TMS values are used in Fig. 3 for the convenience of the direct comparison between the observed and calculated values. The plot shows an excellent correlation (y = −1.52 + 0.942x: R_c² = 0.998), with some systematic deviations. The excellent correlation confirms the high reliability of the calculations. While the data for (CH₃F, CH₂F₂, CHF₃ and CF₄) are on the correlation line, those for (CH₃Cl, CH₂Cl₂, CHCl₃ and CCl₄) and (CH₃Br, CH₂Br₂, CHBr₃ and CBr₄) deviate systematically from the line.

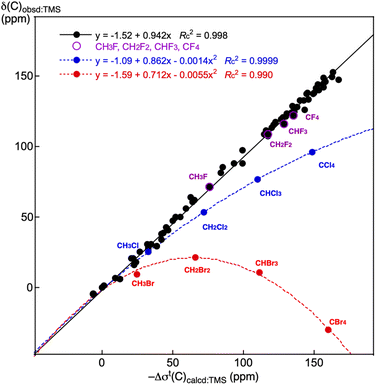Fig. 3 Plots of δ(C: S)_obsd:TMS versus −Δσ^t(C: S)_calcd:TMS for 1–56 and S21–S70, CH₃X, CH₂X₂, CHX₃ and CX₄ (X = F, Cl and Br).

While the data point for CH₃Cl is on the line, that from CH₃Br seems to deviate slightly downside from the correlation. Data for the chlorine and bromine species are analysed using the quadratic functions. The correlations are described by y = −1.09 + 0.862x − 0.0014x²: R_c² = 0.9999 and y = −1.59 + 0.712x − 0.0055x²: R_c² = 0.990, respectively. The relativistic effect must be responsible for the deviations, which will not be discussed here.^{10,11,40–42}

Behaviour of σ^d(C)

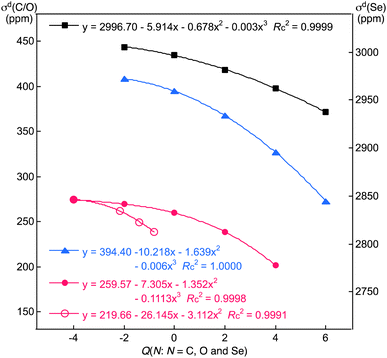
Fig. 4 shows the plot of σ^d(C) versus Q(C) for (C⁴⁺, C²⁺, C⁰, C²⁻ and C⁴⁻). The correlation is excellent if analysed using the cubic function (y = 0.1113x³ − 1.352x² − 7.305x + 259.57: R_c² = 0.9998). The behaviour of the σ^d(C) values can essentially be understood by considering the two factors shown by eqn (3) and (4). If the number of occupied MOs (ψ_i) on C increases, the σ^d(C) values increase, although the magnitude of each σ^d_i(C) will decrease, especially for the outer ψ_i (as shown by σ^d_B3LYP(C: AO)). The average distance of the electrons from C(r_i) in question in ψ_i becomes longer because of the increase in the electron–electron repulsion if the number of occupied MOs increases. In this case, each 〈r_i⁻¹〉 and σ^d_i in eqn (4) decreases. The σ^d_i values collected in Table 4 are well understood as the total effect of the two. Fig. 2 also shows the plot of σ^d(C) versus Q(C) for (C⁴⁻, CH₂²⁻, CH₃⁻, and CH₄). The correlation is also excellent if analysed using the quadratic function (y = −3.112x² − 26.145x + 219.66: R_c² = 0.9998).

Fig. 4 Plots of σ^d(N: N = C, O and Se) versus Q(N) for N⁶⁺, N⁴⁺, N²⁺, N⁰, N²⁻ and/or N⁴⁻, drawn from the red (C), blue (O) and black (Se) curves. The plot of σ^d(C) versus Q(C) for C⁴⁻, CH₂²⁻, CH₃⁻ and CH₄ is also shown by the red hollow circles.

Fig. 4 contains similar plots for (O⁶⁺, O⁴⁺, O²⁺, O⁰ and O²⁻)¹⁶ and (Se⁶⁺, Se⁴⁺, Se²⁺, Se⁰ and Se²⁻),⁹ whose correlations are excellent (y = −0.006x³ − 1.639x² − 10.218x + 394.40: R_c² = 1.0000 for O and y = 0.003x³ − 0.678x² − 5.914x + 2996.70: R_c² = 0.9999 for Se). The correlations become less sharp in the order of N = O > C > Se. The Δσ^d(N^2−:2+) (=(σ^d(N²⁻) − σ^d(N²⁺)) value was divided by the overall chemical shift width for each N. The values were compared with each other to estimate roughly the contributions of σ^d(N) to σ^t(N). The ratio is 0.103 (=31.0/300) for C, 0.016 (=41.1/2500) for O and 0.003 (=23.9/8000) for Se. The results show that the contributions of σ^d(N) to the overall chemical shifts decreased in the order of N = C ≫ O >> Se. As a result, the σ^d(C) term should be considered carefully for N = C relative to the cases of O and Se.

Fig. 5 shows the plot of σ^d(C: S) versus Q(C) for 1–56 in Table 4, except for those plotted in Fig. 4 (1–5). The σ^d(C: S) values are analysed separately by the types of S: RH₂C⁻ (6–11), RCH₃ (12–16), RMeCH₂ (17–20), RMe₂CH (21–25), RH₂C⁺ (26–30), RMeHC⁺ (31–34), RMe₂C⁺ (35 and 36) and CH₃X (37–50), together with C₂H₄ (51), C₂H₂ (52), C₆H₆ (53), H₂C=O (54) and H(HO)C=O (55). The range of σ^d(C) in each plot is less than approximately 15 ppm, except for that of RMeCH₂ (17–20), which ranges from 30 ppm. The σ^d(C: S) values increase in the order of R = Me < Et < i-Pr < t-Bu for RH₂C⁻ and RCH₃. However, the behaviour seems complex for others.

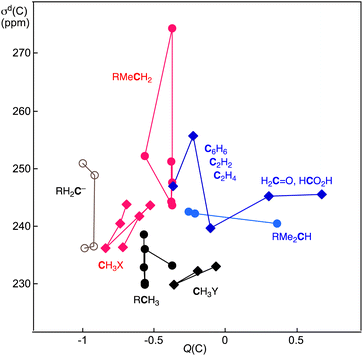Fig. 5 Plots of σ^d(C) versus Q(C) for various species, 1–56, except for H_kC^(4−k)− (1–4), collected in Table 4.

The origin and mechanisms of the effects are discussed next, using an approximated image derived from eqn (6).

Origin of the pre-α effect

The analysis of the ¹³C NMR chemical shifts starts from the pre-α effect,⁹ this is the important starting point of our NMR analysis. The pre-α effect is evaluated by the (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values. The average values from C⁴⁻ to H₄C are (−8.9, −12.4, −21.3 ppm) (see Table 4), which are calculated per unit group (per H in this case). The pre-α effect is theoretically predicted to be a downfield shift of 21 ppm based on the average value of Δσ^t(C)_e from C⁴⁻ to H₄C. The solvent effect is not considered for the pre-α effect on each process from C⁴⁻ to CH₄, although the negative charge would also be of importance (see Scheme 3).

Table 5 lists the σ^d(C), σ^p(C) and σ^t(C) values of C⁴⁻, H₂C²⁻, H₃C⁻ and H₄C, separately by each MO. The inner MO of ψ₁ is formed by the 1s(C) AO; therefore, it greatly contributes to σ^d(C) but not σ^p(C). The second inner ψ₂ is constructed mainly by the 2s(C) AO; therefore, it contributes substantially to σ^d(C) but slightly to σ^p(C). The outer MOs of ψ₃, ψ₄ and ψ₅ are constructed mainly by the 2p_x(C), 2p_y(C) and 2p_z(C) AOs with 1s(H) AO(s), if any. Therefore, they contribute greatly to σ^p(C) but slightly to σ^d(C), although σ^p(C) = 0 ppm for all the MOs in C⁴⁻. The MOs of ψ₃, ψ₄ and ψ₅ in C⁴⁻ are equivalent; therefore, the total values of the three are given in the Table, as are ψ₃ and ψ₄ in H₃C⁻.

Table 5 The σ^d(C), σ^p(C) and σ^t(C) values for C⁴⁻, H₂C²⁻, H₃C⁻ and H₄C, given separately by each MO^a

MO (i in ψi)	σ^di(C)	σ^pi(C)	σ^ti(C)
a Calculated with the GIAO-DFT method under B3LYP/BSS-A.b MOs of ψ1, ψ2, ψ3, ψ4 and ψ5 of C^4− are constructed mainly by 1s(C), 2s(C), 2px(C), 2py(C) and 2pz(C) AOs, respectively.
C^4^– (Oh)^b
1 (A1g)	200.45	0.00	200.45
2 (A1g)	31.72	0.00	31.72
3 (T1u)–5 (T1u)	42.04	0.00	42.04
Total	274.39	0.00	274.39
H2C^2^− (C2v)
1 (A1)	200.37	0.00	200.37
2 (A1)	23.73	−8.06	15.68
3 (B2)	1.27	−93.29	−92.02
4 (A1)	20.18	−16.17	4.01
5 (B1)	16.41	197.59	214.00
ψocc to ψocc		57.39
Total	261.96	137.46	399.42
H3C^− (C3v)
1 (A1)	200.32	0.00	200.32
2 (A1)	24.93	−3.19	21.74
3 (E)–4 (E)	3.28	−148.47	−145.19
5 (A1)	21.00	24.22	45.22
ψocc to ψocc		125.17
Total	249.52	−2.26	247.26
H4C (Td)
1 (A1)	200.28	0.00	200.28
2 (A1)	26.97	0.33	27.30
3 (T2)–5 (T2)	11.73	−175.52	−163.83
ψocc to ψocc		125.55
Total	238.98	−49.66	189.32

---

The protonation of C⁴⁻ introduces σ(C–H) and σ*(C–H) orbitals in the resulting species, resulting in the asymmetrical distribution of electrons. The symmetrical and unsymmetrical components of the electron distribution produce σ^d(C) and σ^p(C), respectively, as mentioned above. The σ^p(C) terms are caused through orbital-to-orbital transitions, such as the ψ_i→ψ_a transition, where σ(C–H) and σ*(C–H) are expected to operate as the typical ψ_i and ψ_a, respectively, in the transitions. Table 6 lists the ψ_i→ψ_a transitions that contributed mainly to σ^p_i→a:kk(C: k = x, y and/or z) for H₂C²⁻ and H₄C. The magnitudes of σ^p_i→a(C), which are greater than 10 ppm in magnitude, are provided in Table 6. In the case of H₂C²⁻, the ψ₃→ψ₉ (σ^p_3→9:zz(C) = −113.8 ppm) and ψ₄→ψ₉ (σ^p_4→9:yy(C) = −87.6 ppm) transitions largely contribute to σ^p_i→a(C), with large positive contributions from the ψ₄→ψ₇, ψ₅→ψ₆, ψ₅→ψ₇ and ψ₅→ψ₈ transitions. The ψ₃→ψ₁₅, ψ₃→ψ₁₆, ψ₄→ψ₁₄, ψ₄→ψ₁₆, ψ₅→ψ₁₄ and ψ₅→ψ₁₅ transitions contribute greatly to σ^p(C) (σ^p_i→a:kk(C) = −33.3 ppm) in H₄C.

Table 6 Main contributions from the occupied-to-unoccupied orbital transitions on σ^p(C), exemplified by H₂C^2– and H₄C.^a

i→a^b	σ^pi→a:xx(C)	σ^pi→a:yy(C)	σ^pi→a:zz(C)	σ^pi→a(C)
a Calculated with the GIAO method under B3LYP/BSS-A.b The magnitudes of σ^pi→a(C) larger than 10 ppm are shown. In ψi→ψa.
H2C^2^− (C2v)
3→9	0.00	0.00	−113.76	−37.92
4→7	72.46	0.00	0.00	24.15
4→9	0.00	−87.63	0.00	−29.21
5→6	0.00	216.63	0.00	72.21
5→7	0.00	0.00	225.75	75.25
5→8	0.00	143.42	0.00	47.81
CH4 (Td)
3→15	−33.27	0.00	0.00	−11.09
3→16	0.00	−33.27	0.00	−11.09
4→14	−33.27	0.00	0.00	−11.09
4→16	0.00	0.00	−33.27	−11.09
5→14	0.00	−33.27	0.00	−11.09
5→15	0.00	0.00	−33.27	−11.09

---

Fig. 6a and b illustrate the selected ψ_i→ψ_a transitions for H₂C²⁻ and H₄C, respectively, along with the characteristics of ψ_i and ψ_a and the orbital energies. Fig. 6a shows the ψ₃→ψ₉, ψ₄→ψ₇, ψ₄→ψ₉, ψ₅→ψ₆, ψ₅→ψ₇ and ψ₅→ψ₈ transitions in H₂C²⁻, whereas the ψ₃→ψ₁₅, ψ₃→ψ₁₆, ψ₄→ψ₁₄, ψ₄→ψ₁₆, ψ₅→ψ₁₄ and ψ₅→ψ₁₅ transitions in H₄C are shown in Fig. 6b.

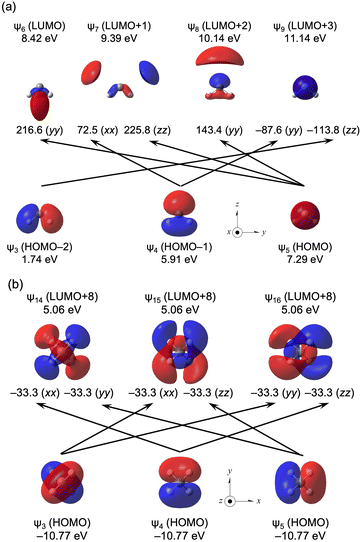Fig. 6 Contributions from each ψ_i→ψ_a transition to the components of σ^p(C) in H₂C²⁻ (a) and H₄C (b) with an isovalue of 0.04 au.

Origin of the α effect

A downfield shift of approximately 10–15 ppm is usually observed for the α effect, which is well supported by the calculated (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values of (−0.4, −15.6, −15.9 ppm) for CH₃CH₃ from CH₄ (see Table 4 and Scheme 3).

Table 7 lists the σ^d(C), σ^p(C) and σ^t(C) values of C₂H₆, separately for each MO. Similar to the case of H₄C, the first and second inner MOs of ψ₁ and ψ₂ are constructed by the 1s(C) AOs; therefore, they greatly contribute to σ^d(C) but not σ^p(C). The third and fourth inner MOs of ψ₃ and ψ₄ are formed mainly by the 2s(C) AOs; therefore, they contribute to σ^d(C) and σ^p(C), more or less. The outer MOs of ψ₅–ψ₉ are constructed mainly by the 2p(C) AOs with the 1s (H) AOs; therefore, they contribute largely to σ^p_i(C) (−36.6 to −42.3 ppm), with very small contributions to σ^d(C) (−4.1 to 8.0 ppm). Table 8 lists the ψ_i→ψ_a transitions contributing to σ^p_i→a:kk(C: k = x, y and/or z), where a larger than ca. 20 ppm in magnitude. The ψ_i→ψ_a transitions of ψ₅→ψ₂₉ (σ^p_5→29:yy(C) = −21.0 ppm), ψ₆→ψ₂₉ (σ^p_6→29:xx(C) = −20.5 ppm), ψ₇→ψ₂₆ (σ^p_7→26:xx(C) = −25.5 ppm), ψ₇→ψ₂₇ σ^p_7→27:yy(C) = −25.5 ppm), ψ₈→ψ₂₇ (σ^p_8→27:zz(C) = −21.1 ppm) and ψ₉→ψ₂₆ (σ^p_9→26:zz(C) = −21.2 ppm) contribute a lot to σ^p_i→a:kk(C: k = x, y and/or z).

Table 7 The σ^d(C), σ^p(C) and σ^t(C) values contributed from each MO of CH₃CH₃ (D_3d)^a

MO (i in ψi)	σ^di(C)	σ^pi(C)	σ^ti(C)
a Calculated with the GIAO-DFT method under B3LYP/BSS-A.
1 (A1g); 2 (A2u)	200.29	0.00	200.29
3 (A1g)	15.73	−3.49	12.24
4 (A2u)	17.28	5.92	23.20
5 (Eu)	2.78	−36.60	−33.81
6 (Eu)	2.78	−36.74	−33.95
7 (A1g)	7.97	−42.31	−34.34
8 (Eg)	−4.12	−36.94	−41.06
9 (Eg)	−4.12	−36.94	−41.06
ψocc to ψocc		121.88
Total	238.60	−65.21	173.39

---

Table 8 Main contributions from the ψ_i→ψ_a transitions on σ^p_i→a:kk(C: k = x, y and/or z) of CH₃CH₃ (D_3d)^a,b

i→a^b	σ^pi→a:xx(C)	σ^pi→a:yy(C)	σ^pi→a:zz(C)	σ^pi→a(C)
a Calculated with the GIAO method under B3LYP/BSS-A. Magnitudes of σ^pi→a(C) larger than 6 ppm are shown.b In ψi→ψa.
5→29	0.00	−20.97	0.00	−6.99
6→29	−20.53	0.00	0.00	−6.84
7→26	−25.48	0.00	0.00	−8.49
7→27	0.00	−25.47	0.00	−8.49
8→27	0.00	−0.54	−21.14	−7.23
9→26	0.00	−0.54	−21.16	−7.23

---

Fig. 7 shows the selected transitions of CH₃CH₃ (D_3d), as shown in Table 8. The occupied-to-unoccupied MO transitions play an important role in the α effect in CH₃CH₃. While the HOMO of ψ₉ acts as a good donor, the LUMOs of ψ₁₀ and ψ₁₁–ψ₂₅ do not seem to contribute substantially to the transitions.

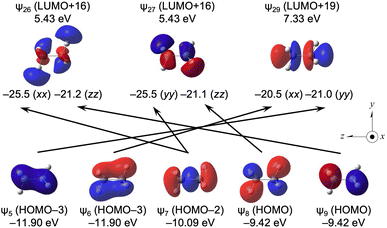Fig. 7 Contributions from each ψ_i→ψ_a transition to the σ^p_i→a:kk(C: k = x, y and/or z) in CH₃CH₃ with an isovalue of 0.04 au.

Origin of the β effect

A downfield shift of approximately 10 ppm is often observed for the β effect. The β effect is evaluated for CH₃CH₂CH₃ (C_2v), (CH₃)₂CHCH₃ (C_3v) and (CH₃)₃CCH₃ from the corresponding species. The calculated (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values for the species are (−5.8, −3.5, −9.3 ppm), (−4.2, −4.3, −8.5 ppm) and (−2.9, −4.5, −7.4 ppm), respectively, which reproduce the observed β effect well (see Table 4 and Scheme 3).

Table 9 lists the σ^d(C), σ^p(C) and σ^t(C) values for CH₃CH₂CH₃ (C_2v) separately by ψ_i. The contributions from ψ₇, ψ₈, ψ₁₁, ψ₁₂ and ψ₁₃ to σ^p_i(C) are large (−21.6 to −48.7 ppm), although the contributions seem to be widely distributed to ψ_i. Table 10 shows the main ψ_i→ψ_a transitions contributing to σ^p_i→a:kk(C: k = x, y and/or z). The contributions are relatively large for ψ₈→ψ₄₁ (σ^p_8→41:xx(C) = −15.2 ppm) and ψ₁₁→ψ₃₆ (σ^p_11→36:zz(C) = −20.1 ppm).

Table 9 The σ^d(C), σ^p(C) and σ^t(C) values contributed from each MO of CH₃CH₂CH₃ (C_2v)^a

MO (i in ψi)	σ^d(C)	σ^p(C)	σ^t(C)
a Calculated with the GIAO-DFT method under B3LYP/BSS-A.
1 (A1)–3 (A1)	200.29	0.00	200.29
4 (A1)	16.20	−2.72	13.48
5 (B2)	6.36	−1.23	5.13
6 (A1)	16.89	4.51	21.39
7 (B1)	4.00	−33.20	−29.20
8 (A1)	7.27	−21.55	−14.28
9 (B2)	11.57	2.10	13.68
10 (A2)	−0.60	−2.62	−3.22
11 (B2)	0.28	−29.63	−29.35
12 (A1)	−5.18	−48.71	−53.89
13 (B1)	−5.87	−41.71	−47.58
ψocc to ψocc		83.64
Total	251.23	−91.12	160.10

---

Table 10 Main contributions from the ψ_i→ψ_a transitions on σ^p_i→a:kk(C: k = x, y and/or z) in CH₃CH₂CH₃ (C_2v)^a,b

i→a^c	σ^pi→a:xx(C)	σ^pi→a:yy(C)	σ^pi→a:zz(C)	σ^pi→a(C)
a Calculated with the GIAO method under B3LYP/BSS-A.b The magnitudes of σ^pi→a(C) larger than 5 ppm are shown.c In ψi→ψa.
8→41	−15.15	0.00	0.00	−5.05
11→36	0.00	0.00	−20.07	−6.69

---

Fig. 8 shows the ψ₈→ψ₄₁ and ψ₁₁→ψ₃₆ transitions, together with the orbital energies and the axes of CH₃CH₂CH₃. The transitions are well visualized. However, it is curious that ψ₁₄ (LUMO) and those near it seem not to operate effectively as acceptors in the transitions. Similar results are obtained for EtMeCH₂, i-PrMeCH₂ and t-BuMeCH₂ from the corresponding species. The calculated (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values are (−6.9, −2.5, −9.4 ppm), (−1.8, −5.5, −7.4 ppm) and (0.2, −7.0, −6.8 ppm), respectively, for the species. For ionic EtH₂C⁻, t-BuH₂C⁻ and EtH₂C⁺, the calculated (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values are predicted to be (−2.0, 16.3, 14.3 ppm), (−4.9, 12.2, 7.3 ppm) and (0.4, 79.4, 79.8 ppm) respectively, from the corresponding species. The (large) upfield shifts are again predicted for the β effect for the ionic species. A large positive Δσ^t(C)_e value of 79.8 ppm is predicted for EtH₂C⁺ from the corresponding species. The vacant 2p(C) orbital in EtH₂C⁺ is responsible for these results.

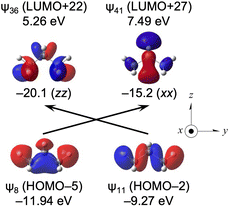Fig. 8 Contributions from each ψ_i→ψ_a transition to the σ^p_i→a:kk(C: k = x, y and/or z) of CH₃CH₂CH₃ with an isovalue of 0.04 au.

Origin of the γ and δ effects

An upfield shift of ∼2 ppm is often encountered for the γ effect. The conformational effect cannot be avoided in the γ and δ effects,⁹ contrary to the α and β effects in the cases of CH₄, CH₃CH₃ and CH₃CH₂CH₃, as discussed above. The γ and δ effects are not discussed further here since they are negligibly small.

Origin of the α-X and β-X effects

The α-X effect is examined for CH₃–X from CH₄ and CH₃CH₂–X from CH₃CH₃ (X = OH, SH, SeH, SSCH₃, F, Cl, Br, I, CO₂Me, CN, NH₂ and/or NO₂) (see Scheme 3, Table 4 and Table S11 of the ESI†). The (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values of (−18.7–40.3, −76.4–−11.1, −82.3–−4.4 ppm) are predicted for the species. The β-X effect is similarly examined for CH₃CH₂–X from CH₃CH₃ (X = OH, SH, SeH, SSCH₃, F, Cl, Br, I, CO₂Me, CN, NH₂ and NO₂) (see Scheme 3, Table 4 and Table S11 of the ESI†). The (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values of (−16.8–0.9, −66.9–14.1, −77.2–−1.3 ppm) are calculated for the species. It seems difficult to find a good relation between the α-X and β-X effects in the same species, as a whole. However, such relation could be found is the species are divided to some groups, as shown in Fig. S10 of the ESI.† The β-X effect of −77.2 ppm for X = F is notable.

Table 11 lists the σ^d(C), σ^p(C) and σ^t(C) values for CH₃CH₂OH and CH₃CH₂OH, separately for each MO. The outer MOs of HOMO (ψ₁₃), HOMO–1 (ψ₁₂), HOMO-4 (ψ₉) and HOMO–5 (ψ₈) contribute greatly to σ^p(C) in CH₃CH₂OH. On the other hand, the outer MOs of HOMO-2 (ψ₁₁) and HOMO–3 (ψ₁₀) contribute greatly to σ^p(C) in CH₃CH₂OH. Table 12 lists the ψ_i→ψ_a transitions contributing to σ^p_i→a:kk(C: k = x, y and/or z), which are greater than 5 ppm in magnitude. The contributions from the ψ_i→ψ_a transitions seem greater for ψ₈→ψ₃₈ (σ^p_8→33:xx(C) = −13.1 ppm and σ^p_8→33:yy(C) = −3.2 ppm) in CH₃CH₂OH. The contributions are greater for ψ₁₀→ψ₃₁ (σ^p_10→31:yy(C) = −28.7 ppm), ψ₁₀→ψ₃₅ (σ^p_10→35:zz(C) = −17.1 ppm) and ψ₁₀→ψ₅₉ (σ^p_10→59:zz(C) = −15.36 ppm) in CH₃CH₂OH.

Table 11 The σ^d(C), σ^p(C) and σ^t(C) values of CH₃CH₂OH, given separately by each ψ_i^a

MO (i in ψi)	σ^di(C)	σ^pi(C)	σ^ti(C)
a Calculated with the GIAO method under B3LYP/BSS-A.
CH3CH2OH (Cs)
1 (A′)–3 (A′)	200.33	0.00	200.32
4 (A′)–6 (A′)	30.44	−6.12	24.33
7 (A′)	4.08	−28.13	−24.05
8 (A′′)	4.62	−50.64	−46.02
9 (A′)	−4.90	−48.07	−52.97
10 (A′)	−2.22	−9.91	−12.13
11 (A′′)	−1.61	−16.19	−17.80
12 (A′)	1.21	−47.21	−46.00
13 (A′′)	−6.00	−27.71	−33.70
ψocc to ψocc		125.61
Total	225.95	−108.36	117.60
CH3CH2OH (Cs)
1 (A′)–3 (A′)	200.27	−0.03	200.24
4 (A′)–6 (A′)	30.09	0.84	31.14
7 (A′)	2.12	−5.52	−3.41
8 (A′′)	3.12	−18.92	−15.80
9 (A′)	15.42	−6.30	9.12
10 (A′)	−3.19	−72.62	−75.82
11 (A′′)	−2.25	−50.07	−52.31
12 (A′)	0.94	−20.25	−19.32
13 (A′′)	−1.18	−2.31	−3.50
ψocc to ψocc		93.77
Total	245.33	−81.19	164.14

---

Table 12 Main contributions from the ψ_i→ψ_a transitions on σ^p_i→a:kk(C: k = x, y and/or z) in CH₃CH₂OH^a,b

i→a^c	σ^pi→a:xx(C)	σ^pi→a:yy(C)	σ^pi→a:zz(C)	σ^pi→a(C)
a Calculated with the GIAO method under B3LYP/BSS-A.b The magnitudes of σ^pi→a(C) larger than 5 ppm are shown.c In ψi→ψa.
CH3CH2OH (Cs)
8→33	−13.09	−3.24	0.00	−5.44
CH3CH2OH (Cs)
10→31	−3.47	−28.67	0.00	−10.71
10→35	0.00	0.00	−17.07	−5.69
10→59	0.00	0.00	−15.29	−5.10

---

Fig. 9a shows the ψ₈→ψ₃₃ transition in CH₃CH₂OH and the ψ₁₀→ψ₃₁, ψ₁₀→ψ₃₅ and ψ₁₀→ψ₅₉ transitions in CH₃CH₂OH are illustrated in Fig. 9b. The α-X and β-X effects are well visualized, employing the ψ_i→ψ_a transitions.

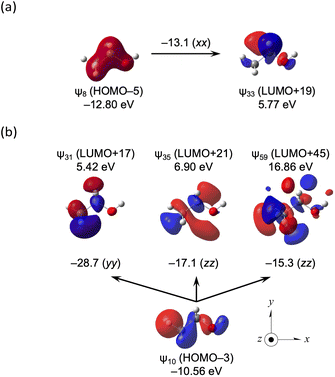Fig. 9 Contributions from each ψ_i→ψ_a transition to the components of σ^p(C) for CH₃CH₂OH (a) and CH₃CH₂OH (b), together with the axes with an isovalue of 0.04 au.

The α-X effect is also typical detected in CH₃NH₂ and CH₃NO₂. The σ^d(C), σ^p(C) and σ^t(C) values for CH₃NH₂ and CH₃NO₂ are listed in Table S13 of the ESI,† separately for each MO. In the case of CH₃NH₂, which has a very strong electron donating X of NH₂, the outer MOs of the HOMO–1 (ψ₈) ∼ HOMO–3 (ψ₆) contribute greatly to σ^p(C). In the case of CH₃NO₂, with the very strong electron accepting group X of NO₂, the somewhat more inner HOMO–3 (ψ₁₃) and HOMO–4 (ψ₁₂) also strongly affect σ^p(C). The ψ_i→ψ_a transitions contributing to σ^p_i→a:kk(C: k = x, y and/or z) from the species are collected in Table S14 of the ESI.† The contributions to CH₃NH₂ are large for the ψ_i→ψ_a transitions of ψ₇→ψ₂₆ (σ^p_7→26:zz(C) = −19.9 ppm), ψ₇→ψ₄₁ (σ^p_7→41:zz(C) = −18.8 ppm), ψ₈→ψ₂₃ (σ^p_8→23:yy(C) = −31.4 ppm) and ψ₈→ψ₂₆ (σ^p_8→26:xx(C) = −22.9 ppm). Those in CH₃NO₂ are large for ψ₁₂→ψ₂₈ (σ^p_12→28:xx(C) = −28.7 ppm) and ψ₁₂→ψ₂₉ (σ^p_12→29:yy(C) = −29.2 ppm) and ψ₁₃→ψ₂₈ (σ^p_13→28:zz(C) = −31.6 ppm). The ψ_i→ψ_a transitions of ψ₇→ψ₂₆, ψ₇→ψ₄₁, ψ₈→ψ₂₃ and ψ₈→ψ₂₆ for CH₃NH₂ and those of ψ₁₂→ψ₂₈, ψ₁₂→ψ₂₉, ψ₁₃→ψ₂₈ and ψ₁₃→ψ₃₀ for CH₃NO₂ are shown in Fig. S11a and b of ESI,† respectively. The α-X effect is well visualized both for X of a very good donor and a very good acceptor, employing ψ_i→ψ_a transitions.

Effect from ethene and ethyne and the origin

Large downfield shifts in δ(C) are reported for ethene (∼120 ppm) and ethyne (∼60 ppm) from ethane.^1–4 The calculated (Δσ^d(C)_e, Δσ^p(C)_e and Δσ^t(C)_e) values for H₂C=CH₂ and HC≡CH from CH₃CH₃ are (8.3, −129.6, −121.3 ppm) and (17.0, −80.4, −63.3 ppm), respectively, which reproduce the observed results well.

Table 13 lists the σ^d(C), σ^p(C) and σ^t(C) values of H₂C=CH₂ (D_2h) and HC≡CH (D_∞h), separately for each MO, whereas HOMO–1 (ψ₇) ∼ HOMO–3 (ψ₅) contribute a lot to σ^p(C) in H₂C=CH₂ (D_2h), HOMO–2 (ψ₅) and HOMO–3 (ψ₄) strongly affect HC≡CH (D_∞h). Table 14 shows that the ψ_i→ψ_a transitions largely contribute to σ^p(C) in H₂C=CH₂ (D_2h) and HC≡CH (D_∞h). The ψ_i→ψ_a transitions of ψ₆→ψ₉ (σ^p_6→9:yy(C) = −175.0 ppm), ψ₆→ψ₁₇ (σ^p_6→17:yy(C) = −47.7 ppm), ψ₆→ψ₃₇ (σ^p_6→37:yy(C) = −31.9 ppm), ψ₇→ψ₉ (σ^p_7→9:zz(C) = −126.0 ppm) and ψ₇→ψ₁₇ (σ^p_7→17:zz(C) = −32.1 ppm) provide great contributions to H₂C=CH₂ (D_2h). Similarly, the transitions of ψ₅→ψ₁₀ (σ^p_5→10:yy(C) = −84.2 ppm), ψ₅→ψ₁₁ (σ^p_5→11:xx(C) = −84.2 ppm), ψ₅→ψ₁₇ (σ^p_5→17:xx(C) = −48.7 ppm) and ψ₅→ψ₁₈ (σ^p_5→18:yy(C) = −48.7 ppm) greatly contribute to HC≡CH (D_∞h).

Table 13 The σ^d(C), σ^p(C) and σ^t(C) values of H₂C=CH₂ (D_2h) and HC≡CH (D_∞h), given separately by each ψ_i^a

MO (i in ψi)	σ^di(C)	σ^pi(C)	σ^ti(C)
a Calculated with the GIAO method under B3LYP/BSS-A.
H2C=CH2 (D2h)
1 (Ag); 2 (B1u)	200.30	0.02	200.32
3 (Ag)	16.54	−10.56	5.98
4 (B1u)	13.95	−0.39	13.56
5 (B2u)	1.14	−33.89	−32.75
6 (Ag)	5.18	−112.14	−106.96
7 (B3g)	−7.49	−87.51	−94.99
8 (B3u)	17.28	−19.65	−2.37
ψocc to ψocc		69.30
Total	246.91	−194.83	52.08
HC≡CH (D∞h)
1 (Σg); 2 (Σu)	200.21	−0.46	199.74
3 (Σg)	17.82	−22.76	−4.95
4 (Σu)	2.99	−34.63	−31.64
5 (Σg)	−2.03	−131.94	−133.97
6 (Πu)	18.32	−10.20	8.12
7 (Πu)	18.32	0.04	18.36
ψocc to ψocc		54.39
Total	255.62	−145.56	110.06

---

Table 14 Main contributions from the ψ_i→ψ_a transitions in the σ^p(C) of H₂C=CH₂ (D_2h) and HC≡CH (D_∞h)^a,b

i→a^c	σ^pi→a:xx(C)	σ^pi→a:yy(C)	σ^pi→a:zz(C)	σ^pi→a(C)
a Calculated with the GIAO method under B3LYP/BSS-A.b The magnitudes of σ^pi→a(C) larger than 5 ppm are shown.c In ψi→ψa.
H2C=CH2 (D2h)
6→9	0.00	−174.98	0.00	−58.33
6→17	0.00	−47.66	0.00	−15.89
6→37	0.00	−31.93	0.00	−10.64
7→9	0.00	0.00	−126.04	−42.01
7→17	0.00	0.00	−32.05	−10.68
7→19	−21.82	0.00	0.00	−7.27
7→37	0.00	0.00	−16.43	−5.48
HC≡CH (D∞h)
5→10	0.00	−84.16	0.00	−28.05
5→11	−84.16	0.00	0.00	−28.05
5→17	−48.66	0.00	0.00	−16.22
5→18	0.00	−48.66	0.00	−16.22
5→30	−22.78	0.00	0.00	−7.59
5→31	0.00	−22.78	0.00	−7.59
5→37	−23.40	0.00	0.00	−7.80
5→38	0.00	−23.40	0.00	−7.80

---

Fig. 10a shows the ψ₆→ψ₉, ψ₆→ψ₁₇, ψ₆→ψ₃₇, ψ₇→ψ₉ and ψ₇→ψ₃₇ transitions in H₂C=CH₂ (D_2h), and Fig. 10b shows the ψ₅→ψ₁₀, ψ₅→ψ₁₁, ψ₅→ψ₁₇ and ψ₅→ψ₁₈ transitions in HC≡CH (D_∞h). The MO energies and axes are also shown in the figure. The main characteristics of ψ₆, ψ₇, ψ₉, ψ₁₇ and ψ₃₇ with H₂C=CH₂ are occupied σ(C=C), σ(C–H), vacant π*(C=C), σ*(C–C) and σ*(C–H), respectively. The LUMO of ψ₉ acts as a great acceptor in the transition, whereas the HOMO of ψ₈ does not seem to do so. The main characteristic of ψ₅ in HC≡CH is the occupied σ(C–C), whereas those of ψ₁₀ and ψ₁₁ are the vacant π*(C=C), and those of ψ₁₇ and ψ₁₈ seem to be higher vacant π*(C=C). The HOMO and LUMO in HC≡CH seem not to act as good donors and acceptors, respectively.

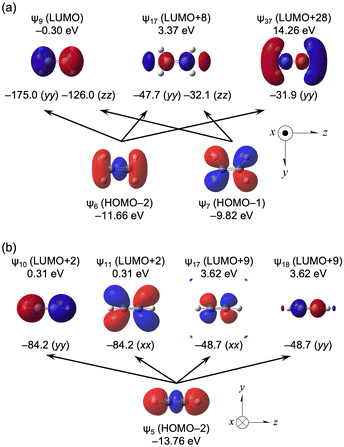Fig. 10 Contributions from each ψ_i→ψ_a transition to the components of σ^p(C) in H₂C=CH₂ (D_2h) (a) and HC≡CH (D_∞h) (b), together with the axes with an isovalue of 0.04 au.

Effect of benzene and its origin

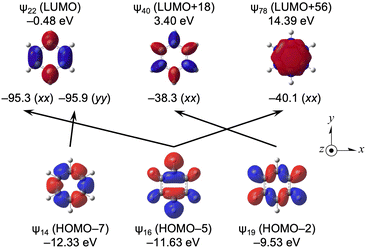
Large downfield shifts in δ(C) (∼127 ppm) are reported for benzene.^1–4 The calculated (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values from CH₃CH₃ are (1.1, −127.5, −126.4 ppm). The calculations reproduced the observed results well.

Table 15 lists the σ^d(C), σ^p(C) and σ^t(C) values of C₆H₆, separately, by ψ_i. The contributions from HOMO–2 (ψ₁₉), HOMO–5 (ψ₁₆) and HOMO–7 (ψ₁₄) are very large, together with HOMO–3 (ψ₁₈). Table 16 lists the ψ_i→ψ_a transitions that greatly contribute to σ^p(C). The transitions of ψ₁₄→ψ₂₂ (σ^p_14→22:yy(C) = −95.9 ppm), ψ₁₆→ψ₂₂ (σ^p_16→22:xx(C) = −95.3 ppm), ψ₁₆→ψ₇₈ (σ^p_16→78:xx(C) = −40.1 ppm) and ψ₁₉→ψ₄₀ (σ^p_19→40:xx(C) = −38.3 ppm) contribute greatly, together with ψ₁₈→ψ₄₀ (σ^p_18→40:yy(C) = −43.9 ppm) and ψ₁₈→ψ₅₀ (σ^p_18→50:yy(C) = −31.2 ppm).

Table 15 The σ^d(C), σ^p(C) and σ^t(C) values of C₆H₆ (D_6h), given separately by each ψ_i^a

MO (i in ψi)	σ^di(C)	σ^pi(C)	σ^ti(C)
a Calculated with the GIAO method under B3LYP/BSS-A.
1 (A1g)	33.37	−0.01	33.37
2 (E1u)–6 (B1u)	167.08	0.17	167.23
7 (A1g)	5.82	−5.41	0.42
8 (E1u)	2.95	−4.84	−1.89
9 (E1u)	11.07	−3.02	8.05
10 (E2g)	0.88	−15.67	−14.78
11 (E2g)	7.07	2.34	9.41
12 (A1g)	1.95	−11.67	−9.72
13 (B2u)	3.33	−10.46	−7.13
14 (B1u)	2.84	−48.38	−45.54
15 (E1u)	6.87	−0.43	6.44
16 (E1u)	−19.97	−107.31	−127.28
17 (A2u)	8.37	−9.28	−0.91
18 (E2g)	1.65	−30.56	−28.91
19 (E2g)	−5.76	−48.14	−53.90
20 (E1g)	11.06	−11.58	−0.51
21 (E1g)	2.08	−1.36	0.72
ψocc to ψocc		111.93
Total	240.68	−193.67	47.00

---

Table 16 Main contributions from the ψ_i→ψ_a transitions in the σ^p(C) of C₆H₆ (D_6h)^a,b

i→a^c	σ^pi→a:xx(C)	σ^pi→a:yy(C)	σ^pi→a:zz(C)	σ^pi→a(C)
a Calculated with the GIAO method under B3LYP/BSS-A.b The magnitudes of σ^pi→a(C) larger than 8 ppm are shown.c In ψi→ψa.
3→22	−36.14	0.00	0.00	−12.05
14→22	0.00	−95.93	0.00	−31.98
15→22	0.00	−27.30	0.00	−9.10
16→22	−95.30	0.00	0.00	−31.77
16→68	0.00	0.00	−26.05	−8.68
16→78	−40.08	0.00	0.00	−13.36
16→93	0.00	0.00	−25.58	−8.53
16→117	0.00	0.00	−28.12	−9.37
18→40	0.00	−43.94	0.00	−14.65
18→50	0.00	−31.15	0.00	−10.38
19→40	−38.27	0.00	0.00	−12.76
19→50	−26.96	0.00	0.00	−8.99
19→59	0.00	0.00	−26.04	−8.68

---

Fig. 11 shows the ψ_i→ψ_a transitions in C₆H₆, shown in Table 16, although they are limited to those discussed above, together with the MO energies and axes. The main characteristics of ψ₁₄, ψ₁₆ and ψ₁₉ are the occupied σ(C–C), σ(C–C) with σ(C–H) and σ(C–C) with σ(C–H), respectively, whereas those of ψ₂₂, ψ₄₀ and ψ₇₈ are vacant π*(C=C), π*(C₆H₆), and much higher π*(C₆H₆), respectively. The LUMO of ψ₂₂ acts as a great acceptor in the transition, whereas the HOMO does not seem to do so.

Fig. 11 Contributions from each ψ_i→ψ_a transition to the components of σ^p(C) in C₆H₆ (D_6h), together with their axes by the isovalue of 0.04 au.

Origin of the i-X effect

The i-X effect is examined for C₆H₅–X from C₆H₆ (X = OH, SH, SeH, F, Cl, Br, I, NH₂, CO₂Me, CN and NO₂) (see Scheme 3, Table 4 and Table S11 of the ESI†). The calculated (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values are (−82.5–35.2, −74.9–70.5, −39.7–14.0 ppm) for the species.

The σ^d(C), σ^p(C) and σ^t(C) values of C₆H₅OH, are listed in Table S15 of the ESI,† separately for each MO. The outer MOs of HOMO–3 (ψ₂₂), HOMO–8 (ψ₁₇) and HOMO–9 (ψ₁₆) contribute greatly to σ^p(C). The ψ_i→ψ_a transitions contributing to σ^p_i→a:kk(C: k = x, y and/or z), greater than 18 ppm, are listed in Table S16 of the ESI.† The ψ_i→ψ_a transitions of ψ₁₆→ψ₂₈ (σ^p_16→28:yy(C) = −53.5 ppm), ψ₁₇→ψ₂₈ (σ^p_17→28:xx(C) = −25.5 ppm), ψ₁₇→ψ₈₇ (σ^p_17→87:xx(C) = −24.9 ppm) and ψ₂₂→ψ₄₄ (σ^p_22→44:yy(C) = −28.1 ppm) contribute a lot to σ^p_i→a:kk(C: k = x, y and/or z). The ψ_i→ψ_a transitions of ψ₁₆→ψ₂₈, ψ₁₇→ψ₂₈, ψ₁₇→ψ₈₇ and ψ₂₂→ψ₄₄ are drawn in Fig. S15 of the ESI,† where the transitions of large contributions are omitted if the contributions from ψ_i are small in C₆H₅OH. The i-X effect is well visualized through the occupied-to-unoccupied orbital transitions.

Effect of the carbonyl group and its origin

Very large downfield shifts of δ(¹³C) (∼200 ppm) are usually observed for the carbonyl group.^1–4 The calculated (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values for H₂C=O from MeOH are (13.1, −159.0, −145.9 ppm), which explains the observed results well.

Table 17 lists the σ^d(C), σ^p(C) and σ^t(C) values of H₂C=O, separately, by ψ_i. The outer MOs of HOMO (ψ₈), HOMO–2 (ψ₆) and HOMO–3 (ψ₅) contribute a lot to σ^p(C), whose values amount to −95.7, −118.8 and −64.5 ppm, respectively. The ψ_i→ψ_a transitions of ψ₅→ψ₉ (σ^p_5→9:zz(C) = −62.6 ppm), ψ₆→ψ₉ (σ^p_6→9:yy(C) = −195.3 ppm), ψ₆→ψ₁₃ (σ^p_6→13:yy(C) = −30,3 ppm) and ψ₈→ψ₉ (σ^p_8→9:zz(C) = −185.7 ppm) contribute predominantly to σ_i→a^p, as shown in Table 18.

Table 17 The σ^d(C), σ^p(C) and σ^t(C) values of H₂C=O (C_2v), given separately by each ψ_i^a

MO (i in ψi)	σ^d(C)	σ^p(C)	σ^t(C)
a Calculated with the GIAO method under B3LYP/BSS-A.
1 (A1); 2 (A1)	200.29	−0.02	200.27
3 (A1)	7.42	−21.88	−14.46
4 (A1)	22.01	−2.20	19.82
5 (B2)	6.81	−64.47	−57.66
6 (A1)	1.98	−118.84	−116.86
7 (B1)	14.00	−13.21	0.79
8 (B2)	−7.32	−95.73	−103.05
ψocc to ψocc		52.70
Total	245.20	−263.64	−18.44

---

Table 18 Main contributions from the ψ_i→ψ_a transitions on the σ^p(C) of H₂C=O (C_2v)^a,b

i→a^c	σ^pi→a:xx(C)	σ^pi→a:yy(C)	σ^pi→a:zz(C)	σ^pi→a(C)
a Calculated with the GIAO method under B3LYP/BSS-A.b The magnitudes of σ^pi→a(C) larger than 10 ppm are shown.c In ψi→ψa.
5→9	0.00	0.00	−62.57	−20.86
6→9	0.00	−195.32	0.00	−65.11
6→13	0.00	−30.34	0.00	−10.11
8→9	0.00	0.00	−185.66	−61.89

---

Fig. 12 shows the ψ₆→ψ₉ and ψ₈→ψ₉ transitions of H₂C=O, along with the MO energies and the molecular axes. The main characteristics of ψ₆, ψ₈ and ψ₉ are the occupied σ(C=O), n_p(C) and vacant π*(C=O), respectively. HOMO (ψ₈) and LUMO (ψ₉) act as excellent donors and acceptors, respectively, to produce very large σ^p(C) values in H₂C=O. HOMO–1 (ψ₇) (π(C=O)) in H₂C=O does not seem to act as a good donor, contrary to the excellent donors of HOMO (ψ₈) (n_p(C)) and HOMO–2 (ψ₆) (σ(C=O)).

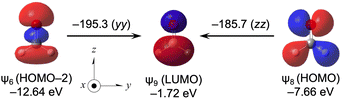Fig. 12 Contributions from each ψ_i→ψ_a transition to the components of σ^p(C) in H₂C=O (C_2v), together with the axes with an isovalue of 0.04 au.

Effect of the carboxyl group and its origin

The carboxyl effect is closely related to the carbonyl effect. Very large downfield shifts of δ(¹³C) (∼180 ppm) are usually recorded for the carboxyl group.^1–4 The calculated (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values are (13.3, −123.9, −111.5 ppm) for H(OH)C=O from MeOH, which explains the observed results well.

Table 19 lists the σ^d(C), σ^p(C) and σ^t(C) values of H(HO)C=O, separately, by ψ_i. The contributions from HOMO–2 (ψ₁₀) and HOMO–5 (ψ₇) to σ_i^p(C) are very large, with values of −86.2 and −68.8 ppm, respectively. Table 20 lists the ψ_i→ψ_a transition in H(HO)C=O, which mainly contributes to σ^p_i→a:kk(C: k = x, y and/or z), larger than approximately 10 ppm. The ψ_i→ψ_a transitions of ψ₇→ψ₁₃ (σ^p_7→13:xx(C) = −83.7 ppm with σ^p_7→13:yy(C) = −12.7 ppm), ψ₈→ψ₁₃ (σ^p_8→13:yy(C) = −38.1 ppm) and ψ₁₀→ψ₁₃ (σ^p_10→13:yy(C) = −108.6 ppm with σ^p_10→13:xx(C) = −29.2 ppm) contribute predominantly to σ^p_i→a(C), together with ψ₅→ψ₁₃ (σ^p_5→13:yy(C) = −30.6 ppm) and ψ₁₂→ψ₁₃ (σ^p_12→13:xx(C) = −45.6 ppm).

Table 19 The σ^d(C), σ^p(C) and σ^t(C) values of H(HO)C=O (C_s), given separately by each ψ_i^a

MO (i in ψi)	σ^d(C)	σ^p(C)	σ^t(C)
a Calculated with the GIAO method under B3LYP/BSS-A.
1 (A′)–3 (A′)	200.31	−0.03	200.28
4 (A′)	8.56	−8.27	0.29
5 (A′)	3.00	−23.65	−20.65
6 (A′)	13.84	−11.59	2.25
7 (A′)	6.02	−68.76	−62.74
8 (A′)	5.29	−30.62	−25.34
9 (A′′)	14.46	−20.58	−6.13
10 (A′)	−4.35	−86.16	−90.51
11 (A′′)	1.96	−0.95	1.01
12 (A′)	−3.59	−24.60	−28.19
ψocc to ψocc		46.69
Total	245.49	−228.53	16.97

---

Table 20 Main contributions from the ψ_i→ψ_a transitions on σ^p(C) of H(HO)C=O (C_s)^a,b

i→a^c	σ^pi→a:xx(C)	σ^pi→a:yy(C)	σ^pi→a:zz(C)	σ^pi→a(C)
a Calculated with the GIAO method under B3LYP/BSS-A.b The magnitudes of σ^pi→a(C) larger than 10 ppm are shown.c In ψi→ψa.
5→13	−0.10	−30.55	0.00	−10.22
7→13	−83.72	−12.66	0.00	−32.13
8→13	−0.90	−38.10	0.00	−13.00
10→13	−29.23	−108.63	0.00	−45.95
12→13	−45.55	2.78	0.00	−14.25

---

Fig. 13 shows the ψ₇→ψ₁₃ and ψ₁₀→ψ₁₃ transitions in H(HO)C=O, along with the MO energies and the molecular axes. The characters of ψ₇ and ψ₁₀ are the occupied σ(O–C=O) of A′ spread over the whole molecule, whereas that of ψ₁₃ is the vacant π*(O–C=O). While ψ₇ and ψ₁₀ operate as excellent donors, ψ₁₃ (LUMO) is an excellent acceptor in H(HO)C=O.

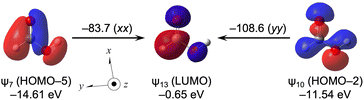Fig. 13 Contributions from each ψ_i→ψ_a transition to the components of σ^p(C) in H(HO)C=O (C_s), together with the axes with an isovalue of 0.04 au.

The (Δσ^d(C)_e, Δσ^p(C)_e, Δσ^t(C)_e) values are (13.3, −123.9, −111.5 ppm) for H(HO)C=O from CH₃OH, as mentioned above. However, the values for the conversion of H(HO)C=O from H₂C=O are also of interest. The values are (0.3, 35.1, 35.4 ppm). Specifically, the NMR signal of H(HO)C=O is predicted to appear at a higher field of approximately 35 ppm than that of H₂C=O. The specific π-allyl type O–C=O interaction is responsible for these results. The charge on C of H(HO)C=O is less positive than that of H₂C=O because of the donation from HO to C=O in H(HO)C=O, which should lead to an upfield shift.

It is necessary to consider the effect of the wider extension of the MOs over the entire molecule in H(HO)C=O. One explanation is as follows: It does not directly increase the σ^p(C) value when the occupancy of electrons becomes higher at the carbon atom in question in an important orbital of H(HO)C=O relative to the case of H₂C=O. The energy differences between the two orbitals that make up the transitions also affect σ^p(C). Nevertheless, a more upfield shift in σ^p(C) is expected to be predicted when the charge on C becomes less positive. However, more complex mechanisms control the real shift values.

The analysis of H₂C=O and H(HO)C=O will help to understand the δ(C) values of similar structures. The upfield shifts in RC(=O)NHR' and ROC(=O)OR' relative to R₂C=O can also be understood based on the structural similarities to R(R’O)C=O. However, further investigations are necessary to understand the much greater downfield shifts of the species containing low-lying vacant orbitals, such as some cationic species, carbenes and radicals.

Illustration of the terms used to control Δσ^t(C)

The Δσ^d(C), Δσ^p(C), Δσ^t(C) (=Δσ^d(C) + Δσ^p(C)) values and the components are plotted for CH₃CH₃, CH₂=CH₂, CH≡CH, C₆H₆ and H₂C=O. Fig. 14 shows the plot. The Δσ^d(C) and Δσ^p(C) values are all negative for the species, where C^4– is taken as the standard. However, the contributions from the occupied-to-occupied (occ-to-occ) orbital (ψ_i→ψ_j) transitions are all positive for the species shown in Fig. 14. The magnitudes of Δσ^d(C) seem almost constant for the species, whereas those of Δσ^p(C) change widely depending on the structure of the species, which increases the variety of the Δσ^t(C) values. The magnitudes of Δσ^t(C) (=Δσ^d(C) + Δσ^p(C)) increase in the order of S=CH₃CH₃ < CH≡CH < CH₂=CH₂ < C₆H₆ < H₂C=O, as expected. The σ^p(C) values originate from the unsymmetric component of the electron distribution derived from the unsymmetric MOs on the unsymmetric structure of the species.

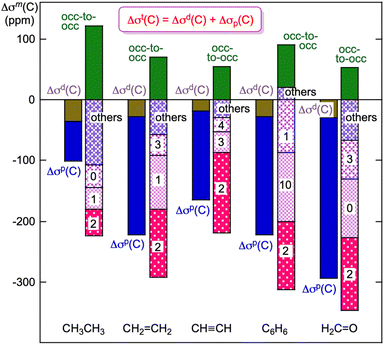Fig. 14 Plots of Δσ^d(C), Δσ^p(C), Δσ^t(C) and the components for CH₃CH₃, CH₂=CH₂, CH≡CH, C₆H₆ and H₂C=O. Each MO contributing to σ^p(C) is shown by n in HOMO–n.

The unsymmetric MOs are constructed mainly by the 2p_x(C), 2p_y(C) and 2p_z(C) AOs. These MOs are expected to exist near the HOMO; however, they sometimes reside in (much) deeper areas. The magnitudes of the terms, such as Δσ^d(C), Δσ^p(C), Δσ^t(C) and the components, are well visualized in Fig. 14, which helps us to understand the plain rules founded in theory, supported by the origin and mechanism, for ¹³C NMR chemical shifts.

The occupied-to-occupied orbital (ψ_i→ψ_j) transitions arise through the redistribution of electrons in a species under an applied magnetic field. They are usually not considered to be important; therefore, they are often neglected in analyses and discussions. However, they contribute to σ^p(C) more than those expected in some cases, as shown in Fig. 14. Specifically, the occupied-to-occupied orbital transitions may play an important role in the (observed) ¹³C NMR chemical shifts, which are hidden in the unconscious realm of the measurers.

Conclusions

The plain rules associated with the origin and mechanism for δ(C) are intended to be established, without compromising theoretical requirements, in this work. The rules should be simple, easily imaged and easily understood for experimental scientists, who are not specialists. The rules should help experimental scientists image the role of C at a specific position in a species over the empirical rules usually employed in assigning the spectra. The δ(C) values are analysed by employing the calculated σ^d, σ^p and σ^t terms. The contributions from σ^d(C) to σ^t(C) are approximately one tenth of those from σ^p(C), although the ratio changes depending on the species. The plot of σ^d(C) versus Q(C) for C⁴⁺, C²⁺, C⁰, C²⁻ and C⁴⁻ gave excellent correlations if analysed via a cubic regression curve, as did the plots for C⁴⁻, CH₂²⁻, CH₃⁻ and CH₄ with a quadratic curve. The σ^d(C) values can be understood based on Q(C) for the species; however, σ^d(C) of those other than those above do not correlate with Q(C). The relationship between σ^p(C) and Q(C) was not examined further, which would be hidden in the complex combinations of the ψ_i→ψ_a transitions, as shown in eqn (6).

The pre-α effect of an approximately 20 ppm downfield shift is theoretically predicted based on the average value of Δσ^t(C)_e from C^4– to H₄C. The α and β effects of approximately 10 ppm downfield shifts are reproduced well by the calculated Δσ^t(C)_e values. The variety of the α-X, β-X and i-X effects are clarified by the calculations. Large downfield shifts by ethene (∼120 ppm), benzene (∼127 ppm) and ethyne (∼60 ppm) and very large downfield shifts by the carbonyl group (∼200 ppm) and carboxyl group (∼180 ppm) are also well reproduced by the calculations.

The orbital-to-orbital transitions in σ^p(C) are widely employed to clarify the origin and the mechanism for δ(C) in this work. The occupied-to-unoccupied orbital (ψ_i→ψ_a) transitions in σ^p(C) enable us to visualize the origin and the mechanism. The occupied-to-occupied orbital (ψ_i→ψ_j) transitions, which are usually neglected, are also examined: The contributions from the ψ_i→ψ_j transitions are greater than those expected in some cases. The examination provided useful information for σ^p(C). As a result, the plain rules with the origin and the mechanism are formulated for δ(C). The origin and the mechanism for δ(C) can be imaged and understood more easily based on the treatments also by experimental scientists. The results will help in understanding the role of C in question in the specific position of a compound. By expanding the image of the orbital-to-orbital transitions, it would be possible to envision the molecular orbitals around the carbon in question in the compound and their interactions. The expansion will hopefully lead to the development of the highly functionality based on the inherent properties of the compound. Namely, this work also has the potential to provide an understanding δ(C) of unknown species and facilitate new concepts for strategies to create highly functional materials on the basis of the δ(C) values.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

W. N. and S. H. formulated the project and organized the data; contributed to supervision, data curation and resources; and wrote, reviewed and edited the paper. K. M. contributed to the investigation. All of the authors have read and agreed to the published version of the manuscript.

Conflicts of interest

The authors declare that they have no conflicts of interest.

Acknowledgements

The authors are very grateful to Prof. Masahiko Hada and Dr Daisuke Yamaki of Tokyo Metropolitan University for the utility programs.

Notes and references

1. J. Pople, W. G. Schneider and H. J. Bernstein, High-resolution Magnetic Resonance, McGraw-Hill, New York, 1959.
2. J. B. Stothers, Carbon-13 NMR Spectroscopy, Academic Press, New York and London, 1972.
3. H.-O. Kalinowski, S. Berger and S. Braun, Carbon-13 NMR Spectroscopy, John Wiley & Sons: New York, 1988.
4. Annual Reports on NMR Spectroscopy, ed. G. A. Webb, Academic Press, vol. 83, 2014.
5. Encyclopedia of Nuclear Magnetic Resonance, ed. D. M. Grant and R. K. Harris, John Wiley & Sons, New York, 1996.
6. Encyclopedia of Nuclear Magnetic Resonance, ed. R. K. Harris and R. E. Wasylishen, John Wiley & Sons, New York, 2012.
7. Nuclear Magnetic Shieldings and Molecular Structure, ed. J. A. Tossell, Kluwer Academic Publishers, Dordrecht, Boston, London, 1993.
8. Calculation of NMR and EPR Parameters; Theory and Applications, ed. M. Kaupp, M. Bühl and V. G. Malkin, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2004.
9. W. Nakanishi, S. Hayashi and M. Hada, Chem. E. J., 2007, 13, 5282–5293.
10. K. Kanda, H. Nakatsuji and T. Yonezawa, J. Am. Chem. Soc., 1984, 106, 5888–5892.
11. Molecular Quantum Mechanics, ed. P. W. Atkins and R. S. Friedman), Oxford: New York, 1997, Chapter 13.
12. Indeed, this decomposition includes small arbitrariness due to the coordinate origin dependence, but it does not damage our insights into the ¹³C NMR spectroscopy.
13. The occupied-to-unoccupied orbital (ψ_i→ψ_a) transitions mainly contribute to σ^p, whereas the occupied-to-occupied orbital (ψ_i→ψ_j) transitions sometimes play an important role in σ^p.
14. Based on the second-order perturbation theory at the level of the HF and single-excitation CI approximation, σ^p_i→a on a resonance nucleus N is shown to be proportional to reciprocal orbital energy gap (ε_a − ε_i)⁻¹ as expressed in eqn (5), where ψ_k is the k-th orbital function, L̂_z,N is orbital angular momentum around the resonance nucleus, and r_N is the distance from the nucleus N.
15. L. P. Hammett, Chem. Rev., 1935, 17, 125–136.
16. K. Matsuzaki, S. Hayashi and W. Nakanishi, RSC Adv., 2024, 14, 14340–14356.
17. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
18. A. D. Becke, Phys. Rev., 1988, A38, 3098–3100.
19. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
20. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785–789.
21. B. Miehlich, A. Savin, H. Stall and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206.
22. T. Yanai, D. P. Tew and N. C. A. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
24. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6169.
25. T. M. Henderson, A. F. Izmaylov, G. Scalmani and G. E. Scuseria, J. Chem. Phys., 2009, 131, 044108.
26. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
27. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
28. J. Gauss, J. Chem. Phys., 1993, 99, 3629–3643.
29. J. Gauss and B. Bunsenges, Phys. Chem., 1995, 99, 1001–1008.
30. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260.
31. K. Wolinski and A. Sadlej, Mol. Phys., 1980, 41, 1419–1430.
32. R. Ditchfield, Mol. Phys., 1974, 27, 789–807.
33. R. McWeeny, Phys. Rev., 1962, 126, 1028–1034.
34. F. London, J. Phys. Radium, 1937, 8, 397–409.
35. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO Version 6.0. 2013.
36. The utility program was provided by Prof. Hada and Dr Yamaki of Tokyo Metropolitan University. It is derived from the NMR program in the Gaussian program, which made some processes, necessary for our discussion, possible to be printed out, such as the contributions from the occupied orbitals and/or the orbital-to-orbital transitions.⁴³.
37. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
38. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
39. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
40. W. Nakanishi, S. Hayashi, D. Shimizu and M. Hada, Chem.–Eur. J., 2006, 12, 3829–3846.
41. W. Nakanishi, S. Hayashi, Y. Katsura and M. Hada, J. Phys. Chem. A, 2011, 115, 8721–8730.
42. S. Hayashi, K. Matsuiwa and W. Nakanishi, RSC Adv., 2014, 4, 44795–44810.
43. Essentially the same analysis can be achieved by using the ADF program.

---

Footnote

† Electronic supplementary information (ESI) available: Additional tables and the fully optimized structures given by Cartesian coordinates, together with total energies. See DOI: https://doi.org/10.1039/d4ra05980h

---