Open Access Article
Open Access ArticlePhase stability, electronic, mechanical, lattice distortion, and thermal properties of complex refractory-based high entropy alloys TiVCrZrNbMoHfTaW with varying elemental ratios†
Sahib Hasan ab,
Puja Adhikaria,
Saro Sana and
Wai-Yim Ching
ab,
Puja Adhikaria,
Saro Sana and
Wai-Yim Ching *a
*a
aDepartment of Physics and Astronomy, University of Missouri-Kansas City, Kansas City, MO 64110, USA. E-mail: chingw@umkc.edu
bDepartment of Sciences, College of Basic Education, Al Muthanna University, Samawah 66001, Iraq
First published on 21st January 2025
Abstract
This study examines the intricate area of refractory-based high entropy alloys (RHEAs), focusing on a series of complex compositions involving nine diverse refractory elements: Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W. We investigate the phase stability, bonding interactions, electronic structures, lattice distortions, mechanical, and thermal properties of six RHEAs with varying elemental ratios using VASP and OLCAO DFT calculations. Through comprehensive analysis, we investigate the impact of elemental variations on the electronic structure, interacting bond dynamics, lattice distortion, thermodynamic, mechanical, and thermal properties within these RHEAs, providing an insight into how these specific elemental variations in composition give rise to changes in the calculated properties in ways that would guide future experimental and computational efforts. The correlation between the lattice distortion, mechanical, and thermal properties is explored in detail in this work. Our findings reveal significant insights into how these factors contribute to the unique properties of RHEAs, such as enhanced strength, ductility, and resistance to corrosion and wear. This research not only advances our understanding of the fundamental aspects of RHEAs but also opens new avenues for the design and application of these materials in various industrial sectors.
1 Introduction
High Entropy Alloys (HEAs) represent a remarkable class of materials that have fascinated the materials science community due to their unique combination of properties, which include exceptional strength,1 ductility,2 corrosion resistance,3 high-temperature stability,4,5 fatigue resistance,6,7 high wear resistance,8 dielectric,9 and superconducting10 properties. HEAs concept was proposed for the first time in 2004 by Yeh et al.11,12 An alloy with entropy larger than 1.5R where R is the gas constant (8.3144 J K−1 mol−1), is considered a HEA.13–15 HEAs can provide a significant performance and efficiency in many applications, such as aerospace propulsion systems, gas turbines, nuclear reactors, heat exchangers, and rocket engine nozzles.16–18 These materials are unique for their multi-principal element composition, unlike conventional alloys with one or two major constituents. Traditional alloys obviously no longer meet the growing demands of rapidly advancing technologies. The concept of high entropy stabilizes the solid solution phase, leading to novel microstructures and properties that cannot be seen in traditional alloys, such as the so-called cocktail effect and significant lattice distortion.19,20 The cocktail effect describes any emergent property that cannot be described by the presence of any individual components of HEA. On the other hand, the severe lattice distortion in HEAs is caused by the randomly distributed mismatch of ionic mass and sizes.21 The variation in bond energy, bond length, and bond strength between the components in HEAs can also lead to severe lattice distortion22 that ultimately impacts some of their properties such as thermoelectric (TE) properties.23 Such severe lattice distortion increases the phonons scattering, thus reducing the lattice thermal conductivity (κL).11,24,25 Large numbers of distributed solute atoms (more than 5 atoms) with different atomic sizes and characteristics result in distorted lattices with large long-range lattice friction,2,26,27 which reduces the mobility of phonons and dislocations in HEAs. Hence, the lattice distortion may cause an increase in the yield strength of the solid solution alloys even with very small changes in the microstructure.28A single-phase solid-solution alloy containing multi-principal elements with equimolar or near-equimolar atomic ratios is the original definition of HEAs.29 HEAs have been extended to include refractory-based high-entropy alloys (RHEAs) by Senkov et al.30,31 Refractory elements such as rhenium (Re), tungsten (W), molybdenum (Mo), tantalum (Ta), niobium (Nb), hafnium (Hf), titanium (Ti), chromium (Cr), and zirconium (Zr) are the main constituents in this type of HEA.13 To improve the properties, some non-refractory light elements, such as Al and Ni, can also be included to design RHEAs with less density for some applications.32 Senkov et al. found that MoNbTaW, MoNbTaVW, and TaNbHfZrTi have higher melting temperature than the traditional alloys with yield strength of 1058 MPa and 1246 MPa at room temperature. Senkov's alloys also possessed an excellent yield strength of 405 MPa and 477 MPa at high temperature (1600 °C), which is considered much better than that of nickel-based alloys, making them promising materials for high-temperature applications.33 Due to the potential slow diffusion of refractory elements and solid-solution strengthening, RHEAs keep its remarkable strengths even at elevated temperatures.13,29,34 After Senkov et al., many RHEAs were developed, however, most of these RHEAs exhibited limited ductility or negligible tensile ductility at room-temperature,35–37 except for HfNbTaTiZr with BCC structure which exhibits good tensile ductility at room temperature.38 Due to their constituent elements, such as Ta, Nb, Ti, and Mo, which could form passive films in corrosive environment, RHEAs are considered promising materials for their excellent corrosion resistance.39–41 Another RHEAs such as TiZrNbTaMo, AlNbTiVZrx, and MoNbTaTiW have been extensively studied for their excellent mechanical properties.42–44 RHEAs possessing a single body centered cubic (BCC) structure have much better mechanical properties than other HEAs with face centered cubic (FCC) structure.
The present study focuses on a specific group of RHEAs composed of nine elements: titanium (Ti), vanadium (V), chromium (Cr), zirconium (Zr), niobium (Nb), molybdenum (Mo), hafnium (Hf), tantalum (Ta), and tungsten (W). These elements were chosen for their diverse atomic sizes, valency, and electron configurations, which contribute to the complex microstructure and properties of the resulting alloys. By manipulating the ratios of these elements, we aim to explore the complicated balance between high entropy effects, lattice distortion, mechanical, thermal, and electronic structure contributions in the behaviour of these materials. This investigation is structured around several key areas of interest. Firstly, we test the phase stability of these six alloys via study thermodynamic parameters and other affecting factors such as entropy of mixing (ΔSmix), enthalpy of mixing (ΔHmix), change in Gibbs free energy (ΔGmix), valence electron concentration (VEC), the atomic size difference (δ), and electronegativity difference (Δχ). Secondly, the electronic structure of these complex alloys is studied to provide insights into the role of electron behaviour in determining overall material properties. Thirdly, the study examines into the atomic-scale interactions, focusing on bond order (BO), a measure of the bond strength, and total bond order density (TBOD), to clarify the role of electron density distribution in defining the materials structural stability and mechanical characteristics. TBOD is a single quantum mechanical metric to describe the internal cohesion of the RHEA. Fourthly, we examine the mechanical properties of these RHEAs, such as bulk modulus, Young modulus, shear modulus, Pugh ratio, Vickers hardness, Cauchy pressure, and machinability index, and their correlation with TBOD to understand how the high entropy nature contributes to their enhanced performance. Lattice distortion (LD), an assurance feature of RHEAs, is analysed in relation to its impact on dislocation movement and, consequently, mechanical and thermal properties. Finally, we study the thermoelectric (TE) performance of RHEAs models by calculating several crucial parameters such as Debye temperature, minimum thermal conductivity, Grüneisen parameter, lattice thermal conductivity, melting temperature, and thermal expansion. Then we analyze the effect of LD and Grüneisen parameter on lattice thermal conductivity. By systematically exploring these aspects, the current study aims to contribute significantly to the fundamental understanding of RHEAs, thereby guiding the development of new materials with tailored properties for advanced applications in aerospace, automotive, and energy sectors, among others.
2 Computational methods
The initial model of the RHEA was developed using a Nb Body-Centered Cubic (BCC) unit cell, identified by space group 229. This model was then enhanced through the incorporation of various refractory metals (Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W) using a random ratio including equiatomic and non-equiatomic RHEAs. A specialized Python script was used to determine the lattice parameters, considering the inclusion of these transition metals within their specific cells. This Python script is available in the ESI file.† To simulate a disordered atomic arrangement, we constructed 8 × 8 × 8 supercells of BCC structure, leading to the formation of six RHEAs random solid solutions containing 1024 atoms each. For TiVCrZrNbMoHfTaW, two configurations (m1 and m2) were studied, while one structure was studied for each of the remaining four compositions. The ball and stick figure for m1 is shown in Fig. 1. These six distinct RHEA models (listed in Table 1) were subsequently optimized using the Vienna Ab initio Simulation Package (VASP).45 VASP optimizations employed the Projector Augmented Wave (PAW) of Perdew, Burke, and Ernzerhof (PBE)46 method within the Generalized Gradient Approximation (GGA) to address the exchange-correlation potential. We selected the plane wave expansion kinetic energy cutoff of 500 eV, with the electronic and ionic relaxations requiring convergence thresholds of 1.0 × 10−6 eV and −1.0 × 10−4 eV Å−1, respectively. The Monkhorst scheme47 is used with k-point meshes of 1 × 1 × 1 for all these RHEAs solid solutions. The optimized structures from VASP were used to calculate the elastic tensors by employing a stress–strain response approach. The calculation of the elastic coefficient Cij matrix involved solving a linear equation where the stress σi is a function of the applied strains εj. This linear equation, also called the Hooke's law:48,49
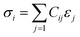 | (1) |
| Model | Composition | a, b, c (Å) | α, β, γ in deg. | Vol (Å3) | NN (Å) | SNN (Å) |
|---|---|---|---|---|---|---|
| m1 | TiVCrZrNbMoHfTaW | 25.9, 25.9, 25.8 | 89.9, 90.2, 90.1 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 386.70 386.70 |
2.804 | 3.238 |
| m2 | TiVCrZrNbMoHfTaW | 25.9, 25.9, 25.9 | 90.2, 89.9, 89.8 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 391.71 391.71 |
2.805 | 3.239 |
| m3 | Ti114V114Cr138Zr90Nb114Mo138Hf90Ta113W113 | 25.7, 25.8, 25.7 | 89.9, 90.2, 90.1 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 957.03 957.03 |
3.211 | 2.781 |
| m4 | Ti164V65Cr118Zr118Nb99Mo118Hf104Ta119W119 | 26.1, 25.9, 25.9 | 90.2, 89.9, 90.0 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 510.73 510.73 |
3.246 | 2.811 |
| m5 | Ti114V114Cr171Zr57Nb114Mo171Hf57Ta113W113 | 25.4, 25.4, 25.4 | 90.1, 90.2, 90.2 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 381.24 381.24 |
2.749 | 3.175 |
| m6 | Ti114V114Cr228Nb114Mo228Ta113W113 | 24.9, 24.9, 24.9 | 90.0, 90.0, 90.1 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 430.82 430.82 |
2.695 | 3.112 |
Eqn (1) can be solved to obtain the elastic coefficient, Cij, with both indices ranging from 1 to 6, at strains of ±0.50%. From these Cij matrices, bulk modulus (K), shear modulus (G), Young's modulus (E), and Poisson's ratio (η) were derived using the Voigt–Reuss–Hill (VRH) approximation,50,51 which is applicable to polycrystalline materials. More details on mechanical properties calculation are described in ESI.† The Orthogonalized Linear Combination of Atomic Orbitals (OLCAO)52 technique was applied to investigate the electronic structure and chemical bonding, using the structure refined by VASP as the starting point. OLCAO method, which is an all-electron approach, uses the local density approximation (LDA) as the exchange and correlation potential. OLCAO utilizes Gaussian-type orbitals (GTO) to form the atomic orbitals that are part of the basis set for expanding the Bloch functions. OLCAO has been successfully applied in DFT calculations of both crystalline,53–59 non-crystalline materials,60,61 HEAs,62,63 and complex bio-molecular systems.64,65 A 1 × 1 × 1 Monkhorst k-points mesh was used for OLCAO density of states (DOS) calculations. Within this framework, OLCAO determines the bond order (BO) and effective charge (Q*) metrics, drawing on Mulliken's analysis.66 The bond order, indicative of bond strength, is calculated as the overlap population ρα,β between atom pairs (α,β) at a given bond length:
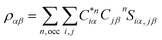 | (2) |
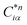 , the coefficient Cjβn, and the overlap integral Siα,jβ across the orbital indices i and j. For effective charge
, the coefficient Cjβn, and the overlap integral Siα,jβ across the orbital indices i and j. For effective charge 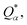 the calculation aggregates the products of eigenvector coefficients and the overlap integrals over all bands and orbitals, reflecting the charge distribution deviation from a neutral state. Additionally, the partial charge (PC) for each atom was assessed in every model, defined as the difference between the effective
the calculation aggregates the products of eigenvector coefficients and the overlap integrals over all bands and orbitals, reflecting the charge distribution deviation from a neutral state. Additionally, the partial charge (PC) for each atom was assessed in every model, defined as the difference between the effective 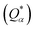 and neutral atomic charges (Q0α).
and neutral atomic charges (Q0α).
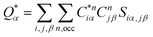 | (3) |
The aggregation of all bond orders within a model yields the total bond order (TBO), which, when normalized by the model's volume, provides the total bond order density (TBOD). TBOD serves as a quantum mechanical measure of the alloy's structural integrity.67 The optimized structure parameters along with first and second nearest neighbors are listed in Table 1. Notice that the only difference between model m1 and model 2 is the way that these nine elements are distributed in the model.
3 Results and discussion
3.1. Parameters affecting RHEAs formation
The Hume-Rothery rules68,69 play a crucial role in predicting phase formation of HEAs. These rules are based on enthalpy of mixing, atomic-size difference, electronegativity difference, and valence electron concentration. The formation of HEAs is inevitably linked to the energy of the system, so thermodynamic factors are vital for the study and design of HEAs when discussing their formation process. Thermodynamic parameters can predict the phase of the HEAs. The first three principal components that affect the phase formation are: the entropy of mixing (ΔSmix), enthalpy of mixing (ΔHmix), and Gibbs free energy (ΔGmix):70
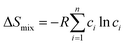 | (4) |
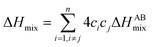 | (5) |
| ΔGmix = ΔHmix − TΔSmix | (6) |
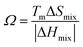 | (7) |
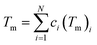 | (8) |
| Model | ΔHmix (kJ mol−1) | ΔSmix (J.K−1 mol−1) | δ% | VEC | Tm (K) |
|---|---|---|---|---|---|
| m1 | −4.790120 | 18.26669 | 7.6378 | 4.99995 | 2618.42 |
| m2 | −4.790120 | 18.26669 | 7.6378 | 4.99995 | 2618.42 |
| m3 | −5.061120 | 18.19895 | 7.0564 | 5.10054 | 2631.89 |
| m4 | −5.000125 | 18.08030 | 7.4853 | 4.97060 | 2611.79 |
| m5 | −5.188510 | 17.80139 | 7.3409 | 5.22854 | 2646.13 |
| m6 | −4.800360 | 15.71158 | 7.1213 | 5.45254 | 2671.05 |
When all constituent atoms (with different sizes) of a HEA are placed together in a certain lattice, a severely distorted lattice results from the presence of large atomic size difference. In 2008, Zhang et al.70 suggested a new parameter, namely, the atomic size difference (δ), to characterize such an atomic size effect in HEAs as follows:
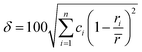 | (9) |
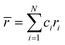 . Experimentally, the formation of metallic glasses favors larger values of δ (∼δ > 11%) while HEAs formation favors less values of δ. δ is widely used nowadays to predict the formation of HEAs. However, the value of δ cannot give an accurate estimation of local lattice distortions. Yang and Zhang74 suggested a critical condition for solid solution formation which is δ ≤ 6.6. Multicomponent systems with higher δ than critical condition may form intermetallic compounds. Guo et al. and Nutor et al. showed that solid solution phases can form when the parameter δ is in the range: 0 ≤ δ ≤ 8.5,80 while bulk metallic glasses form in the region δ ≥ 9.78 δ for the six RHEAs is listed in Table 2. All these six RHEAs have large values of δ (∼7). Dong et al. and Poletti et al.81,82 showed that HEAs with high δ (∼7) form laves phase plus BCC solid solutions phase. From Zhang et al.’s work,29 HEAs having large δ (∼7) form solid solutions plus intermetallic compounds. Thermodynamic approach can be combined with the geometrical information (lattice characteristics and atomic radius) by the parameter ∧. Singh et al.83 developed the ∧ parameter (named the combination parameter) to predict the formation of disordered solid solution as follows:
. Experimentally, the formation of metallic glasses favors larger values of δ (∼δ > 11%) while HEAs formation favors less values of δ. δ is widely used nowadays to predict the formation of HEAs. However, the value of δ cannot give an accurate estimation of local lattice distortions. Yang and Zhang74 suggested a critical condition for solid solution formation which is δ ≤ 6.6. Multicomponent systems with higher δ than critical condition may form intermetallic compounds. Guo et al. and Nutor et al. showed that solid solution phases can form when the parameter δ is in the range: 0 ≤ δ ≤ 8.5,80 while bulk metallic glasses form in the region δ ≥ 9.78 δ for the six RHEAs is listed in Table 2. All these six RHEAs have large values of δ (∼7). Dong et al. and Poletti et al.81,82 showed that HEAs with high δ (∼7) form laves phase plus BCC solid solutions phase. From Zhang et al.’s work,29 HEAs having large δ (∼7) form solid solutions plus intermetallic compounds. Thermodynamic approach can be combined with the geometrical information (lattice characteristics and atomic radius) by the parameter ∧. Singh et al.83 developed the ∧ parameter (named the combination parameter) to predict the formation of disordered solid solution as follows:
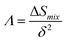 | (10) |
The main idea of ∧ is that high ΔSmix and low δ stabilize the single-phase solid solution. According to Singh's proposal for ∧ parameter, single-phase solid solution requires ∧ > 0.96, two phases solid solution form when 0.24 < ∧ < 0.96, while intermetallic compounds form at ∧ < 0.24. The values of ∧ listed in Table S3† are about 0.3 for all models. This may indicate forming another phase along with BCC solid solution phase in these RHEAs. Calculating the valence electron concentration (VEC) is also important to predict the formation of stable crystalline structures and stability for FCC and BCC phases of HEAs.84 VEC is the total number of valence electrons per atom. VEC can be calculated as follows:78
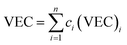 | (11) |
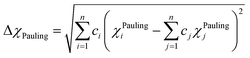 | (12) |
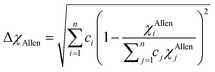 | (13) |
Electronegativity is the ability of atoms to attract charges toward itself.96 The atoms in a HEA can attract electrons uniformly when the electronegativity difference has low value, thus stable solid solutions can form. While the formations of amorphous structures favors high electronegativity difference.97 ΔχPauling and ΔχAllen for these six RHEAs are listed in Table S3.† These six alloys have uniquely large ΔχPauling due to the existence of Mo and W elements which have much larger electronegativity than the other elements (see Table S2†). Dong et al.81 showed that the topologically close-packed (TCP) phases form at ΔχPauling > 0.133. Thus, these six RHEAs may form laves phase and TCP phases along with BCC solid solution. These RHEAs have ΔχAllen higher than 8.0%. Yurchenko et al.98 showed that the formation of laves phase can be observed at ΔχAllen > 7.0%.
3.2. Electronic structure analysis
These six BCC RHEAs solid solutions are made with varying proportions of components. The new local chemical environment of the different elements: Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W results in a huge deformation. Some properties such as electronic structure and interatomic bonding can be affected by this deformation. The electronic structure of a material may reflect the stability of that material. Density of states (DOS) and partial density of states (PDOS) of the models m1 and m6 are demonstrated in Fig. 2, while Fig. S1 in the ESI† contains the figures of DOS and PDOS of all models. The DOS predominantly originated from the 3d orbitals in Ti, V, and Cr, the 4d orbitals in Zr, Nb, and Mo, and the 5d orbitals in Hf, Ta, and W. DOS has no minimum at Fermi energy (EF) for all models. However, the minimum or dip in DOS of m6 is very close to EF, which indicates its stability compared to other models. Notably the N(EF) values in Table 3 show that m5 and m6 a lower dip or minimum in the DOS at EF. This is because m5 and m6 contain higher percentage of 3d and 4d elements (Cr and Mo).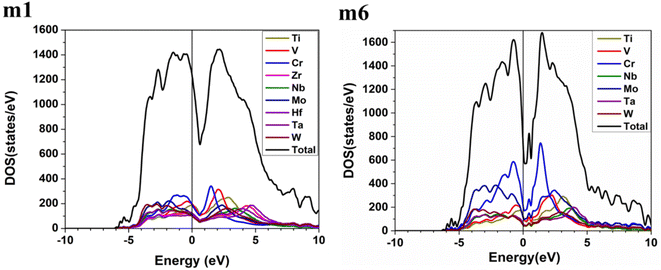 | ||
| Fig. 2 Calculated total density of states (TDOS) and partial density of states (PDOS) of m1 and m6 RHEAs models from −10 eV to 10 eV. | ||
| # | Model | N(EF) | N (first peak) | E (eV) | N (second peak) | E (eV) |
|---|---|---|---|---|---|---|
| 1 | m1 | 1235 | 1420 | −1.48 | 1442 | 2.12 |
| 2 | m2 | 1222 | 1437 | −0.65 | 1462 | 1.99 |
| 3 | m3 | 1197 | 1445 | −0.53 | 1466 | 2.01 |
| 4 | m4 | 1140 | 1447 | −0.76 | 1381 | 2.29 |
| 5 | m5 | 1119 | 1528 | −0.62 | 1514 | 1.80 |
| 6 | m6 | 732 | 1620 | −0.77 | 1677 | 1.52 |
Table 4 and Fig. S2† show that the highest contributions to the TDOS at EF in m1 and m2 are from V atom, whereas the highest contributions to the TDOS at EF in m3 and m4 are from Cr and Ti respectively. The highest contributions to the TDOS at EF in m5 and m6 are from Cr atom. On the other hand, Table 3 shows that m1 and m2 have the largest values of TDOS at EF of 1235 state per eV and 1222 state per eV respectively, attributed to the contribution from V. While m6 has the lowest TDOS value at EF of 732 stat per /eV, with N(EF) of m3, m4, and m5 are somewhere in between. It is well known that N(EF) is related to the electrical conductivity and m1 and m2 should have higher electrical conductivity than the other four RHEAs models. m6 should have lowest electrical conductivity amongst other RHEAs models.
| # | Model | Ti | V | Cr | Zr | Nb | Mo | Hf | Ta | W |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | m1 | 187.05 | 190.04 | 178.96 | 112.28 | 100.79 | 113.68 | 102.87 | 124.49 | 103.22 |
| 2 | m2 | 178.76 | 197.69 | 190.86 | 110.55 | 100.01 | 104.09 | 95.24 | 116.34 | 87.19 |
| 3 | m3 | 177.63 | 167.31 | 190.55 | 77.38 | 78.88 | 108.62 | 74.41 | 109.89 | 89.27 |
| 4 | m4 | 273.19 | 113.33 | 154.62 | 101.43 | 93.31 | 100.81 | 95.50 | 105.32 | 85.32 |
| 5 | m5 | 165.06 | 159.02 | 225.99 | 43.13 | 80.49 | 120.96 | 36.92 | 84.67 | 68.28 |
| 6 | m6 | 125.67 | 116.41 | 202.86 | — | 56.43 | 113.57 | — | 62.20 | 48.49 |
3.3. Partial charge and interatomic bonding characteristics
The valence electron count (VEC) is a fixed charge quantity for each element in the periodic table regardless of its pure environment and can be used only in that pure environment. On the other hand, the average partial charge (PC) and effective charge (Q*), calculated using the methods described in Section 2 (Computational methods), are important aspect of the electronic structure and are much more meaningful than VEC. In HEAs, the local environment and structure of a certain atom can significantly change when interacting with other atoms in the complex structure. Thus, the interpretation of VEC in HEAs in some published literature is misleading. The calculated PC and Q* on each atom in the six RHEAs models are shown in Table 5 and Table 6 respectively. The values of PC and Q* vary from one model to another depending on their compositions. As shown in Table 5, in general, Ti, Cr, and Mo atoms gain charges in all models, while Zr, Nb, Hf, and Ta atoms lose charges in all models.| # | Model | Ti | V | Cr | Zr | Nb | Mo | Hf | Ta | W | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | m1 | −0.05 | −0.08 | −0.68 | 0.34 | 0.25 | −0.41 | 0.56 | 0.06 | 0 | 5.0007 |
| 2 | m2 | −0.04 | −0.08 | −0.72 | 0.35 | 0.25 | −0.42 | 0.57 | 0.07 | 0 | 5.0018 |
| 3 | m3 | −0.01 | −0.02 | −0.66 | 0.38 | 0.30 | −0.35 | 0.59 | 0.13 | 0.05 | 5.1026 |
| 4 | m4 | −0.15 | −0.16 | −0.65 | 0.41 | 0.16 | −0.34 | 0.49 | 0.19 | 0.11 | 4.9696 |
| 5 | m5 | −0.05 | 0.05 | −0.63 | 0.47 | 0.35 | −0.30 | 0.68 | 0.21 | 0.15 | 5.2305 |
| 6 | m6 | −0.20 | 0.16 | −0.54 | 0.43 | −0.18 | — | 0.35 | 0.28 | 5.4565 | |
| 7 | VEC | 4 | 5 | 6 | 4 | 5 | 6 | 4 | 5 | 6 |
| # | Model | TBOD | Average effective charge(Q*) |
|---|---|---|---|
| 1 | m1 | 0.0453 | Ti (4.05), V(5.08), Cr (6.68), Zr (3.66), Nb (4.75), Mo (6.41), Hf (3.44), Ta (4.94), W (6) |
| 2 | m2 | 0.0452 | Ti (4.04), V(5.08), Cr (6.72), Zr (3.65), Nb (4.75), Mo (6.42), Hf (3.43), Ta (4.93), W (6) |
| 3 | m3 | 0.0472 | Ti (4.01), V(5.02), Cr (6.66), Zr (3.62), Nb (4.70), Mo (6.35), Hf (3.41), Ta (4.87), W (5.95) |
| 4 | m4 | 0.0454 | Ti (4.15), V(5.16), Cr (6.65), Zr (3.59), Nb (4.84), Mo (6.34), Hf (3.51), Ta (4.81), W (5.89) |
| 5 | m5 | 0.0499 | Ti (3.95), V(4.95), Cr (6.63), Zr (3.53), Nb (4.65), Mo (6.30), Hf (3.32), Ta (4.79), W (5.85) |
| 6 | m6 | 0.0547 | Ti (3.80), V(4.84), Cr (6.54), Nb (4.57), Mo (6.18), Ta (4.65), W (5.72) |
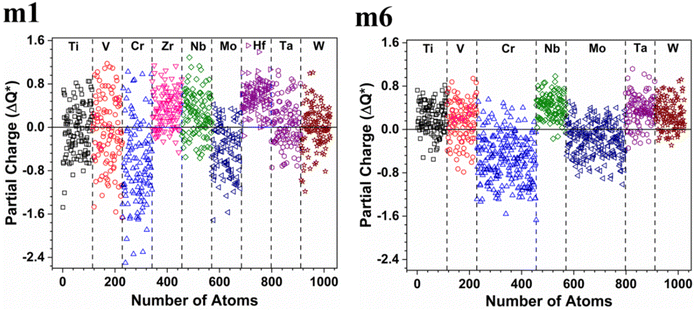
W atom loses charges in the models from m3 to m6. V atom gains charges in the models from m1 to m4 and loses charges in m5 and m6. The distribution of the calculated PC for each element in each RHEA model is shown in Fig. 3 for m1 and m6, and Fig. S3 (m1–m6) in the ESI† for all models. The values of PC in Table 5 are average values. However, a closer look at Fig. 3 and S3† indicates that all elements in these six RHEAs models gain and lose charges within the same model in different percentages. As can be seen in Fig. S3,† the PC activity vary in these six RHEAs models. A recent study99 showed that a larger PC activity between the elements in a HEA model may indicate a larger lattice distortion. Fig. 3 shows much larger PC activity in m1 than in m6, suggesting increased lattice distortion (LD) in m1 (see Section 3.5). The average overall 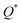 of each HEA can be obtained from the formula:
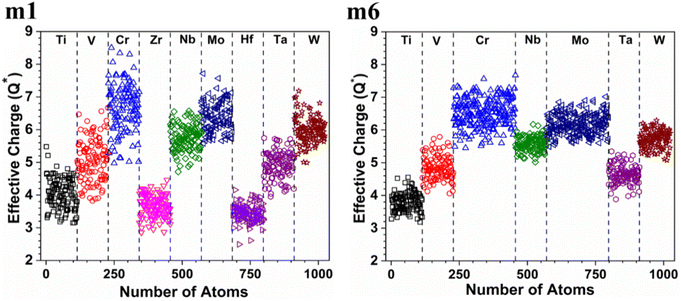
of each HEA can be obtained from the formula: 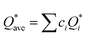 , where ci is the composition of the components. The calculated
, where ci is the composition of the components. The calculated 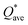 for each model of the six RHEAs models are listed in Table 5. The highest
for each model of the six RHEAs models are listed in Table 5. The highest 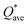 is in m5 and m6 while the lowest
is in m5 and m6 while the lowest 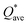 is in m1. These numbers are important for designing HEAs because they correlate with total energy and other properties such as mechanical properties (see Section 3.4). The distribution of the calculated Q* for each atom in each RHEA model is shown in Fig. 4 for m1 and m6, and Fig. S4† (m1–m6) in the SI for all models. Cr and Mo have the highest Q* in m1, m2, m3, m5, and m6 whereas Ti has the highest Q* in m4. Fig. 4 shows that Q* is much more scattered in m1 than m6 which indicates a higher Q* activity and thus a larger lattice distortion in m1 than m6 (see Section 3.5).
is in m1. These numbers are important for designing HEAs because they correlate with total energy and other properties such as mechanical properties (see Section 3.4). The distribution of the calculated Q* for each atom in each RHEA model is shown in Fig. 4 for m1 and m6, and Fig. S4† (m1–m6) in the SI for all models. Cr and Mo have the highest Q* in m1, m2, m3, m5, and m6 whereas Ti has the highest Q* in m4. Fig. 4 shows that Q* is much more scattered in m1 than m6 which indicates a higher Q* activity and thus a larger lattice distortion in m1 than m6 (see Section 3.5).
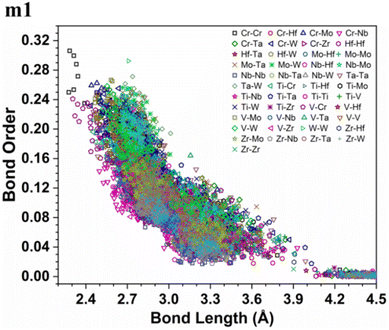
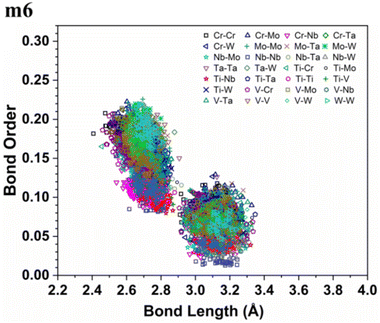
More details about the nature of interatomic interactions between different elements in these six RHEAs models could be revealed via using bond order (BO) and bond length (BL) data. The distribution of BO versus BL for each model is shown in Fig. S5† while the distribution of BO versus BL for all types of bonds in these six RHEAs models is shown in Fig. S6 in the ESI.† These six RHEAs models are constituted from nine metallic elements (Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, W), Therefore, there is a presence of metallic bonds. To comprehend the formation of these six RHEAs models, it is important to understand the nature of these metallic bonds. The lack of information about the metallic bonding for this class of RHEAs motivated us to investigate this bonding. Sharing the valence electrons of all nearby atoms is the origin of metallic bonds.
As an atom making a bond pair transition from the first nearest neighbour to the next nearest neighbour and beyond, the bond's strength decreases. In metallic bonding, there could be several possible values of BO for one certain distance of separation for a pair of atoms, and there could be many possible pairs of atoms for the same distance of separation. A significant implication of interatomic bonding analysis can provide an opportunity to investigate the lattice distortion (LD) in RHEAs. In Fig. 5, and 6, we plotted BO versus BL data for m1 and m6 models. These two figures show that bonds in m1 have much broader distribution than m6 which hints the lattice is much more distorted in m1. Deep analysis of our calculations for BO and BL data and observations can be found in the ESI.†
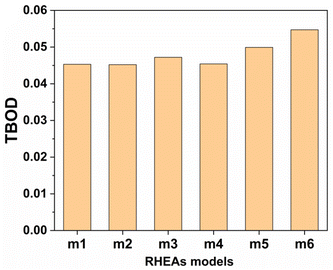
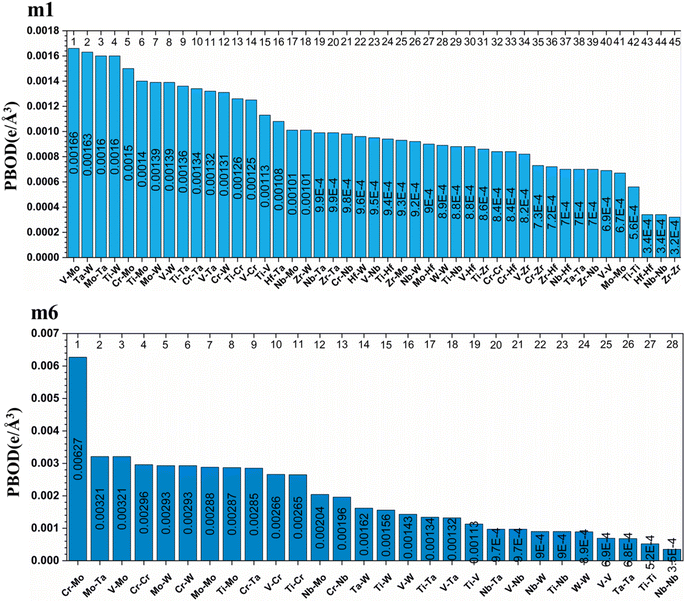
From these observations in ESI,† we conclude that most bonds in the models from m1 to m4 are scatterd in long BLs indicating larger lattice distortion. In contrast, most bonds in m5 and all bonds in m6 are concentrated or assembled in shorter BLs, indicating small lattice distortion in these two models. In Section 3.5, we discuss lattice distorion in these six RHEAs models in detail. m6 uniquely contains 7 elements instead of 9, providing an opportunity to investigate the impact of the element count on HEA properties. The summation of all bond order values for all bond pairs in the corresponding RHEA model is called total bond order (TBO). TBO can be normalized by the volume of the cell to obtain the total bond order density (TBOD). TBOD describes the internal cohesion in a HEA model. TBOD values for all RHEAs models are listed in Table 6 and plotted in Fig. 7. Models m1 and m2 have the lowest TBOD whereas m6 has the largest TBOD among other models. To obtain more insights and reveal the details of interatomic interactions in these RHEAs, we resolved the TBOD into partial bond order density (PBOD) based on the volume defined. Quantum mechanical calculations were used to derive both TBOD and PBOD. The PBOD of the six RHEAs models is displayed in the bar charts in Fig. 8 for m1 and m6, and S7† for all models. As can be seen, each type of bond pair has its unique characteristic, and the PBOD of these bond pairs vary among these six models. So, in both figures the x-axis is ordered in decreasing order of PBOD. In m1, the highest PBOD is from V–Mo and Ta–W bond pairs. In m2, Ta–W and Cr–Ta pairs have the highest PBOD. In m3, the highest PBOD is from Cr–Ta and V–Mo bond pairs, while Ti–Hf and Ta–W have the highest PBOD in m4. Cr–Mo bonds have the highest PBOD in m5 and m6.
3.4. Mechanical properties
In current work, VASP is used to calculate the mechanical properties of these RHEAs models. The response of a material toward a certain stress is described by the elastic constants. The calculated elastic constants (C11, C12, and C44) are listed in Table 7. The resistance of a material against the deformation along [100] direction can be described by C11. Large value of C11 refers to incompressibility under uniaxial stress along x-axes. Changing only the elemental distribution in m2 leads to small changes in elastic constants and mechanical moduli whereas noticeable changes in hardness and lattice distortion (see Section 3.5). One of the key factors to manipulate the properties of these alloys is mainly changing (reducing or increasing) the composition (the atomic fractions) of the Cr, Mo, Ti, Zr, and Hf elements. Cr and Mo along with V elements have the smallest atomic radius whereas Zr and Hf have the largest atomic radius (see Table S2†). Ti is the lightest element among these nine refractory elements. Manipulating the compositions of these five elements can lead to severe lattice distortion (or less lattice distortion), leading to extreme changes in the properties of these six RHEAs. In addition, Mo and Cr have BCC structure and the highest elemental VEC (VEC = 6), whereas Ti, Zr, and Hf have HCP structure and the lowest elemental VEC (VEC = 4). Therefore, altering the atomic fraction of these elements significantly impacts the VEC value of these six RHEAs, leading to notable changes in their mechanical properties. Considering these factors, the atomic fraction of the five elements were selected for adjustment. However, the specific values of the atoms fractions were chosen randomly. For example, increasing the compositions of Cr and Mo from 0.111 in m1 and m2 to 0.135 in m3 and reducing the compositions of Zr and Hf from 0.111 in m1 and m2 to 0.088 in m3 resulted in larger elastic constants, mechanical moduli, and hardness, whereas a noticeable reduce in lattice distortion (see Tables 7 and 8).| Model | C11 | C12 | C44 | K | G | E | η | G/K | HV | HV(S12) | μM | CP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m1 | 225.43 | 127.72 | 32.48 | 160.22 | 38.24 | 106.27 | 0.390 | 0.239 | 2.381 | 2.980 | 4.933 | 95.24 |
| m2 | 228.01 | 126.22 | 34.46 | 160.09 | 40.29 | 111.51 | 0.384 | 0.252 | 2.624 | 3.269 | 4.646 | 91.76 |
| m3 | 246.77 | 132.38 | 35.48 | 170.38 | 42.99 | 118.95 | 0.384 | 0.252 | 2.755 | 3.396 | 4.802 | 96.90 |
| m4 | 223.29 | 124.98 | 38.75 | 157.72 | 42.60 | 117.24 | 0.376 | 0.270 | 2.958 | 3.662 | 4.070 | 86.23 |
| m5 | 276.32 | 139.41 | 39.56 | 184.82 | 49.35 | 135.95 | 0.377 | 0.267 | 3.241 | 3.939 | 4.673 | 99.85 |
| m6 | 345.93 | 148.40 | 50.35 | 213.68 | 66.17 | 179.94 | 0.360 | 0.310 | 4.720 | 5.569 | 4.244 | 98.05 |
| # | Model | FWHM 1 | FWHM 2 | Sum. | Ave. |
|---|---|---|---|---|---|
| 1 | m1 | 0.25788 | 0.33363 | 0.59151 | 0.29576 |
| 2 | m2 | 0.26008 | 0.30319 | 0.56327 | 0.28164 |
| 3 | m3 | 0.25425 | 0.28274 | 0.53699 | 0.26850 |
| 4 | m4 | 0.25177 | 0.32682 | 0.57859 | 0.28930 |
| 5 | m5 | 0.21093 | 0.24131 | 0.45224 | 0.22612 |
| 6 | m6 | 0.15054 | 0.16812 | 0.31866 | 0.15933 |
Hf is heavy element and reducing its composition leads to less lattice distortion in m3 (see Table 8). In m4, Ti composition was increased from 0.111 to 0.1604; the compositions of Ta and W were increased from 0.111 to 0.116; the compositions of Cr, Zr, and Mo were increased from 0.111 to 0.115; while the compositions of V and Nb were reduced from 0.111 to 0.064 and 0.097 respectively. This caused an increase in lattice distortion and hardness while elastic constants (C11 and C12) and bulk modulus reduced significantly in m4. Lattice distortion effect is going to be discussed in detail in the next section. From Table 7, C11 has significantly increased in m5 and m6 (276.3 GPa and 345.9 GPa, respectively) comparing to m1, m2, and m4 due to the increase of Cr and Mo content from 114 atoms in m1to 228 atoms in m5 and m6 models. Increasing the Cr and Mo compositions in this class of RHEAs could be the key factor in improving the yield strength. C44 determines the exact resistance against the shear deformation in the (100) plane. Possessing the highest C44 values, m5 and m6 exhibit the lowest shearability (less responsive to shear stress) amongst all studied solid solutions. Higher Cr and Mo content in m5 and m6 results in significantly increased elastic constants compared to m1 and m4. This suggests that m5 and m6 experience lower elastic strains under stress. Increasing Ti content from 114 atoms in m1 to 164 atoms in m4 led to a significant decrease in C11. The calculated elastic constants in Table 7 satisfy the mechanical stability criteria of a cubic structure: C44 > 0, C11 > |C12|, and C11 + 2C12 > 0.100 This suggests that these alloys are expected to be mechanically stable.
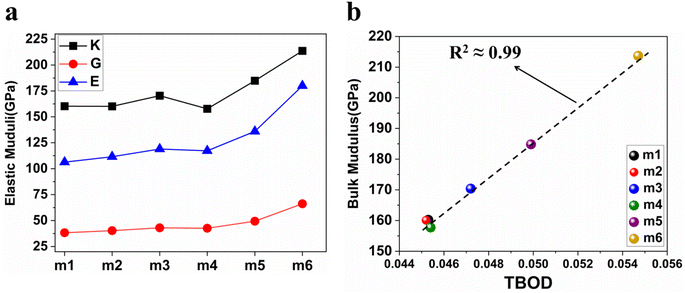
We obtained the mechanical parameters: bulk modulus (K), Young's modulus (E), shear modulus (G), and Poisson's ratio (η) from elastic coefficient Cij using Voigt–Reuss–Hill (VRH) approximation.101,102 The compliance tensor Sij (Sij = 1/Cij) was also employed in the calculation. These derived properties are presented in Table 7 and Fig. 9(a). Young's modulus measures the change in length. Bulk modulus determines the resistance to compressibility or change in volume under pressure and shear modulus measures the resistance against shear distortion. A significant increase of K, E and G moduli in m5 and m6 due to the increased compositions of Cr and Mo. Fig. 9(a) show the model m6 has the highest values for K, G, and E, m4 exhibits the lowest values for K, and m1 exhibits the lowest values for both G and E. All these six RHEAs models are considered incompressible due to the high values of bulk modulus (higher than 40 GPa). It is crucial to determine the machinability index (μM) to assess the applications in different materials. Machinability is the ease with which the materials can be machined at a low cost. Eqn (S10) in the ESI† is used to calculate μM. Table 7 shows minimal variation in μM across the different compositions of the refractory elements in these six models. Pugh's modulus ratio,102,103 defined as the ratio of shear modulus (G) to the bulk modulus (K), can sometimes be used to predict the brittle or ductile behavior of a material. Materials with G/K larger than 0.571 tend to be brittle while those with less than 0.571 tend to be ductile.103,104 Based on Pugh's modulus ratio values in Table 7, all the six RHEAs models show a strong ductile behaviour.
Pettifor proposed the Cauchy pressure (CP)105 as the difference between the elastic constants C12 and C44: CP = C12 − C44. A negative CP indicates dominance of covalent bonding and likely to have brittleness, while a positive CP indicates dominance of metallic bonding106 and likely to have ductility.107,108 As shown in Table 7, the metallic bonding is dominant in all six models. Vicker's hardness (HV)109,110 has been calculated using eqn (S11) based on the elastic constants.111–113 The calculated values of HV for the six RHEAs solid solutions are listed in Table 7. With these values of HV, these RHEAs solid solutions cannot be considered as super hard materials. Another formula (S12)† was used to estimate HV. These values of HV are presented in the column eleven of Table 7. Formula (S12)† shows that these six models have higher HV than when using formula (S11),† however, m6 still has the highest HV amongst other models. A relationship between the mechanical properties and the electronic structure is explored. For example, Fig. 9(b) illustrates the correlation between TBOD and bulk modulus. This correlation exhibits a closer-to-linear nature with their coefficient of determination (R2) equaling 0.99. This observation suggests the potential future prediction of bulk modulus based on TBOD. Fig. 10 illustrates the positive correlation between bulk modulus (K) and 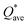 with their coefficient of determination (R2) equaling 0.996, and this refers to the extreme importance of
with their coefficient of determination (R2) equaling 0.996, and this refers to the extreme importance of 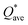 in designing HEAs.
in designing HEAs.
 | ||
Fig. 10 Calculated 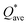 versus bulk modulus K for the set of 6 BCC RHEAs. The dashed line denotes linear fit. versus bulk modulus K for the set of 6 BCC RHEAs. The dashed line denotes linear fit. | ||
Finally, it is worthwhile to investigate the effects of incorporating HCP structures (the favored structure for Ti, Zr, and Hf under standard conditions) in these six RHEAs.
The type of crystalline structure (HCP or BCC) have a huge effect on the values of bulk modulus (K), Young's modulus (E), and VEC of RHEAs. K or E is one of the intrinsic nature of materials. Hf has HCP structure, while Ti and Zr can have either HCP or BCC structure. Therefore, changing the composition of these three elements may result in a dramatic change on the values of K, E, and VEC. K and E are also strongly correlated with VEC. Increasing proportion of HCP structures (Ti and Zr) while reducing BCC structure (V) within a BCC structure of a RHEA stabilize HCP structure (and destabilize BCC structure). This results in a significant decrease of K, E, and VEC values, as observed in m4 (see Tables 2 and 7). While reducing the composition of Zr and Hf and increasing the composition of Cr and Mo (BCC structures) stabilize BCC structure and result in larger K, E, and VEC values as observed in m3 and m5 (see Tables 2 and 7). The same trend can be seen in m6. We conclude that the type of crystalline structure (HCP or BCC) plays an important role in K, E, and VEC values of these RHEAs.
3.5. Lattice distortion
Lattice distortion (LD) has a huge effect on the properties of HEAs2 such as mechanical and thermal properties. More large elastic-strains could be induced by LD which in return may hinder the dislocation motion during deformation.114 LD can significantly modify the dislocation core structure115 which suggests a correlation between LD and strength/ductility in HEAs.116 Quantifying LD in HEAs is difficult beyond the simple geometric parameters. It is also difficult to capture LD in experiments. However, LD can be obtained from the BO vs. BL data. It is difficult to provide a precise description for LD due to the lack of a basic reference for the undistorted lattice in HEAs. In this work, LD is obtained by plotting the histogram distribution of BL data of interatomic pairs in Fig. 11 for m1 and m6, and Fig. S8† for all RHEAs models. Basically, the two peaks in these figures belong to the first nearest neighbor (NN) and second nearest neighbor (SNN) interatomic pairs.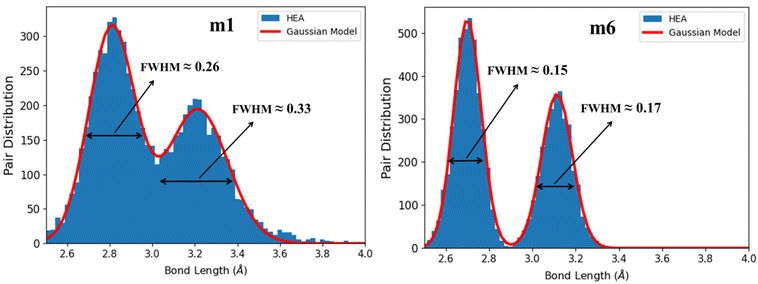 | ||
| Fig. 11 Lattice distortion (LD) in m1 and m6 RHEAs models. FWHM of the Gaussian curve fitted to the histogram distribution of the bimodal peaks. The two peaks denote the NN and SNN. | ||
These data were fitted with two Gaussians exhibiting a bimodal distributions for the NN and SNN. The full width at half maximum (FWHM) values obtained from BO values are presented in Table 8. Notable peaks show the structure integrity, whereas the pair distribution between the peaks denotes structure's LD. The larger the two FWHM and their sum, the greater the LD. From Table 8, m1 model displays the higher degree of LD while m6 displays the lower degree of LD. This indicates equimolar atomic ratios for these nine elements may result in larger LD. Increasing the compositions of Cr and Mo from 0.111 in m1 and m2 to 0.223 in m6 and reducing the compositions of Zr and Hf from 0.111 in m1 and m2 to zero in m6 resulted in much less LD and much higher elastic properties and hardness. This feature can be used to guide future experimental and computational works. In literature, the correlation between LD and ductility of HEAs is ambiguous and misleading. LD may be used as a parameter to predict the ductility of arbitrary HEAs. LD can significantly modify the dislocation core structure. Large elastic-strains could be induced by large LD which in return hinders the dislocation motion during the deformation99,114 affecting the ductility and strength of HEAs.117–121 Several parameters are used to predict the ductility of RHEAs: Cauchy pressure, Pugh's ratio, and Poisson's ratio. Small Pugh's ratio and large Poisson's ratio indicate ductile behavior. In Fig S9,† Pugh's ratio decreases with increase of LD and Poisson's ratio increases with increase in LD, indicating a strong correlation between LD and ductility of these six RHEAs models.
LD has a huge effect on many crucial properties including mixing entropies, electrical transport, and mechanical properties of HEAs as many previous studies have reported.23,26,122 Thus, it is significant to explore the effect of LD on mechanical properties for these six RHEAs models by plotting LD (average value of FWHM1 and FWHM2 from Table 8) versus bulk (K) and shear (G) moduli in Fig. S10,† LD versus Young's modulus (E) and Vicker's hardness (HV) in Fig. S11,† and LD versus elastic constants (C11 and C44) in Fig. S12.† Fig. S10, S11, and S12† show that K, G, E, HV, C11, and C44 decrease with increase of LD, showing that LD generally decreases the strength and hardness of these six RHEAs models. The present results uncover that LD obviously lessen the elastic properties, which is consistent with some of previous findings.27,123,124 This effect may be universal phenomenon irrespective of lattice structure of RHEAs. Fig. S11(b)† shows that LD and HV are inversely correlated with a small deviation in m4.
3.6. Thermal properties
It is crucial to calculate thermal properties such as Debye temperature and thermal conductivity of the six RHEAs models since they determine the thermoelectric (TE) performance. TE performance of materials is the ability to convert heat into electricity under a temperature gradient. TE technology could be one of the green solutions to mitigate the energy and environmental crisis via reducing the pollution resulting from using fossil fuels.125 TE performance is determined by so called figure of merit (ZT) which is given as: ZT = S2σT/κ, where σ is the electrical conductivity, S is the Seebeck coefficient, T is the absolute temperature, and κ is the thermal conductivity.Due to the significant reduced κ, HEAs could be promising TE materials. The severe LD and chemical disorder may result in a significant phonon scattering and reduced κ. Several thermal characteristics could be described by the value of Debye temperature (ΘD), such as the specific heat, thermal conductivity (κ), melting temperature, and the nature of bonding. In this work, we used Anderson's method (shown in eqn (S13) in the ESI†) to calculate ΘD. The average sound velocity (vm), transverse (shear) sound velocity (vs), and the longitudinal sound velocity (vl) were calculated using eqn (S14)–(S16)† respectively.
The calculated νs, νl, νm, and ΘD for the six RHEAs models are listed in Table 9. m6 has the highest ΘD and vm, while m1 has the smallest vm and ΘD. This may indicate that m1 has the weakest bond strength and lowest thermal conductivity whereas m6 has the strongest bonds and higher thermal conductivity. This result suggests a possible link between TBOD and these properties as m6 has the highest TBOD (see Table 6) and is a more cohesive structure. Low ΘD is usually associated with low melting temperature while materials with high ΘD tend to have stronger interatomic bonding and higher melting temperature.48,126
| Model | ρ (Kg m−3) | νs (m s−1) | νl (m s−1) | νm (m s−1) | ΘD (K) | νE (m s−1) |
|---|---|---|---|---|---|---|
| m1 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 571.57 571.57 |
1901.907 | 4469.759 | 2149.883 | 249.03 | 3170.558 |
| m2 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568.52 568.52 |
1952.502 | 4497.870 | 2205.391 | 255.44 | 3248.252 |
| m3 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 553.26 553.26 |
2018.322 | 4645.027 | 2279.650 | 266.27 | 3357.291 |
| m4 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483.81 483.81 |
2015.790 | 4523.498 | 2274.441 | 262.84 | 3344.093 |
| m5 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 516.87 516.87 |
2166.209 | 4881.628 | 2444.596 | 288.85 | 3595.394 |
| m6 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 417.72 417.72 |
2520.254 | 5383.319 | 2837.257 | 341.99 | 4156.020 |
The performance of heat transfer through a material can be determined by the thermal conductivity (κ).127 Calculating minimum thermal conductivity (κmin) and lattice thermal conductivity (κL) in HEAs is important to verify the TE performance. In this work, we used Clarke's model128 (see eqn (S17)†), Cahill's model129 (see eqn (S18)†), Slack's model130 (see eqn (S19)†), and mixed model (see eqn (S23)†) to obtain an estimation for κmin and κL of the six RHEAs models 300 K and they are listed in Table 10. m1 has the lowest κmin and κL according to Clarke's, Cahill's, and Slack's models while m6 has the highest κmin and κL. From Table 10, m1 has the smallest value of νs. The significantly dampened transverse phonon modes (νs) may strengthen the scattering of phonons131 which in return results in a reduced lattice thermal conductivity (κL).
| Model | Clarke model κmin (W m−1 K−1) | Cahill model κmin (W m−1 K−1) | Slack model κL (W m−1 K−1) | Mixed model κL (W m−1 K−1) | γα | Tmelt (K) | α (×10−5) |
|---|---|---|---|---|---|---|---|
| m1 | 0.5765 | 0.5367 | 0.4641 | 0.6636 | 2.506 | 1885.29 | 4.184 |
| m2 | 0.5905 | 0.5432 | 0.5253 | 0.7388 | 2.447 | 1900.54 | 3.971 |
| m3 | 0.6207 | 0.5707 | 0.5807 | 0.8044 | 2.444 | 2011.41 | 3.722 |
| m4 | 0.6052 | 0.5482 | 0.6104 | 0.8439 | 2.368 | 1872.64 | 3.756 |
| m5 | 0.6802 | 0.6177 | 0.7521 | 1.0070 | 2.381 | 2186.05 | 3.242 |
| m6 | 0.8183 | 0.7208 | 1.3466 | 1.6919 | 2.214 | 2597.45 | 2.418 |
The Grüneisen parameter (γα) describes the bond anharmonicity and the nature of the interatomic interaction inside a material.132 Large value of γα indicates strong anharmonic vibrations of atoms or molecules, and thus higher phonon scattering and lower κL. Formula (S21)† was used to calculate γα values and they are summarized in Table 10. With the highest γα, m1 is the lowest influenced under high temperature (depressed and temperature-independent lattice thermal conductivity) whereas m6 with lowest γα is the highest influenced under high temperature (higher and temperature-dependent lattice thermal conductivity). A higher ΘD may indicate a higher κL and vice versa according to Callaway–Debye theoretical model.133 Fig. S13(a)† shows that ΘD is positively correlated (close-linear) with κL for the six RHEAs models and in agreement with Callaway–Debye model.
We also calculated melting temperature (Tmelt) using formula (S24) in the ESI.† Tmelt is an important parameter in high temperature applications. Tmelt is usually correlated to ΘD and κL. The calculated Tmelt for the six RHEAs models is presented in Table 10. As expected, m6 has the highest Tmelt whereas m4 has the lowest Tmelt. The tendency of a material to change the shape, volume, and density in response to a change in temperature is described by thermal expansion coefficient (α). α for the six RHEAs models can be estimated from the formula (S25).† Table 10 shows that m1 has the largest α whereas m6 has the smallest α.
The random distribution of mismatch of atomic size in HEAs leads to a severe LD. Thus, LD should have a huge impact on thermal properties.24,134,135 For example, higher LD causes stronger anharmonic vibrations (higher γα) (see Fig. S13(b)†) and this leads to higher phonon scattering and lower κL. According to this criterion, we plotted LD (average value of FWHM1 and FWHM2 from Table 8) versus ΘD in Fig. S14(a)† and noticed that with the increase in LD, ΘD significantly decreases. The same exact trend was noticed in Fig. S14(b) and S15(a).† With the increase in LD, νs and κL significantly decrease. This shows that LD strongly affects the thermal transport process. Small deviation could be noticed for m4. Strong anharmonic vibrations (high γα) indicates higher phonon scattering and lower κL, and this trend can be seen in Fig. S15(b).† With the increase in γα, κL significantly decreases.
4 Conclusion
In current study, electronic structure, bonding, mechanical, lattice distortion, and thermal properties of six BCC refractory-based HEAs (or RHEAs): TiVCrZrNbMoHfTaW(m1), TiVCrZrNbMoHfTaW(m2),Ti114V114Cr138Zr90Nb114Mo138Hf90Ta113W113(m3), Ti164V65Cr118Zr118Nb99Mo118Hf104Ta119W119(m4), Ti114V114Cr171Zr57Nb114Mo171Hf57Ta113W113(m5), and Ti114V114Cr228Nb114Mo228Ta113W113(m6) were investigated via first-principles calculations. Phase stability of these six RHEAs has been tested via calculating thermodynamic parameters and other parameters. Random solid solution model (RSSM) was used for alloying these six RHEAs models with large super-cells of 1024 atoms each.The effect of total bond order density (TBOD) as a valuable parameter in understanding the bonding characteristics of RHEAs is highlighted. The average partial charge 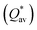 for each model was calculated. It is shown that TBOD and
for each model was calculated. It is shown that TBOD and 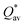 are positively correlated with the mechanical properties, especially with bulk modulus. Based on our calculations, all these six RHEAs models are mechanically stable. m5 and m6 have the largest Young's, bulk, and shear moduli, whereas m1 and m2 have the lowest Young's, bulk, and shear moduli. Reducing the composition of Hf element from 114 atoms into 57 atoms, and increasing the composition of Cr and Mo elements to 171 atoms each in m5 resulted in larger elastic moduli (Young's, bulk, and shear) compared with other models. Reducing the composition of Hf and Zr elements into zero and increasing the composition of Cr and Mo elements into 228 atoms each in m6 resulted in larger elastic moduli (even larger than m5) and large elastic constants (C11 and C44) compared with other models indicating higher hardness with higher fracture toughness and melting temperature. Larger elastic moduli indicates higher difficulty to compress and elongate.
are positively correlated with the mechanical properties, especially with bulk modulus. Based on our calculations, all these six RHEAs models are mechanically stable. m5 and m6 have the largest Young's, bulk, and shear moduli, whereas m1 and m2 have the lowest Young's, bulk, and shear moduli. Reducing the composition of Hf element from 114 atoms into 57 atoms, and increasing the composition of Cr and Mo elements to 171 atoms each in m5 resulted in larger elastic moduli (Young's, bulk, and shear) compared with other models. Reducing the composition of Hf and Zr elements into zero and increasing the composition of Cr and Mo elements into 228 atoms each in m6 resulted in larger elastic moduli (even larger than m5) and large elastic constants (C11 and C44) compared with other models indicating higher hardness with higher fracture toughness and melting temperature. Larger elastic moduli indicates higher difficulty to compress and elongate.
Different atomic configurations can result in a significant different property. For example, the total density of states of m2 and partial density of states (PDOS) at Fermi energy of most elements in m2 lowered compared to m1 indicating that m2 is more stable than m1(see Tables 3 and 4). Elastic constants (C11 and C44), shear and Young's moduli, Pugh's ratio, and Vicker's hardness increased in m2 comparing to m1. This indicates that mechanical properties can be improved via changing the atomic configurations in HEAs. The atomic configuration has also an effect on lattice distortion and thermal properties. Different atomic configurations can cause either higher or lower lattice distortion which in return results in different mechanical and thermal properties. Lattice thermal conductivity increased in m2 comparing to m1, whereas lattice distortion decreased (see Tables 7, 8, and 10). If the atomic configuration can influence the lattice distortion, it indeed influences the dislocation dynamics and further in mechanical properties of HEAs. This suggests that manipulating the atomic configuration would be an effective strategy to enhance the mechanical properties. Similarly, changing atomic configurations can be carried out for each model from m3 to m6 to produce other new different models with different physical properties. However, this process would be very computationally expensive in the current study.
Controlling the VEC value is a key factor in achieving either high or low Young's modulus (E) and bulk modulus (K). Both E and K are positively correlated to VEC as shown in Fig. S16.† This strongly suggests that increasing the composition of elements with low VEC value such as Ti, Zr, and Hf lowers the VEC of the RHEA, thereby reducing E and K (as observed in m4). Conversely, decreasing the composition of Ti, Zr, and Hf while increasing the proportion of elements with high VEC values, such as Cr, Mo, and W, raises the VEC of the RHEA, resulting in significantly higher E and K (as seen in m5 and m6). VEC values can also control melting point (Tm) (see Table 2) of RHEAs. Fig. S17† shows that the correlation between Tm and VEC of the six RHEAs is almost positively linear with (R2 ≈ 0.995). VEC along with the type of crystalline structure can be used to manipulate the mechanical and thermal properties of RHEAs. This analysis can open new avenues for the designing more RHEAs for multiple applications.
Thermal properties and TE performance of these six RHEAs were investigated. m1 and m2 have the smallest velocity of a sound (vs., vl, vm), ΘD, and κL, whereas m5 and m6 have the largest vs., vl, vm, ΘD, and κL. The velocity of a sound is usually determined by two factors: the elastic properties and density (ρ), and the relationship is described by the following equation:
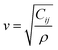 | (14) |
Reducing the composition of Hf and Zr elements to zero in m6 affected thermal properties significantly. m6 has the lowest density among other models. Larger ΘD in m5 and m6 indicates stronger interatomic bonding and as a result, sound waves travel faster in these two models. The larger ΘD positively correlates with TBOD. High sound velocities or high phonon speeds indicates larger κL. This feature makes the m5 and m6 models less applicable for TE applications, whereas m1 and m2 are more applicable for TE applications. These six RHEAs models were investigated for their lattice distortion (LD). m1, m2, and m4 have the highest LD while models m5 and m6 have the lowest LD. We showed that LD is correlated to the ductility of these six RHEAs models. LD is correlated with lattice thermal conductivity (κL). A high LD indicates higher phonon scattering and thus low κL, while a small LD indicates higher κL. This new finding from our current calculations could be facilitated to design new RHEAs for multiple uses. The promising current results inspire us to do more research in this direction for more complex refractory-based high-entropy materials. We believe our results can be facilitated to design new high-entropy materials with wider applications.
Data availability
The authors declare that the main data supporting the findings of this study are available within the article and its ESI files.† Any additional information, such as codes used in this study, is available either in the ESI† or upon request via contacting the first author at: E-mail: sahibhasan81@gmail.com.Author contributions
Wai-Yim Ching (W. C.) conceived and directed the project. W. C., Saro San (S. S.), and Sahib Hasan (S. H.) performed the calculations. S. S. and S. H. made all figures. S. H., Puja Adhikari, and W. C. drafted the paper. All authors participated in the discussion and interpretation of the results. All authors edited and proofread the final manuscript.Conflicts of interest
The authors declare no competing or conflicts of interests.Acknowledgements
This research used the resources of the National Energy Research Scientific Computing Center supported by DOE under Contract No. DE-AC03-76SF00098 and also the Research Computing Support Services (RCSS) of the University of Missouri System. This project was funded by Missouri Institute for Defense and Energy [Gift Account].References
- C. J. Tong, et al., Mechanical performance of the AlxCoCrCuFeNi high-entropy alloy system with multiprincipal elements, Metall. Mater. Trans. A, 2005, 36, 1263–1271 CrossRef.
- C. Lee, et al., Lattice distortion in a strong and ductile refractory high-entropy alloy, Acta Mater., 2018, 160, 158–172 CrossRef CAS.
- Y. Shi, et al., Corrosion of Al xCoCrFeNi high-entropy alloys: Al-content and potential scan-rate dependent pitting behavior, Corros. Sci., 2017, 119, 33–45 CrossRef CAS.
- O. N. Senkov, G. B. Wilks, D. B. Miracle, C. P. Chuang and P. K. Liaw, Refractory high-entropy alloys, Intermetallics, 2010, 18, 1758–1765 CrossRef CAS.
- W. R. Wang, W. L. Wang and J. W. Yeh, Phases, microstructure and mechanical properties of AlxCoCrFeNi high-entropy alloys at elevated temperatures, J. Alloys Compd., 2014, 589, 143–152 CrossRef CAS.
- Y. L. Chou, J. W. Yeh and H. C. Shih, Effect of Inhibitors on the Critical Pitting Temperature of the High-Entropy Alloy Co1.5CrFeNi1.5Ti0.5Mo0.1, J. Electrochem. Soc., 2011, 158, C246 CrossRef CAS.
- Y. F. Kao, T. D. Lee, S. K. Chen and Y. S. Chang, Electrochemical passive properties of AlxCoCrFeNi (x = 0, 0.25, 0.50, 1.00) alloys in sulfuric acids, Corros. Sci., 2010, 52, 1026–1034 CrossRef CAS.
- Y. Geng, et al., Remarkable Wear Resistance in a Complex Concentrated Alloy with Nanohierarchical Architecture and Composition Undulation, Research, 2023, 6, 1–14 Search PubMed.
- D. Bérardan, S. Franger, D. Dragoe, A. K. Meena and N. Dragoe, Colossal dielectric constant in high entropy oxides, Phys. Status Solidi Rapid Res. Lett., 2016, 10, 328–333 CrossRef.
- K. Stolze, J. Tao, F. O. Von Rohr, T. Kong and R. J. Cava, Sc-Zr-Nb-Rh-Pd and Sc-Zr-Nb-Ta-Rh-Pd High-Entropy Alloy Superconductors on a CsCl-Type Lattice, Chem. Mater., 2018, 30, 906–914 CrossRef CAS.
- M. H. Tsai, Physical properties of high entropy alloys, Entropy, 2013, 15, 5338–5345 CrossRef CAS.
- J. W. Yeh, et al., Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes, Adv. Eng. Mater., 2004, 6, 299–303 CrossRef CAS.
- D. B. Miracle and O. N. Senkov, A critical review of high entropy alloys and related concepts, Acta Mater., 2017, 122, 448–511 CrossRef CAS.
- Z. Li, S. Zhao, R. O. Ritchie and M. A. Meyers, Mechanical properties of high-entropy alloys with emphasis on face-centered cubic alloys, Prog. Mater. Sci., 2019, 102, 296–345 CrossRef CAS.
- S. Gorsse, J. P. Couzinié and D. B. Miracle, From high-entropy alloys to complex concentrated alloys, Compt. Rendus Phys., 2018, 19, 721–736 CrossRef CAS.
- O. N. Senkov, D. B. Miracle, K. J. Chaput and J. P. Couzinie, Development and exploration of refractory high entropy alloys - A review, J. Mater. Res., 2018, 33, 3092–3128 CrossRef CAS.
- J. Han, B. Su, J. Meng, A. Zhang and Y. Wu, Microstructure and composition evolution of a fused slurry silicide coating on MoNbTaTiW refractory high-entropy alloy in high-temperature oxidation environment, Materials, 2020, 13, 3592 CrossRef CAS.
- A. Ostovari Moghaddam, A. Cabot and E. A. Trofimov, Does the pathway for development of next generation nuclear materials straightly go through high-entropy materials?, Int. J. Refract. Met. Hard Mater., 2021, 97, 105504 CrossRef CAS.
- J. W. Yeh, Alloy design strategies and future trends in high-entropy alloys, Jom, 2013, 65, 1759–1771 CrossRef CAS.
- D. Juliusz, Z. Marek, W. Kucza, G. C. slak, K. Berent, T. Czeppe and M. D. Tadeusz Kulik, Demystifying the sluggish diffusion effect in high entropy alloys, J. Alloys Compd., 2019, 783, 193–207 CrossRef.
- J.-W. Yeh, C. Shou-Yi, H. Yu-Der and S.-J. L. Swe-Kai Chen, Anomalous decrease in X-ray diffraction intensities of Cu–Ni–Al–Co–Cr–Fe–Si alloy systems with multi-principal elements, Mater. Chem. Phys., 2007, 103, 41–46 CrossRef CAS.
- B. Jiang, et al., High-entropy-stabilized chalcogenides with high thermoelectric performance, Science, 2021, 371, 830–834 CrossRef CAS PubMed.
- H. Song, et al., Local lattice distortion in high-entropy alloys, Phys. Rev. Mater., 2017, 1, 1–8 Search PubMed.
- C. M. Rost, et al., Electron and phonon thermal conductivity in high entropy carbides with variable carbon content, Acta Mater., 2020, 196, 231–239 CrossRef CAS.
- K. Y. Tsai, M. H. Tsai and J. W. Yeh, Sluggish diffusion in Co-Cr-Fe-Mn-Ni high-entropy alloys, Acta Mater., 2013, 61, 4887–4897 CrossRef CAS.
- S. S. Sohn, et al., Ultrastrong Medium-Entropy Single-Phase Alloys Designed via Severe Lattice Distortion, Adv. Mater., 2019, 31, 1–8 Search PubMed.
- B. Feng and M. Widom, Elastic stability and lattice distortion of refractory high entropy alloys, Mater. Chem. Phys., 2018, 210, 309–314 CrossRef CAS.
- L. Xiang, Microstructure and Mechanical Properties of TaNbVTiAlx Refractory High-Entropy Alloys, Entropy, 2020, 22, 282 CrossRef CAS.
- Y. Zhang, et al., Microstructures and properties of high-entropy alloys, Prog. Mater. Sci., 2014, 61, 1–93 CrossRef CAS.
- O. N. Senkov, G. B. Wilks, J. M. Scott and D. B. Miracle, Mechanical properties of Nb25Mo25Ta 25W25 and V20Nb20Mo 20Ta20W20 refractory high entropy alloys, Intermetallics, 2011, 19, 698–706 CrossRef CAS.
- O. N. Senkov, J. M. Scott, S. V. Senkova, D. B. Miracle and C. F. Woodward, Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy, J. Alloys Compd., 2011, 509, 6043–6048 CrossRef CAS.
- S. K. Bachani, C. J. Wang, B. S. Lou, L. C. Chang and J. W. Lee, Microstructural characterization, mechanical property and corrosion behavior of VNbMoTaWAl refractory high entropy alloy coatings: Effect of Al content, Surf. Coating. Technol., 2020, 403, 126351 CrossRef CAS.
- O. N. Senkov, S. Gorsse and D. B. Miracle, High temperature strength of refractory complex concentrated alloys, Acta Mater., 2019, 175, 394–405 CrossRef CAS.
- E. P. George, W. A. Curtin and C. C. Tasan, High entropy alloys: A focused review of mechanical properties and deformation mechanisms, Acta Mater., 2020, 188, 435–474 CrossRef CAS.
- Y. Zou, S. Maiti, W. Steurer and R. Spolenak, Size-dependent plasticity in an Nb25Mo25Ta25W25 refractory high- entropy alloy ScienceDirect Size-dependent plasticity in an Nb 25 Mo 25 Ta 25 W 25 refractory high-entropy alloy, Acta Mater., 2017, 65, 85–97 CrossRef.
- Y. Zou, H. Ma and R. Spolenak, Ultrastrong ductile and stable high-entropy alloys at small scales, Nat. Commun., 2015, 6, 7748 CrossRef.
- S. Y. Chen, et al., Peierls barrier characteristic and anomalous strain hardening provoked by dynamic-strain-aging strengthening in a body-centered-cubic high-entropy alloy, Mater. Res. Lett., 2019, 7, 475–481 CrossRef CAS.
- O. N. Senkov, J. M. Scott, S. V. Senkova, F. Meisenkothen, D. B. Miracle and C. F. Woodward, Microstructure and elevated temperature properties of a refractory TaNbHfZrTi alloy, J. Mater. Sci., 2012, 47, 4062–4074 CrossRef CAS.
- Q. T. Song and J. Xu, TiZrNbTa)90Mo10 high-entropy alloy: Electrochemical behavior and passive film characterization under exposure to Ringer's solution, Corros. Sci., 2020, 167, 108513 CrossRef CAS.
- J. Li, X. Yang, R. Zhu and Y. Zhang, Corrosion and Serration Behaviors of TiZr0.5NbCr0.5VxMoy High Entropy Alloys in Aqueous Environments, Metals, 2014, 4, 597–608 CrossRef.
- Q. Zhou, et al., Corrosion behavior of Hf0.5Nb0.5Ta0.5Ti1.5Zr refractory high-entropy in aqueous chloride solutions, Electrochem. Commun., 2019, 98, 63–68 CrossRef CAS.
- S. P. Wang and J. Xu, TiZrNbTaMo high-entropy alloy designed for orthopedic implants: As-cast microstructure and mechanical properties, Mater. Sci. Eng. C, 2017, 73, 80–89 CrossRef CAS PubMed.
- N. Y. Yurchenko, N. D. Stepanov, S. V. Zherebtsov, M. A. Tikhonovsky and G. A. Salishchev, Structure and mechanical properties of B2 ordered refractory AlNbTiVZrx (x = 0–1.5) high-entropy alloys, Mater. Sci. Eng., A, 2017, 704, 82–90 CrossRef CAS.
- Z. D. Han, et al., Effect of Ti additions on mechanical properties of NbMoTaW and VNbMoTaW refractory high entropy alloys, Intermetallics, 2017, 84, 153–157 CrossRef CAS.
- G. Kresse, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis se, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillonin-zone integrations, Phys. Rev. B, 1976, 13, 5188 CrossRef.
- A. Yang, L. Bao, M. Peng and Y. Duan, Explorations of elastic anisotropies and thermal properties of the hexagonal TMSi2 (TM = Cr, Mo, W) silicides from first-principles calculations, Mater. Today Commun., 2021, 27, 102474 CrossRef CAS.
- A. J. Wang, et al., Structural and elastic properties of cubic and hexagonal TiN and AlN from first-principles calculations, Comput. Mater. Sci., 2010, 48, 705–709 CrossRef CAS.
- A. Reuss, Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle, J. Appl. Math. Mech., 1929, 9, 49–58 CAS.
- R. HILL, The Elastic Behaviour of a Crystalline Aggregate, Proc. Phys. Soc., 1952, 65(5), 349 CrossRef.
- Y. Mo, P. Rulis and W. Y. Ching, Electronic structure and optical conductivities of 20 MAX-phase compounds, Phys. Rev. B Condens. Matter, 2012, 86, 1–10 CrossRef.
- S. Hasan, P. Adhikari, K. Baral and W. Y. Ching, Conspicuous interatomic bonding in chalcogenide crystals and implications on electronic, optical, and elastic properties, AIP Adv., 2020, 10, 7 CrossRef.
- S. Hasan, K. Baral, N. Li and W. Y. Ching, Structural and physical properties of 99 complex bulk chalcogenides crystals using first-principles calculations, Sci. Rep., 2021, 11, 1–18 CrossRef.
- C. Dharmawardhana, M. Bakare, A. Misra, W. Y. Ching and J. Bullard, Nature of Interatomic Bonding in Controlling the Mechanical Properties of Calcium Silicate Hydrates, J. Am. Ceram. Soc., 2016, 99, 2120–2130 CrossRef CAS.
- L. Poudel, C. Tamerler, A. Misra and W. Y. Ching, Atomic-Scale Quantification of Interfacial Binding between Peptides and Inorganic Crystals: The Case of Calcium Carbonate Binding Peptide on Aragonite, J. Phys. Chem. C, 2017, 121, 28354–28363 CrossRef CAS.
- S. San, N. Li, Y. Tao, W. Zhang and W. Y. Ching, Understanding the atomic and electronic origin of mechanical property in thaumasite and ettringite mineral crystals, J. Am. Ceram. Soc., 2018, 101, 5177–5187 CrossRef CAS.
- S. Hasan, S. San, K. Baral, N. Li, P. Rulis and W. Y. Ching, First-principles calculations of thermoelectric transport properties of quaternary and ternary bulk chalcogenide crystals, Materials, 2022, 15, 8 Search PubMed.
- S. Hasan, P. Rulis and W.-Y. Ching, First-Principles Calculations of the Structural, Electronic, Optical, and Mechanical Properties of 21 Pyrophosphate Crystals, Crystals, 2022, 12, 8 CrossRef.
- B. Hunca, C. Dharmawardhana, R. Sakidja and W. Y. Ching, Ab initio calculations of thermomechanical properties and electronic structure of vitreloy Z r41.2 T i13.8 C u12.5 N i10 B e22.5, Phys. Rev. B, 2016, 94, 1–10 CrossRef.
- W. Y. Ching, et al., First-principles study in an inter-granular glassy film model of silicon nitride, J. Am. Ceram. Soc., 2018, 101, 2673–2688 CrossRef CAS.
- S. Hasan, P. Adhikari, S. San, P. Rulis and W. Y. Ching, First-principles calculation of lattice distortion, electronic structure, and bonding properties of GeTe-based and PbSe-based high-entropy chalcogenides, J. Appl. Phys., 2024, 135, 085101 CrossRef CAS.
- S. H. Saro San, Designing Quaternary and Quinary Refractory-Based High-Entropy Alloys: Statistical Analysis of Their Lattice Distortion, Mechanical, and Thermal Properties, Metals, 2023, 13, 1953 CrossRef.
- L. Poudel, R. Twarock, N. F. Steinmetz, R. Podgornik and W. Y. Ching, Impact of Hydrogen Bonding in the Binding Site between Capsid Protein and MS2 Bacteriophage ssRNA, J. Phys. Chem. B, 2017, 121, 6321–6330 CrossRef CAS PubMed.
- P. Adhikari, et al., Intra- And intermolecular atomic-scale interactions in the receptor binding domain of SARS-CoV-2 spike protein: Implication for ACE2 receptor binding, Phys. Chem. Chem. Phys., 2020, 22, 18272–18283 RSC.
- R. S. Mulliken, Electronic population analysis on LCAO-MO molecular wave functions. I, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- C. C. Dharmawardhana, A. Misra and W. Y. Ching, Quantum mechanical metric for internal cohesion in cement crystals, Sci. Rep., 2014, 4, 1–8 Search PubMed.
- W. Hume-Rothery, The Engel-Brewer theories of metals and alloys, Prog. Mater. Sci., 1968, 13, 229–265 CrossRef.
- E. C. STONER, Atomic Theory Students of Metallurgy, Nature, 1947, 159, 78–79 CrossRef.
- Y. Zhang, Y. J. Zhou, J. P. Lin, G. L. Chen and P. K. Liaw, Solid-solution phase formation rules for multi-component alloys, Adv. Eng. Mater., 2008, 10, 534–538 CrossRef CAS.
- A. Takeuchi and A. Inoue, Classification of Bulk Metallic Glasses by Atomic Size Difference , Heat of Mixing and Period of Constituent Elements and Its Application to Characterization of the Main Alloying Element, Mater. Trans., 2005, 46, 2817–2829 CrossRef CAS.
- A. Raza, H. J. Ryu and S. H. Hong, Strength enhancement and density reduction by the addition of Al in CrFeMoV based high-entropy alloy fabricated through powder metallurgy, Mater. Des., 2018, 157, 97–104 CrossRef CAS.
- W. Guo, et al., Microstructures and mechanical properties of ductile NbTaTiV refractory high entropy alloy prepared by powder metallurgy, J. Alloys Compd., 2019, 776, 428–436 CrossRef CAS.
- X. Yang and Y. Zhang, Prediction of high-entropy stabilized solid-solution in multi-component alloys, Mater. Chem. Phys., 2012, 132, 233–238 CrossRef CAS.
- O. N. Senkov and D. B. Miracle, Effect of the atomic size distribution on glass forming ability of amorphous metallic alloys, Mater. Res. Bull., 2001, 36, 2183–2198 CrossRef CAS.
- B. Chanda and J. Das, Composition Dependence on the Evolution of Nanoeutectic in CoCrFeNiNb x (0.45 ≤ x ≤ 0.65) High Entropy Alloys, Adv. Eng. Mater., 2018, 20, 0–9 CrossRef CAS.
- U. Bhandari, H. Ghadimi, C. Zhang, S. Yang and S. Guo, Predicting Elastic Constants of Refractory Complex Concentrated Alloys Using Machine Learning Approach, Materials, 2022, 15, 1–16 CrossRef.
- S. Guo and C. T. Liu, Phase stability in high entropy alloys : Formation of solid-solution phase or amorphous phase, Prog. Nat. Sci.:Mater. Int., 2011, 21, 433–446 CrossRef.
- S. Guo, C. Ng, J. Lu and C. T. Liu, Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys, J. Appl. Phys., 2011, 109, 103505 CrossRef.
- R. K. Nutor, et al., Phase Selection, Lattice Distortions, and Mechanical Properties in High-Entropy Alloys, Adv. Eng. Mater., 2020, 22, 1–36 CrossRef.
- Y. Dong, Y. Lu, L. Jiang, T. Wang and T. Li, Effects of electro-negativity on the stability of topologically close- packed phase in high entropy alloys, Intermetallics, 2014, 52, 105–109 CrossRef CAS.
- M. G. Poletti and L. Battezzati, ScienceDirect Electronic and thermodynamic criteria for the occurrence of high entropy alloys in metallic systems, Acta Mater., 2014, 75, 297–306 CrossRef CAS.
- A. K. Singh, A geometrical parameter for the formation of disordered solid solutions in multi-component alloys, Intermetallics, 2014, 53, 112–119 CrossRef CAS.
- F. Tian, L. K. Varga, N. Chen, J. Shen and L. Vitos, Intermetallics Empirical design of single phase high-entropy alloys with high hardness, Intermetallics, 2015, 58, 1–6 CrossRef CAS.
- X. F. Wang, Y. Zhang, Y. Qiao and G. L. Chen, Novel microstructure and properties of multicomponent CoCrCuFeNiTi x alloys, Intermetallics, 2007, 15, 357–362 CrossRef CAS.
- M.-R. Chen, Microstructure and Properties of Al0:5CoCrCuFeNiTix (x ¼ 0{2:0) High-Entropy Alloys, Mater. Trans., 2006, 47, 1395–1401 CrossRef CAS.
- Y. F. Ye, Q. Wang, J. Lu, C. T. Liu and Y. Yang, High-entropy alloy: challenges and prospects, Mater. Today, 2016, 19, 349–362 CrossRef CAS.
- C. C Tung, J. W. Yeh, T. Shun, S. K. Chen, Y. S. Huang and H. C. Chen, On the elemental effect of AlCoCrCuFeNi high-entropy alloy system, Mater. Lett., 2007, 61(1), 1–5 CrossRef CAS.
- C. Tsai, J. Yeh & P. Lee Effect of the substitution of Co by Mn in Al-Cr-Cu-Fe-Co-Ni high-entropy alloys. ( 2006) doi: DOI:10.3166/acsm.31.685-698.
- C. Li, Microstructure and properties of AlTiNiMnBx high entropy alloys, Mater. Sci. Technol., 2008, 459 Search PubMed.
- Z. Wang, S. Guo & C. T. Liu Phase Selection in High-Entropy Alloys : From Nonequilibrium to EquilibriumJOM ( 2014)1996 doi: DOI:10.1007/s11837-014-0953-8.
- Y. Yuan, et al., Formation, structure and properties of biocompatible TiZrHfNbTa high-entropy alloys, Mater. Res. Lett., 2019, 7, 225–231 CrossRef CAS.
- X. Yang and Y. Zhang, Prediction of high-entropy stabilized solid-solution in multi-component alloys Prediction of high-entropy stabilized solid-solution in multi-component alloys, Mater. Chem. Phys., 2017, 132, 233–238 CrossRef.
- S. Fang, X. Xiao, L. Xia, W. Li and Y. Dong, Relationship between the widths of supercooled liquid regions and bond parameters of Mg-based bulk metallic glasses, J. Non-Cryst. Solids, 2003, 321(1–2), 120–125 CrossRef CAS.
- S. Fang, Z. Zhou, J. Zhang, M. Yao, F. Feng and D. Northwood, Two mathematical models for the hydrogen storage properties of AB2 type alloys, J. Alloys Compd., 1999, 293–295, 10–13 CrossRef CAS.
- L. Pauling and G. W. Wheland, The Nature of the Chemical Bond. V, J. Chem. Phys., 1934, 2, 482 CrossRef.
- I. Toda-Caraballo and P. E. J. Rivera-Díaz-Del-Castillo, A criterion for the formation of high entropy alloys based on lattice distortion, Intermetallics, 2016, 71, 76–87 CrossRef CAS.
- N. Yurchenko, N. Stepanov and G. Salishchev, Laves-phase formation criterion for high-entropy alloys, Mater. Sci. Technol., 2016, 33(1), 17–22 CrossRef.
- P. Singh, et al., A ductility metric for refractory-based multi-principal-element alloys, Acta Mater., 2023, 257, 1–36 CrossRef.
- F. Mouhat and F. X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B Condens. Matter, 2014, 90, 0–3 CrossRef CAS.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. R. Soc. Edinb. Sect. A, 1952, 65, 349–354 CrossRef.
- S. F. Pugh, Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Philos. Mag. Ser. 7, 1954, 45(367), 823–843 CrossRef CAS.
- M. Ali, Md. Hossain, M. Rayhan, M. Hossain, M. R. Uddin, K. Ostrikov, A. Islam and S. Naqib, First-principles study of elastic, electronic, optical and thermoelectric properties of newly synthesized K2Cu2GeS4 chalcogenide, J. Alloys Compd., 2019, 781, 37–46 CrossRef CAS.
- D. Heciri, et al., Insight into the structural, elastic and electronic properties of tetragonal inter-alkali metal chalcogenides CsNaX (X=S, Se, and Te) from first-principles calculations, Mater. Chem. Phys., 2019, 221, 125–137 CrossRef CAS.
- D. G. Pettifor, Theoretical predictions of structure and related properties of intermetallics, Mater. Sci. Technol., 1992, 8, 345–349 CrossRef CAS.
- G. Surucu, M. Isik, A. Candan, X. Wang and H. H. Gullu, Investigation of structural, electronic, magnetic and lattice dynamical properties for XCoBi (X: Ti, Zr, Hf) Half-Heusler compounds, Phys. B Condens. Matter, 2020, 587, 412146 CrossRef CAS.
- L. Bao, D. Qu, Z. Kong and Y. Duan, Anisotropies in elastic properties and thermal conductivities of trigonal TM2C (TM = V, Nb, Ta) carbides, Solid State Sci., 2019, 98, 106027 CrossRef CAS.
- M. M. Hossain, et al., Influence of Se doping on recently synthesized NaInS2-xSex solid solutions for potential thermo-mechanical applications studied via first-principles method, Mater. Today Commun., 2021, 26, 101988 CrossRef CAS.
- X. Q. Chen, H. Niu, D. Li and Y. Li, Modeling hardness of polycrystalline materials and bulk metallic glasses, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS.
- Y. Tian, B. Xu and Z. Zhao, Microscopic theory of hardness and design of novel superhard crystals, Int. J. Refract. Met. Hard Mater., 2012, 33, 93–106 CrossRef CAS.
- Z. T. Y. Liu, X. Zhou, D. Gall and S. V. Khare, First-principles investigation of the structural, mechanical and electronic properties of the NbO-structured 3d, 4d and 5d transition metal nitrides, Comput. Mater. Sci., 2014, 84, 365–373 CrossRef CAS.
- Z. T. Y. Liu, X. Zhou, S. V. Khare and D. Gall, Structural, mechanical and electronic properties of 3d transition metal nitrides in cubic zincblende, rocksalt and cesium chloride structures: A first-principles investigation, J. Phys. Condens. Matter, 2014, 26, 025404 CrossRef CAS PubMed.
- X. Zhou, D. Gall and S. V. Khare, Mechanical properties and electronic structure of anti-ReO3 structured cubic nitrides, M3N, of d block transition metals M: An ab initio study, J. Alloys Compd., 2014, 595, 80–86 CrossRef CAS.
- Y. Zhang, X. Yang and P. K. Liaw, Alloy design and properties optimization of high-entropy alloys, Jom, 2012, 64, 830–838 CrossRef CAS.
- S. Lyu, W. Li, Y. Xia, Y. Chen and A. H. W. Ngan, Effects of chemical randomness on strength contributors and dislocation behaviors in a bcc multiprincipal element alloy, Phys. Rev. Mater., 2023, 7, 1–10 Search PubMed.
- J. Li, K. Yamanaka and A. Chiba, Significant lattice-distortion effect on compressive deformation in Mo-added CoCrFeNi-based high-entropy alloys, Mater. Sci. Eng., A, 2022, 830, 142295 CrossRef CAS.
- S. I. Rao, Atomistic Simulations of Dislocations in a Model BCC Multicomponent Concentrated Solid Solution Alloy, Acta Mater., 2017, 125, 311–320 CrossRef CAS.
- F. Maresca and W. A. Curtin, Theory of screw dislocation strengthening in random BCC alloys from dilute to “High-Entropy” alloys, Acta Mater., 2020, 182, 144–162 CrossRef CAS.
- Q. J. Li, H. Sheng and E. Ma, Strengthening in multi-principal element alloys with local-chemical-order roughened dislocation pathways, Nat. Commun., 2019, 10, 1–11 CrossRef.
- C. Lee, et al., Temperature dependence of elastic and plastic deformation behavior of a refractory high-entropy alloy, Sci. Adv., 2020, 6, 1–12 Search PubMed.
- F. Wang, et al., Multiplicity of dislocation pathways in a refractory multiprincipal element alloy, Science, 2020, 370, 95–101 CrossRef CAS PubMed.
- S. Mu, S. Wimmer, S. Mankovsky, H. Ebert and G. M. Stocks, Influence of local lattice distortions on electrical transport of refractory high entropy alloys, Scr. Mater., 2019, 170, 189–194 CrossRef CAS.
- H. Meng, et al., Influence of Local Lattice Distortion on Elastic Properties of Hexagonal Close-Packed TiZrHf and TiZrHfSc Refractory Alloys, Phys. Status Solidi B, 2021, 258, 1–9 CrossRef.
- S. min Zheng, W. qiang and S. qing Wang, Elastic properties of high entropy alloys by MaxEnt approach, Comput. Mater. Sci., 2018, 142, 332–337 CrossRef CAS.
- J. He and T. M. Tritt, Advances in thermoelectric materials research: Looking back and moving forward, Science, 2017, 357, 6358 Search PubMed.
- H. Ma, X. Zhang and F. Wang, First-principles study of the lattice vibration, elastic anisotropy and thermodynamical properties of Tantalum Silicide with the different crystal structures, Vacuum, 2021, 191, 110410 CrossRef CAS.
- Y. Shen, D. R. Clarke and P. A. Fuierer, Anisotropic thermal conductivity of the Aurivillus phase, bismuth titanate (Bi4Ti3O12): A natural nanostructured superlattice, Appl. Phys. Lett., 2008, 93, 1–4 Search PubMed.
- D. R. Clarke, Materials selections guidelines for low thermal conductivity thermal barrier coatings, Surf. Coating. Technol., 2003, 163–164, 67–74 CrossRef CAS.
- D. G. Cahill, S. K. Watson and R. O. Pohl, Lower limit to the thermal conductivity of disordered crystals, Phys. Rev. B, 1992, 46, 6131–6140 CrossRef CAS PubMed.
- D. T. Morelli and G. A. Slack, High lattice thermal conductivity solids, High Therm. Conduct. Mater., 2006, 37–68 CAS.
- X. Y. Li, et al., Observation of High-Frequency Transverse Phonons in Metallic Glasses, Phys. Rev. Lett., 2020, 124, 1–6 Search PubMed.
- R. Knura, T. Parashchuk, A. Yoshiasa and K. T. Wojciechowski, Origins of low lattice thermal conductivity of Pb 1 − x Sn x Te alloys for thermoelectric applications, Dalton Trans., 2021, 50, 4323–4334 RSC.
- J. Feng, et al., Electronic structure, mechanical properties and thermal conductivity of Ln2Zr2O7 (Ln = La, Pr, Nd, Sm, Eu and Gd) pyrochlore, Acta Mater., 2011, 59, 1742–1760 CrossRef CAS.
- A. Sarkar, et al., High-Entropy Oxides: Fundamental Aspects and Electrochemical Properties, Adv. Mater., 2019, 31, 1970189 CrossRef.
- D. Berardan, A. K. Meena, S. Franger, C. Herrero and N. Dragoe, Controlled Jahn-Teller distortion in (MgCoNiCuZn)O-based high entropy oxides, J. Alloys Compd., 2017, 704, 693–700 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra07460b |
| This journal is © The Royal Society of Chemistry 2025 |