DOI:
10.1039/D4RA07861F
(Paper)
RSC Adv., 2025,
15, 1425-1437
Efficiency of carbon dioxide capture with metal substitutions in the MIL-88A metal–organic framework
Received
4th November 2024
, Accepted 25th December 2024
First published on 16th January 2025
Abstract
Carbon dioxide capture is a vital approach for mitigating air pollution and global warming. In this context, metal–organic frameworks are promising candidates. Particularly, MIL-88A (M), where the metal nodes (M) are connected to fumarate linkers in its structure, has demonstrated significant potential for CO2 capture. However, to date, no studies have investigated the effects of metal substitutions in MIL-88A (M) on CO2 capture performance. Therefore, the present work aims to address this gap by examining metal substitutions with M = Al, Sc, Ti, V, and Ga. To quantitatively understand the CO2 capture capabilities of MIL-88A (M), we employed grand canonical Monte Carlo simulations to study both excess and total CO2 uptakes. Our findings indicated that MIL-88A with Al and Ga as metal nodes exhibited the best performance for CO2 capture. Furthermore, the adsorption energy of the CO2 molecule in MIL-88A (M), obtained through van der Waals-corrected density functional theory calculations, indicated the following order of preference for CO2 adsorption: Ti > V > Sc > Ga ≈ Al. The adsorption strength of the CO2 molecule in MIL-88A (Ga and Al) was the weakest among the considered metals. However, MIL-88A (Al) exhibited the largest specific surface area and hence offered the best excess and total gravimetric uptakes, while MIL-88A (Ga), together with MIL-88A (Al), had the largest pore volumes. Therefore, they exhibited the best excess and total volumetric uptakes. The electronic density of states revealed that the interaction between the 3σg, 2πu, and 1πg peaks of the CO2 molecule and the O and C px and py orbitals of MIL-88A (M) was found to be significant for understanding the physical interaction between CO2 and MIL-88A (M). Thus, our findings provide valuable insights for the rational design of metal–organic frameworks for gas capture and storage applications.
1 Introduction
Harnessing the power of fossil fuels and natural gas for energy production has resulted in the release of significant amounts of carbon dioxide (CO2) into the atmosphere, contributing to climate change and environmental degradation. Therefore, to combat this issue, it is crucial to not only promote the use of renewable energy sources, such as solar and wind, but also actively work towards reducing CO2 emissions. Several methods, including pre-combustion, post-combustion, oxyfuel combustion, gas-mixture separation, and CO2 capture using solid adsorbents, have been employed to address this challenge.1–4 Particularly noteworthy is the CO2 capture by solid adsorbents, which has garnered significant attention due to their remarkable properties, including high capacity, rapid adsorption and desorption, and high selectivity in capturing CO2 based on adsorption phenomena.2–4 Among the solid adsorbents, metal–organic frameworks (MOFs) have emerged as leading candidates, surpassing traditional porous zeolites and activated carbons owing to their ultra-large surface areas, adjustable pore sizes, high stability, and flexible design.5,6 Owing to their outstanding CO2 capture capacity, MOFs and MOF-based compounds have found applications in numerous areas, such as water pollutant removal, electrocatalysis, photocatalysis, gas sensing, and gas capture and separation.7
To date, several MOFs have been synthesized and investigated for CO2 capture.8,9 For instance, MIL-101 (Cr),10 Ni-MOF-74,11 and AS-2-600 (ref. 12) demonstrated gravimetric uptakes of 3.81 mmol g−1 at 348 K, 5.22 mmol g−1 at 298 K, and 4.8 mmol g−1 at 298 K, respectively, at a pressure of 1 bar. Mg2(dobdc) exhibited a capacity of approximately 9.0 mmol g−1.13,14 MOF-177 showed a high CO2 uptake capacity of 33.5 mmol g−1 at room temperature and 35 bar. Nu-100 provided an excess gravimetric CO2 uptake of 2043 mg g−1 or 46.4 mmol g−1 at 298 K and 40 bar.15 The best MOFs for gravimetric CO2 capture thus far are MOF-200 and MOF-210, achieving approximately 2400 mg g−1 at 298 K and 50 bar.16 Additionally, volumetric uptake is important for automobile applications. JLU-MOF58 (ref. 17) and NKU-521a18 exhibited a volumetric uptake of 49 cm3 g−1 and 139 cm3 g−1 at 273 K, respectively. Also, a high volumetric uptake was observed for Mg-MOF-74 (165 cm3 (STP) cm−3) and opt-UiO-66(Zr)–(OH)2 (172 cm3 (STP) cm−3) at 298 K and 1 bar,19 and IRMOF-74III-CH2–NH2 (73.2 cm3 g−1 at 298 K and 800 Torr).20 The CO2 loading of Cu-1 was 180 cm3 g−1 at 273 K and 128.77 cm3 g−1 at 298 K, both measured at 1 bar pressure.21 IRMOF-1 and MIL-101 (Cr) achieved CO2 volumetric loadings of 290 cm3 (STP) cm−3 at 298 K and 35 bar, and 390 cm3 (STP) cm−3 at 304 K and 50 bar, respectively.22
Recently, the MIL-88 series has attracted significant attention because of its superior stability in humid and liquid environments.23,24 Thus, it has been utilized in many applications, such as drug delivery,25 catalysis,26,27 and hydrogen storage.28–30 A theoretical study has shown that organic-linker substitutions can significantly impact the CO2 uptake in the MIL-88 series, with MIL-88A being identified as the most effective for capturing CO2 in terms of both gravimetric and volumetric loadings.31 However, to date, an experimental investigation of CO2 capture has only been conducted on MIL-88A.32
Many strategies have been developed to enhance the performance of MOFs for CO2 capture. These strategies include organic ligand modification, metal substitution, and incorporating metal nanoparticles, metal sulfides, metal oxides, metal phosphides, MXenes, carbon materials, aerogels, and polymers.7 The first two methods involve modifying the main structure of MOFs, while the remaining methods involve adding foreign components to the MOF structure. For example, MIL-88A/polyacrylate and MIL-88A(Fe)/MoS2 photocatalysts have been utilized for the degradation of organic pollutants with a catalytic efficiency of over 97%.33,34 Moreover, the MIL-88A(Fe)/PDINH compound was prepared for the photocatalytic degradation of chloroquine phosphate.35 Additionally, NH2-MIL-88(Fe) and MIL-88(Fe) were employed for photocatalytic applications.36 Among the MIL-88 series, MIL-88A has been found to be the most effective MOF,30 which has been modified using various methods for different applications. However, there is a lack of research addressing the impacts of metal substitution in MIL-88A(M) for CO2 capture. Therefore, this study aims to address this gap using grand canonical Monte Carlo (GCMC) simulations in combination with van der Waals-dispersive correction density functional theory (vdW-DF) calculations. The GCMC simulations were performed to quantitatively assess the CO2 uptake capacity in MIL-88A(M), while the vdW-DF approach was employed to elucidate the physical interactions between CO2 and MIL-88A(M), where M = Al, Ga, Sc, Ti, and V. We substituted these metals because previous works showed that they are the most competent substituents in the MIL-family.37–39
2 Computational techniques
We computed the absolute uptake (nabs) and the excess adsorption (nex) capacity of CO2 capture via the following relationship,40where ρgas and Vp are the density of CO2 molecules in the bulk gas phase and the pore volume of MIL-88A(M), respectively. If nabs is divided by the mass of the unit cell, one can obtain the absolute gravimetric uptake capacity of CO2 (in units of g CO2 g−1).41 The excess uptake can be deduced from eqn (1). We conducted the GCMC simulations with μVT ensembles using the RASPA package for obtaining nabs and nex.42 The unit cell for the GCMC simulations consisting of 1224 atoms was built by repeating 3 × 3 × 2 times of the primitive unit cell along the x, y, and z directions, respectively. During the simulations, the carbon dioxide molecules were allowed to freely move in the unit cell without restrictions following the translating, rotating, inserting, and deleting operators to reach the equilibrium state, while the atoms of MIL-88A(M) were immobile. The interaction between the C and O atoms of the CO2 molecule and the (C, O, H, and M = Al, Ga, Sc, Ti, V) atoms of the MIL-88A(M) was described through the Lennard-Jones and coulombic potentials, between a pair of the ith and jth atoms at the distance of rij, as follows:| |
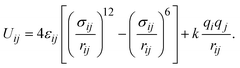 | (2) |
where the force field parameters εij and σij are the Lennard-Jones potential-well depth and diameter, respectively. k is Coulomb's constant. The Lorentz–Berthelot mixing rules were employed to calculate the εij and σij parameters for a pair of dissimilar atomic species.| |
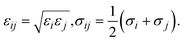 | (3) |
where σi and εi for each atom type of MIL-88A(M) are the generic force field parameters for MOFs (UFF for metals and DREIDING for the other atoms)43,44 and the parameters for CO2 come from the EPM2 model of the universal force field.44–46 For the partial charge qi of the atoms in the unit cell, we first designed the primitive unit cell of MIL-88A(M), then optimized the primitive unit cell size and its geometry structure, calculated the charge density using our vdW-DF calculations, and finally computed the partial point charge of the atoms with the aid of the DDEC6 package.47–50 The cut-off radius for the LJ and coulombic interactions was 13 Å, which was large enough for the convergent results of the GCMC simulations. Using the present force field method and the rigid structure of MIL-88A(M), our previous work31 showed that the gravimetric uptake for M = Fe is in good agreement with the available experiment, where the data is 4.00 mmol g−1 at 303 K and 1 bar. This value is about 19% lower than the experimental value of 4.95 mmol g−1 under the same condition.32 We tested the accuracy of the GCMC simulations against the experimental data for several points and found that the accuracy was approximately 20%. This discrepancy between the calculation and the experiment is acceptable. Furthermore, the EPM2 model was also found to reasonably describe CO2 in another MOF.51
We performed the vdW-DF52 density functional theory calculations using the VASP software53,54 with the revPBE version of the generalized gradient approximation for exchange-correlation energy.55 The plane wave basis set was expanded at the cut-off energy of 700 eV. The ion-valence electron interaction was described by the projector-augmented wave method.56,57 The special k-point mesh of 3 × 3 × 3 following the Monkhorst–Pack scheme58 was used to optimize the geometric structure and calculate the total energy and charge density for MIL-88A(M) and the MIL-88A(M)@CO2 system. The geometric structure was optimized until the force acting on each atom reached 0.001 eV Å−1. We performed both spin-polarized and non-spin-polarized calculations. To increase the convergent speed of the calculations, the Methfessel–Paxton smearing of order 1 with the smearing width of 0.1 eV was used.59
The adsorption energy of the CO2 molecule in the primitive unit cell of MIL-88A(M), according to our vdW-DF calculations, was obtained to elucidate the effects of electronic interaction on its binding strength to MIL-88A(M), as follows:60
| | |
Eads = EgMIL − (EMIL + Eg).
| (4) |
where the total energy of MIL-88A(M) with the adsorbed CO
2 molecule is
EgMIL. The total energy of the clean MIL-88(M) and the isolated CO
2 molecule is
EMIL and
Eg, respectively.
To analyse the information on the interaction between the CO2 molecules and MIL-88A(M), we computed the density of states using the following formula:61
| |
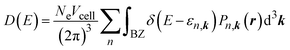 | (5) |
where
Pn,k(
r) = |
φn,k(
r)|
2 is the probability of finding an electron, the electron wavefunction and wavevector are denoted by
φn,k(
r) and
k, and the spin-degeneracy factor and the unit cell volume are
Ne and
Vcell, respectively.
3 Results and discussion
3.1 Preparing primitive unit cell and force field parameters
We previously designed the primitive unit cell of MIL-88A(M),28,30 as shown in Fig. 1a (three-dimensional view) and Fig. 1b (top view). MIL-88A(M) has a three-dimensional hexagonal structure. Each metal node trimer with the chemical formula M3O (including three cyan-colour polyhedra) is connected to three fumarate organic linkers with the chemical formula (–O2C–C2H2–CO2–)3. The primitive unit cell has a = b ≠ c, α = β = 90°, and γ = 120°, where the a, b, and c lattice constants were optimized with our vdW-DF calculations for M = Al and Ga metal substitutions in the present study (for M = Sc, Ti, and V, found in our previous publications30), while the shape of the primitive unit cell was kept fixed with the unchanged α, β, and γ angles. The positions of the atoms in the primitive unit cell were relaxed before performing the optimization of the lattice constants according to the following steps: (1) for each value of c/a ratio, we varied the value of a = b, and then computed the total energy of the primitive unit cell. (2) We fitted the total energy versus the unit cell volume following Murnaghan's equation of state,62,63 where the unit cell volume was calculated by 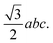 64 The optimized lattice constants for MIL-88A(M) with M = Al and Ga are presented in Table 1. We also calculated the specific surface area (SSA) and pore volume of these MOFs. By comparing the results with that in our previous work,30 we found that the distance dM–O between the metal atom (M) to the oxygen atom (O) and the primitive unit cell volume of MIL-88A(M) follows the order of Sc > Ti > V > Ga > Al and Sc > Ti > Ga ≈ V > Al, while the specific surface area and the pore volume follow the order of Al > Ti > V > Sc > Ga and Al > Ga > Ti ≈ Sc > V, respectively. Notably, the distance and the primitive unit cell volume of MIL-88A(Al) are the smallest; however, its specific surface area and pore volume are the largest, while the distance and the primitive unit cell volume of MIL-88A(Sc) are the largest among the metal substitutions. The obtained dM–O distance, a, b, and c lattice constants, primitive unit cell volume, specific surface area, and pore volume are similar to the computational and experimental values found in the literature.24,65 It is worth emphasizing that these parameters are almost the same for both the spin-polarized and non-spin-polarized vdW-DF calculations in the present work. After obtaining the optimized lattice constants and geometric structure for the primitive unit cell, we calculated the charge density, and then the partial point charges of the atoms of MIL-88A(M). We found that the difference between the partial charges obtained by spin-polarized and non-spin-polarized versions is insignificant. The partial point charges and the force field parameters for the GCMC simulations are given in Table 2. Notably, the Lennard-Jones potential-well depth and diameter of Al and Ga are much larger than that of Sc, Ti, and V. The denotation of the atoms is described in Fig. 2. We use the optimized unit cell of MIL-88A(M) for M = Al and Ga obtained in this work and that for M = Sc, Ti, and V from our previous works30 to investigate the CO2 adsorption and uptake capacities of MIL-88A(M) in the next sections. We must emphasize that although the optimized unit cell for M = Sc, Ti, and V was found in our previous publication, the investigation of the CO2 adsorption and CO2 uptake capacities is completely new for MIL-88A(M) with M = Al, Ga, Sc, Ti, and V. During the discussion, we will also compare the results of this work with the previous theoretical and experimental results for MIL-88A(Fe).31,32
64 The optimized lattice constants for MIL-88A(M) with M = Al and Ga are presented in Table 1. We also calculated the specific surface area (SSA) and pore volume of these MOFs. By comparing the results with that in our previous work,30 we found that the distance dM–O between the metal atom (M) to the oxygen atom (O) and the primitive unit cell volume of MIL-88A(M) follows the order of Sc > Ti > V > Ga > Al and Sc > Ti > Ga ≈ V > Al, while the specific surface area and the pore volume follow the order of Al > Ti > V > Sc > Ga and Al > Ga > Ti ≈ Sc > V, respectively. Notably, the distance and the primitive unit cell volume of MIL-88A(Al) are the smallest; however, its specific surface area and pore volume are the largest, while the distance and the primitive unit cell volume of MIL-88A(Sc) are the largest among the metal substitutions. The obtained dM–O distance, a, b, and c lattice constants, primitive unit cell volume, specific surface area, and pore volume are similar to the computational and experimental values found in the literature.24,65 It is worth emphasizing that these parameters are almost the same for both the spin-polarized and non-spin-polarized vdW-DF calculations in the present work. After obtaining the optimized lattice constants and geometric structure for the primitive unit cell, we calculated the charge density, and then the partial point charges of the atoms of MIL-88A(M). We found that the difference between the partial charges obtained by spin-polarized and non-spin-polarized versions is insignificant. The partial point charges and the force field parameters for the GCMC simulations are given in Table 2. Notably, the Lennard-Jones potential-well depth and diameter of Al and Ga are much larger than that of Sc, Ti, and V. The denotation of the atoms is described in Fig. 2. We use the optimized unit cell of MIL-88A(M) for M = Al and Ga obtained in this work and that for M = Sc, Ti, and V from our previous works30 to investigate the CO2 adsorption and uptake capacities of MIL-88A(M) in the next sections. We must emphasize that although the optimized unit cell for M = Sc, Ti, and V was found in our previous publication, the investigation of the CO2 adsorption and CO2 uptake capacities is completely new for MIL-88A(M) with M = Al, Ga, Sc, Ti, and V. During the discussion, we will also compare the results of this work with the previous theoretical and experimental results for MIL-88A(Fe).31,32
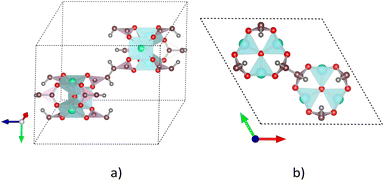 |
| | Fig. 1 Primitive unit cell structure of MIL-88A(M), where M (cyan), O (red), C (brown), and H (grey). The red, green, and blue arrows represent the directions of the a, b, and c dimensions along the x, y, and z axes, respectively. (a) Three-dimensional view. (b) Two-dimensional (top) view. | |
Table 1 Optimized structural parameters for the primitive unit cell of MIL-88A(M)
| MIL-88A(M) |
a = b (Å) |
c (Å) |
dM–O (Å) |
Primitive unit cell volume (Å3) |
SSA (m2 g−1) |
Pore volume (cm3 g−1) |
| Found in ref. 30. |
| Al |
11.284 |
14.599 |
1.775 |
1609.83 |
1326.95 |
0.745 |
| Ga |
11.245 |
14.973 |
1.871 |
1639.65 |
959.41 |
0.571 |
| Sca |
11.165 |
15.315 |
2.020 |
1653.26 |
1102.97 |
0.550 |
| Tia |
11.192 |
15.196 |
1.950 |
1648.36 |
1129.05 |
0.551 |
| Va |
11.187 |
15.122 |
1.904 |
1638.97 |
1119.34 |
0.542 |
Table 2 Lennard-Jones potential parameters42 and partial charges for the atoms of MIL-88A(M) and the CO2 molecule
| Atoms |
ε/kB (K) |
σ (Å) |
Partial charge (e) |
| Al_MOF |
156.00 |
3.91 |
1.75 |
| Ga_MOF |
208.84 |
3.90 |
1.54 |
| Sc_MOF |
9.56 |
2.94 |
2.09 |
| Ti_MOF |
8.55 |
2.83 |
1.90 |
| V_MOF |
8.05 |
2.80 |
1.76 |
| H_MOF |
7.65 |
2.85 |
0.12 |
| C1_MOF |
47.86 |
3.47 |
0.73 |
| C2_MOF |
|
|
−0.18 |
| O1_MOF |
48.16 |
3.03 |
−0.57 |
| O2 (μ3-O) |
|
|
−0.88 |
| C_CO2 (ref. 45 and 46) |
28.129 |
2.757 |
0.6512 |
| O_CO2 (ref. 45 and 46) |
80.507 |
3.033 |
−0.3256 |
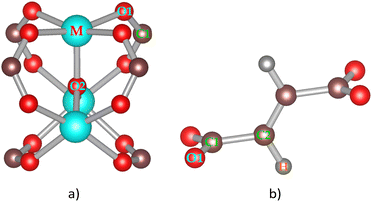 |
| | Fig. 2 Secondary building blocks of MIL-88A(M) with M = Al, Ga, Sc, Ti, and V: metal oxide node (a) and fumarate linker (b). | |
3.2 CO2 capture capacity in MIL-88A(M)
Using the primitive unit cell in Section 3.1, we successively repeated 3 × 3 × 2 times along the x, y, and z directions, and then exported data on the obtained supercell size, its atomic positions, and the force field parameters (Table 2) to the RASPA package for performing the GCMC simulations. Fig. 3a and b show the gravimetric and volumetric CO2 uptake for pressures up to 50 bar, respectively. The dashed and solid lines indicate the excess and total uptake, respectively. We found that the CO2 uptake is enhanced quickly at low pressures (below 10 bar), then increases slowly to the maximum value at 50 bar for the total gravimetric and volumetric CO2 uptake (the solid lines), and to the maximum value at 25 bar for the excess gravimetric and volumetric CO2 uptake (the dashed lines). Fig. 3a exhibits that the excess and total gravimetric uptake for M = Al are clearly distinguished over the other metal substitutions, while the excess and total volumetric uptake for Al are close to that for Ga (Fig. 3b). The zoom-in of the excess isotherms at low pressures, as presented in Fig. 3c and d, reveals the CO2 capture ability of the MOFs based on adsorption phenomena. We found that below 0.2 bar, Sc is the best for both excess gravimetric and volumetric adsorption isotherms; however, above 0.2 bar, the best candidates are Al and Ga for excess gravimetric and volumetric uptake, respectively. The capture ability of MIL-88A(M) can be explained by examining the relationship among the uptake, ionic radius, specific surface area, and pore volume, as analysed in Fig. 7 and 8 in the subsequent section.
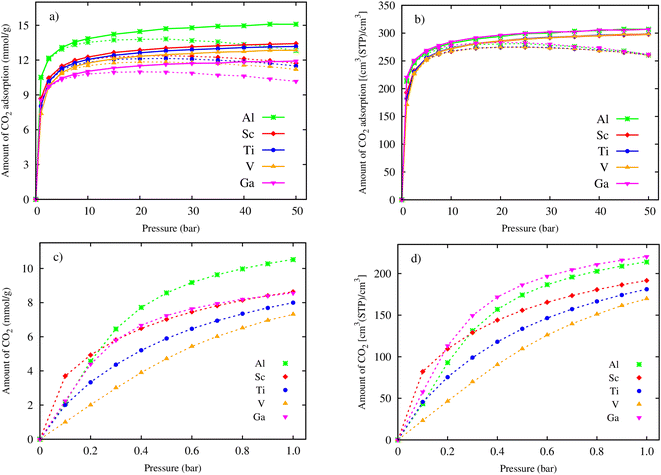 |
| | Fig. 3 Excess (dashed lines) and absolute (solid lines) CO2 adsorption isotherms of MIL-88A(M), where M = Al, Ga, Sc, Ti, and V: (a) gravimetric uptake and (b) volumetric uptake for pressures of up to 50 bar. Zoom-in for gravimetric (c) and volumetric (d) CO2 adsorption isotherms at low pressures (0–1.0 bar). | |
The maximum excess adsorption isotherms at the saturated pressure of 25 bar for M = Al, Sc, Ti, and V, and 20 bar for M = Ga, and the maximum absolute uptake at 50 bar are displayed in Table 3. We found that the excess gravimetric uptake (in columns 2 and 4) and the total gravimetric uptake (in columns 3 and 5) of CO2 follow the order of Al > Sc > Ti > V > Ga. Noticeably, the excess and absolute volumetric uptake show a different order of Ga > Al > Sc ≈ Ti ≈ V. The reason for this difference may be that the excess uptake is attributed to the adsorption phenomenon of CO2 on the surface of MIL-88A. However, besides the adsorption effects, the absolute uptake also considers the storage capacity within the pore volume, which is influenced by pressure. Under pressure, CO2 molecules can also be compelled to enter the available space within the pore volume. We found that replacing the metals improved the excess and total uptake for both gravimetric and volumetric terms significantly compared to that obtained for MIL-88A(Fe).31
Table 3 Maximum excess (at 25 bar) and absolute (at 50 bar) CO2 capture capacity in MIL-88A(M) at ambient temperature (298 K). The ionic radii of the metal atoms in their +3 oxidation state66
| MIL-88A(M) |
Gravimetric uptake (mmol g−1) |
Gravimetric uptake (mg g−1) |
Volumetric uptake (cm3 (STP) cm−3) |
Metal ionic radius |
| Excess |
Absolute |
Excess |
Absolute |
Excess |
Absolute |
| Maximum excess uptake for MIL-88A(Ga) at 20 bar. |
| M = Al |
13.82 |
15.09 |
608.20 |
663.99 |
281.16 |
306.95 |
0.68 |
| M = Sc |
12.38 |
13.42 |
544.67 |
590.44 |
274.80 |
297.90 |
0.89 |
| M = Ti |
12.15 |
13.18 |
534.43 |
579.80 |
275.23 |
298.62 |
0.81 |
| M = V |
11.83 |
12.85 |
520.53 |
565.48 |
274.56 |
298.27 |
0.78 |
| M = Ga |
10.99a |
11.92 |
483.47a |
524.45 |
283.01a |
307.00 |
0.76 |
Furthermore, we also calculated the excess CO2 adsorption uptake in mmol g−1 as a function of temperature. Fig. 4 shows that the excess isotherms monotonically decrease when the temperature increases. Also, increasing the pressure to the saturated value (20 bar for M = Ga and 25 bar for the others) enhances the excess uptake by about three folds that of MIL-88A(Fe) at the low pressure of 1 bar,31 and all the metal substitutions give rise to a higher excess uptake of CO2 than that of Fe under the saturated pressure condition.31 Particularly, the excess uptake is higher by 0.93, 1.25, 1.48, and 2.92 mmol g−1 for MIL-88A (V, Ti, Sc, and Al) compared to 10.9 mmol g−1 (theoretical value at 303 K, 25 bar)31 and 4.95 mmol g−1 (experimental value at 303 K, 1 bar)32 for MIL-88A(Fe).
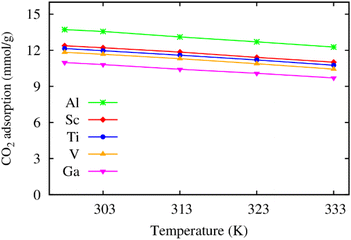 |
| | Fig. 4 Temperature dependence of the excess gravimetric loading of CO2 in MIL-88A(M) at the saturated pressure of 20 bar for M = Ga and 25 bar for the other metal substitutions. | |
3.3 Adsorption sites and strength of CO2 in MIL-88A(M)
To understand the stable adsorption sites for the CO2 molecule at the vdW-DF level in the optimized structure of the primitive unit cell of MIL-88A(M), we designed a CO2 molecule with various initial positions and configurations. We classified the adsorption positions into metal, hollow, and linker sites, as shown in Fig. 5, respectively. The metal site is where the CO2 molecule can adsorb on the top of a metal atom. The hollow and linker sites are in the middle region of four oxygen atoms and the fumarate linker, respectively. After that, we performed the geometrical structure relaxation of the designed CO2@MIL-88A(M) system to obtain its optimized structure, and then calculated the adsorption energy of the CO2 molecule following definition (4). The favourable side-on and end-on configurations of CO2 on the metal, hollow, and linker positions are obtained and presented in Fig. 5, where the shortest average distance from the nearest atoms of CO2 to the atoms of MIL-88A(M) is d1, d2, d3, d4, d5, and d6 for the side-on metal, end-on metal, side-on hollow, end-on hollow, side-on linker, and end-on linker, respectively. The detailed value of the distances is listed in Table 4. We found that for each adsorption site, i.e., metal, hollow, and linker, the average distance is shorter for the CO2 molecule in the end-on configuration than in the side-on configuration. The distance for the side-on configuration follows the order of metal < hollow < linker, i.e., d1 < d3 < d5. Particularly, the distance d2 is the shortest among the end-on configurations on the metal, hollow, and linker positions, i.e., d2 ≪ d4 ≈ d6. The geometry structure of the CO2 adsorption sites from the GCMC simulations, as presented in Fig. 6, shows that the CO2 molecules prefer to gather near the metal sites (presented by the frames) more than the other sites (presented by coloured spots). Furthermore, the distribution of the CO2 molecules is more dispersive in MIL-88A (Al and Ga), but more localized in MIL-88A (Sc, Ti, and V).
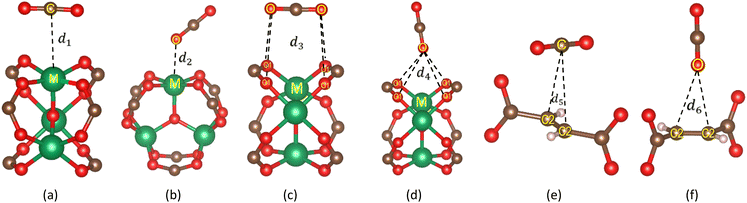 |
| | Fig. 5 Favourable adsorption sites and configurations of the CO2 molecule in MIL-88A(M) with M = Al, Ga, Sc, Ti, and V, where M (green), O (red), C (brown), and H (light pink). (a) Side-on metal. (b) End-on metal. (c) Side-on hollow. (d) End-on hollow. (e) Side-on linker. (f) End-on linker | |
Table 4 Bond distances (d in Å) between the CO2 molecule and the nearest atoms of MIL-88A(M) with M = Al, Ga, Sc, Ti, and V for the most favourable adsorption configuration of the CO2 molecule
| CO2@MIL-88A(M) |
M = Al |
M = Ga |
M = Sc |
M = Ti |
M = V |
| Metal |
Side-on, d1 |
3.27 |
3.39 |
3.19 |
3.24 |
3.25 |
| End-on, d2 |
2.44 |
2.46 |
2.45 |
2.49 |
2.34 |
| Hollow |
Side-on, d3 |
3.43 |
3.45 |
3.39 |
3.46 |
3.45 |
| End-on, d4 |
3.06 |
3.09 |
3.12 |
3.10 |
3.15 |
| Linker |
Side-on, d5 |
3.51 |
3.52 |
3.55 |
3.51 |
3.53 |
| End-on, d6 |
3.07 |
3.00 |
3.10 |
3.11 |
3.06 |
 |
| | Fig. 6 Visualization of CO2 adsorption in MIL-88A(M) at 1 bar. At this low pressure, the distribution of gas molecules distributed within the pores of the MOF is primarily governed by adsorption phenomena. (a) CO2@MIL-88A(Al). (b) CO2@MIL-88A(Gc). (c) CO2@MIL-88A(Sc). (d) CO2@MIL-88A(Ti). (e) CO2@MIL-88A(V). | |
According to formula (4), the more negative the adsorption energy, the more favourable the adsorption configuration of the CO2 molecule. Table 5 shows the adsorption energy together with the magnetic moment in units of magneton Bohr per primitive unit cell. It must be noted that we performed both spin-polarized and non-spin-polarized vdW-DF calculations and compared both results to find the most stable configuration of the CO2 molecule for each adsorption site. In Table 5, the system without the information of magnetic moment is the one that has no magnetic property. We found that the CO2 molecule adsorbed on the metal site is much more stable with the end-on configuration than the side-on configuration. Alternatively, for adsorption on the hollow and linker sites, the side-on configuration is more favourable than the end-on configuration. Among the adsorption sites and configurations, we found that the metal end-on structure is the best, where the favourability of the metal substitutions follows the order of Ti > V > Sc > Ga ≈ Al. However, regarding the overall effect of the metal substitutions based on all the adsorption sites, the average adsorption energy over six configurations of the CO2 molecule for each metal shows that the adsorption favourability follows the order of Ti > Sc > V > Ga ≈ Al. This implies that M = Al and Ga cause the weakest adsorption strength of the CO2 molecule at the metal site. Therefore, as shown in Fig. 6, we found that the distribution of the CO2 molecules is more dispersive in MIL-88A (Al and Ga). However, it is very interesting to emphasize that they are the best among the samples for the gravimetric and volumetric uptake, as analysed above, respectively.
Table 5 Adsorption energy (Eads in kJ mol−1) of CO2 in MIL-88A(M) with M = Al, Sc, Ti, V, and Ga. The magnetic moment values (in units of Bohr magnetons per primitive unit cell) are provided in parentheses
| CO2@MIL-88A(M) |
M = Al |
M = Sc |
M = Ti |
M = V |
M = Ga |
| Metal |
Side-on |
−7.40 (1.99) |
−45.44 |
−14.82 |
−8.22 (14.00) |
−8.50 (1.94) |
| End-on |
−44.62 (1.97) |
−46.61 (2.00) |
−62.63 |
−48.84 (13.83) |
−44.95 (1.89) |
| Hollow |
Side-on |
−28.03 |
−37.19 |
−53.13 |
−39.23 |
−37.95 |
| End-on |
−24.76 (1.99) |
−23.68 |
−33.62 |
−25.08 |
−22.60 |
| Linker |
Side-on |
−26.75 (1.99) |
−27.72 |
−31.96 |
−27.18 (14.00) |
−25.24 (1.95) |
| End-on |
−25.75 (1.99) |
−13.97 |
−22.23 |
−13.87 (14.00) |
−15.63 (1.96) |
| Average Eads for 6 sites |
−26.22 |
−32.44 |
−36.40 |
−27.07 |
−25.81 |
Here, we clarify the relationship between the excess and total uptake with macroscopic parameters or structural characteristics of MIL-88A(M), such as specific surface area, pore volume, and metal ionic radius. Fig. 7a shows that although the trend is not monotonic in the middle range of the curve, the excess and total gravimetric uptake proximately increase as the specific surface area increases. MIL-88A(Ga) and MIL-88A(Al) with the smallest and largest surface area have the lowest and highest excess and total gravimetric uptake of CO2, as discussed in the previous part, respectively. Fig. 7b exhibits that the excess and total volumetric uptake in MIL-88A(Ga) and MIL-88A(Al) have step behaviours, where M = Ga and Al with higher pore volumes can improve about ten units of the volumetric isotherm compared to M = Sc, Ti, and V. Besides, according to Fig. 7c and d, we found that the gravimetric uptake does not have a close correlation, while the volumetric uptake has a good correlation with the metal ionic radius66 (see Table 3). Notably, as shown in Fig. 7c, the excess and total gravimetric uptake of MIL-88A(Al) are large, while the Al ionic radius is small. This data point is outside the increasing trend of the gravimetric curves. However, as shown in Fig. 7d, Ga and Al with smaller ionic radii have better volumetric uptake than Sc, Ti, and V with larger ionic radii. According to the above-mentioned analysis, we somehow found a simple correlation among the volumetric uptake, pore volume, and metal ionic radius, while the gravimetric uptake is correlated with only the specific surface area. Indeed, Fig. 8 shows that an increase in the metal ionic radius causes a decrease in pore volume but does not show a simple trend with the specific surface area. We guess that the specific surface area is influenced not only by the ionic radius but also by a variety of other parameters in a more complex manner. These parameters include the electronic effects of the linkers, the size of the linkers, and the electronic properties of the metals.
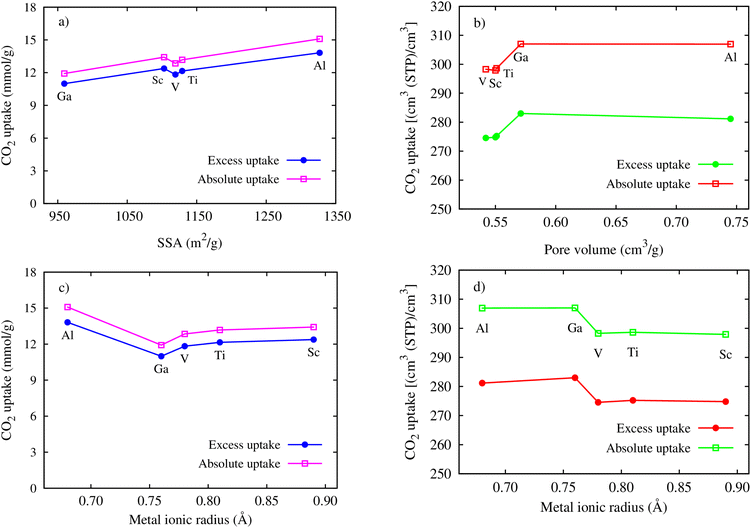 |
| | Fig. 7 Relationship between the maximum gravimetric uptakes and SSA (a), the metal ionic radii (c), the maximum volumetric uptakes and pore volume (b), and the metal ionic radii (d). | |
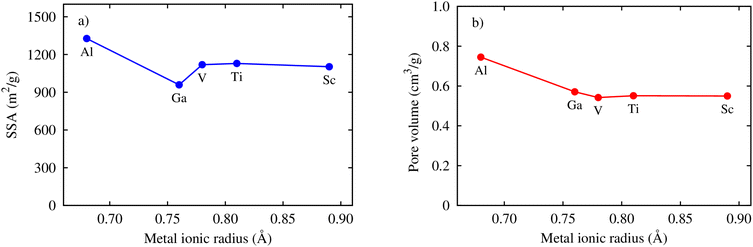 |
| | Fig. 8 Relationship between the specific surface area (SSA) and (a) the pore volume (b) the metal ionic radii. | |
3.4 Electronic structure properties
The atomic point charges calculated by the Bader partition technique67,68 can expose the interaction nature between the CO2 molecule and MIL-88A(M), focusing on the effects of metal substitution. The atomic point charge for the CO2@MIL-88A(M) systems was calculated in three steps, as follows: (1) computing the charge density by the vdW-DF method, (2) computing the atomic point charge from the charge density using the Bader partition technique, and (3) deducting the atomic neutral charge from the atomic point charges obtained in step (2). The Bader point charges in Table 6 show that the C and O atoms of the adsorbed CO2 molecule and MIL-88A(M) of the CO2@MIL-88A(M) systems always lose and gain a negative charge (e−), while the metal (M) and hydrogen (H) atoms always donate and accumulate negative charge, respectively. However, the total charge of the adsorbed CO2 molecule is negligible because it is less than the error (0.005e−) of the charge calculations for M = Al and Sc, while it is a small value for M = Ti, V, and Ga. This result implies that the interaction between the CO2 molecule and MIL-88A (Al and Sc) is electrostatic attraction, while it is the weak charge exchange between the CO2 molecule and MIL-88A (Ti, V, and Ga). In the weak charge exchange, the CO2 molecule donates the charge in e− units to MIL-88A (Ti, V, and Ga) with the highest charge donation from the adsorbed CO2 molecule to MIL-88A(Ga). According to the charge exchange analysis, the interaction between the adsorbate and the adsorbent can occur in two distinct ways, i.e., with charge exchange and without charge exchange. In the case of charge exchange, the interaction is strong enough to facilitate the transfer of charge between the adsorbate and the adsorbent. Conversely, when there is no charge exchange, the interaction is insufficient to transfer charge, but the charge clouds rearrange themselves to create local charge dipoles within the structures of both the adsorbate and the adsorbent, thereby establishing a connection between the two via electrostatic interaction.
Table 6 Bader point charges (in units of e−) for the atoms in the CO2@MIL-88A(M) systems with M = Al, Sc, Ti, V, and Ga at the most stable adsorption site and configuration of the CO2 molecule. The error in charge calculation is 0.005 e−. Atomic indices are shown in Fig. 2. The plus and minus signs indicate the negative charge gain and loss, respectively
| CO2@MIL-88A(M) |
M = Al |
M = Sc |
M = Ti |
M = V |
M = Ga |
| 1C_CO2 |
−2.135 |
−2.077 |
−2.089 |
−2.084 |
−2.082 |
| 2 O_CO2 |
+2.136 |
+2.080 |
+2.079 |
+2.066 |
+2.057 |
| CO2 |
+0.001 |
+0.003 |
−0.010 |
−0.018 |
−0.025 |
| 6 M_MIL |
−14.895 |
−12.161 |
−10.552 |
−9.982 |
−10.214 |
| 12H_MIL |
+0.175 |
+0.206 |
+0.156 |
+0.054 |
+0.119 |
| 12C1_MIL |
−17.492 |
−18.401 |
−17.784 |
−18.558 |
−17.939 |
| 12C2_MIL |
−0.863 |
−0.731 |
−0.976 |
−0.690 |
−0.879 |
| 2 O1_MIL |
+29.816 |
+28.622 |
+27.081 |
+27.145 |
+26.695 |
| 24 O2_MIL |
+3.258 |
+2.462 |
+2.086 |
+2.049 |
+2.243 |
| MIL-88A(M) |
−0.001 |
−0.003 |
+0.010 |
+0.018 |
+0.025 |
The charge density difference (Fig. 9) shows that there are always positive charge clouds in the interface region between the adsorbed CO2 molecule and MIL-88A(M) for the side-on adsorption configurations at the metal, hollow, and linker (Fig. 9a, c, and e) of the CO2 molecule, while negative charge clouds for the end-on configurations at the hollow and linker (Fig. 9d and f) except for the end-on configuration of the CO2 molecule at the metal site (Fig. 9b), respectively. The charge clouds in the interface region become an adhesive glue to bind with the opposite charge clouds of the CO2 molecule and MIL-88A(M), establishing the interaction of the CO2 molecule and the MIL-88A(M) structure by forming charge dipoles.
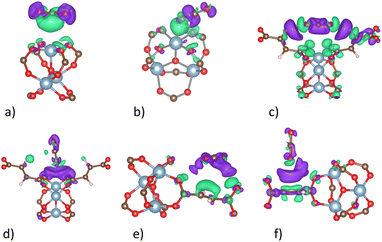 |
| | Fig. 9 Charge density difference of the CO2@MIL-88A(Al) system at the favourable adsorption sites. Green and violet colours describe the positive and negative charge clouds, respectively. The isosurface value is 0.0003 e Bohr−3 isosurface. A similar charge cloud distribution was also found for MIL-88A (Sc, Ti, Vi, and Ga). (a) Side-on metal. (b) End-on metal. (c) Side-on hollow. (d) End-on hollow. (e) Side-on linker. (f) End-on linker. | |
The total electronic density of states (DOS) for the CO2 molecule in the isolated and adsorbed states is presented in Fig. 10. This figure shows that in the energy range below 10 eV, there are five main DOS peaks (the black curve) for the isolated CO2 molecule, including 3σg, 2πu, 1πg, 1πu/2σu, and 2σg located at around 8.0, 7.5, 0.0, −4.0, and −5.0 eV, respectively.69 The adsorption of the CO2 molecule in the MIL-88A(M) structure shifts these peaks downward to lower energy levels by about 5.0 eV. However, the new position of the 2πu peak almost remains unoccupied (above the Fermi level), which agrees with the Bader point charge analysis, where there is only weak or no charge exchange between the adsorbed CO2 molecule and the MIL-88A(M). It must be emphasized that if there are significant charge exchanges, a large portion of the occupied and unoccupied states will cross the Fermi level to become the unoccupied and occupied states, respectively.
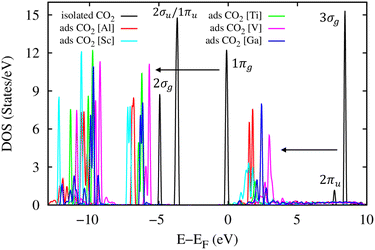 |
| | Fig. 10 Total electronic density of states for the CO2 molecule in the isolated and adsorbed states. The Fermi level is set to 0 eV. | |
The atomic-projected electronic density of states (the left panels in Fig. 11) displays that the DOS of metal atoms and the O and C atoms dominate around the Fermi level for M = (Sc, Ti, V, and Ga) and M = Al, respectively. However, in the negative energy range below the Fermi level, the DOS of the O and C atoms of MIL-88A(M) is more dominant than the DOS of the metal atoms for all the metal substitutions. The attraction between the DOS of MIL-88A(M) and that of the CO2 molecule is the reason for the interaction between MIL-88A(M) and the CO2 molecule. The occupied states of MIL-88A(M) near the Fermi level attract the unoccupied states, the 3σg and 2πu peaks, of the CO2 molecule and shift these peaks closer to the Fermi level, causing the peak resonance between the 3σg and 2πu peaks of the CO2 molecule and the DOS peaks of MIL-88A(M) at the energy of around 2.0 eV. The resonance is a partial overlapping of the DOS states of the metal, C, and O atoms for M = Al and Ga (Fig. 11a1 and e1) and complete overlapping of the DOS states of the metal, C, and O atoms for M = Sc, Ti, and V (Fig. 11b1–d1) with the 3σg and 2πu peaks at 2.0 eV, respectively. Besides, resonance is also found at around −6.5 eV due to the overlapping between the 1πg peak of the adsorbed CO2 molecule and the DOS of MIL-88A(M). However, the overlapping level between the DOS peaks of MIL-88A (Sc, Ti, and V) and that of the adsorbed CO2 molecule is higher than that between the DOS peaks of MIL-88A (Al and Ga) and the 3σg, 2πu, and 1πg peaks of the adsorbed CO2 molecule. Therefore, the adsorption energy of the CO2 molecule at the metal site is greater on MIL-88A (Sc, Ti, and V) than on MIL-88A (Al and Ga), as shown in Table 5.
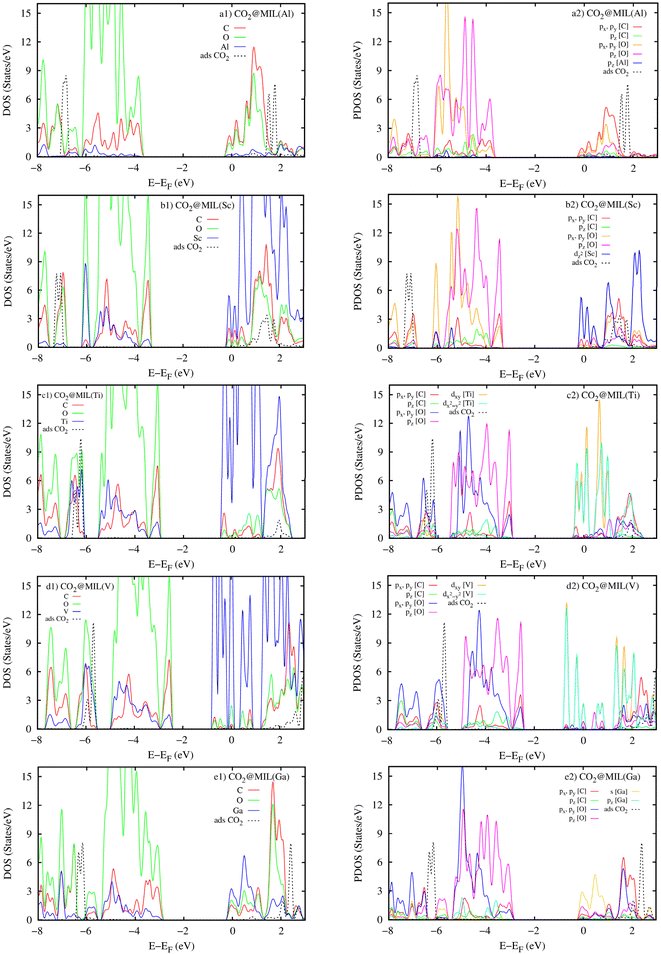 |
| | Fig. 11 Atomic projected density of states (the left panels) and orbital projected density of states (the right panels) for the CO2@MIL-88A(M) systems with M = Al, Sc, Ti, V, and Ga. | |
The orbital-projected DOS (the right panels of Fig. 11) explains the detailed interaction between the orbitals of MIL-88A(M) and that of the adsorbed CO2 molecule. We found that the 3σg, 2πu, and 1πg peaks of the adsorbed CO2 molecule have main interactions with the O and C px and py orbitals of MIL-88A(M), respectively. Noticeably, the Sc dz2, (Ti and V) dxy and dx2−y2, Ga s orbitals of the metals also have a great contribution to the interaction between MIL-88A(M) and the adsorbed CO2 molecule.
4 Conclusions
We explored the effects of Al, Sc, Ti, V, and Ga substitutions in the structure of MIL-88A(M) on CO2 capture using vdW-DF density functional theory calculations in combination with grand canonical Monte Carlo simulations. We found that MIL-88A(Al) is the best candidate for both gravimetric and volumetric CO2 uptake, while MIL-88 (Ga) is the best for volumetric CO2 uptake only. The analysis exhibited that the excess and total gravimetric uptake have a loose connection with the specific surface area, i.e., they increase as the surface area increases. However, the excess and total volumetric uptake showed a close correlation with the pore volume of MIL-88A(M) and the metal ionic radius. The smaller the metal ionic radius, the larger the pore volume of MIL-88A(M), and the better the excess and volumetric CO2 uptake. The interaction between the CO2 molecule and MIL-88A(M) is due to the electrostatic attraction for M = Al and Sc, and the weak charge exchange for M = Ti, V, and Ga. The density of states showed that this interaction is established mainly due to the 3σg, 2πu, and 1πg peaks of the adsorbed CO2 molecule and the O and C px and py orbitals of MIL-88A(M), respectively. Besides, there are also significant contributions from the Sc dz2, (Ti and V) dxy and dx2−y2, Ga s orbitals, while Al has negligible contribution to the interaction.
Data availability
The data supporting this article has been included as part of this manuscript.
Author contributions
Conceptualization (DNS), investigation (NTXH, DNS), formal analysis (DNS), resources (DNS, VC), supervision (DNS, VC), validation (DNS), visualization (NTXH), writing manuscript (DNS), reviewing and editing (DNS, NTXH, VC).
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
This research is funded by Vietnam National University Ho Chi Minh City (VNU-HCM) under grant number VL2022-20-01.
References
- S. E. M. Elhenawy, M. Khraisheh, F. Almomani and G. Walker, Catalysts, 2020, 10, 1–33 CrossRef
 .
. - D. Y. C. Leung, G. Caramanna and M. M. Maroto-valer, Renewable Sustainable Energy Rev., 2014, 39, 426–443 CrossRef CAS
 .
. - J. Y. Jung, F. Karadas, S. Zulqar, E. Deniz, S. Aparicio, M. Atilhan, C. T. Yavuz and S. M. Han, Phys. Chem. Chem. Phys., 2013, 15, 14319–14327 RSC
 .
. - W. S. Drisdell, R. Poloni, T. M. McDonald, T. A. Pascal, L. F. Wan, C. Das Pemmaraju, B. Vlaisavljevich, S. O. Odoh, J. B. Neaton, J. R. Long, D. Prendergast and J. B. Kortright, Phys. Chem. Chem. Phys., 2015, 17, 21448–21457 RSC
 .
. - A. J. Howarth, Y. Liu, P. Li, Z. Li, T. C. Wang, J. T. Hupp and O. K. Farha, Nat. Rev. Mater., 2016, 1, 1–15 Search PubMed
 .
. - T. T. T. Huong, P. N. Thanh, N. T. X. Huynh and D. N. Son, VNU J. Sci. Math. –Phys., 2016, 32, 67–85 Search PubMed
 .
. - Y. Qian, F. Zhang, D. J. Kang and H. Pang, Energy Environ. Mater., 2023, 6, e12414 CrossRef CAS
 .
. - M. Ding, R. W. Flaig, H.-L. Jiang and O. M. Yaghi, Chem. Soc. Rev., 2019, 48, 2783–2828 RSC
 .
. - M. Younas, M. Rezakazemi and M. Daud, et al., Prog. Energy Combust. Sci., 2020, 80, 100849 CrossRef
 .
. - S. Mutyala, M. Jonnalagadda, H. Mitta and R. Gundeboyina, Chem. Eng. Res. Des., 2019, 143, 241–248 CrossRef CAS
 .
. - C. Chen, X. Feng, Q. Zhu, R. Dong, R. Yang, Y. Cheng and C. He, Inorg. Chem., 2019, 58, 2717–2728 CrossRef CAS PubMed
 .
. - M. Sevilla and A. B. Fuertes, Energy Environ. Sci., 2011, 4, 1765–1771 RSC
 .
. - D. Britt, H. Furukawa, B. Wang, T. G. Glover and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20637–20640 CrossRef CAS PubMed
 .
. - W. L. Queen, M. R. Hudson, E. D. Bloch, J. A. Mason, M. I. Gonzalez, J. S. Lee, D. Gygi, J. D. Howe, K. Lee, T. A. Darwish, M. James, V. K. Peterson, S. J. Teat, B. Smit, J. B. Neaton, J. R. Long and C. M. Brown, Chem. Sci., 2014, 5, 4569–4581 RSC
 .
. - O. K. Farha, A. Özgür Yazaydın, I. Eryazici, C. D. Malliakas, B. G. Hauser, M. G. Kanatzidis, S. T. Nguyen, R. Q. Snurr and J. T. Hupp, Nat. Chem., 2010, 2, 944–948 CrossRef CAS PubMed
 .
. - H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. O. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428 CrossRef CAS PubMed
 .
. - X. Sun, J. Gu, Y. Yuan, C. Yu, J. Li, H. Shan, G. Li and Y. Liu, Inorg. Chem., 2019, 58, 7480–7487 CrossRef CAS PubMed
 .
. - N. Li, Z. Chang, H. Huang, R. Feng, W.-W. He, M. Zhong, D. G. Madden, M. J. Zaworotko and X.-H. Bu, Small, 2019, 15, 1900426 CrossRef PubMed
 .
. - Z. Hu, Y. Wang, B. B. Shah and D. Zhao, Adv. Sustainable Syst., 2019, 3, 1800080 CrossRef
 .
. - A. M. Fracaroli, H. Furukawa, M. Suzuki, M. Dodd, S. Okajima, F. Gándara, J. A. Reimer and O. M. Yaghi, J. Am. Chem. Soc., 2014, 136, 8863–8866 CrossRef CAS PubMed
 .
. - Z. L. Ma, P. X. Liu, Z. Y. Liu, J. J. Wang, L. B. Li and L. Tian, Inorg. Chem., 2021, 60, 6550–6558 CrossRef CAS PubMed
 .
. - P. L. Llewellyn, S. Bourrelly, C. Serre, A. Vimont, M. Daturi, L. Hamon, G. De Weireld, J. Chang, D. Hong, Y. K. Hwang and S. H. Jhung, Langmuir, 2008, 24, 7245–7250 CrossRef CAS PubMed
 .
. - P. Horcajada, F. Salles, S. Wuttke, T. Devic, D. Heurtaux, A. Vimont, M. Daturi, O. David, E. Magnier, N. Stock, Y. Filinchuk, D. Y. Popov, C. Riekel, G. Férey, C. Serre, G. Maurin and D. Popov, J. Am. Chem. Soc., 2011, 133, 17839–17847 CrossRef CAS PubMed
 .
. - S. Surblé, C. Serre, C. Mellot-Draznieks, F. Millange, G. Férey, S. Surble, C. Serre, C. Mellot-Draznieks, F. Millange and G. Ferey, Chem. Commun., 2006, 284–286 RSC
 .
. - S. N. Kim, C. G. Park, B. K. Huh, S. H. Lee, C. H. Min, Y. Y. Lee, Y. K. Kim, K. H. Park and Y. Bin Choy, Acta Biomater., 2018, 79, 344–353 CrossRef CAS PubMed
 .
. - J. Wang, J. Wan, Y. Ma, Y. Wang, M. Pu and Z. Guan, RSC Adv., 2016, 6, 112502–112511 RSC
 .
. - W.-T. Xu, L. Ma, F. Ke, F.-M. Peng, G.-S. Xu, Y.-H. Shen, J.-F. Zhu, L.-G. Qiu and Y.-P. Yuan, Dalton Trans., 2014, 43, 3792–3798 RSC
 .
. - N. T. X. Huynh, V. Chihaia and D. N. Son, J. Mater. Sci., 2019, 54, 3994–4010 CrossRef
 .
. - N. T. X. Huynh, O. M. Na, V. Chihaia and D. N. Son, RSC Adv., 2017, 7, 39583–39593 RSC
 .
. - N. T. X. Huynh, V. Chihaia and D. N. Son, Adsorption, 2020, 26, 509–519 CrossRef CAS
 .
. - N. T. X. Huynh, O. K. Le, T. P. Dung, V. Chihaia and D. N. Son, RSC Adv., 2023, 13, 15606–15615 RSC
 .
. - S. Wongsakulphasatch, W. Kiatkittipong, J. Saupsor, J. Chaiwiseshphol, P. Piroonlerkgul, V. Parasuk and S. Assabumrungrat, Greenhouse Gases:Sci. Technol., 2016, 7, 383–394 CrossRef
 .
. - B. Xue, L. Du, J. Jin, H. Meng and J. Mi, Appl. Surf. Sci., 2021, 564, 150404 CrossRef CAS
 .
. - M. Govarthanan, R. Mythili, W. Kim, S. Alfarraj and S. A. Alharbi, J. Hazard. Mater., 2021, 414, 125522 CrossRef CAS PubMed
 .
. - X.-H. Yi, H. Ji, C.-C. Wang, Y. Li, Y.-H. Li, C. Zhao, A. Wang, H. Fu, P. Wang, X. Zhao and W. Liu, Appl. Catal., B, 2021, 293, 120229 CrossRef CAS
 .
. - D. Wang, R. Huang, W. Liu, D. Sun and Z. Li, ACS Catal., 2014, 4, 4254–4260 CrossRef CAS
 .
. - L. Mitchell, B. Gonzalez-Santiago, J. P. S. Mowat, M. E. Gunn, P. Williamson, N. Acerbi, M. L. Clarke and P. A. Wright, Catal. Sci. Technol., 2013, 3, 606–617 RSC
 .
. - Y. Jiao, Z. Li, Y. Ma, G. Zhou, S. Wang and G. Lu, AIP Adv., 2017, 7, 085009 CrossRef
 .
. - B. E. Keshta, H. Yu and L. Wang, Sep. Purif. Technol., 2023, 322, 124301 CrossRef CAS
 .
. - A. L. Myers and P. A. Monson, Langmuir, 2002, 18, 10261–10273 CrossRef CAS
 .
. - Y. Basdogan and S. Keskin, CrystEngComm, 2014, 17, 261–275 RSC
 .
. - D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101 CrossRef CAS
 .
. - S. L. Mayo, B. D. Olafson and W. A. Goddard III, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS
 .
. - A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS
 .
. - J. G. Harris and K. H. Yungt, J. Phys. Chem., 1995, 99, 12021–12024 CrossRef CAS
 .
. - K. Makrodimitris, G. K. Papadopoulos and D. N. Theodorou, J. Phys. Chem. B, 2001, 105, 777–788 CrossRef CAS
 .
. - T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC
 .
. - N. G. Limas and T. A. Manz, RSC Adv., 2016, 6, 45727–45747 RSC
 .
. - T. A. Manz, RSC Adv., 2017, 7, 45552–45581 RSC
 .
. - N. G. Limas and T. A. Manz, RSC Adv., 2018, 8, 2678–2707 RSC
 .
. - I. Erucar and S. Keskin, Ind. Eng. Chem. Res., 2013, 52, 3462–3472 CrossRef CAS
 .
. - M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed
 .
. - G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
 .
. - G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
 .
. - Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS
 .
. - P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
 .
. - G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys.B, 1999, 59, 1758–1775 CrossRef CAS
 .
. - H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef
 .
. - M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed
 .
. - D. N. Son, P. N. Thanh, N. D. Quang, K. Takahashi and M. P. Pham-Ho, J. Appl. Electrochem., 2017, 47, 747–754 CrossRef CAS
 .
. - L. Lodeiro and T. Rauch, Comput. Phys. Commun., 2022, 277, 108384 CrossRef CAS
 .
. - F. D. Murnaghan, Finite Deformation of an Elastic Solid, Wiley, New York, 1st edn., 1951 Search PubMed
 .
. - N. T. Xuan Huynh, V. T. Ngan, N. T. Yen Ngoc, V. Chihaia and D. N. Son, RSC Adv., 2024, 14, 19891–19902 Search PubMed
 .
. - O. K. Le, V. Chihaia, V. Van On and D. N. Son, RSC Adv., 2021, 11, 8033–8041 RSC
 .
. - Z. U. Zango, N. S. Sambudi, K. Jumbri, N. H. H. Abu Bakar and B. Saad, IOP Conf. Ser.: Earth Environ. Sci., 2020, 549, 12061 CrossRef
 .
. - R. D. Shannon, Acta Crystallogr., 1976, A32, 751–767 CrossRef CAS
 .
. - P. Thi Hong Hoa, V. Chihaia, O. Kim Le, P. T. Hai, D. L. Quan, H. T. Thanh and D. N. Son, Phys. Chem. Chem. Phys., 2022, 24, 20491–20505 RSC
 .
. - G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef
 .
. - D. N. Son, T. T. Thuy Huong and V. Chihaia, RSC Adv., 2018, 8, 38648–38655 RSC
 .
.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Viorel Chihaia
*ab,
Viorel Chihaia c and
Nguyen Thi Xuan Huynh
c and
Nguyen Thi Xuan Huynh *d
*d
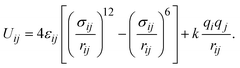
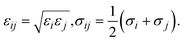
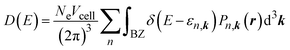
 64 The optimized lattice constants for MIL-88A(M) with M = Al and Ga are presented in Table 1. We also calculated the specific surface area (SSA) and pore volume of these MOFs. By comparing the results with that in our previous work,30 we found that the distance dM–O between the metal atom (M) to the oxygen atom (O) and the primitive unit cell volume of MIL-88A(M) follows the order of Sc > Ti > V > Ga > Al and Sc > Ti > Ga ≈ V > Al, while the specific surface area and the pore volume follow the order of Al > Ti > V > Sc > Ga and Al > Ga > Ti ≈ Sc > V, respectively. Notably, the distance and the primitive unit cell volume of MIL-88A(Al) are the smallest; however, its specific surface area and pore volume are the largest, while the distance and the primitive unit cell volume of MIL-88A(Sc) are the largest among the metal substitutions. The obtained dM–O distance, a, b, and c lattice constants, primitive unit cell volume, specific surface area, and pore volume are similar to the computational and experimental values found in the literature.24,65 It is worth emphasizing that these parameters are almost the same for both the spin-polarized and non-spin-polarized vdW-DF calculations in the present work. After obtaining the optimized lattice constants and geometric structure for the primitive unit cell, we calculated the charge density, and then the partial point charges of the atoms of MIL-88A(M). We found that the difference between the partial charges obtained by spin-polarized and non-spin-polarized versions is insignificant. The partial point charges and the force field parameters for the GCMC simulations are given in Table 2. Notably, the Lennard-Jones potential-well depth and diameter of Al and Ga are much larger than that of Sc, Ti, and V. The denotation of the atoms is described in Fig. 2. We use the optimized unit cell of MIL-88A(M) for M = Al and Ga obtained in this work and that for M = Sc, Ti, and V from our previous works30 to investigate the CO2 adsorption and uptake capacities of MIL-88A(M) in the next sections. We must emphasize that although the optimized unit cell for M = Sc, Ti, and V was found in our previous publication, the investigation of the CO2 adsorption and CO2 uptake capacities is completely new for MIL-88A(M) with M = Al, Ga, Sc, Ti, and V. During the discussion, we will also compare the results of this work with the previous theoretical and experimental results for MIL-88A(Fe).31,32
64 The optimized lattice constants for MIL-88A(M) with M = Al and Ga are presented in Table 1. We also calculated the specific surface area (SSA) and pore volume of these MOFs. By comparing the results with that in our previous work,30 we found that the distance dM–O between the metal atom (M) to the oxygen atom (O) and the primitive unit cell volume of MIL-88A(M) follows the order of Sc > Ti > V > Ga > Al and Sc > Ti > Ga ≈ V > Al, while the specific surface area and the pore volume follow the order of Al > Ti > V > Sc > Ga and Al > Ga > Ti ≈ Sc > V, respectively. Notably, the distance and the primitive unit cell volume of MIL-88A(Al) are the smallest; however, its specific surface area and pore volume are the largest, while the distance and the primitive unit cell volume of MIL-88A(Sc) are the largest among the metal substitutions. The obtained dM–O distance, a, b, and c lattice constants, primitive unit cell volume, specific surface area, and pore volume are similar to the computational and experimental values found in the literature.24,65 It is worth emphasizing that these parameters are almost the same for both the spin-polarized and non-spin-polarized vdW-DF calculations in the present work. After obtaining the optimized lattice constants and geometric structure for the primitive unit cell, we calculated the charge density, and then the partial point charges of the atoms of MIL-88A(M). We found that the difference between the partial charges obtained by spin-polarized and non-spin-polarized versions is insignificant. The partial point charges and the force field parameters for the GCMC simulations are given in Table 2. Notably, the Lennard-Jones potential-well depth and diameter of Al and Ga are much larger than that of Sc, Ti, and V. The denotation of the atoms is described in Fig. 2. We use the optimized unit cell of MIL-88A(M) for M = Al and Ga obtained in this work and that for M = Sc, Ti, and V from our previous works30 to investigate the CO2 adsorption and uptake capacities of MIL-88A(M) in the next sections. We must emphasize that although the optimized unit cell for M = Sc, Ti, and V was found in our previous publication, the investigation of the CO2 adsorption and CO2 uptake capacities is completely new for MIL-88A(M) with M = Al, Ga, Sc, Ti, and V. During the discussion, we will also compare the results of this work with the previous theoretical and experimental results for MIL-88A(Fe).31,32






.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.





