Microfluidic reactor development for isothermal kinetic measurements of sugar hydrolysis and global kinetics determination by the model-fitting approach†
Saartjie M.
Gouws
 a,
Julien
Brocus
a,
Julien
Brocus
 a,
Laurent
Cassayre
a,
Laurent
Cassayre
 b,
Jean-Jacques
Letourneau
a and
Marion
Carrier
b,
Jean-Jacques
Letourneau
a and
Marion
Carrier
 *a
*a
aRAPSODEE, CNRS UMR 5203, Université de Toulouse, IMT Mines Albi, Campus Jarlard, 81013 Albi CT Cedex 09, France. E-mail: marion.carrier@mines-albi.fr
bLaboratoire de Génie Chimique, Université de Toulouse, CNRS, INP, UPS, F-31 432 Toulouse, France
First published on 24th September 2024
Abstract
In this study, a novel method was developed to understand the liquid-state reactions occurring inside the intermediate liquid component (ILC) during biomass fast pyrolysis. A new experimental setup using a heated 300 μm inner diameter capillary microchannel with flow visualization was designed to study isothermal kinetics and reaction mechanisms of liquid-state sugar hydrolysis reactions. Heat- and flow patterns were investigated to confirm the intrinsic character of the kinetic measurements. Following the conventional dimensional analysis, observations with a high-speed camera and computational fluid dynamics modelling (CFD) in COMSOL Multiphysics® were used to confirm the hydrodynamic slug-flow pattern and the scale function of the temperature. The microfluidic reactor can operate within a temperature range of 453–533 K, up to 7 MPa, and a residence time within the hot section of 5 to 80 s, which is controlled by the volumetric flow rate. The novelty of this reactor is that under the specified operating conditions and residence times, it can provide isothermal measurements of intrinsic reaction kinetics, which have never been reported for hydrolysis systems. After hydrolysis in the microfluidic reactor, liquid samples were analysed off-line through HPLC to determine the sugar conversion and product yields. A fitting kinetic approach was developed to treat the kinetic data and extract intrinsic kinetic parameters describing sugar hydrolysis, key reactions occurring in the softening phase of biomass fast pyrolysis that are too often overlooked. It is proposed to integrate this experimental kinetic information into complete biomass fast pyrolysis models to take into consideration the solvent-like reactional environment.
1. Introduction
The production of bio-based energy and products via biomass liquefaction is a promising strategy to allow the phasing out of fossil fuels.1 The scientific and industrial community's interest in producing renewable carbon-based liquid fractions (via both pyrolysis and hydrotreatment) has increased significantly over the past 40 years.2 Typically, the levels of water content within lignocellulosic feedstocks determine the choice of the conversion technology. High water-content feedstocks are generally hydrotreated while low water-content ones are processed through dry thermochemical routes. To maximize the yields of liquid fractions (bio-oil), high volumetric or surface energy density is applied to the system. In a dry environment, fast and flash pyrolysis is used, which requires levels of heating intensity that are not necessarily needed under hydrothermal or hot-compressed water conditions.The commercialization of biomolecule production technologies relies on the progress made in the fields of modelling and simulation advances that also depend on the modelling strategies adopted, ranging from detailed mechanistic models to full-physical models.3 Moreover, the measurements of intrinsic kinetics of such complex systems are paramount but extremely challenging due to the substrate complexity and the multiphasic nature of the thermal process.4 The study of solid and liquid-state kinetics under fast heating has been of high interest. In the field of biomass fast pyrolysis, intrinsic kinetics determination has been intensively scrutinized. Observations and experimental kinetic measurements of biomass fast pyrolysis reflect the result of a combination of various intertwined chemical, thermodynamical and transport phenomena, all influencing each other if no precautions are taken.5 Therefore, the study of fast pyrolysis kinetics requires the careful selection of a reactor configuration and operating conditions designed to isolate and control chemical events.6
Although significant progress has been made in the field of biomass fast pyrolysis kinetics, the collection of reliable experimental data remains challenging. An important parameter to consider during thermal conversion, which has often been overlooked, is the reaction environment. In most studies, kinetic measurements have been based on the pyrolysis of solid samples of biomass (or other model components) in an inert gas environment (Table 1). However, Mettler et al.7 and Mamleev et al.8 suggested that the liquid phase reaction environment of the intermediate liquid compound (ILC) affects both the primary and secondary pyrolysis chemistries and therefore this liquid phase should be taken into consideration. In the first study, the authors hypothesized that the ILC plays the role of a solvent and alters both the thermodynamics and the transition states of reaction intermediates, thereby changing the activation energy of the reactions. This hypothesis was based on the theoretical ab initio calculations of Assary et al.9 who estimated that the presence of an aqueous reaction environment (solvent) can (through its participation in the reaction mechanisms) change the energy barrier for the conversion of sugars to furans by as much as 59 kJ mol−1. The work of Maduskar et al.10 and Maliekkal et al.11 also demonstrated that when the pyrolysis of cellulose was carried out using thick samples (>70 μm), the ILC (solvent) played a significant role in the reaction chemistry. Indeed, the reactive hydroxyl groups of intermediate compounds in the ILC acted as catalysts for the glycosidic bond cleavage of cellulose and thereby promoted the formation of levoglucosan in the liquid phase. Meanwhile, when thin film samples were used (ensuring the absence of the ILC), the formation of levoglucosan (in the gas phase) was significantly lower. These results demonstrate the important role of the reaction environment in favouring specific reaction pathways through selective catalysis of certain mechanisms. Therefore, controlling the extent of the liquid phase may be a key process strategy in controlling product selectivity. Furthermore, Mamleev et al.8 suggested that rationalizing the environment chemistry inside the cellulose matrix is paramount to elaborate kinetic models applicable to both slow and fast pyrolysis. In this regard, Antal,12 during a correspondence with Mamleev, proposed that a liquid water environment is a closer representative of the true reaction environment inside solid cellulose. He justified this statement by referring to experimental work with alcohols13 and acids14 in hot compressed water and pointed out that the reaction mechanisms proposed for the thermal breakdown of these compounds corresponded well to those used to rationalize the products observed from biomass pyrolysis. Moreover, the hydrolysis reaction that occurs during biomass pyrolysis (due to the presence of water) is significant and has been included in the detailed mechanistic model of biomass fast pyrolysis.15
| Reactor system | Sample heating rate (K s−1) | Temperature range (K) | Environment, residence time (s) | Kinetic measurement strategy | Advantages | Disadvantages | Ref. |
|---|---|---|---|---|---|---|---|
| TGA | 0.1–3.3 | 303–1173 | Inert gas, >1 | Online scale with rapid measurement | - Widely available | - Limited to low heating rates | 16–19 |
| - Different stages of biomass pyrolysis may be identified | - No direct measurement of sample temperature | ||||||
| - Reaction may be sensitively tracked | |||||||
| Tube reactor | NR | 573–623 | Liquid water, 0.05–30 | Quenching of liquid solutions followed by offline HPLC analysis | - Liquid reaction environment | - Presence of mass and heat transfer limitations | 20–23 |
| - Precise control of reactant and product residence time | - Insoluble compounds cannot be analysed | ||||||
| - Cheap and easy to manufacture | |||||||
| Tube reactor | NR | 773–823 | Inert gas, 1.5 | Quenching of volatiles followed by offline analysis | - Precise control of product vapour residence time | - No direct measurement of sample temperature | 24 |
| - Laminar and plug flow confirmed in reactor | - Absence of heat and mass transfer not confirmed | ||||||
| Tube reactor | 27 | 773 | Inert gas, 7.1 | Quenching of volatiles followed by offline analysis | - Large amount of product volatiles quantified | - Long product vapour residence times | 25 |
| - Absence of heat and mass transfer not confirmed | |||||||
| Micro-pyrolyzer | 110–216 | 373–773 | Inert gas, ∼0.02 | Online mass spectrometer with delay of ∼50 ms | - Widely available | - Significant heating time (4–6 s to reach 500 °C) | 26–28 |
| -Reaction-controlled conditions | |||||||
| - No direct measurement of sample temperature | |||||||
| - Delayed response for tracking volatile production | |||||||
| - Presence of secondary vapour phase reactions | |||||||
| Pyroprobe | 50–2000 | 723–1023 | Inert gas, ∼1 | Direct flushing of volatiles into GC-MS system and offline analysis | - Widely available | - No direct measurement of sample temperature | 29 |
| - High heating rates | - Presence of secondary vapour phase reactions | ||||||
| Wire-mesh reactor | 50–7000 | 523–973 | Inert gas, 0.015–0.02 | Quenching of volatiles followed by offline gravimetric measurement | - Very high heating rates | - Very small amount of bio-oil available for subsequent analyses (<0.05 g) | 30–32 |
| - Reaction-controlled conditions | - Relatively slow quenching of volatiles | ||||||
| - Direct and fast measurement of sample temperature | - Expensive and difficult to acquire | ||||||
| - Limited secondary vapour phase reactions | |||||||
| PHASR | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875 875 |
648–823 | Inert gas, 0.1–2 | Quenching of volatiles followed by offline GC analysis | - Very high heating rates | - Analysis of volatiles is limited to compounds with boiling points below 300 °C | 33–35 |
| - Reaction-controlled conditions | |||||||
| - Direct and fast measurement of sample temperature | - Expensive and difficult to acquire | ||||||
| - Fast quenching of volatiles | |||||||
| - No liquid phase secondary reactions | |||||||
| - No secondary vapour phase reactions | |||||||
| Micro-fluidic reactor | 721–5333 | 453–533 | Liquid water, 0.1 | Quenching of liquid solutions followed by offline HPLC and GC analysis | - Liquid reaction environment | - Insoluble compounds cannot be analysed | This study |
| (Section 2.3.2) | - Precise control of reactant and product residence time | - Limited range of operating temperatures and pressures | |||||
| - No heat and concentration gradients | |||||||
| - Reaction-controlled conditions |
Another motivation for studying hydrolysis kinetics in a liquid phase environment is that in comparison with solid phase particles, it is significantly easier to avoid mass and heat transfer limitations in a homogeneously mixed solution. For example, when studying intrinsic solid-phase kinetics, the significant impact of temperature–time profiles36 and response delay37 on intrinsic kinetics has recently been demonstrated in a down-fall36 and a pulse-heated analysis of solid reaction (PHASR) micropyrolyzer.10 During solid phase pyrolysis, heat transfer phenomena should be adequately identified to confirm heat transfer coefficients according to particle shape38 and ensure the absence of temperature gradients within the particles.36 The evaluation of intra- and external particle mass transfer must also be assessed considering the microstructure organization of particles and physical medium changes (e.g., the presence of an intermediate liquid phase). Suuberg et al.39 extensively studied the matter considering physical properties of solid/fluids such as diffusion coefficients during coal pyrolysis and scrutinized the reaction and diffusion time scales. Depending on the properties of the solid and fluid medium in which the volatiles evolved, mass transfer mechanisms will change. In solids, significant retention of volatiles in the pore structure can be observed and in liquids, bubble transport mechanisms are greatly affected. As a result, the time scales for mass transfer in the ILC and the solid particle largely differ, which significantly complicates the attempts to obtain intrinsic kinetic measurements. However, in the case of a liquid homogenous solution, the type of mass transfer limitation related to a porous solid is completely avoided, and mass transfer limitations in the liquid can be overcome by sufficient mixing. Consequently, the study of intrinsic kinetics in a liquid phase reaction environment is an attractive option.
In the last decade, a few authors have carried out kinetic studies of cellulose (and other model components) in aqueous solution by using continuous flow tube reactors.20–23 An advantage of this type of reactor is that the residence time of reactants and products can be precisely controlled by varying the liquid flow rate. However, Xu et al.13 reported a 3 K temperature variation throughout their tube reactor, confirming the presence of heat transfer limitations. Furthermore, the authors did not provide any details regarding concentration gradients, which may also have affected the kinetic measurements. A need therefore exists to develop a flow reactor system where both heat and concentration gradients are absent to better study primary reactions while minimizing secondary reactions.
Microfluidic reactor systems have gained wide interest among researchers of various fields due to their unique flow, mixing and control abilities as well as the possibility of process intensification.40 Lu et al.41 estimated that the heat transfer coefficient in a microfluidic reactor could reach 10 kW m−2 K−1, which is significantly higher compared to heat transfer coefficients reported for solid phase pyrolysis down-fall reactors (0.17–0.24 kW m−2 K−1).42 High mass transfer coefficients (0.005–0.115 s−1) have also been reported for these reactors.42 Microfluidic reactors are composed of micro-capillary tubes (internal diameters in the range of 10–500 μm) and may be operated using single- or multiphasic flow.43 Among the various flow regimes, the Taylor flow regime (slug flow) is often a favourable choice due to the improved mass and heat transfer together with the narrow residence time distribution (RTD) that may be achieved under these operating conditions.44 During Taylor flow, toroidal recirculation occurs within the liquid slugs, enabling enhanced mixing which improves heat and mass transport (further details in section 2.2).45 At the same time, the small diameter of the reactor (10–500 μm) allows laminar and plug flow to be easily attained and therefore ensures an identical residence time for all the molecules passing through the reactor.42 Each liquid slug in the segmented flow may then be regarded as a perfectly mixed unit batch reactor.46 These advantages combined with the ability to precisely control the reaction time in microfluidic reactors make them a well-suited tool for kinetic studies.
Although microfluidic reactors have attracted interest in performing kinetic studies in several fields,47 to our knowledge this type of device has never been implemented to the area of biomass fast pyrolysis kinetics and, although a consensus on the presence of the ILC under fast heating has been reached,7 its description is still debated. Furthermore, the majority of experimental pyrolysis kinetic studies have been conducted under non-isothermal conditions; however, this complicates the analysis of the true sigmoidal character of a reaction as illustrated in the critical review of Burnham et al.48 For example, during non-isothermal heating, it is challenging to deconvolute the effects of the heat-up process and the sigmoidal reaction characteristics. However, recognizing the sigmoidal characteristics is more straightforward in isothermal data because the rate constant remains constant. Therefore, the shape of the kinetic curve is solely determined by the reaction model itself. Meanwhile under non-isothermal conditions, both the rate constant and the reaction model vary simultaneously, resulting in sigmoidal α vs. t curves. This simultaneous variation makes it more challenging to recognize the specific reaction model type. Therefore, providing isothermal kinetic data is of great interest for kinetic modelling.
Many studies have focused on the fast pyrolysis of biomass in an inert gas reaction environment, whereas it has been suggested that a liquid environment is a closer representative of the true conditions of the ILC inside the cellulose matrix. In this context, the focus of this paper is to provide a proof of concept of a new method for measuring isothermal hydrolysis kinetics. A novel heated microfluidic system was developed, and it was demonstrated that intrinsic kinetic data could be collected under isothermal conditions in this setup. The case of the reaction of glucose and cellobiose hydrolysis was chosen to investigate the role of the liquid reaction environment in the degradation of emblematic cellulose model compounds.
2. Materials and methods
2.1 Chemicals
A 10 g L−1 (or 1.1 wt%) solution of D-(+)-glucose (D-(+)-glucopyranose, Sigma Aldrich, 96 wt%), a 10 g L−1 (or 0.8 wt %) solution of D-(+)-cellobiose (β-D-(+)-glucopyranosyl (1 → 4)D-glucopyranose, Sigma Aldrich, 96 wt%) and ultra-pure water (Purelab Classic DI, ELGA LabWater) were prepared as aqueous reactant solutions. Although glucose may undertake different conformations, the most represented cyclic form of glucose in water is the β-form (around 64% β-form versus 36% α-form, and traces of the linear form). In addition, Mayes et al.49 confirmed that there was no statistically significant difference in the product yields obtained during fast pyrolysis of either α-glucose or β-glucose.For HPLC quantification of the products, D-fructose (β-D-fructopyranose), levoglucosan (1,6-anhydro-β-D-glucopyranose) and 5-hydroxymethylfurfural were purchased respectively from Merck and Sigma-Aldrich at 99 wt% purity for both products. These compounds were used as the organic standards. According to Lichtenthaler et al.,50 the most represented form of D-fructose in an aqueous solution at 298 K is the pyranose β-form (around 73% β-D-fructopyranose, around 2% α-D-fructopyranose, around 5% α-D-fructofuranose and around 20% β-D-fructofuranose). However, these different forms of D-fructose could not be separated on the HPLC and appeared as a single peak.
Polydimethylsiloxane (PDMS) DC 200 (Fluka Chemika) with a relative density, d204, of 1, a refractive index, η20D, of 1.406 and a viscosity of 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mPa s at 298 K was selected as the non-aqueous phase for transporting the segmented aqueous slugs through the microfluidic reactor. Nitrogen (Linde France, 99.995% purity) was used to pressurize pump 3 (Fig. 1).
000 mPa s at 298 K was selected as the non-aqueous phase for transporting the segmented aqueous slugs through the microfluidic reactor. Nitrogen (Linde France, 99.995% purity) was used to pressurize pump 3 (Fig. 1).
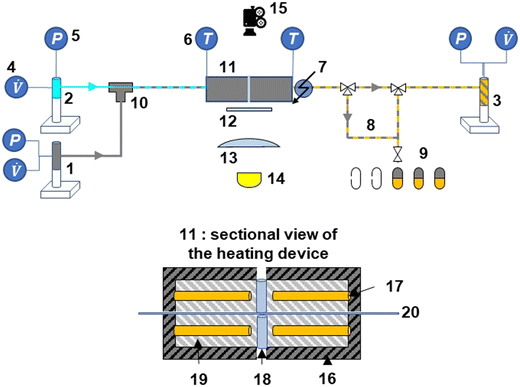 | ||
| Fig. 1 Experimental set-up: microfluidic reactor, flow regulation, and imaging systems with the following items: 1 syringe pump PDMS, 2 syringe pump aqueous solution, 3 syringe pump phase mixture, 4 volumetric flow rate controller, 5 pressure transducer, 6 temperature indicator (thermocouple), 7 cooling device (airflow), 8 sampling loop, 9 collecting samples, 10 coaxial injection device, 11 heating device,12 frosted glass, 13 lens, 14 high power LED, 15 highspeed camera, 16 insulating coating (mica), 17 heating cartridge, 18 quartz cylinder, 19 aluminium block, 20 micro-capillary. Fig. S1† shows another 3D sectional view of the heated microfluidic reactor. | ||
In this study, the thermal behaviour of two-phase flow (aqueous glucose/cellobiose solution–PDMS) was studied. The physico-chemical properties (e.g., viscosity, density, thermal conductivity, heat capacity) of this diphasic system were chosen to guarantee the immiscibility between the two components and to ease the flow within the capillary (minimizing the interfacial effects). The overview of the physical properties of the liquid–liquid system is provided in the ESI† Data S1.
2.2 Description of the microfluidic reactor set-up
The experimental set-up consists of 3 sections, namely the co-axial injection system,46 a heating/cooling section, and a product collection section (Fig. 1). Two Teledyne 260D ISCO pumps (capacity: 266 mL, flow range: 0.001–107 mL min−1, flow accuracy: 0.5% of the set point, pressure range: 0.7 to 517 bar, pressure accuracy: 0.5% of the full scale) were used to feed the reactant solution (pump 1) and PDMS (pump 2) to a T-junction inlet. At this inlet, the fluids each entered a different polyimide-coated silica capillary (with different diameters), purchased from Polymicro Technologies. The reactant solution entered through the smaller capillary (OD 151 μm, ID 75 μm), whereas the PDMS was fed into the larger capillary (OD 793 μm, ID 300 μm). Further details of this inlet system are provided in Deleau et al.46After achieving the slug flow at the inlet section of the larger capillary, the fluids flowed into the heating section, where the capillary was heated between two aluminium heating blocks (length 22 cm, Fonderie Gillet, Albi). The heating system was specifically designed to heat the 20 cm-length capillary and aluminium was chosen to ensure quick capillary heating. The heating of the two blocks was achieved using a four cartridge-type tubular electric heater (1/4′′ FIREROD cartridge heater) that was installed into the blocks. A K-type thermocouple in contact with the capillary was used to control the reaction temperature at 453–533 K. The reaction time was varied (5–80 s) by controlling the flow rates of the reactant solution and PDMS (6–20 μL min−1).
To maintain the slugs under liquid–liquid state and control the slug velocity during their heating (ESI† Data S3), a 500D Teledyne ISCO pump (pump 3) (capacity: 507 mL, flow range: 0.001–204 mL min−1, flow accuracy: 0.5% of the set point, pressure range: 0.7 to 258.6 bar, pressure accuracy: 0.5% of the full scale) was used to control the volumetric flow at a constant value. This has the advantage of maintaining a periodic flow at a constant pressure. The pump was initially pressurized with nitrogen gas (Linde France, 99.995% purity). Furthermore, the same pump was used to collect the waste liquids passing through the reactor under unsteady state conditions at the start of each run.
At the reactor outlet, the rapid cooling of the products was ensured using a compressed air-cooling system and the collection of the entire aqueous phase provided a representative sample obtained from the degradation process. By varying the flow rates, it was possible to obtain a sample of the reaction products at different residence times. The collection of these samples was started only once the steady-state two-phase flow was stabilized. Once a sample volume of 0.5 mL was obtained, the collection was stopped. The product samples were then analysed using HPLC-UV/RID analysis (section 2.4). Each experiment was performed in triplicate and the maximum deviation was determined to be 3.3% for the glucose solutions and 5.4% for the cellobiose solutions (ESI† Data S5).
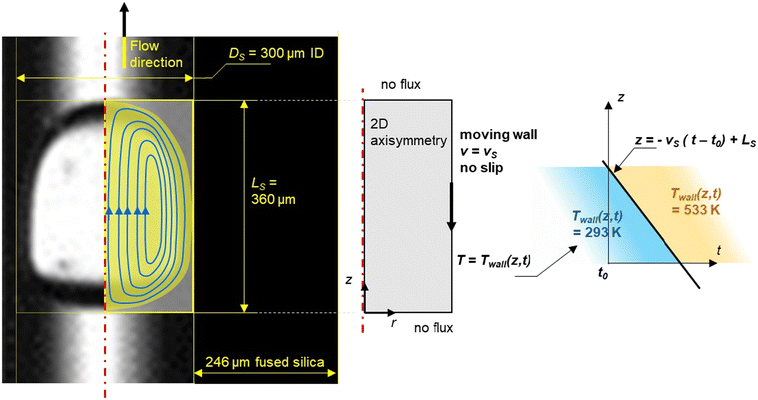
A small opening (5 mm diameter) was drilled in the middle of the heating blocks of the microreactor (at L/2) to allow the capture of images of the slug flow inside the capillary (Fig. 2). This hole is hidden behind the diffuser plane (between the bright light and the zone of interest) to enhance diffusion. A lens was placed between the diffuser and the backlight to collimate light from the high-power UV LED (CXB3590 3000 K 80 CRI, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 lumens). A high-speed camera (xiB-64, Ximea) was horizontally aligned with the lighting system. The pictures were taken at a rate of 1648 frames per second at a resolution of 6.8 μm per pixel. Within the hole, two quartz cylinders were placed to minimise heat loss. Some examples of images taken at different flow ratios of aqueous reactant solution and non-aqueous PDMS are shown in Fig. 3.
000 lumens). A high-speed camera (xiB-64, Ximea) was horizontally aligned with the lighting system. The pictures were taken at a rate of 1648 frames per second at a resolution of 6.8 μm per pixel. Within the hole, two quartz cylinders were placed to minimise heat loss. Some examples of images taken at different flow ratios of aqueous reactant solution and non-aqueous PDMS are shown in Fig. 3.
 | ||
| Fig. 2 A photo of the heated analysis of the liquid reaction system with the reactor, heating system, optics and camera. | ||
Slug geometric characteristics and velocity field measurements were secured by the imaging set-up. The reproducibility of the fully developed slug flow in the heated zone is confirmed by the regular slug length and shape (Fig. 3) with total flow rates varying from 0.01 to 0.19 mL min−1 at an aqueous-to-PDMS volumetric flow ratio of 0.5, 1 and 2. The diphasic liquid–liquid flow is steady after a few minutes. These flow rates correspond to different slug velocities from 0.003 to 0.044 m s−1 and therefore various slug residence times from 5 to 80 s according to measurements and corroborated by the calculations in the ESI† Data S6. The slug velocity was calculated by measuring the displacement of the slug tip between two successive high-speed images to calculate an average slug velocity.
This microfluidic device has allowed the study of hydrolysis kinetics by collecting values for the concentration of the reaction products as a function of the reaction time under high pressure. This was made possible thanks to three major features of the device: (i) working under pressure avoids vaporizing the aqueous phase containing the reagents; thus, the flow can be described using an incompressible model. (ii) Using flow rates ranges (6–20 μL min−1) that are small enough to assimilate both heating and cooling ramps to a perfect temperature step but still large enough to favour convection inside the aqueous slug and ensure the uniformity in reagent concentration (perfectly stirred mini-reactors).51 (iii) Finally, because of the relatively low velocities, the pressure drop in the micro-reactor is not high enough to take into account the influence of pressure on the values of the transport properties (viscosity and density).
These features, which are demonstrated in the following sections, provide a better understanding of the measurement campaign. Each aqueous slug is regarded as a micro-reactor in which all the reactants in solution are subjected to the same operating conditions.
2.3 Evaluation of heat and mass transfer
To guarantee the measurement of intrinsic chemical kinetics in the microfluidic reactor, a dimensional analysis combined with a CFD simulation of a simplified system was conducted.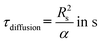 | (1) |
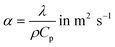 | (2) |
The convection time can be expressed as follows:
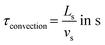 | (3) |
The required time without convection, τdiffusion, to reach the desired temperature is equal to 0.13–0.14 s respectively for 453 and 533 K, whereas the necessary time for a slug, τconvection, to entirely enter the hot capillary is between 0.003 and 0.052 s. To validate the hypothesis of a temperature step function, it is necessary that the ratio 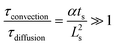 be satisfied, which is the case as this ratio ranges from 39–219. This preliminary empirical investigation that confirms the absence of a temperature gradient was completed by a numerical simulation to understand the role of the convection phenomena.
be satisfied, which is the case as this ratio ranges from 39–219. This preliminary empirical investigation that confirms the absence of a temperature gradient was completed by a numerical simulation to understand the role of the convection phenomena.
For the internal temperature gradient, the calculation of the Peclet number that correlates convective and diffusive transport phenomena to study both mass and heat transfer52 is of interest. The ratio of convection transport to diffusion transport is referred to as PeM, whereas the ratio of convection transport to heat transport is referred to as PeH. The equations for these dimensionless numbers (eqn (4) and (5)) were obtained from Rapp.52
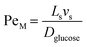 | (4) |
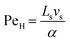 | (5) |
From these calculations PeM was determined to be between 35–540 and PeH between 0.3–4.3, the former being significantly larger. Therefore, it was concluded that the convection transport inside the unit slug seems to be the major factor (over conduction) in driving temperature and concentration uniformity in the slug. As a result, a CFD simulation was required to fully investigate the interplay between conduction, convection, and diffusion and determine the magnitude of the heating ramp.
A computational domain is shown in Fig. 4 where a 2-D axisymmetric model revolving around the z axis reduces the aqueous slug by half. The width and the length of the yellow rectangle represent the radius of the capillary and the length of the aqueous slug, respectively. The immiscible character of the liquid–liquid flow and the periodic regime (the constant residence time of the slug) were two hypotheses drawn from the above observations (Fig. 3). It was also assumed that the PDMS did not undergo any chemical change during the time the slugs move through the length of the heated capillary (ESI† Data S3). The co-axial feeding system allowed a rapid establishment of a laminar profile.
Both phases were assumed to be incompressible and Newtonian. Fluid flow was numerically represented by the non-isothermal Navier–Stokes equations using CFD calculations (finite element methods) with the following boundary conditions: slip or no flux conditions when the slug's walls are in contact with PDMS, and the no-slip condition was applied when the slug's walls are in contact with the capillary's walls. For the simulation, the slug was assumed to be held stationary while the wall of the capillary moved with a constant velocity, which was the average velocity, vs, in the reference frame of the slug.
For the simulations, the related laminar flow module was used. Indeed, based on the observations, the shape and volume of the slugs remained the same during the chemical reaction. The flow was laminar due to the small Reynolds number. Despite changes in mean flow speed, the laminar flow was maintained between 453 K (Re = 0.8 < 200) and 533 K (Re = 10.8 < 200). A step function displayed in Fig. 4 to describe the temperature along the reactor was implemented and a pressure value was given at a specific point. The mesh setting involved nearly 6000 triangle elements.
Dependent variables were solved using the time-dependent solver, parallel direct solver (PARDISO). Simulations were converged with an absolute tolerance of 0.05. In addition, a sensitivity study of mesh was carried out. The maximum element size of the mesh was in the range of 1 to 64 μm. The influence of the maximum element size was determined at a specific localization of the slug and at a time in the dynamic heating step. The temperature at several positions and the overall energy balance results were stable at 1 to 16 μm. Therefore, this element size of 2 μm was retained. The number of elements describing the slug is 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 for the domain and 514 for the boundary. We considered a ‘no flux’ boundary condition between each slug as shown in Fig. 4 because of the stiffness of the heating step, which allows us to simplify the numerical simulation to a single slug and not to a train of slugs.
246 for the domain and 514 for the boundary. We considered a ‘no flux’ boundary condition between each slug as shown in Fig. 4 because of the stiffness of the heating step, which allows us to simplify the numerical simulation to a single slug and not to a train of slugs.
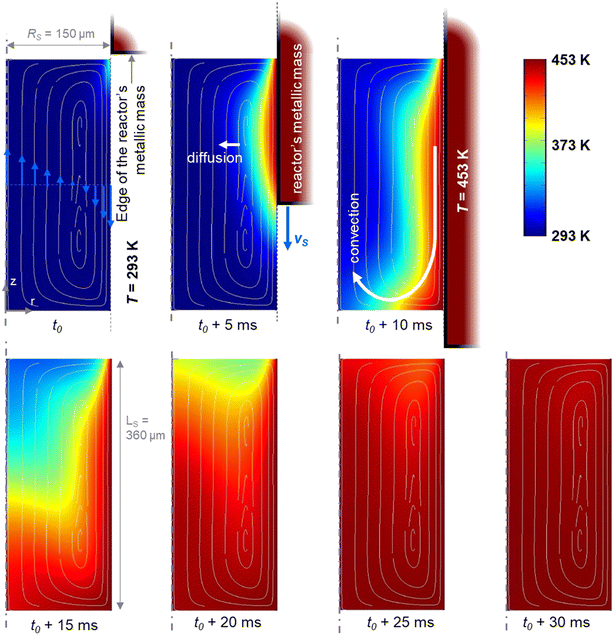
To study the passive mixing, which was based on solving a general convection–diffusion equation (Navier–Stokes equation), the flow field was solved under time-dependent (transient) conditions due to the small Reynolds number. The simulations (Fig. 5) confirm the presence of a toroidal flow pattern inside the aqueous phase plug in the two extreme cases at 453 K and 533 K (the latter is not shown).
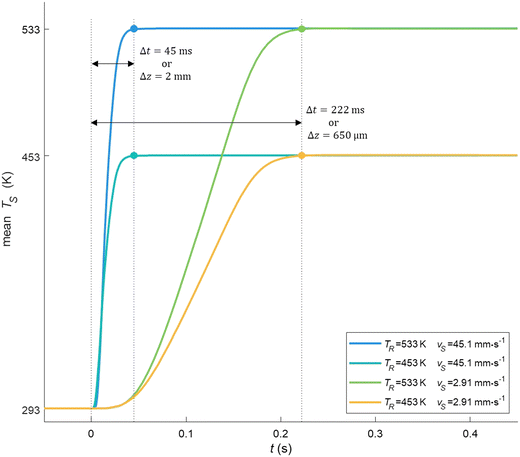
The presence of internal circulatory flow patterns inside the slug was confirmed, and useful to enhance the mass transfer.51 Each slug was exposed to the same hydrodynamics and then similar heating ramps. Once the hydrodynamics stabilized, the heating rate of the slug was determined by considering the time for the slug initially at ambient temperature to reach the desired temperature (Fig. 6). The mean temperature of the slug versus time for the minimum and maximum heating times at 453 K and 533 K, respectively at the slowest and fastest slug velocities, indicated quasi-isothermal conditions along the heated capillary section (>99%). From 453 to 533 K, the heating rate of the aqueous slug increased from 721 K s−1 to 5333 K s−1 at the least favourable flow values.
To summarise, the actual setup and operating conditions allowed an accurate measurement of the average velocity of the slug in the capillary. The pressurizing of the setup was inevitable to avoid uncontrolled expansion of the liquid slug into the gas phase upon entering the heated section (ESI† Data S3) and therefore maintain the liquid–liquid system in a liquid state. As a result, the setup can operate in the temperature range of 453–533 K and pressure up to 7 MPa. Under these conditions, the heating rate of the slug varies between 721 and 5333 K s−1, with a velocity of 2.9–45.1 mm s−1 and a resulting residence time of 45–222 ms. Both theoretical and experimental data are reported in Tables S3 and S4.†
2.4 HPLC analysis of liquids
The HPLC-UV/RID analyses of the products were performed using an Agilent Technologies system with a diode array detector (1260 Infinity II, Agilent). The samples were filtered through 45 μm polypropylene filters and subsequently separation was performed using a 300 mm × 7.8 mm Aminex HPX-87 hydrogen form cation exchange resin-based column (Bio-Rad) following the method of Liu et al.53 Ultra-pure water with 0.00025 M H2SO4 was used as the mobile phase with a flow rate of 0.6 mL min−1 and the column temperature was set to 308 K. The injection volume was 20 μL. The sugars (cellobiose, glucose, fructose and levoglucosan) were detected by the RID, whereas 5-hydroxymethylfurfural (5-HMF) was detected using UV detection. The wavelength was set at 280 nm. Calibrations curves for 5 model compounds (cellobiose, glucose, fructose, levoglucosan, 5-HMF) were obtained and are shown in the ESI† Data (S4). Each experimental run was repeated 3 times, and the maximum deviation was determined to be 3.3% for glucose and 5.4% for cellobiose (ESI† Data (S5)).An organic carbon balance was carried out for each experiment using eqn (6)46 and based on the product concentration determined by the above-described HPLC analysis, which allowed the assessment of the extent of unidentified byproducts.
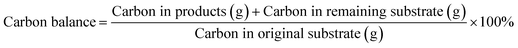 | (6) |
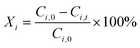 | (7) |
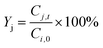 | (8) |
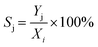 | (9) |
2.5 Determination of kinetic parameters
Previous heat and mass transfer investigations confirmed that each slug can be considered as a microreactor perfectly stirred in a periodic and isothermal flow as evidenced in process intensification strategies. Under those conditions, first-order reactions are considered and parameters such as reactant and product concentrations vary only with time and not in space. The variation in pressure and its possible influence on kinetics of liquid-phase reactions was neglected because of small pressure drops (Table S3†) along the reactor due to microflows. Chen et al.54 previously suggested that for liquid-phase organic reactions, changes in pressure in the order of kbar (∼100 MPa) are needed before any effect on activation energies can be noted. In this paper, a two-step process was followed to determine kinetic parameters. First, global kinetic parameters were determined (section 2.5.1) and then these estimates were used as input data to a kinetic model consisting of a series of differential equations (section 2.5.2). The kinetic parameters in this model were determined via regression using the experimental data.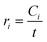 | (10) |
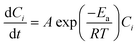 | (11) |
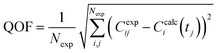 | (12) |
3. Results and discussion
In this section, the results of the isothermal hydrolysis of glucose and cellobiose solutions in the microfluidic reactor are discussed. The product distribution for the sugar hydrolysis at different reaction times is presented in section 3.1 from which a degradation scheme is proposed. Thereafter, global kinetic parameters are obtained from the experimental data in section 3.2. Finally, a kinetic model is derived in section 3.3 where the global kinetic parameters (section 3.2) are used as input values in the regression process.3.1 Glucose and cellobiose conversion: product distribution
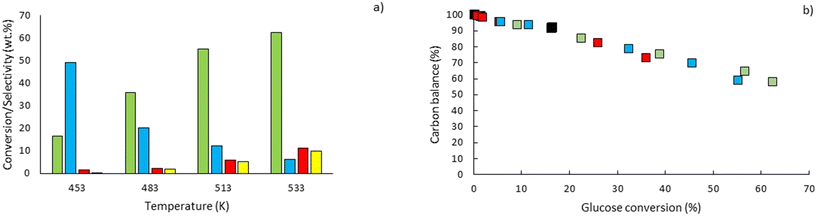
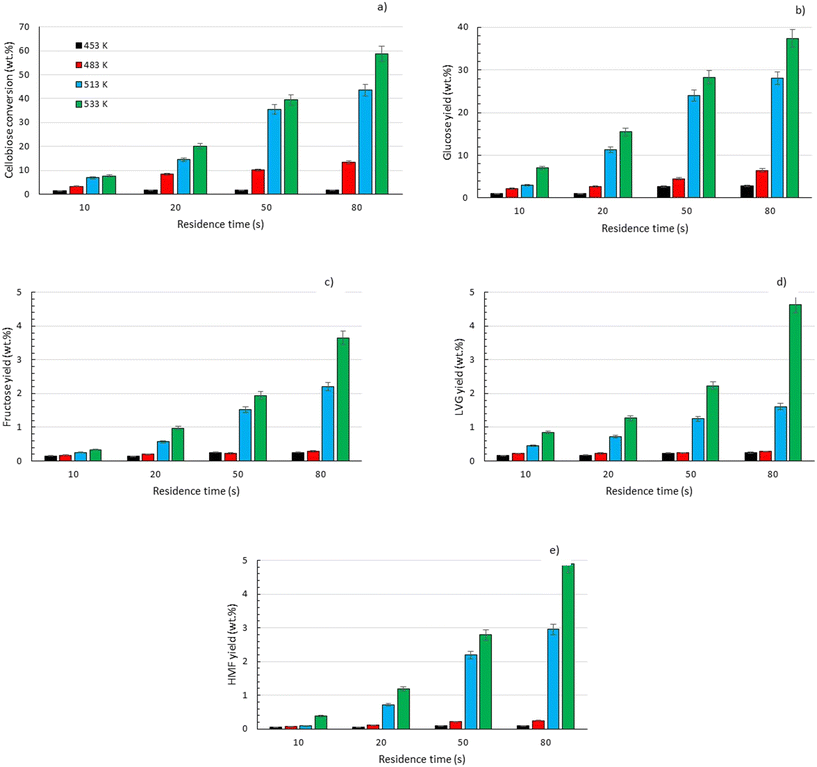
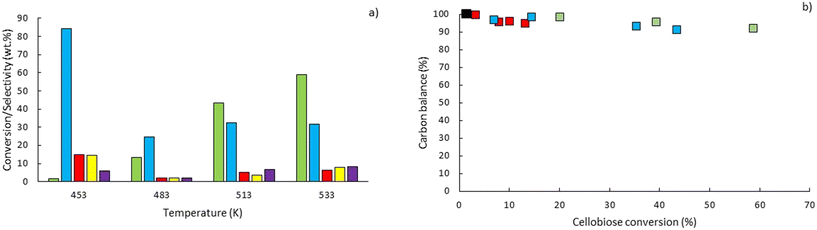
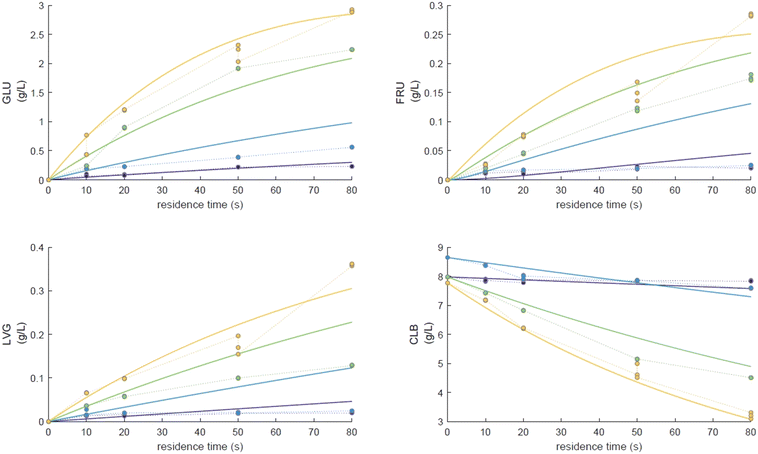
To explore the potential of the microreactor in the conversion of sugars, the effect of temperature (453–533 K) and residence/reaction time (5–80 s) is displayed in Fig. 7a–d. The conversion of glucose as well as yields of the byproducts detected and quantified (fructose, levoglucosan and 5-HMF) confirms that fructose (FRU) and levoglucosan (LVG) are two of the main products with the respective highest yield of 8.6 wt% (obtained at 513 K for 20 s of reaction) and 7.0 wt% (at 533 K and 80 s). The production of LVG is low due to limited operating conditions; indeed, without a catalyst higher LVG yields could not be expected as the formation mechanism of LVG, transglycosylation, occurs optimally at 773 K.57 With respect to the FRU yield, the isomerization reaction, which is known to be equilibrium limited, is expected to occur at low temperatures, <573 K.20,58 The selectivity towards fructose of 49% is high at low temperature (453 K) for long reaction times (80 s), whereas for the same reaction time at the maximum temperature (533 K), this selectivity decreases dramatically to 6.3%, clearly demonstrating that the isomerization of glucose to fructose is a primary reaction that is favoured at low temperatures (Fig. 8a). The production of both 5-HMF and levoglucosan was favoured at the highest temperature (533 K) and longest residence time (80 s), with yields reaching up to 6.1 wt% and 6.9 wt% (Fig. 7c and d); production ranges are quite comparable to those obtained in glucose fast pyrolysis, 4.9 wt% and 8.1 wt% for 5-HMF and LVG, respectively.59 The concentration of fructose initially increased due to the isomerization reaction with glucose but decreased for reaction times >20 s. This demonstrates a reaction-in-series behaviour after 20 s where fructose was subsequently converted into other byproducts. Also note that fructose degradation at higher temperature was necessary to overcome the thermodynamic equilibrium and allow further glucose conversion and therefore other byproducts such as LVG and HMF were produced.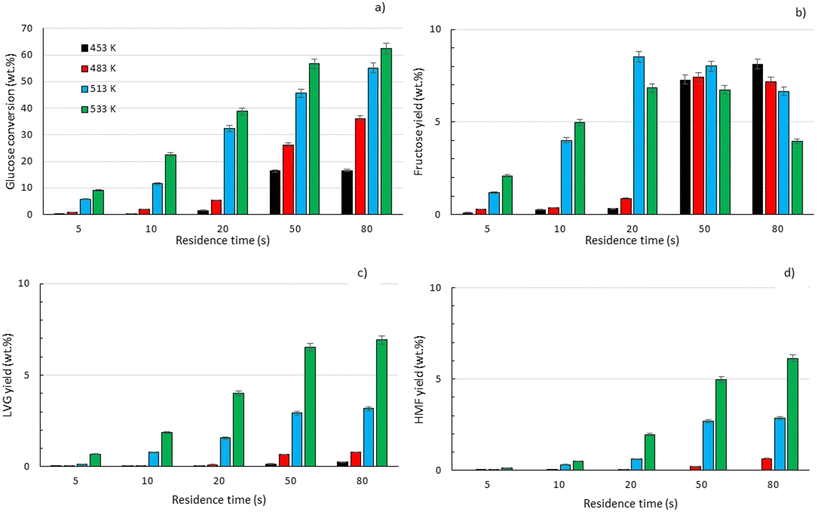 | ||
Fig. 7 Conversion of a) glucose and yields of b) fructose, c) levoglucosan and d) 5-HMF at temperatures of 453 K (■), 483 K ( ), 513 K ( ), 513 K ( ) and 533 K ( ) and 533 K ( ) and residence times between 5 and 80 s. ) and residence times between 5 and 80 s. | ||
For longer reaction times and higher temperatures, the selectivity towards LVG and HMF was also significant, respectively 11.1 and 9.8%, which was possible due to higher glucose conversions, up to 62.4 wt% at 533 K (Fig. 8a). The yield of HMF increased gradually with increasing temperatures and reaction times (Fig. 7d), conditions that favour successive dehydration of fructose to form 5-HMF. The results confirm that higher temperatures and extended exposure to those temperatures are beneficial to the conversion of primary products into water-soluble low molecular-weight secondary compounds. According to the literature, levoglucosan is formed directly from the dehydration of D-glucose.60
Furthermore, the regular decrease of the carbon balance with the glucose conversion (Fig. 8b), down to 58% at the highest reaction temperature and longest reaction time, confirms the presence of byproducts that were not identified by HPLC analyses. Previous investigations on cellulose hydrolysis have established more intricate glucose degradation mechanism networks in which the presence of furfural,61 levulinic and formic acids62 has been evidenced. These compounds were not quantified in this study and might account for the carbon missing at high glucose conversion yields.
Eager to further understand the role of the intermediate liquid compound (ILC), which consists of depolymerized anhydrous oligomers, cellobiose hydrolysis was also carried out (Fig. 9a–d). Among the primary products obtained from isomerization and hydrolysis,55 only glucose, the hydrolysis product, was tracked and a yield of up to 37 wt% was obtained under the most severe conditions (533 K and 80 s). This is coherent when high initial concentrations of cellobiose, 0.8 wt%, are used as the formation of GLU is suspected to be catalyzed by acidic products from cellobiose decomposition.55 On the other hand, secondary byproducts (FRU, LVG, HMF) remained below 5 wt% (Fig. 9b–d). The selectivity towards glucose (Fig. 8a) increased with temperature (from 24.5 to 31.8%) when sufficient cellobiose conversion was reached (13.3%). Severe conditions are preferred to degrade cellobiose and promote the formation of secondary products. The carbon balance demonstrated that under the most severe conditions, 91 wt% of the original carbon in the cellobiose could be recovered in the quantified products. This confirms the limited extent of cellobiose degradation and that the quantification of major cellobiose primary decomposition reactions has been depicted, which demonstrates that the setup allows detailed investigation of primary reactions. Similar to what has been reported for cellulose pyrolysis,15 glucose was also an intermediate product during the hydrolysis of cellobiose in water, although the selectivity to glucose (up to 31.8% at 533 K) is beyond the conventional selectivity recorded, 6–27%.55 Under the experimental conditions, the mechanism responsible for cellobiose primary decomposition into glucose cannot be considered as a minor conversion pathway anymore, confirming that at higher temperatures the hydrolysis of cellobiose is promoted, being catalyzed by protons.55 The low yields of fructose and HMF confirm that the secondary reactions of the glucose product were limited which also explains why the glucose concentration does not start to decrease within the reaction time. In comparison with the initial glucose conversion, it is evident that cellobiose takes longer to convert initially. For example, to reach a conversion of 20% at 553 K, a reaction time of 10 s is required for glucose, whereas for cellobiose a reaction time of 20 s is required. This might also explain why more by-products were formed in the case of glucose hydrolysis and why reaction-in-series behaviour is not observed in the cellobiose case. Meanwhile in the case of glucose, the fructose yield went through a maximum, illustrating the serial kinetic pathway with fructose as the main primary product (Fig. 7b).
The levels of levoglucosan obtained via cellobiose hydrolysis (<5 wt% at 533 K, Fig. 10) remain limited compared to those recorded under cellobiose fast pyrolysis (27 wt% at 773 K (ref. 59)). This result confirms that if significant release of LVG must be achieved, the direct hydrolysis of cellobiose into glucose should be avoided as well as acidic conditions to avoid the conversion of LVG into glucose.63
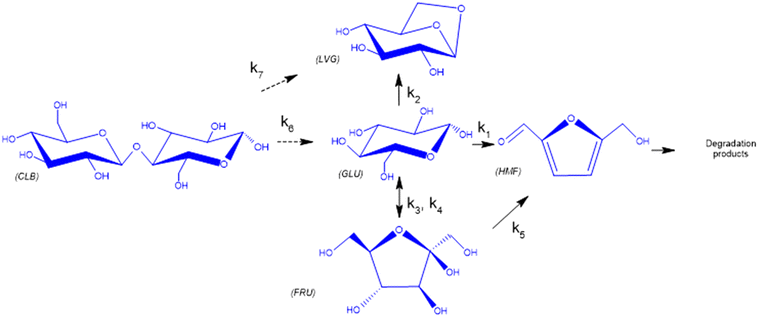
Based on the detected and identified byproducts as well as the trends that have been compared to previous degradation patterns found for hydrolysis conditions,64–67 a conversion network is provided in Fig. 11. This network will be used in section 3.3 to derive a kinetic model and determine kinetic parameters for the different reactions. Under hot compressed water, the β(1,4)-glycosidic bond linkage of cellobiose (CLB) is mainly cleaved by a hydrophobic water molecule releasing two moles of glucose (reaction 6, k6). In addition, the nonreducing end of CLB can be transformed into LVG (reaction 7, k7).64 This anhydrosugar can also be produced from the dehydration of GLU (reaction 2, k2), which also undergoes isomerization into D-fructose (FRU) and/or dehydration of the reducing end into HMF (reactions 3, 4 & 1, k3, k4 & k1).68 This latter can also be obtained from FRU (reaction 5, k5). Under those mild operating conditions, trends of LVG and HMF yields did not show any sign of decline (Fig. S2 and S3†), indicating that their further degradation (Fig. 8b) could be balanced out by their production. No coloration of the samples indicated the absence of condensed products such as humins. The global kinetic models developed for cellobiose and glucose hydrolysis in the next section will consider the degradation pathways shown in Fig. 11.
3.2 Global kinetic measurements for glucose and cellobiose hydrolysis
To obtain estimates of the kinetic parameters of the reactions shown in Fig. 11, global kinetic measurements were first carried out. The Arrhenius plots for the initial rate of reactant decomposition and main product formation are shown in Fig. S7 and S8† and a summary of the kinetic parameters is provided in Table 2. The global activation energies for the decomposition of glucose and the formation of fructose, levoglucosan and 5-HMF were 110.3 ± 5.4 kJ mol−1, 73.6 ± 6.9 kJ mol−1, 102.8 ± 11.8 kJ mol−1, and 70.0 ± 10.1 kJ mol−1, respectively. In general, the activation energies for hydrolysis in the microfluidic reactor are lower than the ones reported in the literature for the hydrolysis reaction occurring during solid-phase glucose pyrolysis. For example, Mayes et al.69 carried out a computational and experimental investigation of glucose pyrolysis and reported activation energies of 146.9 kJ mol−1 for the water-assisted isomerization of β-glucose into D-fructose and 201.7 kJ mol−1 for the dehydration of the chair conformation of β-D-glucose into levoglucosan (Table 2). Furthermore, Mayes et al.69 reported an activation energy of 356.9 kJ mol−1 for the successive dehydration of β-D-fructose into 5-HMF, which is significantly higher than the global activation energy determined for the formation of 5-HMF in the microfluidic reactor (70.1 kJ mol−1).| Reactant/product | E a (kJ mol−1) | A (s−1) |
|---|---|---|
| Glucose as substrate | ||
| Glucose (GLU), | 110.3 ± 5.4 | 1.8 × 109 |
| Fructose (FRU) | 73.6 ± 6.9 | 7.0 × 106 |
| Levoglucosan (LVG) | 102.8 ± 11.8 | 1.2 × 109 |
| 5-HMF (HMF) | 70.1 ± 10.1 | 1.3 × 105 |
| Cellobiose as substrate | ||
|---|---|---|
| Cellobiose (CLB) | 43.3 ± 1.1 | 2.1 × 102 |
| Glucose | 76.3 ± 7.8 | 2.9 × 107 |
| Fructose | 49.9 ± 9.4 | 3.4 × 103 |
| Levoglucosan | 52.4 ± 10.7 | 7.6 × 103 |
| 5-HMF | 83.2 ± 12.5 | 8.5 × 106 |
Therefore, the results obtained in the microfluidic reactor suggest that the liquid solvent (water in this case) has a significant catalytic effect on both the isomerization of β-glucose into D-fructose and the dehydration of β-D-glucose into levoglucosan, when compared to the literature on hydrolysis reactions during solid pyrolysis. These results demonstrate the significant impact of the reaction environment on the activation energies of hydrolysis reactions. As a first attempt to include the effects of the molten phase in mechanistic fast pyrolysis kinetic models (such as the model by Zhou et al.70), it may be suggested to replace the existing input activation energies of glucose hydrolysis (determined under solid phase pyrolysis conditions) by the activation energies of the hydrolysis reactions determined in the microfluidic reactor (that already include the catalytic effect of a solvent).
Similar to the case of glucose decomposition, the activation energies for cellobiose product formation were lower compared to those reported under solid pyrolysis conditions. For example, Vinu & Broadbelt15 used an activation energy of 142 kJ mol−1 to describe the thermohydrolysis reaction of cellobiose in their mechanistic model for fast pyrolysis, whereas a global activation energy of 43.3 kJ mol−1 was determined in the microfluidic reactor. The presence of the solvent (water) therefore significantly impacted the global kinetics. When comparing the results from the microfluidic reactor to the range of activation energies reported in the literature for the decomposition of cellobiose in sub- and supercritical water, a clearer agreement is visible. Park & Park71 obtained an activation energy of 51.1 kJ mol−1 for cellobiose dehydration in sub- and supercritical water at 593–693 K and 40 MPa. Furthermore, the results of our study are also comparable to the activation energies found for hydrolysis of cellobiose to glucose under hydrothermal conditions. Shafie et al.72 reported activation energies of 81–151 kJ mol−1 for cellobiose hydrolysis (at temperatures of 473–548 K and 10 MPa pressure). These results demonstrate that the reaction environment and conditions greatly affect the reaction rate of the hydrolysis of cellobiose and suggest that the presence of a molten phase during biomass fast pyrolysis, containing a large amount of reactive water (up to 20 wt% in the case of glucose fast pyrolysis) due to dehydration reactions, can significantly alter the hydrolysis rates.59 For both glucose and cellobiose, global activation energies for hydrolysis reactions in a liquid environment are around 50–100 kJ mol−1 lower than those for a solid environment. Although future kinetic measurements and studies are required to fully understand and model the impact of the ILC (melted oligomers) during fast pyrolysis, the microfluidic reactor has proven to be a useful tool for measuring kinetics in a liquid reaction environment.
3.3 Kinetic modelling of cellobiose/glucose hydrolysis
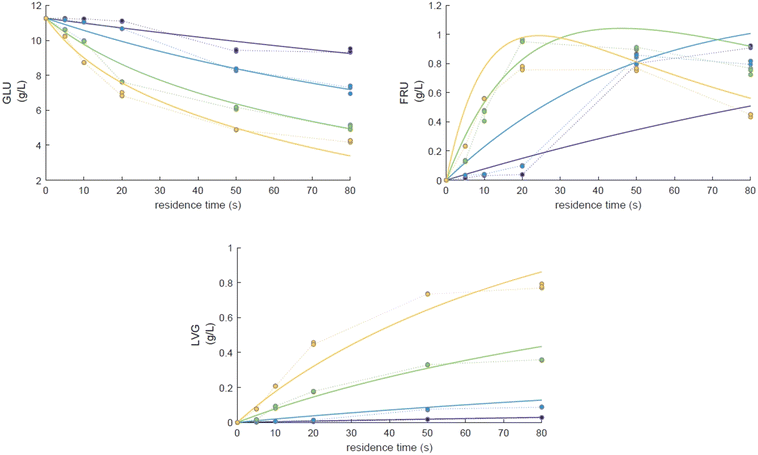
After obtaining global kinetic parameters (section 3.2), a kinetic model based on the general scheme displayed in Fig. 11 (obtained from the detection and quantification of products (section 3.1)) was constructed. Khajavi et al.73 previously reported that sugar hydrolysis reactions in subcritical water are well described by first-order kinetics, therefore all reactions were assumed to be first-order. The assumed steady state leads to simple non-linear algebraic equations derived from a sequence of first-order reactions. Two ODE systems respectively describe the glucose degradation (model A, eqn (13)–(16)) and that of cellobiose (model B, eqn (17)–(19)):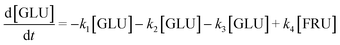 | (13) |
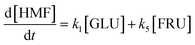 | (14) |
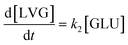 | (15) |
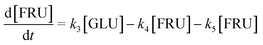 | (16) |
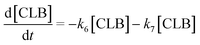 | (17) |
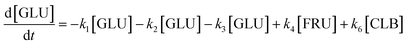 | (18) |
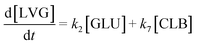 | (19) |
| Reactant | Conditions | Mechanisms | E a (kJ mol−1) | A (s−1 for unimolecular) | Ref. |
|---|---|---|---|---|---|
| a n.r. – not reported. | |||||
| α-β-D-glucose | Pyrolysis | Water-assisted isomerization of β-glucose into D-fructose | 146.9 | 2.3 × 1011 | 49 |
| Dehydration of the chair conformation of β-D-glucose into LVG | 201.7 | 1.4 × 1013 | |||
| Successive dehydration of β-D-fructose into 5-HMF | 356.9 | 6.8 × 1011 | |||
| α-β-D-glucose | Pyrolysis | Water-assisted isomerization of inverted-chair β-D-glucose to D-glucose | 96.7 | 8.13 × 1011 | 49, 74 |
| Inverted-chair β-D-glucose to levoglucosan, type C1 | 192.9 | 5.10 × 1013 | |||
| Glucose | Subcritical water | Glucose global degradation | 155 | 2.9 × 1013 | 73 |
| Cellobiose | Hydrolysis | Cellobiose + water | 134 | 1.4 × 1013 | 75 |
| Cellobiose | Pyrolysis | Thermohydrolysis of cellobiose | 142 | 1.0 × 1014 | 76 |
| Cellobiosan | Pyrolysis | Transglycosylation to LVG | 113 | 4.2 × 107 | 57 |
| Cellobiose | Sub- and supercritical water | Hydrolysis of cellobiose | 51.05 | n.r.a | 71 |
| Cellobiose | Hydrothermal | Hydrolysis of cellobiose | 81–151 | n.r. | 55 |
| Reaction type | A (s−1) | E a (kJ mol−1) | QOFabsolute |
|---|---|---|---|
| Model A, including only glucose degradation dataset | |||
| GLU → HMF dehydration of reducing end, k1 | 896.4 | 49.4 | 0.19 |
| GLU → LVG dehydration, k2 | 8.033 × 106 | 98.1 | |
| GLU → FRU isomerization, k3 | 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 917 917 |
70.1 | |
| FRU → GLU isomerization, k4 | 12.706 × 106 | 83.6 | |
| FRU → HMF dehydration, k5 | 0.62201 | 52.2 | |
| Model B, including only cellobiose degradation dataset | |||
|---|---|---|---|
| GLU → HMF dehydration, k1 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 294 294 |
71.6 | 0.15 |
| GLU → LVG dehydration, k2 | 216.7 | 86.8 | |
| GLU → FRU isomerization, k3 | 2.3747 × 105 | 63.0 | |
| FRU → GLU isomerization, k4 | 3.8675 × 108 | 75.8 | |
| FRU → HMF dehydration, k5 | 713.71 | 40.4 | |
| CLB → GLU hydrolysis, k6 | 1.8773 × 105 | 73.9 | |
| CLB → LVG transglycosylation - dehydration, k7 | 399.54 | 58.2 | |
| Model B, including both glucose + cellobiose degradation datasets | |||
|---|---|---|---|
| GLU → HMF dehydration, k1 | 938.68 | 49.6 | 0.13 |
| GLU → LVG dehydration, k2 | 1.8357 × 107 | 101.8 | |
| GLU → FRU isomerization, k3 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
64.1 | |
| FRU → GLU isomerization, k4 | 8.024 × 105 | 71.7 | |
| FRU → HMF dehydration, k5 | 0.00486 | 9.7 | |
| CLB → GLU hydrolysis, k6 | 2.6907 × 105 | 75.1 | |
| CLB → LVG transglycosylation - dehydration, k7 | 356.31 | 63.8 | |
Values of kinetic constants were calculated at 453 and 533 K (Table 5). The nature of the substrate has a strong influence on all the rates. Isomerization and dehydration reaction rates, k3, k4 and k5, for GLU are slower than those for CLB. The conversion of CLB is mainly achieved through hydrolysis into GLU with a rate constant, k6, greater than that of its transglycosylation into LVG, k7. GLU is preferably dehydrated into HMF at lower temperatures, a pathway that competes with its isomerization into FRU at higher temperatures. When considering the values of k5, CLB appears to be a better substrate for HMF production than GLU.
| Rate constant (s−1) at 453 K | |||||||
|---|---|---|---|---|---|---|---|
| Substrate | k 1 | k 2 | k 3 | k 4 | k 5 | k 6 | k 7 |
| GLU | 0.0018 | 3.88 × 10−5 | 0.000697 | 0.0029 | 6.03 × 10−7 | — | — |
| CLB | 0.00023 | 2.14 × 10−8 | 0.0129 | 0.702 | 0.0156 | 5.65 × 10−4 | 7.79 × 10−5 |
| Rate constant (s−1) at 533 K | |||||||
|---|---|---|---|---|---|---|---|
| Substrate | k 1 | k 2 | k 3 | k 4 | k 5 | k 6 | k 7 |
| GLU | 0.0129 | 0.00193 | 0.0114 | 0.0812 | 4.82 × 10−6 | — | — |
| CLB | 0.0039 | 6.799 × 10−7 | 0.1585 | 14.39 | 0.078 | 0.0107 | 7.9 × 10−4 |
4. Conclusion
In this paper, a new experimental microfluidic setup was developed for measuring thermohydrolysis kinetics of key biomass model compounds under isothermal conditions. The microfluidic reactor was operated under controlled liquid–liquid slug flow conditions, up to 533 K and 7 MPa. Moreover, heat and mass transfer inside the liquid slugs were investigated, and flow patterns were simulated. The calculated heat ramps and measured slug velocities confirmed that the sugar solutions were exposed to a temperature function with a slope varying from 721 to 5333 K s−1. Furthermore, the simulations of the flow patterns also confirmed perfect mixing inside the liquid slugs. The controlled operating conditions (temperature and reaction time) allowed the conduction of a kinetic study under isothermal conditions. Global kinetic parameters were determined for the main products formed during the primary decomposition of glucose and cellobiose at 453–533 K. These parameters demonstrated the key role of the water environment in the production of levoglucosan and hydroxymethylfurfural. For example, the global activation energies for the isomerization (74 kJ mol−1) and dehydration (103 kJ mol−1) reactions of glucose were lower than the ones reported for these reactions under solid-state pyrolysis conditions, suggesting a catalytic effect of the water reaction environment. For cellobiose decomposition, glucose was the main product formed, demonstrating that the hydrolysis reaction was more dominant than the retro-aldol condensation reactions.Following the determination of global kinetic parameters, a multi-mechanism degradation model was developed to investigate the major primary mechanisms in the presence of water under fast heating (which is a first step in simulating the intermediate liquid component formed during fast pyrolysis). The results showed that the nature of the substrate had a significant influence on the reaction rates. For example, isomerization and dehydration rates were slower for glucose compared to cellobiose. Furthermore, hydrolysis of cellobiose to glucose was more dominant than its transglycosylation into levoglucosan.
The microfluidic system and related kinetic modelling approach that has been developed in this paper provide an important foundation for future research to fully understand the role of fast heating conditions in the conversion of biopolymers in the melt-phase. Therefore, this paper should be regarded as the first proof of concept to pursue investigations into the description and isothermal kinetic measurements of melt-phase reactions during biomass fast pyrolysis. Moreover, this paper has made a significant contribution towards understanding the flow system (surface-to-volume ratio, slug flow, temperature, pressure) within the capillary microreactor developed in this paper.
Nomenclature
| D sS | Diameter of the capillary slug (m) |
| L R | Length of the heated capillary (m) |
| LsS | Slug length (m) |
| R sS | Slug radius internal radius of capillary (m) |
| S s | Cross-section of the slug capillary (m2) |
| T R | Reactor temperature (K) |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif)
| Volumetric flow rate (m3 s−1) |
| c P | Mass heat capacity (J kg−1 K−1) |
| ṁ | Mass flow rate (kg s−1) |
| v Ss | Mean slug's mean velocity (m s−1) |
| Re | Reynolds number |
| V | Volume volume (m3) |
| z | z-axis |
| ΔP | Pressure pressure drop (Pa) |
| τ convection | Convection time (s) |
| τ diffusion | Diffusion time (s) |
Greek letters
| α | Thermal diffusivity (m2 s−1) |
| λ | Thermal conductivity (W m−1 K−1) |
| μ | Viscosity (Pa s) |
| ρ | Density (kg m−3) |
Acronyms
| CFD | Computational fluid dynamics |
| ILC | Intermediate liquid component |
| PDMS | Polydimethylsiloxane |
Data availability
The data supporting this article has been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the French scientific program MOPGA (reference ANR-18-MPGA-0013) managed by the National Research Agency and financially supported by the “Investissements d'Avenir” and Region Occitanie (18016004).References
- A. Sharma, V. Pareek and D. Zhang, Biomass pyrolysis—A review of modelling, process parameters and catalytic studies, Renewable Sustainable Energy Rev., 2015, 50, 1081–1096, DOI:10.1016/j.rser.2015.04.193.
- S. M. Gouws, M. Carrier, J. R. Bunt and H. W. J. P. Neomagus, Co-pyrolysis of coal and raw/torrefied biomass: A review on chemistry, kinetics and implementation, Renewable Sustainable Energy Rev., 2021, 135, 110189, DOI:10.1016/j.rser.2020.110189.
- M. Sharifzadeh, M. Sadeqzadeh, M. Guo, T. N. Borhani, N. V. S. N. Murthy Konda, M. C. Garcia, L. Wang, J. Hallett and N. Shah, The multi-scale challenges of biomass fast pyrolysis and bio-oil upgrading: Review of the state of art and future research directions, Prog. Energy Combust. Sci., 2019, 71, 1–80, DOI:10.1016/j.pecs.2018.10.006.
- S. Maduskar, G. G. Facas, C. Papageorgiou, C. L. Williams and P. J. Dauenhauer, Five Rules for Measuring Biomass Pyrolysis Rates: Pulse-Heated Analysis of Solid Reaction Kinetics of Lignocellulosic Biomass, ACS Sustainable Chem. Eng., 2018, 6, 1387–1399, DOI:10.1021/acssuschemeng.7b03785.
- M. Brennan Pecha, J. I. M. Arbelaez, M. Garcia-Perez, F. Chejne and P. N. Ciesielski, Progress in understanding the four dominant intra-particle phenomena of lignocellulose pyrolysis: Chemical reactions, heat transfer, mass transfer, and phase change, Green Chem., 2019, 21, 2868–2898, 10.1039/c9gc00585d.
- S. Vyazovkin, K. Chrissafis, M. L. di Lorenzo, N. Koga, M. Pijolat, B. Roduit, N. Sbirrazzuoli and J. J. Suñol, ICTAC Kinetics Committee recommendations for collecting experimental thermal analysis data for kinetic computations, Thermochim. Acta, 2014, 590, 1–23, DOI:10.1016/j.tca.2014.05.036.
- M. S. Mettler, D. G. Vlachos and P. J. Dauenhauer, Top ten fundamental challenges of biomass pyrolysis for biofuels, Energy Environ. Sci., 2012, 5, 7797–7809, 10.1039/c2ee21679e.
- V. Mamleev, S. Bourbigot, M. le Bras and J. Yvon, The facts and hypotheses relating to the phenomenological model of cellulose pyrolysis. Interdependence of the steps, J. Anal. Appl. Pyrolysis, 2009, 84, 1–17, DOI:10.1016/j.jaap.2008.10.014.
- R. S. Assary, P. C. Redfern, J. R. Hammond, J. Greeley and L. A. Curtiss, Computational studies of the thermochemistry for conversion of glucose to levulinic acid, J. Phys. Chem. B, 2010, 114, 9002–9009, DOI:10.1021/jp101418f.
- S. Maduskar, V. Maliekkal, M. Neurock and P. J. Dauenhauer, On the Yield of Levoglucosan from Cellulose Pyrolysis, ACS Sustainable Chem. Eng., 2018, 6, 7017–7025, DOI:10.1021/acssuschemeng.8b00853.
- V. Maliekkal, S. Maduskar, D. J. Saxon, M. Nasiri, T. M. Reineke, M. Neurock and P. Dauenhauer, Activation of Cellulose via Cooperative Hydroxyl-Catalyzed Transglycosylation of Glycosidic Bonds, ACS Catal., 2019, 9, 1943–1955, DOI:10.1021/acscatal.8b04289.
- M. J. Antal Jr., Private correspondence, 2007 Search PubMed.
- X. Xu, M. J. Antal and D. G. M. Anderson, Mechanism and Temperature-Dependent Kinetics of the Dehydration of tert-Butyl Alcohol in Hot Compressed Liquid Water, Ind. Eng. Chem. Res., 1997, 36, 23–41, DOI:10.1021/ie960349o.
- M. Carlsson, C. Habenicht, L. C. Kam, M. Jerry Antal, N. Bian, R. J. Cunningham and M. Jones, Study of the Sequential Conversion of Citric to Itaconic to Methacrylic Acid in Near-Critical and Supercritical Water, Ind. Eng. Chem. Res., 1994, 33, 1989–1996, DOI:10.1021/ie00032a014.
- R. Vinu and L. J. Broadbelt, A mechanistic model of fast pyrolysis of glucose-based carbohydrates to predict bio-oil composition, Energy Environ. Sci., 2012, 5, 9808–9826, 10.1039/c2ee22784c.
- S. A. El-Sayed and M. E. Mostafa, Pyrolysis characteristics and kinetic parameters determination of biomass fuel powders by differential thermal gravimetric analysis (TGA/DTG), Energy Convers. Manage., 2014, 85, 165–172, DOI:10.1016/j.enconman.2014.05.068.
- Y. C. Lin, J. Cho, G. A. Tompsett, P. R. Westmoreland and G. W. Huber, Kinetics and mechanism of cellulose pyrolysis, J. Phys. Chem. C, 2009, 113, 20097–20107, DOI:10.1021/jp906702p.
- M. van de Velden, J. Baeyens, A. Brems, B. Janssens and R. Dewil, Fundamentals, kinetics and endothermicity of the biomass pyrolysis reaction, Renewable Energy, 2010, 35, 232–242, DOI:10.1016/j.renene.2009.04.019.
- P. T. Williams and S. Besler, The pyrolysis of rice husks in a thermogravimetric analyser and static batch reactor, Fuel, 1993, 72, 151–159 CrossRef CAS.
- B. M. Kabyemela, T. Adschiri, R. M. Malaluan and K. Arai, Kinetics of Glucose Epimerization and Decomposition in Subcritical and Supercritical Water, Ind. Eng. Chem. Res., 1997, 36, 1552–1558, DOI:10.1021/ie960250h.
- M. Sasaki, Z. Fang, Y. Fukushima, T. Adschiri and K. Arai, Dissolution and hydrolysis of cellulose in subcritical and supercritical water, Ind. Eng. Chem. Res., 2000, 39, 2883–2890, DOI:10.1021/ie990690j.
- B. M. Kabyemela, M. Takigawa, T. Adschiri, R. M. Malaluan and K. Arai, Mechanism and Kinetics of Cellobiose Decomposition in Sub-and Supercritical Water, Ind. Eng. Chem. Res., 1998, 37, 357–361, DOI:10.1021/ie9704408.
- X. Liang, A. Montoya and B. S. Haynes, Mechanistic Insights and Kinetic Modeling of Cellobiose Decomposition in Hot Compressed Water, Energy Fuels, 2017, 31, 2203–2216, DOI:10.1021/acs.energyfuels.6b02187.
- E. Hoekstra, R. J. M. Westerhof, W. Brilman, W. P. M. Van Swaaij, S. R. A. Kersten, K. J. A. Hogendoorn and M. Windt, Heterogeneous and homogeneous reactions of pyrolysis vapors from pine wood, AIChE J., 2012, 58, 2830–2842, DOI:10.1002/aic.12799.
- M. Carrier, M. Windt, B. Ziegler, J. Appelt, B. Saake, D. Meier and A. Bridgwater, Quantitative Insights into the Fast Pyrolysis of Extracted Cellulose, Hemicelluloses, and Lignin, ChemSusChem, 2017, 10, 3212–3224, DOI:10.1002/cssc.201700984.
- F. Nardella, M. Mattonai and E. Ribechini, Evolved gas analysis-mass spectrometry and isoconversional methods for the estimation of component-specific kinetic data in wood pyrolysis, J. Anal. Appl. Pyrolysis, 2020, 145 DOI:10.1016/j.jaap.2019.104725.
- Y. M. Kim, T. U. Han, B. A. Hwang, Y. Lee, A. Watanabe, N. Teramae, S. S. Kim, Y. K. Park and S. Kim, New approach for the kinetic analysis of cellulose using EGA-MS, Polym. Test., 2017, 60, 12–17, DOI:10.1016/j.polymertesting.2017.02.004.
- A. A. Boateng, K. B. Hicks and K. P. Vogel, Pyrolysis of switchgrass (Panicum virgatum) harvested at several stages of maturity, J. Anal. Appl. Pyrolysis, 2006, 75, 55–64, DOI:10.1016/j.jaap.2005.03.005.
- S. Thangalazhy-Gopakumar, S. Adhikari, R. B. Gupta and S. D. Fernando, Influence of pyrolysis operating conditions on bio-Oil components: A microscale study in a pyroprobe, Energy Fuels, 2011, 25, 1191–1199, DOI:10.1021/ef101032s.
- E. Hoekstra, W. P. M. van Swaaij, S. R. A. Kersten and K. J. A. Hogendoorn, Fast pyrolysis in a novel wire-mesh reactor: Decomposition of pine wood and model compounds, Chem. Eng. J., 2012, 187, 172–184, DOI:10.1016/j.cej.2012.01.118.
- Y. Zhang, Y. Niu, H. Zou, Y. Lei, J. Zheng, H. Zhuang and S. Hui, Characteristics of biomass fast pyrolysis in a wire-mesh reactor, Fuel, 2017, 200, 225–235, DOI:10.1016/j.fuel.2017.03.070.
- A. A. Zabaniotou, G. Kalogiannis, E. Kappas and A. J. Karabelas, Olive residues (cuttings and kernels) rapid pyrolysis product yields and kinetics, Biomass Bioenergy, 2000, 411–420, DOI:10.1016/S0961-9534(00)00002-7.
- V. Maliekkal, S. Maduskar, D. J. Saxon, M. Nasiri, T. M. Reineke, M. Neurock and P. Dauenhauer, Activation of Cellulose via Cooperative Hydroxyl-Catalyzed Transglycosylation of Glycosidic Bonds, ACS Catal., 2019, 9, 1943–1955, DOI:10.1021/acscatal.8b04289.
- S. Maduskar, G. G. Facas, C. Papageorgiou, C. L. Williams and P. J. Dauenhauer, Five Rules for Measuring Biomass Pyrolysis Rates: Pulse-Heated Analysis of Solid Reaction Kinetics of Lignocellulosic Biomass, ACS Sustainable Chem. Eng., 2018, 6, 1387–1399, DOI:10.1021/acssuschemeng.7b03785.
- C. Krumm, J. Pfaendtner and P. J. Dauenhauer, Millisecond Pulsed Films Unify the Mechanisms of Cellulose Fragmentation, Chem. Mater., 2016, 28, 3108–3114, DOI:10.1021/acs.chemmater.6b00580.
- M. Nasfi, M. Carrier and S. Salvador, Reconsidering the potential of micropyrolyzer to investigate biomass fast pyrolysis without heat transfer limitations, J. Anal. Appl. Pyrolysis, 2022, 165 DOI:10.1016/j.jaap.2022.105582.
- M. Nasfi, M. Carrier and S. Salvador, Kinetic modelling of biomass fast devolatilization using Py-MS: Model-free and model-based approaches, J. Anal. Appl. Pyrolysis, 2023, 174 DOI:10.1016/j.jaap.2023.106128.
- M. B. Pecha, M. Garcia-Perez, T. D. Foust and P. N. Ciesielski, Estimation of Heat Transfer Coefficients for Biomass Particles by Direct Numerical Simulation Using Microstructured Particle Models in the Laminar Regime, ACS Sustainable Chem. Eng., 2017, 5, 1046–1053, DOI:10.1021/acssuschemeng.6b02341.
- E. M. Suuberg, Mass Transfer Effects in Pyrolysis of Coals: A Review of Experimental Evidence and Models, in Chemistry of Coal Conversion, ed. R. H. Schlosberg, Springer US, Boston, MA, 1985, pp. 67–119, DOI:10.1007/978-1-4899-3632-5_4.
- P. N. Nge, C. I. Rogers and A. T. Woolley, Advances in microfluidic materials, functions, integration, and applications, Chem. Rev., 2013, 113, 2550–2583, DOI:10.1021/cr300337x.
- Y. Lu, D. Xin, J. Zhang and G. Luo, Modeling ethyl diazoacetate synthesis in an adiabatic microchemical system, Chem. Eng. J., 2015, 273, 406–412, DOI:10.1016/j.cej.2015.03.028.
- M. N. Kashid, A. Renken and L. Kiwi-Minsker, Gas-liquid and liquid-liquid mass transfer in microstructured reactors, Chem. Eng. Sci., 2011, 66, 3876–3897, DOI:10.1016/j.ces.2011.05.015.
- Z. Chen, J. Xu and Y. Wang, Gas-liquid-liquid multiphase flow in microfluidic systems – A review, Chem. Eng. Sci., 2019, 202, 1–14, DOI:10.1016/j.ces.2019.03.016.
- Z. Yan, J. Tian, C. Du, J. Deng and G. Luo, Reaction kinetics determination based on microfluidic technology, Chin. J. Chem. Eng., 2022, 41, 49–72, DOI:10.1016/j.cjche.2021.08.023.
- K. Shimizu, K. Kato, T. Kobayashi, Y. Komoda and N. Ohmura, Flow and mixing characteristics of gas-liquid slug flow in a continuous Taylor-Couette flow reactor with narrow gap width, Chem. Eng. Process., 2023, 183 DOI:10.1016/j.cep.2022.109226.
- T. Deleau, M. H. H. Fechter, J. J. Letourneau, S. Camy, J. Aubin, A. S. Braeuer and F. Espitalier, Determination of mass transfer coefficients in high-pressure two-phase flows in capillaries using Raman spectroscopy, Chem. Eng. Sci., 2020, 228 DOI:10.1016/j.ces.2020.115960.
- H. Shi, K. Nie, B. Dong, M. Long, H. Xu and Z. Liu, Recent progress of microfluidic reactors for biomedical applications, Chem. Eng. J., 2019, 361, 635–650, DOI:10.1016/j.cej.2018.12.104.
- A. K. Burnham, X. Zhou and L. J. Broadbelt, Critical review of the global chemical kinetics of cellulose thermal decomposition, Energy Fuels, 2015, 29, 2906–2918, DOI:10.1021/acs.energyfuels.5b00350.
- H. B. Mayes, M. W. Nolte, G. T. Beckham, B. H. Shanks and L. J. Broadbelt, The alpha-bet(a) of glucose pyrolysis: Computational and experimental investigations of 5-hydroxymethylfurfural and levoglucosan formation reveal implications for cellulose pyrolysis, ACS Sustainable Chem. Eng., 2014, 2, 1461–1473, DOI:10.1021/sc500113m.
- F. W. Lichtenthaler, Towards improving the utility of ketoses as organic raw materials, Carbohydr. Res., 1998, 313, 69–89, DOI:10.1016/S0008-6215(98)00222-5.
- M. N. Kashid, I. Gerlach, S. Goetz, J. Franzke, J. F. Acker, F. Platte, D. W. Agar and S. Turek, Internal Circulation within the Liquid Slugs of a Liquid−Liquid Slug-Flow Capillary Microreactor, Ind. Eng. Chem. Res., 2005, 44, 5003–5010, DOI:10.1021/ie0490536.
- B. E. Rapp, Fluids, in: Microfluidics: Modelling, Mechanics and Mathematics, Elsevier, 2017, pp. 243–263, DOI:10.1016/B978-1-4557-3141-1.50009-5.
- X. Liu, N. Ai, H. Zhang, M. Lu, D. Ji, F. Yu and J. Ji, Quantification of glucose, xylose, arabinose, furfural, and HMF in corncob hydrolysate by HPLC-PDA-ELSD, Carbohydr. Res., 2012, 353, 111–114, DOI:10.1016/j.carres.2012.03.029.
- B. Chen, R. Hoffmann and R. Cammi, Druckeffekte auf organische Reaktionen in Fluiden – eine neue theoretische Perspektive, Angew. Chem., 2017, 129, 11278–11295, DOI:10.1002/ange.201705427.
- Z. Mohd Shafie, Y. Yu and H. Wu, Insights into the Primary Decomposition Mechanism of Cellobiose under Hydrothermal Conditions, Ind. Eng. Chem. Res., 2014, 53, 14607–14616, DOI:10.1021/ie5027309.
- J. C. Lagarias, J. A. Reeds, M. H. Wright and P. E. Wright, Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions, SIAM J. Optim., 1998, 9, 112–147 CrossRef.
- V. Maliekkal, S. Maduskar, D. J. Saxon, M. Nasiri, T. M. Reineke, M. Neurock and P. Dauenhauer, Activation of Cellulose via Cooperative Hydroxyl-Catalyzed Transglycosylation of Glycosidic Bonds, ACS Catal., 2019, 9, 1943–1955, DOI:10.1021/acscatal.8b04289.
- B. M. Kabyemela, T. Adschiri, R. M. Malaluan and K. Arai, Glucose and fructose decomposition in subcritical and supercritical water: detailed reaction pathway, mechanisms, and kinetics, Ind. Eng. Chem. Res., 1999, 38, 2888–2895, DOI:10.1021/ie9806390.
- X. Zhou, H. B. Mayes, L. J. Broadbelt, M. W. Nolte and B. H. Shanks, Fast pyrolysis of glucose-based carbohydrates with added NaCl part 1: Experiments and development of a mechanistic model, AIChE J., 2016, 62, 766–777, DOI:10.1002/aic.15106.
- K. Takahashi, H. Satoh, T. Satoh, T. Kakuchi, M. Miura, A. Sasaki, M. Sasaki and H. Kaga, Formation kinetics of levoglucosan from glucose in high temperature water, Chem. Eng. J., 2009, 153, 170–174, DOI:10.1016/J.CEJ.2009.06.027.
- M. S. R. Dos Santos Rocha, B. Pratto, R. De Sousa, R. M. R. G. Almeida and A. J. G. Da Cruz, A kinetic model for hydrothermal pretreatment of sugarcane straw, Bioresour. Technol., 2017, 228, 176–185, DOI:10.1016/j.biortech.2016.12.087.
- N. V. Gromov, O. P. Taran, C. Aymonier and V. N. Parmon, Kinetic modeling of the multistep hydrolysis-dehydration of cellulose to platform molecules over a solid carbon acid catalyst in pure water, React. Kinet., Mech. Catal., 2020, 130, 669–684, DOI:10.1007/s11144-020-01814-8.
- R. M. Abdilla, C. B. Rasrendra and H. J. Heeres, Kinetic studies on the conversion of levoglucosan to glucose in water using brønsted acids as the catalysts, Ind. Eng. Chem. Res., 2018, 57, 3204–3214, DOI:10.1021/acs.iecr.8b00013.
- Y. Matsumura, M. Sasaki, K. Okuda, S. Takami, S. Ohara, M. Umetsu and T. Adschiri, SUPERCRITICAL WATER TREATMENT OF BIOMASS FOR ENERGY AND MATERIAL RECOVERY, Combust. Sci. Technol., 2006, 178, 509–536, DOI:10.1080/00102200500290815.
- D. Soukup-Carne, X. Fan and J. Esteban, An overview and analysis of the thermodynamic and kinetic models used in the production of 5-hydroxymethylfurfural and furfural, Chem. Eng. J., 2022, 442, 136313, DOI:10.1016/j.cej.2022.136313.
- I. Itabaiana Junior, M. Avelar Do Nascimento, R. O. M. A. De Souza, A. Dufour and R. Wojcieszak, Levoglucosan: a promising platform molecule?, Green Chem., 2020, 22, 5859–5880, 10.1039/D0GC01490G.
- L. Vilcocq, É. Rebmann, Y. W. Cheah and P. Fongarland, Hydrolysis of Cellobiose and Xylan over TiO _2 -Based Catalysts, ACS Sustainable Chem. Eng., 2018, 6, 5555–5565, DOI:10.1021/acssuschemeng.8b00486.
- T. Nomura, E. Minami and H. Kawamoto, Hydroxymethylfurfural as an Intermediate of Cellulose Carbonization, ChemistryOpen, 2021, 10, 609, DOI:10.1002/open.202100115.
- H. B. Mayes, M. W. Nolte, G. T. Beckham, B. H. Shanks and L. J. Broadbelt, The alpha-bet(a) of glucose pyrolysis: Computational and experimental investigations of 5-hydroxymethylfurfural and levoglucosan formation reveal implications for cellulose pyrolysis, ACS Sustainable Chem. Eng., 2014, 2, 1461–1473, DOI:10.1021/sc500113m.
- X. Zhou, M. W. Nolte, H. B. Mayes, B. H. Shanks and L. J. Broadbelt, Experimental and mechanistic modeling of fast pyrolysis of neat glucose-based carbohydrates. 1. Experiments and development of a detailed mechanistic model, Ind. Eng. Chem. Res., 2014, 53, 13274–13289, DOI:10.1021/ie502259w.
- J. H. Park and S. D. Park, Kinetics of Cellobiose Decomposition under Subcritical and Supercritical Water in Continuous Flow System, Korean J. Chem. Eng., 2002, 19(6), 960–966, DOI:10.1007/BF02707218.
- Z. M. Shafie, Y. Yu and H. Wu, Insights into the primary decomposition mechanism of cellobiose under hydrothermal conditions, Ind. Eng. Chem. Res., 2014, 53, 14607–14616, DOI:10.1021/ie5027309.
- S. H. Khajavi, S. Ota, R. Nakazawa, Y. Kimura and S. Adachi, Hydrolysis Kinetics of Trisaccharides Consisting of Glucose, Galactose, and Fructose Residues in Subcritical Water, Biotechnol. Prog., 2006, 22, 1321–1326, DOI:10.1021/BP060086L.
- V. Seshadri and P. R. Westmoreland, Concerted Reactions and Mechanism of Glucose Pyrolysis and Implications for Cellulose Kinetics, J. Phys. Chem. A, 2012, 116, 11997–12013, DOI:10.1021/jp3085099.
- H. M. Pilath, M. R. Nimlos, A. Mittal, M. E. Himmel and D. K. Johnson, Glucose Reversion Reaction Kinetics, J. Agric. Food Chem., 2010, 58, 6131–6140, DOI:10.1021/jf903598w.
- R. Vinu and L. J. Broadbelt, A mechanistic model of fast pyrolysis of glucose-based carbohydrates to predict bio-oil composition, Energy Environ. Sci., 2012, 5, 9808, 10.1039/c2ee22784c.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4re00297k |
| This journal is © The Royal Society of Chemistry 2025 |