 Open Access Article
Open Access ArticleThe hole mass in Car–Parrinello molecular dynamics: insights into the dynamics of excitation†
Sherif Abdulkader
Tawfik
 *a and
Tiffany R.
Walsh
*a and
Tiffany R.
Walsh
 b
b
aApplied Artificial Intelligence Institute, Deakin University, Geelong, Victoria 3216, Australia. E-mail: s.abbas@deakin.edu.au
bInstitute for Frontier Materials, Deakin University, Geelong, Victoria 3216, Australia
First published on 1st May 2025
Abstract
In the Car–Parrinello molecular dynamics (CPMD) formalism, orbitals can be assigned different effective masses according to whether the orbital is occupied by a hole or an electron, and such masses affect the response of the orbitals to their environment. Inspired by this, we introduce and implement a novel modification of CPMD, HoleMass CPMD, in which a hole, which is a partially empty orbital, is assigned a fictitious mass that is different from fully occupied orbitals. Despite the simplicity of the approach, we find that it solves a key problem in first principles molecule dynamics simulation: for a set of carefully assigned mass values, the method is able to successfully simulate photoinduced chemical reactions, exemplified here by the ring-opening reaction in oxirane within a few femtoseconds, and cyclobutene, within a few picoseconds. Our method can reproduce the CO ring-opening of oxirane, and the correct isomerization sequence for cyclobutene: when the ring opens, the first isomer that forms is the cis isomer, followed by the trans isomer. Our method has been implemented in the Car–Parrinello package of QuantumEspresso and is available as an open-source contribution. The HoleMass CPMD method provides a new quantum chemistry tool for the simulation of excitation dynamics in molecules, and can also be applied for modelling charge localization effects in materials systems.
1. Introduction
Navigating the potential energy surface (PES) of molecules is the “holy grail” of understanding chemical reactivity.1,2 Tracing the structural and electronic changes along the reaction pathway of a chemical system, provides important details about the quantum states of the system before a chemical reaction takes place. Exploration of the reaction pathway at the zero-time, zero-temperature limit can be performed at high computational accuracy and precision by using quantum chemistry transition state calculations. To incorporate the impact of entropy (temperature), one can use less computationally expensive and approximate time-dependent methods. While high computational accuracy achieves the theoretical requirement of “chemical accuracy”, the time- and temperature-dependence can incorporate “chemical relevance”: that is, what is actually taking place in a reaction as opposed to what might take place under ideal conditions.A number of time- and temperature-dependent quantum-based computational approaches have been developed for the simulation of the coupled electronic and molecular dynamics at finite temperatures. Born–Oppenheimer molecular dynamics (BOMD), described as the “gold standard” for molecular dynamics,3 separates the nuclear and electronic degrees of freedom based on the Born–Oppenheimer approximation, and evolves the nuclear degrees of freedom based on Newtonian mechanics. It does not directly evolve the electronic degrees of freedom; instead, electronic wavefunctions are optimized at every step of the evolution, and therefore the nuclear dynamics evolve based on the ground state of the electrons. Realizing that the ground state calculation in BOMD is a computational bottleneck, there have been several proposals in the literature towards the development of less computationally complex methods for the propagation of the wavefunctions, the most significant of which are the Ehrenfest time-dependent density functional theory (Ehrenfest TDDFT)4 and Car–Parrinello molecular dynamics (CPMD).5 The nuclear dynamics in both Ehrenfest TDDFT dynamics and CPMD are handled classically like BOMD. The key difference in these methods is that Ehrenfest TDDFT propagates the electronic wavefunctions by integrating the time-dependent Schrödinger equation, whereas CPMD propagates the electronic wavefunctions based on a fictitious kinetic energy term in the system's modified Lagrangian. CPMD gained massive popularity since its inception in 1985, mainly because of its high computational efficiency as compared to both BOMD and Ehrenfest TDDFT.4
The PES modelled by BOMD and CPMD is the adiabatic PES, in which the saddle points indicate the presence of potential crossing into the excited state PES, but the crossing is forbidden. Thus, these methods cannot model the dynamics of reactions that involve electronic excitation, such as photocatalytic and photoinduced reactions. These two methods, however, were reported to model non-adiabaticity after applying fundamental modifications to the computational method. For example, application of constrained-DFT was demonstrated to recover the photoisomerization reaction of azobenzene,6 and adding the Tully's fewest switches surface hopping (FSSH) algorithm to BOMD was shown simulate the breaking of the oxirane ring.7 A modified version of CPMD was demonstrated to reproduce the ring-opening reaction in cyclobutene and the complex isomerization of Si6H8.8 As for ETDDFT, the latter allows electrons to propagate along a mixture of adiabatic states, and therefore it can model the nonadiabatic dynamics of electronic state in principle, such as intersystem crossing. However, ETDDFT requires a methodological modification, such as a surface hopping add-on, to reproduce nonadiabatic effects such as the H2 dissociation on gold nanoclusters, as reported in ref. 9.
In this work, we introduce a new approach, HoleMass CPMD, that can enable CPMD to simulate the nonadiabatic dynamics of chemical reactions. The approach is based on assigning fictitious masses to orbitals according to the orbital occupations and constraining the occupation during the CPMD simulation. We demonstrate the ability of the method to simulate the photoinduced ring-opening reaction in two example molecules, oxirane and cyclobutene.
2. The hole mass in CPMD
In the Car–Parrinello molecular dynamics (CPMD), the Lagrangian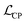 is given by
is given by | (1) |
 is a kinetic energy term for the electronic states. This term treats the electronic states as classical particles, and assigns the electrons a mass-like coefficient, μ, and is thus known as the fictitious kinetic energy. The second term is the nuclear kinetic energy; the third term is the total Kohn–Sham energy and the last term imposes the orthonormalization of the occupied orbitals. From (1), one can derive the following equations of motion,
is a kinetic energy term for the electronic states. This term treats the electronic states as classical particles, and assigns the electrons a mass-like coefficient, μ, and is thus known as the fictitious kinetic energy. The second term is the nuclear kinetic energy; the third term is the total Kohn–Sham energy and the last term imposes the orthonormalization of the occupied orbitals. From (1), one can derive the following equations of motion,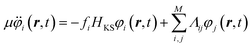 | (2) |
 | (3) |
 | (4) |
The kinetic energy term in (1) gives rise to a fictitious equation of motion, and hence fictitious dynamics, for the electrons, eqn (2). This equation reduces to the time-independent Kohn–Sham equation, where the Λij terms become the energy eigenvalues of the system, in the limit of self-consistency of the electronic states (![[small phi (variant), Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a4.gif) i(r) = 0), eqn (2) reduces to
i(r) = 0), eqn (2) reduces to
 | (5) |
 | (6) |
This equation establishes a relationship between the Lagrange multipliers Λij and the eigenvalues, as well as between Λij and fi. Although unoccupied states cannot be directly modelled within the standard CPMD because the first term in eqn (2) would vanish, a recent proposal by Medina et al.10 sought to model the evolution of unoccupied states by modifying the form of the orthonormalization matrix (Λ) to accommodate zero values for fi, where all orbitals are assigned the same fictitious mass. Several authors have also implemented various strategies to model fractional occupations using CPMD in the case of metallic systems11–13 and for modelling excited electrons.14
Freezing electronic orbitals, such as in constrained DFT (CDFT), can be used for the calculation of photoexcitation phenomena in crystal defects15 and molecules (also known as ΔSCF).16 The general principle is to freeze the occupation of the orbitals during the energy minimization to approximate the structure and energetics of an excited state. For example, the excitation of the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO) can be simulated by setting the HOMO occupation to 0, and the LUMO occupation to 1. Constraining the density during the molecular dynamics simulation was previously reported ref. 17 and 18, in which the occupation numbers are fixed and the electron density is frozen during the simulation. These methods require and additional force term in due to the density constraint. Here we examine the constraining of the occupation numbers during CPMD, which will not require a force term.
In this work we consider a modification of eqn (2),
 | (7) |
Although the standard CPMD formalism warrants reasonable latitude in assigning the value for the electron mass in a CPMD wavefunction propagation calculation, there is, in principle, the option to assign a different electron mass value for each electron. The evolution of the energy and temperature is very sensitive to the choice of the electron mass, and one must experiment with multiple values in a microcanonical ensemble (in which energy is conserved) to ensure that the dynamics of the system will not lead to a drift in the total energy, which violates the energy conservation of the ensemble. It should be noted here that, in standard CPMD, the choice of the electron mass can be system-specific: several values for the electron mass have been reported in the literature. In this work we examine a range of values for the hole and the unoccupied electron masses and use the energy conservation of the system dynamics to identify the range of valid mass values.
Given that the total energy should be conserved, what happens to the temperature? One approach is to fix the temperature at a particular value, say 300 K, by using an artificial thermostat such as velocity rescaling. This was done by Tavernelli et al.19 in their application of TDDFT for simulating the isomerization process. They justified the velocity rescaling approach as mimicking the intermolecular collisions. The authors also reported that removing the thermostat yielded several crossings between the ground and excited states, but no isomerization events were observed.
As test cases, we examine the photoinduced ring-opening reaction of two molecules: ethylene oxide or oxirane (C2H4O, displayed in Fig. 1(a)) and cyclobutene (C4H6, displayed in Fig. 1(b)). The C2H4O ring structure is the simplest epoxide ring which has been a model system for photoinduced ring opening.7,20,21 The ring opening reaction is fundamental to its polymerisation into the poly-ethylene oxide, which can be induced by UV-irradiation.22 There are three stoichiometric minima with this molecular formula: acetaldehyde and ethanol. The transition to the acetaldehyde structure starts with a CO bond breaking, followed by a CC bond breaking, and is known as the Gomer–Noyes mechanism.21 The entire Gomer–Noyes mechanism was simulated by Tapavicza et al.20 using TDDFT-FSSH, by initiating the simulation in the S1 state (HOMO → LUMO). Later, it was simulated by Krenz et al.7 using constrained-DFT by forcing the electronic transitions HOMO → LUMO (S1), HOMO → LUMO + 1 (S2) and HOMO → LUMO + 2 (S3).
The C4H6 cyclobutene molecule possesses multiple configurations, which have been thoroughly examined by Nguyen and Gordon23 and Sakai.24 The lowest energy structure is the trans-butadiene conformation,23 but the molecule has a wealth of isomers and undergoes various isomerization reactions. Among the metastable configurations of this molecule are the cyclobutene,8,24cis-butadiene,23,24 bicyclobutane23,24 and skewed conformers.25 The cis-butadiene conformation undergoes a ring-closing isomerization reaction upon optical excitation to either cyclobutene or bicyclobutane.24 The ring-opening reaction of cyclobutene to trans-butadiene faces a thermal energy barrier of ∼30 kcal mol−1.26
Even though there are potentially multiple isomerization pathways for the molecule, the energy barriers associated with these pathways are not insignificant. Finding the right approach to navigate the PES of the molecule in a time-dependent dynamical simulation has been an important research objective. Cyclobutene has particularly been an interesting case for molecular dynamics simulations because it should follow a disrotatory stereochemistry upon photoexcitation, according to the Woodward–Hoffmann (WH) rules.27 However, various photoisomerization reaction products that are WH-forbidden have been observed, and the use of different theoretical methods yield different results with respect to WH rules: BOMD simulations that demonstrate the onset of disrotatory movement within 15 fs of the simulation, confirming the WH rule,28 and TDDFT-FSSH simulations predicted the existence of a WH-forbidden product.29 Iannuzzi et al.8 examined the ground state reactivity of this molecule using a modified CPMD theory for the modelling the free energy surface, and demonstrated the ability of their approach to successfully cross the high isomerization energy barriers, but their work did not incorporate the photoexcitation physics in the simulation, nor did it reflect on the WH stereochemistry in their analysis of the reaction pathway. It is worth mentioning that cyclobutene and its derivatives were the subject of several investigations that examined the mechanochemical ring-opening effect in which the ring-opening reaction is driven by mechanical force.30–33 In that case, the molecule undergoes disrotatory movement, in violation of WH rules for non-photoinduced ring-opening of the molecule.33 In the present work, we use the signatures of disrotatory movement as a qualitative validation of the hole mass method.
In the present investigation, we demonstrate the ability of the hole mass formalism in crossing the isomerization energy barrier in a reasonable simulation time, with the advantage of incorporating the effect of photoexcitation explicitly (in terms of freezing the partial occupation of the molecular orbitals). For a range of hole mass parameters, we monitor the dynamics of the ring-opening reactions using various structural parameters, including bond lengths, dihedral and disrotatory angles, and use these parameters to suggest the best hole mass parameters for organic reactions.
3. Computational details
All calculations were performed using the Quantum Espresso code.34 The generalized-gradient approximation using the (PBE) parametrization35 was applied. The initial structures of the molecules were obtained from the CCCDB database, where the structures were optimized using the Hartree–Fock self-consistent field (SCF) method, using the dAug-cc-pVTZ basis set. We display in Fig. 1 the two isomers of C2H4O, oxirane and acetaldehyde, and the three isomers of C4H6, cyclobutene, cis-butadiene and trans-butadiene.In the HoleMass CPMD simulation process, the electronic orbitals of cyclobutene were first optimized with an energy cut-off of 10−7 Ha, and then the molecule was equilibrated with velocity rescaling at a temperature of 300 K using the Verlet integrator.36 This was followed by a calculation within the energy-conserving microcanonical ensemble (NVE). We chose the NVE ensemble, rather than a temperature-based thermostat, to exclude the influence of the thermostat on the excitation dynamics. This was previously reported in ref. 10. It is noted here that imposing a thermostat on the dynamics of systems that undergo electronic excitations can be counterproductive for systems in which the excitation leads to isomerization. This is because the isomerization process is likely to involve bond fission, during which the velocities of the atoms increase rapidly. Having a thermostat in place can limit the evolution of bond fission by reducing the velocity of the atoms in the system.36 A time step of 3 a.u. (0.073 fs) was used in the simulations.
4. Results and discussion
Hole mass parameter values
We first determined the range of suitable values for the fictitious masses μo, μh and μu by performing simulations of the HOMO → LUMO transitions for O2, C2H4, C4H6, C6H8 and azobenzene. We examined two different fractional occupancies for the electronic transitions for each of the molecules: fh = 0.1, fu = 0.9 and fh = 0.5, fu = 0.5. The ranges of values for the fictitious masses considered in this work are μo = 200, 400, 600 amu, μh = 500, 1000 amu and μu = 100, 200, 300 amu. Our calculations show that specifying fh = 0.1, fu = 0.9 will violate the energy conservation of the ensemble for most mass values except in the cases where μo = 200 amu, whereas specifying fh = 0.5, fu = 0.5 can result in conserved ensemble energies if, for both values of μh considered, or if μo = 200 amu and μu, = 100, 200, 300 amu. When μo = 200 amu, only the value μu = 100 amu converges to the initial temperature of the system, whereas setting μu = 200 amu or 300 amu led to loss of thermalization (that is, the temperature dropped far below the initial temperature).In the following, we focussed on the six mass values (with μh = 500, 1000 amu and μo = 2μu). We label each combination of mass values as displayed in Table 1.
| μ o | μ h | μ u | |
|---|---|---|---|
| μ A | 200 | 500 | 100 |
| μ B | 200 | 1000 | 100 |
| μ C | 400 | 500 | 200 |
| μ D | 400 | 1000 | 200 |
| μ E | 600 | 500 | 300 |
| μ F | 600 | 1000 | 300 |
Oxirane
We monitored the ring-opening reaction in oxirane by measuring the bond length dCC and bond angle dCCOθ as indicated in Fig. 1(a). We display the results of the simulations for the hole mass parameter values μA, μC, and μE in Fig. 2. We do not display the results for the parameter values μB, μD, and μF because of their similarity to the results obtained with the previous parameters.The CO ring opening reaction occurs during the first few fs of the simulations using each of the hole mass parameters. In terms of the CO bond distance, the largest observed opening happens with the μE parameter values, and we display the structure of the opened ring in the inset of Fig. 2(i). This structure is similar to that displayed in Fig. 8 of ref. 20 for the ring-opening of oxirane which was obtained using TDDFT-FSSH. The CO bond length for the C atom bonded to O increases, but does not increase enough for a bond scission. The maximum values of the CO bonds are 1.44 Å for μA, 1.45 Å for μC and 1.55 Å for μE.
The simulations reported in ref. 20 yielded the scission of oxirane into CH4 and CO, as well as the radicals  and CHO˙, while our simulations only yielded the CO ring-opening product. Both our simulations and those in ref. 20 do not reproduce the result of the experimental photoinduced decomposition of oxirane reported by Kawasaki et al.37 in which the most dominant reaction product is the oxygen abstraction reaction: C2H4O + hv → O + C2H4 + H2. Oxygen abstraction does not involve H tautomerisation that was reported in ref. 20, but is likely to evolve from the oxirane structure with CO ring-opening after exposure to high energy light, as was performed in the experiment by Kawasaki et al.37 The difference between the results of our simulations and those in ref. 20 is most likely due to the application of the FSSH scheme by ref. 20, and would not emerge from the computation of the electronic structure because both our calculations and ref. 20 apply the plane-wave basis sets. The way the FSSH scheme navigates the PES is fundamentally different from the method we applied in our work, because of the probabilistic nature of FSSH. Both studies do not reproduce the decomposition of oxirane, which is most likely due to their divergence from the true PES. Additionally, the representation of a photoinduced chemical reaction either via surface hopping or forced electronic transitions might not capture specific aspects of the physics of the phenomenon, which can only be accounted for by the incorporation of the photon energy within the formalism.
and CHO˙, while our simulations only yielded the CO ring-opening product. Both our simulations and those in ref. 20 do not reproduce the result of the experimental photoinduced decomposition of oxirane reported by Kawasaki et al.37 in which the most dominant reaction product is the oxygen abstraction reaction: C2H4O + hv → O + C2H4 + H2. Oxygen abstraction does not involve H tautomerisation that was reported in ref. 20, but is likely to evolve from the oxirane structure with CO ring-opening after exposure to high energy light, as was performed in the experiment by Kawasaki et al.37 The difference between the results of our simulations and those in ref. 20 is most likely due to the application of the FSSH scheme by ref. 20, and would not emerge from the computation of the electronic structure because both our calculations and ref. 20 apply the plane-wave basis sets. The way the FSSH scheme navigates the PES is fundamentally different from the method we applied in our work, because of the probabilistic nature of FSSH. Both studies do not reproduce the decomposition of oxirane, which is most likely due to their divergence from the true PES. Additionally, the representation of a photoinduced chemical reaction either via surface hopping or forced electronic transitions might not capture specific aspects of the physics of the phenomenon, which can only be accounted for by the incorporation of the photon energy within the formalism.
Cyclobutene
We monitored the ring-opening reaction in cyclobutene by measuring the bond length dC3–C4, as indicated in Fig. 1(b). The conversion from cis to trans was monitored by calculating the dihedral angle dC3124θ. The disrotatory motion was monitored by calculating the absolute value of the disrotatory angle, which is given by |(β1 + β2) − (β3 + β4)|, where the dihedrals βi are indicated in Fig. 1.We applied the hole mass values to the simulation of the ring-opening reaction and ran the simulations for ∼10 ps. The simulation with μh = 1000, μo = 400 did not result in a ring-opening reaction within the simulation time. The results of the six simulations are presented in Fig. 3–6. We display in Fig. S1 and S2† the Fourier transform of the bond vibrations displayed in Fig. 5 and 6 to explore the vibrational modes prior bond scission.
 | ||
| Fig. 3 Cyclobutene ring-opening simulations: the evolution of the relative energy E(t)–E(0) (Ha) as a function of time (in ps) for the six mass values in Table 1: (a) μA, (b) μB, (c) μC, (d) μD, (e) μE, and (f) μF. | ||
 | ||
| Fig. 4 Cyclobutene ring-opening simulations: the evolution of the temperature (K) as a function of time (in ps) for the six mass values in Table 1: (a) μA, (b) μB, (c) μC, (d) μD, (e) μE, and (f) μF. | ||
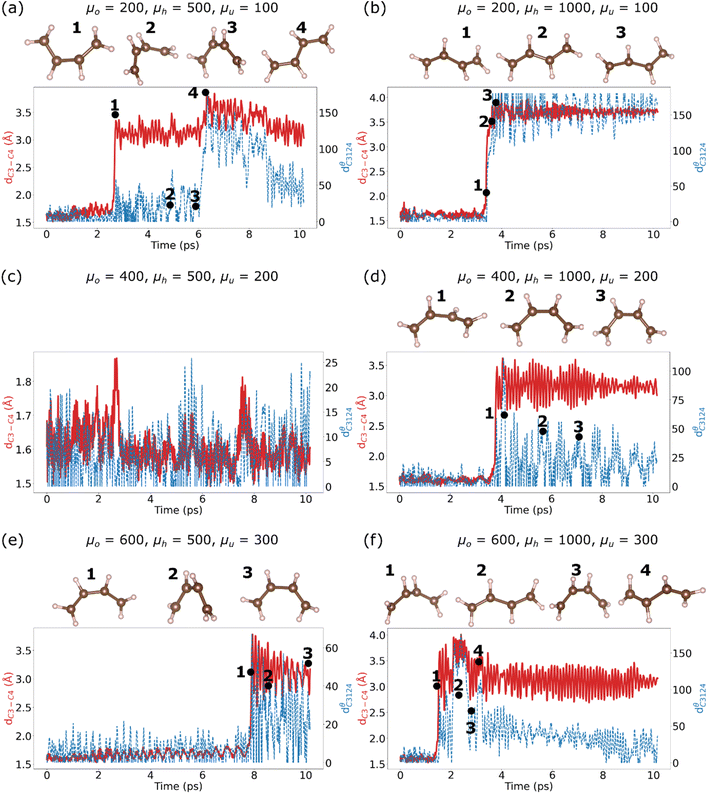 | ||
| Fig. 5 Cyclobutene ring-opening simulations: the evolution of the C3–C4 bond length (Å, dC3–C4) and the dihedral angle (degrees, dC3124θ) for the six mass values in Table 1: (a) μA, (b) μB, (c) μC, (d) μD, (e) μE, and (f) μF. | ||
 | ||
| Fig. 6 Cyclobutene ring-opening simulations: the evolution of the C1–C2 bond length (Å, dC1–C2) and the disrotatory angle (degrees) for the six mass values in Table 1: (a) μA, (b) μB, (c) μC, (d) μD, (e) μE, and (f) μF. | ||
In all simulations, the switch to the NVE ensemble resulted in a large increase in temperature within the first 1 ps, followed by a drop in temperature to values around 300 K. The evolution of the temperature, as well as the dynamics of the ring-opening reaction, clearly depends on the choice of mass values. We examined the ring breaking in μA in three additional trajectories using different initial random velocities, and obtained the ring opening reaction in these cases as well. The earliest onset of ring-opening (after about 2 ps of NVE dynamics) occurs for μE (Fig. 3(e), 4(e), 5(e) and 6(e)), while the ring-opening reaction takes the longest time to occur for μD (Fig. 3(d), 4(d), 5(d) and 6(d)). Once the reaction takes place, the temperature drops gradually to ∼200 K, except in Fig. 4(e).
We display the structure of the molecule at various points along the time axis after the ring-opening reaction in the subfigures of Fig. 5. For μA (Fig. 3(a), 4(a), 5(a) and 6(a)), the ring breaks as depicted in the cis structure 1, which then undergoes several configurational changes for about 3 ps until it converts to the trans structure 4. The conversion from cis to trans occurs at ∼6 ps, which follows the ring-opening reaction by ∼2.5 ps. Later, the trans structure gradually converts to the cis structure. The disrotatory angle (Fig. 6(a)) exhibits a rapid rise after ∼2.5 ps, which agrees with the WH rules for this molecule.
In the case of μB (Fig. 3(b), 4(b), 5(b) and 6(b)), the transition from the cyclobutene structure to the trans structure occurs more abruptly, as can be seen in the stabilization of dC3124θ at 180° for the remaining simulation time. However, the trajectory of the disrotatory angle (Fig. 5(b)) is opposite to that of μA: the angle starts at a value > 100°, and then drops to values < 50° after the ring-opening. Thus, the simulation leads to anti-WH dynamics. The simulation using μD (Fig. 3(d), 4(d), 5(d) and 6(d)) displayed a rapid change in the dihedral angle after ∼4 ps, which corresponded to the ring-opening reaction followed by the transition to a structure close to the trans structure (dC3124θ ∼ 100°), and then the system changed to the cis structure. Such incomplete transition to the trans-butadiene structure also occurred in the simulation that applied μE (Fig. 5(e)); after ∼8 ps, the ring-opening reaction yields a distorted cis structure, and continued in this manner for the duration of the simulation. In both μE and μF the disrotatory angles drop after the onset of the ring-opening reaction, indicating anti-WF dynamics. Applying μF (Fig. 5(f)) yields a ring-opening reaction after ∼2 ps, with a transition to a structure close to the trans structure (dC3124θ ∼ 160°), followed by several re-configurations within the same dihedral angle (labelled 2 and 4 in Fig. 5(f)), and then followed by transitioning to the cis structure. The disrotatory angle in this case is similar to that in μA, where the angle increases after the onset of ring-opening, conforming to the WH rules.
We examine the vibrational modes of the cyclobutene molecules prior to the ring breaking reaction by computing the Fourier transform of the CC bonds. Fig. S1† displays Fourier transform of dC3–C4, and Fig. S2† displays the Fourier transform of dC1–C2. Cyclobutene has characteristic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond stretching modes around 1500 cm−1,38 and we can observe vibrational models around 1500 cm−1 in the Fourier transform of the C1–C2 bond length (Fig. S2†), which does not break throughout the simulation. However, Fig. S1† shows a lack of the modes around 1500 cm−1, while active modes in Fig. S1† are between 500 cm−1 and 1000 cm−1. These modes are related to the ring expansion and deformation, and CH2 rocking, twisting, wagging and C–H out-of-plane bending.38 This mixture of vibrational modes shows the disruptive dynamics of the ring prior to the breaking of the C
C bond stretching modes around 1500 cm−1,38 and we can observe vibrational models around 1500 cm−1 in the Fourier transform of the C1–C2 bond length (Fig. S2†), which does not break throughout the simulation. However, Fig. S1† shows a lack of the modes around 1500 cm−1, while active modes in Fig. S1† are between 500 cm−1 and 1000 cm−1. These modes are related to the ring expansion and deformation, and CH2 rocking, twisting, wagging and C–H out-of-plane bending.38 This mixture of vibrational modes shows the disruptive dynamics of the ring prior to the breaking of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond.
C bond.
A key feature that can aid in identifying the most valid combination of mass values is by inspecting the order of isomerization: which isomer occurs first? In all simulations μA, μD and μF, the first structure that emerges is the cis isomer, followed later by the trans isomer. The cis–trans transition took the longest time (3.6 ps), whereas the other two simulations took less than 1 ps for the transition to take place. Only the case of μB produced the trans isomer as the first conformer after the ring-opening reaction, but the structure remained in the trans state for the duration of the simulation. Comparing these results with the structural transitions in ref. 20, the cis isomer is a transition state in this reaction, and this is accurately reproduced in our simulation. Given that both μA and μF yield WH-confirming dynamics, they can accurately predict the correct sequence and dynamics of transitions in a simulation.
Forced hole mass excitation
We examined the impact of a forced excitation on the dynamics of the cyclobutene molecule. In the forced excitation scheme, the electronic orbitals of the molecule were equilibrated using the occupations fh = 0.9, fu = 0.1 to approximate a ground state electronic structure, followed by a short molecular equilibration step under the same occupations, and then the simulation was conducted with the occupations fh = 0.5, fu = 0.5. We performed these calculations with μh = 500, 1000 and μo = 2μu (a total of six simulations) and found that the dynamics strongly violated the mass conservation in all cases except that of μo = 200 amu, μu = 100 amu and μh = 500 amu. In that case, the energy is nearly conserved, the temperature fluctuations are much larger than in the case without forced excitation, and the ring-opening reaction does not take place. We therefore did not pursue this simulation further.Ring breaking with standard CPMD
We propagated the evolution of cyclobutene using standard CPMD (with no electronic excitation) with no thermostat. For the duration of 23.8 ps, only minor variations were noted in the equilibrium bond length dC3–C4 (Fig. 1(b)) and the temperature dropped from 300 K to 30–50 K, indicating the inability of standard CPMD to realize the bond-breaking reaction.Computational cost
We note that, within the QuantumEspresso code, the cost of running the CPMD dynamics using the Hole Mass method is close to the cost of running CPMD using default settings: running CPMD for the cyclobutene molecule costs 0.77 s per simulation step, while running CPMD with the Hole Mass code costs 0.81 s per simulation step. These simulations were run on 24 cores on a HPE Cray EX architecture.Application to periodic systems
Given that the QuantumEspresso code we used implicitly applies periodic boundary conditions, it is in principle possible to apply the hole mass formalism to electronic photoinduced reactions in periodic systems. Moreover, one can compute the effective mass of the orbitals in periodic systems by performing band structure calculations at regular intervals during the simulation, and then using the computed masses to set the hole mass in subsequent simulation steps. However, this has not been feasible because the QuantumEspresso code: only supports forced electronic transitions (CDFT), such as those applied in ref. 15, at the Γ point. The VASP code39 supports proper CDFT across all points in momentum space, but it does not support CPMD.5. Conclusions
Inspired by the identification of masses to hole orbitals in solid state physics, we assigned different fictitious masses to orbitals in Car–Parrinello molecular dynamics (CPMD) to model the dynamics of photoinduced reactions. This new method, HoleMass CPMD, was applied to two example photoinduced ring-opening reactions; the breaking of the oxirane ring, and the breaking of the cyclobutene ring to form the trans-butadiene molecule. Our simulations could reproduce the CO ring-opening of oxirane, as well as the expected order of isomeric transition in cyclobutene in which cyclobutene transitions to the cis isomer, then to the trans isomer. Based on the analysis of the disrotatory angle, we identified hole mass parameter values that produced outcomes which conform with the Woodward–Hoffmann rules of the photoinduced ring-opening reaction in the molecule. HoleMass CPMD can be utilized for the simulation of photoinduced chemical reactions in molecular systems, as well as for solid state systems. For example, the dynamics of frontier orbitals in semiconductors can be simulated using HoleMass CPMD, and such investigations are currently underway. The source code of HoleMass CPMD is available at ref. 40.Data availability
All the simulation input and output files for oxirane and cyclobutene can be uploaded from the repository https://doi.org/10.5281/zenodo.14994469.Author contributions
S. A. T. conceived and designed the calculations and wrote the manuscript. All authors discussed the results and revised the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. A. T. recognizes the support of the Alfred Deakin Postdoctoral Research Fellowship from Deakin University. This work was supported by computational resources provided by the Australian Government through the National Computational Infrastructure National Facility and the Pawsey Supercomputer Centre. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231.References
- H. B. Schlegel, Exploring Potential Energy Surfaces for Chemical Reactions: An Overview of Some Practical Methods, J. Comput. Chem., 2003, 24(12), 1514–1527, DOI:10.1002/jcc.10231.
- F. Bernardi, M. Olivucci and M. A. Robb, Potential Energy Surface Crossings in Organic Photochemistry, Chem. Soc. Rev., 1996, 25(5), 321, 10.1039/cs9962500321.
- A. M. N. Niklasson, Extended Born-Oppenheimer Molecular Dynamics, Phys. Rev. Lett., 2008, 100(12), 123004, DOI:10.1103/PhysRevLett.100.123004.
- X. Andrade, A. Castro, D. Zueco, J. L. Alonso, P. Echenique, F. Falceto and Á. Rubio, Modified Ehrenfest Formalism for Efficient Large-Scale Ab Initio Molecular Dynamics, J. Chem. Theory Comput., 2009, 5(4), 728–742, DOI:10.1021/ct800518j.
- R. Car and M. Parrinello, Unified Approach for Molecular Dynamics and Density-Functional Theory, Phys. Rev. Lett., 1985, 55(22), 2471–2474, DOI:10.1103/PhysRevLett.55.2471.
- M. L. Tiago, S. Ismail-Beigi and S. G. Louie, Photoisomerization of Azobenzene from First-Principles Constrained Density-Functional Calculations, J. Chem. Phys., 2005, 122(9), 094311, DOI:10.1063/1.1861873.
- M. Krenz, U. Gerstmann and W. G. Schmidt, Photochemical Ring Opening of Oxirane Modeled by Constrained Density Functional Theory, ACS Omega, 2020, 5(37), 24057–24063, DOI:10.1021/acsomega.0c03483.
- M. Iannuzzi, A. Laio and M. Parrinello, Efficient Exploration of Reactive Potential Energy Surfaces Using Car-Parrinello Molecular Dynamics, Phys. Rev. Lett., 2003, 90(23), 238302, DOI:10.1103/PhysRevLett.90.238302.
- Q. Wu, L. Zhou, G. C. Schatz, Y. Zhang and H. Guo, Mechanistic Insights into Photocatalyzed H2 Dissociation on Au Clusters, J. Am. Chem. Soc., 2020, 142(30), 13090–13101, DOI:10.1021/jacs.0c04491.
- A. Castañeda Medina and R. Schmid, Verlet-like Algorithms for Car-Parrinello Molecular Dynamics with Unequal Electronic Occupations, J. Chem. Phys., 2017, 147(11), 114102, DOI:10.1063/1.4987005.
- N. Marzari, D. Vanderbilt and M. C. Payne, Ensemble Density-Functional Theory for Ab Initio Molecular Dynamics of Metals and Finite-Temperature Insulators, Phys. Rev. Lett., 1997, 79(7), 1337–1340, DOI:10.1103/PhysRevLett.79.1337.
- M. Stengel and A. De Vita, First-Principles Molecular Dynamics of Metals: A Lagrangian Formulation, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(23), 15283–15286, DOI:10.1103/PhysRevB.62.15283.
- G. Pastore, E. Smargiassi and F. Buda, Theory of Ab Initio Molecular-Dynamics Calculations, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44(10), 6334–6347, DOI:10.1103/PhysRevA.44.6334.
- A. Alavi, J. Kohanoff, M. Parrinello and D. Frenkel, Ab Initio Molecular Dynamics with Excited Electrons, Phys. Rev. Lett., 1994, 73(19), 2599–2602, DOI:10.1103/PhysRevLett.73.2599.
- S. A. Tawfik, S. Ali, M. Fronzi, M. Kianinia, T. T. Tran, C. Stampfl, I. Aharonovich, M. Toth and M. J. Ford, First-Principles Investigation of Quantum Emission from hBN Defects, Nanoscale, 2017, 9(36), 13575–13582, 10.1039/C7NR04270A.
- T. Kowalczyk, S. R. Yost and T. V. Voorhis, Assessment of the ΔSCF Density Functional Theory Approach for Electronic Excitations in Organic Dyes, J. Chem. Phys., 2011, 134(5), 054128, DOI:10.1063/1.3530801.
- C. Li and G. A. Voth, Using Constrained Density Functional Theory to Track Proton Transfers and to Sample Their Associated Free Energy Surface, J. Chem. Theory Comput., 2021, 17(9), 5759–5765, DOI:10.1021/acs.jctc.1c00609.
- H. Oberhofer and J. Blumberger, Charge Constrained Density Functional Molecular Dynamics for Simulation of Condensed Phase Electron Transfer Reactions, J. Chem. Phys., 2009, 131(6), 064101, DOI:10.1063/1.3190169.
- I. Tavernelli, U. F. Röhrig and U. Rothlisberger, Molecular Dynamics in Electronically Excited States Using Time-Dependent Density Functional Theory, Mol. Phys., 2005, 103(6–8), 963–981, DOI:10.1080/00268970512331339378.
- E. Tapavicza, I. Tavernelli, U. Rothlisberger, C. Filippi and M. E. Casida, Mixed Time-Dependent Density-Functional Theory/Classical Trajectory Surface Hopping Study of Oxirane Photochemistry, J. Chem. Phys., 2008, 129(12), 124108, DOI:10.1063/1.2978380.
- R. Gomer and W. A. Noyes, Photochemical Studies. XLII. Ethylene Oxide, J. Am. Chem. Soc., 1950, 72(1), 101–108, DOI:10.1021/ja01157a029.
- J. Herzberger, K. Niederer, H. Pohlit, J. Seiwert, M. Worm, F. R. Wurm and H. Frey, Polymerization of Ethylene Oxide, Propylene Oxide, and Other Alkylene Oxides: Synthesis, Novel Polymer Architectures, and Bioconjugation, Chem. Rev., 2016, 116(4), 2170–2243, DOI:10.1021/acs.chemrev.5b00441.
- K. A. Nguyen and M. S. Gordon, Isomerization Of Bicyclo[1.1.0]Butane to Butadiene, J. Am. Chem. Soc., 1995, 117(13), 3835–3847, DOI:10.1021/ja00118a020.
- S. Sakai, Theoretical Study on the Photochemical Reactions of Butadiene, Cyclobutene and Bicyclobutane, Chem. Phys. Lett., 2000, 319(5–6), 687–694, DOI:10.1016/S0009-2614(00)00167-6.
- R. L. Lipnick and E. W. Garbisch, Conformational Analysis of 1,3-Butadiene, J. Am. Chem. Soc., 1973, 95(19), 6370–6375, DOI:10.1021/ja00800a034.
- A. Michalak and T. Ziegler, First-Principle Molecular Dynamic Simulations along the Intrinsic Reaction Paths, J. Phys. Chem. A, 2001, 105(17), 4333–4343, DOI:10.1021/jp0041297.
- R. B. Woodward and R. Hoffmann, The Conservation of Orbital Symmetry, Angew Chem., Int. Ed. Engl., 1969, 8(11), 781–853, DOI:10.1002/anie.196907811.
- M. Ben-Nun and T. J. Martínez, Direct Observation of Disrotatory Ring-Opening in Photoexcited Cyclobutene Using Ab Initio Molecular Dynamics, J. Am. Chem. Soc., 2000, 122(26), 6299–6300, DOI:10.1021/ja9943896.
- E. Tapavicza, G. D. Bellchambers, J. C. Vincent and F. Furche, Ab Initio Non-Adiabatic Molecular Dynamics, Phys. Chem. Chem. Phys., 2013, 15(42), 18336, 10.1039/c3cp51514a.
- P. Dopieralski, P. Anjukandi, M. Rückert, M. Shiga, J. Ribas-Arino and D. Marx, On the Role of Polymer Chains in Transducing External Mechanical Forces to Benzocyclobutene Mechanophores, J. Mater. Chem., 2011, 21(23), 8309, 10.1039/c0jm03698f.
- J. Ribas-Arino, M. Shiga and D. Marx, Unravelling the Mechanism of Force-Induced Ring-Opening of Benzocyclobutenes, Chem.–Eur. J., 2009, 15(48), 13331–13335, DOI:10.1002/chem.200902573.
- M. J. Kryger, A. M. Munaretto and J. S. Moore, Structure–Mechanochemical Activity Relationships for Cyclobutane Mechanophores, J. Am. Chem. Soc., 2011, 133(46), 18992–18998, DOI:10.1021/ja2086728.
- M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martínez, First Principles Dynamics and Minimum Energy Pathways for Mechanochemical Ring Opening of Cyclobutene, J. Am. Chem. Soc., 2009, 131(18), 6377–6379, DOI:10.1021/ja8095834.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials, J. Phys.:Condens. Matter, 2009, 21(39), 395502, DOI:10.1088/0953-8984/21/39/395502.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- L. Verlet, Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules, Phys. Rev., 1967, 159(1), 98–103, DOI:10.1103/PhysRev.159.98.
- M. Kawasaki, T. Ibuki, M. Iwasaki and Y. Takezaki, Vacuum-Ultraviolet Photolysis of Ethylene Oxide, J. Chem. Phys., 1973, 59(4), 2076–2082, DOI:10.1063/1.1680294.
- R. C. Lord and D. G. Rea, The Vibrational Spectra and Structure of Cyclobutene and Cyclobutene-d61, J. Am. Chem. Soc., 1957, 79(10), 2401–2406, DOI:10.1021/ja01567a017.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- HoleMass, https://github.com/sheriftawfikabbas/holemasscpmd Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc00175g |
| This journal is © The Royal Society of Chemistry 2025 |


