 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accurate and efficient machine learning interatomic potentials for finite temperature modelling of molecular crystals†
Flaviano
Della Pia
 a,
Benjamin X.
Shi
a,
Benjamin X.
Shi
 a,
Venkat
Kapil
a,
Venkat
Kapil
 abc,
Andrea
Zen
abc,
Andrea
Zen
 de,
Dario
Alfè
de,
Dario
Alfè
 cde and
Angelos
Michaelides
cde and
Angelos
Michaelides
 *a
*a
aYusuf Hamied Department of Chemistry, University of Cambridge, Cambridge CB2 1EW, UK. E-mail: am452@cam.ac.uk; v.kapil@ucl.ac.uk
bDepartment of Physics and Astronomy, University College London, London, UK
cThomas Young Centre and London Centre for Nanotechnology, University College London, London WC1E 6BT, UK
dDipartimento di Fisica Ettore Pancini, Università di Napoli Federico II, Monte S. Angelo, I-80126 Napoli, Italy
eDepartment of Earth Sciences, University College London, London WC1E 6BT, UK
First published on 23rd May 2025
Abstract
As with many parts of the natural sciences, machine learning interatomic potentials (MLIPs) are revolutionizing the modelling of molecular crystals. However, challenges remain for the accurate and efficient calculation of sublimation enthalpies – a key thermodynamic quantity measuring the stability of a molecular crystal. Specifically, two key stumbling blocks are: (i) the need for thousands of ab initio quality reference structures to generate training data; and (ii) the sometimes unreliable nature of density functional theory, the main technique for generating such data. Exploiting recent developments in foundation models for chemistry and materials science alongside accurate quantum diffusion Monte Carlo benchmarks, offers a promising path forward. Herein, we demonstrate the generation of MLIPs capable of describing molecular crystals at finite temperature and pressure with sub-chemical accuracy, using as few as ∼200 data structures; an order of magnitude improvement over the current state-of-the-art. We apply this framework to compute the sublimation enthalpies of the X23 dataset, accounting for anharmonicity and nuclear quantum effects, achieving sub-chemical accuracy with respect to experiment. Importantly, we show that our framework can be generalized to crystals of pharmaceutical relevance, including paracetamol and aspirin. Nuclear quantum effects are also accurately captured as shown for the case of squaric acid. By enabling accurate modelling at ambient conditions, this work paves the way for deeper insights into pharmaceutical and biological systems.
1. Introduction
Research and development in molecular crystals drives innovation across several impactful fields, from organic semiconductors1,2 and optoelectronics3 to life-saving pharmaceuticals.4,5 In pharmaceuticals, the structures of molecular crystals dictate not just the stability of compounds, but also how effectively a drug can be absorbed, its efficacy, and even its safety. Computational approaches have become essential for aiding experimental structure determination.6–10 Accurate predictions are especially important for sublimation processes, as the sublimation enthalpy of pharmaceutical compounds affects stability and drug solubility, which in turn influences therapeutic dosage, toxicity, and bioavailability.11–15Unfortunately, the routine modelling of molecular crystals is constrained by a cost-accuracy trade-off. Classical force fields are a commonly adopted approach for modelling the potential energy surface (PES) of molecular crystals, offering computational efficiency and enabling the estimation of sublimation enthalpies under ambient conditions. Substantial advancements have been made using empirical descriptions of intermolecular interactions.6,16–18 However, their reliance on empirical parametrization sometimes compromises accuracy, undermining predictive reliability.6,18,19 Significant progress has been achieved in modelling the PES of molecular crystals using electronic structure theory approaches.9,10,16,20–34 Density Functional Theory (DFT) represents the first step up the accuracy-cost ladder beyond empirical force fields. However, the higher cost of DFT force evaluations typically implies approximations for the vibrational contributions, such as the harmonic or quasi-harmonic approximation (QHA). Even within the QHA framework, computational costs scale significantly with system size, requiring up to 3N force calculations for N atoms in the simulation cell (for a system with no symmetry). In addition, the QHA inherently lacks a full description of anharmonicity and nuclear quantum effects (NQEs), which can be critical for molecular crystals, especially in pharmaceutical applications.19,35 While anharmonicity can be incorporated via finite-temperature classical molecular dynamics (MD), and both effects are captured by path integral MD (PIMD), these methods are computationally prohibitive. Hundreds of thousands of force evaluations are generally needed, making them impractical for large systems. In addition, even DFT approximations often fall short in accuracy, struggling to capture the complex intermolecular interactions that characterize molecular crystals. Such interactions, particularly in systems with competing polymorphs where small energy differences dictate stability, often require the accuracy of expensive beyond DFT methods.27,29–31,36
Machine learning interatomic potentials (MLIPs) represent a promising alternative, aiming to combine the accuracy of ab initio approaches with the efficiency of less computationally intensive force evaluations. MLIPs, either trained with periodic unit cells or molecular cluster approaches, have provided a significant leap towards the calculation of accurate thermodynamic stabilities of molecular crystals,10,35,37–45 although often previous calculations have been restricted to zero temperature lattice energies. Nonetheless, the widespread application of MLIPs was still constrained by notable limitations. Training an MLIP typically necessitates costly ab initio MD (AIMD) simulations to generate the required training datasets. In addition, even models trained on thousands of structures may yield training errors comparable to chemical accuracy (conventionally ∼4 kJ mol−1), potentially undermining the reliability of their predictions for the relative stabilities of molecular crystals. However, recent algorithmic improvements have transformed the landscape of MLIP development.46–48 Improvement in data efficiency and reductions in training errors have facilitated the creation of foundation models for chemistry and materials science.46,48–55 These models provide qualitative – and in many cases, quantitative – accuracy across a substantial portion of the periodic table, and they have the promising potential to be fine-tuned to high accuracy for specific applications with minimal additional data.56
In this work, we exploit the training performance of the MACE MLIP architecture47,57 to deliver data-efficient MLIPs that achieve sub-chemical accuracy for molecular crystals with respect to the underlying DFT PES with as few as ∼200 data points, an approximately order of magnitude data efficiency improvement compared to previous work.35 In detail, we fine-tune the MACE-MP-0b3 (ref. 57) foundation model for each molecular crystal in the X23 dataset. X23 is a diverse dataset of 23 molecular crystals characterised by a delicate interplay of intermolecular interactions including hydrogen bonding and dispersion forces, for which a large number of experimental measurements of the sublimation enthalpy is available.58–61 On the other hand, accurate estimates of the sublimation enthalpies via computational approaches have been sought for decades.24,62,63 Our fine-tuned models achieve excellent accuracy on lattice energies, equation of state (EOS), and quasi-harmonic vibrational energies compared to the reference DFT functional (vdW-DF2), which was chosen based on a benchmark against DMC reference lattice energies30 reported in Appendix A. We apply the fine-tuned models to compute the vibrational contribution to the sublimation enthalpies of the X23 dataset with the inclusion of anharmonicity and NQEs, which is added to the reference DMC lattice energy to obtain the final sublimation enthalpies. The sublimation enthalpies computed in this work agree with available experimental estimates with an average error <4 kJ mol−1, and come at a cost within the recently suggested threshold for applicability of a computational method to be economically viable for routine screening of molecular crystals stabilities.40
In addition, we showcase the reliability and robustness of our framework by fine tuning MLIPs that achieve excellent accuracy (with respect to vdW-DF2) for systems of pharmaceutical interest such as paracetamol, aspirin, and squaric acid. This work highlights how state-of-the-art MLIPs facilitate the routine modelling of molecular crystals at finite temperatures and pressures with sub-chemical accuracy. We hope this work will contribute to achieving first-principles accuracy in the study of systems relevant to pharmaceuticals and biology.
2. Framework for data-efficient MLIPs with sub-chemical accuracy
We begin by describing the procedure used to fine-tune so-called foundation machine learning models to produce accurate MLIPs for molecular crystals. Our approach relies on foundation models for chemistry and materials science, i.e. MLIPs trained on large DFT datasets that qualitatively reproduce the underlying PES for a wide range of materials. Specifically, we use the MACE-MP-0b3 (ref. 57) model, pre-trained on MPtrj, a subset of optimised inorganic crystals from the Materials Project database.64 This model has been shown to have PBE-level accuracy for numerous systems, and serves as a useful starting point for improving the potential for a given problem with minimal data.The main idea behind the current approach is summarised in Fig. 1, with each step of the fine tuning framework described in the following.
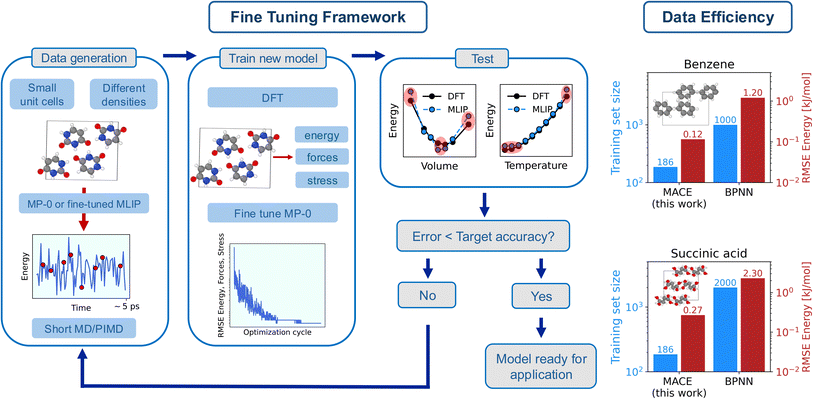 | ||
| Fig. 1 (left) Framework used in this work to fine-tune MACE-MP-0b3 to reproduce the potential energy surface of molecular crystals with sub-chemical accuracy. Each step of ‘Fine Tuning Framework’, i.e. ‘Data generation’, ‘Train new model’, and ‘Test’ is described in the text, with additional computational details reported in the Methods section and in Sec. S3 of the ESI.† (right) Data efficiency and energy errors of the fine-tuned models. The figure reports a comparison on the training set size (blue bars) and the root mean square error (RMSE) of the energy in the validation set (red bars) for benzene and succinic acid between this work and state-of-the-art Behler Parrinello Neural Network (BPNN) MLIPs.35 | ||
Our goal is to develop an accurate potential for NPT simulations to simulate molecular crystals at desired temperatures and pressures rigorously, hence a correct description of a system at different densities is required. Therefore, we first generate a minimal training set by sampling a molecular crystal phase space around the equilibrium volume at low temperatures (‘Data generation’ in Fig. 1). In particular, we run short MD simulations for different cells across the EOS, as described in Methods and in Sec. S2 of the (ref. 65) (ESI).† The key aspect here is that the MD simulations are directly run with the foundation model in the first iteration, and with the fine-tuned model in subsequent training iterations. This allows us to avoid the extremely costly step of producing data with AIMD. The initial training set is then generated by sampling (randomly) a few structures (∼10 per volume) from the MD trajectories. The MACE-MP-0b3 model is then fine-tuned by optimizing its parameters to minimize errors on energy, forces, and stress (‘Train new model’ in Fig. 1). Subsequently, we test the fine-tuned model (‘Test’ in Fig. 1). In particular, we test the models on the EOS (total electronic energy per molecule of the solid as a function of the volume) and its vibrational energy (total energy per molecule as a function of the temperature) in the quasi-harmonic approximation (QHA). The training set is then gradually augmented (with ∼5 structures per volume) until the tested properties are obtained with chemical (or sub-chemical) accuracy. Details of the models performance on the EOS and QHA vibrational properties are reported in Sec. S10 of the ESI.†
We further demonstrate the potential and applicability of the fine-tuned models for the simulation of molecular crystals at ambient temperature with the inclusion of anharmonicity and NQEs. For this reason, the training set of each molecular crystal has been additionally augmented with the inclusion of structures sampled at higher temperatures in PIMD simulations as well as structures for the gas phase. Additional computational details on each step of the fine tuning framework are reported in the Methods section. The breakdown of the cost of each step of the framework (including the calculations of reference DFT EOS, vibrational properties, and training data, as well as the cost of the fine tuning of each model) and the number of structures in the training set for each system is reported in Sec. S3 of the ESI.†
Finally, we discuss the data efficiency of the framework. In fact, we achieve a sub-chemical accuracy reproduction of the PES of molecular crystals by using training sets with an average of approximately ∼200 data points and a computational costs of ∼30 CPU node-hours. The computational cost (estimated on one Ice Lake node on the Cambridge Service for Data Driven Discovery (CSD3)66 with 76 cores and 256 GB of RAM) includes the calculations of the DFT energy, forces and stresses for the training set, and it does not include the calculation of the reference EOS and vibrational frequencies. As showcased in Fig. 1 for the cases of benzene and succinic acid (‘Data efficiency’), this represents about an order of magnitude improvement on data efficiency (i.e., the amount of data needed to achieve the desired accuracy on the training errors) and energy training errors (see Table S27 of the ESI†) compared to Behler Parrinello Neural Network (BPNN) MLIPs for molecular crystals.35
3. Anharmonic sublimation enthalpies of molecular crystals with nuclear quantum effects
The fine tuning procedure described above delivers data efficient and accurate MLIPs for molecular crystals. The efficacy and accuracy of the fine-tuned models is now showcased by tackling a long standing challenge in the computational study of molecular crystals: a fast and accurate computation of fully anharmonic finite temperature thermodynamic stabilities. In particular, we consider the X23 dataset,24,62,63 the most widely used dataset for molecular crystals. A large number of experimental measurements of the sublimation enthalpies of molecules in the X23 dataset is available,58–61 and it was shown that for several systems the experimental uncertainty is larger than ∼4 kJ mol−1, and it can be as large as ∼20 kJ mol−1.30The X23 sublimation enthalpies have been previously computed with DFT with the QHA62,63 and with the inclusion of thermal expansion.24 Hence, the accuracy of the available estimates can in principle be affected by both the accuracy of the electronic structure method (e.g., the choice of the functional in the DFT calculations) and the statistical mechanics description of the nuclei (i.e., lack of anharmonicity and NQEs). Here, we leverage recent reference DMC values of the X23 lattice energies30 to benchmark several DFT approximations and determine a functional that achieves chemical accuracy on the dataset (see Sec. S1 of the ESI†). Subsequently, we train 23 fine-tuned MACE models, one for each molecular crystal in X23. The fine-tuned models achieve sub-chemical accuracy errors compared to the reference functional (vdW-DF2) on the lattice energy, the EOS, and the quasi harmonic vibrational properties (see Sec S10 of the ESI†). We then use the fine-tuned models to compute the vibrational contribution to the sublimation enthalpies of X23 with three different approximations: (i) the QHA; (ii) the inclusion of anharmonicity with a classical description of the nuclei (referred to as MD); and (iii) the inclusion of anharmonicity with a quantum description of the nuclei (referred to as PIMD). The zero temperature electronic contribution to the sublimation enthalpies, i.e. the lattice energy, is finally corrected to the DMC accuracy as described in Methods. We note here that although the DFT functional was selected based on a lattice energy benchmark, the lattice energy typically represents the major contribution (∼80%) of the sublimation enthalpy. In addition, the choice of the functional (among “reliable” ones) plays a minor role in the determination of the vibrational contribution, as shown in Sec. S11 of the ESI.†
In Fig. 2, we report the analysis of the sublimation enthalpies of the X23 dataset. In Fig. 2(a), we show the scatter plot of the sublimation enthalpies computed with the PIMD approach against the median of the experimental values. The vertical error bars take into account the uncertainty on the DMC lattice energy and the statistical sampling error of the PIMD simulations, computed with reblocking. The horizontal bars represent the uncertainty on the experimental numbers and go from the minimum to the maximum experimental value. The grey shaded area represents an uncertainty of ∼4 kJ mol−1. The figure shows that the MLIPs trained in this work reproduce the experimental sublimation enthalpies with chemical accuracy. In Fig. 2(c) we report the sublimation enthalpies computed with the three different approaches for each system in X23 and compare with the median of the experimental values. The grey shaded bars represent the uncertainty on the experimental estimates, which often reflects the number of available measurements, as discussed in ref. 30. Importantly, when taking into account the large uncertainty on the experimental numbers as well as the error bars on the computational sublimation enthalpies, we find that the sublimation enthalpies of the X23 dataset are well reproduced also with the MD approach and even at the QHA level. Measuring the performance of the computational approaches as a mean absolute error (MAE) with respect to the median of the experimental data, we obtain MAEQHA ∼ 2.7 ± 0.8 kJ mol−1, MAEMD ∼ 3.0 ± 0.8 kJ mol−1, and MAEPIMD ∼ 3.3 ± 0.9 kJ mol−1. On average, the sublimation enthalpies are predicted with chemical accuracy with all three approaches, with all three approaches equivalent within the error bars. Overall, the large uncertainties on the experimental sublimation enthalpies30 and the error bars on the computational estimates do not allow for a rigorous assessment of the three different approaches.
 | ||
| Fig. 2 Sublimation enthalpies of the X23 dataset. (a) Scatter plot of the sublimation enthalpies of the X23 dataset computed with the PIMD approach against the median of the experimental value for each system.58–61 The horizontal error bars represent the experimental uncertainty and go from the minimum to the maximum measured value. (b) Estimated computational cost of the sublimation enthalpies for a single molecular crystal with the three different approaches used in this work, QHA, MD and PIMD. The cost is estimated for 1,4-cyclohexanedione with ∼200 atoms in the simulated supercell. The reported cost of the sublimation enthalpy calculations does not include the training of the model. (c) Comparison between experiments and the computational sublimation enthalpies obtained with the three different approaches considered in this manuscript. The figure shows, for each system in X23, the difference between the computational sublimation enthalpies ΔHcompsub and the median of the experimental sublimation enthalpies ΔHexpsub, for the QHA (blue squares), the MD (light blue triangles) and the PIMD (navy circles). The grey shaded bars represent the uncertainty on the experimental estimates. | ||
However, anharmonicity and NQEs are expected to play a greater role in larger and more flexible molecular crystals. Hence the importance of this work, which showcases the feasibility of finite temperature modelling of molecular crystals with NQEs.
While the data-efficiency of the approach has been discussed, in Fig. 2(b) now we discuss the computational cost. We report the approximate computational cost (in GPU-hours) of the calculation of the sublimation enthalpies with QHA, MD, and PIMD for a showcase system from X23: 1,4-cyclohexanedione. The reported cost does not include the cost of the fine tuning of the model nor the cost of the DMC lattice energy correction. It was recently suggested that the acceptable amount of CPU time required for a single free-energy calculation for a method to be economically feasible in screening molecular crystals structures was about 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 core-hours.40 The simulations in this work were performed on GPUs (single NVIDIA A100-SXM-80GB GPU on CSD3 (ref. 66)), therefore we evaluate the efficiency of our method in terms of the actual monetary cost and notably find that the cost of our simulations is approximately within the threshold even with the inclusion of NQEs (see ref. 67 for details of the cost evaluation).
000 core-hours.40 The simulations in this work were performed on GPUs (single NVIDIA A100-SXM-80GB GPU on CSD3 (ref. 66)), therefore we evaluate the efficiency of our method in terms of the actual monetary cost and notably find that the cost of our simulations is approximately within the threshold even with the inclusion of NQEs (see ref. 67 for details of the cost evaluation).
Now, we focus on a comparison among the sublimation enthalpies computed with the three different approaches. In Fig. 3(a) we report the scatter plot of the difference between ΔHPIMDsub and the sublimation enthalpies computed with the QHA and MD approaches, against the PIMD values. Overall, we observe that the inclusion of NQEs can account for a ∼4 kJ mol−1 change in the sublimation enthalpy, which can be non negligible when computing energy differences with chemical accuracy. The system in X23 where anharmonicity plays a major role is succinic acid, which is highlighted with red circles. In Sec. S14 of the ESI,† we show that the torsion angle of the four carbon atoms in the gas phase oscillates between ∼75°, ∼180° and ∼290°. This anharmonic feature cannot be described with the harmonic approximation, where only small displacements of the atoms are allowed. Therefore, the contribution of anharmonicity and NQEs is larger and more significant for succinic acid, accounting for a ∼11 kJ mol−1 change in the sublimation enthalpy.
Similarly, in Fig. 3(b) and (c) we report the scatter plots of the kinetic energy K (b) and potential energy U (c) contributions to the sublimation enthalpy differences plotted in panel (a) (see the Methods section for a breakdown of each contribution to the sublimation enthalpy in each approximation). For the majority of the X23 systems where anharmonicity and NQEs play a minor role, we observe that a similar correction of ∼2 kJ mol−1 affects the kinetic and potential energy contribution to the sublimation enthalpy. For succinic acid, where anharmonicity plays a major role, the main correction is due to the potential energy contribution, with ΔUQHAsub − ΔUPIMDsub ∼ 10 kJ mol−1. This analysis suggests that the effect of anharmonicity and NQEs on the sublimation enthalpy of a highly anharmonic molecular crystal can be primarily estimated by the calculation of the potential energy contribution.
4. Extension of the framework to pharmaceutical crystals
The robust fine-tuning framework presented here is not limited to the X23 dataset. In fact, in this work we tested the validity of the framework for the description of systems of pharmaceutical interest, as well as a highly polymorphic and ubiquitous system like ice. The ice polymorphs application is presented in Sec. S12 of the ESI,† where we show that an MLIP fine-tuned on ∼464 structures correctly reproduces the zero temperature relative stability of 15 ice polymorphs, including two polymorphs not explicitly represented in the training set. Here in the main manuscript, we focus on the generalization of the framework's applicability to pharmaceutical systems of interest, namely paracetamol and aspirin. We also consider squaric acid, known for the highly quantum nature of its hydrogen bond.68 As shown in the Sec. S15,† the fine-tuned MLIPs correctly reproduce the reference DFT, with errors <0.5 kJ mol−1 for the lattice energy and <2 kJ mol−1 on the QHA vibrational energy.In Fig. 4(a–c), we report the room-temperature sublimation enthalpies of paracetamol (a), aspirin (b), and squaric acid (c) using four different approximations: the zero-temperature perfect lattice approximation (negative of the lattice energy Elatt), QHA, MD, and PIMD.
 | ||
| Fig. 4 Generalization of the framework to systems of pharmaceutical interest. We report the sublimation enthalpies of (a) form I of paracetamol, (b) form I of aspirin, and (c) squaric acid. The experimental sublimation enthalpies of paracetamol and squaric acid are ∼117.9 ± 0.7 kJ mol−1 (ref. 61 and 69) at room temperature and ∼152 kJ mol−1 (ref. 61 and 70) at ∼486 K, respectively. Each plot shows the sublimation enthalpy ΔHsub (in kJ mol−1) computed with the perfect lattice approximation (the negative of the lattice energy Elatt), the QHA, MD and PIMD. In each panel we show the structure of the considered system, with oxygen atoms in red, hydrogen atoms in white, carbon atoms in grey and nitrogen atoms in blue. The 1 × 2 × 1 supercell is shown for squaric acid, to help visualize the in-plane hydrogen bonded molecules. (d) Conventional Ubbelodhe effect for squaric acid. The plot shows the distribution of the Δ(O–O) = (O–O)H − (O–O)D in room temperature PIMD simulations. The average of the distribution is reported with a black dashed line. | ||
We first address the importance of finite temperature contributions. These contributions have a noticeable impact on the sublimation enthalpy (variations of ∼4 kJ mol−1), underscoring the need to go beyond the perfect lattice approximation. Using fast and accurate MLIPs, the QHA contribution can be computed in as little as 0.2 GPU-hours.
For paracetamol and aspirin, as with most molecular crystals in the X23 dataset, anharmonicity and NQEs make minimal corrections to the QHA, with differences between ΔHQHAsub and ΔHMD/PIMDsub of <4 kJ mol−1. However, for squaric acid, the inclusion of anharmonicity and NQEs is more significant, with ΔHPIMDsub − ΔHQHAsub ∼ 4 kJ mol−1 and ΔHPIMDsub − ΔHMDsub ∼ 8 kJ mol−1.
We now comment on the accuracy of the sublimation enthalpy with respect to experiment, for which we found available estimates for paracetamol61,69 and squaric acid.61,70 As mentioned above, the fine-tuned MLIPs correctly reproduce the underlying DFT level of theory with sub-chemical accuracy errors (<2 kJ mol−1) on lattice energies and QHA vibrational energy. However, for these systems we find that the chosen DFT functional does not appear to perform well. Although experimental values of molecular crystals' sublimation enthalpies might have larger uncertainties than those reported in a single experiment,30 the sublimation enthalpies computed in this work differ by ∼15–20 kJ mol−1 from experiment. As described in Sec. S15.3,† the sublimation enthalpies of paracetamol, aspirin, and squaric acid do not contain the correction to the zero temperature contribution (−Elatt) computed with DMC. Therefore, the larger errors between the computational and experimental sublimation enthalpies could be ascribed to the DFT functional used in our calculations (selected on a benchmark for the X23 dataset). Future work will be related to the extension of reference DMC calculations to the challenging systems described in this section.
Finally, we discuss the importance of NQEs. NQEs can influence the interaction strength and consequently the structure of H-bonded systems.71,72 In H-bonded crystals, this effect is known as the Ubbelohde effect, where replacing H with deuterium (D) causes a change of the O–O distance, and consequently of the ferroelectric phase-transition temperature.73 Squaric acid yields an elongation of its lattice constant and O–O distance upon deuteration, an effect known as conventional Ubbelohde effect (as opposed to the negative Ubbelohde effect, where O–O decreases upon deuteration).68 In Fig. 4(d) we show that the Ubbelodhe effect at room temperature is correctly described with our model. In fact, we report the change in the O–O distance between hydrogenated [(O–OH)] and deuterated [(O–OD)] squaric acid. In particular, we plot the distribution of the difference Δ(O–O) = (O–O)H − (O–O)D in the PIMD simulations. The mean elongation ∼0.03 Å correctly describes the conventional Ubbelodhe effect, and agrees with the previously reported value68 of ∼0.04 Å obtained with ab initio PIMD, but comes at a fraction of the computational cost.
5. Discussion and conclusion
In this work, we leverage recent developments on MLIPs and insight into molecular crystal lattice energies with DMC to study finite temperature stabilities of molecular crystals with sub-chemical accuracy by fine tuning a foundation model for chemistry and materials science. In particular, we fine-tune the MACE-MP-0b3 foundation model to obtain MLIPs that accurately reproduce lattice energies, equations of state, and quasi-harmonic thermodynamic properties of the X23 dataset. The procedure followed in this work builds on recent preliminary work, where some of us reported the data-efficient generation of an MLIP for three ice polymorphs.56 Importantly, in this work we consider organic molecular crystals that are not represented in the original training set of the pre-trained model.57 Moreover, the generation of the training set in this work was directly run with MACE-MP-0b3 rather than with AIMD, which significantly reduces the overall computational cost. The training sets contain as few as ∼200 data points and required ∼30 node-hours of DFT calculations (cost estimated on one Ice Lake node with 76 cores and 256 GB of RAM), which represents an almost order of magnitude improvement compared to the state-of-the-art. In summary, while fine tuning is known in general to be a powerful approach towards improving the accuracy of machine learning models, here we show that for molecular crystals unprecedented accuracy can be obtained with few data points.The fine-tuned models are used to compute the vibrational contribution to the sublimation enthalpies of the X23 dataset with three different approximations: QHA, anharmonicity with a classic description of the nuclei, and anharmonicity with inclusion of NQEs. The sublimation enthalpies reported in this work agree with experiment with sub-chemical accuracy for all the considered systems, and notably come at a cost that is within the recently suggested threshold for the widespread applicability of a method to the calculation of finite temperature free energies for molecular crystals.40 In addition, we show that our framework can be applied to deliver MLIPs that efficiently reproduce the DFT PES for systems such as paracetamol, aspirin, and squaric acid. The results showcase that the strategy followed in this manuscript is robust, and provides a way to obtain MLIPs that achieve excellent accuracy with respect to the reference PES with low data and computational cost even for systems of pharmaceutical interest.
We now discuss the limitations of our work and potential improvements for the near future. Two main aspects merit consideration: (i) enhancing the framework from a technical and methodological standpoint; and (ii) expanding its range of applicability. The former involves two key technical aspects: the accuracy of the training data and a systematic understanding of how data requirements depend on the starting foundation model.
Regarding training data accuracy, as evidenced by the sublimation enthalpies of paracetamol and squaric acid, the choice of the DFT functional – critical for accurate lattice energy calculations – remains a significant challenge in modelling molecular crystals. Future work will focus on leveraging the low data requirements of our framework to directly learn the PESs obtained from explicitly correlated methods.74–77 In fact, some of us recently showcased how Random Phase Approximation accuracy could be reached for the prototypical case of hexagonal ice.56
With respect to the starting foundation model, foundation model development and fine-tuning strategies are rapidly evolving research areas. Interesting future directions involve: (i) testing our framework with recent MACE foundation models trained on larger datasets such as Alexandria78 and OMat,79 the pre-trained organic machine learning force field MACE-OFF23,55 or models with different architectures such as Orb,80 MatterSim,81 and more; and (ii) exploring new fine tuning strategies to possibly lower the data-requirement of our framework.82,83
We now turn to future potential applications of our framework, which include: extending our approach to larger and more complex drug-like compounds and analysing highly polymorphic organic molecular crystals. The ice polymorphs test reported in the ESI† serves as a stringent benchmark for polymorphic systems, as their energies lie within a range comparable to chemical accuracy. Interestingly, the fine-tuned model correctly predicts the energetics of polymorphs which are not included in the training set. However, the systems presented in this manuscript are still relatively limited in size, flexibility, and molecular complexity. In the future, it would be particularly interesting to test our approach on more challenging and highly polymorphic organic systems, e.g. compounds from the 7th blind test challenge,16 or to compute the phase diagram of larger pharmaceutical compounds.40 As mentioned above, for such systems, questions arise both regarding the accuracy of the underlying DFT PES as well as the data requirement necessary for its accurate description with MLIPs.
Finally, we discuss the relevance of our work to crystal structure prediction (CSP), an exciting field with recent developments both in the structure generation16,84,85 and polymorph ranking tasks.16,42,86 Here, we focused on developing a modular pipeline to compute the sublimation enthalpy associated with a single crystal structure. A different and exciting research direction for the application of MLIPs in the modelling of molecular crystals is the determination of the most stable polymorph among numerous candidates in CSP ranking tasks, e.g. the blind test challenges.16,87–92 CSP ranking is a multi-fidelity screening problem, typically requiring a hierarchy of models with increasing accuracy. In general, different models are used to first screen among thousands of generated structures to identify the most promising candidates, and then predict relative energies of a handful of final candidates. For the initial screening, one is often interested in shortlisting structures within a few kcal mol−1 of the lowest-energy structures. Here, one could desire a general and transferable model accurate for “all” molecular crystals. In Sec. S13 of the ESI† we report a comparison between the 23 different fine-tuned models and a single “global” model, trained on the 23 joined training sets, showing that comparable accuracy can be obtained with the two procedures. The global model was used to generate initial training data for paracetamol, aspirin, and squaric acid, and achieves reliable performance on the description of the vibrational properties with the QHA. These preliminary tests show that this framework could be a promising route towards developing an accurate and transferable MLIP for molecular crystals. Nonetheless, this task faces significant challenges, especially for the inclusion of long range interactions and the development of a training set for accurate modelling of complex structures such as salts and co-crystals. For the final re-ranking step, explicit DFT calculations are typically used and our approach could be applied to further accelerate this process. As mentioned above, this will require exploring strategies to extend our framework to predict full energy landscapes for multiple polymorphs with minimal data requirements.
In conclusion, this work demonstrates that employing state-of-the-art MLIPs helps to bridge the gap toward routine accurate modelling of molecular crystals under realistic thermodynamic conditions. We hope that this research will support the pursuit of first-principles accuracy in systems relevant to pharmaceutical and biological studies.
6. Methods
The work conducted in this manuscript is based on four fundamental steps. These steps are: (A) generating training set configurations with the MACE-MP-0b3 potential; (B) computing energy, forces, and stress for the training set configurations with DFT; (C) fine tuning the MACE-MP-0b3 potential for the training set from steps (A and B); and (D) computing the sublimation enthalpy with three different approximations: QHA, MD, and PIMD. In this section, we describe theory and computational details for each step.6.1. Training set generation
To generate the training set for the MLIP, we initially computed the EOS of each system in X23 with the vdW-DF2 (ref. 93) functional. Details of the DFT calculations are reported in Sec. 6.2. For each molecular crystal in X23, the initial training set for the MLIP is generated by running short (∼5 ps) classical MD simulations with MACE-MP-0b3 in the NVT ensemble (constant number of particles, volume, and temperature) with small unit cells at each volume of the solid EOS and for the gas phase. The volumes for the EOS were obtained by optimizing with DFT the unit cell at the pressures 0, ±1, ±2, ±4 kbar. The MD simulations are run at a relatively low temperature, T ∼ 100 K. The initial training set is obtained by randomly selecting ∼10 structures per volume (∼7 volumes) from the NVT simulations. The training set was subsequently augmented with structures sampled at the volumes V where the difference on the EOS between the model and DFT was larger. Finally, the training set was augmented with ∼5 structures per volume obtained from PIMD simulations at higher temperatures T ∼ 300 K. Overall, the training set for each molecular crystal comprises ∼200 structures. The exact training set size for each model is reported in Sec. S4 of the ESI.† The MD simulations are performed with the i-PI94 code by using the atomistic simulation environment (ASE)95 as the force provider.6.2. Density functional theory
The MLIP has been trained on DFT energies, forces, and stresses computed with the vdW-DF2 (ref. 93) functional with VASP.96–99 The vdW-DF2 functional was chosen based on the benchmark of the X23 lattice energies against reference DMC values,30 reported in Appendix A. In all the DFT calculations, the projector-augmented plane wave method (PAW) has been used with hard pseudo-potentials100,101 with a dense FFT grid, a PAW energy cut-off of 1000 eV, and a break condition in the self consistent loop of 10−7 eV. The total energy of the solid phase is computed with a dense system specific k-point grid that ensures a convergence of each molecular crystal lattice energy with a threshold of 1 meV. The k-point grids used for each molecular crystal are reported in Table S1 of the ESI.† The total energies of the gas phase are computed at the Γ point in cubic boxes of ∼20 Å.6.3. Fine tuning of MACE-MP-0
The MLIP is obtained by fine tuning the “medium” foundation model MACE-MP-0b3 (the exact starting point is provided on GitHub). In each fine tuning iteration, we train the new model starting from the initial parameters of MACE-MP-0b3. Each optimization cycle is performed with 2000 epochs. The script used to fine-tune the initial model is provided on GitHub.6.4. Sublimation enthalpy
The fine-tuned MLIPs are finally used to compute the sublimation enthalpies of the X23 dataset. The sublimation enthalpy is defined as the difference between the enthalpy of the gas phase (Hgas) and the enthalpy per molecule of the solid (Hsol):| ΔHsub = Hgas − Hsol. | (1) |
The total enthalpy of both gas and solid phases is defined as the sum of the total internal energy and the pressure–volume term:
| H = E + pV, | (2) |
| Hgas = Eelgas + Evibgas + Etransgas + Erotgas + pV. | (3) |
 | (4) |
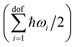 is explicitly taken into account in the (quantum) QHA. Given the number of atoms in the molecule N, the number of degrees of freedom is dof = 3N − 6 for non-linear molecules and dof = 3N − 5 for linear molecules (only CO2 in the X23 dataset). In the ideal gas approximation, we have Etransgas = (3/2)RT, Erotgas = (3/2)RT for non linear molecules and Erotgas = RT for linear molecules, and pV = RT.
is explicitly taken into account in the (quantum) QHA. Given the number of atoms in the molecule N, the number of degrees of freedom is dof = 3N − 6 for non-linear molecules and dof = 3N − 5 for linear molecules (only CO2 in the X23 dataset). In the ideal gas approximation, we have Etransgas = (3/2)RT, Erotgas = (3/2)RT for non linear molecules and Erotgas = RT for linear molecules, and pV = RT.
The total enthalpy of the solid phase is computed as the sum of the electronic and vibrational energy and the pV term:
| Hsol = Eelsol + Evibsol + pV. | (5) |
The pV term for the solid is usually <0.05 kJ mol−1 and is typically neglected. The vibrational energy of the solid in the QHA is computed as:
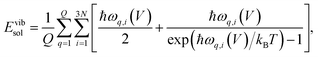 | (6) |
In this work, we use the MLIP trained at the vdW-DF2 functional to estimate the vibrational contribution to the sublimation enthalpy, while the zero temperature electronic contribution is given by the DMC reference lattice energy calculations from ref. 30. Hence, the equation used to compute the sublimation enthalpies with the QHA is:
| ΔHQHAsub = Eel,DMCgas − Eel,DMCsol + Evib,MLIPgas − Evib,MLIPsol + 4RT, | (7) |
6.4.1.1. Computational details. The vibrational frequencies in the QHA are obtained with the small displacement method using a displacement of ∼0.01 Å. The solid phase vibrational energies are computed with the code PHON.102 The reference DFT forces are computed with VASP, while the MLIP forces are obtained with ASE. The reference frequencies and vibrational energies of the gas phase are computed directly with VASP, while the MLIP frequencies and vibrational energies of the gas phase are computed with ASE. The VASP, PHON, and ASE input files used to obtain the vibrational energies are provided on GitHub.
| 〈H〉sol = 〈K〉NPTsol + 〈U〉NPTsol + p〈V〉NPTsol, | (8) |
 | (9) |
As for the QHA approximation, we use the MLIP trained at the vdW-DF2 functional to estimate the vibrational contribution to the sublimation enthalpy, while the zero temperature electronic contribution is corrected to the DMC reference lattice energy calculations from ref. 30. Hence, the equation used to compute the sublimation enthalpies with the MD approach is:
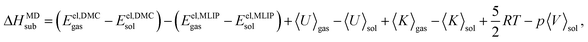 | (10) |
6.4.2.1. Computational details. The MD simulations are performed with i-PI using a time step of 1 fs and the generalized Langevin equation (GLE) barostat-thermostat. In particular, we run ∼500 ps NPT simulations at p ∼ 1 bar and T = T* for the solid phase, and ∼1 ns NVT simulations at T = T* for the gas phase. The statistical error bar on the averaged quantity were computed with reblocking averaging. Further details on the supercells used for the MD simulations are provided in Table S28 of the ESI.† The input files used for the classical MD simulations are provided on GitHub.
| 〈H〉sol = 〈E〉NPTsol + p〈V〉NPTsol, | (11) |
| 〈H〉gas = 〈E〉NVTgas + RT. | (12) |
As for the previous cases, we use the MLIP trained at the vdW-DF2 functional to estimate the vibrational contribution to the sublimation enthalpy, while the zero temperature electronic contribution is corrected to the DMC reference lattice energy calculations from ref. 30. Hence, the equation used to compute the sublimation enthalpies with the PIMD approach is:
| ΔHPIMDsub = (Eel,DMCgas − Eel,DMCsol) − (Eel,MLIPgas − Eel,MLIPsol) + 〈Kcv + U〉gas − 〈Kcv + U〉sol + RT − p〈V〉sol, | (13) |
6.4.3.1. Computational details. The PIMD simulations are performed with i-PI using 32 replicas, a time step of 1 fs, the GLE barostat and the path integral Langevin equation (PILE) thermostat.104 In particular, we run ∼200 ps NPT simulations at p ∼ 1 bar and T = T* for the solid phase, and ∼1 ns NVT simulations at T = T* for the gas phase. The statistical error bar on the averaged quantity were computed with reblocking averaging. The input files for the PIMD simulations are provided on GitHub.
Appendices
Appendix A: Benchmark of DFT functionals against diffusion Monte Carlo
The key initial ingredient to train an MLIP that achieves chemical accuracy compared to the experiment is to determine a DFT functional that achieves the desired accuracy. To identify reliable functionals for the description of the X23 molecular crystals, we perform a benchmark of the X23 lattice energies against the reference quantum diffusion Monte Carlo (DMC) estimates from ref. 30. The geometries used in the DFT calculations are the same as those used for the DMC calculations,30 which were optimised with the optB88-vdW functional. In Fig. 5, we report the performance of several DFT functionals measured as a Mean Absolute Error (MAE) against the DMC estimates of the lattice energies. The tested functionals are reported in order of decreasing performance (from left to right), i.e. higher MAE. The error bar on each column represents the average statistical error bar of the DMC reference values.30 The majority of the calculations have been performed with VASP96–99 using the same set-up described in the Methods section. The B86bPBE functional with the exchange-hole dipole moment (XDM)23 dispersion correction has been tested both with Quantum Espresso105 (QE in the figure) with pseudopotentials, and with FHI-aims106 (FHI in the figure) with the all electron calculation. The hybrids B86bPBE + XDM with 25% and 50% delocalization correction have been also tested with FHI-aims. Overall, we find that several functionals, namely PBE + MBD, SCAN + rVV10, vdW-DF2, B86bPBE + XDM(50%), B86bPBE + XDM(25%), and B86bPBE + XDM, achieve the chemical accuracy limit with a MAE ∼ 4 kJ mol−1. Their performance are approximately equivalent taking into account the DMC statistical error bars. The functional used in this work is vdW-DF2, which was chosen considering its reliable performance and its cost comparable to GGA calculations. We acknowledge that other functionals could have been chosen based on the reported benchmark. However, we notice that: (1) the minimal data strategy and framework proposed in the main manuscript should not be highly dependent on the selected functional (this statement is also supported by the test on the ice polymorphs reported in Sec. S12†); and (2) the choice of the functional defines major differences on the computation of the zero temperature lattice energies (which account for ∼80% of the sublimation enthalpy), and not of the vibrational contribution. This is evident from the comparison between the QHA sublimation enthalpies computed in this work and in previous work, reported in Sec. S11. Since the zero temperature contribution is corrected to the DMC values (as explained in the Methods section and in Sec. S9 of the ESI†), we expect the choice of the DFT functionals (among the reliable ones) to play a minor role in the sublimation enthalpies reported in Table S29.† Further details on the DFT benchmark – including tabulated results for each functional – are reported in Section S1 of the ESI.† | ||
| Fig. 5 Benchmark of DFT functionals against reference DMC values30 on the lattice energies of the X23 dataset. The functionals are listed from left to right in order of decreasing performance (higher MAE). The reported error bar is the average statistical error bar of the DMC reference values. “QE” and “FHI” mean that the number have been respectively computed with Quantum Espresso105 or FHI-aims.106 | ||
Data availability
The data supporting the findings of this work, including the training set and the fine-tuned models, together with scripts and input and output are provided on GitHub and in the ESI.†Author contributions
Investigation and Data curation: F. D. P. and B. X. S.; methodology and formal analysis: all authors; conceptualization: all authors; project administration: A. M. and V. K.; writing – original draft: F. D. P; writing – review & editing: all authors; resources: A. M., V. K., A. Z., and D. A.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the computational resources from Cambridge Service for Data Driven Discovery (CSD3) operated by the University of Cambridge Research Computing Service, provided by Dell EMC and Intel using Tier-2 funding from the Engineering and Physical Sciences Research Council (capital grant EP/T022159/1 and EP/P020259/1), and DiRAC funding from the Science and Technology Facilities Council (https://www.dirac.ac.uk). We are further grateful for computational support from the UK national high performance computing service, ARCHER2, for which access was obtained via the UKCP consortium and funded by EPSRC grant ref EP/X035891/1, and the Swiss National Supercomputing Centre under project s1288. V. K. acknowledges support from the Ernest Oppenheimer Early Career Fellowship and the Sydney Harvey Junior Research Fellowship. A. M. and B. X. S acknowledge support from the European Union under the “n-AQUA” European Research Council project (grant no. 101071937). D. A. and A. Z. acknowledge support from Leverhulme grant no. RPG-2020-038, and from the European Union under the Next generation EU (projects 20222FXZ33 and P2022MC742).References
- J. Mei, Y. Diao, A. L. Appleton, L. Fang and Z. Bao, Integrated Materials Design of Organic Semiconductors for Field-Effect Transistors, J. Am. Chem. Soc., 2013, 135(18), 6724–6746 Search PubMed.
- G. Gryn'ova, K. H. Lin and C. Corminboeuf, Read between the Molecules: Computational Insights into Organic Semiconductors, J. Am. Chem. Soc., 2018, 140(48), 16370–16386 CrossRef PubMed.
- O. Ostroverkhova, Organic Optoelectronic Materials: Mechanisms and Applications, Chem. Rev., 2016, 116(22), 13279–13412 CrossRef CAS PubMed.
- C. Y. Ma, A. A. Moldovan, A. G. P. Maloney and K. J. Roberts, Exploring the CSD Drug Subset: An Analysis of Lattice Energies and Constituent Intermolecular Interactions for the Crystal Structures of Pharmaceuticals, J. Pharm. Sci., 2023, 112(2), 435–445 CrossRef CAS PubMed.
- S. Datta and D. J. W. Grant, Crystal structures of drugs: advances in determination, prediction and engineering, Nat. Rev. Drug Discovery, 2004, 3, 42–57 CrossRef CAS PubMed.
- S. L. Price, Predicting crystal structures of organic compounds, Chem. Soc. Rev., 2014, 43, 2098–2111 RSC.
- G. M. Day, Current approaches to predicting molecular organic crystal structures, Crystallogr. Rev., 2011, 17(1), 3–52 CrossRef.
- J. Hoja, A. M. Reilly and A. Tkatchenko, First-principles modeling of molecular crystals: structures and stabilities, temperature and pressure, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2017, 7(1), e1294 Search PubMed.
- G. J. O. Beran, Modeling Polymorphic Molecular Crystals with Electronic Structure Theory, Chem. Rev., 2016, 116(9), 5567–5613 CrossRef CAS PubMed.
- J. Hoja, H. Y. Ko, M. A. Neumann, R. Car, R. A. DiStasio and A. Tkatchenko, Reliable and practical computational description of molecular crystal polymorphs, Sci. Adv., 2019, 5(1), eaau3338 CrossRef PubMed.
- H. G. Brittain, S. J. Bogdanowich, D. E. Bugay, J. DeVincentis, G. Lewen and A. W. Newman, Physical Characterization of Pharmaceutical Solids, Pharm. Res., 1991, 8(8), 963–973 Search PubMed.
- K. R. Chaudhuri, Crystallisation within transdermal rotigotine patch: is there cause for concern?, Expet Opin. Drug Deliv., 2008, 5(11), 1169–1171 CrossRef CAS PubMed.
- I. B. Rietveld and R. Céolin, Rotigotine: Unexpected Polymorphism with Predictable Overall Monotropic Behavior, J. Pharm. Sci., 2015, 104(12), 4117–4122 CrossRef CAS PubMed.
- J. Bauer, S. Spanton, R. Henry, J. Quick, W. Dziki and W. Porter, et al., Ritonavir: An Extraordinary Example of Conformational Polymorphism, Pharm. Res., 2001, 18(6), 859–866 CrossRef CAS PubMed.
- D. K. Bučar, R. W. Lancaster and J. Bernstein, Disappearing Polymorphs Revisited, Angew. Chem., Int. Ed., 2015, 54(24), 6972–6993 CrossRef PubMed.
- L. M. Hunnisett, N. Francia, J. Nyman, N. S. Abraham, S. Aitipamula and T. Alkhidir, et al., The seventh blind test of crystal structure prediction: structure ranking methods, Acta Crystallogr., Sect. B, 2024, 80(6), 548–574 Search PubMed.
- A. A. Aina, A. J. Misquitta and S. L. Price, A non-empirical intermolecular force-field for trinitrobenzene and its application in crystal structure prediction, J. Chem. Phys., 2021, 154(9), 094123 CrossRef CAS PubMed.
- J. Nyman, O. S. Pundyke and G. M. Day, Accurate force fields and methods for modelling organic molecular crystals at finite temperatures, Phys. Chem. Chem. Phys., 2016, 18, 15828–15837 Search PubMed.
- M. Rossi, P. Gasparotto and M. Ceriotti, Anharmonic and Quantum Fluctuations in Molecular Crystals: A First-Principles Study of the Stability of Paracetamol, Phys. Rev. Lett., 2016, 117, 115702 CrossRef PubMed.
- C. T. Sargent, D. P. Metcalf, Z. L. Glick, C. H. Borca and C. D. Sherrill, Benchmarking two-body contributions to crystal lattice energies and a range-dependent assessment of approximate methods, J. Chem. Phys., 2023, 158(5), 054112 CrossRef CAS PubMed.
- C. H. Borca, Z. L. Glick, D. P. Metcalf, L. A. Burns and C. D. Sherrill, Benchmark coupled-cluster lattice energy of crystalline benzene and assessment of multi-level approximations in the many-body expansion, J. Chem. Phys., 2023, 158(23), 234102 CrossRef CAS PubMed.
- P. M. Nelson and C. D. Sherrill, Convergence of the many-body expansion with respect to distance cutoffs in crystals of polar molecules: Acetic acid, formamide, and imidazole, J. Chem. Phys., 2024, 161(21), 214105 CrossRef CAS PubMed.
- A. J. A. Price, A. Otero-de-la Roza and E. R. Johnson, XDM-corrected hybrid DFT with numerical atomic orbitals predicts molecular crystal lattice energies with unprecedented accuracy, Chem. Sci., 2023, 14, 1252–1262 Search PubMed.
- G. A. Dolgonos, J. Hoja and A. D. Boese, Revised values for the X23 benchmark set of molecular crystals, Phys. Chem. Chem. Phys., 2019, 21, 24333–24344 RSC.
- Y. H. Liang, H. Z. Ye and T. C. Berkelbach, Can Spin-Component Scaled MP2 Achieve kJ/mol Accuracy for Cohesive Energies of Molecular Crystals?, J. Phys. Chem. Lett., 2023, 14(46), 10435–10441 CrossRef CAS PubMed.
- G. J. O. Beran, Frontiers of molecular crystal structure prediction for pharmaceuticals and functional organic materials, Chem. Sci., 2023, 14, 13290–13312 Search PubMed.
- C. Greenwell, J. L. McKinley, P. Zhang, Q. Zeng, G. Sun and B. Li, et al., Overcoming the difficulties of predicting conformational polymorph energetics in molecular crystals via correlated wavefunction methods, Chem. Sci., 2020, 11, 2200–2214 RSC.
- F. Stein and J. Hutter, Massively parallel implementation of gradients within the random phase approximation: Application to the polymorphs of benzene, J. Chem. Phys., 2024, 160(2), 024120 CrossRef CAS PubMed.
- F. Della Pia, A. Zen, D. Alfè and A. Michaelides, DMC-ICE13: Ambient and high pressure polymorphs of ice from diffusion Monte Carlo and density functional theory, J. Chem. Phys., 2022, 157(13), 134701 CrossRef CAS PubMed.
- F. Della Pia, A. Zen, D. Alfè and A. Michaelides, How Accurate Are Simulations and Experiments for the Lattice Energies of Molecular Crystals?, Phys. Rev. Lett., 2024, 133, 046401 CrossRef PubMed.
- A. Zen, J. G. Brandenburg, J. Klimeš, A. Tkatchenko, D. Alfè and A. Michaelides, Fast and accurate quantum Monte Carlo for molecular crystals, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(8), 1724–1729 CrossRef CAS PubMed.
- Y. Kim, M. Sim, M. Lee, S. Kim, S. Song, K. Burke and S. Eunji, Extending Density-Corrected Density Functional Theory to Large Molecular Systems, J. Phys. Chem. Lett., 2024, 16(4), 939–947 CrossRef PubMed.
- P. R. Nagy, State-of-the-art local correlation methods enable affordable gold standard quantum chemistry for up to hundreds of atoms, Chem. Sci., 2024, 15, 14556–14584 RSC.
- C. Červinka and M. Fulem, State-of-the-Art Calculations of Sublimation Enthalpies for Selected Molecular Crystals and Their Computational Uncertainty, J. Chem. Theory Comput., 2017, 13(6), 2840–2850 CrossRef PubMed.
- V. Kapil and E. A. Engel, A complete description of thermodynamic stabilities of molecular crystals, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(6), e2111769119 CrossRef CAS PubMed.
- C. Greenwell and G. J. O. Beran, Inaccurate Conformational Energies Still Hinder Crystal Structure Prediction in Flexible Organic Molecules, Cryst. Growth Des., 2020, 20(8), 4875–4881 CrossRef CAS.
- F. Musil, S. De, J. Yang, J. E. Campbell, G. M. Day and M. Ceriotti, Machine learning for the structure–energy–property landscapes of molecular crystals, Chem. Sci., 2018, 9, 1289–1300 RSC.
- S. Wengert, G. Csányi, K. Reuter and J. T. Margraf, Data-efficient machine learning for molecular crystal structure prediction, Chem. Sci., 2021, 12, 4536–4546 RSC.
- A. K. Gupta, M. M. Stulajter, Y. Shaidu, J. B. Neaton and W. A. de Jong, Equivariant Neural Networks Utilizing Molecular Clusters for Accurate Molecular Crystal Lattice Energy Predictions, ACS Omega, 2024, 9(38), 40269–40282 CAS.
- D. Firaha, Y. M. Liu, J. van de Streek, K. Sasikumar, H. Dietrich and J. Helfferich, et al., Predicting crystal form stability under real-world conditions, Nature, 2023, 623(7986), 324–328 CrossRef CAS PubMed.
- P. W. V. Butler, R. Hafizi and G. M. Day, Machine-Learned Potentials by Active Learning from Organic Crystal Structure Prediction Landscapes, J. Phys. Chem. A, 2024, 128(5), 945–957 CrossRef CAS PubMed.
- C. R. Taylor, P. W. V. Butler and G. M. Day, Predictive crystallography at scale: mapping, validating, and learning from 1000 crystal energy landscapes, Faraday Discuss., 2024, 256, 434–458 RSC.
- A. Nandi, P. Pandey, P. L. Houston, C. Qu, Q. Yu and R. Conte, et al., Δ-Machine Learning to Elevate DFT-Based Potentials and a Force Field to the CCSD(T) Level Illustrated for Ethanol, J. Chem. Theory Comput., 2024, 20(20), 8807–8819 CrossRef CAS PubMed.
- O. T. Unke, M. Stöhr, S. Ganscha, T. Unterthiner, H. Maennel and S. Kashubin, et al., Biomolecular dynamics with machine-learned quantum-mechanical force fields trained on diverse chemical fragments, Sci. Adv., 2024, 10(14), eadn4397 CrossRef CAS PubMed.
- M. Feng, C. Zhao, G. M. Day, X. Evangelopoulos and A. I. Cooper, A Universal Foundation Model for Transfer Learning in Molecular Crystals, 2024 Search PubMed.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han and C. J. Bartel, et al., CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling, Nat. Mach. Intell., 2023, 5(9), 1031–1041 CrossRef.
- I. Batatia, D. P. Kovacs, G. N. C. Simm, C. Ortner and G. Csanyi, MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields, in Advances in Neural Information Processing Systems, 2022 Search PubMed.
- C. Chen and S. P. Ong, A universal graph deep learning interatomic potential for the periodic table, Nat. Comput. Sci., 2022, 2(11), 718–728 CrossRef PubMed.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Scaling deep learning for materials discovery, Nature, 2023, 624, 80–85 CrossRef CAS PubMed.
- K. Choudhary, B. DeCost, L. Major, K. Butler, J. Thiyagalingam and F. Tavazza, Unified graph neural network force-field for the periodic table: solid state applications, Digital Discovery, 2023, 2, 346–355 RSC.
- C. Chen and S. P. Ong, A universal graph deep learning interatomic potential for the periodic table, Nat. Comput. Sci., 2022, 2(11), 718–728 CrossRef PubMed.
- D. Zhang, H. Bi, F. Z. Dai, W. Jiang, X. Liu and L. Zhang, et al., Pretraining of attention-based deep learning potential model for molecular simulation, npj Comput. Mater., 2024, 10(1), 94 CrossRef.
- S. Takamoto, C. Shinagawa, D. Motoki, K. Nakago, W. Li and I. Kurata, et al., Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements, Nat. Commun., 2022, 13(1), 2991 CrossRef CAS PubMed.
- I. Žugec, R. M. Geilhufe and I. Lončarić, Global machine learning potentials for molecular crystals, J. Chem. Phys., 2024, 160(15), 154106 CrossRef PubMed.
- D. P. Kovács, J. H. Moore, N. J. Browning, I. Batatia, J. T. Horton, V. Kapil, et al., MACE-OFF: Transferable Short Range Machine Learning Force Fields for Organic Molecules, arXiv, 2025, preprint, arXiv:2312.15211, DOI:10.48550/arXiv.2312.15211, https://arxiv.org/abs/2312.15211.
- H. Kaur, F. Della Pia, I. Batatia, X. R. Advincula, B. X. Shi and J. Lan, et al., Data-efficient fine-tuning of foundational models for first-principles quality sublimation enthalpies, Faraday Discuss., 2025, 256, 120–138 RSC.
- I. Batatia, P. Benner, Y. Chiang, A. M. Elena, D. P. Kovács, J. Riebesell, et al., A foundation model for atomistic materials chemistry, arXiv, 2024, preprint, arXiv:2401.00096, DOI:10.48550/arXiv.2401.00096, https://arxiv.org/abs/2401.00096.
- J. W. Acree and J. S. Chickos, Phase Transition Enthalpy Measurements of Organic and Organometallic Compounds. Sublimation, Vaporization and Fusion Enthalpies From 1880 to 2010, J. Phys. Chem. Ref. Data, 2010, 39(4), 043101 CrossRef.
- M. A. V. Ribeiro da Silva, M. J. S. Monte and J. R. Ribeiro, Thermodynamic study on the sublimation of succinic acid and of methyl- and dimethyl-substituted succinic and glutaric acids, J. Chem. Therm., 2001, 33(1), 23–31 CrossRef CAS.
- H. G. M. De Wit, J. C. Van Miltenburg and C. G. De Kruif, Thermodynamic properties of molecular organic crystals containing nitrogen, oxygen, and sulphur 1. Vapour pressures and enthalpies of sublimation, J. Chem. Therm., 1983, 15(7), 651–663 CrossRef CAS.
- NIST Web_Book, and references within for accessed: July 2023. See https://webbook.nist.gov/chemistry/name-ser.html Search PubMed.
- A. Otero-de-la Roza and E. R. Johnson, A benchmark for non-covalent interactions in solids, J. Chem. Phys., 2012, 137(5), 054103 Search PubMed.
- A. M. Reilly and A. Tkatchenko, Understanding the role of vibrations, exact exchange, and many-body van der Waals interactions in the cohesive properties of molecular crystals, J. Chem. Phys., 2013, 139(2), 024705 CrossRef PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards and S. Dacek, et al., Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 Search PubMed.
- See the ESI† for: a benchmark of several DFT approximations on the lattice energies of the X23 dataset; the X23 equations of state computed with the vdW-DF2 functional; the training errors of the 23 fine tuned models; extra details on the computational set-up and convergence tests; the values of the sublimation enthalpies computed in this work; a comparison between ours and previous estimates of the QHA sublimation enthalpies; a detailed benchmark of the 23 fine tuned models on the X23 lattice energies, equations of state, and quasi-harmonic vibrational properties; an application of the framework reported in the main manuscript to the ice polymorphs; and a comparison between the 23 fine tuned models (one for each molecular crystal in X23) and a single general model (i.e., one model trained on the joined 23 training sets).
- https://www.csd3.cam.ac.uk/ .
- The cost is estimated on a single GPU on CSD3. The cost of the QMD simulations is estimated by multiplying the cost of the CMD simulations by the number of beads. Currently, the cost of 1 Ice Lake core hour on CSD3 is £0.01. Hence, the cost equivalent of the above mentioned ∼24000 core-hours threshold is ∼£240. The cost of 1 GPU-hour on CSD3 is £0.55. This means that the cost of the simulations performed in this work for a molecular crystals with ∼250 atoms in the supercell is ∼£0.1 for QHA, ∼£9 for CMD, and ∼£285 for QMD. Notably, the cost of our simulations is approximately within the threshold even with the inclusion of QNEs.
- X. Z. Li, B. Walker and A. Michaelides, Quantum nature of the hydrogen bond, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(16), 6369–6373 CrossRef CAS.
- G. L. Perlovich, T. V. Volkova and A. Bauer-Brandl, Polymorphism of paracetamol, J. Therm. Anal. Calorim., 2007, 89(3), 767–774 CrossRef CAS.
- H. G. M. De Wit, J. C. Van Miltenburg and C. G. De Kruif, Thermodynamic properties of molecular organic crystals containing nitrogen, oxygen, and sulphur 1. Vapour pressures and enthalpies of sublimation, J. Chem. Therm., 1983, 15(7), 651–663 CrossRef CAS.
- B. Chen, I. Ivanov, M. L. Klein and M. Parrinello, Hydrogen Bonding in Water, Phys. Rev. Lett., 2003, 91, 215503 CrossRef PubMed.
- X. Z. Li, M. I. J. Probert, A. Alavi and A. Michaelides, Quantum Nature of the Proton in Water-Hydroxyl Overlayers on Metal Surfaces, Phys. Rev. Lett., 2010, 104, 066102 CrossRef PubMed.
- A. R. Ubbelohde and K. J. Gallagher, Acid-base effects in hydrogen bonds in crystals, Acta Crystallogr., 1955, 8(2), 71–83 Search PubMed.
- J. Daru, H. Forbert, J. Behler and D. Marx, Coupled Cluster Molecular Dynamics of Condensed Phase Systems Enabled by Machine Learning Potentials: Liquid Water Benchmark, Phys. Rev. Lett., 2022, 129, 226001 CrossRef CAS PubMed.
- B. Huang, O. A. von Lilienfeld, J. T. Krogel and A. Benali, Toward DMC Accuracy Across Chemical Space with Scalable Δ-QML, J. Chem. Theory Comput., 2023, 19(6), 1711–1721 Search PubMed.
- E. Slootman, I. Poltavsky, R. Shinde, J. Cocomello, S. Moroni and A. Tkatchenko, et al., Accurate Quantum Monte Carlo Forces for Machine-Learned Force Fields: Ethanol as a Benchmark, J. Chem. Theory Comput., 2024, 20(14), 6020–6027 CrossRef CAS PubMed.
- N. O'Neill, B. X. Shi, K. Fong, A. Michaelides and C. Schran, To Pair or not to Pair? Machine-Learned Explicitly-Correlated Electronic Structure for NaCl in Water, J. Phys. Chem. Lett., 2024, 15(23), 6081–6091 Search PubMed.
- J. Schmidt, T. F. T. Cerqueira, A. H. Romero, A. Loew, F. Jäger and H. C. Wang, et al., Improving machine-learning models in materials science through large datasets, Mater. Today Phys., 2024, 48, 101560 Search PubMed.
- L. Barroso-Luque, M. Shuaibi, X. Fu, B. M. Wood, M. Dzamba, M. Gao, et al., Open Materials 2024 (OMat24) Inorganic Materials Dataset and Models, 2024 Search PubMed.
- M. Neumann, J. Gin, B. Rhodes, S. Bennett, Z. Li, H. Choubisa, et al., Orb: A Fast, Scalable Neural Network Potential, arXiv, 2024, preprint, arXiv:2410.22570, DOI:10.48550/arXiv.2410.22570, https://arxiv.org/abs/2410.22570.
- H. Yang, C. Hu, Y. Zhou, X. Liu, Y. Shi, J. Li, et al., MatterSim: A Deep Learning Atomistic Model Across Elements, Temperatures and Pressures, arXiv, 2024, preprint, arXiv:2405.04967, DOI:10.48550/arXiv.2405.04967, https://arxiv.org/abs/2405.04967.
- J. Kim, J. Kim, J. Kim, J. Lee, Y. Park and Y. Kang, et al., Data-Efficient Multifidelity Training for High-Fidelity Machine Learning Interatomic Potentials, J. Am. Chem. Soc., 2025, 147(1), 1042–1054 Search PubMed.
- X. T. Xie, T. Guan, Z. X. Yang, C. Shang and Z. P. Liu, Fine-Tuned Global Neural Network Potentials for Global Potential Energy Surface Exploration at High Accuracy, J. Chem. Theory Comput., 2025, 21(7), 3576–3586 CrossRef CAS PubMed.
- Y. Han, C. Ding, J. Wang, H. Gao, J. Shi and S. Yu, et al., Efficient crystal structure prediction based on the symmetry principle, Nat. Comput. Sci., 2025, 5, 255–267 Search PubMed.
- N. Galanakis and M. E. Tuckerman, Rapid prediction of molecular crystal structures using simple topological and physical descriptors, Nat. Commun., 2024, 15(1), 9757 CrossRef CAS PubMed.
- D. Zhou, I. Bier, B. Santra, L. D. Jacobson, C. Wu and A. Garaizar Suarez, et al., A robust crystal structure prediction method to support small molecule drug development with large scale validation and blind study, Nat. Commun., 2025, 16(1), 2210 CrossRef CAS PubMed.
- J. P. M. Lommerse, W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Gavezzotti and D. W. M. Hofmann, et al., A test of crystal structure prediction of small organic molecules, Acta Crystallogr., Sect. B, 2000, 56(4), 697–714 Search PubMed.
- W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Dzyabchenko, P. Erk and A. Gavezzotti, et al., Crystal structure prediction of small organic molecules: a second blind test, Acta Crystallogr., Sect. B, 2002, 58(4), 647–661 CrossRef PubMed.
- G. M. Day, W. D. S. Motherwell, H. L. Ammon, S. X. M. Boerrigter, R. G. Della Valle and E. Venuti, et al., A third blind test of crystal structure prediction, Acta Crystallogr., Sect. B, 2005, 61(5), 511–527 CrossRef CAS PubMed.
- G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk, H. L. Ammon and S. X. M. Boerrigter, et al., Significant progress in predicting the crystal structures of small organic molecules – a report on the fourth blind test, Acta Crystallogr., Sect. B, 2009, 65(2), 107–125 CrossRef CAS PubMed.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter and D. E. Braun, et al., Towards crystal structure prediction of complex organic compounds – a report on the fifth blind test, Acta Crystallogr., Sect. B, 2011, 67(6), 535–551 CrossRef CAS PubMed.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese and J. G. Brandenburg, et al., Report on the sixth blind test of organic crystal structure prediction methods, Acta Crystallogr., Sect. B, 2016, 72(4), 439–459 Search PubMed.
- K. Lee, E. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Higher-accuracy van der Waals density functional, Phys. Rev. B, 2010, 82, 081101 CrossRef.
- Y. Litman, V. Kapil, Y. M. Y. Feldman, D. Tisi, T. Begušić and K. Fidanyan, et al., i-PI 3.0: A flexible and efficient framework for advanced atomistic simulations, J. Chem. Phys., 2024, 161(6), 062504 CrossRef CAS PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen and M. Dułak, et al., The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29(27), 273002 CrossRef PubMed.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 Search PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 Search PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 Search PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- D. Alfè, PHON: A program to calculate phonons using the small displacement method, Comput. Phys. Commun., 2009, 180(12), 2622–2633 CrossRef , 40 YEARS OF CPC: a celebratory issue focused on quality software for high performance, grid and novel computing architectures.
- M. Ceriotti and D. E. Manolopoulos, Efficient First-Principles Calculation of the Quantum Kinetic Energy and Momentum Distribution of Nuclei, Phys. Rev. Lett., 2012, 109, 100604 CrossRef PubMed.
- M. Ceriotti, M. Parrinello, T. E. Markland and D. E. Manolopoulos, Efficient stochastic thermostatting of path integral molecular dynamics, J. Chem. Phys., 2010, 133(12), 124104 CrossRef PubMed.
- Quantum Espresso, http://www.quantum-espresso.org./.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu and X. Ren, et al., Ab initio molecular simulations with numeric atom-centered orbitals, Comput. Phys. Commun., 2009, 180(11), 2175–2196 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details on the benchmark of several DFT approximations on the lattice energies of the X23 dataset; the X23 equations of state computed with the vdW-DF2 functional; the training errors of the 23 fine-tuned models; extra details on the computational set-up and convergence tests; the values of the sublimation enthalpies computed in this work; a comparison between ours and previous estimates of the QHA sublimation enthalpies; a detailed benchmark of the 23 fine-tuned models on the X23 lattice energies, equations of state, and quasi-harmonic vibrational properties; the application of the framework reported in the main manuscript to the ice polymorphs; a comparison between the 23 fine-tuned models (one for each molecular crystal in X23) and a single general model (i.e., one model trained on the joined 23 training sets); the application of the fine-tuning framework to paracetamol, aspirin, and squaric acid. The training set and the fine-tuned models, together with scripts and input and output files necessary to reproduce the finding of this work are provided on GitHub (https://github.com/water-ice-group/MolCrys-MACE). See DOI: https://doi.org/10.1039/d5sc01325a |
| This journal is © The Royal Society of Chemistry 2025 |

