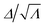Adhesion of a nematic elastomer cylinder

Abstract

Reversible dry adhesion is exploited by lizards and insects in nature, and is of interest to robotics and bio-medicine. In this paper, we use numerical simulation to study how the soft elasticity of liquid crystal elastomers can affect its adhesion and provide a technological opportunity. Liquid crystal elastomers are cross-linked elastomer networks with liquid crystal mesogens incorporated into the main or side chain. Polydomain liquid crystalline (nematic) elastomers exhibit unusual mechanical properties like soft elasticity, where the material deforms at nearly constant stress, due to the reorientation of mesogens. Our study reveals that the soft elasticity of nematic elastomers dramatically affects the interfacial stress distribution at the interface of a nematic elastomer cylinder adhered to a rigid substrate. The stress near the edge of the nematic cylinder under tensile load deviates from the singular behavior predicted for linear elastic materials, and the maximum normal stress reduces dramatically. This suggests that nematic elastomers should display extremely high, but controllable adhesion, consistent with the available experimental observations.

---

Introduction

Adhesion that exploits the surface forces between the material and dry surfaces can be significant, but reversible.¹ This is widely exploited in nature, for example by lizards and insects,² and is of increasing interest in engineering, for example in robotics^3,4 and in medical adhesives.⁵ It is now well recognized that contact mechanics and the distribution of stresses are as critical to this phenomenon as surface energy and chemistry.^1,6 This is because the failure of adhesion occurs by a process of nucleation and growth of an interfacial crack. This has motivated a number of approaches including the use of soft elastomers, shape, and composite materials to affect the stress distribution and consequently the adhesion.^6–9 Recent experimental observations in probe-tack,^10,11 and peeling¹² tests show that liquid crystals elastomers display extremely strong, but controllable, adhesion. In this paper, we explore how the remarkable soft behavior of liquid crystal elastomers can affect its adhesion to dry surfaces.

Liquid crystal elastomers (LCEs) are cross-linked elastomer networks with liquid crystal molecules, also known as mesogens, incorporated into the underlying polymer chains. Mesogens are stiff, rod-like molecules that respond to temperature by changing their orientation distribution. At high temperatures T > T_ni (T_ni denotes the nematic to isotropic transition temperature), the LCE is in the isotropic state where the mesogens are randomly oriented. At lower temperatures T < T_ni, the LCE is in the nematic state where the mesogens are aligned along a preferred direction. The degree of order observed in the mesogens determines the degree of anisotropy. When an isotropic-genesis LCE (one that is cross-linked in the isotropic state) is cooled down, it undergoes a phase transition from its isotropic state to a nematic state and forms an isotropic-genesis polydomain nematic LCE with domains on the order of 1–2 μm;¹³ see Fig. 1A.

Fig. 1 (A) Schematic of an isotropic-genesis polydomain nematic LCE cylinder adhered to a rigid surface. (B) The uniaxial nominal stress–strain curves for linear elastic material, neo-Hookean hyperelastic (r = 1) material, and LCE (r = 6). (C) Distribution of interfacial normal stress σ_zz along the adhered interface of the cylinder in logarithmic scale for materials in (B). (D) Distribution of the state variables Λ, Δ, and ratio for LCE with r = 6 near the adhered region at different applied loads σ_A. The insets show the singular region at the edge of the cylinder.

A fascinating characteristic of isotropic-genesis nematic LCEs is the soft elasticity behavior: when subjected to an external uniaxial tension, the material stretches at almost zero stress, resulting in a soft plateau region in the stress–strain curve.^14–16 This phenomenon is attributed to the reorientation of the mesogens through polydomain–monodomain transition.^13–15,17 Practically, nematic elastomers exhibit a non-ideal ‘semi-softness’ response due to the presence of internal constraints, leading to an initial linear elastic regime before the stress plateau. This produces a non-zero stress plateau until the full chain re-alignment is achieved. Several microscopic mechanisms contribute to this non-ideal semi-softness response including the polydispersity of network chains,¹⁸ the effect of anisotropic cross-linkers,¹⁹ and the entanglement of nematic chains.²⁰ Recent research indicates that the soft elasticity of LCE makes its mechanical behavior differ dramatically from that of rubber in various problems including the wrinkling of thin sheets,²¹ energy absorption in impact,²² and Hertz contact.²³ Interestingly, recent experiments^10,11 exhibit that the adhesion force between glass and a polydomain nematic LCE is higher than that between glass and silicone rubber. In this paper, we study how the soft elasticity of nematic LCE contributes to a stronger adhesion.

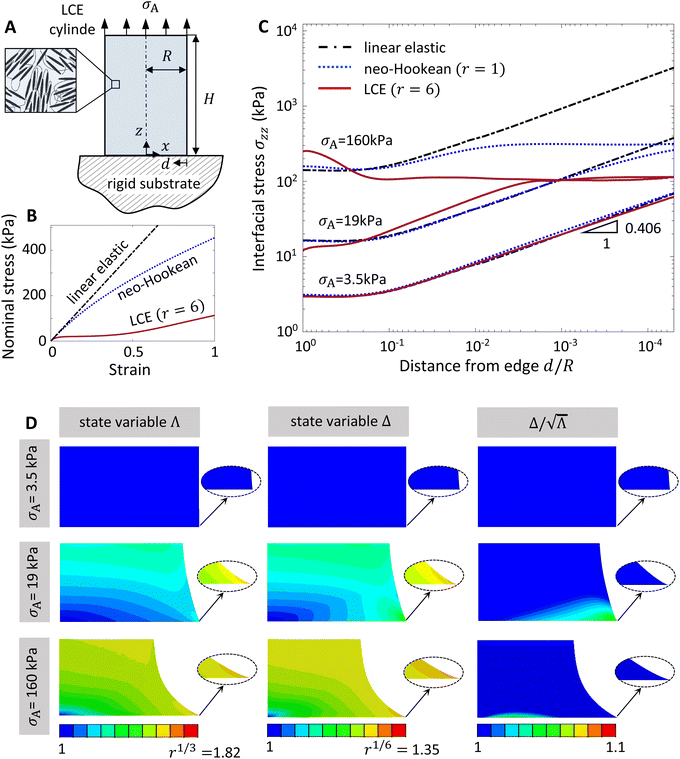
Consider a flat-ended cylinder perfectly attached to a rigid substrate at one end; see Fig. 1A. If the cylinder is linear elastic and subjected to a tensile load at the other end, the maximum normal stress on the cylinder-substrate interface occurs at the edge where the cylinder touches the substrate. In fact, the normal stress distribution is singular at this edge and is of the form σ = Kdⁿ, where the intensity K depends on the applied load, d is the distance from the edge, and n = −0.406.²⁴ This stress singularity results in a crack being initiated at the edge, and this eventually leads to the failure of adhesion. In this work, we examine the stress distribution on an LCE flat-ended cylinder perfectly attached to a rigid substrate at one end and subject to an applied tensile load at the other. We find that the soft elasticity dramatically changes the interfacial stress distribution in the LCE cylinder. The stress is no longer singular at the edge and the location of the maximum stress shifts to the interior. We discuss the implications for adhesion and compare the results with available experimental data.

Model

We consider a cylinder under normal loading as shown in Fig. 1A. The bottom surface of the cylinder is fixed in all directions to model adhesion to a rigid flat substrate, while the top interface of the cylinder is quasi-statically displaced uniformly in the axial or z-direction with no displacement allowed in other directions modeling the fact that the cylinder is bonded to a stiff support plate at the top. The lateral surfaces are traction-free. We consider a relatively long cylinder with overall height H = 10 mm and radius R = 1 mm to eliminate end effects on the stress distribution at the interface. We model the cylinder as a 2D axisymmetric model in the commercial finite element package ABAQUS Standard.²⁵ The cylinder is discretized using four-node bilinear axisymmetric quadrilateral hybrid elements (Abaqus CAX4H).

We use the constitutive model for an isotropic-genesis polydomain nematic elastomer developed by Lee et al.²⁶ We provide a brief overview of the model here. This model introduces two scalar state variables Λ and Δ that describe the spontaneous deformation associated with the local domain pattern. These are closely related to local polydomain order parameters: Λ with the degree of orientation S, and Δ with S + X where X is the degree of biaxial orientation. These state variables describe the spontaneous change in material metric (the Cauchy–Green stretch due to domains) G = P diag(Λ², Δ²/Λ², 1/Δ²)P^T where P is a rotation matrix, and Λ and Δ can take values in the region 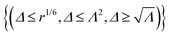where r is the chain anisotropy parameter (related to the degree of nematic order Q). A monodomain has Λ = r^1/3 and Δ = r^1/6 so that G is the step-length tensor [small script l] of the neo-classical theory,²⁷ and an isotropic polydomain state where the nematic directors are equidistributed has Λ = Δ = 1 so that G is identity. The biaxial polydomain state where all the nematic directors are confined to a plane but equidistributed in the plane has Λ = r^1/12 and Δ = r^1/6 so that G = P diag(r^1/12, r^1/12, r^−1/6)P^T. The model postulates a coarse-grained free energy W = W_e + W_r where 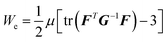is the entropic energy in the polymer chains for a deformation gradient F relative to an isotropic reference state, with μ the rubber modulus, and W_r = C(Δ − 1)/(r^1/6 −Δ)^k is the energy of domain patterns required to overcome fluctuations. The deformation is determined by the equation of mechanical equilibrium while the state variables evolve according to overdamped dynamics 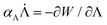, 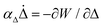. The model has been validated against experiments and verifiably implemented as a UMAT in the finite element package ABAQUS; further details can be found in ref.26. The typical material properties we use in our simulations are μ = 0.26 MPa, C = 0.6 kPa, α_Δ = 30 MPa.s, α_Λ = 0.01α_Δ, k = 2, and r = 6 for a nematic LCE cylinder. Note that we can include the neo-Hookean rubber into this model by setting r = 1.

The exact stress value at the corner of the cylinder is sensitive to the mesh size due to the presence of a singularity. Therefore, a very fine mesh is used close to the corner of the cylinder to increase the accuracy of the results there. The mesh near the contact interface and the free edge is refined, and mesh convergence is verified with further refinement resulting in less than 0.5% difference in the average normal stress. We verify that we resolve the singularity at the edge by plotting the stress on a semi-log plot and verifying the slope against known theoretical values for linear elastic materials as shown in Fig. 1C. We note that as the anisotropy parameter r increases, the model requires finer mesh size for convergence at the corner stress; see, for instance, Fig. S1 in ESI.† Our converged model possesses a total of 26 015 elements with the smallest mesh size of 2 × 10⁻⁶ mm at the corner. We use the same mesh size around the adhesion region for all the simulations resulting in less than 0.5% difference in the average normal stress.

Results and discussion

Interfacial stress distribution

Fig. 1C displays the distribution of normal stress along the adhered interface for a linear elastic material, a neo-Hookean hyperelastic material (LCE with r = 1), and a nematic LCE with r = 6 at various values of the applied load. We present the results in a logarithmic scale to highlight the details of the stress singularity near the edge of the cylinder. For the linear elastic cylinder, a significant stress concentration is generated at the edge of the interface in the form of σ_zz = Kdⁿ with n = −0.406 as anticipated in the classical theory,²⁴ thereby providing a verification of the numerical method. This singularity exists at all values of the applied load, with the intensity K proportional to the applied load. A neo-Hookean hyperelastic cylinder (r = 1) follows the linear elastic theory for small values of the applied load (e.g., 3.5 kPa), but then deviates from it at larger values of the applied load. At σ_A = 160 kPa, there is no singularity at the edge. Further, the value of the normal stress at the edge is significantly less than that in a linear elastic material, but looks similar away from the edge except it is slightly elevated at the center (to give the same average stress).

Finally, we turn to the LCE cylinder with r = 6. At low applied loads (σ_A = 3.5 kPa), the stress distribution follows the linear elastic theory with an exponent n = −0.406. This is because of the initial elastic regime in the stress–strain response of the non-ideal LCE; see the stress–strain curve in Fig. 1B. However, it soon deviates as we increase the load. The singularity at the edge vanishes and the level of stress at the edge is significantly reduced compared to the other two materials, at σ_A = 19 kPa. As the load increases further, the stress distribution is still regular. Further, the value at the edge remains unchanged despite the increased applied load and increases in the center of the cylinder instead, see σ_A = 160 kPa. Thus the stress at the edge is significantly smaller in the LCE compared to that in the other two cases, but higher in the center.

To gain insight into the reason for this dramatically different stress distribution in the LCE, we study the domain pattern and its evolution. Fig. 1D shows the distribution of the state variables Λ and Δ, and the ratio 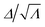in the vicinity of the adhered region at three different applied loads σ_A. The color scale in Fig. 1D for Λ and Δ are chosen so that blue corresponds to the smallest value (1 for both) while red corresponds to the largest theoretical value (r^1/3 = 1.82 for Λ, r^1/6 = 1.35 for Δ). However, the color scale for 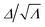is chosen to be limited to be close to 1 (the possible maximum value for 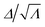is r^1/8 = 1.25 but our scale only goes to 1.1). As the applied load σ_A increases, Λ evolves significantly, especially near the edge of the cylinder with the maximum value at the edge. This maximum Λ at the edge reaches the saturation value of ≈1.71 at the higher applied load (σ_A = 160 kPa) and this is close to the theoretical maximum value of 1.82 (the material hardens significantly as it approaches the maximum value in the constitutive model). We observe that Δ also evolves and reaches the value of ≈1.31 (close to the maximum values of 1.35) at the edge of the cylinder at the higher load. However, the ratio 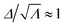everywhere along the adhered interface in all cases. The ratio 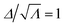indicates a pure uniaxial deformation. Therefore, we conclude that the domain pattern evolves to maintain an uniaxial state of deformation along the adhered interface. Further, Λ ≈ r^1/3 and Δ ≈ r^1/6 at the edge, and thus the LCE is almost in a monodomain state. In other words, the polydomain–monodomain transition suppresses the stress singularity at the edge in an LCE cylinder.

Fig. 2A shows the maximum interfacial normal stress σ_zz^max and the corresponding radial position where it is attained for different applied loads σ_A. The maximum interfacial stress for the neo-Hookean material remains at the edge of the cylinder (a₁–e₁), as exemplified in Fig. 1C. However, LCE exhibits a significantly different trend. At low applied load, the maximum interfacial stress is located at the edge (a₆–c₆), but the location of maximum stress shifts from the edge to the center of the cylinder (d₆–e₆) above a transition applied load σ_A^t; see Fig. 1C. As shown in Fig. 2B, the interfacial stress at the transition applied load σ_A^t is almost uniform along the adhered interface.

Fig. 2 (A) Maximum interfacial stress σ_zz^maxvs. its corresponding radial position along the adhered interface of the cylinder at different applied loads σ_A. The red square data correspond to the nematic LCE cylinder with r = 6 and the blue circle data correspond to the isotropic cylinder (r = 1). (B) Distribution of interfacial normal stress σ_zz along the adhered interface of the cylinder at transition applied load σ_A^t = 94 kPa for LCE with r = 6.

Adhesion

The failure adhesion in a cylinder of sufficiently large diameter occurs by a process of nucleation of a crack either at a pre-existing flaw or stress singularity followed by growth. Tanné et al.²⁸ (also ref. 29), based on an extensive study of experimental and computational observations, proposed a unified criterion for stress nucleation at a point where the opening stress is locally of the form σ ∼ Kdⁿ (so n = 0 for a non-singular stress field, n = −0.406 at the edge of an adhered cylinder, and n = −0.5 for a pre-existing crack). A crack nucleates when

K = K_c: = K_Ic⁻²ⁿσ_c¹⁺²ⁿ (1)

where K_Ic is the fracture toughness and σ_c is the maximum tensile strength. Note that K = K_Ic in the presence of a pre-existing crack and σ = σ_c in the absence of a singularity in agreement with classical fracture mechanics.

We now apply this criterion to the current problem of cylinder adhesion. In a linear elastic cylinder, the stress is singular at the corner with n = −0.406, and therefore, failure initiates at the corner. Therefore, the stress intensity factor K determines the adhesion strength of the cylinder;^7–9 the lower stress intensity at the edge of the cylinder leads to a higher adhesion strength. In a neo-Hookean cylinder, the stress is initially singular at the edge, but then becomes regular. At that point, though the highest stress occurs at the edge (Fig. 2), the stress is quite uniform (Fig. 1). It is also known that in shorter cylinders, the interior stress can also increase.³⁰ For these reasons, failure may occur at the edge or in the interior depending on the specific dimensions and properties.³¹ However, the failure will occur at significantly higher values of the applied load compared to a linear elastic material of similar properties.

In an LCE cylinder, the stress is singular at the edge for small applied loads, but the stress intensity is insufficient to cause failure. The singularity decreases and eventually goes away. Further, the levels of stress are significantly lower in an LCE cylinder compared to that of the neo-Hookean cylinder (Fig. 1 and 2). In other words, there are two mechanisms for the suppression of failure – lack of a stress singularity at the edge, and significantly reduced levels of stress. This leads to a significant increase in the adhesive strength of an LCE cylinder compared to that of a neo-Hookean one. This is consistent with the experimental observation by Farre-Kaga et al.¹⁰ where they tested the adhesion of the polydomain nematic LCE via the probe-tack experiment (rigid cylinder and LCE substrate). Further, since the location of the highest stress is in the interior, we expect the failure to initiate in the interior even for long cylinders.

Effect of temperature

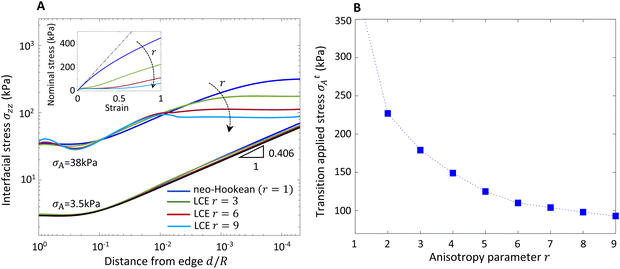
Temperature T significantly affect anisotropy parameter r. At T_ni < T, the LCE is in the isotropic state with r = 1, and at T < T_ni, the LCE is nematic with r > 1. Fig. 3A compares the interfacial stress distribution at different anisotropy parameters r (equivalently, different temperatures) with the corresponding uniaxial stress–strain curves in Fig. 3 (inset). At low load (σ_A = 3.5 kPa), all cases follow the linear elastic theory with the same stress distribution along the interface including a singularity at the edge with the exponent n = −0.406. The singularity vanishes for all the studied cases at the higher applied load (σ_A = 38 kPa). However, the value of the stress at the edge decreases with increasing r (decreasing temperature). These lead us to conclude that lower temperature would lead to stronger adhesion, and this is consistent with experimental observations of Ohzono et al.¹¹Fig. 3B shows the transition applied load σ^t_A at which the point of maximum stress shifts from the edge to the center. We observe that this transition occurs at a smaller load for larger r (lower temperature). Therefore, we anticipate an interior failure at lower temperatures.

Fig. 3 (A) Distribution of interfacial normal stress σ_zz along the adhered interface of the cylinder in logarithmic scale at different anisotropy r. The inset presents the corresponding uniaxial nominal stress–strain curves. (B) Transition applied load σ_A^t as a function of anisotropy parameter r.

Conclusion

We use numerical simulation to study how the remarkable softness of liquid crystal elastomers affects the adhesive behavior of this material on rigid surfaces. We show that the soft behavior of nematic elastomers dramatically affects the interfacial stress distribution at the interface of a nematic elastomer cylinder adhered to a rigid substrate. Specifically, the stress near the edge of the nematic cylinder under tensile load deviates from the singular behavior predicted for linear elastic materials, and the maximum normal stress reduces dramatically. Together, these imply that one would have to apply a much larger macroscopic load to initiate adhesive failure (i.e., nucleate a crack). This would manifest itself as a significantly higher adhesive strength. This is consistent with the experimental observations in probe-tack,^10,11 and peeling¹² tests. Our analysis also shows that the nature of the stress distribution depends on temperature (through the anisotropy parameter), and therefore the apparent adhesion would be temperature-dependent. The fact that the adhesion can be controlled, and the maximum adhesion can be very high, implies that LCEs offer a highly attractive medium for robotic and bio-medical grippers and climbers. In other words, LCEs offer an alternative to the other approaches that exploit shape and composite materials. Future research may explore the adhesion and interfacial stress distribution of nematic LCEs with square or rectangular cross-sectional contact shapes under combined tensile and shear loads. This could pave the way for designing adhesives that offer both strong adhesion and easy removal.

Data availability

All algorithms and data necessary for the analysis are included in the paper and ESI.†

Conflicts of interest

The authors declare that they have no conflict of interests.

Acknowledgements

This work has been funded by the US Office of Naval Research (MURI grant N00014-18-1-2624).

References

1. R. Hensel, K. Moh and E. Arzt, Adv. Funct. Mater., 2018, 28, 1800865.
2. K. Autumn, Y. A. Liang, S. T. Hsieh, W. Zesch, W. P. Chan, T. W. Kenny, R. Fearing and R. J. Full, Nature, 2000, 405, 681–685.
3. S. Song, D.-M. Drotlef, J. Paik, C. Majidi and M. Sitti, Extreme Mech. Lett., 2019, 30, 100485.
4. M. Spenko, Adv. Intell. Syst., 2023, 5, 2100063.
5. M. K. Kwak, H.-E. Jeong and K. Y. Suh, Adv. Mater., 2011, 23, 3949–3953.
6. S. S. Pande and K. T. Turner, Extreme Mech. Lett., 2023, 59, 101969.
7. R. Balijepalli, M. Begley, N. Fleck, R. McMeeking and E. Arzt, Int. J. Solids Struct., 2016, 85, 160–171.
8. R. Balijepalli, S. Fischer, R. Hensel, R. McMeeking and E. Arzt, J. Mech. Phys. Solids, 2017, 99, 357–378.
9. A. Luo, A. Mohammadi Nasab, M. Tatari, S. Chen, W. Shan and K. Turner, Soft Matter, 2020, 16, 9534–9542.
10. H. Farre-Kaga, M. Saed and E. Terentjev, Adv. Funct. Mater., 2022, 32, 2110190.
11. T. Ohzono, M. Saed and E. Terentjev, Adv. Mater., 2019, 31, 1902642.
12. R. Annapooranan, S. Suresh Jeyakumar, R. J. Chambers, R. Long and S. Cai, Adv. Funct. Mater., 2024, 34, 2309123.
13. S. Clarke, E. Terentjev, I. Kundler and H. Finkelmann, Macromolecules, 1998, 31, 4862–4872.
14. J. Biggins, M. Warner and K. Bhattacharya, Phys. Rev. Lett., 2009, 103, 037802.
15. J. Biggins, M. Warner and K. Bhattacharya, J. Mech. Phys. Solids, 2012, 60, 573–590.
16. K. Urayama, E. Kohmon, M. Kojima and T. Takigawa, Macromolecules, 2009, 42, 4084–4089.
17. S. Fridrikh and E. Terentjev, Phys. Rev. E, 1999, 60, 1847.
18. G. Verwey and M. Warner, Macromolecules, 1997, 30, 4189–4195.
19. G. Verwey and M. Warner, Macromolecules, 1997, 30, 4196–4204.
20. S. Kutter and E. Terentjev, Eur. Phys. J. E, 2001, 6, 221–229.
21. P. Plucinsky and K. Bhattacharya, J. Mech. Phys. Solids, 2017, 102, 125–150.
22. S. Jeon, B. Shen, N. Traugutt, Z. Zhu, L. Fang, C. Yakacki, T. Nguyen and S. Kang, Adv. Mater., 2022, 34, 2200272.
23. A. Maghsoodi, M. Saed, E. Terentjev and K. Bhattacharya, Extreme Mech. Lett., 2023, 63, 102060.
24. S. Khaderi, N. Fleck, E. Arzt and R. McMeeking, J. Mech. Phys. Solids, 2015, 75, 159–183.
25. A. v. 6.20, A. v. 6.20, Dassault Systems Simulia Corp., Johnston, RI, USA, 2020.
26. L. Victoria, A. Wihardja and K. Bhattacharya, J. Mech. Phys. Solids, 2023, 179, 105369.
27. M. Warner and E. Terentjev, Liquid Crystal Elastomers, Oxford University Press, 2007.
28. E. Tanné, T. Li, B. Bourdin, J. J. Marigo and C. Maurini, J. Mech. Phys. Solids, 2018, 110, 80–99.
29. C. Hsueh, L. Avellar, B. Bourdin, G. Ravichandran and K. Bhattacharya, J. Mech. Phys. Solids, 2018, 120, 68–78.
30. A. Gent and P. Lindley, Proc. R. Soc. London, Ser. A, 1959, 249, 195–205.
31. H. Yao and H. Gao, J. Mech. Phys. Solids, 2006, 54, 1120–1146.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00606b

---