Open Access Article
Open Access ArticleHelical pitch and thickness-dependent opto-mechanical response in cholesteric liquid crystal elastomers†
Alexis T.
Phillips
a,
Jonathan D.
Hoang
b and
Timothy J.
White
 *ab
*ab
aDepartment of Chemical and Biological Engineering, University of Colorado, Boulder, Colorado, USA
bMaterials Science and Engineering Program, University of Colorado, Boulder, Colorado, USA. E-mail: Timothy.J.White@colorado.edu
First published on 24th February 2025
Abstract
Cholesteric liquid crystalline elastomers (CLCEs) are selectively reflective, deformable materials. We prepared CLCEs with selective reflection spanning the electromagnetic spectrum, from the visible to the mid-wave infrared (MWIR). Within these CLCEs, we systematically investigate the opto-mechanical response and expand upon observations detailed in our previous study where CLCEs with comparatively long pitch lengths do not exhibit total reflection in response to deformation (i.e., mechanically induced depolarization of the selective reflection). By systematically varying the pitch length and/or thickness of the CLCEs we isolate that total reflection in CLCEs is dependent on the number of helical pitches (Np). Optical characterization, including polarized optical microscopy (POM), UV-vis, and FTIR spectroscopy, is complemented by X-ray scattering to uncover the mechanical origins. The tunable and reversible optical properties of CLCEs position them as promising candidates for adaptive optics, sensors, tunable reflectors, and reconfigurable photonic devices.
Introduction
Cholesteric liquid crystals (CLCs) exhibit selective reflection due to the periodic modulation of the refractive index along the optical axis.1,2 This phenomenon arises from the helical arrangement of the nematic director, where one complete rotation defines the helical pitch (P). The handedness of the helix is dictated by the handedness of the chiral dopants that transfer their chirality to achiral liquid crystal mesogens. The selective reflection of CLCs achieves a maximum theoretical reflection efficiency of 50% unpolarized light (dependent on the handedness of the cholesteric helix).The cholesteric phase can be arrested in a liquid crystalline polymer network (LCN). Here we are particularly interested in elastomeric LCNs, in which the molecular weight between crosslinks is high enough to introduce elastic deformability.3 These materials have been referred to as cholesteric liquid crystal elastomers (CLCEs). As elastic media, CLCEs are readily deformed. Experimental and theoretical investigation document blue-shifted tuning of the selective reflection that can be accompanied by “total reflection”. Various stimuli have been utilized to indirectly mechanically deform CLCEs, including heat,4,5 light,6–9 or an electric field.10–12 The extensive range of chemistries and crosslinking strategies available for CLCEs have enabled their development as highly adaptable optical materials considered for potential use in lasing, sensing, wearable devices, and optical filters.13–16
Theoretical analyses have shed light on how mechanical strain affects the CLCE helix.17,18 When stretched perpendicular to the helical axis, the pitch length decreases, causing a blue-shift in the reflected wavelength (λc) as dictated by the relationship λc = ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) P, where
P, where ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) represents the average refractive index. The birefringence (Δn) of a CLCE arises from the difference between the ordinary (no) and extraordinary (neo) refractive indices of the liquid crystal molecules within the polymer network. The birefringence controls the bandwidth of the reflection notch (Δλ = ΔnP). At zero or low strain values, the reflection of CLCE is circularly polarized. However, applied strain can result in total reflection (i.e., eliminate helical handedness) achieving reflection efficiency up to 100% under sufficient deformation.18
represents the average refractive index. The birefringence (Δn) of a CLCE arises from the difference between the ordinary (no) and extraordinary (neo) refractive indices of the liquid crystal molecules within the polymer network. The birefringence controls the bandwidth of the reflection notch (Δλ = ΔnP). At zero or low strain values, the reflection of CLCE is circularly polarized. However, applied strain can result in total reflection (i.e., eliminate helical handedness) achieving reflection efficiency up to 100% under sufficient deformation.18
The transition of cholesteric liquid crystal elastomers (CLCEs) from selective reflection of circularly polarized light to “total reflection” (or depolarization) upon deformation is rooted in the fundamental interplay between their helical structure and mechanical properties, as theorized by Warner and coworkers in the early 2000s and experimentally confirmed by Terentjev and others.17,19–22 In their initial state, CLCEs exhibit a periodic helical arrangement of liquid crystalline molecules, which leads to selective reflection of circularly polarized light with a specific handedness (right-handed or left-handed) depending on the chirality of the system.23–26 This selective reflection occurs due to the photonic bandgap created by the periodic variation of the refractive index along the helix. The incident light with a matching circular polarization state is reflected, while the opposite handedness passes through the material. When mechanical deformation, such as uniaxial strain, is applied perpendicular to the helical axis, the liquid crystal director throughout the CLCE can reorient towards the direction of the strain. Concurrently, as the CLCE stretches, the helical pitch becomes compressed, which reduces the pitch length and results in a blue-shift in the reflected wavelength. As deformation continues, the originally well-ordered, chiral helical structure becomes increasingly distorted, disrupting the uniform periodicity and effectively eliminating the chirality of the periodic nanostructure. This structural disruption alters the refractive index contrast and the periodicity from which the selective, polarized reflection originates.19,20,27
Warner's theoretical models, supported by Terentjev's experimental work, demonstrate that at a critical level of strain, the reorientation and distortion lead to a loss of helical handedness in the reflection.19 At “total reflection”, the CLCE transitions to a state where both right-handed and left-handed circularly polarized light are reflected equally. In other words, the reflection of the CLCE transitions from circularly polarized to unpolarized (or depolarized). This is apparent in transmission spectra of unpolarized light passing through a strained CLCE dropping from 50% to 0%.
Despite these robust theoretical and experimental underpinnings, we recently reported an unexpected finding. CLCEs prepared with long pitch (e.g., infrared reflection) did not exhibit total reflection in response to deformation.28 We speculated that this was the result of the distinctive mechanical properties of CLCEs. Specifically, when subject to uniaxial deformation, CLCEs contract less in the thickness dimension compared to isotropic rubbers due to their helicoidal structure, leading to greater in-plane deformation. The Mao–Terentjev–Warner model predicts that for strain applied along the x-direction (λxx = λ), the corresponding deformations in the z- and y-directions are λ−2/7 and λ−5/7, respectively, assuming elastomer incompressibility.17,29 Beyond the initial linear elastic regime, a semi-soft elastic plateau arises, demarking director reorientation along the strain axis. Further deformation induces asymmetric deformation of the helix which can eliminate polarized reflection and reflects both left- and right-handed light—a phenomenon akin to increasing the incident angle on a CLC helix, where blue-shifting occurs as the effective pitch length seen by the light decreases, resulting in enhanced reflection due to changes in light polarization. The effects of sample thickness and associated change in the number of pitches have been examined in low molar mass CLCs at varying incident angles. These studies indicate that samples with fewer helical rotations require larger incident angles to exhibit total reflection.30–34
In this work, we systematically examine the opto-mechanical deformation of CLCEs with differing thicknesses, pitch counts, and reflection wavelengths. Our findings again highlight novel opto-mechanical phenomena in CLCEs reflecting longer wavelengths, (i.e., longer pitches). We characterize the polymer network structure, optical spectra, LC director behavior, and pitch evolution of these CLCEs subject to deformation provide insights into their distinct opto-mechanical responses.
Experimental
Sample preparation
Cholesteric liquid crystalline elastomers (CLCEs) were synthesized by combining acrylates and hexane dithiol (HDT, Sigma Aldrich) at a molar ratio of 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The liquid crystalline diacrylates used comprised a 60
1. The liquid crystalline diacrylates used comprised a 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 weight percent ratio of C6M (Wilshire Technologies) and C6BAPE (ChemFish). The addition of the chiral diacrylate monomer LC756 (HTP = 64 μm−1) was adjusted to achieve the desired reflection wavelength within the electromagnetic spectrum, as governed by the following relationship:
40 weight percent ratio of C6M (Wilshire Technologies) and C6BAPE (ChemFish). The addition of the chiral diacrylate monomer LC756 (HTP = 64 μm−1) was adjusted to achieve the desired reflection wavelength within the electromagnetic spectrum, as governed by the following relationship: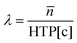 | (1) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is the average refractive index, HTP is the helical twisting power, and [c] is the chiral concentration. To initiate polymerization, 1 wt% Omnirad 819 (IGM Resins) was used as the photoinitiator, with 0.5 wt% 4-methoxyphenol (MeHQ, Sigma Aldrich) added as a stabilizer. All chemicals were used without further purification.
is the average refractive index, HTP is the helical twisting power, and [c] is the chiral concentration. To initiate polymerization, 1 wt% Omnirad 819 (IGM Resins) was used as the photoinitiator, with 0.5 wt% 4-methoxyphenol (MeHQ, Sigma Aldrich) added as a stabilizer. All chemicals were used without further purification.
Alignment cells were fabricated by spin-coating two plasma-cleaned ITO-coated glass slides (Colorado Concepts) with an Elvamide alignment layer. The Elvamide-coated glass was mechanically rubbed with velvet to induce surface alignment. The two glass slides were then assembled so that the ITO layers faced inward, creating a cell adhered with Norland Optical Adhesive mixed with glass spacers of varying thicknesses (5–120 μm). The assembled cells were UV-cured for 3 minutes to set the adhesive.
CLCE mixtures were prepared by melting all components at 149 °C while stirring on a vortexer for one minute to ensure homogeneity. The molten HDT was then pipetted into the mixture and stirred for an additional 30 seconds at 90 °C. The thiol-acrylate mixture was introduced into the alignment cells via capillary action at 90 °C, during the isotropic phase. Once the cells were filled, they were cooled rapidly to 18 °C using a cold plate. For samples 50 μm thick or greater, an electric field (4 V μm−1) was applied to ensure uniform alignment, which was maintained for ∼3 minutes. No voltage was applied to samples thinner than 50 μm. Once uniform alignment was achieved, the CLCEs were cured under 365 nm light at an intensity of 50 mW cm−2 for 10 minutes.
Material characterization
Polarized optical microscope (POM) (Nikon Eclipse CiPOL) was used to verify the phase and alignment of the CLCEs after polymerization. The POM was also employed to measure sample thickness and observe the director profile under strain using a micro-vise tensile stage. The optical properties of CLCEs with reflection wavelengths ranging from 300 nm to 2500 nm were monitored using a UV-vis spectrometer equipped with a universal measurement accessory (UMA) (Agilent Cary 7000). For SWIR and MWIR-reflecting CLCEs, a Fourier transform infrared (FTIR) spectrometer (Thermo Scientific Nicolet iS50) was used in transmission mode. Mechanical stress–strain data were collected using an RSA G2 solids analyzer at a linear strain rate of 5% of the original sample length per minute, with samples having a 1 × 4 aspect ratio.X-ray analysis was conducted using a Xenocs Xeuss 3.0 instrument with a rotating copper anode X-ray source at 8 keV energy. Small-angle X-ray scattering (SAXS) patterns were collected at a sample-to-detector distance of 0.37 m, while wide-angle X-ray scattering (WAXS) data were collected at a distance of 0.043 m. SAXS exposure times were 600 seconds, and WAXS exposure times were 180 seconds. All samples were mounted on a Linkham HFSX350 stage, and measurements were taken under vacuum in transmission geometry. Geometry corrections were performed using silver behenate (SAXS) and lanthanum hexaboride (WAXS) standards. Radial integration for 2D-to-1D data reduction was carried out using the “line-slice” method over the relevant scattering region.
The Herman's orientation parameter (S) was calculated from WAXS patterns using eqn (2) and (3):
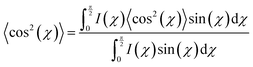 | (2) |
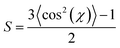 | (3) |
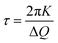 | (4) |
Results & discussion
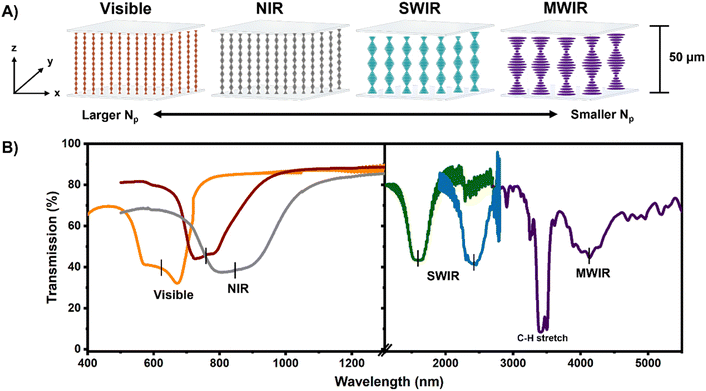
Cholesteric liquid crystal elastomers (CLCEs) were prepared with selective reflection spanning the electromagnetic spectrum. The pitch length of the CLCE increases as the selective reflection wavelength increases. The pitch length of a CLCE is equal to the thickness of the material (d) and the average refractive index (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ) divided by the number of pitches (Np) represented by eqn (5) at normal light incidence.
) divided by the number of pitches (Np) represented by eqn (5) at normal light incidence.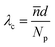 | (5) |
For CLCEs prepared with equivalent thickness and material composition (i.e., the same average refractive index), the variation in pitch length manifests as a change in Np. The association of material thickness, pitch length, and Np is evident in the illustration in Fig. 1A. The transmission spectra of the CLCEs prepared with selective reflection spanning from 600 to 4000 nm are presented in Fig. 1B. The selective reflection is evident as the sharp, stepwise decrease in transmission. At 50 microns, all CLCEs exhibit the maximum ∼50% reflection of right-handed circularly polarized light. These CLCEs are right-handed helixes associated with the right-handed chirality of the LC756* chiral monomer. Sample to sample variability is evident in the spectra in Fig. 1B, with variation in baseline transmission and reflection notch shape.
The central focus of our investigation was exploring the total reflection (i.e., depolarization) of CLCEs under mechanical strain as a function of selective reflection wavelength (i.e., pitch length). When uniaxial mechanical strain is applied perpendicularly to the helical axis, the liquid crystal (LC) director reorients toward the direction of strain, distorting the helical structure and leading to a loss of circular polarization. This behavior has been supported by both theoretical predictions and experimental observations.15–18,20–22,27,37–40 At sufficiently high strains, both left-handed (LH) and right-handed (RH) circularly polarized light are equally reflected due to the periodic structure of alternating refractive index layers. This phenomenon is evident in Fig. 2A, where a 27 μm-thick visible-reflecting CLCE was stretched incrementally in the x-direction, up to 50% strain. As expected, a blue-shift in reflection was observed with increasing strain. At 30% strain, the reflection depth begins to increase and eventually approaches 100% reflection (or 0% transmission) at 50% strain. In our prior report, we detailed the observation that CLCEs prepared with long pitch did not exhibit total reflection.28 Our systematic examination clarifies that this is a manifestation of the number of pitches rather than the pitch length. This is evident in Fig. 2B, in which a 6 μm-thick CLCE with a sufficient number of pitches for reflection of 100% of right-handed circularly polarized light (i.e., unpolarized incident light gets transmitted at 50%) is deformed to 50% strain by 10% strain increments.41 As evident in the transmission spectra, the selective reflection blue shifts due to the associated thickness decreased from the incompressibility of elastomers, but the depth of the reflection remains at 50%. This suggests that the defining variable for a CLCE to exhibit total reflection is the number of pitches.
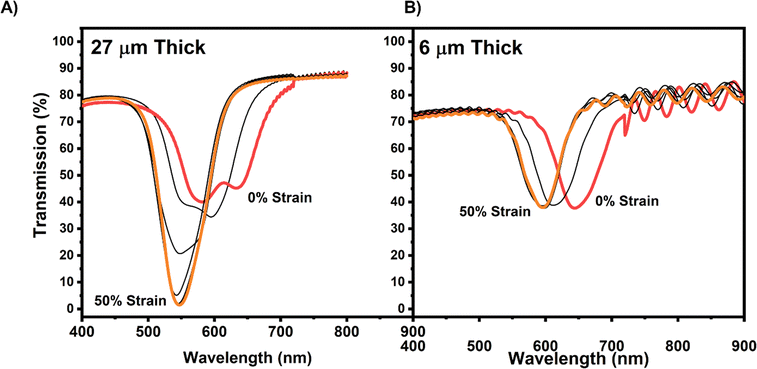 | ||
| Fig. 2 CLCEs were prepared with reflection notches at approximately 600 nm that were (A) 27 μm thick and (B) 6 μm thick and subject to 0–50% strain at 10% strain increments. | ||
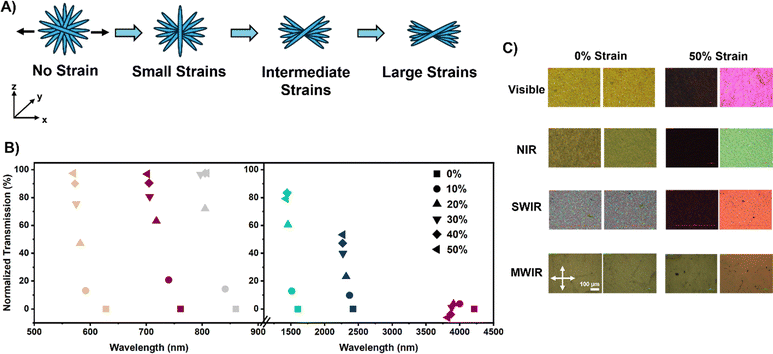
The response of the LC director to applied strain has been described as a gradual rotation within the xz-plane, followed by a dominant reorientation in the xy-plane towards the direction of strain (Fig. 3A). In an undistorted state, the twist angle changes linearly in the pitch direction (i.e., z-axis). As strain is applied, there is a non-linear, stepwise relationship between the twist angle as a function along the pitch which has been previously reported.17–19 This reorientation disrupts the helical structure, leading to an enhancement in LH reflection and a transformation into a periodic, achiral arrangement. To further elucidate the impact of strain, we examined 50 μm-thick CLCEs across the electromagnetic spectrum, straining these materials from 0% to 50% in increments of 10% (Fig. 3B). The visible and near-infrared (NIR) reflective CLCEs exhibited both a blue-shift and depolarization. Comparatively, CLCEs prepared with short-wave IR (SWIR) reflection showed limited depolarization and CLCEs with mid-wave (MWIR) reflection exhibited minimal reflection enhancement before normalized transmission decreased, indicating reflection loss. The transmission spectra for these experiments are presented in Fig. S1 (ESI†). Normalized transmission 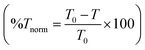 was used to compare all the CLCEs to remove discrepancies in baseline transmittance and reflection from sample to sample. The polarized optical microscope (POM) images taken in reflection mode (Fig. 3C) of visible, NIR, SWIR, and MWIR CLCEs before and after 50% strain revealed birefringence and reflection enhancement in high Np samples, while MWIR CLCEs exhibited only minor changes. High Np and thick CLCEs exhibit complete reorientation of the LC director under strain, resulting in birefringence and increased reflection, while low Np and thin samples show limited reorientation leading to enhanced reflection, as confirmed by the POM images (Fig. 3C). Under mechanical strain, the liquid crystal reorientation alters the macroscopic birefringence viewed under crossed polarizers in high Np CLCEs, but the intrinsic liquid crystal refractive indices (i.e., ne and neo) remain nearly constant thus preserving the bandwidth of the reflection notch.
was used to compare all the CLCEs to remove discrepancies in baseline transmittance and reflection from sample to sample. The polarized optical microscope (POM) images taken in reflection mode (Fig. 3C) of visible, NIR, SWIR, and MWIR CLCEs before and after 50% strain revealed birefringence and reflection enhancement in high Np samples, while MWIR CLCEs exhibited only minor changes. High Np and thick CLCEs exhibit complete reorientation of the LC director under strain, resulting in birefringence and increased reflection, while low Np and thin samples show limited reorientation leading to enhanced reflection, as confirmed by the POM images (Fig. 3C). Under mechanical strain, the liquid crystal reorientation alters the macroscopic birefringence viewed under crossed polarizers in high Np CLCEs, but the intrinsic liquid crystal refractive indices (i.e., ne and neo) remain nearly constant thus preserving the bandwidth of the reflection notch.
To explore the role of sample thickness and Np further, we examined CLCEs with thicknesses ranging from 5 μm to 123 μm. Fig. 4 presents the normalized transmission as a function of strain. The reflection of the CLCEs was broken up into five regions/panels – visible (350–700 nm), NIR (700–1000 nm), SWIR1 (1000–1500 nm), SWIR2 (1500–2500 nm), and MWIR (2500–5000 nm). The inset reveals the calculated Np based on the original sample thickness and reflection wavelength. The legend in each of the panels shows the original reflection wavelength and thickness of the CLCEs. Low Np CLCEs exhibited little to no depolarization upon strain, while high Np and thicker CLCEs achieved full depolarization more readily. Focusing on the visible panel, a sample with 12 Np does not have any enhanced reflection upon strain, and the reflection notch starts to diminish due to the decrease in normalized transmission to lower than 0% indicating loss of periodicity that enables Bragg reflection (similar to the MWIR CLCE in Fig. 3). When a visible reflecting CLCE has an Np = 17, there is no change in the transmittance of the reflection notch under mechanical strain. When a visible reflecting CLCE has an Np > 17, depolarization starts to occur evident in the appearance of LH reflection (i.e., total reflection). Similar results can be observed in the other panels across the CLCEs prepared over a range of pitch lengths. This data clearly isolates the correlation of Np and the manifestation of total unpolarized reflection. Our data also may suggest that the Np to achieve significant reflection enhancement may be pitch dependent as well. Looking at the MWIR CLCE panel, a sample that reflects 4120 nm light and is 123 μm thick having an Np = 48 does not have an increase in the normalized transmission (i.e., enhanced reflection). On the contrary, a 10 μm thick CLCE reflecting 515 nm light has an Np = 28 achieved nearly full depolarization. This suggests as the reflection wavelength increases, a larger Np is required to depolarize the reflection and start reflecting both LH and RH light. From this, we see Np plays a large role in the opto-mechanical properties of a CLCE, and there are clear differences in the LC director reorientation and overall periodicity of high/low Np CLCEs. The rate at which enhanced reflection occurs within the CLCEs of various Np under strain is shown in Fig. S2 (ESI†). This shows that higher Np/thicker CLCEs reach enhanced total reflection (i.e. a normalized transmission of 100%) at a much faster rate when strained compared to CLCEs with lower Np. This phenomenon is similar to what is shown in the literature with thick vs. thin low molar mass CLCs as the incident angle of light is increased.33
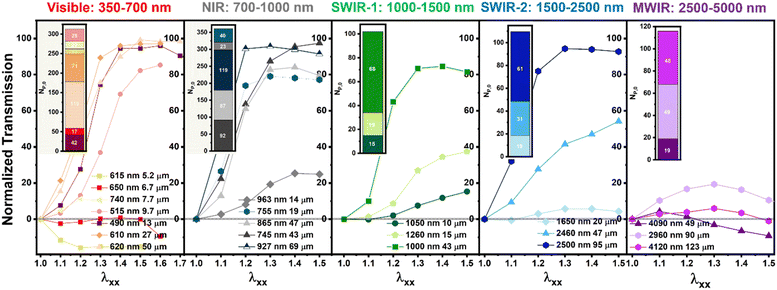 | ||
| Fig. 4 Normalized transmission versus strain for CLCEs of varying thicknesses across different regions of the electromagnetic spectrum. | ||
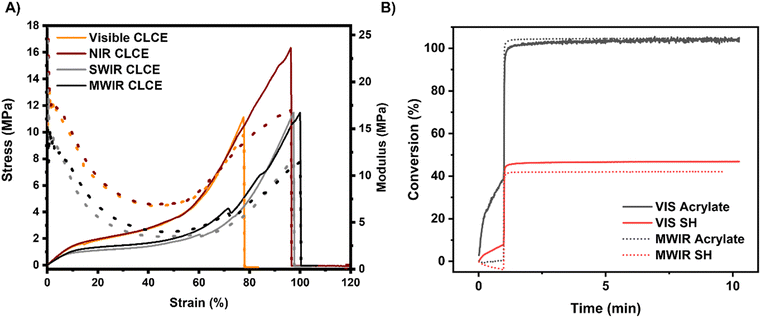
Mechanical characterization revealed differences in the stress–strain behavior of the 50 μm-thick CLCEs reflecting in the visible, NIR, SWIR, and MWIR regions (Fig. 5A). Mechanical characterization revealed that visible and NIR CLCEs exhibited higher Young's moduli compared to SWIR and MWIR samples, and the presence of a longer semi-soft elastic plateau for SWIR and MWIR CLCEs suggesting that more strain is required to achieve full LC director reorientation. This finding is clearly associated with the previously detailed optomechanical response of CLCEs. The softer response in higher reflection wavelength CLCEs could possibly be attributed to a less tightly constrained helical polymer network, allowing for easier deformation and softer mechanical behavior. The differences in mechanical properties while under strain indicates there are differences in how the CLC director reorients and how the polymer distorts with strain. Fig. 5B confirms in two exemplar compositions (VIS and MWIR reflecting CLCE) have similar acrylate and thiol conversions. The photopolymerization kinetic study of these CLCE networks is nearly identical to prior examination of this reaction in the preparation of nematic LCEs regarding the degree of acrylate incorporation, extent of chain extension, and unreacted thiol dangling ends.42,43
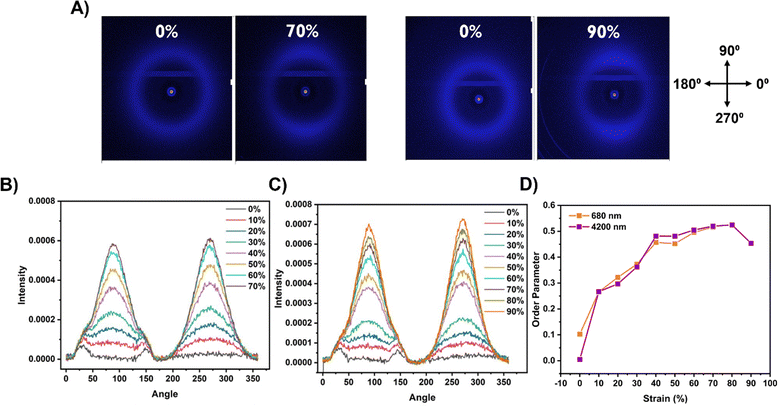
To better understand the behavior of LC director reorientation under strain, we conducted wide-angle X-ray scattering (WAXS) and small-angle X-ray scattering (SAXS) experiments on 50 μm-thick visible (high Np) and MWIR (low Np) reflective CLCEs. WAXS measurements indicate lateral LC mesogen packing/orientation and SAXS measurements indicate head-to-tail mesogen packing/orientation.36 WAXS data (Fig. 6A–C) showed isotropic scattering patterns in the absence of strain, indicative of no macroscopic order. Upon applying strain, peaks around 90° and 270° emerged, confirming mesogen alignment along the strain direction (i.e., 0° and 180° directions, or the x-axis). The orientation parameter was calculated as a function of strain for both CLCEs (Fig. 6D) using the WAXS data and the analysis outlined in the Experimental methods section. As strain is applied to the CLCE, the orientation parameter increases when fit to the 270° peak due to LC mesogen reorientation. Both CLCEs reach an orientation parameter of around 0.5 and have similar responses to strain.
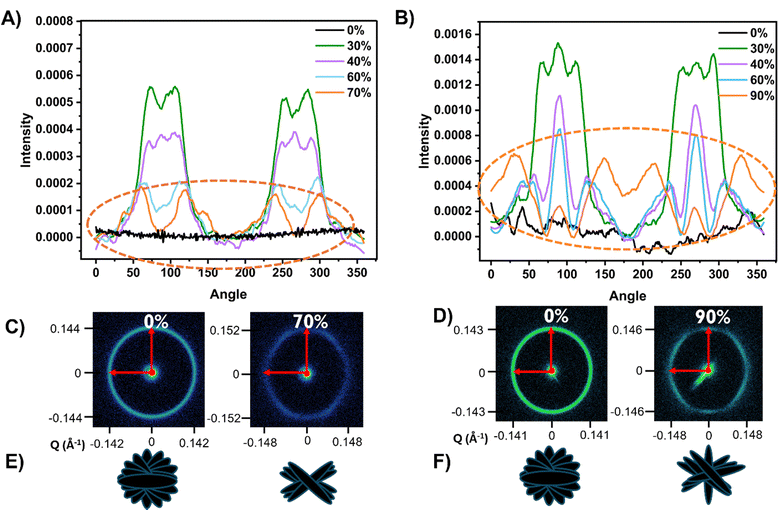
The difference in LC director reorientation between high and low Np CLCEs was further investigated with SAXS. SAXS measurements revealed differences in head-to-tail mesogen packing as well as director reorientation in high (visible) and low (MWIR) Np CLCEs. Fig. 7A and B show the SAXS intensity vs azimuthal angle as a function of applied strain for both 50 micron thick visible and MWIR CLCEs, respectively. Upon strain, visible-reflecting CLCEs exhibit a split peak at higher strains (>30%), indicating LC director rotation around the strain axis as theoretically predicted. In contrast, MWIR CLCEs showed incomplete mesogen reorientation where a small portion of LCs are still pinned in 90° and 270° directions. The SAXS patterns can also provide insight into the d-spacing upon strain by monitoring changes in the scattering vector (i.e., the Q-shift) in both the 0° and 90° directions before and after mechanical strain (Fig. 7C and D). The high Np, visible reflecting CLCE showed ∼ equal increase in the scattering vector in both the 0° and 90° directions, indicating uniform polymer network deformation under strain in all axes. Conversely, MWIR CLCEs exhibited non-uniform deformation in the 0° and 90° directions, suggesting polymer network distortion under strain. The intensity vs. Q graphs for both CLCEs under strain are shown in Fig. S3 (ESI†), and the LC orientation and network distortion is visually represented in Fig. 7E and F for visible and MWIR reflective CLCEs, respectively.
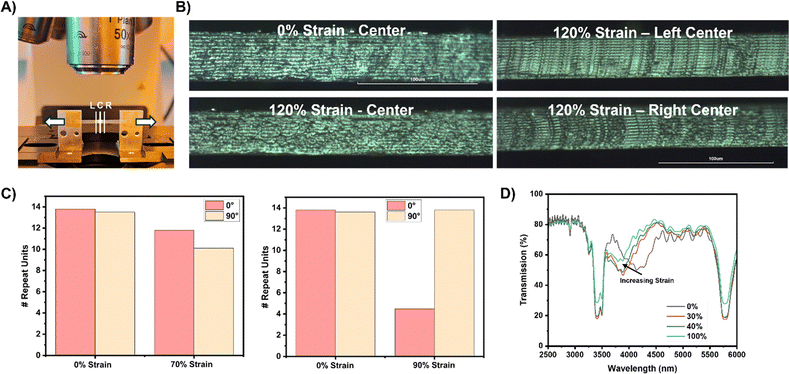
To investigate the association of the polymer network distortion represented in the MWIR CLCE SAXS patterns with the helical distortion, the helical pitch was investigated under the POM using the setup shown in Fig. 8A. The center of the film before deformation has alternating layers of bright and dark regions indicative of the undulations from the rotating director within the helical pitch (Fig. 8B). Straining this CLCE caused the center to have less distinct periodic bright and dark layers compared to the unstrained version. Looking at the sample slight left and right of center illustrates shear in the periodic LC layers. The shearing of the cholesteric layers can be further confirmed by calculating the coherence length and number of repeat units (as described in the Methods section) of the CLCEs before and after strain (Fig. 8C). The more periodic the CLCE is, the larger number of repeat units exist before a disruption in the periodicity is observed. Fig. 8C suggests that periodicity in the strain direction (0°) decreases while remaining constant in the 90° direction for the MWIR CLCE. However, the periodicity remains unchanged after strain in both axes for the visible CLCE. The decrease in the number of repeat units corresponds to the associated observed shear in the helix under strain (Fig. 8B).
Fig. 8D shows the correlation between the shearing effects and the reflection notch. Here, strains up to 30% cause very slight observed depolarization/enhancement of reflection due to mesogen reorientation. However, at strains 40% and larger, the reflection notch depth starts to decrease. The decrease in the reflection notch depth can be attributed to the distortion of periodicity in the CLCE because of polymer network shearing, as shown in the SAXS patterns (Fig. 7). As the MWIR CLCE is strained above 40%, the layered periodicity is getting disrupted leading to loss of overall reflection.
In summary, our results highlight the critical role of Np and thickness in the opto-mechanical response of CLCEs across the electromagnetic spectrum. High Np samples exhibit complete LC director reorientation and enhanced reflection, while low Np samples are prone to polymer network distortion resulting in limited reflection enhancement and eventual loss of reflection. This has been shown for several CLCEs across the electromagnetic spectrum, indicating that the reflection polarization is dependent on the Np, thickness, and pitch length. These findings provide valuable insights for designing CLCEs with tunable opto-mechanical properties for advanced optical applications.
Conclusion
In summary, this work presents the fabrication and detailed characterization of cholesteric liquid crystalline elastomers (CLCEs) with tunable reflection properties across the electromagnetic spectrum. By varying the concentration of the chiral monomer, we achieved precise control over the helical pitch and corresponding optical response. Careful examination of the optical response of CLCE to deformation revealed distinct opto-mechanical behavior based on thickness and pitch count. Thick, high-Np CLCEs exhibited enhanced reflection and complete LC director reorientation under strain, while thinner, low-Np samples showed limited reorientation and did not achieve total reflection due to loss of periodicity and polymer network distortion. Our findings highlight a previously unconsidered dependence of CLCE optomechanics on pitch count, offering new insights for the design and optimization of these materials.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Data availability
Data for this article, including Origin, Excel, and all X-ray files, are available upon request from the corresponding author. Additional data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. T. P acknowledges financial support from the NDSEG Fellowship of the Department of Defense. T. J. W. acknowledges support from the Air Force Office of Scientific Research (AFOSR, FA9550-20-1-0311). The Xenocs Xeuss 3.0 used in this work was purchased through funding from a Defense University Research Instrumentation Program under Grant Number N00014-22-1-2361.References
- W. D. John, W. J. Fritz, Z. J. Lu and D.-K. Yang, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 1191–1198 CrossRef PubMed.
- D. W. Berreman and T. J. Scheffer, Phys. Rev. Lett., 1970, 25, 577–581 CrossRef CAS.
- S. T. Kim and H. Finkelmann, Cholesteric Liquid Single-Crystal Elastomers (LSCE) Obtained by the Anisotropic Deswelling Method, Macromol. Rapid Commun., 2001, 22, 429–433 CrossRef CAS.
- H. Nagai and K. Urayama, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022501 CrossRef PubMed.
- K. R. Schlafmann, M. S. Alahmed, H. M. Pearl and T. J. White, ACS Appl. Mater. Interfaces, 2024, 16(18), 23780–23787 CAS.
- E.-Y. Chuang, W.-H. Huang, T.-L. Ho, P.-C. Wang and Y.-C. Hsiao, Chem. Eng. J., 2022, 429, 132213 CrossRef CAS.
- W. Liu, L.-X. Guo, B.-P. Lin, X.-Q. Zhang, Y. Sun and H. Yang, Macromolecules, 2016, 49, 4023–4030 CrossRef CAS.
- P. Zhang, G. Zhou, L. T. de Haan and A. P. H. J. Schenning, Adv. Funct. Mater., 2021, 31, 2007887 CrossRef CAS.
- H. Yang, J.-J. Liu, Z.-F. Wang, L.-X. Guo, P. Keller, B.-P. Lin, Y. Sun and X.-Q. Zhang, Chem. Commun., 2015, 51, 12126–12129 RSC.
- A. T. Phillips, K. R. Schlafmann, H. E. Fowler and T. J. White, Adv. Opt. Mater., 2022, 10, 2201457 CrossRef CAS.
- W. Zhao, L. T. de Haan, D. J. Broer, Y. Zhang, P. Lv and G. Zhou, Prog. Polym. Sci., 2021, 114, 101365 CrossRef CAS.
- S. Nam, D. Wang, G. Lee and S. S. Choi, Nanophotonics, 2022, 11, 2139–2148 CrossRef CAS PubMed.
- L. Wang, Z. Lou, K. Jiang and G. Shen, Adv. Intell. Syst., 2019, 1, 1900040 CrossRef.
- B. Li, Y. Wu, Y. Sun, W. Ma, L. Jiang, Z. Yang, P. Zhao, Y. Hu, L. Chang, Y. Wang, L. Yang, D. Ge and G. Chen, Adv. Intell. Syst., 2024, 6, 2200415 CrossRef.
- H. Finkelmann, S. T. Kim, A. Muñoz, P. Palffy-Muhoray and B. Taheri, Adv. Mater., 2001, 13, 1069–1072 CrossRef CAS.
- A. Varanytsia, H. Nagai, K. Urayama and P. Palffy-Muhoray, Sci. Rep., 2015, 5, 17739 CrossRef CAS PubMed.
- Y. Mao, E. M. Terentjev and M. Warner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 041803 CrossRef CAS PubMed.
- M. Warner, E. M. Terentjev, R. B. Meyer and Y. Mao, Phys. Rev. Lett., 2000, 85, 2320–2323 CrossRef CAS PubMed.
- P. Cicuta, A. R. Tajbakhsh and E. M. Terentjev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 011703 CrossRef CAS PubMed.
- S. Mori, H. Takagi, N. Shimizu, N. Igarashi, S. Sakurai and K. Urayama, Soft Matter, 2024, 20, 3931–3941 RSC.
- P. V. Shibaev, R. Uhrlass, S. Woodward, C. Schlesier, M. R. Ali and E. Hanelt, Liq. Cryst., 2010, 37, 587–592 CrossRef CAS.
- C. Kwon, S. Nam, S. H. Han and S. S. Choi, Adv. Funct. Mater., 2023, 33, 2304506 CrossRef CAS.
- V. A. Belyakov, V. E. Dmitrienko and V. P. Orlov, Soviet Phys.-Usp., 1979, 22, 64–88 CrossRef.
- N. P. M. Huck, I. Staupe, A. Thirouard and D. K. G. de Boer, Jpn. J. Appl. Phys., 2003, 42, 5189–5194 CrossRef CAS.
- H. L. de Vries, Acta Crystallogr., 1951, 4, 219–226 CrossRef CAS.
- P. A. Bermel and M. Warner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 65, 010702 CrossRef PubMed.
- Y. Geng, R. Kizhakidathazhath and J. P. F. Lagerwall, Nat. Mater., 2022, 21, 1441–1447 CrossRef CAS PubMed.
- A. T. Phillips, J. C. Chen, J. M. McCracken and T. J. White, ACS Appl. Opt. Mater., 2024, 2, 2559–2567 CrossRef CAS.
- V. Lee and K. Bhattacharya, J. Elast., 2024, 155, 671–697 CrossRef.
- M. A. Mossman and L. A. Whitehead, Appl. Opt., 2005, 44, 1601 CrossRef PubMed.
- B. A. Umanskii and I. V. Simdyankin, Crystallogr. Rep., 2017, 62, 448–454 CrossRef CAS.
- A. H. Gevorgyan, Opt. Spectrosc., 2008, 105, 624–632 CrossRef CAS.
- H. Takezoe, Y. Ouchi, M. Hara, A. Fukuda and E. Kuze, Jpn. J. Appl. Phys., 1983, 22, 1080 CrossRef CAS.
- D. Grzelczyk and J. Awrejcewicz, Lat. Am. J. Solids Struct., 2019, 16, e105 CrossRef.
- M. T. Sims, L. C. Abbott, R. M. Richardson, J. W. Goodby and J. N. Moore, Liq. Cryst., 2019, 46, 11–24 CrossRef CAS.
- G. R. Mitchell and A. H. Windle, Dev. Cryst. Polym., 1988, 2, 115–175 Search PubMed.
- R. Kizhakidathazhath, Y. Geng, V. S. R. Jampani, C. Charni, A. Sharma and J. P. F. Lagerwall, Adv. Funct. Mater., 2020, 30, 1909537 CrossRef CAS.
- K. Ku, K. Hisano, K. Yuasa, T. Shigeyama, N. Akamatsu, A. Shishido and O. Tsutsumi, Molecules, 2021, 26, 6193 CrossRef CAS PubMed.
- K. Hisano, S. Kimura, K. Ku, T. Shigeyama, N. Akamatsu, A. Shishido and O. Tsutsumi, Adv. Funct. Mater., 2021, 31, 2104702 CrossRef CAS.
- C. Yang, B. Wu, J. Ruan, P. Zhao, J. Shan, R. Zhang, D. K. Yoon, D. Chen and K. Liu, ACS Appl. Polym. Mater., 2022, 4, 463–468 CrossRef CAS.
- A. Mendoza-Galván, E. Muñoz-Pineda, S. J. L. Ribeiro, M. V. Santos, K. Järrendahl and H. Arwin, J. Opt., 2018, 20, 024001 CrossRef.
- N. P. Godman, B. A. Kowalski, A. D. Auguste, H. Koerner and T. J. White, ACS Macro Lett., 2017, 6, 1290–1295 CrossRef CAS PubMed.
- T. S. Hebner, H. E. Fowler, K. M. Herbert, N. P. Skillin, C. N. Bowman and T. J. White, Macromolecules, 2021, 54, 11074–11082 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00059a |
| This journal is © The Royal Society of Chemistry 2025 |