Open Access Article
Open Access ArticleFinding suitable biobased solvents for extractions from water†
Gerhard
König
 *a,
Pascal
Hauk
b and
Fabrice
Gallou
*a,
Pascal
Hauk
b and
Fabrice
Gallou
 *c
*c
aCentre for Enzyme Innovation, School of Biological Sciences, University of Portsmouth, Portsmouth, UK. E-mail: gerhard.koenig@port.ac.uk
bLaboratoire d'Innovation Moléculaire et Applications (UMR CNRS 7042), Université de Strasbourg, Université de Haute Alsace, ECPM, 67087 Strasbourg, France
cChemical & Analytical Development, Novartis Pharma AG, 4056 Basel, Switzerland. E-mail: fabrice.gallou@novartis.com
First published on 3rd February 2025
Abstract
Solvent usage is one of the most critical factors for the carbon footprint of the chemical and pharmaceutical industries. Therefore, finding suitable green solvents that can be sourced from biomass is necessary for more sustainable manufacturing processes. One of the greenest solvents is water, and chemical transformations in aqueous solution play an increasingly important role. To guide the search for suitable green solvents for extractions from aqueous solution, eleven biobased solvents were systematically evaluated with 132 absolute free energy calculations based on 1728 molecular dynamics simulations. These kinds of calculations are used in modern computer-aided drug discovery for protein–ligand binding because of their high accuracy and the ability to account for dynamic changes of heterogenous nanostructures. Based on the calculations, 1-butanol and cyclopentanol are recommended for extractions of hydrophilic molecules with a decadic logarithm of the partition coefficient between 1-octanol and water (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) below 0.5, while cyclopentyl methyl ether and butyl methyl ether are recommended for hydrophobic solutes with log
P) below 0.5, while cyclopentyl methyl ether and butyl methyl ether are recommended for hydrophobic solutes with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P > 2.6. Ethyl acetate and 1-pentanol are suitable for solutes in the mid-range. These findings are verified based on experimental extraction efficiencies from an aqueous solution in a micelle-enabled cross-coupling transformation. The extraction yields confirm the computational results, and also show that only the six most hydrophilic solvents lead to a clear phase separation in the presence of residual organic solvents and surfactants. This highlights that aqueous micellar media require special extraction solvents. Overall, both molecular level insight and practical considerations are needed for the selection of suitable green solvents.
P > 2.6. Ethyl acetate and 1-pentanol are suitable for solutes in the mid-range. These findings are verified based on experimental extraction efficiencies from an aqueous solution in a micelle-enabled cross-coupling transformation. The extraction yields confirm the computational results, and also show that only the six most hydrophilic solvents lead to a clear phase separation in the presence of residual organic solvents and surfactants. This highlights that aqueous micellar media require special extraction solvents. Overall, both molecular level insight and practical considerations are needed for the selection of suitable green solvents.
Sustainability spotlightThis study reports an in silico approach to identify optimal solvent for pre-treatment of waste water, offering significant benefits in terms of CO2 release ultimately. The process is illustrated with a real case study that shows its impact on the production of an active pharmaceutical ingredient. The process is particularly timely as water-based chemistry has grown significantly in importance in the last 10 years, in particular in the pharmaceutical industry. Within this account, we seek to contribute to the UN Sustainable Development Goals 9 (industry, innovation and infrastructure), 12 (responsible consumption and production), and 13 (climate action). |
1 Introduction
Solvent selection has a major impact on the environmental footprint in chemical production processes, as they represent about 80% of the total life cycle mass and 75% of the total energy consumption.1 Selecting the right solvent can influence reactions by stabilizing certain intermediate states or products relative to the reactants.2,3 The purification and isolation steps often rely on the relative solubility of the product in different phases such as in liquid–liquid extraction,4–6 crystallization,7–9 or distillation.10 However, the most commonly used solvents are still fossil-fuel based, and often problematic for the environment.11 Finding green alternatives to conventional solvents should reconcile two different demands. On the one hand, the solvents should come from renewable resources and exhibit beneficial environmental, health, and safety properties. On the other hand, the green alternatives should still have the correct solubility profiles for the solutes in the application. Unfortunately, the necessary experimental solubility profiles to choose the right solvent for the molecules of interest are often not available, which is why solvent selection often has to rely on chemical intuition.The greenest and most sustainable solvent is water, which, therefore, plays an increasingly important role as a reaction medium for biocatalytic and micelle-enabled processes.12,13 However, the extraction of products from water can be difficult, especially for hydrophilic compounds and biocatalysis.14 Another challenge can be the cleaning of the resulting waste water before disposal,15 which might require extractions with other solvents. Therefore, finding suitable solvents for extractions from water is highly relevant for green chemistry (Fig. 1). From a theoretical point of view, the efficiency of different solvents in extracting a particular solute from water is quantified by the corresponding partition coefficient, P, which is the ratio of the solute concentration between the aqueous and the organic phase at chemical equilibrium. A high partition coefficient indicates better extraction efficiencies, which also means that less organic solvent is required.
To test their suitability for extractions from water, the partition coefficients of a series of common biobased solvents are evaluated with absolute free energy calculations based on molecular dynamics simulations: cyclopentanol, ethyl acetate, 1-butanol, 2-pentanol, 2-methyl tetrahydrofuran, 1-pentanol, cyclopentyl methyl ether, butyl methyl ether, butyl acetate, 1-octanol, and methyl oleate. These solvents were selected to span a range of different levels of hydrophobicity, with cyclopentanol being the most hydrophilic and methyl oleate being the most hydrophobic molecule based on their partition coefficients between water and 1-octanol (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P). Importantly, all of the considered solvents can be sourced from biomass. Cyclopentanol, 2-pentanol, 2-methyl tetrahydrofuran, and 1-octanol can be produced from lignocellulosic biomass,16–19 while n-ethyl acetate, n-butyl acetate, 1-pentanol, and 1-octanol can be synthesized by fermenting sugars.20–23 The production of 1-butanol via acetone–butanol–ethanol fermentation is one of the oldest biotechnological techniques and has been used on an industrial scale since World War I.24N-Butyl methyl ether can be produced electrochemically from biomass-derived valeric acid.25 Finally, methyl oleate is a biodiesel that can be obtained from an esterification reaction of vegetable oil.26
P). Importantly, all of the considered solvents can be sourced from biomass. Cyclopentanol, 2-pentanol, 2-methyl tetrahydrofuran, and 1-octanol can be produced from lignocellulosic biomass,16–19 while n-ethyl acetate, n-butyl acetate, 1-pentanol, and 1-octanol can be synthesized by fermenting sugars.20–23 The production of 1-butanol via acetone–butanol–ethanol fermentation is one of the oldest biotechnological techniques and has been used on an industrial scale since World War I.24N-Butyl methyl ether can be produced electrochemically from biomass-derived valeric acid.25 Finally, methyl oleate is a biodiesel that can be obtained from an esterification reaction of vegetable oil.26
In terms of greenness, life cycle analysis, health and safety, the Pfizer solvent selection guide lists 1-butanol and ethyl acetate as preferred green solvents, and 2-methyl tetrahydrofuran as useable.27 Other solvents were marked as yellow (scores between 4 and 7, where 10 is green) in the GSK solvent selection guide,28 which includes 2-pentanol, butyl acetate, and cyclopentyl methyl ether. The rest of the solvents have not been considered in solvent selection guides so far. Here, the main evaluated application is the cleaning of chemical waste water from pharmaceutical processes with the selected solvents, so no further downstream separation operations to recover the solvents are considered. Importantly, all considered solvents pose a low hazard to water according to the German water hazard class system (WGK 1), which makes them interesting for waste water cleaning before it is released into the environment. Only 2-methyl tetrahydrofuran is classified as hazardous (WGK 2).
The remainder of this paper is structured as follows. First, the underlying theory of distribution coefficients and transfer free energies is explained. Since insufficient experimental data are available for most of the selected solvents, the simulation method is validated in a series of steps. First, the densities from the simulations were compared to experimental values. Second, the correct distribution behaviour of water between the aqueous phase and the organic phase was checked. Third, the partition coefficients between water and 1-octanol were determined for twelve molecules with a broad dynamic range and even spacing of hydrophobicities (Fig. S1 of the ESI†) using all eleven solvents. The results are compared to experimental data to determine any weaknesses in the force field parameters. Fourth, the simulation results for the twelve test solutes are compared to available experimental partition coefficients in 1-octanol and 1-butanol. After validation of the simulation protocols, the partition coefficients of the twelve solutes in the different solvents are presented. Based on the high correlation with the widely available partition coefficients between water and 1-octanol, some guidelines for selecting a suitable solvent for extractions from water are provided. These guidelines are then verified based on experimental extraction efficiencies of an aqueous solution from a micelle-enabled cross-coupling transformation. Finally, the methodological details of the simulations and experiments are described.
2 Theory
The partition coefficient, P, is a dimensionless ratio of the concentrations of a solute that distributes among two immiscible phases.29 It is related to the number of extraction steps that are necessary to remove a given amount of solute from solution, and, therefore, it is a measure of extraction efficiency. Here, the partition coefficients were calculated with a thermodynamic approach in two steps: first, by transferring the solute of interest (S) from aqueous solution (wat) to an ideal gas state. Second, by transferring the solute from the ideal gas state to the wet organic solvent of interest (X). The resulting transfer free energy of the solute from water to the solvent of interest (ΔGSwa![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0074_20d1.gif) X) is related to the partition coefficient (P) via
X) is related to the partition coefficient (P) via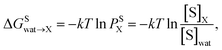 | (1) |
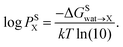 | (2) |
In pharmaceutical applications, the decadic logarithm of the partition coefficient between water and 1-octanol is often abbreviated as “log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P” or “log
P” or “log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow”. To avoid confusion, the abbreviation log
Kow”. To avoid confusion, the abbreviation log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is used for a general partition coefficient. The log
P is used for a general partition coefficient. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P for a specific solvent is denoted as log
P for a specific solvent is denoted as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PX, where X is replaced by the abbreviation of the solvent of interest (for example, log
PX, where X is replaced by the abbreviation of the solvent of interest (for example, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PBU for the decadic logarithm of the partition coefficient between water and 1-butanol). For consistency with the literature, the abbreviation log
PBU for the decadic logarithm of the partition coefficient between water and 1-butanol). For consistency with the literature, the abbreviation log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is used exclusively for the decadic logarithm of the partition coefficient between water and 1-octanol.
P is used exclusively for the decadic logarithm of the partition coefficient between water and 1-octanol.
3 Methods
3.1 Absolute free energy simulations
Absolute free energy simulations are the latest stage in the evolution of rigorous physics-based methods for computational drug discovery, accounting for entropic effects and dynamic structural changes in protein–ligand binding.30–32 To determine the partition coefficients with such free energy simulations, the associated transfer free energies of a series of ligands were calculated from water to the wet organic phase. This transfer process is analogous to the transfer of a ligand from water to a protein binding pocket in protein–ligand binding affinity calculations. The relative binding affinity of a ligand to the wet organic solvent phase with respect to water can be directly converted to partition coefficients.33 The main motivation for using this technique is the possible formation of inverse micelles in the wet organic phase, creating heterogeneous and dynamic nanoenvironments that can accommodate amphiphilic solutes like active pharmaceutical ingredients. The partition coefficients were calculated for a series of different solvents: cyclopentanol, ethyl acetate, 1-butanol, 2-pentanol, 2-methyl tetrahydrofuran, 1-pentanol, cyclopentyl methyl ether, butyl methyl ether, butyl acetate, 1-octanol, and methyl oleate. Twelve simple solutes were evaluated, water, acetamide, methanol, ethanol, tetrahydrofuran, methanethiol, aniline, phenol, ethane, benzene, cyclohexane, and hexane, as used in previous studies.33,34 All molecules are listed in the order of their hydrophobicity, starting with the most hydrophilic molecules and ending with the most hydrophobic molecules, as determined from the partition coefficient between water and 1-octanol.All free energy calculations used CHARMM,35,36 with the CHARMM General Force Field (CGenFF) for molecules.37 In an extensive evaluation of several force fields by Kashefolgheta et al.,38 the CHARMM force field gave the most accurate results for cross-solvation free energies of alcohols. CHARMM has been developed for biomolecular simulations, which makes it suitable for biobased solvents, but it is not suitable for all solvents in general, as it lacks parameters for chlorinated solvents, and can lead to biased results for amines. In addition, CHARMM was used successfully in previous partition coefficient calculations,33 as well as solvation free energy calculations of the selected solutes.34,39 The free energy differences were computed with Bennett's acceptance ratio method, as implemented in the FREN module of CHARMM.40,41 The simulations in water used 2971 TIP3P water molecules,42,43 while the wet organic phases contained 512 solvent molecules, along with water molecules according to the experimental mole fractions (between 0.0053 for cyclopentyl methyl ether and 0.512 for cyclopentanol).44–52 The only exceptions were 1-octanol and methyl oleate, which contained 411 and 189 solvent molecules, respectively. The length of the cubic simulation boxes varied between 4.44 and 4.88 nm.
The temperature was maintained at 300 K with a Nosé–Hoover thermostat. The Particle Mesh Ewald method53 was used for electrostatic interactions, while the Lennard-Jones interactions were switched off between 10 and 12 Å. All solute–solvent pairs were first equilibrated for 1 ns at constant pressure, followed by an additional 1 ns equilibration at constant volume for each λ alchemical transformation state. Production simulations of each phase were conducted for 20 ns. All simulations were performed with a time step of 2 fs, saving frames every 1000 steps. SHAKE54 was used to keep water rigid. To ensure proper sampling of all relevant solute degrees of freedom, λ-Hamiltonian Replica Exchange55 was employed to exchange structures between neighboring λ-points every 1000 steps. Standard deviations were calculated from 10 blocks of 2 ns for each free energy simulation.
The transfer free energies were calculated as described in ref. 56, using a constant volume. The transfer from water to each organic phase was broken down into four steps: First, the charges of the solute were gradually turned off in water (λ = 0.0, 0.2, 0.55, and 1.0). Second, the uncharged solute in aqueous solution was mutated to dummy atoms without any non-bonded interactions (λ = 0.00, 0.15, 0.30, 0.45, 0.60, 0.75, 0.87, 0.96, and 1.00). Third, and fourth, the analogous transformations were performed in the organic phase, where the non-interacting molecule was transferred into the organic solvent, followed by the gradual reintroduction of van der Waals and electrostatic interactions in the organic phase. Soft core potentials, as implemented with the PSSP command in the PERT module of CHARMM, were used to avoid the end point problem in the simulations with dummy atoms.57,58
3.2 Experimental extraction efficiencies
A cross-electrophilic cross-coupling transformation under micellar conditions was used as an example.59,60 The chemistry of this reaction has been developed and demonstrated on a multi-kilogram scale, using one equivalent of aryl bromide and one and a half equivalents of iodopiperidine salt and TPGS-750-M as the surfactant for micellar catalysis. In this process, the product forms smoothly in a highly selective manner, resulting in the desired cross-coupling product formed in 85% isolated yield and purity above 99%, with no protodeboronation, and with only competitive side-reactions on the iodopiperidine. At completion, the solid zinc by-products and zinc were removed by filtration on cellulose, and the crude reaction mixture was extracted with a minimal amount of 2-methyl tetrahydrofuran. The product was finally crystallized from a mixture of 2-methyl tetrahydrofuran (residual), isopropanol, and water, containing the surfactant TPGS-750-M (copper = Cu2O 0.15 mol%).The combined aqueous waste streams from the initial extraction, and the mother liquor, enriched in organic components, were used. The mother liquor was distilled to remove as much of the volatile components as possible. After distillation, TPGS-750-M had started to hydrolyze into vitamin E succinate and PEG-750-M (<10% weight). The bulk remained TPGS-750-M (>90%).
A stirring bar was added to the crude wastewater and stirred until a homogenized solution formed. 5.0 mL of the homogenized waste water at pH 8.5 were removed with an Eppendorf pipette under constant stirring and placed in a 15 mL glass vial equipped with a stirring bar. The exact mass of the waste water was measured and 20% by weight of the organic solvents were added via an Eppendorf pipette. The biphasic mixture was then vigorously stirred for 16 h at room temperature and allowed to rest for 30 min for phase separation. The aqueous phase was then removed carefully via a glass pipette and the mass balance was noted. A 50 mL sample of the extracted wastewater was taken for quantitative NMR analysis with CH2Br2 (20 mL) as the internal standard. The experimental conditions were chosen based on previous work.15
4 Results and discussion
4.1 Validation of the simulation protocol
Several previous studies have used free energy simulations to calculate partition coefficients,61–65 and partition coefficients have become a benchmark system for the accuracy of molecular simulations.56,66–79 Based on the experience from previous free energy simulations, the expected accuracy of such calculations lies between 1 and 5 kcal mol−1. The deviations are mostly expected to arise from misrepresentations of the aqueous phase, as hydration free energies commonly exhibit deviations between 1 and 3 kcal mol−1.80–90 In our previous study of partition coefficients of 1-octanol and 1-butanol, errors of merely 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units were observed, which are on the same order as the statistical uncertainties.33 A blind prediction of the partition coefficient of cis-cyclohexane-1,2-diol between water and 1-butanol yielded an error of just 0.02
P units were observed, which are on the same order as the statistical uncertainties.33 A blind prediction of the partition coefficient of cis-cyclohexane-1,2-diol between water and 1-butanol yielded an error of just 0.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units,33 which further supports the confidence in the simulation results.
P units,33 which further supports the confidence in the simulation results.
Unfortunately, no or very few experimental partition coefficients are available for the selected biobased solvents. For this reason, the validation of the simulation protocol relied on a series of other data. Table S1 of the ESI† lists the densities of the pure solvents obtained from experiments and simulations. The average error is 2.1%, demonstrating that the simulations can yield the correct density. The lowest error is observed for methyl oleate, with a difference of 0.3%. Oleate is a fatty acid, and, therefore, is expected to be well-represented by the CHARMM force field, which was developed for biomolecules. 2-Methyl tetrahydrofuran exhibits the largest deviation with an error of 2.9%, which is well below the reported error of 8.8% for the density of furan of the CHARMM General Force Field.37 Overall, the errors in the observed densities align well with the expected average error of about 2% for the force field.37
Another important solvent property for extractions from water is the water content in the organic phase, which can be quantified by the partition coefficient of water between aqueous solution and the organic phase. Higher, positive partition coefficients for water indicate a higher water content of the organic phase, which is a sign for hydrophilicity. For example, the mole fraction of water in wet 1-butanol is 51%, which means that there are more water molecules than 1-butanol molecules in the organic phase.45 With relatively high water concentrations in the organic phase, inverted micelles of water can form, which also influence the uptake of hydrophilic molecules in the organic phase.33,91
The partition coefficients of water between the aqueous phase and the organic phase are shown in Table S2 of the ESI.† In all cases, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values are negative, because the organic phases represent hydrophobic environments and are immiscible with water. The most hydrophilic solvents are 1-butanol and cyclopentanol, with a log
P values are negative, because the organic phases represent hydrophobic environments and are immiscible with water. The most hydrophilic solvents are 1-butanol and cyclopentanol, with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value for water of about −0.8. Interestingly, according to the simulations, the solvents with the least affinity for water are cyclopentyl methyl ether and butyl methyl ether with log
P value for water of about −0.8. Interestingly, according to the simulations, the solvents with the least affinity for water are cyclopentyl methyl ether and butyl methyl ether with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values of −2.7 and −2.5. Thus, the two most hydrophilic biobased solvents considered here can be converted into the two most hydrophobic environments by forming their corresponding methyl ether. However, according to the experimental partitioning data, methyl oleate is more hydrophobic with a log
P values of −2.7 and −2.5. Thus, the two most hydrophilic biobased solvents considered here can be converted into the two most hydrophobic environments by forming their corresponding methyl ether. However, according to the experimental partitioning data, methyl oleate is more hydrophobic with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value of −2.8, which can be rationalized by its long aliphatic tail. The largest deviations from the experimental values are observed for methyl oleate, and the two esters butyl acetate and ethyl acetate (errors of 0.5, 0.5, and 0.4, respectively), but the observed discrepancies are much lower than the average error of 3.3
P value of −2.8, which can be rationalized by its long aliphatic tail. The largest deviations from the experimental values are observed for methyl oleate, and the two esters butyl acetate and ethyl acetate (errors of 0.5, 0.5, and 0.4, respectively), but the observed discrepancies are much lower than the average error of 3.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units reported for partition coefficient calculations of cyclohexane with a similar protocol.56 Overall, the agreement between the simulated and the experimental partition coefficients for water is excellent, with a mean signed error of around 0.1 and a root mean square error of about 0.3
P units reported for partition coefficient calculations of cyclohexane with a similar protocol.56 Overall, the agreement between the simulated and the experimental partition coefficients for water is excellent, with a mean signed error of around 0.1 and a root mean square error of about 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units.
P units.
As another test of the quality of the force field parameters, the partition coefficients of all solvent molecules between water and 1-octanol were calculated (denoted as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P here, but also known as log
P here, but also known as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow). Within the framework of the European REACH legislation, water–octanol partition coefficients have to be determined for the registration of chemicals to estimate their toxicokinetic behaviour and bioaccumulation potential. Therefore, experimental log
Kow). Within the framework of the European REACH legislation, water–octanol partition coefficients have to be determined for the registration of chemicals to estimate their toxicokinetic behaviour and bioaccumulation potential. Therefore, experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values are available for a wide range of compounds, including the considered biobased solvents.
P values are available for a wide range of compounds, including the considered biobased solvents.
The simulated and experimental partition coefficients between water and 1-octanol for the considered solvent molecules are listed in Table S4.† The largest deviation from the experimental values was again observed for methyl oleate, with an error of 0.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units. However, this error is still within the reported experimental 95% prediction interval of 1.22
P units. However, this error is still within the reported experimental 95% prediction interval of 1.22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units.92 Therefore, the overestimation of the hydrophobicity of methyl oleate is not significant. Similarly, the hydrophobicity of cyclopentyl methyl ether (error of 0.6
P units.92 Therefore, the overestimation of the hydrophobicity of methyl oleate is not significant. Similarly, the hydrophobicity of cyclopentyl methyl ether (error of 0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units) and cyclopentanol (error of 0.6
P units) and cyclopentanol (error of 0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units) was overestimated. Overall, a mean signed error of around 0.2 and a root mean square error of about 0.4
P units) was overestimated. Overall, a mean signed error of around 0.2 and a root mean square error of about 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units were achieved, indicating excellent agreement with experimental data.
P units were achieved, indicating excellent agreement with experimental data.
As a further verification, the accuracy of partition coefficient calculations for the twelve test solutes was evaluated based on available data for water—1-octanol and water—1-butanol. The corresponding results are shown in Table S3.† Similar to the partitioning data in Table S4,† the mean signed error is around 0.2 and the root mean square error is about 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units. This again indicates excellent agreement with experimental data. Also, the agreement of the mean signed error and root mean square error for different solutes (Tables S3 and S4†), and solvents (1-octanol and 1-butanol data in Table S3†) is a sign of consistently good results.
P units. This again indicates excellent agreement with experimental data. Also, the agreement of the mean signed error and root mean square error for different solutes (Tables S3 and S4†), and solvents (1-octanol and 1-butanol data in Table S3†) is a sign of consistently good results.
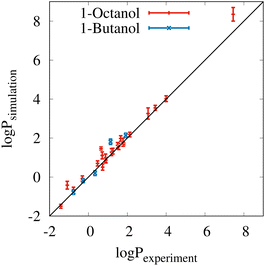
Fig. 2 shows a comparison of the experimental partitioning data (x-axis) and simulated results (y-axis) from Tables S3 and S4 of the ESI.† The black diagonal line indicates what ideal correspondence would look like. The error bars of the individual data points correspond to the standard deviations from ten block averages. In almost all cases, the simulation results are very close to the experimental data, which is also demonstrated by the total mean signed error of 0.18 and the total root mean square error of 0.33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units. The coefficient of determination (R2) is very high at 0.98. The only notable outlier is the partitioning result for methyl oleate between water and 1-octanol in the upper right corner of the plot, but this result is still within the experimental confidence interval.
P units. The coefficient of determination (R2) is very high at 0.98. The only notable outlier is the partitioning result for methyl oleate between water and 1-octanol in the upper right corner of the plot, but this result is still within the experimental confidence interval.
The simulated partition coefficients (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) of the twelve solutes between water and all selected biobased solvents are listed in Table 1. High, positive log
P) of the twelve solutes between water and all selected biobased solvents are listed in Table 1. High, positive log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values indicate high extraction yields. Both the solutes (different rows) and the solvents (different columns) are ordered based on the experimental partition coefficient between water and 1-octanol of the corresponding molecule, going from the most hydrophilic to the most hydrophobic compound. The corresponding standard deviations from ten blocks were all below 0.2
P values indicate high extraction yields. Both the solutes (different rows) and the solvents (different columns) are ordered based on the experimental partition coefficient between water and 1-octanol of the corresponding molecule, going from the most hydrophilic to the most hydrophobic compound. The corresponding standard deviations from ten blocks were all below 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units, with an average standard deviation of 0.11.
P units, with an average standard deviation of 0.11.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) of twelve simple solutes between aqueous solution and the selected biobased solvents: cyclopentanol (CP), ethyl acetate (EA), 1-butanol (BU), 2-pentanol (2P), 2-methyl tetrahydrofuran (2T), 1-pentanol (1P), cyclopentyl methyl ether (CM), butyl methyl ether (BM), butyl acetate (BA), 1-octanol (OC), and methyl oleate (MO). More positive log
P) of twelve simple solutes between aqueous solution and the selected biobased solvents: cyclopentanol (CP), ethyl acetate (EA), 1-butanol (BU), 2-pentanol (2P), 2-methyl tetrahydrofuran (2T), 1-pentanol (1P), cyclopentyl methyl ether (CM), butyl methyl ether (BM), butyl acetate (BA), 1-octanol (OC), and methyl oleate (MO). More positive log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values indicate higher extraction yields
P values indicate higher extraction yields
| CP | EA | BU | 2P | 2T | 1P | CM | BM | BA | OC | MO | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Water | −0.8 | −1.1 | −0.8 | −1.2 | −1.6 | −1.2 | 0.8 | −2.5 | −1.5 | −1.5 | −2.3 |
| Acetamide | 0.2 | −0.4 | 0.1 | 0.0 | −0.6 | 0.0 | −1.5 | −1.3 | −0.7 | −0.4 | −1.6 |
| Methanol | −0.2 | −0.4 | −0.2 | −0.3 | −0.6 | −0.4 | 0.9 | −1.1 | −0.6 | −0.6 | −1.2 |
| Ethanol | 0.2 | 0.1 | 0.2 | 0.1 | 0.0 | 0.1 | 1.9 | −0.6 | −0.1 | −0.1 | −0.7 |
| Tetrahydrofuran | 1.0 | 0.8 | 1.0 | 1.0 | 1.0 | 0.9 | −0.7 | 0.8 | 0.8 | 0.7 | 0.5 |
| Methanethiol | 1.5 | 1.8 | 1.4 | 1.5 | 1.9 | 1.5 | 4.5 | 1.8 | 1.8 | 1.5 | 1.6 |
| Aniline | 1.3 | 1.5 | 1.2 | 1.1 | 1.2 | 1.0 | 4.0 | 0.8 | 1.4 | 0.9 | 0.8 |
| Phenol | 2.2 | 2.6 | 1.8 | 2.1 | 2.4 | 1.9 | 1.7 | 1.7 | 2.5 | 1.6 | 2.0 |
| Ethane | 1.6 | 2.0 | 1.7 | 1.8 | 2.1 | 1.8 | 2.6 | 2.3 | 2.0 | 1.7 | 1.9 |
| Benzene | 2.2 | 2.5 | 2.1 | 2.3 | 2.6 | 2.2 | 2.2 | 2.6 | 2.6 | 2.2 | 2.4 |
| Cyclohexane | 3.3 | 3.7 | 3.2 | 3.5 | 3.8 | 3.5 | −1.2 | 3.9 | 3.8 | 3.5 | 3.7 |
| Hexane | 3.7 | 4.1 | 3.7 | 4.0 | 4.4 | 3.9 | −2.7 | 4.5 | 4.3 | 4.0 | 4.2 |
Since all organic solvents are immiscible with water, the partition coefficients of water (first row) are negative in all cases. The most hydrophilic solvents are cyclopentanol (CP) and 1-butanol (BU). These two solvents also show the highest extraction capabilities for acetamide, methanol, ethanol, and tetrahydrofuran. The best solvent to extract methanethiol from water is 2-methyl tetrahydrofuran (2T). The best solvent for the extraction of aniline and phenol is ethyl acetate (EA). Butyl methyl ether (BM) shows high affinities for ethane, benzene, cyclohexane, and hexane.
4.2 Derivation of guidelines for solvent selection
To identify general trends in the extraction efficiencies of the different solvents, linear regressions with respect to the partition coefficients between water and 1-octanol were performed. This is motivated by the observation of strong correlation between the partition coefficients of 1-octanol and 1-butanol in previous calculations,33 which was also verified experimentally.93 The slope of the regression analysis of the theoretical partitioning data for 1-octanol and 1-butanol for the selected twelve solutes agrees with the corresponding slope of the regression based on experimental data for 173 solutes to the second digit.91 This gives some confidence that a similar analysis can also be performed for the selected biobased solvents. The physical basis for the strong correlation of the partition coefficients between the different solvents is that the free energy contribution of the removal of the solute from the aqueous phase is exactly the same for each solute. Due to the similar densities, the free energy contribution of cavity formation in the organic phase is similar in all cases,94,95 and, relative to water, the dielectric constants of the solvents fall within a narrow range, which also leads to similar electrostatic contributions.
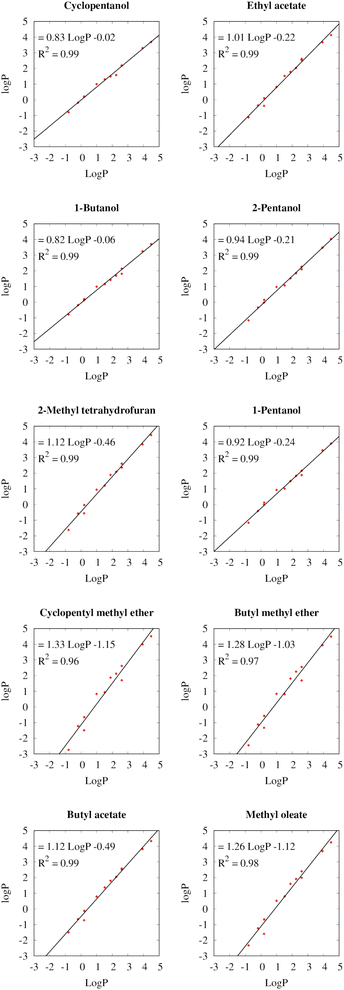
Fig. 3 depicts the relationships between the partition coefficients of the different solvents for the twelve test solutes with the partition coefficients between water and 1-octanol (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P). Because the log
P). Because the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values (also knowns as log
P values (also knowns as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow) are often included in the safety data sheets of chemicals, they can serve as a readily available measure for the hydrophobicity of the compound. The linear regressions of log
Kow) are often included in the safety data sheets of chemicals, they can serve as a readily available measure for the hydrophobicity of the compound. The linear regressions of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P for all selected solvents exhibit coefficients of determination (R2) with the log
P for all selected solvents exhibit coefficients of determination (R2) with the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P between 0.96 and 0.99, which shows that log
P between 0.96 and 0.99, which shows that log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is a useful metric to predict the extraction efficiencies in the different solvents.
P is a useful metric to predict the extraction efficiencies in the different solvents.
Fig. 4 shows a comparison of the linear regressions from Fig. 3 to determine which solvent works best in which range of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. As a reference, the extraction efficiency of 1-octanol is used, therefore the y-axis shows the difference between the log
P. As a reference, the extraction efficiency of 1-octanol is used, therefore the y-axis shows the difference between the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P of the corresponding solvent and the log
P of the corresponding solvent and the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. Positive values show that the solvent is better at extracting compounds from water than 1-octanol. Negative values indicate that the solvent is less efficient than 1-octanol for extractions from water.
P. Positive values show that the solvent is better at extracting compounds from water than 1-octanol. Negative values indicate that the solvent is less efficient than 1-octanol for extractions from water.
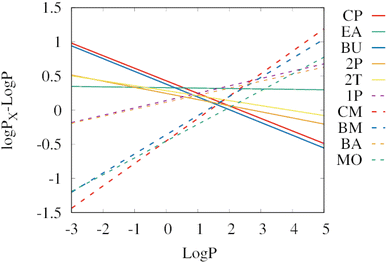 | ||
Fig. 4 Extraction efficiencies from water of the individual biobased solvents relative to 1-octanol (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PX − log PX − log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P). The lines show the linear regressions from Fig. 3. Positive values mean that the solvent exhibits a higher extraction efficiency than 1-octanol. The selected green solvents are abbreviated as cyclopentanol (CP), ethyl acetate (EA), 1-butanol (BU), 2-pentanol (2P), 2-methyl tetrahydrofuran (2T), 1-pentanol (1P), cyclopentyl methyl ether (CM), butyl methyl ether (BM), butyl acetate (BA), and methyl oleate (MO). Some solvents show significantly higher extraction yields than 1-octanol: cyclopentanol, and 1-butanol for hydrophilic solutes (log P). The lines show the linear regressions from Fig. 3. Positive values mean that the solvent exhibits a higher extraction efficiency than 1-octanol. The selected green solvents are abbreviated as cyclopentanol (CP), ethyl acetate (EA), 1-butanol (BU), 2-pentanol (2P), 2-methyl tetrahydrofuran (2T), 1-pentanol (1P), cyclopentyl methyl ether (CM), butyl methyl ether (BM), butyl acetate (BA), and methyl oleate (MO). Some solvents show significantly higher extraction yields than 1-octanol: cyclopentanol, and 1-butanol for hydrophilic solutes (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P < 0.5), as well as cyclopentyl methyl ether and butyl methyl ether for hydrophobic solutes (log P < 0.5), as well as cyclopentyl methyl ether and butyl methyl ether for hydrophobic solutes (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P > 2.6). For log P > 2.6). For log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values in the range between 0.5 and 2.6, ethyl acetate and 1-pentanol are the most efficient extraction solvents from water. P values in the range between 0.5 and 2.6, ethyl acetate and 1-pentanol are the most efficient extraction solvents from water. | ||
For hydrophilic molecules (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P < 0.5), both cyclopentanol (CP, red solid line) and 1-butanol (BU, blue solid line) outperform the other solvents in terms of extraction efficiency. A difference in log
P < 0.5), both cyclopentanol (CP, red solid line) and 1-butanol (BU, blue solid line) outperform the other solvents in terms of extraction efficiency. A difference in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P of 0.5 corresponds to three times higher extraction yields. For hydrophobic solutes (log
P of 0.5 corresponds to three times higher extraction yields. For hydrophobic solutes (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P > 2.6), cyclopentyl methyl ether (CM, red dashed line) and butyl methyl ether (BM, blue dashed line) exhibit the highest extraction yields. This is somewhat surprising, considering that methyl oleate has a much higher log
P > 2.6), cyclopentyl methyl ether (CM, red dashed line) and butyl methyl ether (BM, blue dashed line) exhibit the highest extraction yields. This is somewhat surprising, considering that methyl oleate has a much higher log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P than these two solvents (7.5 versus 1.6 and 1.7), which indicates a higher hydrophobicity. But a higher hydrophobicity does not necessarily imply a high loading capacity for the solute. Another interesting aspect is that the formation of methyl ethers converts the most suitable solvents for hydrophilic molecules into the most suitable solvents for hydrophobic molecules, which might become relevant in the production process of the solvents. In the mid-range of log
P than these two solvents (7.5 versus 1.6 and 1.7), which indicates a higher hydrophobicity. But a higher hydrophobicity does not necessarily imply a high loading capacity for the solute. Another interesting aspect is that the formation of methyl ethers converts the most suitable solvents for hydrophilic molecules into the most suitable solvents for hydrophobic molecules, which might become relevant in the production process of the solvents. In the mid-range of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values, ethyl acetate (EA, green solid line), or 1-pentanol (1P, purple dashed line) perform best.
P values, ethyl acetate (EA, green solid line), or 1-pentanol (1P, purple dashed line) perform best.
4.3 Experimental testing of extraction efficiencies of the selected biobased solvents
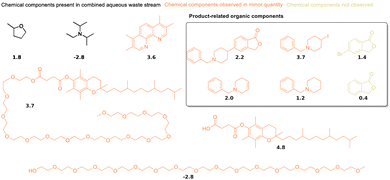
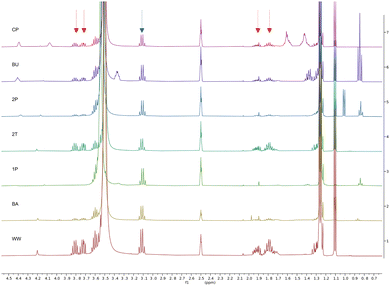
Synthetic reactions in water, particularly those using micellular environments or enzymes, play an increasingly important role in the transition towards greener chemistry.12,13,96 Their use requires reliable and sustainable ways to extract the reaction products from water. Therefore, a recently published micelle-enabled cross-coupling reaction of an active pharmaceutical ingredient59,60 was chosen as the first practical application of the guidelines outlined in the previous section. The selected process was developed to produce an active pharmaceutical ingredient on a multi-kilogram scale, leading to a yield of 85% and a purity above 99%. The product is crystallized with a mixture of 2-methyl tetrahydrofuran, isopropanol and water, which leads to high concentrations of 2-methyl tetrahydrofuran in the aqueous phase.The organic content of the aqueous medium is around 10% by mass, and its main components are 2-methyl tetrahydrofuran and N,N-diisopropylethylamine (highlighted in red in Fig. 5). An NMR analysis of the aqueous medium is shown in Fig. S2 of the ESI.† The aqueous medium was extracted with cyclopentanol (CP), ethyl acetate (EA), 1-butanol (BU), 2-pentanol (2P), 2-MeTHF (2T), 1-pentanol (1P), cyclopentyl methyl ether (CM), butyl methyl ether (BM), butyl acetate (BA), 1-octanol (OC), and methyl oleate (MO). These solvents were selected because of their interesting and promising properties from a sustainability point of view.97,98 Based on the distribution coefficients between water and 1-octanol at pH 7.4 shown in Fig. 5, the best extraction solvents for N,N-diisopropylethylamine (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D of −2.8) should be cyclopentanol or 1-butanol. The log
D of −2.8) should be cyclopentanol or 1-butanol. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D of 2-methyl tetrahydrofuran is 1.8, which indicates preference for 1-pentanol or ethyl acetate. However, the extraction efficiency of several selected biobased solvents is very similar in this range of hydrophobicity, as multiple lines intersect at log
D of 2-methyl tetrahydrofuran is 1.8, which indicates preference for 1-pentanol or ethyl acetate. However, the extraction efficiency of several selected biobased solvents is very similar in this range of hydrophobicity, as multiple lines intersect at log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values between 1 and 2 (see Fig. 4). This makes this experimental test particularly interesting. The average log
P values between 1 and 2 (see Fig. 4). This makes this experimental test particularly interesting. The average log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D of the two main organic components of the aqueous solution is −1, which indicates that cyclopentanol or 1-butanol might show the best average performance for the heterogenous mixture of organic components.
D of the two main organic components of the aqueous solution is −1, which indicates that cyclopentanol or 1-butanol might show the best average performance for the heterogenous mixture of organic components.
Fig. 6 shows the results of the extraction experiments. Notably, only six out of the eleven solvents lead to a clear phase separation (cyclopentanol, ethyl acetate, 1-butanol, 2-pentanol, 2-methyl tetrahydrofuran, and 1-pentanol), which is a necessary condition for straightforward separation. The most hydrophobic solvents resulted in oily materials or emulsions (cyclopentyl methyl ether, butyl methyl ether, 1-octanol, butyl acetate, and methyl oleate). Since all solvents were selected to be immiscible with water, the lack of phase separation can probably be attributed to the presence of organic solvents and surfactants in the aqueous medium. The presence of a surfactant decreases the surface tension, which likely stabilizes the emulsion and allows it to remain stable for a long time. This counterintuitive finding indicates that, for some applications like aqueous micellar media, more hydrophilic extraction solvents can lead to better phase separation.
Table 2 lists the percentage of the total mass extracted from the aqueous phase for each solvent. The results demonstrate that the two alcohols, 1-butanol (recommended for hydrophilic compounds), and 1-pentanol (recommended for mid-range compounds), extracted more than 90% of the organic content. The recommended solvent for hydrophobic compounds, cyclopentyl methyl ether, also extracted high amounts of mass from aqueous solution, but it did not lead to a clear phase separation. In all other cases the extraction of the organic content was below 20%. In the case of 2-methyl tetrahydrofuran (2T) the weight loss of the aqueous phase is negative. This indicates that parts of the organic phase are dissolved into the aqueous phase. The resulting reduced thickness of the organic phase in 2-methyl tetrahydrofuran can also be observed in Fig. 6.
| Solvent | % Extracted mass |
|---|---|
| Cyclopentanol | 15.0% |
| Ethyl acetate | 7.8% |
| 1-Butanol | 24.0% |
| 2-Pentanol | 16.5% |
| 2-Methyl tetrahydrofuran | −0.7% |
| 1-Pentanol | 21.6% |
| Cyclopentyl methyl ether | 21.3% |
| Butyl methyl ether | 19.2% |
| Butyl acetate | 19.3% |
| 1-Octanol | 16.6% |
| Methyl oleate | 17.5% |
Finally, the 1H NMR spectra in Fig. 7 confirm that 1-butanol (BU, 2nd row) and cyclopentanol (CP, 1st row), as well as 1- and 2-pentanol (1P, 5th row, and 2P, 3rd row) exhibit high extraction efficiencies for the organic content of the aqueous waste streams. Peaks of the two main organic components, 2-methyl tetrahydrofuran and N,N-diisopropylethylamine, are marked with red and blue arrows. Notably, 1-butanol is more efficient when it comes to extracting both main organic components at the same time, which might be attributed to the micellular nanostructure of wet 1-butanol.33 The 1H NMR spectra of the corresponding aqueous phase are shown in Fig. S3 of the ESI.†
Compared to the total organic carbon (TOC) of the non-extracted wastewater (1.67%, or 16.7 g L−1), the TOC of the extracted wastewater is reduced to 1.19–1.39%, with most of the remaining carbon being attributed to the less ecotoxic extraction solvent itself. Better extraction efficiencies are expected for larger scale applications. Importantly, none of the hydrophobic chemical entities of the reaction, such as the product, the iodopiperidine starting material, TPGS-750-M, the hydrolyzed vitamin E succinate, or 3,4,6,7-tetramethyl phenanthroline (all with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P > 3), were observed in the aqueous solution after extraction. Besides, 1-butanol, 1-pentanol, and 2-pentanol are known to be biodegradable and only pose a low hazard to waters, suggesting that the release of the extracted aqueous waste stream in standard waste water treatment plants is acceptable. This highlights the practical usefulness of the provided guidelines for more ecofriendly extraction processes.
P > 3), were observed in the aqueous solution after extraction. Besides, 1-butanol, 1-pentanol, and 2-pentanol are known to be biodegradable and only pose a low hazard to waters, suggesting that the release of the extracted aqueous waste stream in standard waste water treatment plants is acceptable. This highlights the practical usefulness of the provided guidelines for more ecofriendly extraction processes.
5 Conclusions
Molecular simulations were employed to fill the gap of missing experimental solubility data for extractions from water using a series of biobased solvents. The simulation results were first verified based on density calculations of the pure solvents, yielding an average error of only 2.1%. The partition coefficients of water between the aqueous phase and all selected solvents lead to a mean signed error of only 0.07 and a root mean square error of 0.28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units, which is in the range of experimental uncertainties. The simulation results were compared to a series of 27 partition coefficients between water and 1-octanol as well as 1-butanol, leading to a mean signed error of 0.18 and a root mean square error of 0.33
P units, which is in the range of experimental uncertainties. The simulation results were compared to a series of 27 partition coefficients between water and 1-octanol as well as 1-butanol, leading to a mean signed error of 0.18 and a root mean square error of 0.33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P units. The coefficient of determination (R2) was 0.98. This demonstrates that partition coefficients for the selected solutes and solvents can be predicted with relatively high accuracy with computer simulations. The simulation results were tested experimentally for extractions of a heterogenous aqueous solution.
P units. The coefficient of determination (R2) was 0.98. This demonstrates that partition coefficients for the selected solutes and solvents can be predicted with relatively high accuracy with computer simulations. The simulation results were tested experimentally for extractions of a heterogenous aqueous solution.
The partition coefficients, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, of all selected solvents exhibit high correlations with the partition coefficients in 1-octanol (log
P, of all selected solvents exhibit high correlations with the partition coefficients in 1-octanol (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, also knowns as log
P, also knowns as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow). Because the log
Kow). Because the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values are often included in the safety data sheets of the compounds, they can be used as an estimate of their hydrophobicity to guide solvent selection. Based on the partition coefficients, some simple guidelines can be provided for extractions from water: Hydrophilic molecules are best extracted with cyclopentanol or 1-butanol, while hydrophobic molecules can be extracted with cyclopentyl methyl ether or butyl methyl ether. For the remainder of the molecules with log
P values are often included in the safety data sheets of the compounds, they can be used as an estimate of their hydrophobicity to guide solvent selection. Based on the partition coefficients, some simple guidelines can be provided for extractions from water: Hydrophilic molecules are best extracted with cyclopentanol or 1-butanol, while hydrophobic molecules can be extracted with cyclopentyl methyl ether or butyl methyl ether. For the remainder of the molecules with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values between 0.5 and 2.6, either ethyl acetate or 1-pentanol might be suitable solvents.
P values between 0.5 and 2.6, either ethyl acetate or 1-pentanol might be suitable solvents.
The computational results were verified by experimental extraction data for a heterogenous aqueous solution from a micelle-enabled cross-coupling reaction. The main organic components of the aqueous medium are 2-methyl tetrahydrofuran and N,N-diisopropylethylamine. Based on the published water–octanol distribution coefficients of the two main organic components, the two solvents 1-butanol and 1-pentanol were predicted to be the most suitable solvents. These predictions were confirmed by the experimental extraction yields. The experimental data show the importance of practical evaluations of extraction efficiency, as only six out of the eleven solvents lead to a clear phase separation in the presence of organic components and surfactants. Here, the amphiphilic surfactants form hydrophobic interactions with the hydrophobic tails of some of the organic solvents at the water–solvent interface. Some hydrophobic solvent molecules are then removed from the organic solvent phase, and encapsulated by surfactant molecules, forming micelles. The micelles lead to turbidity in the aqueous phase, preventing clear phase separation. The hydrophobic effect of slightly more hydrophilic solvents is not strong enough for stable micelle formation, which leads to a better phase separation in the presence of surfactants. This leads to the counterintuitive finding that more hydrophilic solvents might be more suited for extractions in micelle-enabled reactions. Future simulation studies therefore should incorporate the effect of salts, buffers, and surfactants on phase separation by including both phases in one simulation box. Due to the large size of TPGS-750-M (88 heavy atoms and a diameter of more than 6 nm), the surfactants could not be included in the simulation boxes of the present study (4.4–4.9 nm). To include quantum-mechanical effects that are not captured by the force field, the use of methods like COSMO-RS could also be envisioned.99 Such calculations could enable a more sustainable treatment of waste water in industry. We hope that the provided guidelines can support ongoing efforts to transition more processes to biocatalysis and micellular chemistry, and will encourage the use of more biobased solvents.
Data availability
All data supporting the findings of this study are available within the article, and the ESI† file.Conflicts of interest
All authors declare no competing interests.Acknowledgements
This work was partially supported by Research England with E3 funding. Numerical computations were performed on the Sciama High Performance Computing (HPC) cluster which is supported by the ICG, SEPNet and the University of Portsmouth.Notes and references
- C. Jiménez-González, A. D. Curzons, D. J. Constable and V. L. Cunningham, Int. J. Life Cycle Assess., 2004, 9, 114–121 CrossRef.
- H. Struebing, Z. Ganase, P. G. Karamertzanis, E. Siougkrou, P. Haycock, P. M. Piccione, A. Armstrong, A. Galindo and C. S. Adjiman, Nat. Chem., 2013, 5, 952–957 CrossRef CAS PubMed.
- H. Struebing, S. Obermeier, E. Siougkrou, C. S. Adjiman and A. Galindo, Chem. Eng. Sci., 2017, 159, 69–83 CrossRef CAS.
- L. Bruce and A. Daugulis, Biotechnol. Prog., 1991, 7, 116–124 CrossRef CAS PubMed.
- S. H. Ha, N. L. Mai and Y.-M. Koo, Process Biochem., 2010, 45, 1899–1903 CrossRef CAS.
- A. Bednarz, P. Scherübel, A. C. Spiess and A. Pfennig, Chem. Eng. Technol., 2017, 40, 1852–1860 CrossRef CAS.
- B. Shekunov and P. York, J. Cryst. Growth, 2000, 211, 122–136 CrossRef CAS.
- S. Datta and D. Grant, Nat. Rev. Drug Discovery, 2004, 3, 42–57 CrossRef CAS PubMed.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr. Sect. B Struct. Sci., 2011, 67, 535–551 CrossRef CAS PubMed.
- Z. Olujić, M. Jödecke, A. Shilkin, G. Schuch and B. Kaibel, Chem. Eng. Process., 2009, 48, 1089–1104 CrossRef.
- A. Jordan, P. Stoy and H. F. Sneddon, Chem. Rev., 2020, 121, 1582–1622 Search PubMed.
- M. T. Reetz, G. Qu and Z. Sun, Nat. Synth., 2024, 1–14 Search PubMed.
- M. Cortes-Clerget, J. Yu, J. R. Kincaid, P. Walde, F. Gallou and B. H. Lipshutz, Chem. Sci., 2021, 12, 4237–4266 RSC.
- A. Li, A. Ilie, Z. Sun, R. Lonsdale, J.-H. Xu and M. T. Reetz, Angew. Chem., Int. Ed., 2016, 128, 12205–12208 CrossRef.
- C. Krell, R. Schreiber, L. Hueber, L. Sciascera, X. Zheng, A. Clarke, R. Haenggi, M. Parmentier, H. Baguia, S. Rodde and F. Gallou, Org. Process Res. Dev., 2021, 25, 900–915 CrossRef CAS.
- N. Pino, G. Hincapié and D. López, Energy Fuel, 2018, 32, 561–573 CrossRef CAS.
- B. Seemala, R. Kumar, C. M. Cai, C. E. Wyman and P. Christopher, React. Chem. Eng., 2019, 4, 261–267 RSC.
- H. H. Khoo, L. L. Wong, J. Tan, V. Isoni and P. Sharratt, Resour. Conserv. Recycl., 2015, 95, 174–182 CrossRef.
- J. Julis and W. Leitner, Angew. Chem., Int. Ed., 2012, 51, 8615–8619 CrossRef CAS PubMed.
- C. Löser, T. Urit and T. Bley, Appl. Microbiol. Biotechnol., 2014, 98, 5397–5415 CrossRef PubMed.
- J. T. Ku, A. Y. Chen and E. I. Lan, Microb. Cell Fact., 2022, 21, 28 CrossRef CAS PubMed.
- H.-C. Tseng and K. L. Prather, Proc. Natl. Acad. Sci. U.S.A., 2012, 109, 17925–17930 CrossRef CAS PubMed.
- M. K. Akhtar, H. Dandapani, K. Thiel and P. R. Jones, Metab. Eng. Commun., 2015, 2, 1–5 CrossRef PubMed.
- H. G. Moon, Y.-S. Jang, C. Cho, J. Lee, R. Binkley and S. Y. Lee, FEMS Microbiol. Lett., 2016, 363, fnw001 CrossRef PubMed.
- G. Yuan, X. Ren and Q. Wang, et al. , Int. J. Electrochem. Sci., 2018, 13, 3210–3223 CrossRef.
- R. A. Welter, H. Santana, L. G. de la Torre, M. Robertson, O. P. Taranto and M. Oelgemöller, ChemPhotoChem, 2022, 6, e202200007 CrossRef CAS.
- F. P. Byrne, S. Jin, G. Paggiola, T. H. M. Petchey, J. H. Clark, T. J. Farmer, A. J. Hunt, C. R. McElroy and J. Sherwood, Sustain. Chem. Process., 2016, 4, 7 CrossRef.
- R. K. Henderson, C. Jimenez-Gonzalez, D. J. C. Constable, S. R. Alston, G. G. A. Inglis, G. Fisher, J. Sherwood, S. P. Binks and A. D. Curzons, Green Chem., 2011, 13, 854–862 RSC.
- A. Leo, C. Hansch and D. Elkins, Chem. Rev., 1971, 71, 525–616 CrossRef CAS.
- H. Fu, Y. Zhou, X. Jing, X. Shao and W. Cai, J. Med. Chem., 2022, 65, 12970–12978 CrossRef CAS PubMed.
- Y. Khalak, G. Tresadern, M. Aldeghi, H. M. Baumann, D. L. Mobley, B. L. de Groot and V. Gapsys, Chem. Sci., 2021, 12, 13958–13971 RSC.
- T.-S. Lee, B. K. Allen, T. J. Giese, Z. Guo, P. Li, C. Lin, T. D. McGee Jr, D. A. Pearlman, B. K. Radak and Y. Tao, et al. , J. Chem. Inf. Model., 2020, 60, 5595–5623 CrossRef CAS PubMed.
- G. König, M. T. Reetz and W. Thiel, J. Phys. Chem. B, 2018, 122, 6975–6988 CrossRef PubMed.
- G. König, Y. Mei, F. C. Pickard, A. C. Simmonett, B. T. Miller, J. M. Herbert, H. L. Woodcock, B. R. Brooks and Y. Shao, J. Chem. Theory Comput., 2016, 12, 332–344 CrossRef PubMed.
- B. R. Brooks, C. L. Brooks III, A. D. MacKerell Jr, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodošček, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 Search PubMed.
- B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187–217 Search PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. MacKerell Jr, J. Comput. Chem., 2010, 31, 671–690 Search PubMed.
- S. Kashefolgheta, M. P. Oliveira, S. R. Rieder, B. A. Horta, W. E. Acree Jr and P. H. Hünenberger, J. Chem. Theory Comput., 2020, 16, 7556–7580 CrossRef CAS PubMed.
- G. König, F. Pickard, J. Huang, W. Thiel, A. MacKerell, B. Brooks and D. York, Molecules, 2018, 23, 2695 CrossRef PubMed.
- C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268 CrossRef.
- G. König and S. Boresch, J. Comput. Chem., 2011, 32, 1082–1090 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- E. Neria, S. Fischer and M. Karplus, J. Chem. Phys., 1996, 105, 1902–1921 CrossRef CAS.
- M. Männistö, J.-P. Pokki, L. Fournis and V. Alopaeus, J. Chem. Thermodyn., 2017, 110, 127–136 CrossRef.
- A. Maczyński, D. G. Shaw, M. Góral and B. Wiśniewska-Gocłowska, J. Phys. Chem. Ref. Data, 2007, 36, 59–132 CrossRef.
- A. Maczyński, D. G. Shaw, M. Góral and B. Wiśniewska-Gocłowska, J. Phys. Chem. Ref. Data, 2007, 36, 133–190 CrossRef.
- A. Maczyński, D. G. Shaw, M. Góral and B. Wiśniewska-Gocłowska, J. Phys. Chem. Ref. Data, 2007, 36, 399–443 CrossRef.
- A. Maczynski, D. G. Shaw, M. Goral and B. Wisniewska-Goclowska, J. Phys. Chem. Ref. Data, 2007, 36, 685–731 CrossRef CAS.
- M. Góral, D. G. Shaw, A. Maczyński, B. Wiśniewska-Gocłowska and A. Jezierski, J. Phys. Chem. Ref. Data, 2009, 38, 1093–1127 CrossRef.
- M. Góral, D. G. Shaw, A. Maczyński, P. Oracz, B. Wiśniewska-Gocłowska, I. Owczarek and K. Blazej, J. Phys. Chem. Ref. Data, 2010, 39, 013102 CrossRef.
- A. Maczyński, D. G. Shaw, M. Góral and B. Wiśniewska-Gocłowska, J. Phys. Chem. Ref. Data, 2008, 37, 1119–1146 CrossRef.
- A. Maczyński, D. G. Shaw, M. Góral and B. Wiśniewska-Gocłowska, J. Phys. Chem. Ref. Data, 2008, 37, 1147–1168 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- W. F. Van Gunsteren and H. J. C. Berendsen, Mol. Phys., 1977, 34, 1311–1327 CrossRef CAS.
- Y. Sugita, A. Kitao and Y. Okamoto, J. Chem. Phys., 2000, 113, 6042–6050 CrossRef CAS.
- G. König, F. C. Pickard, J. Huang, A. C. Simmonett, F. Tofoleanu, J. Lee, P. O. Dral, S. Prasad, M. Jones, Y. Shao, W. Thiel and B. R. Brooks, J. Comput.-Aided Mol. Des., 2016, 30, 989–1006 CrossRef PubMed.
- T. C. Beutler, A. E. Mark, R. C. van Schaik, P. R. Gerber and W. F. van Gunsteren, Chem. Phys. Lett., 1994, 222, 529–539 CrossRef CAS.
- M. Zacharias, T. P. Straatsma and J. A. McCammon, J. Chem. Phys., 1994, 100, 9025–9031 CrossRef CAS.
- B. Wu, N. Ye, K. Zhao, M. Shi, J. Liao, J. Zhang, W. Chen, X. Li, Y. Han, M. Cortes-Clerget, M. L. Regnier, M. Parmentier, C. Mathes, F. Rampf and F. Gallou, Chem. Commun., 2024, 60, 2349–2352 RSC.
- N. Ye, B. Wu, K. Zhao, X. Ge, Y. Zheng, X. Shen, L. Shi, M. Cortes-Clerget, M. L. Regnier, M. Parmentier and F. Gallou, Chem. Commun., 2021, 57, 7629–7632 RSC.
- J. Michel, M. Orsi and J. W. Essex, J. Phys. Chem. B, 2008, 112, 657–660 CrossRef CAS PubMed.
- N. Bhatnagar, G. Kamath, I. Chelst and J. J. Potoff, J. Chem. Phys., 2012, 137, 014502 CrossRef PubMed.
- N. Hansen, P. H. Hünenberger and W. F. van Gunsteren, J. Chem. Theory Comput., 2013, 9, 1334–1346 CrossRef CAS PubMed.
- S. Genheden, J. Chem. Theory Comput., 2016, 12, 297–304 Search PubMed.
- S. Genheden, J. Comput.-Aided Mol. Des., 2017, 31, 867–876 CrossRef CAS PubMed.
- A. S. Rustenburg, J. Dancer, B. Lin, D. F. Ortwine, D. L. Mobley and J. D. Chodera, J. Comput.-Aided Mol. Des., 2016, 30, 945–958 Search PubMed.
- F. C. Pickard, G. König, F. Tofoleanu, J. Lee, A. C. Simmonett, Y. Shao, J. W. Ponder and B. R. Brooks, J. Comput.-Aided Mol. Des., 2016, 30, 1087–1100 Search PubMed.
- C. C. Bannan, K. H. Burley, M. Chiu, M. R. Shirts, M. K. Gilson and D. L. Mobley, J. Comput.-Aided Mol. Des., 2016, 30, 927–944 CrossRef CAS PubMed.
- A. Klamt, F. Eckert, J. Reinisch and K. Wichmann, J. Comput.-Aided Mol. Des., 2016, 30, 959–967 CrossRef CAS PubMed.
- S. Genheden and J. W. Essex, J. Comput.-Aided Mol. Des., 2016, 30, 969–976 CrossRef CAS PubMed.
- G. Kamath, I. Kurnikov, B. Fain, I. Leontyev, A. Illarionov, O. Butin, M. Olevanov and L. Pereyaslavets, J. Comput.-Aided Mol. Des., 2016, 30, 977–988 CrossRef CAS PubMed.
- S. Diaz-Rodriguez, S. M. Bozada, J. R. Phifer and A. S. Paluch, J. Comput.-Aided Mol. Des., 2016, 30, 1007–1017 CrossRef CAS.
- K.-C. Chung and H. Park, J. Comput.-Aided Mol. Des., 2016, 30, 1019–1033 CrossRef CAS PubMed.
- N. Tielker, D. Tomazic, J. Heil, T. Kloss, S. Ehrhart, S. Güssregen, K. F. Schmidt and S. M. Kast, J. Comput.-Aided Mol. Des., 2016, 30, 1035–1044 CrossRef CAS PubMed.
- I. M. Kenney, O. Beckstein and B. I. Iorga, J. Comput.-Aided Mol. Des., 2016, 30, 1045–1058 CrossRef CAS PubMed.
- D. Santos-Martins, P. A. Fernandes and M. J. Ramos, J. Comput.-Aided Mol. Des., 2016, 30, 1079–1086 CrossRef CAS PubMed.
- S. Bosisio, A. S. J. S. Mey and J. Michel, J. Comput.-Aided Mol. Des., 2016, 30, 1101–1114 CrossRef CAS PubMed.
- T. Luchko, N. Blinov, G. C. Limon, K. P. Joyce and A. Kovalenko, J. Comput.-Aided Mol. Des., 2016, 30, 1115–1127 CrossRef CAS PubMed.
- M. R. Jones, B. R. Brooks and A. K. Wilson, J. Comput.-Aided Mol. Des., 2016, 30, 1129–1138 CrossRef CAS PubMed.
- A. Nicholls, D. L. Mobley, J. P. Guthrie, J. D. Chodera, C. I. Bayly, M. D. Cooper and V. S. Pande, J. Med. Chem., 2008, 51, 769–779 CrossRef CAS PubMed.
- J. P. Guthrie, J. Phys. Chem. B, 2009, 113, 4501–4507 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 4538–4543 CrossRef CAS PubMed.
- M. T. Geballe, A. G. Skillman, A. Nicholls, J. P. Guthrie and P. J. Taylor, J. Comput.-Aided Mol. Des., 2010, 24, 259–279 CrossRef CAS PubMed.
- P. V. Klimovich and D. L. Mobley, J. Comput.-Aided Mol. Des., 2010, 24, 307–316 CrossRef CAS PubMed.
- A. Klamt and M. Diedenhofen, J. Comput. Aid. Mol. Des., 2010, 24, 357–360 CrossRef CAS PubMed.
- R. Ribeiro, A. Marenich, C. Cramer and D. Truhlar, J. Comput. Aid. Mol. Des., 2010, 24, 317–333 CrossRef CAS PubMed.
- J. P. Guthrie, J. Comput.-Aided Mol. Des., 2014, 28, 151–168 CrossRef CAS PubMed.
- D. L. Mobley, K. Wymer and N. M. Lim, J. Comput.-Aided Mol. Des., 2014, 28, 135–150 CrossRef CAS PubMed.
- G. König, F. C. Pickard, Y. Mei and B. R. Brooks, J. Comput.-Aid. Mol. Des., 2014, 28, 245–257 CrossRef.
- P. Mikulskis, D. Cioloboc, M. Andrejić, S. Khare, J. Brorsson, S. Genheden, R. A. Mata, P. Söderhjelm and U. Ryde, J. Comput.-Aid. Mol. Des., 2014, 28, 375–400 CrossRef CAS PubMed.
- M. T. Reetz and G. König, Eur. J. Org Chem., 2021, 2021, 6224–6228 CrossRef CAS.
- H. B. Krop, M. J. van Velzen, J. R. Parsons and H. A. Govers, Chemosphere, 1997, 34, 107–119 CrossRef CAS.
- K. B. Hanson, D. J. Hoff, T. J. Lahren, D. R. Mount, A. J. Squillace and L. P. Burkhard, Chemosphere, 2019, 218, 616–623 CrossRef CAS PubMed.
- G. Hummer, S. Garde, A. E. Garcia, A. Pohorille and L. R. Pratt, Proc. Natl. Acad. Sci. U.S.A., 1996, 93, 8951–8955 CrossRef CAS PubMed.
- G. Hummer, S. Garde, A. Garcia, M. E. Paulaitis and L. R. Pratt, J. Phys. Chem. B, 1998, 102, 10469–10482 CrossRef CAS.
- Y. Liu, J. Yan, Q. Yuan, L. Ma, L. Zhou, Y. He, G. Liu, X. Yue and Y. Jiang, Green Chem., 2024, 26, 6666–6674 RSC.
- L. Pilon, D. Day, H. Maslen, O. P. J. Stevens, N. Carslaw, D. R. Shaw and H. F. Sneddon, Green Chem., 2024, 26, 9697–9711 RSC.
- A. Jordan, C. G. J. Hall, L. R. Thorp and H. Sneddon, Chem. Rev., 2022, 16, 6749–6794 CrossRef PubMed.
- T. Gerlach, S. Müller, A. G. de Castilla and I. Smirnova, Fluid Phase Equilib., 2022, 560, 113472 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Molecular structures of the benchmark solutes, NMR spectra, densities, and partition coefficient data of the solvents. See DOI: https://doi.org/10.1039/d4su00628c |
| This journal is © The Royal Society of Chemistry 2025 |