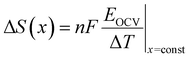Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
From structure to electrochemistry: the influence of transition metal ordering on Na+/vacancy orderings in P2-type NaxMO2 cathode materials for sodium-ion batteries†
Lukas Fridolin
Pfeiffer‡
 *a,
Manuel
Dillenz‡
b,
Nora
Burgard
a,
Premysl
Beran
cd,
Daniel
Roscher
ef,
Maider
Zarrabeitia
*a,
Manuel
Dillenz‡
b,
Nora
Burgard
a,
Premysl
Beran
cd,
Daniel
Roscher
ef,
Maider
Zarrabeitia
 ef,
Paul
Drews
a,
Charles
Hervoches
c,
Daria
Mikhailova
ef,
Paul
Drews
a,
Charles
Hervoches
c,
Daria
Mikhailova
 g,
Ahmad
Omar
g,
Volodymyr
Baran
h,
Neelima
Paul
i,
Mohsen
Sotoudeh
g,
Ahmad
Omar
g,
Volodymyr
Baran
h,
Neelima
Paul
i,
Mohsen
Sotoudeh
 b,
Michael
Busch
b,
Michael
Busch
 jk,
Margret
Wohlfahrt-Mehrens
a,
Axel
Groß
jk,
Margret
Wohlfahrt-Mehrens
a,
Axel
Groß
 b,
Stefano
Passerini
b,
Stefano
Passerini
 ef and
Peter
Axmann
ef and
Peter
Axmann
 *a
*a
aZSW Center for Solar Energy and Hydrogen Research Baden-Württemberg, Helmholtzstraße 8, 89081 Ulm, Germany. E-mail: lukas.pfeiffer@zsw-bw.de; peter.axmann@zsw-bw.de
bInstitute for Theoretical Chemistry, Mez-Starck-Haus, Oberberghof 7, 89081 Ulm, Germany
cNuclear Physics Institute, CAS, Hlavni 130, 250 68 Rez, Czech Republic
dEuropean Spallation Source, ERIC, PO Box 176, 221 00 Lund, Sweden
eHelmholtz Institute Ulm, Helmholtzstraße 11, 89081 Ulm, Germany
fKarlsruhe Institute of Technology, 76021 Karlsruhe, Germany
gLeibniz Institute for Solid State and Materials Research (IFW) Dresden e.V., Helmholtzstr. 20, 01069 Dresden, Germany
hDeutsches Elektronen-Synchrotron (DESY), Notkestraße 85, 22607 Hamburg, Germany
iHeinz Maier-Leibnitz Zentrum, Technische Universität München, Lichtenbergstraße 1, 85747 Garching, Germany
jDivision of Materials Science, Department of Engineering Sciences and Mathematics, Luleå University of Technology, 971 87 Luleå, Sweden
kWallenberg Initiative Materials Science for Sustainability (WISE), Luleå University of Technology, 971 87 Luleå, Sweden
First published on 28th November 2024
Abstract
P2-type layered oxides are attractive cathode active materials for sodium-ion batteries, however, these materials typically suffer from detrimental Na+/vacancy orderings. In this work, we investigate the origin as well as the influence of the transition metal ratio on Na+/vacancy orderings in P2-type cathode materials. A combination of X-ray diffraction (XRD), neutron diffraction, advanced electrochemical methods, operando XRD and DFT calculations is applied to study Na+/vacancy orderings in P2-NaxNi1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2. In P2-NaxNi1/3Mn2/3O2, a honeycomb Ni/Mn superstructure leads to charge ordering within the transition metal slab and pronounced Na+/vacancy orderings, causing distinct voltage jumps at specific sodium contents (x = 2/3, 1/2 and 1/3). For P2-Na0.60Mn3/4Ni1/4O2, the Ni/Mn superstructure is disrupted, resulting in more complex charge orderings within the transition metal slab, partially suppressed Na+/vacancy orderings and an overall smoother potential profile. Based on our findings, guidelines to suppress Na+/vacancy orderings in P2-type cathode materials for sodium-ion batteries are postulated and discussed with respect to electrochemical measurements of various transition metal compositions. These guidelines can serve to predict the tendency towards Na+/vacancy orderings for a given cathode composition or to design new cathode compositions for enhanced cycle life based on the absence of Na+/vacancy orderings.
Introduction
Increasing energy generation from renewables is inevitable to reduce the impact of man-made climate change.1 With that, the need for energy storage is gaining importance.2–4 Today, lithium-ion batteries (LIBs) play a key role in mobile and stationary energy storage,2,5 however, LIBs contain critical raw materials in terms of availability and cost, such as cobalt, nickel, lithium, copper or graphite.6–9Sodium-ion batteries (SIBs), in which sodium replaces lithium as the ionic charge carrier, are currently being developed and commercialized as a sustainable and potentially cost-effective complementary technology to today's LIBs.10–13 SIBs typically utilize the same working principle as LIBs,14 however, critical raw materials are either replaced by more abundant and cost-effective materials or reduced in content.15,16 On the anode side, hard carbon typically replaces graphite as the active material17–20 and aluminium is applied as a current collector instead of copper.15,21,22 As the electrolyte, typically, solutions of NaPF6 in carbonate solvents replace LiPF6 equivalents.15,23,24 On the cathode side, sodium-containing intercalation materials substitute lithium nickel cobalt manganese oxides (NCM) or lithium iron phosphate (LFP) as the active material.10,15,25 Overall, these measures may result in a significantly reduced bill of materials for SIBs and potentially more sustainable batteries.22,26–30 Additionally, SIBs promise more advantages over today's LIBs in terms of low-temperature performance,11 power capability,25 safety, and transportation and storage.31–33 Furthermore, SIBs can be produced on established production equipment, which reduces necessary investment costs and enables a rapid scale-up of the technology (drop-in technology).15 Cumulatively, these aspects make SIBs a sustainable and cost-effective secondary battery technology if their performance can be further enhanced.26
So far, one of the main bottlenecks for SIBs remains the cathode active material. Currently, mainly three material classes are explored as potential cathode active materials for SIBs, namely Prussian-Blue Analogues (PBAs), sodium vanadium fluorophosphates (NVFP) and layered sodium transition metal oxides (NaxMO2).10,25 Among these three broad families, the latter offers attractive potential and capacity, high (crystal) density and can be produced in a similar fashion as today's NCM for LIBs.10,25,34–36
These layered sodium transition metal oxides can be synthesized in an O3, P3 or P2-type structure according to Delmas' notation, where a letter is used as an abbreviation of the alkali metal ion environment (e.g., O = octahedral and P = trigonal prismatic) and a numeral is used to describe the number of transition metal oxygen slabs (MO2) necessary to describe the unit cell fully. A prime is used to indicate distortion of the ideal structure.37
In O3-type layered sodium transition metal oxides, octahedra of adjoining sodium sites share edges. Hence, in these materials the diffusion from one sodium site to another proceeds via an intermediate tetrahedral site (divacancy mechanism), leading to moderate Na conductivities.38,39 In P2-type layered sodium transition metal oxides, prisms of adjoining sodium sites share faces, enabling a single-vacancy mechanism with low activation energy, typically resulting in high diffusion rates.40 Eventually diffusion rates are a function of the sodium content (vacancy concentration) and can be highly influenced by Na+/vacancy orderings.40
P2-type sodium transition metal oxides typically offer high power capability due to fast solid diffusion, high discharge potential and attractive reversible capacities.41 In this material class, P2-type NaxNiyMn1−yO2 is one of the most investigated sodium layered oxides, due to its attractive performance in terms of reversible capacity and mean discharge potential as well as its high power capability.10,42
Synthesis and electrochemistry of P2-Na2/3Ni1/3Mn2/3O2 were first reported by Jeff Dahn and co-workers.43–45 During reversible electrochemical desodiation at room temperature, P2-NaxNi1/3Mn2/3O2 follows a solid-solution-like behaviour, maintaining the P2 structure for x > 1/3.44 For x < 1/3, a reversible two-phase reaction between P2-Na1/3Ni1/3Mn2/3O2 and O2-Nax≈0Ni1/3Mn2/3O2 takes place.44 The potential profile typically exhibits distinct voltage jumps at sodium stoichiometries of x = 2/3, 1/2 and 1/3, which are associated with Na+/vacancy orderings.44,46,47 These potential jumps are enclosed by flat regions (indicating the transition between ordered and disordered sodium configurations) at 3.16 V, 3.31 V & 3.56 V and 3.66 V & 4.10 V corresponding to sodium stoichiometries of approximately x = 2/3 − δ, 1/2 ± δ and 1/3 ± δ with 0.09 ≳ δ ≳ 0.04, respectively.44,48–50 The corresponding Na+/vacancy orderings within the sodium slab have been elucidated using first principles calculations by Meng et al.46 Na+/vacancy ordered compounds are thermodynamically more stable compared to their disordered counterparts, which results in impeded solid diffusion in proximity to the composition of the ordering46,51 and potentially limits the cycle life of the battery.47 Additionally, the potential plateaus caused by Na+/vacancy ordering are challenging for the application of a battery management system (BMS).52
If some of the nickel in P2-Na2/3Ni1/3Mn2/3O2 is substituted by manganese to obtain P2-Na2/3Mn3/4Ni1/4O2, similar performance can be achieved, however, the potential profile is considerably smoother, hinting at largely suppressed Na+/vacancy orderings.53–57
In this work, we investigate the influence of the transition metal ratio on Na+/vacancy ordering in P2-NaxNi1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2 cathode active materials for SIBs. Both materials were synthesized and thoroughly characterized, using advanced electrochemical and analytical techniques as well as first principles calculations, to demonstrate that Na+/vacancy ordering is closely related to charge ordering within the transition metal slab. A general guideline to suppress Na+/vacancy ordering in P2-type cathode materials is postulated and evaluated against various P2-type sodium transition metal oxides and reports in the literature.
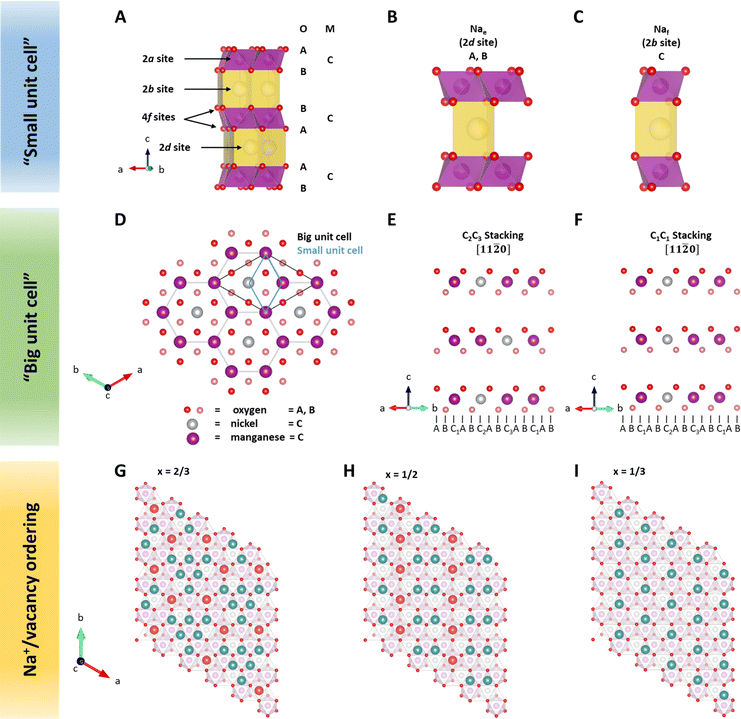
Crystal structure of P2-type NaxNiyMn1−yO2
In layered sodium transition metal oxides, transition metals are octahedrally coordinated by oxygen atoms. Edge-sharing MO6 octahedra form MO2 slabs. These MO2 slabs are separated by sodium slabs. Sodium is preferentially located in a triangular prismatic or octahedral environment with six-fold coordination to the surrounding oxygen atoms of the MO2 slabs.47 As described above, P2-type NaxMO2 structures are characterized by a trigonal prismatic environment of sodium and two MO2 slabs within the unit cell.58Due to similar X-ray scattering length of 3d transition metals,59 the crystal structure of P2-type sodium transition metal oxides as derived from X-ray diffraction (XRD) is typically indexed in space group P63/mmc (SG 194),60–62 here noted as a “small unit cell” (Fig. 1A–C). In this structure model, all transition metals are located on the same 2a site, e.g., C, in the hexagonal stacking sequence. Oxygen atoms are located on 4f sites following the ABBA stacking sequence. Sodium ions in the prismatic environment are located either on 2d sites sharing edges with adjacent MO6 octahedra (Nae) or 2b sites sharing faces (Naf) with the adjacent MO6 octahedra. Please note that the number of available sodium sites is twice the amount of transition metal sites. However, the simultaneous occupation of adjacent Nae and Naf sites would result in close proximity of sodium ions with shared prismatic faces and is therefore considered unlikely.63 According to the principles by Linus Pauling, Nae sites are expected to be energetically more favourable than Naf sites.63
Neutron diffraction (ND) is an invaluable tool for investigating transition metal superstructures due to variant scattering lengths of 3d transition metals.64 In particular, the neutron scattering length of Mn = −3.73 fm is distinctly different from that of Ni = 10.3 fm. Thus, ND is optimal for identifying sites occupied by these transition metal cations. For P2-Na2/3Ni1/3Mn2/3O2, a honeycomb Ni/Mn ordering within the MO2 slab is reported, which can be described using a 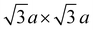 superstructure (P6322, SG 182 or P63, SG 173),51,60,65 here noted as a “big unit cell” (Fig. 1D–F). The in-plane honeycomb Ni/Mn ordering together with the small and big unit cells is presented in Fig. 1D. In the big unit cell, three different transition metal sites, C1, C2 and C3, are available, which can be used to describe the stacking sequence of MO2 slabs in the z-direction. For P2-Na2/3Ni1/3Mn2/3O2, nickel atoms are reported to predominantly occupy alternating C2 and C3 sites in stacked MO2 slabs (C2C3 stacking)60 as presented in Fig. 1E. Interestingly, in the isovalent P2-Na2/3Mg1/3Mn2/3O2, the same Mg/Mn honeycomb ordering is reported within the MO2 slab, however, magnesium atoms are predominantly stacked on top of each other following a C1C1 stacking sequence (P63/mcm, SG 193)60 as presented in Fig. 1F. Simulated ND patterns for the “small unit cell” neglecting any Ni/Mn ordering and the “big unit cell” with Ni/Mn ordering in C1C1 and C2C3 stacking sequences are presented in ESI Fig. S5.† The simulated diffraction patterns clearly differ between Q = 1.3 Å−1 and Q = 2.4 Å−1 due to the presence and stacking sequence of the Ni/Mn honeycomb ordering.
superstructure (P6322, SG 182 or P63, SG 173),51,60,65 here noted as a “big unit cell” (Fig. 1D–F). The in-plane honeycomb Ni/Mn ordering together with the small and big unit cells is presented in Fig. 1D. In the big unit cell, three different transition metal sites, C1, C2 and C3, are available, which can be used to describe the stacking sequence of MO2 slabs in the z-direction. For P2-Na2/3Ni1/3Mn2/3O2, nickel atoms are reported to predominantly occupy alternating C2 and C3 sites in stacked MO2 slabs (C2C3 stacking)60 as presented in Fig. 1E. Interestingly, in the isovalent P2-Na2/3Mg1/3Mn2/3O2, the same Mg/Mn honeycomb ordering is reported within the MO2 slab, however, magnesium atoms are predominantly stacked on top of each other following a C1C1 stacking sequence (P63/mcm, SG 193)60 as presented in Fig. 1F. Simulated ND patterns for the “small unit cell” neglecting any Ni/Mn ordering and the “big unit cell” with Ni/Mn ordering in C1C1 and C2C3 stacking sequences are presented in ESI Fig. S5.† The simulated diffraction patterns clearly differ between Q = 1.3 Å−1 and Q = 2.4 Å−1 due to the presence and stacking sequence of the Ni/Mn honeycomb ordering.
Within the sodium slab, Na+/vacancy orderings at distinct sodium stoichiometries x are reported46 (Fig. 1G–I). At x = 2/3, sodium ions in Naf sites arrange in a large-zig-zag (LLZ) around sodium ions in Nae sites (Fig. 1G). At x = 1/2, the ordering can be described as a row of sodium ions in Naf sites adjacent to two rows of sodium ions in Nae sites (Fig. 1H). At x = 1/3, only Nae sites are occupied, resulting in an altered row ordering (Fig. 1I). These Na+/vacancy orderings are accompanied by distinct potential jumps during galvanostatic (de)sodiation.44,46
For P2-NaxMn3/4Ni1/4O2, a similar crystal structure to that in P2-Na2/3Ni1/3Mn2/3O2 with a honeycomb Ni/Mn superstructure in the MO2 slab is reported, however, with additional manganese atoms located on nickel sites.54 Based on a smoother potential profile and the absence of Na+/vacancy superstructure reflections at x = 0.62, one report54 concludes that the LLZ-ordering is disrupted in P2-Na0.62Mn3/4Ni1/4O2.
In this work, we thoroughly characterize the crystal structure of P2-Na2/3Ni1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2 and investigate the extent of Na+/vacancy ordering and the nature of Na+/vacancy ordered phases in these materials. Furthermore, this report correlates the in-plane Na+/vacancy orderings with transition metal charge ordering arising from the transition metal superstructure in these materials.
Experimental
Material synthesis
Na2/3Ni1/3Mn2/3O2, Na2/3Mn3/4Ni1/4O2 and Na0.60Mn3/4Ni1/4O2 were prepared in a three-step synthesis route following co-precipitation of a hydroxide precursor, mixing of the dried precipitate with NaOH as the sodium source and subsequent calcination at high temperature to obtain the final cathode active material (CAM). The dense, spherical Ni1/3Mn2/3(OH)2 and Mn3/4Ni1/4(OH)2 hydroxide precursors were prepared under vigorous stirring in a continuously stirred tank reactor (CSTR, volume = 1 liter). The reactor was constantly fed with deaerated, aqueous solutions of Mn(NO3)2·4H2O (Carl Roth) and Ni(NO3)2·6H2O (Carl Roth), NH3 (Carl Roth) and NaOH (Carl Roth). The precipitate collected at the reactor outlet was filtered and washed to remove residual salt solutions and dried. Subsequently, these hydroxide precursors were mixed with respective amounts of aqueous NaOH (Sigma-Aldrich) solution and dried at 80 °C following a wet impregnation procedure. The dried mixture was then calcined in a box furnace (Carbolite Gero). Na2/3Ni1/3Mn2/3O2 was calcined for 10 h at 900 °C in a pure oxygen atmosphere, Na2/3Mn3/4Ni1/4O2 was calcined for 10 h at 900 °C in air as described elsewhere56 and Na0.60Mn3/4Ni1/4O2 was calcined for 10 h at 1000 °C in pure oxygen. After passive cooling to 200 °C, the powders were directly transferred into a Büchi glass oven, where they were kept at 200 °C under dynamic vacuum overnight. Subsequently, the CAM powders were transferred without any further contact with ambient air into an Ar-filled glovebox (MBraun, H2O < 0.1 ppm, O2 < 0.1 ppm). Consecutive powder handling, electrode preparation and cell assembly were conducted in the same glovebox.For powder characterization with ND, a second batch of Na2/3Ni1/3Mn2/3O2 and Na0.60Mn3/4Ni1/4O2 was prepared based on the same hydroxide precursor and following the same synthesis procedure. A comparison of the characterization results for the two batches is presented in ESI Fig. S6 with ESI Tables S3 and S4 and ESI Fig. S7 with ESI Tables S5 and S6† for Na2/3Ni1/3Mn2/3O2 and Na0.60Mn3/4Ni1/4O2, respectively.
Additionally, P2-Na2/3Ni1/3Mn2/3O2, P2-Na3/4Ni1/4Li1/12Mn2/3O2, P2-Na2/3Ni1/4Mg1/12Mn2/3O2, P2-Na2/3Ni2/9Al1/9Mn2/3O2 and P2-Na2/3Ni1/3Al1/9Mn5/9O2 were synthesized. The respective synthesis route, main characterization results and electrochemical testing procedure are described in the ESI.†
Material characterization
Inductively coupled plasma optical emission spectroscopy (ICP-OES, Spectro Arcos SOP) with a diluted aqua regia solution was used for analysis of the chemical composition. Fourier transform infrared spectroscopy in attenuated total reflectance mode (ATR-FTIR) was performed using a Bruker Alpha spectrometer with an Alpha-P ATR unit placed in an Ar-filled glovebox. Scanning electron microscopy (SEM) was used to characterize the powder morphology using a Leo 1530VP (Zeiss) equipped with an Everhart–Thornley SE detector at 5 kV acceleration voltage. Powder XRD patterns were collected on a D8Advance (Bruker) in Bragg–Brentano geometry equipped with a Cu X-ray tube and a LynxEye XE-T detector. Neutron diffraction patterns were recorded at MEREDIT instrument at the Nuclear Physics Institute CAS located in Řež near Prague, Czech Republic. A joint refinement of XRD and ND patterns was performed to obtain lattice parameters, Wyckoff sites and site occupations using the FullProf Suite software.66 Lattice parameters were refined independently for XRD and ND patterns, due to potentially different measurement temperatures and the different sensitivities of X-ray and neutron radiation. Instrumental broadening was determined from SiO2 powder on a mosaic Cu(222) monocrystal for ND and NIST640c Si powder for XRD. Based on the results of the joint ND and XRD refinement, FAULTS software67 was deployed to obtain the stacking probability of P3-type stacking faults from the XRD patterns56 and to analyse the stacking probability of C1C1 stacking faults from ND patterns. The refinement procedure is described in more detail in the ESI.† Throughout the manuscript, depictions of the crystal structures were prepared using VESTA software.68Ex situ capillary transmission XRD measurements were performed on the same D8Advance (Bruker) instrument. For this purpose, CR2032 coin cells were galvanostatically (dis)charged to obtain the desired active material sodium content and subsequently opened inside an argon filled glovebox. After rinsing with dimethyl carbonate (DMC), the electrode composite was carefully scratched off the aluminium current collector foil and filled into glass capillaries (Ø 0.3 mm, Hilgenberg). The glass capillaries were sealed inside an argon filled glovebox to avoid any contact with the ambient environment.
Electrochemical investigations
Slurries were prepared by homogeneously dispersing a CAM powder, polyvinylidene difluoride binder (PVDF, Solvay Solef 5130) and conductive carbon (SuperP-Li, Imerys Graphite & Carbon) with an 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio in an appropriate amount of anhydrous N-methyl-2-pyrrolidone (Sigma-Aldrich). These slurries were cast on aluminium current collector foils using the doctor blade technique. Electrodes with Ø12 mm and a typical active material mass loading of approximately 4 mg cm−2 were punched from the dried electrode sheets. The electrodes were further dried in a Büchi glass oven at 130 °C and dynamic vacuum (≈2 × 10−5 bar) overnight. Alumina coated CR2032 coin cells (Hohsen) were prepared using these electrodes, two layers of a glass fibre separator (GFA, Whatman, Ø16 mm), 150 μl of 1 M NaPF6 in propylene carbonate (PC) + 5 wt% fluoroethylene carbonate (FEC) as electrolyte and sodium metal foil as the counter electrode (Acros Organics, Ø16 mm). The galvanostatic intermittent titration technique (GITT) was performed on a VMP3 potentiostat (Biologic) using specific current pulses of 17.3 mA g−1 for 10 min within the voltage range of 1.5–4.3 V. Equilibrium was assumed when the absolute voltage change was <0.0001 V h−1. Entropymetry measurements were performed using the same potentiostat and a programmable temperature chamber (CTS GmbH) with temperature steps at 40 °C, 25 °C and 10 °C. Specific current pulses of 8.7 mA g−1 with various time periods were applied at 40 °C, followed by a relaxation time of 8 h at the same temperature. In the following, the temperature was changed within 15 min to 25 °C, where it was held for 105 min. Subsequently, the temperature was changed to 10 °C following the same procedure before another current pulse was applied at 40 °C. Equilibrium voltages were derived from the average voltage of the last thirty minutes at each temperature step. The sodium stoichiometry was calculated based on the measured charge of the current pulse and the electrode active material mass, assuming that side reactions were negligible. For every sodium stoichiometry, the entropy change was derived from the obtained slope of the cell voltage with temperature as described in the ESI.†
1 weight ratio in an appropriate amount of anhydrous N-methyl-2-pyrrolidone (Sigma-Aldrich). These slurries were cast on aluminium current collector foils using the doctor blade technique. Electrodes with Ø12 mm and a typical active material mass loading of approximately 4 mg cm−2 were punched from the dried electrode sheets. The electrodes were further dried in a Büchi glass oven at 130 °C and dynamic vacuum (≈2 × 10−5 bar) overnight. Alumina coated CR2032 coin cells (Hohsen) were prepared using these electrodes, two layers of a glass fibre separator (GFA, Whatman, Ø16 mm), 150 μl of 1 M NaPF6 in propylene carbonate (PC) + 5 wt% fluoroethylene carbonate (FEC) as electrolyte and sodium metal foil as the counter electrode (Acros Organics, Ø16 mm). The galvanostatic intermittent titration technique (GITT) was performed on a VMP3 potentiostat (Biologic) using specific current pulses of 17.3 mA g−1 for 10 min within the voltage range of 1.5–4.3 V. Equilibrium was assumed when the absolute voltage change was <0.0001 V h−1. Entropymetry measurements were performed using the same potentiostat and a programmable temperature chamber (CTS GmbH) with temperature steps at 40 °C, 25 °C and 10 °C. Specific current pulses of 8.7 mA g−1 with various time periods were applied at 40 °C, followed by a relaxation time of 8 h at the same temperature. In the following, the temperature was changed within 15 min to 25 °C, where it was held for 105 min. Subsequently, the temperature was changed to 10 °C following the same procedure before another current pulse was applied at 40 °C. Equilibrium voltages were derived from the average voltage of the last thirty minutes at each temperature step. The sodium stoichiometry was calculated based on the measured charge of the current pulse and the electrode active material mass, assuming that side reactions were negligible. For every sodium stoichiometry, the entropy change was derived from the obtained slope of the cell voltage with temperature as described in the ESI.†
Operando synchrotron XRD measurements were performed at PETRA III, beamline P02.1 (DESY, Hamburg, Germany).69 2D diffraction images were collected using a VATEX CT4343 area detector (2880 × 2880 pixels, 150 × 150 μm pixel size) for 60 seconds. The obtained data were integrated using the DAWN package.70 An eight-fold coin cell holder, connected to a Biologic Instruments potentiostat, was employed as described elsewhere.71 A wavelength of 0.20734(1) Å was determined by analysis of the positions of reflections of the LaB6 reference material (NIST 660C). Prior to recording the first diffraction pattern, the electrochemical cells were subject to a formation cycle at 8.65 mA g−1 (discharge to 1.5 V followed by charge to 4.2 V). Subsequently, diffraction patterns were collected with the pre-charged cell by first discharging to 1.5 V followed by charge to 4.3 V at a constant current of 8.65 mA g−1. All diffraction patterns were analysed by the Rietveld method with TOPAS V6 software where the reflections of the Al current collector served as the internal reference.
Throughout this work, either cell voltages from two-electrode measurements with a sodium metal counter electrode or potentials against a sodium metal quasi-reference electrode (three-electrode setup) are reported.
Computational methods
Periodic first-principles calculations based on density functional theory (DFT)72,73 were performed to determine the convex hull for the Na intercalation for P2-NaxNi1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2. The projector augmented wave method (PAW)74 was used in conjunction with the PBE75 exchange and correlation functional. In addition, the Grimme D3 correction76 was employed as implemented in the Vienna Ab initio Simulation Package (VASP)77–79 to capture the influence of dispersion effects. The data-driven Hubbard-type U corrections80 of UNi = 6.2 eV and UMn = 3.9 eV (ref. 81 and 82) were used to treat the strongly correlated 3d-electrons of the Ni and Mn atoms. The plane wave cut-off was set to 520 eV and a 3 × 3 × 3 k-point mesh was employed to sample the Brillouin zone. A large supercell containing 24 formula units and ferromagnetic ordering was chosen. The electronic convergence criterion was set to 1 × 10−6 eV and the structures were relaxed until all forces converged below 0.01 eV Å−1. The open circuit potential VOCV in a Na-ion battery is governed by the change in free enthalpy ΔG for the transfer of a Na atom. Thus, the open circuit voltage (OCV) is determined by the difference of the chemical potential μ of Na in the anode and cathode by taking into account the number of transferred electrons ne and the Faraday constant F: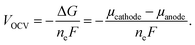 | (1) |
By neglecting pV and the entropic contributions to ΔG, the difference in the chemical potential of the Na atom is approximated using the total energy of DFT calculations EDFT. The calculation of the VOCV for an exemplary layered oxide compound NaxMO2 follows:
| VOCV = EDFT(Nax1+ΔxMO2) − (EDFT(Nax1MO2) + ΔxEDFT(Nametal)). | (2) |
In eqn (2), EDFT is stated in eV and sodium metal is chosen as the reference for the anode. Since the mode of intercalation in these materials deviates from a simple solid-solution behaviour and first order phase transformations at high potentials as well as Na+/vacancy ordering transitions occur, the convex hull for the Na intercalation compound is derived to identify thermodynamically stable configurations. The convex hull is constructed from the formation energy Efx with respect to the decomposition into the Na deficient O2-type structure (x = 0) and the P2-type structure at a Na content of x = 2/3:
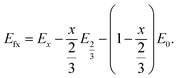 | (3) |
Once the convex hull is constructed by calculating the formation energy per formula unit, the OCV for each stable configuration is obtained using eqn (1). The convex hull calculations for P2-NaxNi1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2 were employed following the previously described procedure for the sodium contents 0 < x < 1/3 (ref. 53 and 83) and by considering the row and large-zig-zag Na+/vacancy orderings at the Na contents x = 1/3, 1/2 and 2/3 as identified by Lee et al.46 and the alternative Na+/vacancy ordering at x = 1/2 proposed by Huang et al.65,83 Additional Na configurations for the Na contents x = 1/3, 5/12, and 7/12 were selected by minimizing the classical Ewald energy84 assuming integer charges for redox inactive atoms (i.e., Na+, O2−) and variable charges for the TM atoms (i.e., Ni2+/3+/4+, and Mn3+/4+) for all possible configurations as implemented in pymatgen.85 Overall, a minimum of 10 configurations per Na content were obtained for the Na composition range 0 < x < 1/3 and 20 configurations for the Na composition range 1/3 ≤ x ≤ 2/3 in steps of x = 1/12 for each compound. Some of the configurations considered in the DFT calculations for NaxNi1/3Mn2/3O2 are equivalent to the publication by Daubner et al.48
Results and discussion
Material characterization
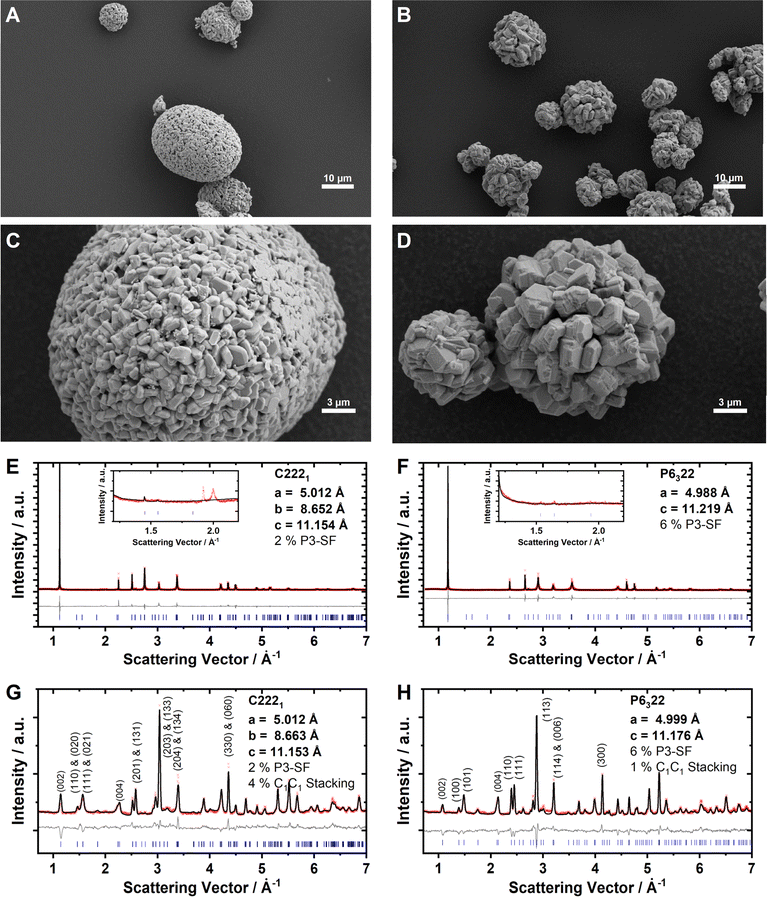
The Na2/3Ni1/3Mn2/3O2 and Na0.60Mn3/4Ni1/4O2 cathode active materials were synthesized in our labs, where the reduced sodium content in the latter material is targeted to minimize surface impurities such as NaOH, NaHCO3 or Na2CO3.86,87 For Na2/3Ni1/3Mn2/3O2, a small amount of Na2CO3 is detected with ATR-FTIR, whereas the absence of these surface impurities is confirmed for Na0.60Mn3/4Ni1/4O2 by ATR-FTIR measurements as presented together with the reproduced batches in ESI Fig. S8.† Elemental analysis with ICP-OES results in Na0.69Ni0.34Mn0.66O2 and Na0.60Mn0.74Ni0.26O2, respectively, which is in good accordance with the targeted stoichiometries. Based on the knowledge that Mn3+/Mn4+ takes place at a lower potential than Ni2+/Ni3+ redox,50,87 we can derive the formal oxidation states Na0.69Ni0.34IIMn0.01IIIMn0.65IVO2 and Na0.60Mn0.08IIIMn0.66IVNi0.26IIO2, respectively. In both samples, nickel is dominantly divalent and manganese is mainly tetravalent. Particle morphology was characterized using SEM (Fig. 2A–D). Both samples consist of secondary particles with a spherical morphology. The crystal structure was characterized using powder XRD and ND. The diffraction patterns for Na2/3Ni1/3Mn2/3O2 and Na0.60Mn3/4Ni1/4O2 are presented in Fig. 2E–H. For both materials, the obtained XRD pattern (Fig. 2E and F) can be indexed with the hexagonal space group P63/mmc (SG 194), indicating phase pure P2-type crystalline structures. For P2-Na2/3Ni1/3Mn2/3O2, the small reflexes located at Q = 1.9 Å−1 and Q = 2.0 Å−1 originate from the LLZ Na+/vacancy ordering (see the inset of Fig. 2E). For P2-Na0.60Mn3/4Ni1/4O2, these superstructure reflexes are absent in accordance with the discrepancy in sodium content (see the inset of Fig. 2F). For P2-Na2/3Ni1/3Mn2/3O2, a subtle split of the (100) and (2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) reflections at Q = 2.5 Å−1 and Q = 4.3 Å−1 in the XRD pattern suggests a slight orthorhombic distortion of the hexagonal unit cell. Additionally, in both XRD patterns the broadening of (10l) reflections hints at stacking faults. The ND patterns of both samples exhibit reflections between Q = 1.3 Å−1 and Q = 2.4 Å−1, indicating the presence of a Ni/Mn honeycomb ordering with predominantly a C2C3 stacking sequence (compare ESI Fig. S5†). Based on these findings, we performed a joint Rietveld refinement of XRD and ND patterns using the “big unit cell” (P6322, SG 182) with a honeycomb Ni/Mn ordering and a C2C3 stacking sequence. For P2-Na2/3Ni1/3Mn2/3O2, C2221 (SG 20) was used to account for the slight orthorhombic distortion (b/a = 1.728). The results are further refined using “P3-type stacking faults” to account for anisotropic broadening56 and C1C1 stacking faults. The refined lattice parameters, occupancies and staking fault probabilities are summarized in Tables 1 and 2. Both materials, Na2/3Ni1/3Mn2/3O2 and Na0.60Mn3/4Ni1/4O2, exhibit a honeycomb Ni/Mn ordering. For the latter one, this Ni/Mn ordering is partially disrupted as 27% of the nickel site is occupied by manganese. Please note that a different Ni/Mn ordering for the higher Mn content in Na0.60Mn3/4Ni1/4O2 was evaluated, however, the corresponding simulated ND pattern does not match with the experimentally observed one (ESI Fig. S9†). To evaluate any potential influence of the sodium content on the Ni/Mn superstructure, a third sample, Na2/3Mn3/4Ni1/4O2, was synthesized and characterized respectively. The characterization results for Na2/3Mn3/4Ni1/4O2 are presented in ESI Fig. S10 and ESI Table S7.† Na2/3Mn3/4Ni1/4O2 exhibits a similar honeycomb Ni/Mn ordering as Na0.60Mn3/4Ni1/4O2 with approximately one quarter of the nickel site being occupied by manganese in accordance with the stoichiometry. Therefore, no influence of the sodium content on the Ni/Mn superstructure is observed.
0) reflections at Q = 2.5 Å−1 and Q = 4.3 Å−1 in the XRD pattern suggests a slight orthorhombic distortion of the hexagonal unit cell. Additionally, in both XRD patterns the broadening of (10l) reflections hints at stacking faults. The ND patterns of both samples exhibit reflections between Q = 1.3 Å−1 and Q = 2.4 Å−1, indicating the presence of a Ni/Mn honeycomb ordering with predominantly a C2C3 stacking sequence (compare ESI Fig. S5†). Based on these findings, we performed a joint Rietveld refinement of XRD and ND patterns using the “big unit cell” (P6322, SG 182) with a honeycomb Ni/Mn ordering and a C2C3 stacking sequence. For P2-Na2/3Ni1/3Mn2/3O2, C2221 (SG 20) was used to account for the slight orthorhombic distortion (b/a = 1.728). The results are further refined using “P3-type stacking faults” to account for anisotropic broadening56 and C1C1 stacking faults. The refined lattice parameters, occupancies and staking fault probabilities are summarized in Tables 1 and 2. Both materials, Na2/3Ni1/3Mn2/3O2 and Na0.60Mn3/4Ni1/4O2, exhibit a honeycomb Ni/Mn ordering. For the latter one, this Ni/Mn ordering is partially disrupted as 27% of the nickel site is occupied by manganese. Please note that a different Ni/Mn ordering for the higher Mn content in Na0.60Mn3/4Ni1/4O2 was evaluated, however, the corresponding simulated ND pattern does not match with the experimentally observed one (ESI Fig. S9†). To evaluate any potential influence of the sodium content on the Ni/Mn superstructure, a third sample, Na2/3Mn3/4Ni1/4O2, was synthesized and characterized respectively. The characterization results for Na2/3Mn3/4Ni1/4O2 are presented in ESI Fig. S10 and ESI Table S7.† Na2/3Mn3/4Ni1/4O2 exhibits a similar honeycomb Ni/Mn ordering as Na0.60Mn3/4Ni1/4O2 with approximately one quarter of the nickel site being occupied by manganese in accordance with the stoichiometry. Therefore, no influence of the sodium content on the Ni/Mn superstructure is observed.
| Refinement of ND and XRD patterns using C 222 1 (SG 20) |
|---|
| ND: a = 5.0122(3) Å, b = 8.6626(4) Å, c = 11.1248(2) Å, V = 483.030(35) Å3, Rp = 4.26, GOF = 2.82 |
| XRD: a = 5.0115(0) Å, b = 8.6516(0) Å, c = 11.1540(0) Å, V = 483.613(2) Å3, Rp = 4.40, GOF = 4.43 |
| P3-type SF: 2.0%, C1C1 SF: 4.4% |
| Atom | x | y | z | Occ | B iso |
|---|---|---|---|---|---|
| Na (4a) | 0 | 0 | 0 | 0 | 2.526 |
| Na (8c) | 0 | 1/3 | 0.0054(8) | 0.2987(63) | 2.526 |
| Na (4a) | 0.3230(8) | 0 | 0 | 0.6211(18) | 2.526 |
| Na (8c) | 0.1557(6) | 0.1557(6) | 1/2 | 0.3657(12) | 2.526 |
| Ni (4a) | 0 | 0 | 1/4 | 0.14 | 0.276 |
| Mn (4a) | 0 | 0 | 1/4 | 0.86 | 0.276 |
| Ni (4b) | 0 | 2/3 | 1/4 | 0 | 0.276 |
| Mn (4b) | 0 | 2/3 | 1/4 | 1 | 0.276 |
| Ni (4b) | 0 | 1/3 | 1/4 | 0.92 | 0.276 |
| Mn (4b) | 0 | 1/3 | 1/4 | 0.08 | 0.276 |
| O (8c) | 0.1744(8) | 0.4913(8) | 0.8397(6) | 1 | 1.105 |
| O (8c) | 0.8150(11) | 0.1577(9) | 0.3427(11) | 1 | 1.105 |
| O (8c) | 0.1592(10) | 0.1682(8) | 0.8430(11) | 1 | 1.105 |
| Refinement of ND and XRD patterns using P 6 3 22 (SG 182) |
|---|
| ND: a = 4.9989(7) Å, c = 11.1759(27) Å, V = 241.859(77) Å3, Rp = 5.05, GOF = 2.95 |
| XRD: a = 4.9875(1) Å, c = 11.2192(5) Å, V = 241.694(13) Å3, Rp = 5.35, GOF = 5.31 |
| P3-type SF: 5.6%, C1C1 SF: 0.7% |
| Atom | x | y | z | Occ | B iso |
|---|---|---|---|---|---|
| Na (4f) | 1/3 | 2/3 | −0.0053(26) | 0.2209(36) | 2.526 |
| Na (2a) | 0 | 0 | 0 | 0.2211(35) | 2.526 |
| Na (6g) | 0.3533(3) | 0 | 0 | 0.3790(12) | 2.526 |
| Ni (2c) | 1/3 | 2/3 | 1/4 | 0.7336(7) | 0.276 |
| Mn (2c) | 1/3 | 2/3 | 1/4 | 0.2664(7) | 0.276 |
| Ni (2d) | 1/3 | 2/3 | 3/4 | 0 | 0.276 |
| Mn (2d) | 1/3 | 2/3 | 3/4 | 1 | 0.276 |
| Ni (2b) | 0 | 0 | 1/4 | 0 | 0.276 |
| Mn (2b) | 0 | 0 | 1/4 | 1 | 0.276 |
| O (12i) | 0.3229(8) | 0.3339(9) | 0.8426(11) | 1 | 1.105 |
Electrochemical characterization
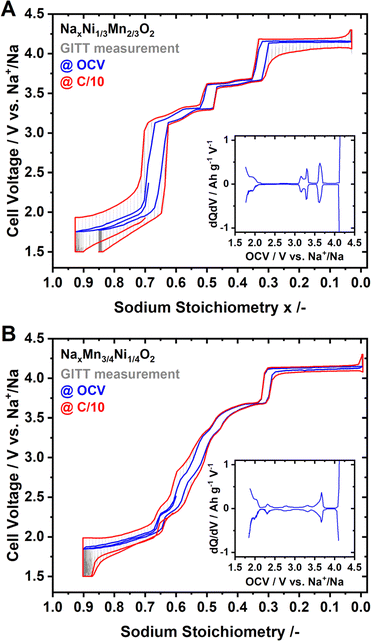
Coin half-cells were assembled using P2-Na2/3Ni1/3Mn2/3O2 or P2-Na0.60Mn3/4Ni1/4O2 as the cathode active material. The galvanostatic intermittent titration technique (GITT) was performed to evaluate the quasi-open circuit voltage (OCV) curve for both materials. The results of the GITT experiments are presented in Fig. 3, where an OCV hull curve is added as a blue line and the on-load hull curve is presented in red colour.For P2-NaxNi1/3Mn2/3O2 both the OCV and on-load voltage curves exhibit distinct voltage jumps at x ≈ 2/3, 1/2 and 1/3 (Fig. 3A). These voltage jumps are accompanied by flat voltage regions as evidenced by the dQ/dV plot (inset of Fig. 3A). In the literature, these voltage jumps are associated with distinct Na+/vacancy orderings.44,46 The flat voltage profiles in proximity to these voltage jumps correspond to order/disorder transitions between unordered and Na+/vacancy ordered phases.48,83,88–92 The voltage profile of P2-NaxMn3/4Ni1/4O2, – both at equilibrium and under current load – is considerably smoother than those of P2-NaxNi1/3Mn2/3O2 (Fig. 3A and B). At the same sodium stoichiometries x = 2/3, 1/2 and 1/3, the voltage profile exhibits small shoulders in accordance with smaller peaks in the dQ/dV analysis (inset of Fig. 3B).
Whereas the nature of the actual Na+/vacancy orderings have been reported in the literature for P2-NaxNi1/3Mn2/3O2, to the best of our knowledge, for P2-NaxMn3/4Ni1/4O2, the nature of Na+/vacancy orderings has not been elucidated so far. However, the similarities in composition and structure suggest similar Na+/vacancy orderings in both materials. The significantly reduced voltage jumps for P2-NaxMn3/4Ni1/4O2 compared to P2-NaxNi1/3Mn2/3O2 hint to partially suppressed or disrupted Na+/vacancy orderings in P2-NaxMn3/4Ni1/4O2.
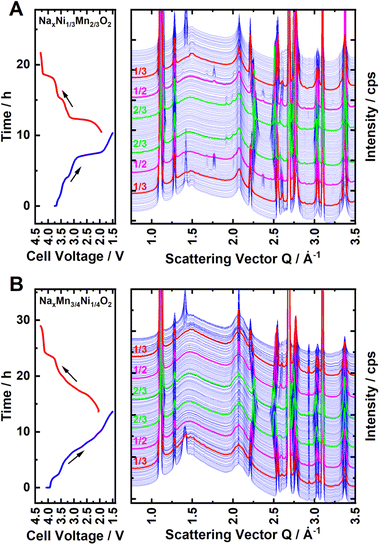
To further investigate the nature and extent of Na+/vacancy orderings in both materials, synchrotron operando XRD measurements were performed. Waterfall diagrams of the obtained diffraction patterns are presented in Fig. 4A and B for P2-NaxNi1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2, respectively. For both materials, the measurements start with sodiation from the charged state. The diffraction patterns corresponding to sodium contents of x = 2/3, 1/2 and 1/3 are highlighted in red, magenta and green colour, respectively. For P2-NaxNi1/3Mn2/3O2, clear superstructure reflections in proximity to the sodium content of x = 2/3, 1/2 and 1/3 are apparent. Simulated diffraction patterns based on the reported in-plane Na+/vacancy ordering by Lee et al.46 and Huang et al.83 are presented in ESI Fig. S11,† in which the range of experimentally found superstructure reflections is highlighted in yellow colour for the ease of comparison. At sodium stoichiometries of x = 2/3 and 1/3, the observed superstructure reflexions match the simulated pattern based on the Na+/vacancy ordering reported by Lee et al.46 For x = 1/2, observed superstructure reflections match the report by Huang et al.83 in accordance with a previous publication.65
For P2-NaxMn3/4Ni1/4O2, similar superstructure reflections in proximity to x = 2/3 and 1/3 are apparent, however, the superstructure reflection at x = 2/3 is very weak. For P2-Na1/2±δMn3/4Ni1/4O2, no superstructure reflection is observed, indicating that no long-range Na+/vacancy ordering exists at this stoichiometry. The comparably low intensity of the Na+/vacancy superstructure reflection in P2-NaxMn3/4Ni1/4O2 is indicative of either decreased long-range order (disrupted ordering) or a smaller weight fraction of the ordered phase (partial ordering). For both materials, the similarity of the superstructure reflection at x = 2/3 and 1/3 supports the assumption that the in-plane Na+/vacancy ordering is the same for both materials. These observations are in accordance with diffraction patterns obtained by ex situ capillary transmission XRD, as presented in ESI Fig. S12.† For both materials, the heat maps of the obtained diffraction patterns as well as the refined lattice parameters (Pawley method) are presented in ESI Fig. S13 and S14.† A good agreement of refined lattice parameters as well as the nature and extent of the detected Na+/vacancy ordering is found for synchrotron operando XRD and ex situ capillary transmission XRD, indicating that the operando measurement is close to equilibrium.
To measure the extent of Na+/vacancy orderings at various stoichiometries, entropymetry measurements were performed. A detailed description of the method is provided in the ESI.† In short, the equilibrium voltage at different sodium contents was measured at 40 °C, 25 °C and 10 °C following a GITT procedure including temperature change at every equilibrium step. The change in measured equilibrium voltage EOCV with the change in temperature ΔT is proportional to the entropy change ΔS at the corresponding sodium content x, according to:
Several factors, such as the configurational entropy, phonon entropy and electronic entropy, can contribute to the entropy change of a material.93 However, the course of the entropy change is reported to be highly dominated by the configurational entropy,93 making entropymetry a valuable tool to investigate it.
The entropy change derived from several independent cells is presented in Fig. 5A and B for P2-NaxNi1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2, respectively. For P2-NaxNi1/3Mn2/3O2, the entropy change curve exhibits a distinct double-S shape in proximity to sodium contents x ≈ 2/3, 1/2 and 1/3. As described in the ESI,† such a double-S shaped course of the entropy change is expected in proximity to Na+/vacancy ordered phases. For P2-NaxMn3/4Ni1/4O2, the entropy change curve follows a double-S shape at x ≈ 2/3, 0.54, 1/2 and 1/3, indicative of Na+/vacancy ordering at these stoichiometries. For P2-NaxMn3/4Ni1/4O2, the variation of entropy change at x ≈ 2/3 and 1/2 is significantly smaller compared to P2-NaxNi1/3Mn2/3O2, indicating a reduced extent of Na+/vacancy orderings in the former material. The double-S shaped course of the entropy change in proximity to x ≈ 0.54 might correspond to a weak Na+/vacancy ordering resembling the reported Na+/vacancy ordering in Na4/7CoO2.90,92,94 We have estimated the expected potential jump based on the measured configurational entropy change and summarized the estimated potential differences due to Na+/vacancy orderings in ESI Table S8.† The results further corroborate more pronounced Na+/vacancy orderings at x = 2/3 and 1/2 for P2-NaxNi1/3Mn2/3O2 compared to P2-NaxMn3/4Ni1/4O2. Furthermore, the measured voltage jumps in GITT measurements (Fig. 3) at x = 2/3, 1/3 in P2-NaxNi1/3Mn2/3O2 and at x = 1/3 in P2-NaxMn3/4Ni1/4O2 significantly exceed the estimated potential jumps due to configurational entropy change (i.e., Na+/vacancy ordering), suggesting additional processes contributing to these voltage jumps. For x = 2/3 in P2-NaxNi1/3Mn2/3O2, the energy difference between Ni2+/3+ redox and Mn3+/4+ redox is expected to significantly contribute to the voltage jump at x = 2/3 in P2-NaxNi1/3Mn2/3O2. For both materials, the onset of the P2–O2 phase transition is expected to contribute to the voltage jump at x = 1/3.
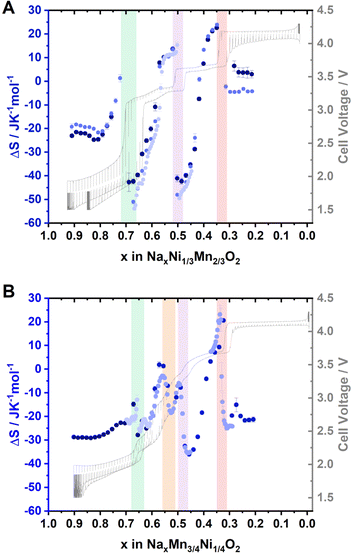 | ||
| Fig. 5 Entropymetry measurements for (A) Na2/3Ni1/3Mn2/3O2 and (B) Na0.60Mn3/4Ni1/4O2. A detailed description of the method is provided in the ESI.† Jumps in the entropy change indicative of Na+/vacancy ordering are highlighted with coloured background. A GITT measurement is provided in grey colour in the background. For both materials, the results from independent cells are presented in different colour. The uncertainty of the linear regression is presented as error bars. | ||
Overall, GITT, operando XRD, ex situ XRD, and entropymetry indicate similar Na+/vacancy orderings at x = 2/3 and 1/3 in P2-NaxNi1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2. For x = 2/3 and x = 1/2, XRD and entropymetry measurements suggest a disrupted Na+/vacancy ordering in P2-NaxMn3/4Ni1/4O2. For x = 1/3, no significant influence of the Ni/Mn ratio on the Na+/vacancy ordering is detected.
In general, Na+/vacancy orderings in these structures result from the high stability (low Gibbs free enthalpy) of the ordered configurations. In Na+/vacancy ordered phases, Gibbs free enthalpy is eventually reduced by (i) minimized Na+–Na+ repulsion within the sodium layer and (ii) advantageous interaction of Na+ with the immediate environment of the MO2 slab (i.e., low energy sodium lattice sites). For the herein investigated materials, the transition metals, nickel and manganese, are known to adopt different formal oxidation states depending on the applied electrode potential.50,87 Hence, the stability of sodium sites is eventually influenced by the transition metals in the immediate environment and the formal oxidation states thereof. The resulting difference in energy for various sodium sites potentially contributes to the preferential occupation of these sites (i.e., preferential occupation of low-energy sodium sites).
Computational
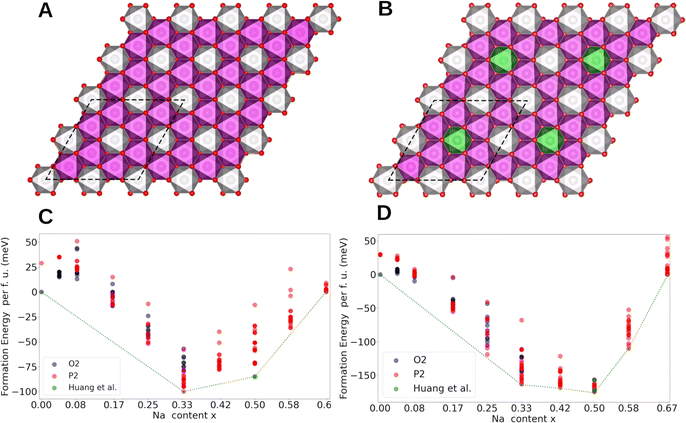
Computational methods were employed to gain further insights into the origin of Na+/vacancy orderings in P2-NaxNi1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2. First, we identify the thermodynamically stable phases. Then, we evaluate the electronic structure and the charge density distribution of the transition metals in these materials. Subsequently, we evaluate the existence of low-energy sodium lattice sites in the absence of Na+–Na+ repulsion. Finally, we analyse the charge ordering within the MO2 slab and correlate these findings with the existence and stability of Na+/vacancy orderings.Spin polarized periodic DFT calculations were performed to determine the thermodynamically stable phases and construct the convex hull for P2-NaxNi1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2. For P2-NaxNi1/3Mn2/3O2, the implemented unit cell includes 24 transition metal atoms arranged in a characteristic honeycomb Ni/Mn ordering in accordance with our characterization results and the literature60 (Fig. 6A). By substituting every fourth Ni by Mn, the unit cell for P2-NaxMn3/4Ni1/4O2 with a defect honeycomb transition metal ordering is obtained according to the characterization results (Fig. 6B). Even though the in-plane sodium arrangement has been reported for the Na+/vacancy orderings at x = 2/3, 1/2 and 1/3 in P2-NaxNi1/3Mn2/3O2,46 to the best of our knowledge, the relation of this in-plane sodium ordering to the honeycomb ordered MO2 slabs has not been analysed so far. To fill this gap, we have calculated the free enthalpy for the reported in-plane sodium vacancy orderings at various sites in these large Ni/Mn ordered superstructure cells. The calculated convex hull is presented in Fig. 6C and D for P2-NaxNi1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2, respectively. For P2-NaxNi1/3Mn2/3O2, solely the O2-structure at x = 0 and the Na+/vacancy ordered P2-structures at x = 1/3, 1/2 and 2/3 are located on the convex hull. At x = 1/2, the Na+/vacancy ordering, as reported by Huang et al.,83 was calculated to be energetically favourable, which is in accordance with our operando XRD results and literature reports for Na1/2CoO2.90,91,95–99 At x = 2/3, the determined stable structure exhibits the same in-plane Na+/vacancy ordering;98,99 however, the stacking sequence differs from reports on P2-Na2/3CoO2.90,100,101 For P2-NaxMn3/4Ni1/4O2, the O2-structure at x = 0 and the P2-structures at x = 1/3, 5/12, 1/2, 7/12 and 2/3 are located on the convex hull. At x = 1/2, the reported ordering by Lee et al.46 was calculated to be slightly more stable than the ordering reported by Huang et al.83 The marginal difference in energy between both orderings is in accordance with the disrupted Na+/vacancy ordering observed with operando XRD and entropymetry measurements.
In general, configurations located on the convex hull (Fig. 6C and D) are stable, whereas all configurations with formation enthalpies above the convex hull are unstable or metastable. The convex hull directly relates to the enthalpy difference between sodium in intercalated and metallic form, whereas the measured OCV curve, as presented in Fig. 3, represents the Gibb's free energy (enthalpic plus entropic contribution) of the same reaction. In the convex hull, segments of solely unstable configurations (e.g., 0 < x < 1/3 in P2-NaxNi1/3Mn2/3O2) represent a miscibility gap between the respective stable endmembers (e.g., O2-Na0Ni1/3Mn2/3O2 and P2-Na1/3Ni1/3Mn2/3O2). The corresponding two-phase reaction results in a characteristic voltage plateau in the electrochemical potential profile.102 Overall, the calculated convex hull well describes the course of the experimentally determined OCV curve, suggesting that the enthalpy change dominates the course of the Gibb's free energy, however, small differences between the convex hull and the experimentally derived OCV curve exist. For P2-NaxNi1/3Mn2/3O2 (Fig. 6C), the miscibility gap in the ranges 1/3 < x < 1/2 and 1/2 < x < 2/3 is expected to cause a voltage plateau. Experimentally, we find two small voltage plateaus associated with the order/disorder transitions in proximity to the respective Na+/vacancy orderings and observe distinct voltage jumps for Na+/vacancy ordered phases. The difference between the expected potential profile based on the convex hull and the measured voltage profile eventually arises from (finite) temperature effects. For P2-NaxMn3/4Ni1/4O2 (Fig. 6D), no miscibility gap is expected between 1/3 < x < 2/3 based on the convex hull in line with the much smoother electrochemical voltage profile in Fig. 3B.
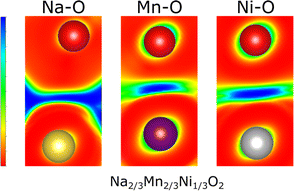
To elucidate the nature of the M–O and Na–O bonds, Density Overlap Regions Indicators (DORI)103 were determined for P2-Na2/3Ni1/3Mn2/3O2 as presented in Fig. 7. The DORI analysis was developed to distinguish covalent from noncovalent interactions, while differences between metallic and ionic bonding cannot be resolved. In this framework, covalent interactions are revealed by localized overlap indicators, while noncovalent interactions are characterized by fully smeared out overlap indicators. This analysis is not restricted to interactions in molecules as similar bonding characteristics exist in solids and DORI was already successfully applied to Mn-oxides.104
Hence, the DORI analysis in Fig. 7 allows tracking qualitative differences in bonding character between the different bonds in the system. Qualitatively identical results were observed independent of Na content and the Ni/Mn ratio and are depicted in ESI Fig. S15.† While the Mn–O and Ni–O bonds are characterized by localized basins of DORI values close to 1, indicating increased covalent character, the Na–O bonds show entirely smeared out overlap indicators implying ionic bonding. The revealed covalent nature of the M–O bond is in good agreement with what has been found for many other comparable oxides104,105 and corresponds to a distribution of the electron density along the M–O bond. Thus, only formal oxidation states, which do not necessarily agree with the true charge at the ion, can be assigned. This observation is in accordance with the calculated Bader charges, which indicate lower electron density at the transition metal ion than that suggested by the formal oxidation state (see Table 3).
| Na content x | Mn | Ni | ||||
|---|---|---|---|---|---|---|
| μ [μB] | Bader [e−] | OS | μ [μB] | Bader [e−] | OS | |
| Na x Ni 1/3 Mn 2/3 O 2 | ||||||
| 1/3 | 3.19 | 1.84 | 4+ | 1.20 | 1.32 | 3+ |
| 1/2 (Lee)46 | 3.18 | 1.84 | 4+ | 1.18; 1.73 | 1.21; 1.31 | 2+; 3+ |
| 1/2 (Huang)83 | 3.18 | 1.84 | 4+ | 1.18; 1.76 | 1.21; 1.31 | 2+; 3+ |
| 2/3 | 3.19 | 1.84 | 4+ | 1.76 | 1.20 | 2+ |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Na x Mn 3/4 Ni 1/4 O 2 | ||||||
| 1/3 | 3.21 | 1.84 | 4+ | 1.19; 1.76 | 1.22; 1.36 | 2+; 3+ |
| 1/2 (Lee)46 | 3.19 | 1.84 | 4+ | 1.76 | 1.21 | 2+ |
| 1/2 (Huang)83 | 3.19 | 1.84 | 4+ | 1.76 | 1.21 | 2+ |
| 2/3 | 3.21; 3.86 | 1.70; 1.83 | 3+; 4+ | 1.76 | 1.21 | 2+ |
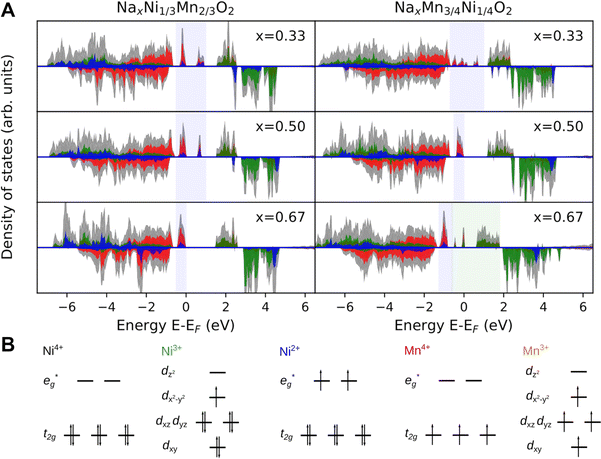
To further elucidate the nature of the M–O bonding, we determined the partial density of states (PDOS) shown in Fig. 8A. Indeed, no Na 2s states are found in the valence band region in agreement with the ionic character of the Na–O bond. In contrast, the M-3d states are found to strongly hybridise with the O-2sp3 states in the valence band region, possibly indicating the prevalence of covalent bonding in the MO2 layer. While this supports the simplified picture of the Na atoms donating their electrons to the MO2 layer, it raises the question of the charge density distribution in the MO2 slab. Specifically, it is of interest whether electrons (e−) are entirely localized in M–O bonds or whether they are delocalized over several transition metal atoms. In fact, transition metal compounds are well known to delocalize electrons through direct exchange or super exchange interactions.106 In the present case, however, no direct overlap between metal 3d orbitals are possible owing to the long metal–metal distance and the ferromagnetic coupling between ions. Instead, delocalisation is achieved through a super-exchange interaction whereby electrons are delocalized through an at least partially covalent M–O–M two electron three center (2e3c) bond. This is a well known bonding scheme in inorganic chemistry106,107 which has also been observed for related compounds such as manganese hydroxo complexes108 and Cu2O.105,109 These observations suggest that similar bonding characteristics can possibly lead to delocalization of e− also in the here investigated samples.
For P2-NaxNi1/3Mn2/3O2 (Fig. 8A), independent of Na content, the low spin Ni t2g orbitals are fully occupied in both spin majority and minority directions and are found in the range from −6 eV to 0 eV. The Ni 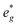 orbitals are either empty (x = 0) and form the conduction band or are partially occupied (x > 0) and situated below the Fermi level, depending on the Na content in the structure. During sodiation of NaxNi1/3Mn2/3O2, first the low lying Ni
orbitals are either empty (x = 0) and form the conduction band or are partially occupied (x > 0) and situated below the Fermi level, depending on the Na content in the structure. During sodiation of NaxNi1/3Mn2/3O2, first the low lying Ni 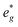 are partially occupied and shifted below the Fermi energy. At a sodium content of x = 1/3 the Ni atoms are formally Ni3+ and undergo a Jahn–Teller splitting of the
are partially occupied and shifted below the Fermi energy. At a sodium content of x = 1/3 the Ni atoms are formally Ni3+ and undergo a Jahn–Teller splitting of the 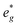 into occupied dx2−y2 and unoccupied dz2 states (Fig. 8B). This is followed by further reduction of Ni from Ni3+ to Ni2+ with increasing Na content leading to fully occupied Ni
into occupied dx2−y2 and unoccupied dz2 states (Fig. 8B). This is followed by further reduction of Ni from Ni3+ to Ni2+ with increasing Na content leading to fully occupied Ni 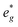 states at a Na content of x = 2/3. Independent of the sodium content x (2/3 > x > 0), Mn t2g orbitals are fully occupied in the spin majority direction and empty in the spin minority direction and are found in the range between −6 eV and 0 eV. The Mn
states at a Na content of x = 2/3. Independent of the sodium content x (2/3 > x > 0), Mn t2g orbitals are fully occupied in the spin majority direction and empty in the spin minority direction and are found in the range between −6 eV and 0 eV. The Mn 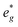 orbitals are situated between 1.5 eV and 2.5 eV independent of the Na content x and hence do not contribute to the electrochemical processes in this material (0 < x < 2/3). The significant potential jump at x = 2/3, as observed in GITT measurements (Fig. 3), is qualitatively supported by the observed energy difference between Ni
orbitals are situated between 1.5 eV and 2.5 eV independent of the Na content x and hence do not contribute to the electrochemical processes in this material (0 < x < 2/3). The significant potential jump at x = 2/3, as observed in GITT measurements (Fig. 3), is qualitatively supported by the observed energy difference between Ni 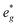 and Mn
and Mn 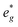 states in PDOS.
states in PDOS.
In P2-NaxMn3/4Ni1/4O2, PDOS features appear similar, however, they are shifted in sodium content. Due to the reduced Ni content in NaxMn3/4Ni1/4O2, the respective Ni redox processes are shifted to lower Na contents and Ni 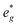 is fully occupied at x = 1/2. For x = 2/3, the Mn
is fully occupied at x = 1/2. For x = 2/3, the Mn 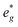 orbitals are partially occupied and shifted below the Fermi level. With increasing sodium content, the continuously increasing occupation of the Ni
orbitals are partially occupied and shifted below the Fermi level. With increasing sodium content, the continuously increasing occupation of the Ni 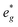 and Mn
and Mn 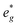 can be rationalized considering octahedral crystal field splitting (Fig. 8B) in conjunction with the formal oxidation states of the transition metal centre. Thus, sodiation beyond x = 1/2 leads to Mn redox activity and the formation of Jahn–Teller active Mn3+ by partial occupation of Mn
can be rationalized considering octahedral crystal field splitting (Fig. 8B) in conjunction with the formal oxidation states of the transition metal centre. Thus, sodiation beyond x = 1/2 leads to Mn redox activity and the formation of Jahn–Teller active Mn3+ by partial occupation of Mn 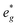 states.
states.
To corroborate the observations in the PDOS, we have analysed local magnetic moments μ and Bader charges of the transition metal atoms and summarized the results in Table 3. The local magnetic moment allows distinguishing between transition metals of different formal oxidation states based on the number of unpaired electrons expected from the crystal field splitting as presented in Fig. 8B. In contrast, Bader charges are determined by charge partitioning of the charge density obtained using DFT and yield qualitative trends for charge situated at the transition metal centre. Despite their fundamentally different methodologies, both methods show similar trends in agreement with the analysis of the PDOS.
For P2-NaxNi1/3Mn2/3O2, with increasing sodium content, the local magnetic moment increases and Bader charges decrease for Ni, whereas both values remain invariant for Mn. Hence, with increasing sodium content, Ni is gradually reduced from Ni3+ at x = 1/3 to Ni2+ at x = 2/3, while Mn is redox inactive. At x = 1/2, Ni3+ and Ni2+ are detected in equal amounts.
For P2-NixMn3/4Ni1/4O2, with increasing sodium content, the local magnetic moment increases and the Bader charges decrease for Ni from x = 1/3 to x = 1/2, whereas Mn remains invariant within this sodium range. Further sodiation from x = 1/2 to x = 2/3, leads to increasing local magnetic moment and decreasing Bader charges for Mn, whereas Ni is invariant. Hence, Ni is redox active for x < 1/2 and Mn is redox active at sodium contents x > 1/2.
Overall, the analysis of PDOS, the local magnetic moment μ and Bader charges, suggest that charge within the MO2 slab is considerably localized at the covalently bonded transition metals, making formal oxidation states an acceptable descriptor for P2-NaxNi1/3Mn2/3O2 and P2-NixMn3/4Ni1/4O2. Please note that similar charge disproportionation has been reported for P2-NaxCoO2 and O′3-NaxMnO2 with experimental and computational methods.83,95–97,110–112
As described above, various transition metal oxidation states within the MO2 slab potentially result in low energy sodium sites. The interplay between the preferential occupation of these low energy sodium sites and Na+–Na+ repulsion eventually results in Na+/vacancy orderings. To deconvolute these two effects, we have calculated sodium site energies at a high vacancy limit by placing one sodium atom in a supercell with 24 transition metals (x = 1/24). The supercell volume was fixed to the one of a calculated, hypothetical empty P2-structure. Subsequently, we analysed the difference in energy between the respective site and the lowest energy site. Since only one sodium atom is placed within the large supercell, Na+–Na+ repulsion can be neglected and solely the influence of the immediate environment is modelled. Please note that these structures constitute a model system and do not reflect the experimentally found configurations (P2–O2 two-phase reaction).
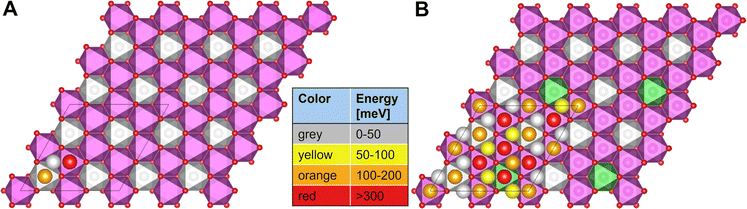
For P2-NaxNi1/3Mn2/3O2, the honeycomb arrangement of the metal atoms distinguishes the Naf sites in NaMn–Mnf and NaMn–Nif that either sit in between two Mn octahedra (Mn–Na–Mn dumbbell) or in between a Ni and a Mn octahedra (Ni–Na–Mn dumbbell), respectively, while all Nae are equivalent. In P2-Na1/24Ni1/3Mn2/3O2, the sodium site energies follow the trend Nae < NaMn–Nif < NaMn–Mnf as presented in Fig. 9A. This qualitative trend can be rationalized when considering that the insertion of one Na atom leads to the reduction of one Ni centre from Ni4+ to Ni3+. Since the Na–O bond is ionic, Na+ interacts with the charge density distribution in the MO2 slab and Na sites in vicinity of Ni centres are beneficial due to their lower formal oxidation state. In P2-Ni1/24Mn3/4Ni1/4O2, the substitution of 1/12 of the Ni atoms by Mn atoms leads to further inequivalence of the Na sites when the nearest neighbour transition metals are considered, which is reflected in the sodium site energies as presented in Fig. 9B. The Na site energy is substantially increased for Naf sites in Mn–Na–Mn dumbbells and the surrounding Nae sites. This phenomenon is caused by the redox-inactive nature of the Mn atoms at such small sodium contents. Mn atoms remain in the formal 4+ oxidation state and therefore lead to significant electrostatic repulsion of the adjacent Na cations. The charge is compensated by a reduction of nearest-neighbour Ni atoms, which are considerably far from the particular high-energy sodium lattice sites. Overall, the calculated sodium site energies suggest preferential occupation of Nae sites over Naf sites in accordance with expectations based on Pauling's principles.63 For P2-NaxNi1/3Mn2/3O2 (Fig. 9A), two energetically different Naf sites are available, which arrange in a distinct pattern. For P2-NixMn3/4Ni1/4O2 (Fig. 9B), additional Mn–Na–Mn dumbbells result in an energy penalty for corresponding Naf sites and adjacent Nae sites. For P2-NixMn3/4Ni1/4O2, the simple site energy pattern, as observed for P2-NaxNi1/3Mn2/3O2, is disrupted. In this model experiment, site energies differ in more than 200 mV, suggesting a potentially strong influence of site energies on Na+/vacancy orderings.
Encouraged by these results, we have analysed the most stable structures for x = 2/3, 1/2 and 1/3 in terms of charge ordering within the MO2 slab and its relation to Na+/vacancy ordering. Please note that the analysed structures are in accordance with the experimental characterization and therefore most likely resemble the physical reality. Respective structure files are provided in the ESI.† A depiction of the calculated most stable structures following the in-plane Na+/vacancy orderings as reported by Lee et al.46 is presented in Fig. 10A and B for P2-NaxNi1/3Mn2/3O2 and P2-NixMn3/4Ni1/4O2, respectively. For x = 1/2, an additional comparison between the Na+/vacancy orderings reported by Lee et al.46 and Huang et al.83 is presented in ESI Fig. S16.† In both figures, the three-dimensional crystal structure is presented as stacking of three slices with [0 0 1] orientation. Charge ordering within the transition metal slab as derived from magnetic moments and Bader charges (Table 3) is depicted in the colour code. In-plane Na+/vacancy orderings are presented in red colour for occupied Naf sites and petrol colour for occupied Nae sites (following the colour code in the publication by Lee et al.46). Occupied sodium sites are categorized by their closest neighbour transition metals and the respective oxidation state.
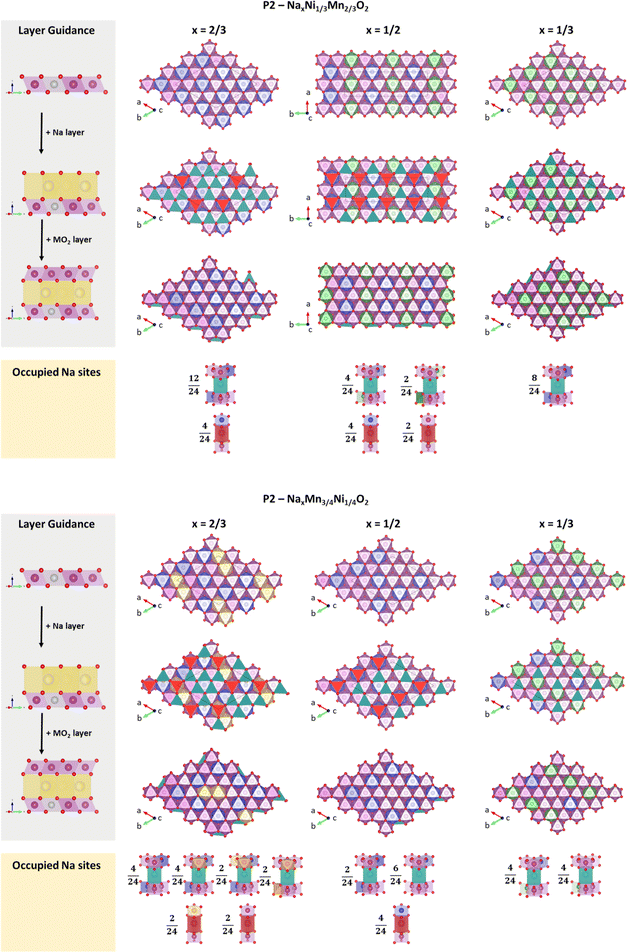 | ||
| Fig. 10 Most stable structures following the in-plane Na+/vacancy ordering reported by Lee et al.46 in relation to the respective transition metal charge ordering for (A) P2-NaxNi1/3Mn2/3O2 and (B) P2-NaxMn3/4Ni1/4O2. Ni2+, Ni3+, Mn3+ and Mn4+ are presented in blue, green, yellow and magenta colour, respectively. Occupied Nae sites are presented in petrol colour and Naf sites are presented in red colour. | ||
Orderings following Lee et al.46 (Fig. 10) – for P2-NaxNi1/3Mn2/3O2, solely Ni2+ and Ni3+ next to Mn4+ are observed at x = 2/3 and 1/3, respectively, resulting in simple hexagonal charge orderings within the MO2 slab. At x = 1/2, Ni2+ and Ni3+ arrange in alternating lines, which is in contrast to a more homogeneous charge distribution within the MO2 slab following a hexagonal pattern. A similar charge ordering in lines has been observed for Na1/2CoO2.83,95–97 For P2-NixMn3/4Ni1/4O2, the change in Ni/Mn stoichiometry leads to a shift to lower oxidation states as discussed above. At x = 2/3, the addition of manganese to the structure leads to two adjacent Mn3+ atoms. At x = 1/2, solely Ni2+ and Mn4+ is present. At x = 1/3, a line ordering of Ni3+ and Ni2+/Mn4+ is observed. Overall, the simple charge orderings observed in P2-NaxNi1/3Mn2/3O2 are disrupted in P2-NixMn3/4Ni1/4O2. As a result of the simple charge orderings in P2-NaxNi1/3Mn2/3O2, Naf sites are exclusively occupied if one of the nearest neighbour transition metals is Ni2+. For each sodium stoichiometry, all occupied Nae sites exhibit the same transition metal oxidation state environment. For P2-NixMn3/4Ni1/4O2, the disrupted charge ordering within the MO2 slab causes more diverse nearest-neighbour environments for occupied Nae and Naf sites.
Ordering following Huang et al.83 (ESI Fig. S16†) – for both P2-Na1/2Ni1/3Mn2/3O2 and P2-Na1/2Mn3/4Ni1/4O2, we find the same transition metal charge orderings for the in-plane Na+/vacancy ordering reported by Huang et al.83 and Lee et al.46 Independent of the Ni/Mn ratio, two Naf sites with different nearest-neighbour environments (Mn4+–Na+f–Ni2+ and Mn4+–Na+f–Mn4+) and two energetically different Nae sites are occupied. The nearest-neighbour environment of these Nae sites is influenced by the Ni/Mn ratio, eventually influencing the stability of the Na+/vacancy ordering.
Comparison of evaluated Na+/vacancy orderings at x = 1/2 – both operando XRD experiments and DFT calculations indicate that the Na+/vacancy ordering as reported by Huang et al.83 is present in P2-Na1/2Ni1/3Mn2/3O2. For P2-Na1/2Mn3/4Ni1/4O2, no indication for long-range Na+/vacancy ordering is found in operando XRD experiments and DFT calculations suggest a marginal energy benefit for the ordering reported by Lee et al.46 Please note that the ordering reported by Huang et al.83 incorporates a lower fraction of Nae sites (Nae/Naf = 1) compared to the reported in-plane Na+/vacancy ordering by Lee et al.46 (Nae/Naf = 2). Furthermore, the ordering reported by Huang et al.83 is characteristic for increased mean squared Na+–Na+ distances, resulting in an energy benefit by minimizing in-plane Na+–Na+ repulsion. For P2-Na1/2Ni1/3Mn2/3O2, the minimized Na+–Na+ repulsion (Huang ordering) seems to prevail over the effect of low energy sodium sites (Lee ordering). For P2-Na1/2Mn3/4Ni1/4O2, the disruption of the transition metal charge ordering destabilizes the ordering reported by Huang et al.83 As a result, none of both Na+/vacancy orderings results in a significant energy gain and long-range Na+/vacancy ordering is disrupted.
Influence of Ni/Mn stoichiometry on Na+/vacancy orderings – if we compare the same Na+/vacancy ordered structure for P2-NaxNi1/3Mn2/3O2 and P2-NaxMn3/4Ni1/4O2 (vertical comparison in Fig. 10 and ESI fig. S16†), Na+–Na+ distances remain constant. Therefore, the relative stability of the compared Na+/vacancy orderings is solely influenced by the transition metal environment. At x = 2/3, the decrease in the Ni/Mn ratio from P2-NaxNi1/3Mn2/3O2 to P2-NaxMn3/4Ni1/4O2 leads to the occupation of energetically more diverse sodium sites. Consequently, the Na+/vacancy ordering is partially disrupted in P2-NixMn3/4Ni1/4O2. At x = 1/2, the transition metal charge ordering in rows in P2-NaxNi1/3Mn2/3O2 is disrupted when the Ni/Mn ratio is increased (P2-NaxMn3/4Ni1/4O2). As a result, the energy benefit of the Huang ordering is lost and any long-range Na+/vacancy ordering is suppressed. At x = 1/3, no influence of the Ni/Mn ratio and the transition metal charge ordering on Na+/vacancy ordering is found. Enabled by the relatively low sodium content, only low energy sodium sites are occupied in both materials and we conclude that Na+/vacancy ordering at x = 1/3 is dominated by the effect of Na+–Na+ repulsion.
Guideline and discussion
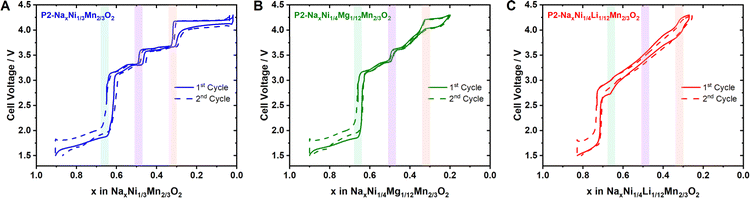
Based on the above findings, we can deduce that the Na+/vacancy orderings in P2-type NaxMO2 at sodium contents of x = 2/3 and 1/2 are considerably influenced by the charge ordering in the MO2 slab. Therefore, these Na+/vacancy orderings can be suppressed if the transition metal charge orderings are disrupted. The Na+/vacancy ordering at x = 1/3 is dominated by Na+–Na+ repulsion and therefore is largely independent of charge ordering within the MO2 slab.To crosscheck this hypothesis, we have synthesized P2-Na2/3Ni1/4Mg1/12Mn2/3O2 and P2-Na3/4Ni1/4Li1/12Mn2/3O2. Within the applied potential range (1.5–4.3 V), Li+ and Mg2+ remain redox inactive.113–115 For P2-Na2/3Ni1/4Mg1/12Mn2/3O2, the expected formal oxidation states (assuming Na+ and O2−) are Na2/3Ni1/4IIMg1/12IIMn2/3IVO2. According to Delmas et al.58 the hexagonal transition metal ordering within the MO2 slab results from the difference in ionic radii during synthesis. Based on the ionic radii (Ni2+ = 0.69 Å, Mg2+ = 0.72 Å, and Mn4+ = 0.53 Å),116 we anticipate hexagonal ordering of small Mn4+ ions surrounding larger Ni2+ & Mg2+ ions. This honeycomb ordering is in accordance with literature reports.51,60
As a result, we expect the following formal oxidation states at x = 2/3, 1/2 and 1/3: Na2/3[Ni1/4IIMg1/12II]Mn2/3IVO2, Na1/2[Ni1/12IINi2/12IIIMg1/12II]Mn2/3IVO2 and Na1/3[Ni2/12IIINi1/12IVMg1/12II]Mn2/3IVO2 (“C1 site” in parenthesis). Therefore, a perfect honeycomb charge ordering is expected at x = 2/3, whereas a disrupted charge ordering is expected for x = 1/2 and 1/3. Following our guideline, we expect a potential jump caused by Na+/vacancy ordering at x = 2/3 and a potential shoulder at x = 1/2. As discussed above, no effect of charge ordering on the Na+/vacancy ordering at x = 1/3 is expected. The corresponding first cycle potential profile is presented in Fig. 11B. In accordance with literature reports,51,113,117,118 the potential profile exhibits a distinct jump at x = 2/3 (approx. 3.0 V) and a smoothed jump at x = 1/2 (approx. 3.5 V). Similar to P2-Na2/3Ni1/3Mn2/3O2, the change from Ni2+/3+ to Mn3+/4+ redox most likely contributes to the significant voltage jump at x = 2/3.
For P2-Na3/4Ni1/4IILi1/12IMnIV2/3O2, the expected formal oxidation states are Na3/4Ni1/4IILi1/12IMn2/3IVO2, resulting in a hexagonal ordering of large Ni2+ & Li+ (Li+ = 0.76 Å)116 surrounded by small Mn4+ within the MO2 slab. In accordance with the literature,113 superstructure reflections in the XRD pattern support the honeycomb superstructure within the MO2 slab (ESI Fig. S17†). At the relevant sodium contents for Na+/vacancy ordering, the corresponding formal oxidation states are Na2/3[Ni1/6IINi1/12IIILi1/12I]Mn2/3IVO2, Na1/2[Ni1/4IIILi1/12I]Mn2/3IVO2 and Na1/3[Ni1/12IIINi1/6IVLi1/12I]Mn2/3IVO2. Following the guideline above, we expect highly disrupted charge ordering at x = 2/3, 1/2 and 1/3, leading to a considerably smooth potential profile for x > 1/3. The corresponding first cycle potential profile, as presented in Fig. 11C, is smooth and solely exhibits a small shoulder at x = 2/3 and a slight jump at x = 1/3 in accordance with earlier reports.113,115,119 The significant voltage jump at x = 3/4 is most likely caused by the transition from Ni2+/3+ to Mn3+/4+ redox.
Further results, obtained by Al substitution for either Ni or Mn in P2-Na2/3Ni1/3Mn2/3O2, are presented in ESI Fig. S19.† Al substitution for Mn is expected to have only minor effects on the transition metal charge ordering in the MO2 slab. Experimentally, we find no significant impact on the potential jumps indicative for Na+/vacancy orderings at x = 2/3, 1/2 and 1/3. In contrast, Al substitution for Ni is expected to disrupt the transition metal charge ordering in the MO2 slab. The experimentally found potential profile is significantly smoothened at x = 2/3 and 1/2 in accordance with earlier reports.120
The experimentally observed potential profiles for the undoped, Mg- and Li-doped samples (Fig. 11), as well as Al-substitutions (ESI Fig. S19†), comply with the expectations based on the herein postulated guideline, underlining the significant impact of transition metal charge ordering on Na+/vacancy ordering. The cycling stability of the undoped, Mg- and Li-doped samples increases with decreasing tendency for Na+/vacancy ordering (ESI Fig. S20†). Analogously to the above-discussed materials, the herein postulated guideline also holds for Zn-113,121 and Cu-doping.113,122–124
High entropy materials – lately, “high entropy” materials are explored as promising future cathode materials.125–130 Per definition, high entropy materials are single-phase materials consisting of at least five (near)-equimolar species, resulting in an ideal configurational entropy Sideal ≥ 1.609 kB per transition metal site, where kB is the Boltzmann constant.125,131,132 In view of this work, the tendency for a smooth potential profile of “high entropy layered sodium transition metal oxides” can be rationalized. The presence of various transition metals with diverse formal oxidation states eliminates long-range charge ordering, which then results in suppressed Na+/vacancy orderings and a smooth potential profile. Please note that high entropy cathode materials may exhibit further potential advantages, such as minimized strain or enhanced solid diffusion,125,130,133–138 which are beyond the scope of this work.
Conclusion
Within this work, we have demonstrated the significance of charge ordering within the transition metal slab on the presence and extent of Na+/vacancy orderings in P2-type cathode materials for sodium-ion batteries. Simple charge ordering patterns within the MO2 slab support the tendency towards Na+/vacancy orderings. Disrupted charge ordering patterns lead to disrupted or suppressed Na+/vacancy orderings.The herein proposed guideline enables the prediction of Na+/vacancy orderings and the associated potential jumps solely on the transition metal composition, the consideration of formal oxidation states and well-known atomic crystal radii. In the first step, the presence of a honeycomb transition metal superstructure is analysed based on either experimental data or by considering the formal oxidation states and ionic radii of the transition metals in the as-synthesized material. In the second step, the formal oxidation states of the transition metals are calculated for sodium stoichiometries x = 2/3, 1/2 and 1/3. Combining the structural information (e.g., honeycomb superstructure ordering within the MO2 slab) with the formal oxidation states enables the prediction of charge ordering and, as a consequence, the tendency for Na+/vacancy ordering.
Besides estimating the tendency for detrimental Na+/vacancy orderings in a given transition metal composition, this rather simple framework can as well serve to design and optimize cathode compositions with suppressed Na+/vacancy orderings and therefore improved long-term cycling stability.
Data availability
Experimental data, including diffraction data and electrochemical data, are publicly available via the zenodo repository at https://doi.org/10.5281/zenodo.13911290. The complete computational data sets are available via the NOMAD repository at https://doi.org/10.17172/NOMAD/2024.10.10-2.Author contributions
L. F. P. – writing original draft, conceptualization, formal analysis, methodology, visualization. M. D. – writing original draft, conceptualization, formal analysis, methodology, visualization. N. B. – investigation, software, formal analysis, methodology. P. B. – formal analysis, software. D. R. – investigation, formal analysis. M. Z. – investigation, data curation. P. D. – investigation. C. H. – investigation. D. M. – investigation, data curation. A. O. – investigation, data curation. V. B. – investigation, resources. N. P. – resources, formal analysis. M. S. – investigation, formal analysis, visualization. M. B. – investigation, formal analysis, methodology. M. W. M. – supervision, funding acquisition, methodology. A. G. – supervision, funding acquisition. S. P. – supervision, project administration, funding acquisition. P. A. – supervision, project administration, funding acquisition. All authors reviewed and edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the German Federal Ministry of Education and Research (BMBF) in the projects TRANSITION (03XP0186C, 03XP0186A), transition transfer (03XP0533A, 03XP0533B) and ExcellBattMat (03XP0257A, 03XP0257C and 03XP0254D) and by the German Research Foundation (DFG) in the project POLIS Cluster of Excellence (ProjectID 390874152). Computational resources have been provided by the state of Baden-Wuerttemberg through bwHPC and the German Research Foundation (DFG) through Grant No. INST 40/575-1 FUGG (JUSTUS 2 cluster). Neutron diffraction measurements were carried out at the CANAM infrastructure of the NPI CAS Rez using the CICRR infrastructure supported by MEYS project LM2023041, both of which are acknowledged. We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at the P02.1 beamline. The authors thank Gisela Arnold (ZSW) for ICP-OES analysis and Wolfgang Weirather (ZSW) for precipitation of hydroxide precursors.References
- IPCC, Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Geneva, Switzerland, ed. Core Writing Team, H. Lee and J. Romero, 2023, p. 184, DOI:10.59327/IPCC/AR6-9789291691647.
- S. Passerini, L. Barelli, M. Baumann, J. Peters and M. Weil, Emerging Battery Technologies to Boost the Clean Energy Transition, Springer International Publishing, Cham, 2024 Search PubMed.
- T. M. Gür, Energy Environ. Sci., 2018, 11, 2696–2767 RSC.
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- M. Armand, P. Axmann, D. Bresser, M. Copley, K. Edström, C. Ekberg, D. Guyomard, B. Lestriez, P. Novák, M. Petranikova, W. Porcher, S. Trabesinger, M. Wohlfahrt-Mehrens and H. Zhang, J. Power Sources, 2020, 479, 228708 CrossRef CAS.
- European Commission, Directorate General for Internal Market, Industry, Entrepreneurship and SMEs., Study on the Critical Raw Materials for the EU 2023: Final Report, Publications Office, 2023 Search PubMed.
- L. Boer, A. Pescatori and M. Stuermer, Discussion Papers 1976, 2021, https://www.diw.de/de/diw_01.c.826751.de/publikationen/diskussionspapiere/2021_1976/energy_transition_metals.html Search PubMed.
- International Energy Agency (IEA), The Role of Critical Minerals in Clean Energy Transitions, World Energy Outlook Special Report, 2021 Search PubMed.
- D. Gielen, Critical Materials for the Energy Transition, International Renewable Energy Agency, [Abu Dhabi], 2021 Search PubMed.
- N. Tapia-Ruiz, A. R. Armstrong, H. Alptekin, M. A. Amores, H. Au, J. Barker, R. Boston, W. R. Brant, J. M. Brittain, Y. Chen, M. Chhowalla, Y.-S. Choi, S. I. R. Costa, M. C. Ribadeneyra, S. A. Cussen, E. J. Cussen, W. I. F. David, A. V. Desai, S. A. M. Dickson, E. I. Eweka, J. D. Forero-Saboya, C. P. Grey, J. M. Griffin, P. Gross, X. Hua, J. T. S. Irvine, P. Johansson, M. O. Jones, M. Karlsmo, E. Kendrick, E. Kim, O. V. Kolosov, Z. Li, S. F. L. Mertens, R. Mogensen, L. Monconduit, R. E. Morris, A. J. Naylor, S. Nikman, C. A. O'Keefe, D. M. C. Ould, R. G. Palgrave, P. Poizot, A. Ponrouch, S. Renault, E. M. Reynolds, A. Rudola, R. Sayers, D. O. Scanlon, S. Sen, V. R. Seymour, B. Silván, M. Tahar Sougrati, L. Stievano, G. S. Stone, C. I. Thomas, M.-M. Titirici, J. Tong, T. J. Wood, D. S. Wright and R. Younesi, JPhys Energy, 2021, 3, 31503, DOI:10.1088/2515-7655/ac01ef.
- A. Rudola, A. J. R. Rennie, R. Heap, S. S. Meysami, A. Lowbridge, F. Mazzali, R. Sayers, C. J. Wright and J. Barker, J. Mater. Chem. A, 2021, 9, 8279–8302 RSC.
- A. Bauer, J. Song, S. Vail, W. Pan, J. Barker and Y. Lu, Adv. Energy Mater., 2018, 8, 1702869, DOI:10.1002/aenm.201702869.
- Y.-S. Hu and Y. Li, ACS Energy Lett., 2021, 6, 4115–4117 CrossRef CAS.
- Y.-K. Sun, ACS Energy Lett., 2020, 5, 1278–1280 CrossRef CAS.
- J.-M. Tarascon, Joule, 2020, 4, 1616–1620 CrossRef , https://www.sciencedirect.com/science/article/pii/S2542435120302403..
- Sodium-Ion Batteries, ed. M.-M. Titirici, P. Adelhelm and Y.-S. Hu, Wiley, 2022 Search PubMed.
- F. Xie, Z. Xu, Z. Guo and M.-M. Titirici, Prog. Energy, 2020, 2, 42002 CrossRef.
- H. Moon, A. Innocenti, H. Liu, H. Zhang, M. Weil, M. Zarrabeitia and S. Passerini, ChemSusChem, 2023, 16, e202201713 CrossRef CAS PubMed.
- H. Moon, M. Zarrabeitia, E. Frank, O. Böse, M. Enterría, D. Saurel, I. Hasa and S. Passerini, Batteries Supercaps, 2021, 4, 960–977 CrossRef CAS.
- M. Thompson, Q. Xia, Z. Hu and X. S. Zhao, Mater. Adv., 2021, 2, 5881–5905 RSC.
- D. Larcher and J.-M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed , https://www.nature.com/articles/nchem.2085#change-history..
- C. Vaalma, D. Buchholz, M. Weil and S. Passerini, Nat. Rev. Mater., 2018, 3, 1–11 CrossRef , https://www.nature.com/articles/natrevmats201813..
- K. Kubota, M. Dahbi, T. Hosaka, S. Kumakura and S. Komaba, Chem. Rec., 2018, 18, 459–479 CrossRef CAS PubMed.
- K. Kubota and S. Komaba, J. Electrochem. Soc., 2015, 162, A2538–A2550 CrossRef CAS.
- I. Hasa, S. Mariyappan, D. Saurel, P. Adelhelm, A. Y. Koposov, C. Masquelier, L. Croguennec and M. Casas-Cabanas, J. Power Sources, 2021, 482, 228872 CrossRef CAS , https://www.sciencedirect.com/science/article/pii/S0378775320311769..
- W. Zuo, A. Innocenti, M. Zarrabeitia, D. Bresser, Y. Yang and S. Passerini, Acc. Chem. Res., 2023, 56, 284–296 CrossRef CAS PubMed.
- J. F. Peters, M. Baumann, J. R. Binder and M. Weil, Sustainable Energy Fuels, 2021, 5, 6414–6429 RSC.
- J. Peters, M. Baumann, M. Weil and S. Passerini, in Sodium-Ion Batteries, ed. M.-M. Titirici, P. Adelhelm and Y.-S. Hu, Wiley, 2022, vol. 24, pp. 551–571 Search PubMed.
- F. B. Jasper, J. Späthe, M. Baumann, J. F. Peters, J. Ruhland and M. Weil, J. Cleaner Prod., 2022, 366, 132899 CrossRef CAS.
- J. Peters, A. Peña Cruz and M. Weil, Batteries, 2019, 5, 10 CrossRef CAS.
- A. Rudola, C. J. Wright and J. Barker, Energy Mater. Adv., 2021, 2021, 37 Search PubMed.
- S. Kuze, J.-i. Kageura, S. Matsumoto, T. Nakayama, M. Makidera, M. Saka, T. Yamaguchi, T. Yamamoto and K. Nakane, Development of a Sodium Ion Secondary Battery, R&D Report, 2013 Search PubMed.
- Q. Zhou, Y. Li, F. Tang, K. Li, X. Rong, Y. Lu, L. Chen and Y.-S. Hu, Chin. Phys. Lett., 2021, 38, 76501 CrossRef CAS.
- E. Gonzalo, M. Zarrabeitia, N. E. Drewett, L. del Amo, J. Miguel and T. Rojo, Energy Storage Mater., 2021, 34, 682–707 CrossRef , https://www.sciencedirect.com/science/article/pii/S2405829720303883..
- E. Goikolea, V. Palomares, S. Wang, I. R. de Larramendi, X. Guo, G. Wang and T. Rojo, Adv. Energy Mater., 2020, 10, 2002055, DOI:10.1002/aenm.202002055.
- N. Ortiz-Vitoriano, N. E. Drewett, E. Gonzalo and T. Rojo, Energy Environ. Sci., 2017, 10, 1051–1074 RSC , https://rsc.66557.net/en/content/articlelanding/2017/ee/c7ee00566k..
- C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81–85 CrossRef CAS , https://www.sciencedirect.com/science/article/pii/0378436380902144..
- S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. Ma and G. Ceder, Energy Environ. Sci., 2011, 4, 3680 RSC.
- A. van der Ven, G. Ceder, M. Asta and P. D. Tepesch, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 16 CrossRef.
- Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2014, 26, 5208–5214 CrossRef CAS.
- P. Gupta, S. Pushpakanth, M. A. Haider and S. Basu, ACS Omega, 2022, 7(7), 5605–5614 CrossRef CAS PubMed.
- J. Zhang, W. Wang, W. Wang, S. Wang and B. Li, ACS Appl. Mater. Interfaces, 2019, 11, 22051–22066 CrossRef CAS PubMed.
- J. M. Paulsen and J. R. Dahn, Solid State Ionics, 1999, 126, 3–24 CrossRef CAS.
- Z. Lu and J. R. Dahn, Chem. Mater., 2001, 148, A1225 CAS.
- Z. Lu and J. R. Dahn, Chem. Mater., 2001, 13, 1252–1257 CrossRef CAS.
- D. H. Lee, J. Xu and Y. S. Meng, Phys. Chem. Chem. Phys., 2013, 15, 3304–3312 RSC.
- R. J. Clément, P. G. Bruce and C. P. Grey, J. Electrochem. Soc., 2015, 162, A2589, DOI:10.1149/2.0201514jes.
- S. Daubner, M. Dillenz, L. F. Pfeiffer, C. Gauckler, M. Rosin, N. Burgard, J. Martin, P. Axmann, M. Sotoudeh, A. Gross, D. Schneider and B. Nestler, npj Comput. Mater., 2024, 10, 1020 Search PubMed.
- J. Mao, X. Liu, J. Liu, H. Jiang, T. Zhang, G. Shao, G. Ai, W. Mao, Y. Feng, W. Yang, G. Liu and K. Dai, J. Electrochem. Soc., 2019, 166, A3980–A3986 CrossRef CAS.
- T. Risthaus, D. Zhou, X. Cao, X. He, B. Qiu, J. Wang, L. Zhang, Z. Liu, E. Paillard, G. Schumacher, M. Winter and J. Li, J. Power Sources, 2018, 395, 16–24 CrossRef CAS.
- N. Tapia-Ruiz, W. M. Dose, N. Sharma, H. Chen, J. Heath, J. W. Somerville, U. Maitra, M. S. Islam and P. G. Bruce, Energy Environ. Sci., 2018, 11, 1470–1479 RSC.
- L. Lu, X. Han, J. Li, J. Hua and M. Ouyang, J. Power Sources, 2013, 226, 272–288 CrossRef CAS.
- C. Gauckler, M. Dillenz, F. Maroni, L. F. Pfeiffer, J. Biskupek, M. Sotoudeh, Q. Fu, U. Kaiser, S. Dsoke, H. Euchner, P. Axmann, M. Wohlfahrt-Mehrens, A. Groß and M. Marinaro, ACS Appl. Energy Mater., 2022, 5, 13735–13750 CrossRef CAS.
- A. Gutierrez, W. M. Dose, O. Borkiewicz, F. Guo, M. Avdeev, S. Kim, T. T. Fister, Y. Ren, J. Bareño and C. S. Johnson, J. Phys. Chem. C, 2018, 122, 23251–23260 CrossRef CAS.
- P. Manikandan, D. Ramasubramonian and M. M. Shaijumon, Electrochim. Acta, 2016, 206, 199–206 CrossRef CAS.
- L. F. Pfeiffer, N. Jobst, C. Gauckler, M. Lindén, M. Marinaro, S. Passerini, M. Wohlfahrt-Mehrens and P. Axmann, Front. Energy Res., 2022, 10, 305 Search PubMed.
- L. F. Pfeiffer, Y. Li, M. Mundszinger, J. Geisler, C. Pfeifer, D. Mikhailova, A. Omar, V. Baran, J. Biskupek, U. Kaiser, P. Adelhelm, M. Wohlfahrt-Mehrens, S. Passerini and P. Axmann, Chem. Mater., 2023, 35, 8065–8080 CrossRef CAS.
- C. Delmas, D. Carlier and M. Guignard, Adv. Energy Mater., 2021, 11, 2001201 CrossRef CAS.
- B. L. Henke, E. M. Gullikson and J. C. Davis, At. Data Nucl. Data Tables, 1993, 54, 181–342 CrossRef CAS.
- J. M. Paulsen, R. A. Donaberger and J. R. Dahn, Chem. Mater., 2000, 12, 2257–2267 CrossRef CAS.
- J. M. Paulsen and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 2478 CrossRef CAS.
- R. Balsys, Solid State Ionics, 1997, 93, 279–282 CrossRef CAS.
- L. Pauling, J. Am. Chem. Soc., 1929, 51, 1010–1026 CrossRef CAS.
- V. F. Sears, Neutron News, 1992, vol. 3, pp. 26–37 Search PubMed.
- J. W. Somerville, A. Sobkowiak, N. Tapia-Ruiz, J. Billaud, J. G. Lozano, R. A. House, L. C. Gallington, T. Ericsson, L. Häggström, M. R. Roberts, U. Maitra and P. G. Bruce, Energy Environ. Sci., 2019, 12, 2223–2232 RSC.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- M. Casas-Cabanas, M. Reynaud, J. Rikarte, P. Horbach and J. Rodríguez-Carvajal, J. Appl. Crystallogr., 2016, 49, 2259–2269 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- A.-C. Dippel, H.-P. Liermann, J. T. Delitz, P. Walter, H. Schulte-Schrepping, O. H. Seeck and H. Franz, J. Synchrotron Radiat., 2015, 22, 675–687 CrossRef CAS PubMed.
- J. Filik, A. W. Ashton, P. C. Y. Chang, P. A. Chater, S. J. Day, M. Drakopoulos, M. W. Gerring, M. L. Hart, O. V. Magdysyuk, S. Michalik, A. Smith, C. C. Tang, N. J. Terrill, M. T. Wharmby and H. Wilhelm, J. Appl. Crystallogr., 2017, 50, 959–966 CrossRef CAS PubMed.
- M. Herklotz, J. Weiß, E. Ahrens, M. Yavuz, L. Mereacre, N. Kiziltas-Yavuz, C. Dräger, H. Ehrenberg, J. Eckert, F. Fauth, L. Giebeler and M. Knapp, J. Appl. Crystallogr., 2016, 49, 340–345 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 1049 Search PubMed.
- L. Wang, T. Maxisch and G. Ceder, Am. Mineral., 2006, 73, 603 Search PubMed.
- Q. Huang, M. L. Foo, J. W. Lynn, H. W. Zandbergen, G. Lawes, Y. Wang, B. H. Toby, A. P. Ramirez, N. P. Ong and R. J. Cava, J. Solid State Chem., 2004, 16, 5803–5814 CAS.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- W. Zuo, J. Qiu, X. Liu, F. Ren, H. Liu, H. He, C. Luo, J. Li, G. F. Ortiz, H. Duan, J. Liu, M.-S. Wang, Y. Li, R. Fu and Y. Yang, Nat. Commun., 2020, 11, 3544 CrossRef CAS PubMed.
- W. Zuo, Z. Xiao, M. Zarrabeitia, X. Xue, Y. Yang and S. Passerini, ACS Mater. Lett., 2022, 4, 1074–1086 CrossRef CAS.
- H. Xia, L. Lu, Y. S. Meng and G. Ceder, J. Power Sources, 2007, 154, A337 CAS.
- L. W. Shacklette, T. R. Jow and L. Townsend, J. Electrochem. Soc., 1988, 135, 2669–2674 CrossRef CAS.
- R. Berthelot, D. Carlier and C. Delmas, Nat. Mater., 2011, 10, 74–80 CrossRef CAS PubMed.
- H. W. Zandbergen, M. Foo, Q. Xu, V. Kumar and R. J. Cava, Solid State Ionics, 2004, 70, 431 Search PubMed.
- D. Igarashi, Y. Miyazaki, T. Kajitani and K. Yubuta, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235 Search PubMed.
- Y. Reynier, J. Graetz, T. Swan-Wood, P. Rez, R. Yazami and B. Fultz, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 753 CrossRef.
- M. Blangero, R. Decourt, D. Carlier, G. Ceder, M. Pollet, J.-P. Doumerc, J. Darriet and C. Delmas, Inorg. Chem., 2005, 44, 9299–9304 CrossRef CAS PubMed.
- Q. Huang, M. L. Foo, R. A. Pascal, J. W. Lynn, B. H. Toby, T. He, H. W. Zandbergen and R. J. Cava, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 453 Search PubMed.
- P. Zhang, R. B. Capaz, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 165 Search PubMed.
- M. L. Foo, Y. Wang, S. Watauchi, H. W. Zandbergen, T. He, R. J. Cava and N. P. Ong, Phys. Rev. Lett., 2004, 92, 247001 CrossRef PubMed.
- Y. S. Meng, Y. Hinuma and G. Ceder, J. Chem. Phys., 2008, 128, 104708 CrossRef PubMed.
- Y. Hinuma, Y. S. Meng and G. Ceder, Solid State Ionics, 2008, 77, 165 Search PubMed.
- H. Alloul, I. R. Mukhamedshin, T. A. Platova and A. V. Dooglav, Europhys. Lett., 2009, 85, 47006 CrossRef.
- T. A. Platova, I. R. Mukhamedshin, H. Alloul, A. V. Dooglav and G. Collin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224106 CrossRef.
- R. A. Huggins, Advanced Batteries, Materials Science Aspects, Springer US, Boston, MA, 2009 Search PubMed.
- P. de Silva and C. Corminboeuf, J. Chem. Theory Comput., 2014, 10, 3745–3756 CrossRef CAS PubMed.
- M. Busch, R. B. Wang, A. Hellman, J. Rossmeisl and H. Grönbeck, J. Phys. Chem. C, 2018, 122, 216–226 CrossRef CAS.
- A. Visibile, R. B. Wang, A. Vertova, S. Rondinini, A. Minguzzi, E. Ahlberg and M. Busch, Chem. Mater., 2019, 31, 4787–4792 CrossRef CAS.
- C. Elschenbroich, Organometallchemie, Teubner, Wiesbaden, 5th edn, 2005 Search PubMed.
- A. F. Holleman, N. Wiberg and E. Wiberg, Lehrbuch der Anorganischen Chemie, Walter de Gruyter, 2007 Search PubMed.
- M. Busch, E. Ahlberg and I. Panas, Phys. Chem. Chem. Phys., 2011, 13, 15069–15076 RSC.
- A. Visibile, A. Vertova, S. Rondinini, A. Minguzzi, E. Ahlberg and M. Busch, Chem. Phys. Lett., 2020, 755, 137799 CrossRef CAS.
- I. R. Mukhamedshin and H. Alloul, Phys. B, 2015, 460, 58–63 CrossRef CAS.
- X. Chen, Y. Wang, K. Wiaderek, X. Sang, O. Borkiewicz, K. Chapman, J. LeBeau, J. Lynn and X. Li, Adv. Funct. Mater., 2018, 28, 385 Search PubMed.
- X. Li, X. Ma, D. Su, L. Liu, R. Chisnell, S. P. Ong, H. Chen, A. Toumar, J.-C. Idrobo, Y. Lei, J. Bai, F. Wang, J. W. Lynn, Y. S. Lee and G. Ceder, Nat. Mater., 2014, 13, 586–592 CrossRef CAS PubMed.
- Y. Li, K. A. Mazzio, N. Yaqoob, Y. Sun, A. I. Freytag, D. Wong, C. Schulz, V. Baran, A. S. J. Mendez, G. Schuck, M. Zając, P. Kaghazchi and P. Adelhelm, Adv. Mater., 2024, e2309842 CrossRef PubMed.
- R. A. House, U. Maitra, L. Jin, J. G. Lozano, J. W. Somerville, N. H. Rees, A. J. Naylor, L. C. Duda, F. Massel, A. V. Chadwick, S. Ramos, D. M. Pickup, D. E. McNally, X. Lu, T. Schmitt, M. R. Roberts and P. G. Bruce, Chem. Mater., 2019, 31, 3293–3300 CrossRef CAS.
- R. J. Clément, J. Xu, D. S. Middlemiss, J. Alvarado, C. Ma, Y. S. Meng and C. P. Grey, J. Mater. Chem. A, 2017, 5, 4129–4143 RSC.
- R. D. Shannon, Acta Crystallogr., 1976, 32, 751–767 CrossRef.
- H. Hou, B. Gan, Y. Gong, N. Chen and C. Sun, Inorg. Chem., 2016, 55, 9033–9037 CrossRef CAS PubMed.
- P.-F. Wang, Y. You, Y.-X. Yin, Y.-S. Wang, L.-J. Wan, L. Gu and Y.-G. Guo, Angew. Chem., Int. Ed. Engl., 2016, 55, 7445–7449 CrossRef CAS PubMed.
- J. Xu, D. H. Lee, R. J. Clément, X. Yu, M. Leskes, A. J. Pell, G. Pintacuda, X.-Q. Yang, C. P. Grey and Y. S. Meng, Chem. Mater., 2014, 26, 1260–1269 CrossRef CAS.
- I. Hasa, S. Passerini and J. Hassoun, J. Mater. Chem. A, 2017, 5, 4467–4477 RSC.
- X. Wu, G.-L. Xu, G. Zhong, Z. Gong, M. J. McDonald, S. Zheng, R. Fu, Z. Chen, K. Amine and Y. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 22227–22237 CrossRef CAS PubMed.
- K. Kubota, Y. Yoda and S. Komaba, J. Electrochem. Soc., 2017, 164, A2368, DOI:10.1149/2.0311712jes.
- L. Wang, Y.-G. Sun, L.-L. Hu, J.-Y. Piao, J. Guo, A. Manthiram, J. Ma and A.-M. Cao, J. Mater. Chem. A, 2017, 5, 8752–8761 RSC.
- L. Zheng, J. Li and M. N. Obrovac, Chem. Mater., 2017, 29, 1623–1631 CrossRef CAS.
- B. Ouyang and Y. Zeng, Nat. Commun., 2024, 15, 973 CrossRef CAS PubMed.
- A. Sarkar, L. Velasco, D. Wang, Q. Wang, G. Talasila, L. de Biasi, C. Kübel, T. Brezesinski, S. S. Bhattacharya, H. Hahn and B. Breitung, Nat. Commun., 2018, 9, 3400 CrossRef PubMed.
- F. Strauss, M. Botros, B. Breitung and T. Brezesinski, J. Appl. Phys., 2024, 135, 420 CrossRef.
- R. Guo, Y. Yang, C. Zhao, F. Huo, J. Xue, J. He, B. Sun, Z. Sun, H. K. Liu and S. X. Dou, Adv. Funct. Mater., 2023, 19, 2022 Search PubMed.
- Y. Ma, Y. Ma, Q. Wang, S. Schweidler, M. Botros, T. Fu, H. Hahn, T. Brezesinski and B. Breitung, Energy Environ. Sci., 2021, 14, 2883–2905 RSC.
- B. Wang, J. Ma, K. Wang, D. Wang, G. Xu, X. Wang, Z. Hu, C. -W. Pao, J. -L. Chen, L. Du, X. Du and G. Cui, Adv. Energy Mater., 2024, 35, 38 Search PubMed.
- E. P. George, D. Raabe and R. O. Ritchie, Nat. Rev. Mater., 2019, 4, 515–534 CrossRef CAS.
- J. -W. Yeh, S. -K. Chen, S. -J. Lin, J. -Y. Gan, T. -S. Chin, T. -T. Shun, C. -H. Tsau and S. -Y. Chang, Adv. Eng. Mater., 2004, 6, 299–303 CrossRef CAS.
- F. Ding, C. Zhao, D. Xiao, X. Rong, H. Wang, Y. Li, Y. Yang, Y. Lu and Y.-S. Hu, J. Am. Chem. Soc., 2022, 144, 8286–8295 CrossRef CAS PubMed.
- S. L. Dreyer, R. Zhang, J. Wang, A. Kondrakov, Q. Wang, T. Brezesinski and J. Janek, JPhys Energy, 2023, 5, 35002 CrossRef CAS.
- J. Liu, W. Huang, R. Liu, J. Lang, Y. Li, T. Liu, K. Amine and H. Li, Adv. Funct. Mater., 2024, 34, 2315437 CrossRef CAS.
- K. Tian, H. He, X. Li, D. Wang, Z. Wang, R. Zheng, H. Sun, Y. Liu and Q. Wang, J. Mater. Chem. A, 2022, 10, 14943–14953 RSC.
- J. Wang, S. L. Dreyer, K. Wang, Z. Ding, T. Diemant, G. Karkera, Y. Ma, A. Sarkar, B. Zhou, M. V. Gorbunov, A. Omar, D. Mikhailova, V. Presser, M. Fichtner, H. Hahn, T. Brezesinski, B. Breitung and Q. Wang, Mater. Futures, 2022, 1, 35104 CrossRef CAS.
- C. Zhao, F. Ding, Y. Lu, L. Chen and Y.-S. Hu, Angew. Chem., Int. Ed. Engl., 2020, 59, 264–269 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta04786a |
| ‡ Lukas Fridolin Pfeiffer and Manuel Dillenz contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |