Open Access Article
Open Access ArticleThe devil in the details: lessons from Li6PS5X for robust high-throughput workflows†
Asif Iqbal
Bhatti
 ab,
Sandeep
Kumar
ab,
Sandeep
Kumar
 ab,
Catharina
Jaeken
ab,
Catharina
Jaeken
 c,
Michael
Sluydts
c,
Michael
Sluydts
 c,
Danny E. P.
Vanpoucke
c,
Danny E. P.
Vanpoucke
 ad and
Stefaan
Cottenier
ad and
Stefaan
Cottenier
 *ab
*ab
aDepartment of Electromechanical, Systems and Metal Engineering, Ghent University, Belgium. E-mail: stefaan.cottenier@ugent.be
bCenter for Molecular Modeling, Ghent University, Belgium
cePotentia, Belgium
dHasselt University and imec, Institute for Materials Research (imo-imomec), Quantum & Artificial inTelligence Design of Materials (QuATOMs), Belgium
First published on 14th November 2024
Abstract
High-throughput computational screening has become a powerful tool in materials science for identifying promising candidates for specific applications. However, the effectiveness of these methods relies heavily on the accuracy and appropriateness of the underlying models and assumptions. In this study, we use the popular argyrodite solid-state electrolyte family Li6PS5X (X = Cl, Br, I) as a case study to critically examine key steps in high-throughput workflows and highlight potential pitfalls. We demonstrate some of these pitfalls by highlighting the importance of careful structural considerations, including symmetry breaking and site disorder, and examine the difference between 0 K thermodynamic stability and finite-temperature stability based on temperature-dependent Gibbs free energy calculations. Furthermore, we explore the implications of these findings for the ranking of candidate materials in a mini-throughput study in a search space of isovalent analogs to Li6PS5Cl. As a result of these findings, our work underscores the need for balanced trade-offs between computational efficiency and accuracy in high-throughput screenings, and offers guidance for designing more robust workflows that can better bridge the gap between computational predictions and experimental realities.
1 Introduction
Computationally screening extensive material spaces using computational tools to identify new materials with optimal properties for specific technological applications has become a standard practice in materials science.1–8 This method, known as high-throughput screening, holds great promise; however, like any tool, it must be applied critically. In this paper, we address several lesser-known issues that need to be considered when planning, executing, or evaluating a high-throughput study. Our aim is to contribute to the improved design of high-throughput studies and to foster more realistic expectations regarding the outcomes such studies can deliver.To illustrate our points, we will use a toy case to conduct a “mini-throughput study”. Our starting point is Li6PS5Cl, a crystal extensively studied in recent years as a candidate for solid-state electrolytes in Li-ion batteries (see Section 2). Following the common assumption that similar materials may exhibit equally favorable properties, we construct a material space derived from Li6PS5Cl and investigate whether other materials in this space exhibit similar or superior properties for use as solid-state electrolytes. In this example, we focus on a single property: thermodynamic stability. Our pretended goal is to identify all members in the space that are at least as thermodynamically stable as Li6PS5Cl with respect to decomposition into other crystals.
The objective of this paper is not to actually identify new electrolytes. Instead, we use this toy case to highlight the following critical, yet common, issues that do not always receive the attention they deserve when planning, performing, or analyzing high-throughput studies: (1) the importance of starting from the correct crystal structure, (2) the relevance (or lack thereof) of 0 K results for room temperature properties, and (3) the modification of property rankings with increasing levels of theoretical complexity.
2 Battery context
In the pursuit of ever better batteries, the development of Li-ion batteries with a solid electrolyte rather than a liquid electrolyte is a major goal. They combine a higher energy density with increased stability, high ionic conductivity and improved safety.9,10 One family of candidate solid-state electrolytes that has received considerable attention is the Li6PS5X family, with X being a halogen element. The most studied member of this family is Li6PS5Cl,7,8 whose properties (ionic conductivity and chemical stability) can be altered by substituting the halogen.11 They are stable at room temperature, and their Li ion conductivity approaches the values found in liquid electrolytes.12–14 There is often a trade-off: while X = Cl offers higher conductivity, there are concerns about its stability. Conversely, X = I improves chemical stability at the cost of lower ionic conductivity.13,15–22Chemical stability is a property that can be studied using first-principles methods, and such studies have been conducted for Li6PS5X.23–26 Making meaningful rankings of candidate materials, however, requires understanding the uncertainty on the predicted properties, several of which are independent of the first-principles method used. We will examine two sources of uncertainty: crystal structure and temperature. While the crystal structure of Li6PS5Cl has been experimentally determined, it cannot be considered fully resolved due to the effect of disorder. At the same time, chemical stability is a temperature-dependent property. We will examine how chemical stability evolves if the temperature is explicitly included in the simulations. Finally, we will illustrate how the rankings in our search space are affected by dealing with these two sources of uncertainty at various levels of sophistication. By quantifying these effects we hope to inspire the synthesis of new materials which have been previously discarded in high-throughput studies.
3 Computational methodology
For structural relaxation and total energy calculations, we used Density Functional Theory (DFT) as implemented in the Vienna Ab initio Simulation Package (VASP) code.27 The electron core energy was approximated with plane wave-based projector-augmented wave (PAW) pseudopotentials.28 After extensive convergence tests, the energy cutoff was set to 650 eV. The common Perdew–Burke–Ernzerhof (PBE) generalized-gradient approximation was used for the exchange–correlation functional.29 As PAW potentials, we used the so-called GW-ready set, known for its high overall precision.30,31 Specifically, we chose the following potentials: Li_sv_GW, Cl_GW, P_GW, V_sv_GW, As_GW, S_GW, and Bi_d_GW. Brillouin zone integration was performed using a Γ-centered k-point grid scheme generated via the Monkhorst–Pack method,32 and the first-order Methfessel–Paxton method33 with 0.03 eV was used for smearing. In all calculations, we used the van der Waals Grimme DFT-D3 corrections as implemented in the VASP code34 to model the long-range interactions. This choice was based on test calculations for a series of argyrodite crystals, which showed that without van der Waals (VDW) corrections, volumes and ion channel sizes were overestimated. All calculations were carried out as non-spin-polarized, except for V5S8, which is known to be ferrimagnetic.35–38 For geometry optimizations, the initial structure was relaxed until the forces on each atom were below 0.01 meV Å−1.For dynamic stability analysis, we performed first-principles phonon calculations on geometry-optimized unit cells with 52 atoms using the finite displacement method as implemented in the VASP code.39 Thermodynamic properties were computed with the phonopy code.40 All phonon band structures were plotted with the sumo code.41
To compute the distance to the convex hull for Li6PS5X and the different x-Li3PS4 phases, we used the Pymatgen code.42,43Pymatgen determines this energy distance ΔEhull based on the total energies of the relevant decomposition products it identifies from the Materials Project database.44 We modified the Pymatgen code to consistently add the VDW corrections as an additional correction to the final energy of each composition in the phase diagram, without further altering the crystal structure.
3.1 Predicting thermodynamic phase stability
In order to predict the stability of a crystal at different temperatures, we calculate its Gibbs free energy with respect to its decomposition into a set of simpler crystals chosen to minimize this energy difference. A general example of a crystal AmBn formed by the elements A and B could be:| AmBn ⇌ cpqApBq + crsArBs + cvAv + cwBw | (1) |
| ΔG(T) = ΔH + ΔFvib − TΔSmix | (2) |
| ΔH = Eleft − ∑cright,iEright,i | (3) |
The second term in eqn (2) is the vibrational free energy difference, given by ΔFvib = ΔEZPE − TΔSvib, with EZPE the zero-point energy of each of the crystals and ΔSvib the vibrational contribution to their entropy. In the harmonic approximation,40Fvib is given by
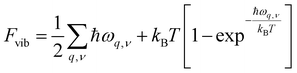 | (4) |
As for the last term in eqn (2), the mixing entropy difference is important for crystals that are not completely ordered. When two elements compete for the same lattice site, this can be approximated by the mixing entropy difference of two ideal gases. The expression for this is given by
ΔSmix = −nR[f1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(f1) + (1 − f1)ln(1 − f1)] ln(f1) + (1 − f1)ln(1 − f1)] | (5) |
ΔSmix = −NkB[f1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(f1) + (1 − f1)ln(1 − f1)] ln(f1) + (1 − f1)ln(1 − f1)] | (6) |
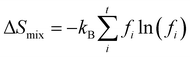 | (7) |
Under the constraints and approximations listed above, the ΔG(T) of eqn (2) is entirely computable, which can be exploited to predict temperature-dependent phase stability (as done, for instance, in ref. 26 and 45 for crystals similar to the ones studied in the present paper). At T = 0, ΔG(T = 0) simplifies to the total energy difference between the left and right-hand sides of eqn (1), plus the (small) zero-point energy difference. Therefore, the total energy difference ΔE is a good approximation for ΔG(T = 0). We will use the notation ΔE when referring to a total energy difference at 0 K without considering zero-point corrections. With zero-point corrections, this will be noted as ΔG. For T > 0 K, there is no ambiguity, and we write it as ΔG(T). When the simpler crystals on the right-hand side of eqn (1) are selected to be those that provide the smallest possible energy difference with the crystal on the left-hand side, those simpler crystals must be on the convex hull of the corresponding crystal space. In that case, we will write the energy differences with a ‘hull’ subscript: ΔEhull, ΔGhull, and ΔGhull(T).
4 Results and discussion
4.1 Ambiguities in the argyrodite crystal structure
In order to perform meaningful first principles calculations for Li6PS5Cl, partial information about its crystal structure needs to be known as input: which space group, which Wyckoff sites are occupied by which elements, …. Such information is usually provided by experiments, e.g. by X-ray diffraction. While experimental information on the positions occupied by elements can be highly accurate, it often represents global averages, that can be affected by defects or disorder. As will become clear from the following overview, the experimental information available about the crystal structure of Li6PS5Cl does not suggest in a straightforward way which structure to use as input for the first-principles calculations (Fig. 1 and Table 1). On the other hand, quantitative aspects of the crystal structure, such as the lattice parameters, unit cell angles or the position coordinates that are not fixed by symmetry, can be obtained as output from the first principles calculations.| Elements | Wyckoff position | ||||
|---|---|---|---|---|---|
| Deiseroth et al.,14 ICSD 418490, 2008 | Rayavarapu et al.46 2012 | Kraft/Gautam et al.13,47 2017/2021 | Hanghofer et al.48 2019 | Yu et al.49 2016 | |
| Li | 48h (0.56) | 48h (0.44) | 48h (0.50) | 24g (1.00) | 48h (0.47) |
| P | 4b (1.00) | 4b (1.00) | 4b (1.00) | 4b (1.00) | 4b (1.00) |
| S | 16e (1.00) | 16e (1.00) | 16e (1.00) | 16e (1.00) | 16e (1.00) |
| 4c (1.00)(?) | 4c (0.37) | 4c (0.38) | 4c (0.39) | 4c (0.29) | |
| — | 4a (0.63) | 4a (0.61) | 4a (0.62) | 4a (0.71) | |
| Cl | 4a (1.00)(?) | 4a (0.37) | 4a (0.38) | 4a (0.39) | 4a (0.29) |
| — | 4c (0.63) | 4c (0.61) | 4c (0.62) | 4c (0.71) | |
| Exp | XRD | XRD/NPD | NPD | XRD/NMR | NPD |
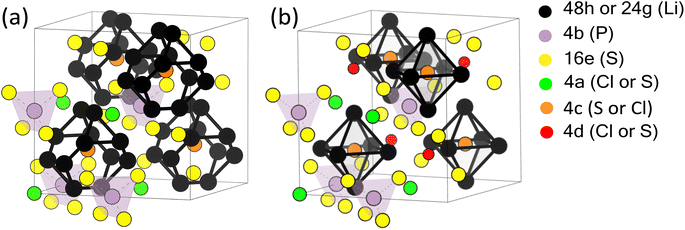
There is no ambiguity about the space group, which is universally accepted to be the face-centered cubic group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (ITA 216). The P atoms occupy Wyckoff position 4b, and 4 out of the 5 S atoms occupy Wyckoff position 16e ((x,x,x), x = 0.625 (ref. 49)). These P and S atoms form tetrahedral cages, with P in the center of the cage and S on its vertices. Similarly, the Li atoms form cages around the 4c positions. These cages are either regular octahedra, with a Li atom at each of its 6 vertices (Wyckoff site 24g, ref. 48), or they are pyritohedra with 12 vertices, of which roughly 50% are occupied by Li atoms (Wyckoff site 48h, ref. 13, 14, 46 and 47).
3m (ITA 216). The P atoms occupy Wyckoff position 4b, and 4 out of the 5 S atoms occupy Wyckoff position 16e ((x,x,x), x = 0.625 (ref. 49)). These P and S atoms form tetrahedral cages, with P in the center of the cage and S on its vertices. Similarly, the Li atoms form cages around the 4c positions. These cages are either regular octahedra, with a Li atom at each of its 6 vertices (Wyckoff site 24g, ref. 48), or they are pyritohedra with 12 vertices, of which roughly 50% are occupied by Li atoms (Wyckoff site 48h, ref. 13, 14, 46 and 47).
The 4c positions at the center of these Li-cages are either fully occupied by the fifth S atom (ref. 14, although the authors note they could not distinguish between S and Cl), or by a mixture of S (38%) and Cl (62%) (ref. 13 and 46–48). The 4a site, which lies outside the Li cages, is the mirror image of this, with either 100% Cl (ref. 14) or a mixture of S (62%) and Cl (38%) (ref. 13 and 46–48). The 4a site forms an fcc-pattern at the corners and face centers of the unit cell.
Several experimental papers mention a 4d Wyckoff site for S or Cl. As pointed out in ref. 50, this is due to a different origin choice and a possible inversion. This 4d site is identical to what we call 4c. In the present work, we strictly adhere to the ITA standard setting, called ‘setting 2, not inverted’ in ref. 50. With this choice, the 4c position is at 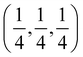 and is surrounded by a Li octahedron formed by the 24g sites. These octahedra themselves form a tetrahedral arrangement, with one octahedron in the first octant. The 4d position (unoccupied) is at the center of each of the four octants where no Li octahedron is located and is tetrahedrally surrounded by four S atoms at 16e. When other choices are made, the names of 4c and 4d can be reversed.50 In this work, all literature data have been converted to the ITA standard setting, ensuring that 4c is always a site at the center of the octahedron. As an additional verification that the 4d site is not occupied, some test calculations were performed with 4d occupied by S or Cl (see Table 2 and its discussion).
and is surrounded by a Li octahedron formed by the 24g sites. These octahedra themselves form a tetrahedral arrangement, with one octahedron in the first octant. The 4d position (unoccupied) is at the center of each of the four octants where no Li octahedron is located and is tetrahedrally surrounded by four S atoms at 16e. When other choices are made, the names of 4c and 4d can be reversed.50 In this work, all literature data have been converted to the ITA standard setting, ensuring that 4c is always a site at the center of the octahedron. As an additional verification that the 4d site is not occupied, some test calculations were performed with 4d occupied by S or Cl (see Table 2 and its discussion).
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), orthorhombic S (Fddd), and orthorhombic Cl2 (Cmce))
), orthorhombic S (Fddd), and orthorhombic Cl2 (Cmce))
| Elements | Materials project mp-985592 | D'Amore et al. ‘Model 2’, ref. 26 | Variant 1 | Variant 2 | Variant 3 | Variant 4 [chosen model] |
|---|---|---|---|---|---|---|
| Cubic | Distorted | Distorted | Distorted | Distorted | Distorted | |
| Wyckoff position | ||||||
| Li | 24g | 24g | 24g | 24g | 24g | 24g |
| P | 4b | 4b | 4b | 4b | 4b | 4b |
| S | 16e | 16e | 16e | 16e | 16e | 16e |
| 4c | 4c | 4d | 4a | 4a | 4c | |
| Cl | 4a | 4a | 4a | 4d | 4c | 4a |
| ΔE [eV per atom] | −1.129 | −1.160 | −1.193 | −1.206 | ||
Given the experimentally observed site disorder for both Li and S/Cl (see Table 1), the question arises of which ordered model crystal structure should be used as the input structure for first-principles calculations. The requirement is to capture the essential features of Li6PS5Cl without entering the combinatorial explosion of possibilities by explicitly considering the site disorder. Table 2 shows two choices made in the literature, as well as a comparison between four extreme cases tested in this paper. This table demonstrates that swapping S and Cl between the 4c and 4a sites involves almost no energy change, consistent with the observed experimental disorder over these two sites. Variant 4, with S on 4c and Cl on 4a, has the lowest energy and is taken as our model system. This is the same choice as in Materials Project (mp-985592, ref. 44) and in ref. 26.
Unless explicitly mentioned, we will always use ‘variant 4′ from Table 2 throughout this paper. This model is visualized in Fig. 1b, assuming 4a is occupied by Cl, 4c by S, and 4d is empty.
As discussed in ref. 24, 26 and 51, the cubic version of Li6PS5Cl is metastable: its phonon band structure shows soft modes (see Fig. 5a). When a geometry optimization is performed starting from the cubic cell but with a small random displacement of all atoms, a non-cubic phase with a lower energy is found. Its cell parameters and formation energy are documented in Table 3 for the lowest energy case (‘variant 4′). Although this structure is not far from the original cubic cell, it has less symmetry (space group 7) and can only be documented by its explicit cif file (see ESI, Section 1.4,† once in space group 7 and once in space group 1 (P1)). It corresponds to the ‘LT’ phase discussed in ref. 15, whereas the cubic structure corresponds to the ‘HT’ phase. This is a result of each Li atom at 24g choosing one of the 48h positions it can access. A phonon band structure calculation for this non-cubic cell does not show any soft modes (see Fig. 5d), in contrast to the cubic cell. This confirms that the distorted cell not only has a more negative formation energy but is also dynamically stable, meaning there is no further way to lower its energy without crossing a barrier. Table 3 documents two intermediate cases as well, where the unit cell was constrained to be cubic and only the atom positions were randomly displaced and subsequently allowed to relax. Once the volume was constrained to the one of the initial cubic structure, once to the one of the distorted structure. The energies in the last column demonstrate that the distortion of the cell shape has a minor effect. The energy reduction is due to the repositioning of the atoms, which leads to a volume reduction.
| Volume | a | b | c | α | β | γ | ΔE | |
|---|---|---|---|---|---|---|---|---|
| Cubic | 1022.15 | 10.073 | 10.073 | 10.073 | 90 | 90 | 90 | −1.122 |
| Cubic (high volume) | 1022.15 | 10.073 | 10.073 | 10.073 | 90 | 90 | 90 | −1.186 |
| Cubic (low volume) | 907.43 | 9.681 | 9.681 | 9.681 | 90 | 90 | 90 | −1.205 |
| Distorted | 907.43 | 9.832 | 9.609 | 9.609 | 89.1 | 88.8 | 88.8 | −1.206 |
For the isovalent crystals Li6PS5Br and Li6PS5I, there are fewer experimental data. Kraft et al.13 showed that in Li6PS5Br, Li is distributed over the 48h (44.1%) and 24g (11.9%) sites, while Br occupies 77.9% of the 4a sites and 22.1% of the 4c sites. In Li6PS5I, Li occupies 39.1% of the 48h site and 21.9% of the 24g site, while iodine only occupies the 4a site, and the 4c sites are entirely occupied by S. This is very similar to the ‘variant 4′ model from Table 2. Therefore, we can state that Li6PS5Br and Li6PS5I have qualitatively the same crystal structure as Li6PS5Cl, with a different mixture of Br/I and S on the 4a and 4c sublattices. Over the series Cl–Br–I, the S content of the 4a site takes the values 62%, 22%, and 0% (with a complementary behavior for the S content of the 4c site). This is attributed to the similarity in ionic radii for S, Cl, and Br, whereas the ionic radii for S and I are more different.48 For the Li position, various interpretations range from full occupation of 24g, partial occupation of 48h, to a mixture of both. This variety likely reflects the inherently mobile nature of Li atoms in this crystal, which is, after all, the reason these crystals are being studied. We will always place Li at 24g, representing an average position.
The discussion above illustrates that determining the most meaningful input structure for a first-principles calculation can be more involved than ‘simply adopting the experimental structure’. Nomenclature issues must be identified and resolved (4c/4d), average high symmetry features may need to be broken to find the actual lowest energy structure (we will see in Fig. 4 how this can affect computational predictions), and if site disorder appears, the most meaningful ordered model must be chosen (the entropy term that accounts for site disorder will be considered in Fig. 4). This is even more relevant if the chosen structure model will be used as a template for a high-throughput study: every mistake at this stage will proliferate through the entire high-throughput workflow.
Having decided on the most realistic model for the crystal structure, we can proceed to compute ground state and temperature-dependent properties for this model.
4.2 Thermodynamic stability of Li6PS5X at T = 0 K
Having verified the dynamical stability of (non-cubic) Li6PS5Cl in the previous section, we now focus on its thermodynamic stability. A crystal is thermodynamically stable if, at a given temperature, there is no other combination of crystals with a lower Gibbs free energy. Importantly, the number and type of atoms on both sides of the equation must be identical. Proving thermodynamic stability is challenging, as it requires knowledge not only of the crystal under consideration but also of any other possible crystal that can be formed with the given elements. There is an infinite number of such crystals, necessitating a large (and ideally infinite) database of known structures and energies. Databases such as Materials Project44 or the Open Quantum Materials Database (OQMD)52 are invaluable in this respect. They can document the thermodynamic stability of a given crystal with respect to all other crystals present in the database. If a crystal is found to be thermodynamically unstable, it will also be unstable with respect to an ideal infinite database. However, if a crystal is found to be thermodynamically stable with respect to a given database, this remains a conditional conclusion: a very stable crystal missing from the database could potentially alter the results. The lowest-energy combination of crystals from a given database consists of a set of crystals that are themselves thermodynamically stable with respect to that database. These crystals are on the so-called convex hull of the phase diagram for the considered elements. The energy difference between the studied crystal and this particular decomposition is called the (convex) hull energy (ΔEhull or ΔGhull(T)).For argyrodite-type crystals, there is a general decomposition reaction that typically points to the relevant crystals:18
| Li12−x−mMm+S6−xXx ⇌ Li8−mMm+S4 + (2 − x)Li2S + xLiX | (8) |
| Li6PS5X ⇌ Li3PS4 + Li2S + LiX | (9) |
If eqn (9) is used to compare the energies of the crystals involved, the energies should be expressed per formula unit (see eqn (10) for a different formulation). Li3PS4 can adopt different structures (see Section 4.3), with γ-Li3PS4 being the ground state structure. γ-Li3PS4 is thermodynamically stable (though it is not currently listed in the Materials Project database). Li2S, LiCl, LiBr, and LiI each have only one possible structure, with space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, and are all thermodynamically stable. It can be verified that for every element, the number of atoms on the left and right sides of eqn (9) is identical, as required.
m, and are all thermodynamically stable. It can be verified that for every element, the number of atoms on the left and right sides of eqn (9) is identical, as required.
The 0 K property ΔEhull has been computed for Li6PS5Cl. Deng et al. found it to be unstable by 21 meV per atom (ref. 25) with respect to decomposition into Li3PS4, Li2S, and LiCl. Schwieter et al. reported a similar value of about 30 meV per atom (Fig. 2a in ref. 54), while the Materials Project reports 80 meV per atom. We find ΔEhull to be 90.0 meV per atom (Table 4). The corresponding values for Li6PS5Br (ΔEhull = 60.3 meV per atom) and Li6PS5I (ΔEhull = 17.7 meV per atom) also predict these two crystals to be unstable. This contrasts with the fact that they are experimentally known to exist, and Li6PS5Cl can even be commercially bought. This contradiction may be due to limitations of the theoretical level (particularly the exchange–correlation functional used in DFT), it may indicate a metastable crystal structure that will decompose over a long time, or it may be a temperature-induced stability (unstable at 0 K but stable at higher temperatures). To better distinguish between these possibilities, we will calculate the temperature-dependent Gibbs free hull energy ΔGhull(T) in Sections 4.3 and 4.4.
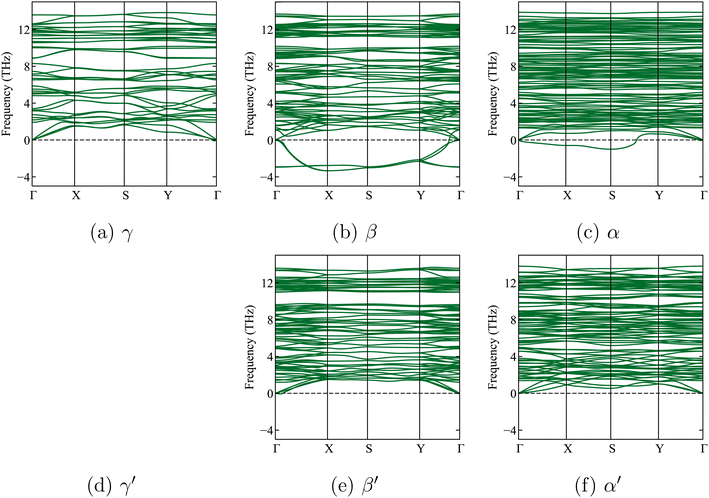 | ||
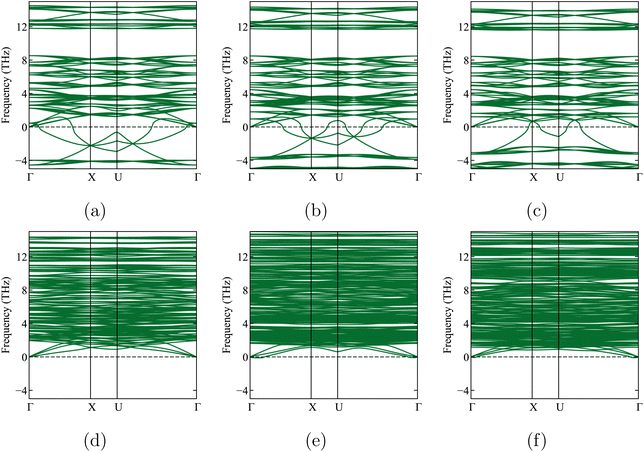
| Fig. 2 Calculated phonon band structures of the three x-Li3PS4 phases, without symmetry breaking (top, (a–c)) and with further symmetry breaking (bottom, (e and f)) (symmetry breaking had no effect for the γ phase). The dashed horizontal line shows the zero frequency. Soft modes (‘negative frequencies’) are clearly visible for the β and α phases without symmetry breaking. With symmetry breaking, the soft modes for β′ and α′ vanish. The very small negative frequencies near the Γ point in the γ phase are within an acceptable numerical error range of −0.3 THz, as previously reported in a study by Brivio et al.53 They are due to small residual stresses in the relaxed structure. | ||
| Phases | #Atoms | ΔE (eV per atom) | ΔEhull (meV per atom) | a (Å) | b (Å) | c (Å) |
|---|---|---|---|---|---|---|
| α-LPS | 32 | −0.982 | 9.0 | 8.602 | 9.048 | 7.817 |
| α-LPS′ | 32 | −0.978 | 5.3 | 8.481 | 9.135 | 7.985 |
| Exp | 8.643 | 9.046 | 8.477 | |||
| β-LPS | 32 | −0.984 | 2.4 | 12.945 | 7.821 | 6.013 |
| β- LPS′ | 32 | −0.986 | 1.2 | 12.874 | 7.875 | 6.045 |
| Exp | 12.819 | 8.219 | 6.123 | |||
| γ-LPS | 16 | −0.997 | 0.0 | 7.587 | 6.495 | 6.111 |
| γ-LPS′ | 16 | −0.997 | 0.0 | 7.587 | 6.495 | 6.111 |
| Exp | 7.708 | 6.535 | 6.136 | |||
| LPSCl | 52 | −1.130 | 90.0 | 10.052 | 10.052 | 10.052 |
| LPSCl′ | 52 | −1.215 | 12.6 | 9.832 | 9.609 | 9.609 |
| Exp | 9.857 | 9.857 | 9.857 | |||
| LPSBr | 52 | −1.124 | 60.3 | 10.083 | 10.083 | 10.083 |
| LPSBr′ | 52 | −1.179 | 5.24 | 9.818 | 9.884 | 9.727 |
| Exp | 9.986 | 9.986 | 9.986 | |||
| LPSI | 52 | −1.111 | 17.7 | 10.115 | 10.115 | 10.115 |
| LPSI′ | 52 | −1.139 | 0.0 | 9.953 | 10.002 | 9.923 |
| Exp | 10.145 | 10.145 | 10.145 | |||
| Li2S | 12 | −1.44 | 0.0 | 5.587 | 5.587 | 5.587 |
| Exp | 0.0 | 5.708 | 5.708 | 5.708 | ||
| LiCl | 8 | −1.89 | 0.0 | 5.046 | 5.046 | 5.046 |
| Exp | 0.0 | 5.129 | 5.129 | 5.129 | ||
| LiBr | 8 | −1.60 | 0.0 | 5.385 | 5.385 | 5.385 |
| Exp | 0.0 | 5.489 | 5.489 | 5.489 | ||
| LiI | 8 | −1.24 | 0.0 | 5.968 | 5.968 | 5.968 |
| Exp | 29.0 | 6.00 | 6.00 | 6.00 |
4.3 Li3PS4 as a test case for the temperature dependence formalism
We now leave Li6PS5X for a while and focus on one of its decomposition products: Li3PS4. Three known experimental structures of Li3PS4 as a function of temperature have been described in the literature.11,22,45,55,60,61 From the lowest temperatures up to 573 K, the γ-Li3PS4 phase has been reported.55,56,61 This is an orthorhombic structure with space group Pmn2a (ITA 31). For T > 573 K, a transformation to β-Li3PS4 occurs. This structure is also orthorhombic, with space group Pnma (ITA 62). The high-temperature α structure appears above 773 K.55,56,61 Homma et al. reported the latter phase as Li2PS4, i.e., with an incorrect stoichiometry, and with the space group ‘Pbcn’.62 Later, Kaup et al. showed by neutron powder diffraction that α has space group symmetry ‘Cmcm’ (ITA 63)55 and maintains the Li3PS4 stoichiometry. At high pressures, there is a δ-Li3PS4 phase that is not relevant to this study.61 We will apply a phase transition prediction formalism to Li3PS4 and compare the results with the aforementioned transition sequence and temperatures. If this approach works well for Li3PS4, it will increase confidence in its application to the temperature-dependent phase transformations in Li6PS5X.Starting from the experimental structures for the three different x-Li3PS4 phases, we perform DFT calculations at 0 K, optimize their geometry, and determine their formation energies. We subsequently check their dynamic stability by calculating the phonon spectra of the geometry-optimized structures at 0 K. We find that the low-temperature γ-Li3PS4 phase has no soft modes (Fig. 2a). However, the β-Li3PS4 and α-Li3PS4 phases do show soft modes when the cubic symmetry is maintained (Fig. 2b and c). This indicates that there are collective motions of atoms that will disintegrate the crystal rather than settle into a vibration mode with a finite amplitude. These soft modes disappear when the symmetry of the β and α phases is broken by applying a small random displacement to all atoms, followed by a new geometry optimization (Fig. 2e and f). The cif files for these structures, before and after breaking the symmetry, are provided in Section 1.3 of the ESI.†
In Table 4, the calculated lattice parameters for, among others, the three x-Li3PS4 phases are shown. The lattice parameters after symmetry breaking vary at the 0.1 Å level. For γ-Li3PS4, the structural change is at the noise level, as evidenced by its values for ΔEhull, ΔE, and the lattice parameters.
The coordinates and simulated XRD spectra for these cases are provided in the ESI (Sections 1.2 and 1.3).† As shown in Table 4, the symmetry breaking lowers the formation energies, confirming that these are indeed more stable configurations. Moreover, the formation energies become less negative along the series γ → β → α, consistent with the experimentally observed phases when increasing the temperature.
According to the Materials Project database, β-Li3PS4 (mp-985583, ref. 44) cannot lower its energy by a phase transformation or by decomposition into other crystals. In other words, it lies on the convex hull of the Li–P–S phase diagram. However, based on our calculations and literature,61 we know that γ-Li3PS4 (not yet documented in the Materials Project database) has an even lower energy. Therefore, γ-Li3PS4 lies on the convex hull. We can thus assign it a reference energy of zero and express the energy of the other crystals relative to this reference. These values are given in Table 4 in the column with the header ΔEhull – indicating the energy distance to the convex hull.
With the ground state energies and phonon information known, we can now use eqn (2) to obtain the temperature-dependent Gibbs free energy for all three Li3PS4 phases (the mixing entropy term in eqn (2) is zero here, as these are ordered crystals). Fig. 3 shows these Gibbs free energies as a function of temperature, plotted with respect to the Gibbs free energy of the γ-phase, which is taken to be zero at every temperature (horizontal blue line). It can be concluded from this figure that at the lowest temperatures, the γ-phase has the lowest Gibbs free energy and is therefore the most stable phase in this temperature range. This aligns with the experimental findings.56 As the temperature increases to approximately 330 K, the β-phase becomes stable, followed by the α-phase around 800 K. These results are summarized in the lower inset of Fig. 3 and compared with the experimentally observed phase transition temperatures. We conclude that the phase sequence is correctly predicted. The predicted transition temperatures quantitatively deviate notably from the experimental values, but on a scale of 1000 K, they are at least in the right range. This is the level of accuracy that can be expected for such properties, and deviations from the experiment are due to imperfections in the exchange–correlation functional used in the DFT calculations. If the (unknown) exact exchange–correlation functional would give energy differences that are only 0.005 eV per atom different from the PBE values, the transition temperatures can easily change by several hundred Kelvin. This example for Li3PS4 suggests that by this procedure, qualitatively correct phase stability predictions can be made for Li6PS5X – something we will do in Section 4.4.
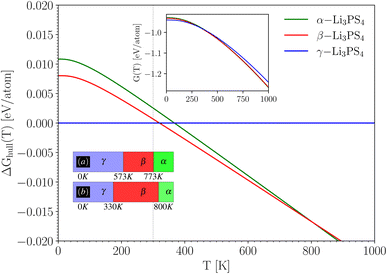 | ||
| Fig. 3 Temperature dependent Gibbs free energy difference ΔGhull(T) with respect to the convex hull (i.e. w.r.t. γ-Li3PS4) using eqn (2). The upper inset shows the individual Gibbs free energy curves G(T), which is for the γ-phase multiplied by a factor of 2 to match the number of formula units of the other polymorphs. The box diagram in the lower inset shows (a) the experimental temperature range for each phase, and (b) the temperature ranges deduced from taking the phase with the lowest calculated G at any T. | ||
4.4 Thermodynamic stability of Li6PS5X at T > 0 K
We will now use the same approach as in Section 4.3 to predict temperature-dependent phase transformations or decompositions for Li6PS5X (X = Cl, Br, I). We start by performing a geometry optimization and phonon calculation in the cubic state and find soft modes not only for Li6PS5Cl (Section 4.1) but for all three crystals (Fig. 5a–c). Breaking the symmetry and optimizing the geometry again, as was done for Li3PS4, results in structures with lower energy and no soft modes (Fig. 5d–f and Table 4).The relaxed coordinate files (cif) are given in the ESI, Section 1.4.† Looking at Table 4, we see that the symmetry breaking lowers the lattice parameters by about 0.2 Å for all three crystals.
Using the structures with broken symmetry, which are now demonstrated to be dynamically stable, the next step is to apply eqn (2). In contrast to the Li3PS4 example in Section 4.3, the entropy term does play a role here.
The mixing entropy term is approximated viaeqn (6). It represents the entropy contribution due to X/S anion site disorder at the 4a and 4c sites, while the rest of the atoms have defined Wyckoff positions (see Table 1 and references therein). Rather than using the actual S fractions (e.g. f = 0.62 for Li6PS5Cl), we used f = 0.5 instead. This maximizes the entropy contribution. As we will see, the entropy contribution is a small effect after all, and the results would not be significantly different if the actual fractions were used. For Li6PS5I, the I and S atoms are fully ordered at the 4a and 4c sites. Therefore, the entropy term was not included for Li6PS5I. Fig. 4a and c illustrate the effect of the entropy term for Li6PS5Cl and Li6PS5Br.
According to the Materials Project database, none of these Li6PS5X crystals lies on the convex hull of the Li–P–S–X phase diagram at 0 K. This means they will decompose into a combination of simpler crystals, with each of the decomposition products being on the convex hull. The decomposition products are always γ-Li3PS4, Li2S, and LiX. If the energies are expressed per atom, and considering that these four crystals have 52, 32, 12, and 8 atoms per unit cell, respectively, this is the translation of eqn (9) with the proper coefficients:
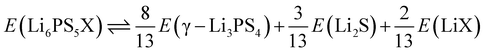 | (10) |
This is a realization of the general example in eqn (1). In order to calculate the T-dependent stability, we first geometry-optimize LiCl, LiBr, LiI, and Li2S, and calculate their phonon spectrum (γ-Li3PS4 has been done in Section 4.3, and these data are re-used). There were no soft modes. The Gibbs free energies for all three crystals (left-hand side of eqn (10)) and for the weighted sum of the simpler crystals (right-hand side of eqn (10)) are shown in Fig. 4. At any given temperature, the lowest among those curves represents the most stable situation at that temperature.
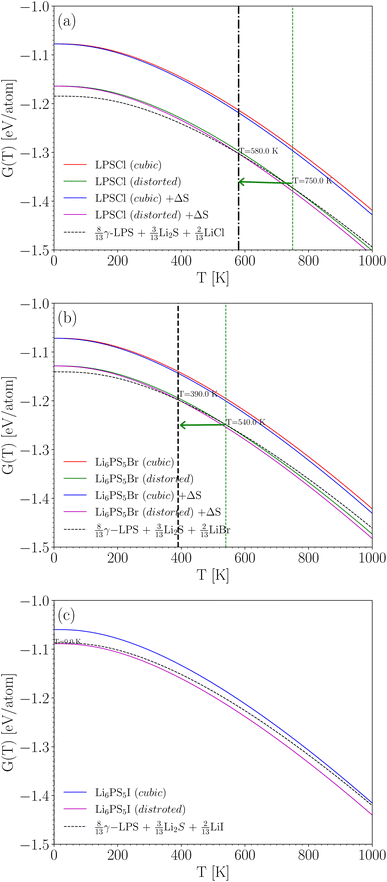
Fig. 4a shows the results for Li6PS5Cl. If cubic symmetry is kept, then the energy of Li6PS5Cl would be about 0.1 eV per atom above the energy of the weighted sum of simpler crystals (at 0 K). Indeed, this is essentially the same as the 0.09 eV per atom found in Table 4, with the only difference being that now the small zero-point energy difference is taken into account. When allowing for the symmetry breaking, the energy of Li6PS5Cl is only slightly higher than that of the decomposition products at low temperature and lower than that of the decomposition products above 580 K. This means that above 580 K, Li6PS5Cl is predicted to be thermodynamically stable against decomposition. This prediction is very consistent with the measured experimental crystallization temperature of 603 K.49,63 Note that the minor shift due to the entropy term is relevant here; without the entropy term, the temperature above which Li6PS5Cl is predicted to be stable rises to 750 K. The disorder on the S/Cl sublattices plays, therefore, a meaningful role in the stabilization of this crystal.
The situation is quite similar for Li6PS5Br, as shown in Fig. 4b. Li6PS5Br becomes thermodynamically stable above 390 K (this would have been 540 K without the entropy term). For Li6PS5I in Fig. 4c, the entropy term does not play a role (S and Cl are on their own Wyckoff sites, without mixing), but even without this term the energy of Li6PS5I is always lower than the energy of the decomposition products: Li6PS5I is predicted to be stable over the entire temperature range. Taken together, Fig. 4 indicates an increasing stability of Li6PS5X from X = Cl to X = I.
In conclusion, we can state that total energy and phonon calculations at the given level of theory (PBE-DFT with van der Waals corrections), combined with the proper structural information (allowing for symmetry reduction, including site disorder and the corresponding entropy contribution), provide an effective method to predict the thermodynamic stability of argyrodite-type solid-state electrolytes as a function of temperature.
4.5 Isovalent analog to Li6PS5Cl
When searching for materials optimized for a particular technological application, it has become possible to perform computational high-throughput searches: a large space of candidate materials is computationally screened for a specific property. Only those materials with the most attractive values for that property are taken to the next stage, where a computationally more expensive property is determined. By applying this procedure multiple times, a vast space can be filtered down to a handful of candidates that exhibit desirable values for all considered properties, without having to calculate the most expensive properties for the entire space.The underlying assumption in this screening approach is that the approximations used at different stages do not influence each other. If the ranking of materials after stage 1 changes considerably at stage 2, then selecting the subset of best-ranked materials after stage 1 could discard materials that would have been better-ranked at stage 2.
In this work, we do not perform a high-throughput study but rather examine a methodological question using a ‘mini-throughput’ approach as a model. The reasoning is as follows:
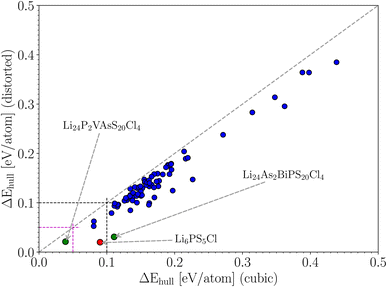
Argyrodite-type Li6PS5Cl is a known candidate for a solid-state electrolyte, and we have demonstrated in the previous sections that we can predict its stability as a function of temperature with reasonable accuracy. There are 4 P atoms in the unit cell of this crystal. We could define a family of crystals where phosphorus is replaced by (a combination of) other elements, assuming that the crystal structure is qualitatively maintained. A subset of this family is formed by combinations of 4 atoms that are collectively isovalent to four phosphorus atoms (this makes it more likely that there will be no crystal structure phase transitions). For instance, two W atoms (valence +5), one Os (+6), and one Te (+4) have an average valence of +5 per atom, which is identical to the valence of P. Such isovalent substitutions (which we restrict to a maximum of 3 different elements) are least likely to fundamentally alter the properties of Li6PS5Cl, while still offering ways to fine-tune some properties. By pseudo-randomly replacing the 4 phosphor atoms by up to 3 other elements (omitting elements that are too expensive, toxic or radioactive, or just implausible), and by considering only valence states that are normal for each element, a list of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 candidates was made. After applying the constraint of an isovalent substitution, 91 of those survived. They form the space for a “mini-throughput study”. They are listed in Table S1 of the ESI.† For each of these crystals, we calculated the total energy in the cubic phase and in the distorted phase, as was done before with Li6PS5X. The former is a relatively fast calculation, while the latter requires much more involved geometry optimization and should preferably be avoided in a full-fledged high-throughput study. The energy distance to the convex hull (ΔEhull) was calculated for both series and was plotted with respect to each other in Fig. 6. The distance to the convex hull is positive for all 91 cases, regardless of whether symmetry was broken or not. This means that none of these crystals is thermodynamically stable. The values of the energy distance are spread within the interval [0, 0.5] eV per atom. The energies in the distorted phase are systematically lower than the energies in the cubic phase, indicating that the tendency for symmetry lowering is present in all cases. There is a fair correlation between both data sets, which would lead at first sight to the conclusion that it is not necessary to calculate the geometry optimization for the distorted structures for all cases. However, the correlation is far from perfect, and therefore a considerable safety margin must be built in. If we want to avoid discarding cases with an energy below 0.05 eV per atom in the distorted set, we need to include all crystals with energies up to 0.12 eV per atom in the cubic set. If we want to avoid discarding cases with an energy below 0.10 eV per atom, we need to keep all high-symmetry crystals with an energy below 0.20 eV per atom. It is a rule of thumb in high-throughput studies that crystals up to 0.05 eV per atom above the convex hull still have a chance to be thermodynamically stable when experimentally tested.64 This level of disagreement is due to limitations in the level of theory (e.g. the XC-functional in DFT), the effect of thermal vibrations, or kinetic effects (stabilization of metastable states by energy barriers). This rule of thumb is valid for situations where the crystal structure is unambiguous. It means we need to apply this rule of thumb to the vertical axis of Fig. 6. If we had only the cubic data, we would need to keep all cubic crystals with an energy below 0.12 eV per atom (there are 12 of them, or 13% of the set) in order to find the 3 distorted crystals (3% of the set) with an energy below 0.05 eV per atom. The difference may not seem large, but if this were applied to a real high-throughput study starting from, say, 50
000 candidates was made. After applying the constraint of an isovalent substitution, 91 of those survived. They form the space for a “mini-throughput study”. They are listed in Table S1 of the ESI.† For each of these crystals, we calculated the total energy in the cubic phase and in the distorted phase, as was done before with Li6PS5X. The former is a relatively fast calculation, while the latter requires much more involved geometry optimization and should preferably be avoided in a full-fledged high-throughput study. The energy distance to the convex hull (ΔEhull) was calculated for both series and was plotted with respect to each other in Fig. 6. The distance to the convex hull is positive for all 91 cases, regardless of whether symmetry was broken or not. This means that none of these crystals is thermodynamically stable. The values of the energy distance are spread within the interval [0, 0.5] eV per atom. The energies in the distorted phase are systematically lower than the energies in the cubic phase, indicating that the tendency for symmetry lowering is present in all cases. There is a fair correlation between both data sets, which would lead at first sight to the conclusion that it is not necessary to calculate the geometry optimization for the distorted structures for all cases. However, the correlation is far from perfect, and therefore a considerable safety margin must be built in. If we want to avoid discarding cases with an energy below 0.05 eV per atom in the distorted set, we need to include all crystals with energies up to 0.12 eV per atom in the cubic set. If we want to avoid discarding cases with an energy below 0.10 eV per atom, we need to keep all high-symmetry crystals with an energy below 0.20 eV per atom. It is a rule of thumb in high-throughput studies that crystals up to 0.05 eV per atom above the convex hull still have a chance to be thermodynamically stable when experimentally tested.64 This level of disagreement is due to limitations in the level of theory (e.g. the XC-functional in DFT), the effect of thermal vibrations, or kinetic effects (stabilization of metastable states by energy barriers). This rule of thumb is valid for situations where the crystal structure is unambiguous. It means we need to apply this rule of thumb to the vertical axis of Fig. 6. If we had only the cubic data, we would need to keep all cubic crystals with an energy below 0.12 eV per atom (there are 12 of them, or 13% of the set) in order to find the 3 distorted crystals (3% of the set) with an energy below 0.05 eV per atom. The difference may not seem large, but if this were applied to a real high-throughput study starting from, say, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 crystals, it would mean that 6600 rather than 1650 crystals survive the first filtering stage. This implies that significantly more computation time would be required for the next stage.
000 crystals, it would mean that 6600 rather than 1650 crystals survive the first filtering stage. This implies that significantly more computation time would be required for the next stage.
The methodological lesson learned from this mini-throughput model is that in crystal sets where there is uncertainty involved in the structure, rather coarse limits on ΔEhull must be used to avoid eliminating too many candidates from the next stage. A more general way to formulate this is as follows: if a computational shortcut (here: using the cubic symmetry) changes the properties of interest (here: ΔEhull) to such an extent that the list of promising candidates is significantly altered, then this shortcut should probably not be used.
Having data in Fig. 6 for 91 broken-symmetry isovalent substitutions for Li6PS5Cl, it can be interesting to inspect whether there are crystals among them with stability similar to or better than that of Li6PS5Cl. To that end, the data point for Li6PS5Cl has been added to Fig. 6 as well. There are two other data points with similarly low ΔEhull on the vertical axis. One of them, where the four P atoms had been replaced by P2VAs, had a low ΔEhull in the cubic phase too, and would have been found with a tight limit on ΔEhull. The other one, where the four P atoms were replaced by As2BiP, has an equally small ΔEhull on the vertical axis but a much larger ΔEhull on the horizontal axis. It is an example of an interesting case that would have been discarded if a too coarse limit on ΔEhull had been used.
As a sidenote, we applied the same procedure to these two crystals that was used in the preceding sections to calculate the temperature-dependent thermodynamical stability of Li6PS5Cl. The decomposition into simpler crystals is more involved due to the larger number of elements present. It can be found by applying the phase diagram tool as implemented in the Pymatgen code43 (rather than formula units, all atoms in the unit cell are counted):
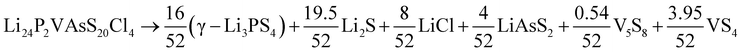 | (11) |
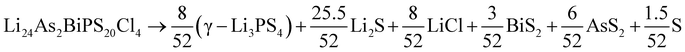 | (12) |
Among the 9 different decomposition products, 3 crystals are also present in the Li6PS5Cl decomposition. The others result from the presence of the elements V, As, and Bi. For these two predicted crystals, we performed phonon calculations for each of the decomposition products and the reactants, as described in Section 3. No soft modes were found, indicating that all crystals involved are dynamically stable.
Comparing the results in Fig. 7 to Fig. 4a for Li6PS5Cl, we conclude that neither of these two crystals is competitive with Li6PS5Cl in terms of stability. Note that the energy differences at T = 0 K in Fig. 7b and c (0.06 and 0.04 eV per atom) differ slightly from the values in Fig. 6 and Table S1.† This is because, in Fig. 7, zero-point corrections are included, and all reaction products were geometry-optimized with high precision. In Fig. 6, however, there are no zero-point corrections, and energies are taken directly from the Materials Project database.
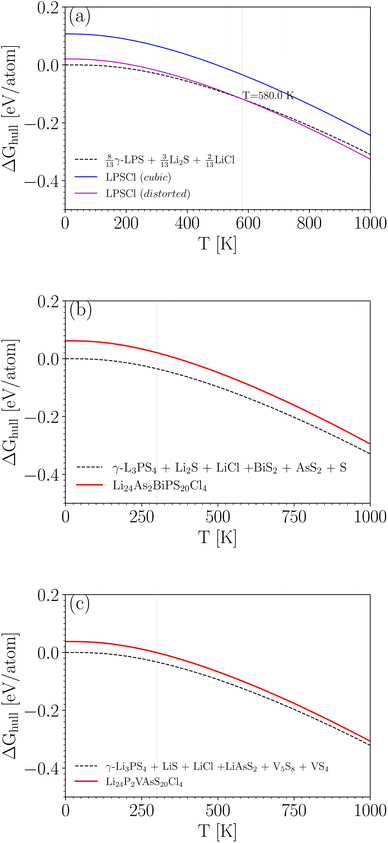 | ||
| Fig. 7 ΔGhull(T) for Li6PS5Cl (a) compared to two selected crystals that are analogous to Li6PS5Cl (b and c). The energy for the decomposition products at T = 0 K is taken as reference (zero). | ||
5 Conclusions
This work aims to illustrate, using the example of Li6PS5X, several aspects of high-throughput studies that are not always explicitly discussed. We highlighted potential issues when formulating the template crystal structure for first-principles calculations: the importance of understanding nomenclature and conventions in the experimental literature (cfr. 4c/4d), the necessity to recognize that experimental symmetry determination can represent an averaged higher symmetry that needs to be broken for more meaningful DFT energies, and the need to account for site disorder. Inspecting phonon band structures for soft modes is an effective method for removing artificially high symmetries.Moreover, for computational efficiency, high-throughput screening is often limited to information at 0 K. We demonstrated that more comprehensive stability information can be obtained from temperature-dependent calculations. Relying solely on 0 K information can be misleading. Finally, imposing overly strict filters can exclude potentially interesting cases from the search set, especially if the simplifications in calculations at one stage significantly alter the ranking of candidate materials. This was shown here by the fact that the stability ranking based on the energies of high-symmetry crystals differed substantially from the ranking based on energies from broken-symmetry structures.
We hope that this work will contribute to enhancing the quality of high-throughput studies and to setting appropriate expectations for interpreting the results they provide, allowing for a more realistic integration of high-throughput screening into materials design workflows for battery materials and other applications.
Data availability
Data for this article, including cif files and VASP input and output files are available at Zenodo at https://doi.org/10.5281/zenodo.13744522. A selection of this data as well as some additional pictures have been included as part of the ESI.†Author contributions
M. S. and S. C. were responsible for the conceptualization of the study. A. I. B., S. K., C. J., and M. S. handled data curation. Formal analysis was conducted by A. I. B. Funding acquisition was handled by M. S. and S. C. A. I. B., S. K., C. J. and M. S. were involved in the investigation. The methodology was developed by S. C. and M. S., with additional contributions from D. V., C. J. and A. I. B. S. C. and M. S. provided supervision and dealt with project administration. Software development and coding were carried out by C. J., M. S. and D. V. The validation process was overseen by S. C. and carried out by A. I. B., S. K. and D. V. Visualization tasks were performed by A. I. B. The original draft of the manuscript was prepared by A. I. B. and S. C., with critical writing, review, and editing contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been funded as an innovation project by the VLAIO agency (Flanders Innovation & Entrepreneurship), with the acronym SCONE, and by a bilateral Umicore/Ghent University project with the acronym BRIDGE. The authors gratefully acknowledge discussions and collaboration with the SCONE project partners from Umicore (Vishank Kumar, Alexander Hofmann and Florencia Marchini) and CICe (Alfonso Gallo and Javier Carrasco). The computational resources and services used in this work were provided by the VSC (Flemish Supercomputer Center). S. C. acknowledges financial support from OCAS NV by an OCAS-endowed chair at Ghent University.References
- S. Luo, T. Li, X. Wang, M. Faizan and L. Zhang, High-throughput computational materials screening and discovery of optoelectronic semiconductors, WIREs Comput. Mol. Sci., 2021, 11(1), e1489, DOI:10.1002/wcms.1489.
- C. Chen, D. T. Nguyen and S. J. Lee, et al., Accelerating computational materials discovery with artificial intelligence and cloud high-performance computing: From large-scale screening to experimental validation, J. Am. Chem. Soc., 2024, 146(29), 20009–20018, DOI:10.1021/jacs.4c03849.
- M. T. Dunstan, A. Jain and W. Liu, et al., Large scale computational screening and experimental discovery of novel materials for high temperature co2 capture, Energy Environ. Sci., 2016, 9, 1346–1360, 10.1039/C5EE03253A.
- A. M. Mroz, V. Posligua, A. Tarzia, E. H. Wolpert and K. E. Jelfs, Into the unknown: How computation can help explore uncharted material space, J. Am. Chem. Soc., 2022, 144(41), 18, DOI:10.1021/jacs.2c06833.
- J. Hu, S. Stefanov and Y. Song, et al., Materialsatlas.org: A materials informatics web app platform for materials discovery and survey of state-of-the-art, npj Comput. Mater., 2022, 8(1), 65, DOI:10.1038/s41524-022-00750-6.
- P. Borlido, J. Schmidt, H.-C. Wang, S. Botti and M. A. L. Marques, Computational screening of materials with extreme gap deformation potentials, npj Comput. Mater., 2022, 8(1), 156, DOI:10.1038/s41524-022-00811-w.
- Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, A sulphide lithium super ion conductor is superior to liquid ion conductors for use in rechargeable batteries, Energy Environ. Sci., 2014, 7, 627–631, 10.1039/C3EE41655K.
- F. Zheng, M. Kotobuki, S. Song, M. O. Lai and L. Lu, Review on solid electrolytes for all-solid-state lithium-ion batteries, J. Power Sources, 2018, 389, 198–213, DOI:10.1016/j.jpowsour.2018.04.022.
- M. Weiss, F. J. Simon and M. R. Busche, et al., From liquid- to solid-state batteries: Ion transfer kinetics of heteroionic interfaces, Electrochem. Energy Rev., 2020, 3, 221–238, DOI:10.1007/S41918-020-00062-7.
- W. Zhao, J. Yi, P. He and H. Zhou, Solid-state electrolytes for lithium-ion batteries: Fundamentals, challenges and perspectives, Electrochem. Energy Rev., 2019, 2(4), 574–605, DOI:10.1007/S41918-019-00048-0.
- W. G. Suci, H. K. Aliwarga, Y. R. Azinuddin, R. B. Setyawati, K. N. R. Stulasti and A. Purwanto, Review of various sulfide electrolyte types for solid-state lithium-ion batteries, Open Eng., 2022, 12, 409–423, DOI:10.1515/eng-2022-0043.
- S. Wang, Y. Zhang and X. Zhang, et al., High-conductivity argyrodite li6ps5cl solid electrolytes prepared via optimized sintering processes for all-solid-state lithium-sulfur batteries, ACS Appl. Mater. Interfaces, 2018, 10(49), 42, DOI:10.1021/acsami.8b15121.
- M. A. Kraft, S. P. Culver and M. Calderon, et al., Influence of lattice polarizability on the ionic conductivity in the lithium superionic argyrodites li6ps5x (x = cl, br,i), J. Am. Chem. Soc., 2017, 139, 10, DOI:10.1021/jacs.7b06327.
- H.-J. Deiseroth, S.-T. Kong and H. Eckert, et al., Li6ps5x: A class of crystalline li-rich solids with an unusually high li+ mobility, Angew. Chem., Int. Ed., 2008, 47(4), 755–758, DOI:10.1002/anie.200703900.
- H.-J. Deiseroth, J. Maier, K. Weichert, V. Nickel, S.-T. Kong and C. Reiner, Li7ps6 and li6ps5x (x: Cl, br,i): Possible three-dimensional diffusion pathways for lithium ions and temperature dependence of the ionic conductivity by impedance measurements, Z. Anorg. Allg. Chem., 2011, 637(10), 1287–1294, DOI:10.1002/zaac.201100158.
- R. P. Rao and S. Adams, Studies of lithium argyrodite solid electrolytes for all-solid-state batteries, Phys. Status Solidi A, 2011, 208(8), 1804–1807, DOI:10.1002/pssa.201001117.
- S. Boulineau, J.-M. Tarascon, J.-B. Leriche and V. Viallet, Electrochemical properties of all-solid-state lithium secondary batteries using li-argyrodite li6ps5cl as solid electrolyte, Solid State Ionics, 2013, 242, 45–48, DOI:10.1016/j.ssi.2013.04.012.
- H. M. Chen, C. Maohua and S. Adams, Stability and ionic mobility in argyrodite-related lithium-ion solid electrolytes, Phys. Chem. Chem. Phys., 2015, 17, 16, 10.1039/c5cp01841b.
- O. Pecher, S.-T. Kong and T. Goebel, et al., Atomistic characterisation of li+ mobility and conductivity in Li7−xPS6−xIx argyrodites from molecular dynamics simulations, solid-state nmr, and impedance spectroscopy, Chem.—Eur. J., 2010, 16(28), 8347–8354, DOI:10.1002/chem.201000501.
- S. Boulineau, M. Courty, J.-M. Tarascon and V. Viallet, Mechanochemical synthesis of li-argyrodite li6ps5x (x=cl, br,i) as sulfur-based solid electrolytes for all solid state batteries application, Solid State Ionics, 2012, 221, 1–5, DOI:10.1016/j.ssi.2012.06.008.
- R. P. Rao, N. Sharma, V. Peterson and S. Adams, Formation and conductivity studies of lithium argyrodite solid electrolytes using in-situ neutron diffraction, Solid State Ionics, 2013, 230, 72–76, DOI:10.1016/j.ssi.2012.09.014 , Special Issue for the E-MRS Spring Meeting Symposium C: “Solid State Ionics: Mass and Charge Transport Across and Along Interfaces of Functional Material” Strasbourg/France, May 14-17, 2012.
- N. Minafra, M. A. Kraft and T. Bernges, et al., Local charge inhomogeneity and lithium distribution in the superionic argyrodites li6ps5x (x = cl, br,i), Inorg. Chem., 2020, 59, 11, DOI:10.1021/ACS.INORGCHEM.0C01504.
- B. J. Morgan, Mechanistic origin of superionic lithium diffusion in anion-disordered li6ps5x argyrodites, Chem. Mater., 2021, 33, 2004–2018, DOI:10.1021/ACS.CHEMMATER.0C03738.
- Z. Wang and G. Shao, Theoretical design of solid electrolytes with superb ionic conductivity: Alloying effect on li+ transportation in cubic li6pa5x chalcogenides, J. Mater. Chem. A, 2017, 5, 21, 10.1039/c7ta06986c.
- Z. Deng, Z. Zhu, I. H. Chu and S. P. Ong, Data-driven first-principles methods for the study and design of alkali superionic conductors, Chem. Mater., 2017, 29, 281–288, DOI:10.1021/acs.chemmater.6b02648.
- M. D'Amore, L. E. Daga and R. Rocca, et al., From symmetry breaking in the bulk to phase transitions at the surface: A quantum-mechanical exploration of lpscl argyrodite superionic conductor, Phys. Chem. Chem. Phys., 2022, 24, 22, 10.1039/d2cp03599e.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11, DOI:10.1103/PhysRevB.54.11169.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775, DOI:10.1103/PhysRevB.59.1758.
- M. Ernzerhof and G. E. Scuseria, Assessment of the perdew-burke-ernzerhof exchange-correlation functional, J. Chem. Phys., 1999, 110, 5029–5036, DOI:10.1063/1.478401.
- E. Bosoni, L. Beal and M. Bercx, et al., How to verify the precision of density-functional-theory implementations via reproducible and universal workflows, Nat. Rev. Phys., 2024, 6(1), 45–58, DOI:10.1038/s42254-023-00655-3.
- K. Lejaeghere, G. Bihlmayer and T. Björkman, et al., Reproducibility in density functional theory calculations of solids, Science, 2016, 351(6280), aad3000, DOI:10.1126/science.aad3000.
- H. J. Monkhorst and J. D. Pack, Special points for brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192, DOI:10.1103/PhysRevB.13.5188.
- M. Methfessel and A. T. Paxton, High-precision sampling for brillouin-zone integration in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621, DOI:10.1103/PhysRevB.40.3616.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465, DOI:10.1002/jcc.21759.
- H. Nishihara, H. Yasuoka, Y. Oka, K. Kosuge and S. Kachi, Nmr of 51v in the antiferromagnetic state of v5s8, J. Phys. Soc. Jpn., 1977, 42(3), 787–790, DOI:10.1143/JPSJ.42.787.
- H. Nozaki, M. Umehara, Y. Ishizawa, M. Saeki, T. Mizoguchi and M. Nakahira, Magnetic properties of v5s8 single crystals, J. Phys. Chem. Solids, 1978, 39(8), 851–858, DOI:10.1016/0022-3697(78)90144-0.
- S. Funahashi, H. Nozaki and I. Kawada, Magnetic structure of v5s8, J. Phys. Chem. Solids, 1981, 42(11), 1009–1013, DOI:10.1016/0022-3697(81)90064-0.
- M. Knecht, H. Ebert and W. Bensch, Electronic and magnetic properties of, J. Phys.: Condens. Matter, 1998, 10(42), 9455, DOI:10.1088/0953-8984/10/42/011.
- Y. L. Page and P. Saxe, Symmetry-general least-squares extraction of elastic coefficients from ab initio total energy calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 174, DOI:10.1103/PhysRevB.63.174103.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5, DOI:10.1016/J.SCRIPTAMAT.2015.07.021.
- A. M. Ganose, A. J. Jackson and D. O. Scanlon, Sumo: Command-line tools for plotting and analysis of periodic *ab initio* calculations, J. Open Source Softw., 2018, 3(28), 717, DOI:10.21105/joss.00717.
- S. P. Ong, A. Jain, G. Hautier, B. Kang and G. Ceder, Thermal stabilities of delithiated olivine mpo4 (m=fe, mn) cathodes investigated using first principles calculations, Electrochem. Commun., 2010, 12, 427–430, DOI:10.1016/J.ELECOM.2010.01.010.
- S. P. Ong, L. Wang, B. Kang and G. Ceder, Li - fe - p - o2 phase diagram from first principles calculations, Chem. Mater., 2008, 20, 1798–1807, DOI:10.1021/cm702327g.
- A. Jain, S. P. Ong and G. Hautier, et al., Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011, DOI:10.1063/1.4812323.
- R. L. Kam, K. J. Jun, L. Barroso-Luque, J. H. Yang, F. Xie and G. Ceder, Crystal structures and phase stability of the li2s-p2s5 system from first principles, Chem. Mater., 2023, 35, 9111–9126, DOI:10.1021/ACS.CHEMMATER.3C01793.
- P. R. Rayavarapu, N. Sharma, V. K. Peterson and S. Adams, Variation in structure and li +-ion migration in argyrodite-type li 6ps 5x (x = cl, br, i) solid electrolytes, J. Solid State Electrochem., 2012, 16, 1807–1813, DOI:10.1007/s10008-011-1572-8.
- A. Gautam, M. Ghidiu, E. Suard, M. A. Kraft and W. G. Zeier, On the lithium distribution in halide superionic argyrodites by halide incorporation in Li7-xPS6-xClx, ACS Appl. Energy Mater., 2021, 4, 7309–7315, DOI:10.1021/acsaem.1c01417.
- I. Hanghofer, B. Gadermaier and H. M. R. Wilkening, Fast rotational dynamics in argyrodite-type Li6PS5x (X: Cl, Br, I) as seen by 31P nuclear magnetic relaxation - on cation-anion coupled transport in thiophosphates, Chem. Mater., 2019, 31, 4591–4597, DOI:10.1021/acs.chemmater.9b01435.
- C. Yu, L. van Eijck, S. Ganapathy and M. Wagemaker, Synthesis, structure and electrochemical performance of the argyrodite li6ps5cl solid electrolyte for li-ion solid state batteries, Electrochim. Acta, 2016, 215, 93–99, DOI:10.1016/J.ELECTACTA.2016.08.081.
- S.-T. Kong, H.-J. Deiseroth and C. Reiner, et al., Lithium argyrodites with phosphorus and arsenic: Order and disorder of lithium atoms, crystal chemistry, and phase transitions, Chem.—Eur. J., 2010, 16(7), 2198–2206, DOI:10.1002/chem.200902470.
- A. Golov and J. Carrasco, Molecular-level insight into the interfacial reactivity and ionic conductivity of a li-argyrodite li6ps5cl solid electrolyte at bare and coated li-metal anodes, ACS Appl. Mater. Interfaces, 2021, 13(36), 43, DOI:10.1021/acsami.1c127533.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Materials design and discovery with high-throughput density functional theory: The Open Quantum Materials Database (OQMD), JOM, 2013, 65(11), 1501–1509, DOI:10.1007/s11837-013-0755-4.
- F. Brivio, J. M. Frost and J. M. Skelton, et al., Lattice dynamics and vibrational spectra of the orthorhombic, tetragonal, and cubic phases of methylammonium lead iodide, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144–308, DOI:10.1103/PHYSREVB.92.144308.
- T. K. Schwietert, V. A. Arszelewska and C. Wang, et al., Clarifying the relationship between redox activity and electrochemical stability in solid electrolytes, Nat. Mater., 2020, 19, 428–435, DOI:10.1038/s41563-019-0576-0.
- K. Kaup, L. Zhou, A. Huq and L. F. Nazar, Impact of the li substructure on the diffusion pathways in alpha and beta li3ps4: An: In situ high temperature neutron diffraction study, J. Mater. Chem. A, 2020, 8, 12, 10.1039/d0ta02805c.
- K. Homma, M. Yonemura, T. Kobayashi, M. Nagao, M. Hirayama and R. Kanno, Crystal structure and phase transitions of the lithium ionic conductor li3ps4, Solid State Ionics, 2011, 182, 53–58, DOI:10.1016/j.ssi.2010.10.001.
- E. Zintl, A. Harder and B. Dauth, Gitterstruktur der oxyde, sulfide, selenide und telluride des lithiums, natriums und kaliums, Z. Elektrochem. Angew. Phys. Chem., 1934, 40(8), 588–593, DOI:10.1002/bbpc.19340400811.
- A. Levin’sh, M. Straumanis and K. Karlsons, Präzisions Bestimming von Gitterkonstanten hygroskopischer Verbindungen (Li Cl, Na Br), Z. Phys. Chem., Abt. B, 1938, 40, 146–150 Search PubMed.
- H. Ott, Die raumgitter der lithiumhalogenide, Phys. Z., 1923, 24, 209–213 CAS.
- M. S. Lim and S. H. Jhi, First-principles study of lithium-ion diffusion in β-li3ps4 for solid-state electrolytes, Curr. Appl. Phys., 2018, 18, 541–545, DOI:10.1016/j.cap.2018.03.002.
- S. Iikubo, K. Shimoyama and S. Kawano, et al., Novel stable structure of Li3PS4 predicted by evolutionary algorithm under high-pressure, AIP Adv., 2018, 8(1), 015008, DOI:10.1063/1.5011401.
- K. Homma, M. Yonemura, M. Nagao, M. Hirayama and R. Kanno, Crystal structure of high-temperature phase of lithium ionic conductor, li3ps4, J. Phys. Soc. Jpn., 2010, 79, 90–93, DOI:10.1143/JPSJS.79SA.90.
- R. P. Rao, N. Sharma, V. K. Peterson and S. Adams, Formation and conductivity studies of lithium argyrodite solid electrolytes using in-situ neutron diffraction, Solid State Ionics, 2013, 230, 72–76, DOI:10.1016/j.ssi.2012.09.014.
- M. Aykol, S. S. Dwaraknath, W. Sun and K. A. Persson, Thermodynamic limit for synthesis of metastable inorganic materials, Sci. Adv., 2018, 4(4), 0148, DOI:10.1126/sciadv.aaq0148.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta06603k |
| This journal is © The Royal Society of Chemistry 2025 |