Raman spectroscopy study of K-birnessite single crystals

Abstract

Raman studies of manganese dioxide (MnO₂), a crucial material for sustainable and innovative solutions in energy storage and environmental remediation, have predominantly been conducted on fine-grained aggregates, leaving the identification of Raman peaks open to debate. To address this, in this study the Raman spectra of potassium (K)-birnessite single crystals with varying crystal thickness, temperature, and polarization configuration are measured. An acoustic phonon mode of birnessite is identified, which is found to be sensitive to both crystal thickness and interlayer spacing, with its frequency increasing by approximately 35% when the c-axis lattice parameter is reduced from 0.70 to 0.65 nm by the removal of interlayer water. In contrast, the dependence of the optical phonon modes on crystal thickness and interlayer spacing is not particularly noticeable. It is demonstrated that the characteristic Raman peak of K-birnessite, observed at approximately 559 cm⁻¹, originates from a two-dimensional hexagonal configuration of cations and water molecules within the interlayer space, rather than from the MnO₆ octahedra. Additionally, the doubly degenerate vibrational mode of MnO₆ octahedra, corresponding to the motion of oxygen atoms in the basal plane, splits into two, confirming that the MnO₆ octahedra are distorted by the Jahn–Teller effect.

---

Introduction

One of the numerous polymorphs of manganese dioxide (MnO₂) is birnessite (δ-MnO₂), a material comprising layers of edge-sharing MnO₆ octahedra arranged in the c-axis direction with charge-balancing cations and structural water intercalated in the interlayer space.^1–3 In comparison to the tunnels of other MnO₂ polymorphs, such as α-MnO₂, β-MnO₂, and λ-MnO₂ with spinel structures,^4–6 the interlayer space of birnessite has a larger volume and surface area, allowing more ions or molecules to intercalate into or deintercalate from the material. Birnessite exhibits an excellent ion exchange capacity, electrochemical activity, and catalytic performance, making it a versatile material suitable for a wide range of industries focused on sustainability and pollution control, including environmental remediation, energy storage, catalysis, and sensing.^6–12

In birnessite, interlayer cations and water molecules coordinate with adjacent MnO₂ layers to modulate the oxidation state of manganese, thereby causing Jahn–Teller distortions of the MnO₆ octahedra with Mn³⁺ centers and adjusting the relative positions of the MnO₆ octahedra above and below.^13–16 It has been reported that the symmetry of birnessite decreases from hexagonal to monoclinic or triclinic by Jahn–Teller distortions as more Mn⁴⁺ is replaced with Mn³⁺.^17,18 The quantity and configuration of interlayer cations and water molecules are intimately related to the structural stability and functionality of layered materials, and it has been postulated that they form complex ordered or disordered hydrogen-bonded structures. Based on density functional theory (DFT) calculations, Sudare et al. proposed that in layered double hydroxides, interlayer water molecules form two-dimensional (2D) or three-dimensional (3D) irregular hydrogen-bonded structures with interlayer ions, depending on the quantity of interlayer ions and water.¹⁹ On the other hand, Matsui et al. proposed that interlayer water molecules in monoclinic Na-birnessite with C2/m symmetry are hydrated around cations bound to the MnO₆ sites with Mn³⁺ centers, forming 2D hexamer-like structures.²⁰

Raman spectroscopy, a powerful and non-destructive analytical technique for observing the vibrational modes of materials down to the micrometer scale without special sample preparation,^21,22 has been applied to the study of MnO₂ in a variety of ways. These include the identification and differentiation of different polymorphs of MnO₂, the monitoring of structural changes during synthesis or electrochemical processes, and the analysis of the oxidation states of manganese ions.^2,3,23–27 Since the pioneering studies conducted by Julien and colleagues,^28,29 Raman spectroscopic studies of MnO₂ have made significant progress over the past two decades. However, Raman studies have predominantly been conducted on aggregates of fine grains with different crystallinities, structures, and crystallographic orientations. Furthermore, the presence of impurities, interlayer cations, and water molecules poses inherent challenges to the accurate and precise analysis of Raman spectra. Consequently, inaccuracies or discrepancies persist not only in the identification of Raman peaks but also in the correlation between the crystal structure and Raman peaks, which are fundamental aspects of MnO₂ Raman spectroscopy for its characterization and applications.

In order to address this limitation, in this study, the Raman spectra of potassium ion intercalated layered MnO₂ (K-birnessite) single crystals were measured down to 50 cm⁻¹ for the first time, considering variations in crystal thickness, temperature, and polarization configuration. By measuring the Raman spectra of impurity-free K-birnessite single crystals in air and a vacuum, we were able to identify both the acoustic phonon mode of birnessite and the splitting of the doubly degenerate vibrational mode of MnO₆ octahedra. Moreover, the Raman peak at 559 cm⁻¹ was verified to originate from the 2D hexagonal arrangement of K⁺ ions and water molecules within the interlayer space. This provides an explanation for the observation of this peak in birnessite,^2,3,26,30,31 which has a relatively large and flexible 2D interlayer space. The interlayer spacing exerts a significant influence on the frequency of the acoustic phonon mode of birnessite, whereas its effect on the frequency of the optical phonon modes is negligible. The new insights into the Raman properties of K-birnessite obtained in this work are expected to play an important role in the characterization and applications of MnO₂ in a variety of contexts, including determination of its crystal structure and symmetry as well as investigation of the ion storage mechanism.

Experimental

K-birnessite single crystals were grown on c-sapphire substrates; details of the crystal growth process are described in a previous study.³¹ The thickness of the crystals was measured in a laboratory environment using tapping mode atomic force microscopy (AFM). An X-ray diffractometer (RIGAKU, SmartLab) equipped with a CuKα source was used to obtain X-ray diffraction (XRD) data. Micro-Raman spectra were collected in a 180° backscattering configuration using a 532 nm laser line focused on the crystal surface through a 50× long working distance objective (numerical aperture = 0.8) as excitation light. The scattered light was analyzed using a Horiba Jobin Yvon LabRAM HR spectrometer, which was equipped with a grating of 1800 grooves per mm and a cooled charge-coupled device with 1024 × 256 pixels. Each Raman spectrum was obtained by conducting two measurements with an acquisition time of 60 s and averaging the two spectra. The laser power on the crystals was maintained below 0.3 mW to ensure that the Raman spectrum remained unaltered even after multiple measurements at the same location, confirming that the effect of laser heating was negligible. The temperature of the crystals was controlled by placing the sample in contact with thermal paste on a heating stage in a home-built vacuum chamber, where the vacuum was maintained below 40 mTorr. The A_1g peak of c-sapphire at 417.3 cm⁻¹ for 532 nm incident light, calibrated to the T_2g peak of Si at 520.7 cm⁻¹ in a laboratory environment, was employed as an internal reference to calibrate the frequencies of the Raman peaks of K-birnessite.

Results and discussion

Shape and polarization configuration effect

Crystals grown on the c-sapphire substrate³¹ showed a blue, yellow, or purple color under a light microscope. They were predominantly triangular in shape, with some trapezoidal or irregular shapes; on rare occasions, a hexagonal shape was observed (ESI Fig. S1†). Blue crystals grew to over 15 μm on one side, while yellow crystals were up to 7 to 8 μm in size and purple crystals were even smaller. The thicknesses of the blue, yellow, and purple crystals employed for Raman spectral measurements were typically within the ranges of 30–50, 60–80, and 90–105 nm, respectively, indicating that as the color of the crystals changed from blue to yellow to purple, the thickness exhibited a corresponding increase (ESI Fig. S2†). In a laboratory environment (∼25 °C and air), only the (001) and (002) peaks at 2θ = 12.54° and 25.26°, respectively, were observed in XRD patterns obtained using the CuKα line, indicating that the c-axis of the crystals was oriented perpendicular to the c-sapphire substrate.³¹

Optical images of blue and yellow crystals and their typical Raman spectra are presented in Fig. 1. It can be observed that the frequency of each Raman peak and the relative intensity of the peaks exhibit minimal variation across different crystals (ESI Fig. S4†). Furthermore, the Raman spectra of different regions within a crystal exhibit high similarity, confirming the single crystal structure (ESI Fig. S5†). All crystals display Raman features characteristic of monoclinic birnessite:^3,26 (i) a ν₁ peak with much lower intensity compared to the ν₂ peak, (ii) two peaks, ν₃ and ν₄, rather than a single peak at around 500 cm⁻¹, and (iii) the appearance of a ν₆ peak. The ω₁ peak is commonly observed in birnessite and varies in position and intensity depending on the type of cation, particularly in K-birnessite where it appears as a distinct peak rather than as a weak shoulder of the ν₂ peak.^2,31 Accordingly, the Raman spectra reveal single crystals of monoclinic K-birnessite on the c-sapphire substrate.

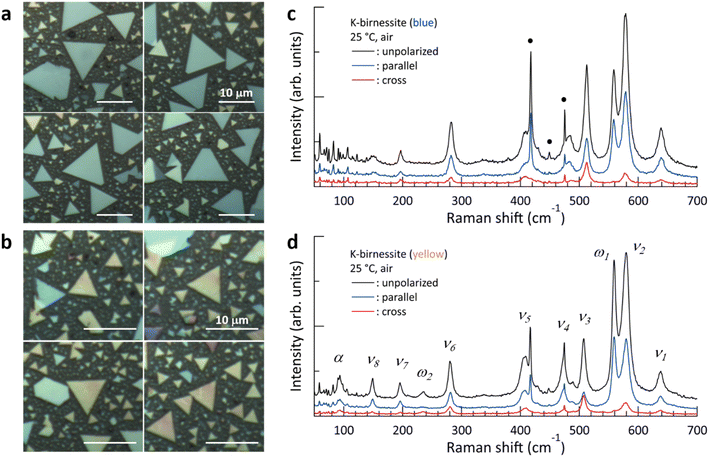Fig. 1 (a and b) Light microscopy images of blue and yellow crystals, respectively. (c and d) Typical Raman spectra of blue and yellow crystals obtained in a laboratory environment. The blue (parallel) and red (cross) spectra were obtained with parallel and perpendicular polarization directions, respectively, of the incident and scattered light. The black spectra (unpolarized) were obtained with no analyzer in the scattered light path. For the sake of convenience, each peak is named as in (d). The weak, narrow peaks below 150 cm⁻¹ and those marked with black circles (●) represent the Raman peaks of the c-sapphire substrate (ESI Fig. S3†).

The following differences were observed in the Raman spectra of the yellow crystals compared to those of the blue crystals: (i) a significant increase in the relative intensity of the ω₁ peak compared to the other Raman peaks, accompanied by the appearance of the ω₂ peak at 235 cm⁻¹ and (ii) the appearance of the α peak at 97 cm⁻¹. A Raman peak below 100 cm⁻¹ was recently observed in K-birnessite by Post et al.,² but its identity remains unknown. The Raman spectra were analyzed by fitting them with Lorentzian functions (ESI Fig. S6†), and the results are summarized in Table 1. The electrical and optical properties of layered materials are known to be influenced by interlayer interactions and interfacial effects, and these effects on material properties are observed to diminish gradually with an increase in the number of layers.^22,32 Here, the frequencies of the ν₃, ν₄, and α peaks in the blue and yellow crystals exhibit notable differences from one another in comparison to the other peaks. Additionally, the ω₂ peak emerges in the case of the thicker yellow crystals. However, there was little overall difference between the Raman spectra of the yellow and purple crystals.

Table 1 Raman peak frequencies of blue and yellow K-birnessite single crystals measured in a laboratory environment. The asterisk (*) indicates the frequency measured at 30 °C in a vacuum. In the case of the blue crystal, no birnessite Raman peak was observed between 50 and 100 cm⁻¹ in the laboratory environment, but it appeared in a vacuum. The Raman peak frequencies were obtained by averaging the results of five blue and yellow crystals each

	α	ν 8	ν 7	ω 2	ν 6	ν 5	ν 4	ν 3	ω 1	ν 2	ν 1
Blue crystal (cm^−1)	63.2*	150.3	196.7	—	281.7	406.9	482.0	511.8	558.3	578.2	638.7
Yellow crystal (cm^−1)	96.5	148.9	196.5	234.8	280.9	407.6	473.0	507.6	559.6	579.4	638.5

---

There are nine active Raman modes (3A_g + 6B_g) in monoclinic birnessite with point group C_2h. It is known that the Raman spectrum of MnO₂ consists of the vibrational modes of MnO₆ octahedra in the high-frequency region above 500 cm⁻¹ and those of the structures formed by coordination between oxygen in the MnO₂ layers and interlayer cations/water in the low-frequency region.² In particular, the ν₆ peak is attributed to the stretching mode of the MO₆ (M = alkali) group, while the ν₅ peak is attributed to the asymmetric stretching mode of M–O tetrahedra, with some oxygen atoms from the MnO₂ layer.^2,3,26–28 However, these are still under debate.

The totally symmetric A_1g mode of the c-sapphire with a hexagonal structure at 417 cm⁻¹ almost disappears in the cross Raman spectra.³³ The ν₁ peak is the A_g mode of the MnO₆ octahedra, in which the six Mn–O bonds stretch and compress in phase while Mn remains stationary in its equilibrium position.³⁴ In the case of chalcophanite, which consists of undistorted MnO₆ octahedra with all Mn in the 4+ valence state, the depolarization ratio (ρ = I_cross/I_parallel) of the ν₁ peak at 670 cm⁻¹ is approximately zero, confirming a totally symmetric mode.² However, the depolarization ratio of the ν₁ peak in Fig. 1 is approximately 0.2, indicating that as some Mn⁴⁺ are replaced by Mn³⁺ and vacancies in K-birnessite, the symmetry of the MnO₆ octahedra is broken due to Jahn–Teller distortion, and the frequency of the peak is redshifted to 639 cm⁻¹ by the increase in the average distance of Mn–O.

Previously, the ν₂ and ω₁ peaks were attributed to the motion of oxygen atoms in the basal plane of MnO₆. The ν₂ peak was identified as the A_g mode, while the ω₁ peak was attributed to the asymmetric B_g mode.² In contrast, Rasouli et al. attributed the ω₁ peak to out-of-plane vibrational modes of Mn–O bonds.³¹ However, Fig. 1 demonstrates that the depolarization ratio of the ω₁ peak is approximately zero, indicating that the ω₁ peak is a totally symmetric vibrational mode of the structure that will be revealed later. The α, ν₁, ν₂, and ω₁ peaks will be discussed in detail in subsequent sections. The depolarization ratio of the ν₃ peak at around 510 cm⁻¹ is considerable, at times reaching more than 1 depending on the crystal as illustrated in Fig. 1d, indicating that it is the B_g mode.^23,35 For the same reason, we attribute the ω₂ peak to the asymmetric vibrational mode of the structure that is responsible for the ω₁ peak. In the high-frequency region, where the Raman peaks are dominated by MnO₆ deformations, the depolarization ratios of the ν₁, ν₂, and ν₄ peaks are approximately 0.2 or less, with the exception of the ν₃ peak. It is noteworthy that the α and ω₁ peaks exhibit a markedly different behavior when compared to the other peaks. The frequencies of the α peaks observed in the blue and yellow crystals differ considerably by approximately 30 cm⁻¹. The polarization configuration dependence of the ω₁ peak, which was previously reported to be the B_g mode of the MnO₆ octahedra, differs from all other peaks but is identical to that of the A_1g mode of c-sapphire with sixfold symmetry (ESI Fig. S3†).

Temperature effect

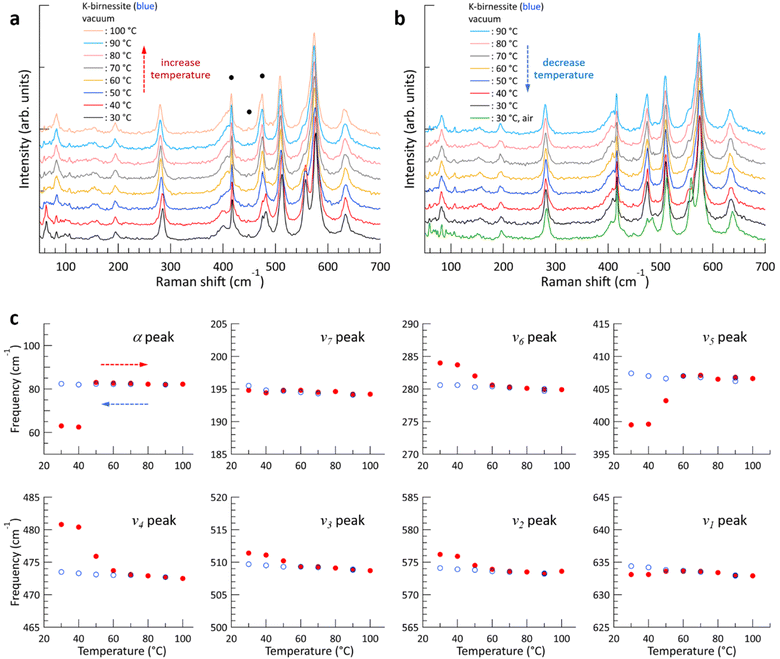
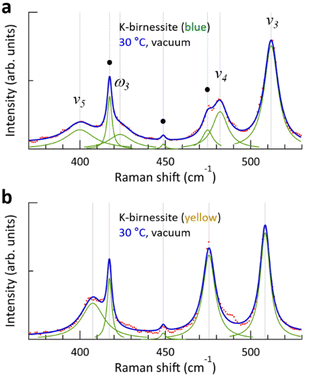
Fig. 2 shows the changes in the Raman spectrum of blue K-birnessite single crystals as the temperature increases and subsequently decreases in a vacuum. The Raman spectra demonstrate that crystals maintain a monoclinic structure at temperatures up to 100 °C. The α peak, which was undetectable in air, is clearly discernible at 63 cm⁻¹ in a vacuum due to the elimination of the air damping effect, which refers to the attenuation of acoustic phonon amplitudes by interactions with the surrounding air. As the temperature increases, the intensity of the ω₁ peak begins to decrease, becoming very weak at 50 °C and manifesting only as a faint shoulder of the ν₂ peak at 60 °C. No further discernible change in the intensity of the ω₁ peak is observed as the temperature continues to increase to 100 °C. However, the intensity of all the other peaks remains relatively constant throughout the temperature increase to 100 °C. As the ω₁ peak diminishes, the frequency of the α peak increases from 63 to 83 cm⁻¹, representing a considerably more pronounced change compared to any of the other peaks. Once the ω₁ peak has almost disappeared, its intensity does not recover even when the temperature is decreased to 30 °C. The frequency of all peaks increases slightly due to the decrease in interatomic distances that occurs with decreasing temperature. But upon the introduction of air into the chamber at 30 °C, the intensity of the ω₁ peak rapidly recovers, and likewise the frequencies of all the peaks return to their initial state at 30 °C in air. As the temperature increased and then decreased between 30 and 100 °C, the frequency of the c-sapphire exhibited a linear change (ESI Fig. S7†), confirming that the temperature of the sample reached each set temperature with precision.

Fig. 2 (a and b) Typical changes in the Raman spectrum of blue K-birnessite single crystals with increasing (a) and then decreasing (b) temperature in a vacuum. Measurements were started after pumping the vacuum chamber for 1–2 h at room temperature, and each Raman spectrum was obtained 10 min after reaching each target temperature. The green spectrum was obtained after decreasing the temperature to 30 °C and injecting air into the chamber. The small and narrow peaks below 150 cm⁻¹ and those marked with black circles (●) represent the Raman peaks of the c-sapphire substrate. Each Raman spectrum is shifted along the intensity axis for clarity. (c) Change in frequency of each Raman peak with increasing (red closed circles) and decreasing (blue open circles) temperature. Each frequency was obtained by performing the same experiment on three different crystals and averaging the results.

To elucidate the reason for the change in Raman spectra with temperature, XRD patterns were measured, where a change was indicated in the c-axis lattice parameter, namely a decrease from 0.70 to 0.65 nm with increasing temperature above 60 °C in a vacuum (ESI Fig. S8†). This suggests that interlayer water is removed from the crystal, resulting in an increase in interlayer interaction.^11,28 Based on thermogravimetric measurements on Na-birnessite in a vacuum, Matsui et al. reported that strongly hydrated water molecules around Na⁺, which serve as structural water, begin to deintercalate at approximately 40 °C, with some remaining at 110 °C. On the other hand, weakly hydrated water can be removed even at room temperature in a vacuum,²⁰ which is in accordance with our XRD measurements in a vacuum and air at 30 °C. It is noteworthy that the removal of interlayer water results in a more pronounced shift in the frequencies of the ν₄, ν₅, and ν₆ peaks, which lie below 500 cm⁻¹, in comparison to the ν₁, ν₂, and ν₃ peaks, which are the vibrational modes of the MnO₆ octahedra.

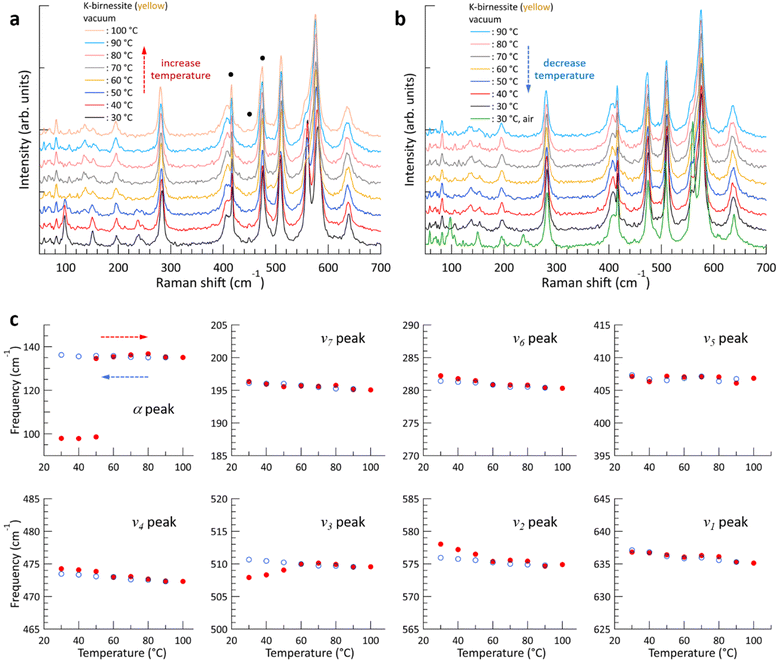
The evolution of the Raman spectrum of yellow K-birnessite single crystals with increasing and then decreasing temperature in a vacuum is depicted in Fig. 3. As the temperature increases, the intensities of the two peaks ω₁ and ω₂ diminish and almost disappear at 60 °C. The experimental results indicate that the ω₁ and ω₂ peaks do not originate from the MnO₆ octahedra, but are closely related to water molecules and K⁺ ions in the interlayer space. This is consistent with the observation that the depolarization ratio of the ω₁ peak in Fig. 1 is approximately zero, in contrast to all other Raman peaks of K-birnessite. As the quantity of interlayer water decreases from 40 °C, the intensities of the ω₁ and ω₂ peaks exhibit a gradual decline. Nevertheless, the ω₁ peak persists as a faint shoulder on the low-frequency side of the ν₂ peak even at 100 °C due to the presence of residual water molecules.²⁰ Measurements were also conducted on crystals covered with a 30 nm thick layer of Al₂O₃ deposited by atomic layer deposition. In this case, the Raman spectrum remained unaltered when the temperature of the sample was elevated to 100 °C in a vacuum, as the Al₂O₃ layer effectively prevented interlayer water from escaping from the crystal (ESI Fig. S9†).

Fig. 3 (a and b) Typical changes in the Raman spectrum of yellow K-birnessite single crystals with increasing (a) and then decreasing (b) temperature in a vacuum. Measurements were started after pumping the vacuum chamber for 1–2 h at room temperature, and each Raman spectrum was obtained 10 min after reaching each target temperature. The green spectrum was obtained after decreasing the temperature to 30 °C and injecting air into the chamber. The small and narrow peaks below 150 cm⁻¹ and those marked with black circles (●) represent the Raman peaks of the c-sapphire substrate. Each Raman spectrum is shifted along the intensity axis for clarity. (c) Change in frequency of each Raman peak with increasing (red closed circles) and decreasing (blue open circles) temperature. Each frequency was obtained by performing the same experiment on three different crystals and averaging the results.

The overall trend of the Raman spectrum change with temperature for the yellow crystals is almost identical to that for blue crystals; however, there are some notable differences. In the case of the blue crystal, the frequencies of the ν₄, ν₅, and ν₆ peaks undergo a significant change due to the deintercalation of interlayer water during the temperature increase to 60 °C. In contrast, the yellow crystal exhibits a minimal change in frequency. Fig. 3 illustrates that, with the exception of the α, ν₂, and ν₃ peaks, the frequency of each Raman peak remains largely unchanged at a given temperature before and after the interlayer water is removed. Even in the case of the ν₂ and ν₃ peaks, the difference in frequency before and after the change in interlayer spacing is not significant. This phenomenon is characteristic of optical phonons, which correspond to the relative motion of atoms. Consequently, the frequency of these phonons is primarily determined by the interatomic distances and local bonding environment.

The α peak shows markedly distinct behaviors compared to the other peaks, as follows. (i) It appears in a much lower frequency range than the other peaks. (ii) Its frequency is highly susceptible to alterations in crystal thickness and interlayer spacing. The frequency of the α peak of the yellow crystal increases significantly from 98 to 135 cm⁻¹ as the ω₁ peak disappears in a vacuum. (iii) The α peak of the blue crystal shows a pronounced air damping effect. However, this is observed in both air and vacuum in thicker yellow crystals, where bulk properties become more dominant, due to a reduced air damping effect. The α peak exhibits typical characteristics of acoustic phonon modes of layered materials, providing compelling evidence to assign it as an acoustic phonon mode of K-birnessite. The acoustic phonon mode is indicative of the collective motion of each MnO₂ layer; accordingly, the frequency of this mode, particularly the shear mode, increases significantly as the interlayer interaction is increased by increasing the number of layers or decreasing interlayer spacing.^36–38 It is observed that the frequency of the α peak for both blue and yellow crystals increases by approximately 35 ± 3% as the interlayer spacing decreases due to the removal of interlayer water. At 50 °C, the intensity of the α peak at 98 cm⁻¹ decreases, while a weak peak appears at 135 cm⁻¹. This suggests the coexistence of two types of interlayer spaces during the transition: those in which a substantial amount of interlayer water remains and those in which interlayer water has been largely removed.

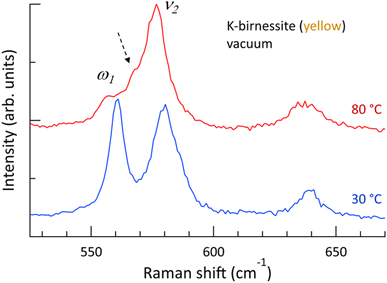
Fig. 1 shows that the depolarization ratio of the ν₁ peak is approximately 0.2 due to unequal Mn–O bond lengths of MnO₆ octahedra by Jahn–Teller distortion, which results in symmetry-breaking of the octahedra. The ν₂ peak, which is assigned to the motion of oxygen atoms in the basal plane of MnO₆, is the doubly degenerate mode (E-mode) of undistorted MnO₆ octahedra.³⁴ If the degeneracy is removed by breaking the symmetry of the MnO₆ octahedra, the ν₂ peak is expected to split into two peaks, as observed in transition metal dichalcogenide materials.³⁹ The Raman spectra of yellow crystals at 30 and 80 °C in a vacuum are shown in Fig. 4, which details the region near the ν₂ peak. At 30 °C, only the two strong peaks ν₂ and ω₁, which are in close proximity, are discernible. However, above 60 °C, the ω₁ peak almost disappears and a new peak appears as a shoulder of the ν₂ peak. The frequency difference between the two peaks is approximately 9 cm⁻¹ (ESI Fig. S10†). It is postulated that the ν₂ peak is also split at 30 °C but the weak shoulder is masked by the two strong peaks ω₁ and ν₂ located in close proximity. Although Scheitenberger et al. recently claimed that the ν₁ peak originates from interlayer water,³ our results confirm that the ν₁ peak is indicative of in-phase stretching and compressing of the six Mn–O bonds and that the ν₂ peak is associated with the motion of oxygen atoms in the basal plane of the MnO₆ octahedra.

Fig. 4 Raman spectra of yellow K-birnessite single crystals at 30 °C (blue) and 80 °C (red) between 525 and 670 cm⁻¹ in a vacuum. As the ω₁ peak diminishes, a shoulder appears on the low frequency side of the ν₂ peak, as indicated by the dashed arrow.

In-plane angle-resolved polarized Raman scattering

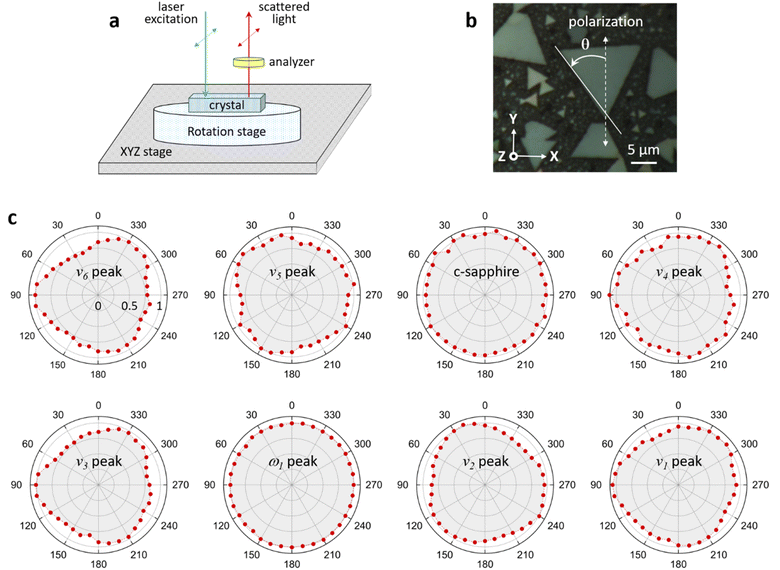
In-plane angle-resolved polarized Raman scattering (ARPRS) measurements were performed with a parallel polarization direction of the incident and scattered light (i.e., parallel polarization configuration) in order to examine the symmetry properties of each Raman mode.^40,41 The angle between the polarization direction of the incident light and the crystal axis was varied in 10° steps by rotating the crystal using the measurement configuration shown in Fig. 5a. To prevent thermal damage and fluctuations, each Raman spectrum was obtained by raster scanning the incident laser over a 5 × 5 μm² surface of the crystal, with an acquisition time of 120 s. As the crystal was rotated, the intensities of the c-sapphire and ω₁ peaks remained unchanged. However, the intensities of all other Raman peaks exhibited a slight modulation with a 120° period, which differed from the 90° or 180° period observed in a previous study.⁴² The intensity of each Raman peak reaches a maximum when the bisection direction through the vertices of the triangle is parallel to the polarization direction of the incident light. In a recent study, Ilchenko et al. conducted ARPRS measurements on a (111) silicon plane and observed that the Raman intensity exhibited a period of 120° for off-axis (45°) measurements, which was in good agreement with theoretical calculations based on Raman tensors.⁴³ They also observed that the Raman intensity was slightly modulated with a period of 120° for on-axis measurements. In our experiments, the c-plane of the crystal has a hexagonal structure, but the MnO₆ octahedra are tilted with respect to the XY plane (ESI Fig. S11†), so it is postulated that the intensities of the Raman peaks of K-birnessite single crystals are slightly modulated by a 120° period.

Fig. 5 Angle-resolved polarized Raman scattering (ARPRS) measurement of K-birnessite single crystals. (a) Configuration of the ARPRS measurements. (b) Optical image of K-birnessite single crystals. The polarizations of the incident and scattered light were fixed in the direction of the y-axis of the laboratory coordinate system (XYZ), and the crystal rotation angle (θ) was defined as shown. (c) Polar plots of the angle-dependent Raman peak intensity of a blue K-birnessite single crystal measured in the laboratory environment.

The Raman peak of c-sapphire at 413 cm⁻¹ exhibits an isotropic polarization angle dependence, which is characteristic of backscattering measurements on a crystal plane with a hexagonal structure, such as the basal planes in MoS₂ or highly ordered pyrolytic graphite.^44,45 Post et al. postulated that K⁺ and water molecules form a hexagonal close-packed arrangement in the interlayer space to explain the results of Rietveld refinement and the pseudo-hexagonal arrangement observed in a selected area electron diffraction pattern corresponding to the normal direction on a K-birnessite plate.¹ In addition, based on the infrared spectra of Na-birnessite and Post et al.‘s¹ Rietveld refinement, Matsui et al. argued that interlayer structural water molecules hydrate Na⁺ ions, forming a quasi-planar hexamer-like structure.²⁰ Our results confirm that the ω₁ peak is a totally symmetric vibrational mode of the hexagonal arrangement of interlayer cations and water molecules. This result elucidates the reason for the occurrence of the ω₁ peak in birnessite, which has a relatively large and highly flexible interlayer space that can accommodate various cations and water molecules to form clusters of 2D hexamer-like structures, but not in tunnel-structured MnO₂ polymorphs.^1,2,23

Interlayer water effect

In our experiments, increasing the temperature in a vacuum had a negligible effect on the frequency of the ν₁ peak of the crystals, which are sensitive to the fraction of Mn³⁺. Additionally, the ω₁ peak was immediately restored when air was reintroduced into the chamber at 30 °C, indicating that K⁺ ions are strongly bound to the MnO₆ sites with Mn³⁺ centers and are not removed from the interlayer space even when the temperature is increased to 100 °C in a vacuum. The frequency and intensity of the ν₁ peak have previously been reported to correlate positively with interlayer spacing (i.e., interlayer water content);^3,24,27 however, Fig. 2 and 3 demonstrate that they have little to do with the interlayer spacing. During anodic potential sweep in aqueous solution, the quantity of cations in the interlayer space decreases while water content increases, resulting in increased frequency and intensity of the ν₁ peak and interlayer spacing. It thus appeared that the interlayer spacing itself has an effect on the frequency and intensity of the ν₁ peak. Our results indicate that the frequency and intensity of the ν₁ peak are governed by the average Mn–O distance, which depends on the fraction of Mn³⁺, and have little correlation with the interlayer spacing. Furthermore, Fig. 3 demonstrates that the interlayer spacing exerts a minimal influence on the optical phonon modes below 500 cm⁻¹ and only a limited effect on the ν₂ and ν₃ peaks.

As illustrated in Fig. 2 and 3, the temperature-dependent alterations of the ν₄ and ν₅ peaks during the temperature elevation to 60 °C exhibit notable distinctions between blue and yellow crystals. As water is removed during the temperature increase, the frequencies of the two peaks undergo a significant change for the blue crystal, whereas they remain largely unaltered for the yellow crystal. A more detailed examination of the Raman spectra in this region reveals the presence of a weak peak (ω₃) at 423 cm⁻¹ for the blue crystal, which is not observed in the yellow crystal, as illustrated in Fig. 6. As the temperature increases and interlayer water is removed, the ω₃ peak disappears along with the ω₁ and ω₂ peaks (ESI Fig. S12†), which is consistent with the results by Chen et al. that two peaks appear at around 400 cm⁻¹ when the interlayer space is rich in water, but only a single peak is observed when the amount of water decreases.²⁷ Through DFT calculations, Sudare et al. reported that cations and water molecules form 2D or tetrahedral 3D structures depending on the amounts of cations and water molecules in the interlayer space.¹⁹ On the other hand, Scheitenberger et al. used the peak at around 400 cm⁻¹ as one of the indicators of the crystal structure of birnessite: as the symmetry of the crystal structure changes from monoclinic to hexagonal, the peak splits into two, accompanied by a significant enhancement of the ν₁ peak.²⁶ This is inconsistent with our results, which show that the intensity of the ν₁ peak remains largely unaltered.

Fig. 6 (a and b) Deconvolution of the Raman peaks between 370 and 530 cm⁻¹ of blue and yellow K-birnessite single crystals into Lorentzian curves. The red dots represent the experimental results, the green lines represent the individual peaks, and the blue lines represent the fit. The black circles (●) represent the Raman peaks of the c-sapphire substrate. In (b), the c-sapphire peak at 475 cm⁻¹ is obscured by the ν₄ peak.

It is postulated that the ω₃ peak originates from the tetrahedral 3D structure of cations and water molecules formed in the interlayer space. The majority of cations and water molecules form a 2D hexagonal structure in the yellow crystal, while some of them also form a 3D structure in the blue crystal. This is consistent with the observation that the relative intensity of the ω₁ peak is greater in the yellow crystals compared to the blue crystals. Once the 2D and 3D structures of cations and water molecules are removed, the interlayer environments of the blue and yellow crystals become almost identical, resulting in the frequencies of all optical phonons in the two crystals being very close to each other. Further studies are required to pinpoint the reasons for the subtle differences in the structures formed by interlayer cations and water molecules in blue and yellow crystals. At present, it can be speculated that differences in interlayer interaction strength may play a role.

Conclusions

The effects of thickness, polarization configuration, and temperature on the Raman spectra of K-birnessite single crystals have been quantified. Distortion of the MnO₆ octahedra was confirmed by observing that the depolarization ratio of the totally symmetric mode (ν₁) is approximately 0.2, while the doubly degenerate mode (ν₂) splits into two peaks. An acoustic phonon mode (α peak) of birnessite was identified for the first time. The α peak was found to be highly sensitive to changes in interlayer spacing: when the c-axis parameter was reduced from 0.70 to 0.65 nm by water evaporation, the frequency increased by approximately 35%. In contrast, the impact of interlayer spacing on the frequency of optical phonon modes is relatively modest. We conducted a comprehensive analysis of the ω₁ peak at 559 cm⁻¹, which was previously attributed to the motion of oxygen atoms in the basal plane of MnO₆. The depolarization ratio of the ω₁ peak was approximately zero, and in angle-resolved polarized Raman scattering measurements in parallel polarization configuration, its intensity was found to be constant for crystal rotation from 0° to 360°, which is in striking contrast to the behaviors observed for all other Raman peaks of K-birnessite single crystals. The ω₁ peak was therefore assigned as a totally symmetric vibrational mode of the 2D hexagonal arrangement of interlayer cations and water molecules. This provides a clear explanation as to why the ω₁ peak is observed in birnessite, which has a relatively large and highly flexible 2D interlayer space that can accommodate various cations and water molecules, allowing them to form 2D hexagonal clusters.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

D. H. Ha: conceptualization, project administration, investigation and writing – original draft. G. Noh: resources, investigation and writing – original draft. H. Kim: investigation and validation. D. H. Kim: investigation and validation. J. Kim: resources and investigation. S. Jung: investigation, funding acquisition and writing – review & editing. C. Hwang: resources and funding acquisition. H. Y. Lee: investigation and validation. Y. J. Yun: validation and writing – review & editing. J. Y. Kwak: resources and validation. K. Kang: resources and funding acquisition. S. N. Yi: conceptualization, formal analysis, validation and writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. Jung was supported by a research grant for basic research funded by the Korea Research Institute of Standards and Science (no. KRISS-GP2024-0014-10). K. Kang was supported by the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (grant no. RS-2023-00030-4068).

References

1. J. E. Post and D. R. Veblen, Am. Mineral., 1990, 75, 477–489.
2. J. E. Post, D. A. McKeown and P. J. Heaney, Am. Mineral., 2021, 106, 351–366.
3. P. Scheitenberger, H. Euchner and M. Lindén, J. Mater. Chem. A, 2021, 9, 18466–18476.
4. J. E. Post, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 3447–3454.
5. T. Hatakeyama, N. L. Okamoto and T. Ichitsubo, J. Solid State Chem., 2022, 305, 122683.
6. S. Tajima, S. Fuchida and C. Tokoro, J. Environ. Sci., 2022, 121, 136–147.
7. M. Shi, Q. Li, Q. Wang, X. Yan, B. Li, L. Feng, C. Wu, R. Qiu, H. Zhang, Z. Yang, W. Yang, Q. Liao and L. Chai, J. Environ. Sci., 2024, 139, 496–515.
8. X. Zhang, Z. Wei, K. N. Dinh, N. Chen, G. Chen, F. Du and Q. Yan, Small, 2020, 16, 2002700.
9. A. Gao, M. Li, N. Guo, D. Qiu, Y. Li, S. Wang, X. Lu, F. Wang and R. Yang, Adv. Energy Mater., 2019, 9, 1802739.
10. R. Yang, Z. Guo, L. Cai, R. Zhu, Y. Fan, Y. Zhang, P. Han, W. Zhang, X. Zhu, Q. Zhao, Z. Zhu, C. K. Chan and Z. Zeng, Small, 2021, 17, 2103052.
11. X. Tian, L. Yang, X. Qing, K. Yu and X. Wang, Sens. Actuators, B, 2015, 207, 34–42.
12. P. Wuamprakhon, A. Krittayavathananon, S. Kosasang, N. Ma, T. Maihom, J. Limtrakul, N. Chanlec, P. Kidkhunthod and M. Sawangphruk, Inorg. Chem., 2020, 59, 15595–15605.
13. K. P. Lucht and J. L. Mendoza-Cortes, J. Phys. Chem. C, 2015, 119, 22838–22846.
14. S. Zhu, Y. Wang, J. Zhang, J. Sheng, F. Yang, M. Wang, J. Ni, H. Jiang and Y. Li, Energy Environ. Mater., 2023, 6, e12382.
15. J. Liu, L. Yu, E. Hu, B. S. Guiton, X.-Q. Yang and K. Page, Inorg. Chem., 2018, 57, 6873–6882.
16. L. D. Kulish, P. Nukala, R. Scholtens, A. G. M. Uiterwijk, R. Hamming-Green and G. R. Blake, J. Mater. Chem. C, 2021, 9, 1370–1377.
17. V. A. Drifts, E. Silvester, A. I. Gorshkov and A. Manceau, Am. Mineral., 1997, 82, 946–961.
18. F. T. Ling, J. E. Post, P. J. Heaney and E. S. Ilton, Chem. Geol., 2018, 479, 216–227.
19. T. Sudare, T. Yamaguchi, M. Ueda, H. Shiiba, H. Tanaka, M. Tipplook, F. Hayashi and K. Teshima, Nat. Commun., 2022, 13, 6448.
20. H. Matsui, J. Ju, T. Odaira and N. Toyota, J. Phys. Soc. Jpn., 2009, 78, 074801.
21. H. -J. Kim, D. Kim, S. Jung, M. -H. Bae, Y. J. Yun, S. N. Yi, J. -S. Yu, J. -H. Kim and D. H. Ha, J. Raman Spectrosc., 2018, 49, 1938–1944.
22. D. H. Lee, N.-H. Kim, S. Jung, J. Park, B.-K. Kim, M.-H. Bae, Y. J. Yun, S. N. Yi and D. H. Ha, Adv. Mater. Interfaces, 2023, 10, 2300002.
23. J. E. Post, D. A. McKeown and P. J. Heaney, Am. Mineral., 2020, 105, 1175–1190.
24. Y.-K. Hsu, Y.-C. Chen, Y.-G. Lin, L.-C. Chen and K.-H. Chen, Chem. Commun., 2011, 47, 1252–1254.
25. H. An, Z. Chen, J. Yang, Z. Feng, X. Wang, F. Fan and C. Li, J. Catal., 2018, 367, 53–61.
26. P. Scheitenberger, S. Brimaud and M. Lindén, Mater. Adv., 2012, 2, 3940–3953.
27. D. Chen, D. Ding, X. Li, G. H. Waller, X. Xiong, M. A. El-Sayed and M. Liu, Chem. Mater., 2015, 27, 6608–6619.
28. C. Julien, M. Massot, R. Baddour-Hadjean, S. Franger, S. Bach and J. P. Pereira-Ramos, Solid State Ionics, 2003, 159, 345–356.
29. C. M. Julien and M. Massot, Mater. Sci. Eng., B, 2003, 97, 217–230.
30. M. Tu, H. Lu, S. Luo, H. Peng, S. Li, Y. Ke, S. Yuan, W. Huang, W. Jie and J. Hao, ACS Appl. Mater. Interfaces, 2020, 12, 24133.
31. H. R. Rasouli, J. Kim, N. Mehmood, A. Sheraz, M.-K. Jo, S. Song, K. Kang and T. S. Kasirga, Nano Lett., 2021, 21, 3997–4005.
32. M. Y. Chan, K. Komatsu, S.-L. Li, Y. Xu, P. Darmawan, H. Kuramochi, S. Nakaharai, A. Aparecido-Ferreira, K. Watanabe, T. Taniguchi and K. Tsukagoshi, Nanoscale, 2013, 5, 9572–9576.
33. G. Pezzotti and W. Zhu, Phys. Chem. Chem. Phys., 2014, 17, 2608–2627.
34. H. Meskine and S. Satpathy, J. Appl. Phys., 1999, 85, 4346–4348.
35. D. Tuschel, Spectroscopy, 2014, 29, 14–22.
36. A. Molina-Sánchez and L. Wirtz, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 155413.
37. H. Zeng, B. Zhu, K. Liu, J. Fan, X. Cui and Q. M. Zhang, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 86, 241301(R).
38. P. H. Tan, W. P. Han, W. J. Zhao, Z. H. Wu, K. Chang, H. Wang, Y. F. Wang, N. Bonini, N. Marzari, N. Pugno, G. Savini, A. Lombardo and A. C. Ferrari, Nat. Mater., 2012, 11, 294–300.
39. J.-U. Lee, S. Woo, J. Park, H. C. Park, Y.-W. Son and H. Cheong, Nat. Commun., 2022, 8, 1370.
40. D. Tuschel, Spectroscopy, 2012, 27, 2–6.
41. D. Rawat, A. Singh, N. K. Singh and A. Soni, Phys. Rev. B, 2023, 107, 155203.
42. Q. Song, X. Pan, H. Wang, K. Zhang, Q. Tan, P. Li, Y. Wan, Y. Wang, X. Xu, M. Lin, X. Wan, F. Song and L. Dai, Sci. Rep., 2016, 6, 29254.
43. O. Ilchenko, Y. Pilgun, A. Kutsyk, F. Bachmann, R. Slipets, M. Todeschini, P. O. Okeyo, H. F. Poulsen and A. Boisen, Nat. Commun., 2019, 10, 5555.
44. Y. Ding, W. Zheng, M. Jin, Y. Zhu, R. Zhu, Z. Lin and F. Huang, Opt. Lett., 2020, 45, 1313–1316.
45. X.-L. Liu, X. Zhang, M.-L. Lin and P.-H. Tan, Chin. Phys. B, 2017, 26, 067802.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta06118g

---